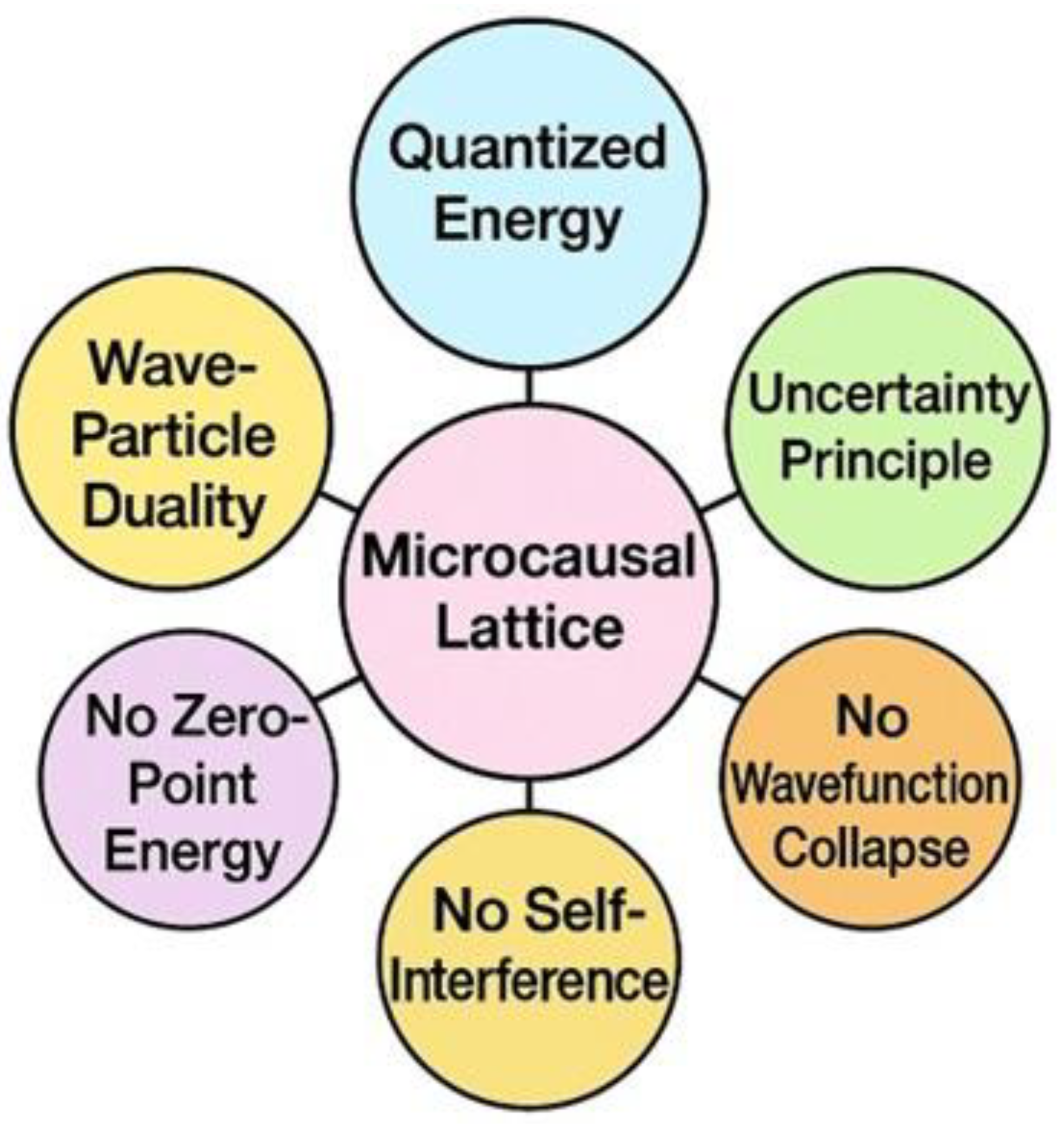
I. Introduction
Modern physics faces deep conceptual and mathematical challenges, particularly in reconciling quantum field theory (QFT) [
1] with general relativity [
2]. Both frameworks rest on the assumption that spacetime is a smooth, continuous manifold. This assumption gives rise to persistent paradoxes such as ultraviolet divergences [
3], infinite vacuum energy [
4], and gravitational singularities [
5]—problems that hint at an incomplete understanding of nature’s most fundamental structure.
A notable example is the vacuum catastrophe [
6], in which QFT predicts a vacuum-energy density exceeding astronomical observations by over 120 orders of magnitude [
7]. This enormous discrepancy arises from summing zero-point energies [
8] of field modes within a continuum spacetime, despite the absence of experimental evidence for such energy density.
Renormalization [
9] provides a practical way to remove infinities but offers no physical explanation. Likewise, general relativity predicts singularities of infinite curvature at black-hole centers and at the Big Bang [
10], signaling the breakdown of the continuum picture at the Planck scale [
11]. These issues suggest that the assumption of an infinitely divisible spacetime must be replaced by a quantized causal structure [
12].
We therefore propose a micro-causal, quantized spacetime in which space and time are composed of discrete, causally ordered units. This lattice-like geometry enforces finite information propagation and replaces differential equations with finite-difference relations. Remarkably, this structure alone reproduces key quantum principles—uncertainty [
13], energy quantization [
13], and wave–particle duality [
14]—without appealing to canonical quantization [
15] or oscillator models [
16].
This approach resolves multiple long-standing paradoxes in a unified way:
Zero-point energy and vacuum divergence are eliminated.
Ultraviolet divergences are avoided through a natural lattice cutoff.
Mass arises from geometric U(1)-symmetry breaking, eliminating the need for a Higgs field [
17].
Singularities are replaced by bounded causal structure at small scales.
A concrete experimental prediction also emerges. By reinterpreting the Casimir effect renormalization [
18] as a thermal-radiation phenomenon, the model predicts that the Casimir force should vary with temperature—a falsifiable distinction from QFT’s vacuum-fluctuation interpretation. Confirmation would constitute strong empirical evidence for spacetime discreteness.
By grounding quantum behavior in a finite causal lattice, this framework provides a divergence-free, geometrically intuitive foundation for quantum physics and suggests a route toward reconciling quantum theory, gravity, and cosmology.
II. Causal Quantized Spacetime: A Geometric Origin for Quantum Behavior
This section develops the mathematical foundation of the causal lattice-spacetime model and demonstrates how quantum behavior—especially uncertainty, wave–particle duality, and energy quantization—emerges naturally from discrete causal geometry. Each mathematical step is accompanied by its physical interpretation to clarify the underlying logic.
2.1. Discrete Spacetime and Lattice Operators
Consider a two-dimensional causal lattice where spatial and temporal coordinates are integer multiples of fundamental units
and
. Define displacement operators
and
that shift states along the lattice:
These finite shifts form the basis of the operator algebra. Position and momentum-like operators are defined as
Their commutation relation,
reduces to the canonical form
in the continuum limit. Thus, non-commutativity arises geometrically from finite causal shifts rather than being imposed as a postulate.
2.2. Emergence of the Uncertainty Principle
Define a unitary displacement operator
.Applying the Baker–Campbell–Hausdorff identity [
19] yields
which implies
The Heisenberg uncertainty relation [
20], therefore, arises naturally from the discrete causal ordering of spacetime, providing a geometric origin for quantum indeterminacy rather than an axiomatic one.
2.3. Complex Wave Functions and Wave–Particle Duality
Because lattice translation operators are intrinsically non-commutative, their eigenfunctions must be vector- or matrix-valued. The lowest-order representation is
, equivalent to a complex scalar function. Hence, the complex nature of the quantum wavefunction and the wave–particle duality emerge automatically from the algebra of discrete causal operators rather than from de Broglie’s hypothesis [
21].
2.4. Absence of Zero-Point Vacuum Energy
In standard QFT, harmonic-oscillator quantization produces a vacuum energy of
per mode. In the lattice framework, creation and annihilation operators are defined directly from discrete position and momentum operators:
satisfying
. The Hamiltonian becomes
For the ground state , the energy is exactly zero. Thus, vacuum energy arises only from real excitation modes, eliminating ultraviolet divergences and the vacuum catastrophe from first principles.
2.5. Quaternionic Representation of Spatial Displacement
To preserve isotropy and causal order, spatial displacement operators are assigned to quaternionic imaginary units:
maintaining the invariant
This representation provides a geometric foundation for the spatial structure of quantum fields and suggests a natural extension of quaternions [
22] to octonionic [
23] and sedenionic algebras [
24], while keeping time real and causally ordered.
2.6. Violation of the Klein–Gordon Equation and U(1) Symmetry [25]
Discretizing the massless Klein–Gordon equation [
26] with second-order finite differences leads to a modified dispersion relation,
Unlike the continuum case , this relation shows that massless fields acquire a finite effective mass due solely to lattice discreteness. Consequently, both global and local U(1) symmetries are broken geometrically, producing mass generation without invoking a Higgs field.
2.7. Summary of Lattice vs. Continuum Frameworks
To clearly contrast the predictions of the causal-lattice model with those of standard QFT,
Table 1 summarizes their key conceptual and structural differences.
This causal-lattice formulation re-interprets the foundations of quantum mechanics as consequences of geometry and causality, offering a self-consistent, divergence-free description of nature that can be tested through measurable phenomena such as the thermal dependence of the Casimir effect.
III. Comparative Analysis of Quantum Field Theories: Continuum vs. Causal Lattice Framework
To clarify the implications of a discrete, causal spacetime, we now compare the proposed framework directly with the conventional quantum field theory (QFT) built on a continuous manifold. While standard QFT rests on postulated operator algebra, harmonic oscillators, and renormalization, the causal lattice model reconstructs quantum phenomena from the geometry and algebra of finite causal intervals. This comparison highlights how changing the underlying spacetime ontology—from continuous to discrete, from symmetric to causally ordered—resolves many of the long-standing inconsistencies of QFT.
3.1. Summary of Core Differences
Table 2 presents a systematic comparison between standard QFT and the proposed causal-lattice framework, emphasizing how the change from a continuous to a discrete spacetime resolves major inconsistencies.
3.2. Interpretive Shift: Geometry Over Axioms
In conventional QFT, operator algebra, complex wavefunctions, and quantization conditions are introduced axiomatically. By contrast, the causal lattice approach shows that these same properties emerge naturally from geometry. Non-commutativity, complex state representation, and energy quantization are not imposed—they are consequences of finite causal separation within spacetime itself.
This shift in perspective transforms quantization from a procedural assumption into a geometric inevitability. The fundamental structure of spacetime—not the postulation of wavefunctions or operators—becomes the source of quantum behavior.
3.3. Physical Consequences
This ontological and mathematical reformulation leads to significant physical advantages:
Vacuum Catastrophe Eliminated – The absence of zero-point energy removes the 120-order-of-magnitude discrepancy between QFT and cosmological observation.
Renormalization Unnecessary – No infinities arise; the lattice imposes a natural high-energy cutoff.
Finite Spectrum of Field Modes – Ultraviolet divergences are suppressed by construction.
No Singularities – Fields remain finite at all scales, avoiding the infinite curvature of the continuum.
These results demonstrate that discrete causal structure is not a numerical convenience (as in lattice QCD) [
27] but a fundamental physical principle capable of resolving long-standing theoretical paradoxes.
3.4. Visual Representation
To aid intuition,
Figure 1 contrasts the two frameworks:
Left panel: Standard QFT, depicting continuous spacetime filled with harmonic oscillators, zero-point fluctuations, and renormalization loops.
Right panel: The causal lattice model, showing discrete spacetime points connected by causal arrows and finite shift operators that generate energy quantization without vacuum energy.
Figure 1 provides a visual comparison between the standard continuum-based QFT and the discrete causal-lattice framework, illustrating how the replacement of continuous fields with finite causal connections eliminates divergences and vacuum fluctuations.
IV. Experimental Proposal: Testing the Thermal Nature of the Casimir Effect
A central strength of the causal-lattice framework is that it yields falsifiable predictions distinct from those of standard QFT. One of the most direct and measurable differences appears in the interpretation of the Casimir effect—traditionally regarded as a manifestation of vacuum fluctuations.
4.1. Rethinking the Casimir Effect
In standard QFT, the Casimir force between two uncharged, parallel conducting plates arises from changes in the zero-point vacuum energy caused by boundary conditions. The vacuum is assumed to possess physically real energy, and the force is considered temperature-independent.
In the causal lattice framework, vacuum energy is identically zero. The Casimir force instead originates from a thermal-radiation pressure imbalance: electromagnetic radiation between the plates is partly excluded, creating a net force that depends on the surrounding thermal environment. Therefore, the Casimir force should vary systematically with temperature—a prediction absent in QFT.
4.2. Experimental Design
To test this hypothesis, we propose a precision measurement of the Casimir force between two neutral, metallic plates under controlled thermal conditions.
Table 3 lists the proposed experimental parameters for measuring the Casimir force under controlled thermal conditions to test the model’s temperature-dependent prediction.
The plates are mounted within a vacuum chamber whose wall temperature can be independently varied. According to our model, increasing the wall temperature enhances the thermal radiation intensity, producing a measurable increase in the Casimir force. Standard QFT predicts no such dependence.
4.3. Expected Outcomes and Contrast with QFT
To highlight the contrasting predictions of standard QFT and the causal-lattice model regarding the Casimir effect,
Table 4 summarizes their expected outcomes.
A clear, temperature-dependent change in the measured force would decisively favor the lattice interpretation.
4.4. Prior Evidence and Feasibility
Previous high-precision Casimir experiments (e.g., Lamoreaux 1997; Mohideen & Roy 1998) confirmed the force’s existence but did not systematically vary temperature under vacuum. Recent advances—atomic-force microscopy, optical-levitation sensors, and cryogenic control—now permit sub-pico-Newton sensitivity, enabling the proposed test with high accuracy. The experiment could thus decisively determine whether the Casimir effect is a vacuum or thermal phenomenon.
4.5. Broader Implications of a Positive Result
If the Casimir force is experimentally shown to vary with temperature, several far-reaching implications follow:
Refutation of vacuum zero-point energy as a physical entity.
Empirical validation of spacetime discreteness and geometric origin of quantization.
Elimination of renormalization as a fundamental requirement in field theory.
New direction for quantum gravity, based on micro-causal geometry rather than vacuum fluctuations.
Such a result would not only support the proposed framework but also redefine the physical meaning of the vacuum, providing experimental grounding for a divergence-free theory of quantum reality.
V. Discussion and Broader Implications
The causal lattice spacetime framework presented here offers a fundamentally new way of viewing quantum theory. By replacing the assumption of a continuous manifold with a discrete, causally ordered geometry, quantum phenomena emerge as structural consequences of spacetime itself. This perspective unifies several puzzles of modern physics and provides a divergence-free, testable foundation for quantum and cosmological dynamics.
5.1. Resolution of Foundational Problems in Quantum Field Theory
The proposed model addresses several long-standing theoretical challenges that plague conventional QFT:
Standard QFT predicts a vacuum-energy density vastly exceeding cosmological observations. In our model, this divergence is absent because vacuum energy is identically zero; no subtraction or renormalization is required.
The continuum theory’s infinite mode density is replaced by a finite spectrum determined by the lattice spacing. Divergences disappear naturally due to this built-in cutoff.
The discrete lattice violates global and local U(1) symmetry geometrically, producing mass generation without introducing an ad hoc scalar field or spontaneous symmetry breaking.
The Heisenberg uncertainty principle arises directly from the non-commutativity of lattice shift operators, making uncertainty an intrinsic property of spacetime rather than an imposed axiom.
Collectively, these features replace the need for renormalization and fine-tuning with geometric consistency—a hallmark of a deeper physical theory
5.2. Philosophical Shift: From Postulates to Structure
Conventional quantum mechanics builds upon postulates—canonical commutation relations, wavefunctions, and quantization rules—that work remarkably well yet lack physical justification.In contrast, the causal lattice framework derives these principles from three structural premises:
Discreteness: Spacetime is composed of indivisible units with finite intervals.
Causality: All displacements respect light-speed-limited propagation.
Algebraic Structure: Quaternionic or higher hypercomplex elements encode spatial and internal symmetries.
From these premises, quantization, complex state representation, and even the uncertainty principle arise naturally.Quantization thus becomes a manifestation of geometry, not an independent assumption—transforming the philosophical foundations of quantum theory.
5.3. Implications for Cosmology and Gravity
The model’s implications extend far beyond particle physics:
Minimum spatial and temporal intervals prevent infinite curvature, replacing singularities with bounded causal regions. This allows for non-singular black holes and cyclic cosmological models where the universe undergoes periodic expansion and contraction.
The discrete, divergence-free structure provides a foundation for a finite quantum gravity [
28] without quantizing the metric. Gravity may emerge as a macroscopic manifestation of micro-causal connectivity.
Dark Energy [
29] Reinterpretation:
If vacuum energy is not physical, the cosmological constant problem must be reconsidered. Dark energy could instead represent thermal or geometric pressure associated with a large-scale lattice structure.
These consequences suggest that quantum mechanics, gravity, and cosmology may be unified through the same underlying causal geometry.
5.4. Compatibility with Gauge Theories
Standard gauge theories, such as quantum electrodynamics (QED) and quantum chromodynamics (QCD), are formulated on continuous spacetime and rely on perturbative renormalization.
The causal lattice framework opens the possibility of reformulating these interactions non-perturbatively on discrete geometry:
Future work will extend the causal lattice approach to include:
Gauge boson dynamics and conserved currents,
Fermionic fields with spinor representations, and
Quark confinement and asymptotic freedom emerging from finite lattice topology.
These developments could yield a fully geometric understanding of internal symmetries and gauge interactions.
5.5. Anticipated Critiques and Responses
Table 5 addresses common questions and criticisms likely to arise regarding the causal-lattice framework and provides concise responses to each.
5.6. Summary of Theoretical Contributions
In summary, the causal lattice framework:
Eliminate vacuum and ultraviolet divergences without renormalization,
Explains mass generation through geometric U(1) symmetry breaking,
Predicts experimentally testable deviations (e.g., temperature-dependent Casimir effect),
Provides a geometric origin for quantization and uncertainty,
Avoids cosmological and gravitational singularities, and
Lays the foundation for a unified, divergence-free quantum theory of spacetime.
This synthesis unites quantum mechanics and geometry into a coherent, testable theory of reality.
VI. Conclusions and Outlook
6.1. Conclusions
This work introduces a causal lattice spacetime framework as a fundamental reformulation of quantum field theory. By replacing the continuum assumption with a discrete, causally ordered structure, we show that the core features of quantum mechanics—energy quantization, wave–particle duality, and uncertainty—emerge geometrically, without invoking wavefunctions, canonical operators, or harmonic oscillators.
The formulation eliminates key conceptual problems in QFT:
Zero-point vacuum energy is absent due to the non-oscillator-based Hamiltonian.
Ultraviolet divergences are prevented by the finite mode spectrum.
Renormalization becomes unnecessary since no infinities arise.
Singularities disappear due to the existence of minimum spacetime intervals.
Mass generation occurs naturally via geometric U(1)-symmetry breaking, removing the need for a Higgs field.
Equally important, the model yields a falsifiable experimental prediction: the Casimir force should vary with temperature if it originates from thermal radiation pressure rather than vacuum fluctuations. A positive experimental outcome would strongly support the causal-lattice interpretation and redefine our understanding of quantum vacuum and mass.
6.2. Outlook and Future Directions
This foundational study opens multiple directions for continued research:
Extend the framework to Dirac and Majorana fermions using quaternionic or octonionic spinor algebra.
- 2.
Lattice Gauge Field Dynamics
Develop SU(2) and SU(3) gauge theories compatible with causal lattice structure, enabling divergence-free descriptions of electroweak and strong interactions.
- 3.
Quantum Gravity and Geometry
Construct a background-independent, finite quantum gravity based on micro-causal geometry, unifying spacetime and field dynamics.
- 4.
Higher Algebraic Extensions
Explore octonionic and sedenionic formulations to encode coupling constants, symmetry hierarchies, and charge quantization.
- 5.
Numerical Simulations and Visualization
Implement direct lattice simulations to visualize causal propagation, field excitations, and cosmological evolution.
- 6.
Cosmological Applications
Investigate cyclic cosmology, singularity resolution, and reinterpretation of dark energy as geometric or thermal phenomena.
This framework is not a mathematical regularization or computational tool but an ontological shift in our understanding of nature. By treating quantum phenomena as emergent properties of causal geometry, we obtain a finite, physically transparent, and testable theory that bridges quantum physics, gravity, and cosmology.
VII. Summary of Core Results
This study introduces a micro-causal, discrete spacetime lattice as the geometric foundation of quantum physics, providing a divergence-free and physically consistent reformulation of quantum field theory.The following summarizes the key conceptual and quantitative results of the framework:
A. Spacetime Structure and Ontology
Classical continuous spacetime is replaced by an intrinsic causal lattice characterized by minimum spatial and temporal intervals .
Causality is preserved through ordered connections, ensuring finite signal propagation at or below the speed of light.
Quaternionic and octonionic algebraic structures encode spatial and internal symmetries, linking spacetime geometry to particle interactions.
Lorentz symmetry is approximately recovered at macroscopic scales but violated near the Planck scale in a controlled and physically meaningful way.
This lattice ontology redefines the vacuum as a zero-energy geometric state, not as a fluctuating medium.
B. Emergent Quantum Foundations
Planck’s energy quantization arises directly from discrete temporal evolution, eliminating the need for harmonic oscillators or boundary quantization.
The uncertainty principle is derived from the intrinsic non-commutativity of finite shift operators, giving a geometric origin to quantum indeterminacy.
Wave–particle duality emerges naturally from the algebraic structure of the lattice rather than from de Broglie’s postulate.
The complex wavefunction is reinterpreted as a compact representation of discrete causal relations, replacing the traditional probabilistic postulate with geometric necessity.
Quantum mechanics thus emerges not from axioms but from causal spacetime structure.C. Physical Consequences
Zero-point vacuum energy is eliminated; the ground state energy of all fields is exactly zero.
Ultraviolet divergences and the vacuum catastrophe vanish due to the finite mode spectrum of the lattice.
The Casimir effect is reinterpreted as a thermal radiation pressure imbalance, leading to a direct, testable prediction of temperature-dependent force variation.
Mass generation arises from geometric violation of U(1) symmetry, requiring no Higgs boson or spontaneous symmetry breaking.
Singularities such as those predicted in black holes and the Big Bang are avoided, replaced by bounded lattice structure ensuring finite curvature.
Together, these results demonstrate that the apparent infinities of modern physics are artifacts of the continuum assumption.
D. Experimental and Theoretical Outlook
A precision Casimir experiment is proposed to test for temperature dependence, providing a clear, falsifiable distinction from QFT predictions.
The lattice framework offers a foundation for constructing divergence-free formulations of quantum electrodynamics (QED), quantum chromodynamics (QCD), and quantum gravity.
Extensions into octonionic and sedenionic algebra may describe gauge hierarchies and coupling constants within a unified algebraic geometry.
The framework supports cyclic cosmological models and reinterprets dark energy as an emergent geometric or thermal effect rather than vacuum pressure.
This model transforms quantum theory from a system of abstract postulates into a geometric and causal structure with direct experimental relevance.
Final Statement
By deriving quantum behavior from causal geometry rather than imposing it axiomatically, this framework provides a finite, testable, and conceptually transparent description of nature.It resolves long-standing paradoxes—wavefunction collapse, vacuum catastrophe, renormalization infinities, and spacetime singularities—while unifying the foundations of quantum theory, gravity, and cosmology under a single geometric principle.
If validated experimentally, particularly through the temperature-dependent Casimir effect, this theory could mark a paradigm shift toward a quantum reality governed by discrete causal spacetime, offering a new path to the ultimate unification of physics.
Funding Statement
The author is a retired professor with no funding.
Declaration Statement
All images are created by oneself
The author knows the details of the contributing author, including the affiliated institution
This work is purely theoretical and does not involve experiments on live subjects
The author follows the ethics and approval statement
The author declares no competing interests with any financial and non-financial interests, such as business or family interests
The author declares there are no differences between the manuscript file and personal information
Author Contributions
J. Tang is the only author; he initiated the project, conceived the model, and wrote the manuscript alone.
Data Availability Statement
This report presents analytical equation derivations without the use of computer numerical simulations. All reasonable questions about the derivations can be requested by contacting the corresponding author.
References
- Peskin, M. E., and Schroeder, D. V., An Introduction to Quantum Field Theory. Westview Press, 1995.
- Wald, R. M., General Relativity. University of Chicago Press, 1984.
- Weinberg, S., The Quantum Theory of Fields. Vol. 1: Foundations. Cambridge University Press, 1995.
- Weinberg, S., The Cosmological Constant Problem. Reviews of Modern Physics, Vol. 61, No. 1, 1989, pp. 1–23.
- Penrose, R., Gravitational Collapse and Space-Time Singularities. Physical Review Letters, Vol. 14, No. 3, 1965, pp. 57–59.
- Dirac, P. A. M., The Principles of Quantum Mechanics. 4th ed., Oxford University Press, 1958.
- Heisenberg, W., The Physical Principles of the Quantum Theory. University of Chicago Press, 1930.
- Feynman, R. P., and Hibbs, A. R. Quantum Mechanics and Path Integrals. McGraw–Hill, 1965.
- Dyson, F., The Radiation Theories of Tomonaga, Schwinger, and Feynman , Physical Review, 75, 1949), pp. 486–502.
- Tomonaga, S., On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. Progress of Theoretical Physics, Vol. 1, 1946, pp. 27–42.
- Dyson, F. J., The Radiation Theories of Tomonaga, Schwinger, and Feynman. Physical Review, Vol. 75, 1949, pp. 486–502.
- Planck, M., On the Theory of the Energy Distribution Law of the Normal Spectrum. Annalen der Physik, Vol. 4, 1901, pp. 553–563.
- Einstein, A., On a Heuristic Viewpoint Concerning the Production and Transformation of Light. Annalen der Physik, Vol. 17, 1905, pp. 132–148.
- de Broglie, L., Non-Linear Wave Mechanics: A Causal Interpretation. Elsevier, 1960.
- Bohr, N. , The Quantum Postulate and the Recent Development of Atomic Theory. Nature, Vol. 121, 1928, pp. 580–590.
- Heisenberg, W., Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, Vol. 43, 1927, pp. 172–198.
- Higgs, P. W., Broken Symmetries and the Masses of Gauge Bosons , Physical Review Letters, Vol. 13, p. 508 (1964).
- ’t Hooft, G., and Veltman, M., Regularization and Renormalization of Gauge Fields. Nuclear Physics B, Vol. 44, 1972, pp. 189–213.
- Casimir, H. B. G., On the Attraction Between Two Perfectly Conducting Plates. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Vol. 51, 1948, pp. 793–795.
- Lamoreaux, S. K., Demonstration of the Casimir Force in the 0.6 to 6 μm Range. Physical Review Letters, Vol. 78, 1997, pp. 5–8.
- Mohideen, U., and Roy, A. Precision Measurement of the Casimir Force from 0.1 to 0.9 μm. Physical Review Letters, Vol. 81, 1998, pp. 4549–4552.
- Jackson, J. D., Classical Electrodynamics. 3rd ed., John Wiley & Sons, 1999.
- Hawking, S. W., and Ellis, G. F. R. The Large Scale Structure of Space-Time. Cambridge University Press, 1973.
- Misner, C. W., Thorne, K. S., and Wheeler, J. A. Gravitation. W. H. Freeman, 1973.
- Rovelli, C., Quantum Gravity. Cambridge University Press, 2004.
- Smolin, L. Three Roads to Quantum Gravity. Basic Books, 2001.
- Ashtekar, A., New Variables for Classical and Quantum Gravity. Physical Review Letters, Vol. 57, 1986, pp. 2244–2247.
- Laughlin, R. B., Emergent Relativity. International Journal of Modern Physics A, Vol. 18, 2003, pp. 831–854.
- Barrow, J. D., The Constants of Nature: From Alpha to Omega. Pantheon Books, 2002.
- Penrose, R., The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape, 2004.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).