Quantum Gravity I—Emergent Hypercomplex Operator Gauge Theory for Microcausal Lattice Spacetime

1. Introduction

The unification of quantum mechanics [1] and general relativity [2] remains one of the most profound challenges in theoretical physics. Traditional approaches—ranging from quantum field theory on curved spacetimes [3] to string theory [4], M-theory [5], and loop quantum gravity [6]—have encountered persistent obstacles: ultraviolet divergences [7], singularities [8], lack of experimental falsifiability, and unresolved ontological paradoxes such as wavefunction collapse [9] and the measurement problems [10].

This work, as the first part I of a two-part work on quantum gravity, introduces a fundamentally new approach: quantum gravity [11] as an emergent phenomenon from algebraic microcausality [12] over a discrete causal lattice [13]. Rather than quantizing classical fields or geometries [14], we begin with a more primitive structure—hypercomplex [15] algebraic relations among displacement operators—and allow both quantum behavior and spacetime geometry to arise as emergent features.

In Part I (this paper), we focus on laying the algebraic and causal foundations. We introduce the discrete causal lattice and show how operator commutation relations encode both the geometry of spacetime and the non-classical structure of quantum mechanics. Key quantum features—including Panck’s quantized energy [6]. Heisenberg’s uncertainty principle [17], de Broglie’s particle-wave duality [18], quantum entanglement [19], self-interference in double-slit interference [20], wavefunction collapse upon measurement problems [21], and quantum statistics [22]—are derived from first principles using operator algebra. Importantly, this framework avoids the use of wavefunctions, path integrals, or Hilbert space axioms, instead interpreting quantum phenomena as consequences of non-commutative operator dynamics.

Part II, to be developed and submitted separately, will build upon this foundation to derive gravitational dynamics, explore the resolution of singularities, and show how internal gauge symmetries and cosmological expansion naturally emerge from extensions of the operator algebra into hypercomplex structures such as sedenions. In the sequel, Part II, we will address grand unification [23] and cosmological implications beyond Einstein’s general relativity [24] and the Standard Model [25].

This separation into two parts allows for a clear and focused exposition. Part I provides theoretical and mathematical scaffolding; Part II will present the physical consequences and phenomenological extensions. Our goal is to offer not merely reinterpretation, but a new derivation of the essential features of modern physics—grounded in a microcausal operator algebra that unifies space, time, and matter at the most fundamental level.

2. Operator Foundations of Microcausal Spacetime

2.1. Discrete Causal Lattice: Motivation and Definitions

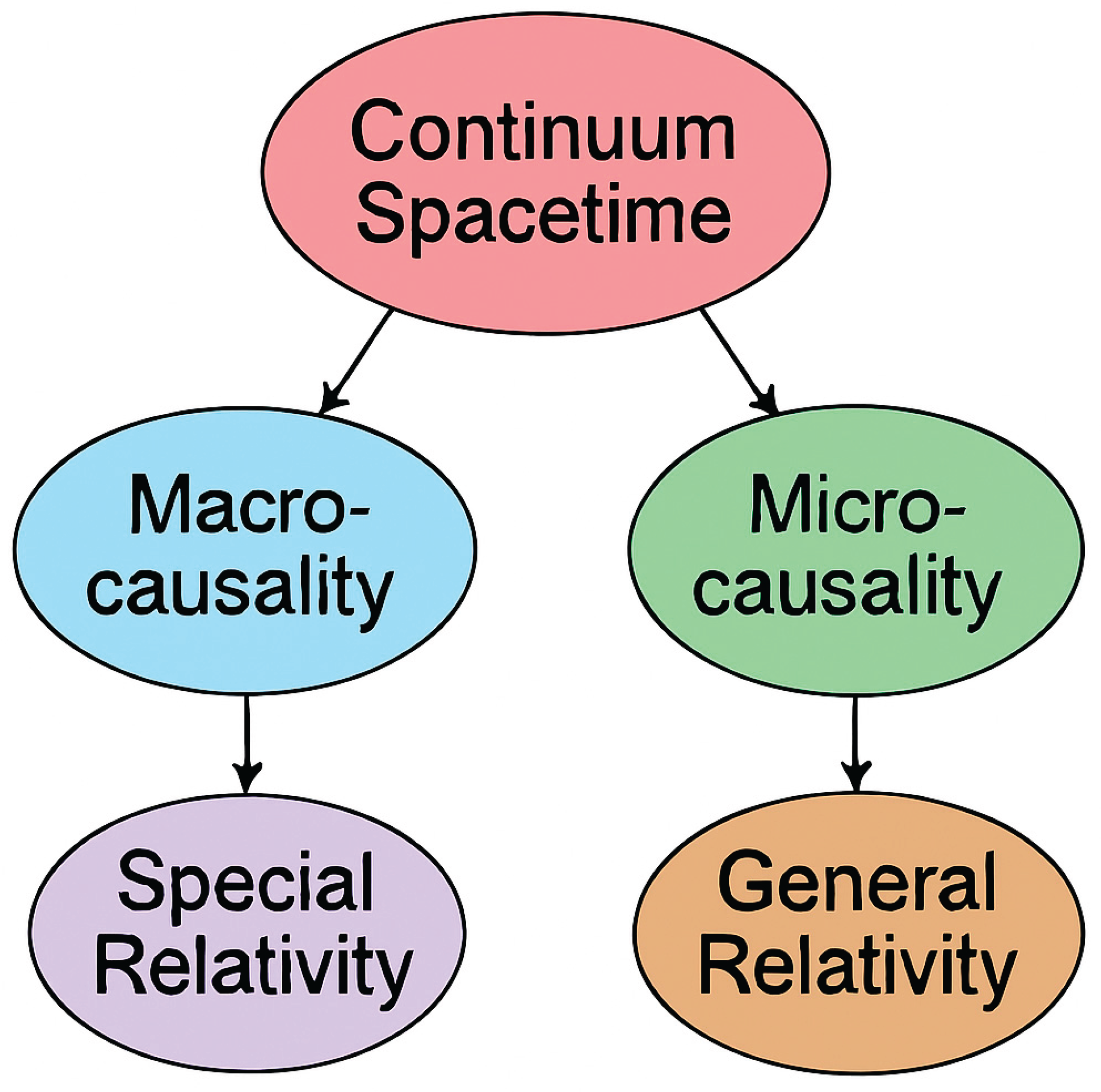
Relativity and quantum theory are two pillars of modern physics since the dawn of the 20^th century. The finite propagation speed of light, as the origin of macrocausality, is the fundamental basis for Einstein’s special relativity [26] for reference frames with a constant speed. Such a property is validated by the experiments and is consistent with the invariance of Maxwell's equations of the electromagnetic fields. In the presence of a gravitational field, the reference frames are no longer moving at a constant speed but with an acceleration, the macrocausality must be replaced by the microcausality that is encoded in differential geodesics as postulated in Einstein’s general relativity.

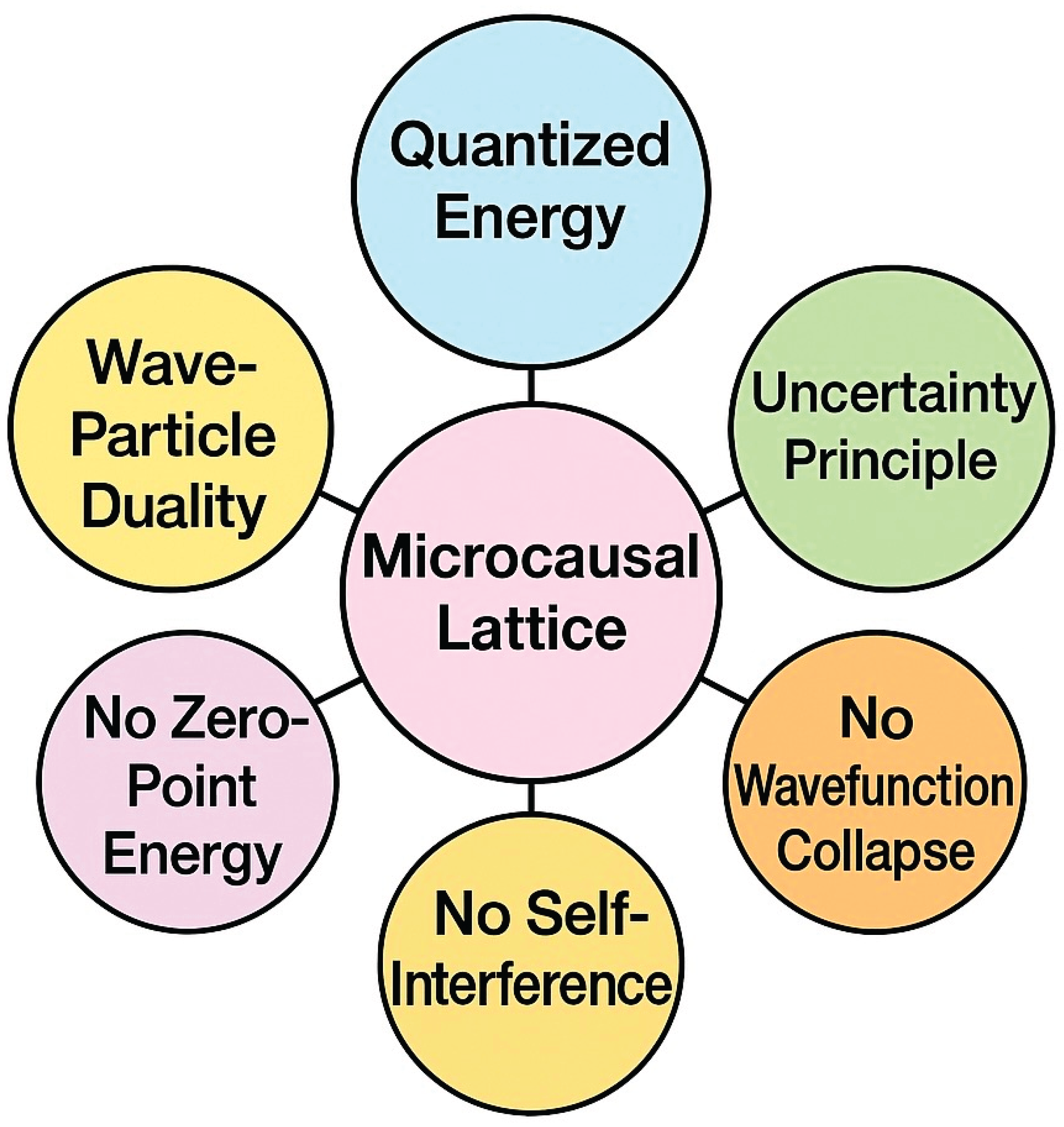
To understand the fundamental implications of microcausality on quantum theory, we outline the core principles that emerge from the structure of a microcausal lattice, as illustrated in Figure 1.

In conventional quantum field theory, spacetime is modeled as a smooth, continuous manifold where fields evolve through differential equations. However, this framework leads to a cascade of foundational problems, including ultraviolet (UV) divergences [27], the cosmological vacuum catastrophe [28], and singularities in gravitational collapse [29]. These issues suggest that the continuum approximation may break down at the Planck scale [30], where quantum gravitational effects become dominant.

To resolve these inconsistencies, we replace the continuum with a fundamentally discrete spacetime structure: a causal lattice, defined by two postulates:

1. Spacetime consists of quantized, finite-length intervals, labeled by a minimal spatial unit L and a corresponding temporal unit T = L / c, where c is the speed of light.

2. Causality is preserved through a directed acyclic graph (DAG) structure [31]. Each lattice point is connected only to its forward or backward causal neighbors, forming a microcausally ordered network.

Let x^μ ∈ ℤ⁴ , where ℤ represents integers, L denote the discrete spacetime coordinates on the lattice, where μ = 0, 1, 2, 3 index time and spatial directions. The fundamental dynamical elements are displacement operators D_μ, which act algebraically to propagate fields from one lattice node to its neighbor:

D_μ ψ(x) = ψ(x + L e_μ).

(1)

Here, e_μ is the unit vector in the μ-th direction. These operators replace the role of infinitesimal derivatives in the continuum and are algebraically richer, supporting non-commutative behavior.

Importantly, time is algebraically distinguished by assigning an imaginary coefficient to the temporal operator:

D₀ → i D₀.

(2)

This substitution enforces a strict causal direction in field evolution and explicitly breaks time-reversal symmetry at the fundamental level. The temporal step is not merely a coordinate increment, but a complex displacement that generates irreversible dynamics.

Together, these features define a microcausally ordered, discrete spacetime lattice. Unlike ad hoc lattices used for regularization (e.g., in lattice gauge theory), this structure is taken to be physically fundamental. It acts as both a regulator and a geometric substrate, embedding causality, directionality, and minimal length and time scales directly into the kinematic fabric of the theory.

At large scales, the continuum approximation is recovered as an emergent symmetry, but at Planckian scales, the granular structure of spacetime becomes dynamically relevant. This approach lays the groundwork for encoding curvature, fields, and quantum behavior not through smooth metrics, but through operator algebra on a discrete causal substrate.

2.2. Microcausality as an Algebraic Constraint

A central principle of this framework is microcausality, which asserts that all fundamental field operations must respect the local causal structure of discrete spacetime. In contrast to continuum theories, where causality is preserved globally through Lorentz invariance, our model implements causality directly in the algebra of displacement operators.

We begin by defining microcausality through the non-commutativity of displacement operators. Let D_μ and D_ν be displacement operators acting on lattice points in spacetime directions μ and ν, respectively. At the macroscopic scale, the order of these operations becomes irrelevant, and the commutator vanishes:

[D_μ, D_ν] = 0 (macrocausal regime).

(3)

However, at Planckian resolution, displacements no longer commute:

[D_μ, D_ν] ≠ 0 (microcausal regime).

(4)

This algebraic non-commutativity implies that the order of operations encodes temporal and causal information. The lattice thus defines a partially ordered set (poset) of events, forming a directed acyclic graph (DAG) structure. Temporal ordering is embedded not in coordinate time but in the algebraic structure of operators.

To enforce this ordering, we distinguish the temporal direction explicitly by assigning an imaginary factor to the time displacement operator:

D₀ → i D₀.

(5)

This algebraic step breaks time-reversal symmetry intrinsically and ensures that field propagation occurs only along forward-directed causal links. Each lattice node is connected to a finite number of causally prior nodes, and closed timelike loops are prohibited by construction.

This causal operator ordering also ensures a discrete form of signal propagation: fields propagate only when the operator sequence preserves causality, meaning all non-zero contributions to field evolution must arise from microcausally valid paths.

In this way, causality is not an emergent feature of spacetime geometry but a foundational constraint in the operator algebra itself. This shift has profound implications: the geometry of spacetime becomes inseparable from the algebra governing field dynamics, and causality is no longer a global symmetry to be preserved but a local algebraic condition embedded in every dynamical step.

This causal algebraic structure replaces Lorentz symmetry as the guiding principle at short distances, while allowing approximate Lorentz invariance to emerge in the continuum limit.

2.3. Displacement Operators and Commutation Algebra

The fundamental dynamical elements of the discrete causal lattice are displacement operators D_μ, which replace derivatives in conventional field theory. These operators shift a field ψ(x) from one lattice site to its neighbor in the μ-direction by a fixed unit length L:

D_μ ψ(x) = ψ(x + L e_μ).

(6)

Here, e_μ is the unit vector in the spacetime direction μ ∈ {0, 1, 2, 3}. The operator D_μ acts as a finite, algebraic translation. The inverse operator D_μ⁻¹ shifts in the opposite direction.

To define observables such as position and momentum, we construct an algebra of these operators. Let X be the position operator, acting by multiplication:

X ψ(x) = x ψ(x).

(7)

The non-commutativity of X and D_x reflects the discrete structure of space. Their algebraic commutator is:

[X, D_x] = L D_x.

(8)

Similarly, defining the time operator T and the temporal displacement D_t, we obtain:

[T, D_t] = T D_t^.

(9)

These commutation relations are discrete analogs of the canonical commutation relations in continuous quantum mechanics. In particular, this algebra naturally leads to uncertainty principles without invoking wavefunctions or Hilbert spaces.

To define momentum, we construct a dimensionless conjugate operator P̂ from the algebra of displacement and position operators. Using a symmetrized difference form:

P̂ = (i / 2) [D⁻¹ X̂ D - D X̂ D⁻¹],

(10)

where X̂ = X / L is the dimensionless position operator. It follows that:

[X̂, P̂] = i.

(11)

This relation reproduces the familiar Heisenberg algebra, but as an emergent feature of operator geometry, not as a quantization rule. It shows that quantum uncertainty and discreteness of measurement arise from the algebra of field propagation on the lattice, not from axiomatic postulates.

Moreover, the algebra is consistent across all lattice directions and inherently non-associative when generalized to more complex number systems (e.g., quaternions, octonions), which will become important in later sections for encoding internal symmetries.

Thus, the displacement operator algebra plays a dual role: it governs causal propagation and encodes the geometry of measurement and uncertainty. It offers a unified language for space, time, and momentum, rooted in operator actions rather than background geometry or wavefunction evolution.

2.4. Lorentz Symmetry from Discrete Causality

A fundamental challenge of discretized spacetime models is the apparent loss of continuous Lorentz symmetry [32]. Naively, introducing a lattice breaks translation and rotation invariance, especially when a preferred grid orientation exists. However, in our framework, Lorentz symmetry is not imposed a priori but instead emerges as an effective symmetry in the long-wavelength limit from the underlying causal algebra.

The key idea is that the discrete causal lattice, despite being composed of directed links between nodes, preserves the causal light-cone structure. The local causal order encoded in the directed acyclic graph (DAG) formed by the displacement operators respects a maximum signal propagation speed c. That is, no sequence of displacement operators can connect two events in a time interval shorter than allowed by light-speed constraints.

This causal restriction effectively reproduces the structure of local Minkowski neighborhoods in the continuum approximation. Since microcausality enforces a light-cone boundary, and since field propagation occurs along operator paths constrained by this boundary, the resulting dynamics approximate Lorentz invariance at scales much larger than the lattice spacing L.

To illustrate, consider the massless dispersion relation in our lattice formulation. The field evolution governed by operator paths satisfies a difference-based wave equation. In the continuum limit L → 0, the discrete evolution approximates:

E² = c² p².

(12)

This is precisely the Lorentz-invariant relation [33] for massless particles. At finite L, the dispersion becomes:

E² = (4 / L²) Σ_i sin²(L p_i / 2ħ).

(13)

This expression reduces to the continuum result as p_i → 0, confirming that Lorentz symmetry is an emergent symmetry of the causal operator lattice.

Moreover, the use of algebraic displacement operators avoids fixed coordinate axes; the operators define relative displacement, not fixed embedding. This allows local frame covariance even on a discrete structure, with boost transformations reinterpreted as changes in operator composition paths across DAG.

In short, Lorentz symmetry is not destroyed but encoded algebraically and recovered effectively. The causal operator framework thereby preserves relativistic invariance at large scales while naturally encoding Planck-scale deviations that could serve as observational signatures.

2.5. Emergence of Time and Directionality

In standard formulations of physics, time is treated as a coordinate — symmetric with space in relativistic theories — and reversible in both classical mechanics and unitary quantum evolution. However, such symmetry is in direct tension with the irreversibility observed in thermodynamic processes, quantum measurement, and cosmological expansion.

In our framework, time is not a background parameter but an emergent feature of operator algebra on the causal lattice. The temporal displacement operator D₀, unlike its spatial counterparts, is defined with an intrinsic imaginary factor:

D₀ → i D₀.

(14)

This imaginary component introduces non-Hermiticity into the temporal evolution algebra, explicitly breaking time-reversal symmetry at the fundamental level. Rather than treating t and –t as physically equivalent, the system evolves along a directed chain of causal operator actions. This directionality is built into the formalism, not imposed as an external condition.

At each lattice node, the only permitted operator compositions are those that advance the causal ordering — backward evolutions are either undefined or algebraically forbidden. The resulting structure forms a directed acyclic graph (DAG) of events, with a strict partial order encoded in the operator algebra. Each node x has incoming arrows only from its causal past, and outgoing arrows only to its causal future.

This asymmetric structure has two immediate implications:

1. Irreversibility emerges naturally: There is no need to invoke entropy increase or stochastic collapse to explain the arrow of time — the irreversible operator action itself defines forward temporal flow.

2. No closed timelike curves: Since operators can only move forward in causal order, looped causal structures (which plague some classical general relativistic solutions) are eliminated by construction.

Moreover, the imaginary nature of the time displacement operator connects to the Feynman path integral's complex phase structure, offering a reinterpretation of quantum amplitudes as geometric consequences of causal operator composition.

Thus, in this model, time is not a coordinate to be quantized, but a macroscopic approximation of algebraic directionality. The emergent temporal flow is the result of the local microcausal ordering defined by operator dynamics. This directly supports later developments of thermodynamic emergence (Section 3.5) and quantum measurement theory (Section 3.8).

2.6. Operator Algebra vs. Wavefunction Ontology

The foundational shift introduced by our framework involves a rejection of wavefunction-based ontology in favor of a more primitive structure: the algebra of operators defined over a discrete causal lattice. This represents a major departure from conventional quantum theory, where the wavefunction ψ(x) is central to defining quantum states, evolution, and probabilities.

In standard quantum mechanics, the wavefunction evolves unitarily under a Hamiltonian operator and collapses during measurement — a process that is inherently non-unitary and introduces interpretational paradoxes. These include the measurement problem, the observer-dependence of collapse, and the metaphysical ambiguity of superposition.

In contrast, our theory is built upon operator sequences acting over a lattice. The quantum state is no longer a complex-valued function over spacetime, but a history of operator displacements:

ψ(x) ~ D_μn ... D_μ2 D_μ1 I.

(15)

Here, the "state" is encoded in a sequence of causal displacements from an origin point I (an identity or vacuum node). Each path through operator space represents a specific field history, and amplitudes arise from operator algebra, not from Hilbert space inner products.

This view carries several conceptual advantages:

1. No wavefunction collapse is required: Measurements correspond to algebraic projections onto causal subgraphs — no special postulates or observer-triggered processes are needed.

2. No self-interference or paradoxical duality: Particles do not interfere with themselves through multiple paths; rather, interference is encoded in the non-commutativity of composite operator sequences.

3. No need for global configuration space: The formalism remains local and compositional; each operator encodes only local shifts, and quantum phenomena emerge from the global structure of operator interactions.

Furthermore, the operator algebra naturally includes uncertainty and entanglement, not as axioms or mysterious phenomena, but as emergent properties of algebraic non-commutativity and path-dependence. As shown previously:

[X̂, P̂] = i.

(16)

This uncertainty arises not from the probabilistic interpretation of wavefunctions, but from the incompatibility of measurement operators on a causal lattice.

This reorientation frees the theory from the ontological baggage of the wavefunction and reframes quantum mechanics as a dynamical system of algebraic propagation — closer in spirit to quantum computation or category theory than to classical mechanics.

It also enables a seamless transition to field theory and gravity, where the same operator structures that define propagation also generate curvature, internal symmetries, and thermodynamic behavior — as developed in later sections.

2.7. Natural Planck Cutoffs and Ultraviolet Finiteness

A persistent challenge in quantum field theory (QFT) [32] is the appearance of ultraviolet (UV) divergences at high energies and short distances. These infinities manifest in loop integrals, self-energy corrections, and vacuum energy density, requiring renormalization schemes that are mathematically effective but physically unsatisfying.

Our framework eliminates UV divergences at the root by replacing the continuum with a Planck-scale causal lattice. The lattice spacing L and temporal step T = L / c are not arbitrary regulators but fundamental physical constants. All operator actions occur over finite, irreducible displacements, which introduces an intrinsic minimal resolution in both space and time.

This discreteness modifies the behavior of field modes at high momentum. In contrast to continuum QFT, where momenta are unbounded and integrations extend to infinity, the lattice imposes a finite Brillouin zone:

|p_i| ≤ πħ / L.

(17)

This upper bound ensures that energy and momentum values remain bounded, and any sums over momentum space become finite, naturally cutting off divergent terms.

Moreover, the dispersion relation itself reflects this ultraviolet behavior. As seen earlier, the lattice-modified energy spectrum becomes:

E² = (4 / L²) Σ_i sin²(L p_i / 2ħ).

(18)

Unlike the continuum E² = c² p², this expression saturates at high p, flattening the energy spectrum and preventing runaway contributions.

Crucially, this cutoff is not added manually, as in Pauli-Villars [34] or dimensional regularization, but emerges directly from the causal structure. Since the displacement operators act only over discrete causal links, field evolution is bounded both spatially and temporally. This is structurally incompatible with divergences.

This has multiple implications:

- No vacuum catastrophe [35]: The infinite zero-point energy [36] contribution in standard QFT is avoided. The number of allowed modes is finite, and the vacuum energy density remains naturally small.

- No need for renormalization counter-terms [37]: Physical quantities like charge and mass are well-defined from the outset, without requiring arbitrary subtractions or scale-dependent redefinitions.

- Robust against trans-Planckian breakdowns: Since no physical quantity can resolve distances smaller than L, the theory remains well-defined even under extreme boosts or black hole horizons [38].

The causal lattice thus functions not merely as a discretization trick, but as a physical substrate that ensures the ultraviolet finiteness of quantum field theory by construction.

2.8. Operator Saturation and Singularities

A major problem in general relativity and quantum field theory is the appearance of singularities — points where curvature, energy density, or field values diverge, rendering the theory physically meaningless. In standard formulations, such singularities appear in black hole cores [39], the Big Bang [40], or in renormalized quantities like self-energy [41].

In our causal operator framework, singularities are avoided not by imposing external constraints, but as a natural consequence of operator saturation. Since all physical evolution is governed by discrete displacement operators acting on a causal lattice, there exists a finite density of operator actions per region of spacetime. This places strict bounds on the accumulation of energy and information.

Each lattice point can be connected to a finite number of causal neighbors, defined by the directed acyclic graph (DAG) structure. The number of distinct operator paths that can reach a node in a finite number of steps is also finite. Therefore, any attempt to encode infinite curvature or energy into a finite region violates the operator algebra and becomes undefined.

This is evident in the energy density expression derived from the lattice dispersion relation:

E² = (4 / L²) Σ_i sin²(L p_i / 2ħ).

(19)

As p_i → πħ / L, the energy saturates. No further increase in momentum leads to greater energy, and hence curvature and field strength are naturally bound. This saturation prevents blow-ups in the energy-momentum tensor or Riemann curvature tensor analogs.

Moreover, since operator composition is non-associative in generalized algebras (e.g., octonionic or sedenionic extensions), multiple operator applications within a confined region cannot be arbitrarily nested. The algebra itself restricts the complexity of evolution paths, functioning as a dynamical firewall against singular configurations.

This has several physical consequences:

- Black hole cores do not form singularities, but regions where displacement operators are saturated. These cores exhibit non-geometric behaviors — more akin to algebraic boundaries than spacetime punctures.

- Cosmological singularities, such as the Big Bang, are reinterpreted as operator-boundary conditions in a maximally compressed lattice region, with no need for diverging curvature scalars.

- Information loss is avoided because all operator paths are traceable through a finite causal structure, even near what would be singularities in classical theory.

In short, singularities are artifacts of continuum assumptions. In a discrete, algebraic spacetime, the limits of resolution, energy, and operator composition are built in. Saturation replaces divergence, and algebraic boundaries replace geometric breakdowns.

2.9. Internal vs. External Degrees of Freedom

In traditional field theory and general relativity, there exists a clear distinction between external (spacetime) and internal (gauge or flavor) degrees of freedom. Spacetime dynamics are governed by geometric curvature and coordinate transformations, while internal symmetries (e.g., SU(3) for color or SU(2) for weak isospin) are appended through independent group structures.

Our operator-based framework blurs and ultimately unifies this distinction. In this formalism, both external and internal degrees of freedom arise from the same algebraic origin — namely, the structure and representation of displacement operators acting over a causal lattice. The apparent separation between “spacetime” and “internal” symmetries is thus emergent, not fundamental.

External (Spacetime) Degrees:Spacetime displacement operators D_μ act on lattice sites and encode causal structure, directionality, and propagation. These operators define external observables such as position, time, and momentum via their commutation relations with position operators:

[X_μ , D_ν] ~ δ_μν D_ν.

(20)

The action of these operators maps fields from one causal node to another, thereby defining the geometry of spacetime.

Internal Degrees as Algebraic Extensions:

Internal symmetries emerge when displacement operators are extended into higher-dimensional algebras. For example:

- Complex numbers support phase symmetry (U(1)),

- Quaternions accommodate SU(2)-like structures,

- Octonions and sedenions support non-associative generalizations of SU(3), SU(5), etc.

These internal structures do not act on position but on the algebraic index structure of the field operators themselves. That is, fields carry components in internal algebraic directions (e.g., color, flavor, generation), which transform under internal commutators of generalized displacement operators:

[𝔇_a, 𝔇_b] = f^c_ab 𝔇_c.

(21)

Here, 𝔇_a denotes generalized displacement operators in both internal and external directions, and f^c_ab are the structure constants [42] of the algebra (potentially non-Lie, if non-associative).

Unified Interpretation:

In this view, external and internal degrees of freedom are not fundamentally distinct. Instead:- External degrees emerge from causal relations between nodes,

- Internal degrees emerge from algebraic multiplicities at each node.

This framework implies that spacetime geometry and gauge fields are both manifestations of the same operator algebra — differing only in how the operator indices are interpreted and composed.

Additionally, this unification hints at a geometric origin of particle quantum numbers, including spin, charge, and generation structure. These may correspond not to fundamental attributes, but to the algebraic topologies of operator paths on the causal lattice — a direction developed more fully in Section 5.

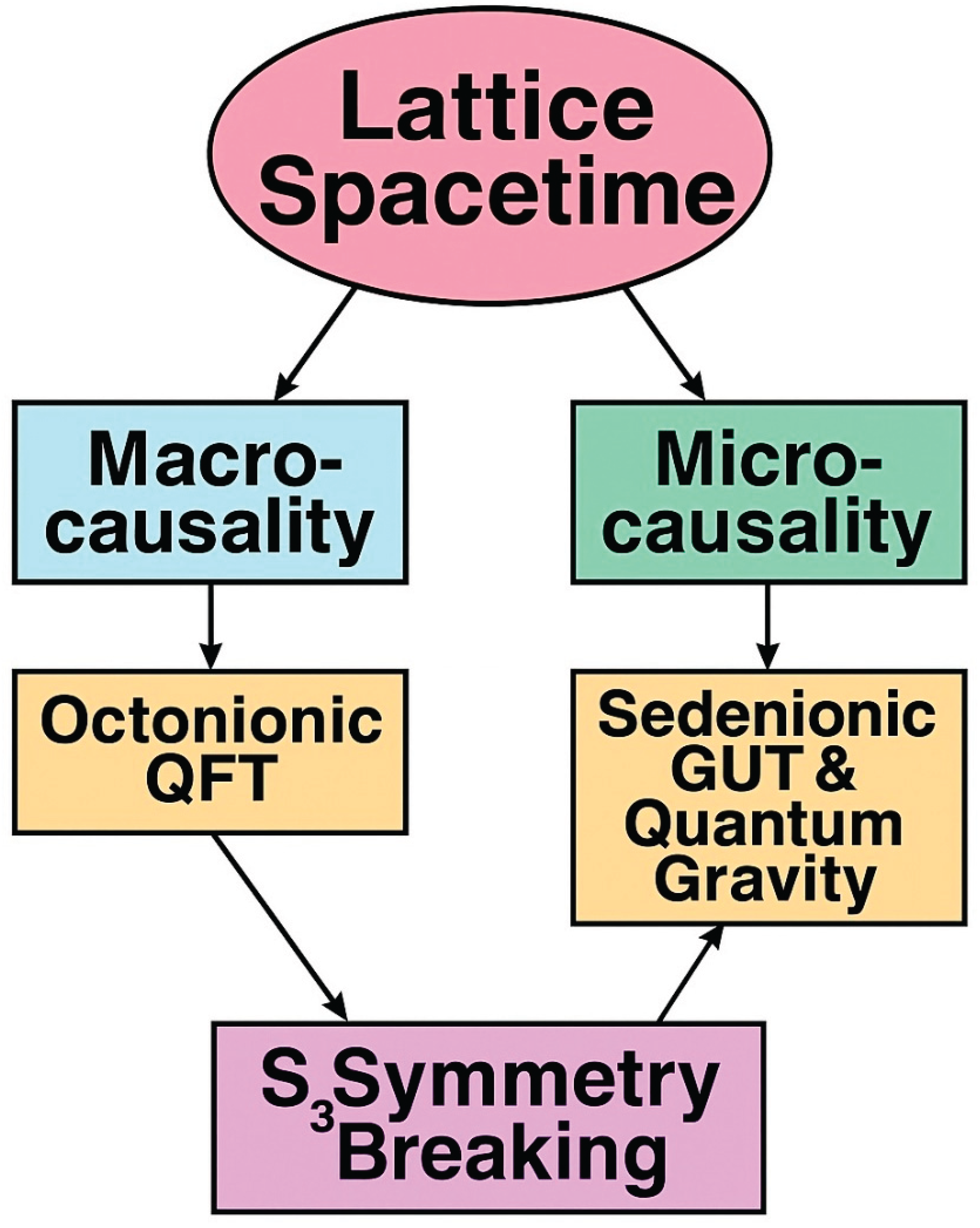
Building upon this foundation, Figure 2 presents a conceptual framework in which lattice spacetime gives rise to both macro- and microcausality, ultimately leading to symmetry breaking and the emergence of a unified quantum field and gravity theory."

3. Quantum Mechanics from Operator Algebra

3.1. Uncertainty Principle from Commutators

In traditional quantum mechanics, the Heisenberg uncertainty principle is derived from the non-commutativity of operators in Hilbert space:

[x̂, p̂] = iħ.

(22)

This relation implies that position and momentum cannot simultaneously be known with arbitrary precision. The uncertainty is typically interpreted as an intrinsic property of quantum states described by wavefunctions.

In our operator-based causal lattice framework, uncertainty is not a statistical property of wavefunctions, but a structural feature of the operator algebra that governs physical evolution. The uncertainty principle arises directly from the non-commuting nature of displacement and position operators on the lattice.

We define the dimensionless position operator X̂ and the conjugate momentum operator P̂ algebraically as:

X̂ ψ(x) = (x / L) ψ(x),

P̂ ψ(x) = (i / 2) [D⁻¹ X̂ D - D X̂ D⁻¹] ψ(x).

(23)

These operators satisfy the canonical commutation relation:

[X̂, P̂] = i.

(24)

This algebra emerges purely from the discrete translation structure of the lattice and the finite displacement operators. It leads to a geometric derivation of the uncertainty principle that is independent of wavefunctions or probability distributions.

We can express the uncertainty relation in its usual form:

ΔX ΔP ≥ ½.

(25)

But here, ΔX and ΔP refer to the spread of operator eigenvalue support over the lattice, rather than statistical variances derived from measurement outcomes. The inequality reflects the incompatibility of simultaneously sharp operator paths for X̂ and P̂, rooted in the non-commuting operator algebra of field evolution.

This formulation offers several advantages:

- No probabilistic interpretation is required: Uncertainty is topological, not epistemic.

- Applies even in finite systems: The lattice has intrinsic resolution limits; the uncertainty principle reflects this.

- Generalizes to other observables: Any pair of non-commuting operators will exhibit similar algebraic uncertainty.

Moreover, because operator paths define the causal structure of the system, uncertainty becomes a manifestation of causal indeterminacy. It encodes the impossibility of resolving both the origin and direction of propagation at sub-Planck scales — a geometric property of the causal lattice itself.

This foundational reinterpretation will be extended in the next subsection, where classical wave-like behavior, including the de Broglie relations, are shown to arise naturally from operator geometry — without invoking wavefunctions or path integrals.

3.2. de Broglie Relations Without Wavefunctions

In conventional quantum mechanics, the de Broglie relations:

p = ħk, E = ħω.

(26)

link wave-like quantities (wavevector k, frequency ω) to particle properties (momentum p, energy E). These relations rely on associating particles with wavefunctions — solutions to the Schrödinger or Klein-Gordon equations — and interpreting their Fourier components as modes of propagation.

In our causal operator framework, these relations emerge geometrically, not from wavefunctions, but from the algebraic structure of displacement operators on a discrete lattice.

Displacement Operators and Phase Evolution:

Consider a field defined over a causal lattice with uniform spacing L and time step T = L / c. Define the spatial displacement operator D_x and temporal displacement operator D_t, acting on lattice nodes as:

D_x ψ(x) = ψ(x + L), D_t ψ(t) = ψ(t + T)

(27)

A sequence of displacement operations generates an evolution history:

ψ_n(x, t) = D_xⁿ D_t^m I.

(28)

Because each displacement is a unit step on the causal graph, the system accumulates discrete phase shifts associated with each operator:

D_x ~ e^{i k L}, D_t ~ e^{-i ω T..}

(28)

The eigenvalues of these operators encode momentum and energy. Matching the periodicity of the lattice leads directly to the de Broglie relations:

p = (ħ / L) θ_x = ħk, E = (ħ / T) θ_t = ħω.

(30)

Here, θ_x, θ_t are the discrete angular phases per unit step in space and time, respectively.

No Wavefunctions, Just Operator Geometry:

This derivation does not rely on a continuous wavefunction. Instead, the field is defined entirely in terms of operator displacements and their algebraic eigenvalues. The wave-like behavior emerges from the cyclic structure of operator products — much like phase factors in quantum gates or modular arithmetic.

In this view:

- p and E are emergent labels of causal translation rates.

- k and ω are phase increments from discrete propagation.

- The Planck constant ħ serves as a conversion factor between lattice phases and physical quantities.

This approach has several conceptual advantages:

- No superposition assumption: Interference emerges from non-commutative operator history, not overlapping wave amplitudes.

- No path integrals needed: Evolution paths are actual operator sequences, not virtual histories.

- No collapse or delocalization: Particles do not "spread" across space; they follow definite but algebraically constrained causal paths.

The de Broglie relations therefore reflect a deep algebraic resonance condition in the causal lattice — a rhythm of operator action — rather than any duality between waves and particles.

3.3. Entanglement via Nested Operator Histories

In standard quantum mechanics, entanglement is viewed as a nonlocal correlation between subsystems that share a joint wavefunction. The resulting phenomena — such as violations of Bell inequalities [43] and measurement-induced collapse — are often interpreted through probabilistic or information-theoretic lenses.

In contrast, our framework interprets entanglement not as a superposition of states, but as a property of operator history nesting on the causal lattice. That is, quantum correlations arise from overlapping, interdependent sequences of displacement operators, rather than from shared wavefunctions in configuration space.

Causal Histories and Nested Paths:

Let two quantum subsystems A and B evolve independently on separate regions of the lattice via their respective displacement operators D_A and D_B. In a non-entangled case, their histories are factorizable:

ψ_AB = D_A⁽ⁿ⁾ D_B⁽ᵐ⁾ I = ψ_A ⊗ ψ_B.

(31)

However, when their histories share causal overlaps — such as a shared ancestor node or an interleaved sequence of operator actions — the system forms a nested operator history:

ψ_AB = D_A⁽ᵏ⁾ D_B⁽ˡ⁾ D_AB⁽ʲ⁾ I.

(32)

Here, D_AB represents a joint sequence of displacement operators that link the two histories. This introduces algebraic coupling between otherwise independent causal paths, leading to non-factorizable evolution.

Algebraic Source of Correlation:

Because operators do not generally commute, the order of operations matters. If the displacement operators D_A and D_B satisfy:

[ D_A, D_B] ≠ 0 ,

(33)

then the nesting of histories implies a path-dependent interference structure. This gives rise to correlations between measurement outcomes, even in the absence of a wavefunction description.

These correlations can be traced to shared causal ancestry and operator overlap on the lattice. In this sense:

- Entanglement is causal, not statistical.

- Measurement correlations reflect shared operator geometry.

- Nonlocality emerges from topological constraints, not action-at-a-distance.

Measurement without Collapse:In this framework, there is no need for wavefunction collapse to explain measurement correlations. A measurement is modeled as an algebraic projection on the operator path — i.e., constraining the set of allowable displacements based on boundary conditions.

This projection alters the structure of the operator history, which can have global consequences due to the nested nature of prior paths. As such:- The “collapse” is a reconfiguration of operator possibilities, not a discontinuous jump.- Entangled correlations persist due to consistency in shared causal structure, not instantaneous communication.

This view aligns with a fully relational interpretation of quantum mechanics, where what matters is how systems are linked via operator histories, not what individual systems “are” in isolation. Entanglement becomes a structural consequence of algebraic entwinement on a causal lattice, offering a concrete and geometrical origin for one of quantum theory’s most mysterious features.

3.4. No Wavefunction Collapse or Self-Interference

A central puzzle in standard quantum mechanics is the notion of wavefunction collapse [44]: upon measurement, a quantum system discontinuously transitions from a superposed state into a definite eigenstate. Alongside this is the phenomenon of self-interference, where a single particle seems to interfere with itself when no other particles are present — as in the double-slit experiment.

These effects challenge classical intuition and have led to philosophical debates over the meaning of measurement, observer effect, and reality itself.

Our operator-based framework resolves these puzzles by removing wavefunctions altogether. Instead of assuming that quantum systems are described by continuous, delocalized wavefunctions, we model them as algebraic sequences of displacement operators acting on a causal lattice. All “evolution” is defined by operator histories, not by state vectors.

No Collapse — Just Operator Path Constraint:

Measurement in this framework is not a collapse of a state, but a constraint on the allowable future operator paths. When an observable is measured, it restricts the evolution by selecting a subset of compatible operator sequences consistent with the measurement interaction.

Suppose a measurement operator M projects the system along a certain causal direction. The full operator history is filtered as:

ψ → M ψ = P_M D ... D I.

(34)

This “collapse” is algebraic and deterministic. It represents a change in boundary conditions, not an ontological discontinuity. The system continues to evolve via the same operator algebra, only now subject to new constraints imposed by the measurement history.

Self-Interference as Path Entanglement:

What about interference patterns observed in single-particle experiments? In our view, these do not result from a particle traversing two paths simultaneously. Instead, they emerge from the non-commutative structure of overlapping operator histories.

In a double-slit setup, the field evolves via two causally distinct paths:

ψ = D₁⁽ⁿ⁾ + D₂⁽ⁿ⁾.

(35)

Because D₁ and D₂ do not commute in general, their combined action depends on the full operator sequence and their algebraic overlaps. The interference pattern is a manifestation of how operator paths interfere geometrically, not probabilistically.

This resolves the paradox of “which-path” information:

- If path constraints are imposed (e.g., a detector at one slit), certain operator sequences are disallowed.

- The interference pattern disappears, not because of observation, but due to loss of algebraic overlap between the sequences.

Key Takeaways:

- Collapse is a misinterpretation: It’s a projection on operator paths, not a physical event.

- Self-interference is not literal: It arises from the algebraic structure of non-commuting displacements, not from a single object traversing multiple paths.

- Measurement is fully local: Outcomes are determined by causal constraints, not observer knowledge or external triggers.

By reformulating quantum behavior in terms of algebraic causal evolution, we dissolve the conceptual tension of collapse and interference. These effects are seen not as paradoxes, but as natural consequences of a discrete operator geometry.

3.5. Emergence of Thermodynamic Time

The arrow of time — the unidirectional flow from past to future — remains one of the deepest puzzles in physics. While microscopic laws are mostly time-reversible, macroscopic systems evolve irreversibly toward equilibrium. This tension underlies the second law of thermodynamics, entropy increase, and the emergence of classical causality.

In standard quantum theory, time is treated as a background parameter, and thermodynamic time [45] is often derived through statistical interpretations of large ensembles or decoherence. However, these approaches depend on approximations and assumptions, external to the theory’s algebraic core.

In our causal operator framework, thermodynamic time is emergent and algebraic. It arises from the structure of nested displacement operators on a directed causal lattice, where the very act of operator composition generates an intrinsic asymmetry.

Time as Directional Operator Growth:

Each operator application corresponds to a causal displacement: a directed link on the lattice graph. As systems evolve, their histories are encoded in sequences of such displacements:

ψₙ = D⁽ⁿ⁾ I.

(36)

As operator paths accumulate, the number of accessible configurations increases. Because operator composition is generally non-commutative (and in some cases non-associative), the order and structure of operations matter. This creates a natural time ordering on histories — a hierarchy of evolution paths that cannot be reversed without violating the algebra.

Entropy as Operator Multiplicity:

We define algebraic entropy not as a function of microstate probabilities, but as the logarithm of the number of operator sequences consistent with a given macro-observable constraint:

S_op = log (number of operator paths compatible with boundary conditions).

(37)

As the system evolves forward in causal steps, this operator entropy typically increases. There are more ways to build long operator paths than short ones, reflecting the combinatorial expansion of causal possibilities.

This entropy is inherently relational and causal, reflecting the multiplicity of ways systems can connect through operator histories — not any underlying ignorance or probabilistic spread.

Irreversibility from Algebra, Not Probability:

In this framework:

- Irreversibility is built into the operator algebra, not added statistically.

- Time is not a background parameter, but a direction in operator composition.

- The second law emerges from the irreducibility of operator sequences — you cannot “un-compose” a nested history without algebraic violation.

Thus, thermodynamic time is a shadow of causal operator growth: a byproduct of how systems unfold on the lattice through irreversible, non-commuting actions.

3.6. Quantum Statistics from Algebraic Permutations

Quantum statistics — bosonic and fermionic — are typically derived from the symmetrization postulate applied to wavefunctions: indistinguishable particles must have wavefunctions that are either symmetric (bosons) or antisymmetric (fermions) under exchange. This leads to the Bose-Einstein [46] and Fermi-Dirac distributions [47] as well as phenomena like Pauli exclusion and superfluidity.

In our framework, which is built on operator algebra over a causal lattice, the need for wavefunction symmetry is replaced by algebraic permutation constraints on the displacement operators themselves. That is, the statistical behavior of quantum systems emerges from how operator sequences permute and interfere under causal evolution.

Operator Sequences and Permutability:

Consider two identical particles, represented not by state vectors, but by displacement operator histories D₁ and D₂. These histories are sequences of algebraic operations on the causal lattice. The joint evolution is represented by:

ψ = D₁ D₂ I.

(38)

Swapping the two operator paths yields:

ψ' = D₂ D₁ I.

(39)

If the operators commute:

[D₁, D₂] = 0 ⇒ ψ = ψ'.

(40)

This corresponds to bosonic symmetry: indistinguishable paths that interfere constructively.

If the operators anti-commute:

{D₁, D₂} = 0 ⇒ ψ = -ψ'.

(41)

This leads to fermionic antisymmetry and enforces the Pauli exclusion principle: repeated application of the same operator yields zero.

Algebraic Statistics Without States:

Thus, quantum statistics arise not from properties of abstract state vectors, but from the algebraic relationships between displacement operators. This has profound implications:

- Particle identity is defined by operator action, not by internal labels.

- Exchange statistics are structural — encoded in the underlying commutation relations.

- No need for a “state space” or symmetrization rule — the algebra defines everything.

In more complex systems, algebraic permutations generalize beyond simple commutators. In particular, non-associative algebras (e.g., octonions and sedenions) may support exotic statistics not described by standard boson/fermion dichotomies. These generalizations become important in high-energy regimes or theories with extended symmetry.

Summary:

- Bosons and fermions are defined algebraically through permutation of displacement operators.- Quantum statistics is an emergent algebraic effect, not a postulate about symmetrized wavefunctions.

- The Pauli principle follows from nilpotency in operator combinations, not from antisymmetric states.

This operator-centric view not only simplifies the foundations of quantum statistics, but also opens new paths for understanding non-standard particles, quasi-statistics, and the emergence of field modes in many-body quantum systems — all grounded in causal algebraic structure.

3.7. Effective Field Theories as Coarse-Grained Operators

Effective field theories (EFTs) are a cornerstone of modern physics, allowing complex high-energy dynamics to be approximated by simpler low-energy models with a finite number of degrees of freedom. Traditionally, EFTs are constructed by integrating out short-distance fluctuations in path integrals or renormalizing Lagrangian terms.

In our framework, EFTs arise not from functional integrals or Lagrangians, but from coarse-graining the operator algebra that governs field evolution on the causal lattice. This process reflects how fine-grained operator sequences can be approximated by effective composite operators that preserve relevant long-distance dynamics.

Coarse-Graining Operator Histories:

Consider a sequence of causal displacements:

ψ = Dₙ Dₙ₋₁ ... D₁ I..

(42)

At very short scales (e.g., near the Planck length), these operators may exhibit complex non-commutative behavior. But when viewed over many lattice steps, clusters of operators can be approximated by effective displacement operators D_eff, which encode the net causal shift over a larger region.

This defines a renormalized algebra:

D_eff = Dₙ Dₙ₋₁ ... D₁

(43)

The effective operator D_eff may obey approximately simpler algebraic relations (e.g., near-commutativity or emergent symmetries), even if the underlying constituents do not.

Emergence of Field Modes and Propagators:At coarse scales, effective operators organize into modes that satisfy simplified dispersion relations, much like how plane waves emerge in continuum quantum field theory. The propagation of these effective modes can be described by algebraic propagators, which are not Green’s functions, but operator mappings between lattice nodes.

This leads to emergent analogs of mass, spin, and gauge behavior:

- Mass terms arise from local operator loops that resist displacement.

- Gauge-like symmetries emerge from redundancy in operator path representations.

- Kinetic terms reflect translation structure in the effective operator algebra.

Thus, EFT behavior is recovered without path integrals or fields, but from the collective structure of causal operators acting at mesoscopic scales.

Operator Renormalization and Scaling:

Renormalization in this framework is not about rescaling coupling constants, but about constructing equivalence classes of operator paths that yield the same algebraic action at coarse scale. These equivalence classes define the RG (renormalization group) flow of the operator algebra.

Importantly:

- High-energy behavior is encoded in fine operator sequences.

- Low-energy predictions depend only on the algebraic structure of D_eff.

- UV divergences are avoided because the lattice naturally regularizes operator products.

Summary:

- EFTs arise from coarse-graining nested displacement operators, not from Lagrangians.

- Effective modes emerge algebraically, with approximate dispersion relations.

This approach provides a non-perturbative, non-functional foundation for EFTs — one that naturally avoids infinities, preserves causality, and allows new insights into how macroscopic physics emerges from fundamental operator geometry.

3.8. Microcausal Interpretation of Quantum Measurement

Measurement in standard quantum mechanics is notoriously enigmatic. The “measurement problem” stems from the idea that physical quantities do not have definite values until observed, and that wavefunction collapse must occur — seemingly instantaneously and nonlocally — during a measurement. This has led to many-worlds interpretations, decoherence theory, and epistemic models of quantum states.

In contrast, the microcausal operator framework avoids this problem entirely by treating measurement as a local causal constraint on operator sequences, not a metaphysical discontinuity. The key idea is that observables are defined by their ability to restrict allowed displacement operators on the lattice, and thus directly shape the algebraic history of the system.

Measurement as Projection on Causal Paths:

Let a quantum system evolve via a nested set of displacement operators:

ψ = Dₙ Dₙ₋₁ ... D₁ .I

A measurement imposes a projection constraint P that filters allowable operator sequences. This is not a collapse, but a selection rule:

ψ' = P ψ = P Dₙ ... D₁ I.

(44)

Here, P is a local operator that enforces microcausal consistency with the measuring apparatus — itself a part of the lattice with its own operator history.

In this way:

- Measurement is causally local, not instantaneous or global.

- The outcome is contextual, depending on how the measuring path entangles with the system path.

- No probabilistic collapse is invoked; only algebraic consistency is required.

Observer-System Interactions as Operator Coupling:

The observer is not a special agent, but a subgraph of the lattice with its own operator algebra. When the system and measuring device interact, their respective operator paths intertwine.

This leads to a coupled operator algebra, where:

- Measurement outcomes are determined by the joint structure of entangled histories.

- Correlations reflect the overlapping causal influence, not hidden variables or epistemic states.

- Repeatability follows from the stability of algebraic projection paths.

Probabilities from Operator Multiplicity:

The familiar probabilistic outcomes of quantum measurement — the Born rule — can be reinterpreted as a count of compatible operator paths. That is:

P(a) ∝ number of causal operator histories leading to outcome a

Probabilities are not fundamental, but emergent from the combinatorial structure of the operator network. This is similar in spirit to entropy but applied to measurement outcomes instead of thermodynamic ensembles.

Summary:

- Measurement is a local causal projection, not a wavefunction collapse.

- Outcomes reflect operator compatibility, not observer knowledge.

- Probabilities arise from path multiplicities, not axiomatic rules.

The microcausal interpretation provides a geometrically grounded, observer-independent explanation for quantum measurement — dissolving one of the field’s most enduring paradoxes.

3.9. Hypercomplex Gauge Structures from Causal Constraints

The algebraic formulation of quantum mechanics developed in this work not only reconstructs canonical quantum phenomena, but also reveals deeper structural consequences of causal constraints in lattice spacetime. Specifically, the macrocausal and microcausal constraints on discrete operator dynamics lead naturally to successive symmetry breakings and the emergence of hypercomplex number systems — each corresponding to different classes of gauge interactions and internal symmetries.

At the first level, macro-causality, which enforces consistent displacement ordering across extended regions of the lattice, breaks global U(1) symmetry and gives rise to a quaternionic gauge structure. This aligns with the known correspondence between quaternions and the compact form of Maxwell’s equations, suggesting that electromagnetism can be understood as the first emergent layer of gauge behavior resulting from causal alignment constraints.

At the second level, micro-causality, which restricts operator commutativity at infinitesimal spacetime separations, leads to further symmetry breaking and the emergence of an octonionic algebra. Octonions naturally accommodate non-associative structures and have long been considered candidates for encoding fermionic structure and SU(3) color dynamics due to their 7-imaginary-dimensional framework and Fano plane multiplicative relations.

Finally, when considering permutation symmetry breaking at the level of operator ordering — particularly through S₃ symmetry, which reflects the loss of full symmetry among triplets of causal sequences — we encounter the need for sedenionic structure. Unlike octonions, sedenions are not division algebras, and their rich zero-divisor structure enables encoding of causal singularities, entropy bounds, and gravitational interactions, as explored in Part II. This points to a deep structural analogy: just as quaternions are indispensable in formulating Maxwell’s equations in the continuum, sedenions are essential for constructing a consistent operator-based theory of quantum gravity.

Thus, each layer of causal constraint corresponds to a natural mathematical generalization of number systems:

• ℍ (quaternions) from macrocausality
• 𝕆 (octonions) from microcausality
• 𝕊 (sedenions) from discrete symmetry breaking (e.g., S₃)

These hypercomplex algebras are not mathematical artifacts but reflect physical realities: the topological excitations of the lattice and the operator symmetries that define the identity and interaction of elementary particles. They provide a unified mathematical language in which discrete causal dynamics, internal symmetries, and field quantization arise from a single structural foundation.

The key distinctions and structural innovations introduced by this framework, compared to the conventional QFT-based Standard Model, are summarized in the following Table 1 for conceptual clarity.

4. Discussion and Conclusions

The operator-theoretic framework presented in this work challenges the conventional foundations of quantum theory and spacetime. Rather than beginning with a continuous manifold or assuming the existence of wavefunctions, we introduced a discrete causal lattice governed by microcausality and encoded through displacement operator algebra. From this minimal and algebraic foundation, we have reconstructed many core aspects of quantum mechanics, including the uncertainty principle, de Broglie relations, quantum statistics, and entanglement — all without the need for Hilbert space postulates or probabilistic wavefunction interpretation.

A central outcome is the realization that non-commutativity of displacement operators, constrained by microcausality, gives rise to spacetime structure, temporal directionality, and observable quantum effects. This reformulation replaces the ontological role of the wavefunction with a structural ontology, where algebraic relations between operators encode all physically meaningful quantities and dynamics. The notion of measurement, often plagued by interpretational paradoxes in conventional quantum theory, is here reinterpreted as the emergence of coarse-grained operator effects within a causal network, avoiding the need for collapse postulates or observer-dependent transitions.

Another significant insight is the presence of natural Planck-scale cutoffs, which regularize the theory and preclude the divergences that afflict conventional quantum field theories. The discrete lattice structure, together with operator saturation constraints, suggests an intrinsic ultraviolet finiteness that may obviate the need for renormalization altogether. The framework further distinguishes between internal and external degrees of freedom, setting the stage for the emergence of internal symmetries and gauge interactions in more extended algebraic settings.

Conceptually, this approach also offers a new resolution to the measurement problem and the origins of thermodynamic time. The directionality of time emerges from operator non-commutativity and lattice causality rather than being imposed externally or derived statistically. Quantum indeterminacy arises not from epistemic ignorance but as a structural feature of the causal lattice's algebraic constraints.

From a methodological standpoint, this reformulation demands a rethinking of what constitutes a “quantum theory.” Here, the theory is defined not by a wavefunction and evolution equation, but by an operator algebra and causal constraints — a shift analogous to replacing geometry with algebra in the transition from classical to noncommutative geometry.

In this Part I paper, we have deliberately restricted our focus to the foundational operator algebra framework and its implications for quantum phenomena. A detailed comparative analysis with other prominent quantum gravity approaches—such as string theory, loop quantum gravity, causal set theory, and non-commutative geometry—is beyond the scope of this foundational part. These comparisons, including a critical evaluation of similarities, divergences, and possible synthesis, will be addressed comprehensively in Part II, where we extend the operator formalism to gravitational dynamics, gauge unification, and cosmological applications.

This paper has been concerned exclusively with the algebraic and quantum foundations of the operator framework. In doing so, we have deliberately deferred the inclusion of dynamical spacetime curvature, gravitational interaction, and internal symmetry structures. These are not absent from the theory, but rather emerge at a higher level of algebraic organization, which we reserve for the next stage of development.

The following Figure 3 further elaborates how the interplay between algebraic structures and causal dynamics within lattice spacetime leads to the emergence of fundamental particle generations and interactions, setting the stage for a unified framework of quantum field theory and gravity.

5. Summary and Outlook

This paper has introduced a foundational rethinking of quantum physics and spacetime, grounded in the algebra of displacement operators over a discrete causal lattice. We replaced the traditional wavefunction-based formalism with a framework built upon operator non-commutativity and microcausal constraints, treating spacetime, quantum behavior, and physical observables as emergent consequences of a deeper algebraic structure.

In Section 2, we formulated the concept of discrete causal spacetime using minimal postulates. We defined displacement operators, encoded their commutation relations, and imposed algebraic microcausality to restrict operator interactions on the lattice. This yielded a discretized framework with built-in directionality, intrinsic Planck cutoffs, and a novel operator interpretation of locality and saturation.

In Section 3, we demonstrated how canonical quantum behavior naturally arises within this structure. The uncertainty principle and de Broglie relations were derived as algebraic consequences of commutators, not postulates. Entanglement emerged from nested causal operator histories, and quantum statistics followed from the permutation symmetries of operator sequences. Crucially, the entire quantum formalism was reconstructed without invoking wavefunctions, Hilbert spaces, or collapse mechanisms. Time, measurement, and thermal behavior all found new interpretations grounded in lattice causality and algebraic structure.

These results suggest that quantum mechanics is not a fundamental theory of nature, but rather an emergent behavior arising from deeper causal-algebraic relations. The operator framework developed here offers not only mathematical elegance but also conceptual clarity — removing long-standing paradoxes and divergences that have plagued quantum theory and quantum field theory for decades.

In our recent work [53], we applied the sedenionic gauge framework to derive, from first principles, the masses of leptons, quarks, weak bosons, and the Higgs boson. The resulting theoretical values show remarkable agreement with experimental measurements. In a separate study [x54, we computed the g−2 magnetic anomalies of electrons with a precision comparable to quantum electrodynamics (QED), and with even greater accuracy for muons. These results strongly suggest that a hypercomplex algebraic approach offers a promising route toward the ultimate grand unification of all four fundamental forces. Ongoing investigations aim to extend this framework to a complete theory of quantum gravity, the details of which will be reported in future work.

Looking ahead, this work lays the foundation for a broader synthesis. In the forthcoming Part II, we extend the operator algebra framework to include:

- Spacetime curvature via nested commutators of displacement operators, leading to Einstein-like gravitational field equations without metric quantization.

- Hypercomplex algebraic extensions (quaternions, octonions, sedenions) to encode internal symmetries, fermion-boson structure, and SU(3) × SU(2) × U(1) gauge groups.

- Black hole entropy bounds, causal horizons, and singularity resolution as natural consequences of operator saturation and microcausal locality.

- Cosmological signatures, including dark energy as emergent operator pressure, CMB polarization modes beyond tensor structure, and gravitational wave spectra that distinguish this framework from standard GR and quantum field theory.

These extensions are not speculative add-ons but structural consequences of deepening the algebraic symmetry of the operator space. As such, they provide an ultraviolet-complete, ontologically minimal, and testable path forward for quantum gravity and unification.

We believe this approach reframes many of the deepest puzzles in modern physics and opens a new avenue for research at the intersection of algebra, causality, and the foundations of space and matter. In the Appendix A, we list a table of contents for our sequel manuscript on quantum gravity. Because of length considerations, it will be submitted and published separately.