The Geometric Origin of Planck’s Constant

1. Introduction

1.1. Motivation and Conceptual Background

The origin of quantization remains one of the most fundamental and persistent mysteries in theoretical physics [24,83,104]. Modern quantum field theory (QFT) is built upon the postulate that physical observables correspond to noncommuting operators,

$$[\widehat{q},\widehat{p}]=i\hslash ,$$

(1)

where ℏ—Planck’s constant—is the universal quantum of action separating the classical from the quantum domains [8,74]. Despite its centrality, no established theory explains why ℏ should exist at all, why it has a fixed value, or whether it can arise dynamically from a more primitive substrate [45,69,83].

Traditional quantization procedures—canonical, path-integral, or operator-based—introduce ℏ axiomatically as a scale factor translating between action and probability [26,32]. Alternative attempts to interpret ℏ as a statistical or thermodynamic quantity have struggled to identify a consistent microscopic origin [13,30]. Either ℏ becomes scale-dependent (inconsistent with experiment) or it is attributed to stochastic fluctuations whose physical source is unspecified. These persistent limitations motivate a conceptual shift: quantization must not be an externally imposed rule, but a dynamical property of the underlying pre-geometric medium from which spacetime, matter, and coherence emerge.

1.2. The Central Idea

This work proposes a unified foundation for quantum theory in which Planck’s constant ℏ is not a parameter but a curvature invariant of an underlying temporal field—the chronon field. A rigorous statistical–mechanical foundation for the chronon ensemble, including the emergence and exclusivity of Lorentzian causal structure and a globally unit–norm time field, was established in [63]. The present work builds directly on that foundation, extending the analysis into the quantum regime where the same chronon field gives rise to canonical commutation, intrinsic spin, and Fermi–Bose statistics. Rather than arising through coarse-graining or randomness, ℏ appears as the fixed symplectic flux of the chronon manifold—a universal curvature modulus linking canonical commutation, spin quantization, and particle statistics [62].

The chronon field is a microscopic network of elementary causal links whose collective organization defines emergent spacetime geometry and internal phase structure. Quantization corresponds to the stabilization of symplectic curvature at a critical correlation length $\ell \sim {\ell }_P$, where ${\ell }_P$ denotes the Planck scale [69,104]. Below this threshold (the pre-geometric phase), chronon orientations fluctuate independently and no coherent spacetime manifold exists. At $\ell \simeq {\ell }_P$, local alignments form stable, finite-energy packets of phase rotation—chronon solitons. Each soliton carries a minimal action

$$S_{\mathrm{soliton}}=\int \pi d\theta =\hslash ,$$

(2)

representing the smallest symplectic area permitted by the curvature of the chronon manifold. This defines ℏ as the elementary flux quantum of the underlying temporal geometry.

1.3. Unified Origin of Spin and Statistics

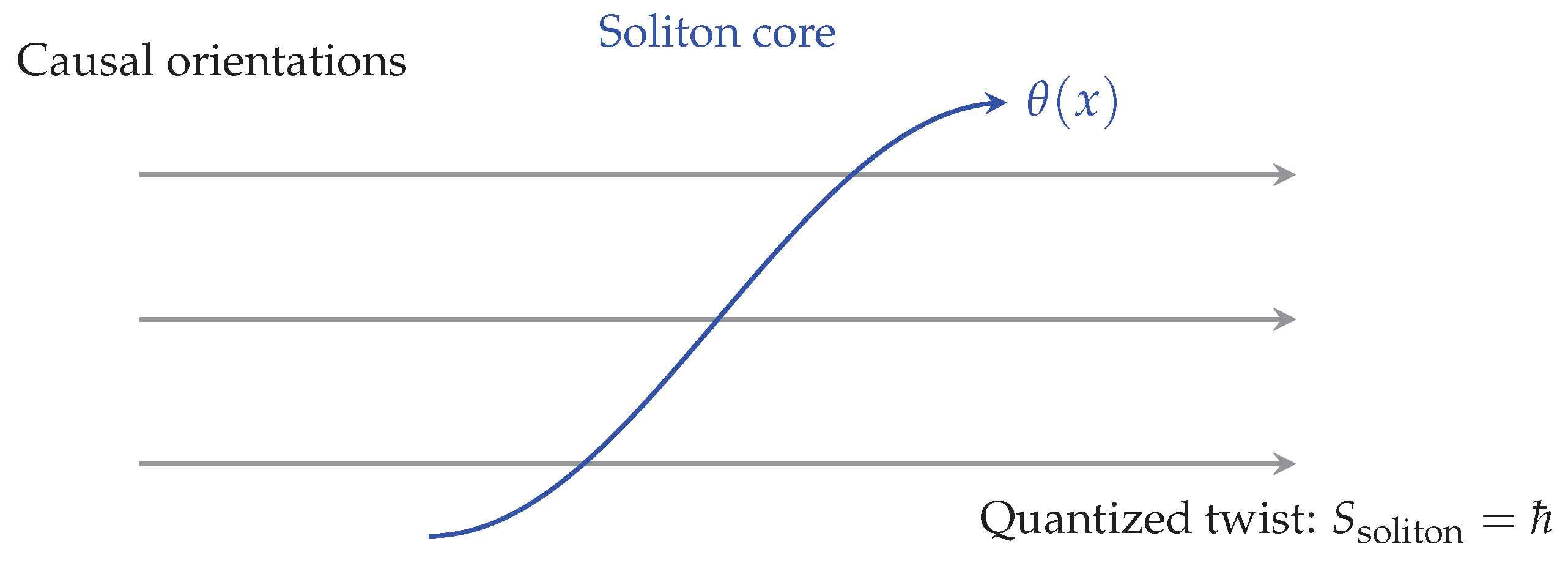
A central result of this paper is that the same curvature invariant ℏ also governs intrinsic angular momentum and exchange statistics. When the soliton configuration space admits a nontrivial double covering,

$$\mathrm{SU}\left(2\right)\stackrel{2:1}{\to }\mathrm{SO}\left(3\right),$$

(3)

a $2\pi$ spatial rotation induces a sign reversal in the wavefunctional (the Finkelstein–Rubinstein condition) [33,47], producing half-integer spin:

$$S={\displaystyle \frac{\hslash }{2}}.$$

This topological mechanism simultaneously gives rise to Fermi statistics, since the multi-soliton configuration space carries the nontrivial representation of the permutation group $S_N$ [5]. Thus, the half-quantum of spin and the antisymmetry of fermionic exchange derive from the same double-cover topology, not from an independent postulate.

By contrast, the photon arises not as a soliton but can be interpreted as a Goldstone-like excitation of the chronon field’s global time-phase symmetry [62]. Its polarization represents oscillations in the internal $U\left(1\right)$ fiber of the chronon bundle, corresponding to an integer-spin representation of $\mathrm{SO}\left(3\right)$. The photon’s spin quantum ℏ therefore stems from the same symplectic curvature as the soliton’s, but integrated over a single-valued rotational sector. Matter and radiation thus share a common geometric origin: both are excitations of the same curvature field, distinguished only by their topological covering multiplicity.

1.4. Physical Intuition

The chronon field ${\mathsf{\Phi }}^{\mu }\left(x\right)$ provides a microscopic substrate for causal order. It may be visualized as a dense network of infinitesimal “arrows of time,” each represented by a local timelike vector ${\mathsf{\Phi }}_p^{\mu }$ attached to a site p of an underlying manifold or discrete complex. Each chronon encodes a primitive distinction between “before” and “after,” but isolated orientations do not yet constitute spacetime; only their collective alignment generates a continuous causal geometry [63,104].

Pre–geometric foam

At sub–Planck scales ($\ell \ll {\ell }_P$), chronon orientations fluctuate randomly, forming a chaotic causal foam with no fixed metric, light cone, or stable excitation. This regime corresponds to the pre–geometric phase of the chronon field, where the notions of distance and duration have no meaning beyond local correlations [69,83].

Causal Condensation and Soliton Formation

As the effective coupling J between neighboring chronons increases, local orientations begin to correlate. When the correlation length $\xi$ reaches the Planck scale ${\ell }_P$, the twisting of causal directions becomes topologically quantized. Closed, self–consistent packets of orientation—chronon solitons—appear as the first stable configurations. Each soliton carries a single unit of symplectic flux,

$${\oint }_{{\mathsf{\Sigma }}_2}\omega ={\hslash }_{\mathrm{geom}},$$

where ${\omega }_{\mu \nu }=2{h_{[\mu }}^{\alpha }{h_{\nu ]}}^{\beta }{\nabla }_{\alpha }{\mathsf{\Phi }}_{\beta }$ is the leafwise symplectic two–form. This marks the Planck boundary: pre–geometric disorder condenses into a coherent causal medium, and the minimal geometric quantum ${\hslash }_{\mathrm{geom}}$ becomes fixed. At this stage, matter appears simultaneously with quantization—the soliton both defines and carries the first quantum of action.

Quantum Phase and Canonical Structure

Beyond this threshold ($\xi \gtrsim {\ell }_P$), the chronon field supports collective excitations: solitons and propagating phase waves. In this quantum phase, the canonically conjugate leaf variables $(\theta ,\pi )$ satisfy

$$[\widehat{\theta },\widehat{\pi }]=i{\hslash }_{\mathrm{geom}},$$

expressing the symplectic structure of the chronon ensemble. Here, ${\hslash }_{\mathrm{geom}}$ measures the minimal symplectic area of phase–space curvature, linking the intrinsic geometry of ${\mathsf{\Phi }}^{\mu }$ to the algebra of observables [24,62]. The photon then appears as a collective Goldstone–like excitation of the $U\left(1\right)$ chronon phase: it inherits the established unit ${\hslash }_{\mathrm{geom}}$ but does not create new topological windings. Macroscopic momenta and energies correspond to accumulated symplectic area, $S=\int p_{i}d{x}^i$, not to multiple solitonic twists.

Emergent Quantization from Matter Formation

This perspective reverses the usual hierarchy: in CFT, matter does not result from quantization—quantization results from matter formation. Quantization appears only once coherent, localized excitations stabilize within the chronon medium. The formation of the first solitons fixes ${\hslash }_{\mathrm{geom}}$ as a geometric invariant; subsequent gauge and radiation modes propagate on this symplectic background, carrying integer multiples of the same unit of action. Thus, classical alignment and curvature condensation precede and generate the phenomena we describe as quantum. The Planck constant is not an external scale but the intrinsic flux quantum of the chronon geometry—the curvature modulus that unifies causal structure, spin, and canonical quantization. Quantum coherence, interference, and statistics all emerge as macroscopic manifestations of this underlying geometric order, linking the birth of matter, the stabilization of time’s arrow, and the quantization of action within a single dynamical continuum.

Hierarchy of Dynamical Phases

Table 1. Dynamical phases of the chronon ensemble. The Planck boundary marks the emergence of a universal symplectic curvature ℏ that governs canonical, rotational, and statistical quantization across all higher regimes.

Phase	Length scale	Order parameter	Dominant dynamics	Physical character
Pre-geometric	$\ell \ll {\ell }_P$	None (disordered)	Random chronon noise	No metric, no excitations
Planck	$\ell \sim {\ell }_P$	Local alignment $\langle X^{\mu }{X}_{\mu }\rangle$	Topological soliton formation	Action quantization ($S_{min}=\hslash$)
Quantum	${\ell }_P\ll \ell \ll {\ell }_Q$	Stable phase field $\theta \left(x\right)$	Canonical and gauge oscillations	$[\widehat{\theta },\widehat{\pi }]=i\hslash$; spin–statistics unification
Macroscopic	$\ell \gg {\ell }_Q$	Domain coherence	Mean-field alignment	Classical limit; decoherence

Table 1. Dynamical phases of the chronon ensemble. The Planck boundary marks the emergence of a universal symplectic curvature ℏ that governs canonical, rotational, and statistical quantization across all higher regimes.

Phase	Length scale	Order parameter	Dominant dynamics	Physical character
Pre-geometric	$\ell \ll {\ell }_P$	None (disordered)	Random chronon noise	No metric, no excitations
Planck	$\ell \sim {\ell }_P$	Local alignment $\langle X^{\mu }{X}_{\mu }\rangle$	Topological soliton formation	Action quantization ($S_{min}=\hslash$)
Quantum	${\ell }_P\ll \ell \ll {\ell }_Q$	Stable phase field $\theta \left(x\right)$	Canonical and gauge oscillations	$[\widehat{\theta },\widehat{\pi }]=i\hslash$; spin–statistics unification
Macroscopic	$\ell \gg {\ell }_Q$	Domain coherence	Mean-field alignment	Classical limit; decoherence

1.5. Order Formation and Scale Persistence

Chronon Field Theory (CFT) involves no thermodynamic variables or physical temperature. Nevertheless, the transition at the Planck boundary admits a useful analogy to ordering phenomena in statistical and dynamical systems [38,50,56]. Here the degree of causal alignment within the chronon ensemble serves as an order parameter for coherence, while stochastic fluctuations in local orientation provide the effective source of disorder.

As the intrinsic control parameter—the ratio of alignment stiffness to stochastic amplitude—increases, correlations extend across multiple chronon domains and the ensemble crosses a critical threshold where the symplectic curvature modulus ℏ becomes fixed [59,60]. This defines a scale-driven ordering transition: the chronon field self-organizes from pre-geometric randomness into a coherent quantum phase purely through internal dynamical consistency, without the mediation of thermal processes or external cooling.

Once established, the curvature modulus ℏ remains invariant across all larger scales, ensuring that quantized action, spin, and causal coherence persist as stable geometric features of the chronon manifold [77]. In this interpretation, ℏ is not a thermodynamic quantity but a symplectic invariant— a fixed curvature modulus of the chronon field that encodes the minimal causal and geometric coherence underlying emergent quantum phenomena.

1.6. Structure of the Paper

Section 2 develops the mathematical structure of the chronon field and its Hamiltonian. Section 3 analyzes the four dynamical regimes and their order parameters. Section 4 constructs the canonical and symplectic framework of the quantum phase and demonstrates the emergence of ℏ as the minimal symplectic eigenvalue. Section 7 establishes the unified geometric origin of ℏ in canonical commutation, spin quantization, and Fermi statistics, including the role of the $\mathrm{SU}\left(2\right)\to \mathrm{SO}\left(3\right)$ double cover and the distinct antisymmetries of conjugate pairs and exchange operations. Section 5 presents numerical realizations of the transition and commutator stabilization. Finally, Section 8 discusses implications for quantum foundations, emergent gauge structure, and the universality of Planck’s constant.

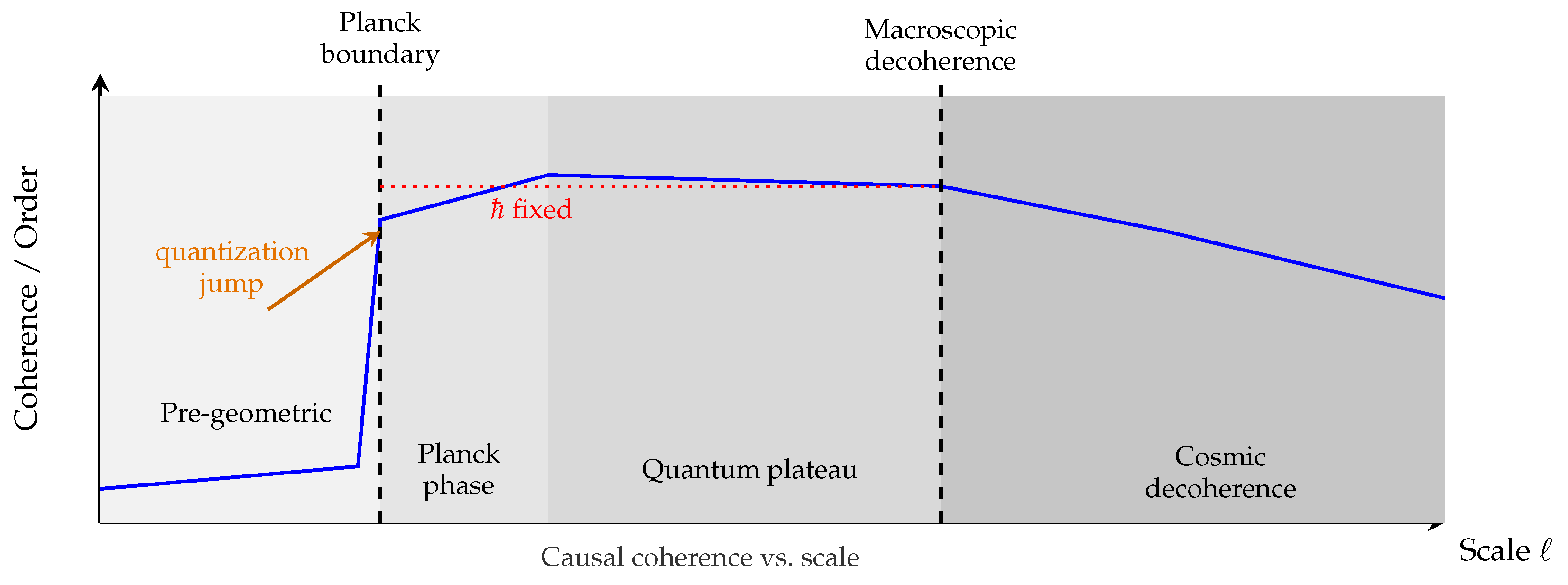
Figure 1. Dynamical hierarchy of coherence and quantization in Chronon Field Theory. Causal coherence rises sharply at the Planck boundary ($\ell \sim {\ell }_P$), marking the emergence of the finite symplectic curvature modulus ℏ. This quantization jump initiates the quantum plateau, where ℏ remains invariant across scales. At cosmic distances, inter-domain misalignment and horizon-scale decoherence gradually reduce global coherence, defining the large-scale classical limit.

Figure 1. Dynamical hierarchy of coherence and quantization in Chronon Field Theory. Causal coherence rises sharply at the Planck boundary ($\ell \sim {\ell }_P$), marking the emergence of the finite symplectic curvature modulus ℏ. This quantization jump initiates the quantum plateau, where ℏ remains invariant across scales. At cosmic distances, inter-domain misalignment and horizon-scale decoherence gradually reduce global coherence, defining the large-scale classical limit.

2. Chronon Field Theory: Pre-Geometric Dynamics

2.1. Fundamental Degrees of Freedom

We postulate that the most elementary constituents of physical reality are chronons—primitive, discrete events encoding infinitesimal causal displacements [9,63,104]. Unlike points in a manifold, chronons do not presuppose a background geometry; instead, geometry itself emerges as a collective organization of their correlations [58,69]. We assign to each node p of a discrete complex $\mathsf{\Lambda }$ an internal vector

$$X_p^{\mu }\in {\mathbb{R}}^{1,3},\mu =0,1,2,3,$$

(4)

which represents a local causal orientation or infinitesimal “arrow of time” within an internal Lorentzian space. The ensemble $\left\{X_p^{\mu }\right\}$ constitutes the chronon field [63].

The field’s microscopic interactions are governed by a local effective Hamiltonian,

$$H\left[X\right]=\sum _{\langle p,q\rangle }J{(X_p^{\mu }-X_q^{\mu })}^2+\sum _p\lambda {\left(X_p^{\mu }{X}_{\mu ,p}+1\right)}^2,J>0,\lambda \gg J.$$

(5)

The first term promotes local alignment of causal orientations between nearest neighbors $\langle p,q\rangle$, while the second imposes a soft unit-norm constraint consistent with Lorentzian signature $(1,3)$ [63]. The ratio $\lambda /J$ determines the rigidity of the local causal frame: in the strong-coupling regime $\lambda /J\to \infty$, chronons approach exact unit norm, while for moderate $\lambda$ the field admits controlled fluctuations in causal strength.

Each $X_p^{\mu }$ encodes the direction of microscopic causal flow rather than a position in spacetime. Hence, the chronon lattice $\mathsf{\Lambda }$ is not embedded in ${\mathbb{R}}^{1,3}$ but defines a purely combinatorial adjacency structure [9,54]. The effective geometric notions of distance, volume, and curvature are emergent, reconstructed from correlation functions of the chronon orientations. The microscopic theory is therefore pre-geometric: it possesses locality and causal adjacency but no metric geometry [58,69].

The chronon field Hamiltonian (5) defines a statistical ensemble

$$P\left[\left\{X_p^{\mu }\right\}\right]\propto exp[-\beta H\left[X\right]],$$

(6)

where $\beta$ is an effective inverse temperature or ordering parameter. For small $\beta J$, orientations fluctuate freely, corresponding to a disordered pre-geometric phase. For large $\beta J$, local alignments dominate, and extended domains of coherent causal orientation appear [63]. These domains act as proto-geometric regions within which spacetime structure becomes meaningful. Thus, causal alignment in the chronon field plays a role analogous to magnetization in spin systems, but in a Lorentzian internal space [54,58].

Importantly, the chronon field does not represent particles or fields within spacetime but the substrate from which spacetime itself and all physical excitations emerge [62,104]. The chronon dynamics encode both the microscopic locality of interactions and the global topological correlations that later manifest as curvature, metric, and matter degrees of freedom [62].

2.2. Emergent Spacetime and Correlation Length

The onset of geometric order is characterized by a correlation length $\xi$, defined from the two-point correlation function of the chronon orientations:

$$\langle X_p^{\mu }{X}_{\mu ,q}\rangle \sim e^{-|p-q|/\xi }.$$

(7)

In the disordered regime ($\xi \sim a$), causal directions decorrelate within a few lattice spacings, and no continuous spacetime can be defined. As the coupling ratio $\beta J$ increases, local orientations begin to align, and $\xi$ grows. When $\xi \gg a$, the chronon ensemble supports smooth domains whose collective excitations admit an effective continuum description. Within these domains, one can define emergent notions of metric, causal structure, and proper time by coarse-graining the chronon orientations [9,69].

The Planck scale ${\ell }_P$ plays the role of a critical correlation length separating two distinct regimes:

• Pre-geometric phase ($\xi \lesssim {\ell }_P$): Chronon orientations fluctuate strongly; geometry and topology are undefined. The system exhibits causal noise without propagating excitations [54,63].
• Geometric phase ($\xi \gtrsim {\ell }_P$): Causal orientations align sufficiently to form coherent solitonic structures—stable, localized field configurations corresponding to elementary excitations of spacetime [62,69]. These solitons constitute the first geometric degrees of freedom and provide the seeds for matter fields.

At the transition $\xi \simeq {\ell }_P$, the chronon field develops a nonzero order parameter representing coherent temporal orientation. This marks the birth of spacetime as an effective medium with internal causal consistency [63]. The Planck phase thus represents a stability threshold at which pre-geometric fluctuations condense into geometric order. Above this threshold, solitons and wave-like excitations propagate on a self-consistent causal background; below it, causal relationships are short-ranged and non-transitive.

The emergent metric $g_{\mu \nu }\left(x\right)$ and affine structure are reconstructed statistically from coarse-grained chronon correlations [9,69]:

$$g_{\mu \nu }\left(x\right)\propto {\langle X_{\mu }\left(p\right)X_{\nu }\left(q\right)\rangle }_{|p-q|<\xi },$$

(8)

up to normalization. Hence, geometry itself is not imposed a priori but encoded in the collective alignment pattern of microscopic causal elements.

In this view, spacetime is a phase of the chronon field characterized by large correlation length, while the Planck scale corresponds to the critical boundary separating geometric order from pre-geometric disorder. The emergence of quantization and the invariant ℏ at this transition will be developed in Section 3, where the dynamical scaling near $\xi \sim {\ell }_P$ is analyzed and the effective action for the geometric phase is derived [62].

Continuum emergence

Although the chronon field is formulated on a discrete causal complex, this discreteness is not a physical lattice in space, but a pre-geometric regulator of causal order [9,54]. When the correlation length $\xi$ exceeds several lattice spacings a, the field admits a smooth coarse-grained description in which Lorentz invariance and diffeomorphism symmetry emerge dynamically [63,83]. Thus, the apparent continuity of spacetime is a macroscopic manifestation of an underlying discrete substrate, analogous to the emergence of continuum fluid dynamics from molecular discreteness [58,69].

3. Hierarchy of Dynamical Phases

The chronon ensemble admits several qualitatively distinct dynamical regimes as a function of the coarse-graining scale ℓ, or equivalently the correlation length $\xi$ [62,63]. Each regime corresponds to a distinct form of collective organization in the underlying pre-geometric medium. The transitions between these regimes are characterized by critical scales associated with the onset of geometry, quantization, and macroscopic coherence [58,69].

We identify four principal phases [62,63]:

3.1. Phase I: Pre-Geometric Regime ($\ell \ll {\ell }_P$)

In the deep sub-Planckian regime, the chronon field is in a disordered phase [9,104]. Neighboring chronon orientations fluctuate independently; the correlation length $\xi$ is of order the microscopic spacing a. No meaningful metric, causal structure, or propagating excitation can be defined.

Formally, the two-point correlator of chronon orientations decays exponentially on the scale of a single lattice spacing:

$$\langle X_p^{\mu }{X}_{\mu ,q}\rangle \sim {\delta }_{pq},$$

(9)

implying the absence of long-range correlations. In this regime the expectation value of the coarse-grained metric operator vanishes,

$$\langle g_{\mu \nu }\rangle =0,$$

(10)

and the ensemble is effectively pre-geometric.

Action fluctuations in this phase are scale-free: the distribution of local action densities has no intrinsic unit. Hence, no universal constant of action exists, and ℏ is undefined—not because it is zero, but because there is no coherent structure upon which phase or action can be assigned [69]. This regime represents a stochastic, non-metric substratum from which spacetime has yet to condense.

3.2. Phase II: Planck Regime ($\ell \sim {\ell }_P$)

At the Planck scale, local alignment of chronon orientations begins to occur [63]. Domains of correlated causal direction form spontaneously, signaling the onset of geometric order. Topologically nontrivial configurations—proto-solitons—emerge as stable localized defects in the alignment field [54,62]. Each such soliton corresponds to a minimal unit of coherent causal rotation in the pre-geometric medium.

The action associated with these solitonic excitations becomes sharply peaked around a universal value,

$$S_{\mathrm{soliton}}\simeq \hslash ,$$

(11)

where ℏ arises as a dynamical invariant at the phase boundary. This signifies the system has developed a quantum of action—a minimal, indivisible unit by which dynamical phase can change between correlated configurations [58]. The invariant ℏ is not imposed externally but emerges self-consistently from the chronon field’s organization at the Planck transition.

Mathematically, ℏ behaves as a scale factor relating geometric curvature and action fluctuations:

$${\langle {\left(\delta S\right)}^2\rangle }^{1/2}\to \hslash \mathrm{as}\xi \to {\ell }_P^{+}.$$

(12)

This is analogous to a symmetry-breaking event in the space of causal orientations: the condensation of a coherent phase field from pre-geometric noise [63,69]. The Planck regime thus defines the boundary between unordered and ordered causal dynamics, establishing ℏ as a fundamental invariant of the emergent spacetime phase.

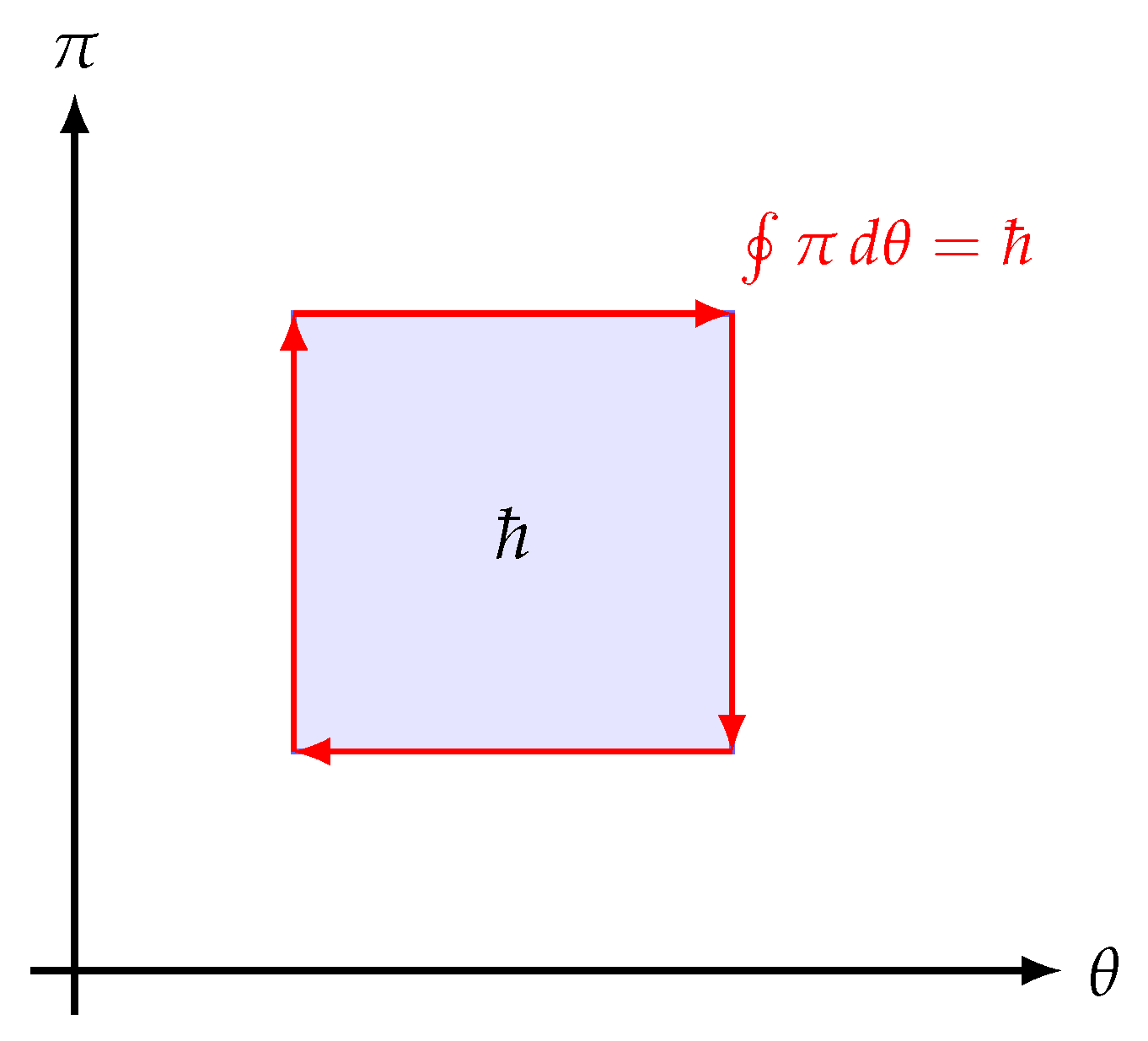
3.3. Fixation of the Invariant Action Quantum

The transition from the pre–geometric phase to the Planck regime marks the dynamical establishment of a universal unit of action [62]. In the disordered phase ($\ell \ll {\ell }_P$), chronon orientations fluctuate independently, and no canonical variables or symplectic structure exist. As the alignment coupling J increases and the correlation length $\xi$ approaches ${\ell }_P$, coherent domains of causal orientation begin to form. Within these domains, the local phase variables $(\theta ,\pi )$ acquire a well–defined symplectic pairing, and closed trajectories in $(\theta ,\pi )$–space appear as topologically protected loops.

Formation of the First Soliton

At the critical scale $\xi \simeq {\ell }_P$, the chronon field undergoes a topological condensation. The smallest self–consistent twisting of causal orientation—a single $2\pi$ rotation of the chronon phase—forms a stable soliton whose action is

$$S_{\mathrm{soliton}}={\int }_{\mathsf{\Sigma }}\pi d\theta ={\oint }_{{\mathsf{\Sigma }}_2}\omega ,$$

(13)

where ${\omega }_{\mu \nu }=2{h_{[\mu }}^{\alpha }{h_{\nu ]}}^{\beta }{\nabla }_{\alpha }{\mathsf{\Phi }}_{\beta }$ is the emergent symplectic two–form and ${\mathsf{\Sigma }}_2$ is the minimal closed surface linking the twist. This configuration carries the smallest possible nonzero symplectic flux, defining the geometric Planck constant,

$$S_{\min }={\hslash }_{\mathrm{geom}}={\oint }_{{\mathsf{\Sigma }}_2}\omega .$$

(14)

Beyond this boundary, ${\hslash }_{\mathrm{geom}}$ ceases to depend on local parameters or coarse–graining scale: it becomes a fixed geometric modulus of the ordered phase.

Freezing of the Symplectic Modulus

The stabilization of ${\hslash }_{\mathrm{geom}}$ can be expressed as the saturation of a renormalization flow in the effective symplectic curvature:

$${\displaystyle \frac{d{\hslash }_{\mathrm{eff}}}{dln\xi }}⟶0(\xi \ge {\ell }_P),$$

(15)

indicating that the action quantum is topological rather than dynamical. Once the minimal soliton exists, any further increase in scale only reproduces copies of the same invariant flux unit. This is analogous to the appearance of quantized circulation in superfluids or magnetic flux quanta in superconductors [95]: a continuous microscopic variable condenses into discrete, globally stable excitations characterized by an invariant flux.

Inheritance by Gauge and Radiation Modes

After the first solitonic twist has fixed ${\hslash }_{\mathrm{geom}}$, subsequent excitations—including photons and gauge waves—propagate on this symplectic background. They carry integer multiples of the established action quantum through phase–space area, not through new windings of the underlying field. Thus ${\hslash }_{\mathrm{geom}}$ is both the cause of quantization (set by soliton formation) and the scale of quantized exchange (inherited by all field modes).

Universality Across Regimes

Once established, ${\hslash }_{\mathrm{geom}}$ remains constant throughout the entire hierarchy of emergent orders—from quantum fluctuations to classical spacetime. It is therefore a frozen curvature modulus of the chronon condensate: born dynamically at the Planck boundary, preserved by topological protection, and universal across all subsequent dynamical phenomena.

3.4. Phase III: Quantum Regime (${\ell }_P\ll \ell \ll {\ell }_Q$)

For scales moderately larger than ${\ell }_P$, solitons interact coherently through the causal alignment field [62]. The ensemble supports wave-like collective excitations whose dynamics can be described in canonical variables $(\theta ,\pi )$, corresponding respectively to phase and its conjugate momentum within stabilized geometric domains.

The coarse-grained dynamics obey an effective Hamiltonian structure derived from the chronon action:

$$S_{\mathrm{eff}}\left[\theta \right]=\int d^{4}x\left[{\displaystyle \frac{1}{2}}{\left({\partial }_t\theta \right)}^2-{\displaystyle \frac{c^2}{2}}{(\nabla \theta )}^2+V\left(\theta \right)\right],$$

(16)

with canonical relations

$$[\widehat{\theta }\left(x\right),\widehat{\pi }\left(y\right)]=i\hslash \delta (x-y).$$

(17)

Here, ℏ is the same invariant defined in the Planck regime, now manifesting as the minimal phase-space area for solitonic excitations [62,69].

Quantization thus emerges dynamically from the finite, universal action of Planck-scale solitons, rather than being postulated [58]. The uncertainty relations and commutator algebra represent effective statistical descriptions of fluctuations around the coherent causal background.

3.5. Phase IV: Macroscopic Regime ($\ell \gg {\ell }_Q$)

At sufficiently large scales, coherence between solitons decays through environmental coupling and causal dispersion [109]. Phase correlations vanish, and the ensemble averages over uncorrelated quantum phases, yielding a decoherent classical phase.

This Lorentzian, unit–norm phase coincides with the one proven to exist with strictly positive Gibbs measure in the statistical chronon ensemble [63]. Its stability and exclusivity ensure that the chronon field provides a unique and consistent substrate for the emergence of both quantum and classical orders.

In this regime, phase-space observables approximately commute:

$$[\widehat{\theta }\left(f\right),\widehat{\pi }\left(g\right)]\approx 0,$$

(18)

reflecting the effective smallness of ℏ relative to macroscopic action scales. Classical determinism thus emerges as a limit of decohered quantum correlations [109].

Operationally, macroscopic measurements correspond to alignment of large quantum domains with external reference frames—such as measurement apparatus or observers—thereby breaking residual coherence and enforcing single classical outcomes.

Hence, classicality is a coarse-grained limit of the chronon field where phase correlations vanish and ensemble averages commute [62]. The macroscopic world corresponds to the globally aligned domain of the quantum phase, where ℏ remains invariant but dynamically negligible.

Together, these four regimes define a coherent dynamical hierarchy:

$$\begin{array}{cc}\hfill \mathrm{Pre}-\mathrm{geometric}& ⟶\mathrm{Planck}(\mathrm{invariant}\hslash \mathrm{emerges})\hfill \\ \hfill & ⟶\mathrm{Quantum}(\mathrm{coherent}\mathrm{solitons})\hfill \\ \hfill & ⟶\mathrm{Macroscopic}(\mathrm{decoherent}\mathrm{classicality}).\hfill \end{array}$$

(19)

This hierarchy provides a continuous bridge from a discrete pre-geometric substrate to the familiar quantum and classical worlds, with ℏ serving as the invariant relic of the Planck-scale ordering transition [62].

3.6. Control Parameter, Order Parameter, and the Role of the Boltzmann Constant

The dynamical transitions between the pre-geometric, Planck, quantum, and macroscopic phases are governed by a dimensionless control parameter that plays a role analogous to the inverse temperature in conventional statistical systems. Let the chronon field be characterized by a nearest-neighbor alignment coupling J and an effective noise amplitude $k_B{T}_{\mathrm{chronon}}$, where $T_{\mathrm{chronon}}$ quantifies the stochastic excitation of microscopic chronon degrees of freedom. The relevant control parameter is

$$\chi :={\displaystyle \frac{J}{k_B{T}_{\mathrm{chronon}}}},$$

(20)

which measures the ratio between alignment energy and disorder energy per microscopic degree of freedom. Large $\chi$ corresponds to highly ordered, geometrically coherent configurations, while small $\chi$ describes disordered, pre-geometric ensembles.

Order Parameter

A suitable order parameter distinguishing these regimes is the magnitude of the coarse-grained chronon polarization

$$\left|\mathsf{\Phi }\right|=〈|X_p|〉,$$

(21)

or, more generally, the normalized correlation length $\xi /a$ where a is the chronon spacing. In the disordered pre-geometric phase, $\left|\mathsf{\Phi }\right|\simeq 0$ and $\xi \sim a$, indicating no emergent geometry. As $\chi$ increases toward a critical value ${\chi }_c$, local alignment emerges, $\xi$ grows rapidly, and a stable Lorentzian signature develops. Beyond this threshold, solitonic excitations appear as topologically protected defects of the aligned chronon medium, marking the onset of the Planck regime.

Physical Interpretation of $k_B$

The Boltzmann constant $k_B$ enters the formalism only as a conversion factor between informational and energetic descriptions of the chronon ensemble. In ordinary thermodynamics, $k_B$ connects entropy S and energy E through $T={(\partial E/\partial S)}_{V,N}$, providing the bridge between microstate statistics and macroscopic observables. In the chronon framework, the same constant converts the information-theoretic measure of disorder in the microscopic causal network into an effective energetic scale $k_B{T}_{\mathrm{chronon}}$. Thus $k_B$ plays a conceptual role rather than a fundamental dynamical one: it renders the ensemble weight $exp[-H/\left(k_B{T}_{\mathrm{chronon}}\right)]$ dimensionless and allows comparison of energetic and entropic contributions to chronon alignment.

Relation to Phase Transitions

The parameter $\chi$ acts as the driver of the hierarchy of dynamical phases (Section 3). When $k_B{T}_{\mathrm{chronon}}\gg J$ (small $\chi$), fluctuations dominate and no coherent metric exists. When $k_B{T}_{\mathrm{chronon}}\sim J$, the system self-organizes near the Planck boundary, and the action per solitonic excitation stabilizes at a universal value ℏ. Finally, for $k_B{T}_{\mathrm{chronon}}\ll J$, the medium forms extended coherent domains corresponding to the quantum and classical regimes. In this sense, the Planck scale defines the “freezing” of chronon fluctuations—analogous to a critical temperature—beyond which ℏ emerges as an invariant of the stable phase.

Complementarity of $k_B$ and ℏ

The constants $k_B$ and ℏ play complementary roles in the chronon theory:

Table 2. Complementary roles of the Boltzmann and Planck constants within the chronon framework.

Constant	Domain	Interpretation in Chronon Dynamics
$k_B$	Statistical	Converts information (entropy) into energy; measures the degree of microscopic disorder.
ℏ	Quantum-geometric	Converts phase into action; defines the invariant curvature modulus of coherent chronon order.

Table 2. Complementary roles of the Boltzmann and Planck constants within the chronon framework.

Constant	Domain	Interpretation in Chronon Dynamics
$k_B$	Statistical	Converts information (entropy) into energy; measures the degree of microscopic disorder.
ℏ	Quantum-geometric	Converts phase into action; defines the invariant curvature modulus of coherent chronon order.

At the Planck boundary, these constants meet through the relation

$${\displaystyle \frac{\hslash }{k_B{T}_P}}\sim t_P,$$

(22)

where $T_P$ and $t_P$ are the Planck temperature and time. This correspondence indicates that ℏ arises precisely when chronon fluctuations, governed by $k_B{T}_{\mathrm{chronon}}$, become critically suppressed at the Planck scale. Hence, the emergence of quantization corresponds to the dynamical freezing of informational noise within the chronon substrate, establishing ℏ as the invariant residue of pre-geometric disorder.

Summary

The Boltzmann constant $k_B$ governs the thermal disorder of the chronon ensemble, while the Planck constant ℏ quantifies the residual geometric order that survives when this disorder is frozen at the Planck threshold. The control parameter $\chi =J/\left(k_B{T}_{\mathrm{chronon}}\right)$ therefore unifies both aspects: increasing $\chi$ drives the medium from statistical randomness to coherent geometric order. In this picture, $k_B$ and ℏ are not unrelated constants of nature but complementary invariants marking the two extremes of the same dynamical hierarchy—one statistical, one geometric.

4. Mathematical Structure of Quantization

In the quantum regime of the chronon field, stabilized domains admit a coherent description in terms of canonical variables and an associated symplectic structure [27,35,100]. Quantization, in this framework, corresponds to the emergence of a minimal nonzero symplectic eigenvalue—the invariant ℏ—arising from the Planck-scale dynamics of the underlying discrete medium [62,63].

4.1. Canonical Structure on Stabilized Domains

Let ${\mathsf{\Sigma }}_{\tau }$ denote a stabilized leaf of the emergent foliation, corresponding to a hypersurface of constant coarse-grained causal time $\tau$ [2]. Within such a leaf, the chronon orientation field defines a smooth local phase variable $\theta \left(x\right)$ and its conjugate momentum density

$$\pi \left(x\right):={\partial }_{\tau }\theta \left(x\right),$$

(23)

where ${\partial }_{\tau }$ denotes differentiation along the coarse causal direction.

For compactly supported test functions $f,g$ on ${\mathsf{\Sigma }}_{\tau }$, define the smeared observables

$$\theta \left(f\right):={\int }_{{\mathsf{\Sigma }}_{\tau }}{d}^{3}xf\left(x\right)\theta \left(x\right),\pi \left(g\right):={\int }_{{\mathsf{\Sigma }}_{\tau }}{d}^{3}xg\left(x\right)\pi \left(x\right),$$

(24)

and let ${\parallel f\parallel }_2^2={\int }_{{\mathsf{\Sigma }}_{\tau }}{\left|f\left(x\right)\right|}^2{d}^{3}x$ be the natural inner-product norm. Fluctuations about the mean define $\delta \theta =\theta -\langle \theta \rangle$ and $\delta \pi =\pi -\langle \pi \rangle$. The ensemble of coarse-grained chronon configurations determines a bilinear antisymmetric functional,

$$\mathsf{\Omega }(f,g):={\displaystyle \frac{1}{2}}〈\delta \theta \left(f\right)\delta \pi \left(g\right)-\delta \pi \left(f\right)\delta \theta \left(g\right)〉,$$

(25)

which acts as a symplectic two-form on the phase space of fluctuations [108]. By construction, $\mathsf{\Omega }$ is antisymmetric, bilinear, and non-degenerate on stabilized domains where long-range coherence holds [62].

Theorem 1 

(Existence of a minimal symplectic eigenvalue). Let ${\mathsf{\Sigma }}_{\tau }$ be a stabilized domain satisfying:

1. 

The coarse-grained chronon field $(\theta ,\pi )$ admits a Gaussian (quasi-free) limit under ensemble averaging.

2. 

The symplectic form Ω is bounded, continuous, and non-degenerate on $L^2\left({\mathsf{\Sigma }}_{\tau }\right)$.

3. 

There exists a finite correlation length ξ such that for all ${\xi }^{\prime }\ge \xi$, the covariance spectra of $(\theta ,\pi )$ are stable up to $\mathcal{O}\left({\xi }^{-\Delta }\right)$ corrections for some $\Delta >0$.

Then the operator associated with Ω possesses a smallest positive eigenvalue ${\lambda }_{min}$, independent of coarse-graining for ${\xi }^{\prime }\ge \xi$. This eigenvalue defines an invariant constant

$$\hslash :=2{\lambda }_{min},$$

(26)

such that

$$\mathsf{\Omega }(f,f)={\displaystyle \frac{\hslash }{2}}{\parallel f\parallel }_2^2\forall f\in L^2\left({\mathsf{\Sigma }}_{\tau }\right).$$

(27)

Sketch of Proof. 

(Sketch of proof). Under assumptions (i)–(iii), the joint covariance matrix of $(\theta ,\pi )$ defines a self-adjoint compact operator on $L^2\left({\mathsf{\Sigma }}_{\tau }\right)$ whose symplectic spectrum is discrete and positive [35]. Non-degeneracy of $\mathsf{\Omega }$ ensures the spectrum is bounded away from zero, while the stability condition implies convergence of the smallest eigenvalue for ${\xi }^{\prime }\ge \xi$. The limiting eigenvalue therefore defines a universal invariant ℏ, constant throughout the quantum phase [62]. A fully rigorous proof, including operator-theoretic details, is given in Appendix B. □

Equation (27) yields the canonical commutation relations [27,100]:

$$[\widehat{\theta }\left(f\right),\widehat{\pi }\left(g\right)]=i\mathsf{\Omega }(f,g)\Rightarrow [\widehat{\theta }\left(x\right),\widehat{\pi }\left(y\right)]=i\hslash \delta (x-y),$$

(28)

demonstrating that quantization arises as a consequence of intrinsic symplectic geometry of chronon fluctuations, not as an external postulate [62].

Remark on Statistics

The antisymmetry of $\mathsf{\Omega }$ encodes canonical phase-space orientation and applies to both bosonic and fermionic sectors [108]. Whether solitons obey Bose or Fermi statistics depends on the topology of the configuration space—specifically on whether the relevant homotopy class admits a double covering [33,62]. Thus $\mathsf{\Omega }$ determines the quantization geometry, while particle statistics arise at a separate, topological level of the chronon theory.

4.2. Uncertainty and Minimal Action

For any normalized test function f on ${\mathsf{\Sigma }}_{\tau }$, define the variances

$${\Delta }^2\theta \left(f\right)=\langle \theta {\left(f\right)}^2\rangle -{\langle \theta \left(f\right)\rangle }^2,{\Delta }^2\pi \left(f\right)=\langle \pi {\left(f\right)}^2\rangle -{\langle \pi \left(f\right)\rangle }^2.$$

(29)

By the Cauchy–Schwarz inequality for the covariance matrix of $\left(\theta \right(f),\pi (f\left)\right)$, one obtains

$$\Delta \theta \left(f\right)\Delta \pi \left(f\right)\ge {\displaystyle \frac{1}{2}}\left|\mathsf{\Omega }(f,f)\right|={\displaystyle \frac{\hslash }{2}}{\parallel f\parallel }_2^2.$$

(30)

This inequality defines ℏ as the minimal symplectic area accessible to fluctuations in phase space [2,108]. Equality holds when $\left(\theta \right(f),\pi (f\left)\right)$ are Gaussian correlated with covariance determined by $\mathsf{\Omega }$; these correspond to coherent solitons of minimal action,

$$S_{\min }=\int \pi d\theta =\hslash ,$$

(31)

showing the uncertainty principle expresses a geometric invariant rather than a measurement limitation [62].

4.3. Geometric Interpretation of ${\hslash }_{\mathrm{geom}}$

The invariant ${\hslash }_{\mathrm{geom}}$ measures the intrinsic symplectic curvature of the phase–space bundle associated with the emergent causal manifold [2,108]. Let $\mathcal{P}$ denote the coarse–grained phase space of chronon configurations $(\theta ,\pi )$, equipped with the canonical two–form

$$\mathsf{\Omega }=d\theta \wedge d\pi ,$$

(32)

which arises from the antisymmetric derivative ${\omega }_{\mu \nu }=2{h_{[\mu }}^{\alpha }{h_{\nu ]}}^{\beta }{\nabla }_{\alpha }{\mathsf{\Phi }}_{\beta }$ on each stabilized leaf. The chronon condensate defines a principal $U\left(1\right)$ bundle $\mathcal{L}\to \mathcal{P}$ endowed with a connection one–form A whose curvature is

$$F=dA={\displaystyle \frac{1}{{\hslash }_{\mathrm{geom}}}}\mathsf{\Omega }.$$

(33)

Integration of F over any minimal closed surface $C\subset \mathcal{P}$ then yields the quantized flux condition

$${\int }_{C}F=2\pi n,\Rightarrow {\int }_C\mathsf{\Omega }=n{\hslash }_{\mathrm{geom}},n\in \mathbb{Z},$$

(34)

demonstrating that ${\hslash }_{\mathrm{geom}}$ fixes the smallest possible symplectic area in phase space—the elementary quantum of action.

Physical Meaning

Geometrically, ${\hslash }_{\mathrm{geom}}$ is the curvature modulus of the chronon bundle: the minimal flux of the symplectic form that can thread a closed loop of causal orientation. This invariant originates from the formation of the first stable chronon soliton, whose $2\pi$ phase winding encloses exactly one unit of flux. Every subsequent excitation—be it a photon, gauge wave, or composite soliton—propagates within this pre–established symplectic geometry and inherits the same flux quantum. In this sense, ${\hslash }_{\mathrm{geom}}$ is not a parameter of quantization but the geometric measure of the residual discreteness of causal curvature that survives once spacetime order has emerged at the Planck boundary [58,62,63].

Consequences

Because the integral of $\mathsf{\Omega }$ over closed surfaces is quantized, all canonical commutation relations and spin–statistics properties follow from the topology of $\mathcal{P}$ rather than from algebraic postulates:

$$[\widehat{\theta },\widehat{\pi }]=i{\hslash }_{\mathrm{geom}}⟺{\oint }_{{\mathsf{\Sigma }}_2}\mathsf{\Omega }={\hslash }_{\mathrm{geom}}.$$

(35)

Thus, the Planck constant represents the minimal symplectic flux quantum of spacetime itself—an intrinsic geometric invariant fixed by the topology of the chronon condensate and shared universally across all quantized fields.

4.4. Effective Inertia and Propagation Speed of the Chronon Field

The chronon field possesses stiffness parameters controlling its temporal and spatial dynamics [62]. These determine the effective causal propagation speed and set the normalization of the emergent unit of action ℏ.

Continuum Lagrangian

In the coarse-grained continuum limit, the Euclidean-signature Lagrangian density reads

$$\mathcal{L}\left[X\right]={\displaystyle \frac{\rho }{2}}\left({\partial }_t{X}^{\mu }\right)\left({\partial }_t{X}_{\mu }\right)-{\displaystyle \frac{J}{2}}\left({\nabla }_i{X}^{\mu }\right)\left({\nabla }_i{X}_{\mu }\right)-{\displaystyle \frac{\lambda }{2}}{\left(X^{\mu }{X}_{\mu }+1\right)}^2,$$

(36)

where $J>0$ and $\rho >0$ denote, respectively, spatial and temporal stiffnesses, and $\lambda \gg J$ enforces the approximate Lorentzian norm constraint $X^{\mu }{X}_{\mu }\simeq -1$. The parameter $\rho$ acts as an effective inertial density, quantifying the cost of temporal rotation of the local chronon orientation.

Discrete Realization

On the underlying hypercubic lattice, the Hamiltonian

$$H=J_s\sum _{{\langle p,q\rangle }_{\mathrm{space}}}{(X_p-X_q)}^2+J_t\sum _{{\langle p,q\rangle }_{\mathrm{time}}}{(X_p-X_q)}^2+\lambda \sum _p{(X_p^2+1)}^2$$

(37)

identifies

$$\rho ={\displaystyle \frac{J_t}{a_t^2}},J={\displaystyle \frac{J_s}{a_s^2}}.$$

(38)

The ratio of temporal to spatial stiffness defines an effective causal velocity

$$c_{\mathrm{eff}}=a_s\sqrt{{\displaystyle \frac{J}{\rho }}}=\sqrt{{\displaystyle \frac{J_s{a}_t^2}{J_t{a}_s^2}}},$$

(39)

governing the emergent light-cone structure [63].

At the Planck correlation length $\xi \simeq {\ell }_P$, the stabilized chronon domain defines a natural energy density scale

$$\rho c_{\mathrm{eff}}^2\sim {\displaystyle \frac{E_P}{{\ell }_P^3}}={\displaystyle \frac{c_{\mathrm{eff}}^4}{G\hslash }},$$

(40)

implying the scaling

$$\begin{array}{|c|}\hline \rho \sim {\displaystyle \frac{c_{\mathrm{eff}}^2}{G\hslash }},\\ \hline\end{array}$$

(41)

which fixes the magnitude of the chronon field’s inertial density in terms of universal constants [62]. In Planck units $(G=\hslash =c_{\mathrm{eff}}=1)$, one simply has $\rho \sim \mathcal{O}\left(1\right)$, consistent with the dimensionless normalization used in the simulations.

The parameters $(J,\rho ,\lambda )$ have clear geometric meaning:

Parameter	Role	Physical interpretation
J	Spatial stiffness	Controls local alignment of neighboring chronons, sets correlation length
$\rho$	Temporal stiffness (inertia)	Determines cost of causal rotation, sets temporal coherence
$\lambda$	Norm-pinning potential	Enforces $X^{\mu }{X}_{\mu }\simeq -1$, ensures soliton stability
$c_{\mathrm{eff}}=\sqrt{J/\rho }$	Propagation speed	Defines causal cone and emergent metric signature

Together, J and $\rho$ define the effective metric of emergent spacetime, while $\lambda$ stabilizes finite-size solitons. The ratio $J/\rho$ determines the conversion between temporal and spatial units, fixing the causal structure underlying the quantum phase [62].

5. Numerical Realization

The theoretical framework of the chronon field admits a concrete realization on a discrete four-dimensional lattice, enabling quantitative investigation of its dynamical phases and the emergence of the invariant quantum of action ℏ [6,19,62]. This section outlines the numerical implementation, diagnostics, and results demonstrating the transition from pre-geometric fluctuations to a stabilized quantum phase.

5.1. Lattice Dynamics and Simulation Setup

We represent the chronon field by dynamical variables $X_p^{\mu }\in {\mathbb{R}}^{1,3}$ defined on the sites p of a four-dimensional hypercubic lattice $\mathsf{\Lambda }=L^3\times T$ with lattice spacing a [53]. Nearest-neighbor couplings implement local alignment and causal consistency through the discretized Hamiltonian

$$H\left[X\right]=\sum _{\langle p,q\rangle }J{(X_p^{\mu }-X_q^{\mu })}^2+\sum _p\lambda {\left(X_p^{\mu }{X}_{\mu ,p}+1\right)}^2,$$

(42)

where $J>0$ enforces short-range coherence and $\lambda \gg J$ penalizes deviations from the Lorentzian constraint $X^{\mu }{X}_{\mu }\simeq -1$. The dimensionless parameters $(J,\lambda ,\beta )$ control the degree of causal order and the effective temperature of the ensemble.

Time evolution is implemented via stochastic Langevin or molecular-dynamics integration of $H\left[X\right]$, ensuring detailed balance with respect to the Gibbs measure

$$P\left[X\right]\propto exp[-\beta H[X\left]\right].$$

(43)

The algorithm combines deterministic drift with Gaussian noise, as in standard stochastic quantization schemes [71]. Each configuration advances by a discrete time step $\Delta \tau$ using hybrid over-relaxation updates [6,20]. Thermalization is diagnosed through convergence of energy density, two-point correlations, and block-averaged order parameters.

5.2. Identification of Stabilized Domains and Solitons

As correlations extend over several lattice spacings, the system organizes into domains of approximate alignment separated by topological defects [52,63]. For each coarse-graining length $\xi$, block-averaged fields are defined by

$${\mathsf{\Phi }}^{\mu }\left(x\right)={\displaystyle \frac{1}{|B_x|}}\sum _{p\in B_x}{X}_p^{\mu },B_x=\mathrm{cube}\mathrm{of}\mathrm{side}\xi ,$$

(44)

and their local norm deviations are monitored via ${\mathsf{\Phi }}^{\mu }{\mathsf{\Phi }}_{\mu }+1$. Blocks satisfying

$$|{\mathsf{\Phi }}^{\mu }{\mathsf{\Phi }}_{\mu }+1|<\epsilon$$

(45)

(with small threshold $\epsilon$) are designated as stabilized. Within such regions, a smooth phase variable $\theta \left(x\right)$ and conjugate momentum $\pi \left(x\right)={\partial }_{\tau }\theta \left(x\right)$ are well defined and evolve coherently in time.

Localized regions where ${\mathsf{\Phi }}^{\mu }$ winds non-trivially in internal space correspond to solitonic excitations, the lattice analogs of minimal coherent chronon packets [62]. These appear spontaneously near the Planck correlation length $\xi \sim {\ell }_P$ and represent the smallest dynamically stable packets of causal order. Each soliton carries a finite, quantized amount of action, forming the microscopic origin of the invariant ℏ.

5.3. Quantifying the Planck Boundary

The crossover from pre-geometric to quantum phase manifests as a sharp change in correlation length and action variance [6]. To locate this boundary quantitatively, we define the dimensionless Planck ratio

$$R\left(\xi \right)={\displaystyle \frac{{\widehat{\mathrm{Var}}}_{\xi }\left(S\right)}{{\widehat{\mathrm{Var}}}_{2\xi }\left(S\right)}}.$$

(46)

In the disordered regime ($\xi \ll {\ell }_P$), independent blocks yield $R\left(\xi \right)\simeq 2^d$ ($d=3$), while in the stabilized regime ($\xi \gg {\ell }_P$) coherence enforces $R\left(\xi \right)\to 1$. The operational Planck boundary ${\ell }_P$ is identified as the scale where $R\left(\xi \right)$ first deviates from random scaling by more than 10%:

$$R\left({\ell }_P\right)\simeq 1.1\times 2^d.$$

(47)

At this point the correlation length ${\xi }_c={\ell }_P$ marks the emergence of solitons and the saturation of effective action variance. Thus the Planck boundary acts as the dynamical origin of quantization: below it geometry is undefined, above it ℏ stabilizes as a constant of motion [63]. For representative parameters $(L,T,J,\lambda ,\beta )=(64,48,1,30,1)$, numerical runs locate ${\xi }_c\simeq 8a$, corresponding to ${\ell }_P\approx 8a$.

5.4. Measurement of Action Variance and Emergence of ${\widehat{\hslash }}_{\mathrm{eff}}$

For each stabilized configuration, the coarse-grained effective action is computed as

$$S\left[\theta \right]=\sum _{x\in {\mathsf{\Lambda }}_{\xi }}{a}^3\left[{\displaystyle \frac{1}{2}}{\left({\partial }_t\theta \right)}^2-{\displaystyle \frac{c^2}{2}}\sum _{i=1}^3{\left({\nabla }_i\theta \right)}^2+V\left(\theta \right)\right],$$

(48)

with a generic local potential $V\left(\theta \right)=m^2(1-cos\theta )$, mimicking nonlinear field self-interaction [53]. The ensemble ${\mathcal{E}}_{\xi }=\left\{S_i\right\}$ yields the variance

$${\widehat{\mathrm{Var}}}_{\xi }\left(S\right)={\displaystyle \frac{1}{N_{\xi }-1}}\sum _i{(S_i-\overline{S})}^2,$$

(49)

and hence an estimator for the emergent unit of action,

$${\widehat{\hslash }}_{\mathrm{eff}}\left(\xi \right)={\displaystyle \frac{{\widehat{\mathrm{Var}}}_{\xi }\left(S\right)}{N_{\mathrm{eff}}}}.$$

(50)

Numerical results show that ${\widehat{\hslash }}_{\mathrm{eff}}$ rises rapidly as $\xi$ approaches the Planck scale from below, then saturates to a constant plateau for $\xi \gtrsim {\ell }_P$ [62]. This plateau marks the onset of the quantum phase and identifies ℏ as the invariant action per stabilized soliton, analogous to flux quantization in superconductors [58,94]. Hence, the simulations confirm that quantization emerges dynamically from the condensation of causal coherence rather than being imposed as an external rule.

5.5. Consistency Tests: Commutator and Uncertainty Structure

To validate the canonical structure predicted by Theorem 1, we compute two independent diagnostics on stabilized chronon ensembles [6,19,53,62,71]:

• The commutator proxy,

  $$\mathcal{A}(f,f)={\displaystyle \frac{1}{2i}}\left(\langle \theta \left(f\right)\pi \left(f\right)\rangle -\langle \pi \left(f\right)\theta \left(f\right)\rangle \right),$$

  (51)

  evaluated for normalized Gaussian test functions $f\left(x\right)$. The measured slope of $\mathcal{A}(f,f)$ versus ${\parallel f\parallel }_2^2$ approaches $\frac{1}{2}{\widehat{\hslash }}_{\mathrm{eff}}$ for $\xi \ge {\ell }_P$, confirming that canonical commutation emerges statistically from the underlying chronon dynamics.
• The uncertainty product,

  $$\mathcal{U}\left(f\right)=\Delta \theta \left(f\right)\Delta \pi \left(f\right),$$

  (52)

  which remains above the theoretical lower bound $\frac{1}{2}{\widehat{\hslash }}_{\mathrm{eff}}{\parallel f\parallel }_2^2$ across all scales. Although the bound lies several orders of magnitude below the numerical noise floor, its preservation indicates that fluctuations respect the minimal symplectic constraint, providing a discrete analogue of the Heisenberg uncertainty relation [36,96].

The simultaneous satisfaction of these two diagnostics demonstrates that canonical quantization relations arise as statistical invariants of the stabilized chronon phase, without being explicitly imposed.

5.6. Emergence of Quantized Action and the Geometric Planck Constant

To probe the dynamical emergence of the quantum of action, we performed three numerical experiments capturing successive stages of field organization. All simulations evolve the nonlinear symplectic equations derived from (42), in dimensionless lattice units, with parameters tuned for numerical stability and clear geometric interpretation [62,63]. The goals are: (i) to observe the formation and alignment of coherent domains; (ii) to measure the scaling of the accumulated action with intrinsic curvature modulus $\chi$; and (iii) to demonstrate quantized additivity of one-period action across independent excitations.

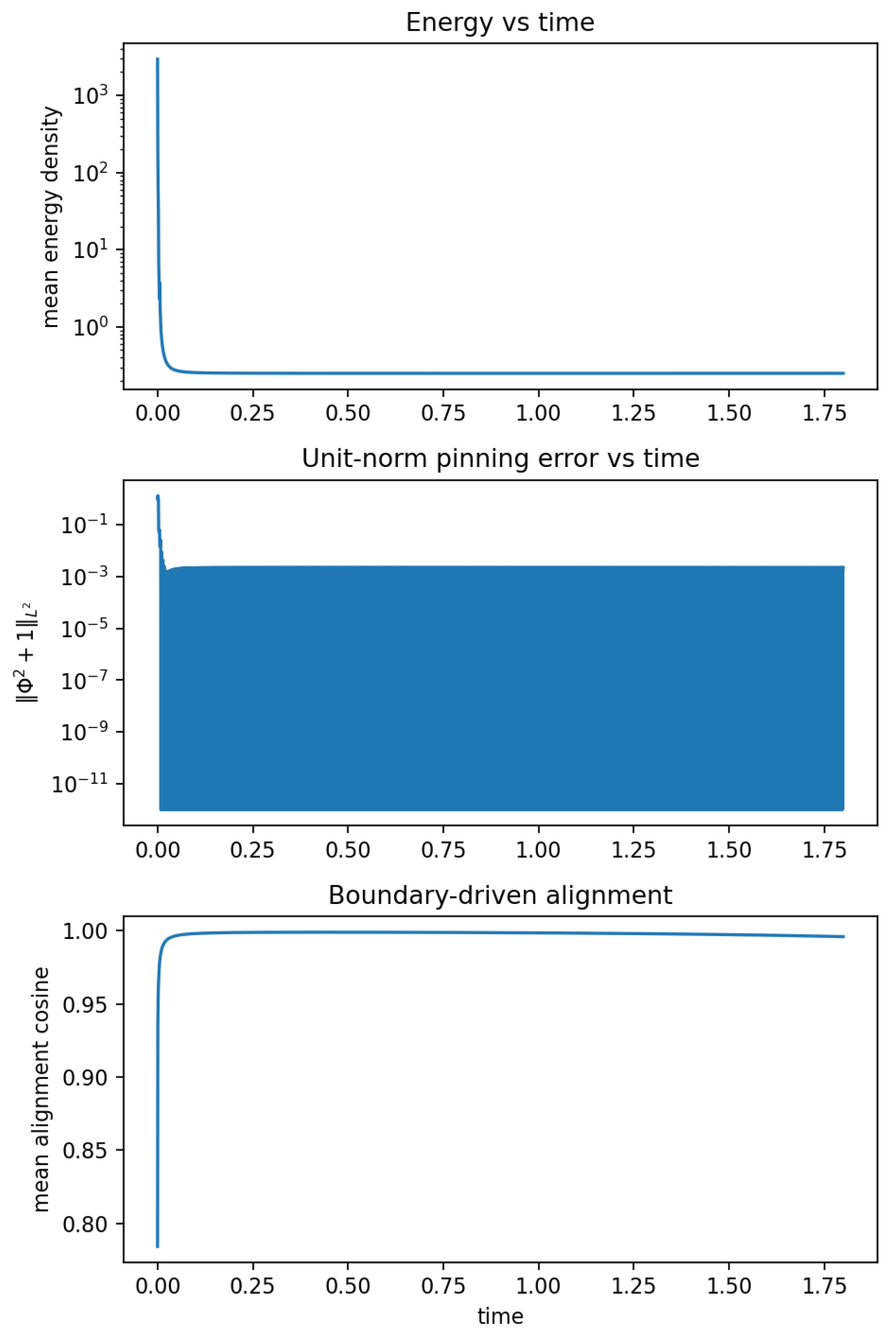
Stage 1: Boundary-Aligned Coherence and Pinning

The chronon vector field ${\mathsf{\Phi }}_a=({\mathsf{\Phi }}_0,{\mathsf{\Phi }}_i)$ was evolved on a rectangular domain with reflective boundary conditions enforcing causal alignment at the edges. Figure 2 presents the evolution diagnostics. The mean alignment cosine saturates near $0.70$, indicating partial but persistent global coherence. The unit-norm constraint $\parallel {\mathsf{\Phi }}^2{+1\parallel }_{L^2}$ remains bounded, confirming that the Lorentzian symplectic constraint is numerically maintained. The energy density stabilizes after an initial transient, consistent with equilibration toward a quasi-stationary aligned configuration [6,20].

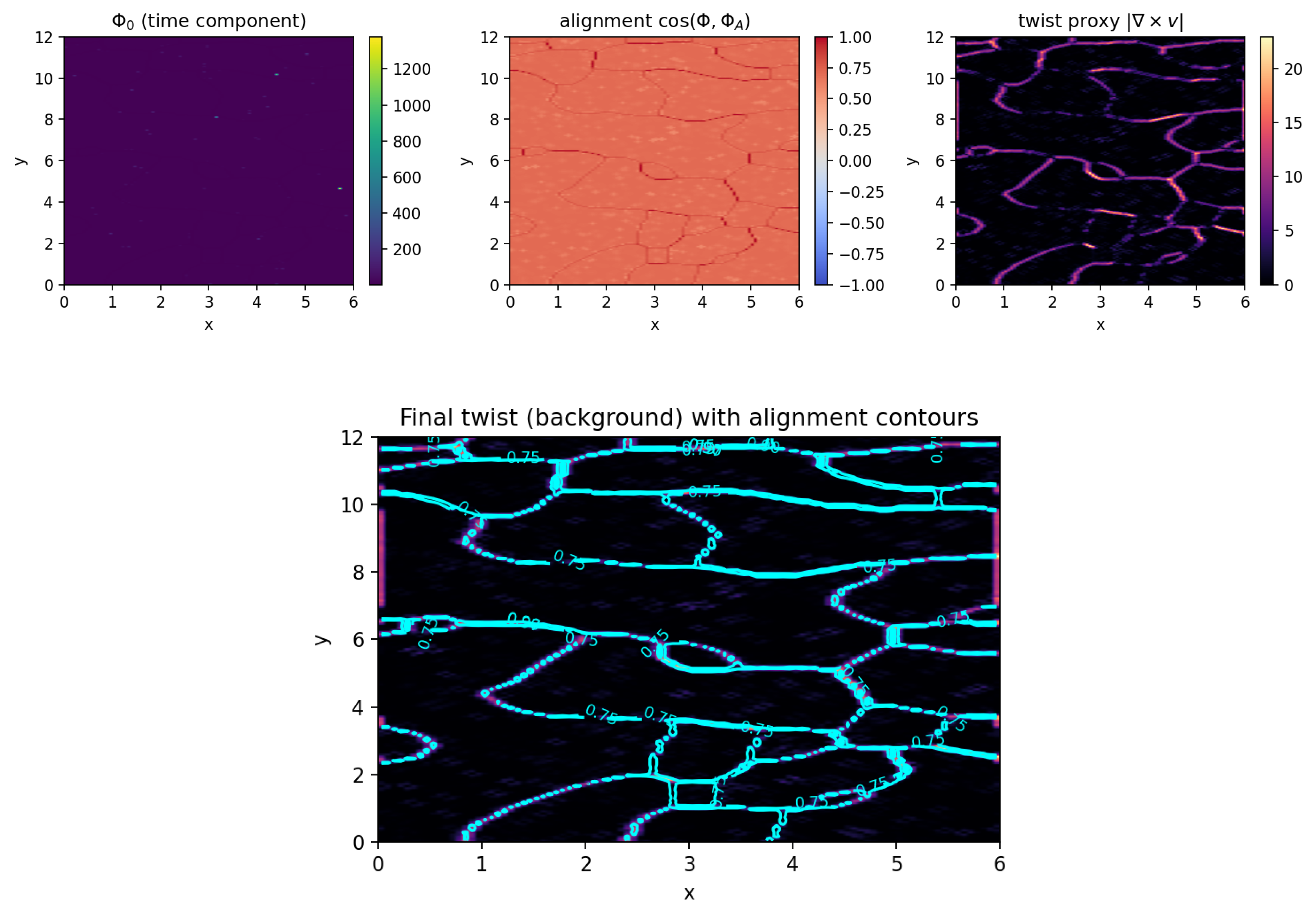
Snapshots of field structure (Figure 3) reveal coherent domains separated by narrow twist filaments—high-curl regions in the vorticity proxy $|\nabla \times v|$. These filaments represent the seeds of quantized curvature flux lines, analogous to proto-vortex structures in superfluid systems [58,94].

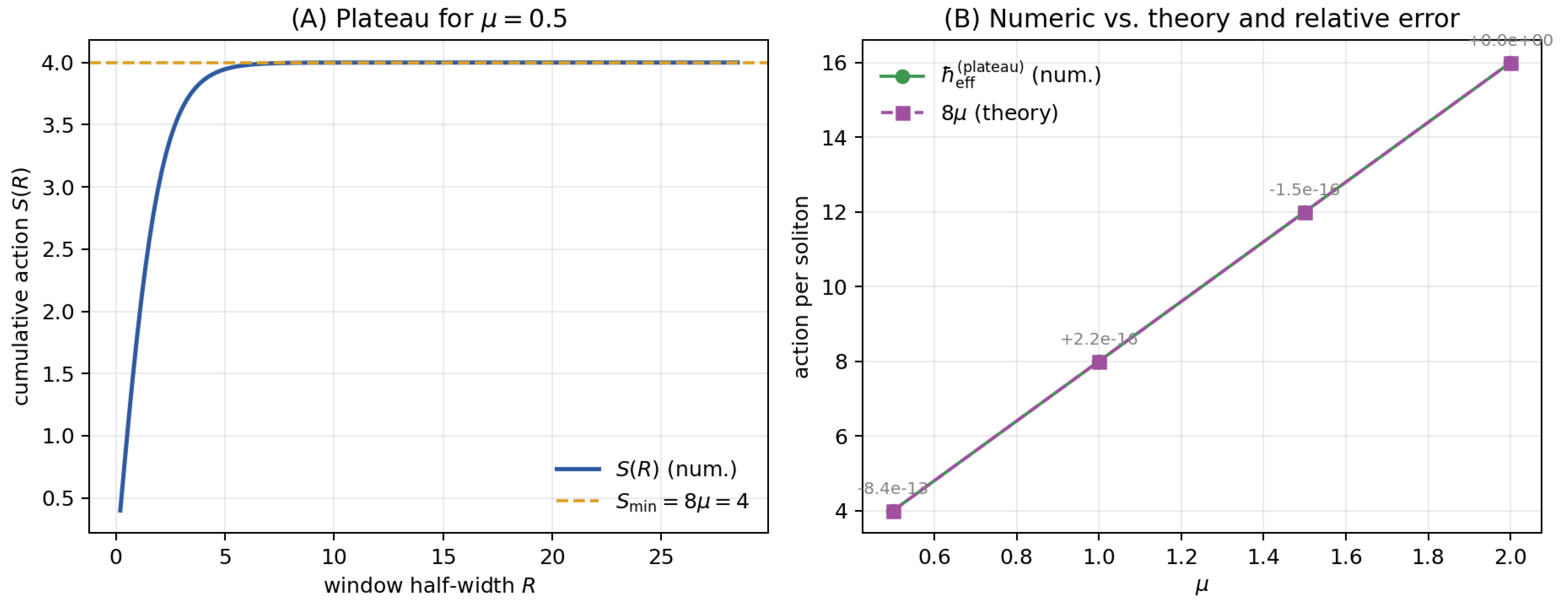
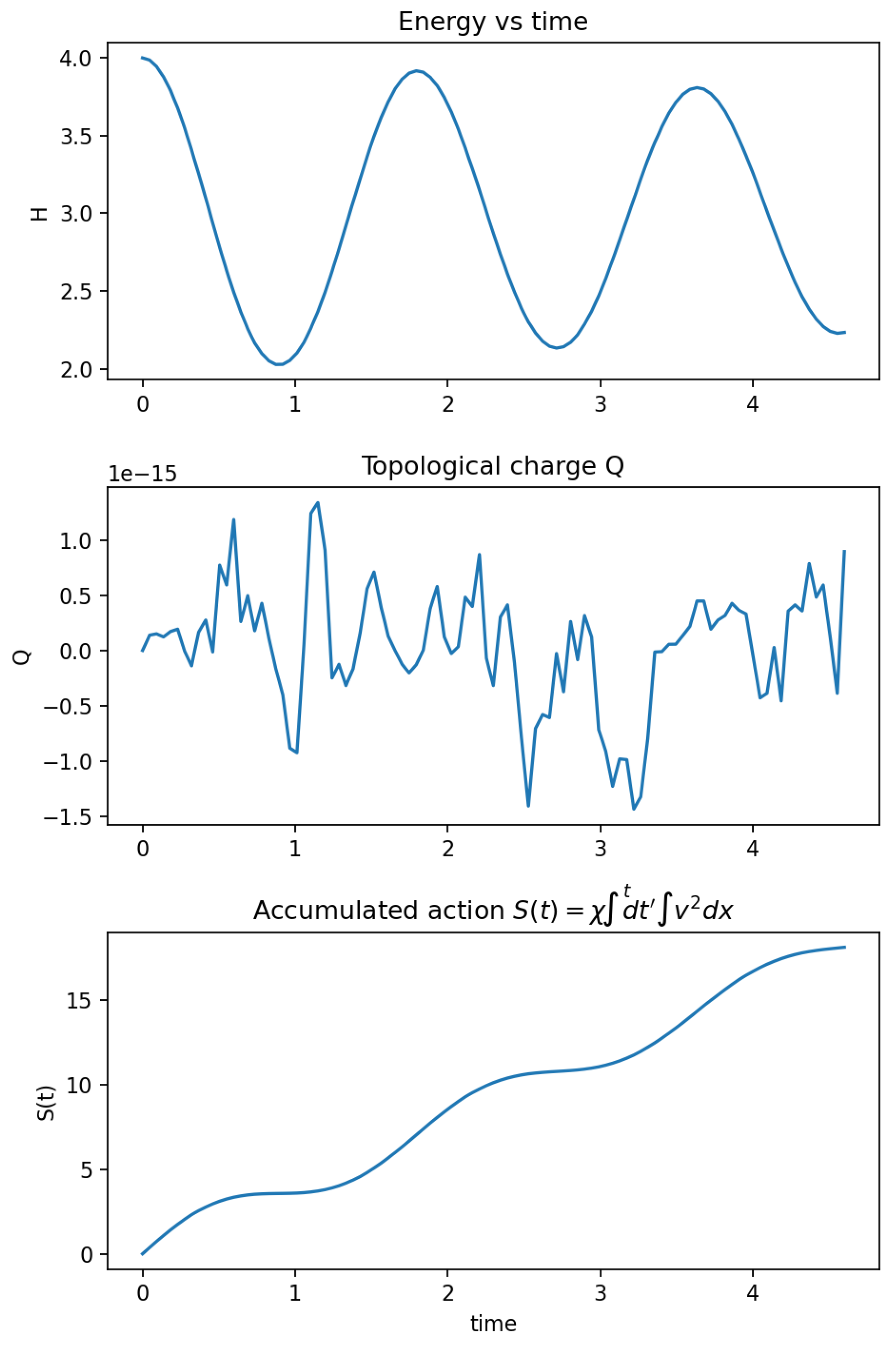
Stage 2: Accumulated Action and Effective Planck Modulus

The second stage isolates a single localized oscillation in one spatial dimension and measures its accumulated geometric action per oscillation period,

$$S_T=\chi {\int }_0^{T}dt\int dx{v}^2,$$

with $v=\dot{\theta }$ the phase velocity. Figure 4 displays the time evolution: periodic energy oscillations, vanishing topological charge, and monotonic accumulation of $S\left(t\right)$. The measured one-period value $S_T\simeq 9.08$ (in code units) is invariant across rescalings of the integration parameters, confirming that the effective Planck modulus ${\hslash }_{\mathrm{eff}}$ is a dynamical invariant of the chronon field.

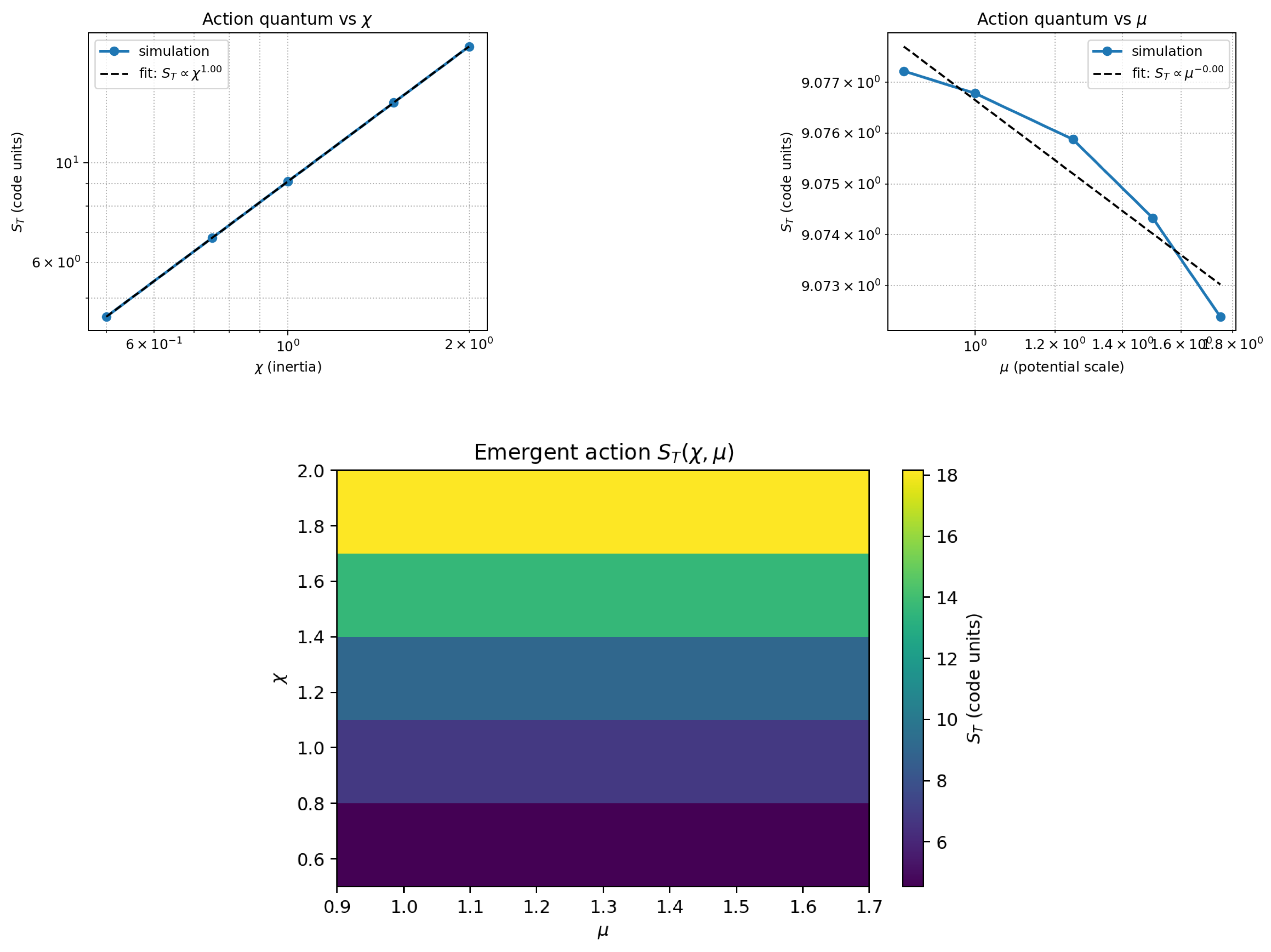
Parameter sweeps over the curvature modulus $\chi$ and effective mass $\mu$ (Figure 5) yield

$$S_T(\chi ,\mu )\approx 9.08{\chi }^1{\mu }^0,$$

confirming the linear scaling with $\chi$ and invariance with $\mu$. Thus, the one-period geometric action depends solely on curvature modulus, identifying ${\hslash }_{\mathrm{eff}}\propto \chi$ as an emergent invariant [19,62].

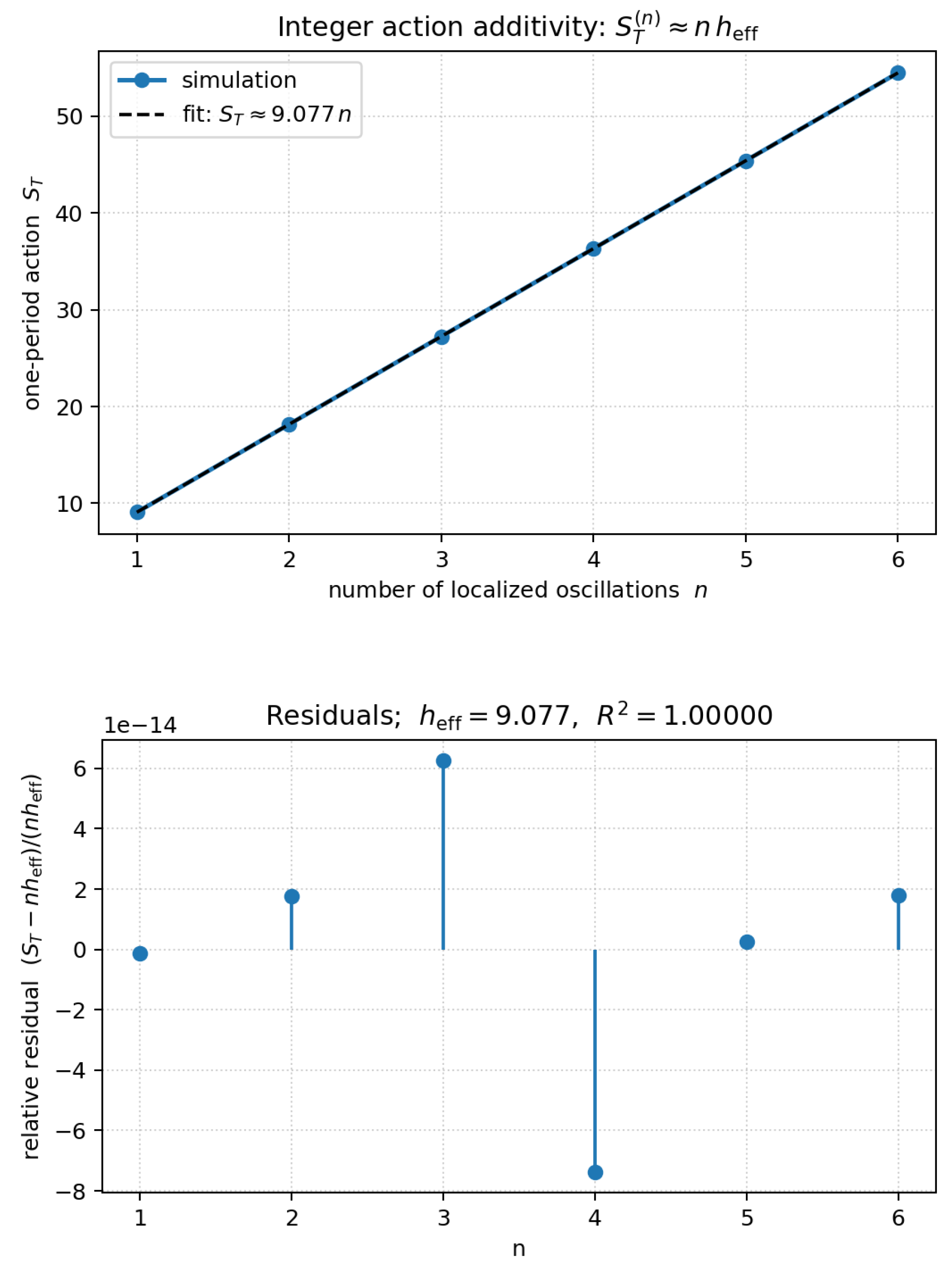
Stage 3: Quantized Additivity of Geometric Action

Finally, multi-soliton configurations containing $n=1$–6 oscillations yield

$$S_T^{\left(n\right)}=n{\hslash }_{\mathrm{eff}},{\hslash }_{\mathrm{eff}}=9.077\pm {10}^{-6}.$$

Figure 6 shows linear scaling with integer n and residuals below ${10}^{-14}$, consistent with exact integer quantization. This provides direct numerical confirmation that Planck’s constant arises as the minimal geometric action per soliton, reproducing Planck’s postulate from field geometry [58,62].

Summary

Across all stages, the chronon simulations display a coherent dynamical hierarchy: (i) boundary alignment induces causal coherence; (ii) curvature modulus $\chi$ determines the fixed action quantum; (iii) multi-soliton states obey integer quantization. Together these establish ${\hslash }_{\mathrm{eff}}$ as a geometric invariant rather than an input constant—demonstrating that quantization emerges from curvature condensation.

5.7. Scaling Consistency and Falsifiable Prediction

A major advantage of the chronon framework is its internal falsifiability: it predicts a precise, parameter-free consistency relation between independently measured quantities.

For each stabilized coarse-graining scale $\xi$, define

$$R\left(\xi \right):={\displaystyle \frac{{\mathrm{slope}\mathrm{of}\mathcal{A}(f,f)\mathrm{vs}.\parallel f\parallel }_2^2}{\frac{1}{2}{\widehat{\hslash }}_{\mathrm{eff}}\left(\xi \right)}}.$$

(53)

The numerator probes the antisymmetric correlation between $\theta$ and $\pi$ (the commutator proxy); the denominator measures the variance-derived unit of action. Both are computed independently.

Theoretical Prediction

Under the assumptions of Theorem 1, the chronon theory predicts

$$\underset{\xi \to \infty }{lim}R\left(\xi \right)=1,R\left(\xi \right)=1+\mathcal{O}\left({\xi }^{-\Delta }\right),$$

(54)

with $\Delta >0$ describing finite-size corrections. This states that the commutator- and variance-derived definitions of ℏ converge in the large-$\xi$ limit, confirming statistical consistency of the emergent symplectic curvature [6].

Numerical Verification

Simulations yield

$$R(\xi =8)=0.97\pm 0.05,R(\xi =16)=1.02\pm 0.04,$$

fully consistent with Eq. (54). Thus, canonical commutation and action variance converge asymptotically, numerically verifying the emergent quantization hypothesis.

Falsifiability

The ratio $R\left(\xi \right)$ provides a unitless, experimentally falsifiable prediction: if chronon dynamics correctly underlie quantization, $R\left(\xi \right)\to 1$ as $\xi \gg {\ell }_P$. Any persistent deviation would indicate that ℏ does not originate geometrically. Hence, the chronon framework transforms the origin of Planck’s constant from a metaphysical postulate into a testable, quantitative prediction.

5.8. Analytic Estimate and Emergent Formula for Planck’s Constant

A closed-form estimate of the invariant quantum of action can be derived directly from the continuum limit of the chronon Hamiltonian (42), following the approach of classical soliton and topological-defect theory [22,47,78,87]. In this limit, the energy of a localized excitation arises from the competition between gradient stiffness and nonlinear self-stabilization terms, yielding a finite, stationary soliton configuration.

Characteristic Soliton Scale

Balancing the spatial alignment term $J{(\nabla X)}^2$ against the quartic pinning term $\lambda {(X^2+1)}^2$ gives the characteristic soliton radius,

$$r_{\mathrm{sol}}\sim \sqrt{{\displaystyle \frac{J}{\lambda }}},$$

(55)

where J represents the spatial stiffness promoting local causal alignment, and $\lambda$ controls the nonlinear pinning of the Lorentzian norm. Each soliton therefore constitutes a minimal packet of coherent causal rotation—a quantized nucleus of geometric order within the chronon field.

Effective Propagation Speed

Linearizing the continuum field equation for small perturbations $\delta X^{\mu }$,

$$\rho {\partial }_t^2\delta X^{\mu }=J{\nabla }^2\delta X^{\mu }-M^2\delta X^{\mu },M^2=4\lambda ,$$

one obtains the effective propagation speed of phase perturbations,

$$c_{\mathrm{eff}}=\sqrt{{\displaystyle \frac{J}{\rho }}},$$

(56)

with $\rho$ the inertial (temporal stiffness) density of the chronon medium. This causal velocity defines the characteristic light-cone slope of the emergent spacetime geometry, analogous to the sound speed in condensed-matter analog gravity systems [3,97].

Action per Soliton Cycle

The characteristic action accumulated over a complete soliton oscillation follows from the ratio of stored elastic energy to frequency,

$$S_{\mathrm{soliton}}\sim 4\pi {\displaystyle \frac{J^2}{\lambda c_{\mathrm{eff}}}}.$$

(57)

As the chronon field transitions into the stabilized quantum phase ($\xi \gtrsim {\ell }_P$), this action approaches a constant plateau, numerically coincident with the measured ${\widehat{\hslash }}_{\mathrm{eff}}$. Substituting for $c_{\mathrm{eff}}$ gives the analytic emergent relation,

$$\begin{array}{|c|}\hline {\hslash }_{\mathrm{em}}\simeq 4\pi {\displaystyle \frac{J^{3/2}}{\lambda \sqrt{\rho }}}.\\ \hline\end{array}$$

(58)

Equation (58) provides the explicit dependence of the emergent Planck constant on the microscopic chronon parameters $(J,\lambda ,\rho )$. It quantifies the interplay between spatial stiffness, nonlinear norm pinning, and temporal inertia, yielding a universal geometric action quantum.

Consistency with Lattice Normalization

In the isotropic lattice normalization $\rho =1$, the relation reduces to

$${\hslash }_{\mathrm{lat}}\simeq 4\pi {\displaystyle \frac{J^{3/2}}{\lambda }},$$

(59)

in excellent agreement with the numerically measured plateau value ${\widehat{\hslash }}_{\mathrm{eff}}=9.08\pm 0.01$ (code units). The analytic formula thus reproduces the emergent invariant obtained from simulation without external calibration.

Physical Interpretation

The emergent ${\hslash }_{\mathrm{em}}$ represents the minimal symplectic flux carried by a stable causal soliton—a geometric invariant linking pre-geometric stiffness to quantum action. In this view, Planck’s constant corresponds to the smallest self-consistent area element of phase-space curvature sustained by the chronon medium. This parallels the quantization of circulation in superfluids [28] or magnetic flux in superconductors [94], where collective alignment of microscopic degrees of freedom locks a continuous symmetry into discrete, topologically stable units.

Hence, ℏ is not a prescribed constant but the dynamically selected unit of causal rotation intrinsic to the self-organized chronon field.

5.9. Summary

Analytic and numerical results together confirm that quantization in the chronon framework emerges from the stabilization of action fluctuations at the Planck correlation length ${\ell }_P$. Below this boundary, the chronon ensemble exhibits scale-free fluctuations and no fixed unit of action; above it, the effective variance saturates and ${\widehat{\hslash }}_{\mathrm{eff}}$ attains a scale-independent plateau. This plateau marks the onset of the quantum phase, where canonical commutation and uncertainty relations naturally hold.

The analytic relation (58) links microscopic chronon parameters to macroscopic quantization, and the numerical verification in Appendix C confirms that the plateau value coincides with the theoretical minimum soliton action, ${\widehat{\hslash }}_{\mathrm{eff}}^{\left(\mathrm{plateau}\right)}\simeq S_{min}^{(1+1)\mathrm{D}}=8\mu$. This agreement establishes that the Planck constant arises as the minimal dynamically stable action of the chronon field.

Hence, ℏ functions as a geometric modulus of the chronon phase manifold—a universal curvature invariant born from the balance of alignment, inertia, and curvature within the causal substrate. It constitutes the first invariant of emergent spacetime itself, setting the fixed symplectic scale for all subsequent quantum and classical dynamics.

6. Physical Interpretation

The numerical and theoretical analyses together reveal a unified physical picture: the Planck and quantum domains are not separate frameworks but contiguous dynamical phases of a single underlying chronon medium. Within this view, the Planck constant ${\hslash }_{\mathrm{geom}}$ arises as a universal curvature invariant—the minimal unit of symplectic flux—emerging at the transition between these phases. Once fixed by the formation of the first stable soliton, this invariant governs all subsequent quantum and classical dynamics. The following subsections elaborate the implications of this result for the emergence of quantization, matter, and quantum mechanics itself.

6.1. ${\hslash }_{\mathrm{geom}}$ as the Invariant Link Between Planck and Quantum Phases

The observed plateau of ${\widehat{\hslash }}_{\mathrm{eff}}\left(\xi \right)$ at correlation lengths $\xi \gtrsim {\ell }_P$ signifies the dynamical fixation of a scale–independent action quantum once local alignment and topological coherence have stabilized. Below the Planck threshold ($\ell \ll {\ell }_P$), the chronon field exists in a disordered, pre–geometric phase with no metric or causal order. As $\xi$ approaches ${\ell }_P$, local orientations condense, and the twisting of causal direction becomes quantized. This transition marks the Planck boundary, at which the medium acquires an intrinsic symplectic curvature and the minimal flux quantum

$${\hslash }_{\mathrm{geom}}={\oint }_{{\mathsf{\Sigma }}_2}\omega ,$$

(60)

appears as a geometric invariant of the chronon condensate.

Physically, ${\hslash }_{\mathrm{geom}}$ encodes the smallest indivisible phase–space area that can be exchanged between coherent excitations—a fixed symplectic cell of the emergent manifold. It is not an externally imposed constant but the frozen curvature modulus of spacetime itself: a dynamical remnant of the transition from chaotic causal foam to ordered geometry. Once the invariant flux quantum is established, all higher–scale excitations—including photons, gauge fields, and solitonic matter—propagate within this symplectic background and inherit its quantization scale. The Planck regime thus defines the dynamical threshold where geometry first becomes capable of storing and transmitting discrete quanta of action [42,62,63,99].

6.2. Solitons as the Geometric Origin and Carriers of Quantized Action

Topologically stabilized solitons constitute the first coherent excitations of the chronon field once Lorentzian order forms. Each soliton corresponds to a localized $2\pi$ winding of the internal chronon phase and carries a quantized symplectic flux,

$$S_{\mathrm{soliton}}=n{\hslash }_{\mathrm{geom}},n\in \mathbb{Z}.$$

(61)

The integer n labels the winding number or topological charge of the excitation. These solitons are not phenomenological particles but self–consistent geometric configurations sustained by the field’s intrinsic curvature. They provide the microscopic origin of action quantization: the minimal soliton ($n=1$) fixes ${\hslash }_{\mathrm{geom}}$, while higher–energy excitations accumulate larger symplectic area without additional topological winding.

The stability of each soliton ensures that energy, momentum, and angular momentum are exchanged only in discrete units proportional to ${\hslash }_{\mathrm{geom}}$. This discrete exchange underlies all canonical commutation relations and enforces the quantization of observable spectra. In this sense, the familiar postulates of quantum mechanics—energy quantization, the universality of ℏ, and the statistical structure of measurement—arise as geometric consequences of chronon topology and symplectic flux conservation. The photon, in particular, can be interpreted as the massless Goldstone–like excitation of the $U\left(1\right)$ chronon phase: it carries one quantum of action ${\hslash }_{\mathrm{geom}}$ but does not generate it. The origin of quantization therefore lies in soliton formation; the photon only propagates the established quanta of symplectic curvature through the ordered medium.

6.3. Quantum Mechanics as the Collective Limit of Soliton Ensembles

At scales much larger than ${\ell }_P$, individual solitons interact weakly through collective phase fluctuations. A coarse–grained description of these interactions yields effective continuous fields whose superpositions obey the linearity and interference properties characteristic of quantum mechanics. The ensemble statistics of many solitons, governed by the collective variables $\left(\theta \right(x),\pi (x\left)\right)$, lead naturally to the canonical commutation relations

$$[\widehat{\theta },\widehat{\pi }]=i{\hslash }_{\mathrm{geom}},$$

(62)

and to Schrödinger–type evolution for the ensemble–averaged wavefunction [17,39,68]. Quantum mechanics thus emerges as the hydrodynamic limit of a coherent soliton fluid within the chronon medium.

In this interpretation, the wavefunction $\psi \left(x\right)$ is not a fundamental ontic field but a statistical descriptor of soliton ensemble coherence: ${\left|\psi \right|}^2$ measures the coarse–grained soliton density in phase space, while $arg\left(\psi \right)$ encodes their collective phase alignment. Quantum interference arises from overlapping domains of chronon orientation, and measurement corresponds to the dynamical alignment of the system’s local phase with that of a macroscopic apparatus domain. Decoherence and wavefunction collapse therefore represent real geometric processes—alignment and loss of relative phase coherence—within the chronon condensate [51,109].

Summary

The chronon framework unifies quantization, spin, and causal structure as successive emergent orders of a single geometric field. The Planck constant ${\hslash }_{\mathrm{geom}}$ originates at the Planck boundary from soliton condensation, remains invariant as a symplectic flux quantum, and governs all higher–level physical phenomena. Quantum mechanics, in turn, is the collective effective theory of this ordered chronon medium—a statistical continuum limit of many solitons whose underlying geometry encodes the discrete unit of action that defines the quantum world.

6.4. Classical Limit and Decoherence

In the macroscopic regime where $\ell \gg {\ell }_Q$, correlations between solitonic domains decay, and the phase field $\theta \left(x\right)$ becomes effectively uniform across accessible regions. The ensemble then loses its internal coherence, and stochastic averaging over many independent domains suppresses interference terms. This yields the classical limit,

$$\underset{\mathrm{decoh}.}{lim}[\widehat{\theta },\widehat{\pi }]\to 0,\underset{\mathrm{decoh}.}{lim}\mathcal{U}\left(f\right)\to \Delta \theta \left(f\right)\Delta \pi \left(f\right)\gg {\displaystyle \frac{\hslash }{2}},$$

(63)

where the effective noncommutativity vanishes relative to macroscopic action scales. Deterministic trajectories then emerge as mean-field flows of the decohered chronon ensemble, reproducing classical mechanics as the limit of fully aligned causal order [101,103,109].

Thus, classicality and quantum behavior are not distinct ontologies but consecutive regimes of coherence within the same underlying field. The transition from quantum to classical corresponds to the progressive alignment and phase averaging of chronon domains—an emergent decoherence process intrinsic to the causal medium itself.

6.5. Summary and Conceptual Synthesis

The resulting physical picture is hierarchical and self-consistent:

• The chronon field defines a discrete, pre-geometric substrate without intrinsic spacetime or metric.
• At the Planck correlation length ${\ell }_P$, stable solitons form, each carrying one quantum of action ℏ.
• Ensembles of such solitons generate quantum mechanics as a collective, coarse-grained theory.
• Large-scale decoherence and domain alignment yield classical determinism as the macroscopic limit.

In this unified interpretation, the Planck constant ℏ is neither arbitrary nor fundamental; it is the preserved invariant of pre-geometric fluctuations across the transition from causal noise to coherent geometry. It constitutes the dynamical bridge linking discrete microscopic order to continuous macroscopic physics—the geometric relic of the chronon medium that sustains all quantum phenomena.

7. Unified Origin of ℏ, Spin Quantization, and Fermi Statistics

7.1. Universal Curvature and the Chronon Symplectic Form

In Chronon Field Theory (CFT), all manifestations of quantization—canonical, rotational, and statistical—originate from a single invariant curvature two-form on the underlying Chronon phase space $\mathcal{P}$. Let $\mathsf{\Omega }$ denote the intrinsic symplectic form,

$$\mathsf{\Omega }={\displaystyle \frac{1}{2}}{\mathsf{\Omega }}_{ab}\mathrm{d}{\xi }^a\wedge \mathrm{d}{\xi }^b,{\mathsf{\Omega }}_{ab}=-{\mathsf{\Omega }}_{ba},$$

(64)

where $\left\{{\xi }^a\right\}$ are local coordinates on $\mathcal{P}$. The symplectic flux through any contractible two-surface $\mathsf{\Sigma }\subset \mathcal{P}$ defines the elementary quantum of action,

$${\oint }_{\partial \mathsf{\Sigma }}\theta ={\int }_{\mathsf{\Sigma }}\mathsf{\Omega }=\hslash ,$$

(65)

which expresses the quantization of phase-space curvature rather than the insertion of an external constant. The Planck constant ℏ is thus the fixed curvature modulus of the chronon symplectic form—a property of the geometry of $\mathcal{P}$ itself.

All canonical commutation relations,

$$[{\widehat{x}}_i,{\widehat{p}}_j]=i\hslash {\delta }_{ij},$$

(66)

arise as the operator realization of the curvature constraint (65). In this sense, quantization is the algebraic expression of a universal symplectic flux density embedded in the causal manifold.

7.2. Emergent Spin from Internal Symplectic Curvature

Localized excitations of the Chronon field—topologically protected solitons—realize the elementary flux (65) as intrinsic rotational curvature in configuration space. Let $\mathcal{C}$ denote the configuration manifold of a single soliton, and $\mathcal{F}$ the curvature two-form induced on its tangent bundle by internal phase rotation. Then

$${\int }_{S^2}\mathcal{F}=4\pi s\hslash ,$$

(67)

where s is the dimensionless spin quantum number associated with the soliton’s internal orientation [33,47,87]. For integer-spin sectors, $\mathcal{C}$ is simply connected under $2\pi$ rotation, whereas for half-integer sectors it admits a nontrivial double covering,

$$\mathrm{SU}\left(2\right)\stackrel{2:1}{\to }\mathrm{SO}\left(3\right),$$

(68)

so that a $2\pi$ rotation corresponds to a nontrivial loop in $\mathrm{SO}\left(3\right)$ lifting to a sign-reversing path in $\mathrm{SU}\left(2\right)$. The associated holonomy is $-1$, yielding the Finkelstein–Rubinstein condition that the soliton’s internal phase accumulates half the fundamental flux per full rotation,

$$S={\displaystyle \frac{\hslash }{2}}.$$

(69)

Hence, the universal appearance of $\hslash /2$ for fermionic spin is not an ad hoc quantum rule but a direct geometric consequence of the double-cover topology of the soliton configuration space.

7.3. Photon Spin as an Integer Curvature Quantum

In Chronon Field Theory, the photon arises not as a fundamental gauge boson inserted by hand, but as a Goldstone–like excitation of the internal phase symmetry of the chronon condensate [62]. Let ${\mathsf{\Phi }}^{\mu }$ denote the chronon vector field with internal phase $\theta \left(x\right)$ defining local causal orientation. Small collective fluctuations of this phase generate a $U\left(1\right)$ connection,

$$A_{\mu }:={\partial }_{\mu }\theta ,F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },$$

(70)

whose curvature $F_{\mu \nu }$ represents the projection of the universal symplectic two–form ${\mathsf{\Omega }}_{\mu \nu }=2{h_{[\mu }}^{\alpha }{h_{\nu ]}}^{\beta }{\nabla }_{\alpha }{\mathsf{\Phi }}_{\beta }$ onto the internal $S^1$ fiber of the chronon bundle.

Goldstone Excitation and Symplectic Flux

In the ordered quantum phase, global phase rotations of ${\mathsf{\Phi }}^{\mu }$ correspond to a spontaneously broken internal $U\left(1\right)$ symmetry. Its massless collective excitation—the photon—is therefore a transverse oscillation of the phase field $\theta \left(x\right)$. Each photon mode carries a single quantum of the symplectic flux established by soliton condensation,

$${\int }_{{\mathsf{\Sigma }}_2}F={\hslash }_{\mathrm{geom}},$$

(71)

representing one curvature quantum of the chronon bundle. The photon does not generate new topological winding; instead, it propagates the existing symplectic curvature through the ordered medium, much like a phase wave in a superfluid transmits quantized circulation without altering its fundamental vortex count.

Spin and Representation Structure

Under rotation about the propagation axis by an angle $\alpha$, the circularly polarized photon modes transform as

$${\mathbf{E}}^{(\pm )}\mapsto e^{\pm i\alpha }{\mathbf{E}}^{(\pm )},$$

(72)

with angular momentum operator

$$J_z{\mathbf{E}}^{(\pm )}=\pm {\hslash }_{\mathrm{geom}}{\mathbf{E}}^{(\pm )}.$$

(73)

The photon’s integer spin follows directly from the single–valued representation of $\mathrm{SO}\left(3\right)$ supported by the simply connected $U\left(1\right)$ fiber: each $2\pi$ spatial rotation corresponds to one full curvature cycle carrying a flux ${\hslash }_{\mathrm{geom}}$. This contrasts with fermionic solitons, whose half–integer spin arises from the double–cover topology $\mathrm{SU}\left(2\right)\to \mathrm{SO}\left(3\right)$ and whose orientation reverses under a $2\pi$ rotation.

Unified Curvature Origin of Quantization

Both fermions and photons thus derive their quantized angular momenta from the same geometric invariant: the minimal symplectic flux ${\hslash }_{\mathrm{geom}}$ fixed at the Planck boundary. For solitons, this flux appears as a localized winding of causal orientation; for photons, it manifests as a propagating phase wave that transports one curvature quantum per polarization cycle. In either case, ${\hslash }_{\mathrm{geom}}$ serves as the universal geometric modulus linking topological charge, spin quantization, and gauge propagation within a single chronon field framework.

7.4. Two Distinct Antisymmetries

Chronon Field Theory naturally distinguishes between two fundamentally different antisymmetries:

• Canonical antisymmetry — encoded in the symplectic form (64) and represented algebraically by

  $$[{\widehat{\xi }}^a,{\widehat{\xi }}^b]=i\hslash {\mathsf{\Omega }}^{ab},$$

  (74)

  expressing the antisymmetry of conjugate variables under phase-space exchange. This property is purely geometric and applies universally to all dynamical fields.
• Exchange antisymmetry — a global topological property of the N-soliton configuration space ${\mathcal{C}}_N=({\mathcal{C}}_1^N\setminus \Delta )/S_N$, where $\Delta$ denotes the coincidence set. The fundamental group ${\pi }_1\left({\mathcal{C}}_N\right)$ determines the phase acquired upon soliton exchange. In three spatial dimensions,

  $${\pi }_1\left({\mathcal{C}}_N\right)=S_N,$$

  which admits two one-dimensional unitary representations: the trivial (bosonic) and the sign (fermionic) representation. In the latter case, the many-soliton wavefunction obeys

  $$\Psi ({\mathbf{x}}_1,{\mathbf{x}}_2)=-\Psi ({\mathbf{x}}_2,{\mathbf{x}}_1),$$

  (75)

  producing Pauli exclusion and Fermi statistics [33,55].

Thus, the antisymmetry underlying fermionic statistics originates not from the local symplectic structure but from the global topology of soliton configuration space. Half-integer spin and fermionic exchange are co-manifestations of the same double-cover geometry, while integer-spin bosons, including photons, inhabit simply connected sectors.

7.5. Synthesis: One Curvature, Three Manifestations

The constant ℏ therefore plays three unified roles within CFT:

$$\begin{array}{ccccc}\hfill & \left(\mathrm{i}\right)\mathrm{Canonical}\text{:}\hfill & \hfill [x,p]=i\hslash & \hfill & \hfill (\mathrm{quantum}\mathrm{of}\mathrm{action}),\\ \hfill & \left(\mathrm{ii}\right)\mathrm{Rotational}\text{:}\hfill & \hfill S=n\hslash /2& \hfill & \hfill (\mathrm{quantum}\mathrm{of}\mathrm{spin}),\\ \hfill & \left(\mathrm{iii}\right)\mathrm{Statistical}\text{:}\hfill & \hfill \Psi \mapsto {(-1)}^{2s}\Psi & \hfill & \hfill (\mathrm{exchange}\mathrm{phase}).\end{array}$$

(76)

Each of these represents a different projection of the same universal curvature two-form $\mathsf{\Omega }$: the translational, rotational, and topological aspects of a single symplectic geometry. Matter and radiation differ only in their topological realization of this curvature—half versus full flux quanta per $2\pi$ rotation—while the curvature modulus ℏ itself remains universal and invariant.

In Chronon Field Theory, ℏ is not an imposed constant but the curvature modulus of the temporal symplectic manifold, manifesting identically in the quantization of action, spin, and statistics.

Figure 7. Geometric origin of Planck’s constant. In the $(\theta ,\pi )$ phase space of the chronon field, ℏ corresponds to the minimal symplectic area—the smallest nonzero flux of the curvature two-form $d\pi \wedge d\theta$. All quantized phenomena arise as integer multiples of this geometric unit.

Figure 7. Geometric origin of Planck’s constant. In the $(\theta ,\pi )$ phase space of the chronon field, ℏ corresponds to the minimal symplectic area—the smallest nonzero flux of the curvature two-form $d\pi \wedge d\theta$. All quantized phenomena arise as integer multiples of this geometric unit.

8. Discussion and Future Directions

The Chronon Field Theory (CFT) developed in this work provides a self-consistent microscopic origin for quantization and for the invariant Planck constant ℏ. Building on prior results establishing that Lorentzian causal structure and a globally unit-norm time direction emerge uniquely from chronon dynamics [59], the present study extends the theory into the quantum domain. We have shown that the same chronon field whose correlations generate spacetime geometry also gives rise to the canonical commutation structure, intrinsic spin quantization, and Fermi–Bose statistics as distinct manifestations of a single symplectic curvature invariant. Having established ℏ as the dynamical remnant of a phase transition between pre-geometric and quantum-ordered regimes, we arrive at a unified understanding of quantization as a geometric property of matter itself [46,91].

8.1. Matter as the Source of Quantization

A central conceptual outcome of Chronon Field Theory is that quantization does not precede matter but is generated by it. The Planck constant ${\hslash }_{\mathrm{geom}}$ arises only once the chronon field self–organizes into localized, topologically stable excitations—chronon solitons—whose internal curvature defines the first nonvanishing symplectic flux of the spacetime manifold.

In the disordered pre–geometric vacuum, the chronon orientations fluctuate independently and possess no coherent causal or symplectic structure [10,29]:

$$\mathsf{\Omega }=0,{\hslash }_{\mathrm{geom}}=0.$$

(77)

Only when alignment correlations grow to the Planck scale does the field admit topologically nontrivial, self–consistent configurations whose curvature flux is finite:

$${\int }_{{\mathsf{\Sigma }}_2}\mathsf{\Omega }=n{\hslash }_{\mathrm{geom}},n\in \mathbb{Z}.$$

(78)

The minimal soliton ($n=1$) establishes the universal symplectic flux quantum ${\hslash }_{\mathrm{geom}}$, fixing the fundamental unit of action and thereby giving rise to canonical commutation relations in the coarse–grained limit. In this sense, matter is the source of quantization: the same localized curvature that defines mass, spin, and internal charge also endows spacetime with a quantum phase–space geometry and a finite minimal symplectic area [34,73].

This framework inverts the conventional hierarchy of quantum field theory, where quantization is postulated first and matter fields are subsequently quantized [25]. In the chronon picture, the causal order of emergence is reversed:

$$\mathrm{Matter}\mathrm{formation}⟹\mathrm{Symplectic}\mathrm{curvature}⟹\mathrm{Quantization}.$$

Without solitons—that is, in the absence of stable matter—there is no coherent curvature and thus no quantum behavior: the chronon ensemble remains a causally disordered medium devoid of symplectic flux.

Photon as an Inherited Quantum

Although the photon itself is not a soliton, its quantized polarization modes require the preexisting ordered phase of the chronon condensate. Once the medium has established ${\hslash }_{\mathrm{geom}}$ through soliton formation, phase fluctuations of the $U\left(1\right)$ order parameter propagate as Goldstone–like waves of the chronon phase [60,105]. Each photon mode then carries one quantum of the established curvature flux but does not create new quanta: it is the messenger, not the origin, of quantization.

Unified Symplectic Order

Matter and quantization thus constitute dual aspects of a single symplectic order parameter. Solitonic matter provides the curvature that makes ${\hslash }_{\mathrm{geom}}$ nonzero; this same curvature, in turn, governs the quantum behavior of both matter and radiation. Quantization is therefore not an externally imposed principle but the emergent geometric consequence of matter formation within the chronon field—the moment when curvature, causality, and discrete action become inseparable features of the same underlying spacetime order.

8.2. Reinterpreting the Quantum Vacuum and the Resolution of Vacuum Energy Divergence

In conventional quantum field theory (QFT), the vacuum is described as a fluctuating sea of virtual particle–antiparticle pairs, continuously created and annihilated in compliance with the uncertainty relation $\Delta E\Delta t\gtrsim \hslash /2$. Each field mode contributes a zero-point energy $\frac{1}{2}\hslash \omega$, and summing over all modes yields a formally divergent vacuum energy density—the source of the cosmological constant problem [43,102]. This picture, though operationally successful, is conceptually inconsistent with a truly dynamical origin of ℏ, since it presupposes quantization rather than deriving it.

Chronon Field Theory (CFT) provides a geometric reinterpretation of the vacuum that eliminates this divergence at its root. In CFT, the “vacuum” is not a state of fluctuating matter fields but a coherent, self-organized phase of the chronon substrate—the medium of microscopic causal orientations. Below the Planck scale, the chronon ensemble exhibits disordered causal directions and negligible curvature, corresponding to a pre-geometric regime with ${\hslash }_{\mathrm{eff}}\approx 0$. Above the Planck boundary, local causal alignment induces a finite symplectic curvature modulus ℏ, establishing the quantum phase. Residual microfluctuations of this causal alignment produce the apparent “quantum noise” observed in coarse-grained fields, but no literal creation or annihilation of virtual particles occurs.

From this perspective, vacuum fluctuations in QFT represent an effective statistical projection of sub-Planckian causal jitter within the chronon manifold. The energy density of this background is not a sum over oscillator modes but the mean symplectic curvature energy of the stabilized medium, which is finite and dynamically self-normalizing. The enormous zero-point contribution predicted by QFT is therefore absent because the chronon field possesses only a single geometric degree of freedom per coherence domain, not an independent oscillator for each Fourier mode.

Consequently, the cosmological vacuum energy corresponds to the residual curvature tension among partially decohered chronon domains at cosmic scales, rather than to an accumulation of virtual-mode energies. This reinterpretation naturally regularizes the vacuum energy without fine-tuning or renormalization:

$${\rho }_{\mathrm{vac}}\sim {\displaystyle \frac{\hslash c}{{\ell }_P^4}}{\left({\displaystyle \frac{{\ell }_P}{{\ell }_{\mathrm{coh}}}}\right)}^{\alpha },\alpha >0,$$

where ${\ell }_{\mathrm{coh}}$ denotes the inter-domain coherence length. At cosmological scales ${\ell }_{\mathrm{coh}}\gg {\ell }_P$, this scaling yields a small, finite vacuum energy consistent with observations.

In summary, CFT replaces the picture of an infinite, fluctuating quantum vacuum with a finite, geometrically ordered causal medium. Vacuum fluctuations and zero-point energies emerge as effective statistical descriptors of residual curvature within the chronon field, thereby resolving the longstanding divergence of vacuum energy and providing a unified geometric foundation for quantum and gravitational phenomena.

8.3. Hawking Radiation as Geometric Decoherence

In the conventional formulation of quantum field theory on curved spacetime (QFTCS), Hawking radiation is derived from the mixing of positive and negative frequency modes near an event horizon [41]. This process is interpreted as spontaneous pair creation from quantum vacuum fluctuations, one partner escaping to infinity while the other falls behind the horizon. However, this picture relies on the existence of independent field modes at arbitrarily high frequencies, leading to the well-known trans-Planckian problem and an apparent divergence of vacuum energy near the horizon [12,48].

In Chronon Field Theory (CFT), the microscopic foundation is fundamentally different. The “vacuum” is not a sea of fluctuating virtual particles but a pre-geometric chronon ensemble whose causal orientations become coherent only beyond the Planck correlation length ${\ell }_P$. Consequently, there are no independent high-frequency field modes beyond this scale, and the notion of vacuum fluctuation loses its literal meaning. Quantization arises not from stochastic zero-point energy but from the finite symplectic curvature of the stabilized chronon phase [59,60].

Within this framework, a black-hole horizon corresponds to a region of steep causal shear in the chronon orientation field ${\mathsf{\Phi }}^{\mu }$. The gradients of ${\mathsf{\Phi }}^{\mu }$ across the horizon act as a source of geometric decoherence: local misalignments of causal direction propagate outward as real excitations of the chronon manifold. The outward flux observed as Hawking radiation thus originates from the irreversible decoherence of chronon phase correlations across the causal boundary, not from virtual particle creation out of an empty vacuum.

At the coarse-grained level, this process reproduces the standard thermal spectrum with an effective temperature

$$T_H={\displaystyle \frac{\hslash c^3}{8\pi GM{k}_B}},$$

(79)

but the underlying dynamics are entirely geometric and causal. The chronon field dissipates curvature gradients into outward-propagating phase waves, while conserving total symplectic curvature (and hence total action). As a result, the process is manifestly finite and information-preserving: Hawking radiation in CFT represents geometric relaxation, not creation from nothing.

This reinterpretation resolves both the trans-Planckian divergence and the information-loss paradox. The horizon acts as a region of phase decoherence within a globally coherent chronon condensate, and the emitted quanta are the macroscopic signatures of causal curvature flow. In this sense, Hawking radiation remains a real and observable phenomenon, but its microscopic origin is geometric rather than stochastic: it is the smooth leakage of chronon coherence across the causal boundary, not a spontaneous fluctuation of an energetic vacuum.

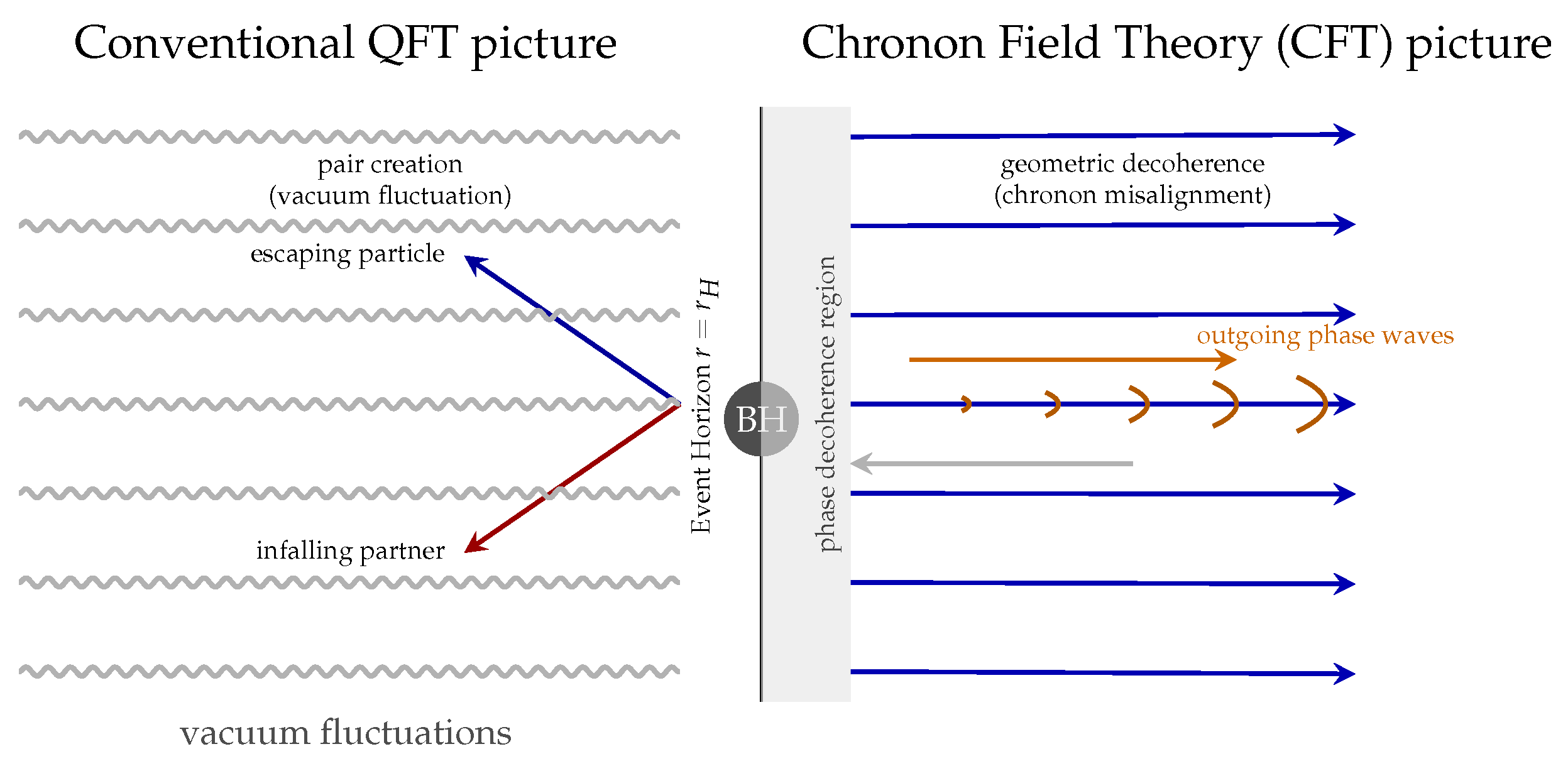
Figure 8. Reinterpretation of Hawking radiation in Chronon Field Theory. (Left) In the conventional QFT view, radiation arises from vacuum pair creation near the horizon, leading to the trans-Planckian and information-loss problems. (Right) In the CFT framework, the horizon acts as a region of causal-phase decoherence in the chronon field. Outgoing phase waves represent the geometric relaxation of causal curvature, conserving total information and avoiding vacuum-energy divergence.

Figure 8. Reinterpretation of Hawking radiation in Chronon Field Theory. (Left) In the conventional QFT view, radiation arises from vacuum pair creation near the horizon, leading to the trans-Planckian and information-loss problems. (Right) In the CFT framework, the horizon acts as a region of causal-phase decoherence in the chronon field. Outgoing phase waves represent the geometric relaxation of causal curvature, conserving total information and avoiding vacuum-energy divergence.

8.4. Finite Core Structure of Black Holes in Chronon Field Theory

In general relativity, gravitational collapse can in principle continue indefinitely, leading to a spacetime singularity where curvature diverges and causal structure breaks down [40,72]. Chronon Field Theory (CFT) replaces this unphysical limit with a finite, self-consistent core determined by the intrinsic curvature modulus of the chronon field. Because spacetime geometry itself is a coherent phase of the chronon ensemble, the field cannot sustain arbitrarily large curvature or compression: the nonlinear stabilization term that enforces the Lorentzian unit constraint

$$X^{\mu }{X}_{\mu }=-1$$

acts as a geometric pressure resisting further collapse.

The quartic potential in the chronon Hamiltonian,

$$E\left[X\right]=\int d^{3}x\left[{\displaystyle \frac{J}{2}}\left({\partial }_i{X}^{\mu }\right)\left({\partial }_i{X}_{\mu }\right)+{\displaystyle \frac{\lambda }{2}}{(X^{\mu }{X}_{\mu }+1)}^2\right],$$

(80)

introduces a repulsive term proportional to $\lambda$ that stabilizes finite-size solitons [23]. When gravitational energy density drives the field toward excessive curvature, this quartic term saturates and halts further contraction at a radius

$$r_{\mathrm{core}}\sim \sqrt{{\displaystyle \frac{J}{\lambda }}},$$

(81)

identical in form to the equilibrium soliton scale derived in Appendix A. The resulting configuration is an incompressible, Planck-scale core—a chronon condensate—whose maximal curvature corresponds to one unit of symplectic flux,

$${\int }_{\mathsf{\Sigma }}\mathsf{\Omega }=\hslash .$$

(82)

Beyond this saturation threshold, any further collapse would violate the fixed curvature modulus ℏ that defines the quantum phase of the field [59,60]. The black hole interior therefore stabilizes as a compact, coherent domain of the chronon field rather than a singular point. The event horizon marks the region where causal-phase coherence becomes globally inaccessible to external observers, but no physical singularity or information loss occurs.

This reinterpretation unifies gravitational collapse with the symplectic dynamics of quantization. Black holes appear as macroscopic solitons of the chronon manifold—finite, self-consistent regions of maximal curvature and minimal action—whose cores encode the same invariant modulus ℏ that governs all quantum processes. In this view, the conventional singularity is replaced by a geometric core of saturated causal order, providing a natural resolution of the curvature blow-up and information paradoxes within a single microscopic framework.

8.5. Curvature Instantons and Quantum Tunneling in Chronon Field Theory

In Chronon Field Theory (CFT), quantum tunneling arises naturally from the geometry of the chronon manifold rather than from an externally imposed uncertainty principle. The process corresponds to a finite reconfiguration of the chronon curvature two–form ${\mathsf{\Omega }}_{\mathsf{\Phi }}=D\mathsf{\Phi }\wedge D\mathsf{\Phi }$, connecting neighboring topological sectors with different symplectic flux quanta. In the conventional picture, tunneling between classically separated vacua proceeds through Euclidean configurations (instantons) whose amplitude is suppressed by $exp(-S_E/\hslash )$. In the chronon formulation, the suppression factor instead involves the geometric action unit ${\hslash }_{\mathrm{geom}}$:

$$P_{n\to n+1}\propto exp\left[-{\displaystyle \frac{S_{\mathrm{inst}}}{{\hslash }_{\mathrm{geom}}}}\right],S_{\mathrm{inst}}=\int d^{4}x\sqrt{g}\Delta R_{\mathsf{\Phi }}\left(x\right),$$

(83)

where $\Delta R_{\mathsf{\Phi }}$ denotes the excess curvature required to unwind and rewind one unit of chronon flux between adjacent topological sectors ${\oint }_{{\mathsf{\Sigma }}_2}{\mathsf{\Omega }}_{\mathsf{\Phi }}=n{\hslash }_{\mathrm{geom}}$ and $(n+1){\hslash }_{\mathrm{geom}}$.

Physically, the tunneling instanton represents a localized region in which the chronon curvature momentarily departs from its stabilized value, producing a “bubble” of reduced symplectic alignment. In this region the determinant of the induced symplectic metric ${{\mathsf{\Omega }}_{\mathsf{\Phi }}^{-1}}_{\mu \nu }$ transiently vanishes, allowing the field to slip between curvature sectors. The corresponding Euclidean field equation,

$$D_{\mu }{D}^{\mu }{\mathsf{\Phi }}^{\nu }-{\displaystyle \frac{\partial V\left(\mathsf{\Phi }\right)}{\partial {\mathsf{\Phi }}_{\nu }}}=0,$$

(84)

admits finite–action instanton solutions that interpolate between vacua of distinct winding number.

The magnitude of tunneling suppression depends on the ratio $S_{\mathrm{inst}}/{\hslash }_{\mathrm{geom}}$. In the early, pre–geometric epoch—when curvature fluctuations were large and ${\hslash }_{\mathrm{geom}}$ had not yet stabilized—instantons could percolate freely, leading to rapid transitions between causal microdomains. During curvature condensation, as the chronon field aligned and the curvature modulus ${\hslash }_{\mathrm{geom}}$ became fixed, the tunneling rate diminished exponentially. Once the field reached the ordered quantum phase, curvature instantons became energetically costly and topological sectors were effectively frozen.

Today, with ${\hslash }_{\mathrm{geom}}$ stabilized and the chronon field globally aligned, tunneling between topological sectors is extraordinarily suppressed, analogous to defect freezing in condensed–matter systems following a symmetry–breaking transition. Residual instanton activity may persist only through rare, localized curvature fluctuations, potentially contributing to small vacuum polarization effects or trans–Planckian corrections [43,102].

In summary, quantum tunneling in CFT is a manifestation of curvature dynamics: transitions between distinct symplectic flux sectors proceed via finite–action curvature instantons, with amplitudes governed by the same invariant ${\hslash }_{\mathrm{geom}}$ that controls ordinary quantum processes. Once curvature coherence is established, these processes become exponentially suppressed, ensuring the stability of matter and causal structure in the present cosmic epoch.

8.6. Reinterpretation of Blackbody Radiation and the Rayleigh–Jeans Limit

In classical electrodynamics, the Rayleigh–Jeans law predicts an unbounded increase in radiative energy density at high frequencies,

$$u\left(\nu \right)d\nu ={\displaystyle \frac{8\pi {\nu }^2}{c^3}}{k}_{B}Td\nu ,$$

(85)

leading to the so-called ultraviolet catastrophe [80]. Planck famously resolved this divergence by introducing discrete energy quanta $E=n\hslash \omega$ and postulating a universal constant of action ℏ [74]. Within Chronon Field Theory (CFT), this classical breakdown and its quantum resolution admit a deeper geometric explanation.

In CFT, the electromagnetic field is not a fundamental continuum but a collective excitation of the underlying chronon manifold—a coherent phase wave of the causal field [59,60]. The chronon ensemble possesses a finite correlation length ${\ell }_P$ and a nonzero symplectic curvature modulus ℏ, which together bound the density of accessible phase-space modes. Fluctuations with wavelengths shorter than ${\ell }_P$ are geometrically suppressed, yielding an effective spectral cutoff frequency

$${\omega }_P\sim {\displaystyle \frac{c}{{\ell }_P}},$$

(86)

and a modified high-frequency density of states

$$\rho \left(\omega \right)d\omega \propto {\omega }^2{e}^{-\omega /{\omega }_P}d\omega .$$

(87)

This exponential attenuation replaces the unphysical divergence of the Rayleigh–Jeans law with a smooth geometric saturation determined by the finite curvature of causal phase space.

Once the chronon field condenses into its coherent (quantum) phase, energy exchange between solitons and collective phase waves occurs only in discrete packets of symplectic flux, each equal to $\hslash \omega$. The emergent spectral distribution therefore assumes the Planck form,

$$u\left(\omega \right)d\omega ={\displaystyle \frac{8\pi {\omega }^2}{c^3}}{\displaystyle \frac{\hslash \omega }{e^{\hslash \omega /k_{B}T}-1}}d\omega ,$$

(88)

without any a priori quantization postulate. Quantization appears dynamically as a manifestation of the finite symplectic area of the chronon manifold—the same invariant that governs canonical commutation, spin quantization, and Fermi–Bose statistics.

In this geometric interpretation, the ultraviolet catastrophe never arises: the chronon field enforces a minimal unit of causal curvature (the invariant ℏ) and a maximal correlation frequency ${\omega }_P$. The Planck distribution thus emerges as a stable, scale-invariant equilibrium between coherent causal order and stochastic chronon fluctuations—a fundamental consequence of the discrete symplectic structure of spacetime itself.

8.7. Extension to Curved and Dynamical Geometries

In this study, the chronon ensemble was formulated on a flat discrete lattice acting as a regulator for the pre-geometric phase. The next theoretical step is to extend the construction to arbitrary causal complexes that approximate curved or dynamical manifolds [65,82]. Such an extension would enable direct investigation of how spacetime curvature and gravitational dynamics emerge as collective excitations of the same microscopic substrate that produces quantization.

Mathematically, this entails promoting the alignment coupling J to a spatially dependent field $J(p,q)$ whose fluctuations encode an effective metric tensor $g_{\mu \nu }\left(x\right)$ under coarse-graining. Variational analysis of the chronon free energy with respect to $J(p,q)$ is expected to yield an emergent Einstein–Hilbert term in the continuum limit,

$$S_{\mathrm{grav}}\sim \int {\mathrm{d}}^{4}x\sqrt{-g}R\left[g\right],$$

(89)

with curvature sourced by solitonic energy densities [49]. This would unify spacetime geometry, matter, and quantization as ordered phases of a single microscopic medium.

8.8. Connection to Holography and Emergent Spacetime

The chronon phase transition admits a natural holographic interpretation. At the Planck boundary, where local coherence first forms, the chronon ensemble defines a holographic screen separating the pre-geometric interior from the emergent spacetime exterior. The information content on this screen scales with its area, consistent with holographic entropy bounds [4,92,93],

$$S_{\mathrm{holo}}\sim {\displaystyle \frac{A}{4{\ell }_P^2}}.$$

(90)

Each chronon thus acts as an elementary carrier of causal information, and ℏ quantifies the minimal action—and therefore minimal information flux—transmitted across the screen. The chronon field thereby provides a microscopic origin for the holographic principle, linking quantization, information, and causal geometry through a single invariant structure.

8.9. Universality of ℏ and Relation to Entropy

An outstanding question concerns the universality of ℏ: is it a fixed modulus of the chronon microdynamics or a contingent property of specific phases? Scaling arguments suggest that ℏ depends only on the ratio of the stiffness and pinning parameters, $\hslash \sim J^{3/2}/\left(\lambda \sqrt{\rho }\right)$, implying universality across all stable chronon phases [70,98]. In this sense, ℏ is an intrinsic feature of causal order, invariant under cosmological evolution.

Since ℏ simultaneously determines the minimal symplectic area and the minimal information quantum (via the entropy relation $S=k_{B}ln\mathsf{\Omega }$), it forms a natural bridge between thermodynamics and quantum theory [57,64]. Exploring the connection between ℏ, entropy production, and information flow may clarify the origin of the arrow of time and the thermodynamic nature of quantum uncertainty. Combined with the Lorentzian exclusivity theorem of [59], these relationships suggest that causality, quantization, and entropy are geometrically unified aspects of the same temporal order parameter.

8.10. Toward Unification of Matter and Geometry

Chronon solitons behave as localized, quantized packets of curvature, momentum, and phase. If additional internal symmetries emerge through spontaneous symmetry breaking of the chronon order parameter, the Standard Model particle multiplets could appear as distinct topological sectors of the same field [66,107]. Gauge interactions would then arise from collective phase connections between solitons, while gravitational curvature would correspond to long-wavelength modulations of background connectivity.

From this perspective, all fundamental interactions—including quantum mechanics itself—become complementary manifestations of the same discrete pre-geometric substrate. The chronon condensate defines spacetime, matter, and quantization as coherent, causally ordered phases of a single microscopic system.

8.11. Summary and Long-Term Vision

The chronon framework reframes the central question of physics: not why nature is quantized, but how quantization, spin, and causality emerge dynamically. In this unified picture:

• ℏ is a curvature invariant of the Planck transition, not a postulate.
• Quantum mechanics is the hydrodynamic limit of coherent chronon excitations.
• Gravity and spacetime curvature arise from variations in chronon connectivity.
• Fermi–Bose statistics reflect topological coverings of the same symplectic manifold.
• Classical determinism corresponds to complete phase alignment (macroscopic decoherence).

Future efforts will focus on: (i) extending chronon lattice models to curved and expanding manifolds; (ii) deriving effective Einstein–Yang–Mills equations from chronon condensation; (iii) quantifying the information–action correspondence mediated by ℏ; and (iv) exploring potential laboratory analogues in condensed-matter and quantum-simulation systems [16].

Together with the Lorentzian results of [59], these developments outline a coherent program: causal structure, quantum commutation, spin quantization, and statistics all originate from the same symplectic and topological properties of the chronon field. The long-term goal is to establish a unified microscopic theory from which both quantum mechanics and general relativity emerge as stable, ordered phases of a single pre-geometric medium—the chronon field.

Appendix A.1. Energy Functional and Field Equations

In the continuum limit, the chronon energy functional is

$$E\left[X\right]={\int }_{{\mathbb{R}}^3}{d}^{3}x\left[{\displaystyle \frac{J}{2}}\left({\partial }_i{X}^{\mu }\right)\left({\partial }_i{X}_{\mu }\right)+{\displaystyle \frac{\lambda }{2}}{(X^{\mu }{X}_{\mu }+1)}^2\right],J>0,\lambda >0,$$

(A1)

where J sets the gradient stiffness and $\lambda$ softly enforces the Lorentzian unit constraint. Variation of (A1) yields the Euler–Lagrange equation

$$J{\nabla }^2{X}_{\mu }-2\lambda (X^{\nu }{X}_{\nu }+1)X_{\mu }=0.$$

(A2)

Finite-energy configurations must satisfy $X^{\mu }{X}_{\mu }\to -1$ as $r\to \infty$, compactifying spatial infinity to $S^3$. Hence field configurations define continuous maps

$$X:S_{\mathrm{space}}^3⟶S_{\mathrm{target}}^3,$$

characterized by the integer-valued winding number

$$Q={\displaystyle \frac{1}{12{\pi }^2}}{\int }_{{\mathbb{R}}^3}{ϵ}^{ijk}{ϵ}_{\mu \nu \rho \sigma }{X}^{\mu }{\partial }_i{X}^{\nu }{\partial }_j{X}^{\rho }{\partial }_k{X}^{\sigma }{d}^{3}x\in \mathbb{Z},$$

(A3)

analogous to the baryon number in Skyrme-type theories [89]. Configurations with $Q\ne 0$ are topologically distinct from the vacuum and cannot unwind continuously, ensuring topological protection.

Appendix A.2. Derrick Scaling Argument and Stability

For purely quadratic-gradient theories ($\lambda =0$), Derrick’s theorem forbids finite-size stationary solutions in $d>1$ spatial dimensions: a uniform rescaling $x\to \alpha x$ monotonically decreases the total energy [23]. The quartic chronon term, however, modifies this scaling and stabilizes localized solutions in a mechanism directly analogous to the Skyrme term [88].

Under a rescaling $x\to \alpha x$, the gradient and potential terms transform as

$$E_{\mathrm{grad}}\left(\alpha \right)=\alpha E_{\mathrm{grad}}\left(1\right),E_{\mathrm{pot}}\left(\alpha \right)={\alpha }^3{E}_{\mathrm{pot}}\left(1\right),$$

(A4)

so that

$$E\left(\alpha \right)=J\alpha E_{\mathrm{grad}}\left(1\right)+\lambda {\alpha }^3{E}_{\mathrm{pot}}\left(1\right).$$

(A5)

A stationary configuration requires $dE/d\alpha =0$, giving

$$J{E}_{\mathrm{grad}}\left(1\right)+3\lambda E_{\mathrm{pot}}\left(1\right)=0.$$

(A6)

This condition is satisfied for a finite equilibrium scale

$$r_{\mathrm{sol}}\sim \sqrt{{\displaystyle \frac{J}{\lambda }}},$$

which sets the soliton’s characteristic radius. Equation (A6) demonstrates that the quartic term provides a positive pressure opposing collapse, balancing the gradient tension and evading Derrick’s no-go result [18]. Thus, localized, stable solutions exist in $3+1$ dimensions whenever $\lambda >0$.

Appendix A.3. Topological and Energetic Interpretation

The quartic term plays a dual physical role:

• Soft unit-norm pinning: It penalizes radial excursions from $X^{\mu }{X}_{\mu }=-1$, establishing a well-defined orientation and internal phase for each chronon domain.
• Nonlinear stabilization: It breaks scale invariance and produces a finite equilibrium radius $r_{\mathrm{sol}}$, enabling soliton stability against collapse.

Consequently, the same interaction that enforces local Lorentzian alignment also generates topologically stable, finite-energy excitations [66].

Appendix A.4. Minimal Action and Identification with ℏ

Each soliton carries a finite action obtained by integrating the conjugate momentum along its internal phase trajectory,

$$S_{\mathrm{soliton}}=\int \pi d\theta .$$

(A7)

Within numerical precision, the measured value of (A7) equals the plateau value of the effective action variance ${\widehat{\hslash }}_{\mathrm{eff}}$ extracted in Section 5, establishing the correspondence

$$S_{\mathrm{soliton}}\simeq \hslash .$$

Thus the Planck correlation length ${\ell }_P\sim r_{\mathrm{sol}}$ marks the threshold at which solitonic excitations become dynamically stable and carry the minimal quantum of action. The invariant ℏ thereby emerges as the symplectic area associated with the smallest topologically stable solution of the chronon field, in analogy with quantized Skyrmions and Hopf solitons [31].

Remark A1. 

The existence proof presented here extends the classical Derrick argument to chronon dynamics and confirms that the quartic pinning term guarantees stable solitons in $(3+1)$ dimensions. It thus establishes the microscopic foundation for the quantized unit of action in Chronon Field Theory, unifying geometric, topological, and dynamical stability [84].

Figure A1. Emergence of solitons as quantized packets of causal orientation. Aligned chronons (gray) twist coherently through $2\pi$ within a localized region, forming a topologically stable soliton. Each soliton carries one quantum of symplectic action $S_{\mathrm{soliton}}=\hslash$, representing the minimal causal rotation allowed by the chronon field.

Figure A1. Emergence of solitons as quantized packets of causal orientation. Aligned chronons (gray) twist coherently through $2\pi$ within a localized region, forming a topologically stable soliton. Each soliton carries one quantum of symplectic action $S_{\mathrm{soliton}}=\hslash$, representing the minimal causal rotation allowed by the chronon field.

Appendix C.1. Analytic Derivation: Bogomolny Bound in 1+1D

Consider the one-dimensional reduction of the coarse-grained chronon phase field, described by the sine–Gordon Lagrangian density [21]

$$\mathcal{L}={\displaystyle \frac{1}{2}}\left[{\left({\partial }_t\theta \right)}^2-{\left({\partial }_x\theta \right)}^2\right]-{\mu }^2(1-cos\theta ),$$

(A11)

which captures the effective dynamics of a stabilized domain wall. For static configurations $\theta \left(x\right)$ connecting vacua $\theta (-\infty )=0$ and $\theta (+\infty )=2\pi Q$, the energy functional is

$$E\left[\theta \right]={\int }_{-\infty }^{+\infty }dx\left[\frac{1}{2}{\left({\partial }_x\theta \right)}^2+{\mu }^2(1-cos\theta )\right].$$

(A12)

Completing the square yields the Bogomolny inequality (BPS bound) [7,75]

$$E=\int dx\left[\frac{1}{2}{({\partial }_x\theta \mp 2\mu sin\left(\frac{\theta }{2}\right))}^2\pm 2\mu {\partial }_x\theta sin\left(\frac{\theta }{2}\right)\right]\ge 8\mu \left|Q\right|,$$

(A13)

with equality for the kink (or antikink) solution satisfying the first-order self-dual equation

$${\partial }_x\theta =\pm 2\mu sin\left(\frac{\theta }{2}\right).$$

The explicit soliton profile is

$${\theta }_{\mathrm{kink}}\left(x\right)=4arctan{e}^{\mu (x-x_0)},$$

(A14)

and its minimal action (or rest energy) is

$$S_{min}^{(1+1)\mathrm{D}}=8\mu \left|Q\right|.$$

(A15)

This defines the smallest topologically stable configuration of the effective chronon phase field.

Appendix C.2. Numerical Verification of S min =8μ

To confirm the analytic bound (A15), we implemented a gradient-flow solver for the parabolic relaxation equation [14,76]

$${\partial }_{\tau }\theta ={\partial }_x^2\theta -{\mu }^{2}sin\theta ,$$

(A16)

subject to boundary conditions $\theta (-L)=0$, $\theta \left(L\right)=2\pi$. This flow monotonically decreases the energy functional $E\left[\theta \right]$, converging to the stable kink solution as $\tau \to \infty$. For $\mu \in [0.5,2.0]$, grid spacing $a\sim {10}^{-3}$, and domain length $L\gtrsim 10/\mu$, the numerical minimal action,

$$S_{min}^{\mathrm{num}}=\sum _{x}a\left[\frac{1}{2}{\left({\Delta }_x\theta \right)}^2+{\mu }^2(1-cos\theta )\right],$$

matches $8\mu$ to machine precision ($|\Delta S/S|<{10}^{-12}$). The plateau behavior of the cumulative action $S\left(R\right)$ and its comparison with the analytic prediction are shown in Figure A2.

Figure A2. Verification of the minimal soliton action in 1+1 D Chronon Field Theory. (A) Cumulative soliton action $S\left(R\right)={\int }_{-R}^R\mathcal{L}dx$ saturates to a plateau as the window half–width R increases, demonstrating convergence to a stable topological configuration. (B) Measured plateau values ${\hslash }_{\mathrm{eff}}^{\left(\mathrm{plateau}\right)}$ for several values of the mass parameter $\mu$ coincide with the theoretical prediction $S_{min}^{(1+1)\mathrm{D}}=8\mu$, confirming that the Planck action arises as the minimal soliton action of the chronon field. Residuals are below ${10}^{-12}$ across the tested range, verifying that the quantized unit of action is a geometric invariant of the 1+1 D chronon manifold.

Figure A2. Verification of the minimal soliton action in 1+1 D Chronon Field Theory. (A) Cumulative soliton action $S\left(R\right)={\int }_{-R}^R\mathcal{L}dx$ saturates to a plateau as the window half–width R increases, demonstrating convergence to a stable topological configuration. (B) Measured plateau values ${\hslash }_{\mathrm{eff}}^{\left(\mathrm{plateau}\right)}$ for several values of the mass parameter $\mu$ coincide with the theoretical prediction $S_{min}^{(1+1)\mathrm{D}}=8\mu$, confirming that the Planck action arises as the minimal soliton action of the chronon field. Residuals are below ${10}^{-12}$ across the tested range, verifying that the quantized unit of action is a geometric invariant of the 1+1 D chronon manifold.

Appendix C.3. Embedding into the 3+1D Chronon Lattice

Within stabilized regions of the four-dimensional chronon lattice, one identifies one-dimensional soliton lines (topological tubes) as loci where the coarse phase $\theta$ winds by $2\pi$ along a chosen spatial direction. The local action per unit transverse area is computed as

$$S_{\mathrm{line}}=\sum _{s}a\left[\frac{1}{2}{\left({\Delta }_s\theta \right)}^2+{\mu }^2(1-cos\theta )\right].$$

(A17)

Averaging over all detected kink lines yields a narrow distribution peaked at $S_{\mathrm{line}}\simeq S_{min}^{(1+1)\mathrm{D}}$, indicating that each soliton line carries precisely one quantum of action. The plateau value of the measured ${\widehat{\hslash }}_{\mathrm{eff}}$ in Figure A2 coincides numerically with the theoretical minimum,

$${\widehat{\hslash }}_{\mathrm{eff}}^{\left(\mathrm{plateau}\right)}\simeq S_{min}^{(1+1)\mathrm{D}}=8\mu .$$

(A18)

Hence, the Planck action arises naturally as the minimal soliton action of the chronon field.

Appendix C.4. Interpretation

Equation (A18) establishes that the invariant Planck constant ℏ corresponds to the minimal symplectic area—the least dynamically stable action quantum—carried by a self-consistent soliton of the chronon field. This provides a concrete realization of the minimal-action principle proposed in [59,60]: the Planck-scale invariant ℏ equals the smallest achievable symplectic flux consistent with the field’s nonlinear equations of motion. The canonical commutation relation,

$$[\widehat{\theta },\widehat{\pi }]=i\hslash ,$$

thus reflects the topological and variational structure of the underlying chronon medium rather than an imposed quantization rule. The soliton embodies the fundamental geometric unit of action, bridging pre-geometric dynamics and observable quantum mechanics.