The Schrödinger Equation for a Free Particle: Generalized Bessel Solutions

1. Introduction

The Schrödinger equation for a free particle remains a subject of enduring importance, standing as one of the foundational pillars of non-relativistic quantum mechanics. Despite its deceptively simple form, the free-particle problem reveals a remarkably rich mathematical structure, providing a conceptual and computational framework that underpins a wide range of phenomena in quantum theory. Its solutions form the basis for understanding more complex scenarios, including scattering processes, the evolution and dispersion of wave packets, and the manifestation of symmetries in quantum systems, which play a crucial role in the classification of quantum states and the derivation of conservation laws [1,2,3]. Beyond its pedagogical and theoretical value, the free-particle problem serves as a testing ground for analytical methods and approximation techniques, bridging the gap between abstract formalism and experimentally observable effects.

Furthermore, the study of free-particle solutions highlights the profound interplay between quantum mechanics and special functions, a connection that becomes particularly evident when the problem is formulated in alternative coordinate systems. For instance, in spherical coordinates, the separation of variables naturally leads to the emergence of Bessel and spherical Bessel functions, which encode the radial dependence of the wavefunction and reflect the underlying rotational symmetry of the system. These functions are not only mathematically elegant, but also provide essential tools for the construction of eigenstates with well-defined angular momentum, the analysis of scattering amplitudes, and the development of more general solutions in external potentials or constrained geometries. Similar analyses have been extended to cylindrical geometries, where the Schrödinger equation is solved using Bessel functions to describe nondiffracting solutions [4] and quantum scattering from circular or rectangular barriers [5]. In this sense, the Schrödinger equation for free particles exemplifies how fundamental quantum systems, even in their simplest form, can give rise to rich mathematical structures that inform both foundational theory and practical applications in modern quantum physics [6,7,8].

In three spatial dimensions, the dynamics of a free particle is described by the time-dependent Schrödinger equation,

$$i{\displaystyle \frac{\partial \psi (\mathbf{r},t)}{\partial t}}=-{\displaystyle \frac{1}{2}}{\nabla }^2\psi (\mathbf{r},t),$$

(1)

where natural units, $\hslash =m=1$, are adopted, as well as throughout this work. The vector $\mathbf{r}=(x,y,z)$ denotes the position, and ${\nabla }^2={\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial y^2}}+{\displaystyle \frac{{\partial }^2}{\partial z^2}}$ represents the three-dimensional Laplacian operator. The general solution of Equation (1) can be constructed using the separation of variables in spherical coordinates, which decomposes the wave function into radial and angular parts. In this representation, the elementary solutions take the form

$${\psi }_{E,l,m}(r,\theta ,\varphi ,t)=C_{l,m}\left(E\right)e^{-iEt}{Y}_l^m(\theta ,\varphi )j_l\left(\sqrt{2E}r\right),$$

(2)

where E is the continuous energy eigenvalue, $Y_l^m(\theta ,\varphi )$ are the spherical harmonics with $l\in {\mathbb{N}}_0$ and $m\in \{-l,\dots ,l\}$, $j_l\left(z\right)$ denotes the spherical Bessel functions of the first kind, and $C_{l,m}\left(E\right)$ are normalization constants that can depend on the energy. The radial part of the wavefunction, given by $j_l\left(\sqrt{2E}r\right)$, satisfies the reduced one-dimensional Schrödinger equation obtained after factoring out the angular dependence, and the angular part, given by $Y_l^m(\theta ,\varphi )$, satisfies the eigenvalue equation of the squared angular momentum operator. The combination of these functions provides a complete set of orthogonal solutions that span the Hilbert space of free-particle states in three dimensions. This construction allows for the analysis of physical phenomena such as the evolution of localized wave packets, scattering by central potentials, and the imposition of boundary conditions in confined geometries. Although the standard treatment focuses on spherical Bessel functions, other classes of functions can be used to represent solutions under different boundary conditions or coordinate systems, where the Schrödinger equation is solved in cylindrical coordinates using Neumann and Hankel functions [9,10]. This motivates the present work to explore new families of solutions beyond the conventional framework.

This work is organized as follows. Section 2 presents the one-dimensional solution of the Schrödinger equation for a free particle with initial conditions given by Bessel functions, introducing the generalized Bessel function formalism. Section 3 extends the recursion relations to three dimensions, deriving key operator identities for the radial Laplacian acting on Bessel-type functions, and we construct the exact solution of the three-dimensional Schrödinger equation for free particles with Bessel initial conditions, expressing the time-evolved wavefunction in compact form using generalized Bessel functions. Section 4 discusses the extension to arbitrary initial radial functions through Bessel series expansions, highlighting applications to Gaussian wavepackets and other physically relevant profiles. Finally, we present our conclusions and outline potential directions for future research.

2. One Dimensional Solution for an Initial Bessel Function

In natural units where $m=1$ and $\hslash =1$, the one-dimensional Schrödinger equation for a free particle is written as

$$i{\displaystyle \frac{\partial \psi (x,t)}{\partial t}}=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2\psi (x,t)}{\partial x^2}}.$$

(3)

The above equation defines the time evolution of the quantum state $\psi (x,t)$ in terms of the second spatial derivative, which represents the kinetic energy operator in one dimension. The formal solution can be expressed as

$$\psi (x,t)=exp\left(i{\displaystyle \frac{t}{2}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}\right)\psi (x,0),$$

(4)

where ${\displaystyle \frac{\partial }{\partial x}}$ denotes the partial derivative with respect to x, and the exponential of the differential operator acts on the initial condition $\psi (x,0)$. This operator form is equivalent to the application of the propagator in position space and can be expanded as a power series to obtain the time evolution of any sufficiently smooth initial wavefunction. The representation emphasizes the linearity of the Schrödinger equation and the role of the kinetic operator in generating dynamics through repeated differentiation.

If the initial wave function is chosen as a Bessel function of the first kind, $\psi (x,0)=J_n\left(\eta x\right)$, with $\eta$ an arbitrary constant, the recursion relations of the Bessel functions can be used to evaluate the repeated derivatives appearing in the series expansion. The standard recursion relation is ${\displaystyle \frac{d{J}_n\left(x\right)}{dx}}={\displaystyle \frac{1}{2}}[J_{n-1}\left(x\right)-J_{n+1}\left(x\right)]$, which is generalized with the scaled argument to

$${\displaystyle \frac{d{J}_n\left(\eta x\right)}{dx}}={\displaystyle \frac{\eta }{2}}\left[J_{n-1}\left(\eta x\right)-J_{n+1}\left(\eta x\right)\right].$$

(5)

This relation allows to express higher-order derivatives in terms of linear combinations of Bessel functions with shifted indices. In particular, applying s derivatives yields

$${\left({\displaystyle \frac{d}{dx}}\right)}^s{J}_n\left(\eta x\right)={\left({\displaystyle \frac{\eta }{2}}\right)}^s\sum _{j=0}^s{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{s}{j}}\right)J_{n-s+2j}\left(\eta x\right),$$

(6)

which provides a systematic method for evaluating the action of the operator series $exp\left(i{\displaystyle \frac{t}{2}}{\displaystyle \frac{\partial }{\partial x^2}}\right)$ on the initial condition. Using this expression, the time evolution of the wavefunction can be written as

$$\psi (x,t)=\sum _{s=0}^{\infty }{\displaystyle \frac{1}{s!}}{\left({\displaystyle \frac{it}{2}}\right)}^s{\left({\displaystyle \frac{d^2}{d{x}^2}}\right)}^s{J}_n\left(\eta x\right)=\sum _{s=0}^{\infty }{\left({\displaystyle \frac{i{\eta }^{2}t}{8}}\right)}^s\sum _{j=0}^{2s}{\displaystyle \frac{{(-1)}^j}{s!}}\left({\displaystyle \genfrac{}{}{0pt}{}{2s}{j}}\right)J_{n-2s+2j}\left(\eta x\right).$$

(7)

This double summation shows explicitly how the propagation mixes different Bessel function orders and generates the complete solution from a single initial mode. It also provides a convenient framework for numerical evaluation or for analytical manipulations involving generating functions or operator methods.

An alternative and compact representation involves generalized two-variable Bessel functions, denoted ${\mathcal{J}}_n(x_1,x_2;s_1)$. As shown in [11], the solution to (1) with the initial condition $\psi (x,0)=J_n\left(\eta x\right)$, can be expressed as

$$\psi (x,t)=exp\left(-i{\displaystyle \frac{{\eta }^{2}t}{4}}\right){\mathcal{J}}_n\left(\eta x,{\displaystyle \frac{{\eta }^{2}t}{4}};i\right),$$

(8)

where the generalized Bessel functions are defined by the series [12,13,14]

$${\mathcal{J}}_n(x_1,x_2;s_1)=\sum _{l=-\infty }^{\infty }{s}_1^l{J}_{n-2l}\left(x_1\right)J_l\left(x_2\right),n\in \mathbb{Z}.$$

(9)

Here, $J_m\left(z\right)$ are ordinary Bessel functions of the first kind, and $s_1$ is a complex parameter. This representation makes explicit the dependence on both the spatial coordinate and the evolution parameter and allows a direct connection with operator-based techniques and generating functions. Using this definition, the generalized Bessel function can be expanded as

$${\mathcal{J}}_n\left(\eta x,{\displaystyle \frac{{\eta }^{2}t}{4}};i\right)=exp\left(i{\displaystyle \frac{{\eta }^{2}t}{4}}\right)\sum _{s=0}^{\infty }{\displaystyle \frac{1}{s!}}{\left(i{\displaystyle \frac{{\eta }^{2}t}{8}}\right)}^s\sum _{j=0}^{2s}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{2s}{j}}\right)J_{n-2s+2j}\left(\eta x\right).$$

(10)

This result, derived from the exponential expansion of the operator, provides the foundation for analyzing the propagation of an initial Bessel-type wavefunction and establishes the framework for extending the analysis to generalized or multiparameter Bessel states.

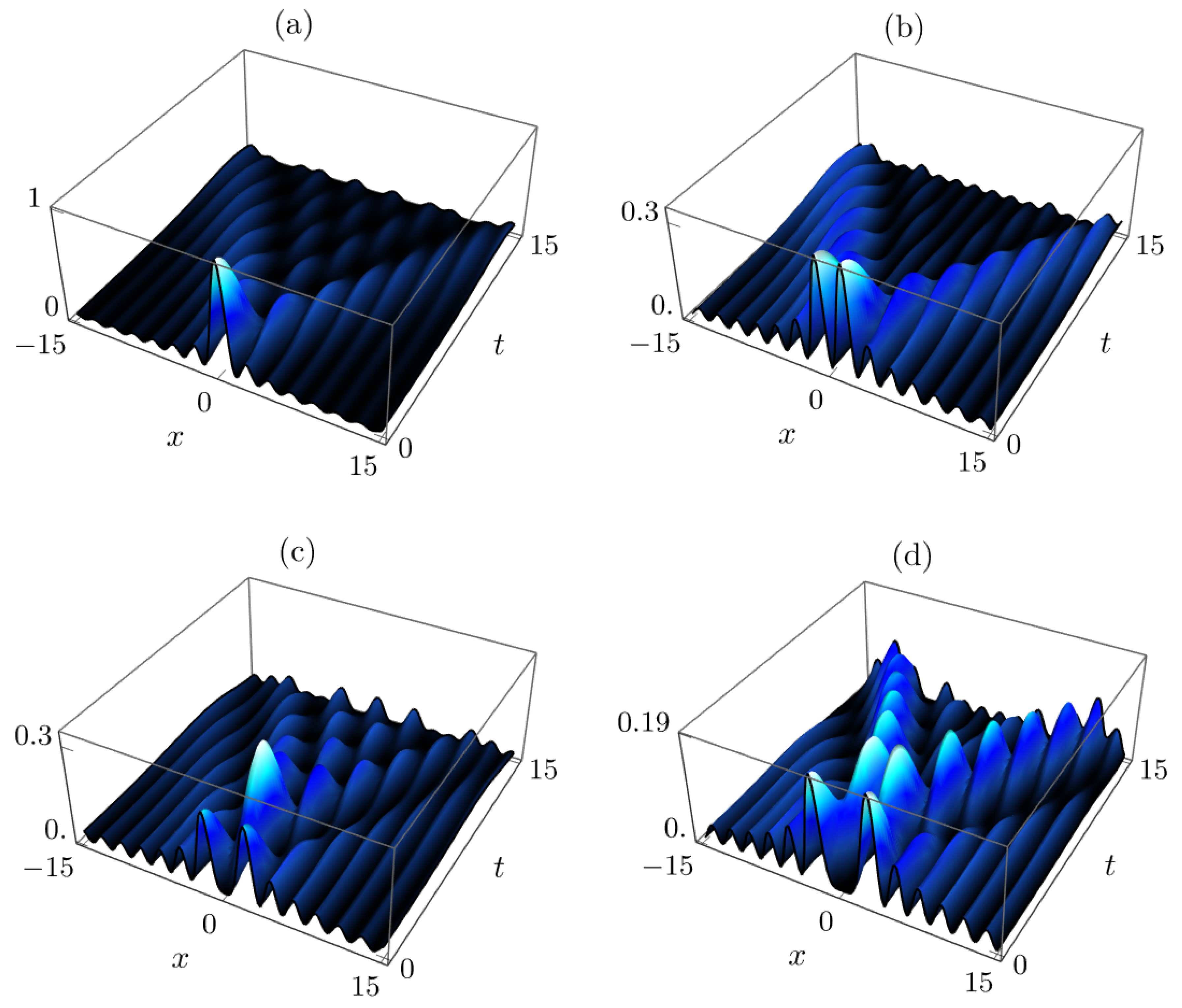
Figure 1 shows the probability density ${\left|\psi (x,t)\right|}^2$ of the exact free-particle wavefunction from Equation (8), for the quantum numbers $n=0,1,2,3$ and the parameter $\eta =1.5$. These solutions, corresponding to the initial conditions $\psi (x,0)=J_n\left(\eta x\right)$, are compactly expressed through the generalized Bessel function ${\mathcal{J}}_n(x_1,x_2;s_1)$ with parameters $x_1=\eta x$, $x_2={\displaystyle \frac{{\eta }^{2}t}{4}}$, and $s_1=i$. As n increases, the spatial probability density exhibits progressively more complex oscillatory structures, marked by additional lobes and nodal points. This behavior stems from the high-order Bessel function composition of the initial state and reveals interference among multiple Bessel components in the series expansion of Equation (10). The temporal evolution maintains these oscillatory features while showing dispersion-induced modulation, which is in agreement with the expected dynamics of free-particle wavepackets.

3. Generalization of the Recursion Relation to 3D

To extend our analysis to three-dimensional systems with spherical symmetry, we begin by expressing the Laplace operator in spherical coordinates,

$${\nabla }^{2}f={\displaystyle \frac{{\partial }^{2}f}{\partial r^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial f}{\partial r}}+{\displaystyle \frac{1}{r^{2}sin\theta }}\left(cos\theta {\displaystyle \frac{\partial f}{\partial \theta }}+sin\theta {\displaystyle \frac{{\partial }^{2}f}{\partial {\theta }^2}}\right)+{\displaystyle \frac{1}{r^2{sin}^2\theta }}{\displaystyle \frac{{\partial }^{2}f}{\partial {\phi }^2}}.$$

(11)

For problems exhibiting radial symmetry, where the wave function depends exclusively on the radial coordinate $f=f\left(r\right)$, all angular derivatives vanish and the Laplacian simplifies considerably to its radial component: ${\nabla }^{2}f={\displaystyle \frac{d^{2}f}{d{r}^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{df}{dr}}$. Motivated by this reduction, we examine the particular case $f\left(r\right)={\displaystyle \frac{J_n\left(\eta r\right)}{r}}$, a form that arises naturally in quantum systems with spherical or cylindrical symmetry and serves as a fundamental basis for constructing more general solutions. For this specific functional form, the Laplacian operation yields: ${\nabla }^2\left[{\displaystyle \frac{J_n\left(\eta r\right)}{r}}\right]={\displaystyle \frac{{\eta }^2}{r}}{\displaystyle \frac{d^2{J}_n\left(\eta r\right)}{d{r}^2}}$. Using the one-dimensional recurrence relation established in Equation (5), we now derive its three-dimensional counterpart:

$${\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2\left[{\displaystyle \frac{J_n\left(\eta r\right)}{r}}\right]={\displaystyle \frac{J_{n-2}\left(\eta r\right)}{r}}-2{\displaystyle \frac{J_n\left(\eta r\right)}{r}}+{\displaystyle \frac{J_{n+2}\left(\eta r\right)}{r}}.$$

(12)

This fundamental relation reveals how the Laplacian operator connects Bessel functions of different orders in the radial coordinate. Applying the operator ${\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2$ a second time yields

$${\left({\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2\right)}^2{\displaystyle \frac{J_n\left(\eta r\right)}{r}}={\displaystyle \frac{1}{r}}\left[J_{n+4}\left(\eta r\right)-4J_{n+2}\left(\eta r\right)+6J_n\left(\eta r\right)-4J_{n-2}\left(\eta r\right)+J_{n-4}\left(\eta r\right)\right],$$

(13)

which can be expressed as:

$${\left({\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2\right)}^2{\displaystyle \frac{J_n\left(\eta r\right)}{r}}={\displaystyle \frac{1}{r}}\sum _{j=0}^4{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{4}{j}}\right)J_{n+4-2j}\left(\eta r\right).$$

(14)

The emerging binomial pattern suggests a general formula, which we prove by mathematical induction to hold for an arbitrary integer $s\ge 0$:

$${\left({\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2\right)}^s{\displaystyle \frac{J_n\left(\eta r\right)}{r}}={\displaystyle \frac{1}{r}}\sum _{j=0}^{2s}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{2s}{j}}\right)J_{n+2s-2j}\left(\eta r\right).$$

(15)

This recurrence relation provides the mathematical foundation for deriving exact solutions to the three-dimensional Schrödinger equation when the initial conditions are specified in terms of Bessel functions. Facilitates the systematic evaluation of how the time evolution operator acts on radial wavefunctions, thereby enabling the construction of complete time-dependent solutions.

The formal solution to the three-dimensional Schrödinger equation for a free particle, Equation (1), is given by the exponential operator expression

$$\psi (\mathbf{r},t)=exp\left(i{\displaystyle \frac{t}{2}}{\nabla }^2\right)\psi (\mathbf{r},0).$$

(16)

When the initial condition takes the form $\psi (\mathbf{r},0)={\displaystyle \frac{J_n\left(\eta r\right)}{r}}$, the solution becomes

$$\begin{array}{cc}\hfill \psi (r,t)& =exp\left(i{\displaystyle \frac{t}{2}}{\nabla }^2\right){\displaystyle \frac{J_n\left(\eta r\right)}{r}}\hfill \\ \hfill & =\sum _{s=0}^{\infty }{\displaystyle \frac{1}{s!}}{\left({\displaystyle \frac{it}{2}}\right)}^s{\left({\nabla }^2\right)}^s{\displaystyle \frac{J_n\left(\eta r\right)}{r}}\hfill \\ \hfill & =\sum _{s=0}^{\infty }{\displaystyle \frac{1}{s!}}{\left({\displaystyle \frac{i{\eta }^{2}t}{8}}\right)}^s{\left({\displaystyle \frac{4}{{\eta }^2}}{\nabla }^2\right)}^s{\displaystyle \frac{J_n\left(\eta r\right)}{r}},\hfill \end{array}$$

(17)

where the second line expands the exponential as a power series in the Laplacian operator, and the third line rescales the expansion parameter to explicitly show the dependence on $\eta$. Applying the recurrence relation from Equation (15), which expresses the s-th power of the rescaled Laplacian acting on the Bessel function, produces the double series expansion

$$\psi (r,t)={\displaystyle \frac{1}{r}}\sum _{s=0}^{\infty }{\displaystyle \frac{1}{s!}}{\left({\displaystyle \frac{i{\eta }^{2}t}{8}}\right)}^s\sum _{j=0}^{2s}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{2s}{j}}\right)J_{n+2s-2j}\left(\eta r\right).$$

(18)

This expression shows that the time evolution generates a superposition of Bessel functions of different orders, with coefficients determined by a binomial distribution. Comparison with the series definition of the generalized Bessel function in Equation (10) shows that this double series is equivalent to the compact form

$$\psi (r,t)={\displaystyle \frac{exp\left(-i\frac{{\eta }^{2}t}{4}\right)}{r}}{\mathcal{J}}_n\left(\eta r,{\displaystyle \frac{{\eta }^{2}t}{4}};i\right).$$

(19)

This result provides the complete time evolution of the wave function for a free particle in three dimensions starting from the initial condition ${\displaystyle \frac{J_n\left(\eta r\right)}{r}}$, expressed in closed form using the generalized Bessel function with complex parameter $s_1=i$, with the generalized Bessel function ${\mathcal{J}}_n(x_1,x_2;s_1)$ [11,12,13], and with parameters $x_1=\eta r$, $x_2={\displaystyle \frac{{\eta }^{2}t}{4}}$.

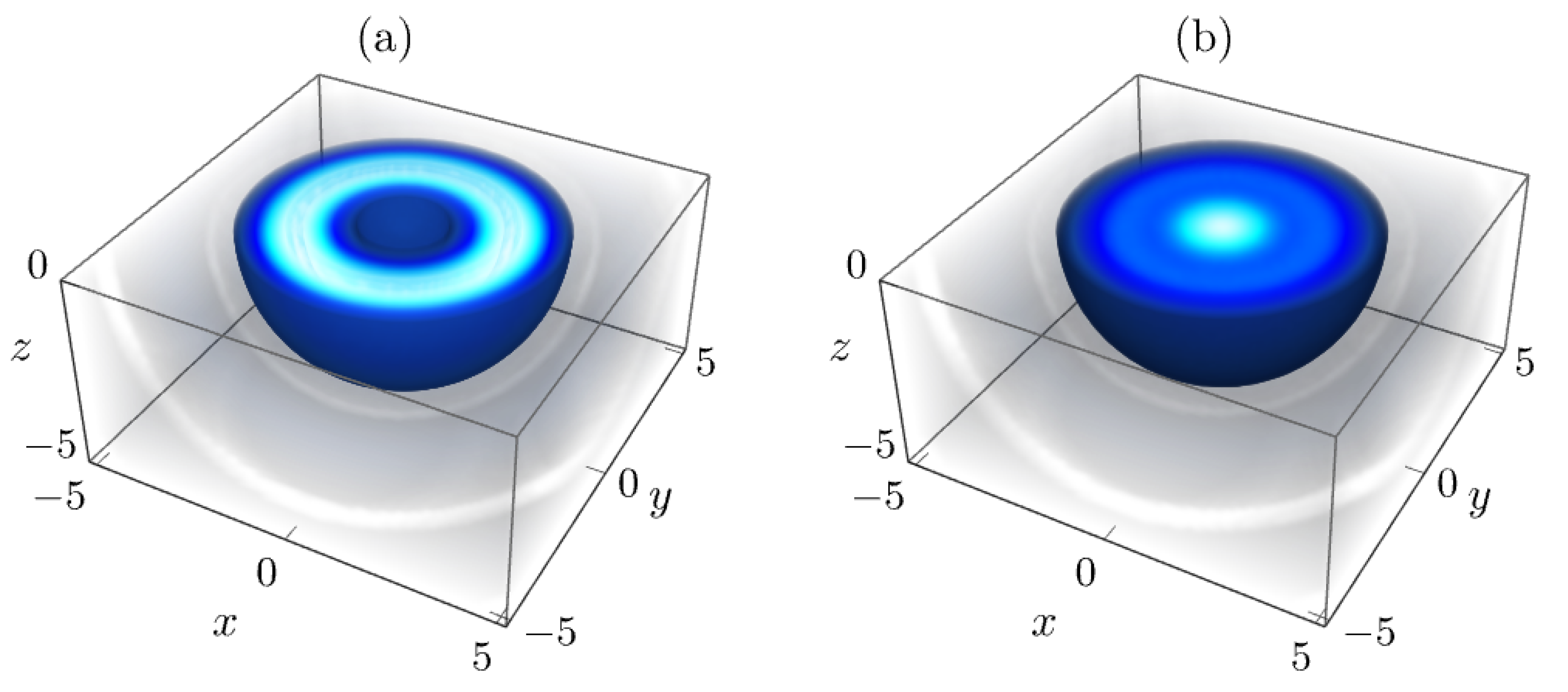
Figure 2 displays the squared modulus ${\left|\psi (r,t)\right|}^2$ from Equation (19) at times $t=0$ and $t=1$ for $\eta =1.5$ and $n=3$. The initial wave function $\psi (r,0)={\displaystyle \frac{J_n\left(\eta r\right)}{r}}$ evolves under Laplacian dynamics while preserving radial symmetry. This solution utilizes generalized Bessel functions ${\mathcal{J}}_n(x_1,x_2;s_1)$, providing an analytical alternative to the standard spherical Bessel treatment in Equation (2) for wavefunctions of the form $f=f\left(r\right)$.

4. Arbitrary Function

Given that we have obtained explicit solutions to the Schrödinger equation for a free particle in terms of Bessel functions of the first kind, it is natural to consider the extension of these results to arbitrary initial conditions. Since a wide class of functions can be represented as series involving Bessel functions, the formalism developed here allows for the propagation of such arbitrary wavefunctions. However, it is important to note that there exist multiple methods for expanding a function in terms of Bessel functions, each with its own mathematical structure and domain of applicability. Among the most relevant are the Fourier–Bessel series, which are constructed using the orthogonality of Bessel functions over finite intervals and involve the positive roots of $J_n\left(x\right)=0$, and the Neumann expansion, which expresses a function as a series of Bessel functions of increasing order and is applicable over infinite domains. The Fourier–Bessel series is particularly useful when the function is defined in a bounded interval and satisfies specific boundary conditions, while the Neumann expansion provides a more general framework, often involving contour integrals and Neumann polynomials for the computation of coefficients. These representations enable the construction of solutions to the time-dependent Schrödinger equation for a broad class of initial states and highlight the versatility of the Bessel function formalism in quantum dynamics.

Examples of functions that can be expanded in terms of Bessel functions include:

• Gaussian functions, such as $f\left(r\right)=exp(-\eta r^2)$, admit Neumann-type expansions because of their smoothness and decay at infinity.
• Step functions or rectangular profiles defined on finite intervals, which can be expanded using Fourier–Bessel series.
• Polynomial functions, such as $f\left(r\right)=r^j$, can be represented as finite or infinite series of Bessel functions depending on the domain.
• Oscillatory functions, such as $f\left(r\right)=sin\left(\mu r\right)$ or $cos\left(\mu r\right)$, which admit expansions involving Bessel functions through known integral transforms.

These expansions are not merely formal tools; they have concrete applications in physical problems. For instance, the propagation of a Gaussian wave packet in free space can be analyzed using Neumann-type expansions, providing insight into dispersion and coherence properties. Similarly, the Fourier–Bessel expansion is essential in solving problems with cylindrical symmetry, such as the radial propagation of matter waves in optical fibers or Bose–Einstein condensates confined in harmonic traps. The ability to represent arbitrary initial conditions within the Bessel framework thus extends the applicability of the method to a wide range of scenarios in quantum mechanics and wave physics.

5. Conclusions

This work has established a comprehensive framework for solving the time-dependent Schrödinger equation for free particles using generalized Bessel functions. We first developed the one-dimensional case, showing that initial Bessel functions $J_n\left(\eta x\right)$ evolve according to $\psi (x,t)=exp(-i{\eta }^{2}t/4){\mathcal{J}}_n(\eta x,{\eta }^{2}t/4;i)$, where the generalized Bessel function ${\mathcal{J}}_n$ encapsulates the full spacetime dynamics through its series representation.

Building on this foundation, we extended the analysis to three dimensions by deriving novel recursion relations that connect the Laplacian operator with Bessel functions of different orders. This enabled the exact evaluation of the time evolution operator acting on radial wavefunctions of the form $\psi (\mathbf{r},0)=J_n\left(\eta r\right)/r$, resulting in the compact solution $\psi (r,t)=exp(-i{\eta }^{2}t/4){\mathcal{J}}_n(\eta r,{\eta }^{2}t/4;i)/r$.

The generalized Bessel function approach provides several concrete advantages over conventional methods: it offers exact closed-form solutions that explicitly reveal the interference mechanisms between different Bessel components during temporal evolution; it enables efficient computation of quantum dynamics without recourse to numerical integration of the Schrödinger equation; and it establishes a mathematical structure that naturally accommodates the spherical symmetry of three-dimensional systems. Furthermore, the formalism can be extended to arbitrary radial functions through appropriate Bessel series expansions, making it applicable to a wide range of physically relevant initial conditions.

These results provide new analytical tools for studying quantum wavepacket dynamics, with potential applications in scattering theory, matter wave optics, and the analysis of quantum systems in confined geometries. The mathematical framework developed here may also find utility in related wave phenomena in optics and acoustics, where Bessel functions naturally arise in the description of propagation dynamics.