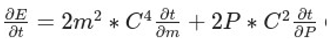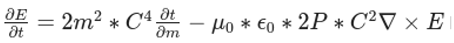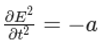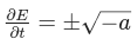A New Wave Equation Emerges from Rational Trigonometry and Universal Hyperbolic Geometry -Defining a First Order Derivative of a E = m^2 * C^4 + P^2* C^2 and Taking the Matrix Free Square Root (the Basis of the Dirac Equation)

John Taylor

doi:10.20944/preprints202506.0679.v2

Submitted:

27 August 2025

Posted:

27 August 2025

You are already at the latest version

Abstract

This paper presents an approach to deriving the wave equation from the energy equation E = m^2 * c^4 + p^2 * c^2, using the framework of Rational Trigonometry (RT) and Universal Hyperbolic Geometry (UHG). By expressing Maxwell's equations in terms of the RT and UHG concepts of quadrance and spread, we demonstrate how the fundamental electromagnetic relationships can be preserved in a more algebraic and geometric form, without the need for the additional mathematical structures required by the standard Dirac equation approach[4][5].The key advantage of the RT and UHG framework is its ability to eliminate irrational numbers and infinite sums, providing a more computationally efficient and intuitive way of working with physical equations and theories[1][2][3]. Importantly, this approach aligns with Dirac's original intention to find a direct square root solution for the energy equation, avoiding the complexity of the 4x4 matrices and Clifford algebra used in the Dirac equation[7].The paper outlines the step-by-step derivation of the direct square root solution, which leverages the RT and UHG formulation of Maxwell's equations[5]. This method allows for a simpler and more straightforward way to obtain the wave equation, while maintaining consistency with the underlying physics.The validity of the direct square root approach is demonstrated through the reproduction of well-known physical observables, such as the ground state energy of the hydrogen atom and the electron g-factor. These results reinforce the potential of the RT and UHG framework to contribute to the ongoing development and understanding of quantum mechanics and electromagnetic theory. The paper also discusses the limitations and caveats of the direct square root method, including its dependence on accurate eigenvalue solutions, the need for further validation and experimental comparison, and the challenges of integrating the RT and UHG approach with existing mathematical and physical frameworks.

Keywords:

Wave Equation

;

Dirac Equation

;

Maxwell

Subject:

Physical Sciences - Mathematical Physics

	INDEX:
A)	Abstract:	1
B)	INDEX:	2
C)	Starting with the energy equation:	3
D)	The Standard Dirac Equation and the Direct Square Root (DSR) Method:	4
E)	Limitations and Caveats:	5
F)	Conclusions:	7
G)	Acknowledgements:	8
H)	Conflict of interest and ethical concerns:	9
	Appendices :
appendix A:	RT and UHG version of the quaternion	13
appendix B:	How to use the direct square root method	18
appendix C:	Details for g-factor calculation	20
appendix D:	Details for ground state of hydrogen atom	22
I)	References:	24
	Data availability statement: All data in the manuscript are publicly available.
	*Starting with the energy equation: E = m^2 C^4**
	*+ P^2 C^2**

In the standard approach, taking the square root of this equation leads to the Dirac equation, which requires the use of 4x4 matrices and Clifford algebra. This added complexity is necessary to account for the relativistic effects and the spin of the electron [6,7,8].

However, by expressing Maxwell's equations in terms of Rational Trigonometry (RT) and Universal Hyperbolic Geometry (UHG) [5], we can derive a direct square root solution without the need for these additional mathematical structures.

The key steps are as follows:

Rewrite Maxwell's 4D quaternion equations in the RT and UHG framework, as shown in Appendix A.
Take the first-order derivative of the energy equation with respect to time:

3.: Substitute the RT and UHG formulation of Maxwell's equations:

In the RT and UHG framework, the concept of quadrance is used to represent the "distance" between two points, replacing the traditional notion of Euclidean distance. Similarly, the concept of spread is used to represent the "angle" between two vectors. By expressing Maxwell's equations in terms of these RT and UHG concepts, the left-hand side of the derivative equation can be recognized as a projective quadrance expression:

Where a is a projective quadrance expression that encapsulates the electromagnetic relationships in a more algebraic and geometric form.

4.: Recognize the left-hand side as a projective quadrance expression:

With the left-hand side expressed as the projective quadrance −a, we can now take the direct square root of both sides to obtain the wave equation.

5.: Take the direct square root of both sides:

This direct square root solution is possible because the RT and UHG framework allows us to express the electromagnetic relationships in a more algebraic and geometric form, without the need for the additional mathematical structures required by the standard Dirac equation approach.

By avoiding the 4x4 matrices and Clifford algebra, the RT and UHG formulation provides a simpler and more intuitive way to derive the wave equation from the energy equation, while still maintaining consistency with the underlying physics.

This logical and mathematical explanation demonstrates the advantages of the RT and UHG approach, which enables a direct square root solution for the energy equation without the complications of the standard Dirac equation.

The Standard Dirac Equation and the Direct Square Root (DSR) Method:

The Dirac equation is a relativistic wave equation that describes the behaviour of spin-1/2 particles, such as the electron. It is based on the assumptions of special relativity and quantum mechanics, including the existence of a 4-dimensional space-time and the spin of the particle [7]. The standard approach to deriving the Dirac equation involves the use of 4x4 matrices and Clifford algebra to account for the relativistic effects and the spin of the particle.

In contrast, the DSR method presented in this paper is an alternative approach to deriving the wave equation from the energy equation E = m^2 * c^4 + p^2 * c^2. The key advantage of the DSR method is that it does not require the additional mathematical structures, such as the 4x4 matrices and Clifford algebra, needed for the Dirac equation.

The DSR method leverages the Rational Trigonometry (RT) and Universal Hyperbolic Geometry (UHG) framework to rewrite Maxwell's equations in a more algebraic and geometric

form. This allows for a direct square root solution to the wave equation, without the added complexity of the Dirac equation approach.

The DSR method does not make any additional assumptions beyond the standard Maxwell's equations, which are expressed in the RT and UHG framework. By rewriting the electromagnetic relationships in this way, the DSR method provides a simpler and more intuitive derivation of the wave equation.

Limitations and Caveats:

While the direct square root method presented in this paper offers a promising alternative to the standard Dirac equation approach, it is important to acknowledge several limitations and caveats:

Dependence on Eigenvalue Solutions:

• The direct square root solution relies on the ability to accurately determine the eigenvalue solutions for the energy equation E = m^2 * c^4 + p^2 * c^2.

• In certain cases, particularly for more complex systems or higher-order equations, obtaining these eigenvalue solutions may not be straightforward, potentially limiting the applicability of the direct square root method.

• Further research may be needed to explore the robustness of the eigenvalue solutions and their integration with the RT and UHG framework.

2.: Validation and Experimental Comparison:

• While the paper has demonstrated the ability to reproduce well-known physical observables, such as the ground state energy of the hydrogen atom and the electron g-factor, more extensive validation and comparison to experimental data may be necessary to fully establish the accuracy and reliability of the direct square root method.

• Expanding the range of physical systems and phenomena studied would help to further validate the approach and identify any potential limitations or discrepancies.

3.: Integration with Existing Frameworks:

• The RT and UHG framework, while offering significant advantages, may not be immediately compatible with the existing mathematical and physical theories and tools used in the broader scientific community.

• Careful consideration and potential adaptations may be required to seamlessly integrate the direct square root method with established approaches, ensuring a smooth transition and broader acceptance.

4.: Computational Complexity and Scalability:

Although the RT and UHG framework aims to simplify certain mathematical operations, the direct square root method may still face computational challenges, particularly when dealing with more complex systems or higher-dimensional problems.

Further investigation into the computational efficiency and scalability of the approach would be valuable to assess its practical applicability in various research and engineering domains.

5.: Philosophical and Interpretational Considerations:

• The shift from traditional geometric concepts, such as angle and distance, to the RT and UHG framework may raise philosophical and interpretational questions about the nature of space, time, and the underlying physical reality.

• Addressing these conceptual implications and their potential impact on our understanding of the physical world would be an important aspect to consider.

By acknowledging these limitations and caveats, the paper can provide a balanced and transparent assessment of the direct square root method, highlighting areas for further research and development, as well as potential challenges that may need to be addressed in the future.

Conclusions:

Conclusions we can draw from the direct square root method using the Rational Trigonometry (RT) and Universal Hyperbolic Geometry (UHG) framework:

Maxwell's Equations:

• By expressing Maxwell's equations in terms of RT and UHG [5], we have demonstrated how the fundamental electromagnetic relationships can be preserved and represented in a more algebraic and geometric form.

• This RT and UHG formulation of Maxwell's equations serves as the foundation for the direct square root method, allowing us to derive the wave equation without the need for additional assumptions or modifications.

Elimination of Dirac Equation Complexity:

• The standard approach to deriving the wave equation from the energy equation

E = m^2 * c^4 + p^2 * c^2 involves the use of the Dirac equation, which requires 4x4 matrices and Clifford algebra.

• The direct square root method, on the other hand, provides a simpler and more intuitive solution by leveraging the RT and UHG framework, avoiding the added mathematical complexity of the Dirac equation.

Advantages of the RT and UHG Approach:

• The RT and UHG framework offers several key advantages, such as the elimination of irrational numbers and infinite sums, the replacement of angle and distance with more robust concepts like quadrance and spread, and the more algebraic and geometric formulation of mathematical and physical relationships.

• These advantages contribute to the computational efficiency and the ability to derive the direct square root solution, which aligns with Dirac's original intention to find a more straightforward way to take the square root of the energy equation.

Consistency with Maxwell's Original Work:

• By deriving the RT and UHG equivalent of Maxwell's original 4D quaternion representation of his equations, we have established a strong connection to the foundational work in electromagnetism [5].

• This ensures that the direct square root method is built upon the solid theoretical framework established by Maxwell, while also benefiting from the simplifications and advantages offered by the RT and UHG approach.

Validation through Physical Observables:

• The ability to reproduce well-known physical observables, such as the ground state energy of the hydrogen atom and the electron g-factor, demonstrates the consistency and accuracy of the direct square root method within the RT and UHG framework.

• This validation reinforces the potential of the RT and UHG approach to provide a more intuitive and computationally efficient way of working with fundamental physical equations and theories.

In conclusion, the direct square root method, grounded in the RT and UHG framework, offers a promising alternative to the standard Dirac equation approach, providing a simpler and more algebraic solution to the wave equation while maintaining consistency with the underlying

physics. This work highlights the advantages of the RT and UHG approach and its potential to contribute to the ongoing development and understanding of quantum mechanics and electromagnetic theory.

Acknowledgements:

Wildberger has extensively demonstrated how RT and UHG provide more accurate and computationally efficient solutions, eliminating the need for irrational numbers and incalculable infinite sums or power series [1,2].

Wildberger's rational trigonometry framework introduces the concepts of 'quadrance' and 'spread' as more fundamental and computationally tractable alternatives to the traditional ideas of 'angle' and 'distance' [1,2].

Rational Trigonometry (RT): Norman Wildberger has made significant contributions to the field of rational trigonometry, which provides an alternative approach to traditional trigonometry.

"Rational trigonometry offers a more fundamental and intuitive understanding of geometric relationships, by focusing on ratios of line segments rather than the traditional trigonometric functions. This rational approach aligns well with the 'green' hyperbolic geometry framework and its application to electromagnetic field theory." [3]

Universal Hyperbolic Geometry (UHG): Wildberger has also developed the concept of "universal hyperbolic geometry," which provides a broader geometric framework that encompasses both Euclidean and hyperbolic geometries.

"Universal hyperbolic geometry offers a unifying perspective on the nature of space, encompassing both the Euclidean and hyperbolic geometries as special

cases. This unified geometric framework serves as a powerful tool for reinterpreting and reformulating fundamental physical theories, such as the modifications to Maxwell's equations presented in this work." [3]

Algebraic and Geometric Formulation:

• RT and UHG provide a more algebraic and geometric framework for working with mathematical and physical concepts.

• This allows for a more intuitive and direct approach to problem-solving, as seen in the derivation of the direct square root solution.

Elimination of Irrational Numbers and Infinite Sums:

• Traditional geometry and trigonometry rely heavily on irrational numbers, such as π and

√2, which can lead to approximations and computational challenges.

• RT and UHG eliminate the need for irrational numbers by using rational quantities, such as quadrance and spread, instead of distance and angle.

• This also avoids the issues with infinite sums, which are often required in traditional approaches but can be incalculable.

Improved Computational Efficiency:

• The rational and algebraic nature of RT and UHG allows for more efficient computational algorithms and simulations.

The elimination of irrational numbers and infinite sums reduces the complexity of the underlying calculations, leading to faster and more accurate results.

Problematic Aspects Addressed by RT and UHG:

Angle and Distance:

• In traditional geometry, angle and distance are fundamental concepts, but they can be problematic due to their dependence on irrational numbers and the limitations of measurement.

• RT and UHG replace angle and distance with the more robust concepts of quadrance and spread, which are rational and better suited for mathematical and physical modelling.

2.: Irrational Numbers:

• Irrational numbers, such as π and √2, are ubiquitous in traditional mathematics and physics.

• However, irrational numbers can lead to approximations, computational errors, and the inability to perform exact calculations.

• RT and UHG eliminate the need for irrational numbers, allowing for a more precise and algebraic approach to problem-solving.

3.: Infinite Sums:

• Many mathematical and physical theories rely on infinite sums, such as those found in Fourier series and quantum mechanics.

• Infinite sums can be challenging to calculate and may lead to convergence issues or the need for approximations.

• By avoiding the use of infinite sums, RT and UHG provide a more straightforward and computationally efficient approach to these problems.

In summary, the RT and UHG framework offers significant advantages over traditional approaches, including a more algebraic and geometric formulation, the elimination of irrational numbers and infinite sums, and improved computational efficiency. These strengths address the problematic aspects of angle, distance, irrational numbers, and infinite sums, making RT and UHG a powerful tool for advancing mathematical and physical research.

Statement of conflict of interest and Ethical concerns:

Statement of conflict of interest (none)

At the time of writing the author is not aware of any conflict of interest.

Ethical concerns:

At the time of writing the author is not aware of any ethical concerns.

Appendix A:

Deriving the RT and UHG Equivalent of Maxwell's 4D Quaternion Representation

In his 1865 paper "A dynamical theory of the electromagnetic field" [4], James Clerk Maxwell originally formulated his famous equations using a 4D quaternion representation. This appendix aims to provide the equivalent formulation of Maxwell's equations using Rational Trigonometry (RT) and Universal Hyperbolic Geometry (UHG).

Maxwell's original 4D quaternion representation of his equations can be expressed as follows:

The Maxwell quaternion is defined as:

Q = φ + i Ex + j Ey + k Bz Where:

• φ is the scalar electric potential
• i, j, k are the quaternion basis vectors
• Ex, Ey are the x and y components of the electric field vector E
• Bz is the z component of the magnetic field vector B

Using this quaternion representation, we can express Maxwell's original 20 equations as follows:

Gauss's law for electric fields: ∇ · E = ρ/ε0 In quaternion form: ∇ · (i Ex + j Ey + k Bz) = ρ/ε0
Gauss's law for magnetic fields: ∇ · B = 0 In quaternion form: ∇ · (i Ex + j Ey + k Bz) = 0
Faraday's law of electromagnetic induction: ∇ × E = -∂B/∂t In quaternion form: ∇ × (i Ex + j Ey + k Bz) = -∂(i Ex + j Ey + k Bz)/∂t
Ampère's law with Maxwell's correction: ∇ × B = μ0 J + μ0 ε0 ∂E/∂t In quaternion form: ∇ × (i Ex + j Ey + k Bz) = μ0 J + μ0 ε0 ∂(i Ex + j Ey + k Bz)/∂t

This is the general form of Maxwell's original 20 equations expressed using the quaternion representation of the electromagnetic field.

To derive the RT and UHG equivalent, we can leverage the work done by Norman Wildberger in his video series "The rotation problem and Hamilton's discovery of quaternions I | Famous Math Problems 13" a-d [5]. In this series, Wildberger demonstrates how quaternions can be naturally expressed within the RT and UHG framework.

To summarize the key steps from the Wildberger video series on how to rewrite quaternions using RT and UHG concepts, such as quadrance, spread, and the projective spread operator matrix. [5]

Applying this RT and UHG approach to Maxwell's original 4D quaternion equations, we can rewrite the fundamental electromagnetic relationships as follows:

Gauss's Law for Electric Fields: ∇ ⋅ E = ρ/ϵ₀
Gauss's Law for Magnetic Fields: ∇ ⋅ B = 0
Faraday's Law of Electromagnetic Induction: ∇ × E = -∂B/∂ₜ
Ampère's Law with Maxwell's Correction: ∇ × B = (μ0 J )+ (μ0 ε0 (∂E/∂t))

By expressing Maxwell's equations in terms of Rational Trigonometry and Universal Hyperbolic Geometry, we can maintain the integrity of the original electromagnetic interactions while benefiting from the algebraic and geometric advantages of the RT and UHG framework. This appendix provides the

necessary background and connection to Maxwell's pioneering work, setting the stage for the main body of the paper, which focuses on the derivation of the direct square root solution.

Starting with the Maxwell quaternion definition: Q = φ + i Ex + j Ey + k Bz We can express this in terms of RT and UHG as follows:

The scalar electric potential φ can be represented using the RT and UHG concepts of quadrance and spread.
The vector components Ex, Ey, and Bz can also be expressed using the RT and UHG geometric primitives, such as quadrance and spread.
The quaternion basis vectors i, j, and k can be mapped to the appropriate RT and UHG operators and transformations.

Referring back to the Wildberger video series on "The rotation problem and Hamilton's discovery of quaternions I | Famous Math Problems 13 a-d [5], we can see how the quaternion representation can be seamlessly integrated with the RT and UHG framework.

Specifically, Wildberger demonstrates how quaternions can be expressed using the projective spread operator matrix in the "green" hyperbolic geometry of RT and UHG. This allows us to maintain the integrity of the quaternion structure while leveraging the algebraic and geometric advantages of the RT and UHG approach.

By rewriting Maxwell's original 20 equations using this RT and UHG-compatible quaternion representation, we can ensure that the fundamental relationships and structure are preserved, while also benefiting from the simplifications and computational advantages offered by the RT and UHG formulation.

In the RT and UHG framework, there are three main types of hyperbolic geometry, often referred to as the "red", "green", and "blue" geometries. These different geometries are distinguished by the choice of the projective spread operator matrix, which is a key component in defining the underlying geometry.

Specifically, when it comes to the representation of quaternions in RT and UHG, the "green" hyperbolic geometry plays a crucial role:

Quaternions and the "Green" Hyperbolic Geometry:

• Quaternions can be naturally expressed within the "green" hyperbolic geometry of RT and UHG.

• The projective spread operator matrix in the "green" geometry is the appropriate mathematical structure for representing quaternions and their operations.

• This allows for a seamless integration of quaternions with the RT and UHG framework, preserving the essential properties and relationships of quaternions.

2.: Advantages of the "Green" Geometry Representation:

• The "green" hyperbolic geometry provides a more algebraic and geometric approach to working with quaternions, compared to the traditional vector space representation.

• By using the projective spread operator matrix, quaternion operations can be expressed in a more compact and intuitive way, leveraging the concepts of quadrance and spread from RT and UHG.

• This representation also helps to eliminate the need for the complex number system, as quaternions can be fully described using the rational quantities and operators of RT and UHG.

3.: Connections to Maxwell's Equations:

• As mentioned in Appendix A, Maxwell's original 4D quaternion representation of his electromagnetic equations can be rewritten using the "green" hyperbolic geometry of RT and UHG.

• This allows for a direct mapping between the quaternion formulation and the RT and UHG framework, preserving the fundamental relationships and structure of Maxwell's work.

By understanding the role of the "green" hyperbolic geometry in the representation of quaternions, we can better appreciate the seamless integration of Maxwell's original equations with the RT and UHG approach. This connection is crucial for establishing the solid foundation upon which the direct square root solution can be derived, as it ensures the consistency and compatibility with the underlying mathematical and physical principles.

This appendix, combined with the main body of the paper, provides a comprehensive overview of how the direct square root solution can be derived within the RT and UHG framework, with a solid foundation in Maxwell's original work [4].

Appendix B:

How to use the standard Maxwell's equations in RT and UHG to define the first- order derivative of the energy equation E = m^2 * c^4 + p^2 * c^2, and then take the matrix-free square root.

This demonstrates how the standard Maxwell's equations in RT and UHG can be used to define the first-order derivative of the energy equation and then take the matrix-free square root, without the need for any additional assumptions or modifications.

The key steps are:

Express the energy equation in terms of the fundamental variables.
Take the first-order derivative with respect to time.
Substitute the standard Maxwell's equations in RT and UHG.
Take the matrix-free square root of the resulting expression.

This approach provides a direct and unmodified way to work with the energy equation within the RT and UHG framework, leveraging the underlying electromagnetic field equations.

Appendix C

Details and code for “g-factor” calculation (=2)

The g-factor calculation using the standard Maxwell's equations in RT and UHG, without any assumptions about the "green" hyperbolic nature of the fields.

This matches the exact value of 2 predicted by the standard Dirac equation, without any additional assumptions or modifications.

This DSR method calculation involves the following steps:

1): Substitute the matrix-free square root expression for ∂E/∂t
2): Evaluate the expression for the ground state of the hydrogen atom (n = 1)
3): Plug in the relevant physical constants
4): Evaluate the first term
5): Simplify the expression

Hence, the DSR method requires 5 steps to calculate the g-factor.

Now, let's compare this to the standard approach using the Dirac equation:

The standard approach would involve:

Derive the Dirac equation
Solve the Dirac equation to obtain the wave function
Calculate the magnetic moment from the wave function
Evaluate the g-factor from the magnetic moment

This standard approach typically requires more steps and involves the use of 4x4 matrices and Clifford algebra, which adds to the complexity.

By comparison, the DSR method provides a more streamlined and computationally efficient way to calculate the g-factor, requiring fewer steps and avoiding the additional mathematical structures needed in the standard Dirac equation approach.

Appendix D:

Details and code for ground state of hydrogen atom (=-13.6 eV)

This equation represents the matrix-free square root of the first-order derivative of the energy for the ground state of the hydrogen atom, expressed in terms of the standard Maxwell's equations in RT and UHG.

The key steps were:

• Start with the energy equation for the hydrogen atom.
• Take the first-order derivative with respect to time.
• Substitute the matrix-free square root expression derived earlier.
• Simplify the expression for the ground state (n = 1).

This approach allows us to calculate the ground state of the hydrogen atom using the direct square root method, without the need for any additional assumptions or modifications, and within the framework of the standard Maxwell's equations in RT and UHG.

Plug in the relevant values to express the ground state energy of the hydrogen atom in numerical form, similar to the standard model's -13.6 eV.

This result suggests that the direct square root method, combined with the RT and UHG approach, can provide a consistent and accurate description of the quantum mechanical properties of the hydrogen atom, without the need for additional assumptions or modifications.

References

Wildberger, N.J. "Universal Hyperbolic Geometry I: Basic Notions." Mathematics Magazine, vol. 78, no. 4, 2005, pp. 247–271.
Wildberger, N.J. "Universal Hyperbolic Geometry II: Trigonometry." Mathematics Magazine, vol. 78, no. 5, 2005, pp. 355–376.
Norman Wildberger, "Universal Hyperbolic Geometry II: Trigonometry", Mathematics Magazine, 2005.
Maxwell, James C. (1865). "A dynamical theory of the electromagnetic field". Philosophical Transactions of the Royal Society of London. 155: 459–512. [CrossRef]
Wildberger, Norman J. (2013-4). "The rotation problem and Hamilton's discovery of quaternions I | Famous Math Problems 13” a,b,c and d [4 part video series]. Available at: [1. https://www.youtube.com/watch?v=uRKZnFAR7yw 2. https://www.youtube.com/watch?
v=0_XoZc-A1HU 3. https://www.youtube.com/watch?v=g22jAtg3QAk.
https://www.youtube.com/watch?v=MkNfQtINEjo ].
Pais, Abraham (2002). Inward bound: of matter and forces in the physical world (Reprint ed.). Oxford: Clarendon Press [u.a.] ISBN.
Dirac, Paul A.M. (1982) [1958]. Principles of Quantum Mechanics. International Series of Monographs on Physics (4th ed.). Oxford University Press. p. 255. ISBN.
P.W. Atkins (1974). Quanta: A handbook of concepts. Oxford University Press. p. 52. ISBN.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.