The Halo Effect and Quantum Vortices. Not so Dark with Alena Tensor

1. Introduction

Research on the dark sector has been ongoing for many years [1] and there is still no theoretical consensus [2] or convincing experimental evidence regarding its nature [3]. We have not found dark matter signals for the WIMP models [4], axions/ALPs [5], SIDM [6], despite new experimental approaches [7], experiments in underground detectors [3], LZ experiments [4], XENON-nT [8] or SuperCDMS [9], and the latest observational data (e.g., "Hubble tension", ”Sigma-8 tension”) make the issue of the dark sector even more puzzling [10]. The dominant theoretical model is still $\mathrm{\Lambda }CDM$ with dark matter haloes [11], although alternative theories such as MOND/relativistic generalizations [12,13], dark photons [14], TeVeS/related constructions [12], f(R) [15], black holes [16], or the recently popular ”emergent/entropic gravity” [17] have achieved some success at selected scales. However, all these approaches experience ups and downs depending on the subsequent observational data [4,8,10,18].

There is also considered the possibility of hybrid models (e.g. a superfluid DM combining features of MOND and DM) [19], or even incorrect/weakened estimates of baryon masses and systematic errors in the M/L estimate [20], and the interaction of dark matter and energy [21] but so far this entire massive effort by the scientific community has not yielded a definitive conclusion. We have more certainty about dark energy because the universe is definitely expanding, and there are ample, multiple, independent confirmations, eg. from SN Ia, BAO, and CMB [11,22]. It is still uncertain whether the cosmological constant is indeed constant, although recent DESI (BAO) analyses indicate the possibility of w(z) dynamics [23], and the Euclid mission is rapidly delivering high-quality weak lensing maps and surveys that will be crucial for measuring the dark energy equation of state [24].

The Alena Tensor is a relatively young field of research and has not had much relevance to the dark sector until now. Previous work has focused on developing a dual description for physical systems with matter and fields in which the metric tensor is not a feature of spacetime but only a method of describing it. Its aim was to provide a smooth transition between curvilinear description consistent with GR [25] and a flat (classical and quantum [26]) description for simple cases with dust [27], which was analyzed mainly for physical systems with electromagnetic fields [28]. This paper will demonstrate that extending the Alena Tensor to the general case yields results, that provide a representation of the spherical dark matter halo and, naturally, provide an explanation for the cosmological constant. The obtained picture of GR equations leads to a potential explanation of the dark matter phenomenon based on the energy associated with the rotation itself and for about 100 diverse galaxies from the SPARC database [29] gives a fairly good approximation of the observed rotation curves.

In the first part of the paper, an introduction to the Alena Tensor model for dust will be presented, then this approach will be extended to the general form of the matter energy-momentum tensor, leading to the "dark matter halo effect". The results will be analyzed and discussed and shown to lead to the conclusions described in the abstract.

2. Results

In this chapter, the conclusions reached so far regarding the Alena Tensor will be recalled, the notation will be introduced, and the reasoning from the previous articles will be generalized to all gauge fields and all forces acting in the physical system. The obtained results will be then used to formulate conclusions regarding the dark matter and compared with observational data. The author uses the Einstein summation convention, metric signature $(+,-,-,-)$ and commonly used notations.

2.1. Transforming Curved Path into Geodesic for Dust

As a first step, one may generalize the solution proposed in [27] in such a way that the forces resulting from all gauge fields are related to the metric tensor of curved spacetime.

One may begin the reasoning by introducing tensor $F^{\mu \nu \alpha \beta }$ defined in terms of the gauge field tensors ${\mathbb{F}}_A^{\mu \nu }$ for each gauge group A, and the stress-energy tensor ${\mathrm{{\rm Y}}}^{\mu \nu }$ for such generalized field

$$F^{\mu \nu \alpha \beta }\equiv \sum _A{\mathbb{F}}_A^{\mu \nu }\otimes {\mathbb{F}}_A^{\alpha \beta };{\mathrm{{\rm Y}}}^{\mu \nu }\equiv F^{\mu \alpha \nu \beta }{g}_{\alpha \beta }-g^{\mu \nu }{\displaystyle \frac{1}{4}}{F}^{\alpha \gamma \beta \delta }{g}_{\alpha \beta }{g}_{\gamma \delta }$$

(1)

and denote the invariant of this field as $p_{\mathrm{\Lambda }}$. Following reasoning from [27] let this field invariant be defined dually as follows

$$p_{\mathrm{\Lambda }}\equiv {\displaystyle \frac{1}{4}}{F}^{\alpha \gamma \beta \delta }{g}_{\alpha \beta }{g}_{\gamma \delta }\equiv p_o{\mathbb{k}}^2;\mathbb{k}\equiv {\mathbb{k}}_{\mu \nu }{g}^{\mu \nu }$$

(2)

where $p_o$ is certain constant (or simply invariant, independent of the metric) and where ${\mathbb{k}}^{\mu \nu }$, as raised in [26], in this approach is a metric tensor describing a curved spacetime in which all motion occurs along geodesics. By making variation on $-p_{\mathrm{\Lambda }}$ with respect to metric $g_{\mu \nu }$ (Hilbert’s method) one obtains the energy-momentum tensor of the field from (1) expressed dually as

$${\mathrm{{\rm Y}}}^{\mu \nu }=p_{\mathrm{\Lambda }}\left({\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\mu \nu }-g^{\mu \nu }\right)$$

(3)

Such approach, exactly as shown in [27], establishes a relationship between the field and the metric tensor ${\mathbb{k}}^{\mu \nu }$ and in the spacetime considered as described by the metric tensor $g^{\mu \nu }\to {\mathbb{k}}^{\mu \nu }$, one obtains $\mathbb{k}=4$ what yields that in curvilinear description of the system, energy-momentum tensor of the field ${\mathrm{{\rm Y}}}^{\mu \nu }$ vanishes, maintaining continuity of function. As shown in previous articles, this causes the presence of a field in curved spacetime to manifest itself solely through curvature, which replaces the four-force densities in flat spacetime.

In flat spacetime, one may assume that the equations of motion for the gauge fields A are satisfied, thus one obtains gauge four-currents $J_A^{\nu }\equiv D_{\mu }{\mathbb{F}}_A^{\mu \nu }$. Therefore, the total density of the Yang-Mills four-forces [30,31]$f_{YM}^{\nu }$ is

$$f_{YM}^{\nu }={\partial }_{\mu }{\mathrm{{\rm Y}}}^{\mu \nu }=\sum _A{J}_A^{\alpha }{\mathbb{F}}_{A\alpha }^{\nu }$$

(4)

where the self-interactions of gauge fields in a non-Abelian theory are reducing. Then, following the reasoning presented in [27] one may define coefficient ${\chi }_m\equiv {\displaystyle \frac{\varrho c^2}{p_{\mathrm{\Lambda }}}}$ where $\varrho$ represents matter density and is associated with the translational current ${\chi }_m{U}^{\mu }$. In the Alena Tensor approach, the existence of matter is thus a manifestation of the existence of fields what ensures, that without fields matter does not exist.

This allows to define the Lagrangian ${\mathcal{L}}_{dust}$ and obtain from it the strest-energy tensor (Alena Tensor) for the system with dust $T_{dust}^{\mu \nu }$ by variation on the metric

$${\mathcal{L}}_{dust}\equiv p_{\mathrm{\Lambda }}(1-{\chi }_m)\to T_{dust}^{\mu \nu }\equiv \varrho U^{\mu }{U}^{\nu }-(1-{\chi }_m){\mathrm{{\rm Y}}}^{\mu \nu }$$

(5)

In accordance with [28], assuming ${\varrho }_o$ as rest mass density, four-momentum density is defined as $\varrho U^{\alpha }\equiv {\varrho }_o\gamma U^{\alpha }$ what takes into account motion and Lorentz contraction of the volume. Total translational four-force density acting on matter is therefore defined as

$$f^{\nu }\equiv {\partial }_{\mu }\varrho U^{\mu }{U}^{\nu }=\varrho U^{\mu }{\partial }_{\mu }{U}^{\nu }=\varrho {\displaystyle \frac{d{U}^{\nu }}{d\tau }};{\partial }_{\mu }\varrho U^{\mu }=0$$

(6)

As shown in [26], the above amendment introduces a natural property concerning curved spacetime, assuming that for dust, geodetic motion is expected

$$\begin{array}{c}\hfill {\partial }_{\alpha }\varrho U^{\alpha }=0\to U_{,\alpha }^{\alpha }=-{\displaystyle \frac{d\gamma }{dt}}\to U_{;\alpha }^{\alpha }=0\end{array}$$

(7)

$$\begin{array}{c}\hfill U^{\alpha }{U}_{;\alpha }^{\beta }=0\to {\displaystyle \frac{D{U}^{\beta }}{D\tau }}=0;{\left(\varrho U^{\alpha }{U}^{\beta }\right)}_{;\alpha }=0\end{array}$$

(8)

Now it can be noticed, that in flat spacetime the four-divergence of the above tensor $T_{dust}^{\mu \nu }$ can be interpreted as the density of the four-forces acting on matter $f^{\nu }$ reduced by the density of the field-related four-forces

$$f_{field}^{\nu }\equiv {\partial }_{\mu }\left[(1-{\chi }_m){\mathrm{{\rm Y}}}^{\mu \nu }\right]=(1-{\chi }_m)f_{YM}^{\nu }+f_{gr}^{\nu };f_{gr}^{\nu }\equiv {\mathrm{{\rm Y}}}^{\mu \nu }{\partial }_{\mu }(1-{\chi }_m)=-{\mathrm{{\rm Y}}}^{\mu \nu }{\partial }_{\mu }{\chi }_m$$

(9)

As shown in [26], $f_{gr}^{\nu }$ can be associated with the existence of gravity in the system, while $f_{rr}^{\nu }\equiv {\chi }_m{f}_{YM}$ behaves as a radiation-reaction force, reducing the value of forces due to the field and upholding the conservation of energy, ensuring that the increasing energy density associated with matter $\varrho c^2$ does not exceed the total energy density $p_{\mathrm{\Lambda }}$ available in the system

$${\partial }_{\mu }{T}_{dust}^{\mu \nu }=f^{\nu }-f_{field}^{\nu }=f^{\nu }-f_{YM}^{\nu }-f_{gr}^{\nu }+f_{rr}^{\nu }$$

(10)

where $\underset{{\chi }_m\to 1}{lim}{f}_{field}^{\nu }=0$. Presented approach also indicates the anstaz for the Kerr-Schild type metrics for curved spacetime

$${\mathbb{k}}^{\mu \nu }\equiv \sum _i{c}_i{l}_i^{\mu }{l}_i^{\nu }+{\displaystyle \frac{\mathbb{k}}{4}}{\eta }^{\mu \nu };0={\eta }_{\mu \nu }{l}_i^{\mu }{l}_i^{\nu }$$

(11)

where $l_i^{\mu }$ are null vectors and $c_i$ are related coefficients.

In the next section, the above model will be expanded to include rotation-related components, which will prove crucial for describing dark sector phenomena and allow to obtain a description that agrees with the observational results.

2.2. Rotational Energy

It can be noticed that the radiation reaction force should take into account the total energy associated with the body, so in addition to the energy associated with the translational motion, it seems necessary to take into account the rotational energy.

One may thus introduce a projector ${\Delta }^{\mu \nu }$, flow vorticity tensor ${\omega }^{\mu \nu }$, positive coefficient ${\chi }_{\omega }$ equal to the rotational energy ${\mathcal{E}}_{rot}$ up to $p_{\mathrm{\Lambda }}$ and some metric independent auxiliary $\alpha$ with the dimension of the square of time

$$\begin{array}{c}\hfill {{\Delta }^{\mu }}_{\nu }\equiv {g^{\mu }}_{\nu }-{\displaystyle \frac{1}{c^2}}{U}^{\mu }{U}_{\nu };{\omega }_{\mu \nu }\equiv {{\Delta }_{\mu }}^{\alpha }{{\Delta }_{\nu }}^{\beta }{\nabla }_{[\alpha }{U}_{\beta ]};{\chi }_{\omega }\equiv {\displaystyle \frac{\alpha }{2}}{\omega }^{\mu \nu }{\omega }_{\mu \nu };{\mathcal{E}}_{rot}\equiv p_{\mathrm{\Lambda }}{\chi }_{\omega }\end{array}$$

(12)

Defining Lagrangian density ${\mathcal{L}}_T$ for the whole system and tensor $S^{\lambda \mu \nu }$ to describe emerging boundary terms

$$\begin{array}{c}\hfill {\mathcal{L}}_T=p_{\mathrm{\Lambda }}\left(1-{\chi }_{\omega }-{\chi }_m\right);S^{\lambda \mu \nu }\equiv p_{\mathrm{\Lambda }}\alpha \left(U^{\lambda }{\omega }^{\mu \nu }-U^{(\mu }{\omega }^{\nu )\lambda }\right)\end{array}$$

(13)

and introducing ${\Xi }^{\mu \nu }$ tensor related to rotational properties of the system

$$\begin{array}{c}\hfill -{\Xi }^{\mu \nu }\equiv \alpha p_{\mathrm{\Lambda }}\left({\omega }^{\mu \gamma }{{\omega }^{\nu }}_{\gamma }-{\displaystyle \frac{1}{2}}{\Delta }^{\mu \nu }{\omega }^{\alpha \beta }{\omega }_{\alpha \beta }\right)+{\nabla }_{\lambda }{S}^{\lambda \left(\mu \nu \right)}\end{array}$$

(14)

one obtains Alena Tensor $T^{\mu \nu }$ for the system derived with help of variational method on ${\mathcal{L}}_T$ in the form

$$\begin{array}{c}\hfill T^{\mu \nu }=\varrho U^{\mu }{U}^{\nu }-{\Xi }^{\mu \nu }-\left(1-{\chi }_{\omega }-{\chi }_m\right){\mathrm{{\rm Y}}}^{\mu \nu };T^{\mu \nu }{g}_{\mu \nu }=\varrho c^2-{\mathcal{E}}_{rot}\end{array}$$

(15)

Considering description in curved spacetime, described by the metric tensor ${\mathbb{k}}^{\mu \nu }$, the field tensor ${\mathrm{{\rm Y}}}^{\mu \nu }$ vanishes, the system tensor reduces to the form $T_{matt}^{\mu \nu }\equiv \varrho U^{\mu }{U}^{\nu }-{\Xi }^{\mu \nu }$ and its vanishing four-divergence means that any deviations from the geodesic motion with $a^{\mu }\equiv U^{\nu }{\nabla }_{\nu }{U}^{\mu }$ are compensated by rotation related forces. Using the standard kinematic decomposition one may calculate

$$\begin{array}{c}\hfill \epsilon \equiv {\displaystyle \frac{1}{c^2}}{T}_{matt}^{\mu \nu }{U}_{\mu }{U}_{\nu }=\varrho c^2+2{\mathcal{E}}_{rot};T_{matt}^{\mu \nu }{U}_{\nu }=\left(\varrho c^2+2{\mathcal{E}}_{rot}\right)U^{\mu }-\alpha p_{\mathrm{\Lambda }}\left(a_{\nu }{\omega }^{\nu \mu }+{\displaystyle \frac{c^2}{2}}{{\Delta }^{\mu }}_{\nu }{\nabla }_{\lambda }{\omega }^{\lambda \nu }\right)\end{array}$$

(16)

where the element in brackets in last equation represents in fact the purely spatial vorticity divergence. Assuming the classical definition of the energy flux $q^{\alpha }$ one also gets

$$\begin{array}{c}\hfill q^{\alpha }\equiv {\displaystyle \frac{1}{c^2}}{{\Delta }^{\alpha }}_{\mu }{T}_{matt}^{\mu \nu }{U}_{\nu }=-\alpha p_{\mathrm{\Lambda }}\left(a_{\nu }{\omega }^{\nu \mu }+{\displaystyle \frac{c^2}{2}}{{\Delta }^{\mu }}_{\nu }{\nabla }_{\lambda }{\omega }^{\lambda \nu }\right)\end{array}$$

(17)

Introducing classical shear tensor ${\sigma }^{\mu \nu }$ and effective vortex stress tensor ${\tau }^{\mu \nu }$ as

$$\begin{array}{c}\hfill {\sigma }^{\mu \nu }\equiv {\Delta }^{\mu \alpha }{\Delta }^{\nu \beta }{\nabla }_{(\alpha }{U}_{\beta )}-{\displaystyle \frac{1}{3}}{\nabla }_{\alpha }{U}^{\alpha }{\Delta }^{\mu \nu };{\tau }^{\mu \nu }\equiv {\displaystyle \frac{p_{\mathrm{\Lambda }}\alpha }{2}}\left({{\sigma }^{\mu }}_{\lambda }{\omega }^{\nu \lambda }+{{\sigma }^{\nu }}_{\lambda }{\omega }^{\mu \lambda }\right)\end{array}$$

(18)

one may thus rewrite $T_{matt}^{\mu \nu }$ in curved spacetime as

$$\begin{array}{c}\hfill T_{matt}^{\mu \nu }={\displaystyle \frac{\epsilon }{c^2}}{U}^{\mu }{U}^{\nu }+{\displaystyle \frac{1}{c^2}}\left(U^{\mu }{q}^{\nu }+U^{\nu }{q}^{\mu }\right)-{\mathcal{E}}_{rot}{\Delta }^{\mu \nu }-{\tau }^{\mu \nu }\end{array}$$

(19)

One may notice, that the system has a built-in anisotropic stress described by ${\tau }^{\mu \nu }$, but its source is not viscosity, but the coupling between shear and vorticity (between flow deformation and local spin angular momentum).

Considered in flat spacetime such approach introduces additional four-force density $f_{\Xi }^{\nu }$ acting on matter and also changes $f_{gr}^{\nu }$ and the radiation reaction $f_{rr}^{\nu }$ to the form

$$\begin{array}{c}\hfill f_{\Xi }^{\nu }\equiv {\partial }_{\mu }{\Xi }^{\mu \nu };f_{rr}^{\nu }=\left({\chi }_m+{\chi }_{\omega }\right)f_{YM}^{\nu };f_{gr}^{\nu }={\mathrm{{\rm Y}}}^{\mu \nu }{\partial }_{\mu }\left(1-{\chi }_{\omega }-{\chi }_m\right)\end{array}$$

(20)

One may now consider the impact of the above expansion of the Alena Tensor on quantum equations and GR equations.

2.2.1. Noether Tensor and Quantum Interpretation

Introducing for simplicity $\xi \equiv 1-{\chi }_{\omega }-{\chi }_m$ one may in flat spacetime define Belinfante superpotential $Q^{\lambda \mu \nu }$ referring to (13) and improvement $I^{\mu \nu }$ resulting from the variable $\xi$ as

$$\begin{array}{c}\hfill Q^{\lambda \mu \nu }\equiv {\displaystyle \frac{1}{2}}\left(S^{\mu \nu \lambda }+S^{\nu \mu \lambda }-S^{\lambda \mu \nu }\right);I^{\mu \nu }\equiv {\partial }_{\lambda }{Q}^{\lambda \mu \nu }+{\eta }^{\mu \nu }\left({\partial }_{\lambda }ln\xi \right){\mathbb{C}}^{\lambda }-({\partial }^{(\mu }ln\xi ){\mathbb{C}}^{\nu )}\end{array}$$

(21)

where

$$\begin{array}{c}\hfill {\mathbb{C}}^{\mu }\equiv {\mathrm{\Pi }}^{\mu \alpha }{U}_{\alpha }-\sum _A{\mathbb{F}}_A^{\mu \lambda }{{\mathbb{A}}_{\lambda }}_A;{\mathrm{\Pi }}^{\mu \alpha }\equiv {\displaystyle \frac{\partial {\mathcal{E}}_{rot}}{\partial \left({\partial }_{\mu }{U}_{\alpha }\right)}}=\alpha p_{\mathrm{\Lambda }}{{\Delta }^{\alpha }}_{\rho }{{\Delta }_{\beta }}^{\mu }{\omega }^{\rho \beta };D_{\mu }={\partial }_{\mu }-i\sum _A{g}_A{\mathbb{A}}_{\mu A}{T}_A,\end{array}$$

(22)

with $g_A$ denoting the gauge couplings, ${\mathbb{A}}_{\mu A}$ the corresponding gauge fields, and $T_A$ the generators of the gauge group in the representation of the matter field. In flat spacetime, one therefore obtains the Noether tensor with Belinfante correction $T_{Bel}^{\mu \nu }$ as

$$\begin{array}{c}\hfill T_{Bel}^{\mu \nu }\left[{\mathcal{L}}_T\right]={\displaystyle \frac{i}{4}}\overline{\psi }{\gamma }^{(\mu }{\overleftrightarrow{D}}^{\nu )}\psi -\xi {\mathrm{{\rm Y}}}^{\mu \nu }-\xi {\Xi }^{\mu \nu }-{\eta }^{\mu \nu }{\mathcal{L}}_T\end{array}$$

(23)

where ${\overleftrightarrow{D}}^{\nu )}$ denotes the two-way derivative. By the Rosenfeld–Belinfante identity, which equates the Hilbert energy-momentum tensor obtained by metric variation with the Belinfante-improved Noether tensor (on-shell), one obtains Alena Tensor as

$$\begin{array}{c}\hfill T^{\mu \nu }=T_{Bel}^{\mu \nu }+I^{\mu \nu }=\varrho U^{\mu }{U}^{\nu }-{\Xi }^{\mu \nu }-\xi {\mathrm{{\rm Y}}}^{\mu \nu }\end{array}$$

(24)

It may be noticed, that ${\partial }_{\mu }{I}^{\mu \nu }=0$ becomes zero on-shell, using the equations of motion and smooth boundary conditions. In flat spacetime the derivatives commute, thus

$$\begin{array}{c}\hfill {\partial }_{\mu }{\partial }_{\lambda }{Q}^{\lambda \mu \nu }=\frac{1}{2}\left({\partial }_{\mu }{\partial }_{\lambda }-{\partial }_{\lambda }{\partial }_{\mu }\right)Q^{\lambda \mu \nu }=0\to {\partial }_{\mu }\left({\partial }_{\lambda }{Q}^{\lambda \mu \nu }\right)=0\end{array}$$

(25)

Using above one obtains

$$\begin{array}{ccc}\hfill {\partial }_{\mu }{I}^{\mu \nu }& =& {\partial }^{\nu }\left[({\partial }_{\lambda }ln\xi ){\mathbb{C}}^{\lambda }\right]-{\partial }_{\mu }\left[({\partial }^{(\mu }ln\xi ){\mathbb{C}}^{\nu )}\right]=({\partial }^{\nu }{\partial }_{\lambda }ln\xi ){\mathbb{C}}^{\lambda }+({\partial }_{\lambda }ln\xi ){\partial }^{\nu }{\mathbb{C}}^{\lambda }\hfill \\ & -& {\displaystyle \frac{1}{2}}\left[(\square ln\xi ){\mathbb{C}}^{\nu }+({\partial }^{\mu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\nu }\right]-{\displaystyle \frac{1}{2}}\left[({\partial }_{\mu }{\partial }^{\nu }ln\xi ){\mathbb{C}}^{\mu }+({\partial }^{\nu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\mu }\right]\hfill \end{array}$$

(26)

The equations of motion for $U_{\mu }$ and gauge fields ${\mathbb{A}}_{\mu A}$ derived from the Lagrangian ${\mathcal{L}}_T=\xi p_{\mathrm{\Lambda }}$ imply the following two relations

$$\begin{array}{c}\hfill {\partial }_{\mu }{\mathbb{C}}^{\mu }=({\partial }_{\lambda }ln\xi ){\mathbb{C}}^{\lambda };{\partial }^{\nu }{\mathbb{C}}^{\lambda }-{\partial }^{\lambda }{\mathbb{C}}^{\nu }=\left({\partial }^{\nu }ln\xi \right){\mathbb{C}}^{\lambda }-\left({\partial }^{\lambda }ln\xi \right){\mathbb{C}}^{\nu }\end{array}$$

(27)

The full expansion of the above is obtained by explicitly writing the Euler–Lagrange equations for $U_{\mu }$ and ${\mathbb{A}}_{\mu A}$ with ${\mathcal{L}}_T$, contracting with $U_{\alpha }$ and with $A_{\lambda A}$, and arranging the terms with the derivatives of $\xi$.

The first relation is the Euler equality for the component $U_{\mu }$ (with ${\mathrm{\Pi }}^{\mu \alpha }$ as the momentum conjugate to ${\partial }_{\mu }{U}_{\alpha }$) after taking into account the fact that ${\mathcal{L}}_T$ has variable $\xi$.

The second relation follows from the gauge field equations ${\partial }_{\mu }\left(\xi {\mathbb{F}}_A^{\mu \nu }\right)={\mathbb{J}}_A^{\nu }$ and from the definition of the "virial" part ${\sum }_A{\mathbb{F}}_A^{\mu \lambda }{\mathbb{A}}_{\lambda A}$ in ${\mathbb{C}}^{\mu }$, which ensures the proper gauge covariance. From this relation one gets

$$\begin{array}{c}\hfill ({\partial }^{\nu }{\partial }_{\lambda }ln\xi ){\mathbb{C}}^{\lambda }-{\displaystyle \frac{1}{2}}({\partial }_{\mu }{\partial }^{\nu }ln\xi ){\mathbb{C}}^{\mu }-{\displaystyle \frac{1}{2}}(\square ln\xi ){\mathbb{C}}^{\nu }=0\end{array}$$

(28)

which makes the whole part with second derivatives $ln\xi$ zero in (26). Using first relation in (26) and using the second relation again, one therefore gets

$$\begin{array}{ccc}\hfill {\partial }_{\mu }{I}^{\mu \nu }& =& ({\partial }_{\lambda }ln\xi ){\partial }^{\nu }{\mathbb{C}}^{\lambda }-{\displaystyle \frac{1}{2}}({\partial }^{\mu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\nu }-{\displaystyle \frac{1}{2}}({\partial }^{\nu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\mu }\hfill \\ & =& {\displaystyle \frac{1}{2}}\left[({\partial }_{\lambda }ln\xi ){\partial }^{\nu }{\mathbb{C}}^{\lambda }-({\partial }^{\nu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\mu }\right]+{\displaystyle \frac{1}{2}}\left[({\partial }_{\lambda }ln\xi ){\partial }^{\nu }{\mathbb{C}}^{\lambda }-({\partial }^{\mu }ln\xi ){\partial }_{\mu }{\mathbb{C}}^{\nu }\right]\hfill \\ & =& {\displaystyle \frac{1}{2}}\left[({\partial }_{\lambda }ln\xi )\left({\partial }^{\nu }{\mathbb{C}}^{\lambda }-{\partial }^{\lambda }{\mathbb{C}}^{\nu }\right)-({\partial }^{\nu }ln\xi )\left({\partial }_{\mu }{\mathbb{C}}^{\mu }-({\partial }_{\mu }ln\xi ){\mathbb{C}}^{\mu }\right)\right]=0\hfill \end{array}$$

(29)

As one may notice, the above derivation establishes a symmetric and conserved energy-momentum tensor, suitable for quantization. In the quantum description $T^{\mu \nu }$ may be promoted to an operator ${\widehat{T}}^{\mu \nu }$ whose expectation values reproduce the classical results, while $I^{\mu \nu }$ accounts for the spin and coupling corrections in the operator formalism.

It may be calculated, that the inclusion of the rotational energy term allows to construct below quantum-effective Lagrangian density

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{eff}}=\underset{\mathrm{fermionic}\mathrm{matter}}{\underbrace{\overline{\psi }(i{\gamma }^{\mu }{D}_{\mu }-m)\psi }}+\underset{\mathrm{spin}-\mathrm{vorticity}}{\underbrace{g\overline{\psi }{\mathrm{\Sigma }}^{\mu \nu }{\omega }_{\mu \nu }\psi }}+\underset{\mathrm{phase}\mathrm{field}U\left(1\right)}{\underbrace{|D_{\mu }{\varphi |}^2-V\left[\right|\varphi \left|\right]}}\\ \hfill -\underset{\mathrm{gauge}\mathrm{fields}}{\underbrace{{\displaystyle \frac{\xi }{4}}{\sum }_A{\mathbb{F}}_A^{\mu \nu }{\mathbb{F}}_{\mu \nu A}}}+\underset{\text{"}\mathrm{stiffness}\text{"}/\mathrm{core}}{\underbrace{{\displaystyle \frac{p_{\mathrm{\Lambda }}}{2}}\alpha \left[\right|\varphi \left|\right]{\omega }^{\mu \nu }\left[J\right]{\omega }_{\mu \nu }\left[J\right]}}\end{array}$$

(30)

where

$$\begin{array}{c}\hfill {\mathrm{\Sigma }}^{\mu \nu }=\frac{i}{2}[{\gamma }^{\mu },{\gamma }^{\nu }];J_{\mu }(\varphi ,A)\equiv \mathrm{Im}\left({\varphi }^{*}{D}_{\mu }\varphi \right);U_{\mu }\left[J\right]\equiv {\displaystyle \frac{c{J}_{\mu }}{\sqrt{J_{\mu }{J}^{\mu }}}}\end{array}$$

(31)

and where g is the spin-vorticity coupling constant, the function $\alpha \left(\right|\varphi \left|\right)$ satisfies $\alpha \left(0\right)=0$ and $\alpha \left(v\right)>0$ to ensure a finite-energy vortex core configuration. The local U(1) phase of $\varphi =\sqrt{\rho }{e}^{i\theta }$ (Madelung decomposition) guarantees quantization of circulation, $V\left[\right|\varphi \left|\right]$ is a symmetry-breaking potential with a minimum at $\left|\varphi \right|=v$, and the resulting Euler-Lagrange equations reproduce the same stress-energy tensor in the classical limit.

2.2.2. General Relativity Interpretation

One may now repeat the reasoning from [27] and define the generalized Ricci and Einstein tensors, where it is used for simplicity $\xi \equiv 1-{\chi }_{\omega }-{\chi }_m$, the ^˜ sign indicates normalization with the constant $\kappa /2={\displaystyle \frac{4\pi G}{c^4}}$, and additional tensor ${\mathrm{\Theta }}^{\mu \nu }$ as

$$\begin{array}{ccc}\hfill {\tilde{R}}^{\mu \nu }& \equiv & 2T_{matt}^{\mu \nu }+2{\chi }_{\omega }{\mathrm{{\rm Y}}}^{\mu \nu }+\left(p_{\mathrm{\Lambda }}+{\mathcal{E}}_{rot}-\varrho c^2\right)g^{\mu \nu }\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill \tilde{R}& \equiv & {\tilde{R}}^{\mu \nu }{g}_{\mu \nu }=4p_{\mathrm{\Lambda }}+2{\mathcal{E}}_{rot}-2\varrho c^2\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\tilde{G}}^{\mu \nu }& \equiv & {\tilde{R}}^{\mu \nu }-{\displaystyle \frac{\tilde{R}}{2}}{\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\mu \nu }={\tilde{R}}^{\mu \nu }-{\displaystyle \frac{\tilde{R}}{2}}{g}^{\mu \nu }-{\displaystyle \frac{\tilde{R}}{2p_{\mathrm{\Lambda }}}}{\mathrm{{\rm Y}}}^{\mu \nu }=2T_{matt}^{\mu \nu }-\left(1+\xi \right){\mathrm{{\rm Y}}}^{\mu \nu }-p_{\mathrm{\Lambda }}{g}^{\mu \nu }\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\mathrm{\Theta }}^{\mu \nu }& \equiv & -\left({\chi }_m+{\chi }_{\omega }\right){\mathrm{{\rm Y}}}^{\mu \nu }\to {\tilde{G}}^{\mu \nu }+p_{\mathrm{\Lambda }}{g}^{\mu \nu }=2T^{\mu \nu }+{\mathrm{\Theta }}^{\mu \nu }\hfill \end{array}$$

(35)

where the last equality holds in any considered spacetime and for $G^{\mu \nu }={\displaystyle \frac{\kappa }{2}}{\tilde{G}}^{\mu \nu }$, $\mathrm{\Lambda }={\displaystyle \frac{\kappa }{2}}{p}_{\mathrm{\Lambda }}$ becomes the classical GR equation in curved spacetime (in curved spacetime ${\mathrm{{\rm Y}}}^{\mu \nu }$ and ${\mathrm{\Theta }}^{\mu \nu }$ vanish).

The Lagrangian ${\mathcal{L}}_{\mathrm{\Theta }}$ for ${\mathrm{\Theta }}^{\mu \nu }$ may be obtained the same way as in [27] with the use of the interpolating path method $g^{\mu \nu }\left(\lambda \right)=(1-\lambda ){\mathbb{k}}^{\mu \nu }+\lambda g^{\mu \nu }$. Using this method one obtains

$$\sqrt{-g}{\mathcal{L}}_{\mathrm{\Theta }}\equiv {\displaystyle \frac{1}{2}}{\int }_0^{1}d\lambda \sqrt{-g\left(\lambda \right)}{\mathrm{\Theta }}_{\mu \nu }\left[g^{\mu \nu }\left(\lambda \right)\right]{\partial }_{\lambda }{g}^{\mu \nu }\left(\lambda \right)$$

(36)

Since the variation of the functional is located on the boundary $\lambda =1$, thus ${\mathrm{\Theta }}_{\mu \nu }={\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \left(\sqrt{-g}{\mathcal{L}}_{\mathrm{\Theta }}\right)}{\delta g^{\mu \nu }}}$.

In the last equation of (35) considered in curved spacetime $(g^{\mu \nu }\to {\mathbb{k}}^{\mu \nu })$ field invariant $p_{\mathrm{\Lambda }}$ acts as double the vacuum energy density (vacum pressure). This equation may be derived from the Lagrangian density ${\mathcal{L}}_G$ in the form

$${\mathcal{L}}_G\equiv 2{\mathcal{L}}_T+{\mathcal{L}}_{\mathrm{\Theta }}={\mathcal{L}}_{matt}+{\displaystyle \frac{1}{2}}\tilde{R}-2{\mathcal{E}}_{rot};{\mathcal{L}}_{matt}\equiv {\mathcal{L}}_{\mathrm{\Theta }}-p_{\mathrm{\Lambda }}\left({\chi }_m+{\chi }_{\omega }\right)$$

(37)

where the variation by Hilbert’s method on ${\mathcal{L}}_{matt}$ gives $T_{matt}^{\mu \nu }\equiv \varrho U^{\mu }{U}^{\nu }-{\Xi }^{\mu \nu }$.

The equation (34) considered in curved spacetime simplifies to ${\tilde{G}}^{\mu \nu }={\tilde{R}}^{\mu \nu }-{\displaystyle \frac{\tilde{R}}{2}}{g}^{\mu \nu }$ where ${\mathrm{{\rm Y}}}^{\mu \nu }$ and thus also ${\mathrm{\Theta }}^{\mu \nu }$ vanishes. It is also worth noting that in flat spacetime the generalized Einstein tensor is associated with the four-divergence of ${\mathrm{\Theta }}^{\mu \nu }$

$${\partial }_{\mu }{\tilde{G}}^{\mu \nu }={\partial }_{\mu }{\mathrm{\Theta }}^{\mu \nu }=f_{gr}^{\nu }-f_{rr}^{\nu }$$

(38)

so the curvature it describes in curved spacetime replaces this four-force density, where $f_{gr}^{\nu }$ is related to gravity and $f_{rr}^{\nu }$ is the density of radiation-reaction four-force. The presence of the radiation-reaction force has already been discussed in previous works [25], and it now prevents the matter energy and rotational energy from increasing beyond the maximum energy density $p_{\mathrm{\Lambda }}$ available in the system.

It is worth noting that internal energy density and rotational energy, essentially exhaust the possible forms of energy that can be attributed to material bodies (other forms of energy, e.g., chemical energy, can be treated as their components) which could be present in the radiation reaction force. This means that the model proposed here seems complete (with the possible extension of $\alpha$ to a tensor form for more complex systems) and should allow for reproducing the results obtained from GR, as well as reproducing observational results that are inconsistent (such as the dark sector) with currently used interpretation of GR.

Alena Tensor approach therefore allows to look at Einstein’s equations in a new light and analyze the possibilities of explaining the dark sector in a consistent mathematical framework that allows analysis in both flat and curved spacetime. Importantly, it is also possible to analyze the system using a quantum approach (in the description for flat spacetime) and to use standard tools of continuum mechanics for continuous media in flat and curved spacetime, where the description of the behavior of matter has been separated into effects related to fundamental interactions $f_{YM}^{\nu }$, gravity and radiation reaction $f_{gr}^{\nu }-f_{rr}^{\nu }$, and forces related to the distribution of matter $f_{\Xi }^{\nu }$.

2.3. The Halo Effect

The obtained result de facto means that Alena Tensor ensures correct operation of the standard continuum mechanics equations and GR equations (Euler equations, EOS, TOV, first integrals for rotating stars, etc.), with assumption that the energy density used in them is $\epsilon =\varrho c^2+2{\mathcal{E}}_{rot}$ and pressure is equal to ${\mathcal{E}}_{rot}$. In the next steps, this approach will be analyzed to show that it leads to consistency with the observational data.

It’s worth starting with a simple approximation. Denoting $u_{rot}$ as rotational velocity and assuming

$$p_{\mathrm{\Lambda }}\alpha ={\displaystyle \frac{1}{c^2\kappa }};{\varrho }_{rot}\equiv {\displaystyle \frac{2{\mathcal{E}}_{rot}}{c^2}}={\displaystyle \frac{{\omega }^{\alpha \beta }{\omega }_{\alpha \beta }}{8\pi G}}\to \underset{r\to \infty }{lim}{\varrho }_{rot}={\displaystyle \frac{u_{rot}^2}{4\pi G{r}^2}}$$

(39)

one may notice, that $p_{\mathrm{\Lambda }}\alpha$ in (14) plays the role of the density of the moment of inertia, while ${\varrho }_{rot}$ increases the body’s effective mass within its own frame. This would allow to consider galaxies as continuous media, where the effective mass $M_{eff}$ and its density ${\varrho }_{eff}$ responsible for gravity ${\varrho }_{eff}\equiv {\displaystyle \frac{\epsilon }{c^2}}=\varrho +{\varrho }_{rot}$ from (16) increases with the galactic disk size and angular velocity, causing the halo effect.

For far regions, denoting $M_b$ as baryonic mass, for spherical symmetry one obtains from Poisson’s equation simple linear ODE in the Newtonian limit. In the far regions it could determine a constant rotation speed and might be used to measure of deviation from the vacuum solution.

Vacuum solution in curved spacetime from (15) and (16) yields

$$\begin{array}{c}\hfill \tilde{R}=0;p_{\mathrm{\Lambda }}=2\epsilon \to \varrho c^2=-3{\mathcal{E}}_{rot};p_{\mathrm{\Lambda }}=-2{\mathcal{E}}_{rot};\mathrm{\Lambda }=-\kappa {\mathcal{E}}_{rot};0={\tau }^{\mu \nu }=U^{(\mu }{q}^{\nu )};{\mathcal{L}}_T=0\end{array}$$

(40)

This means that Kepplerian profiles are still possible for systems that can be approximated by a vacuum solution or does not rotate $({\mathcal{E}}_{rot}\approx 0)$.

Going into a more detailed analysis, one may consider $\left(0={\tau }^{\mu \nu }=U^{(\mu }{q}^{\nu )}\right)$ for a simple ideal fluid system with pressure $p\equiv {\mathcal{E}}_{rot}$ according to (16) and (19). In the GR equations one may consider above with an axisymmetric, spherical metric

$$\begin{array}{ccc}\hfill d{s}^2& =& N^2{c}^{2}d{t}^2-A^2\left(d{r}^2+r^{2}d{\theta }^2\right)-B^2{r}^2{sin}^2\theta {\left(d\varphi -\omega dt\right)}^2\hfill \\ \hfill T_{ideal}^{\mu \nu }& \equiv & \left(\varrho +{\displaystyle \frac{2p}{c^2}}\right)U^{\mu }{U}^{\nu }-p{\Delta }^{\mu \nu };\Omega \equiv {\displaystyle \frac{d\varphi }{dt}}\hfill \end{array}$$

(41)

Analyzing Euler’s energy and momentum equations in ${\nabla }_{\mu }{T}_{ideal}^{\mu \nu }=0$ one may notice, that $u_{ZAMO}$ is not a geodetic movement, and on the equator it takes the value

$$\begin{array}{c}\hfill {\displaystyle \frac{u_{ZAMO}^2}{c^2}}={\displaystyle \frac{{\left(Br\right)}^2}{N^2}}{\left(\Omega -\omega \right)}^2=r{\partial }_{r}lnN+{\gamma }_p^2-1;{\gamma }_p^2\equiv 1-r{\displaystyle \frac{p^{\prime }}{\varrho c^2+3p}}\end{array}$$

(42)

where ${\gamma }_p$ coefficient determines the deviation from the geodetic. One may therefore define pressure according to conclusions from previous section as follows, what yields

$$\begin{array}{c}\hfill \kappa p\equiv {\displaystyle \frac{u_{ZAMO}^2}{r^2{c}^2}}\to {\displaystyle \frac{d{M}_{eff}}{dr}}=4\pi r^2\varrho \left(r\right)+{\displaystyle \frac{u_{ZAMO}^2}{G}}\to {\displaystyle \frac{d}{dr}}{u}_{ZAMO}^2=4\pi Gr\varrho \left(r\right)\end{array}$$

(43)

In obtained picture the velocity increase depends solely on the baryon mass distribution, while the flattening of the tail is maintained by the rotational energy. This precisely corresponds to the expected behavior of a dark matter "halo."

The introduction of $q^{\mu }$ and ${\tau }^{\mu \nu }$ into a system can be approximated by defining parameter $\chi \left(r\right)$ changing oryginal p used for isotropic model

$$\begin{array}{c}\hfill p_r\equiv \alpha p;p_{\theta }\equiv \beta p;p_{\varphi }\equiv p\to \chi =\alpha +\beta ;3p_{\chi }\to (1+\chi )p;2p\to \chi p\end{array}$$

(44)

In practice, even a constant $\chi$ should be sufficient for analyzing the fit of galaxy rotation curves. Using a constant $\chi$ also provides a simpler ODE and the ability to quickly perform preliminary fits of $\chi$ to observational data for large amounts of data.

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{M}_{eff}}{dr}}& =& 4\pi r^2\varrho \left(r\right)+{\displaystyle \frac{\chi }{2}}{\displaystyle \frac{u_{ZAMO}^2}{G}}\to {\displaystyle \frac{d}{dr}}{u}_{ZAMO}^2=4\pi Gr\varrho \left(r\right)+\left({\displaystyle \frac{\chi }{2}}-1\right){\displaystyle \frac{u_{ZAMO}^2}{r}}\hfill \\ \hfill \underset{\varrho \to 0}{lim}{u}_{ZAMO}^2& \propto & r^{{\displaystyle \frac{\chi }{2}}-1}\hfill \end{array}$$

(45)

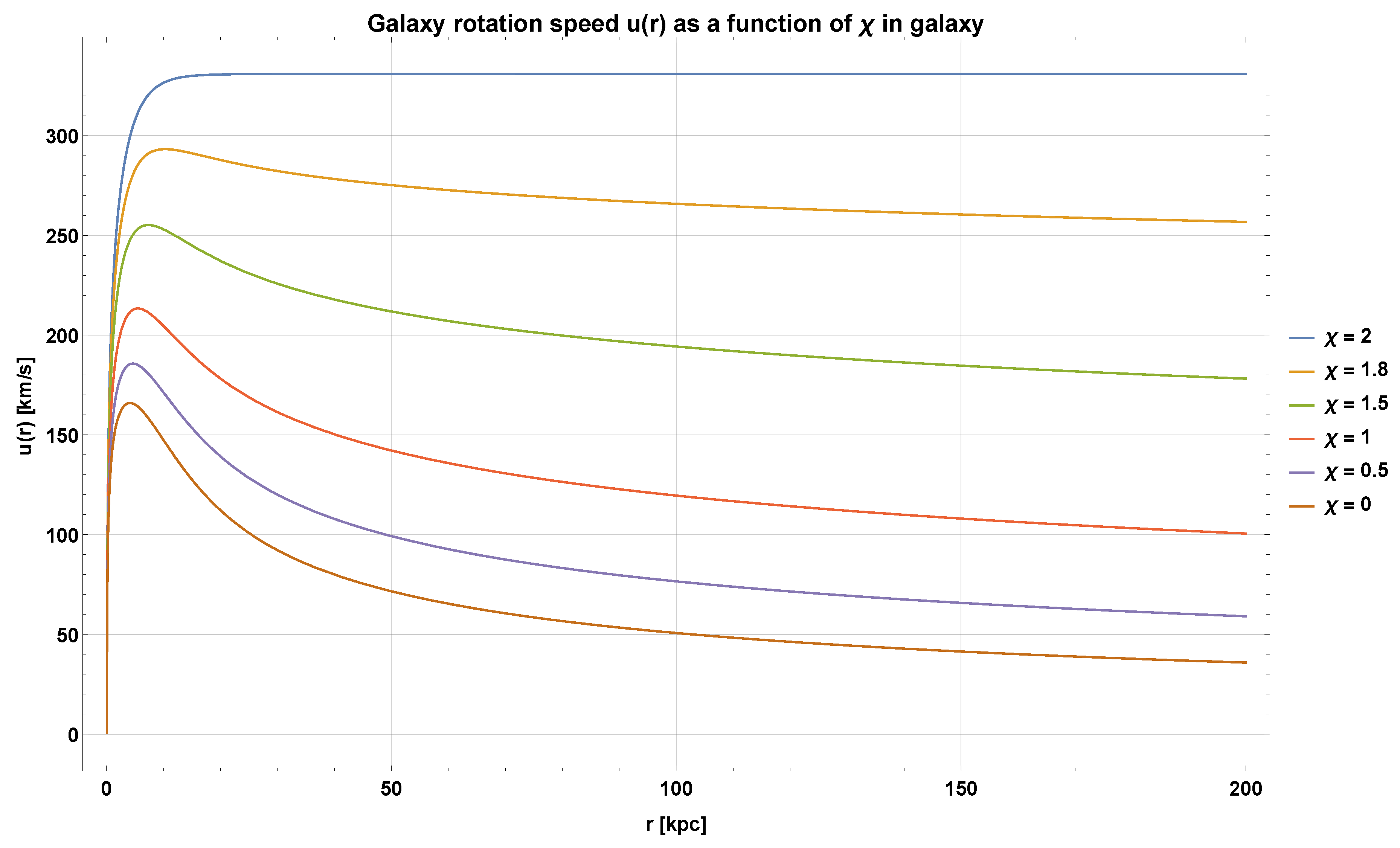
Below one may find the expected course of the rotation curves depending on the assumed constant $\chi$. The calculations used an averaged Hernquist bulge baryon model ${\varrho }_{bulge}$ and a ”spherical proxy” of the exponential disk ${\varrho }_{disc}$

$$\begin{array}{ccc}\hfill {\varrho }_{bulge}& =& {\displaystyle \frac{M_{bulge}}{2\pi }}{\displaystyle \frac{a}{r{(r+a)}^3}};M_{bulge}={10}^{10}{M}_{\odot };a=1kpc\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill {\varrho }_{disc}& =& {\displaystyle \frac{M_{disc}}{4\pi R_d^2}}{\displaystyle \frac{e^{-r/R_d}}{r}};R_d=3kpc\hfill \end{array}$$

(47)

with total baryon density ${\varrho }_b\left(r\right)={\varrho }_{bulge}+{\varrho }_{disc}$, standard G value, anisotropy and energy stream simulated by constant $\chi$. As can be seen from the graph, the increasing anisotropy towards the outskirts of the galaxy $\chi (r=0)=0;\underset{r\to \infty }{lim}\chi \left(r\right)=const$ would allow the graph to align with the expected curve shapes for spiral galaxies.

Figure 1. Approx. rotation curves in Alena Tensor model

Figure 1. Approx. rotation curves in Alena Tensor model

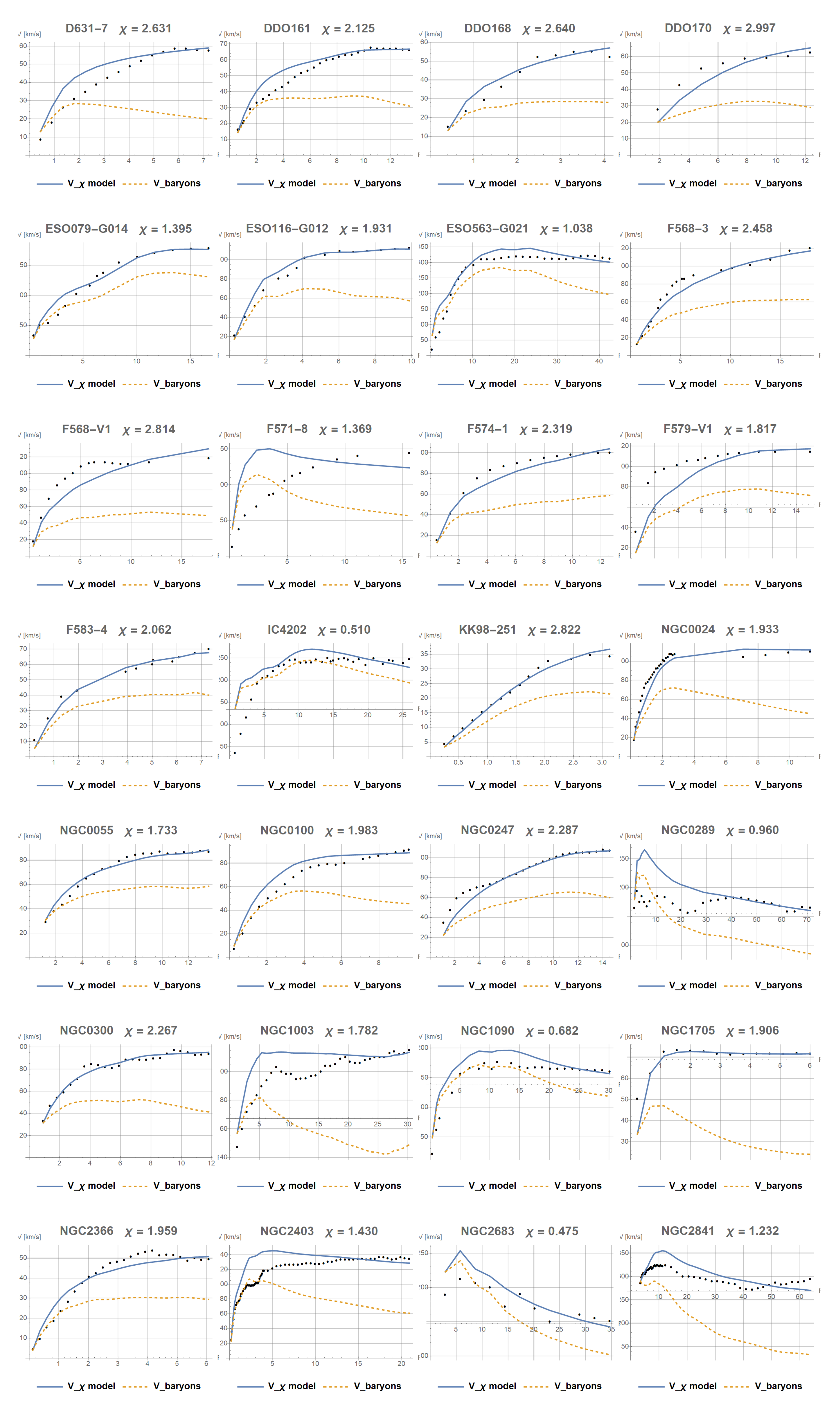
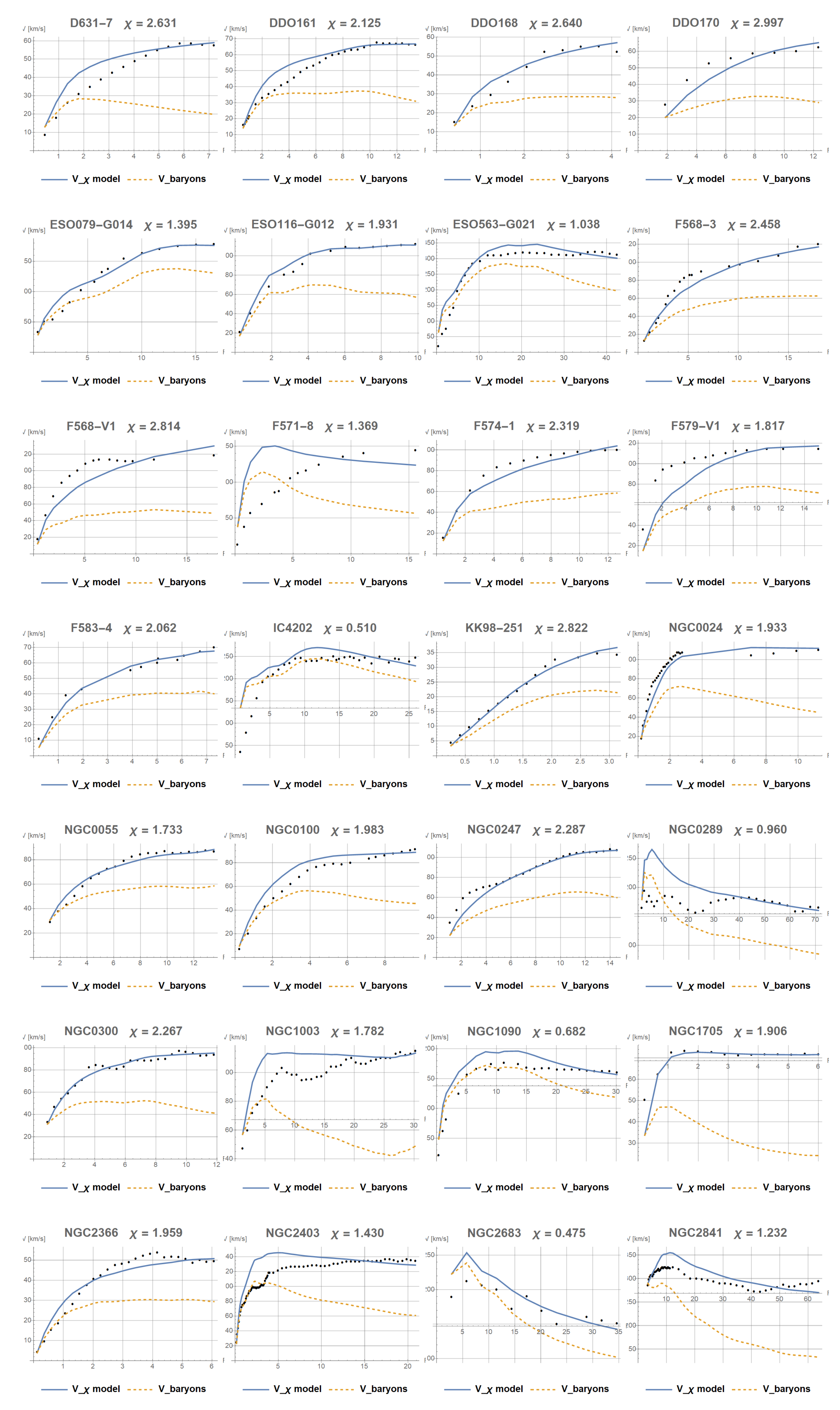
As it appears, constant $\chi$ actually allows to tune the rotation velocity distribution for some part of galaxies what gives an overview of the method and may help in further analysis and tuning of $\chi \left(r\right)$ function to achieve full agreement with observations. The Appendix A presents the results of tuning the $\chi$ constant for about 100 galaxies from the SPARC catalog. The results seem encouraging, and worth further analysis with the $\chi \left(r\right)$ function or with the full $T^{\mu \nu }$ tensor representation. For most galaxies the fit is very good, and for the rest it is obtainable by introducing a simple function $\chi \left(r\right)$ which provides $\chi \left(r\right)\approx 0$ for small r (chaotic motions in the center, no ordered rotation) to a stabilized rotation in the outskirts with a fixed $\chi$.

The $\chi$ parameter was adjusted for each galaxy by iteratively solving the radial motion differential equation resulting from (45), with the condition of normalizing the rotation rate in the outer disk ${\langle V_{\chi }\rangle }_{\mathrm{outer}}={\langle V_{\mathrm{obs}}\rangle }_{\mathrm{outer}}$. The entire procedure, including reading the rotation data from the SPARC catalog, interpolating the baryonic component $V_{\mathrm{bar}}\left(r\right)$, numerically solving the equation for $V_{\chi }(r,\chi )$ and saving the resulting plots in PDF format, was fully automated in the Mathematica script, and run in an environment with the SPARC source data. The script is included in the supplementary files.

3. Discussion and Conclusions

As seen in the above article, supplementing the Alena Tensor with the energy associated with the rotation of bodies naturally leads to the creation of halo effects, known from dark matter studies. Preliminary analysis allows for a fairly good match of this effect to observational results, although this obviously requires further development and verification for a larger number of cosmological objects.

Importantly, the proposed approach does not require modification of the GR equations, but rather fits naturally into the applied GR equations and continuum mechanics. Since the source is described in this approach by $\epsilon =\varrho c^2+2{\mathcal{E}}_{rot}$, this means that the observed increase in effective mass also affects gravitational lensing to an extent precisely corresponding to the increase in effective mass by the energy associated with (in this case - rotational) ”dark matter”. This is precisely what is obtained in observations [32,33].

The proposed solution fits quite well with the research direction represented by [34,35,36] and also [37] (including baryotropy), who investigated anisotropic fluid in cosmology and its potential connections with the dark sector. However, it complements these studies with the natural halo effect resulting directly from the GR equations for the Alena Tensor. The proposed model also expands and, in a sense, substantiates the hypothesis posed by C. Rourke [38], complementing the research [39,40,41,42] with a justification for linking rotation with the halo effect. The idea that rotation-related effects can mimic dark matter is not new, but Alena Tensor gives it some additional structure, making it a direct consequence of a coherent mathematical model.

Importantly, the Alena Tensor also provides a natural interpretation of dark energy. The value of $p_{\mathrm{\Lambda }}$ is an invariant of the field tensor and becomes constant (or, at least, metric-independent invariant) in curvilinear description. In a sense, a nonzero value of $\mathrm{\Lambda }$ can therefore be interpreted as a scale of deviation from pure wave solutions, without matter (for example, for the electromagnetic field, $p_{\mathrm{\Lambda }}=0$ would mean that the electric and magnetic fields are equal, so the solutions must be pure electromagnetic waves). Since the value of $p_{\mathrm{\Lambda }}$ measured in flat spacetime is $p_{\mathrm{\Lambda }}=p_o{\left({\mathbb{k}}_{\mu \nu }{\eta }^{\mu \nu }\right)}^2$, it is a measure of the "flatness" of spacetime, or more precisely, a measure of how much the metric tensor for the curvilinear description deviates from the Minkowski tensor. This interpretation seems particularly interesting in the context of the works [43,44], because it strengthens and details the conclusions described therein, providing a geometric, anisotropic source that can be interpreted as a specific backreaction mechanism leading to acceleration.

This approach could be applied to many other continuous systems (e.g., stars or black holes) and seems worth to describe the extreme in which $\varrho =0$ and all the energy in the system is rotational energy. Although at first glance it seems absurd, one may notice, that the source in vacuum solution (40) is indeed solely rotational energy. Replacing rotation with vorticity and treating it as a consequence of the circulating field could potentially help model, for example, elementary particles as quasi-stable systems of three-dimensional vortices, driven by their own rotational energy. For example, varying ${\mathcal{L}}_{\mathrm{eff}}$ from (30) with respect to $\overline{\psi }$ gives the modified Dirac equation

$$\left(i{\gamma }^{\mu }{D}_{\mu }-m+g{\mathrm{\Sigma }}^{\mu \nu }{\omega }_{\mu \nu }\right)\psi =0$$

(48)

For a thin circular vortex, corresponding to a phase winding $n\in \mathbb{Z}$ in $\varphi =\sqrt{\rho }{e}^{in\vartheta }$, the energy of a loop of radius R can be expressed entirely in terms of quantities already defined in ${\mathcal{L}}_{\mathrm{eff}}$, as

$$E\left(R\right)\simeq 2\pi R\mathcal{T}+{\displaystyle \frac{k{n}^2}{R}};R_{*}=\sqrt{{\displaystyle \frac{k{n}^2}{2\pi \mathcal{T}}}}$$

(49)

In above,

$$\mathcal{T}\equiv \int d^2{x}_{\perp }\left(|D_i{\varphi |}^2+V\left[\right|\varphi \left|\right]+{\displaystyle \frac{\xi }{4}}{\mathbb{F}}_{ij}{\mathbb{F}}^{ij}\right)$$

(50)

is the core line energy per unit length built from the scalar-gauge sector of ${\mathcal{L}}_{\mathrm{eff}}$, and

$$k\equiv \pi p_{\mathrm{\Lambda }}\alpha \left(\left|\varphi \right|\to v\right)$$

(51)

is the rotational stiffness fixed by the ${\displaystyle \frac{p_{\mathrm{\Lambda }}}{2}}\alpha {\omega }_{\mu \nu }{\omega }^{\mu \nu }$ term evaluated at the asymptotic field value $\left|\varphi \right|\to v$. The first term, $2\pi R\mathcal{T}$, corresponds to the contracting line energy of the vortex core, while the second, $k{n}^2/R$, originates from the rotational-energy density ${\displaystyle \frac{p_{\mathrm{\Lambda }}}{2}}\alpha {\omega }_{\mu \nu }{\omega }^{\mu \nu }$ of the circular flow (scaling as $n^2/R$). Their balance yields a finite stable radius $R_{*}$. Hence, the model admits particle-like, topologically stabilized vortices, naturally emerging from the improved Belinfante tensor structure. One may also notice, that the last term in (48) actually represents a local spin-vorticity coupling, formally analogous to the Mashhoon effect [45,46], leading to spin-dependent energy shifts in rotating or vortical systems.

It is thus possible, taking into account the conclusions from 2.2.1, to further develop the idea of rotation in quantum systems. In quantum field theory systems with significant local vorticity, the inclusion of a rotational-energy contribution in the energy-momentum tensor implies a new spin-vorticity coupling term, which may lead to measurable spin polarization of fermions as predicted e.g. in heavy-ion physics [47]. Such additional rotational energy terms effectively modify the Hamiltonian density and thus alter propagators or dispersion relations of excitations in the medium, analogous to how vorticity-induced spin currents appear in hydrodynamic and condensed-matter contexts as in [48]. Since in considered approach the modified tensor now couples orbital angular momentum and intrinsic spin via the rotational energy density, therefore the renormalization group flows and transport coefficients (like shear viscosity or spin diffusion) may pick up new contributions, offering a potential probe of vorticous quantum media such as the quark-gluon plasma [49].

Equally interesting direction of further analysis could be e.g. the use of the possibilities of quantum description of the dark sector in the Alena Tensor model, for further development of works such as [50]. It also seems that describing matter (e.g. a neutron star, as in [51,52]) using the mechanism proposed here for GR, would be the simplest way to confirm or falsify the Alena Tensor, due to the high symmetry of such a solution. However, all these analyses deserve separate articles.

In conclusion, it remains an open question whether the Alena Tensor is a correct way to describe physical systems, but this paper shows that, beyond the compliances with available knowledge achieved so far, it naturally leads to the existence of halo effects and also proposes an interpretation of dark energy. The author hopes that the results obtained in this paper will facilitate further use and development of the discussed approach and, potentially, many similar concepts. It also seems that further analysis of Alena Tensor may provide useful descriptions of the transformation between curved and flat spacetime and bring new insights that will contribute to a better understanding of issues related to the broadly understood unification of physical theories.