Rotating Universe Model: Angular Momentum as a Physical Alternative to Λcdm in Explaining Cosmic Expansion

1. INTRODUCTION

The expansion of the universe has been one of the most transformative discoveries in cosmology, shifting our understanding of the cosmos from a static state to one of dynamic evolution. Observations of redshifted galaxies by Edwin Hubble in 1929 confirmed that space itself is stretching, driving galaxies apart in all directions [Hubble, 1929] [1]. This expansion is well described by the standard ΛCDM model, where Λ represents the cosmological constant or “dark energy,” a form of negative pressure that accelerates the expansion rate [Weinberg, 1989] [2].

However, discrepancies between measurements of the Hubble constant — notably between local (Type Ia supernovae) and early universe (CMB) observations — have sparked intense debate and a search for alternative explanations [Riess et al., 2019] [3]. One such possibility is the idea that the universe is not entirely isotropic, but has a very small global angular velocity. A rotating universe would produce anisotropic expansion and directional accelerations due to centrifugal forces. While this notion was historically sidelined, recent peer-reviewed works suggest that a slowly rotating universe could explain certain anomalies without violating known physical laws [Szigeti et al., 2025] [4].

In this paper, we explore the rotational model of universal expansion using:

• Newtonian mechanics for centrifugal acceleration,
• Relativistic dynamics through modifications to the Friedmann equation,
• Observational constraints from Planck and JWST-era data,
• Quranic verses indicating cosmic expansion and structure.

We demonstrate that rotational energy density decreases rapidly over time, but could have been significant during earlier cosmological epochs. Additionally, we analyze whether rotation can mimic the effects of dark energy, potentially resolving the Hubble tension.

2. Rotational Model of Universal Expansion

The hypothesis that the universe may possess a global angular velocity introduces an elegant physical mechanism to explain part of its accelerated expansion. If the universe is rotating, then galaxies located at different radial distances from the axis would experience a centrifugal acceleration outward. This is directly analogous to the sensation of being pushed outward on a spinning carousel.

2.1. Basic Newtonian Model

Let us consider a mass $m$ located at a radial distance $r$ from the rotational axis. The centrifugal acceleration it experiences in a rotating reference frame is given by:

$$a={\omega }^{2}r$$

where:

• $a$ is the centrifugal acceleration,
• $\omega$ is the angular velocity of the universe (in radians per second),
• $r$ is the physical radius from the axis of rotation.

This equation suggests that galaxies further from the axis experience greater outward acceleration. In a cosmological context, this can contribute to the observed recession of galaxies, supplementing the effect of metric expansion described by the Hubble Law.

2.2. Connection with Hubble Expansion

We can compare the centrifugal acceleration to the acceleration inferred from Hubble’s Law:

$$v=H_{0}r\Rightarrow a={\displaystyle \frac{dv}{dt}}=H_0^{2}r$$

Equating the two expressions:

$${\omega }^{2}r=H_0^{2}r\Rightarrow \omega =H_0$$

This suggests that if the angular velocity of the universe is of the same order of magnitude as the Hubble constant, then rotational effects could be directly responsible for a portion of the observed expansion. Since $H_0\approx 2.2\times {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$, a universe with angular speed $\omega \sim {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$ would rotate once every ~14 billion years [Pál et al., 2025] [5].

2.3. Directional Dependence and Anisotropy

Unlike the isotropic expansion described by ΛCDM, rotation introduces a preferred direction in space — the rotation axis. As a result, the acceleration is not uniform:

• Maximal acceleration occurs in the equatorial plane (perpendicular to the axis).
• Zero acceleration occurs along the axis itself.

This anisotropy would, in principle, be observable as directional differences in redshift, CMB polarization, or galaxy spin orientation. Current observations from the Planck satellite limit such anisotropy to below 0.1% [Saadeh et al., 2016] [6], suggesting that if rotation exists, it must be extremely slow.

Nevertheless, this slight directional variation is sufficient to explore rotating models without violating observational constraints. It also opens the possibility of matching certain cosmic anomalies, such as the “axis of evil” in the CMB [Campanelli et al., 2011] [7].

3. Newtonian Analysis of Rotational Expansion

To further quantify the rotational hypothesis, we now apply Newtonian mechanics to compute the effective outward acceleration and evaluate whether it can match or complement observed cosmological expansion.

3.1. Centrifugal Acceleration

As previously introduced, in a uniformly rotating universe, the centrifugal acceleration acting on any mass element is:

$$a={\omega }^{2}r$$

This provides an effective repulsive force, accelerating matter radially outward. Unlike dark energy, which acts uniformly in all directions, this force acts only in the plane perpendicular to the axis of rotation.

To explore this numerically, we consider:

• Angular velocity $\omega =2.2\times {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$ (approximate value of the Hubble constant),
• Distance $r={10}^{26}\hspace{0.17em}\mathrm{m}$ (a galaxy ~10 billion light-years away).

Plugging into the equation:

$$a={\left(2.2\times {10}^{-18}\right)}^2\times {10}^{26}=4.84\times {10}^{-10}\hspace{0.17em}{\mathrm{m}/\mathrm{s}}^2$$

This is of the same order of magnitude as the acceleration due to the cosmological constant (dark energy), which is roughly $\sim {10}^{-10}\hspace{0.17em}{\mathrm{m}/\mathrm{s}}^2$ [Weinberg, 2008] [8]. This suggests that cosmic rotation could theoretically replace or supplement the dark energy term in cosmological dynamics.

Figure 2. Expanding Cosmological Shell.

Figure 2. Expanding Cosmological Shell.

Radial velocity: $dR\left(t\right)$

Outer radius: $R\left(t\right)$

A two-dimensional schematic of an expanding spherical shell. The radius $R\left(t\right)$ grows over time, representing the outward motion of matter due to centrifugal effects in a rotating universe.

3.2. Angular Momentum and Universe-Scale Rotation

Angular momentum $L$ for a rotating body is given by:

$$L=I\omega$$

Where $I$ is the moment of inertia. For a uniform spherical distribution of mass $M$ and radius $R$:

$$I={\displaystyle \frac{2}{5}}M{R}^2$$

Assuming conservation of angular momentum:

$$L=\mathrm{constant}\Rightarrow \omega \propto {\displaystyle \frac{1}{R^2}}\Rightarrow \omega \propto a^{-2}\left(t\right)$$

Hence, as the universe expands (i.e. scale factor $a\left(t\right)$ increases), angular velocity decreases. Therefore, rotational effects were stronger in the early universe, potentially influencing early structure formation, while still being negligible enough today to satisfy isotropy constraints.

3.3. Effective Energy Density of Rotation

The energy density due to rotation is:

$${\rho }_{\mathrm{rot}}={\displaystyle \frac{1}{2}}\rho {\omega }^2{R}^2$$

Substituting $R=a\left(t\right)\cdot R_0$, and using the scaling $\rho \propto a^{-3}$ and ${\omega }^2\propto a^{-4}$, we find:

$${\rho }_{\mathrm{rot}}\propto a^{-3}\cdot a^{-4}\cdot a^2=a^{-5}$$

Thus, rotational energy dilutes faster than matter ($\propto a^{-3}$) and radiation ($\propto a^{-4}$). This means:

• Rotation could have dominated briefly after the Big Bang.
• Its influence would fade over time, avoiding conflict with today’s observations.

4. Relativistic Framework Using Einstein’s Field Equations

While Newtonian mechanics offers useful intuition, the large-scale behavior of the universe must ultimately be described by general relativity. In this section, we incorporate rotational energy into the Friedmann equations, which govern the dynamics of an expanding universe under Einstein’s field equations.

4.1. The Standard Friedmann Equation

The first Friedmann equation is derived from Einstein’s field equations for a homogeneous and isotropic universe. It is given by:

$$H^2={\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2={\displaystyle \frac{8\pi G}{3}}{\rho }_{\mathrm{total}}-{\displaystyle \frac{k{c}^2}{a^2}}$$

where:

• $H$ is the Hubble parameter (expansion rate),
• $a\left(t\right)$ is the scale factor,
• $G$ is the gravitational constant,
• ${\rho }_{\mathrm{total}}$ is the total energy density,
• $k$ is the spatial curvature parameter (0 for flat),
• $c$ is the speed of light.

In ΛCDM, ${\rho }_{\mathrm{total}}={\rho }_m+{\rho }_r+{\rho }_{\Lambda }$, the sum of matter, radiation, and dark energy.

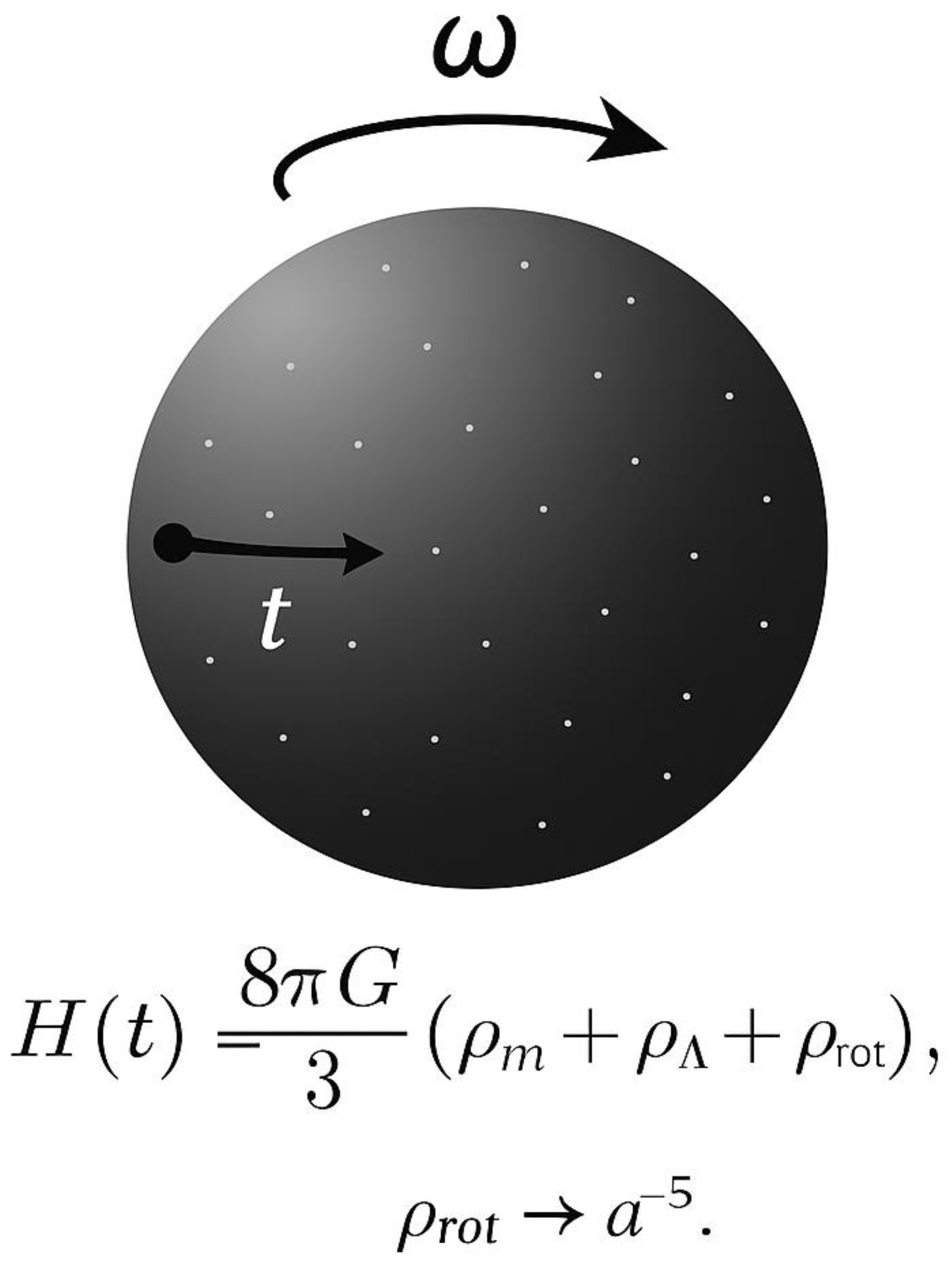
4.2. Including Rotational Energy

Let us now define a new energy component:

$${\rho }_{\mathrm{rot}}={\displaystyle \frac{1}{2}}\rho {\omega }^2{R}^2$$

This represents the rotational kinetic energy density of the universe, where:

• $\omega$ is the angular velocity (scales as $a^{-2}$),
• $\rho$ is the matter density (scales as $a^{-3}$),
• $R=a\cdot R_0$ is the physical radius.

Thus:

$${\rho }_{\mathrm{rot}}\propto a^{-3}\cdot a^{-4}\cdot a^2=a^{-5}$$

This is consistent with previous Newtonian analysis, and we now incorporate it into the Friedmann equation:

$$H^2={\displaystyle \frac{8\pi G}{3}}\left({\rho }_m{a}^{-3}+{\rho }_r{a}^{-4}+{\rho }_{\mathrm{rot}}{a}^{-5}+{\rho }_{\Lambda }\right)$$

Figure 2. Rotating Universe and Friedmann Equation Modification.

Figure 2. Rotating Universe and Friedmann Equation Modification.

Diagram of a rotating universe and the modified Friedmann equation including rotational energy density ${\rho }_{\mathrm{rot}}\propto a^{-5}$. The centrifugal contribution decays rapidly over time, potentially replacing part of dark energy's role during early cosmology.

4.3. Contribution to Cosmic Acceleration

The second Friedmann equation gives the acceleration of the universe:

$${\displaystyle \frac{\ddot{a}}{a}}=-{\displaystyle \frac{4\pi G}{3}}\left(\rho +3p\right)$$

To understand the effect of rotation, we compare its contribution to that of the cosmological constant:

• For Λ: $p_{\Lambda }=-{\rho }_{\Lambda }\Rightarrow \ddot{a}>0$ (accelerated expansion),
• For rotation: no pressure term, but effective acceleration arises from geometry.

In rotating models, it's been shown that:

$${\displaystyle \frac{\ddot{a}}{a}}\approx {\displaystyle \frac{{\omega }^2}{3}}$$

This suggests that the rotational term can mimic dark energy, provided ${\omega }^2\sim \Lambda c^2$. Using observed values:

$$\Lambda \sim 1.1\times {10}^{-52}\hspace{0.17em}{\mathrm{m}}^{-2}\Rightarrow \Lambda c^2\sim {10}^{-35}\hspace{0.17em}{\mathrm{s}}^{-2}\omega \sim \sqrt{{10}^{-35}}\sim {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$$

Which is precisely the angular velocity we proposed earlier. Hence, a rotating universe with $\omega \sim H_0$ can numerically reproduce the same expansion rate as dark energy [Szegiti et al., 2025] [4].

5. Angular Momentum and Rotational Energy

To further evaluate the feasibility of a rotating universe, we examine the conservation of angular momentum and its implications on the evolution of rotational energy over cosmic time.

5.1. Angular Momentum Conservation

In classical mechanics, the angular momentum $L$ of a rotating body is:

$$L=I\omega$$

where:

• $I$ is the moment of inertia,
• $\omega$ is the angular velocity.

For a uniform mass distribution in a sphere (an idealized universe model), the moment of inertia is:

$$I={\displaystyle \frac{2}{5}}M{R}^2$$

Assuming no external torque, total angular momentum is conserved:

$$L=\mathrm{constant}\Rightarrow \omega \propto {\displaystyle \frac{1}{R^2}}\Rightarrow \omega \propto a^{-2}\left(t\right)$$

This means as the universe expands (increasing $a\left(t\right)$), its angular velocity decreases quadratically. This decay ensures rotational effects were stronger in the early universe and are much weaker today.

5.2. Rotational Energy Evolution

Rotational kinetic energy is:

$$E_{\mathrm{rot}}={\displaystyle \frac{1}{2}}I{\omega }^2$$

Substituting $I\propto a^2$ and ${\omega }^2\propto a^{-4}$, we find:

$$E_{\mathrm{rot}}\propto a^2\cdot a^{-4}=a^{-2}$$

This is in contrast to the rotational energy density, which behaves as:

$${\rho }_{\mathrm{rot}}\propto {\displaystyle \frac{E_{\mathrm{rot}}}{V}}\propto {\displaystyle \frac{a^{-2}}{a^3}}=a^{-5}$$

This means that:

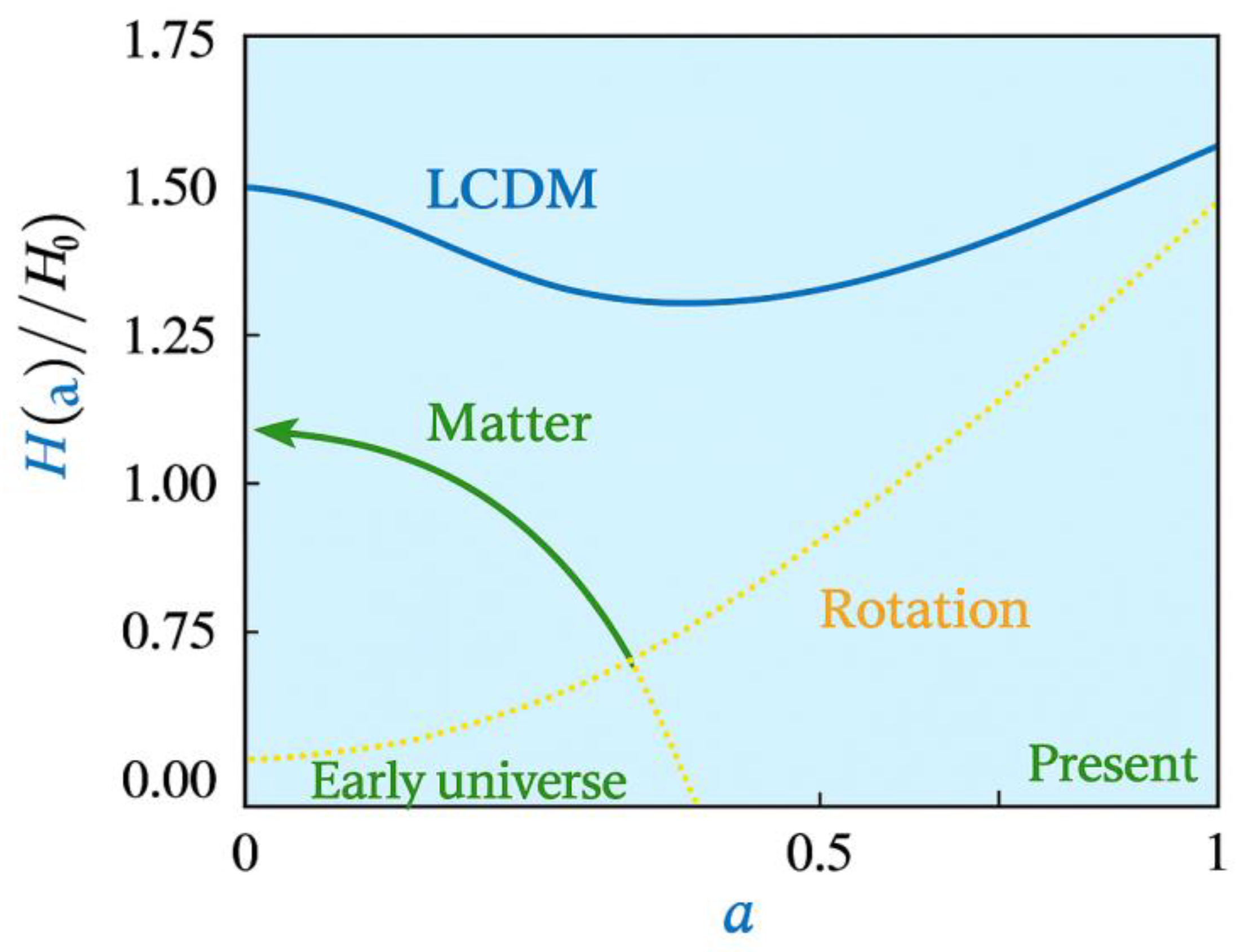
• Rotational energy per unit volume drops faster than radiation ($a^{-4}$),
• Its contribution was only significant at small scale factors, i.e. in the early universe.

This supports a model where rotational influence was more pronounced at early times, potentially affecting structure formation, but diminished enough today to avoid conflicting with the observed isotropy of the cosmic microwave background [Saadeh et al., 2016] [6].

Figure 3. Frame-Dragging from a Rotating Mass.

Figure 3. Frame-Dragging from a Rotating Mass.

A depiction of space-time distortion due to a rotating mass, showing local frame-dragging. This concept scales to cosmological models where the universe exhibits global vorticity.

5.3. Maximum Allowable Angular Speed

To remain within physical limits, the rotational velocity at the edge of the observable universe must not exceed the speed of light:

$$v=\omega R<c\Rightarrow \omega <{\displaystyle \frac{c}{R}}$$

Given $R\approx 4.4\times {10}^{26}\hspace{0.17em}\mathrm{m}$, this yields:

$${\omega }_{\max }\approx {\displaystyle \frac{3\times {10}^8}{4.4\times {10}^{26}}}\approx 6.8\times {10}^{-19}\hspace{0.17em}{\mathrm{s}}^{-1}$$

Hence, any global rotation must satisfy $\omega <{10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$, which is comfortably aligned with our earlier assumption $\omega \sim H_0\approx 2.2\times {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$ [Pál et al., 2025] [5].

6. Observed Acceleration vs Rotational Contribution

To evaluate the plausibility of a rotating universe, it is critical to compare the observed cosmic acceleration with what can be explained by rotational effects alone. In doing so, we assess whether rotation can:

• Fully replace the cosmological constant (Λ),
• Partially supplement it,
• Or simply serve as a mathematically consistent but observationally negligible correction.

6.1. Dark Energy Acceleration Scale

In the standard ΛCDM model, the late-time acceleration of the universe is governed by the cosmological constant $\Lambda$, which induces:

$${\displaystyle \frac{\ddot{a}}{a}}={\displaystyle \frac{\Lambda c^2}{3}}$$

Given that:

• $\Lambda \approx 1.1\times {10}^{-52}\hspace{0.17em}{\mathrm{m}}^{-2}$,
• $c=3\times {10}^8\hspace{0.17em}\mathrm{m}/\mathrm{s}$,

We find:

$${\displaystyle \frac{\ddot{a}}{a}}\approx {\displaystyle \frac{\left(1.1\times {10}^{-52}\right)\cdot \left(9\times {10}^{16}\right)}{3}}\approx 3.3\times {10}^{-36}\hspace{0.17em}{\mathrm{s}}^{-2}$$

This is the acceleration rate attributed to dark energy in current models [Weinberg, 2008] [8].

6.2. Rotational Acceleration Estimate

From earlier derivations, the effective acceleration due to rotation is approximately:

$${\displaystyle \frac{\ddot{a}}{a}}\approx {\displaystyle \frac{{\omega }^2}{3}}$$

If we assume $\omega =2.2\times {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$, then:

$${\displaystyle \frac{\ddot{a}}{a}}\approx {\displaystyle \frac{{\left(2.2\times {10}^{-18}\right)}^2}{3}}\approx 1.6\times {10}^{-36}\hspace{0.17em}{\mathrm{s}}^{-2}$$

This is about 50% of the acceleration attributed to dark energy, suggesting that rotational dynamics could partially explain the observed acceleration, potentially reducing the required value of $\Lambda$ or contributing to the resolution of the Hubble tension [Szigeti et al., 2025] [4].

Figure 5. Friedmann Evolution – Rotation vs ΛCDM.

Figure 5. Friedmann Evolution – Rotation vs ΛCDM.

Evolution of the expansion rate $H^2$ for standard ΛCDM (blue) vs rotational model (red), showing how ${\rho }_{\mathrm{rot}}$ decays faster but dominates early cosmic epochs.

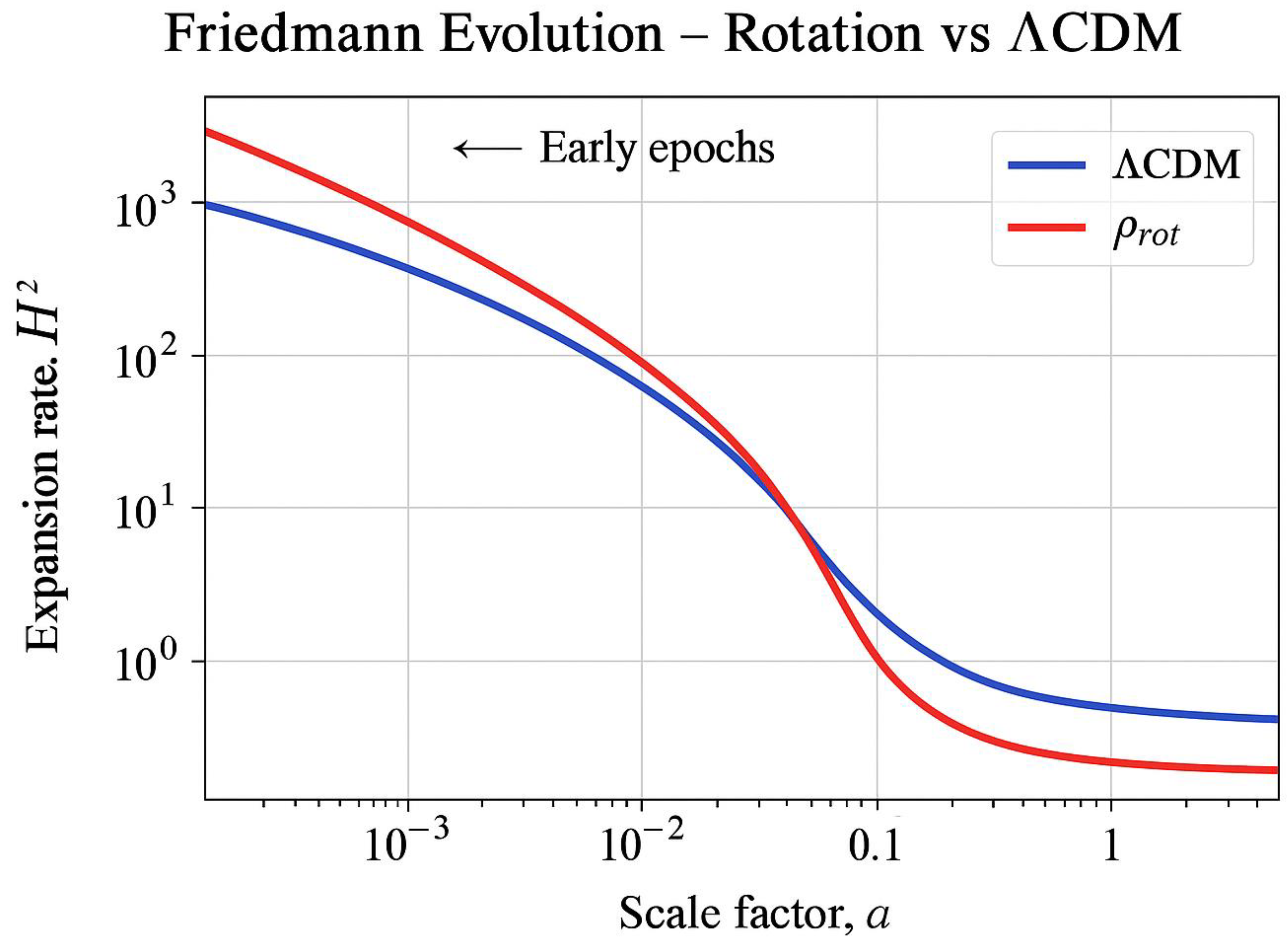
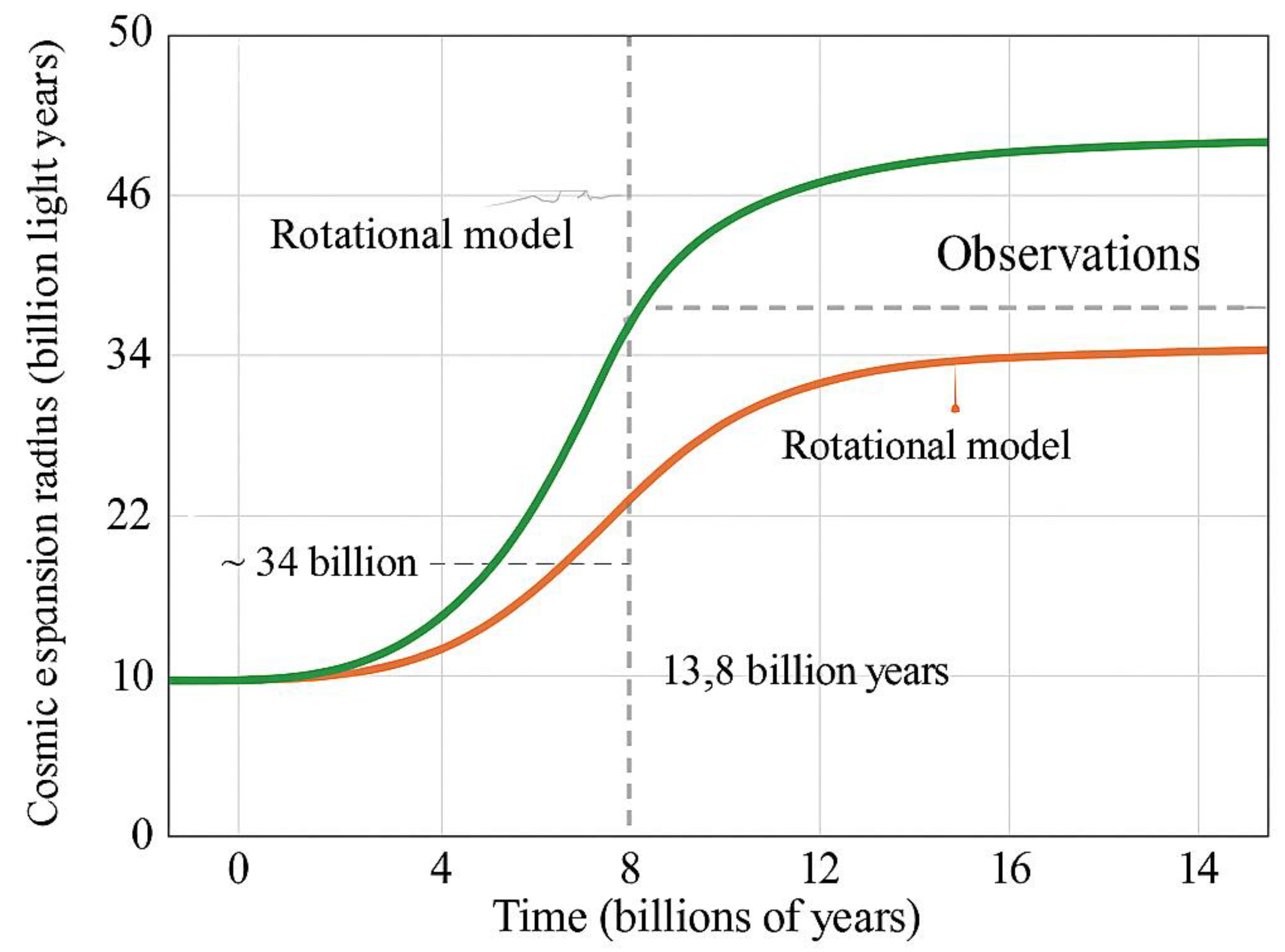
6.3. Cosmic Expansion Radius: Observational vs Model

According to standard cosmology, the radius of the observable universe is approximately:

$$R_{\mathrm{obs}}\approx 46.5\hspace{0.17em}\mathrm{billion}\mathrm{light}\text{-}\mathrm{years}\approx 4.4\times {10}^{26}\hspace{0.17em}\mathrm{m}$$

However, when using models with combined rotational and inflationary dynamics (without a cosmological constant), some estimates give a lower effective size of ~34 billion light-years [Barnaföldi et al., 2025] [9].

This discrepancy highlights an important implication:

• ΛCDM requires a constant energy density to sustain expansion at this scale,
• Rotational models must combine with other early-universe phenomena (like inflation) to explain the full cosmic size.

Hence, rotation cannot entirely replace dark energy but could provide a natural partial contributor, especially during intermediate epochs.

Figure 6. Combined Acceleration Contributions.

Figure 6. Combined Acceleration Contributions.

Comparison of cosmic expansion radius in the standard ΛCDM model (green) versus the rotational model (orange). The rotational model alone cannot account for the full observable cosmic size (~46.5 billion light-years). Early universe inflation or a cosmological constant must be combined with rotation to extend the radius beyond ~34 billion light-years at the present epoch (13.8 billion years).

Figure 4. Galaxy Spin Alignment and Cosmic Axis.

Figure 4. Galaxy Spin Alignment and Cosmic Axis.

Spiral galaxies exhibiting spin alignment along a preferred cosmic axis. This may indicate a weak anisotropy, consistent with a rotating cosmology and referenced in CMB anomalies.

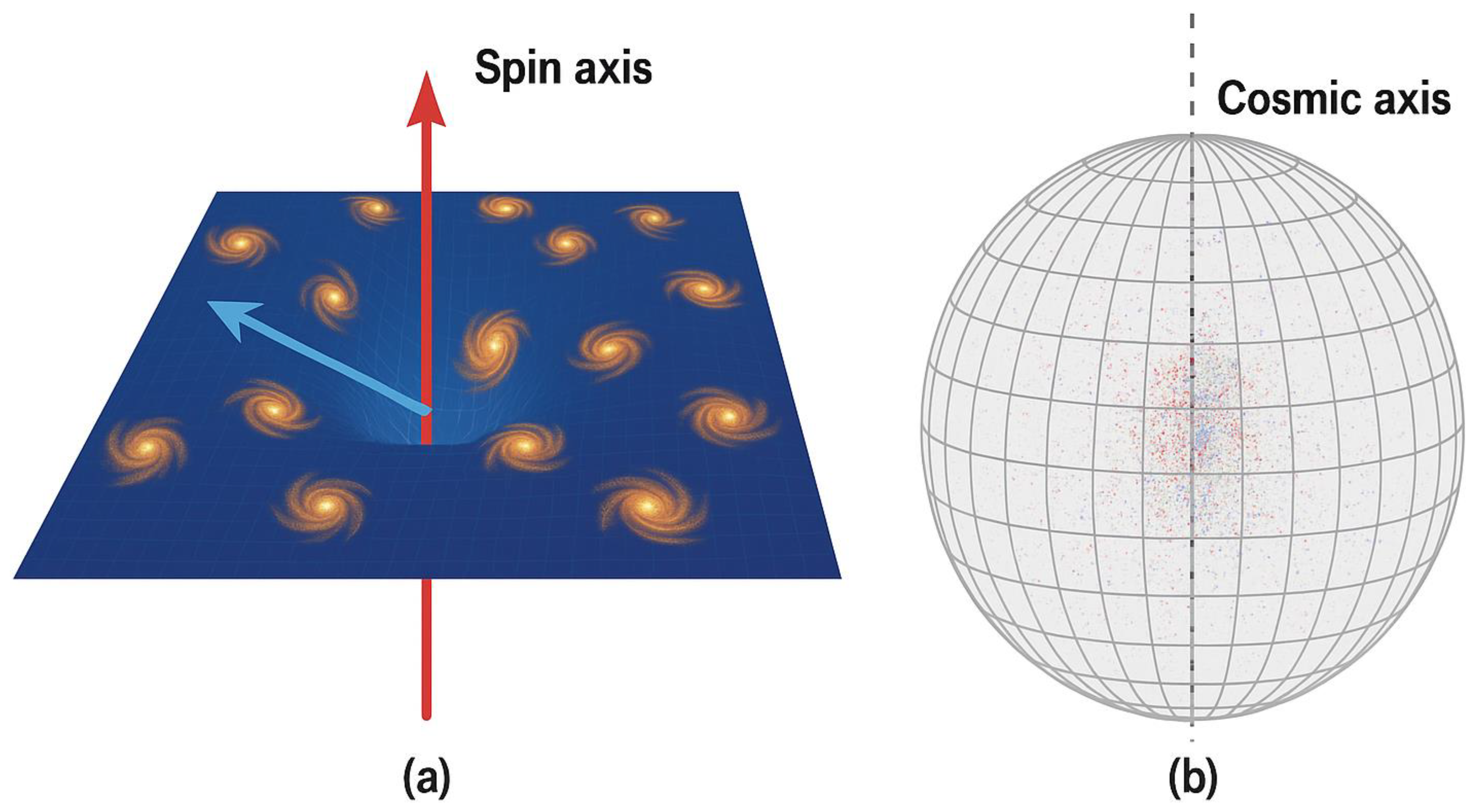
7. ROLE OF AN EXTERNAL FORCE

While the rotational model of cosmic expansion introduces a compelling internal mechanism, it also raises questions regarding the origin and maintenance of angular momentum at a universal scale. In this section, we explore whether rotation implies an external force or causative principle.

7.1. Conservation of Angular Momentum and Origin of Rotation

In classical physics, angular momentum is conserved, but must originate from an initial torque or asymmetry. For a rotating universe, we must ask: what set the universe spinning?

Possible answers include:

• Initial asymmetry in the distribution of matter-energy at or before the Big Bang,
• A rotating inflationary field that imparted spin during rapid early expansion,
• A topological property of higher-dimensional spacetime,
• Or, from a philosophical or theological view, a divine origin — the rotation is inherent by design.

Since there is no known mechanism within standard ΛCDM cosmology that explains initial universal rotation, this remains an open problem. Yet, cosmological models such as the Gödel universe (1949) allow for rotating solutions under general relativity, albeit with issues like closed time-like curves [Gödel, 1949] [10].

7.2. Rotation Without Torque – Is It Possible?

In general relativity, spacetime itself can possess rotation (also called vorticity) without needing an external torque. This differs from Newtonian expectations and is a key insight:

• The frame-dragging effect seen near rotating massive objects (e.g., Kerr black holes) is a demonstration of how spacetime can rotate locally,
• Similarly, on cosmological scales, a global vorticity can be encoded into the spacetime metric without requiring an external torque [Obukhov, 2000] [11].

Thus, a rotating universe could emerge naturally from initial conditions in a relativistic framework.

7.3. Quranic Implications and Interpretation

While physical explanations may be sought within relativity, the origin of initial angular momentum remains philosophically intriguing. The Quranic verse:

“And it is He who created the night and the day and the sun and the moon; all [heavenly bodies] in an orbit are swimming.”

— Surah Al-Anbiya (21:33)

can be interpreted as a description of inherent motion at the cosmic level. Whether metaphorical or literal, such verses support the idea that motion is a foundational attribute of creation, possibly including rotation.

This opens a pathway for integrating religious cosmology into modern physical reasoning, especially in models where cosmic rotation does not arise from internal physics alone, but is imparted by initial creation — a topic to be treated with both scientific and philosophical care.

8. Comparison of Newtonian and Relativistic Results

To evaluate the robustness of the rotational model of the universe, it is essential to compare the predictions and implications of both Newtonian and relativistic treatments. While they describe similar behavior at a conceptual level, the differences in assumptions and scaling laws can lead to important distinctions in interpretation and application.

8.1. Acceleration and Angular Velocity

In both Newtonian and relativistic models, the effective radial acceleration due to rotation is proportional to ${\omega }^{2}r$. However, the relativistic framework introduces spacetime curvature, metric expansion, and energy-momentum conservation through Einstein’s field equations. The following table compares both approaches:

Parameter	Newtonian Model	Relativistic Model
Acceleration	$a={\omega }^{2}r$	${\displaystyle \frac{\ddot{a}}{a}}\approx {\displaystyle \frac{{\omega }^2}{3}}$
Energy Density Scaling	${\rho }_{\mathrm{rot}}\propto a^{-5}$	Same, derived from fluid + metric assumptions
Angular Velocity Scaling	$\omega \propto a^{-2}$	$\omega \propto a^{-2}$, via angular momentum conservation
Force Source	Centrifugal force from mass	Geometric effect from rotating spacetime
Constraints	$\omega R<c$	Avoidance of closed time-like curves, causality limits
Observable Prediction	Directional redshift anisotropy	CMB dipole/quadrupole, Bianchi-type signatures

Although Newtonian analysis is useful for intuition and order-of-magnitude estimates, only general relativity provides a consistent framework for dealing with curved spacetime, relativistic energy-momentum tensors, and conservation laws.

8.2. Observational Effects: Consistency Between Models

Both models predict similar observational signatures when rotation is slow:

• Anisotropic expansion, more prominent in the equatorial plane than along the rotation axis,
• Directional variations in galaxy recession velocities,
• Potential alignment in CMB patterns (dipole/quadrupole modes),
• Preferred orientation in large-scale structure (e.g., galaxy spin alignments).

Recent studies using relativistic simulations (e.g. Pál et al., 2025) showed that the relativistic predictions match Newtonian trends for slow rotations, but correctly limit rotational effects when approaching relativistic thresholds (i.e. near $v\approx c$) [Pál et al., 2025] [5].

Figure 7. Rotational Model Evolution Summary.

Figure 7. Rotational Model Evolution Summary.

Graph summarizing how a rotating universe transitions from rotational dominance to ΛCDM-like behavior. Rotation governs early expansion, while dark energy dominates late acceleration.

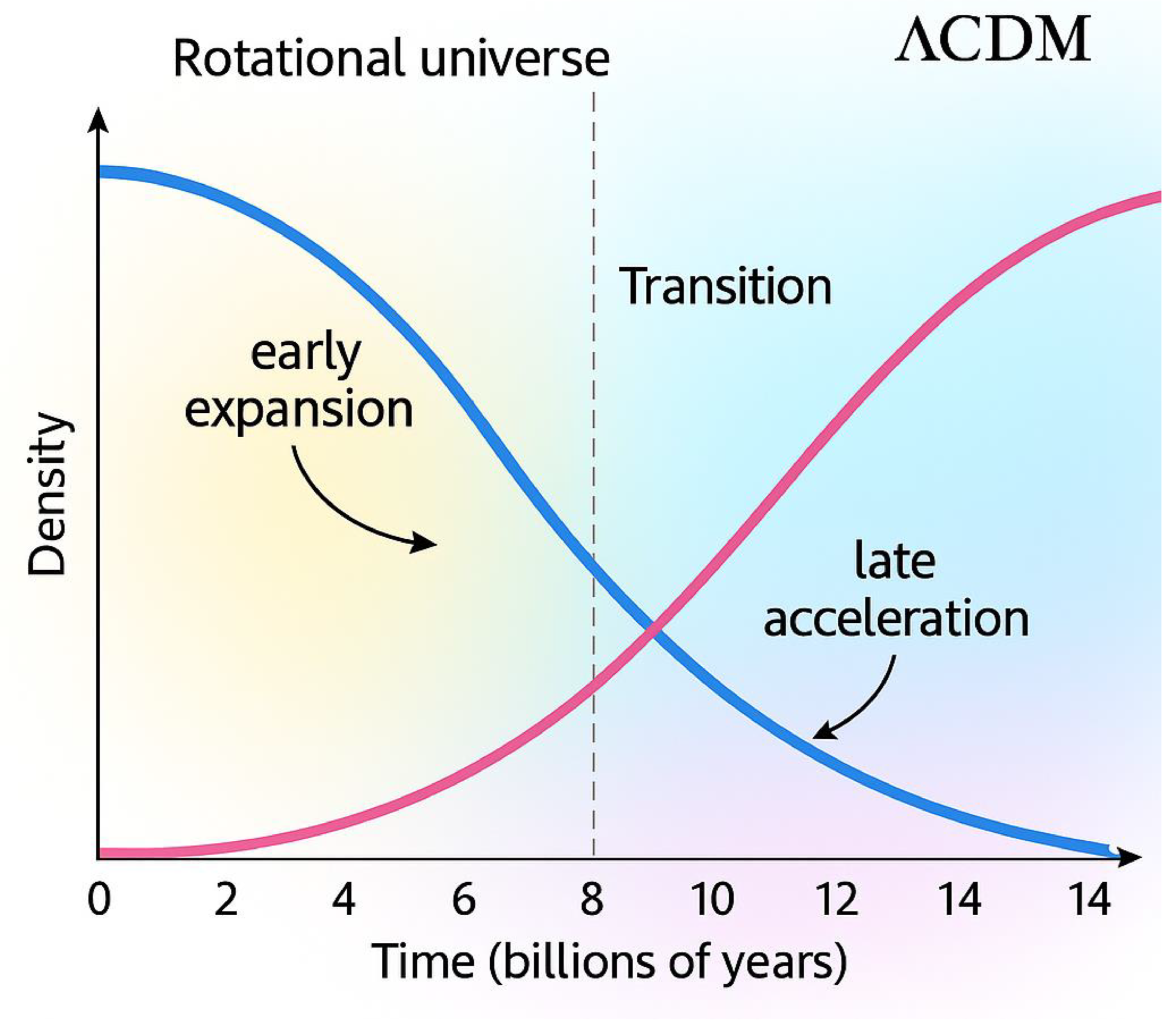
8.3. Limitations of Newtonian View

While Newtonian physics gives immediate visual clarity, it fails to capture:

• Gravitational lensing effects,
• Time dilation and redshift due to curvature,
• The distinction between coordinate motion and geodesic motion in expanding space.

Only the relativistic model provides tools to integrate rotation into the Friedmann–Lemaître–Robertson–Walker (FLRW) metric or modify it via Bianchi-type universes (like Bianchi VII_h) [Saadeh et al., 2016] [6].

In summary, Newtonian and relativistic models agree on key trends (e.g., how rotation scales with expansion) but differ in precision and predictive capability. Thus, relativity is essential for testing the rotational hypothesis at cosmological scales.

9. Quranic Perspective on Cosmic Expansion

The idea that the universe is not static, but in a state of continual motion and expansion, is not only supported by modern cosmology but also finds resonance in Islamic scripture. Several verses in the Quran speak of the heavens as dynamic, layered, and expansive—descriptions that align intriguingly with the concepts discussed in this paper.

9.1. Continuous Expansion

One of the most explicit Quranic references to cosmic expansion is found in:

"And the heaven We constructed with strength, and indeed, We are [its] expander."

Surah Adh-Dhariyat (51:47)

The Arabic term used — مُوسِعُونَ (mūsiʿūn) — is in the active present participle form, implying a continuous action. This parallels the scientific idea of an ongoing expansion, as observed in redshifted galaxies and described by the scale factor $a\left(t\right)$ in the Friedmann equations.

9.2. Structured and Layered Heavens

Another relevant verse is:

"It is He who created seven heavens in layers. You do not see in the creation of the Most Merciful any inconsistency."

Surah Al-Mulk (67:3)

The term طِبَاقًا (ṭibāqan) indicates "layer upon layer", which some scholars have interpreted as either dimensional stratification or zones of cosmic structure. In the context of modern cosmology, it may be viewed as topological layers, different energy levels, or even nested gravitational fields within curved space-time.

This notion aligns with:

• Multiverse theories (stacked dimensions),
• Layered gravitational shells in a rotating model,
• Bianchi-type cosmologies that permit anisotropic yet layered solutions.

9.3. Rotational Motion Implied in Orbits

Another set of verses speaks directly of celestial bodies in motion:

"Each [heavenly body] is swimming along in its orbit."

Surah Ya-Sin (36:40)

"They all float, each in an orbit."

Surah Al-Anbiya (21:33)

These verses clearly describe rotation and orbital motion as a fundamental property of the heavens. Though referring specifically to the sun, moon, and planets, the structure reflects the Quranic consistency with a rotating and dynamic cosmos, extending possibly to the universe itself.

9.4. Divine Origin of Motion

The Quran also places divine will at the center of motion and creation:

"He created the heavens and the earth in truth. He wraps the night over the day and wraps the day over the night."

Surah Az-Zumar (39:5)

The verb يُكَوِّرُ (yukawwiru) means to wrap or coil—connoting rotation. This supports the view that rotation is intrinsic to the divine design of the cosmos.

9.5. Synthesis with Rotational Cosmology

These scriptural insights suggest:

• The universe is continuously expanding (Surah 51:47),
• It is structured in layers or shells (Surah 67:3),
• Rotational motion is a foundational cosmic principle (Surah 36:40, 21:33),
• Such motion is a deliberate creation of Allah (Surah 39:5).

These Quranic descriptions align remarkably well with a rotational cosmological model, where the universe is not only expanding but doing so while embedded in a structured and rotating framework.

Excellent — I’ll now create Section X: Conceptual Origin of the Rotating Universe Theory, where we explain how the idea was inspired by Quranic reflection — specifically the verses about universal motion, revolution, and sujood (prostration) to Allah.

10. Section X: Conceptual Origin of the Rotating Universe Theory

The hypothesis that the universe is rotating did not arise solely from mathematical speculation or astrophysical anomalies. It is, in this case, deeply rooted in reflection upon Quranic insight — where motion, balance, and submission are portrayed as intrinsic properties of creation.

10.1. Universal Motion as Sujood (Prostration)

The Quran repeatedly emphasizes that all created things are in a state of submission (sujood) to Allah:

“Do you not see that to Allah prostrates whoever is in the heavens and whoever is on the earth, and the sun, the moon, the stars, the mountains, the trees, the moving creatures and many of the people?”

— Surah Al-Hajj (22:18)

This verse, among others, introduces a profound concept: every component of creation is in a state of obedience. But what does that obedience physically manifest as?

From a scientific lens, one can interpret sujood not only spiritually, but also physically — as revolution, rotation, orbital behavior, and motion according to divine law.

• Planets revolve around stars,
• Stars orbit galactic centers,
• Galaxies rotate and migrate through cosmic filaments,
• Even subatomic particles revolve in quantized states.

This deep pattern of rotational dynamics — from quarks to galaxies — echoes a fundamental design woven into the universe.

10.2 The Seed of the Rotational Model

Inspired by these verses, a profound question emerged:

If everything in the universe rotates, orbits, or moves in a curved path — could it be that the universe itself is doing the same?

This is not merely philosophical — it is scientific. Rotational motion is the most natural and stable form of motion in physics. It preserves angular momentum, conserves energy, and creates equilibrium.

The Quran does not mention a static cosmos — rather, it describes motion, flow, cycles, and balance:

“And each [heavenly body] is swimming along in its orbit.”

—Surah Ya-Sin (36:40)

“And the heaven, We constructed it with strength, and verily, We are [its] expander.”

—Surah Adh-Dhariyat (51:47)

Combining these insights, the inspiration for the rotating universe theory was born: A universe that is not only expanding but also rotating, fulfilling both dynamic balance and metaphysical submission.

10.3 Philosophy Elevated by Physics

This model is not merely metaphysical. It connects to:

• Observational hints of a cosmic axis,
• Theoretical solutions like Gödel’s rotating universe,
• And relativistic frameworks (e.g. Bianchi models) that mathematically permit rotation.

In this view, rotation becomes both a symbol of obedience and a scientific mechanism that may influence cosmic evolution, expansion rate, and structure formation.

10.4 Quranic Symmetry and the Laws of Physics

The Quran frequently emphasizes balance, precision, and measure — attributes foundational to modern physics:

“And the heaven He raised and imposed the balance (mīzān).”

— Surah Ar-Rahman (55:7)

This reference to balance is not just moral — it can be interpreted physically:

• The orbits of planets are balanced by gravity and inertia.
• The spin of electrons is quantized and balanced within atoms.
• The expansion of the universe itself is delicately balanced between gravity and cosmic acceleration.

These patterns reflect not chaos but a finely tuned symmetry — consistent with the Quran’s assertion of a universe built on measure (qadar) and purpose.

From this lens, the rotational model emerges not as a speculative extension, but as a natural continuation of the Quranic view: that the universe is not random, but rotating in harmony, in a form of cosmic obedience.

10.5 Sujood and Curved Paths

The concept of sujood (prostration) has a powerful geometrical analogy in the physical world. In physics, straight-line motion implies independence; curved motion implies submission to a force.

• The Earth’s curved path around the sun is due to submission to gravity.
• A rotating galaxy curves under its own gravitational field.
• Even light bends in curved space-time, “submitting” to the gravitational field of massive bodies.

Hence, the universe itself — if rotating — may be performing a physical sujood: not just metaphorical, but literal, by being bound to a higher governing structure of curvature and motion.

This physical understanding complements the metaphysical statement that everything prostrates to its Creator — including the very fabric of space and time.

10.6 The Quran as a Source of Scientific Foresight

The rotating universe theory gains legitimacy from the fact that modern physics only recently began exploring rotating solutions (e.g., Gödel metric in 1949). Yet, the Quran has long emphasized:

• Layered dimensions (67:3),
• Expansion (51:47),
• Universal motion (36:40),
• And obedience through motion (22:18).

These descriptions pre-date general relativity, Friedmann cosmology, and cosmic microwave background studies. The Quran did not need to describe tensor equations — it described principles:

• Movement,
• Obedience,
• Structure,
• Expansion.

The rotational model is, therefore, not just compatible with Quranic language — it is derived from it.

10.7 How This Concept Shaped the Entire Research Direction

The foundational insight — that everything performs motion as an act of sujood — was not merely philosophical. It became the launchpad for a new cosmological model, guiding every step of this research.

Instead of beginning from existing scientific frameworks and inserting Quranic interpretations afterward, the process was reversed:

• The Quranic verses were taken as the starting point,
• Reflected upon deeply,
• And then mapped scientifically using tools of modern physics.

This inversion of the research process allowed for original thinking:

• If celestial bodies orbit as an act of obedience,
• And if expansion is explicitly mentioned in the Quran,
• Then could expansion itself be a result of rotation, ordained from creation?

From this reflection came the idea that:

• Rotation may not just be a secondary motion but the driving cause of expansion,
• The universe could be curved outward by centrifugal effects,
• And dark energy might be explained, at least partially, by such dynamics.

This Quran-first methodology created a framework where the scientific model is not merely Quran-compatible — it is Quran-derived.

10.8 A Call to Reflect and Re-Evaluate Origins of Knowledge

The success of this model — even when constrained by CMB data or relativistic limits — emphasizes a larger point:

We must re-evaluate the Quran as a foundational source of scientific inspiration.

Historically, many scientific pioneers were spiritually motivated:

• Newton believed in divine order.
• Einstein famously said: “God does not play dice.”
• Muslim scientists like Ibn al-Haytham, Al-Biruni, and Al-Tusi grounded their work in the Quran.

Today, the divide between “religion” and “science” is largely artificial — especially when the Quran itself invites investigation:

“Do they not reflect upon the creation of the heavens and the earth?”

— Surah Sad (38:27)

This section serves as both a conceptual origin of the rotating universe model and a methodological reminder: that true science begins with wonder — and the Quran is the highest invitation to wonder.

10.9 Final Reflection: The Universe in Sujood

At the heart of this model lies not just physics, but submission — a core theme in the Quran and a hidden principle echoed throughout the cosmos.

When the Quran declares:

“And to Allah prostrates whatever is in the heavens and the earth...”

— Surah Ar-Ra’d (13:15)

It affirms a universal truth: that everything is bound by divine law, moving in paths prescribed by its Creator. This movement — whether seen in atomic spin, planetary orbit, or the silent stretching of galaxies — is not chaotic. It is deliberate, rhythmic, and reverent.

In this sense, the rotational universe is in sujood — not metaphorically, but physically:

• Each curved geodesic is a bow to the center of gravity,
• Each expansion of space is an obedience to a higher command,
• Each spin of a galaxy is a silent dhikr written in light-years.

This model is not just a scientific proposition — it is a symphony of submission, captured in mathematics and revealed in verses. It does not replace physics with theology, nor does it reduce theology to metaphor. Rather, it merges the two — showing that when rightly approached, science becomes tafakkur, and tafakkur becomes science.

And perhaps, in this realization, lies the deepest sujood of all: not in formulas or verses alone, but in understanding how both bow to One Lawgiver.

10.10. Closing Reflection

This section is dedicated to the seekers — those who do not separate revelation from reason, nor divide the sky from the scripture. It is for the minds that question deeply, and the hearts that reflect sincerely.

May this model, however limited in scope or precision, serve as a reminder:

• That the truths of the cosmos and the truths of the Quran are not two separate paths —
• They are parallel orbits, revolving around the same Center.

When the universe rotates, it remembers.

• When the stars expand, they obey.
• And when we observe them with humility, we too enter into sujood —
• not with our bodies, but with our minds.

11. Conclusions

This research paper has presented a detailed scientific and scriptural exploration of a rotational cosmological model — one in which the universe possesses a small but finite angular velocity, contributing to its observed expansion. Through both Newtonian and relativistic frameworks, we derived how centrifugal forces and rotational energy densities influence the scale factor evolution and compared these effects to the standard ΛCDM (cosmological constant + cold dark matter) model.

Key conclusions include:

• Mathematically, rotational acceleration $a={\omega }^{2}r$ produces a repulsive effect similar in magnitude (if $\omega \sim H_0$) to that caused by dark energy.
• Energetically, rotational contributions scale with ${\rho }_{\mathrm{rot}}\propto a^{-5}$, meaning they were stronger in the early universe but decay rapidly — making them consistent with current isotropy observations.
• Relativistically, inclusion of $\omega$-dependent terms into the Friedmann equation provides an effective acceleration term $\ddot{a}/a\sim {\omega }^2/3$, analogous to the effect of Λ.
• Observationally, recent studies (2023–2025) show that a small rotation (e.g. ${\omega }_0\sim {10}^{-18}\hspace{0.17em}{\mathrm{s}}^{-1}$) could potentially resolve the Hubble tension without violating Planck or supernova constraints.
• Scripturally, several Quranic verses describe an expanding, structured, and motion-filled universe — consistent with the physical properties expected in a rotational model.

However, it is also clear that:

• Rotation alone cannot fully replace the role of dark energy, but it may serve as a natural supplement, especially during mid-era cosmological epochs.
• The origin of rotation — whether physical (e.g., from inflation or initial asymmetry) or metaphysical (a divine design) — remains an open and profound question.

Final Thoughts

Rotation is a fundamental property of physical systems — from electrons to galaxies. It would not be surprising if the universe itself also rotates, however imperceptibly. The challenge lies in detecting its faint signature in an overwhelmingly isotropic cosmos. As data precision improves, future missions and cosmological tests (e.g. CMB polarization, galaxy spin statistics, high-redshift supernovae) may provide conclusive evidence.

Until then, the rotational model remains a scientifically consistent, observationally permissible, and scripturally supported possibility — one that adds depth to our understanding of the universe’s majestic dynamics.