Revisiting The Universe Expansion and Dark Energy Problem

1. Introduction

The general understanding today is that the Universe is expanding and accelerating based on experimental evidence and modeling considerations [1,2]. However there have been reservations questioning the acceleration evidence [e.g. [3,4]) mainly due to data and interpretation uncertainties. One of the key parameters affecting universe expansion is the Hubble Parameter (H), (e.g. [5]), quantifying the rate at which the universe is expanding at any given time (t):

$$H\left(t\right)={\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}$$

(1)

where R(t) is the length scale factor, describing how distances in the universe expand with time.

On the other hand, the general relativity formulated by Einstein [6], is the prevailing theoretical framework to describe the Universe evolution and dynamics. More specifically, the Friedman equations are the set of equations in cosmology that govern the expansion of space in homogeneous and isotropic models of the universe. They are derived from Einstein's field equations of general relativity under the assumption of the Friedmann–Lemaître–Robertson–Walker (FLRW) metric (e.g. [5]). These equations describe the universe expansion, acceleration and energy conservation. A widely used approach to study universe dynamics, is based on the introduction of dark energy described through the cosmology constant (Λ) [6,7]. In practice, Λ has been introduced into the original Friedmann Equations leading to modification (e.g. [5]).

It is noticed that the nature of dark energy has not been fully understood today and the constant value of Λ although it has been extensively used, it lacks yet adequate global acceptance. In fact, there are findings giving a preference towards a more dynamic behavior of the dark energy (e.g. [8]).

It should be noticed in addition, that quantum theory based on Heisenberg Uncertainty principle, predicts a rather significant energy density for empty space, but astronomical observations show that the energy density associated with the above cosmological constant, is quite small in serious discrepancy with the above quantum field theory predictions [9]. It is noticed that this very high discrepancy consists one of the major unresolved problems in cosmology today.

Another major challenge to the standard model is the “Hubble tension”—a significant discrepancy between measurements of the Hubble constant obtained from the early Universe (via cosmic microwave background data) and those derived from the local Universe (using Type Ia supernovae and Cepheid variables) [10]. Despite increasing precision on both fronts, the disagreement persists and has prompted speculation about possible new physics beyond the standard ΛCDM framework.

It is noticed, in addition, that several dynamic dark energy models have been proposed, including quintessence [11], phantom fields [12], and k-essence [13], though these often introduce additional scalar fields and free parameters, increasing model complexity without resolving the above-mentioned foundational tensions.

From the discussion above, it becomes clear that there are significant open questions surrounding the expansion of the universe and the nature of dark energy—questions that warrant a careful and foundational re-examination. The present study aims to contribute to this re-examination by returning to first principles, guided by the logical principle of parsimony (“simplicity first”), and by constructing a conceptual framework grounded in fundamental physical reasoning.

Rather than proposing a complete and final theory, this work introduces a new conceptual framework intended as a starting point for deeper analysis. The goal is to identify internally consistent relationships that could illuminate unresolved issues, particularly those involving the cosmological constant problem and the Hubble tension. By anchoring the discussion in basic cosmological quantities—such as the Hubble parameter and total energy density—and by modifying the treatment of dark energy, the framework seeks to open pathways toward alternative explanations for the universe's observed behavior.

Finally, it is essential to clarify that the two central elements of the proposed framework are formulated as hypotheses rather than assumptions. This distinction is deliberate and methodologically significant. By presenting them as hypotheses, the present study adopts a stance of open scientific inquiry, emphasizing that these propositions are subject to testing, refinement, or potential falsification through theoretical analysis and observational data. Given the foundational nature of the questions addressed—such as the nature of dark energy and the dynamics of cosmic expansion—this hypothesis-driven approach is both necessary and appropriate. It allows for conceptual innovation while maintaining adherence to the scientific method.

2. The Present Approach and the Results

In this work, the Universe spatial curvature is considered flat (k=0). It has been a common approximation since several observations show that universe is very close to flat (e.g. [5]).

2.1. The Present Conceptual Framework and the General Relativity Theory

As mentioned above, the Hubble parameter (H(t)) is given by Equation (1). A range of estimations for the H(t) for present time (H0) based on observation data and their analysis [14,15] is:

H0 ≈ (2,17÷2.37) × 10-18 sec-1

The above value seems to correlate rather well with the age of Universe (t0 ≈ 4.4 x 1017 sec) (e.g. [5]):

$$H_0\approx {\displaystyle \frac{1}{t_0}}\approx 2.29\times {10}^{-18}{sec}^{-1}$$

(2)

a value well within the range given above.

It is logical to examine to what degree such an observation might not be a coincidence. Therefore, we are introducing the following two key hypotheses:

1st Key Hypothesis: The Hubble parameter is proposed to be given for the whole universe time by the following equation:

$$H\left(t\right)={\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}={\displaystyle \frac{1}{t}}$$

(3)

where t is the elapsed time after the Big Bang.

In consistency with above hypothesis, we introduce the additional key hypothesis.

2st Key Hypothesis: The concept of dark energy remains as the repulsive gravity constituent directly related to the attractive gravity constituents (e.g. matter, radiation). Such a hypothesis introduces a dynamic form of dark energy expressed through the dark energy density $\left({\rho }_{de}\right).$ Thus, the total energy density (ρ) consists of the sum of the attractive gravity constituents $\left({\rho }_{ag}\right)$ (mainly matter (${\rho }_m)$ and radiation $\left({\rho }_{rad}\right))$ and the repulsive gravity constituent (i.e. dark energy $\left({\rho }_{de}\right)):$

$$\rho ={{\rho }_{ag}+{\rho }_{de}\approx \rho }_m+{\rho }_{rad}+{\rho }_{de}$$

(4)

Equation (4) underlines the assumption that in the present concept, the universe exists due to the balancing coexistence of gravity attractive and gravity repulsing forces pointing out towards the 3rd Newton Law of Motion [16] concept.

It should be emphasized from the beginning, that the two hypotheses above, are considered as an inseparable part of the General relativity theory. More specifically, the standard Friedmann equations, in a flat Friedmann–Lemaître–Robertson–Walker (FLRW) universe, are valid:

The 1st Friedmann Equation (Hubble equation):

$$H^2=({\displaystyle \frac{\dot{R}}{R}}{)}^2={\displaystyle \frac{8\pi G}{3c^2}}\rho$$

(5)

The 2nd Friedmann Equation (Acceleration equation):

$${\displaystyle \frac{\ddot{R}}{R}}=-{\displaystyle \frac{4\pi G}{3c^2}}(\rho +3P)$$

(6)

The Friedmann Energy Equation:

$$\dot{\rho }=-3{\displaystyle \frac{\dot{R}}{R}}(\rho +P)$$

(7)

Adopting a dynamic form of dark energy as mentioned above, the density ρ in the Friedmann equations refers to the total density as defined by equation (4).

In is noticed that the equations (3) - (7) form the basis, on quantitative terms of the present conceptual frame. The key questions here are: (a) to what degree such a frame meets the reality and (b) can it generate new knowledge useful to lead to new considerations on Universe nature and evolution?

2.2. The Universe Total Density

We concentrate first at the total density evolution. Equation (5) can be used directly to estimate the total density ($\rho$) as a function of time, taking into consideration equation (3):

$$\rho \left(t\right)={\displaystyle \frac{3c^2}{8\pi G}}·{\displaystyle \frac{1}{t^2}}$$

(8)

Equation (8) can be used to estimate the present time density value (${\rho }_{0 }$) using the $H_0$ value of equation (2).

$${\rho }_0\approx 8.46\times {10}^{-10} Joules/m^3$$

(9)

a value rather close to the critical density given in literature (e.g. [5]): $7.8\times {10}^{-10} Joules/sec$

Equation (8) indicates that according to the present theory, the universe density decays as $t^{-2}$. The range of application is expected to start from Planck time ($t_{Pl})$ forward. It is reminded that $t_{Pl}$ is scaled as follows [17]

$$t_{Pl}~\sqrt{{\displaystyle \frac{h·G}{2\pi c^5}}}=5.39\times {10}^{-44} sec$$

(9)

We can also use equation (8) to see what the present theory is able to predicts as the universe density$\left( {\rho }_{Pl}^{pred}\right)$ at $t_{Pl}$ time, given by equation (9). The obtained result has as follows:

$${\rho }_{Pl}^{pred}~{\displaystyle \frac{3c^2}{8\pi G}}·{\displaystyle \frac{2\pi c^5}{hG}}={\displaystyle \frac{3c^7}{4h{G}^2}}=5.5\times {10}^{112} Joules/m^3$$

(10)

Recall that the Planck density (${\rho }_{Pl})$ is scaled as follows [17]:

$${\rho }_{Pl}~{\displaystyle \frac{2\pi c^7}{h{G}^2}}=4.63\times {10}^{113 }Joules/m^3$$

(11)

Comparing the two densities from the relationships (10) and we find

$${\displaystyle \frac{{\rho }_{Pl}^{pred}}{{\rho }_{Pl}}}~0.12$$

(12)

Taking into consideration that we are dealing with scales and not the exact values, the equation (12) clearly indicates that $\left( {\rho }_{Pl}^{pred}\right)$ and ( ${\rho }_{Pl})$ are comparable.

This result is quite interesting if one takes also into consideration, that Planck energy density is directly related to the vacuum energy density $\left({\rho }_{QFT}\right)$ arising from quantum fluctuations of fields in space, when confined within the Planck regime.

It is derived by summing the zero-point energies of quantum fields up to the Planck scale [15]18.

$${\rho }_{QFT}~{{\rho }_{Pl}~10}^{113}Joules /m^3$$

(13)

Thus, the above findings and more specifically equations (8) and (13), lead to the following proposal for the universe energy density estimation:

$$\rho \left(t\right) ~{ \rho }_{Pl}·({\displaystyle \frac{t}{t_{Pl}}}{)}^{-2}{ ~ \rho }_{QFT}·({\displaystyle \frac{t}{t_{Pl}}}{)}^{-2}$$

(14)

It should be underlined that equation (14) expresses a very important finding, i.e. it seems to resolve the cosmological constant problem controversy as mentioned above.

Before proceeding and trying to have a better understanding, let us examine the problem in the inverse way. Recall from above, that ${\rho }_{QFT}~{10}^{113}Joules /m^3$and ${\rho }_0~{10}^{-9} Joules/m^3.$Thus, we can estimate the ratio: ${\displaystyle \frac{{\rho }_{QFT}}{{\rho }_0}}~{10}^{122}Joules/m^3$.

On the other hand, by taking the estimations: $t_0\approx 4.4 x{10}^{17}$sec and $t_{Pl}\approx 5.39\times {10}^{-44} sec,$

$$\mathrm{we} \mathrm{obtain}\text{:} {\displaystyle \frac{t_0}{t_{PL}}}~{10}^{61}.$$

If we try to fit those two ratios into a power function with exponent n , the solution is clear: n= -2, i.e. reproducing equation (8).

It should be also undelined that by setting n= -2 we end up, through the Friedmann equation (5), to the 1^st hypothesis equation (3).

The conclusion that can be derived here, is that if the present conceptual frame proved to be valid, the cosmological constant problem does not exist anymore.

2.3. The Universe Expansion and Total Energy

Let us return back to 1^st hypothesis and rewrite equation (3) as $R=t\dot{R}$ . We differentiate with respect to time: $\dot{R}=\dot{R}+t\ddot{R}$ . This leads to:

$$\ddot{R}\left(\mathrm{t}\right)=0$$

(15)

Equation (15) marks a significant departure from the present understanding on university acceleration. As discussed before, the latter seems to be widely supported but without full universal acceptance. It is worth noting, that Nielsen et al. [3] have revisited the existing evidence for the universe accelerated expansion by analyzing the dataset of Type Ia SuperNovae (SN Ia) [19]. A key conclusion was that the data were quite consistent with a constant rate of universe expansion.

The solution of equation (13) gives the universe expansion:

$$R=c·t$$

(16)

Let us recall the 2^nd Friedmann equation (6). The condition (15) translates the equation (6) to:

$$P=-{\displaystyle \frac{1}{3}}·\rho$$

(17)

To what degree equation (17) can make sense, it is discussed in the remainder.

First, in order to get the whole picture, we consider the Friedmann energy equation (7). Recall that the universe total energy (E) can be approximated:

$$\mathrm{E}\approx \mathsf{\rho }·{\displaystyle \frac{4\pi }{3}}{\mathrm{R}}^3$$

(18)

We differentiate:

$${\displaystyle \frac{\partial \mathrm{E}}{\partial \mathrm{t}}}\approx {\displaystyle \frac{4\pi }{3}}(\dot{\mathsf{\rho }}·{\mathrm{R}}^3+3{\mathrm{R}}^2\mathsf{\rho })$$

(19)

Substituting $\dot{\mathsf{\rho }}$ given by equation (7), we end up with the following relation regarding universe energy rate (ER):

$$ER={\displaystyle \frac{\partial \mathrm{E}}{\partial \mathrm{t}}}\approx -4\pi ·\dot{\mathrm{R}}·{\mathrm{R}}^2·\mathrm{P}$$

(20)

Equation (20) indicates that the universe energy evolution is controlled by the pressure P and consequently by the factors shaping up this pressure. Negative pressure is directly related to the energy inflow, contributing to the universe expansion.

Substituting now the pressure given by equation (17) in the equation (20), we obtain for the energy rate (ER):

$$ER={\displaystyle \frac{4\pi }{3}}·\dot{\mathrm{R}}·{\mathrm{R}}^2·\rho ={\displaystyle \frac{4\pi }{3}}·H\left(t\right)·R^3·\rho$$

(21)

Taking into consideration equations (3), (16), and (8) we can express ER as follows:

$$\mathrm{E}\mathrm{R}\approx {{\displaystyle \frac{\mathrm{c}}{2\mathrm{G}}}}^5=1.81·{10}^{52}\mathrm{J}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}/\mathrm{s}\mathrm{e}\mathrm{c}$$

(22)

This result is quite interesting: ER is a constant. If this is true, energy is pumped into the universe with a constant rate. In other words, the universe evolution is characterized by an additional global constant (ER): the expectation value of the universe inflow Energy Rate (ER).

It should be noted, in addition, that the relation (22) is expected to be valid up to the Planck epoch.

Recall that the Planck time scale (${\mathrm{t}}_{\mathrm{P}\mathrm{l}}$ ) is given by equation (9) whereas the Planck energy scale (${\mathrm{E}}_{\mathrm{P}\mathrm{l}}$ ) is given by the relationship [17]:

$$E_{Pl}~\sqrt{{\displaystyle \frac{h·c^5}{2\pi G}} ~}{10}^9 Joules$$

(23)

The relations (9) and (23) can lead to the following scaling for ER:

$$ER\approx {\displaystyle \frac{c^5}{2G}}~{\displaystyle \frac{E_{Pl}}{t_{Pl}}}$$

(24)

The above relationship, if it is true, is quite significant at least for the following reasons:

The Universe seems to have its roots within its Planck regime providing vacuum energy at a rate ER.

The expectation value of ER is continuous and constant i.e. another new universal constant dictating the Universe dynamics.

We are closing this specific topic by estimating the universe total energy evolution by integrating equation (24):

$$(E-E_{Pl})\approx ER ·(t-t_{Pl})$$

(25)

In obtaining equation (25) we have made the plausible assumption that the initial energy is scaled by the Planck energy $E_{Pl}$.

2.4. Universe Composition and Pressure

We have to go back to equation (17) addressing the pressure vs density relationship. Recall that the pressure P is the sum of partial pressures of its constituents introduced in the equation (4) i.e.

$$P\approx P_m+P_{rad}+P_{de}$$

(26)

Following the state of the art, for the attractive gravity constituents the corresponding equations of state are given by the relations (e.g. [5])

$$P_m\approx 0$$

(27a)

$$P_{rad}={\displaystyle \frac{1}{3}}·{\rho }_{rad}$$

(27b)

Concerning dark energy, the common formulation of equation of state is

$$P_{de}=w_{de}·{\rho }_{de}$$

(28)

$w_{de}$ is a negative number reflecting the repulsive gravity property of dark energy. However, there is no full consensus of its precise value. The most widely used value is $w_{de}\approx -1$ . This value is based on observation data analysis and dark energy description through the cosmology constant(Λ). There have been studies considering $w_{de}$ as a variable suggesting higher values up to $w_{de}\approx -0.8$ [20]. In addition, they have been theoretical approaches considering a dynamic behavior of dark energy, like the quintessence (e.g. [11]11), in which $w_{de}$ is a variable with values always greater than -1.

In the present conceptual frame, the dark energy is tightly related to the attractive gravity constituents and therefore, is logical to assume, even as a starting point, that the corresponding equation of state is given by the relationship (28), considering however, $w_{de}$ as a constant and not as a variable.

It is also logical to estimate $w_{de}$ exploiting our knowledge of the universe as it stands today. Keeping in mind that (a) the present study is concentrating more on setting rather refine the present concept and (b) seeking for first order approximations drawn from the state of the art, we can claim that at the present time the matter energy density (${\rho }_{0,m}$ ) is given by the relationship ${\rho }_{0,m}\approx {\displaystyle \frac{1}{3}}{\rho }_0$ , which implies for the dark energy density $\left({\rho }_{0,de}\right)$:

$${\rho }_{0,de}\approx {\displaystyle \frac{2}{3}}·{\rho }_0$$

(29)

It is widely accepted that the matter related pressure is negligible and therefore, the universe total pressure mainly consists of the dark energy related pressure. Thus, for the present time:

$$P_0\approx {\mathrm{p}}_{0,\mathrm{d}\mathrm{e}}=w_{de}·{\mathsf{\rho }}_{0,\mathrm{d}\mathrm{e}}\approx {\displaystyle \frac{2}{3}}·{w_{de}·\rho }_0$$

(30)

From equation (17) and taken into consideration equation (30), we end up with the following relationship for $w_{de}$ :

$$w_{de}\approx -{\displaystyle \frac{1}{2}}$$

(31)

which leads for the following dark energy equation of state:

$$P_{de}\approx -{\displaystyle \frac{1}{2}}·{\rho }_{de}$$

(32)

It should be noted at this point, that the equation (32) is a logical consequence of the condition (17). In other words, its validity depends mainly on the validity of the equation (17).

Departing from the present time and moving backwards to the early universe, we are entering the regime where the main attractive gravity constituent is mainly radiation. Taking into consideration that in this case, $w_{ag}\approx {\displaystyle \frac{1}{3}}$ we can estimate from equation (17), the dark energy density for early universe:

$${\rho }_{de}\approx {\displaystyle \frac{4}{5}}·\rho$$

(33)

If this is the case, we can observe that as we move from early universe to the universe of today, a mild decrease of the dark energy content from 0.8 to 0.7 is taking place.

Those findings need further investigation, especially how the inflow energy is transformed to the various universe components over time.

Finally, it should be underlined that present approach highlights the key role of the dark energy, in ensuring a sustainable expansion of the universe, acting as a reactive force to gravity force, in conceptual agreement with the 3rd Newton Law of motion. The corresponding forcing symmetry is expressed through the conservation of ‘universe total pressure (PT)’ defined as follows:

$$PT=P-{\displaystyle \frac{1}{3}}·\rho =0$$

(34)

2.5. The Hubble Tension Problem

It is also worth examining to what degree the present theory affects the Hubble tension problem mentioned in Section 1. Looking for a representative set of observation data to work with, we ended up with the data presented in [21]. It is a collection of data covering a good range of redshift z=0.07- 3.30. Let us call them for convenience, ‘observed’ data.

It is noted that the application of equation (3), leads to the following simple relationship for the Hubble parameter H(z):

$${\displaystyle \frac{H\left(z\right)}{H_0}}=1+z$$

(35)

It is reminded that value of $H_0$ is given in equation (2).

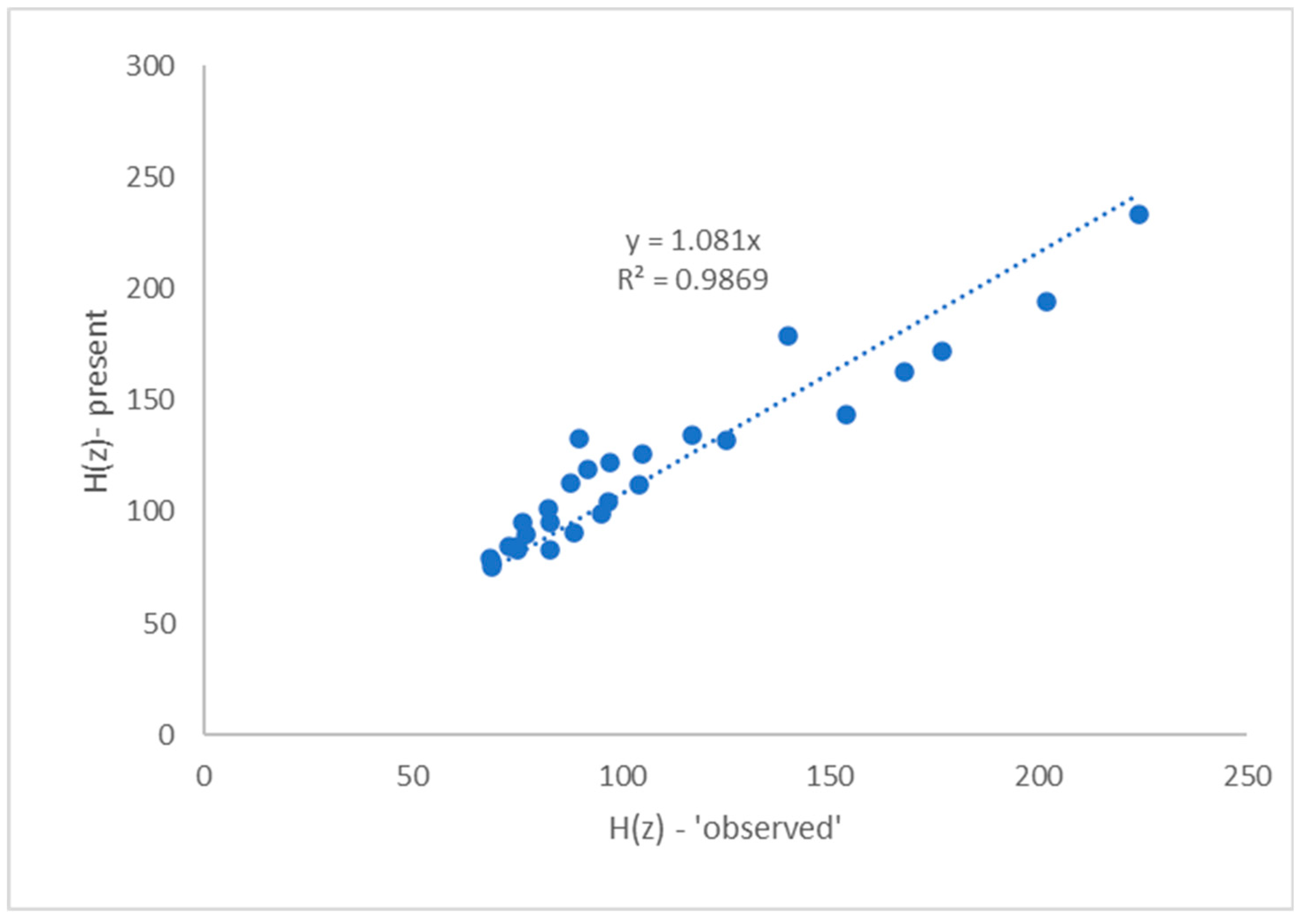
Figure 1 compares the presently produced H(z) values against the corresponding mean values reported in [21]. The results are quite comparable if one takes into consideration that the present model shows an average overprediction over 8% which is well within the reported uncertainties. 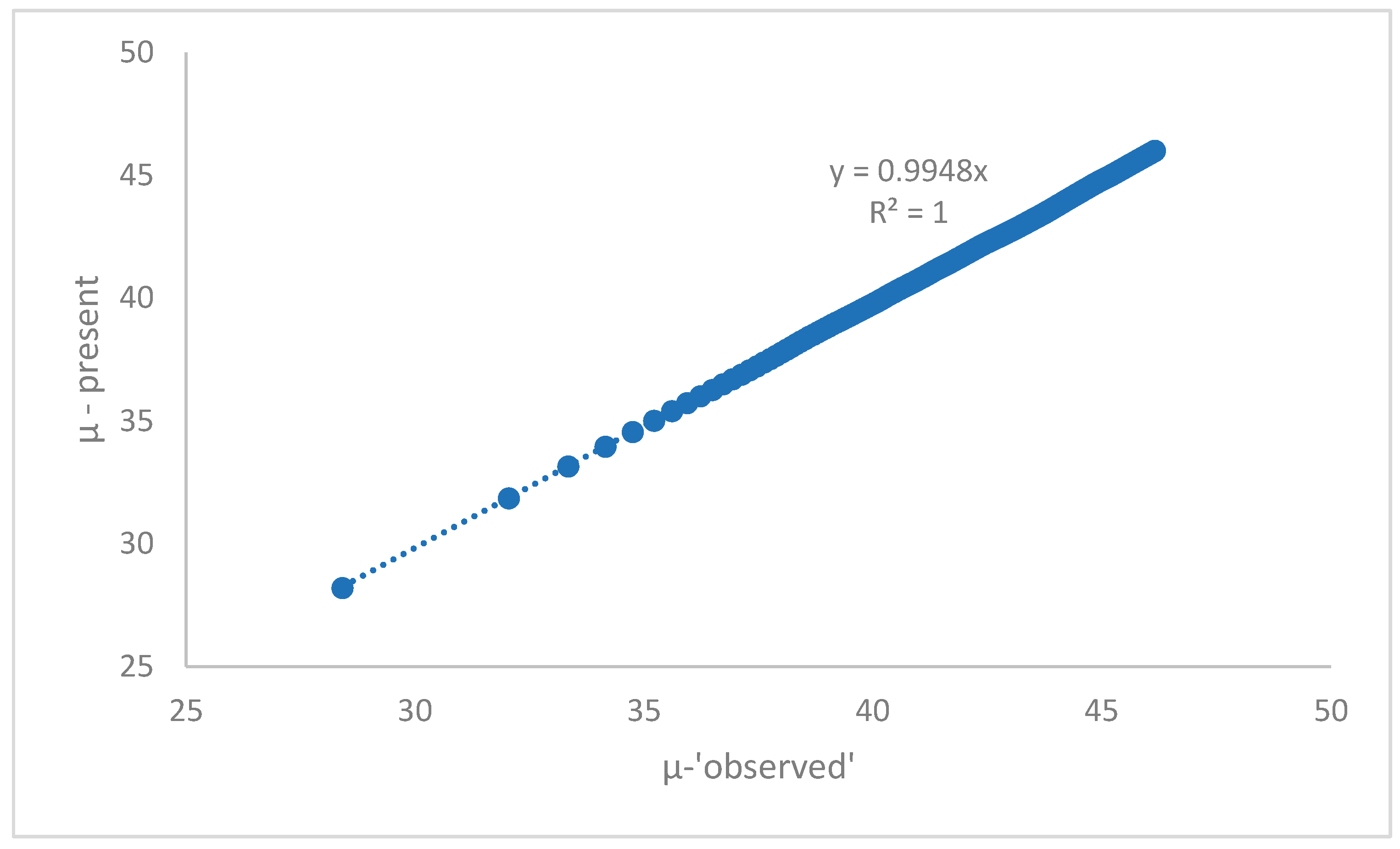It is noticed that the H(z) data give an uncertainty which in terms of standard deviation over mean ratio, exceeds the 18% [21]. It is also interesting to see how theses difference in H(z) affect the estimations of the corresponding Distance Modulus (μ), a key bridge between observation and theory. Figure 2 shows that the μ - differences here are marginal.

In conclusion the obtained results seem to confront with success the Hubble tension problem since it does not appear as a problem under the present theory. The recommendation is the present approach to be seriously considered for further observation data analysis

2.6. Some FurtherConsiderations

Let us go back to the universe constant energy rate (ER) as derived in subsection 2.3. and try to understand further its physical meaning. It is reminded that its expectation value and Planck scaling, are given by Equation (25). The Equation (25) in terms of Planck parameterization(Eq 24) can be rewritten as follows :

$$E~\left[E_{Pl}+{\displaystyle \frac{E_{Pl}}{t_{PL}}}·\left(t-t_{Pl}\right)\right]=[E_{Pl}+E_{Pl}\left({\displaystyle \frac{t}{t_{PL}}}-1\right)]$$

(36)

which leads to

$$E\left(t\right)~\left({\displaystyle \frac{t}{t_{Pl}}}\right)·E_{Pl}$$

(37)

Let us consider that we able to observe universe total energy (E) with a time resolution, the Planck time ($t_{Pl}$) and not less than that. In this case, the time ratio ${\displaystyle \frac{t}{t_{Pl}}}$ can be read as an integer ($n_t$), with $n_t$=1 initial value at $t=t_{Pl}$ , i.e.

$${\displaystyle \frac{t}{t_{Pl}}}\approx n_t={\displaystyle \frac{t_n}{t_{PL}}}$$

(38)

Then Equation (37) becomes

$$E\left(t\right)\approx E\left(t_n\right)~n_t·E_{Pl}$$

(39)

In reality Equation (39) is suggesting as natural units for quantification of time and energy in universe, the Planck time and the Planck energy respectively.

On the other hand if we multiply $t_{PL}$and $E_{Pl}$ and use the Plack scales expressions [Equations (9) and (23)], we can derive :

$$E_{Pl}·t_{Pl}~{\displaystyle \frac{h}{2\pi }}$$

(40)

which leads to

$$E_{Pl}~h·{\nu }_{Pl}$$

(41)

where ${\nu }_{Pl}$ is the Planck frequency (i.e. ${\nu }_{Pl}=1/t_{Pl}$)

Substituting Equation (41) to Equation (39) we end up with:

$$E\left(t_n\right)~n_t·h·{\nu }_{Pl}$$

(42)

and

$$t_n=n_t·t_{Pl}$$

(43)

Equations (42) and (43) point out clearly, towards theories of time and energy quantization. In this case the quantum of time is scaled by $t_{Pl}$ and the quantum of energy is scaled by $E_{Pl}$Thus, the derivation and above reformulation of the universe’s constant energy rate (ER) using Planck-scale parameterization strongly suggest a natural quantization of both time and energy. By expressing time as integer multiples of Planck time and energy in terms of Planck energy, the framework naturally leads to a discrete structure underpinning the continuum of spacetime, aligning with established theoretical proposals in quantum gravity.

Equations (42) and (43) reinforce this quantization perspective, indicating that the Planck time and frequency serve as fundamental units in the temporal evolution of the universe. This finding resonates with the work of Haug [22], who proposes observational implications of Planck time, and aligns with the broader inquiry into quantum gravity dynamics at the Planck scale, as discussed by Jacobs [23].

Thus, the present conceptual framework contributes to the growing body of theoretical evidence that discrete spacetime at the Planck scale may be a necessary feature of any unified theory of quantum gravity. Future work could expand on these results by exploring how this quantization may manifest in observable phenomena or be incorporated into existing quantum gravity models.

3. Concluding Remarks

Revisiting the universe expansion and dark energy problems through first-principles reasoning, this study introduces a conceptual framework centered on two testable hypotheses (Section 2.1). The framework is fully compatible with general relativity and the Friedmann equations, yet it circumvents the need for a cosmological constant. Instead, the expansion is described by a Hubble parameter inversely proportional to cosmic time and a dynamically balancing dark energy component.

The model leads to a time-dependent universe energy density that evolves as $t^{-2}$, producing predictions that are remarkably close to the vacuum energy density expected from quantum field theory at Planck scales. This alignment offers a potential resolution to the longstanding cosmological constant discrepancy. The derived constant energy inflow rate (ER) suggests that the universe is sustained by a stable vacuum energy inflow, governed by a new universal constant. The framework also introduces a pressure-density relationship that aligns with Newton’s third law, treating dark energy as a reactive force countering gravity and ensuring dynamical balance.

Moreover, the proposed model successfully addresses the Hubble tension by offering a unified expression for H(z) that aligns closely with observational data across a wide redshift range. While these results are preliminary, they demonstrate internal consistency and empirical promise.

Crucially, further analysis of ER through Planck-scale parameterization reveals that time and energy may be inherently quantized. Expressing total universe energy and temporal evolution in terms of Planck energy and Planck time suggests a discrete underlying structure of spacetime. This perspective is consistent with proposals in quantum gravity and recent theoretical work emphasizing Planck-scale dynamics as fundamental.

While numerous dynamic dark energy models—such as quintessence, phantom fields, and k-essence—have been proposed in recent decades, they often introduce additional complexities such as scalar fields, arbitrary potential functions, and multiple tuning parameters. Despite their theoretical richness, these models have not yet provided convincing or widely accepted resolutions to the cosmological constant problem or the Hubble tension. In contrast, the present hypothesis-driven framework is rooted in conceptual simplicity, involving minimal inputs and no additional fields beyond those already encompassed by general relativity. Remarkably, it already yields predictions consistent with both Planck-scale quantum field expectations and observed Hubble parameter behavior. This simplicity not only enhances clarity but also enables direct empirical testing. That said, the present work does not dismiss the value of more complex models. Should contradictions arise in future theoretical developments or observational comparisons, existing dynamic dark energy models—and the insights they offer—may prove essential.

Crucially, further analysis of ER through Planck-scale parameterization reveals that time and energy may be inherently quantized. Expressing total universe energy and temporal evolution in terms of Planck energy and Planck time suggests a discrete underlying structure of spacetime. This perspective is consistent with proposals in quantum gravity and recent theoretical work emphasizing Planck-scale dynamics as fundamental.

Importantly, this work does not claim to present a final theory but rather a hypothesis-driven starting point for rethinking foundational cosmological concepts. Future work should focus on refining this approach, comparing it with a broader dataset, and exploring its theoretical underpinnings—potentially from quantum field theory or quantum gravity perspectives. A more extensive study is needed to validate, challenge, or extend this framework. Nonetheless, the findings presented here suggest that revisiting cosmic dynamics through a fresh lens may reveal new and valuable directions for cosmological theory.