Exploring Adsorption Refrigeration for Integration with Hydrogen Production Systems

1. Introduction

Solar-driven adsorption refrigeration systems have gained increased attention in recent years due to their environmental compatibility and low energy requirements. These systems operate using natural refrigerants and are typically powered by low-grade thermal sources, including solar heat and industrial waste heat [1,2,3,4,5]. Their simplicity, scalability, and non-dependence on electricity make them suitable for off-grid cooling applications.

This study aims to develop a dynamic simulation model of a silica gel–water adsorption refrigeration machine using Simulink, focusing on the optimization of key operating parameters, particularly adsorption and desorption temperatures. The model is used to evaluate the system’s feasibility for integration into a hydrogen production process under Tunisian climatic conditions. The ultimate objective is to identify optimal thermal conditions that maximize system COP, cooling capacity, and energy efficiency in a sustainable and renewable configuration.

These systems are particularly suitable for rural or sun-rich regions such as North Africa [6]. The growing concern regarding greenhouse gas emissions, reinforced by international agreements such as the Montreal and Kyoto protocols, has further stimulated research in adsorption cooling as a clean alternative to conventional vapor-compression systems [7,8]. Solar energy, being abundant and diffusely distributed, offers a compelling energy input for such systems. However, its intermittency and dependence on environmental factors like geographic location, time of day, and atmospheric conditions require careful thermal management in practical applications [9,10].

Among various adsorbent–adsorbate pairs, the silica gel–water combination is widely studied due to its favorable thermophysical properties, including high adsorption capacity (up to 40% by dry mass) and regeneration capability at temperatures below 100 °C [11,12,13,14]. These characteristics make it highly compatible with solar heat and waste heat sources [15]. Recent investigations have explored the performance enhancement of silica gel-based systems via hybrid materials, composite adsorbents, and optimized heat exchangers [16,17,18,19].

Liu et al. demonstrated that a silica gel–water adsorption chiller could achieve cooling capacities above 6 kW with a coefficient of performance (COP) near 0.4 under suitable thermal conditions [20]. Later developments incorporating mass and heat recovery reported COP values up to 0.5 [21,22]. Similarly, two- and three-bed cycle configurations have been proposed to improve system continuity and reduce thermal downtime [23,24,25].

Moreover, the integration of adsorption cooling with other thermal systems—such as desalination units, combined cooling and power (CCHP), or hydrogen production—has emerged as a promising research direction. These hybrid systems optimize energy flows and improve the global efficiency of renewable energy utilization [26,27,28].

In regions like Tunisia, where solar irradiation is consistently high, adsorption systems can be adapted to local climatic conditions for synergistic integration with hydrogen production, either via thermochemical cycles or electrolysis requiring low-temperature cooling [29,30].

2. Materials and Methods

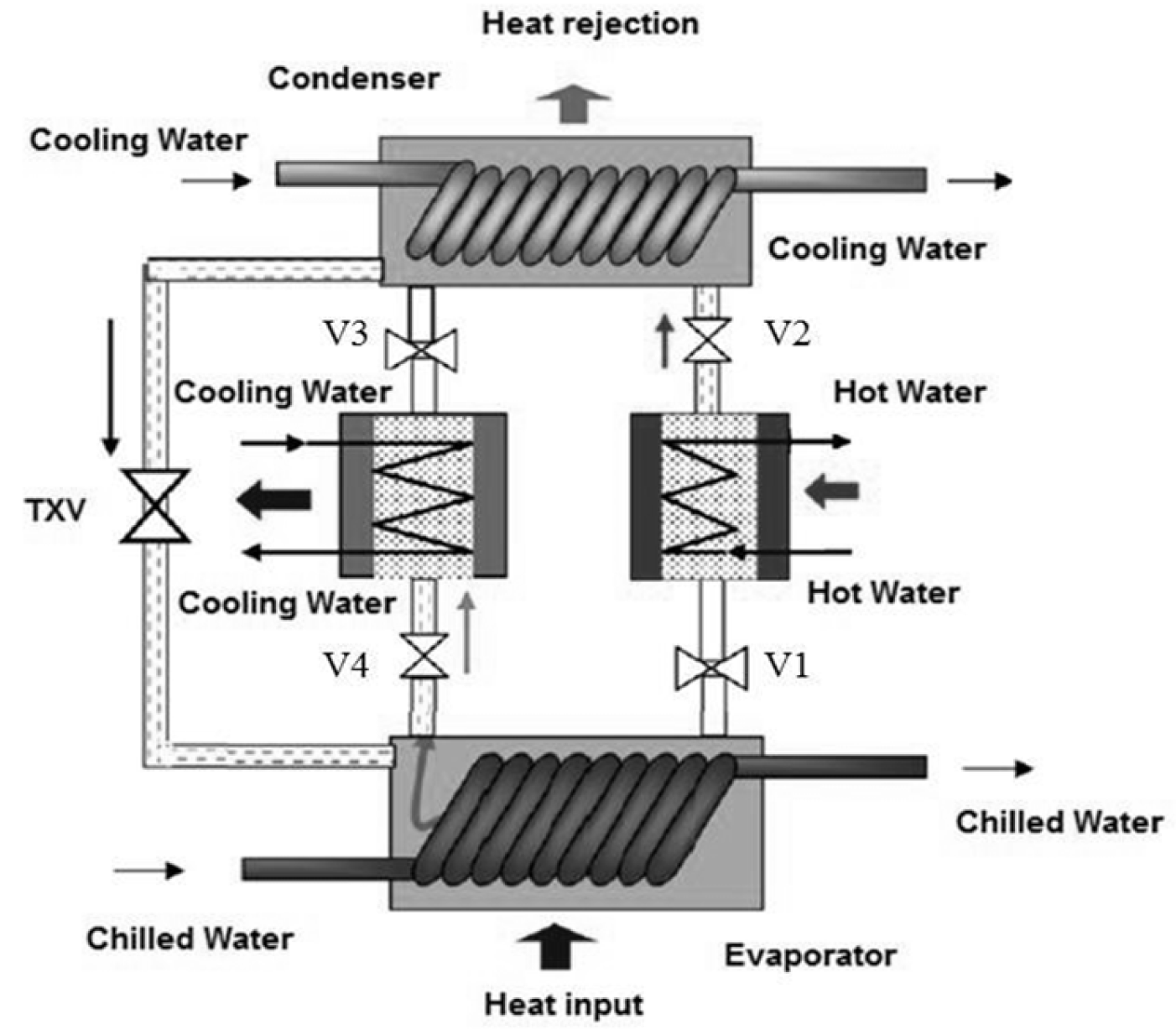
2.1. Working Principle of A Two-Bed Adsorption Chiller

An adsorption chiller operates on the basis of cyclic adsorption and desorption processes, driven by a low-grade heat source. In this system, an adsorbent material—typically silica gel—is used to alternately adsorb and desorb a refrigerant, commonly water vapor. The cycle begins with the desorption phase, wherein thermal energy is supplied to the adsorbent bed (desorber). This input heat—often derived from solar energy—causes the adsorbed water vapor to be released from the adsorbent matrix. The desorbed vapor subsequently flows into a condenser, where it is liquefied by releasing latent heat to a cooling medium.

The resulting condensate is then directed into an evaporator, operating under low pressure. In the evaporator, the liquid water absorbs heat from a chilled water loop or another cooling load, thereby producing the cooling effect. As the water evaporates, it is again drawn into another adsorbent bed (adsorber), which has been previously cooled using cooling water to facilitate the adsorption phase. This process is exothermic and must be continuously maintained to ensure proper cycle regeneration.

In a two-bed adsorption system, two adsorbent reactors (beds) operate alternately—one undergoing desorption while the other undergoes adsorption. This alternating mode ensures a quasi-continuous refrigeration output, thereby improving overall system performance and thermal stability.

In the case of a solar-driven configuration, the heat required for desorption is supplied by solar collectors. Solar radiation is absorbed and converted into thermal energy, which is stored in a thermal storage tank and delivered to the desorber via a circulating pump. The integration of solar energy aligns well with the temperature range required for silica gel–water systems, typically between 70–95 °C.

A key innovation in this study lies in the method of applying the adsorbent material: silica gel is directly coated onto the surfaces of the heat exchangers within the adsorption beds. This approach is adopted to significantly enhance heat transfer between the adsorbent and the thermal fluid. In conventional packed-bed systems, poor thermal contact between the metallic surfaces and granular adsorbents results in a high thermal resistance, which severely limits the effective utilization of the heat source and causes variability in the system performance. By contrast, the coated-bed configuration reduces thermal resistance and improves the thermal response of the adsorbent, thereby enhancing the system’s overall cooling capacity and coefficient of performance (COP).

A schematic diagram illustrating the cycle components and flow sequence is shown in Figure 1.

3. Analysis and Modelling

3.1. Assumptions

To develop a reliable and tractable mathematical model of the two-bed adsorption chiller, the following assumptions are made:

• Uniform distribution: The temperature, pressure, and the quantity of adsorbed water vapor are assumed to be spatially uniform within each adsorbent bed. This assumption simplifies the model to a lumped-parameter approach.
• Adiabatic insulation: All components, including the adsorber and desorber, are considered to be perfectly insulated, thus neglecting any heat losses to the ambient environment.
• Ideal vapor transport: The water vapor desorbed from the adsorbent is assumed to flow instantaneously and completely into the condenser, without accumulation or delay.
• Ideal condensate flow: The condensate from the condenser is assumed to flow immediately and without resistance into the evaporator.
• Instantaneous evaporation and adsorption: The liquid water entering the evaporator is presumed to evaporate instantaneously under vacuum conditions, and the generated vapor is assumed to be adsorbed instantaneously in the cooled adsorber bed.
• Phase modeling: The adsorbed water is considered to exist in liquid phase, while the water vapor behaves as an ideal gas. This allows the use of the ideal gas law in mass and energy balance equations.
• Negligible hydraulic resistance: Pressure losses and flow resistances in the pipelines and valves are neglected.
• Constant properties: The thermophysical properties of the adsorbent material, working fluid (water), heat exchanger tubes (metal), and water vapor are considered to be constant throughout the cycle.

These assumptions allow the simplification of the highly nonlinear, transient behavior of the system, making it possible to derive the governing energy and mass balance equations for each component (adsorber, desorber, evaporator, and condenser). The resulting model captures the essential thermal dynamics and provides a foundation for optimization and performance prediction.

Rate of Adsorption/desorption

The rate of adsorption or desorption is calculated by the linear driving force kinetic equation, The coefficients of LDF equation for silica gel/water are determined by Chihara and Suzuki and are given in the below:

$${\displaystyle \frac{\partial \mathbf{w}}{\partial \mathbf{t}}}={\mathbf{K}}_{\mathbf{s}}({\mathbf{w}}^{\mathrm{*}}-\mathbf{w})(\mathrm{k}\mathrm{g}/\mathrm{k}\mathrm{g}.\mathrm{s})$$

(1)

The effective mass transfer coefficient inside the pores ks is given by:

$${\mathbf{K}}_{\mathbf{s}}={\mathbf{F}}_0{\displaystyle \frac{{\mathbf{D}}_{\mathbf{s}}}{{\mathbf{R}}_{\mathbf{p}}^2}}(\mathrm{s}-1)$$

(2)

The effective diffusivity is defined as follows

$${\mathbf{D}}_{\mathbf{s}}={\mathbf{D}}_{\mathbf{s}0}{\mathbf{e}}^{{\displaystyle \raisebox{1ex}{${-\mathbf{E}}_{\mathbf{a}}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{R}\mathbf{T}$}\right.}}(\mathrm{m}²/\mathrm{s})$$

(3)

Where :

Dso= 2.54 10-4 m²/s, RP = 1.7 10-4 mEa = 4.2 104 J/mol, F0 = 15

R = 8,314 J/mol K

The equilibrium uptake of silica gel- water pair is estimated using the equation developed by Boelman.

$${\mathbf{w}}^{\mathrm{*}}=0.346{\left({\displaystyle \frac{{\mathbf{P}}_{\mathbf{s}}\left({\mathbf{T}}_{\mathbf{r}}\right)}{{\mathbf{P}}_{\mathbf{s}}\left({\mathbf{T}}_{\mathbf{a}}\right)}}\right)}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1.6$}\right.}}$$

(4)

Where Ps(Tr) and Ps(Ts) are respectively the corresponding saturated vapor pressures of the refrigerant at temperatures Tr (water vapor) and Ta (adsorbent). Ps for water vapor is estimated using the following equation:

$${\mathbf{P}}_{\mathbf{s}\mathbf{a}\mathbf{t}}\left(\mathbf{T}\right)=133,32\mathbf{e}\mathbf{x}\mathbf{p}(18,3-{\displaystyle \frac{3820}{\mathbf{T}-46,1}})$$

(5)

Energy balance of adsorber

The adsorption energy balance is described by:

$${(\mathbf{m}}_{\mathbf{a}\mathbf{d}}{\mathbf{c}}_{\mathbf{a}\mathbf{d}}+{\mathbf{m}}_{\mathbf{a}}{\mathbf{c}}_{\mathbf{a}}+{\mathbf{m}}_{\mathbf{a}}\mathbf{w}{\mathbf{c}\mathbf{p}}_{\mathbf{r}}){\displaystyle \frac{\mathbf{d}{\mathbf{T}}_{\mathbf{a}\mathbf{d}}}{\mathbf{d}\mathbf{t}}}={\mathbf{m}}_{\mathbf{a}}∆{\mathbf{H}}_{\mathbf{a}\mathbf{d}\mathbf{s}}{\displaystyle \frac{\mathbf{d}\mathbf{w}}{\mathbf{d}\mathbf{t}}}+{\mathbf{m}}_{\mathbf{a}}{\mathbf{c}\mathbf{p}}_{\mathbf{r},\mathbf{v}}{\displaystyle \frac{\mathbf{d}\mathbf{w}}{\mathbf{d}\mathbf{t}}}\left({\mathbf{T}}_{\mathbf{e}\mathbf{v}}-{\mathbf{T}}_{\mathbf{a}\mathbf{d}}\right)+{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{a}\mathbf{d}}{\mathbf{c}\mathbf{p}}_{\mathbf{f}}({\mathbf{T}}_{\mathbf{f},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{f},\mathbf{o}\mathbf{u}\mathbf{t}})$$

(6)

The outlet temperature of cooling water can be expressed as

$${\mathbf{T}}_{\mathbf{a}\mathbf{d},\mathbf{o}\mathbf{u}\mathbf{t}}={\mathbf{T}}_{\mathbf{a}\mathbf{d}}+({\mathbf{T}}_{\mathbf{a}\mathbf{d},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{a}\mathbf{d}})\mathbf{e}\mathbf{x}\mathbf{p}(-{\displaystyle \frac{{\mathbf{U}}_{\mathbf{a}\mathbf{d}}{\mathbf{A}}_{\mathbf{a}\mathbf{d}}}{{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{a}\mathbf{d}}{\mathbf{c}\mathbf{p}}_{\mathbf{f},\mathbf{a}\mathbf{d}}}})$$

(7)

Energy balance of desorber

The desorption energy balance is described by:

$${(\mathbf{m}}_{\mathbf{d}\mathbf{e}}{\mathbf{c}}_{\mathbf{d}\mathbf{e}}+{\mathbf{m}}_{\mathbf{a}}{\mathbf{c}}_{\mathbf{a}}+{\mathbf{m}}_{\mathbf{a}}\mathbf{w}{\mathbf{c}\mathbf{p}}_{\mathbf{r}}){\displaystyle \frac{\mathbf{d}{\mathbf{T}}_{\mathbf{d}\mathbf{e}}}{\mathbf{d}\mathbf{t}}}={\mathbf{m}}_{\mathbf{a}}∆{\mathbf{H}}_{\mathbf{a}\mathbf{d}\mathbf{s}}{\displaystyle \frac{\mathbf{d}\mathbf{w}}{\mathbf{d}\mathbf{t}}}{\dot{+\acute{\mathbf{m}}}}_{\mathbf{f},\mathbf{d}\mathbf{e}}{\mathbf{c}\mathbf{p}}_{\mathbf{f}}({\mathbf{T}}_{\mathbf{f},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{f},\mathbf{o}\mathbf{u}\mathbf{t}})\left(\mathrm{k}\mathrm{W}\right)$$

(8)

The outlet temperature of hot water can be expressed as

$${\mathbf{T}}_{\mathbf{d}\mathbf{e},\mathbf{o}\mathbf{u}\mathbf{t}}={\mathbf{T}}_{\mathbf{d}\mathbf{e}}+({\mathbf{T}}_{\mathbf{d}\mathbf{e},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{d}\mathbf{e}})\mathbf{e}\mathbf{x}\mathbf{p}(-{\displaystyle \frac{{\mathbf{U}}_{\mathbf{d}\mathbf{e}}{\mathbf{A}}_{\mathbf{d}\mathbf{e}}}{{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{d}\mathbf{e}}{\mathbf{c}\mathbf{p}}_{\mathbf{f}}}})$$

(9)

Energy balance of condenser

The condenser energy balance equation can be written as

$${{(\mathbf{m}}_{\mathbf{r},\mathbf{c}\mathbf{d}}{\mathbf{c}\mathbf{p}}_{\mathbf{r}}+\mathbf{m}}_{\mathbf{c}\mathbf{d}}{\mathbf{c}}_{\mathbf{c}\mathbf{d}}){\displaystyle \frac{\mathbf{d}{\mathbf{T}}_{\mathbf{c}\mathbf{d}}}{\mathbf{d}\mathbf{t}}}=-{\mathbf{m}}_{\mathbf{a}}{\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{d}\mathbf{e}\mathbf{s}}}{\mathbf{d}\mathbf{t}}}{\mathbf{L}}_{\mathbf{v}}-{\mathbf{m}}_{\mathbf{a}}{\mathbf{c}\mathbf{p}}_{\mathbf{r},\mathbf{v}}{\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{d}\mathbf{e}\mathbf{s}}}{\mathbf{d}\mathbf{t}}}\left({\mathbf{T}}_{\mathbf{d}\mathbf{e}}-{\mathbf{T}}_{\mathbf{c}\mathbf{d}}\right)+{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{c}\mathbf{d}}{\mathbf{c}\mathbf{p}}_{\mathbf{f}}({\mathbf{T}}_{\mathbf{f},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{f},\mathbf{o}\mathbf{u}\mathbf{t}}\left)\left(\mathrm{k}\mathrm{W}\right)\right)$$

(10)

The outlet temperature of cooling water can be expressed as

$${\mathbf{T}}_{\mathbf{c}\mathbf{d},\mathbf{o}\mathbf{u}\mathbf{t}}={\mathbf{T}}_{\mathbf{c}\mathbf{d}}+({\mathbf{T}}_{\mathbf{c}\mathbf{d},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{c}\mathbf{d}})\mathbf{e}\mathbf{x}\mathbf{p}(-{\displaystyle \frac{{\mathbf{U}}_{\mathbf{c}\mathbf{d}}{\mathbf{A}}_{\mathbf{c}\mathbf{d}}}{{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{c}\mathbf{d}}{\mathbf{c}\mathbf{p}}_{\mathbf{f},\mathbf{c}\mathbf{d}}}})$$

(11)

Energy balance of evaporator

The energy balance in the evaporator is expressed as

$${(\mathbf{m}}_{\mathbf{e}\mathbf{v}}{\mathbf{c}}_{\mathbf{e}\mathbf{v}}+{\mathbf{m}}_{\mathbf{r},\mathbf{e}\mathbf{v}}{\mathbf{c}}_{\mathbf{p},\mathbf{r}}){\displaystyle \frac{\mathbf{d}{\mathbf{T}}_{\mathbf{e}\mathbf{v}}}{\mathbf{d}\mathbf{t}}}=-{\mathbf{m}}_{\mathbf{a}}{\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{a}\mathbf{d}\mathbf{s}}}{\mathbf{d}\mathbf{t}}}{\mathbf{L}}_{\mathbf{v}}-{\mathbf{m}}_{\mathbf{a}}{\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{d}\mathbf{e}\mathbf{s}}}{\mathbf{d}\mathbf{t}}}{\mathbf{c}}_{\mathbf{p},\mathbf{r}}({\mathbf{T}}_{\mathbf{c}\mathbf{d}}-{\mathbf{T}}_{\mathbf{e}\mathbf{v}})+{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{e}\mathbf{v}}{\mathbf{c}}_{\mathbf{p},\mathbf{f}}({\mathbf{T}}_{\mathbf{f},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{f},\mathbf{o}\mathbf{u}\mathbf{t}}\left)\right(\mathrm{k}\mathrm{W})$$

(12)

The outlet temperature of chilled water can be written as

$${\mathbf{T}}_{\mathbf{e}\mathbf{v},\mathbf{o}\mathbf{u}\mathbf{t}}={\mathbf{T}}_{\mathbf{e}\mathbf{v}}+({\mathbf{T}}_{\mathbf{e}\mathbf{v},\mathbf{i}\mathbf{n}}-{\mathbf{T}}_{\mathbf{e}\mathbf{v}})\mathbf{e}\mathbf{x}\mathbf{p}(-{\displaystyle \frac{{\mathbf{U}}_{\mathbf{e}\mathbf{v}}{\mathbf{A}}_{\mathbf{e}\mathbf{v}}}{{\dot{\mathbf{m}}}_{\mathbf{f},\mathbf{e}\mathbf{v}}{\mathbf{c}\mathbf{p}}_{\mathbf{f},\mathbf{e}\mathbf{v}}}})$$

(13)

Mass balance in the evaporator

The mass balance for the refrigerant can be expressed by neglecting the gas phase as:

$${\displaystyle \frac{\mathbf{d}{\mathbf{m}}_{\mathbf{r},\mathbf{e}\mathbf{v}}}{\mathbf{d}\mathbf{t}}}=-{\mathbf{m}}_{\mathbf{a}}({\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{a}\mathbf{d}\mathbf{s}}}{\mathbf{d}\mathbf{t}}}+{\displaystyle \frac{\mathbf{d}{\mathbf{w}}_{\mathbf{d}\mathbf{e}\mathbf{s}}}{\mathbf{d}\mathbf{t}}})$$

(14)

Where, ${\mathbf{m}}_{\mathbf{a}}$ is the adsorbent mass.

System performance equations

The COP value is defined by the following equation:

$$\mathbf{C}\mathbf{O}\mathbf{P}={\displaystyle \frac{{\mathbf{Q}}_{\mathbf{e}\mathbf{v}}}{{\mathbf{Q}}_{\mathbf{d}\mathbf{e}}}}$$

(15)

The cooling capacity of the system is expressed by:

$${\mathrm{Q}}_{\mathrm{e}\mathrm{v}}={\displaystyle \frac{{\int }_0^{{\mathrm{t}}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}}{\dot{\mathrm{m}}}_{\mathrm{f},\mathrm{e}\mathrm{v}}{\mathrm{c}\mathrm{p}}_{\mathrm{f}}\left({\mathrm{T}}_{\mathrm{e}\mathrm{v},\mathrm{i}\mathrm{n}}-{\mathrm{T}}_{\mathrm{e}\mathrm{v},\mathrm{o}\mathrm{u}\mathrm{t}}\right)\mathrm{d}\mathrm{t}}{{\mathrm{t}}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}}}$$

(16)

Where :

$${\mathrm{Q}}_{\mathrm{d}\mathrm{e}}={\displaystyle \frac{{\int }_0^{{\mathrm{t}}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}}{\dot{\mathrm{m}}}_{\mathrm{f},\mathrm{d}\mathrm{e}}{\mathrm{c}\mathrm{p}}_{\mathrm{f}}\left({\mathrm{T}}_{\mathrm{d}\mathrm{e},\mathrm{i}\mathrm{n}}-{\mathrm{T}}_{\mathrm{d}\mathrm{e},\mathrm{o}\mathrm{u}\mathrm{t}}\right)\mathrm{d}\mathrm{t}}{{\mathrm{t}}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}}}$$

(17)

Specific Cooling Power

$$\mathrm{S}\mathrm{C}\mathrm{P}={\displaystyle \frac{{\mathrm{Q}}_{\mathrm{e}\mathrm{v}}}{{\mathrm{m}}_{\mathrm{a}}}}$$

(18)

Simulation Parameters

Parameter	Value
ma	50 Kg
〖∆H〗_ads	2800 kJ/kg
L_v	2500 kJ/kg
Ccd ,Cev, C_ad	0.386 kJ/kg.K
〖Cp〗_(r,v)	1.85 kJ/kg.K
C_a	0.924 kJ/kg.K
C_pr	4.18 kJ/kg.k
m·_(f,ad)	1.6 m3/h
m·_(f,cd)	3.7 m3/h
m·_(f,ev)	2 m3/h
T_(ev,in)	15 °C
T_(cd,in)	22 °C,
T_(gn,in)	62 °C
t_cycle	840 s

The Carnot coefficient of performance is calculated by the following relation:

$${\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{t}}=\left[{\displaystyle \frac{\overline{{\mathrm{T}}_{\mathrm{a}\mathrm{d}}}-\overline{{\mathrm{T}}_{\mathrm{d}\mathrm{e}}}}{\overline{{\mathrm{T}}_{\mathrm{d}\mathrm{e}}}}}\right]\mathrm{*}\left[{\displaystyle \frac{\overline{{\mathrm{T}}_{\mathrm{e}\mathrm{v}}}}{\overline{{\mathrm{T}}_{\mathrm{a}\mathrm{d}}}-\overline{{\mathrm{T}}_{\mathrm{e}\mathrm{v}}}}}\right]$$

(19)

The adsorption efficiency of the machine is determined by:

$$\mathrm{ɳ}={\displaystyle \frac{\mathrm{C}\mathrm{O}\mathrm{P}}{{\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{t}}}}$$

(20)

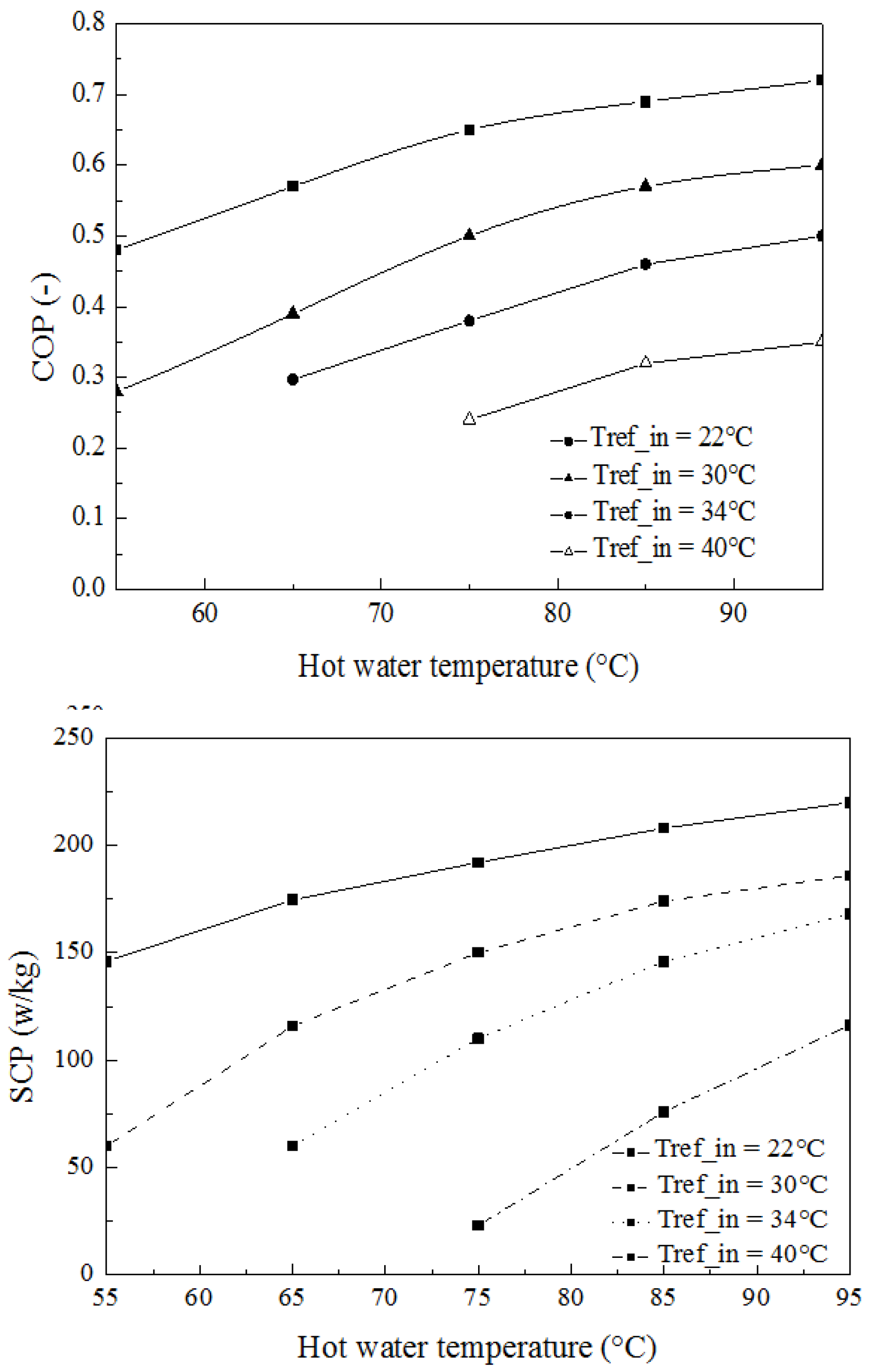
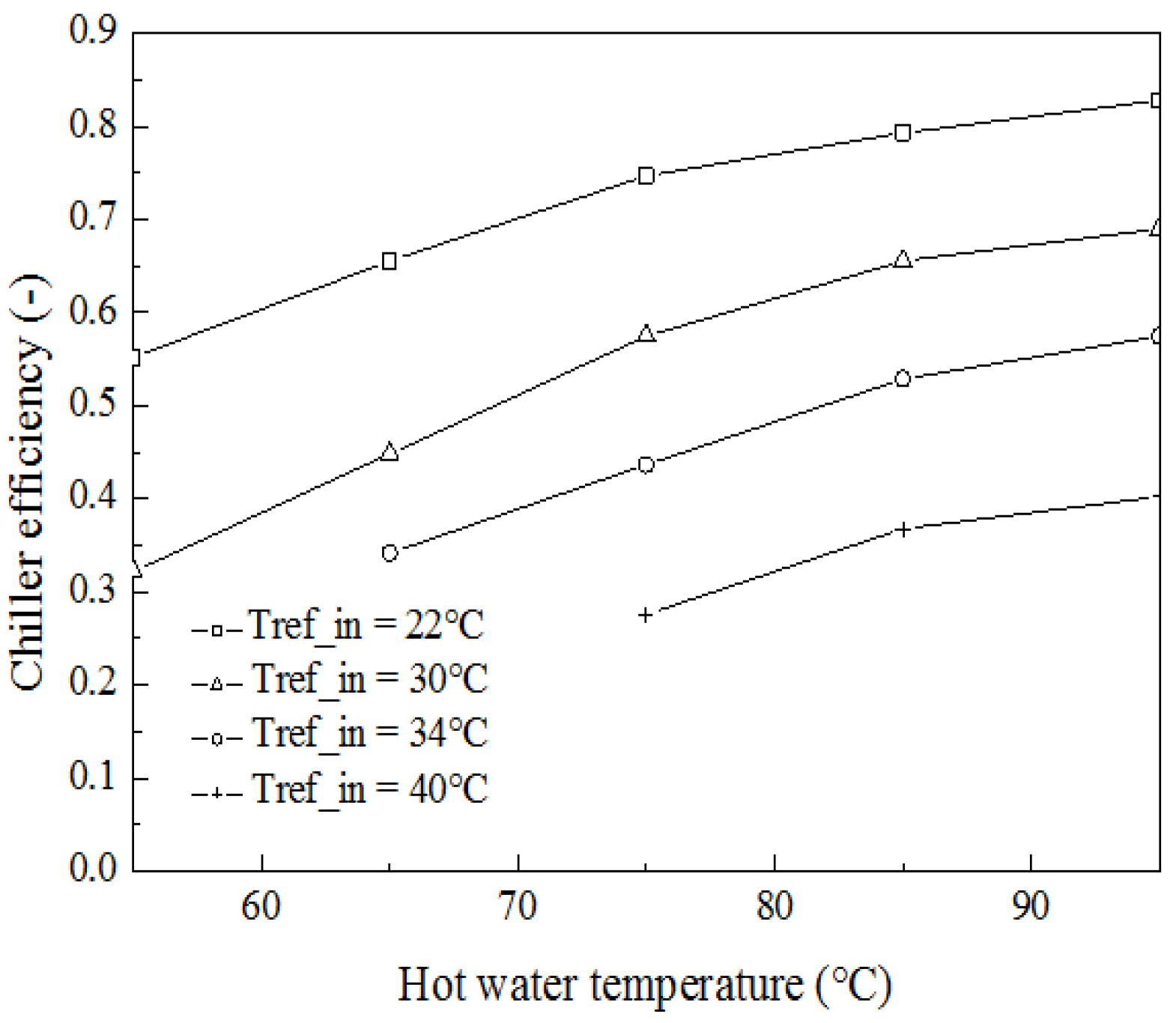
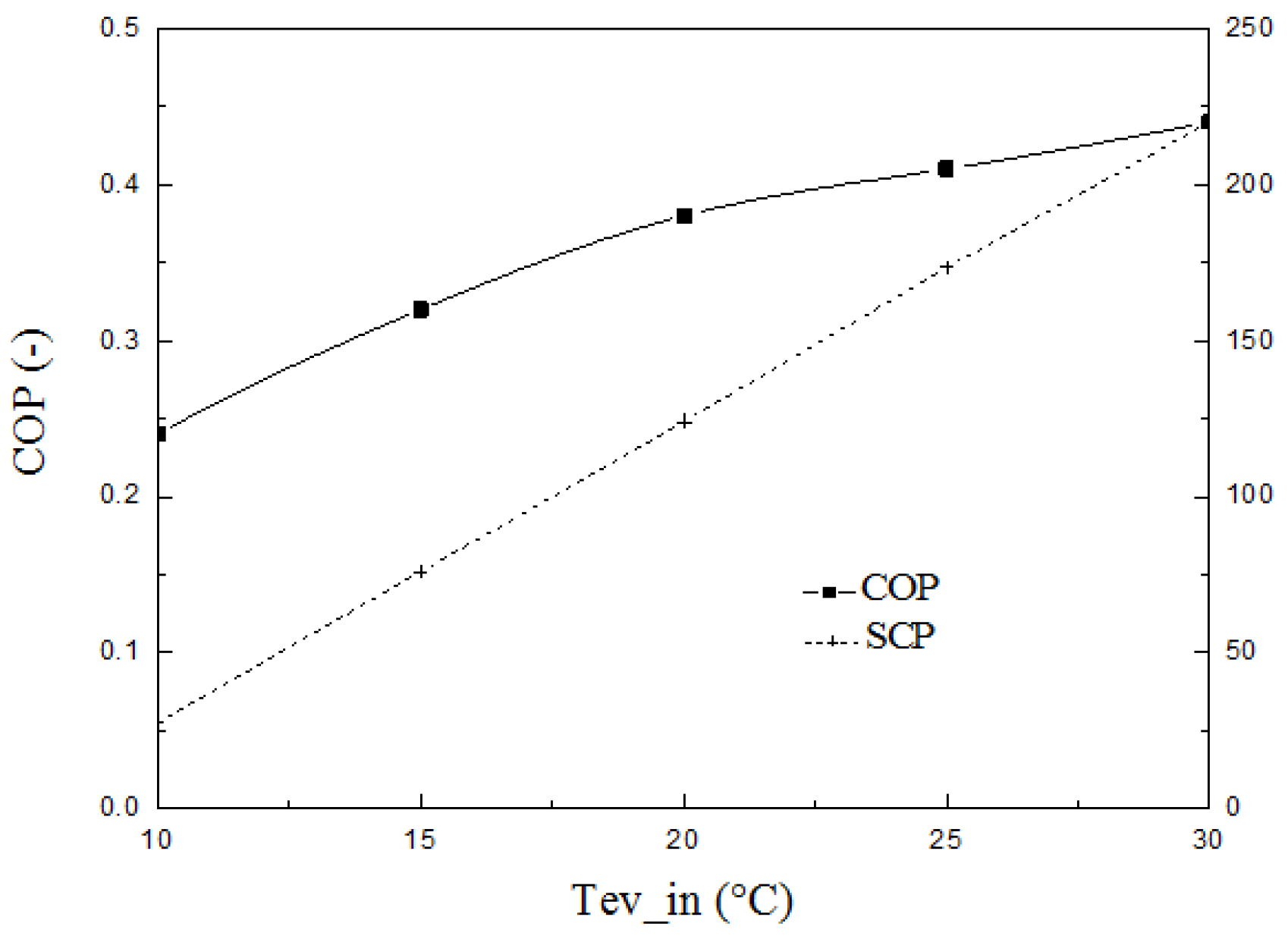
4. Results

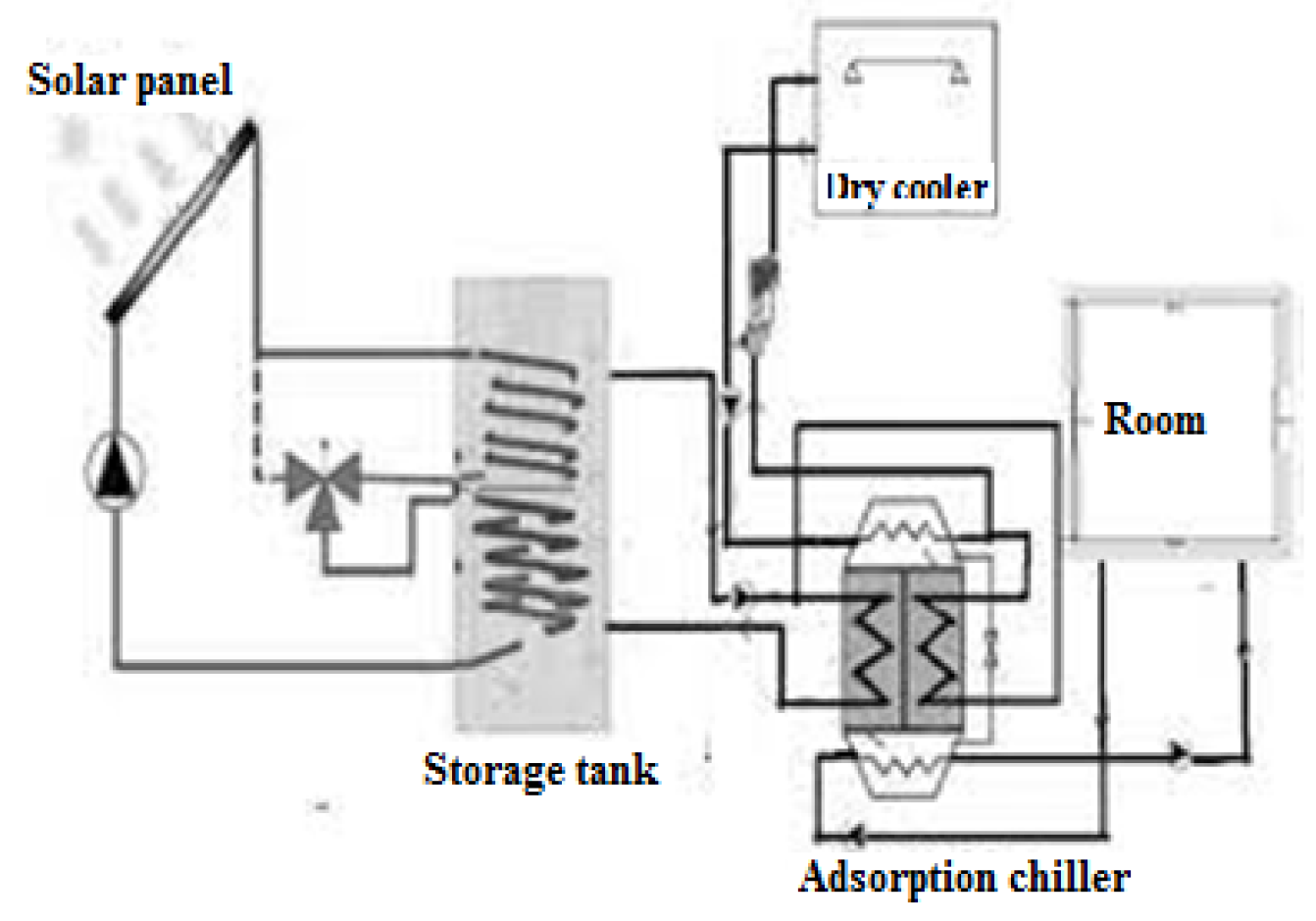
4.1. Experimental Setup

The experimental investigations were carried out using the ENERBAT platform, a solar-assisted tri-generation system installed at the University of Lorraine (Nancy, France), within the Faculty of Science and Technology. A schematic representation of the installation is presented in Figure 2.

ENERBAT is a comprehensive test bed designed to explore renewable energy integration into building thermal management systems. It combines solar thermal energy, gas-based cogeneration, and adsorption refrigeration in a unified platform, thereby enabling the simultaneous generation of cooling, heating, and electricity.

The core components of the platform include:

• A field of solar thermal collectors, responsible for harnessing solar energy and converting it into heat.
• A stratified thermal storage tank, used to store hot water generated by the solar collectors for subsequent use in desorption and domestic heating.
• A gas-fired cogenerator, based on an internal combustion engine, which produces both electricity and thermal energy. The recovered heat is used either for space heating or to supply the adsorption chiller.
• An adsorption refrigeration machine (ARM), which is activated by the thermal energy from the solar tank or cogenerator and delivers chilled water for air-conditioning applications.
• Expansion vessels for system safety, and hydraulic pumps to ensure fluid circulation between components.
• Plate heat exchangers to improve heat transfer in various loops.
• A climatic chamber, constructed from solid glued laminated timber, which consists of two thermally separated compartments, each with a volume of 27 m³. One chamber is conditioned using a chilled ceiling for cooling, while the other uses a heated floor for space heating.

This configuration enables the analysis of dynamic interactions between heat production, storage, and consumption under real environmental conditions, and facilitates the evaluation of the ARM’s performance in a building-integrated application. The integration of adsorption cooling into the tri-generation system serves as a demonstrator for sustainable thermal management in buildings using low-exergy and renewable resources.

Model Validation

The accuracy of the developed dynamic model was assessed by comparing simulated results with experimental data obtained under standard operating conditions. Figure 3 presents the time-evolution profiles of the inlet and outlet temperatures of the heat transfer fluids at key locations in the system: hot water loop, cooling water loop, and chilled water loop.

During the startup phase, the outlet temperature of the hot water loop gradually increases and reaches the inlet temperature after approximately 7 minutes. This stabilization indicates that the silica gel in the desorber has been fully heated, allowing effective desorption of water vapor. At this point, the thermal energy required by the system reaches a minimum, as the energy is now primarily consumed in phase change processes rather than in raising the adsorbent temperature.

In the cooling water circuit, the inlet temperature rises during the pre-cooling and pre-heating periods, and then drops during the desorption/condensation phase. This behavior reflects the system’s need to remove latent heat from the condenser during condensation, as well as from the adsorbent during desorption. The observed cooling of the fluid during these periods confirms effective energy extraction by the cooling loop.

For the evaporator (chilled water loop), the outlet temperature increases during the evaporation/adsorption phase, corresponding to the system delivering cooling power to the thermal load. Conversely, during switching phases (pre-cooling and pre-heating), the chilled water temperature decreases, as evaporation is temporarily halted and no significant cooling is being provided.

Overall, the numerical model successfully reproduces the dynamic thermal behavior observed experimentally, capturing the transient temperature responses in all loops. The consistency between simulated and measured results confirms the validity of the model assumptions and its applicability for parametric studies and optimization of system performance.

Parametric Study of the Adsorption Chiller

The performance of an adsorption refrigeration machine (ARM) is strongly influenced by the temperatures of the working fluids: hot water (driving heat source), cooling water (heat sink), and chilled water (cooling load). This section investigates the impact of hot water inlet temperature on the cooling capacity and the coefficient of performance (COP), under varying cooling water inlet temperatures.

Effect of Cooling and Heating Water Temperatures

A reduction in cooling water inlet temperature enhances both the adsorption rate and the heat rejection process in the adsorber and condenser, leading to an increase in the cooling capacity and an improvement in COP. Conversely, an increase in hot water inlet temperature accelerates the desorption process, increasing the quantity of refrigerant vapor generated and subsequently the refrigeration effect. This leads to an increase in cooling capacity (SCP, specific cooling power). However, depending on the level of the cooling water temperature, this may also result in diminished COP, especially if the thermal energy input outweighs the gain in useful cooling effect.

Effect of Hot Water Inlet Temperature

Figure 4 illustrates the variation of the specific cooling power (SCP) and the coefficient of performance (COP) as functions of the hot water inlet temperature, under different cooling water temperature conditions. All other operating parameters—including cycle duration, chilled water inlet temperature, and flow rates—were maintained at their nominal design values.

As the hot water inlet temperature increases from 55 °C to 95 °C, a consistent enhancement in cooling capacity is observed for all tested cooling water inlet temperatures. This is attributed to the increased desorption rate at higher temperatures, resulting in a greater quantity of refrigerant vapor being released from the adsorbent and consequently an increased evaporation and adsorption capacity in the subsequent cycle.

With respect to COP, a gradual increase is also recorded as the hot water temperature rises, particularly in the range of 55 °C to 85 °C. This is explained by the improved thermal driving force that boosts both desorption and the overall system cooling effect. However, beyond 85 °C, the COP stabilizes or shows diminishing returns, as the additional heat input does not proportionally increase the refrigerant circulation. This suggests the existence of an optimal desorption temperature, beyond which energy efficiency gains become negligible.

These findings highlight the importance of thermal input optimization in solar-assisted or waste-heat-driven adsorption systems, especially when integrated with intermittent renewable energy sources. The optimal balance between heating and cooling conditions must be maintained to maximize both cooling performance and system efficiency.

It is evident from the results that the sorption dynamics are significantly enhanced at higher hot water inlet temperatures. An increase in the driving temperature intensifies the desorption rate, leading to a more rapid liberation of the adsorbed refrigerant. This accelerated desorption enhances thermal exchange within the adsorbent bed and ensures a greater quantity of refrigerant is made available prior to the evaporation/adsorption phase, thereby improving the system’s refrigeration capacity.

Conversely, lower cooling water inlet temperatures yield a notable improvement in both specific cooling power (SCP) and the coefficient of performance (COP). This behavior is attributed to two key mechanisms: first, faster condensation of the desorbed refrigerant due to enhanced heat rejection in the condenser; and second, the increased adsorption rate, which is favored by lower adsorbent temperatures. Both effects contribute to a more efficient refrigeration cycle and improved overall performance.

Furthermore, the thermodynamic efficiency of the adsorption chiller was evaluated by comparing the actual COP to the theoretical maximum COP defined by the inverse Carnot cycle. The ratio between the actual and ideal COPs is presented in Figure 5, offering insight into the exergetic efficiency of the system under various thermal operating conditions. This metric serves as a valuable indicator of how closely the real system approaches ideal thermodynamic performance.

The thermodynamic efficiency of the adsorption chiller is significantly influenced by both the hot water inlet temperature and the cooling water inlet temperature. As observed in Figure 5, increasing the temperature of the heat source (hot water) and decreasing the temperature of the heat sink (cooling water) both lead to a measurable improvement in system efficiency.

This trend is primarily explained by thermodynamic and kinetic factors. An increase in the condenser temperature (due to higher cooling water temperatures) leads to a rise in the saturation pressure of the refrigerant, denoted as Ps(Tcd)P_s(T_{cd})Ps​(Tcd​). This, in turn, affects the adsorption–desorption equilibrium, increasing the amount of refrigerant mass regenerated during desorption. However, while this enhances the cycled mass, it also reduces the overall thermal efficiency, as more heat is required for desorption without a proportional gain in useful cooling. Thus, a higher condenser temperature may decrease the effective COP, especially under suboptimal cooling water conditions.

Effect of Chilled Water Inlet Temperature

To evaluate the influence of chilled water conditions, a series of simulations were conducted by varying the inlet temperature of the chilled water (evaporator side), while keeping the hot water temperature fixed at 85 °C and the cooling water inlet temperature at 40 °C.

Figure 6 illustrates the variation of coefficient of performance (COP) and specific cooling power (SCP) with respect to the evaporator inlet temperature. Results show that increasing the evaporator temperature enhances both COP and SCP. Specifically, a 20 °C increase in evaporator inlet temperature results in a COP increase of 0.2 and an SCP gain of 0.481 kW/kg.

This performance enhancement is attributed to a higher evaporation rate at elevated temperatures, which increases the vapor pressure inside the evaporator, promoting greater refrigerant uptake during the subsequent adsorption phase. As the evaporator pressure rises, the driving potential for mass transfer increases, resulting in higher adsorption capacity at the end of the adsorption cycle. Consequently, both the cooling effect and the efficiency of the cycle improve.

These findings highlight the critical importance of evaporator temperature control in optimizing adsorption chiller performance, particularly in systems operating under variable thermal loads or ambient conditions.

5. Conclusions

This work presented a dynamic and parametric investigation of a solar-powered adsorption refrigeration system using the silica gel–water working pair, with the objective of evaluating its performance under varying thermal conditions and assessing its potential integration with hydrogen production systems. A numerical model was developed and validated to simulate heat and mass transfer phenomena in a two-bed configuration. The parametric study revealed that increasing the hot water inlet temperature (optimal range: 80–95 °C) enhances desorption and boosts cooling capacity, while lowering the cooling water temperature significantly improves the COP—especially under geothermal conditions where values up to 0.7 can be achieved. Additionally, raising the evaporator temperature increases refrigerant uptake, resulting in improved SCP and COP, which confirms the critical role of evaporator-side thermal control. The system showed strong suitability for the Tunisian climate, offering COPs ranging from 0.25 to 0.54 under aerothermal conditions and reaching up to 0.7 with geothermal assistance. Finally, by proposing a coupling with green hydrogen production systems, this study demonstrates that waste heat from electrolysis can be effectively recovered to sustain desorption processes, ensuring continuous cooling even in the absence of solar input. This hybrid configuration enhances energy autonomy, reduces overall consumption, and supports the development of integrated, low-carbon energy infrastructures