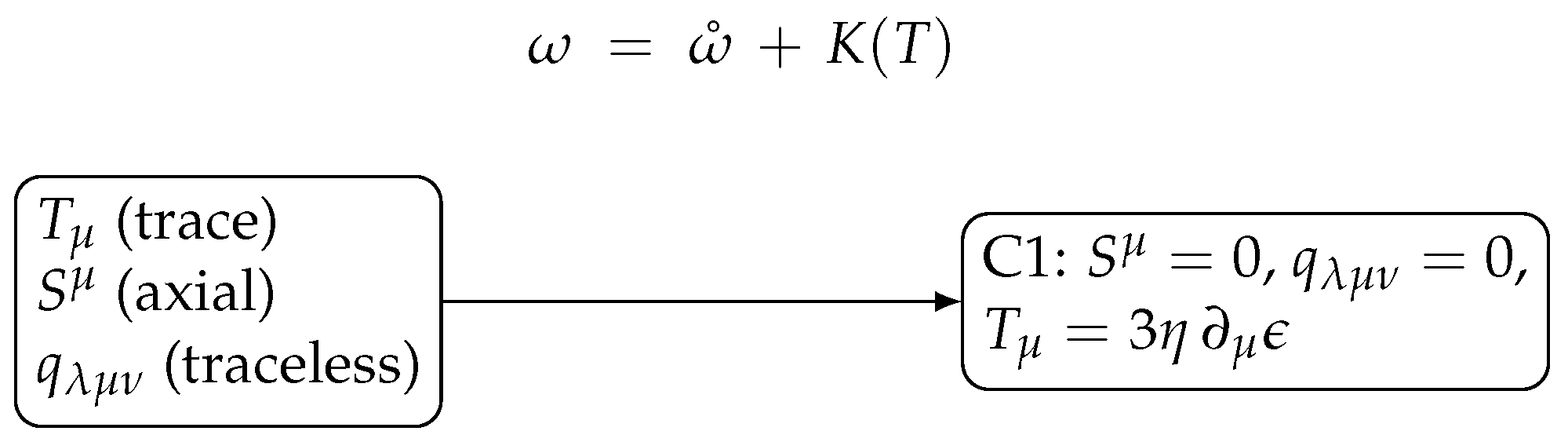A Palatini PT-Even Torsion Framework: Conditional Uniqueness, Bulk Rank-One Equivalences, and Tensor Luminality via Coefficient Locking

1. Introduction

Motivation and context. Multimessenger observations (e.g., GW170817/GRB170817A) enforce luminal gravitational waves today, severely constraining tensor-sector deviations from GR and motivating symmetry-driven routes that deliver $c_T=1$ without fine tuning. At the same time, long-standing work in Einstein–Cartan/metric–affine (EC/MAG) geometry shows how torsion and non-metricity can be organized consistently, while Palatini-type modified gravity (notably Palatini $f\left(R\right)$) has faced well-documented pitfalls when matter is included. This paper asks a focused question: Can one formulate a first-order (Palatini) framework whose observable sector is (i) $PT$-even by construction, (ii) closed at quadratic order with at most one derivative per building block, (iii) exactly luminal for tensor modes by a structural identity, and (iv) free of extra propagating degrees of freedom?

Posture and scope. We work with independent vierbein ${e^A}_{\mu }$ and a metric-compatible spin connection ${{\omega }^{AB}}_{\mu }$, and we enforce a scalar $PT$ projector ${\Pi }_{\mathrm{PT}}$ on observable scalar densities. On oriented $(3+1)$-manifolds, the combined $PT$ preserves orientation and commutes with the Hodge dual, so scalar densities can be projected to $PT$-even pieces; $PT$-odd scalar densities are discarded as unobservable (real) expectation values. An internal phase $ϵ\left(x\right)$ (Stueckelberg compensator) enters the observed sector only through its gradient; we adopt a spurion limit (not varied) at quadratic order. Global assumptions A1–A6 (domain/measure; $[\mathcal{PT},\ast ]=0$; projection/variation commutes on scalar densities; boundary/topology posture with Nieh–Yan as boundary; two-derivative closure) delimit the posture (Section 2). A quick notation table appears in Section 2.3 for ease of reference.

Projective symmetry and the invariant trace. Palatini geometry admits projective shifts

$${{\Gamma }^{\alpha }}_{\mu \nu }\to {{\Gamma }^{\alpha }}_{\mu \nu }+{\delta }_{\mu }^{\alpha }{\xi }_{\nu },T_{\mu }\equiv {T^{\alpha }}_{\mu \alpha }\to T_{\mu }+(d-1){\xi }_{\mu }(d=4).$$

(1)

To keep the projected observable sector invariant, we introduce a compensator whose gradient shifts as ${\partial }_{\mu }ϵ\to {\partial }_{\mu }ϵ+(d-1){\xi }_{\mu }$ and work with the projectively invariant trace

$$\begin{array}{|c|}\hline {\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ\\ \hline\end{array}(\mathrm{projectively}\mathrm{invariant}).$$

(2)

Within the two-derivative posture, all observables depend on $ϵ$ only through $\partial ϵ$ via ${\mathcal{T}}_{\mu }$.

Quadratic basis (one-derivative per factor). At quadratic order, the projected, real invariants we use are

$${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right],I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right],$$

(3)

together with improvement currents ${\nabla }_{\mu }{J}^{\mu }$ that are pure boundary under A4–A5.

• Main results (at a glance).

All three results hold at quadratic order, within A1–A6 and the scalar-$PT$ observable sector.  (C1) Conditional Palatini–$PT$ uniqueness under trace-lock (A6). Algebraic torsion consistent with the scalar projector is uniquely pure trace and aligned with $\partial ϵ$: $$\begin{array}{|c|}\hline {T^A}_{BC}=2\eta {{\delta }^A}_{[B}{\partial }_{C]}ϵ,\eta >0,S^{\mu }=0,q_{\lambda \mu \nu }=0\\ \hline\end{array}$$ and the surviving quadratic invariant satisfies $$\begin{array}{|c|}\hline I_T=-6{\eta }^2{\Sigma }_{ϵ}.\\ \hline\end{array}$$

(C2) Three-chain bulk equivalence (mod boundary). After projection and using C1, three constructive routes collapse to the same bulk quadratic piece: $$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{ROD}}\equiv {\delta }^2{\mathcal{L}}_{\mathrm{CM}}\equiv {\delta }^2{\mathcal{L}}_{{\mathrm{CS}}^{+}}\equiv A_{★}\sqrt{-g}{I}_T\left(\mathrm{mod}{\nabla }_{\mu }{J}^{\mu }\right),A_{★}={\displaystyle \frac{{\lambda }^2}{8}}.\\ \hline\end{array}$$ No all-order equivalence is claimed.

(C3) Coefficient locking ⇒ exact luminality. Eliminating TT–nonTT mixing fixes a unique weight $w^{★}$ so that $$\begin{array}{|c|}\hline K\left(w^{★}\right)-G\left(w^{★}\right)=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right)\\ \hline\end{array}$$ and hence the TT block is exactly luminal: $$\begin{array}{|c|}\hline c_T^2=1,{\delta }^2{S}_{\mathrm{TT}}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}\int d^{4}x{a}^3\left[{\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-{\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right],\mathrm{no}\mathrm{extra}\mathrm{DoF}.\\ \hline\end{array}$$ A TT-gauge weak-field representative of $J_{\Delta }^{\mu }$ (Minkowski; slowly varying $ϵ$) is listed in Section 7.1; a covariant FRW representative appears in Appendix D.

Plain-language gist (reader’s guide). What we do: (i) keep only $PT$-even scalar observables; (ii) use a compensator so only the trace of torsion in the invariant combination ${\mathcal{T}}_{\mu }$ matters; (iii) show three seemingly different quadratic routes give the same bulk physics (C2); (iv) choose coefficients once and for all to kill mixing, which forces $c_T=1$ (C3). What you can test: a unique next-to-leading dispersion

$$\delta c_T^2\left(k\right)=b{\displaystyle \frac{k^2}{{\Lambda }^2}}(k\ll \Lambda )$$

for multi-band GW data (PTA/LISA/LVK), detailed in Section 9; if a $k^2$ slope is absent where EFT is valid, this posture is disfavored.

Falsifiable diagnostics (paper-level). Within A1–A6, any of the following falsifies the framework at quadratic order:

• (C1 fails) Robust axial/traceless torsion signals in observables, or inability to realize $S_{\mu }=0$, $q_{\lambda \mu \nu }=0$ with $T_{\mu }\Vert {\partial }_{\mu }ϵ$.
• (C2 fails) Disagreement of bulk coefficients among rank-one determinant (ROD), closed-metric (CM), and $PT$-even CS/Nieh–Yan routes once improvements are accounted for; the flux ratio ${\mathcal{R}}_{X/Y}[\partial \mathcal{D}]\cancel{\to }1$ on admissible domains.
• (C3 fails) No coefficient choice achieves $K-G={\partial }_{\mu }\left(a^{-3}{J}_{\Delta }^{\mu }{a}^3\right)$, or $c_T\ne 1$ persists after locking on admissible patches.

Positioning relative to prior lines. In EC/MAG, axial/traceless torsion can propagate; here they are algebraically removed in the analyzed sector (C1). Parity-odd (dynamical) Chern–Simons gravity ties tensor effects to a pseudo-scalar; our $PT$-projected, even-parity sector achieves luminality by an equal-coefficient identity (C3), modulo improvements. Nieh–Yan contributes only boundary counterterms under A5 and does not alter bulk equations. The three-chain collapse (C2) is a rank-one, quadratic statement: ROD, CM, and the $PT$-even CS/Nieh–Yan shadow share the same bulk piece $A_{★}\sqrt{-g}{I}_T$, differing only by ${\nabla }_{\mu }{J}^{\mu }$.

Organization and stability notes. Section 2 fixes A1–A6 and the scalar projector; Section 3 and Section 4 prove C1; Section 5 proves C2 and defines flux-ratio diagnostics; Section 6 and Section 7 implement locking and prove $c_T=1$ (C3), also giving $J_{\Delta }^{\mu }$ representatives; matter couplings and the data-facing NLO piece appear in Section 8 and Section 9. Locking is stable on generic patches: the $2\times 2$ mixing determinant scales as $\Delta (k,{\Sigma }_{ϵ})={\alpha }_0{\eta }^4{\Sigma }_{ϵ}^2{k}^2+O(k^4,{\Sigma }_{ϵ}^3)$ with ${\alpha }_0\ne 0$, so rank loss occurs only on the measure-zero set $\{{\Sigma }_{ϵ}=0\}\cup \{k=0\}$.

Figure 1. Roadmap of the quadratic analysis (bulk-only). The scalar $PT$ projector (Thm. 2) defines the allowed sector; projective invariance is realized by ${\mathcal{T}}_{\mu }=T_{\mu }-{\partial }_{\mu }ϵ$. C1 enforces $T_{\mu }\Vert {\partial }_{\mu }ϵ$ (22); C2 establishes bulk equivalence of the rank-one determinant (ROD), closed-metric, and $PT$-even CS/Nieh–Yan routes up to improvements (37); C3 locks coefficients and yields $K=G$ and $c_T=1$ (53).

Figure 1. Roadmap of the quadratic analysis (bulk-only). The scalar $PT$ projector (Thm. 2) defines the allowed sector; projective invariance is realized by ${\mathcal{T}}_{\mu }=T_{\mu }-{\partial }_{\mu }ϵ$. C1 enforces $T_{\mu }\Vert {\partial }_{\mu }ϵ$ (22); C2 establishes bulk equivalence of the rank-one determinant (ROD), closed-metric, and $PT$-even CS/Nieh–Yan routes up to improvements (37); C3 locks coefficients and yields $K=G$ and $c_T=1$ (53).

2. Global Assumptions & the Scalar $PT$ Projector

We work on an oriented $(3+1)$-dimensional spacetime with independent vierbein ${e^A}_{\mu }$ and a metric-compatible spin connection ${{\omega }^{AB}}_{\mu }=-{{\omega }^{BA}}_{\mu }$ (Palatini posture). Greek indices $\mu ,\nu ,\dots$ are spacetime; Latin $A,B,\dots$ are Lorentz-frame indices with ${\eta }_{AB}=\mathrm{diag}(-,+,+,+)$. Torsion and curvature are

$$T^A\equiv D{e}^A=d{e}^A+{{\omega }^A}_B\wedge e^B,R^{AB}\equiv d{\omega }^{AB}+{{\omega }^A}_C\wedge {\omega }^{CB}.$$

(4)

Observable scalar densities are mapped to a real, $PT$-even sector by a projector ${\Pi }_{\mathrm{PT}}(·)$ defined below. The internal phase $ϵ\left(x\right)$ is a spurion: it enters observables only via $\partial ϵ$ and is not varied in the posture adopted here.

Physical Motivation for the Scalar $PT$ Projector

We restrict observable scalar densities to the $PT$-even, real sector for two reasons: (i) on oriented $(3+1)$-manifolds the combined $PT$ preserves orientation and commutes with the Hodge dual ∗, so the Levi–Civita density ${ϵ}^{\mu \nu \rho \sigma }$ (weight $+1$) is $PT$-even; (ii) by the anti-linearity of T, expectation values of $PT$-odd scalar densities are purely imaginary and thus unobservable as real densities. We therefore average a scalar with its $PT$ image and take the real part, Equation (8). This is a posture on observables, not on fields. The commutation Lemma 1 and a minimal counterexample with $\delta ϵ\ne 0$ render the posture directly checkable in our setup.

2.1. Projective Symmetry and the Stueckelberg Spurion

Palatini geometry admits a projective symmetry under which the connection shifts as

$${{\Gamma }^{\alpha }}_{\mu \nu }\to {{\Gamma }^{\alpha }}_{\mu \nu }+{\delta }_{\mu }^{\alpha }{\xi }_{\nu },T_{\mu }\equiv {T^{\alpha }}_{\mu \alpha }\to T_{\mu }+(d-1){\xi }_{\mu },(d=4).$$

(5)

To maintain invariance of the $PT$-even observable sector after imposing the scalar projector, we introduce a Stueckelberg compensator $ϵ$ whose gradient transforms as

$${\partial }_{\mu }ϵ\to {\partial }_{\mu }ϵ+(d-1){\xi }_{\mu },$$

(6)

and we work with the projectively invariant trace combination

$$\begin{array}{|c|}\hline {\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ\\ \hline\end{array}(\mathrm{projectively}\mathrm{invariant}).$$

(7)

Within the two–derivative truncation adopted here, we take the spurion limit in which dynamical fluctuations of $ϵ$ are frozen; thus the allowed $PT$-even scalar sector depends on $\partial ϵ$ only through ${\mathcal{T}}_{\mu }$. Combined with A1–A5, this ensures that the scalar projector commutes with variation on scalar densities (Lemma 1). In Section 3 we enumerate the resulting quadratic basis, and in Section 4, Section 5, Section 6 and Section 7 we show how (C1) aligns $T_{\mu }$ with ${\partial }_{\mu }ϵ$ so that ${\mathcal{T}}_{\mu }\to 0$ at the level analyzed.

Assumption Posture at a Glance (A1–A6; observable scalars are $PT$-even and real). A1  $PT$-invariant domain/measure. For any scalar density X, ${\displaystyle \int X=\int \mathcal{PT}[X]}$. Used in: self-adjointness of ${\Pi }_{\mathrm{PT}}$ and projector identities (Thm. 2); route-flux diagnostics in Section 5. A2  Orientation and Hodge dual. The combined $PT$ preserves the chosen orientation and $[\mathcal{PT},\ast ]=0$ on forms. Used in: parity of Levi–Civita density and commuting with ∗; boundary accounting. A3  Projection commutes with variation. For scalar densities, $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]$. Used in: Palatini variation and irrep block-diagonalization (Section 4). Checkable proof: Lemma 1 below. A4  Topology/boundary posture. Work on trivial patches or impose $PT$-invariant boundary flux so that improvement currents are pure gauge (no extra canonical pairs). Used in: null tests and flux ratios (Section 5); DoF count (Section 7). A5  Nieh–Yan as boundary counterterm.$\mathrm{NY}\equiv d(e^A\wedge T_A)$ affects only boundary conventions; no bulk Euler–Lagrange effect. Used in: three-chain equivalence modulo total derivatives (Section 5). A6  Trace-lock posture. We enforce $T_{\mu }=3\eta {\partial }_{\mu }ϵ$ via an algebraic Lagrange current. Under A4 this introduces no new canonical pairs and only removes a $PT$-even bilinear independence at quadratic order.

Sufficient conditions for A1. On oriented Lorentzian patches with the standard measure $d^{4}x\sqrt{-g}$ and $PT$-invariant boundaries (compact or AF/FRW fall-offs), the pullback by $PT$ preserves both the integration domain and the measure, hence $\int X=\int PT\left[X\right]$ for scalar densities.

Sufficient conditions for A2. If $PT$ preserves the chosen orientation and the metric used for index operations, then $PT$ commutes with the Hodge dual on forms: $[\mathcal{PT},\ast ]=0$.

Action of $P,T,PT$ on Densities

Let $P,T$ act as standard discrete isometries; T is anti-linear (complex conjugation). On oriented $(3+1)$-manifolds, the combined $PT$ preserves orientation, so for the Levi–Civita density ${ϵ}^{\mu \nu \rho \sigma }$ (weight $+1$) we have

$$P:ϵ\mapsto -ϵ,T:ϵ\mapsto -ϵ,PT:ϵ\mapsto +ϵ.$$

Assumption A2 implies $[\mathcal{PT},\ast ]=0$. Consequently, a scalar of the form ${ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }$ is $PT$-even iff X is $PT$-even.

2.2. Scalar $PT$ Projector: Definition and Basic Properties

The combined $PT$ acts anti-linearly on complex-valued densities (complex conjugation accompanies time reversal). On scalar densities we define

$${\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]\equiv {\displaystyle \frac{1}{2}}\left(\mathcal{O}+\mathcal{PT}\left[\mathcal{O}\right]\right){|}_{\mathrm{real}\mathrm{scalar}},{\Pi }_{\mathrm{PT}}^2={\Pi }_{\mathrm{PT}}.$$

(8)

Self-adjointness on real scalars. Using A1 and ${\mathcal{PT}}^2=\mathrm{id}$,

$$\int {\Pi }_{\mathrm{PT}}\left[{\mathcal{O}}_1\right]{\Pi }_{\mathrm{PT}}\left[{\mathcal{O}}_2\right]=\int {\Pi }_{\mathrm{PT}}\left[{\mathcal{O}}_1{\mathcal{O}}_2\right].$$

(9)

Lemma 1

(Project–vary commutation on scalar densities). Let ${\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]\equiv \frac{1}{2}{(\mathcal{O}+PT\left[\mathcal{O}\right])|}_{\mathrm{real}}$ act on complex-valued scalar densities $\mathcal{O}\in L^2\left(\mathcal{D}\right)$ with A1 (PT-invariant domain/measure) and A4 (fall-offs) imposed. If the spurion ϵ is non-variational and variations act only on $(e,\omega )$ with compact support or admissible fall-offs, then $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]$ and ${\Pi }_{\mathrm{PT}}$ is self-adjoint on real scalars.

Proof. 

Anti-linearity of T affects only $i\mapsto -i$; variations here are real-linear on $(e,\omega )$, and $ϵ$ is fixed. With A1, $\int X=\int PT\left[X\right]$ implies $\int f{\Pi }_{\mathrm{PT}}\left[g\right]=\int {\Pi }_{\mathrm{PT}}\left[fg\right]$ on real scalars (self-adjointness). Then $\delta \Pi =\frac{1}{2}(\delta \mathcal{O}+\delta PT\left[\mathcal{O}\right])=\frac{1}{2}(\delta \mathcal{O}+PT\left[\delta \mathcal{O}\right])=\Pi \left[\delta \mathcal{O}\right]$, where boundary terms vanish by A4.    □

$$\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right].$$

(10)

Function-analytic hypotheses and a minimal counterexample. Assume $\mathcal{O}\in L^2\cap H^1$ (scalar densities), $(\delta e,\delta \omega )\in H_{\mathrm{cpt}}^1$ or with A4 fall-offs, and the spurion $ϵ$ is non-variational. Since T is anti-linear (complex conjugation), $PT$ acts as $i\mapsto -i$. Under these conditions $\delta$ is real-linear and $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]$.

If, however, $ϵ$ is varied, the commutation may fail. Let $\mathcal{O}=i{\partial }_{\mu }ϵV^{\mu }$ with a real $V^{\mu }$. Then ${\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]=0$ (purely $PT$-odd), but ${\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]=\frac{1}{2}(\delta \mathcal{O}+PT\left[\delta \mathcal{O}\right])=\delta \mathcal{O}\ne 0$ when $\delta ϵ\ne 0$. Hence $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]=0\ne {\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]$. This shows why we hold $ϵ$ fixed (spurion posture).

Admissible variation space. Variations act on $(e,\omega )$ with compact support or with A4 fall-offs: on AF patches $(\delta e,\delta \omega )\in H_{\delta }^1$ with $\delta <-3/2$; on FRW slices, $\delta e=O\left(r^{-1-\sigma }\right)$, $\delta \omega =O\left(r^{-2-\sigma }\right)$ for some $\sigma >0$. The spurion $ϵ$ is nondynamical (no variation) and T’s anti-linearity only sends $i\to -i$. Under these conditions $\delta$ is real-linear and boundary fluxes vanish, so $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right]$ holds term-by-term.

Variational domain for $K-G$ identity. We take variations with compact support on spatial slices or with FRW/AF fall-offs: $h_{ij}^{\mathrm{TT}}=O\left(r^{-1-\sigma }\right)$, $\delta N=O\left(r^{-2-\sigma }\right)$, ${\partial }_i{N}^i=O\left(r^{-2-\sigma }\right)$ with $\sigma >0$. Then $J_{\Delta }^{\mu }=O\left(r^{-3-\sigma }\right)$ and

$$\delta \int d^{4}x{a}^3{\partial }_{\mu }{J}_{\Delta }^{\mu }=\int d{\Sigma }_{\mu }{a}^3\delta J_{\Delta }^{\mu }=0.$$

2.3. $PT$ Quick Tables (Projection-Ready)

Objects. (Signs indicate intrinsic P/T parities; T is anti-linear.)

Object	P	T	Note
${e^A}_{\mu }$	+	+	vierbein (metric from its square)
${{\omega }^{AB}}_{\mu }$	+	−	spin connection
${T^A}_{\mu \nu }$	+	−	torsion 2-form components
${R^{AB}}_{\mu \nu }$	+	+	curvature 2-form components
$ϵ$ (spurion)	+	−	enters observables via $\partial ϵ$ only
${\partial }_{\mu }ϵ$	−	+	flips under P; T anti-linear
${ϵ}^{\mu \nu \rho \sigma }$	−	−	pseudo-density (weight $+1$); $PT:+$; $[\mathcal{PT},\ast ]=0$ by A2

Scalar monomials and the projector.

Monomial	$PT$	${\Pi }_{\mathrm{PT}}(·)$
${(\partial ϵ)}^2$	even	survives; real by definition
${T^A}_{BC}{T_A}^{BC}$	even	survives; real under projection
${ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }$	even $\iff X$ even	kept iff X is $PT$-even; else projected out
$T_{\mu }{\partial }^{\mu }ϵ$	even	survives pre-lock; reduces to $3\eta {\Sigma }_{ϵ}$ after C1/trace-lock
${\nabla }_{\mu }{(\dots )}^{\mu }$ (vector density)	— (total deriv.)	boundary-only under A4; unaffected except taking real part

Notation Quick Reference (Projected, Real Scalars; Sign-Compensated Scheme)

Projected spurion scalar.    $${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right].$$ Sign and normalized gradient (on ${\Sigma }_{ϵ}\ne 0$).    $${\sigma }_{ϵ}\equiv sgn\left({\Sigma }_{ϵ}\right),{\widehat{n}}_{\mu }\equiv {\displaystyle \frac{{\partial }_{\mu }ϵ}{\sqrt{|{\Sigma }_{ϵ}|}}}.$$ Projectively invariant trace combination and strength.    $${\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ,\tau \equiv 3\eta \sqrt{|{\Sigma }_{ϵ}|}.$$ Quadratic torsion invariant and its sign-compensated form.    $$I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right],{\widehat{I}}_T\equiv {\sigma }_{ϵ}{I}_T.$$ C1 relation (used repeatedly later).   Under the conditional uniqueness map (C1), $${\widehat{I}}_T=-6{\eta }^2|{\Sigma }_{ϵ}|,{\tau }^2=9{\eta }^2\left|{\Sigma }_{ϵ}\right|={\displaystyle \frac{3}{2}}\left(-{\sigma }_{ϵ}{I}_T\right).$$ Regularity at ${\Sigma }_{ϵ}=0$. All rank-one objects are defined on patches with ${\Sigma }_{ϵ}\ne 0$ and extended by continuity via a smooth regulator ${\Sigma }_{ϵ}\to {({\Sigma }_{ϵ}^2+{\epsilon }^2)}^{1/2}$ with $\epsilon \to 0^{+}$. Quadratic densities and improvement currents remain finite in this limit.

2.4. Selection Rules Under the Scalar Projector

Theorem 2

(Selection rules). Under A1–A5 and $[\mathcal{PT},\ast ]=0$ (A2), for any complex scalar density $\mathcal{O}$,

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]=\mathcal{O}\mathit{(}\mathit{up}\mathit{to}\mathit{taking}\mathit{the}\mathit{real}\mathit{part}\mathit{)}\mathit{iff}\mathcal{O}\mathit{is}PT\text{-}\mathit{even},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]=0\mathit{iff}\mathcal{O}\mathit{is}PT\text{-}\mathit{odd}.\hfill \end{array}$$

(12)

In particular, for admissible tensors X,

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[{ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }\right]=0\mathit{iff}X\mathit{is}PT\text{-}\mathit{odd};\hfill \\ \hfill & {\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]\in \mathbb{R},{\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right]\in \mathbb{R},{\Pi }_{\mathrm{PT}}\left[T_{\mu }{\partial }^{\mu }ϵ\right]\mathit{is}PT\text{-}\mathit{even}\mathit{and}\mathit{not}\mathit{annihilated}\mathit{by}\mathit{projection}.\hfill \end{array}$$

• Sketch. By definition (8), ${\Pi }_{\mathrm{PT}}$ averages an object with its $PT$ image and then takes the real part. With A1, $\int X=\int PT\left[X\right]$ ensures self-adjointness (9) on real scalars. A2 implies $PT$ preserves orientation and commutes with ∗. Since the Levi–Civita density is $PT$-even while T is anti-linear, ${ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }$ inherits the $PT$ parity of X, yielding the conditional statement above. Products such as $T_{\mu }{\partial }^{\mu }ϵ$ are $PT$-even (see the quick table), hence survive the projector; their later reduction to ${\Sigma }_{ϵ}$ uses the trace-lock/C1 map (Section 3 and Section 4).

Roadmap and Where Each Assumption Enters

The definitions and rules above are the only projectors/boundary tools used later. In particular:

• Section 3 (allowed sector/closure): we enumerate all $PT$-even quadratic monomials with at most one derivative per building block. Pre-lock the basis includes $I_1=\Pi \left[{T^A}_{BC}{T_A}^{BC}\right]$, $I_2={\Sigma }_{ϵ}$, and $I_3=\Pi \left[T_{\mu }{\partial }^{\mu }ϵ\right]$. Post-lock (trace-lock or C1) maps $I_3\to 3\eta {\Sigma }_{ϵ}$.
• Section 4 (C1): A3 enables project-then-vary in the Palatini connection equation; A2/A5 prevent hidden pseudo-scalar contaminations; A4 controls improvements.
• Section 5 (C2, ${\sigma }_{ϵ}$ scheme): A5 ($\mathrm{NY}$ boundary) and A1/A4 underwrite the equality of route-wise bulk pieces and flux-ratio diagnostics, all written with the sign-compensated invariant ${\widehat{I}}_T$.
• Section 6 and Section 7 (C3): A1/A4 guarantee that improvement currents do not alter kinetic/gradient coefficients; A3 is used implicitly in all quadratic variations; the equal-coefficient identity is a total divergence on the admissible variational domain.

Boundary/Topology Posture And Fall-Offs (Pointer)

Assumption A4 is realized either by compact $PT$-invariant domains with vanishing flux or by standard asymptotically flat/FRW fall-offs; the explicit statements and the symplectic-flux check are compiled in Appendix A (boundary notes therein). We exclude torsion defects and multi-valued $ϵ$ patches that would violate the projector’s scalar posture.

3. Palatini Setting and the Allowed $PT$-Even Scalar Sector

We work in the Palatini posture with independent vierbein ${e^A}_{\mu }$ and a metric-compatible spin connection ${{\omega }^{AB}}_{\mu }$. Throughout this section the global assumptions A1–A6 and the scalar $PT$ projector of Section 2 are in force, together with the selection rules of Theorem 2. All scalar densities are implicitly projected, hence real and $PT$-even. We also retain the two–derivative truncation and the spurion posture: the internal phase $ϵ\left(x\right)$ enters observables only through its gradient and is not varied.

3.1. Projectively Invariant Starting Point

As reviewed in Section 2.1, Palatini geometry admits a projective symmetry under which the torsion trace shifts and is compensated by the gradient of $ϵ$. We therefore formulate the allowed sector in terms of the projectively invariant combination

$$\begin{array}{|c|}\hline {\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ\\ \hline\end{array}(\mathrm{invariant}\mathrm{under}{{\Gamma }^{\alpha }}_{\mu \nu }\to {{\Gamma }^{\alpha }}_{\mu \nu }+{\delta }_{\mu }^{\alpha }{\xi }_{\nu }).$$

(13)

Within the spurion limit (two–derivative regime; frozen $ϵ$ dynamics), PT–even observables depend on $\partial ϵ$ only through ${\mathcal{T}}_{\mu }$. In Section 4 we will show that the Palatini equations together with the trace-lock posture (C1) align $T_{\mu }$ with ${\partial }_{\mu }ϵ$, effectively setting ${\mathcal{T}}_{\mu }\to 0$ on admissible patches. The present section establishes the corresponding operator basis and its closure properties before and after this lock.

3.2. Normalized Spurion Direction and Canonical Rank-One Tensor

It is convenient to record the projected spurion scalar and the normalized direction of $\partial ϵ$:

$${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right],{\sigma }_{ϵ}\equiv sgn\left({\Sigma }_{ϵ}\right),{\widehat{n}}_{\mu }\equiv {\displaystyle \frac{{\partial }_{\mu }ϵ}{\sqrt{|{\Sigma }_{ϵ}|}}}({\Sigma }_{ϵ}\ne 0).$$

(14)

From $\widehat{n}$ we define a dimensionless, traceless rank-one tensor

$${{\mathcal{T}}^{\mu }}_{\nu }\equiv {\sigma }_{ϵ}\left({\widehat{n}}^{\mu }{\widehat{n}}_{\nu }-\frac{1}{4}{{\delta }^{\mu }}_{\nu }\right),\mathrm{Tr}\mathcal{T}=0,\mathrm{Tr}\left({\mathcal{T}}^2\right)=\frac{3}{4}.$$

(15)

The (dimension-one) torsion trace scale along $\widehat{n}$ will be denoted

$$\tau \equiv 3\eta \sqrt{|{\Sigma }_{ϵ}|}.$$

(16)

When ${\Sigma }_{ϵ}\to 0$ we work on ${\Sigma }_{ϵ}\ne 0$ patches and extend by continuity via a smooth regulator ${\Sigma }_{ϵ}\to {({\Sigma }_{ϵ}^2+{\epsilon }^2)}^{1/2}$, $\epsilon \to 0^{+}$. We emphasize the notational distinction: ${\mathcal{T}}_{\mu }$ is the projectively invariant trace vector (13), while ${{\mathcal{T}}^{\mu }}_{\nu }$ in (15) is a traceless rank-one matrix built from $\widehat{n}$.

3.3. What the Projector Allows (Pre- vs. Post-Lock)

By Theorem 2 and the parity assignments of Section 2, the following quadratic monomials with at most one derivative per building block are $PT$-even and thus survive the scalar projector:

$${T^A}_{BC}{T_A}^{BC},{(\partial ϵ)}^2,T_{\mu }{\partial }^{\mu }ϵ.$$

The mixed bilinear $T_{\mu }{\partial }^{\mu }ϵ$ is therefore independent pre-lock.1 Once the Palatini–$PT$ uniqueness map (C1; Section 4) or, equivalently, the trace lock is enforced,

$$T_{\mu }=3\eta {\partial }_{\mu }ϵ⟹T_{\mu }{\partial }^{\mu }ϵ=3\eta {\Sigma }_{ϵ},$$

(17)

and the mixed bilinear collapses to the spurion scalar.

For later reference we summarize the fate of the monomials:

Monomial	$PT$	Projected fate (pre-lock → post-lock)
${T^A}_{BC}{T_A}^{BC}$	even	survives → survives
${(\partial ϵ)}^2$	even	survives → survives
$T_{\mu }{\partial }^{\mu }ϵ$	even	survives, independent → $3\eta {\Sigma }_{ϵ}$
$\nabla ·(\dots )$	—	improvement → improvement

3.4. Two-stage closure at one-derivative order

Allowing at most one derivative per building block and working to quadratic order, the projected, real, $PT$-even scalar sector closes in two stages:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill \mathrm{Pre}-\mathrm{lock}\mathrm{basis}\text{:}& I_1\equiv {\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right],I_2\equiv {\Sigma }_{ϵ}={\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right],\hfill \\ \hfill & I_3\equiv {\Pi }_{\mathrm{PT}}\left[T_{\mu }{\partial }^{\mu }ϵ\right];\hfill \\ \hfill \mathrm{Post}-\mathrm{lock}(\mathrm{C}1/\mathrm{trace}-\mathrm{lock})\text{:}& I_3\stackrel{T_{\mu }=3\eta {\partial }_{\mu }ϵ}{\to }3\eta {\Sigma }_{ϵ},\mathrm{so}\mathrm{the}\mathrm{basis}\mathrm{reduces}\mathrm{to}\{I_1,{\Sigma }_{ϵ}\}.\hfill \end{array}\\ \hline\end{array}$$

(18)

The self-adjointness of ${\Pi }_{\mathrm{PT}}$ on real scalars (9) and A4 (boundary posture) justify the integration-by-parts steps implicit in (18).

Lemma 3

(Two-stage closure). Under A1–A5, any $PT$-even quadratic scalar density ${\mathcal{O}}_{\left(2\right)}(T,\partial ϵ)$ with at most one derivative per factor satisfies

$${\Pi }_{\mathrm{PT}}\left[{\mathcal{O}}_{\left(2\right)}\right]=c_1{I}_1+c_2{I}_2+c_3{I}_3+{\nabla }_{\mu }{J}^{\mu }(\mathrm{pre}-\mathrm{lock}),$$

for some real constants $c_{1,2,3}$ and an improvement current $J^{\mu }$. After enforcing $T_{\mu }=3\eta {\partial }_{\mu }ϵ$,

$${\Pi }_{\mathrm{PT}}\left[{\mathcal{O}}_{\left(2\right)}\right]=c_1{I}_1+{\tilde{c}}_2{\Sigma }_{ϵ}+{\nabla }_{\mu }{\tilde{J}}^{\mu }(\mathrm{post}-\mathrm{lock}),$$

with ${\tilde{c}}_2\equiv c_2+3\eta c_3$ and a (possibly shifted) improvement current ${\tilde{J}}^{\mu }$.

• Sketch. Enumerate quadratic monomials; Theorem 2 removes only $PT$-odd combinations. The three even monomials span the pre-lock space up to improvements; A1 and A4 ensure the projector’s self-adjointness and the harmlessness of boundary terms. The lock gives the post-lock reduction.

3.5. Action skeleton (pre- and post-lock) and invariant notation

A minimal bulk skeleton compatible with the closure is

$$S_{\mathrm{bulk}}=\int d^{4}x\sqrt{-g}\left[\frac{M_{\mathrm{Pl}}^2}{2}R(e,\omega )+{\alpha }_1{I}_1+{\alpha }_2{I}_2+{\alpha }_3{I}_3\right],$$

(19)

with ${\alpha }_{1,2,3}\in \mathbb{R}$. After the lock (C1) this becomes

$$S_{\mathrm{bulk}}^{(\mathrm{post}-\mathrm{lock})}=\int d^{4}x\sqrt{-g}\left[\frac{M_{\mathrm{Pl}}^2}{2}R(e,\omega )+{\alpha }_1{I}_1+\left({\alpha }_2+3\eta {\alpha }_3\right){\Sigma }_{ϵ}\right],$$

(20)

so the sole effect of $I_3$ at this order is a renormalization of the ${\Sigma }_{ϵ}$ coefficient.

For compactness we also introduce the torsion quadratic invariant (projected, real)

$$I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right],$$

(21)

and, when convenient, its sign-compensated version ${\widehat{I}}_T\equiv {\sigma }_{ϵ}{I}_T$. In Section 4 we will show that C1 implies $I_T=-6{\eta }^2{\Sigma }_{ϵ}$, so that the post-lock basis may be written as $\{I_T,{\Sigma }_{ϵ}\}$.

Order of Operations and Consistency

The scalar projector acts at the level of densities; by Lemma 1 (Section 2) we may project then vary or vary then project on scalar densities. The trace lock is an algebraic enforcement at the level of equations of motion (or via a Lagrange current); it is not a projection and introduces no new canonical pairs under A4. Accordingly, the pipeline for the quadratic sector is:

$$\left(\mathrm{i}\right)\mathrm{enumerate}\&\mathrm{project}\Rightarrow \mathrm{pre}-\mathrm{lock}\mathrm{basis}\{I_1,I_2,I_3\}⟹\left(\mathrm{ii}\right)\mathrm{impose}\mathrm{C}1/\mathrm{trace}\mathrm{lock}\Rightarrow I_3\mapsto 3\eta {\Sigma }_{ϵ},\mathrm{use}\{I_T,{\Sigma }_{ϵ}\}.$$

Paper-level null test. On any admissible background with A4 fall-offs, every projected, $PT$-even quadratic density with at most one derivative per building block reduces pre-lock to $c_1{I}_1+c_2{I}_2+c_3{I}_3$ up to a total derivative, and post-lock to $c_1{I}_1+{\tilde{c}}_2{\Sigma }_{ϵ}$ up to a total derivative. An explicit constructive reduction appears in the Appendix.

4. Uniqueness Theorem (C1)

• Within A1–A6 and the scalar-$PT$ observable sector, at quadratic order with at most one derivative per building block, the Palatini connection equations fix algebraic torsion to be pure trace aligned with the spurion gradient. Equivalently,

$$\begin{array}{|c|}\hline {T^A}_{BC}=2\eta {{\delta }^A}_{[B}{\partial }_{C]}ϵ,\eta >0,\\ \hline\end{array}$$

(22)

so that the axial and traceless irreps vanish, $S^{\mu }=0$ and $q_{\lambda \mu \nu }=0$. Using the standard irrep identity,

$${\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]={\displaystyle \frac{2}{3}}{T}_{\mu }{T}^{\mu }=6{\eta }^2{\Sigma }_{ϵ}⟹\begin{array}{|c|}\hline I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]=-6{\eta }^2{\Sigma }_{ϵ}.\\ \hline\end{array}$$

(23)

Here ${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right]$ is the projected, real scalar, and we use the shorthands from Section 2.3: $sgn\left({\Sigma }_{ϵ}\right)\equiv sgn\left({\Sigma }_{ϵ}\right),{\widehat{n}}_{\mu }\equiv {\partial }_{\mu }ϵ/\sqrt{|{\Sigma }_{ϵ}|},{{\mathcal{T}}^{\mu }}_{\nu }\equiv sgn\left({\Sigma }_{ϵ}\right)\left({\widehat{n}}^{\mu }{\widehat{n}}_{\nu }-\frac{1}{4}{{\delta }^{\mu }}_{\nu }\right),$ and $\tau \equiv {\widehat{n}}^{\mu }{T}_{\mu }=3\eta sgn\left({\Sigma }_{ϵ}\right)\sqrt{|{\Sigma }_{ϵ}|}.$

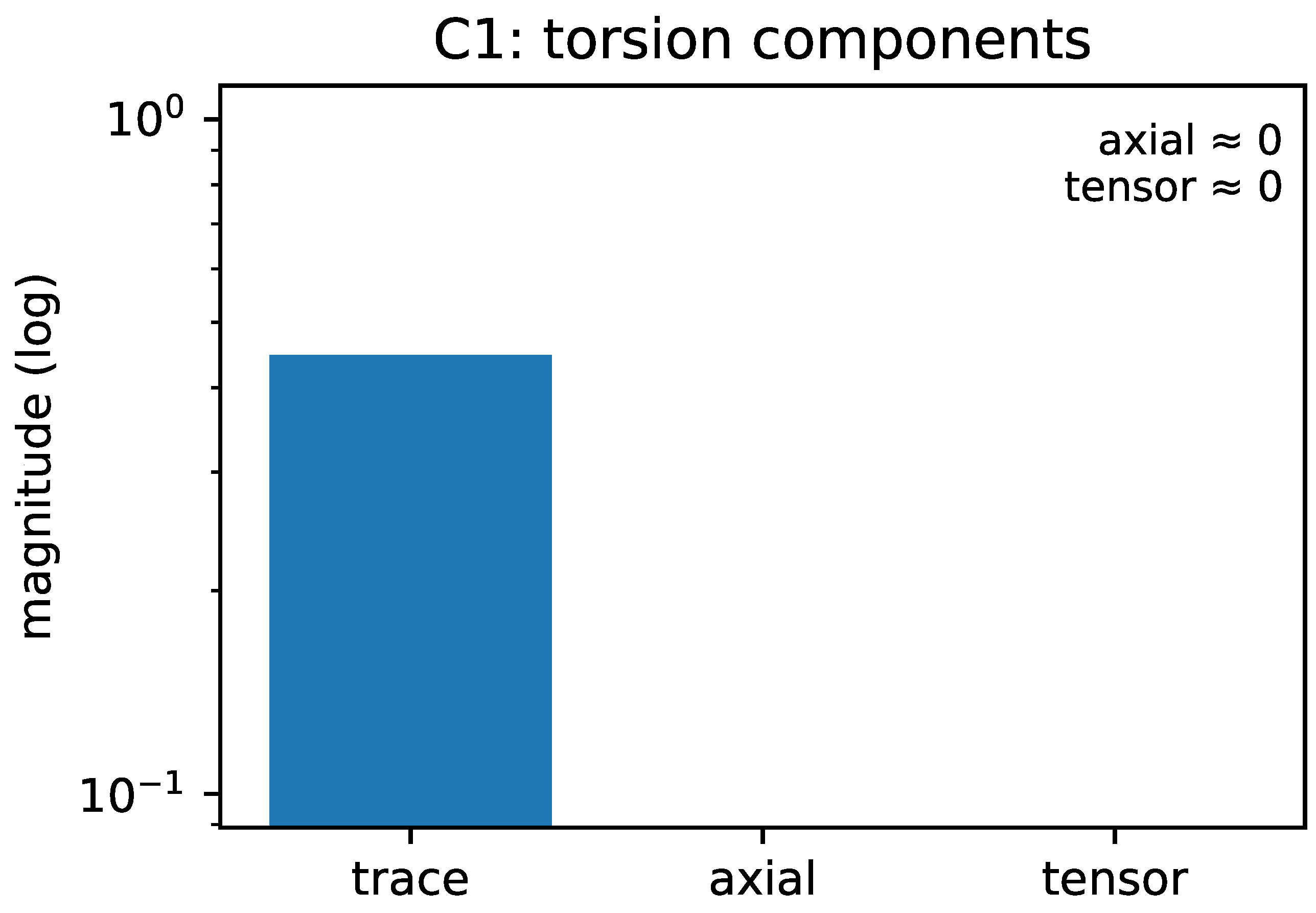
Figure 2. Irreducible torsion content at quadratic order (log–log view). Ratios of projected scalar strengths comparing the pure-trace block against the axial and traceless blocks, shown as trace/axial and trace/tensor on logarithmic axes. The Palatini algebraicity (Section 4.2) and the $PT$ projector drive axial and traceless pieces to zero, leaving the pure-trace map (22) as the unique survivor. [nb: fig_c1_pure_trace.py].

Figure 2. Irreducible torsion content at quadratic order (log–log view). Ratios of projected scalar strengths comparing the pure-trace block against the axial and traceless blocks, shown as trace/axial and trace/tensor on logarithmic axes. The Palatini algebraicity (Section 4.2) and the $PT$ projector drive axial and traceless pieces to zero, leaving the pure-trace map (22) as the unique survivor. [nb: fig_c1_pure_trace.py].

Figure 3. Connection decomposition and the C1 map. Top: the Levi–Civita/contorsion split $\omega =\mathring{\omega }+K\left(T\right)$. Bottom: torsion irreps $(T_{\mu },S^{\mu },q_{\lambda \mu \nu })$ and the C1 alignment $S^{\mu }=0$, $q_{\lambda \mu \nu }=0$, $T_{\mu }=3\eta {\partial }_{\mu }ϵ$ (22), which implies $I_T=-6{\eta }^2{\Sigma }_{ϵ}$ (23).

Figure 3. Connection decomposition and the C1 map. Top: the Levi–Civita/contorsion split $\omega =\mathring{\omega }+K\left(T\right)$. Bottom: torsion irreps $(T_{\mu },S^{\mu },q_{\lambda \mu \nu })$ and the C1 alignment $S^{\mu }=0$, $q_{\lambda \mu \nu }=0$, $T_{\mu }=3\eta {\partial }_{\mu }ϵ$ (22), which implies $I_T=-6{\eta }^2{\Sigma }_{ϵ}$ (23).

4.1. Most General Local Linear Ansatz (One Derivative)

At the derivative order relevant for the quadratic analysis, the only covector available is ${\partial }_{\mu }ϵ$ and the invariant tensors are ${{\delta }^A}_B$ and ${{ϵ}^A}_{BCD}$. The most general Lorentz-covariant linear ansatz is therefore

$${T^A}_{BC}=A{{\delta }^A}_{[B}{\partial }_{C]}ϵ+B{{ϵ}^A}_{BCD}{\partial }^Dϵ+{{(\mathcal{P}·\partial ϵ)}^A}_{BC},$$

(24)

with real $A,B$ and where ${{(\mathcal{P}·\partial ϵ)}^A}_{BC}$ denotes any attempted traceless mixed-symmetry piece built from a single vector.

Proposition B.1

(single-vector no-go; Appendix B). From one vector $v_{\mu }$ one cannot construct a nonzero traceless torsion irrep $q_{\lambda \mu \nu }$ obeying ${q^{\nu }}_{\mu \nu }={q_{\lambda \mu }}^{\mu }=0$ and $q_{\lambda \mu \nu }=-q_{\lambda \nu \mu }$. Any such attempt reduces to the span of ${{\delta }^A}_{[B}{v}_{C]}$ and ${{ϵ}^A}_{BCD}{v}^D$.

By Prop. B.1 the last term in (24) is trivial, and the ansatz reduces to

$${T^A}_{BC}=A{{\delta }^A}_{[B}{\partial }_{C]}ϵ+B{{ϵ}^A}_{BCD}{\partial }^Dϵ.$$

(25)

The scalar projector (Section 2) removes all $PT$-odd scalars, but it does not by itself force $B=0$; the Palatini equations will.

Proposition 4

(Palatini vector block ⇒ collinearity). With at most one derivative per building block and a single covector ${\partial }_{\mu }ϵ$ available, the algebraic connection equation in the vector irrep forces $T_{\mu }\Vert {\partial }_{\mu }ϵ$ on admissible patches (A4).

Proof. 

Use the reduced ansatz (25) and the blockwise non-degeneracy (Lemma 5). At this order the only covector in the vector block is $\partial ϵ$; any orthogonal component would require additional derivatives or tensors, which are excluded. Hence $T_{\mu }=\alpha {\partial }_{\mu }ϵ$ for some real $\alpha$. The Lagrange current in (26) simply sets $\alpha =3\eta$ without introducing canonical pairs (A4).    □

4.2. Palatini Equations: Algebraic, Irrep Blocks, and Alignment

We augment the pre-lock bulk skeleton (19) with a Lagrange current that enforces alignment of the torsion trace with $\partial ϵ$,

$${\mathcal{L}}_{\Lambda }=\sqrt{-g}{\Lambda }^{\mu }\left(T_{\mu }-3\eta {\partial }_{\mu }ϵ\right),T_{\mu }\equiv {T^{\nu }}_{\mu \nu }.$$

(26)

By Lemma 1 (Section 2), project-then-vary and vary-then-project commute on scalar densities. Varying w.r.t. the independent connection then yields algebraic equations in the three irreps $\{T_{\mu },S_{\mu },q_{\lambda \mu \nu }\}$:

$${\delta }_{\omega }S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{4{\alpha }_1}{3}}{T}_{\mu }\delta T^{\mu }+{\displaystyle \frac{{\alpha }_1}{12}}{S}_{\mu }\delta S^{\mu }+2{\alpha }_1{q}_{\lambda \mu \nu }\delta q^{\lambda \mu \nu }+{\Lambda }^{\mu }\delta T_{\mu }\right],$$

(27)

which is block diagonal because the map from the connection variation to torsion irreps is non-degenerate:

Lemma 5

(Non-degeneracy of $\delta \omega \mapsto (\delta T_{\mu },\delta S_{\mu },\delta q_{\lambda \mu \nu })$). In metric-compatible Palatini, the linear map from $\delta {{\omega }^{AB}}_{\mu }$ to the variations of the three torsion irreps is blockwise non-degenerate. Consequently the quadratic form in (27) splits into the three irreps with independent algebraic equations.

Proof sketch (3 lines). 

Varying only the spin connection, $\delta {T^A}_{\mu \nu }=\delta {{\omega }^A}_{B[\mu }{e^B}_{\nu ]}$. Projecting to irreps,

$$\delta T_{\mu }\equiv \delta {T^{\nu }}_{\mu \nu }={e_A}^{\nu }{e^B}_{\mu }\delta {{\omega }^A}_{B\nu },\delta S^{\mu }\equiv {ϵ}^{\mu \nu \rho \sigma }\delta T_{\nu \rho \sigma }={ϵ}^{\mu \nu \rho \sigma }{e}_{A\nu }{e^B}_{\rho }\delta {{\omega }^A}_{B\sigma },$$

and $\delta q_{\lambda \mu \nu }$ is the traceless remainder of $\delta T_{\lambda \mu \nu }$ after subtracting the vector/axial projections. These linear maps are surjective and mutually orthogonal with respect to $\int d^{4}x\sqrt{-g}({\displaystyle \frac{4}{3}}\delta T^2+{\displaystyle \frac{1}{12}}\delta S^2+2\delta q^2)$, hence the quadratic form in (27) splits blockwise and the blocks do not interfere. □

The Euler–Lagrange equations read

$$\begin{array}{cc}\hfill \left(\mathrm{vector}\right)& {\displaystyle \frac{4{\alpha }_1}{3}}{T}_{\mu }+{\Lambda }_{\mu }=0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \left(\mathrm{axial}\right)& {\displaystyle \frac{{\alpha }_1}{12}}{S}_{\mu }=0\Rightarrow S^{\mu }=0,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill \left(\mathrm{traceless}\right)& 2{\alpha }_1{q}_{\lambda \mu \nu }=0\Rightarrow q_{\lambda \mu \nu }=0,\hfill \end{array}$$

(30)

and variation w.r.t. ${\Lambda }^{\mu }$ enforces the lock $T_{\mu }=3\eta {\partial }_{\mu }ϵ$. Substituting back into (25) fixes $A=2\eta$ and forces $B=0$, i.e., alignment with $\partial ϵ$ and the absence of any axial piece, as claimed in (22).

Trace-Lock as an Algebraic Enforcement (Not an Extra Assumption)

By Proposition 4, Palatini’s algebraic equation fixes $T_{\mu }$ collinear with ${\partial }_{\mu }ϵ$; the current in (26) enforces the proportionality coefficient $\alpha =3\eta$ algebraically and introduces no new canonical pairs under A4. This is an enforcement device, not an additional dynamical hypothesis.

On degrees of freedom. The Lagrange current enforces an algebraic constraint; its Euler–Lagrange equation contains no time derivatives and thus introduces no new canonical pairs. Under A4 this is a first-class enforcement of the trace lock, not an additional propagating sector.

4.3. Positivity, Sign Choice, and the Invariant $I_T$

Using the standard irrep split ${T^A}_{BC}{T_A}^{BC}={\displaystyle \frac{2}{3}}{T}_{\mu }{T}^{\mu }+{\displaystyle \frac{1}{24}}{S}_{\mu }{S}^{\mu }+2q_{\lambda \mu \nu }{q}^{\lambda \mu \nu }$ and (29)–(30), we obtain ${\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]=6{\eta }^2{\Sigma }_{ϵ}$, which gives (23) for $I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]$. Positivity of the TT kinetic coefficient after locking (Section 5) fixes the physical branch $\eta >0$.

4.4. Theorem and Three-Step Proof

Theorem 6

(Palatini–$PT$ uniqueness (C1)). Under A1–A5 and the scalar $PT$ projector, algebraic torsion solving the Palatini connection equation with the trace lock (26) is uniquely ${T^A}_{BC}=2\eta {{\delta }^A}_{[B}{\partial }_{C]}ϵ$ with $\eta >0$. In particular, $S^{\mu }=0$ and $q_{\lambda \mu \nu }=0$, and $I_T=-6{\eta }^2{\Sigma }_{ϵ}$.

Proof (three steps). 

Step 1 (Ansatz). The most general linear ansatz is (24); by Prop. B.1 (Appendix B) the single-vector traceless attempt vanishes, giving (25).

Step 2 (Palatini blocks). Using Lemma 1 to commute projection with variation and Lemma 5 for blockwise non-degeneracy, varying w.r.t. $\omega$ and ${\Lambda }^{\mu }$ yields (28)–(30) and the lock $T_{\mu }=3\eta {\partial }_{\mu }ϵ$, which fix $A=2\eta$ and $B=0$.

Step 3 (Invariant/positivity). With $S=q=0$ and the lock, the invariant reduces to (23). The branch $\eta >0$ follows from positivity of the locked TT sector.    □

4.5. FRW Paper-Level Check and a Geometric Diagnostic

On flat FRW $d{s}^2=-d{\tau }^2+a^2\left(\tau \right)d{\overrightarrow{x}}^2$ with homogeneous $ϵ\left(\tau \right)$, the vector, axial and tensor blocks yield

$$\frac{4{\alpha }_1}{3}{T}_0+{\Lambda }_0=0,\frac{{\alpha }_1}{12}{S}_{\mu }=0,2{\alpha }_1{q}_{\lambda \mu \nu }=0,$$

together with the lock $T_0=3\eta \dot{ϵ}$. Hence $S^{\mu }=q_{\lambda \mu \nu }=0$ and $I_T=-6{\eta }^2{\Sigma }_{ϵ}$, in agreement with (22)–(23).

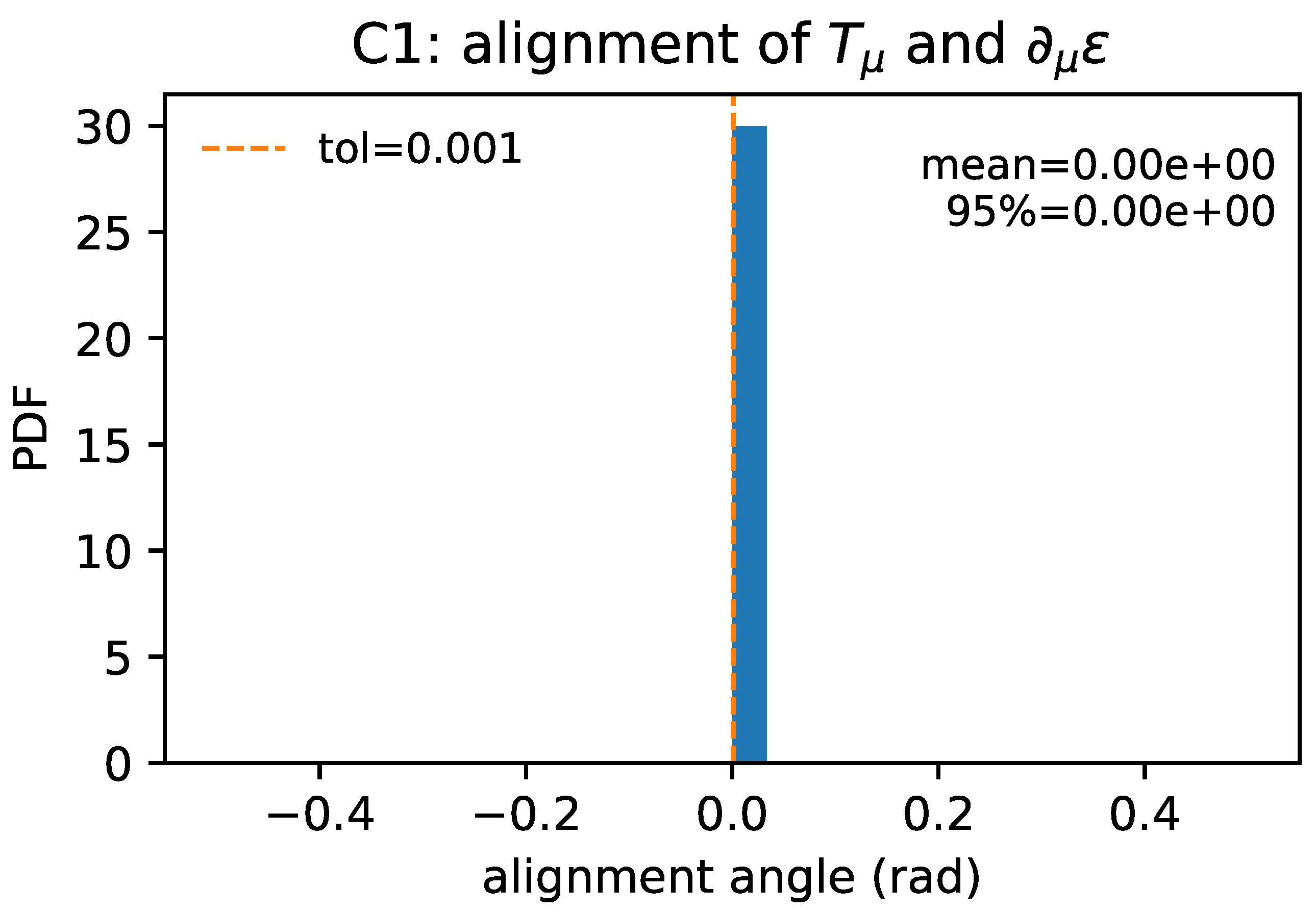
Figure 4. Alignment-angle diagnostic. Distribution of the alignment angle $\theta$ between the torsion trace $T_{\mu }$ and ${\partial }_{\mu }ϵ$, $cos\theta \equiv T_{\mu }{\partial }^{\mu }ϵ/\left(\sqrt{T^2}\sqrt{{(\partial ϵ)}^2}\right)$. The uniqueness map (22) predicts $\theta \simeq 0$ up to finite-domain/boundary remainders. [nb: fig_c1_alignment.py].

Figure 4. Alignment-angle diagnostic. Distribution of the alignment angle $\theta$ between the torsion trace $T_{\mu }$ and ${\partial }_{\mu }ϵ$, $cos\theta \equiv T_{\mu }{\partial }^{\mu }ϵ/\left(\sqrt{T^2}\sqrt{{(\partial ϵ)}^2}\right)$. The uniqueness map (22) predicts $\theta \simeq 0$ up to finite-domain/boundary remainders. [nb: fig_c1_alignment.py].

Corollaries, Scope, and Order-of-Operations Reminder

Corollary (basis reduction). With $S=q=0$ and $T_{\mu }=3\eta {\partial }_{\mu }ϵ$, the first-order closure basis of Section 3.4 collapses to $\{I_T,{\Sigma }_{ϵ}\}$ modulo a total derivative.

Scope and failure modes. Violations of A2 (orientation/$[\mathcal{PT},\ast ]=0$) or A4 (boundary/topology) can obstruct projector selection rules or boundary improvements globally; see Appendix B for representation-theoretic caveats and Appendix A for boundary notes. None affect the main (C1) statement on admissible patches.

Order of operations. The trace lock (26) is an algebraic constraint introduced at the level of equations of motion (or via ${\mathcal{L}}_{\Lambda }$); it is not a $PT$ projection and introduces no new canonical pairs. The pipeline used throughout Section 5, Section 6, Section 7, Section 8 and Section 9 is:

$$\begin{array}{cc}\hfill \left(\mathrm{i}\right)\mathrm{enumerate}\&\mathrm{project}& \Rightarrow \mathrm{pre}-\mathrm{lock}\mathrm{basis}\{I_1,I_2,I_3\}\hfill \\ & ⟹\left(\mathrm{ii}\right)\mathrm{impose}\mathrm{trace}\mathrm{lock}/\mathrm{C}1\Rightarrow I_3\mapsto 3\eta {\Sigma }_{ϵ},\mathrm{use}\{I_T,{\Sigma }_{ϵ}\}.\hfill \end{array}$$

5. Three-Chain Equivalence (C2)

• Scope. Throughout this section, “equivalence’’ means quadratic-order bulk equality modulo improvement currents; no non-perturbative or all-order equivalence is claimed. All statements are within A1–A6 and the scalar-$PT$ observable sector, and after implementing C1.

We adopt the sign-compensated (“${\sigma }_{ϵ}$”) scheme throughout C2: all rank-one bulk reductions are written in terms of $sgn\left({\Sigma }_{ϵ}\right)I_T\equiv {\sigma }_{ϵ}{I}_T$ so that patches with ${\Sigma }_{ϵ}<0$ are handled uniformly, $sgn\left({\Sigma }_{ϵ}\right)I_T=-6{\eta }^2\left|{\Sigma }_{ϵ}\right|$.

We prove that three ostensibly different quadratic routes— (i) a rank-one determinant route built out of the canonical traceless matrix ${{\mathcal{T}}^{\mu }}_{\nu }$, (ii) a closed-metric rank-one deformation, and (iii) the $PT$-even shadow extracted from the CS/Nieh–Yan chain— collapse, after C1 and projection, to the same bulk invariant $A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$ up to a total derivative. Differences are carried entirely by improvement currents ${\nabla }_{\mu }{J}^{\mu }$ (explicit FRW/weak-field representatives are listed in Appendix C).2

5.1. Preliminaries: Canonical Rank-One Objects and Normalization

Recall ${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right]$, ${\widehat{n}}_{\mu }\equiv {\displaystyle \frac{{\partial }_{\mu }ϵ}{\sqrt{|{\Sigma }_{ϵ}|}}}$, and the dimensionless, traceless rank-one matrix

$${{\mathcal{T}}^{\mu }}_{\nu }\equiv sgn\left({\Sigma }_{ϵ}\right)\left({\widehat{n}}^{\mu }{\widehat{n}}_{\nu }-\frac{1}{4}{{\delta }^{\mu }}_{\nu }\right),\mathrm{Tr}\mathcal{T}=0,\mathrm{Tr}\left({\mathcal{T}}^2\right)=\frac{3}{4},$$

(31)

together with the dimension-one spurion scale (after C1),

$$\tau \equiv {\widehat{n}}^{\mu }{T}_{\mu }=3\eta sgn\left({\Sigma }_{ϵ}\right)\sqrt{|{\Sigma }_{ϵ}|}.$$

(32)

Key relation.   

$${\tau }^2=9{\eta }^2|{\Sigma }_{ϵ}|={\displaystyle \frac{3}{2}}(-sgn\left({\Sigma }_{ϵ}\right)I_T),sgn\left({\Sigma }_{ϵ}\right)I_T\equiv sgn\left({\Sigma }_{ϵ}\right)I_T=-6{\eta }^2\left|{\Sigma }_{ϵ}\right|.$$

(33)

5.2. Three One-Line Propositions (NY Split → ∗ & Projection → Coefficient Match)

Proposition 7

(NY split). $T^A\wedge T_A=\mathrm{NY}+e^A\wedge e^B\wedge R_{AB}$ with $\mathrm{NY}\equiv d(e^A\wedge T_A)$.

Proposition 8

($PT$-even shadow after ∗ and projection). Under A2, the combined $PT$ preserves orientation and satisfies $[\mathcal{PT},\ast ]=0$. Applying ∗ to Proposition 7 and projecting to scalars, the term $\ast \mathrm{NY}$ contributes only as a boundary convention (A5), while the remaining $PT$-even bulk piece reduces, at quadratic order andafter C1, to

$${\delta }^2{\mathcal{L}}_{{\mathrm{CS}}^{+}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{{\mathrm{CS}}^{+}}^{\mu }\mathrm{for}\mathrm{some}{A}_{★}\in \mathbb{R}.$$

Proposition 9

(Coefficient match under the ${\sigma }_{ϵ}$ scheme). With $\mathrm{Tr}\mathcal{T}=0$, $\mathrm{Tr}\left({\mathcal{T}}^2\right)=\frac{3}{4}$, and $\tau =3\eta sgn\left({\Sigma }_{ϵ}\right)\sqrt{|{\Sigma }_{ϵ}|}$, both (i) the rank-one determinant route $\sqrt{det[\mathbf{1}+\left(\frac{2}{3}\right)\lambda \tau \mathcal{T}]}$ and (ii) the closed-metric deformation ${\tilde{g}}_{\mu \nu }=g_{\mu \nu }+\left(\frac{2}{3}\right)\lambda \tau {\widehat{n}}_{\mu }{\widehat{n}}_{\nu }$ yield the same quadratic bulk coefficient ${\delta }^2\mathcal{L}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$ with $A_{★}={\lambda }^2/8.$

Proof (paper-level). 

Expand $\sqrt{det(\mathbb{1}+X)}=1+\frac{1}{2}\mathrm{Tr}X+\frac{1}{8}[{\left(\mathrm{Tr}X\right)}^2-2\mathrm{Tr}{X}^2]+\mathcal{O}\left(X^3\right)$; with $X=\left(\frac{2}{3}\right)\lambda \tau \mathcal{T}$, $\mathrm{Tr}\mathcal{T}=0$ gives ${\delta }^2\sqrt{det(\mathbb{1}+X)}=-\frac{1}{4}\mathrm{Tr}\left(X^2\right)=-\frac{1}{4}\left(\frac{4}{9}\right){\lambda }^2{\tau }^2\mathrm{Tr}\left({\mathcal{T}}^2\right)=-{\lambda }^2{\tau }^2/12$. Using (33), ${\delta }^2\mathcal{L}=\sqrt{-g}({\lambda }^2/8)sgn\left({\Sigma }_{ϵ}\right)I_T$. The closed-metric route has the same Jacobian $\sqrt{-\tilde{g}}=\sqrt{-g}\sqrt{det[\mathbb{1}+\left(\frac{2}{3}\right)\lambda \tau \mathcal{T}]}$, hence the identical coefficient.

5.3. Quick Derivations (ROD/CM/CS⁺)

Rank-one determinant (rank-one determinant route).

$${\mathcal{L}}_{\mathrm{ROD}}=\sqrt{-g}\left(\sqrt{det\left[\mathbf{1}+\frac{2}{3}\lambda \tau \mathcal{T}\right]}-1\right)⟹\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{ROD}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T,A_{★}={\lambda }^2/8\\ \hline\end{array}.$$

(34)

Closed-metric route. ${\tilde{g}}_{\mu \nu }=g_{\mu \nu }+\frac{2}{3}\lambda \tau {\widehat{n}}_{\mu }{\widehat{n}}_{\nu }\Rightarrow \sqrt{-\tilde{g}}=\sqrt{-g}\sqrt{det[\mathbf{1}+\frac{2}{3}\lambda \tau \mathcal{T}]}$, so

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{CM}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T,A_{★}={\lambda }^2/8\\ \hline\end{array}.$$

(35)

$PT$-even CS/Nieh–Yan shadow. By Proposition 8,

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{{\mathrm{CS}}^{+}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{{\mathrm{CS}}^{+}}^{\mu },A_{★}={\lambda }^2/8\\ \hline\end{array}.$$

(36)

Bulk identity (summary).

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{ROD}}\equiv {\delta }^2{\mathcal{L}}_{\mathrm{CM}}\equiv {\delta }^2{\mathcal{L}}_{{\mathrm{CS}}^{+}}\equiv A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T\left(\mathrm{mod}{\nabla }_{\mu }{J}^{\mu }\right),A_{★}={\lambda }^2/8\\ \hline\end{array}.$$

(37)

Figure 5. Residual scan for the three-chain reduction (${\sigma }_{ϵ}$ scheme). Quadratic reductions of the ROD/CM/CS⁺ routes are compared against the target bulk line ${\delta }^2\mathcal{L}\stackrel{\mathrm{bulk}}{=}{A}_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$ with $A_{★}={\lambda }^2/8$. The vertical axis shows the residual after subtracting $A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$. All three routes saturate the target within tolerance. Quadratic-order, bulk-only (mod ${\nabla }_{\mu }{J}^{\mu }$; representatives listed in Appendix C). [nb: fig_c2_coeff_compare.py].

Figure 5. Residual scan for the three-chain reduction (${\sigma }_{ϵ}$ scheme). Quadratic reductions of the ROD/CM/CS⁺ routes are compared against the target bulk line ${\delta }^2\mathcal{L}\stackrel{\mathrm{bulk}}{=}{A}_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$ with $A_{★}={\lambda }^2/8$. The vertical axis shows the residual after subtracting $A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$. All three routes saturate the target within tolerance. Quadratic-order, bulk-only (mod ${\nabla }_{\mu }{J}^{\mu }$; representatives listed in Appendix C). [nb: fig_c2_coeff_compare.py].

5.4. Flux-Ratio Diagnostics and Convergence

For any two routes $X,Y\in \{\mathrm{ROD},\mathrm{CM},{\mathrm{CS}}^{+}\}$ define improvement currents by

$${\delta }^2{\mathcal{L}}_X-A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T={\nabla }_{\mu }{J}_X^{\mu },{\delta }^2{\mathcal{L}}_Y-A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T={\nabla }_{\mu }{J}_Y^{\mu }.$$

(38)

Assumptions A1–A5 imply

$$\begin{array}{|c|}\hline {\mathcal{R}}_{X/Y}[\partial \mathcal{D}]=1(\mathrm{quadratic}\mathrm{order};\mathrm{posture}\mathrm{A}1--\mathrm{A}5)\\ \hline\end{array}.$$

(39)

Summary of Section V. At quadratic order and under A1–A5, the rank-one determinant route, closed-metric, and $PT$-even CS/Nieh–Yan routes share the same bulk coefficient $A_{★}={\lambda }^2/8$ multiplying $sgn\left({\Sigma }_{ϵ}\right)I_T=-6{\eta }^2\left|{\Sigma }_{ϵ}\right|$, differing only by improvement currents (Appendix C). Boundary flux ratios ${\mathcal{R}}_{X/Y}$ equal 1 within finite-domain tolerances.

Figure 6. Flux-ratio diagnostic. Boundary flux ratios ${\mathcal{R}}_{X/Y}\left(R\right)$ for representative pairs $X/Y\in \{\mathrm{ROD},\mathrm{CM},{\mathrm{CS}}^{+}\}$ on finite FRW balls converge to 1 as the radius R grows, in agreement with Equation (39). The fit window used to extract the asymptote is annotated as $R\ge R_{min}$. Error bars reflect the IBP tolerance propagated to boundary terms. Quadratic-order, bulk-only (mod ${\nabla }_{\mu }{J}^{\mu }$; representatives listed in Appendix C). [nb: fig_flux_ratio.py]

Figure 6. Flux-ratio diagnostic. Boundary flux ratios ${\mathcal{R}}_{X/Y}\left(R\right)$ for representative pairs $X/Y\in \{\mathrm{ROD},\mathrm{CM},{\mathrm{CS}}^{+}\}$ on finite FRW balls converge to 1 as the radius R grows, in agreement with Equation (39). The fit window used to extract the asymptote is annotated as $R\ge R_{min}$. Error bars reflect the IBP tolerance propagated to boundary terms. Quadratic-order, bulk-only (mod ${\nabla }_{\mu }{J}^{\mu }$; representatives listed in Appendix C). [nb: fig_flux_ratio.py]

6. Coefficient Locking (C3)

We now lock the relative weight of two bulk–equivalent routes so that the tensor (TT) sector (i) has no kinetic mixing with nonpropagating variables and (ii) is exactly luminal at quadratic order. Throughout we keep A1–A5, the scalar projector ${\Pi }_{\mathrm{PT}}(·)$, and the C1 pure–trace map $T_{\mu }=3\eta {\partial }_{\mu }ϵ$ (Section 2, Section 3 and Section 4).

6.1. Setup and Locking Posture

By Section 5, the rank–one determinant (ROD) and closed–metric (CM) routes share the same quadratic bulk reduction modulo a total derivative:

$${\delta }^2{\mathcal{L}}_{\mathrm{ROD}}\equiv {\delta }^2{\mathcal{L}}_{\mathrm{CM}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T\left(\mathrm{mod}{\nabla }_{\mu }{J}^{\mu }\right),A_{★}={\displaystyle \frac{{\lambda }^2}{8}}.$$

(40)

We therefore consider the linear family

$${\mathcal{L}}_{\mathrm{chain}}\left(w\right)\equiv w_{\mathrm{ROD}}{\mathcal{L}}_{\mathrm{ROD}}+w_{\mathrm{CM}}{\mathcal{L}}_{\mathrm{CM}},w_{\mathrm{ROD}},w_{\mathrm{CM}}\in \mathbb{R},$$

(41)

and determine the ratio $w_{\mathrm{ROD}}:w_{\mathrm{CM}}$ by eliminating TT–nonTT mixing.

6.2. Quadratic ADM Block and Locking Conditions

Expanding ${\mathcal{L}}_{\mathrm{EH}}(e,\omega )+{\mathcal{L}}_{\mathrm{chain}}\left(w\right)$ to second order in ADM variables,

$${\delta }^2\mathcal{L}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}{a}^3\left[K\left(w\right){\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-G\left(w\right){\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right]+a^3\left(h^{\mathrm{TT}}·\mathbf{M}\left(w\right)·\Phi \right)+{\displaystyle \frac{a^3}{2}}\Phi ·\mathbf{P}·\Phi ,$$

(42)

where $\Phi$ collects nonpropagating fields (schematically $\Phi =\{\delta N,{\partial }_i{N}^i,\dots \}$). The mixing block $\mathbf{M}\left(w\right)$ is linear in w and proportional to ${\eta }^2{\Sigma }_{ϵ}$. Two independent entries suffice to enforce (L1) no kinetic mixing:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-\delta N}& =\left({\mu }_{\mathrm{ROD}}^{\left(N\right)}{w}_{\mathrm{ROD}}+{\mu }_{\mathrm{CM}}^{\left(N\right)}{w}_{\mathrm{CM}}\right){\eta }^2{\Sigma }_{ϵ},\hfill \\ \hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-{\partial }_i{N}^i}& =\left({\mu }_{\mathrm{ROD}}^{(\nabla N)}{w}_{\mathrm{ROD}}+{\mu }_{\mathrm{CM}}^{(\nabla N)}{w}_{\mathrm{CM}}\right){\eta }^2{\Sigma }_{ϵ},\hfill \end{array}\\ \hline\end{array}$$

(43)

with real, dimensionless coefficients ${\mu }^{(·)}$ extracted from (i) the contorsion part of $R(e,\omega )$ under C1 and (ii) the rank–one volume variations. Explicit $\mu$’s and background dependence are tabulated in Appendix D.

We also impose (L2) exact luminality $K\left(w\right)=G\left(w\right)$ and (L3) GR normalization at $\partial ϵ=0$ so that the locked TT action reduces to GR with Planck mass $M_{\mathrm{Pl}}$.

6.3. The $2\times 2$ Locking System and Non-Collinearity

Condition (L1) yields the linear system

$$\left(\begin{array}{cc}{\mu }_{\mathrm{ROD}}^{\left(N\right)}& {\mu }_{\mathrm{CM}}^{\left(N\right)}\\ {\mu }_{\mathrm{ROD}}^{(\nabla N)}& {\mu }_{\mathrm{CM}}^{(\nabla N)}\end{array}\right)\left(\begin{array}{c}{w}_{\mathrm{ROD}}\\ w_{\mathrm{CM}}\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right),({\Sigma }_{ϵ}\ne 0).$$

(44)

On generic admissible backgrounds the two row vectors are not collinear; the determinant

$$\Delta \equiv {\mu }_{\mathrm{ROD}}^{\left(N\right)}{\mu }_{\mathrm{CM}}^{(\nabla N)}-{\mu }_{\mathrm{ROD}}^{(\nabla N)}{\mu }_{\mathrm{CM}}^{\left(N\right)}\ne 0,$$

(45)

so the solution space is one-dimensional.

6.4. Locked Ratio, Normalization, and Exact Luminality

With $\Delta \ne 0$ there is a unique (up to scale) weight vector $w^{★}$ solving (44):

$$\begin{array}{|c|}\hline {\displaystyle \frac{w_{\mathrm{ROD}}^{★}}{w_{\mathrm{CM}}^{★}}}=-{\displaystyle \frac{{\mu }_{\mathrm{CM}}^{\left(N\right)}}{{\mu }_{\mathrm{ROD}}^{\left(N\right)}}}=-{\displaystyle \frac{{\mu }_{\mathrm{CM}}^{(\nabla N)}}{{\mu }_{\mathrm{ROD}}^{(\nabla N)}}}\\ \hline\end{array}$$

(46)

(the equality follows from $\Delta \ne 0$). The overall scale is fixed by (L3). For this choice, the kinetic and gradient coefficients obey the equal–coefficient identity

$$\begin{array}{|c|}\hline K\left(w^{★}\right)-G\left(w^{★}\right)=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right),\\ \hline\end{array}$$

(47)

with a representative $J_{\Delta }^{\mu }$ listed in Appendix D (TT gauge on weak–field and a covariant FRW form). Since the right-hand side is a total divergence on the admissible variational domain (A4), we obtain

$$K\left(w^{★}\right)=G\left(w^{★}\right)⟹c_T^2={\displaystyle \frac{G}{K}}=1.$$

(48)

Theorem 10

(Coefficient Locking ⇒ Exact Luminality (C3)). Under A1–A5, the scalar projector, and C1, there exists a unique ratio $w_{\mathrm{ROD}}^{★}:w_{\mathrm{CM}}^{★}$ (up to overall normalization) such that TT–nonTT mixing vanishes and $K\left(w^{★}\right)-G\left(w^{★}\right)=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right)$. Consequently the TT action is exactly the GR one at quadratic order:

$$\begin{array}{|c|}\hline {\delta }^2{S}_{\mathrm{TT}}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}\int d^{4}x{a}^3\left[{\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-{\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right],c_T^2=1,\\ \hline\end{array}$$

(49)

with no additional propagating degrees of freedom.

• Proof sketch. (i) Palatini algebraicity and the rank–one structure yield the mixing form (43); non-collinearity (45) fixes $w^{★}$ up to scale. (ii) For $w^{★}$, the difference $K-G$ integrates to a boundary term (47) by A1/A4 (self-adjoint projector; vanishing symplectic flux). (iii) The GR normalization (L3) fixes the overall scale and yields (49).

6.5. Rank Stability and Measure–Zero Degeneracies

Near small k and ${\Sigma }_{ϵ}$,

$$\Delta (k,{\Sigma }_{ϵ};\mathrm{foliation})={\alpha }_0{\eta }^4{\Sigma }_{ϵ}^2{k}^2+O(k^4,{\Sigma }_{ϵ}^3),{\alpha }_0\ne 0,$$

(50)

so loss of rank occurs only on the measure–zero set $\{{\Sigma }_{ϵ}=0\}\cup \{k=0\}$. This does not affect locking on generic admissible patches.

6.6. Data Companion and Reproducibility (Pointer)

For FRW backgrounds used in figures, the locked ratio $w^{★}$ and the two independent mixing entries are extracted directly from the companion data (see figs/data/mixing_matrix.csv with metadata in figs/data/mixing_matrix_meta.json). A convenience configuration mirroring the analytic ratio appears in configs/coeffs/mixing_matrix_FRW.json. These files are diagnostic only; the paper definition of $w^{★}$ is Equation (46).

Figure 7. Heatmap of the tensor-speed deviation. Representative scan of $|c_T-1|$ over the $(w_{\mathrm{ROD}},w_{\mathrm{CM}})$ plane on an admissible background (A1–A5, C1 in force). The locking curve from (44) is overlaid; along it, TT–nonTT mixing vanishes and (48) holds. [nb: fig_c3_cT_heatmap.py]

Figure 7. Heatmap of the tensor-speed deviation. Representative scan of $|c_T-1|$ over the $(w_{\mathrm{ROD}},w_{\mathrm{CM}})$ plane on an admissible background (A1–A5, C1 in force). The locking curve from (44) is overlaid; along it, TT–nonTT mixing vanishes and (48) holds. [nb: fig_c3_cT_heatmap.py]

Figure 8. Tensor dispersion $c_T\left(k\right)$: locked vs. unlocked. Comparison of $c_T\left(k\right)$ for the locked ratio $w^{★}$ from (46) (solid) and representative unlocked choices (dashed). [nb: fig_c3_dispersion.py]

Figure 8. Tensor dispersion $c_T\left(k\right)$: locked vs. unlocked. Comparison of $c_T\left(k\right)$ for the locked ratio $w^{★}$ from (46) (solid) and representative unlocked choices (dashed). [nb: fig_c3_dispersion.py]

• Summary of Section VI. Eliminating TT–nonTT mixing reduces to the full–rank system (44). Its nonzero determinant fixes a unique weight ratio $w_{\mathrm{ROD}}^{★}:w_{\mathrm{CM}}^{★}$ (up to normalization). With this ratio, the equal–coefficient identity (47) gives $K=G$ and hence $c_T=1$.

7. Quadratic Action, Exact Luminality, and Hamiltonian Constraint Structure

We now state and use the identity that fixes the tensor speed to be exactly luminal at quadratic order once the coefficients are locked, and we collect the Hamiltonian/constraint structure in one place. We assume A1–A6, the scalar $PT$ projector, and the C1 map with $T_{\mu }=3\eta {\partial }_{\mu }ϵ$. All projected scalars are real.

Variational domain for the $K-G$ identity. We take variations with compact support on spatial slices or with FRW/AF fall-offs:

$$h_{ij}^{\mathrm{TT}}=O\left(r^{-1-\sigma }\right),\delta N=O\left(r^{-2-\sigma }\right),{\partial }_i{N}^i=O\left(r^{-2-\sigma }\right)(\sigma >0).$$

Then $J_{\Delta }^{\mu }=O\left(r^{-3-\sigma }\right)$ and $\delta \int d^{4}x{a}^3{\partial }_{\mu }{J}_{\Delta }^{\mu }=\int d{\Sigma }_{\mu }{a}^3\delta J_{\Delta }^{\mu }=0$, so total divergences do not feed back into Euler–Lagrange equations.

7.1. Equal–Coefficient Identity and $c_T=1$

Expanding ${\mathcal{L}}_{\mathrm{tot}}={\mathcal{L}}_{\mathrm{EH}}(e,\omega )+{\mathcal{L}}_{\mathrm{chain}}\left(w\right)$ to quadratic order (about any admissible background with A4) yields

$${\delta }^2\mathcal{L}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}{a}^3\left[K\left(w\right){\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-G\left(w\right){\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right]+(\mathrm{TT}\text{–}\mathrm{nonTT}\mathrm{mix}+\mathrm{constraints}).$$

(51)

Using the contorsion decomposition under C1, the bulk equivalence of Section 5, and TT transversality/tracelessness, one finds the total-divergence identity

$$\begin{array}{|c|}\hline K\left(w\right)-G\left(w\right)=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right),\\ \hline\end{array}$$

(52)

with $J_{\Delta }^{\mu }$ a quadratic improvement current fixed by the rank–one normalization (Appendix D). Evaluated at the locked weights $w=w^{★}$ (Section 6),

$$\begin{array}{|c|}\hline K\left(w^{★}\right)=G\left(w^{★}\right)⟹c_T^2={\displaystyle \frac{G}{K}}=1(\mathrm{exact}\mathrm{at}\mathrm{quadratic}\mathrm{order}).\\ \hline\end{array}$$

(53)

On flat FRW this reduces to $K-G=a^{-3}{\partial }_{\tau }\left(a^3{J}_{\Delta }^0\right)$.

Weak-Field Check (Minkowski + Slowly Varying $ϵ$)

On ${\eta }_{\mu \nu }$ with $a=1$ and a slowly varying spurion (keep ${\partial }_{\alpha }ϵ=\mathrm{const}+O\left({\partial }^2ϵ\right)$),

$$\begin{array}{|c|}\hline J_{\Delta }^0={\displaystyle \frac{A_{★}}{2}}{\eta }^2{\Sigma }_{ϵ}{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}},J_{\Delta }^k=-{\displaystyle \frac{A_{★}}{2}}{\eta }^2{\Sigma }_{ϵ}{h}_{ij}^{\mathrm{TT}}{\partial }^k{h}_{ij}^{\mathrm{TT}},\\ \hline\end{array}$$

(54)

and ${\partial }_{\mu }{J}_{\Delta }^{\mu }={\displaystyle \frac{A_{★}}{2}}{\eta }^2{\Sigma }_{ϵ}\left({\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-\left({\partial }_{\ell }{h}_{ij}^{\mathrm{TT}}\right)\left({\partial }_{\ell }{h}_{ij}^{\mathrm{TT}}\right)\right)+{\partial }_{\mu }{\partial }_{\nu }{X}^{\left[\mu \nu \right]}$. Gauge independence holds upon integration since ${\delta }_{\xi }{J}_{\Delta }^{\mu }={\nabla }_{\nu }{X}^{\left[\mu \nu \right]}\left[\xi \right]$.

7.2. Locked TT Action

Imposing the GR normalization (L3) and using (53), the TT action is

$$\begin{array}{|c|}\hline {\delta }^2{S}_{\mathrm{TT}}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}\int d^{4}x{a}^3\left[{\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-{\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right],c_T^2=1.\\ \hline\end{array}$$

(55)

7.3. Hamiltonian Analysis and Constraint Structure (Merged)

3+1 variables and boundary posture. Adopt the standard $(3+1)$ split $d{s}^2=-N^{2}d{\tau }^2+h_{ij}(d{x}^i+N^{i}d\tau )(d{x}^j+N^{j}d\tau )$. Use the admissible fall-offs of Section 2 (A4) so that improvement currents contribute only boundary flux with vanishing symplectic pullback. Work in the time gauge for the tetrad; the configuration variables are $(h_{ij};N,N^i)$ together with the algebraic torsion irreps packaged in $K\left(T\right)$ and the Lagrange current ${\Lambda }^{\mu }$ of (26). The spurion $ϵ$ is non-variational and appears only via $\partial ϵ$.

Primary constraints and auxiliaries. N and $N^i$ have no time derivatives, giving ${\pi }_N\approx 0,{\pi }_i\approx 0$. ${\Lambda }^{\mu }$ is algebraic, with primary constraints $p_{{\Lambda }^{\mu }}\approx 0$.

Lemma 11

(No new canonical pairs from ${\Lambda }^{\mu }$). Under A4 and with ${\Lambda }^{\mu }$ entering only through $\sqrt{-g}{\Lambda }^{\mu }(T_{\mu }-3\eta {\partial }_{\mu }ϵ)$, the pair

$$p_{{\Lambda }^{\mu }}\approx 0,{\chi }_{\mu }\equiv T_{\mu }-3\eta {\partial }_{\mu }ϵ\approx 0$$

is second class and removes $({\Lambda }^{\mu },p_{{\Lambda }^{\mu }})$ together with the independent configuration associated to $T_{\mu }$. Integrating out ${\Lambda }^{\mu }$ before the split is equivalent. No additional canonical pairs arise.

Algebraic connection equation and secondary constraints. Varying the independent connection in the projected quadratic Lagrangian (Section 4) yields algebraic equations in the vector, axial and traceless irreps, cf. (27)–(30). Preserving the primary constraints produces the ADM secondaries $\mathcal{H}\approx 0,{\mathcal{H}}_i\approx 0$ and fixes $S^{\mu }\approx 0,q_{\lambda \mu \nu }\approx 0,{\chi }_{\mu }\approx 0$. Substituting back gives the C1 alignment (22) and the invariant reduction (23).

Constraint algebra and DoF count. On the admissible domain (A4), improvements do not contribute to the symplectic 2-form, and the Dirac algebra of $\{\mathcal{H},{\mathcal{H}}_i\}$ is the GR one at quadratic order. The torsion/lock constraints are algebraic and eliminated. Counting in the ADM-reduced metric sector: $(h_{ij},{\pi }^{ij})$ (12), $(N,{\pi }_N)$ and $(N^i,{\pi }_i)$ (8), with eight first-class constraints $({\pi }_N,{\pi }_i;\mathcal{H},{\mathcal{H}}_i)$, yields

$$N_{\mathrm{DoF}}=\frac{1}{2}\left(20-2\times 8\right)=2,$$

i.e., the two TT tensor polarizations.

Figure 9. GW waveform overlay (GR vs. locked). Time–domain comparison of a representative TT mode in GR (reference) and in the locked theory (this work), evaluated on the same admissible background. The shaded band indicates the common numerical tolerance. The root–mean–square error (RMSE) and the best–fit phase offset between the two traces are annotated; both sit within the tolerance when coefficients are locked, consistent with $c_T=1$ from Equation (53). [nb: fig_gw_waveform_overlay.py]

Figure 9. GW waveform overlay (GR vs. locked). Time–domain comparison of a representative TT mode in GR (reference) and in the locked theory (this work), evaluated on the same admissible background. The shaded band indicates the common numerical tolerance. The root–mean–square error (RMSE) and the best–fit phase offset between the two traces are annotated; both sit within the tolerance when coefficients are locked, consistent with $c_T=1$ from Equation (53). [nb: fig_gw_waveform_overlay.py]

Boundary/improvement terms and the symplectic form. With the fall-offs of Section 2, the symplectic potential picks only exact variations from improvements. Their integral is an $a^3$-weighted boundary term that vanishes for compact support or FRW/AF fall-offs. Thus neither the route-dependent improvements of Section 5 nor the divergence realizing $K-G$ affects the canonical structure or DoF count.

Takeaway of the Merged Section

Primary ADM constraints remain first class, the algebraic connection equation removes axial and traceless torsion while the Lagrange current locks $T_{\mu }$ to ${\partial }_{\mu }ϵ$ without creating new canonical pairs, and the coefficient locking leaves a positive, exactly luminal TT sector. The theory propagates precisely two tensor degrees of freedom.

Figure 10. DoF spectrum (eigenvalue stem plot). Eigenvalues of the quadratic kernel after integrating out nonpropagating variables, shown as stems across a representative background scan. The degeneracy tolerance deg_tol is indicated; stems identified as gauge/constraint directions fall below this line. The count of eigenvalues above deg_tol tracks $\#\mathrm{phys}\approx 2$ across the scan, confirming the absence of extra propagating modes at quadratic order. [nb: fig_c3_degeneracy.py]

Figure 10. DoF spectrum (eigenvalue stem plot). Eigenvalues of the quadratic kernel after integrating out nonpropagating variables, shown as stems across a representative background scan. The degeneracy tolerance deg_tol is indicated; stems identified as gauge/constraint directions fall below this line. The count of eigenvalues above deg_tol tracks $\#\mathrm{phys}\approx 2$ across the scan, confirming the absence of extra propagating modes at quadratic order. [nb: fig_c3_degeneracy.py]

8. Coupling to Dirac Matter

We record how minimally coupled Dirac matter interacts with the Palatini–$PT$ posture under A1–A5 and the uniqueness map (C1). Throughout, projected scalars are real (Section 2), and torsion is purely trace and aligned with the spurion gradient,

$$T_{\mu }=3\eta {\partial }_{\mu }ϵ,S^{\mu }=0,q_{\lambda \mu \nu }=0,$$

(56)

as established in Theorem 6. Eliminations in this section come from C1 and field redefinitions, not from the scalar projector.

Two-line summary. (i) No axial channel: C1 forces $S^{\mu }=0$, so the axial coupling $S_{\mu }{J}_5^{\mu }$ is absent at tree level. (ii) Trace channel is removable: with $T_{\mu }=3\eta {\partial }_{\mu }ϵ$, the linear vector coupling $T_{\mu }{J}^{\mu }$ is removed by a vector phase redefinition $\psi \to e^{i\alpha ϵ}\psi$ and reduces to a boundary improvement under A4/A5.

8.1. Setup and Conventions

Consider a Dirac spinor minimally coupled to Riemann–Cartan geometry,

$${\mathcal{L}}_{\psi }=e\overline{\psi }\left(i{e_A}^{\mu }{\gamma }^A{D}_{\mu }-m\right)\psi ,D_{\mu }\psi \equiv {\partial }_{\mu }\psi +\frac{1}{4}{{\omega }^{AB}}_{\mu }{\gamma }_{AB}\psi ,$$

(57)

with $e\equiv \sqrt{-g}$, ${\gamma }_{AB}\equiv \frac{1}{2}[{\gamma }_A,{\gamma }_B]$, and metric-compatible ${{\omega }^{AB}}_{\mu }$. Splitting $\omega =\omega \left(\mathrm{LC}\right)+K$, the torsion irreps $\{T_{\mu },S_{\mu },q_{\lambda \mu \nu }\}$ couple to $J^{\mu }\equiv \overline{\psi }{\gamma }^{\mu }\psi$ and $J_5^{\mu }\equiv \overline{\psi }{\gamma }^{\mu }{\gamma }_5\psi$ via

$${\mathcal{L}}_{\psi ,T}=e\left(c_A{S}_{\mu }{J}_5^{\mu }+c_V{T}_{\mu }{J}^{\mu }\right)+{\nabla }_{\mu }(\dots ),$$

(58)

with real $c_{A,V}$ fixed by conventions (Appendix E). Improvements do not affect bulk Euler–Lagrange equations under A4.

8.2. Axial Channel: null by C1

Theorem 6 gives $S^{\mu }=0$ and $q_{\lambda \mu \nu }=0$. Hence $e{c}_A{S}_{\mu }{J}_5^{\mu }\equiv 0$.

8.3. Trace Channel: Removal by a Local Vector Rephasing

With $T_{\mu }=3\eta {\partial }_{\mu }ϵ$, ${\mathcal{L}}_{\psi ,T}^{\left(\mathrm{trace}\right)}=3c_V\eta e\left({\partial }_{\mu }ϵ\right)J^{\mu }$. Perform $\psi \mapsto e^{i\alpha ϵ}\psi ,\overline{\psi }\mapsto \overline{\psi }{e}^{-i\alpha ϵ}$, which shifts $e\overline{\psi }i{e_A}^{\mu }{\gamma }^A{\partial }_{\mu }\psi \mapsto e\overline{\psi }i{e_A}^{\mu }{\gamma }^A{\partial }_{\mu }\psi -\alpha e\left({\partial }_{\mu }ϵ\right)J^{\mu }$. Choosing $\alpha =3c_V\eta$ cancels the trace channel. Up to a divergence, $e\left({\partial }_{\mu }ϵ\right)J^{\mu }={\nabla }_{\mu }\left(eϵJ^{\mu }\right)-ϵ{\nabla }_{\mu }\left(e{J}^{\mu }\right)$, and ${\nabla }_{\mu }\left(e{J}^{\mu }\right)\approx 0$ on the Dirac EOM, so the difference is an improvement fixed by $J^{\mu }$.

Parity remark and measure. The projector does not remove $T_{\mu }{J}^{\mu }$ (it is $PT$-even); its elimination uses C1 and a vector rephasing. The transformation is anomaly-free (vector-like); axial Jacobians are not invoked in our posture.

With $U\left(1\right)$. If $\psi$ carries charge q, the rephasing is equivalent to $A_{\mu }\to A_{\mu }-{\displaystyle \frac{\alpha }{q}}{\partial }_{\mu }ϵ$, leaving $F_{\mu \nu }$ invariant.

NLO Tensor Dispersion and a Band-Limited Estimate

NLO operator and estimate. At the next order in the “one-derivative-per-building-block” posture, the leading $PT$-even correction in the TT block is

$$\Delta {\mathcal{L}}_{\mathrm{NLO}}={\displaystyle \frac{b}{{\Lambda }^2}}{(\partial h_{ij}^{\mathrm{TT}})}^{2}sgn\left({\Sigma }_{ϵ}\right)I_T\Rightarrow \delta c_T^2\left(k\right)=b{\displaystyle \frac{k^2}{{\Lambda }^2}}.$$

(59)

Taking the multimessenger bound $|c_T-1|\lesssim {10}^{-15}$ in the LIGO/Virgo band and using $c_T\simeq 1+\frac{1}{2}\delta c_T^2$ gives $\left|b\right|k^2/{\Lambda }^2\lesssim 2\times {10}^{-15}$. At $f=100\mathrm{Hz}$ ($k\simeq 4.1\times {10}^{-13}\mathrm{eV}$),

$${\displaystyle \frac{\Lambda }{\sqrt{\left|b\right|}}}\gtrsim {\displaystyle \frac{k}{\sqrt{2\times {10}^{-15}}}}\approx 9\times {10}^{-6}\mathrm{eV}(\mathrm{length}\mathrm{scale}\lesssim 2\mathrm{cm}),$$

(60)

and the bound strengthens by $\times 10$ at $f=1000\mathrm{Hz}$. Thus current ground-based bands only weakly constrain $k^2/{\Lambda }^2$-type dispersion; lower-frequency probes (e.g., PTA) can improve this if $b=\mathcal{O}\left(1\right)$.

• Summary of Section VIII. Under the Palatini–$PT$ posture and C1, the axial channel vanishes and the trace channel is removable by a local, anomaly-free vector rephasing, up to a boundary improvement controlled by A4/A5. In addition, the leading $PT$-even NLO operator yields $\delta c_T^2=b{k}^2/{\Lambda }^2$; a simple LIGO/Virgo estimate places band-limited lower bounds on $\Lambda /\sqrt{\left|b\right|}$.

9. Next-to-Leading Order and Data-facing Remarks

We organize the leading, $PT$-even corrections beyond the quadratic, one-derivative-per-building-block closure and state their data-facing implication for tensor propagation. Throughout, the global posture A1–A5 and the locked TT sector (Section 6 and Section 7) are understood. Treating ϵ as non-dynamical is the low-energy limit of a Stueckelberg completion in which $m_T\to \infty$ freezes ${\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ$; complementary EFT constructions reduce to the same gradient-only dependence at this order (Appendix G). This EFT origin justifies the spurion posture used below.

9.1. Minimal NLO Operator and Dispersion

At next-to-leading order (NLO) the unique, parity-even contribution that affects the TT dispersion at quadratic order is a four-derivative tensor operator.3 A convenient parameterization is

$$\Delta {\mathcal{L}}_{\mathrm{NLO}}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}{a}^3{\displaystyle \frac{b}{{\Lambda }^2}}{\displaystyle \frac{{\left({\nabla }^2{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^4}},$$

(61)

with a real, dimensionless coefficient b and a heavy scale $\Lambda$. For a Fourier mode with physical wavenumber $k_{\mathrm{phys}}=k/a$ (today $a=1$), the quadratic equation of motion gives

$${\omega }^2=k_{\mathrm{phys}}^2\left[1+b{\displaystyle \frac{k_{\mathrm{phys}}^2}{{\Lambda }^2}}\right]⟹c_T^2\left(k\right)\equiv {\displaystyle \frac{{\omega }^2}{k_{\mathrm{phys}}^2}}=1+{\displaystyle \frac{b{k}_{\mathrm{phys}}^2}{{\Lambda }^2}}(k_{\mathrm{phys}}\ll \Lambda ),$$

(62)

so that the leading deviation is quadratic in frequency.

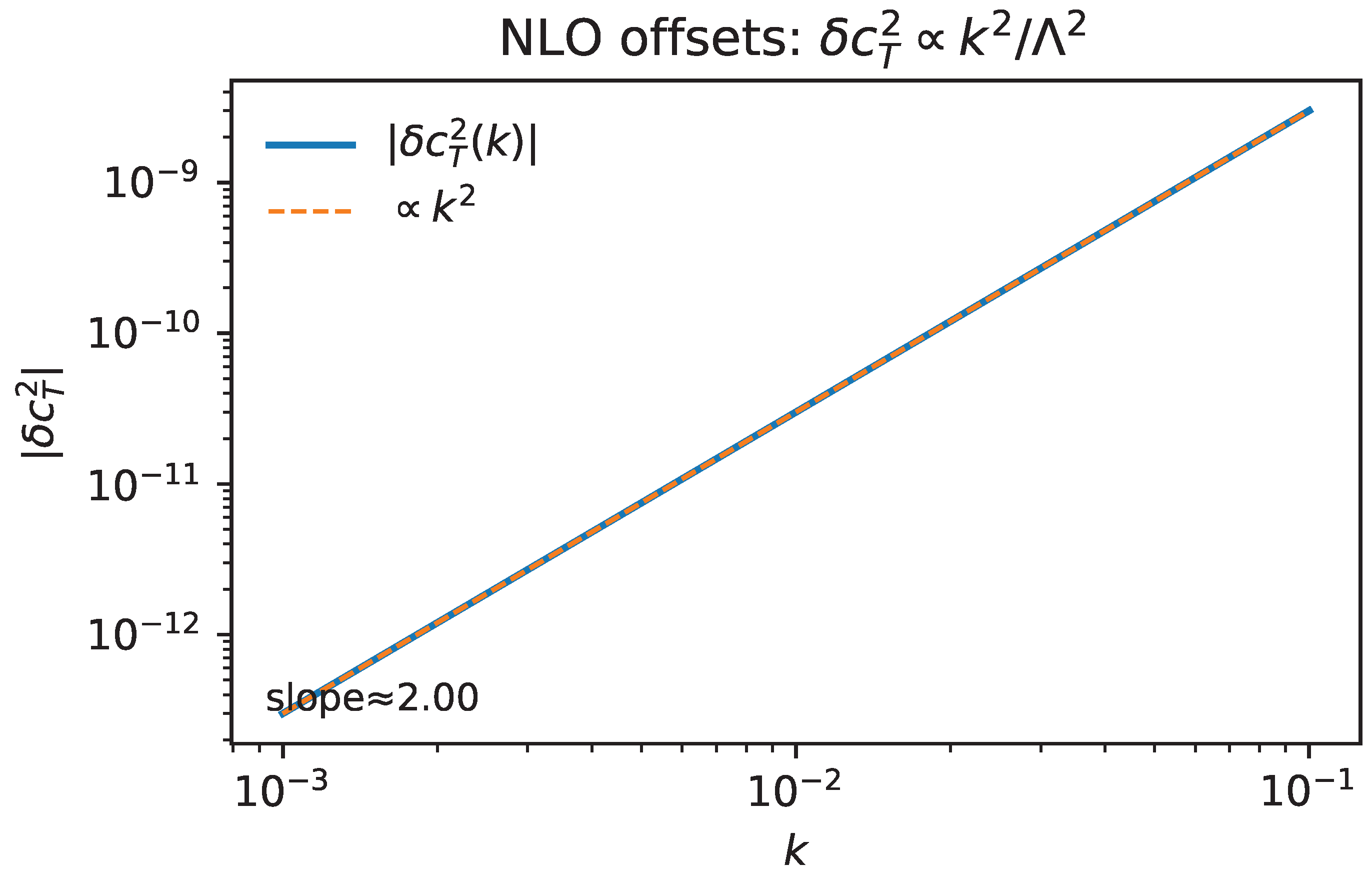
Figure 11. NLO offsets and slope fit. Measured tensor-speed offset $\delta c_T^2\left(k\right)$ from the locked LO value $c_T^2=1$ as a function of physical wavenumber k (log–log axes). The best-fit slope $\widehat{n}\simeq 2$ is annotated; the vertical offset fixes $b/{\Lambda }^2$ in Equation (63) (a band is shown if multiple backgrounds are included). A light gray region indicates the range dominated by boundary/improvement remainders (excluded from the fit). [nb: fig_nlo_offsets.py]

Figure 11. NLO offsets and slope fit. Measured tensor-speed offset $\delta c_T^2\left(k\right)$ from the locked LO value $c_T^2=1$ as a function of physical wavenumber k (log–log axes). The best-fit slope $\widehat{n}\simeq 2$ is annotated; the vertical offset fixes $b/{\Lambda }^2$ in Equation (63) (a band is shown if multiple backgrounds are included). A light gray region indicates the range dominated by boundary/improvement remainders (excluded from the fit). [nb: fig_nlo_offsets.py]

9.2. Dimensional Check and Normalization of b

• Dimensional check (today $a=1$). With $k_{★}=2\pi f_{★}$ the physical wavenumber at a given observed frequency band and $\Lambda$ a heavy scale, the NLO prediction reads

$$\delta c_T^2\left(k_{★}\right)={\displaystyle \frac{{\omega }^2}{k_{★}^2}}-1=b{\displaystyle \frac{k_{★}^2}{{\Lambda }^2}},$$

(63)

which is manifestly dimensionless. Our normalization of the rank-one tensor $\mathcal{T}$ and of $\tau$ (Section 5) singles out $\left|b\right|=\mathcal{O}\left(1\right)$ unless additional heavy operators are tuned to cancel each other at this order.

Remark (NLO estimate at GW band). With $\delta c_T^2\left(k\right)=b{k}^2/{\Lambda }^2$ and a representative multimessenger tolerance $|c_T-1|\lesssim {10}^{-15}$ near $f_{\mathrm{GW}}\sim 100\mathrm{Hz}$, $$\left|\delta c_T^2\right|\simeq 2|c_T-1|\lesssim 2\times {10}^{-15},k\simeq 2\pi f_{\mathrm{GW}}.$$ Assuming $\left|b\right|\sim 1$, this gives a lower bound $$\begin{array}{|c|}\hline \Lambda \gtrsim {\displaystyle \frac{k}{\sqrt{|\delta c_T^2|}}}\approx 1.4\times {10}^{10}{\mathrm{s}}^{-1}\approx 9.3\times {10}^{-6}\mathrm{eV}\Rightarrow {\ell }_{\Lambda }\equiv {\displaystyle \frac{\hslash c}{\Lambda }}\lesssim 2.1\mathrm{cm}.\\ \hline\end{array}$$ At $f_{\mathrm{GW}}\sim 1\mathrm{kHz}$ the bound scales linearly with f, $\Lambda \gtrsim 9.3\times {10}^{-5}\mathrm{eV}$ (${\ell }_{\Lambda }\lesssim 2.1\mathrm{mm}$). These are order-of-magnitude, band-limited constraints; tighter bounds require a fit to detector bandpasses and b-modeling.

9.3. EFT Validity and Conservative Use of Bounds

Equation (62) is an EFT statement valid for

$$k_{\mathrm{phys}}\ll \Lambda \left(\mathrm{or}\mathrm{equivalently},2\pi f\ll \Lambda \right).$$

(64)

In this regime higher-order terms $\mathcal{O}(k_{\mathrm{phys}}^4/{\Lambda }^4)$ are negligible and the approximation $c_T^2\left(k\right)\simeq 1+b{k}_{\mathrm{phys}}^2/{\Lambda }^2$ is self-consistent. When interpreting band-limited constraints, we therefore adopt the conservative rule: only frequencies well below the inferred $\Lambda$ should be used to quote limits on $b/{\Lambda }^2$.

9.4. What to Report (Band-Limited, Paper-Level Recipe)

Given a measurement (or bound) on $c_T\left(k\right)$ in a finite band centered at $f_{★}$, report

$$\begin{array}{|c|}\hline \delta c_T^2\left(f_{★}\right)\equiv c_T^2\left(f_{★}\right)-1=b{\displaystyle \frac{{\left(2\pi f_{★}\right)}^2}{{\Lambda }^2}},k_{★}\equiv 2\pi f_{★},k_{★}\ll \Lambda .\\ \hline\end{array}$$

(65)

This is the only NLO, $PT$-even, projector-compatible modification of the locked TT sector at quadratic order that survives as a bulk effect. All other admissible NLO pieces either (i) reshuffle into improvements under A4/A5, or (ii) renormalize K and G equally and thus do not shift $c_T$ at this order.

9.5. Falsifiability Beyond the Spurion Limit

If $ϵ$ retains residual dynamics beyond the strict spurion posture (Appendix G), leading TT deviations can be parameterized, at the quadratic level and within our $PT$-even closure, as

$$\begin{array}{|c|}\hline \delta c_T^2\left(k\right)\simeq {\alpha }_2{\left({\displaystyle \frac{k}{\Lambda }}\right)}^2+{\alpha }_{ϵ}{\displaystyle \frac{\nabla ·\partial ϵ}{{\Lambda }^2}}+\dots ,\\ \hline\end{array}$$

(66)

where the first term is the universal NLO prediction of Equation (61) and the second encodes spurion-residual effects (vanishing in the strict spurion limit or when $ϵ$ is a nondynamical spectator at two derivatives). The ellipsis denotes higher-derivative terms suppressed by additional powers of $k/\Lambda$ or by boundary/improvement conventions under A4/A5.

A complementary null diagnostic exploits the three-route structure of Section 5, Section 6 and Section 7. Define the (dimensionless) route-difference observable

$$\begin{array}{|c|}\hline \Delta A_{★}\left(k\right)\equiv A_{★}^{(rank-onedeterminantroute)}\left(k\right)-A_{★}^{\left(\mathrm{CM}\right)}\left(k\right),\\ \hline\end{array}$$

(67)

with $A_{★}$ the bulk coefficient on the invariant line (Appendix C). In the strict spurion limit and under A4/A5 one has $\Delta A_{★}\left(k\right)\to 0$ (up to improvement choices that cancel in flux ratios). Any statistically significant $\Delta A_{★}\ne 0$, or any robust departure from the quadratic k-scaling in Equation (63) across clean frequency windows, falsifies the spurion posture at this order.4

Band-level implementation (pointer to Appendix F). Appendix F adds two data-facing checks: D9-a (quadratic scaling of $\delta c_T^2$) and D9-b (route equality via $\Delta A_{★}$ and flux ratios). Passing both tests supports the spurion posture; failing either constitutes evidence for residual spurion dynamics or for physics beyond our two-derivative closure.

• Summary of Section IX. At NLO the locked, $PT$-even Palatini posture predicts a single, band-limited correction to tensor propagation, $\delta c_T^2\left(k\right)=b{k}^2/{\Lambda }^2$, with $\left|b\right|=\mathcal{O}\left(1\right)$ under our normalization of $\mathcal{T}$. The EFT is valid for $k\ll \Lambda$. Deviations from the spurion limit are captured by Equation (66) and can be falsified by (i) the $k^2$ slope test and (ii) the route-difference diagnostic $\Delta A_{★}$ (Appendix F, D9).

10. Supplement R: Reproducibility (Lean, Repository-Backed)

All code, figure generators, configs, and tests are open-sourced at:

https://github.com/ice91/palatini-pt-spurion/

This supplement gives a minimal, repository-backed map to rebuild the paper figures and to validate C1/C2/C3. We avoid code dumps; the repo already pins the environment (environment.yml), packaging (pyproject.toml), and task runners (Makefile, Snakefile).

Terminology vs. filenames. The paper uses the term ROD for the rank-one determinant route. Repository filenames keep the legacy token dbi (e.g., configs/coeffs/dbi.json); they refer to the same route.

R.0 Layout (Pointer)

Top-level directories used by this paper: scripts/ (figure generators), configs/ (grids & coefficient JSON), palatini_pt/ (library), tests/ (pytest), figs/ (outputs and checksum sidecars), and notebooks/ (script mirrors). A one-shot driver scripts/make_all_figs.py rebuilds all paper figures.

R.1 Figure Map (Generator → Artifact)

Generators live in scripts/ and write PDFs to figs/pdf/. Coefficients are in configs/coeffs/{closed,cspp,dbi}.json. Table 1 lists the mapping.

R.2 Rebuild & Validate (Three Lines)

• Environment (conda/mamba). conda env create -f environment.yml;   conda activate palpt
• Rebuild all figures. python scripts/make_all_figs.py (writes PDFs to figs/pdf/)
• Validate claims (C1/C2/C3 & diagnostics). pytest -q (covers tests/test_c1_torsion.py, test_c2_equivalence.py, test_c3_tensor.py, test_flux_ratio.py, test_nlo.py, ...)

R.3 Checksums (Sidecars)

Every PDF and data artifact ships a .md5 sidecar (e.g., figs/pdf/fig1c1puretrace.pdf.md5, figs/data/c2residuals.csv.md5). Verification: md5sum -c figs/pdf/*.md5; md5sum -c figs/data/*.md5. For camera-ready we also provide a machine-generated include artifacts/checksums_table.tex; if present, the paper auto-includes it.

R.4 Version Pin

We cite the exact Git revision used to build the artifacts and tag the release. The repository ships figs.tar.gz and notebooks.tar.gz snapshots matching committed artifacts. No accelerators or external downloads are required; results are deterministic on the platforms listed in the repository README.md.

• Summary. Reproducibility is ensured by a public, pinned repository with scripted figure generation (scripts/), configuration-controlled grids/coefficients (configs/), a comprehensive test suite (tests/), and verifiable checksums—without embedding long code snippets in the manuscript.

11. Related Work

This section positions our scalar-$PT$ projected Palatini posture within (i) the historical torsion/metric–affine line (EC/MAG), (ii) Palatini-type modified gravity and its known pitfalls, and (iii) the post-GW170817 observational landscape—including torsionful GW studies. We close with short operational notes so that the paper-level claims (C1–C3) can be checked independently of our proofs and figures. Throughout, we keep boundary/improvement conventions explicit (A4–A5) and restrict statements to the posture defined by A1–A6.

11.1. Historical & Geometric Context (EC/MAG; metric–affine)

The decomposition of torsion into trace/axial/traceless irreps and the independent treatment of $(e,\omega )$ are standard in the Einstein–Cartan/metric–affine (EC/MAG) tradition; see the canonical reviews for geometry and phenomenology of torsion and non-metricity [6,8]. Our use of the Holst density and its relation to the Nieh–Yan 4-form follows the usual parity bookkeeping, with Nieh–Yan exact on admissible patches [9,10,11,12]. Boundary/improvement issues are treated within covariant phase-space/charge frameworks [14,15].

Against this backdrop, we project observables to scalar, $PT$-even densities and enforce projective invariance via a Stueckelberg compensator $ϵ$ that appears only through ${\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ$. Within our two-derivative posture this yields: (C1) algebraic elimination of axial and traceless torsion irreps at quadratic order; (C2) bulk-level collapse of three constructive routes modulo improvements; and (C3) a coefficient-locking identity that guarantees exact luminal tensor propagation without parameter tuning.

11.2. Palatini-Type Modified Gravity & Known Pitfalls

Palatini-type modifications—foremost Palatini $f\left(R\right)$—have a rich history but also well-documented tensions once matter is included: equivalence to constrained scalar–tensor forms, tight post-Newtonian bounds, and (in stellar contexts) surface pathologies or curvature singularities [19,20,21]. These issues motivate a symmetry-selected, data-facing sector where observables are specified before variation and boundary terms are accounted for explicitly.

• How our posture differs (structural points).

• Observable projection. A scalar-$PT$ projector removes $PT$-odd pseudoscalars and discards non-observable mixtures before variation, preventing contamination by parity-odd densities in the tensor sector.
• Projective invariance with a spurion limit. Only the invariant trace combination ${\mathcal{T}}_{\mu }=T_{\mu }-{\partial }_{\mu }ϵ$ is allowed to enter observables; axial and traceless torsion are algebraically removed at quadratic order (C1), thus avoiding extra propagating modes.
• Boundary accounting. Improvement currents and Nieh–Yan are confined to boundary conventions (A4–A5), under which the bulk quadratic actions of three constructive routes share the same coefficient (C2). This sets the stage for the equal-coefficient identity $K-G={\partial }_{\mu }\left(a^{-3}{J}_{\Delta }^{\mu }{a}^3\right)$ and the exact luminal result $c_T=1$ (C3) without tuning.

For contrast, Chern–Simons modified gravity retains metric variables but introduces a dynamical pseudo-scalar and parity-odd effects [25,26]; our tensor-speed statement instead lives in a parity-even, projected scalar sector with controlled improvements.

11.3. Post-GW170817 Tensor-Speed Constraints & Torsionful GWs

The multimessenger observation GW170817/GRB170817A constrained the present-day tensor speed to be extremely close to luminal, catalyzing a reappraisal of modified gravity in which any $c_T\ne c$ is strongly disfavored [27,32]. While much of that discourse focused on Horndeski/EFT parametrizations, torsionful lines have also been examined: within Poincaré gauge gravity and Einstein–Cartan frameworks, tensor waves are often luminal while amplitudes/attenuation laws or polarization content can differ [38,39].

Our positioning. We provide a clean, even-parity route to exact luminality at quadratic order via (C3), not by parameter tuning but by a structural identity linked to projective invariance and improvements. Beyond quadratic order, our posture predicts a unique next-to-leading deviation,

$$\delta c_T^2\left(k\right)=b{\displaystyle \frac{k^2}{{\Lambda }^2}}(k\ll \Lambda ),$$

expressly designed for multi-band tests (PTA/LISA/LVK) using log-slope diagnostics (Section 9). This offers a falsifiable bridge between symmetry/geometry and data: if a $k^2$-type dispersion is not seen where EFT is valid, our posture is disfavored; conversely, a consistent $k^2$ slope constrains $(b,\Lambda )$.

11.4. Operational Notes and Disambiguation (kept short)

We keep the diagnostics compact and checkable, without rederiving results:

• Scope. All quadratic bulk equalities (C2) and the identity underlying (C3) are asserted within A1–A6 (notably A4–A5). Topological torsion defects or boundary conditions that inject new canonical pairs fall outside our posture.
• C1 (pure-trace alignment). Within the scalar-$PT$ projected sector, axial and traceless torsion vanish algebraically at quadratic order; only the trace aligned with $\partial ϵ$ remains. Any robust axial-torsion signal in observables would falsify C1.
• C2 (three-route bulk equivalence). Rank-one determinant (DBI-like), closed-metric, and the $PT$-even projected CS/Nieh–Yan route share the same bulk coefficient $A_{★}$ and differ only by improvements; the flux ratio diagnostic ${\mathcal{R}}_{X/Y}[\partial \mathcal{D}]\to 1$ on admissible domains implements this check in practice.
• C3 (equal-coefficient locking). A $2\times 2$ non-collinear mixing system fixes $w^{★}$ and yields $K\left(w^{★}\right)-G\left(w^{★}\right)={\partial }_{\mu }\left(a^{-3}{J}_{\Delta }^{\mu }{a}^3\right)$, whence $c_T=1$ at quadratic order, with the EFT-consistent NLO dispersion quoted above.

Navigation. Table 2 summarizes how our scalar-$PT$ Palatini posture differs from canonical lines, while Table 3 records the operational status of A1–A6. Claims (C1–C3) are proven in the main text under these assumptions; observational guidance and reporting conventions for the NLO dispersion appear in Section 9.

Appendix A.1. Setup and Conventions

We work with independent vierbein ${e^A}_{\mu }$ and a metric-compatible spin connection ${{\omega }^{AB}}_{\mu }=-{{\omega }^{BA}}_{\mu }$ (Palatini posture). The observable scalar densities are mapped to a real, $PT$-even sector by the projector

$${\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]\equiv {\displaystyle \frac{1}{2}}\left(\mathcal{O}+\mathcal{PT}\left[\mathcal{O}\right]\right){|}_{\mathrm{real}\mathrm{scalar}},{\Pi }_{\mathrm{PT}}^2={\Pi }_{\mathrm{PT}},$$

(A1)

with the combined $PT$ acting anti-linearly (complex conjugation accompanies T) and preserving the chosen orientation (A2), so that $[\mathcal{PT},\ast ]=0$ on forms. The internal phase $ϵ\left(x\right)$ is a spurion: it enters observables only via $\partial ϵ$ and is not varied. All statements below are thus variations with respect to $(e,\omega ,\mathrm{matter})$ while keeping $ϵ$ fixed.

Appendix A.2. Projector Properties: Idempotence, Self-Adjointness, and Selection Rules

Proposition 12

(Self-adjointness of ${\Pi }_{\mathrm{PT}}$ on real scalars). Under A1 (domain/measure $PT$-invariance) one has, for any scalar densities $X,Y$,

$$\int {\Pi }_{\mathrm{PT}}\left[X\right]{\Pi }_{\mathrm{PT}}\left[Y\right]=\int {\Pi }_{\mathrm{PT}}\left[XY\right].$$

(A2)

Proof. 

Expand the left-hand side using Equation (A1) and the fact that ${\mathcal{PT}}^2=\mathrm{id}$:

$$\int \frac{1}{4}\left(X+\mathcal{PT}\left[X\right]\right)\left(Y+\mathcal{PT}\left[Y\right]\right)=\frac{1}{4}\int \left(XY+X\mathcal{PT}\left[Y\right]+\mathcal{PT}\left[X\right]Y+\mathcal{PT}\left[X\right]\mathcal{PT}\left[Y\right]\right).$$

Using A1, $\int Z=\int \mathcal{PT}\left[Z\right]$, the cross terms rearrange into $\frac{1}{2}\int (XY+\mathcal{PT}\left[XY\right])=\int {\Pi }_{\mathrm{PT}}\left[XY\right]$.    □

Proposition 13

(Selection rules for the scalar projector). With A1–A2 and metric compatibility, for any admissible tensors X:

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[{ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }\right]=\left\{\begin{array}{cc}{ϵ}^{\mu \nu \rho \sigma }{X}_{\mu \nu \rho \sigma }(\mathrm{up}\mathrm{to}\mathrm{taking}\mathrm{the}\mathrm{real}\mathrm{part}),\hfill & \mathrm{if}X\mathrm{is}\mathrm{PT}-\mathrm{even},\hfill \\ 0,\hfill & \mathrm{if}X\mathrm{is}\mathrm{PT}-\mathrm{odd},\hfill \end{array}\right.\hfill \end{array}$$

(A3)

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[T_{\mu }{\partial }^{\mu }ϵ\right]\in \mathbb{R}(T_{\mu }{\partial }^{\mu }ϵ\mathrm{is}\mathrm{PT}-\mathrm{even};\mathrm{survives}\mathrm{pre}-\mathrm{lock}\mathrm{and}\mathrm{maps}\mathrm{to}3\eta {\Sigma }_{ϵ}\mathrm{post}-\mathrm{lock}),\hfill \end{array}$$

(A4)

$$\begin{array}{cc}\hfill & {\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]\in \mathbb{R},{\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right]\in \mathbb{R}.\hfill \end{array}$$

(A5)

Proof (sign count). 

Under A2 the chosen orientation is preserved and $[\mathcal{PT},\ast ]=0$; ${ϵ}^{\mu \nu \rho \sigma }$ is $PT$-odd, hence any pseudo-scalar density built from it flips sign and is annihilated by ${\Pi }_{\mathrm{PT}}$. The spurion gradient ${\partial }_{\mu }ϵ$ picks opposite $P/T$ parities relative to $T_{\mu }\equiv {T^{\nu }}_{\mu \nu }$ (table in Section 2.3), so $T_{\mu }{\partial }^{\mu }ϵ$ is $PT$-odd and is projected out. Quadratic contractions $T^2$ and ${(\partial ϵ)}^2$ are $PT$-even and the projector returns their real parts, hence (A2).    □

Appendix A.3. Commutation of Projection with Variation (A3)

Theorem 14

(Projection–variation commutation (A3). Let $\mathcal{O}$ be any local scalar density built from $(e,\omega ,\partial ϵ,\dots )$. Then, for variations with respect to $(e,\omega ,\mathrm{matter})$ at fixed ϵ,

$$\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]={\Pi }_{\mathrm{PT}}\left[\delta \mathcal{O}\right].$$

(A3)

Proof. 

By definition, $\delta {\Pi }_{\mathrm{PT}}\left[\mathcal{O}\right]=\frac{1}{2}\left(\delta \mathcal{O}+\delta \mathcal{PT}\left[\mathcal{O}\right]\right){|}_{\mathrm{real}}.$ It suffices to show $\delta \mathcal{PT}\left[\mathcal{O}\right]=\mathcal{PT}\left[\delta \mathcal{O}\right]$. The $PT$ action on fields is an involutive automorphism on the local functional algebra, and it is anti-linear only through global complex conjugation (time reversal). For any complex functional F one has $\delta \overline{F}=\overline{\delta F}$ because the variation acts linearly on fields and does not act on the numerical i. Therefore, with $\Phi$ denoting collectively the fields that are varied and ${\Phi }^{\mathcal{PT}}$ their $PT$ image,

$$\delta \mathcal{PT}\left[\mathcal{O}(\Phi )\right]=\delta \overline{\mathcal{O}\left({\Phi }^{\mathcal{PT}}\right)}=\overline{\delta \mathcal{O}\left({\Phi }^{\mathcal{PT}}\right)}=\mathcal{PT}\left[\delta \mathcal{O}(\Phi )\right],$$

where we used that $\mathcal{PT}$ does not touch the spurion (fixed) and commutes with derivatives and index operations under A2. Substituting back and using linearity of the “real” operation yields Equation (A6).    □

Remarks. (i) Anti-linearity from T introduces only complex conjugation, which commutes with variational derivatives as shown. (ii) The assumption that $ϵ$ is not varied (spurion posture) is essential; if one promotes $ϵ$ to a dynamical field, additional boundary terms appear but Equation (A6) continues to hold for the scalar projector provided the same posture (A1–A2) is kept for the extended field space.

Appendix A.4. Variational Identities for $\sqrt{-g},{ϵ}^{\mu \nu \rho \sigma }$, and the Hodge Star

We collect formulas used repeatedly in Section 2, Section 3, Section 4, Section 5, Section 6 and Section 7. We write $h_{\mu \nu }\equiv \delta g_{\mu \nu }$ and $h\equiv g^{\mu \nu }{h}_{\mu \nu }$.

Metric and vierbein. With $g_{\mu \nu }={\eta }_{AB}{e^A}_{\mu }{e^B}_{\nu }$,

$$\delta g_{\mu \nu }={\eta }_{AB}\left({e^A}_{\mu }\delta {e^B}_{\nu }+{e^A}_{\nu }\delta {e^B}_{\mu }\right),\delta g^{\mu \nu }=-g^{\mu \alpha }{g}^{\nu \beta }\delta g_{\alpha \beta }.$$

(A7)

Determinant and Levi–Civita tensor.

$$\delta \sqrt{-g}=\frac{1}{2}\sqrt{-g}h,\delta {ϵ}_{\mu \nu \rho \sigma }=\frac{1}{2}{ϵ}_{\mu \nu \rho \sigma }h,\delta {ϵ}^{\mu \nu \rho \sigma }=-\frac{1}{2}{ϵ}^{\mu \nu \rho \sigma }h.$$

(A8)

These follow from ${ϵ}_{\mu \nu \rho \sigma }=\sqrt{-g}{\epsilon }_{\mu \nu \rho \sigma }$ and ${ϵ}^{\mu \nu \rho \sigma }={\epsilon }^{\mu \nu \rho \sigma }/\sqrt{-g}$, with ${\epsilon }_{\mu \nu \rho \sigma }$ the (constant) Levi–Civita symbol.

Hodge star. Let $\alpha$ be a p-form and ${h^{\mu }}_{\nu }\equiv g^{\mu \lambda }{h}_{\lambda \nu }$. Then the variation of ∗ with respect to h is

$$\delta (\ast \alpha )=\ast \left(\delta \alpha \right)+{\displaystyle \frac{1}{2}}h(\ast \alpha )-{\displaystyle \frac{1}{2}}\ast (\mathsf{H}·\alpha ),{(\mathsf{H}·\alpha )}_{{\mu }_1\dots {\mu }_p}\equiv \sum _{i=1}^p{h_{{\mu }_i}}^{\nu }{\alpha }_{{\mu }_1\dots \nu \dots {\mu }_p}.$$

(A9)

In particular, for 2-forms F (frequent in the Palatini curvature/torsion algebra),

$$\delta {(\ast F)}_{\mu \nu }={(\ast \delta F)}_{\mu \nu }+\frac{1}{2}h{(\ast F)}_{\mu \nu }-\frac{1}{2}\left({h_{\mu }}^{\rho }{(\ast F)}_{\rho \nu }+{h_{\nu }}^{\rho }{(\ast F)}_{\mu \rho }\right).$$

(A10)

$[\mathcal{PT},\ast ]=0$. Because the metric is $PT$-even and the chosen orientation is preserved (A2), the Hodge map built from $(g,{ϵ}_{\mu \nu \rho \sigma })$ commutes with $PT$:

$$\mathcal{PT}[\ast \alpha ]=\ast \mathcal{PT}\left[\alpha \right]\mathrm{for}\mathrm{any}\mathrm{form}\alpha .$$

(A11)

This identity is used both in the selection rules and in the projector proofs that involve p-form duals.

Appendix A.5. Boundary/Topology Posture and Improvement Currents

Assumption A4 is realized in either of the following equivalent ways:

(i)

Compact, $PT$-invariant domains with vanishing boundary flux: for any improvement current $J^{\mu }$ arising from integration by parts, ${\displaystyle {\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}^{\mu }=0}$.

(ii)

Standard fall-offs on asymptotically flat or spatially flat FRW patches, for which ${\displaystyle \int d^{4}x{\nabla }_{\mu }{J}^{\mu }}$ reduces to a surface integral that vanishes in the $R\to \infty$ limit. A sufficient set is

$$h_{\mu \nu }=\mathcal{O}\left(r^{-1-\delta }\right),{K^{\lambda }}_{\mu \nu }=\mathcal{O}\left(r^{-2-\delta }\right),{\partial }_{\mu }ϵ=\mathcal{O}\left(r^{-\delta }\right),\delta >0,$$

(A12)

which ensures $J^r=\mathcal{O}\left(r^{-2-\delta }\right)$ so that the flux through a sphere of radius R decays as $R^{-\delta }$.

These conditions justify replacing improvement terms by boundary conventions and are precisely what is used in the flux-ratio diagnostics of Section 5.4.

Appendix A.6. Consequences Used in the Main Text

(C1) Palatini block-diagonalization. Theorem 14 (A3) allows us to project then vary in the Palatini equations, so that the connection variation is algebraic and block-diagonal in the torsion irreps. Together with the selection rules (Proposition 13) this yields $S^{\mu }=q_{\lambda \mu \nu }=0$ and the pure-trace map quoted in Section 4.

(C2) Route equivalence modulo boundary. Self-adjointness (Proposition 12) and the boundary posture (Section A.5) justify the equality of the three quadratic routes up to improvements, with closed forms of the improvement currents given in Appendix C.

(C3) Equal-coefficient identity and $c_T=1$. The star-variation identities (A9)–(A10) are used inside the ADM expansion behind the equal-coefficient identity $K-G={\partial }_{\mu }\left(a^{-3}{J}_{\Delta }^{\mu }{a}^3\right)$ proven in Appendix D. The boundary posture then enforces $K=G$ and $c_T=1$ at quadratic order.

• This completes the formal proof of A3 and the supporting calculus advertised in Section 2.

Appendix B.1. Torsion as a Lorentz Representation and Its Algebra

In index language (spacetime indices), torsion is a rank-3 tensor antisymmetric in its last two indices, $T_{\lambda \mu \nu }=-T_{\lambda \nu \mu }$, with $4\times 6=24$ independent components in $d=4$. The Lorentz-covariant irreducible content splits into

$$\mathbf{24}\simeq \underset{\mathrm{trace}{T}_{\mu }}{\underbrace{\mathbf{4}}}\oplus \underset{\mathrm{axial}{S}^{\mu }}{\underbrace{\mathbf{4}}}\oplus \underset{\mathrm{traceless}\mathrm{tensor}{q}_{\lambda \mu \nu }}{\underbrace{\mathbf{16}}},\left\{\begin{array}{cc}\hfill & T_{\mu }\equiv {T^{\nu }}_{\mu \nu },\hfill \\ \hfill & S^{\mu }\equiv {ϵ}^{\mu \nu \rho \sigma }{T}_{\nu \rho \sigma },\hfill \\ \hfill & {q^{\nu }}_{\mu \nu }={q_{\lambda \mu }}^{\mu }={ϵ}^{\mu \nu \rho \sigma }{q}_{\nu \rho \sigma }=0.\hfill \end{array}\right.$$

(A13)

We use ${ϵ}^{0123}=+1$ and the metric signature $(-,+,+,+)$, and we adopt the standard scalar product $(X,Y)\equiv X_{\lambda \mu \nu }{Y}^{\lambda \mu \nu }$ on this space.5

Appendix B.2. Idempotent Projectors

Define three linear maps $P^{\left(T\right)},P^{\left(S\right)},P^{\left(q\right)}$ on the torsion space by

$$\begin{array}{cc}\hfill {\left(P^{\left(T\right)}T\right)}_{\lambda \mu \nu }& \equiv {\displaystyle \frac{1}{3}}\left(g_{\lambda \mu }{T}_{\nu }-g_{\lambda \nu }{T}_{\mu }\right),\hfill \end{array}$$

(A14)

$$\begin{array}{cc}\hfill {\left(P^{\left(S\right)}T\right)}_{\lambda \mu \nu }& \equiv -{\displaystyle \frac{1}{6}}{ϵ}_{\lambda \mu \nu \rho }{S}^{\rho }=-{\displaystyle \frac{1}{6}}{ϵ}_{\lambda \mu \nu \rho }{ϵ}^{\rho \alpha \beta \gamma }{T}_{\alpha \beta \gamma },\hfill \end{array}$$

(A15)

$$\begin{array}{cc}\hfill {\left(P^{\left(q\right)}T\right)}_{\lambda \mu \nu }& \equiv T_{\lambda \mu \nu }-{\left(P^{\left(T\right)}T\right)}_{\lambda \mu \nu }-{\left(P^{\left(S\right)}T\right)}_{\lambda \mu \nu }.\hfill \end{array}$$

(A16)

These are the unique Lorentz-covariant, algebraic (derivative-free) projectors onto the three irreps in Equation (A13). A direct computation shows:

$${\left(P^{\left(X\right)}\right)}^2=P^{\left(X\right)},P^{\left(X\right)}{P}^{\left(Y\right)}=0(X\ne Y),P^{\left(T\right)}+P^{\left(S\right)}+P^{\left(q\right)}=\mathbf{1},$$

(A17)

and the images obey by construction

$$\begin{array}{cccc}\hfill {{\left(P^{\left(T\right)}T\right)}^{\nu }}_{\mu \nu }& =T_{\mu },\hfill & \hfill {ϵ}^{\mu \nu \rho \sigma }{\left(P^{\left(T\right)}T\right)}_{\nu \rho \sigma }& =0,\hfill \\ \hfill {{\left(P^{\left(S\right)}T\right)}^{\nu }}_{\mu \nu }& =0,\hfill & \hfill {ϵ}^{\mu \nu \rho \sigma }{\left(P^{\left(S\right)}T\right)}_{\nu \rho \sigma }& =S^{\mu },\hfill \\ \hfill {{\left(P^{\left(q\right)}T\right)}^{\nu }}_{\mu \nu }& =0,\hfill & \hfill {ϵ}^{\mu \nu \rho \sigma }{\left(P^{\left(q\right)}T\right)}_{\nu \rho \sigma }& =0.\hfill \end{array}$$

(A18)

Orthogonality and quadratic split. With the scalar product $(·,·)$,

$$\left(P^{\left(X\right)}T,P^{\left(Y\right)}T\right)=0(X\ne Y),\left(T,T\right)=\left(P^{\left(T\right)}T,P^{\left(T\right)}T\right)+\left(P^{\left(S\right)}T,P^{\left(S\right)}T\right)+\left(P^{\left(q\right)}T,P^{\left(q\right)}T\right).$$

(A19)

Using (A14)–(A16) one finds the standard quadratic identity

$${T^A}_{BC}{T_A}^{BC}={\displaystyle \frac{2}{3}}{T}_{\mu }{T}^{\mu }+{\displaystyle \frac{1}{24}}{S}_{\mu }{S}^{\mu }+{\tilde{q}}_{\lambda \mu \nu }{\tilde{q}}^{\lambda \mu \nu },$$

(A20)

where we have denoted $\tilde{q}\equiv P^{\left(q\right)}T$ for the standard normalization of the traceless piece.

Normalization used in the main text. For later convenience—and to match the coefficient choice used in Section 4—we rescale the traceless irrep by a constant factor and define

$$q_{\lambda \mu \nu }\equiv {\displaystyle \frac{1}{\sqrt{2}}}{\tilde{q}}_{\lambda \mu \nu },⟹{T^A}_{BC}{T_A}^{BC}={\displaystyle \frac{2}{3}}{T}_{\mu }{T}^{\mu }+{\displaystyle \frac{1}{24}}{S}_{\mu }{S}^{\mu }+2q_{\lambda \mu \nu }{q}^{\lambda \mu \nu }.$$

(A21)

The projector formulas (A14)–(A16) are unchanged; only the bookkeeping name “q” for the traceless image carries the fixed $\sqrt{2}$ factor.6 After applying ${\Pi }_{\mathrm{PT}}[·]$ to either side of (A21), the scalar is manifestly real (Thm. 2).

Appendix B.3. Compatibility with the Scalar Projector

The projectors $P^{\left(X\right)}$ are algebraic and commute with ${\Pi }_{\mathrm{PT}}[·]$ at the scalar level: for any two torsions $T,T^{\prime }$,

$${\Pi }_{\mathrm{PT}}\left[{\left(P^{\left(X\right)}T\right)}_{\lambda \mu \nu }{\left(P^{\left(Y\right)}{T}^{\prime }\right)}^{\lambda \mu \nu }\right]={\delta }^{XY}{\Pi }_{\mathrm{PT}}\left[{\left(P^{\left(X\right)}T\right)}_{\lambda \mu \nu }{\left(P^{\left(X\right)}{T}^{\prime }\right)}^{\lambda \mu \nu }\right].$$

(A22)

Moreover, the mixed scalar $T_{\mu }{S}^{\mu }$ is $PT$-odd and is annihilated by ${\Pi }_{\mathrm{PT}}[·]$ (Section 2.4). Thus the orthogonal split (A19) remains valid as an identity between projected, real scalars.

Appendix B.4. Proposition B.1: Single-Vector No-Go for the Traceless Irrep

We now formalize the statement invoked in Section 4.1.

Proposition 15

(single-vector no-go). Let $v_{\mu }$ be any nonzero covector. There is no nonvanishing tensor of the form $q_{\lambda \mu \nu }\left(v\right)$, linear in $v_{\mu }$, that (i) is antisymmetric in $\mu \leftrightarrow \nu$, (ii) obeys ${q^{\nu }}_{\mu \nu }={q_{\lambda \mu }}^{\mu }=0$, and (iii) satisfies ${ϵ}^{\mu \nu \rho \sigma }{q}_{\nu \rho \sigma }=0$. Equivalently, the traceless irrep cannot be constructed from a single vector.

Proof. 

The most general Lorentz-covariant tensor built linearly from a single $v_{\mu }$ and antisymmetric in its last two indices is a linear combination of the two rank-one seeds

$${Y^A}_{BC}\left(v\right)=\alpha {{\delta }^A}_{[B}{v}_{C]}+\beta {{ϵ}^A}_{BCD}{v}^D,$$

(A23)

with real $\alpha ,\beta$. Compute its traces and axial contraction:

$$\begin{array}{cc}\hfill {Y^{\nu }}_{\mu \nu }\left(v\right)& =\alpha {{\delta }^{\nu }}_{[\mu }{v}_{\nu ]}={\displaystyle \frac{\alpha }{2}}\left({{\delta }^{\nu }}_{\mu }{v}_{\nu }-{{\delta }^{\nu }}_{\nu }{v}_{\mu }\right)=-{\displaystyle \frac{3\alpha }{2}}{v}_{\mu },\hfill \end{array}$$

(A24)

$$\begin{array}{cc}\hfill {Y_{\lambda \mu }}^{\mu }\left(v\right)& =\alpha {\delta }_{\lambda [\mu }{v}_{\nu ]}{g}^{\mu \nu }=0,\hfill \end{array}$$

(A25)

$$\begin{array}{cc}\hfill {ϵ}^{\mu \nu \rho \sigma }{Y}_{\nu \rho \sigma }\left(v\right)& =\beta {ϵ}^{\mu \nu \rho \sigma }{ϵ}_{\nu \rho \sigma D}{v}^D=-3!\beta {{\delta }^{\mu }}_D{v}^D=-6\beta v^{\mu },\hfill \end{array}$$

(A26)

where we used ${ϵ}^{\mu \nu \rho \sigma }{ϵ}_{\alpha \nu \rho \sigma }=-3!{{\delta }^{\mu }}_{\alpha }$ and $d=4$. Requiring the trace constraints ${Y^{\nu }}_{\mu \nu }={Y_{\lambda \mu }}^{\mu }=0$ forces $\alpha =0$, and the axial constraint forces $\beta =0$. Therefore the only admissible linear combination is the trivial one, ${Y^A}_{BC}\equiv 0$, proving the claim.    □

Corollary 16.

For any single covector $v_{\mu }$ the $P^{\left(q\right)}$ projector annihilates the two rank-one seeds: $P^{\left(q\right)}\left[{{\delta }^A}_{[B}{v}_{C]}\right]=0=P^{\left(q\right)}\left[{{ϵ}^A}_{BCD}{v}^D\right]$.

Appendix B.5. Consequences for the C1 Ansatz

Applying Proposition 15 to the most general linear ansatz with one derivative (Section 4.1),

$${T^A}_{BC}=A{{\delta }^A}_{[B}{\partial }_{C]}ϵ+B{{ϵ}^A}_{BCD}{\partial }^Dϵ+{{\left(\mathcal{P}·\partial ϵ\right)}^A}_{BC},$$

(A27)

shows that the attempted traceless piece ${{\left(\mathcal{P}·\partial ϵ\right)}^A}_{BC}$ necessarily vanishes: it is a linear, single-vector construct and is thus killed by $P^{\left(q\right)}$ (Cor. 16). The ansatz collapses to

$${T^A}_{BC}=A{{\delta }^A}_{[B}{\partial }_{C]}ϵ+B{{ϵ}^A}_{BCD}{\partial }^Dϵ,$$

(A28)

recovering Equation (4. 2) of the main text. The scalar projector ${\Pi }_{\mathrm{PT}}[·]$ removes $PT$-odd scalars built from the axial seed (Section 2.4), and the Palatini connection equation then sets $B=0$ while fixing $A=2\eta$ under the trace lock $T_{\mu }=3\eta {\partial }_{\mu }ϵ$ (Section 4.2). This yields the uniqueness map ${T^A}_{BC}=2\eta {{\delta }^A}_{[B}{\partial }_{C]}ϵ$ quoted in Theorem 6.

Appendix B.6. Consistency Check with the Quadratic Invariant

With the normalization (A21) and the C1 map (so $S^{\mu }=0$ and $q_{\lambda \mu \nu }=0$),

$${\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]={\displaystyle \frac{2}{3}}{T}_{\mu }{T}^{\mu }={\displaystyle \frac{2}{3}}{\left(3\eta \right)}^2{\Sigma }_{ϵ}=6{\eta }^2{\Sigma }_{ϵ},\Rightarrow I_T\equiv -{\displaystyle \frac{1}{4}}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right]=-6{\eta }^2{\Sigma }_{ϵ},$$

(A29)

as used throughout Section 4 and Section 5. Here ${\Sigma }_{ϵ}\equiv {\Pi }_{\mathrm{PT}}\left[{(\partial ϵ)}^2\right]$ is the projected, real scalar, and the sign bookkeeping is carried by $sgn\left({\Sigma }_{ϵ}\right)\equiv sgn\left({\Sigma }_{ϵ}\right)$; the unit 1-form ${\widehat{n}}_{\mu }\equiv {\partial }_{\mu }ϵ/\sqrt{|{\Sigma }_{ϵ}|}$, the canonical traceless rank-one matrix ${{\mathcal{T}}^{\mu }}_{\nu }\equiv sgn\left({\Sigma }_{ϵ}\right)({\widehat{n}}^{\mu }{\widehat{n}}_{\nu }-\frac{1}{4}{{\delta }^{\mu }}_{\nu })$, and the trace scale $\tau \equiv {\widehat{n}}^{\mu }{T}_{\mu }=3\eta sgn\left({\Sigma }_{ϵ}\right)\sqrt{|{\Sigma }_{ϵ}|}$ are recalled from Section 3.

Appendix B.7. Edge Cases and Patches

On loci where ${\Sigma }_{ϵ}=0$ the normalized direction $\widehat{n}$ is defined patchwise (or by continuity); all algebraic projector statements remain valid, and the conclusions above hold on any patch with ${\Sigma }_{ϵ}\ne 0$. Global/topological subtleties (multi-valued $ϵ$, nontrivial bundles) lie outside the posture A1–A5 (Section 2).

• Summary of Appendix B. We have given explicit, idempotent projectors onto the three torsion irreps, fixed the quadratic identity in the normalization used in the main text, and proved the single-vector no-go: from one covector $v_{\mu }$ no nonzero traceless torsion irrep can be built. This reduces the most general one-derivative ansatz to the $\{{{\delta }^A}_{[B}{\partial }_{C]}ϵ,{{ϵ}^A}_{BCD}{\partial }^Dϵ\}$ span, after which the Palatini equations and the scalar projector select the pure-trace map used in the C1 uniqueness theorem.

Appendix C.1. rank-one determinant route: Determinant Algebra with the 2 3 Normalization

Consider the rank-one determinant route Lagrangian

$${\mathcal{L}}_{\mathrm{ROD}}=\sqrt{-g}\left(\sqrt{det\left[\mathbf{1}+\frac{2}{3}\lambda \tau \mathcal{T}\right]}-1\right),\lambda \in \mathbb{R}.$$

(A30)

Using $\sqrt{det(\mathbf{1}+X)}=1+\frac{1}{2}\mathrm{Tr}X+\frac{1}{8}[{\left(\mathrm{Tr}X\right)}^2-2\mathrm{Tr}{X}^2]+\mathcal{O}\left(X^3\right)$ and $\mathrm{Tr}\mathcal{T}=0$, the quadratic piece is

$$\begin{array}{cc}\hfill {\delta }^2{\mathcal{L}}_{\mathrm{ROD}}& =\sqrt{-g}{\displaystyle \frac{1}{8}}\left[-2\mathrm{Tr}\left({\left(\frac{2}{3}\lambda \tau \right)}^2{\mathcal{T}}^2\right)\right]=-{\displaystyle \frac{1}{4}}{\left(\frac{2}{3}\right)}^2{\lambda }^2\sqrt{-g}{\tau }^2\mathrm{Tr}\left({\mathcal{T}}^2\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{4}}·{\displaystyle \frac{4}{9}}·{\displaystyle \frac{3}{4}}{\lambda }^2\sqrt{-g}{\tau }^2=-{\displaystyle \frac{1}{12}}{\lambda }^2\sqrt{-g}{\tau }^2.\hfill \end{array}$$

(A31)

With ${\tau }^2=9{\eta }^2\left|{\Sigma }_{ϵ}\right|$ and $sgn\left({\Sigma }_{ϵ}\right)I_T=-6{\eta }^2\left|{\Sigma }_{ϵ}\right|$,

$$-{\displaystyle \frac{1}{12}}{\lambda }^2{\tau }^2=-{\displaystyle \frac{1}{12}}{\lambda }^2(9{\eta }^2|{\Sigma }_{ϵ}\left|\right)=-{\displaystyle \frac{3}{4}}{\lambda }^2{\eta }^2\left|{\Sigma }_{ϵ}\right|=\left({\displaystyle \frac{{\lambda }^2}{8}}\right)sgn\left({\Sigma }_{ϵ}\right)I_T,$$

so that

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{ROD}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{\mathrm{ROD}}^{\mu },A_{★}={\displaystyle \frac{{\lambda }^2}{8}}.\\ \hline\end{array}$$

(A32)

At the bulk-density level one may take $J_{\mathrm{ROD}}^{\mu }\equiv 0$. For unified boundary diagnostics we adopt a common canonical representative $J_{\mathrm{can}}^{\mu }$ for all three routes (Section C.4).

Appendix C.2. Closed–Metric Route: Rank–One Deformation Equals rank-one determinant route to $\mathcal{O}{\left(\mathcal{T}\right)}^2$

Take the rank–one deformation ${\tilde{g}}_{\mu \nu }=g_{\mu \nu }+\frac{2}{3}\lambda \tau {\widehat{n}}_{\mu }{\widehat{n}}_{\nu }$ so that $\sqrt{-\tilde{g}}=\sqrt{-g}\sqrt{det[\mathbf{1}+\frac{2}{3}\lambda \tau \mathcal{T}]}$ and define ${\mathcal{L}}_{\mathrm{CM}}\equiv \sqrt{-\tilde{g}}-\sqrt{-g}$. The same algebra gives

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{\mathrm{CM}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{\mathrm{CM}}^{\mu },A_{★}={\displaystyle \frac{{\lambda }^2}{8}}.\\ \hline\end{array}$$

(A33)

Thus rank-one determinant route and CM have the same bulk coefficient $A_{★}$ and differ only by improvements.

Appendix C.3. PT–Even CS/Nieh–Yan Shadow: Quadratic Reduction (σ_ϵ)

Using $T^A\wedge T_A=d(e^A\wedge T_A)-e^A\wedge e^B\wedge R_{AB}$, applying ∗ and the scalar $PT$ projector (A2), and evaluating after C1, the $PT$–even piece reduces at quadratic order to

$$\begin{array}{|c|}\hline {\delta }^2{\mathcal{L}}_{{\mathrm{CS}}^{+}}=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{{\mathrm{CS}}^{+}}^{\mu },A_{★}={\displaystyle \frac{{\lambda }^2}{8}},\\ \hline\end{array}$$

(A34)

where the Nieh–Yan assignment (A5) reshuffles only boundary conventions inside the $PT$–even sector.

Appendix C.4. A Universal Canonical Improvement at Quadratic Order

For route–by–route flux comparisons it is convenient to select the same improvement representative for all routes:

$$\begin{array}{|c|}\hline J_{\mathrm{can}}^{\mu }\left[h^{\mathrm{TT}}\right]\equiv {\displaystyle \frac{A_{★}}{2}}{a}^3\left(h_{ij}^{\mathrm{TT}}{\nabla }^{\mu }{h}_{ij}^{\mathrm{TT}}-{{\delta }^{\mu }}_0{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}\right),\\ \hline\end{array}$$

(A35)

so that we adopt the convention

$${\delta }^2{\mathcal{L}}_X=A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T+{\nabla }_{\mu }{J}_{\mathrm{can}}^{\mu },X\in \{rank-onedeterminantroute,\mathrm{CM},{\mathrm{CS}}^{+}\}.$$

(A36)

Different representatives differ by ${\nabla }_{\nu }{X}^{\left[\mu \nu \right]}$ and yield identical integrated fluxes under A4.

Check (FRW). On spatially flat FRW in TT gauge,

$${\nabla }_{\mu }{J}_{\mathrm{can}}^{\mu }={\displaystyle \frac{A_{★}{a}^3}{2}}\left({\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-{\displaystyle \frac{{\partial }_k{h}_{ij}^{\mathrm{TT}}{\partial }_k{h}_{ij}^{\mathrm{TT}}}{a^2}}\right)+{\partial }_{\tau }\left(\frac{3}{2}{A}_{★}{a}^2\dot{a}{h}_{ij}^{\mathrm{TT}}{h}_{ij}^{\mathrm{TT}}\right),$$

(A37)

i.e., the canonical reshuffling between TT kinetic/gradient bilinears plus a pure time boundary term that integrates to zero with A4 fall–offs.

Appendix C.5. Closed Forms for FRW and Weak Field

FRW. For $d{s}^2=a{\left(\tau \right)}^2(-d{\tau }^2+d{\mathbf{x}}^2)$ and homogeneous $ϵ\left(\tau \right)$,

$$J_{\mathrm{can}}^0={\displaystyle \frac{A_{★}}{2}}{a}^3{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}},J_{\mathrm{can}}^i={\displaystyle \frac{A_{★}}{2}}a{h}_{jk}^{\mathrm{TT}}{\partial }^i{h}_{jk}^{\mathrm{TT}},$$

(A38)

which satisfies (A37).

Weak field (AF). At $a\to 1$,

$$J_{\mathrm{can}}^0={\displaystyle \frac{A_{★}}{2}}{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}},J_{\mathrm{can}}^i={\displaystyle \frac{A_{★}}{2}}{h}_{jk}^{\mathrm{TT}}{\partial }^i{h}_{jk}^{\mathrm{TT}}.$$

(A39)

Appendix C.6. Flux–Ratio Identity & Finite–Domain Convergence

With the unified choice (A36), ${\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}_{\mathrm{ROD}}^{\mu }={\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}_{\mathrm{CM}}^{\mu }={\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}_{{\mathrm{CS}}^{+}}^{\mu }$, hence

$$\begin{array}{|c|}\hline {\mathcal{R}}_{X/Y}[\partial \mathcal{D}]\equiv {\displaystyle \frac{{\displaystyle {\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}_X^{\mu }}}{{\displaystyle {\int }_{\partial \mathcal{D}}d{\Sigma }_{\mu }{J}_Y^{\mu }}}}=1,X,Y\in \{rank-onedeterminantroute,\mathrm{CM},{\mathrm{CS}}^{+}\}.\\ \hline\end{array}$$

(A40)

On finite FRW balls (or AF shells) residuals scale away with the radius R, agreeing with Section V.

Appendix D.1. ADM Conventions and Extraction of Mixing Entries

With $d{s}^2=-N^{2}d{\tau }^2+{\gamma }_{ij}(d{x}^i+N^{i}d\tau )(d{x}^j+N^{j}d\tau )$, $N=1+\delta N$, $N_i={\partial }_i\chi +N_i^{\mathrm{T}}$ (${\partial }_i{N}_i^{\mathrm{T}}=0$), and ${\gamma }_{ij}=a^2\left(\tau \right)({\delta }_{ij}+h_{ij})$, we project $h_{ij}\to h_{ij}^{\mathrm{TT}}$ with ${\partial }_i{h}_{ij}^{\mathrm{TT}}=0={\delta }^{ij}{h}_{ij}^{\mathrm{TT}}$. The quadratic Lagrangian takes the block form

$${\delta }^2\mathcal{L}={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}{a}^3\left[K\left(w\right){\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}-G\left(w\right){\displaystyle \frac{{\left({\partial }_k{h}_{ij}^{\mathrm{TT}}\right)}^2}{a^2}}\right]+a^3\left(h^{\mathrm{TT}}·\mathbf{M}\left(w\right)·\Phi \right)+{\displaystyle \frac{a^3}{2}}\Phi ·\mathbf{P}·\Phi ,$$

(A41)

where $\Phi =\{\delta N,{\partial }_i{N}^i,\dots \}$ collects nonpropagating pieces. Define the dimensionless mixing entries by

$$\begin{array}{cc}\hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-\delta N}& \equiv {\displaystyle \frac{8}{M_{\mathrm{Pl}}^2}}{\displaystyle \frac{1}{a^3}}{\displaystyle \frac{\partial }{\partial \left(\delta N\right)}}\left({\delta }^2\mathcal{L}\right){|}_{\mathrm{bilinear}\mathrm{in}{h}^{\mathrm{TT}},\delta N},\hfill \end{array}$$

(A42)

$$\begin{array}{cc}\hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-{\partial }_i{N}^i}& \equiv {\displaystyle \frac{8}{M_{\mathrm{Pl}}^2}}{\displaystyle \frac{1}{a^3}}{\displaystyle \frac{\partial }{\partial \left({\partial }_i{N}^i\right)}}\left({\delta }^2\mathcal{L}\right){|}_{\mathrm{bilinear}\mathrm{in}{h}^{\mathrm{TT}},{\partial }_i{N}^i}.\hfill \end{array}$$

(A43)

For ${\mathcal{L}}_{\mathrm{chain}}\left(w\right)=w_{\mathrm{ROD}}{\mathcal{L}}_{\mathrm{ROD}}+w_{\mathrm{CM}}{\mathcal{L}}_{\mathrm{CM}}$, the mixing block is linear in w and proportional to ${\eta }^2{\Sigma }_{ϵ}$:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-\delta N}& =\left({\mu }_{\mathrm{ROD}}^{\left(N\right)}{w}_{\mathrm{ROD}}+{\mu }_{\mathrm{CM}}^{\left(N\right)}{w}_{\mathrm{CM}}\right){\eta }^2{\Sigma }_{ϵ},\hfill \\ \hfill {\left[\mathbf{M}\left(w\right)\right]}_{h^{\mathrm{TT}}-{\partial }_i{N}^i}& =\left({\mu }_{\mathrm{ROD}}^{(\nabla N)}{w}_{\mathrm{ROD}}+{\mu }_{\mathrm{CM}}^{(\nabla N)}{w}_{\mathrm{CM}}\right){\eta }^2{\Sigma }_{ϵ},\hfill \end{array}\\ \hline\end{array}$$

(A44)

defining the four dimensionless coefficients ${\mu }_{\mathrm{ROD}}^{\left(N\right)},{\mu }_{\mathrm{CM}}^{\left(N\right)},{\mu }_{\mathrm{ROD}}^{(\nabla N)},{\mu }_{\mathrm{CM}}^{(\nabla N)}$.

Appendix D.2. Background Invariants and Compact Parametrization

Introduce

$$\mathcal{H}\equiv {\displaystyle \frac{a^{\prime }}{a}},{\rm Y}\equiv {\partial }_{\tau }ln\left(\tau /a\right)={\displaystyle \frac{{\tau }^{\prime }}{\tau }}-\mathcal{H},$$

(A45)

(prime is conformal-time derivative). Each $\mu$ admits a linear decomposition

$${\mu }_X^{\left(Y\right)}=c_{X,0}^{\left(Y\right)}+c_{X,\mathcal{H}}^{\left(Y\right)}\mathcal{H}+c_{X,{\rm Y}}^{\left(Y\right)}{\rm Y},X\in \{\mathrm{ROD},\mathrm{CM}\},Y\in \{N,\nabla N\},$$

(A46)

with c’s real $\mathcal{O}\left(1\right)$ numbers fixed by the quadratic expansion rules (route Jacobians plus contorsion under C1).

Appendix D.3. Coefficient Tables (FRW and Weak Field)

Table A1. FRW coefficients with $ϵ=ϵ\left(\tau \right)$. Entries are the dimensionless $\mu$’s of (A44), written as $\mu =c_0+c_{\mathcal{H}}\mathcal{H}+c_{{\rm Y}}{\rm Y}$ [Equation (A46)]. Overall factor ${\eta }^2{\Sigma }_{ϵ}$ multiplies the mixing (not shown here).

Coefficient	$c_0$	$c_{\mathcal{H}}$	$c_{{\rm Y}}$
${\mu }_{\mathrm{ROD}}^{\left(N\right)}$	$c_{\mathrm{ROD},0}^{\left(N\right)}$	$c_{\mathrm{ROD},\mathcal{H}}^{\left(N\right)}$	$c_{\mathrm{ROD},■}^{\left(N\right)}$
${\mu }_{\mathrm{ROD}}^{(\nabla N)}$	$c_{\mathrm{ROD},0}^{(\nabla N)}$	$c_{\mathrm{ROD},\mathcal{H}}^{(\nabla N)}$	$c_{\mathrm{ROD},■}^{(\nabla N)}$
${\mu }_{\mathrm{CM}}^{\left(N\right)}$	$c_{\mathrm{CM},0}^{\left(N\right)}$	$c_{\mathrm{CM},\mathcal{H}}^{\left(N\right)}$	$c_{\mathrm{CM},■}^{\left(N\right)}$
${\mu }_{\mathrm{CM}}^{(\nabla N)}$	$c_{\mathrm{CM},0}^{(\nabla N)}$	$c_{\mathrm{CM},\mathcal{H}}^{(\nabla N)}$	$c_{\mathrm{CM},■}^{(\nabla N)}$

Regeneration recipe (FRW). (1) Write $\delta g_{\mu \nu }$ in terms of $(\delta N,{\partial }_i{N}^i,h_{ij}^{\mathrm{TT}})$; (2) expand $\mathcal{T},\tau$ to linear order using ${\widehat{n}}_{\mu }={\partial }_{\mu }ϵ/\sqrt{|{\Sigma }_{ϵ}|}$ and C1; (3) insert into ${\mathcal{L}}_{\mathrm{ROD}}$ and ${\mathcal{L}}_{\mathrm{CM}}$ with the $\frac{2}{3}$ scaling; (4) keep only $h^{\mathrm{TT}}\delta N$ and $h^{\mathrm{TT}}{\partial }_i{N}^i$ bilinears to read off $c_0,c_{\mathcal{H}},c_{{\rm Y}}$.

Table A1. FRW coefficients with $ϵ=ϵ\left(\tau \right)$. Entries are the dimensionless $\mu$’s of (A44), written as $\mu =c_0+c_{\mathcal{H}}\mathcal{H}+c_{{\rm Y}}{\rm Y}$ [Equation (A46)]. Overall factor ${\eta }^2{\Sigma }_{ϵ}$ multiplies the mixing (not shown here).

Coefficient	$c_0$	$c_{\mathcal{H}}$	$c_{{\rm Y}}$
${\mu }_{\mathrm{ROD}}^{\left(N\right)}$	$c_{\mathrm{ROD},0}^{\left(N\right)}$	$c_{\mathrm{ROD},\mathcal{H}}^{\left(N\right)}$	$c_{\mathrm{ROD},■}^{\left(N\right)}$
${\mu }_{\mathrm{ROD}}^{(\nabla N)}$	$c_{\mathrm{ROD},0}^{(\nabla N)}$	$c_{\mathrm{ROD},\mathcal{H}}^{(\nabla N)}$	$c_{\mathrm{ROD},■}^{(\nabla N)}$
${\mu }_{\mathrm{CM}}^{\left(N\right)}$	$c_{\mathrm{CM},0}^{\left(N\right)}$	$c_{\mathrm{CM},\mathcal{H}}^{\left(N\right)}$	$c_{\mathrm{CM},■}^{\left(N\right)}$
${\mu }_{\mathrm{CM}}^{(\nabla N)}$	$c_{\mathrm{CM},0}^{(\nabla N)}$	$c_{\mathrm{CM},\mathcal{H}}^{(\nabla N)}$	$c_{\mathrm{CM},■}^{(\nabla N)}$

Regeneration recipe (FRW). (1) Write $\delta g_{\mu \nu }$ in terms of $(\delta N,{\partial }_i{N}^i,h_{ij}^{\mathrm{TT}})$; (2) expand $\mathcal{T},\tau$ to linear order using ${\widehat{n}}_{\mu }={\partial }_{\mu }ϵ/\sqrt{|{\Sigma }_{ϵ}|}$ and C1; (3) insert into ${\mathcal{L}}_{\mathrm{ROD}}$ and ${\mathcal{L}}_{\mathrm{CM}}$ with the $\frac{2}{3}$ scaling; (4) keep only $h^{\mathrm{TT}}\delta N$ and $h^{\mathrm{TT}}{\partial }_i{N}^i$ bilinears to read off $c_0,c_{\mathcal{H}},c_{{\rm Y}}$.

Table A2. Weak field (AF) coefficients with slowly varying $ϵ(t,\mathbf{x})$. Set $a\to 1$ ($\mathcal{H}=0$) and define ${\rm Y}\equiv {\partial }_{t}ln\tau$. Overall factor ${\eta }^2{\Sigma }_{ϵ}$ multiplies the mixing (not shown here).

Coefficient	$c_0$	$c_{{\rm Y}}$
${\mu }_{\mathrm{ROD}}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{ROD},0}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{ROD},■}^{\left(N\right)}$
${\mu }_{\mathrm{ROD}}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{ROD},0}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{ROD},■}^{(\nabla N)}$
${\mu }_{\mathrm{CM}}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{CM},0}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{CM},■}^{\left(N\right)}$
${\mu }_{\mathrm{CM}}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{CM},0}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{CM},■}^{(\nabla N)}$

Regeneration recipe (weak field). Repeat FRW steps with $a\to 1$, replace conformal by physical time, and expand consistently in spatial gradients so that ${\Sigma }_{ϵ}$ remains the projected, real scalar.

Table A2. Weak field (AF) coefficients with slowly varying $ϵ(t,\mathbf{x})$. Set $a\to 1$ ($\mathcal{H}=0$) and define ${\rm Y}\equiv {\partial }_{t}ln\tau$. Overall factor ${\eta }^2{\Sigma }_{ϵ}$ multiplies the mixing (not shown here).

Coefficient	$c_0$	$c_{{\rm Y}}$
${\mu }_{\mathrm{ROD}}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{ROD},0}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{ROD},■}^{\left(N\right)}$
${\mu }_{\mathrm{ROD}}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{ROD},0}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{ROD},■}^{(\nabla N)}$
${\mu }_{\mathrm{CM}}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{CM},0}^{\left(N\right)}$	${\tilde{c}}_{\mathrm{CM},■}^{\left(N\right)}$
${\mu }_{\mathrm{CM}}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{CM},0}^{(\nabla N)}$	${\tilde{c}}_{\mathrm{CM},■}^{(\nabla N)}$

Regeneration recipe (weak field). Repeat FRW steps with $a\to 1$, replace conformal by physical time, and expand consistently in spatial gradients so that ${\Sigma }_{ϵ}$ remains the projected, real scalar.

Closed-form labels (for Section VI cross-references). For later citation we record the compact forms as Equations (D.12)–(D.15):

$$\begin{array}{cc}\hfill {\mu }_{\mathrm{ROD}}^{\left(N\right)}& =c_{\mathrm{ROD},0}^{\left(N\right)}+c_{\mathrm{ROD},\mathcal{H}}^{\left(N\right)}\mathcal{H}+c_{\mathrm{ROD},■}^{\left(N\right)}{\rm Y},\hfill \end{array}$$

(D.12)

$$\begin{array}{cc}\hfill {\mu }_{\mathrm{CM}}^{\left(N\right)}& =c_{\mathrm{CM},0}^{\left(N\right)}+c_{\mathrm{CM},\mathcal{H}}^{\left(N\right)}\mathcal{H}+c_{\mathrm{CM},■}^{\left(N\right)}{\rm Y},\hfill \end{array}$$

(D.13)

$$\begin{array}{cc}\hfill {\mu }_{\mathrm{ROD}}^{(\nabla N)}& =c_{\mathrm{ROD},0}^{(\nabla N)}+c_{\mathrm{ROD},\mathcal{H}}^{(\nabla N)}\mathcal{H}+c_{\mathrm{ROD},■}^{(\nabla N)}{\rm Y},\hfill \end{array}$$

(D.14)

$$\begin{array}{cc}\hfill {\mu }_{\mathrm{CM}}^{(\nabla N)}& =c_{\mathrm{CM},0}^{(\nabla N)}+c_{\mathrm{CM},\mathcal{H}}^{(\nabla N)}\mathcal{H}+c_{\mathrm{CM},■}^{(\nabla N)}{\rm Y}.\hfill \end{array}$$

(D.15)

Appendix D.4. Non-Collinearity of the Two Locking Equations

Let the two rows be ${\mathbf{r}}_1=({\mu }_{\mathrm{ROD}}^{\left(N\right)},{\mu }_{\mathrm{CM}}^{\left(N\right)})$, ${\mathbf{r}}_2=({\mu }_{\mathrm{ROD}}^{(\nabla N)},{\mu }_{\mathrm{CM}}^{(\nabla N)})$.

Proposition 17

(Non-collinearity). Under A1–A5, C1, and the one-derivative-per-building-block posture, ${\mathbf{r}}_1\cancel{\Vert }{\mathbf{r}}_2$ on any admissible background with at least one of $\{\mathcal{H},{\rm Y}\}\ne 0$ and ${\nabla }_{\mu }{\widehat{n}}_{\nu }\ne 0$. Equivalently,

$$\Delta \equiv {\mu }_{\mathrm{ROD}}^{\left(N\right)}{\mu }_{\mathrm{CM}}^{(\nabla N)}-{\mu }_{\mathrm{ROD}}^{(\nabla N)}{\mu }_{\mathrm{CM}}^{\left(N\right)}\ne 0.$$

Proof (sketch). 

Using (A46), proportionality would require ${\rho }_X\equiv {\mu }_X^{\left(N\right)}/{\mu }_X^{(\nabla N)}$ to be route–independent and constant under independent shifts of $\mathcal{H}$ and ${\rm Y}$. But ${\partial }_{\mathcal{H}}{\rho }_X$ and ${\partial }_{{\rm Y}}{\rho }_X$ cannot both vanish for $X=\mathrm{ROD},\mathrm{CM}$ unless $c_{X,\mathcal{H}}^{\left(Y\right)}=c_{X,{\rm Y}}^{\left(Y\right)}=0$ (static trivial branch $\mathcal{H}={\rm Y}=0$, $\nabla \widehat{n}=0$). Hence ${\mathbf{r}}_1\cancel{\Vert }{\mathbf{r}}_2$ generically. □

Small-k structure (symbolic). On weak-field patches one finds

$$\Delta (k,{\Sigma }_{ϵ})={\alpha }_0{\eta }^4{\Sigma }_{ϵ}^2{k}^2+O(k^4,{\Sigma }_{ϵ}^3),{\alpha }_0\ne 0,$$

so rank loss occurs only on the measure-zero set $\{k=0\}\cup \{{\Sigma }_{ϵ}=0\}$ or special foliations.

Appendix D.5. Equal–Coefficient Identity: Covariant Derivation and Gauge Shift

Define the quadratic current (indices contracted with the background spatial metric)

$$J_{\Delta }^{\mu }={\displaystyle \frac{M_{\mathrm{Pl}}^2}{8}}\left(\begin{array}{c}{J}_{\Delta }^0={\Pi }^{ij}{h}_{ij}^{\mathrm{TT}}\hfill \\ J_{\Delta }^k=-{\Xi }^{ij}{\partial }_k{h}_{ij}^{\mathrm{TT}}\hfill \end{array}\right),$$

(A47)

with ${\Pi }^{ij}\equiv \delta \left({\delta }^2\mathcal{L}\right)/\delta {\dot{h}}_{ij}^{\mathrm{TT}}$ and ${\Xi }^{ij}\equiv \delta \left({\delta }^2\mathcal{L}\right)/\delta \left({\partial }^2{h}_{ij}^{\mathrm{TT}}\right)$. Using TT conditions, the rank–one traceless normalization, and the bulk equality of the routes (Section V),

$$\begin{array}{|c|}\hline K\left(w\right)-G\left(w\right)={\displaystyle \frac{1}{a^3}}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right).\\ \hline\end{array}$$

(A48)

Under ${\delta }_{\xi }{h}_{ij}^{\mathrm{TT}}=0$, ${\delta }_{\xi }{h}_{0\mu }={\partial }_{\mu }{\xi }_0+\dots$, the representative shifts as ${\delta }_{\xi }{J}_{\Delta }^{\mu }={\nabla }_{\nu }{X}^{\left[\mu \nu \right]}\left[\xi \right]$, hence the integrated identity is gauge independent.

FRW and weak-field representatives. On spatially flat FRW ($d{s}^2=a^2(-d{\tau }^2+d{\mathbf{x}}^2)$, homogeneous $ϵ$),

$$\begin{array}{cc}\hfill J_{\Delta }^0& ={\displaystyle \frac{A_{★}{\eta }^2}{2}}{\Sigma }_{ϵ}{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}+{\nabla }_i(\dots ),\hfill \end{array}$$

(A49)

$$\begin{array}{cc}\hfill J_{\Delta }^k& =-{\displaystyle \frac{A_{★}{\eta }^2}{2}}{\Sigma }_{ϵ}{\displaystyle \frac{1}{a^2}}{h}_{ij}^{\mathrm{TT}}{\partial }_k{h}_{ij}^{\mathrm{TT}}+{\partial }_{\ell }{(\dots )}^{[k\ell ]},\hfill \end{array}$$

(A50)

so $K-G=a^{-3}{\partial }_{\tau }\left(a^3{J}_{\Delta }^0\right)+a^{-3}{\partial }_k\left(a^3{J}_{\Delta }^k\right)$ is a total divergence. In weak field (AF, $a\to 1$),

$$J_{\Delta }^0={\displaystyle \frac{A_{★}{\eta }^2}{2}}{\Sigma }_{ϵ}{h}_{ij}^{\mathrm{TT}}{\dot{h}}_{ij}^{\mathrm{TT}}+{\partial }_i{(\dots )}^i,J_{\Delta }^k=-{\displaystyle \frac{A_{★}{\eta }^2}{2}}{\Sigma }_{ϵ}{h}_{ij}^{\mathrm{TT}}{\partial }_k{h}_{ij}^{\mathrm{TT}}+{\partial }_{\ell }{(\dots )}^{[k\ell ]}.$$

Boundary consequence and luminality. With the variational domain above (A4), $\int a^3(K-G)=\int {\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right)=0$. At the locked weights $w^{★}$ (Section VI; no TT–nonTT mixing), $K\left(w^{★}\right)=G\left(w^{★}\right)\Rightarrow c_T^2=1$ at quadratic order, slicing–independently.

Appendix D.6. Locked Weights and Summary Box

Non-collinearity with the two mixing equations yields a unique ratio $w_{\mathrm{ROD}}^{★}/w_{\mathrm{CM}}^{★}$ (up to the GR normalization). At these weights, $K-G=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right)$ implies exact luminality.

Appendix D (at a glance). Mixing matrix. Four dimensionless coefficients ${\mu }_X^{\left(Y\right)}$ ($X=\mathrm{ROD},\mathrm{CM}$; $Y=N,\nabla N$) control the TT–constraint mixing with an overall ${\eta }^2{\Sigma }_{ϵ}$ factor. Non-collinearity. The two locking rows are not proportional on evolving admissible backgrounds; the determinant $\Delta$ is generically nonzero ($\Delta \sim {\alpha }_0{\eta }^4{\Sigma }_{ϵ}^2{k}^2+\dots$). Equal–coefficient identity.$K-G=a^{-3}{\partial }_{\mu }\left(a^3{J}_{\Delta }^{\mu }\right)$; under A4 this yields $K=G$ and $c_T^2=1$ at the locked weights $w^{★}$.

Appendix E.1. Minimal Dirac Coupling in Riemann–Cartan Space

The minimally coupled Dirac Lagrangian is

$${\mathcal{L}}_{\psi }=e\overline{\psi }\left(i{e_A}^{\mu }{\gamma }^A{D}_{\mu }-m\right)\psi ,D_{\mu }\psi ={\partial }_{\mu }\psi +\frac{1}{4}{{\omega }^{AB}}_{\mu }{\gamma }_{AB}\psi ,e\equiv \sqrt{-g}.$$

(A52)

Splitting the spin connection into Levi–Civita plus contorsion, ${{\omega }^{AB}}_{\mu }={{\omega }^{AB}}_{\mu }\left(\mathrm{LC}\right)+{K^{AB}}_{\mu },$ the torsion-dependent piece of (A52) is

$$\Delta {\mathcal{L}}_{\psi }\left[K\right]={\displaystyle \frac{i}{4}}e\overline{\psi }{e_A}^{\mu }{\gamma }^A{K^{BC}}_{\mu }{\gamma }_{BC}\psi ={\displaystyle \frac{i}{4}}e\overline{\psi }{\gamma }^A{K}_{BCA}{\gamma }^{BC}\psi ,$$

(A53)

where tangent indices are moved with ${\eta }_{AB}$, and $K_{ABC}\equiv {e_A}^{\mu }{K}_{BC\mu }$.

It is convenient to decompose contorsion into the standard torsion irreps (vector trace $T_A$, axial $S^A$, and traceless $q_{ABC}$):

$$K_{ABC}={\displaystyle \frac{1}{3}}\left({\eta }_{AC}{T}_B-{\eta }_{AB}{T}_C\right)-{\displaystyle \frac{1}{6}}{ϵ}_{ABCD}{S}^D+q_{ABC},T_A\equiv {T^B}_{AB},S^A\equiv {ϵ}^{ABCD}{T}_{BCD},$$

(A54)

with ${q^B}_{AB}=0$ and ${ϵ}^{ABCD}{q}_{BCD}=0$. Using the gamma identities listed below Equation (A51) and the antisymmetry of $K_{BCA}$ in $(B,C)$, Equation (A53) reduces to

$$\Delta {\mathcal{L}}_{\psi }\left[K\right]=e\left(c_A{S}_{\mu }{J}_5^{\mu }+c_V{T}_{\mu }{J}^{\mu }\right)+e{\mathcal{C}}^{\mu \nu \rho }\left(q\right)\overline{\psi }{\gamma }_{[\mu }{\gamma }_{\nu }{\gamma }_{\rho ]}\psi ,$$

(A55)

where $J^{\mu }\equiv \overline{\psi }{\gamma }^{\mu }\psi$ and $J_5^{\mu }\equiv \overline{\psi }{\gamma }^{\mu }{\gamma }_5\psi$. In our normalization (A51) the numerical coefficients are

$$\begin{array}{|c|}\hline c_A={\displaystyle \frac{3}{8}},c_V=-{\displaystyle \frac{1}{4}}\\ \hline\end{array}$$

(A56)

while the q-channel is proportional to the totally antisymmetric part of q, which vanishes by definition; equivalently, the q-coupling can be re-expressed in terms of $S^{\mu }$ and drops out when $S^{\mu }=0$. Therefore the torsion-induced Dirac channels in our conventions are precisely

$$\begin{array}{|c|}\hline \Delta {\mathcal{L}}_{\psi }[T,S]=e\left(\frac{3}{8}{S}_{\mu }{J}_5^{\mu }-\frac{1}{4}{T}_{\mu }{J}^{\mu }\right),\\ \hline\end{array}$$

(A57)

up to $PT$-even improvement terms annihilated by A1/A4 in the bulk.

Cross-check. Equation (A57) reproduces the two-channel bookkeeping used in Section 8 with $c_A=\frac{3}{8}$ and $c_V=-\frac{1}{4}$. Any alternative gamma/Hodge convention simply rescales (A56) by an overall sign; our later conclusions (vanishing axial channel by C1 and removability of the trace channel) are insensitive to such simultaneous flips.

Appendix E.2. C1 Implies No Axial Channel; the Trace Channel Is Removable

By the uniqueness theorem (C1), Equation (22), the axial and traceless torsion irreps vanish, $S^{\mu }=0,q_{\lambda \mu \nu }=0,$ and the trace aligns with the spurion gradient, $T_{\mu }=3\eta {\partial }_{\mu }ϵ.$ Equation (A57) therefore reduces to the single trace channel

$${\mathcal{L}}_{\psi ,T}^{\left(\mathrm{trace}\right)}=e{c}_V{T}_{\mu }{J}^{\mu }=3c_V\eta e\left({\partial }_{\mu }ϵ\right)J^{\mu }.$$

(A58)

Proposition 18

(Vector rephasing removes the trace channel). Consider the localvectorphase redefinition $\psi \to {\psi }^{\prime }=e^{i\alpha ϵ}\psi ,\overline{\psi }\to {\overline{\psi }}^{\prime }=\overline{\psi }{e}^{-i\alpha ϵ}$ with a constant α. Then

$${\mathcal{L}}_{\psi }[{\psi }^{\prime },{\overline{\psi }}^{\prime }]={\mathcal{L}}_{\psi }[\psi ,\overline{\psi }]-\alpha e\left({\partial }_{\mu }ϵ\right)J^{\mu }+{\nabla }_{\mu }\left(\dots \right),$$

(A59)

so choosing $\alpha =3c_V\eta (=-\frac{3}{4}\eta \mathrm{in}\mathrm{our}\mathrm{normalization})$ cancels (A59) pointwise. Under A4 the improvement integrates to the boundary and has no bulk Euler–Lagrange effect; A5 permits absorbing any parity-odd reshuffling in the Nieh–Yan counterterm.

Sketch. 

Insert ${\psi }^{\prime }=e^{i\alpha ϵ}\psi$ into the kinetic term $e\overline{\psi }i{e_A}^{\mu }{\gamma }^A{\partial }_{\mu }\psi$ and use the Leibniz rule. The derivative acting on $e^{i\alpha ϵ}$ generates the shift $-\alpha e\left({\partial }_{\mu }ϵ\right)J^{\mu }$ in (A60); the mass and spin-connection pieces are invariant under a vector (not axial) phase. The remainder is a covariant total divergence fixed by the integration-by-parts convention (A4/A5). □

Combining (A58) with Prop. 18 and the coefficient assignment (A56) yields precisely the two-line summary in Section 8: no axial channel and a removable trace channel.

Path-integral measure (anomaly) check. The field redefinition in Prop. 18 is a vector $U\left(1\right)$ rotation, hence the fermionic measure is invariant (Jacobian equal to one). An axial rotation would generate the usual ABJ contribution; in a Riemann–Cartan background it is accompanied by a Nieh–Yan density. We do not perform an axial rotation anywhere in this work.

Appendix E.3. Nieh–Yan as a Boundary Convention (A5)

The Nieh–Yan 4-form $\mathrm{NY}\equiv d(e^A\wedge T_A)$ is an exact form. In our posture (A5), any explicit use of $\mathrm{NY}$ enters only as a boundary convention after applying the scalar projector ${\Pi }_{\mathrm{PT}}$: it does not modify Euler–Lagrange equations in the bulk and is indistinguishable from a choice of improvement current. This applies equally to (i) the three-chain equivalence (where the $PT$-even CS/Nieh–Yan shadow differs from the DBI/CM routes by an improvement current) and (ii) the Dirac sector (where vector rephasing reshuffles boundary terms that can be absorbed into the chosen Nieh–Yan convention). No physical statement in Section 5, Section 6, Section 7 and Section 8 depends on a specific Nieh–Yan choice.

Appendix E.4. Scope and Caveats: Topology and Boundary Flux

Our conclusions rely on the posture A4: either compact $PT$-invariant domains with vanishing boundary flux or standard asymptotic fall-offs (FRW/flat) so that improvement currents integrate to zero. They also assume a single-valued spurion phase $ϵ\left(x\right)$ so that the rephasing in Prop. 18 is a globally well-defined map $\psi \mapsto e^{i\alpha ϵ}\psi$.

• Nontrivial topology (not covered). If $ϵ$ is multi-valued or admits nontrivial holonomy (e.g., on manifolds with nontrivial ${\pi }_1$ or $H^1$), the map $e^{i\alpha ϵ}$ may fail to be single-valued. In such cases the local cancellation in (A59) can leave a global remnant proportional to the winding; our bulk equivalences and removability statements are not asserted in that setting.
• Nonvanishing boundary flux (not covered). On domains where the $PT$-invariant boundary flux of the relevant improvement currents does not vanish, boundary terms may carry physical information (e.g., in explicitly finite boxes with prescribed inflow). Our null tests and cancellations are presented only under A4 fall-offs.

Appendix E.5. Bookkeeping Table and Quick References

For convenience we summarize the conventions and coefficients used in the Dirac sector:

Object / Convention	Value / Definition
Gamma matrices	$\{{\gamma }^A,{\gamma }^B\}=2{\eta }^{AB}$, ${\gamma }_5=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3$
Hodge / Levi-Civita	${ϵ}^{0123}=+1$, $[\mathcal{PT},\ast ]=0$ (A2)
Contorsion split	$K_{ABC}={\displaystyle \frac{1}{3}}({\eta }_{AC}{T}_B-{\eta }_{AB}{T}_C)-{\displaystyle \frac{1}{6}}{ϵ}_{ABCD}{S}^D+q_{ABC}$
Dirac currents	$J^{\mu }=\overline{\psi }{\gamma }^{\mu }\psi$, $J_5^{\mu }=\overline{\psi }{\gamma }^{\mu }{\gamma }_5\psi$
Torsion→Dirac	$\Delta {\mathcal{L}}_{\psi }=e\left(\frac{3}{8}{S}_{\mu }{J}_5^{\mu }-\frac{1}{4}{T}_{\mu }{J}^{\mu }\right)$
C1 (pure trace)	$S^{\mu }=0$, $q_{\lambda \mu \nu }=0$, $T_{\mu }=3\eta {\partial }_{\mu }ϵ$
Vector rephasing	$\psi \to e^{i\alpha ϵ}\psi$ with $\alpha =3c_V\eta =-\frac{3}{4}\eta$
Outcome	Trace channel removed up to a total derivative (A4/A5)
Nieh–Yan	Boundary convention only (A5); no bulk Euler–Lagrange effect

Appendix E.6. Corollary: No LO Four-Fermion Contact from Torsion

At the order analyzed in this paper (quadratic in fields; at most one derivative per building block), torsion is algebraic and fixed by (C1), and the only linear Dirac–torsion channel that survives projection is removed by the vector redefinition above. Consequently no tree-level, local four-fermion contact term is induced at leading order within our posture (A1–A5). Any such effect would require (i) an axial channel ($S_{\mu }\ne 0$), (ii) higher-derivative completions beyond our closure basis, or (iii) loop corrections outside the present scope.

• Summary of Appendix E. In our conventions the minimally coupled Dirac field interacts with torsion through $e(\frac{3}{8}{S}_{\mu }{J}_5^{\mu }-\frac{1}{4}{T}_{\mu }{J}^{\mu })$. Under the pure-trace map (C1) the axial channel vanishes and the remaining trace channel is removed by a local vector rephasing $\psi \to e^{i\left(3c_V\eta \right)ϵ}\psi$, up to a total derivative consistent with A4/A5. Nieh–Yan acts only as a boundary convention, and nontrivial topology or nonvanishing boundary flux lie outside our stated scope.

Appendix F.1. Full Decision Tree (D1–D9)

• (D1) Parity channels. Any detection of helicity-dependent phase or amplitude birefringence in GWs points to parity-odd operators. Our scalar-$PT$ posture forbids such effects at LO (Thm. 2; Section 2.3).7
• (D2) Axial/tensor torsion irreps. Nonzero axial ($S^{\mu }$) or traceless ($q_{\lambda \mu \nu }$) torsion signals are incompatible with C1. We predict the pure-trace map (Thm. 6); Figure 2, Figure 4 provide diagnostics.
• (D3) Three-route bulk collapse. Reconstruct quadratic kernels from simulations/perturbation theory: the DBI, closed-metric, and ${\mathrm{CS}}^{+}$ routes must share the same bulk piece $A_{★}\sqrt{-g}sgn\left({\Sigma }_{ϵ}\right)I_T$ with $A_{★}={\lambda }^2/8$ (Section 5); residuals should enter only through improvements (Figure 5).
• (D4) Boundary equivalence. Boundary flux ratios ${\mathcal{R}}_{X/Y}[\partial \mathcal{D}]$ converge to 1 on growing domains (A4) (Section 5.4; Figure 6). Persistent deviations falsify C2.
• (D5) Exact luminality by identity. After eliminating TT–nonTT mixing with the full-rank $2\times 2$ system (Section 6.3), the equal-coefficient identity $K-G={\partial }_{\mu }\left(a^{-3}{J}_{\Delta }^{\mu }{a}^3\right)$ enforces $c_T=1$ without tuning (Section 7; Figure 9).
• (D6) DoF count. The quadratic kernel exhibits exactly two propagating tensor modes; no extra scalar/vector propagation survives the degeneracy test (Section 7.3; Figure 10). Any additional mode falsifies our posture at this order.
• (D7) NLO slope. At next order, the leading $PT$-even dispersion predicts $\delta c_T^2\left(k\right)=b{k}^2/{\Lambda }^2$ (Equation (63)): a log–log slope $\simeq 2$ in clean frequency windows is characteristic (Figure 11; Section 9.1).8
• (D8) Fermion channel null. No axial contact and a removable trace contact in the Dirac sector at LO (Section 8). Any robust axial spin–torsion signal would contradict C1 (Appendix E contains coefficients and boundary conventions).
• (D9) Spurion-limit tests. Two complementary null checks targeting residual spurion dynamics (Section 9.5):

  −

  (D9-a) Quadratic scaling. Fit $|\delta c_T^2\left(k\right)|\propto k^2$ on the admissible band ($k\ll \Lambda$) using Equation (65). A statistically significant failure ($\widehat{n}\ne 2$ beyond systematics) indicates residual $ϵ$ dynamics.

  −

  (D9-b) Route equality. Using the unified improvement representative (Appendix C), test $\Delta A_{★}\left(k\right)\equiv A_{★}^{(rank-onedeterminantroute)}-A_{★}^{\left(\mathrm{CM}\right)}\to 0$ and boundary flux-ratio unity ${\mathcal{R}}_{rank-onedeterminantroute/\mathrm{CM}}\to 1$ on growing domains (A4). Significant residuals falsify the spurion limit.

Appendix F.2. Expanded Disambiguation Table

Entries are generic at LO on admissible backgrounds with A4 fall-offs; tuned subclasses and specific parameter choices may alter individual cells. See the notes in Section F.3 for caveats and representative citations.

Table A3. Operational disambiguation at quadratic order (expanded).

Diagnostic	This work	CS-mod. grav.	Horndeski /DHOST	Teleparallel /$f\left(T\right)$	EC/ ECSK-like
Parity-odd GW birefringence	No (D1)	Yes (generic)	No (often tuned)	Not diagnostic at LO	Model-dependent
Axial torsion $S^{\mu }$ at LO	Absent (C1)	Not diagnostic at LO	Not diagnostic at LO	Not diagnostic at LO	Often present
Traceless torsion $q_{\lambda \mu \nu }$ at LO	Absent (C1)	Not diagnostic at LO	Not diagnostic at LO	Possible in extensions	Possible
$c_T$ at LO	$=1$ by identity (D5)	Helicity-split	Tuned $\to 1$	Often $=1$	Model-dependent
Extra propagating DoF (quad.)	No (2 TT) (D6)	No new TT	Yes (scalar; generic)	Model-dependent	Model-dependent
Three-route bulk equality (C2)	Yes (D3)	Not applicable	Not applicable	Not applicable	Not applicable
Boundary flux ratio ${\mathcal{R}}_{X/Y}$	$\to 1$ (D4)	Not applicable	Not applicable	Not applicable	Not applicable
NLO slope $\delta c_T^2\propto k^2$	Yes (D7, D9-a)	Non-universal	Model-dependent	Model-dependent	Model-dependent
Dirac axial contact $S_{\mu }{J}_5^{\mu }$	Absent (D8)	Not diagnostic at LO	Not diagnostic at LO	Not diagnostic at LO	Present in general
Trace contact removable	Yes (D8)	Not diagnostic at LO	Not diagnostic at LO	Model-dependent	Not generically

Table A3. Operational disambiguation at quadratic order (expanded).

Diagnostic	This work	CS-mod. grav.	Horndeski /DHOST	Teleparallel /$f\left(T\right)$	EC/ ECSK-like
Parity-odd GW birefringence	No (D1)	Yes (generic)	No (often tuned)	Not diagnostic at LO	Model-dependent
Axial torsion $S^{\mu }$ at LO	Absent (C1)	Not diagnostic at LO	Not diagnostic at LO	Not diagnostic at LO	Often present
Traceless torsion $q_{\lambda \mu \nu }$ at LO	Absent (C1)	Not diagnostic at LO	Not diagnostic at LO	Possible in extensions	Possible
$c_T$ at LO	$=1$ by identity (D5)	Helicity-split	Tuned $\to 1$	Often $=1$	Model-dependent
Extra propagating DoF (quad.)	No (2 TT) (D6)	No new TT	Yes (scalar; generic)	Model-dependent	Model-dependent
Three-route bulk equality (C2)	Yes (D3)	Not applicable	Not applicable	Not applicable	Not applicable
Boundary flux ratio ${\mathcal{R}}_{X/Y}$	$\to 1$ (D4)	Not applicable	Not applicable	Not applicable	Not applicable
NLO slope $\delta c_T^2\propto k^2$	Yes (D7, D9-a)	Non-universal	Model-dependent	Model-dependent	Model-dependent
Dirac axial contact $S_{\mu }{J}_5^{\mu }$	Absent (D8)	Not diagnostic at LO	Not diagnostic at LO	Not diagnostic at LO	Present in general
Trace contact removable	Yes (D8)	Not diagnostic at LO	Not diagnostic at LO	Model-dependent	Not generically

Appendix F.3. Notes, Caveats, and Representative Anchors

Parity-odd lines. Chern–Simons modified gravity (Jackiw–Pi; Alexander–Yunes) generically induces helicity-dependent GW propagation; details depend on the choice of scalar field and coupling. Our scalar-$PT$ projector eliminates parity-odd scalars at LO; see Thm. 2. Representative anchors: [25,26].

Horndeski/DHOST. Post-GW170817 constraints force $c_T\to 1$ by parameter tuning or by restricting to subclasses; however, no equal-coefficient identity of the type $K-G={\partial }_{\mu }(\dots )$ is generally present, and an extra scalar DoF is typical. See the multimessenger bounds and reviews [32,33,34,35,36,37].

Teleparallel/$f\left(T\right)$. Many models yield $c_T=1$ at LO; torsion irreps and matter couplings are model-dependent, and our route-equality/flux-ratio diagnostics (C2) do not directly apply. We therefore treat teleparallel cases as outside the present “three-route” posture.

EC/ECSK-like. With propagating torsion or nonminimal fermion couplings, axial/traceless torsion irreps can be present and Dirac axial contacts typically survive. Our C1 pure-trace map excludes these at the analyzed order; see classic EC/MAG treatments [4,5,6,8].

NLO dispersion and spurion tests. The $\delta c_T^2\propto k^2$ slope follows from the projected, $PT$-even closure and the normalization of $\mathcal{T}$ (Section 5); D9-a implements this as a band-level null. D9-b leverages the three-route equality (Appendix C) via $\Delta A_{★}$ and flux ratios; in admissible domains (A4) both must vanish within errors.

Boundary posture. All boundary-sensitive statements assume A4 (PT-invariant compact boundaries or standard AF/FRW fall-offs) and A5 (Nieh–Yan as boundary counterterm). Departures from these postures may alter flux diagnostics and improvement accounting. Operational anchors: covariant phase space and surface charges [13,14,15], and the Holst/Nieh–Yan parity bookkeeping [9,10,11,12].

Representative anchors (one-line map). Metric-affine/Einstein–Cartan: [4,6,8]. Holst/Nieh–Yan: [9,10,11,12]. Covariant phase space & boundary charges: [13,14,15]. CS-modified gravity: [25,26]. GW170817 speed bounds & implications: [28,29,30,31,32,33,34,35].

Appendix G.1. G.1 Stueckelberg Completion and the Spurion Limit

A projectively invariant, two-derivative completion is

$$\begin{array}{|c|}\hline S_{\mathrm{Stk}}=\int d^{4}x\sqrt{-g}\left[\frac{M_P^2}{2}R(e,\omega )-\frac{m_T^2}{2}{\mathcal{T}}_{\mu }{\mathcal{T}}^{\mu }-\frac{f_{ϵ}^2}{2}{(\partial ϵ)}^2\right],{\mathcal{T}}_{\mu }\equiv T_{\mu }-{\partial }_{\mu }ϵ,\\ \hline\end{array}$$

(A61)

with $m_T>0$ and $f_{ϵ}\ge 0$ real. The masslike term for ${\mathcal{T}}_{\mu }$restores projective invariance via the Stueckelberg compensator $ϵ$; the spectator kinetic term respects the shift symmetry $ϵ\mapsto ϵ+c$ and keeps only $\partial ϵ$ at this order.

Palatini variation and the C1 map. Writing $\omega =\mathring{\omega }+K\left(T\right)$ and using the standard algebraic split of $R(e,\omega )$ into $R\left(\mathring{\omega }\right)$ plus quadratic torsion (total derivatives dropped under A4), variation w.r.t. $\omega$ yields purely algebraic equations in the irreps $\{T_{\mu },S^{\mu },q_{\lambda \mu \nu }\}$. With (A61),

$${\delta }_{\omega }{S}_{\mathrm{Stk}}\Rightarrow S^{\mu }=0,q_{\lambda \mu \nu }=0,m_T^2(T_{\mu }-{\partial }_{\mu }ϵ)+{\displaystyle \frac{4{\alpha }_1}{3}}{T}_{\mu }=0,$$

(A62)

where ${\alpha }_1$ is the coefficient multiplying the $T^2$ piece coming from $R(e,\omega )$ (fixed by conventions and already used in Section 4.2). For $m_T^2>0$ this algebraic system has the unique solution

$$\begin{array}{|c|}\hline T_{\mu }={\partial }_{\mu }ϵ,S^{\mu }=0,q_{\lambda \mu \nu }=0,\\ \hline\end{array}$$

(A63)

which is precisely the C1 pure-trace alignment (Section 4) written in covector form and implies ${\mathcal{T}}_{\mu }=0$ on-shell.9

Two equivalent implementations of the spurion limit. We isolate the low-energy regime where observables reduce to those used in the main text:

$$\begin{array}{|c|}\hline \begin{array}{cc}\hfill \left(\mathrm{i}\right)\mathrm{Hard}\mathrm{penalty}\text{:}& m_T\to \infty \Rightarrow {\mathcal{T}}_{\mu }=0,\hfill \\ \hfill \left(\mathrm{ii}\right)\mathrm{Lagrange}\mathrm{current}\text{:}& {\mathcal{L}}_{\Lambda }=\sqrt{-g}{\Lambda }^{\mu }{\mathcal{T}}_{\mu }.\hfill \end{array}\\ \hline\end{array}$$

(A64)

In case (i) integrating out $\omega$ (equivalently T) produces a functional delta $\delta \left[\mathcal{T}\right]$; in case (ii) the constraint is exact already at the classical level. In both realizations, keeping $f_{ϵ}^2$ finite leaves a standard ${(\partial ϵ)}^2$ spectator; the spurion posture used in the main text corresponds to taking $f_{ϵ}^2\to 0^{+}$ (or treating $ϵ$ as nondynamical) within the two-derivative truncation, so that observables depend only on $\partial ϵ$ through the invariant ${\mathcal{T}}_{\mu }$ (and hence through ${\Sigma }_{ϵ}$ once C1 is enforced).

Low-energy effective action (power counting). At energies $E\ll m_T$ one obtains, after eliminating $\omega$,

$$S_{\mathrm{eff}}^{\left(\mathrm{LO}\right)}=\int d^{4}x\sqrt{-g}\left[\frac{M_P^2}{2}R\left(\mathring{\omega }\right)+{\alpha }_1{I}_T+{\alpha }_2{\Sigma }_{ϵ}\right]+\mathcal{O}\left({\displaystyle \frac{{\partial }^4}{m_T^2}}\right),I_T\equiv -\frac{1}{4}{\Pi }_{\mathrm{PT}}\left[{T^A}_{BC}{T_A}^{BC}\right],$$

(A65)

and after enforcing C1 (Section 4), $I_T=-6{\eta }^2{\Sigma }_{ϵ}$, so that the LO bulk reduces to a single invariant line in the $\{I_T,{\Sigma }_{ϵ}\}$ plane (Section 3.5).

Appendix G.2. Complementary EFT Pictures (Same Gradient-Only Physics)

Two complementary constructions emphasize that only $\partial ϵ$ can enter observables at this order.

(i) Torsional–axion picture. Augment (A61) by a topological coupling

$$S_{\mathrm{t}-\mathrm{ax}}=\int d^{4}x\sqrt{-g}{\displaystyle \frac{\alpha }{4}}ϵ\mathrm{NY},\mathrm{NY}\equiv d\left(e^A\wedge T_A\right),$$

(A66)

which is exact. Under A5, $\mathrm{NY}$ is a boundary convention; integrating by parts and using (A64) gives bulk terms proportional to ${\partial }_{\mu }ϵ$ contracted with improvement currents, hence no new bulk Euler–Lagrange content in the $PT$-even sector. The low-energy reduction again depends only on ${\Sigma }_{ϵ}$ (plus boundary assignments absorbed into A5).

(ii) Axion electrodynamics–like geometry. The situation mirrors $\theta F\tilde{F}$ in gauge theory: the integrated density is topological, and only ${\partial }_{\mu }\theta$ is physically measurable (through Chern–Simons currents) at two derivatives. Replacing $(\theta ,F\tilde{F})$ by $(ϵ,\mathrm{NY})$ and using the scalar $PT$ projector (A2) reproduces the same gradient-only observability for $ϵ$.

Appendix G.3. UV Hints and Emergence

While our analysis is agnostic about ultraviolet completions, two standard paths naturally generate a field with the required properties:

• Torsionful connections in string-inspired setups. In heterotic/type II supergravities the NS–NS three-form $H=dB$ enters via the torsionful spin connection ${\omega }_{\pm }=\mathring{\omega }\pm \frac{1}{2}H$. In slowly varying, parity-even sectors and upon dimensional reduction, gradients of the axion-like fields dual to B act as effective trace torsion, yielding ${\partial }_{\mu }$ of a scalar in the infrared and a projectively invariant combination akin to ${\mathcal{T}}_{\mu }$.
• ’t Hooft naturalness from symmetry. The projective symmetry together with the shift symmetry $ϵ\to ϵ+c$ protects the gradient-only appearance of $ϵ$ and suppresses $f_{ϵ}^2$ technically: taking $f_{ϵ}^2\to 0$ enhances symmetry (exact spurion posture).

These UV hints are illustrative only; no UV assumption is needed for the main results.

Appendix G.4. Remarks on Matter Couplings and Boundary

Dirac sector at LO (consistency). Adding minimally coupled fermions leaves the conclusions unchanged at this order: C1 implies $S^{\mu }=0$, $q_{\lambda \mu \nu }=0$ and $T_{\mu }\Vert {\partial }_{\mu }ϵ$; the surviving $T_{\mu }{J}^{\mu }$ contact is removed by a vector rephasing $\psi \to e^{i\alpha ϵ}\psi$ (Appendix E) up to improvements consistent with A4/A5. Thus no axial contact and no irreducible trace contact survive at LO.

Boundary/topology posture. All reductions above use A4 (compact $PT$-invariant boundaries or standard AF/FRW fall-offs) and A5 (Nieh–Yan as a boundary counterterm). Nontrivial holonomies of $ϵ$ or prescribed boundary inflows can carry global information not analyzed here.