Reframing Graviton Mass and Spin in Emergent Coherence Geometry

1. Introduction

In conventional quantum field theory (QFT), the graviton is modeled as a massless spin-2 particle—an assumption derived from linearized perturbations of the metric tensor in general relativity. Within this linearized framework, perturbations around a flat background yield a symmetric rank-2 tensor field propagating as a quantum excitation with spin-2 and no rest mass. This is viewed as the minimal field-theoretic candidate for mediating the gravitational interaction. String theory further reinforces this perspective by embedding the graviton within the closed string sector, where massless spin-2 excitations emerge naturally from first-quantized string modes.

Despite its mathematical elegance, the assumption of graviton masslessness is not imposed by direct experimental necessity but rather by the requirement for gauge invariance and the avoidance of known theoretical pathologies such as the van Dam–Veltman–Zakharov (vDVZ) discontinuity or the Boulware–Deser ghost in massive gravity models. However, recent developments in gravitational wave astrophysics, precision cosmology, and quantum gravity phenomenology have opened the door to reconsidering this masslessness not as a fundamental feature but as an emergent phenomenon. Observational constraints, such as those from LIGO-Virgo-KAGRA collaborations, now place upper bounds on the graviton mass, but they do not demand strict masslessness.

In this work, we propose a novel conceptual shift: rather than treating graviton mass and spin as intrinsic quantum numbers, we interpret them as emergent properties arising from deeper geometric and coherence-based principles. Specifically, we adopt the Multifaceted Coherence (MC) model and the Dodecahedron Linear String Field Hypothesis (DLSFH) [1,8], which posit that spacetime is underlaid by a discrete, topologically ordered coherence lattice—the Superluminal Graviton Condensate Vacuum (SGCV). Within this framework, mass and spin are not fundamental fields or symmetries, but rather the macroscopic projections of localized tensor coherence deformations across a background structured by high-order dodecahedral symmetry.

This emergent view departs from perturbative string theory by treating spin-2 not as a fixed property of the graviton, but as the lowest-order symmetry-preserving coherence mode of the vacuum. Similarly, graviton mass is not an explicit term in the Lagrangian but is instead interpreted as a second-order curvature response function derived from localized disruptions in tensor coherence. The MC–DLSFH framework therefore allows us to reinterpret mass, spin, and even locality itself as outcomes of deeper coherence-preserving principles—ones that align with causality and unitarity but are not constrained by the limitations of weakly coupled UV completions or perturbative string theory.

Through this lens, the graviton becomes not a fundamental field but a structured coherence artifact: a topological excitation in the quantum vacuum lattice that reflects the minimal symmetry-breaking pathway consistent with long-range information propagation.

1.1. Relation to Swampland Constraints and EFT Breakdown

The emergent interpretation of graviton mass and spin presented in this work also offers an alternative view on long-standing issues associated with the Swampland program in string theory. The Swampland conjectures—such as the Weak Gravity Conjecture (WGC), the Distance Conjecture, and the No Global Symmetries principle—aim to delineate the boundary between low-energy effective field theories (EFTs) that can be consistently embedded in quantum gravity, and those that cannot [6].

Massive spin-2 fields, for instance, are generally believed to lie in the Swampland unless accompanied by an infinite tower of states, as in string theory, or unless carefully constrained by higher-dimensional embeddings. However, in the MC–SGCV framework, mass and spin are not fundamental input parameters within an EFT but instead arise as coherence-driven projections from deeper tensorial order in vacuum geometry. The necessity for a tower of states is automatically satisfied through the natural harmonic extension of coherence modes on the dodecahedral lattice, rather than being imposed externally via compactification or symmetry breaking.

This bypasses the usual EFT cutoff dilemmas because the theory is not organized perturbatively in mass or spin, but hierarchically in terms of coherence modes. Strong coupling is not a pathology here—it is a feature of the superluminal coherence phase space. Moreover, locality is itself an emergent concept, tied to phase-coherent information propagation rather than fundamental metric-based distances.

“In the SGCV model, spin-2 is simply the lowest-coherence mode consistent with causal propagation across a dodecahedral vacuum lattice. Spin-3 and higher modes appear as coherent harmonics, and their activation threshold is governed by curvature-induced decoherence, not by particle-field excitation.” [5]

From this vantage point, much of the Swampland is reinterpreted not as a no-go boundary, but as a region of incomplete phase coherence where tensorial projection rules break down. This calls for a reformulation of what it means for an EFT to be “consistent” with quantum gravity: not merely in terms of UV completion through strings or extra dimensions, but in terms of phase-stable, causality-preserving vacuum structure.

1.2. Causal Propagation and Entropic Flow in SGCV

A central innovation of the SGCV framework is that it redefines causal propagation not in terms of lightcones or metric geodesics, but through the flow of phase-stable coherence encoded in the local tensor structure of the vacuum. Within this model, spacetime is emergent from superluminal graviton condensates that form coherence lattices whose information flows are governed by entropic gradients.

Rather than propagating through a continuous manifold, disturbances in coherence—interpreted as gravitational signals—spread through localized pathways determined by the coherence tensor ${\mathcal{C}}_{\mu \nu }(x,t)$, subject to monotonic decay under entropy increase:

$${\partial }_t{\mathcal{C}}_{\mu \nu }(x,t)=-\kappa (x,t)·{\partial }_{t}S(x,t)$$

(1)

Here, $\kappa (x,t)$ is the local coherence susceptibility, and $S(x,t)$ is the entropy density. When this flow becomes non-differentiable—such as across sharp curvature transitions or coherence collapse thresholds—the local projection of graviton modes breaks down, effectively forming a Swampland horizon beyond which conventional field-theoretic notions of locality and interaction lose meaning.

In these regions, traditional EFT becomes non-viable not because of high energy per se, but due to entropic decoherence. This aligns with the Distance Conjecture in Swampland literature, but recasts the distance not as a geodesic displacement in moduli space, but as a coherence drop-off in vacuum phase space.

“The boundary of EFT validity is not where energy becomes infinite, but where coherence becomes unresolvable.”

This concept introduces a new diagnostic for gravitational and field-theoretic viability: the Coherence Gradient Tensor (CGT), which identifies locations where:

$$|\nabla S(x,t)|>{\sigma }_c\Rightarrow {\mathcal{C}}_{\mu \nu }(x,t)\to 0$$

(2)

This condition marks the breakdown of graviton mode continuity, corresponding to a Swampland-like boundary—not in energy, but in coherence capacity.

2. Mass and Spin in Conventional Theories

In the framework of linearized general relativity, the graviton is modeled as a massless spin-2 field, derived from weak-field perturbations of the Einstein-Hilbert action around flat Minkowski spacetime. This yields a symmetric rank-2 tensor $h_{\mu \nu }$ that satisfies gauge invariance under linearized diffeomorphisms, leading to just two physical degrees of freedom—corresponding to the two transverse polarization states of the graviton. These helicity states ($\pm 2$) are directly analogous to the polarization modes of the photon in electromagnetism, albeit for a spin-2 rather than spin-1 field.

However, introducing a small mass to the graviton fundamentally changes the structure of the theory. A massive spin-2 field carries five degrees of freedom: two transverse-traceless helicity-2 modes, two helicity-1 vector modes, and one scalar (helicity-0) mode. The presence of these additional modes introduces several well-known theoretical challenges.

One major issue is the van Dam–Veltman–Zakharov (vDVZ) discontinuity, which shows that the predictions of massive gravity do not continuously approach those of general relativity in the zero-mass limit [2]. Specifically, the helicity-0 mode does not decouple and leads to observable discrepancies in light bending and perihelion precession—contradicting experimental results unless the graviton mass is exactly zero. Attempts to resolve this via nonlinear interactions led to the development of the Vainshtein mechanism, which screens the helicity-0 mode in high-density regions, but this introduces further complications regarding consistency and predictability.

Another challenge is that massive spin-2 theories generically suffer from strong coupling at relatively low energy scales—far below the Planck scale—meaning that perturbation theory breaks down and the theory loses predictability. Moreover, constructing a ghost-free nonlinear theory of a massive graviton is nontrivial due to the appearance of the Boulware–Deser ghost, an extra scalar degree of freedom with negative kinetic energy that renders the theory unstable.

To address these challenges, de Rham, Gabadadze, and Tolley (dRGT) formulated a class of nonlinear ghost-free massive gravity theories. While dRGT gravity successfully avoids the Boulware–Deser ghost, it still faces questions about ultraviolet (UV) completion and embedding into a consistent high-energy framework, such as string theory.

String theory, in contrast, naturally incorporates a massless spin-2 excitation in the spectrum of closed strings. The masslessness of the graviton arises from the requirement of conformal invariance on the string worldsheet, and its presence is one of the first signs that string theory contains gravity. Crucially, string theory also includes an infinite tower of massive higher-spin states, with increasing masses and spins spaced by the string scale. This tower provides a built-in UV regulator, softening interactions at high energies and resolving many of the divergences encountered in quantum field theory.

However, this resolution comes at a cost: the theory is only well-defined in certain backgrounds, requires compactification to yield a four-dimensional effective theory, and necessitates supersymmetry for anomaly cancellation. Moreover, in all known consistent string compactifications, the graviton remains massless, and no construction has yielded a viable, isolated massive spin-2 state with a large mass gap from the rest of the string spectrum.

Thus, conventional approaches to spin-2 particles remain bifurcated: quantum field theory permits massive gravitons only under stringent consistency conditions, while string theory naturally yields a massless graviton embedded in a higher-dimensional, UV-complete structure. Neither framework fully resolves whether the graviton’s masslessness is fundamental or emergent. This motivates a re-examination of mass and spin from alternative perspectives, such as the coherence-based geometries discussed in this paper.

3. Graviton Mass as Coherence Projection

In MC–SGCV geometry, graviton mass is not fundamental but a response function in curved coherence space. We define:

$$m_g^2\left(x\right)\sim {\displaystyle \frac{{\delta }^2{\mathcal{C}}_{\mu \nu }\left(x\right)}{\delta R_{\alpha \beta }\delta x^{\lambda }}}$$

(3)

where ${\mathcal{C}}_{\mu \nu }\left(x\right)$ is the coherence tensor and $R_{\alpha \beta }$ the local curvature. This view aligns with Markoulakis [4], who interprets graviton mass as emergent from superluminal coherence condensation in curved vacuum lattices.

Figure 1. Coherence lattice geometry used in MC and DLSFH models to define vacuum coherence patterns and symmetry-based projections.

Figure 1. Coherence lattice geometry used in MC and DLSFH models to define vacuum coherence patterns and symmetry-based projections.

4. Spin-2 as a Coherence Symmetry Mode

In the Dodecahedron Linear String Field Hypothesis (DLSFH), spacetime is not modeled as a smooth background continuum but as a discretized, symmetry-rich lattice of coherence nodes. Each node in the lattice corresponds to a localized qubit-like unit, geometrically configured through a dodecahedral symmetry group comprising 20 vertices and 30 edges. These nodes are not merely geometric abstractions—they act as coherence anchors that define the local phase relationships among fundamental field modes. The lattice as a whole forms the underlying informational geometry of the vacuum, from which particle-like excitations and curvature emerge.

Within this framework, the graviton is not treated as a fundamental particle field, but as the lowest-rank tensorial coherence mode that can propagate stably across the lattice. Specifically, the spin-2 mode arises from a symmetric, traceless rank-2 deformation of the coherence tensor ${\mathcal{C}}_{\mu \nu }$, projected across 30-edge link structures in the dodecahedron. This deformation represents the minimal phase-structured oscillation that maintains symmetry while permitting propagation. As such, the spin-2 graviton is interpreted as a collective excitation of the coherence network, not as a standalone particle field with intrinsic quantum numbers.

This interpretation contrasts with standard field theory, where spin is tied to the representations of the Lorentz group and graviton dynamics arise from Lagrangian quantization of the Einstein-Hilbert action. In DLSFH, spin is instead a topological consequence of allowable symmetry-preserving deformations of the vacuum lattice. Thus, spin-2 is not a fixed property, but an emergent symmetry label—defined by the boundary conditions and tensorial structure that preserve coherence across nodes.

Higher-spin excitations emerge naturally as harmonics of the fundamental coherence modes, similar in spirit to the high-spin towers seen in string theory. These harmonics correspond to more complex edge and vertex deformation patterns—such as rank-3 symmetric traceless tensors (spin-3), antisymmetric triplet fields, or spin-4 geometries—all of which exist in the tensor space defined by the lattice topology. Their excitation depends on local entropy gradients, curvature discontinuities, or energetic thresholds within the Superluminal Graviton Condensate Vacuum (SGCV).

Importantly, the DLSFH coherence lattice does not require a truncation at spin-2. Instead, the emergence of higher-spin modes is suppressed dynamically by the curvature coherence scale $\kappa (x,t)$, and only becomes relevant in regions of high spacetime tension or rapid decoherence. This mechanism provides a built-in suppression of ghost modes and exotic fields, while allowing for a graceful transition to higher-order geometries under strong-field conditions—such as near singularities or early-universe topological transitions.

In this view, the graviton as a spin-2 field is simply the lowest-order observable coherence signature permitted by the dodecahedral phase structure. It is not a terminal state, but a default projection mode in regions of stable symmetry. As local coherence breaks down, transitions to spin-3 and higher can occur, albeit transiently and typically nonlocally. These transitions are not random but governed by rules of curvature-coupled coherence evolution, detailed in the coherence tensor flow equation:

$${\partial }_t{\mathcal{C}}_{\mu \nu }(x,t)=-\kappa (x,t)·{\partial }_{t}S(x,t)$$

(4)

where $\kappa (x,t)$ encodes the geometric susceptibility of the lattice to spin-mode perturbations.

This emergent model of spin provides a natural bridge between low-energy gravitational observations and high-dimensional quantum topologies, allowing graviton dynamics to be embedded within a fundamentally geometric and informational substrate. As such, the spin-2 graviton in DLSFH is best understood not as a quantized excitation of a metric, but as a resonant coherence state within a dynamically structured vacuum geometry [1].

5. UV Completion and Causality Constraints

Standard Swampland constraints limit massive spin-2 models [2]. However, the MC framework respects causality and unitarity through local coherence rules:

• Unitarity: ${\sum }_i{P}_i\left(t\right)=1$ maintained via conserved coherence entropy.
• Causality: Propagation of coherence perturbations is spacelike-constrained.

These do not require weakly coupled UV completions, as emphasized in the SGCV work by Markoulakis and Valamontes [5].

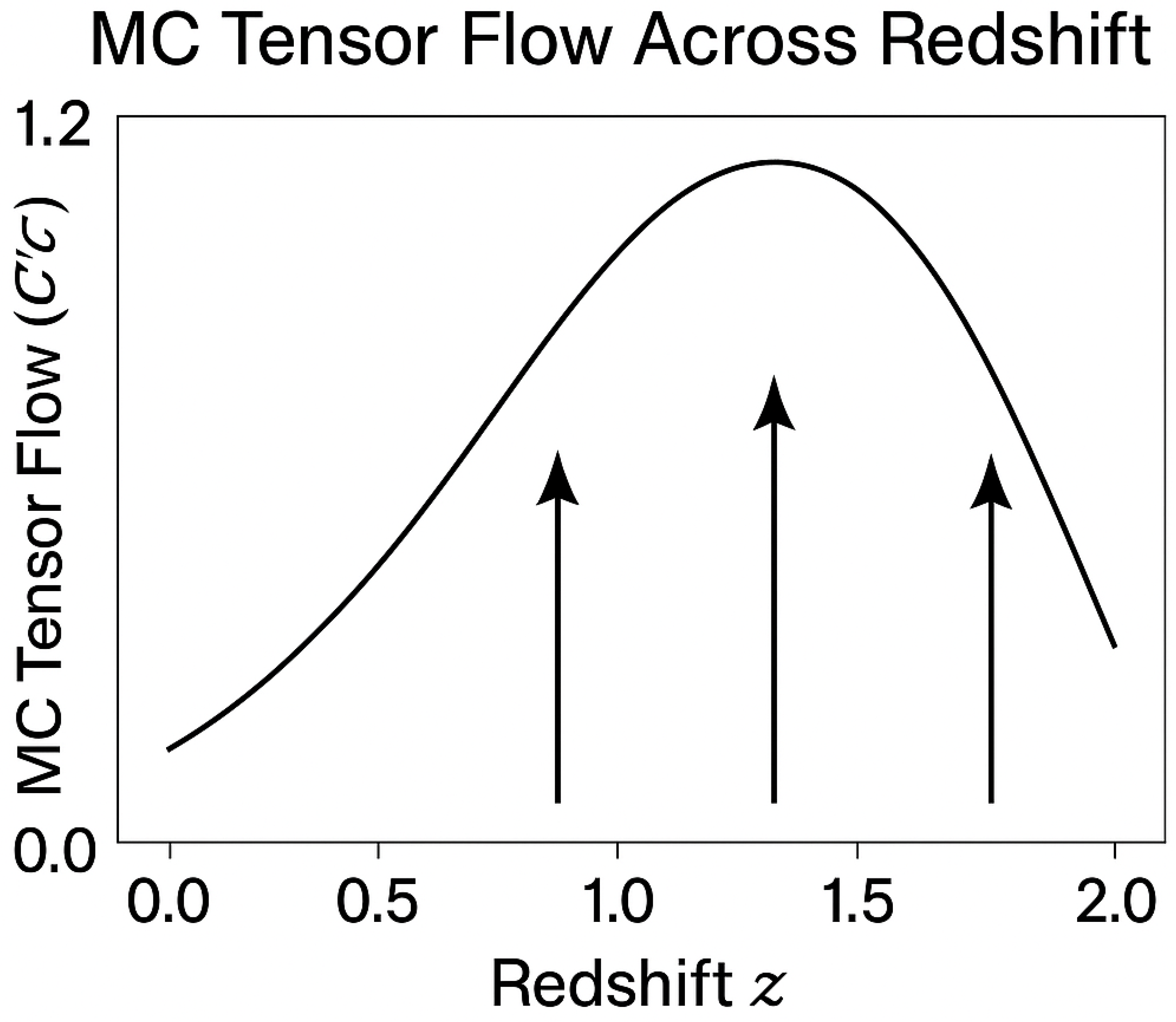
Figure 2. MC tensor coherence evolution across redshift shows structured decay followed by potential recondensation.

Figure 2. MC tensor coherence evolution across redshift shows structured decay followed by potential recondensation.

6. Hierarchy and the “Long Gravity” Conjecture

We hypothesize a coherence-driven hierarchy:

$$m_g<m_{\gamma }<m_{Z,W}$$

(5)

This “Long Gravity Conjecture” suggests that gravity remains the last force active over cosmic distance due to coherence preservation in the SGCV [4]. A graviton with minimal mass would naturally outlast other massive fields in the infrared.

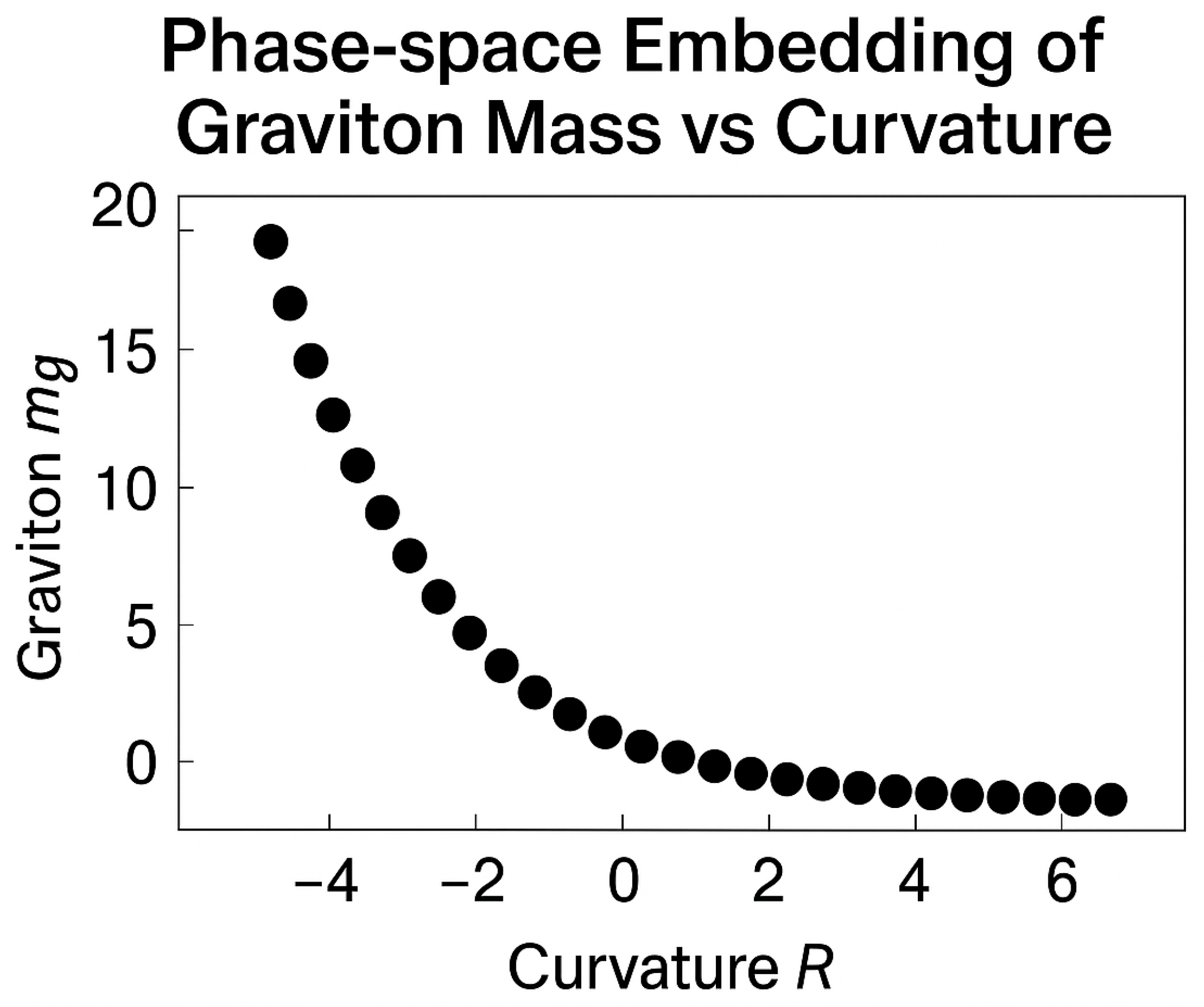
Figure 3. Phase-space embedding showing curvature-coherence transitions as a function of graviton mass. The lower right edge indicates long-distance survival of low-mass coherence states.

Figure 3. Phase-space embedding showing curvature-coherence transitions as a function of graviton mass. The lower right edge indicates long-distance survival of low-mass coherence states.

6.1. Atomic Signatures of Coherence: H-2 to H-3 Transitions

Recent studies have shown that transitions between Hydrogen-2 and Hydrogen-3 isotopes can be coherently mediated by spin-aligned graviton lattices in the SGCV structure, supporting qubit-level projections in atomic vacuum embedding [7].

7. Conclusion

Mass and spin in the graviton sector—traditionally viewed as fundamental and fixed quantum properties—may instead be emergent features of deeper geometric and coherence-based structures. In the framework proposed here, built on the principles of Multifaceted Coherence (MC) and the Dodecahedron Linear String Field Hypothesis (DLSFH), both mass and spin arise not from Lagrangian parameters or gauge symmetries, but from the projection of structured coherence across a vacuum lattice.

This paradigm shift offers a radically different approach to understanding gravitational degrees of freedom. In particular, the spin-2 nature of the graviton is interpreted not as a fundamental representation of the Lorentz group, but as the lowest-order symmetry-preserving mode in a coherence lattice governed by dodecahedral geometry. Graviton mass, similarly, is not introduced by hand via a mass term, but arises from the curvature response of the coherence tensor ${\mathcal{C}}_{\mu \nu }$ under entropy flow. This view naturally aligns with observations while bypassing the theoretical pathologies commonly associated with massive spin-2 fields—such as the vDVZ discontinuity, Boulware–Deser ghosts, and low-scale strong coupling.

The MC–SGCV–DLSFH model also offers a new lens for interpreting Swampland constraints. Rather than treating effective field theory (EFT) breakdown as a failure of UV completion, we reframe it as a breakdown in coherence capacity—a phase-driven boundary where structured vacuum geometry can no longer support graviton-like excitations. This perspective renders traditional Swampland criteria as coherence-based thresholds rather than field-theoretic limits, allowing for stronger connections between low-energy observables and high-energy coherence structure.

Additionally, this framework accommodates hierarchical spin structures and coherence harmonics, suggesting that higher-spin gravitational modes—long considered problematic in field theory—are not only natural, but geometrically required under strong curvature or entropy gradients. These excitations are not free parameters but follow directly from the harmonic content of the lattice geometry, emerging dynamically when coherence structure is distorted.

Ultimately, the MC–DLSFH coherence paradigm reframes gravity not as a force mediated by quantized curvature in smooth spacetime, but as an emergent manifestation of ordered information flow in a quantized vacuum geometry. This approach offers promising paths toward reconciling general relativity, quantum field theory, and string-motivated ideas within a unified, background-independent framework.

These results lay the foundation for a new coherence-based understanding of gravitational phenomena. In the following section, we outline specific future directions—both theoretical and experimental—that build upon this framework and indicate clear next steps for validation and development.

Future Directions

The coherence-based framework developed here opens multiple avenues for further investigation, both at the theoretical frontier and in potential observational validation. One major direction lies in the rigorous formalization of the **coherence tensor algebra** across curved, non-Euclidean vacuum manifolds. While the present work assumes dodecahedral symmetry as a stable coherence base, further study of non-dodecahedral tilings and topological fluctuations could yield new insights into anisotropic or broken-coherence sectors of quantum gravity.

On the phenomenological side, a key challenge is to construct explicit mappings between **coherence gradient thresholds** and known Swampland constraints, particularly the **Swampland Distance Conjecture** and the **Refined de Sitter Conjecture** [9,10,11]. The MC–SGCV formalism offers a candidate mechanism by which phase-space coherence metrics could replace moduli-space geodesics as the dominant diagnostic tool for UV consistency.

Moreover, the emerging **Harlow-Ooguri program** on classifying quantum gravity-consistent theories via constraints on operator algebras and code subspaces presents a promising interface with coherence-based quantization. Specifically, coherence-preserving tensor networks underlying SGCV may serve as concrete implementations of gravitational code subspaces and entanglement wedge reconstruction [12]. These links may clarify how holographic duality and entropic gravity principles emerge naturally from discrete coherence substrates.

Another priority is the extension of the framework to **multi-graviton coherent states** and entangled tensor bundles, as they relate to early-universe dynamics, black hole interiors, and the emergence of time-asymmetry from vacuum information flow. The graviton hierarchy outlined here—beginning with spin-2 and extending through coherence harmonics—may serve as a blueprint for testing predictions in cosmological correlation functions or LIGO/LISA polarization spectrum anomalies.

Finally, the isotope-level coherence effects discussed in the Hydrogen-2 to Hydrogen-3 transition [7] offer a tantalizing opportunity to probe graviton-modulated coherence flows in nuclear systems. High-precision spectroscopy and transition timing analysis may provide indirect signatures of vacuum-mediated coherence reordering and its geometric constraints.

As the coherence tensor framework matures, it may ultimately reframe not only how we approach quantum gravity, but how we define energy, curvature, and causality itself in the presence of structured vacuum information geometry.