Submitted:
14 September 2025
Posted:
16 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
- -
- Up kick versus down kick It is the downkick portion that is the setup in backstroke, while the upkick portion is the propulsive phase. This is the opposite of the Freestyle Kick, but the reality is the same – there is nedeed a great downkick, in order to followthrough with an amazing upkick (Gonzales, L.R. et all, 2023);
- -
- Plantar flexion Just like in the Freestyle Kick, a swimmer should plantarflex their foot while kicking. [....] plantarflexion increases the propulsion a swimmer can create by reducing their drag, increasing the surface area of their foot, and improves their ankle flexibility (Gonzales, L.R. et all, 2023);
- -
- Kick from hips Just like in the Freestyle kick, a swimmer should initiate the Backstroke kick from their hips. The ideal amount of knee bend is the same between these two kicks and that’s about 120degrees of knee bend. You don’t need anymore knee bend than that, and any less—won’t generate much propulsion in your kick at all (Gonzales, L.R. et all, 2023).
2. Material and Methods
3. Result and Discussion
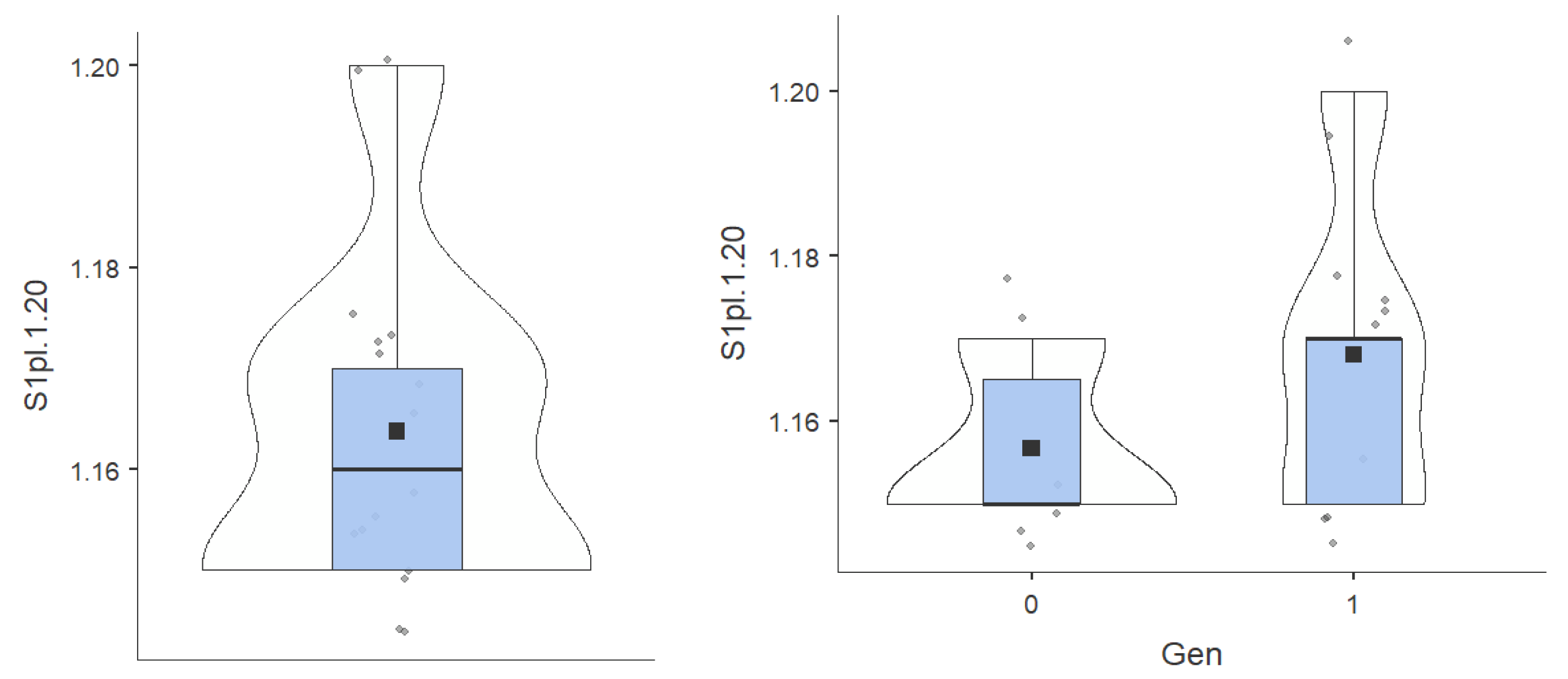
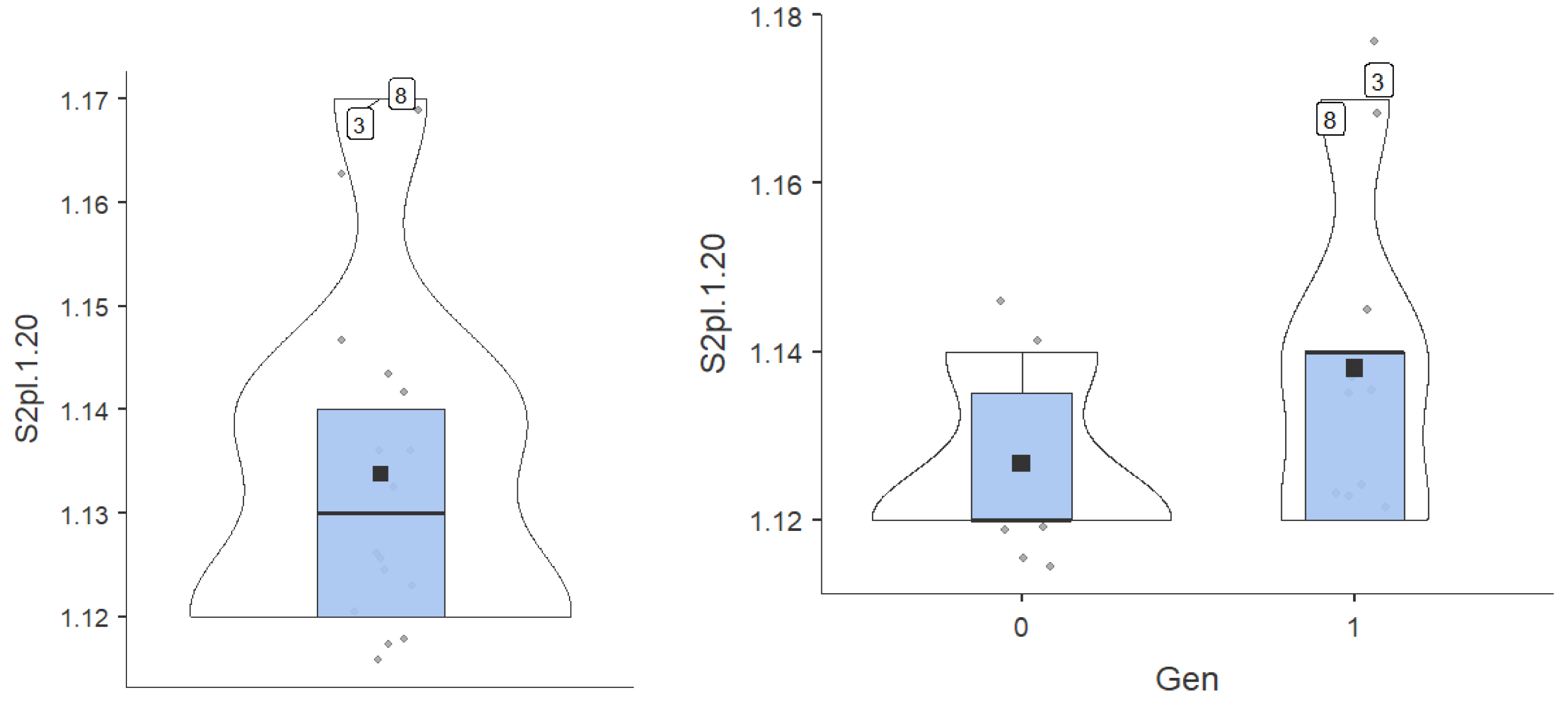
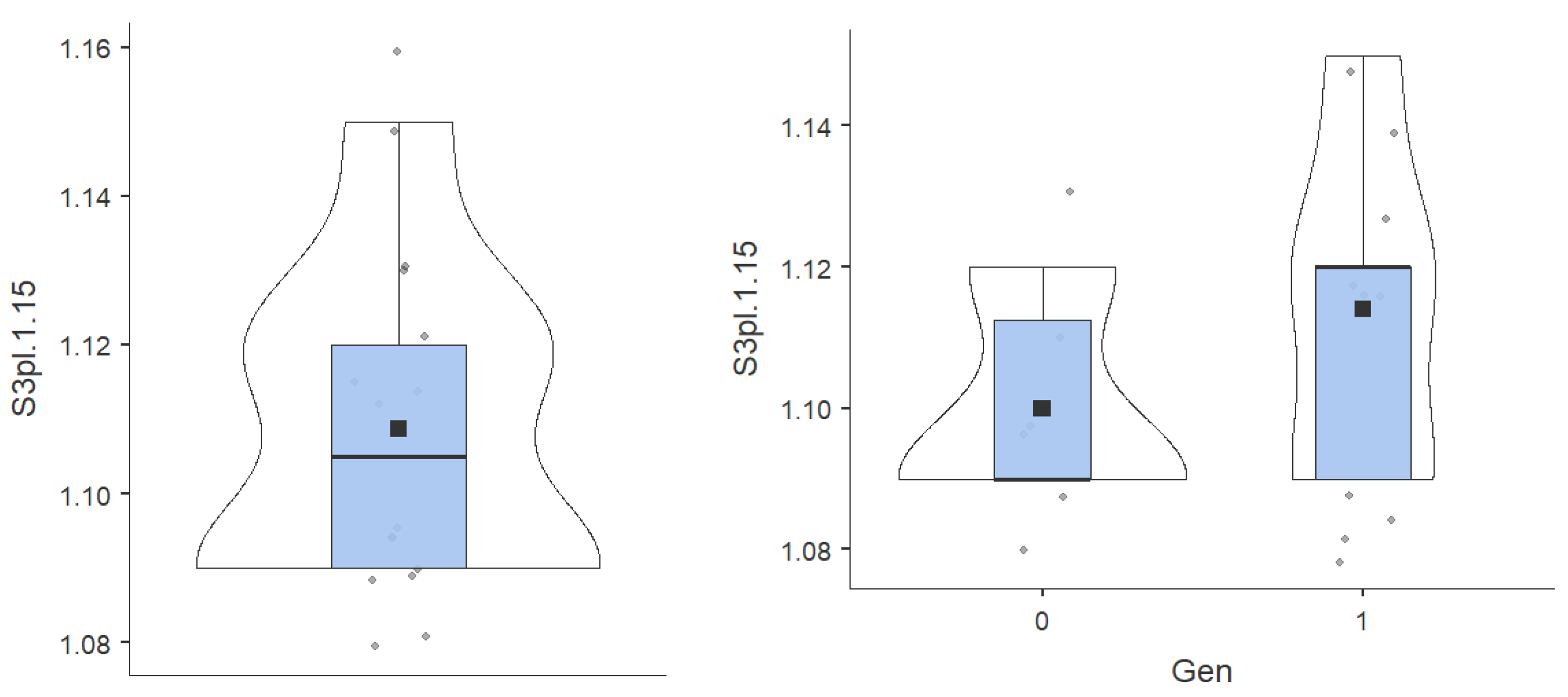
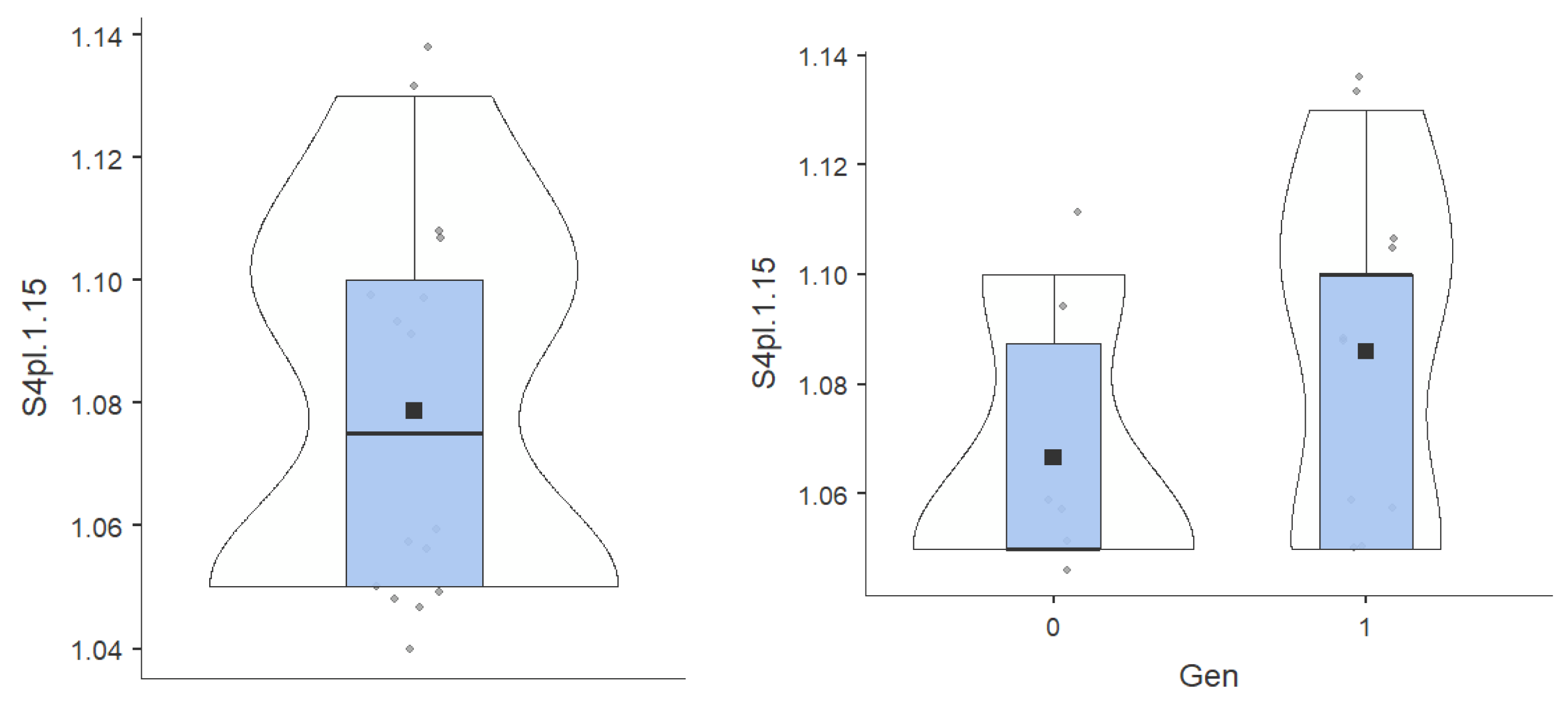
- Average – displays the central tendency of each individual series. (Table 1)
- The standard deviation denotes the degree of dispersion of the data. In general, it is compared to values of the central tendency, to the average. In the case of our variables it is reasonable. (Table 1)
- Standard errors exceed 1 for many variables, so they are too large and calculations are not very accurate. (Table 1)
- Skewness values evaluate the sharpness of the graph. Values in the range [-1.96; 1.96] denotes a graph that closely approximates the Gaussian curve of the normal. Kurtosis values evaluate the shift of the graph to the left or right from the normal values. Values in the range [-1.96; 1.96] denotes a graph that closely approximates the Gaussian curve of the normal. All of our variable values fall within this range, with the exception of S6pl.1.10. (Table 1). At the last test, low and high values were recorded, but not average.
- Min and Max – represent the minimum and maximum values respectively contained in our data series.
- Range – represents the difference between the maximum values and the minimum values.
- The Saphiro-Wilk test can be used to decide whether or not a sample fits a normal distribution and is commonly used for small samples. According to the Shapiro-Wilk test, a p-value greater than 0.05 (p > 0.05) represents the hypothesis that the data were approximately normally distributed (Pearson, 2010). The p-values for perceptions of benefits and effectiveness are all less than 0.05. The Shapiro-Wilk test statistic (Calc W) is basically a measure of how well the ordered and standardized sample quantiles match the standard normal quantiles. The statistic will take a value between 0 and 1, with 1 being a perfect match.

4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hogan, C., Castiglioni, M.T., Abbott, S., Cobley, S., (2021). Talent identification in swimming: A systematic review., Journal of Science and Medicine in Sport 24:S75, November, DOI:10.1016/j.jsams.2021.09.185 Conference: Sports Medicine Australia 2021 https://www.researchgate.net/publication/355788437_Talent_identification_in_swimming_A_systematic_review.
- Paniccia, D., Graziani, G., Lugni, C., Piva, R. (2021). The relevance of recoil and free swimming in aquatic locomotion. Journal of Fluids and Structures, Volume 103, May, 103290. [CrossRef]
- POST, A.K., KONING, R.H., VISSCHER, C., ELFERINK-GENSER, M.T. (2022). The importance of reflection and evaluation processes in daily training sessions for progression toward elite level swimming performance. Phychology of Sport and Exercise, Volume 61, July, 102219. [CrossRef]
- BARBOSA, T. M., BRAGADA, J.A., REIS, V.M., MARINHO, D.A., CARVALHO, C., SILVA, A.J. (2010). Energetics and biomechanics as determining factors of swimming performance: Updating the state of the art. 2010. Journal of Science and Medicine in Sport, Volume 13, Issue 2, March, Pages 262-269. [CrossRef]
- ESKIYECEK, C.G.; GUL,, G.K., GUL M., ULUDAG, B. (2020). The Effect of 8-Week Core Exercises Applied to 10-12 Age Male Swimmers on Swimming Performance. 9(3). [CrossRef]
- HANULA, D. , NARTH, T.; THE SWIM COACHING BIBLE, 1.ST EDITION. (2001). America, Human Kinetics, P.21.
- TAN, M. , LIANG, Y., LV, W., REN, H., CAI, Q. (2023). The effects of inspiratory muscle training on swimming performance: A study on the cohort of swimming specialization students. Physiology and Behavior, Volume 271, 1 November, 114347. [CrossRef]
- GONZALES, L.R., IBANEZ, E.M., MOYA, R.M., GONZALEZ-VALERO, G. (2023). Study of strength training on swimming performance. A systematic review. Science and Sport, Volume 38, Issue 3, May, Pages 217-231. [CrossRef]
- CROWLEY, E. , HARRISON, A.J., LYONS, M. (2017). The Impact of Resistance Training on Swimming Performance: A Systematic Review. Sports Med, Nov;47(11):2285-2307. [CrossRef]
- NUGENT, F.J., COMYNS, T.M., BURROWS, E., WARRINGTON, G.D. (2017). Effects of Low-Volume, High-Intensity Training on Performance in Competitive Swimmers: A Systematic Review. Strength Cond Res. Mar;31(3):837-847. [CrossRef]
- The jamovi project. 2023. jamovi. (Version 2.4) [Computer Software]. Retrieved from https://www.jamovi.org.
- GUO, W., SOH, K.G., ZAKARIA, N.S., BAHARULDIN, M.T.H., GAO, Y. (2022) Effect of Resistance Training Methods and Intensity on the Adolescent Swimmer's Performance: A Systematic Review. http://www.ncbi.nlm.nih.gov/pmc/articles/pmc9013834/.
- WIRTH, K. , KEINER, M., FUHRMANN, S., NIMMERICHTER, A., HAFF, G.G. (2022). Strength Training in Swimming. Environ Res Public Health, Apr 28; 19(9):5369. [CrossRef]

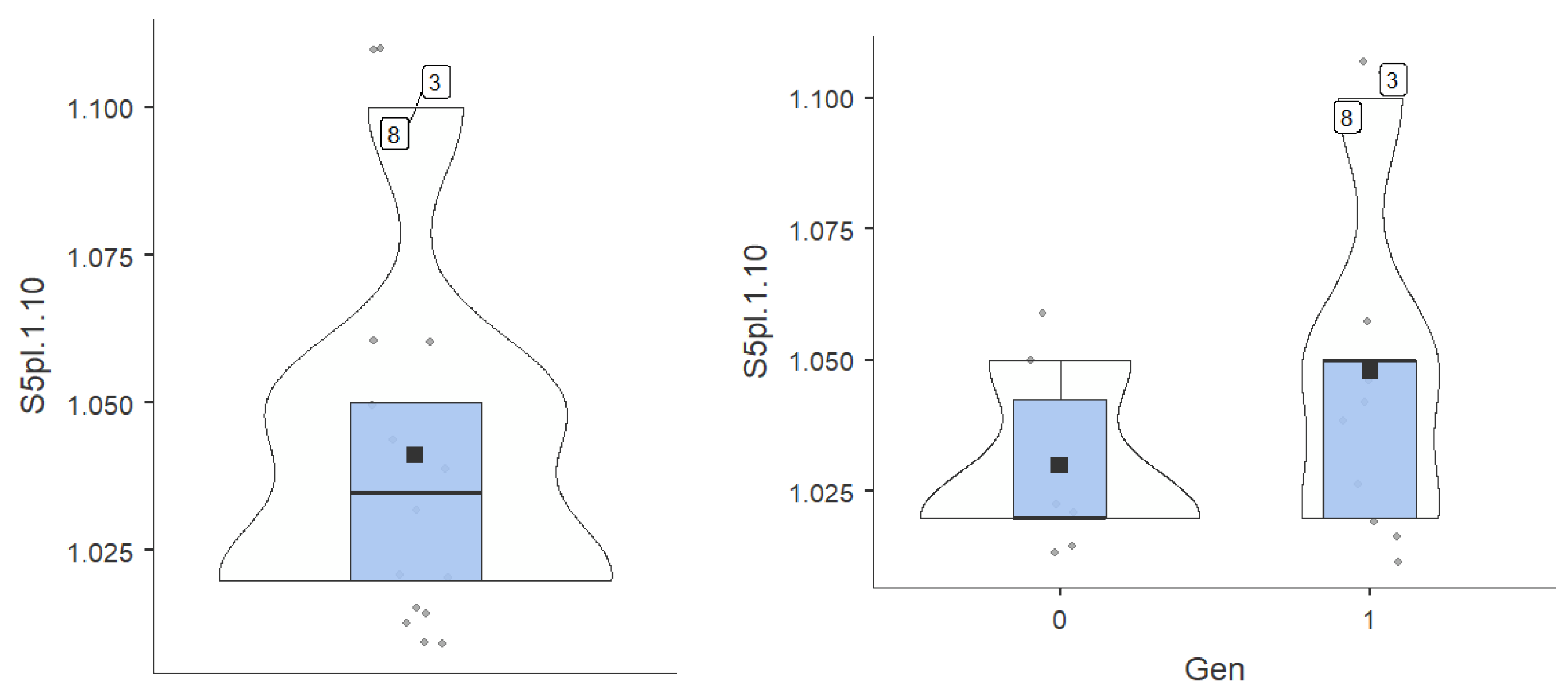
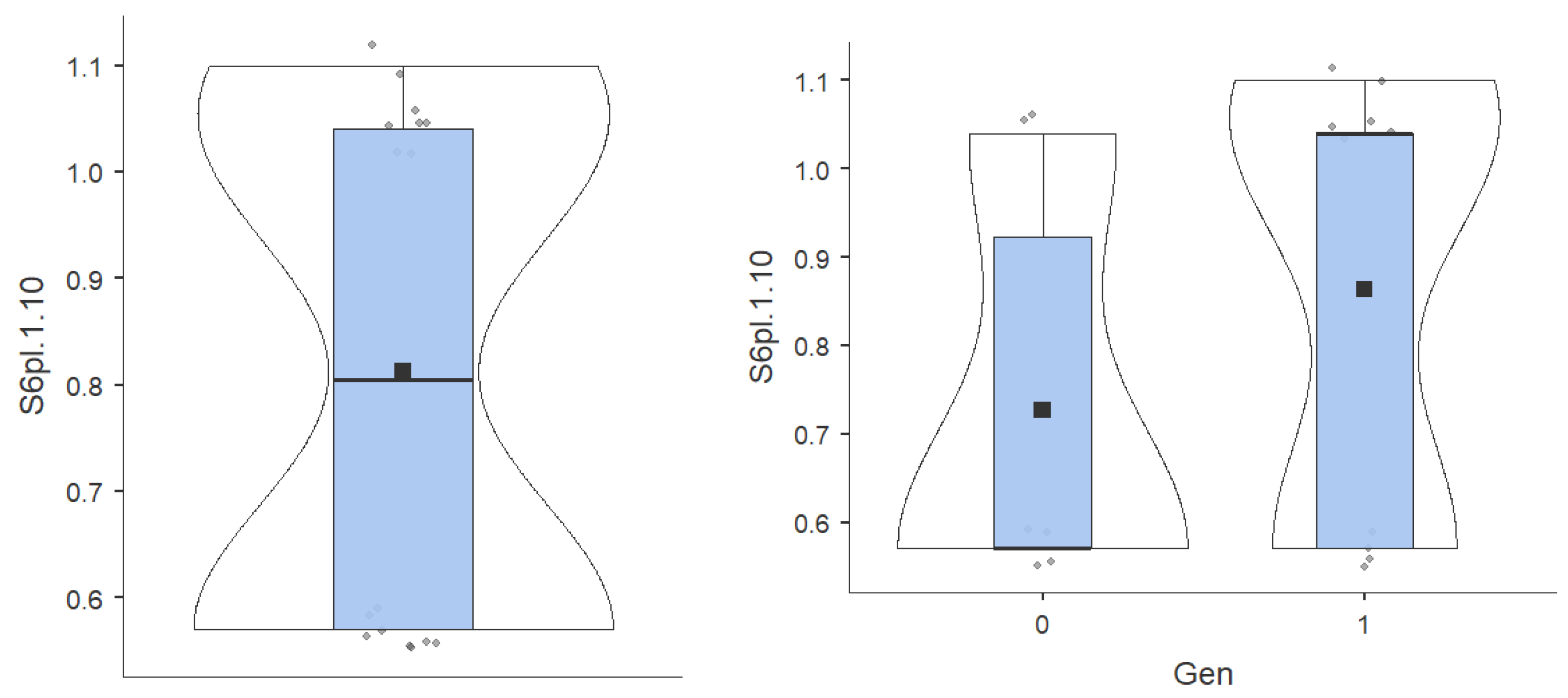
| Descriptives | Gen | TI50m | TF50m | TI100m | TF100m | S1pl.1.20 | S2pl.1.20 | S3pl.1.15 | S4pl.1.15 | S5pl.1.10 | S6pl.1.10 |
| N | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| Missing | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
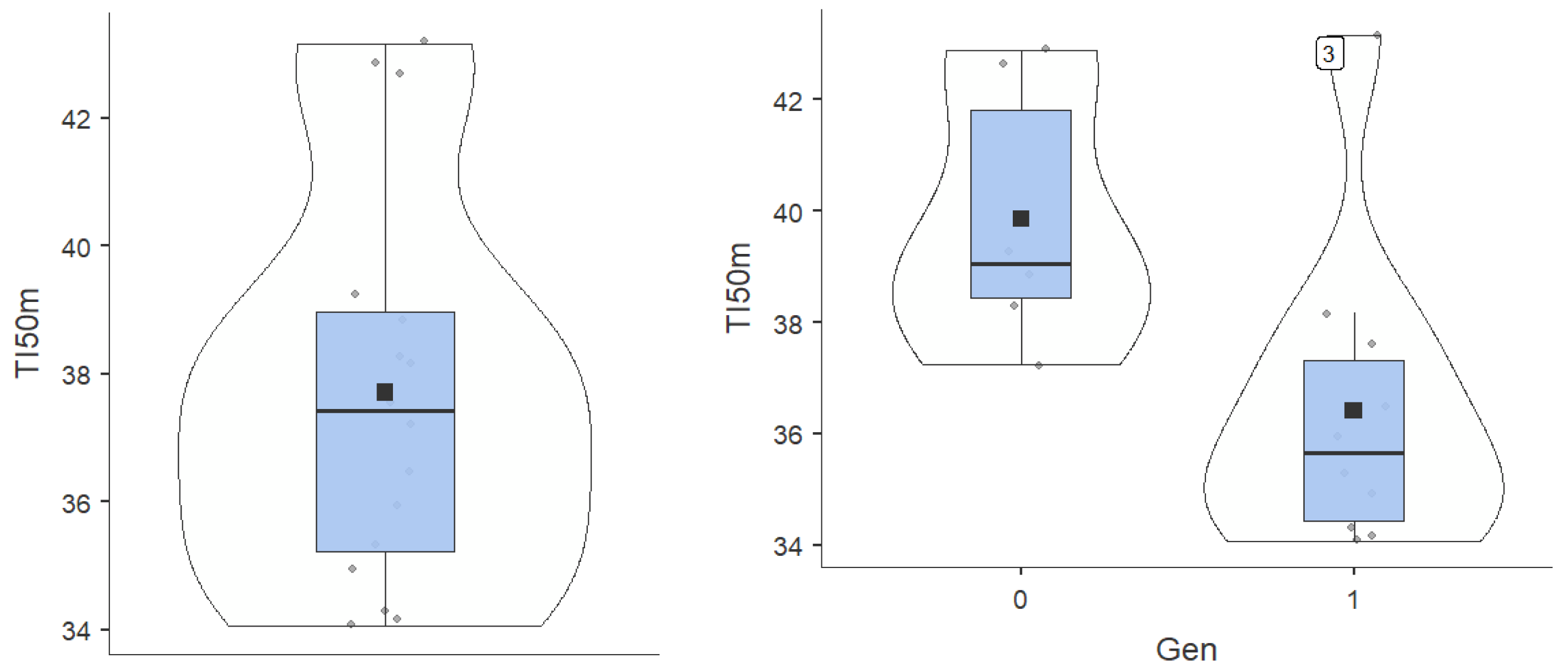
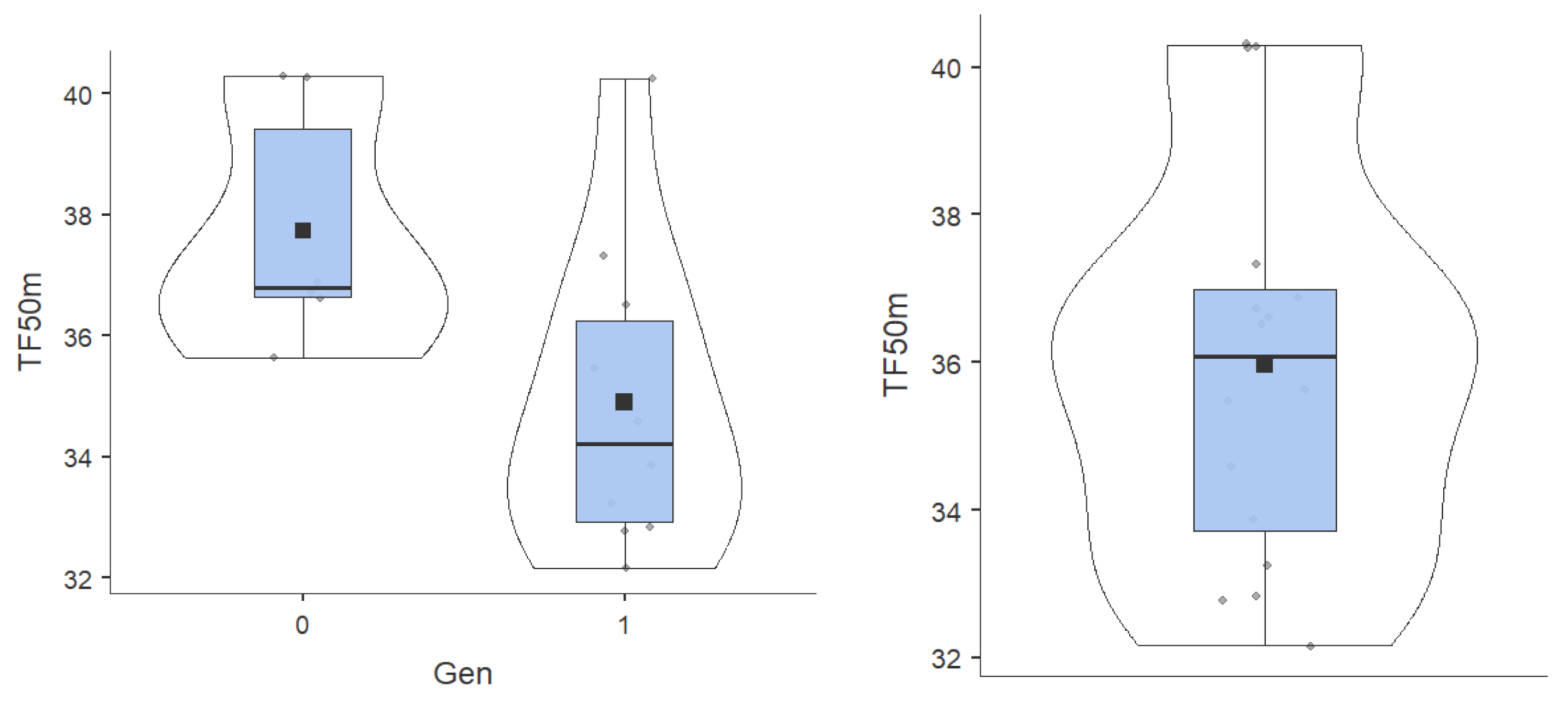
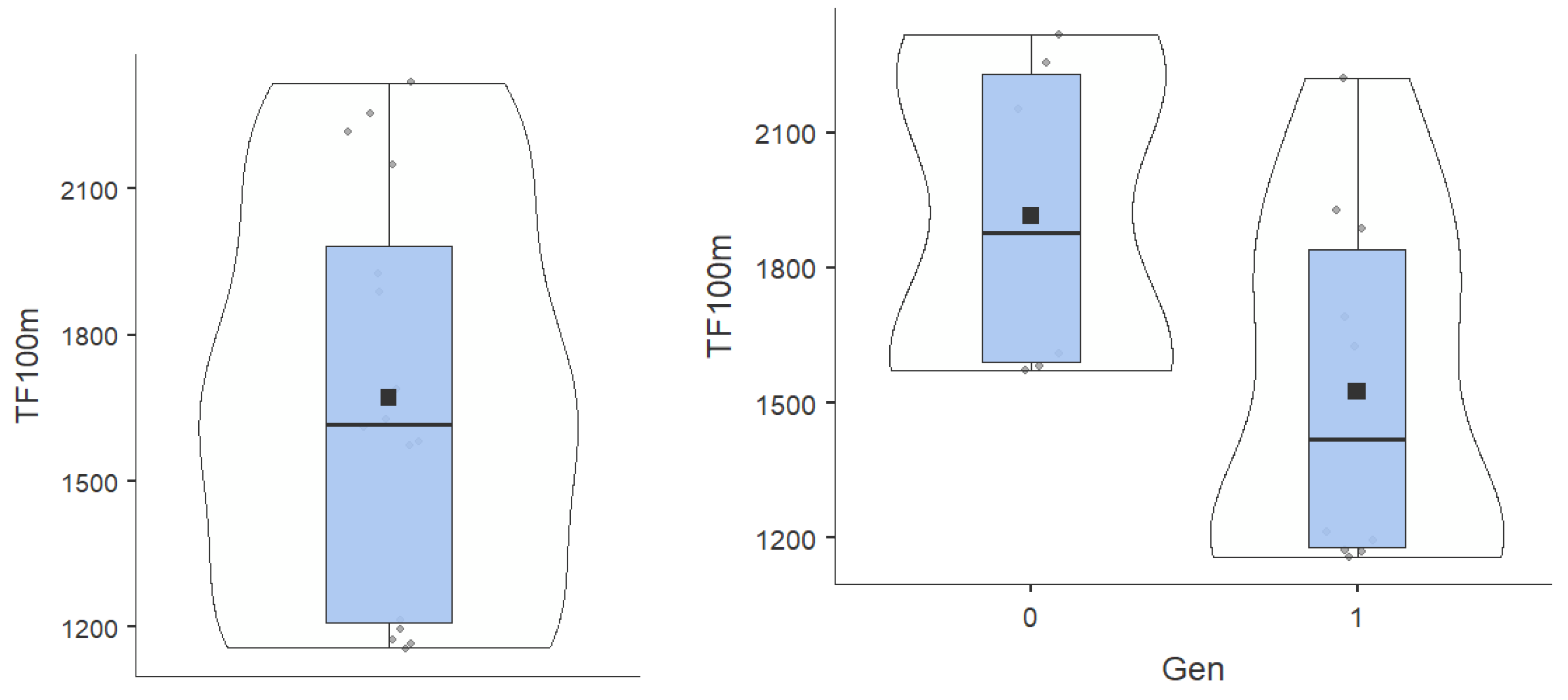
| Mean | 37.7 | 36 | 1762 | 1671 | 1.16 | 1.13 | 1.11 | 1.08 | 1.04 | 0.813 | |
| Median | 37.4 | 36.1 | 1738 | 1617 | 1.16 | 1.13 | 1.1 | 1.08 | 1.04 | 0.805 | |
| Standard deviation | 3.06 | 2.69 | 418 | 419 | 0.0171 | 0.0171 | 0.0216 | 0.0312 | 0.027 | 0.251 | |
| Range | 9.09 | 8.14 | 1144 | 1160 | 0.05 | 0.05 | 0.06 | 0.08 | 0.08 | 0.53 | |
| Minimum | 34.1 | 32.2 | 1215 | 1157 | 1.15 | 1.12 | 1.09 | 1.05 | 1.02 | 0.57 | |
| Maximum | 43.2 | 40.3 | 2359 | 2317 | 1.2 | 1.17 | 1.15 | 1.13 | 1.1 | 1.1 | |
| Skewness | 0.667 | 0.371 | 0.019 | 0.181 | 1.16 | 1.16 | 0.731 | 0.344 | 1.28 | 0.0197 | |
| Std. error skewness | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | 0.564 | |
| Kurtosis | -0.57 | -0.784 | -1.39 | -1.33 | 0.682 | 0.682 | -0.541 | -1.55 | 1.04 | -2.27 | |
| Std. error kurtosis | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 | |
| Shapiro-Wilk W | 0.9 | 0.92 | 0.895 | 0.897 | 0.747 | 0.747 | 0.768 | 0.761 | 0.736 | 0.684 | |
| Shapiro-Wilk p | 0.082 | 0.167 | 0.068 | 0.072 | < .001 | < .001 | 0.001 | < .001 | < .001 | < .001 |
| Spearman's rho | TI50m | TF50m | TI100m | TF100m | S1pl.1.20 | S2pl.1.20 | S3pl.1.15 | S4pl.1.15 | S5pl.1.10 | S6pl.1.10 | Gen | |
| TI50m | Rho | — | ||||||||||
| p-value | — | |||||||||||
| TF50m | Rho | 0.947 | — | |||||||||
| p-value | <.001*** | — | ||||||||||
| TI100m | Rho | 0.829 | 0.835 | — | ||||||||
| p-value | <.001*** | <.001*** | — | |||||||||
| TF100m | Rho | 0.821 | 0.835 | 0.965 | — | |||||||
| p-value | <.001*** | <.001*** | <.001*** | — | ||||||||
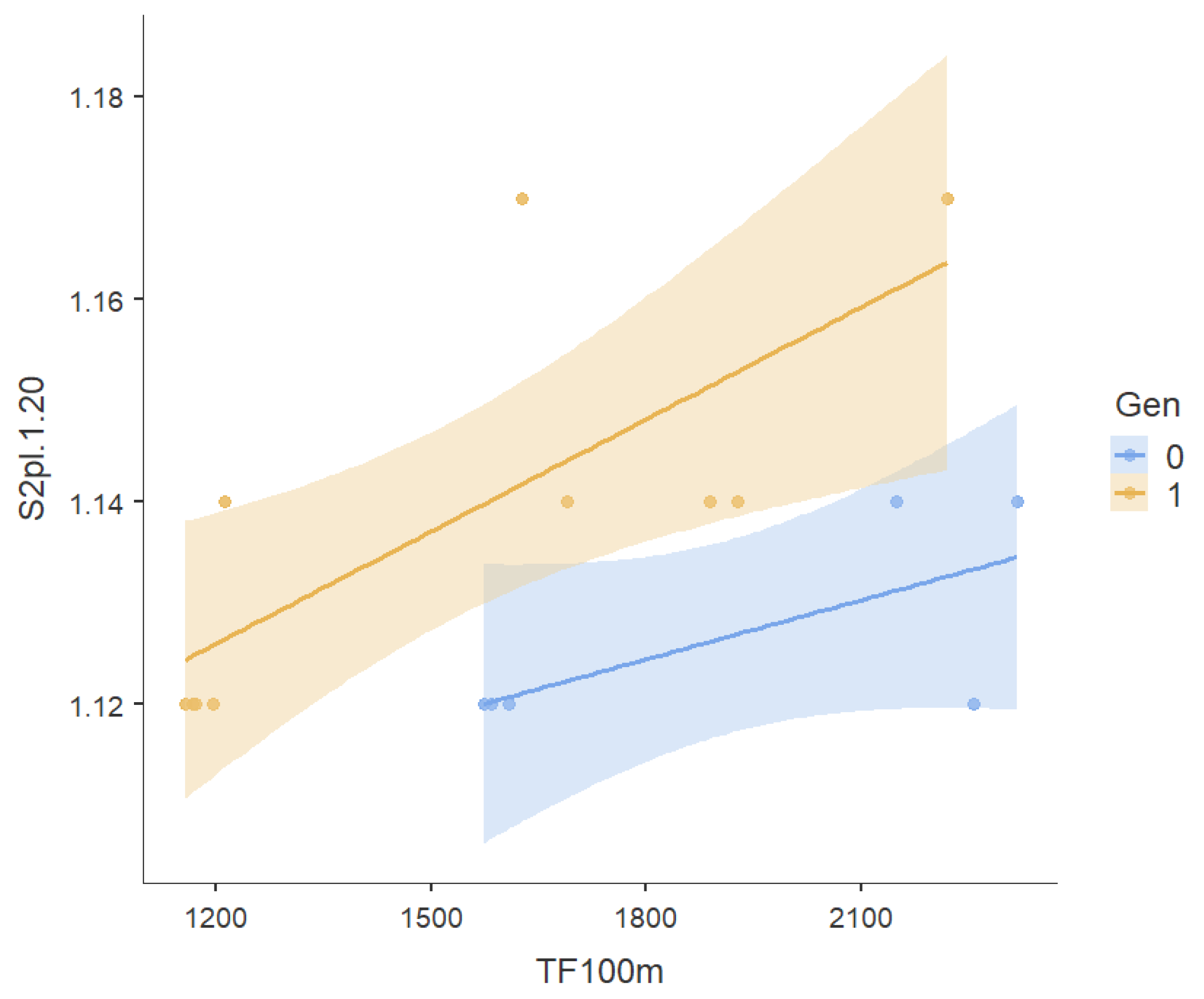
| S1pl.1.20 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | — | ||||||
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | — | |||||||
| S2pl.1.20 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | 1*** | — | |||||
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | <.001 | — | ||||||
| S3pl.1.15 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | 1*** | 1*** | — | ||||
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | <.001 | <.001 | — | |||||
| S4pl.1.15 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | 1*** | 1*** | 1*** | — | |||
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | <.001 | <.001 | <.001 | — | ||||
| S5pl.1.10 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | 1*** | 1*** | 1*** | 1*** | — | ||
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | <.001 | <.001 | <.001 | <.001 | — | |||
| S6pl.1.10 | Rho | 0.366 | 0.402 | 0.486 | 0.577 | 1*** | 1*** | 1*** | 1*** | 1*** | — | |
| p-value | 0.163 | 0.123 | 0.056 | 0.019 | <.001 | <.001 | <.001 | <.001 | <.001 | — | ||
| Gen | Rho | -0.616 | -0.588 | -0.392 | -0.392 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | — |
| p-value | 0.011 | 0.017 | 0.133 | 0.133 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | — | |
| No | Subject | Sex | Class | Age | Initial testing/ 50 m freestyle 11.01.2023 | Final testing/ 50 m freestyle 22.02.2023 | Initial testing/ 100 m freestyle 12.01.2023 | Final testing/ 100 m freestyle 23.02.2023 | Week 1 8x50 pic S/ pl.1.20 | Week 2 8x50 pic S/ pl.1.20 | Week 3 8x50 pic S/ pl.1.15 | Week 4 8x50 pic S/ pl.1.15 | Week 5 8x50 pic S/ pl.1.10 | Week 6 8x50 pic S/ pl.1.10 |
| 1 | A.G. | F | 6 | 13 | 38,86 | 36,72 | 1'21''83 | 1'20''23 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 |
| A.A. | M | 6 | 13 | 34,92 | 33,24 | 1'14''27 | 1'13''73 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| A.N. | M | 6 | 13 | 43,16 | 40,26 | 1'32''06 | 1'30''59 | 1.18-1.20 | 1.16-1.17 | 1.14-1.15 | 1.11-1.13 | 1,10 | 1,10 | |
| B.S. | F | 6 | 13 | 38,29 | 35,63 | 1'22''13 | 1'20''13 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| B.B. | F | 6 | 13 | 42,65 | 40,27 | 1'33''00 | 1'31''97 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| C.S | F | 6 | 13 | 42,88 | 40,30 | 1'33''19 | 1'31''36 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| C.T. | M | 6 | 13 | 34,07 | 32,83 | 1'14''15 | 1'12''87 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| C.I. | M | 6 | 13 | 38,17 | 37,32 | 1'23''26 | 1'21''06 | 1.18-1.20 | 1.16-1.17 | 1.14-1.15 | 1.11-1.13 | 1,10 | 1,10 | |
| I.M. | F | 6 | 13 | 39,25 | 36,87 | 1'31''12 | 1'29''49 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| M.M. | M | 6 | 13 | 34,28 | 32,77 | 1'15''10 | 1'12''92 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| M.D. | M | 6 | 13 | 37,59 | 36,51 | 1'26''88 | 1'25''68 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| N.A. | M | 6 | 13 | 35,32 | 33,87 | 1'15''16 | 1'12''77 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| P.S. | M | 6 | 13 | 34,18 | 32,16 | 1'15''18 | 1'13''55 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 | |
| S.A. | M | 6 | 13 | 35,98 | 34,58 | 1'24''20 | 1'22'10 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| S.D. | M | 6 | 13 | 36,49 | 35,47 | 1'26''93 | 1'25''28 | 1.15-1.17 | 1.13-1.14 | 1.11-1.12 | 1.09-1.10 | 1.04-1.05 | 1,04 | |
| B.D. | F | 6 | 13 | 37,24 | 36,61 | 1'22''29 | 1'20''48 | 1.14-1.15 | 1.10-1.12 | 1.07-1.09 | 1.03-1.05 | 1.00-1.02 | 0.55-0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





