Submitted:
04 September 2025
Posted:
05 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Sample Selection
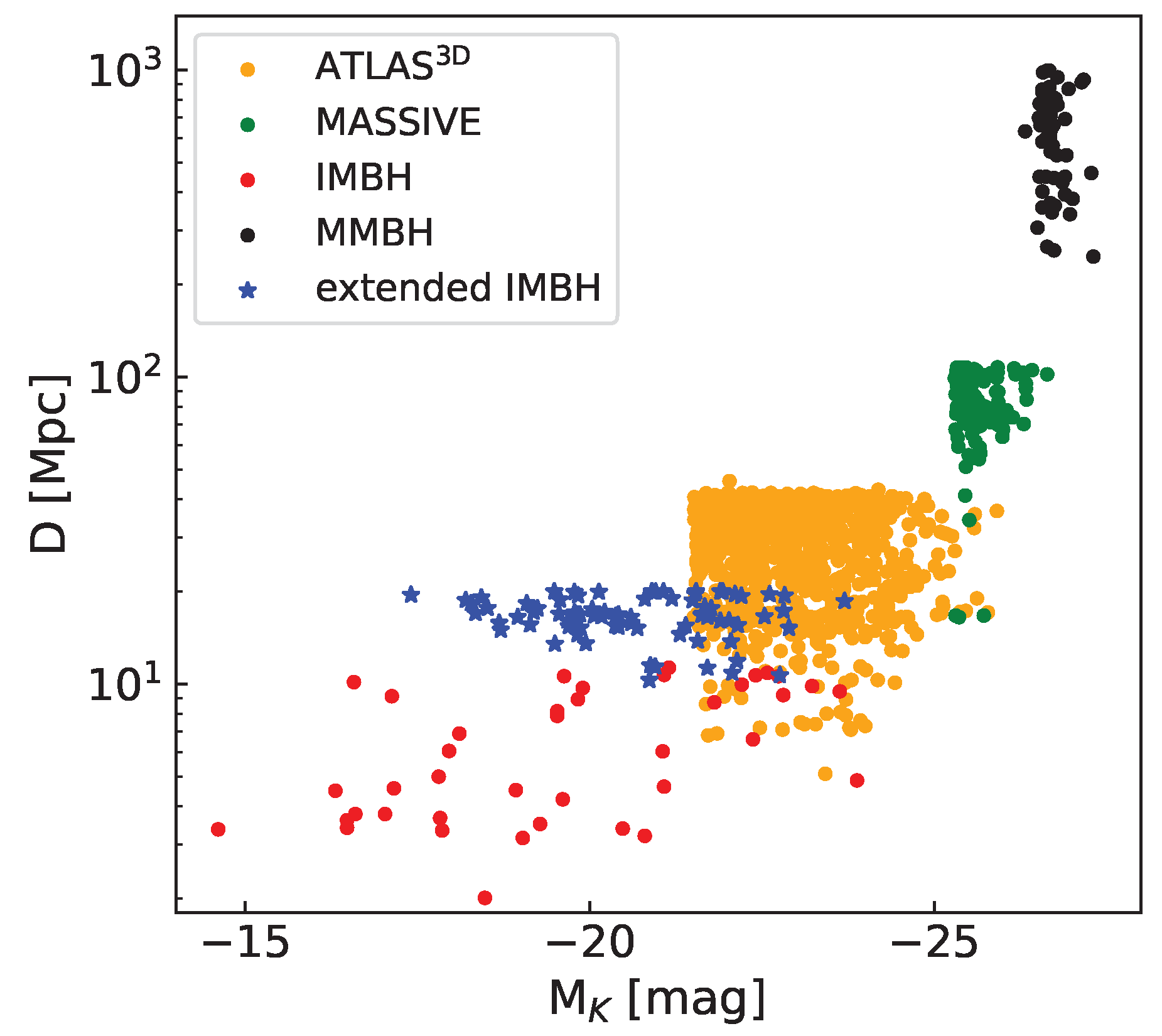
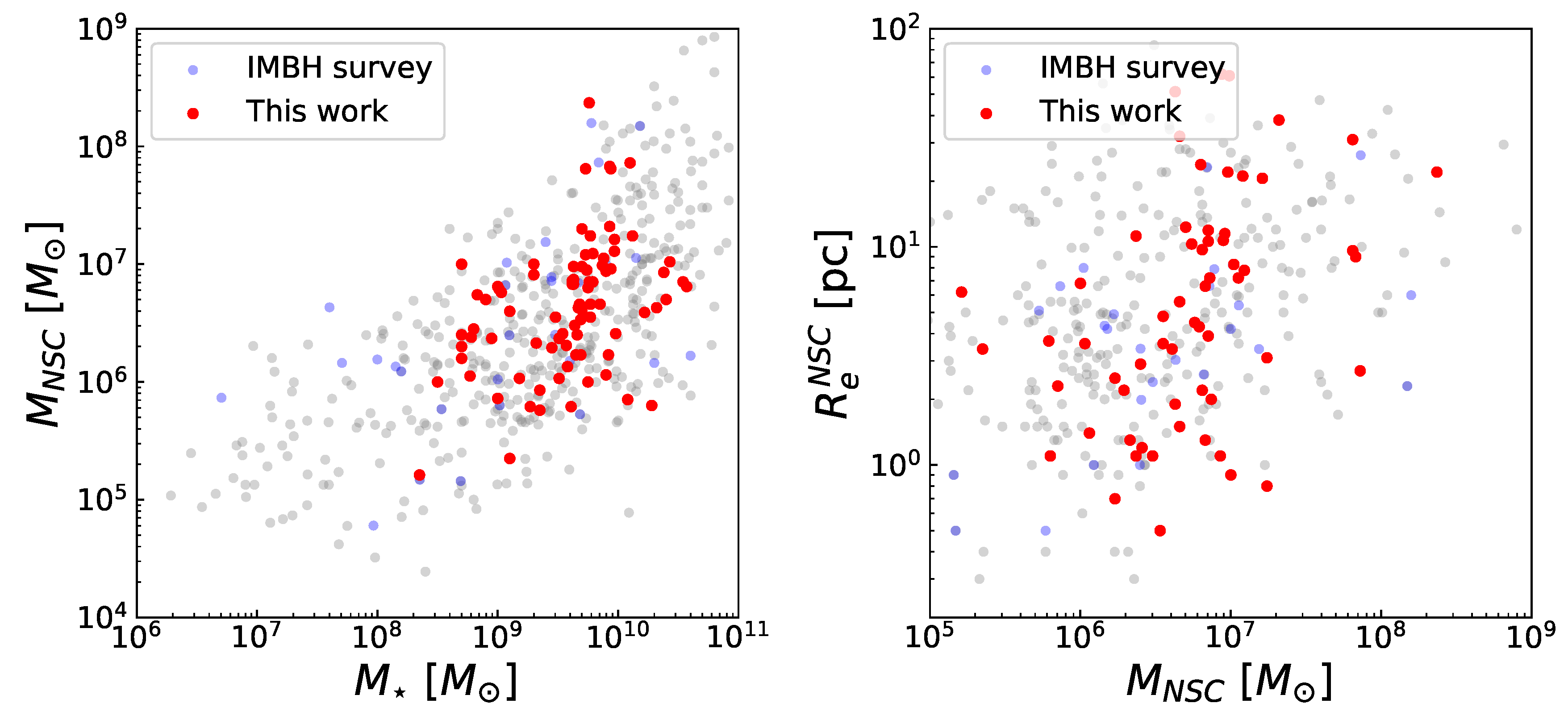
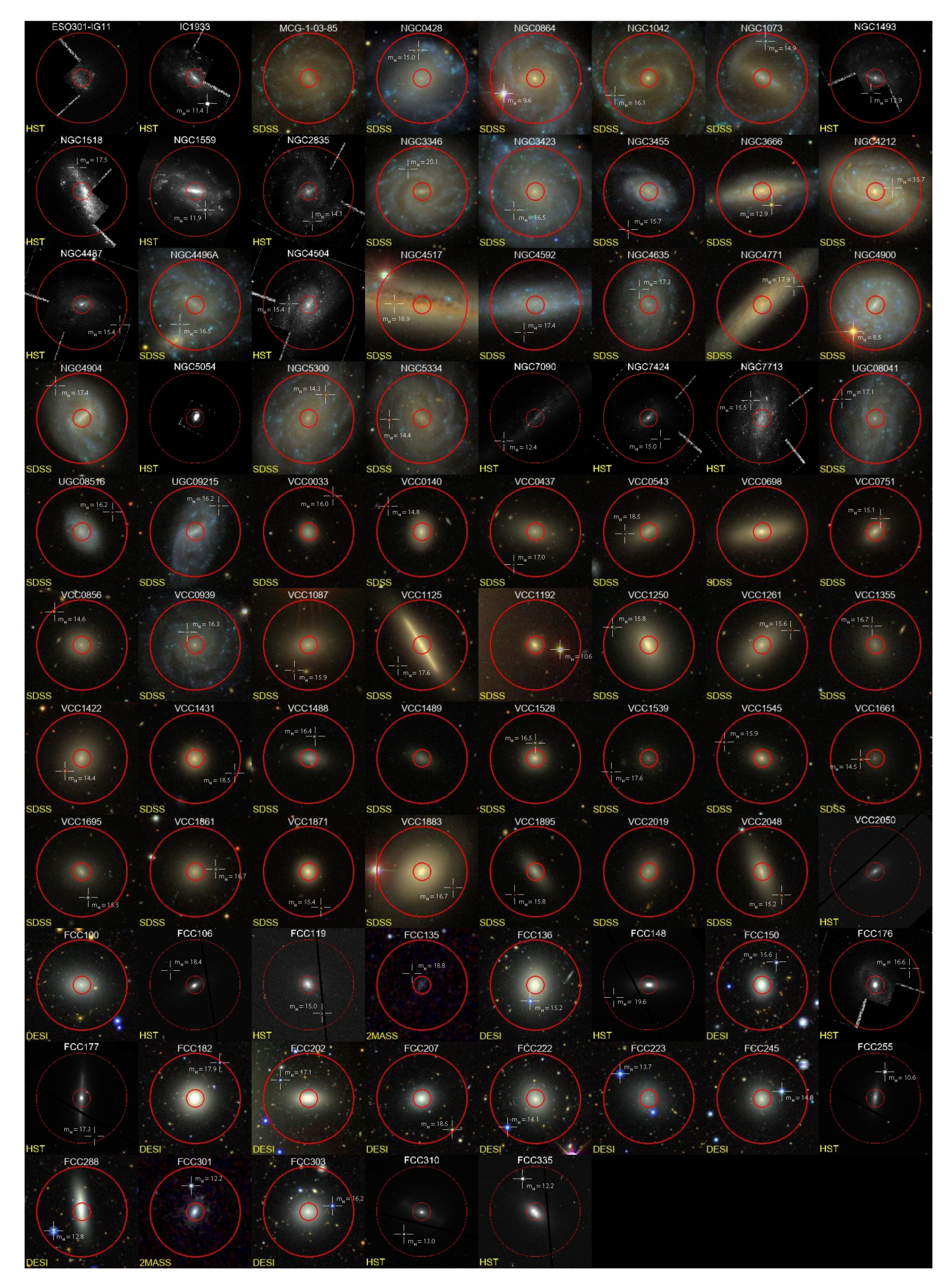
2.1. Sample Selection
2.2. Sample Properties
| No. | Object | RA | Decl. | D | Hubble | Ref. | |||||
| name | (h:m:s) | (d:m:s) | (Mpc) | type | () | (kpc) | () | (pc) | (km s−1) | ||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| 1 | ESO301-IG11 | 03:23:54.21 | −37:30:33.0 | 19.94 | 9.9 | 9.61 | 2.11 | 5.79 | 3.7 | 28.9 | [54] |
| 2 | IC1933 | 03:25:39.97 | −52:47:07.5 | 18.98 | 6.1 | 8.35 | 1.85 | 5.21 | 6.2 | 42.7 | [54] |
| 3 | MCG-1-03-85 | 01:05:04.88 | −06:12:44.6 | 11.38 | 7.0 | 9.66 | 4.04 | 6.40 | 2.9 | 42.0 | [5,54] |
| 4 | NGC0428 | 01:12:55.75 | +00:58:53.5 | 16.54 | 8.6 | 9.54 | 2.63 | 6.41 | 1.2 | 56.9 | [54] |
| 5 | NGC0864 | 02:15:27.64 | +06:00:09.4 | 19.41 | 5.1 | 10.10 | 0.21 | 7.86 | 2.7 | 26.9 | [54,65] |
| 6 | NGC1042 | 02:40:23.97 | −08:26:00.7 | 19.59 | 6.0 | 9.32 | 4.59 | 6.33 | 1.3 | 65.3 | [54] |
| 7 | NGC1073 | 02:43:40.52 | +01:22:34.0 | 13.80 | 5.3 | 9.69 | 0.16 | 6.53 | 0.5 | 24.8 | [54,65] |
| 8 | NGC1493 | 03:57:27.46 | −46:12:38.6 | 15.54 | 6.0 | 9.77 | 4.85 | 6.55 | 3.6 | 51.2 | [54] |
| 9 | NGC1518 | 04:06:49.82 | −21:10:23.5 | 13.50 | 8.2 | 9.10 | 0.83 | 5.35 | 3.4 | 36.6 | [54] |
| 10 | NGC1559 | 04:17:35.77 | −62:47:01.2 | 15.21 | 5.9 | 9.77 | 3.50 | 6.66 | 1.5 | 72.6 | [5,54,130] |
| 11 | NGC2835 | 09:17:52.91 | −22:21:16.8 | 10.86 | 5.0 | 9.70 | 2.80 | 6.61 | 3.4 | 70.7 | [5,54,130] |
| 12 | NGC3346 | 10:43:38.91 | +14:52:18.9 | 17.84 | 5.9 | 9.51 | 3.34 | 6.37 | 1.1 | 49.6 | [54] |
| 13 | NGC3423 | 10:51:14.33 | +05:50:24.1 | 11.27 | 6.0 | 9.45 | 0.12 | 6.29 | 2.2 | 54.6 | [54] |
| 14 | NGC3455 | 10:54:31.08 | +17:17:04.6 | 15.79 | 3.7 | 10.57 | 1.44 | 6.81 | 2.2 | 46.2 | [54] |
| 15 | NGC3666 | 11:24:26.07 | +11:20:32.0 | 19.32 | 5.2 | 9.94 | 0.10 | 7.81 | 9.6 | 60.6 | [54,65] |
| 16 | NGC4212 | 12:15:39.36 | +13:54:05.4 | 17.30 | 4.9 | 10.40 | 4.56 | 6.70 | 12.3 | 61.0 | [54,59] |
| 17 | NGC4487 | 12:31:04.46 | −08:03:14.1 | 19.59 | 6.0 | 10.38 | 3.50 | 6.93 | 1.1 | 51.0 | [54] |
| 18 | NGC4496A | 12:31:39.21 | +03:56:22.1 | 15.49 | 7.6 | 9.65 | 3.10 | 6.23 | 0.7 | 74.9 | [54,65,130] |
| 19 | NGC4504 | 12:32:17.41 | −07:33:48.9 | 14.51 | 6.0 | 10.54 | 2.10 | 6.85 | 3.9 | 53.0 | [54] |
| 20 | NGC4517 | 12:32:45.59 | +00:06:54.1 | 10.67 | 6.0 | 10.08 | 6.50 | 5.85 | 2.3 | 43.8 | [54,65] |
| 21 | NGC4592 | 12:39:18.74 | −00:31:55.0 | 15.21 | 8.0 | 10.28 | 1.84 | 5.80 | 1.1 | 42.6 | [54] |
| 22 | NGC4635 | 12:42:39.23 | +19:56:43.7 | 13.54 | 6.6 | 9.01 | 1.40 | 6.79 | 4.3 | 34.7 | [54] |
| 23 | NGC4771 | 12:53:21.26 | +01:16:09.5 | 16.07 | 6.2 | 10.32 | 2.73 | 6.63 | 1.9 | 64.4 | [54] |
| 24 | NGC4900 | 13:00:39.26 | +02:30:02.7 | 13.73 | 5.2 | 10.12 | 2.59 | 7.24 | 3.1 | 67.1 | [54] |
| 25 | NGC4904 | 13:00:58.64 | −00:01:39.4 | 16.94 | 5.8 | 9.92 | 2.06 | 6.23 | 2.5 | 62.5 | [54] |
| 26 | NGC5054 | 13:16:58.49 | −16:38:05.5 | 18.62 | 4.2 | 10.43 | 0.11 | 7.02 | 8.3 | 57.4 | [5,54] |
| 27 | NGC5300 | 13:48:16.04 | +03:57:03.1 | 16.74 | 5.2 | 9.97 | 2.68 | 7.21 | 20.6 | 54.1 | [54] |
| 28 | NGC5334 | 13:52:54.48 | −01:06:52.0 | 19.63 | 5.2 | 9.79 | 2.96 | 6.85 | 11.9 | 49.5 | [54] |
| 29 | NGC7090 | 21:36:28.81 | −54:33:25.3 | 11.86 | 5.0 | 9.64 | 4.56 | 6.48 | 1.1 | 54.3 | [54] |
| 30 | NGC7424 | 22:57:18.37 | −41:04:14.1 | 11.48 | 6.0 | 9.75 | – | 6.00 | 6.8 | 15.6 | [54,150] |
| 31 | NGC7713 | 23:36:14.99 | −37:56:17.1 | 10.29 | 6.7 | 9.90 | 2.17 | 6.06 | 1.4 | 42.4 | [54] |
| 32 | UGC08041 | 12:55:12.65 | +00:06:59.9 | 17.14 | 6.9 | 8.83 | – | 6.74 | 10.3 | 34.4 | [5,54] |
| 33 | UGC08516 | 13:31:52.59 | +20:00:04.6 | 14.50 | 5.9 | 8.95 | 1.29 | 6.37 | 11.2 | 34.1 | [54] |
| 34 | UGC09215 | 14:23:27.13 | +01:43:34.4 | 19.96 | 6.3 | 9.77 | 2.49 | 7.24 | 0.8 | 41.3 | [54] |
| 35 | VCC0033 | 12:11:07.76 | +14:16:29.3 | 15.00 | −4.0 | 9.62 | 0.72 | 6.86 | 7.2 | 38.9 | [28,80] |
| 36 | VCC0140 | 12:15:12.56 | +14:25:58.4 | 17.15 | −2.2 | 9.79 | 2.10 | 7.09 | 7.8 | 48.7 | [28,80] |
| 37 | VCC0437 | 12:20:48.82 | +17:29:13.4 | 16.90 | −3.2 | 9.90 | 2.96 | 6.94 | 61.8 | 70.7 | [28,80] |
| 38 | VCC0543 | 12:22:19.53 | +14:45:38.8 | 16.04 | −2.7 | 9.74 | 2.19 | 6.95 | 10.7 | 19.2 | [28,46,58,80,112,113] |
| 39 | VCC0698 | 12:24:05.02 | +11:13:05.0 | 18.71 | −2.0 | 9.98 | 1.45 | 6.41 | – | 62.0 | [13,46,58,113] |
| 40 | VCC0751 | 12:24:48.36 | +18:11:42.4 | 15.59 | −2.7 | 9.63 | 1.79 | 6.98 | 22.0 | 65.0 | [28,80] |
| 41 | VCC0856 | 12:25:57.93 | +10:03:13.6 | 16.83 | −3.3 | 9.35 | 1.22 | 5.93 | – | 33.0 | [46,48,58,113] |
| 42 | VCC0939 | 12:26:47.23 | +08:53:04.6 | 16.83 | 6.3 | 9.48 | 4.30 | 6.55 | 4.8 | 45.8 | [5,54] |
| 43 | VCC1087 | 12:28:14.88 | +11:47:23.4 | 16.67 | −4.1 | 9.51 | 1.53 | 6.03 | – | 45.0 | [13,46,58,113,124] |
| 44 | VCC1125 | 12:28:43.31 | +11:45:18.1 | 16.04 | −1.9 | 9.93 | 7.15 | 7.32 | 38.1 | 65.3 | [28,80] |
| 45 | VCC1192 | 12:29:30.25 | +07:59:34.3 | 16.50 | −4.8 | 9.27 | 0.60 | 5.79 | – | 58.2 | [46,58,113,151] |
| 46 | VCC1250 | 12:29:59.08 | +12:20:55.2 | 17.62 | −2.9 | 9.57 | 1.35 | 6.31 | – | 69.0 | [13,46,58,113] |
| 47 | VCC1261 | 12:30:10.33 | +10:46:46.1 | 18.91 | −4.8 | 9.69 | 1.71 | 6.23 | – | 50.0 | [58,112,113] |
| 48 | VCC1355 | 12:31:20.19 | +14:06:54.7 | 16.90 | −5.0 | 9.75 | 1.77 | 6.80 | 23.8 | 64.8 | [28,80] |
| 49 | VCC1422 | 12:32:14.21 | +10:15:05.3 | 15.35 | −4.8 | 9.58 | 1.82 | 6.13 | – | 36.0 | [13,58,113] |
| 50 | VCC1431 | 12:32:23.39 | +11:15:46.7 | 17.50 | −4.8 | 9.97 | 2.43 | 7.11 | – | 55.0 | [28,80] |
| 51 | VCC1488 | 12:33:13.44 | +09:23:50.5 | 18.30 | −3.5 | 9.62 | 0.70 | 6.83 | 1.3 | 18.6 | [28,80] |
| 52 | VCC1489 | 12:33:13.90 | +10:55:42.7 | 18.82 | −5.0 | 9.68 | 0.34 | 6.66 | 5.6 | 25.5 | [28,80] |
| 53 | VCC1528 | 12:33:51.62 | +13:19:20.8 | 15.41 | −4.4 | 9.88 | 1.84 | 7.05 | 7.2 | 51.9 | [28,80] |
| 54 | VCC1539 | 12:34:06.74 | +12:44:29.8 | 16.35 | −5.0 | 9.85 | 0.69 | 6.66 | 32.1 | 28.5 | [28,80] |
| 55 | VCC1545 | 12:34:11.53 | +12:02:56.3 | 17.60 | −5.0 | 9.94 | 1.33 | 6.96 | 11.5 | 45.6 | [28,80] |
| 56 | VCC1661 | 12:36:24.78 | +10:23:04.8 | 17.76 | −5.0 | 9.67 | 1.08 | 6.63 | 51.4 | 64.9 | [28,80] |
| 57 | VCC1695 | 12:36:54.85 | +12:31:12.3 | 16.50 | −3.0 | 9.76 | 2.05 | 6.85 | 10.6 | 54.5 | [28,80] |
| 58 | VCC1861 | 12:40:58.56 | +11:11:04.2 | 15.23 | −4.8 | 9.87 | 2.54 | 6.99 | 60.8 | 58.6 | [28,80] |
| 59 | VCC1871 | 12:41:15.73 | +11:23:14.1 | 15.49 | −5.0 | 9.35 | 0.52 | 5.76 | – | 51.0 | [13,46,58,113] |
| 60 | VCC1883 | 12:41:32.75 | +07:18:53.6 | 16.60 | −2.0 | 10.22 | 2.01 | 6.59 | – | 60.8 | [46,58,113,151] |
| 61 | VCC1895 | 12:41:51.98 | +09:24:10.4 | 15.80 | −3.0 | 9.63 | 0.87 | 6.87 | 2.0 | 25.6 | [28,80] |
| 62 | VCC2019 | 12:45:20.42 | +13:41:33.6 | 17.06 | −3.9 | 9.00 | 1.27 | 5.86 | – | 37.0 | [46,58,112,113] |
| 63 | VCC2048 | 12:47:15.30 | +10:12:12.9 | 16.60 | −4.5 | 9.73 | 2.77 | 7.08 | 21.1 | 67.5 | [28,80] |
| 64 | VCC2050 | 12:47:20.64 | +12:09:59.1 | 17.01 | −4.0 | 9.63 | 0.78 | 6.83 | 6.6 | 26.0 | [28,80] |
| 65 | FCC100 | 03:31:47.58 | −35:03:06.7 | 19.48 | −2.2 | 8.70 | 1.10 | 6.40 | – | 35.0 | [35,39,129] |
| 66 | FCC106 | 03:32:47.65 | −34:14:19.3 | 20.00 | −2.8 | 8.90 | 1.00 | 6.70 | – | 40.0 | [114,129,141] |
| 67 | FCC119 | 03:33:33.84 | −33:34:23.9 | 20.00 | −2.9 | 9.00 | 1.70 | 6.81 | 9.7 | 20.0 | [42] |
| 68 | FCC135 | 03:34:30.86 | −34:17:51.0 | 18.73 | −3.0 | 8.70 | 1.41 | 6.30 | – | 24.0 | [39,110,129] |
| 69 | FCC136 | 03:34:29.48 | −35:32:47.0 | 18.80 | −2.4 | 9.10 | 1.29 | 6.60 | – | 64.3 | [35,129] |
| 70 | FCC148 | 03:35:16.82 | −35:15:56.4 | 20.00 | −2.2 | 9.76 | 2.70 | 8.37 | 22.0 | 56.0 | [42,83,146] |
2.3. Searching Tip-Tilt Stars and Observing Strategies
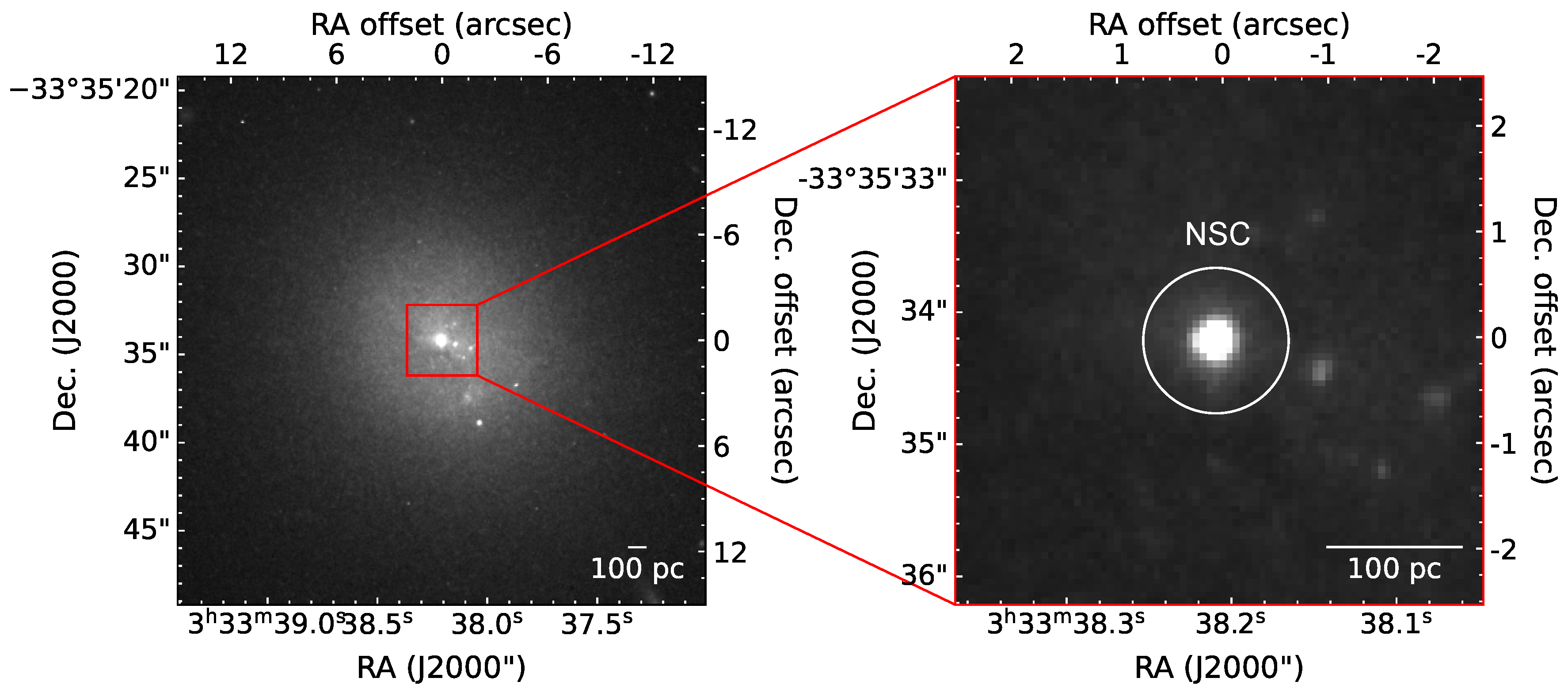
2.4. The Simulated Target: FCC 119
2.5. Fornax & Virgo Clusters
2.5.1. Virgo Cluster
2.5.2. Fornax Cluster
3. Stellar Mass Model of FCC 119
3.1. HST Observations
3.2. HST Point Spread Function (PSF) Simulations
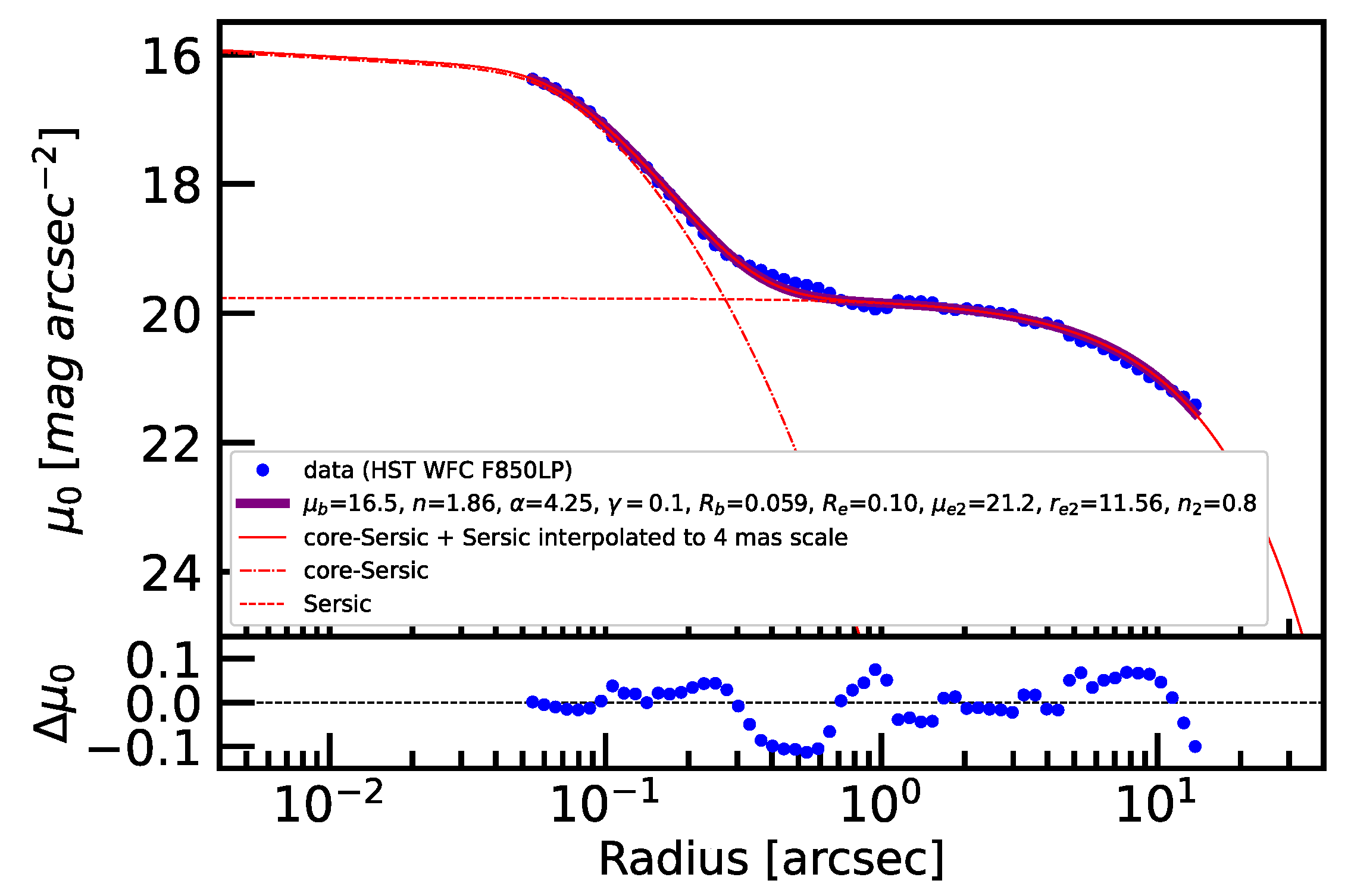
3.3. F850LP Surface Brightness Profile
3.4. MGE Mass Model
4. HARMONI IFS Simulations
4.1. Jeans Anisotropic Model (JAM)
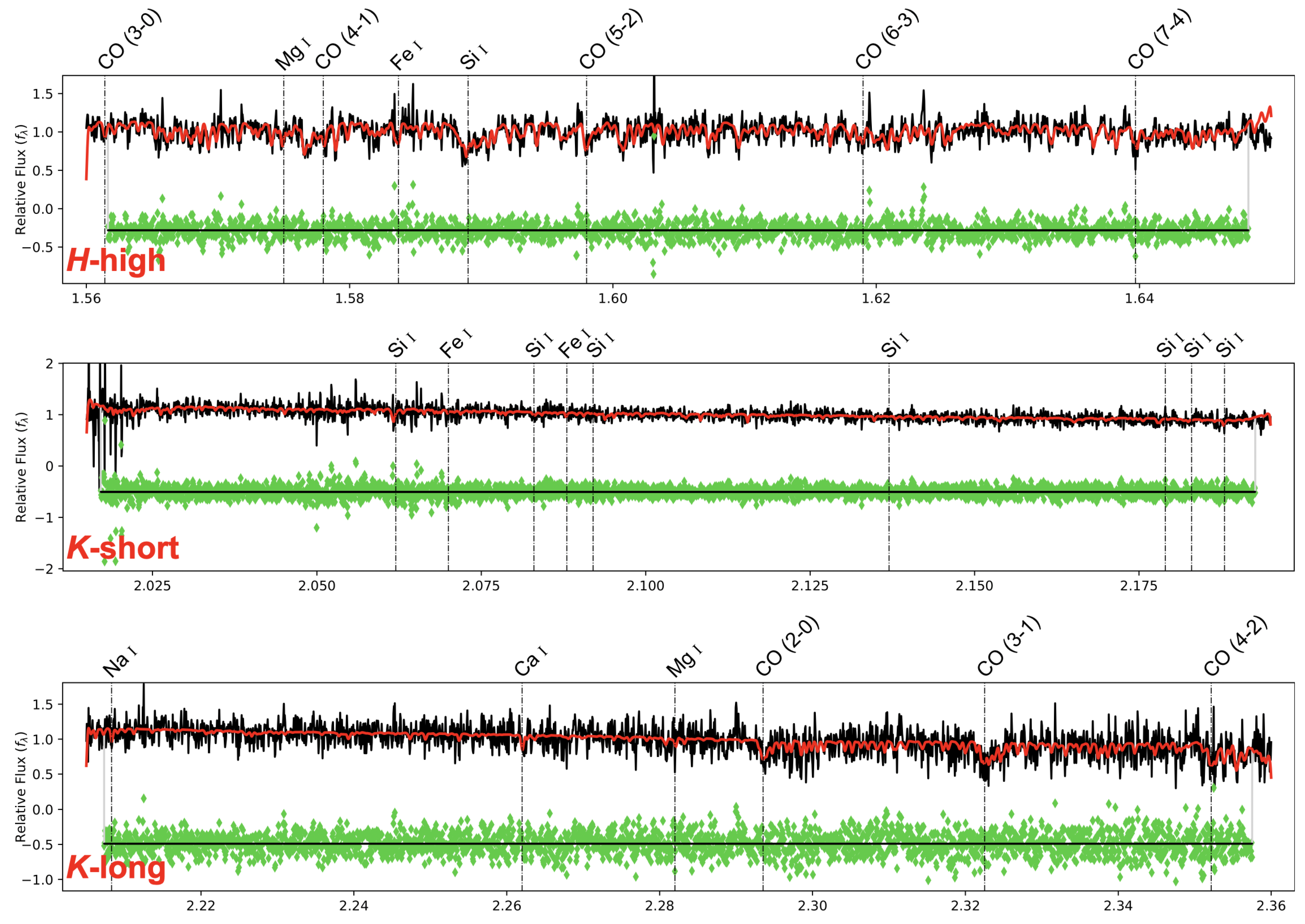
4.2. MARCS Synthetic Library of Stellar Spectra
4.3. HARMONI Instrument and HSIM Simulator
| HARMONI grating | Exposure time (NDIT) | Sensitivity (NDIT) |
| (1) | (2) | (3) |
| H-high | 16 | 12 |
| K-short | 30 | 24 |
| K-long | 20 | 16 |
4.4. HARMONI Simulations
4.4.1. Creation of the Input-Noiseless Cubes for HSIM
4.4.2. HSIM Output Datacubes
5. Results
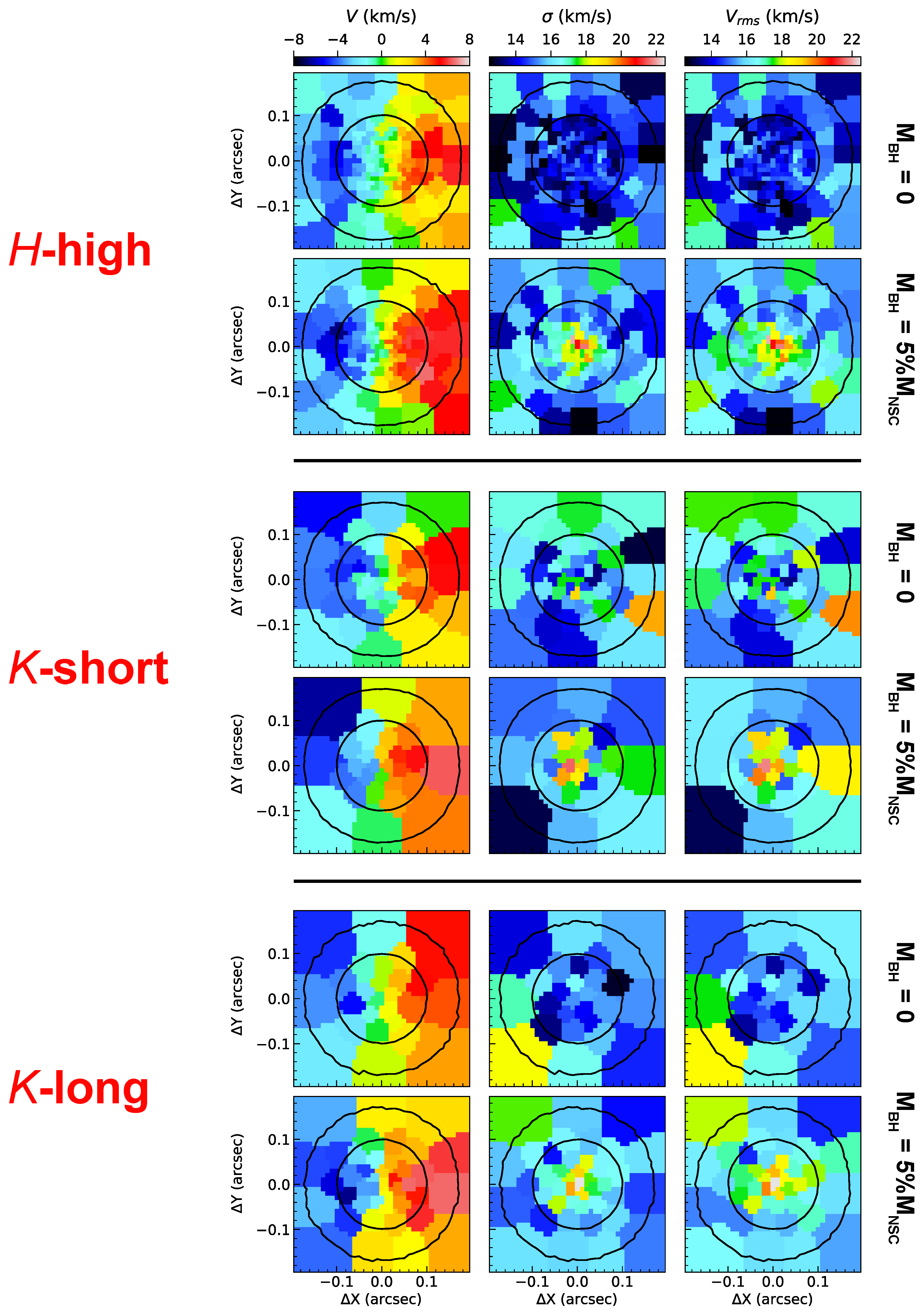
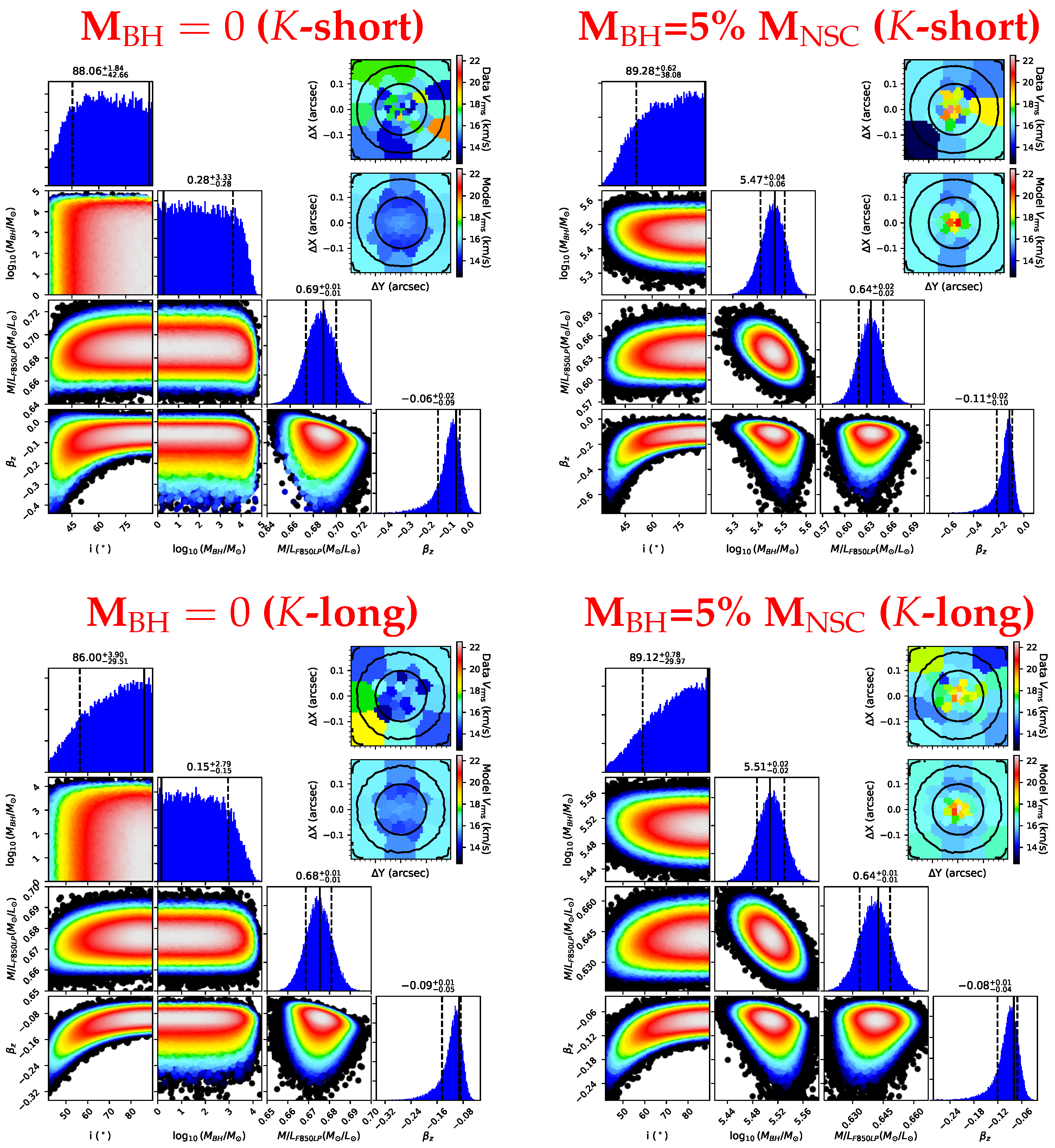
5.1. Stellar Kinematics Extraction
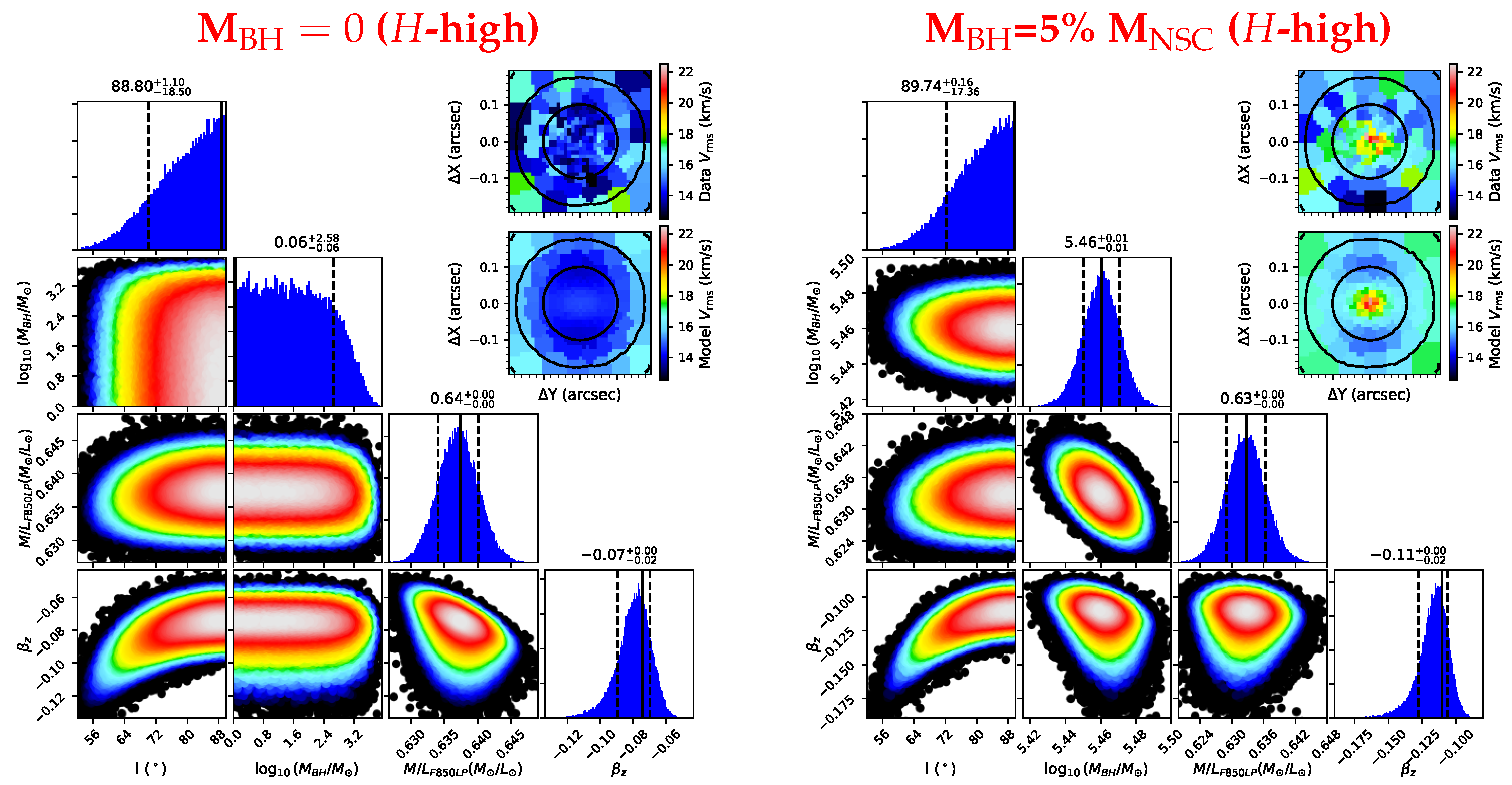
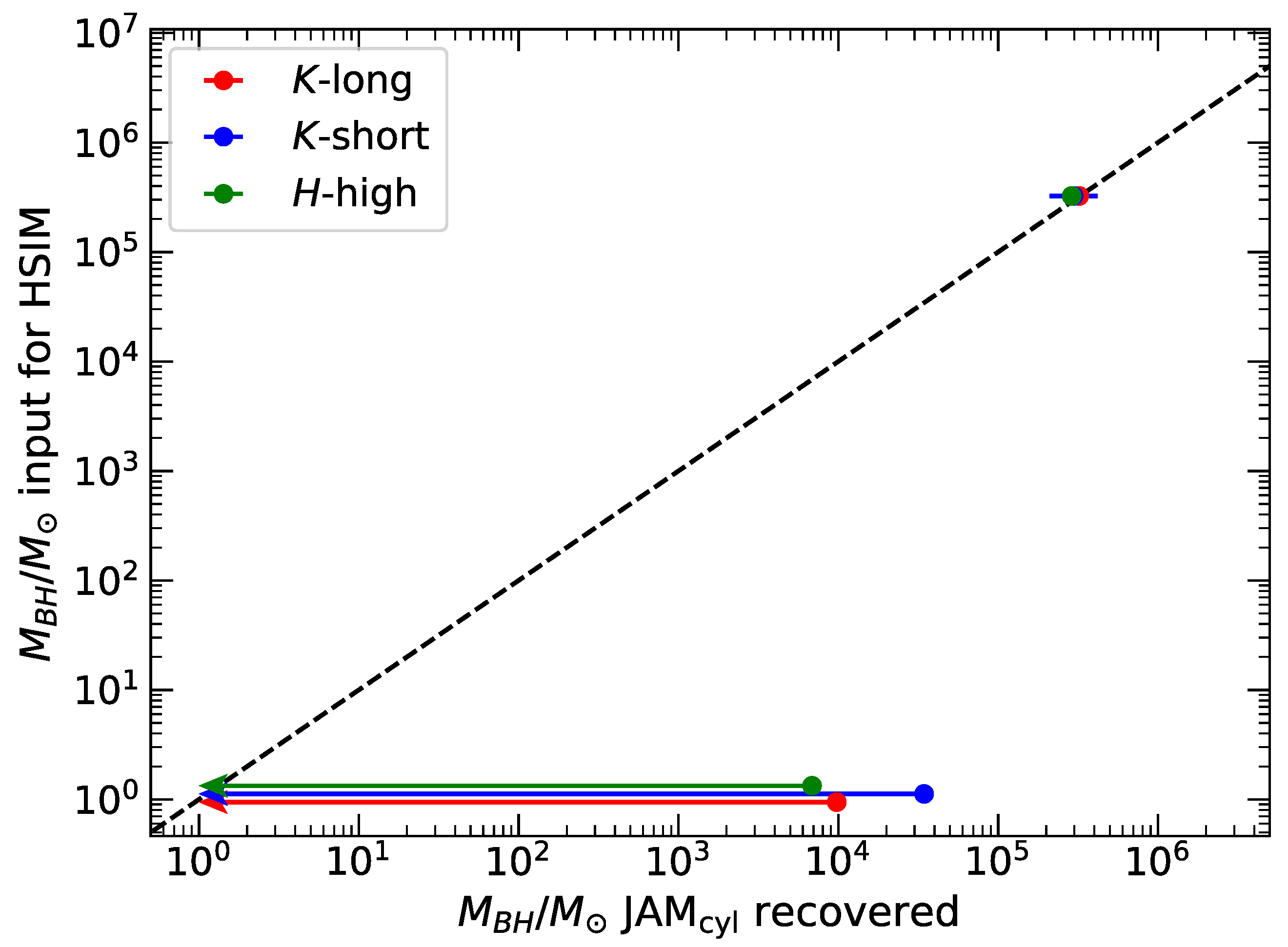
5.2. The Black Hole Mass Recovering
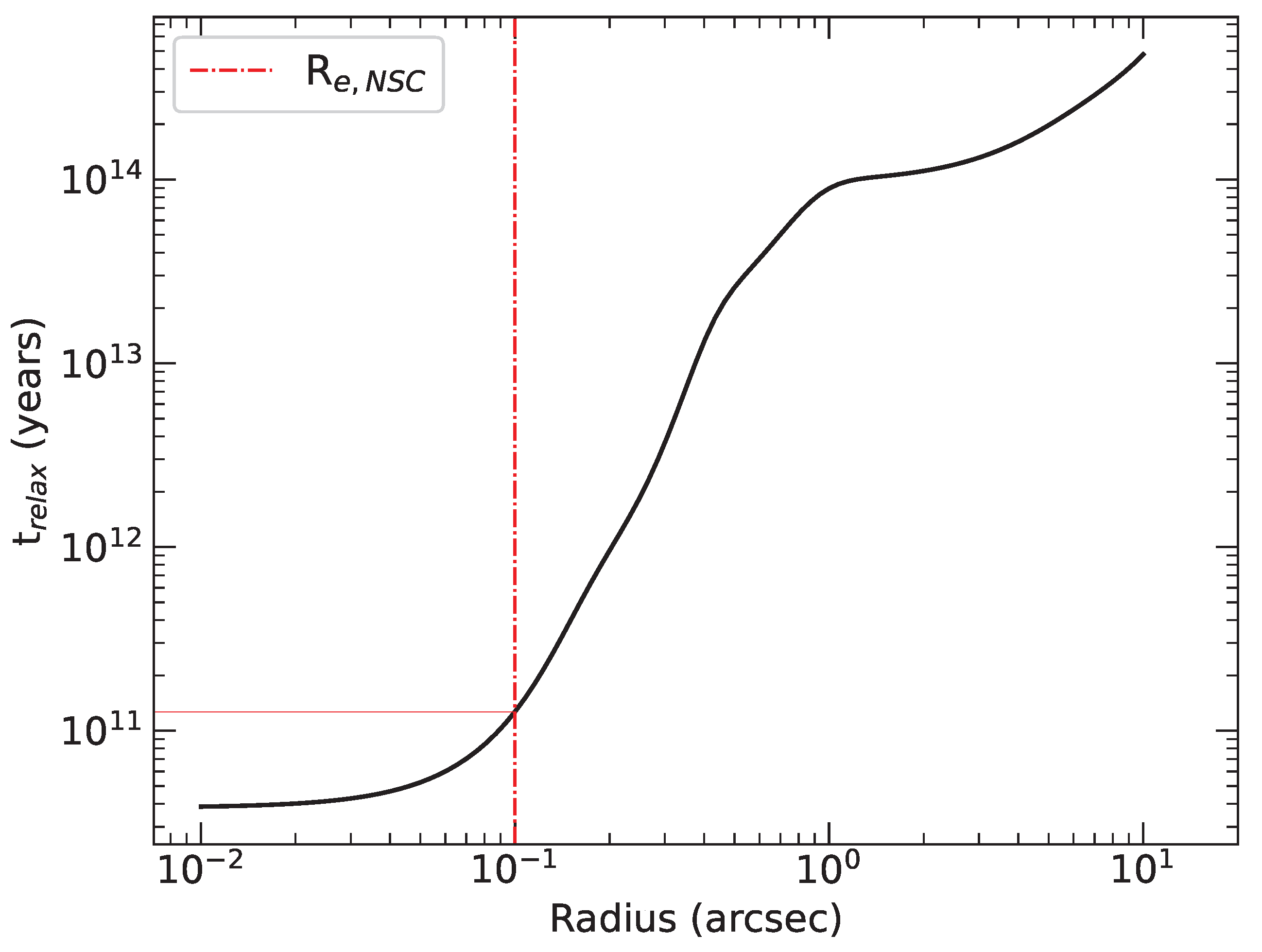
5.3. Dynamical Mass-Segregation in FCC 119 NSC?
5.4. Constraint on Nearby NSC Brightness and Sensitivity
6. Conclusions
Acknowledgements
Data Availability
| 1 | |
| 2 | NASA/IPAC Extragalactic Database: https://ned.ipac.caltech.edu
|
| 3 | HyperLeda: https://leda.univ-lyon1.fr
|
| 4 | |
| 5 | |
| 6 |
SExtractor: https://github.com/astromatic/sextractor/
|
| 7 |
acstools v3.7.0: https://pypi.org/project/acstools/
|
| 8 | |
| 9 | v5.0.15: https://pypi.org/project/mgefit/
|
| 10 |
jampy v7.2.4: https://pypi.org/project/jampy/
|
| 11 | v9.2.1: https://pypi.org/project/ppxf/
|
| 12 | v3.1.5: https://pypi.org/project/vorbin/
|
| 13 | v2.0.9: https://pypi.org/project/adamet/
|
References
- Ahn, C. P., Seth, A. C., Cappellari, M., et al. 2018, The Black Hole in the Most Massive Ultracompact Dwarf Galaxy M59-UCD3, ApJ, 858, 102. [CrossRef]
- Astropy Collaboration, Price-Whelan, A. M., Lim, P. L., et al. 2022, The Astropy Project: Sustaining and Growing a Community-oriented Open-source Project and the Latest Major Release (v5.0) of the Core Package, ApJ, 935, 167. [CrossRef]
- Avila, R. J., Hack, W. J., & STScI AstroDrizzle Team. 2012, in American Astronomical Society Meeting Abstracts, Vol. 220, American Astronomical Society Meeting Abstracts #220, 135.13.
- Bahcall, J. N., & Wolf, R. A. 1977, The star distribution around a massive black hole in a globular cluster. II. Unequal star masses., ApJ, 216, 883. [CrossRef]
- Baldassare, V. F., Stone, N. C., Foord, A., Gallo, E., & Ostriker, J. P. 2022, Massive Black Hole Formation in Dense Stellar Environments: Enhanced X-Ray Detection Rates in High-velocity Dispersion Nuclear Star Clusters, ApJ, 929, 84. [CrossRef]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, The FIRST Survey: Faint Images of the Radio Sky at Twenty Centimeters, ApJ, 450, 559. [CrossRef]
- Bertin, E., & Arnouts, S. 1996, SExtractor: Software for source extraction., A&AS, 117, 393. [CrossRef]
- Bianchini, P., Sills, A., van de Ven, G., & Sippel, A. C. 2017, The relation between the mass-to-light ratio and the relaxation state of globular clusters, MNRAS, 469, 4359, . [CrossRef]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, Studies of the Virgo cluster. II. A catalog of 2096 galaxies in the Virgo cluster area., AJ, 90, 1681. [CrossRef]
- Binggeli, B., Tammann, G. A., & Sandage, A. 1987, Studies of the Virgo Cluster. VI. Morphological and Kinematical Structure of the Virgo Cluster, AJ, 94, 251, . [CrossRef]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, The ACS Fornax Cluster Survey. V. Measurement and Recalibration of Surface Brightness Fluctuations and a Precise Value of the Fornax-Virgo Relative Distance, ApJ, 694, 556, . [CrossRef]
- Böhringer, H., Briel, U. G., Schwarz, R. A., et al. 1994, The structure of the Virgo cluster of galaxies from Rosat X-ray images, Nature, 368, 828. [CrossRef]
- Böker, T., Laine, S., van der Marel, R. P., et al. 2002, A Hubble Space Telescope Census of Nuclear Star Clusters in Late-Type Spiral Galaxies. I. Observations and Image Analysis, AJ, 123, 1389. [CrossRef]
- Boselli, A., Eales, S., Cortese, L., et al. 2010, The Herschel Reference Survey, PASP,, 122, 261. [CrossRef]
- Bradley, L., Sipõcz, B., Robitaille, T., et al. 2024, astropy/photutils: 2.0.2,, 2.0.2 Zenodo, . [CrossRef]
- Busso, G., Cacciari, C., Bellazzini, M., et al. 2022, Gaia DR3 documentation Chapter 5: Photometric data,, Gaia DR3 documentation, European Space Agency; Gaia Data Processing and Analysis Consortium. id. 5. https://gea.esac.esa.int/archive/documentation/GDR3/index.html.
- Cappellari, M. 2002, Efficient multi-Gaussian expansion of galaxies, MNRAS, 333, 400. [CrossRef]
- Cappellari, M. 2008, Measuring the inclination and mass-to-light ratio of axisymmetric galaxies via anisotropic Jeans models of stellar kinematics, MNRAS, 390, 71, . [CrossRef]
- Cappellari, M. 2020, Efficient solution of the anisotropic spherically aligned axisymmetric Jeans equations of stellar hydrodynamics for galactic dynamics, MNRAS, 494, 4819. [CrossRef]
- Cappellari, M. 2023, Full spectrum fitting with photometry in PPXF: stellar population versus dynamical masses, non-parametric star formation history and metallicity for 3200 LEGA-C galaxies at redshift z ≈ 0.8, MNRAS, 526, 3273, . [CrossRef]
- Cappellari, M., & Copin, Y. 2003, Adaptive spatial binning of integral-field spectroscopic data using Voronoi tessellations, MNRAS, 342, 345. [CrossRef]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, The ATLAS3D project - I. A volume-limited sample of 260 nearby early-type galaxies: science goals and selection criteria, MNRAS, 413, 813. [CrossRef]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, The ATLAS3D project - XV. Benchmark for early-type galaxies scaling relations from 260 dynamical models: mass-to-light ratio, dark matter, Fundamental Plane and Mass Plane, MNRAS, 432, 1709, . [CrossRef]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, The Relationship between Infrared, Optical, and Ultraviolet Extinction, ApJ, 345, 245. [CrossRef]
- Charlot, S., & Fall, S. M. 2000, A Simple Model for the Absorption of Starlight by Dust in Galaxies, ApJ, 539, 718, . [CrossRef]
- Ciotti, L. 1991, Stellar systems following the R1/m luminosity law., A&A, 249, 99.
- Ciotti, L., & Bertin, G. 1999, Analytical properties of the R1/m law, A&A, 352, 447. [CrossRef]
- Côté, P., Piatek, S., Ferrarese, L., et al. 2006, The ACS Virgo Cluster Survey. VIII. The Nuclei of Early-Type Galaxies, ApJS, 165, 57. [CrossRef]
- Crespo Gómez, A., Piqueras López, J., Arribas, S., et al. 2021, Stellar kinematics in the nuclear regions of nearby LIRGs with VLT-SINFONI. Comparison with gas phases and implications for dynamical mass estimations, A&A, 650, A149. [CrossRef]
- Davies, J. I., Baes, M., Bendo, G. J., et al. 2010, The Herschel Virgo Cluster Survey. I. Luminosity function, A&A, 518, L48. [CrossRef]
- Davies, J. I., Bianchi, S., Baes, M., et al. 2013, The Herschel Fornax Cluster Survey - I. The bright galaxy sample, MNRAS, 428, 834. [CrossRef]
- Davies, R., Ageorges, N., Barl, L., et al. 2010, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 7735, Ground-based and Airborne Instrumentation for Astronomy III, ed. I. S. McLean, S. K. Ramsay, & H. Takami, 77352A. [CrossRef]
- Davies, R., Hörmann, V., Rabien, S., et al. 2021, MICADO: The Multi-Adaptive Optics Camera for Deep Observations, The Messenger, 182, 17. [CrossRef]
- Davis, T. A., Nguyen, D. D., Seth, A. C., et al. 2020, Revealing the intermediate-mass black hole at the heart of the dwarf galaxy NGC 404 with sub-parsec resolution ALMA observations, MNRAS, 496, 4061. [CrossRef]
- De Rijcke, S., Michielsen, D., Dejonghe, H., Zeilinger, W. W., & Hau, G. K. T. 2005, Formation and evolution of dwarf elliptical galaxies - I. Structural and kinematical properties, A&A, 438, 491, . [CrossRef]
- den Brok, M., Seth, A. C., Barth, A. J., et al. 2015, Measuring the Mass of the Central Black Hole in the Bulgeless Galaxy NGC 4395 from Gas Dynamical Modeling, ApJ, 809, 101, . [CrossRef]
- Ding, Y., Zhu, L., van de Ven, G., et al. 2023, The Fornax3D project: Environmental effects on the assembly of dynamically cold disks in Fornax cluster galaxies, A&A, 672, A84, . [CrossRef]
- Drinkwater, M. J., Gregg, M. D., & Colless, M. 2001, Substructure and Dynamics of the Fornax Cluster, ApJ, 548, L139. [CrossRef]
- Eftekhari, F. S., Peletier, R. F., Scott, N., et al. 2022, The SAMI–Fornax Dwarfs Survey – II. The Stellar Mass Fundamental Plane and the dark matter fraction of dwarf galaxies, Monthly Notices of the Royal Astronomical Society, 517, 4714, . [CrossRef]
- Emsellem, E., Monnet, G., & Bacon, R. 1994, The multi-gaussian expansion method: a tool for building realistic photometric and kinematical models of stellar systems I. The formalism, A&A, 285, 723.
- Erwin, P., & Gadotti, D. A. 2012, Do Nuclear Star Clusters and Supermassive Black Holes Follow the Same Host-Galaxy Correlations?, Advances in Astronomy, 2012, 946368, . [CrossRef]
- Fahrion, K., Lyubenova, M., van de Ven, G., et al. 2021, Diversity of nuclear star cluster formation mechanisms revealed by their star formation histories, A&A, 650, A137, . [CrossRef]
- Fahrion, K., Bulichi, T.-E., Hilker, M., et al. 2022, Nuclear star cluster formation in star-forming dwarf galaxies, A&A, 667, A101. [CrossRef]
- Ferguson, H. C. 1989, Galaxy Populations in the Fornax and Virgo Clusters, Ap&SS, 157, 227. [CrossRef]
- Ferrarese, L., & Merritt, D. 2000, A Fundamental Relation between Supermassive Black Holes and Their Host Galaxies, ApJ, 539, L9, . [CrossRef]
- Ferrarese, L., Côté, P., Jordán, A., et al. 2006, The ACS Virgo Cluster Survey. VI. Isophotal Analysis and the Structure of Early-Type Galaxies, ApJS, 164, 334. [CrossRef]
- Ferrarese, L., Côté, P., Cuillandre, J.-C., et al. 2012, THE NEXT GENERATION VIRGO CLUSTER SURVEY (NGVS). I. INTRODUCTION TO THE SURVEY*, The Astrophysical Journal Supplement Series, 200, 4. [CrossRef]
- Forbes, D. A., Spitler, L. R., Graham, A. W., et al. 2011, Bridging the gap between low- and high-mass dwarf galaxies, MNRAS, 413, 2665. [CrossRef]
- Gallo, E., Treu, T., Jacob, J., et al. 2008, AMUSE-Virgo. I. Supermassive Black Holes in Low-Mass Spheroids, ApJ, 680, 154. [CrossRef]
- Gallo, E., Treu, T., Marshall, P. J., et al. 2010, AMUSE-VIRGO. II. DOWN-SIZING IN BLACK HOLE ACCRETION, The Astrophysical Journal, 714, 25. [CrossRef]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, A Relationship between Nuclear Black Hole Mass and Galaxy Velocity Dispersion, ApJ, 539, L13. [CrossRef]
- Gebhardt, K., Lauer, T. R., Pinkney, J., et al. 2007, The Black Hole Mass and Extreme Orbital Structure in NGC 1399, The Astrophysical Journal, 671, 1321. [CrossRef]
- Georgiev, I. Y., & Böker, T. 2014, Nuclear star clusters in 228 spiral galaxies in the HST/WFPC2 archive: catalogue and comparison to other stellar systems, MNRAS, 441, 3570, . [CrossRef]
- Georgiev, I. Y., Böker, T., Leigh, N., Lützgendorf, N., & Neumayer, N. 2016, Masses and scaling relations for nuclear star clusters, and their co-existence with central black holes, MNRAS, 457, 2122. [CrossRef]
- Ginsburg, A., Sipocz, B. M., Brasseur, C. E., et al. 2019, astroquery: An Astronomical Web-querying Package in Python, AJ, 157, 98. [CrossRef]
- Graham, A. W. 2012, Extending the Mbh–σ diagram with dense nuclear star clusters, Monthly Notices of the Royal Astronomical Society, 422, 1586. [CrossRef]
- Graham, A. W., Erwin, P., Trujillo, I., & Asensio Ramos, A. 2003, A New Empirical Model for the Structural Analysis of Early-Type Galaxies, and A Critical Review of the Nuker Model, AJ, 125, 2951. [CrossRef]
- Graham, A. W., & Soria, R. 2019, Expected intermediate-mass black holes in the Virgo cluster - I. Early-type galaxies, MNRAS, 484, 794. [CrossRef]
- Graham, A. W., Soria, R., & Davis, B. L. 2018, Expected intermediate-mass black holes in the Virgo cluster – II. Late-type galaxies, Monthly Notices of the Royal Astronomical Society, 484, 814, . [CrossRef]
- Greene, J. E. 2012, Low-mass black holes as the remnants of primordial black hole formation, Nature Communications, 3, 1304, . [CrossRef]
- Greene, J. E., Strader, J., & Ho, L. C. 2020, Intermediate-Mass Black Holes, ARA&A, 58, 257, . [CrossRef]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A grid of MARCS model atmospheres for late-type stars. I. Methods and general properties, A&A, 486, 951, . [CrossRef]
- Haario, H., Saksman, E., & Tamminen, J. 2001, An adaptive Metropolis algorithm, Bernoulli, 7, 223.
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Array programming with NumPy, Nature, 585, 357, . [CrossRef]
- Ho, L. C., Greene, J. E., Filippenko, A. V., & Sargent, W. L. W. 2009, A Search for “Dwarf” Seyfert Nuclei. VII. A Catalog of Central Stellar Velocity Dispersions of Nearby Galaxies, ApJS, 183, 1, . [CrossRef]
- Houghton, R. C. W., Magorrian, J., Sarzi, M., et al. 2006, The central kinematics of NGC 1399 measured with 14 pc resolution, MNRAS, 367, 2. [CrossRef]
- Hoyer, N., Neumayer, N., Seth, A. C., Georgiev, I. Y., & Greene, J. E. 2023, Photometric and structural parameters of newly discovered nuclear star clusters in Local Volume galaxies, MNRAS, 520, 4664. [CrossRef]
- Hunter, J. D. 2007, Matplotlib: A 2D graphics environment, Computing In Science & Engineering, 9, 90. [CrossRef]
- Inayoshi, K., Visbal, E., & Haiman, Z. 2020, The Assembly of the First Massive Black Holes, ARA&A, 58, 27, . [CrossRef]
- Iodice, E., Capaccioli, M., Grado, A., et al. 2016, THE FORNAX DEEP SURVEY WITH VST. I. THE EXTENDED AND DIFFUSE STELLAR HALO OF NGC 1399 OUT TO 192 kpc, The Astrophysical Journal, 820, 42, . [CrossRef]
- Iodice, E., Sarzi, M., Bittner, A., et al. 2019, The Fornax3D project: Tracing the assembly history of the cluster from the kinematic and line-strength maps, A&A, 627, A136, . [CrossRef]
- Jedrzejewski, R. I. 1987, CCD surface photometry of elliptical galaxies - I. Observations, reduction and results., MNRAS, 226, 747. [CrossRef]
- Jordan, A., Blakeslee, J. P., Côté, P., et al. 2007, The ACS Fornax Cluster Survey. I. Introduction to the Survey and Data Reduction Procedures, ApJS, 169, 213. [CrossRef]
- Kashibadze, Olga G., Karachentsev, Igor D., & Karachentseva, Valentina E. 2020, Structure and kinematics of the Virgo cluster of galaxies, A&A, 635, A135. [CrossRef]
- Kormendy, J., & Gebhardt, K. 2001, in American Institute of Physics Conference Series, Vol. 586, 20th Texas Symposium on relativistic astrophysics, ed. J. C. Wheeler & H. Martel, 363–381, . [CrossRef]
- Krist, J. E., Hook, R. N., & Stoehr, F. 2011, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 8127, Optical Modeling and Performance Predictions V, ed. M. A. Kahan, 81270J, . [CrossRef]
- Kuijken, K. 2011, OmegaCAM: ESO’s Newest Imager, The Messenger, 146, 8.
- Kuijken, K., Bender, R., Cappellaro, E., et al. 2002, OmegaCAM: the 16k×16k CCD camera for the VLT survey telescope, The Messenger, 110, 15.
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, The UKIRT Infrared Deep Sky Survey (UKIDSS), MNRAS, 379, 1599. [CrossRef]
- Leigh, N., Böker, T., & Knigge, C. 2012, Nuclear star clusters and the stellar spheroids of their host galaxies, MNRAS, 424, 2130. [CrossRef]
- Liu, Y., Peng, E. W., Jordán, A., et al. 2019, The ACS Fornax Cluster Survey. III. Globular Cluster Specific Frequencies of Early-type Galaxies, The Astrophysical Journal, 875, 156, . [CrossRef]
- Loni, A., Serra, P., Kleiner, D., et al. 2021, A blind ATCA HI survey of the Fornax galaxy cluster. Properties of the HI detections, A&A, 648, A31. [CrossRef]
- Lyubenova, Mariya, & Tsatsi, Athanassia. 2019, Nuclear angular momentum of early-type galaxies hosting nuclear star clusters, A&A, 629, A44. [CrossRef]
- Ma, C.-P., Greene, J. E., McConnell, N., et al. 2014, The MASSIVE Survey. I. A Volume-limited Integral-field Spectroscopic Study of the Most Massive Early-type Galaxies within 108 Mpc, ApJ, 795, 158. [CrossRef]
- Maraston, C., & Strömbäck, G. 2011, Stellar population models at high spectral resolution, MNRAS, 418, 2785, . [CrossRef]
- Markwardt, C. B. 2009, in Astronomical Society of the Pacific Conference Series, Vol. 411, Astronomical Data Analysis Software and Systems XVIII, ed. D. A. Bohlender, D. Durand, & P. Dowler, 251, . [CrossRef]
- McDonald, M., Courteau, S., & Tully, R. B. 2009, The near-IR luminosity function and bimodal surface brightness distributions of Virgo cluster galaxies, MNRAS, 394, 2022, . [CrossRef]
- McLaughlin, D. E. 1999, Evidence in Virgo for the Universal Dark Matter Halo, The Astrophysical Journal, 512, L9. [CrossRef]
- Mei, S., Blakeslee, J. P., Côté, P., et al. 2007, The ACS Virgo Cluster Survey. XIII. SBF Distance Catalog and the Three-dimensional Structure of the Virgo Cluster, ApJ, 655, 144, . [CrossRef]
- Mezcua, M. 2017, Observational evidence for intermediate-mass black holes, International Journal of Modern Physics D, 26, 1730021. [CrossRef]
- Mitzkus, M., Cappellari, M., & Walcher, C. J. 2017, Dominant dark matter and a counter-rotating disc: MUSE view of the low-luminosity S0 galaxy NGC 5102, MNRAS, 464, 4789, . [CrossRef]
- Muñoz, R. P., Eigenthaler, P., Puzia, T. H., et al. 2015, Unveiling a Rich System of Faint Dwarf Galaxies in the Next Generation Fornax Survey, ApJ, 813, L15, . [CrossRef]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, The Structure of Cold Dark Matter Halos, ApJ, 462, 563, . [CrossRef]
- Neumayer, N., Seth, A., & Böker, T. 2020, Nuclear star clusters, A&ARv, 28, 4. [CrossRef]
- Neumayer, N., & Walcher, C. J. 2012, Are Nuclear Star Clusters the Precursors of Massive Black Holes?, Advances in Astronomy, 2012, 709038. [CrossRef]
- Nguyen, D. D. 2017, Improved dynamical constraints on the mass of the central black hole in NGC 404, arXiv e-prints, arXiv:1712.02470. [CrossRef]
- Nguyen, D. D. 2019, in ALMA2019: Science Results and Cross-Facility Synergies, 106. [CrossRef]
- Nguyen, D. D., Cappellari, M., & Pereira-Santaella, M. 2023, Simulating supermassive black hole mass measurements for a sample of ultramassive galaxies using ELT/HARMONI high-spatial-resolution integral-field stellar kinematics, MNRAS, 526, 3548, . [CrossRef]
- Nguyen, D. D., Seth, A. C., den Brok, M., et al. 2017, Improved Dynamical Constraints on the Mass of the Central Black Hole in NGC 404, ApJ, 836, 237. [CrossRef]
- Nguyen, D. D., Seth, A. C., Neumayer, N., et al. 2018, Nearby Early-type Galactic Nuclei at High Resolution: Dynamical Black Hole and Nuclear Star Cluster Mass Measurements, ApJ, 858, 118. [CrossRef]
- Nguyen, D. D., Seth, A. C., Neumayer, N., et al. 2019, Improved Dynamical Constraints on the Masses of the Central Black Holes in Nearby Low-mass Early-type Galactic Nuclei and the First Black Hole Determination for NGC 205, ApJ, 872, 104, . [CrossRef]
- Nguyen, D. D., den Brok, M., Seth, A. C., et al. 2020, The MBHBM★ Project. I. Measurement of the Central Black Hole Mass in Spiral Galaxy NGC 3504 Using Molecular Gas Kinematics, ApJ, 892, 68. [CrossRef]
- Nguyen, D. D., Izumi, T., Thater, S., et al. 2021, Black hole mass measurement using ALMA observations of [CI] and CO emissions in the Seyfert 1 galaxy NGC 7469, MNRAS, 504, 4123, . [CrossRef]
- Nguyen, D. D., Bureau, M., Thater, S., et al. 2022, The MBHBM★ Project - II. Molecular gas kinematics in the lenticular galaxy NGC 3593 reveal a supermassive black hole, MNRAS, 509, 2920. [CrossRef]
- Nguyen, D. D., Ngo, H. N., Le, T. Q. T., et al. 2025, Supermassive black hole mass measurement in the spiral galaxy NGC 4736 using JWST/NIRSpec stellar kinematics, A&A, 698, L9, . [CrossRef]
- Nguyen, D. D., Cappellari, M., Ngo, H. N., et al. 2025, Simulating Intermediate Black Hole Mass Measurements for a Sample of Galaxies with Nuclear Star Clusters Using ELT/HARMONI High Spatial Resolution Integral-field Stellar Kinematics, AJ, 170, 124, . [CrossRef]
- Norris, M. A., Kannappan, S. J., Forbes, D. A., et al. 2014, The AIMSS Project - I. Bridging the star cluster-galaxy divide, MNRAS, 443, 1151. [CrossRef]
- Oke, J. B. 1974, Absolute Spectral Energy Distributions for White Dwarfs, ApJS, 27, 21. [CrossRef]
- Ordenes-Briceño, Y., Puzia, T. H., Eigenthaler, P., et al. 2018, The Next Generation Fornax Survey (NGFS). IV. Mass and Age Bimodality of Nuclear Clusters in the Fornax Core Region, ApJ, 860, 4, . [CrossRef]
- Ordenes-Briceño, Y., Eigenthaler, P., Taylor, M. A., et al. 2018, The Next Generation Fornax Survey (NGFS). III. Revealing the Spatial Substructure of the Dwarf Galaxy Population Inside Half of Fornax’s Virial Radius, The Astrophysical Journal, 859, 52, . [CrossRef]
- Pancino, E. 2016, in Astronomical Society of the Pacific Conference Series, Vol. 503, The Science of Calibration, ed. S. Deustua, S. Allam, D. Tucker, & J. A. Smith, 243.
- Pechetti, R., Seth, A., Neumayer, N., et al. 2020, Luminosity Models and Density Profiles for Nuclear Star Clusters for a Nearby Volume-limited Sample of 29 Galaxies, ApJ, 900, 32, . [CrossRef]
- Peng, E. W., Jordán, A., Côté, P., et al. 2008, The ACS Virgo Cluster Survey. XV. The Formation Efficiencies of Globular Clusters in Early-Type Galaxies: The Effects of Mass and Environment*, The Astrophysical Journal, 681, 197. [CrossRef]
- Romero-Gómez, J., Peletier, R. F., Aguerri, J. A. L., et al. 2023, The SAMI–Fornax Dwarfs Survey – III. Evolution of [α/Fe] in dwarfs, from Galaxy Clusters to the Local Group, Monthly Notices of the Royal Astronomical Society, 522, 130. [CrossRef]
- Rossa, J., van der Marel, R. P., Böker, T., et al. 2006, Hubble Space Telescope STIS Spectra of Nuclear Star Clusters in Spiral Galaxies: Dependence of Age and Mass on Hubble Type, AJ, 132, 1074. [CrossRef]
- Sánchez-Janssen, R., Côté, P., Ferrarese, L., et al. 2019, The Next Generation Virgo Cluster Survey. XXIII. Fundamentals of Nuclear Star Clusters over Seven Decades in Galaxy Mass, ApJ, 878, 18. [CrossRef]
- Scharf, C. A., Zurek, D. R., & Bureau, M. 2005, The Chandra Fornax Survey. I. The Cluster Environment, ApJ, 633, 154, . [CrossRef]
- Schipani, P., Noethe, L., Arcidiacono, C., et al. 2012, Removing static aberrations from the active optics system of a wide-field telescope, Journal of the Optical Society of America A, 29, 1359. [CrossRef]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, Measuring Reddening with Sloan Digital Sky Survey Stellar Spectra and Recalibrating SFD, ApJ, 737, 103. [CrossRef]
- Sersic, J. L. 1968, Atlas de galaxias australes (Córdoba: Obs. Astron. Univ. Nacional de Córdoba).
- Seth, A., Agüeros, M., Lee, D., & Basu-Zych, A. 2008, The Coincidence of Nuclear Star Clusters and Active Galactic Nuclei, ApJ, 678, 116. [CrossRef]
- Seth, A. C., Cappellari, M., Neumayer, N., et al. 2010, The NGC 404 Nucleus: Star Cluster and Possible Intermediate-mass Black Hole, ApJ, 714, 713, . [CrossRef]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, The Two Micron All Sky Survey (2MASS), AJ, 131, 1163, . [CrossRef]
- Spavone, M., Iodice, E., van de Ven, G., et al. 2020, The Fornax Deep Survey with VST. VIII. Connecting the accretion history with the cluster density, A&A, 639, A14, . [CrossRef]
- Spavone, M., Iodice, E., D’Ago, G., et al. 2022, Fornax3D project: Assembly history of massive early-type galaxies in the Fornax cluster from deep imaging and integral field spectroscopy, A&A, 663, A135. [CrossRef]
- Spengler, C., Côté, P., Roediger, J., et al. 2017, Virgo Redux: The Masses and Stellar Content of Nuclei in Early-type Galaxies from Multiband Photometry and Spectroscopy, ApJ, 849, 55. [CrossRef]
- Spitzer, L. S. 1987, Dynamical Evolution of Globular Clusters (Princeton University Press). http://www.jstor.org/stable/j.ctt7ztvx4.
- Su, Y., Nulsen, P. E. J., Kraft, R. P., et al. 2017, Gas Sloshing Regulates and Records the Evolution of the Fornax Cluster, ApJ, 851, 69. [CrossRef]
- Su, Alan H., Salo, Heikki, Janz, Joachim, Venhola, Aku, & Peletier, Reynier F. 2022, Photometric properties of nuclear star clusters and their host galaxies in the Fornax cluster, A&A, 664, A167, . [CrossRef]
- Sun, J., Leroy, A. K., Schinnerer, E., et al. 2020, Molecular Gas Properties on Cloud Scales across the Local Star-forming Galaxy Population, The Astrophysical Journal Letters, 901, L8, . [CrossRef]
- Thater, S., Krajnović, D., Nguyen, D. D., Iguchi, S., & Weilbacher, P. M. 2020, in Galactic Dynamics in the Era of Large Surveys, ed. M. Valluri & J. A. Sellwood, Vol. 353, 199–202, . [CrossRef]
- Thater, S., Lyubenova, M., Fahrion, K., et al. 2023a, Effect of the initial mass function on the dynamical SMBH mass estimate in the nucleated early-type galaxy FCC 47, A&A, 675, A18, . [CrossRef]
- Thater, S., Lyubenova, M., Fahrion, K., et al. 2023b, Effect of the initial mass function on the dynamical SMBH mass estimate in the nucleated early-type galaxy FCC 47, A&A, 675, A18, . [CrossRef]
- Thater, S., Krajnović, D., Bourne, M. A., et al. 2017, A low upper mass limit for the central black hole in the late-type galaxy NGC 4414, A&A, 597, A18, . [CrossRef]
- Thater, S., Krajnović, D., Weilbacher, P. M., et al. 2022, Cross-checking SMBH mass estimates in NGC 6958 - I. Stellar dynamics from adaptive optics-assisted MUSE observations, MNRAS, 509, 5416. [CrossRef]
- Thatte, N. A., Clarke, F., Bryson, I., et al. 2016, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9908, Ground-based and Airborne Instrumentation for Astronomy VI, ed. C. J. Evans, L. Simard, & H. Takami, 99081X. [CrossRef]
- Thatte, N. A., Bryson, I., Clarke, F., et al. 2020, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 11447, Ground-based and Airborne Instrumentation for Astronomy VIII, ed. C. J. Evans, J. J. Bryant, & K. Motohara, 114471W, . [CrossRef]
- Tremaine, S., Richstone, D. O., Byun, Y.-I., et al. 1994, A family of models for spherical stellar systems, AJ, 107, 634, . [CrossRef]
- Truemper, J. 1993, ROSAT-A New Look at the X-ray Sky, Science, 260, 1769. [CrossRef]
- Trujillo, I., Erwin, P., Asensio Ramos, A., & Graham, A. W. 2004, Evidence for a New Elliptical-Galaxy Paradigm: Sérsic and Core Galaxies, AJ, 127, 1917. [CrossRef]
- Turner, M. L., Côté, P., Ferrarese, L., et al. 2012, The ACS Fornax Cluster Survey. VI. The Nuclei of Early-type Galaxies in the Fornax Cluster, ApJS, 203, 5, . [CrossRef]
- Urban, O., Werner, N., Simionescu, A., Allen, S. W., & Böhringer, H. 2011, X-ray spectroscopy of the Virgo Cluster out to the virial radius, Monthly Notices of the Royal Astronomical Society, 414, 2101, . [CrossRef]
- Valluri, M., Ferrarese, L., Merritt, D., & Joseph, C. L. 2005, The Low End of the Supermassive Black Hole Mass Function: Constraining the Mass of a Nuclear Black Hole in NGC 205 via Stellar Kinematics, ApJ, 628, 137. [CrossRef]
- van de Sande, J., Kriek, M., Franx, M., Bezanson, R., & van Dokkum, P. G. 2015, The Relation between Dynamical Mass-to-light Ratio and Color for Massive Quiescent Galaxies out to z ~2 and Comparison with Stellar Population Synthesis Models, ApJ, 799, 125. [CrossRef]
- Van Rossum, G., & Drake, F. L. 2009, Python 3 Reference Manual (Scotts Valley, CA: CreateSpace).
- Vanderbeke, J., Baes, M., Romanowsky, A. J., & Schmidtobreick, L. 2011, Optical and near-infrared velocity dispersions of early-type galaxies*, Monthly Notices of the Royal Astronomical Society, 412, 2017, . [CrossRef]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, SciPy 1.0: fundamental algorithms for scientific computing in Python, Nature Methods, 17, 261. [CrossRef]
- Voggel, K. T., Seth, A. C., Neumayer, N., et al. 2018, Upper Limits on the Presence of Central Massive Black Holes in Two Ultra-compact Dwarf Galaxies in Centaurus A, ApJ, 858, 20, . [CrossRef]
- Volonteri, M., Haardt, F., & Gültekin, K. 2008, Compact massive objects in Virgo galaxies: the black hole population, Monthly Notices of the Royal Astronomical Society, 384, 1387, . [CrossRef]
- Walcher, C. J., van der Marel, R. P., McLaughlin, D., et al. 2005, Masses of Star Clusters in the Nuclei of Bulgeless Spiral Galaxies, ApJ, 618, 237. [CrossRef]
- Wegner, G., Bernardi, M., Willmer, C. N. A., et al. 2003, Redshift-Distance Survey of Early-Type Galaxies: Spectroscopic Data, AJ, 126, 2268. [CrossRef]
- White, R. L., Becker, R. H., Helfand, D. J., & Gregg, M. D. 1997, A Catalog of 1.4 GHz Radio Sources from the FIRST Survey, ApJ, 475, 479. [CrossRef]
- Willmer, C. N. A. 2018, The Absolute Magnitude of the Sun in Several Filters, ApJS, 236, 47. [CrossRef]
- Wilson, C. D., Warren, B. E., Israel, F. P., et al. 2009, The James Clerk Maxwell Telescope Nearby Galaxies Legacy Survey. I. Star-Forming Molecular Gas in Virgo Cluster Spiral Galaxies, ApJ, 693, 1736. [CrossRef]
- Zieleniewski, S., Thatte, N., Kendrew, S., et al. 2015, HSIM: a simulation pipeline for the HARMONI integral field spectrograph on the European ELT, MNRAS, 453, 3754, . [CrossRef]
| ELT Observability: | |
| Galaxy zone of avoidance: | |
| Central stellar-velocity dispersion: | km s−1 |
| Distant range: | Mpc |
| Galaxies -band absolute magnitude: | |
| Galaxy stellar mass range: | ≲ M★,gal |
| Effective : | kpc |
| NSC mass range: | |
| NSC effective radius: | pc |
| j | ( | ||
| (1) | (2) | (3) | (4) |
| 1 | 9428.31 | 0.060 | 1.00 |
| 2 | 2535.54 | 0.131 | 1.00 |
| 3 | 175.71 | 0.346 | 1.00 |
| 4 | 91.52 | 2.679 | 1.00 |
| 5 | 243.69 | 6.034 | 1.00 |
| 6 | 187.84 | 9.868 | 0.85 |
| 7 | 68.45 | 13.762 | 0.85 |
| 8 | 10.19 | 17.689 | 0.85 |
| 9 | 0.37 | 21.999 | 0.85 |
| Initial | Input | ||||||
| parameters | JAM guess | best-fit | (16–84)% | (0.14–99.86)% | best-fit | (16–84)% | (0.14–99.86)% |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| H-high | |||||||
| i (°) | 65 | 89 | >19 | >36 | 90 | >17 | >34 |
| /M⊙) | (*) | 0.06 | <2.58 | <3.68 | 5.460 | ±0.010 | ±0.031 |
| (M⊙/L⊙) | 0.6 | 0.637 | ±0.003 | ±0.009 | 0.633 | ±0.004 | ±0.011 |
| 0 | −0.074 | ±0.010 | ±0.039 | −0.110 | ±0.011 | ±0.044 | |
| K-short | |||||||
| i (°) | 65 | 88 | >43 | >56 | 89 | >38 | >56 |
| /M⊙) | (*) | 0.28 | <3.33 | <4.37 | 5.472 | ±0.050 | ±0.150 |
| (M⊙/L⊙) | 0.6 | 0.689 | ±0.013 | ±0.039 | 0.636 | ±0.017 | ±0.050 |
| 0 | −0.057 | ±0.052 | ±0.240 | −0.114 | ±0.062 | ±0.340 | |
| K-long | |||||||
| i (°) | 65 | 86 | >30 | >48 | 89 | >30 | >50 |
| /M⊙) | (*) | 0.15 | <2.79 | <3.92 | 5.507 | ±0.022 | ±0.065 |
| (M⊙/L⊙) | 0.6 | 0.675 | ±0.006 | ±0.019 | 0.643 | ±0.008 | ±0.022 |
| 0 | −0.093 | ±0.029 | ±0.130 | −0.080 | ±0.025 | ±0.230 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





