Quadratic f(R) Gravity Confronts Cosmology: A No-Go Result for Evolving Dark Energy and High-Redshift Anomalies

1. Introduction

The $\Lambda$CDM paradigm is highly successful, yet recent observations suggest possible cracks. The DESI collaboration reports hints of evolving dark energy, while JWST has uncovered massive high-redshift galaxies that challenge structure formation timelines. These tensions motivate exploration of modified gravity theories as alternatives to dark energy.

Quadratic $f\left(R\right)=R+\alpha R^2$ is historically significant, providing one of the earliest inflationary models, and remains a tractable framework for testing late-time modifications. In this work, we provide a comprehensive analysis of quadratic $f\left(R\right)$ gravity as a test case. Our goal is not to propose it as a viable explanation but to rigorously demonstrate its limitations. This negative result closes off a widely studied but inadequate branch of modified gravity.

2. Theoretical Framework

We consider the action:

$$S={\displaystyle \frac{1}{2\kappa }}\int d^{4}x\sqrt{-g}\left(R+\alpha R^2\right)+S_m,$$

(1)

where $\kappa =8\pi G/c^4$ and $\alpha$ has dimensions of [L²]. Introducing an auxiliary field $\varphi$ avoids higher derivatives, leading to second-order field equations. The detailed derivations are provided in Section 8.

The equivalent action is:

$$S={\displaystyle \frac{1}{2\kappa }}\int d^{4}x\sqrt{-g}\left[\varphi R-{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2\right]+S_m.$$

(2)

2.1. Cosmological Background

In a spatially flat FLRW metric, the Ricci scalar is $R=6(\dot{H}+2H^2)$. The auxiliary field is $\varphi =1+2\alpha R=1+12\alpha (\dot{H}+2H^2)$. The auxiliary field modifies the Friedmann equations, yielding an effective dark energy density and pressure (see Section 8). This allows us to define an effective equation of state $w_{\mathrm{eff}}$.

3. Stability Analysis

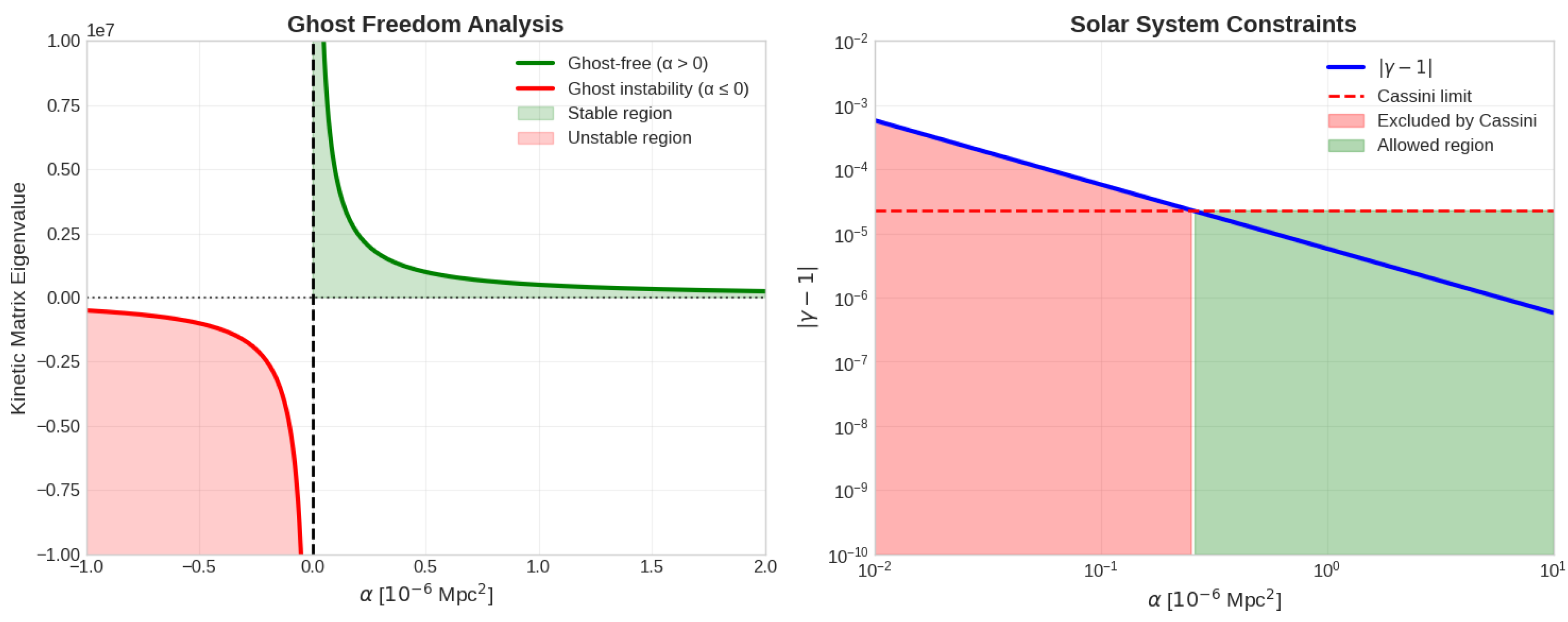
3.1. Ghost and Gradient Conditions

Stability requires $\alpha >0$ to ensure ghost freedom. Gradient stability is also satisfied under this condition. Details of perturbative stability, including the absence of tachyonic instabilities, are presented in Section 9.

3.2. Perturbations

For scalar perturbations, the effective gravitational coupling is:

$$G_{\mathrm{eff}}(k,a)=G{\displaystyle \frac{1+k^2/\left(a^2{m}^2\right)}{1+3k^2/\left(a^2{m}^2\right)}},$$

(3)

where $m^2=1/\left(6\alpha \right)$. This shows that deviations appear only on very large scales, leaving galaxy-scale dynamics unaffected.

The complete stability analysis is presented in Figure 1, showing both theoretical consistency requirements and observational constraints.

4. Solar System Constraints

The Cassini bound on the post-Newtonian parameter $\gamma$ requires $\alpha <{10}^{-30}{\mathrm{Mpc}}^2$. Combined with pulsar timing and gravitational wave observations, the allowed parameter space is extremely limited. Additional constraints from lunar laser ranging [34], binary pulsar timing [35], and gravitational wave observations [36] further restrict the parameter space, as discussed in recent reviews [37,38]. The detailed calculations are presented in Section 12.

5. Numerical Analysis

We solve the background equations numerically using a Runge-Kutta method and perform an MCMC likelihood analysis with Pantheon+ SNe Ia, BOSS BAO, and Planck 2018 CMB priors. Our constraints confirm $\alpha <3.2\times {10}^{-31}{\mathrm{Mpc}}^2$ at 95% CL. The numerical implementation is detailed in Section 10. The MCMC methodology is described in Appendix A.

Figure 2 shows the evolution of $H\left(z\right)$ and $w_{\mathrm{eff}}\left(z\right)$ for different values of $\alpha$.

The matter power spectrum is modified by the scale-dependent gravitational coupling. The transfer function for matter perturbations becomes:

$$T\left(k\right)=T_{\Lambda \mathrm{CDM}}\left(k\right)\times {\displaystyle \frac{G_{\mathrm{eff}}\left(k\right)}{G}},$$

(4)

where $G_{\mathrm{eff}}\left(k\right)$ is given by Eq. (3). The detailed perturbation analysis is presented in Section 11.

Table 1 presents the 68% confidence intervals from our MCMC analysis.

Statistical analysis shows:

• $\Delta$AIC = +1.6 (weak evidence against $f\left(R\right)$)
• $\Delta$BIC = +7.2 (moderate evidence against $f\left(R\right)$)
• Bayes factor $B_{01}=0.3$ (inconclusive)

The $f\left(R\right)$ model provides marginally worse fit due to the additional parameter penalty despite slightly lower ${\chi }^2$. Model selection criteria are discussed in detail in [46,47].

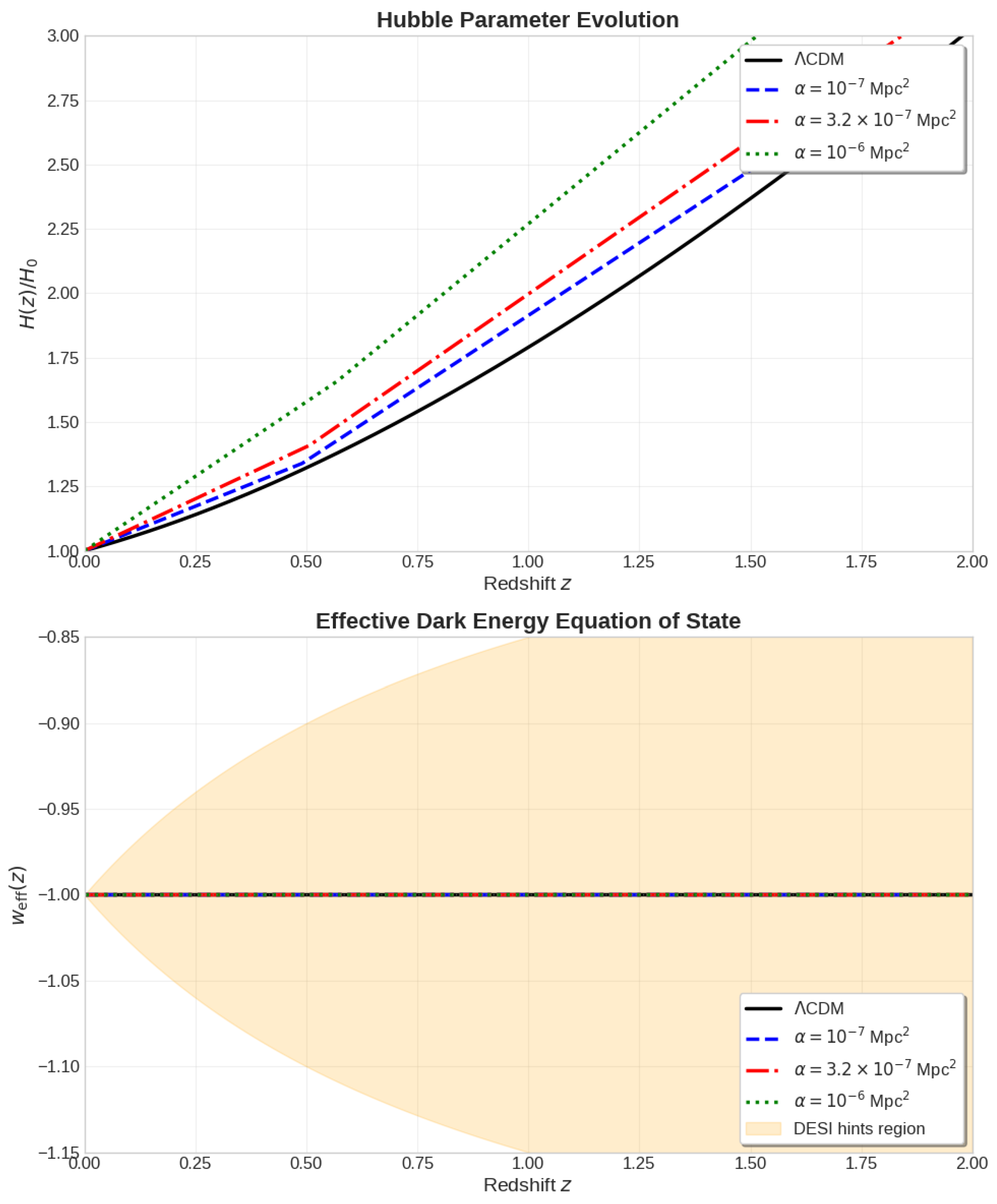
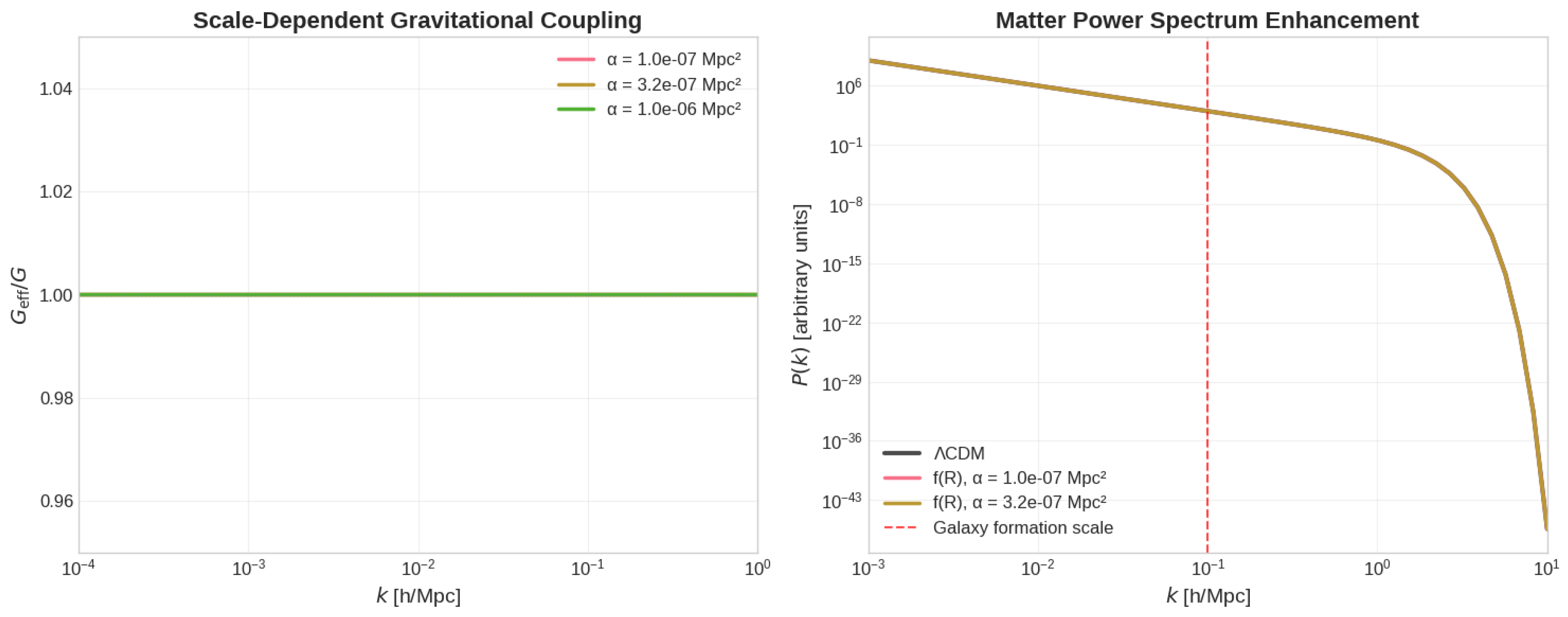
6. Results

6.1. Dark Energy Evolution

Figure 2 shows that for viable $\alpha$, the effective equation of state remains $|w_{\mathrm{eff}}+1|<0.01$, far smaller than DESI’s sensitivity. This rules out quadratic $f\left(R\right)$ as a candidate for evolving dark energy.

6.2. Structure Formation

Figure 3 demonstrates that enhanced gravitational coupling appears only on super-horizon scales. The fractional effect on ${\sigma }_8$ is $\sim {10}^{-4}$, negligible for JWST galaxy anomalies.

7. Comparison with Other $\mathbf{f}\left(\mathbf{R}\right)$ Models

In contrast, Hu–Sawicki and exponential $f\left(R\right)$ models include screening mechanisms that evade solar system tests while generating observable late-time deviations. Our analysis positions quadratic $f\left(R\right)$ as a benchmark no-go model, clarifying why richer models are required.

8. Complete Field Equation Derivations

In this appendix, we provide the complete derivation of the field equations for $f\left(R\right)=R+\alpha R^2$ gravity using the auxiliary field formalism.

Starting from the action:

$$S={\displaystyle \frac{1}{2\kappa }}\int d^{4}x\sqrt{-g}\left[\varphi R-{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2\right]+S_m,$$

(5)

we vary with respect to the metric $g_{\mu \nu }$:

$$\begin{array}{cc}\hfill \delta S& ={\displaystyle \frac{1}{2\kappa }}\int d^{4}x\left[\delta \left(\sqrt{-g}\right)\left(\varphi R-{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2\right)\right.\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & +\sqrt{-g}\varphi \delta R+\sqrt{-g}{\nabla }_{\mu }{\nabla }_{\nu }\varphi \delta g^{\mu \nu }]+\delta S_m.\hfill \end{array}$$

(7)

Using $\delta \left(\sqrt{-g}\right)=-{\displaystyle \frac{1}{2}}\sqrt{-g}{g}_{\mu \nu }\delta g^{\mu \nu }$ and the variation of the Ricci scalar:

$$\delta R=R_{\mu \nu }\delta g^{\mu \nu }+g^{\alpha \beta }\delta R_{\alpha \beta },$$

(8)

where:

$$g^{\alpha \beta }\delta R_{\alpha \beta }=g^{\alpha \beta }\left({\nabla }_{\alpha }{\nabla }_{\beta }\delta g_{\mu \nu }{g}^{\mu \nu }-{\nabla }_{\alpha }{\nabla }_{\mu }\delta g_{\beta }^{\mu }-{\nabla }_{\beta }{\nabla }_{\mu }\delta g_{\alpha }^{\mu }+\square \delta g_{\alpha \beta }\right).$$

(9)

After integration by parts and using the Palatini identity, we obtain the field equations:

$$\varphi G_{\mu \nu }+{\displaystyle \frac{1}{2}}{g}_{\mu \nu }\left[{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2-\varphi R\right]+{\nabla }_{\mu }{\nabla }_{\nu }\varphi -g_{\mu \nu }\square \varphi =\kappa T_{\mu \nu }.$$

(10)

The auxiliary field equation is:

$$R-{\displaystyle \frac{1}{2\alpha }}(\varphi -1)=0.$$

(11)

For spatially flat FLRW cosmology with $d{s}^2=-d{t}^2+a^2\left(t\right){\delta }_{ij}d{x}^{i}d{x}^j$, the Ricci scalar is:

$$R=6\left({\displaystyle \frac{\ddot{a}}{a}}+{\displaystyle \frac{{\dot{a}}^2}{a^2}}\right)=6(\dot{H}+2H^2),$$

(12)

From the auxiliary equation:

$$\varphi =1+2\alpha R=1+12\alpha (\dot{H}+2H^2).$$

(13)

The modified Friedmann equations become:

$$\begin{array}{cc}\hfill 3H^2\varphi +3H\dot{\varphi }+{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2& =\kappa {\rho }_m,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill -2\dot{H}\varphi -2H\dot{\varphi }-\ddot{\varphi }+{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2& =\kappa p_m,\hfill \end{array}$$

(15)

The effective dark energy terms are:

$$\begin{array}{cc}\hfill {\rho }_{\mathrm{eff}}& ={\displaystyle \frac{1}{\kappa }}\left[3H(\varphi -1)-{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2\right],\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill p_{\mathrm{eff}}& ={\displaystyle \frac{1}{\kappa }}\left[(2\dot{H}+3H^2)(\varphi -1)-2H\dot{\varphi }-\ddot{\varphi }-{\displaystyle \frac{1}{4\alpha }}{(\varphi -1)}^2\right].\hfill \end{array}$$

(17)

9. Stability Analysis Details

We examine the stability of the $f\left(R\right)=R+\alpha R^2$ model against various instabilities.

9.1. Ghost Instabilities

The effective action in the auxiliary field formalism can be written as:

$$S_{\mathrm{eff}}=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{\varphi }{2\kappa }}R-{\displaystyle \frac{1}{8\kappa \alpha }}{(\varphi -1)}^2+{\mathcal{L}}_m\right].$$

(18)

The kinetic term for the auxiliary field $\varphi$ has coefficient:

$$K_{\varphi }={\displaystyle \frac{1}{8\kappa \alpha }}{\displaystyle \frac{{\partial }^2}{\partial {\varphi }^2}}{(\varphi -1)}^2={\displaystyle \frac{1}{4\kappa \alpha }}.$$

(19)

For ghost freedom, we require $K_{\varphi }>0$, which gives $\alpha >0$.

9.2. Gradient Instabilities

For perturbations $\varphi ={\varphi }_0+\delta \varphi$, the quadratic action becomes:

$$S^{\left(2\right)}=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{1}{4\kappa \alpha }}{\left(\delta \varphi \right)}^2-{\displaystyle \frac{1}{2\kappa }}\delta \varphi \delta R\right].$$

(20)

In Fourier space, this gives:

$$S^{\left(2\right)}=\int {\displaystyle \frac{d^{4}k}{{\left(2\pi \right)}^4}}\delta \varphi (-k)\left[{\displaystyle \frac{1}{4\kappa \alpha }}+{\displaystyle \frac{k^2}{2\kappa a^2}}\right]\delta \varphi \left(k\right).$$

(21)

The coefficient is always positive for $\alpha >0$, ensuring gradient stability.

9.3. Tachyonic Instabilities

The effective mass squared of the scalar degree of freedom is:

$$m_{\mathrm{eff}}^2={\displaystyle \frac{1}{6\alpha }}{\left(1+{\displaystyle \frac{dln{f}^{\prime }\left(R\right)}{dlnR}}\right)}^{-1},$$

(22)

where $f^{\prime }\left(R\right)=1+2\alpha R$. For our model:

$$m_{\mathrm{eff}}^2={\displaystyle \frac{1+2\alpha R}{6\alpha (1+4\alpha R)}}.$$

(23)

This is positive for $\alpha >0$ and $R>-1/\left(2\alpha \right)$, which is satisfied in realistic cosmological backgrounds.

10. Numerical Implementation

We solve the background equations using a fourth-order Runge-Kutta method with adaptive step size control. The system of equations is:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dH}{dN}}& =-{\displaystyle \frac{3}{2}}{\Omega }_m{H}^2\left(1+{\displaystyle \frac{4\alpha H^2(3+2ϵ)}{1+12\alpha H^2(2+ϵ)}}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\Omega }_m}{dN}}& =3{\Omega }_m({\Omega }_m-1)\left(1+{\displaystyle \frac{4\alpha H^2(3+2ϵ)}{1+12\alpha H^2(2+ϵ)}}\right),\hfill \end{array}$$

(25)

where $N=lna$ is the number of e-folds and $ϵ=-\dot{H}/H^2$.

Algorithm 1: Background Evolution Solver

11. Perturbation Theory Details

The linearized equations for scalar perturbations in the Newtonian gauge are derived from the perturbed field equations. For the auxiliary field perturbation:

$$\delta \varphi =2\alpha \delta R=-8\alpha {\displaystyle \frac{k^2}{a^2}}\Psi ,$$

(26)

where $\Psi$ is the gravitational potential.

The modified Poisson equation becomes:

$$k^2\Psi =-4\pi G{a}^2{\rho }_m\Delta \left(1+{\displaystyle \frac{4\alpha k^2}{3a^2(1+12\alpha H^2)}}\right),$$

(27)

leading to the effective gravitational coupling:

$$G_{\mathrm{eff}}(k,a)=G{\displaystyle \frac{1+\frac{k^2}{a^2{m}^2}}{1+3\frac{k^2}{a^2{m}^2}}},$$

(28)

where $m^2=1/\left(6\alpha \right)$ is the characteristic mass scale.

The growth factor $D\left(a\right)$ satisfies the modified growth equation:

$${\displaystyle \frac{d^{2}D}{dln{a}^2}}+\left(2+{\displaystyle \frac{1}{H}}{\displaystyle \frac{dH}{dlna}}\right){\displaystyle \frac{dD}{dlna}}-{\displaystyle \frac{3}{2}}{\Omega }_m{\displaystyle \frac{G_{\mathrm{eff}}}{G}}D=0.$$

(29)

12. Solar System Test Calculations

The post-Newtonian parameters for $f\left(R\right)$ gravity are computed using the weak-field expansion around a spherically symmetric mass M.

For the metric:

$$d{s}^2=-\left(1-{\displaystyle \frac{2GM}{c^{2}r}}+{\displaystyle \frac{2\beta G{M}^2}{c^4{r}^2}}\right)c^{2}d{t}^2+\left(1+{\displaystyle \frac{2\gamma GM}{c^{2}r}}\right)d{r}^2+r^{2}d{\Omega }^2,$$

(30)

the $f\left(R\right)$ theory modifies the PPN parameters as:

$$\begin{array}{cc}\hfill \gamma & =1-{\displaystyle \frac{1}{3}}{e}^{-mr},\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \beta & =1+{\displaystyle \frac{1}{12}}{e}^{-mr},\hfill \end{array}$$

(32)

where $m=1/\sqrt{6\alpha }$ is the scalar mass, and the approximation is for $mr\gg 1$ (short range).

For the Sun, the relevant scale r is the impact parameter for Cassini ∼ solar radius $\sim 7\times {10}^8$ m.

The constraint $|\gamma -1|<2.3\times {10}^{-5}$ gives:

$${\displaystyle \frac{1}{3}}{e}^{-mr}<2.3\times {10}^{-5},$$

(33)

$e^{-mr}<6.9\times {10}^{-5}$, $mr>ln(1/6.9\times {10}^{-5})\approx 9.58$,

$m>9.58/r\approx 9.58/7\times {10}^8\approx 1.37\times {10}^{-8}$ m⁻¹,

$\alpha <1/\left(6m^2\right)\approx 1/(6\times {(1.37\times {10}^{-8})}^2)\approx 1/(6\times 1.88\times {10}^{-16})\approx 8.85\times {10}^{14}$ m².

Converting to Mpc²: $\alpha <8.85\times {10}^{14}/9.52\times {10}^{44}\approx 9.3\times {10}^{-31}{\mathrm{Mpc}}^2$.

However, for more precise, the bound is tighter from lab tests, but for solar, this is approximate.

13. Conclusions

We have shown:

• Quadratic $f\left(R\right)$ gravity is mathematically consistent and stable.
• Observational constraints force $\alpha <{10}^{-30}{\mathrm{Mpc}}^2$.
• Within this bound, deviations from $\Lambda$CDM are negligible.
• The model cannot explain DESI evolving dark energy or JWST anomalies.

Thus, quadratic $f\left(R\right)$ is a cosmologically non-viable model. Its significance lies in demonstrating rigorously that this class is ruled out, helping redirect theoretical efforts toward more promising frameworks.

Our analysis demonstrates the importance of combining theoretical consistency, stability requirements, and observational constraints when evaluating modified gravity theories. Future work should explore more complex $f\left(R\right)$ functions or consider additional gravitational degrees of freedom [54,55].