Lorentzian Signature as Algebraic Causality in FRC

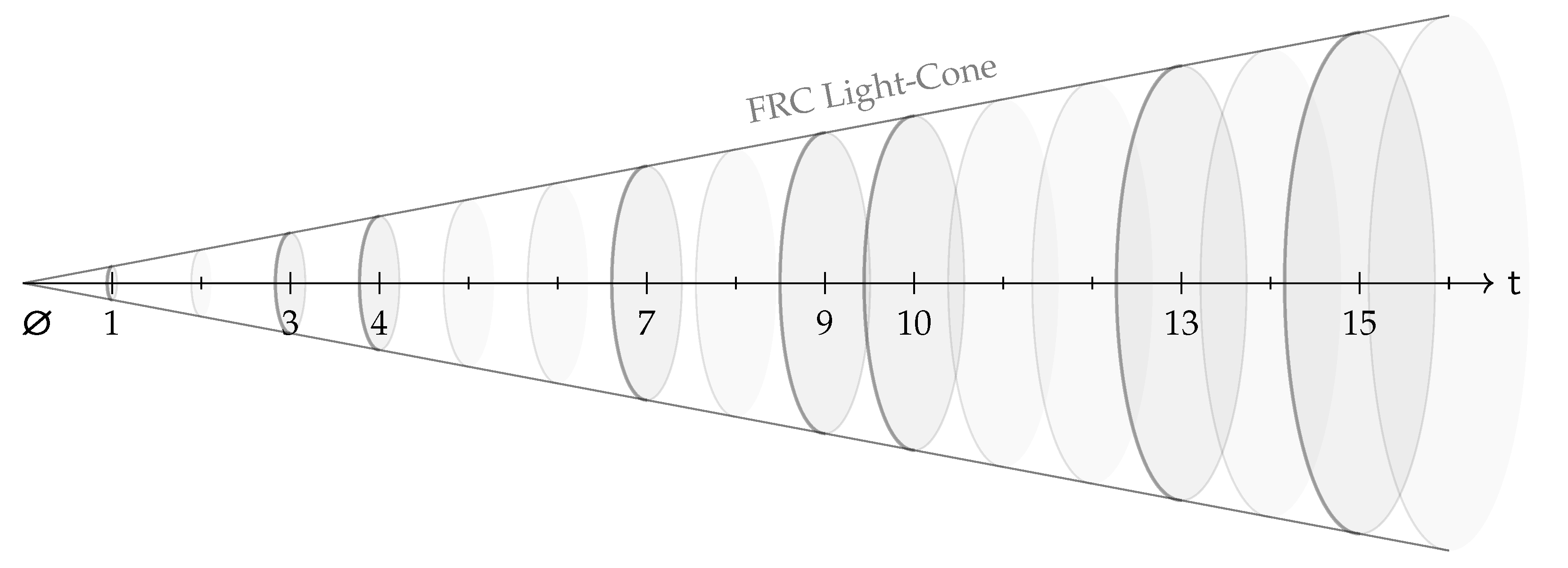
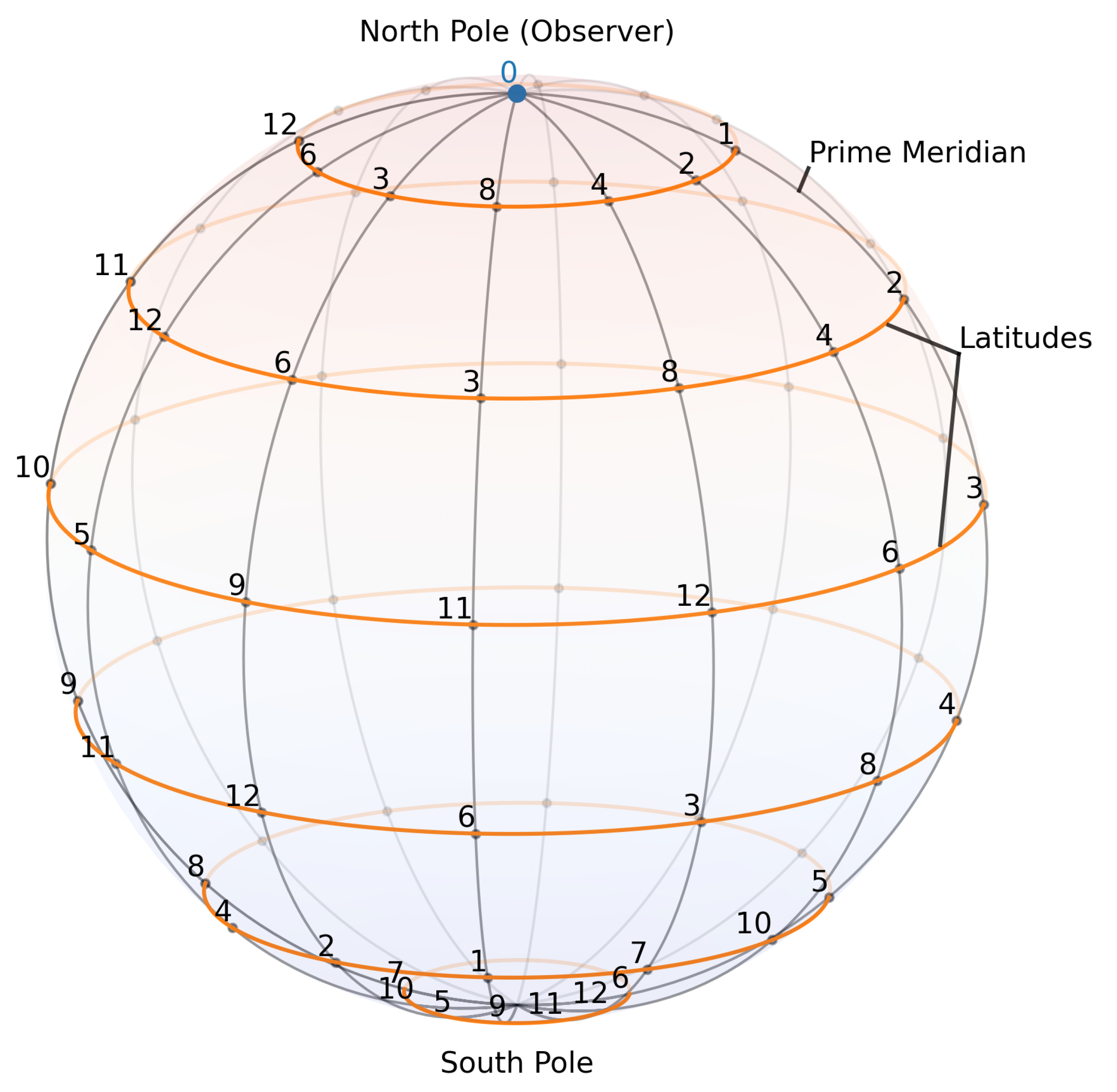
1. Introduction

The present note is framed within the broader programme of Finite Ring Continuum (FRC) [1]. In the physical interpretation of FRC, the universe is modelled by an ensemble of finite arithmetic symmetry shells ${\mathcal{U}}_{\mathsf{t}}$ formed by a succession of finite algebraic rings ${\mathbb{Z}}_{\mathsf{q}}$ with $\mathsf{q}=4\mathsf{t}+1$ and $\mathsf{t}$ being a time-like discrete radial chronon parameter, as illustrated in Figure 1. Each shell supports three fundamental arithmetic actions—translation $T_a$, scaling $S_m$, and powering $P_{ϵ}$—which are interpreted as rotational symmetries and generate a $(1,3)$-dimensional symbolic symmetry space $\mathcal{U}={\bigcup }_{\mathsf{t}}{\mathcal{U}}_{\mathsf{t}}$.

For the specific values of $\mathsf{t}$, such that $\mathsf{p}=4\mathsf{t}+1$ is prime, the resultant geometric structure manifests itself as a combinatorial 2-sphere ${\mathcal{S}}_{\mathsf{p}}$ embedded in a $(1,3)$-D symmetry space $\mathcal{U}$, with meridians and latitudes corresponding to additive and multiplicative rotational symmetries. Physical observables are identified not with individual residues of ${\mathbb{F}}_{\mathsf{p}}$ but with stable symmetry classes (e.g., quadratic residues, Klein-four orbits, etc). In the cosmological reading, the linear succession of shells ${\mathcal{U}}_{\mathsf{t}}$ models the passage of cosmic time, while the complex of internal symmetries ${\mathcal{S}}_{\mathsf{q}}$ of each shell encode the local laws of physics. Within this setting, the present paper isolates a key phenomenon: Lorentzian signature cannot be realized internally to a prime shell, but only through its quadratic extension ${\mathbb{F}}_{{\mathsf{p}}^2}$. We interpret this purely emergent phenomenon as the algebraic origin of causality.

From the perspective of the global FRC timeline, each shell ${\mathcal{S}}_{\mathsf{q}}$ constitutes an accumulation of structure, symmetry, and thus information, as the chronon parameter $\mathsf{t}$ advances. Yet from the perspective of a finite observer with a fixed information horizon, the growing complexity of the ambient symmetry space appears as an irreversible build-up of entropy. This observer-relative distinction between absolute information and perceived entropy provides a natural bridge to the Second Law of Thermodynamics.

More specifically, a prime shell ${\mathcal{S}}_{\mathsf{p}}$ of order $\mathsf{p}=4\mathsf{t}+1$ is formed by a symmetry-complete finite field ${\mathbb{F}}_{\mathsf{p}}$ [1] with fourth roots of unity $\{1,i,-1,-i\}$ and a 3D rotational structure encoded by additive and multiplicative actions; the ambient symmetry space is $\mathcal{U}={\bigcup }_{\mathsf{t}}{\mathcal{U}}_{\mathsf{t}}$, and a 2D orbital complex ${\mathcal{S}}_{\mathsf{p}}\subset \mathcal{U}$ is built by the meridians $M_n\left(a\right)=a{g}^n$ and latitudes $L_a\left(m\right)=a{g}^m$, where g is a primitive root of ${\mathbb{F}}_{\mathsf{p}}$, while freezing the power-map parameter $ϵ$ as depicted in Figure 2.

A persistent question is: how to realize a Lorentzian metric (split signature) on such a shell [2]? We prove that, algebraically, one cannot do this within ${\mathbb{F}}_{\mathsf{p}}$ for $\mathsf{p}\equiv 1(mod4)$. The reason is that a Lorentzian form needs the time coefficient to live in the opposite square class from the spatial coefficients; but if $c\in {\mathbb{F}}_{\mathsf{p}}$, then $c^2$ is a square. Thus, the correct time constant c is not available inside ${\mathbb{F}}_{\mathsf{p}}$; it exists in the next shell ${\mathbb{F}}_{{\mathsf{p}}^2}$, obtained by adjoining a square root of a chosen nonsquare $\nu \in {\mathbb{F}}_{\mathsf{p}}^{\times }$.

This formalizes (and sharpens) the FRC claim that “Minkowski emerges locally” only when one allows the minimal extension beyond the observer’s local algebraic horizon (compare also the “No South Pole in ${\mathbb{F}}_{\mathsf{p}}$” inaccessibility argument).

Contributions.

(i)

A short nonexistence theorem: no $c\in {\mathbb{F}}_{\mathsf{p}}$ with $c^2=\nu$ for any nonsquare $\nu$.

(ii)

A corollary: a genuine split-signature quadratic form requires ${\mathbb{F}}_{{\mathsf{p}}^2}$.

(iii)

A concrete $\mathsf{p}=13$ example. All statements are elementary and reproducible.

Contextual framing. In the broader FRC program, the emergence of a Lorentzian signature is not merely a technical algebraic choice but is tied to the reconstruction of causal structure itself. The distinction between Euclidean and Minkowski forms reflects whether time and space coordinates belong to the same or different square classes in the underlying finite field. When the time coefficient can only be realized in a quadratic extension, causality appears as a form of algebraic inaccessibility: it requires stepping “beyond the shell” of ${\mathbb{F}}_{\mathsf{p}}$. This connects directly with the horizon principles already identified in FRC (e.g., the inaccessibility of the South Pole in the orbital complex). The present note isolates this mechanism in a minimal form, showing that the Lorentzian split is impossible within a single prime shell and arises only in the extension, thereby grounding causal order in the square-class structure of finite fields.

References and context. The algebraic classification underlying our main theorem rests on the standard theory of quadratic forms over finite fields [3], where it is well known that nondegenerate forms in dimension at least three are isotropic and split into two equivalence classes distinguished by square classes of their coefficients; see Lam’s monograph [4] for a comprehensive treatment. On the physics side, our interpretation of the square-class obstruction as “algebraic causality” resonates with relational views of time and causality advocated by Smolin, who emphasizes that causal structure is not fundamental but emergent and relational [5]. Together these sources situate the present note both in the classical algebraic literature and in contemporary discussions of relational physics.

2. Quadratic Extension for Lorentzian Signature

Preliminaries. We recall the minimal algebraic facts needed here.

Definition 1 (Symmetry-complete shell; FRC notation).

Let $\mathsf{p}=4\mathsf{t}+1$ be prime. The multiplicative group ${\mathbb{F}}_{\mathsf{p}}^{\times }$ is cyclic of order $4\mathsf{t}$ and contains the structural set $\{1,i,-1,-i\}$ with $i^2=-1$. The ambient symmetry space $\mathcal{U}$ is formed from 4-tuples $(\mathsf{t};a,m,ϵ)$ modulo the symmetry actions; the orbital complex ${\mathcal{S}}_{\mathsf{p}}\subset \mathcal{U}$ is the 2D skeleton obtained by fixing $ϵ=1$ and combining additive meridians and multiplicative latitudes.

We only use the following basic facts.

(i)

${\mathbb{F}}_{\mathsf{p}}^{\times }$ splits into two square classes: the set of nonzero squares ${\left({\mathbb{F}}_{\mathsf{p}}^{\times }\right)}^2$ and its complement (nonsquares). When $p\equiv 1(mod4)$, $-1$ is a square.

(ii)

If $c\in {\mathbb{F}}_{\mathsf{p}}$, then $c^2\in {\left({\mathbb{F}}_{\mathsf{p}}^{\times }\right)}^2$ is a square.

(iii)

If $\nu \in {\mathbb{F}}_{\mathsf{p}}^{\times }$ is a nonsquare, the polynomial $X^2-\nu$ is irreducible over ${\mathbb{F}}_{\mathsf{p}}$ and defines the quadratic extension ${\mathbb{F}}_{{\mathsf{p}}^2}\simeq {\mathbb{F}}_{\mathsf{p}}\left[X\right]/(X^2-\nu )$.

Main result. The next theorem encodes the algebraic obstruction to Minkowski signature inside ${\mathbb{F}}_{\mathsf{p}}$.

Theorem 1 (Nonexistence of a causal square root in ${\mathbb{F}}_{\mathsf{p}}$).

Let $\mathsf{p}=4\mathsf{t}+1$ and let $\nu \in {\mathbb{F}}_{\mathsf{p}}^{\times }$ be a nonsquare. There is no $c\in {\mathbb{F}}_{\mathsf{p}}$ with $c^2=\nu$. Consequently, for any $c\in {\mathbb{F}}_{\mathsf{p}}$, the form

$$Q(t,x,y,z)=-c^2{t}^2+x^2+y^2+z^2$$

is equivalent over ${\mathbb{F}}_{\mathsf{p}}$ to a positive-definite diagonal form.

Proof. 

If $c\in {\mathbb{F}}_{\mathsf{p}}$, then $c^2$ is a square in ${\mathbb{F}}_{\mathsf{p}}^{\times }$ by definition, so it cannot equal a fixed nonsquare $\nu$. For the consequence: when $\mathsf{p}\equiv 1(mod4)$, $-1$ is a square, hence $-c^2=(-1)·c^2$ is also a square. Thus time and space coefficients lie in the same square class, and the diagonal form is equivalent to a Euclidean form. □

Corollary 1 (Minimal extension for a Lorentzian split).

Fix a nonsquare $\nu \in {\mathbb{F}}_{\mathsf{p}}^{\times }$. The split-signature quadratic form

$$Q_{\nu }(t,x,y,z)=-\nu t^2+x^2+y^2+z^2$$

is not realizable over ${\mathbb{F}}_{\mathsf{p}}$ but is realized canonically over ${\mathbb{F}}_{{\mathsf{p}}^2}\simeq {\mathbb{F}}_{\mathsf{p}}\left[X\right]/(X^2-\nu )$ by choosing $c:=Xmod(X^2-\nu )$ with $c^2=\nu$.

Proof. 

Non-realizability in ${\mathbb{F}}_{\mathsf{p}}$ follows from Theorem 1. Over ${\mathbb{F}}_{{\mathsf{p}}^2}$, the class c of X satisfies $c^2=\nu$ by construction, yielding $Q_{\nu }$. □

Remark 1 (Interpretation in FRC).

In the shell language, c does not exist as an internal element of ${\mathbb{F}}_{\mathsf{p}}$ if one insists that $c^2$ be a fixed nonsquare ν. Therefore, the causal split of square classes (time vs space) requires a pass to the “next shell” ${\mathbb{F}}_{{\mathsf{p}}^2}$. This mirrors the horizon/inaccessibility motif in FRC (cf. the “No South Pole in ${\mathbb{F}}_{\mathsf{p}}$” statement).

Local Minkowski linearization. FRC provides a framed-real embedding that supports local linearization around a frame point $(\mathsf{t};0,1,\mathsf{g})\in {\mathcal{U}}_{\mathsf{t}}$. In that calculus, once $Q_{\nu }$ is available (i.e., over ${\mathbb{F}}_{{\mathsf{p}}^2}$), one obtains a genuine local Minkowski quadratic form

$$d{s}^2=-{\left({\lambda }_{\mathsf{t}}dt\right)}^2+{\left({\lambda }_{1}dx\right)}^2+{\left({\lambda }_{2}dy\right)}^2+{\left({\lambda }_{3}dz\right)}^2,$$

for suitable positive calibrations ${\lambda }_{\mu }$ determined by the framed units. The proof is standard linearization: the discrete tangent and the symmetric bilinearization of $Q_{\nu }$ determine the form; the point is that the algebraic split of square classes needed for Lorentzian signature only exists after adjoining c (Cor. 1). All other steps are routine in the framed setup.

Concrete example. Take $\mathsf{p}=13$. The nonzero squares and nonsquares are

$${\left({\mathbb{F}}_{\mathsf{p}}^{\times }\right)}^2=\{1,3,4,9,10,12\},\mathrm{nonsquares}=\{2,5,6,7,8,11\}.$$

Hence no $c\in {\mathbb{F}}_{\mathsf{p}}$ satisfies $c^2\in \{2,5,6,7,8,11\}$. Pick $\nu =2$. Then $X^2-2$ is irreducible over ${\mathbb{F}}_{\mathsf{p}}$, and

$${\mathbb{F}}_{{\mathsf{p}}^2}\simeq {\mathbb{F}}_{\mathsf{p}}\left[X\right]/(X^2-2),c:=Xmod(X^2-2),c^2=2.$$

Thus

$$Q_2(t,x,y,z)=-2t^2+x^2+y^2+z^2$$

is realized over ${\mathbb{F}}_{{\mathsf{p}}^2}$ and provides the desired split. One can explicitly enumerate null solutions $Q_2=0$ in small boxes to visualize the (finite) light-cone counts; null sets exist in $\ge 3$ variables over finite fields by standard isotropy arguments.

3. Discussion and Outlook

Theorem 1 isolates the minimal algebraic reason why a single prime shell does not carry Lorentzian geometry: the time coefficient must be from a nonsquare class, which forbids its realization as $c^2$ with $c\in {\mathbb{F}}_{\mathsf{p}}$. Corollary 1 shows that the quadratic extension ${\mathbb{F}}_{{\mathsf{p}}^2}$ is sufficient (and minimal) to restore the split, giving a precise sense in which causality emerges “one shell out.” This sharpens the “relativistic algebra” terminology in the FRC Algebra paper [1] by providing an explicit algebraic construction of the local Minkowksi space and a full Lorentz group $O(1,3)$ realized over ${\mathbb{F}}_{{\mathsf{p}}^2}$ within the finite-ring succession.

In FRC, the succession of shells indexed by the chronon parameter $\mathsf{t}$ are interpreted as a discrete informational timeline: each new shell ${\mathcal{S}}_{\mathsf{q}}$ expands the available algebraic symmetries and square-class distinctions, thereby enlarging the catalogue of accessible states. In this view, cosmic time does not simply mark the passage of events but quantifies the accumulation of structural information: the higher the radius $\mathsf{t}$, the greater the informational complexity encoded in the symmetry shell ${\mathcal{S}}_{\mathsf{q}}$. Entropy, in this finite setting, is thus identified with the growth of relational degrees of freedom as one ascends the sequence of shells, with causality emerging precisely at the threshold where information becomes algebraically inaccessible within a local shell and is only revealed “one shell out”.

From the perspective of the global FRC timeline, each shell ${\mathcal{S}}_{\mathsf{q}}$ constitutes an accumulation of structure, symmetry, and thus information, as the chronon parameter $\mathsf{t}$ advances. However, for a finite observer whose informational horizon remains fixed, the ambient symmetry space becomes progressively more complex with each successive shell. Since the observer cannot resolve or assimilate the full algebraic structure beyond their horizon, this expansion manifests not as an accumulation of information but as an apparent growth of entropy. In this sense, the Second Law of Thermodynamics emerges naturally: entropy reflects the mismatch between the bounded horizon of the observer and the build-up of relational complexity in the symmetry shells. Causality and the arrow of time are thus two sides of the same algebraic phenomenon — both arising from the square-class structure that governs algebraic accessibility in finite rings.

Compact numerics. For reproducibility, the $\mathsf{p}=13$ tables above can be checked in a few lines of code; all identities are exact and require no floating-point approximation.

Related work. Square/nonsquare classes and quadratic extensions are textbook facts in finite-field theory and underlie quadratic-form classification over finite fields. The FRC-specific notions of shells ${\mathcal{U}}_{\mathsf{t}}$, the orbital complex ${\mathcal{S}}_{\mathsf{p}}$, framed numbers, and the horizon/inaccessibility perspective (e.g., “No South Pole in ${\mathbb{F}}_{\mathsf{p}}$”) are taken from [1]. The novelty here is the causal interpretation: split signature is equivalent to a square-class separation that is unattainable inside ${\mathbb{F}}_{\mathsf{p}}$ but achieved in the minimal extension, thus tying causality to “next-shell” accessibility.

Outlook. The algebraic obstruction we have identified has immediate consequences for how causal structure may be represented in finite settings. In particular, the passage to ${\mathbb{F}}_{{\mathsf{p}}^2}$ that restores the Lorentzian split also yields nontrivial null sets $Q_{\nu }=0$, which can be viewed as discrete analogues of light-cone structures. This suggests that finite-field shells equipped with square-class separated quadratic forms could serve as toy models for spacetime in discrete or algebraic approaches to physics. Possible applications include finite-field analogues of Minkowski space used in coding theory, or as simplified models for causal order in discrete quantum gravity frameworks. In this sense, algebraic causality provides not only an explanation of why Lorentzian signature emerges in FRC, but also a potential bridge to broader investigations of spacetime geometry in finite or informationally bounded regimes.