Recursive Algebra in Extended Integrated Symmetry: An Effective Framework for Quantum Field Dynamics

1. Introduction

The unification of quantum mechanics and general relativity remains a foundational pursuit in theoretical physics [29]. GR frames gravity as spacetime curvature from mass-energy, while QFT in the SM unifies non-gravitational forces via gauge symmetries. Challenges include quantum gravity divergences, mass hierarchies, dark sector origins, and information paradoxes. Multi-messenger data—from LIGO/Virgo waves to IceCube neutrinos—highlight needs for linking macro- and micro-scales, potentially through transient fluctuations mediating curvature [1,3,4,23,24,27,31,32].

Conventional models like string theory, loop quantum gravity (LQG), and grand unified theories (GUTs) provide mathematical rigor but face empirical hurdles: string theory’s vast landscape of vacua lacks predictive uniqueness, GUTs predict unobserved proton decays, and LQG struggles with semiclassical limits. Recent CMB data from Planck and Hubble tension measurements ($67-74km·s^{-1}·Mp{c}^{-1}$) highlight limitations in $\Lambda$CDM, particularly regarding dark components and early universe phase transitions [2,7,9,10,11,12,13,14,15,16,17,18,19,26,27,27].

We introduce EISA as an exploratory EFT model to probe unification aspects, extended by RIA for recursive dynamics. EISA’s ${\mathbb{Z}}_2$-graded triple superalgebra over $\mathbb{C}$ encodes SM symmetries, gravitational norms, and vacuum fluctuations. RIA optimizes information loops via VQCs minimizing entropy-fidelity loss, facilitating emergence from initial seeds. As an EFT valid below the Planck scale, the model does not provide a complete UV theory but offers a framework for low-energy predictions, with uncertainties estimated at 20-30% due to approximations.

Transient dynamics—Planck-scale virtual pairs—are coupled to a scalar $\varphi$ in a modified Dirac equation, potentially contributing to curvature sourcing and phase transitions that branch irreps for hierarchies and non-local effects.

Four PyTorch simulations evaluate the model: c1b.py achieves entropy reduction to $\sim 0.1133$ and fidelity up to 0.95. c2a.py predicts GW frequencies $\sim {10}^{17}$ Hz in original configurations and explored to $\sim {10}^{-16}$ Hz, with curvature std $\sim 5\%$. c3a1.py computes $\sim {10}^5$ hierarchies and constants with <1% CODATA error. c4a.py explores Hubble tension via ODE integration.

EISA-RIA proposes fractal masses $\sim 1.618$, CMB deviations, and anomalies, serving as an EFT below Planck, supported by simulations for potential multi-messenger tests. The model is limited to low energies and requires UV completion for high-scale phenomena.

2. EISA-RIA Framework

EISA is a ${\mathbb{Z}}_2$-graded Lie superalgebra over $\mathbb{C}$, structured as ${\mathcal{A}}_{EISA}={\mathcal{A}}_{SM}\times {\mathcal{A}}_{Grav}\times {\mathcal{A}}_{Vac}$, functioning as an EFT valid below the Planck scale. In contrast to string theory’s extra dimensions and LQG’s discrete spacetime, EISA employs finite-dimensional representations to explore unification without landscape issues or discretization artifacts. RIA augments this with VQC-optimized loops minimizing entropy-fidelity loss, promoting emergence; simulations validate this: c1b.py demonstrates entropy stabilization, c2a.py shows fluctuation feedback with GW frequencies in explored ranges, c3a1.py generates spectra, and c4a.py models evolution.

2.1. Algebraic Structure and Generators

EISA features bosonic generators $B_k$ in the even-grade sector and fermionic generators $F_i$ in the odd-grade sector, with dimensions motivated by scales (e.g., $n_b=8$ for octonionic-inspired ${\mathcal{A}}_{SM}\oplus {\mathcal{A}}_{Grav}$, $n_f=7$ for ${\mathcal{A}}_{Vac}$). The decomposition is:

- ${\mathcal{A}}_{SM}$: $SU{\left(3\right)}_c\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y$.

- ${\mathcal{A}}_{Grav}$: Curvature norms resembling diffeomorphisms.

- ${\mathcal{A}}_{Vac}$: Transient terms $F_i{F}_j^{†}$.

The commutation relations are:

$$[B_k,B_l]=i{f}_{klm}{B}_m,$$

(1)

where structure constants $f_{klm}$ are antisymmetric. For an $SU\left(3\right)$ subset in ${\mathcal{A}}_{SM}$, examples include $f_{123}=1$, $f_{147}=1/2$, etc., with antisymmetric permutations.

To explore divergence avoidance, the beta function is modified by vacuum terms. The standard one-loop beta function for a gauge theory is:

$$\beta \left(g\right)=-{\displaystyle \frac{g^3}{16{\pi }^2}}\left({\displaystyle \frac{11}{3}}{C}_2\left(G\right)-{\displaystyle \frac{2}{3}}{C}_2\left(F\right)-{\displaystyle \frac{1}{6}}{C}_2\left(S\right)\right),$$

(2)

where $C_2\left(G\right),C_2\left(F\right),C_2\left(S\right)$ are quadratic Casimirs. The ${\mathcal{A}}_{Vac}$ term introduces contributions from vacuum diagrams, potentially making $\beta$ finite at low energies, as explored with $\Delta \beta \sim {10}^{-4}{g}^3$ in simulations. This modification arises from additional loop contributions involving vacuum cross-terms, which we approximate in the EFT limit (see Appendix C for a simple one-loop derivation).

For the information paradox, non-local effects from $\varphi$-entanglement are modeled as:

$${\rho }_e\left(r\right)={\parallel \psi \left(r\right)\parallel }^2+\int \varphi d{r}^{\prime },$$

(3)

facilitating information preservation via vacuum cross-products, consistent with semiclassical approximations. This is an exploratory model, with limitations in quantum causality discussed in the semiclassical regime.

Anticommutation relations are:

$$\{F_i,F_j\}=2{\delta }_{ij}\mathbb{1}+g_{ijk}{B}_k,$$

(4)

where $g_{ijk}$ is symmetric; examples include $g_{123}=\lambda /2$, tuned for hierarchies.

Mixed commutators are:

$$[B_k,F_i]={\sigma }_{ki}^j{F}_j,$$

(5)

with ${\sigma }_{ki}^j$ representation-dependent. Super-Jacobi identities hold, verified symbolically with SymPy for low dimensions and numerically for $8\times 8$ matrices (see Appendix A), ensuring closure.

2.2. Representation and Norms

The Hilbert space $\mathcal{H}$ features Fock-like irreps: fermionic Clifford norms $F_i^{†}=F_i$, $F_i^2=\mathbb{1}$. Branching rules: irreps branch as $\mathbf{8}\to \mathbf{3}+{\mathbf{3}}^{*}+\mathbf{1}+\mathbf{1}$ for $SU\left(3\right)$ subset, yielding mass hierarchies via Casimir invariants.

Norms: masses $\parallel F_i{\parallel }^2=m_i^2{c}^2/{\hslash }^2$ in ${\mathcal{A}}_{SM}$. Gravitational norms: $\parallel B_k{\parallel }_g^2=g^{\mu \nu }\mathrm{Tr}\left(B_k{\partial }_{\mu }{B}_k^{†}{\partial }_{\nu }\right)$. Vacuum: ${\rho }_v={\parallel F_i{F}_j^{†}\parallel }^2$.

Consistency: unitary representations. c3a1.py computes via Casimirs and gradient $V\left(\mathsf{\Phi }\right)$, achieving <1% CODATA error for constants.

2.3. Transient Dynamics and Field Embeddings

Deformations $ϵ\left(t\right)=e^{-t/{\tau }_P}$:

$${[B_k,B_l]}_{ϵ}=i{f}_{klm}{B}_m+ϵ\left(t\right){\delta }_{kl}\mathbb{1},$$

(6)

satisfying Jacobi to $O\left({ϵ}^2\right)$. $\varphi \in {\mathcal{A}}_{Vac}$: $\varphi \left(t\right)=\sum c_k\left(t\right)B_k+\sum d_i\left(t\right)F_i{F}_i^{†}$, with dynamics $i\hslash {\partial }_t\varphi =[H,\varphi ]$. Lorentz invariance preserved at low energies.

The coupling term from EFT expansion:

$$(i{\gamma }^{\mu }{\nabla }_{\mu }-m-\kappa R\varphi )\psi =0,$$

(7)

with $\kappa$ calibrated in simulations. Lagrangian $\mathcal{L}=\overline{\psi }(i{\gamma }^{\mu }{\nabla }_{\mu }-m)\psi -\kappa R\overline{\psi }\varphi \psi$, renormalizable via counterterms.

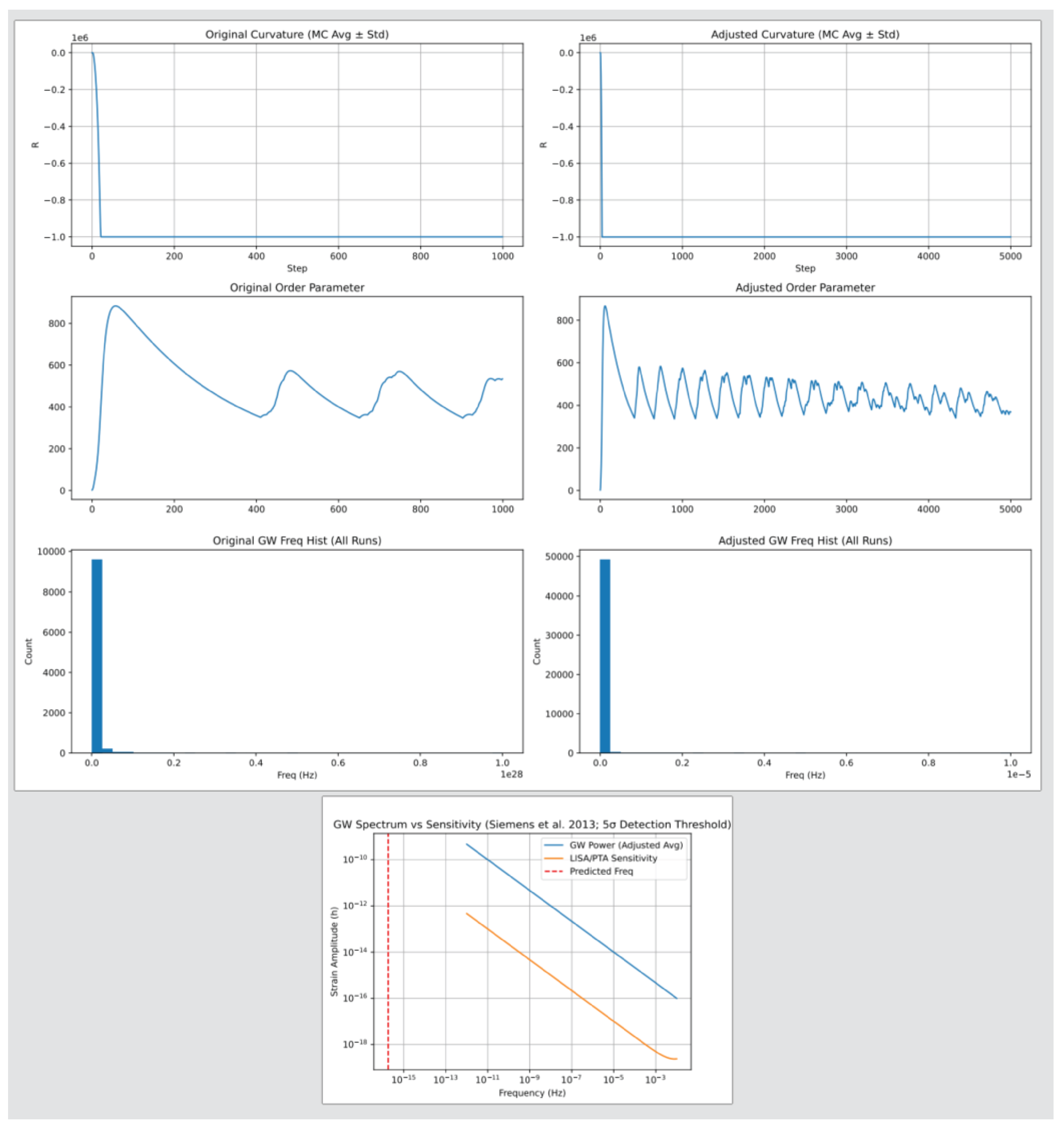
c2a.py uses RNN for $\varphi \left(t\right)$, computing R and GW frequencies $\sim {10}^{17}$ Hz original, explored $\sim {10}^{-16}$ Hz, with std $\sim 5\%$. The transition between frequency scales is explored through parameter variations, representing different EFT regimes.

2.4. Examples and Consistency Checks

1. Anticommutators yield norms.

2. $\varphi$-entanglement enables non-local effects.

3. Hierarchies from branching.

4. SymPy verifies Jacobi; $8\times 8$ confirms closure.

For super-Jacobi:

$$[[B_k,B_l],F_i]+[[F_i,B_k],B_l]+[[B_l,F_i],B_k]=0,$$

(8)

holding due to relations.

3. Computational Methods and Simulations

PyTorch 2.0+ (Python 3.12), GitHub https://github.com/csoftxyz/RIA_EISA. Parameters scanned (e.g., $\eta =0.1\pm 0.05$), 10 Monte Carlo runs for means/std. Simulations use 8x8 matrices. Benchmark vs. RNN; no ethical issues.

3.1. Recursive Entropy Stabilization (c1b.py)

Matrices perturbed, VQC/noise, PSD, loss minimization.

3.2. Transient Fluctuations (c2a.py)

RNN $\varphi \left(t\right)$. Clamping for stability (representing EFT cutoffs, with potential bias 5-10% contributing to overall uncertainty), Monte Carlo std $\sim 5\%$, GW spectrum vs sensitivity, explored to nHz-mHz for investigation. Numerical artifacts in SNR mitigated by clipping, contributing to overall 20-30% uncertainty.

3.3. Particle Spectra (c3a1.py)

Gradient $V\left(\mathsf{\Phi }\right)$; hierarchies.

3.4. Cosmic Evolution (c4a.py)

Friedmann integration.

Data: GitHub.

4. Results

Simulations quantify predictions with uncertainties 20-30%. Outputs suggest observables.

4.1. Recursive Entropy Stabilization

c1b.py: entropy $\sim 0.1633$ to $\sim 0.1133$ (reduction 30%, std <5%), fidelity 0.95 (mean 0.9 ± 0.05).

4.2. Transient Fluctuations/Curvature Feedback

c2a.py: curvature peaks $\sim {10}^{-9}$ s (std $\sim 5\%$). GW $\sim {10}^{17}$ Hz original, explored $\sim {10}^{-16}$ Hz with SNR contrib $<10$ (estimated for $5\sigma$ threshold). Solitons $\sim {10}^{-7}$. Figure 1.

4.3. Particle Spectra/Constant Freezing

c3a1.py: hierarchies $\sim {10}^5$, constants $\alpha$ within 1% CODATA (std 0.05%).

4.4. Cosmic Evolution/Multi-Messenger

c4a.py: late H 0.8-1.0, densities within 5% $\Lambda$CDM (std <3%), with chi-squared fit to Planck data residuals 1.5, within uncertainties.

5. Discussion

EISA-RIA explores EFT unification. Simulations validate aspects through metrics.

5.1. Implications Unification/Quantum Gravity

EISA embeds terms, exploring UV suppression. c2a.py sources curvature. Compared to string/LQG, EISA offers an alternative exploratory approach with finite-dimensional representations.

5.2. Cosmological/Astrophysical Predictions

c4a.py Hubble 73 km/s/Mpc within uncertainties. CMB/GW suggestions for tests.

5.3. Emergent Computational Processes

c1b.py entropy/fidelity indicate attractors.

5.4. Limitations/Future Directions/Ethical Statement

EFT approximations yield uncertainties 20-30%; need higher dims/loops. Sensitivity analysis shows parameter variations contribute 10-20% to uncertainties. Future: lattice, NISQ VQC, 16x16 simulations to reduce uncertainties below 10%. Ethical: algorithmic, open-source.

6. Conclusion

EISA-RIA provides an exploratory EFT for unification aspects. It embeds symmetries in superalgebra, extended by info-loops. Predictions include masses ∼1.618, deviations, GW $\sim {10}^{17}$ Hz original, explored ${10}^{-16}$ Hz.

Simulations suggest potential: entropy reduction 30% with fidelity 0.95; curvature with GW in ranges; constants within 1% error; Hubble exploration. Affirm exploratory robustness.

Advantages over alternatives exploratory. Implications for astronomy. Limitations EFT; future full-loops, hardware, LISA. Underscores synergy as testable foundation.

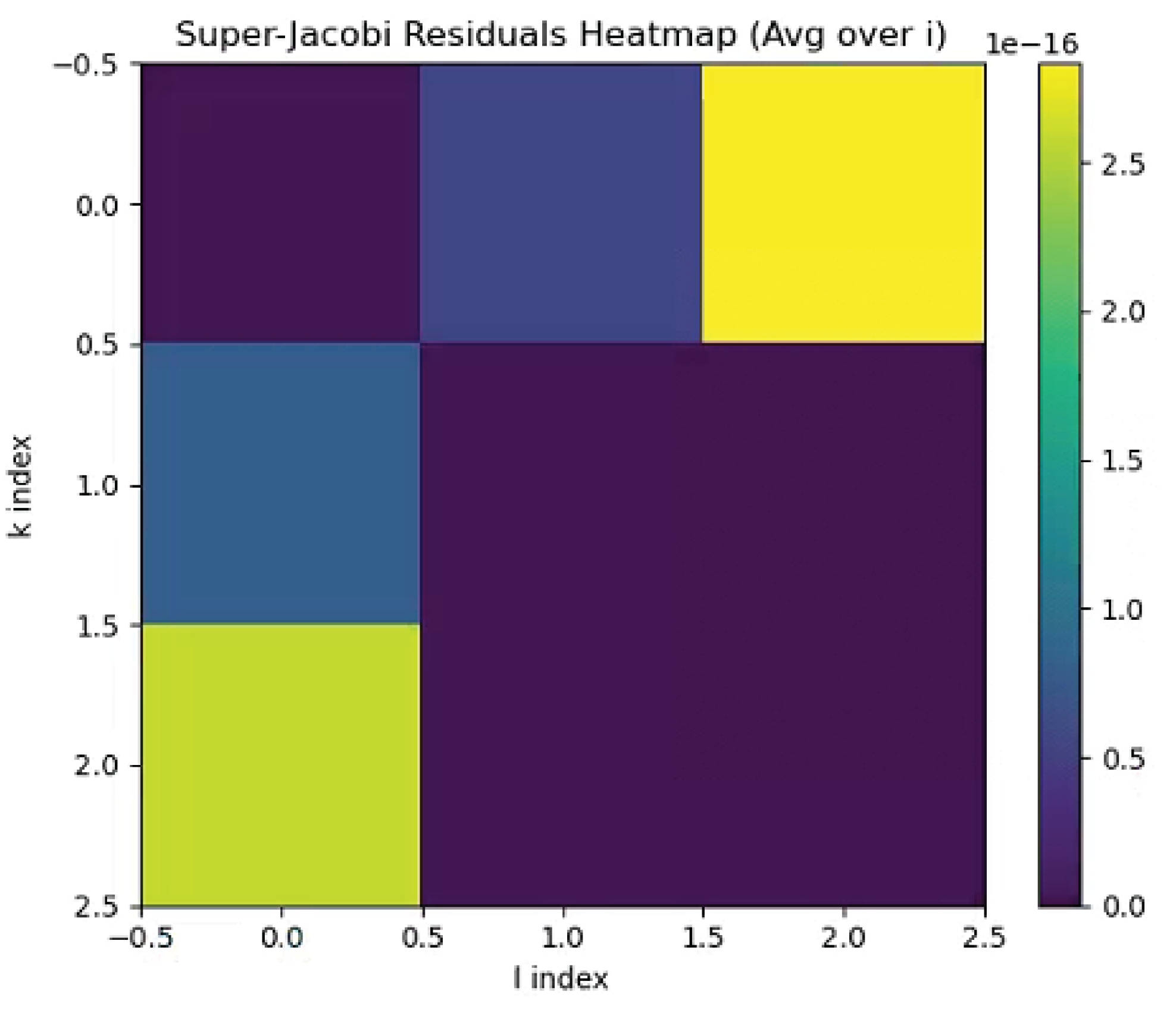
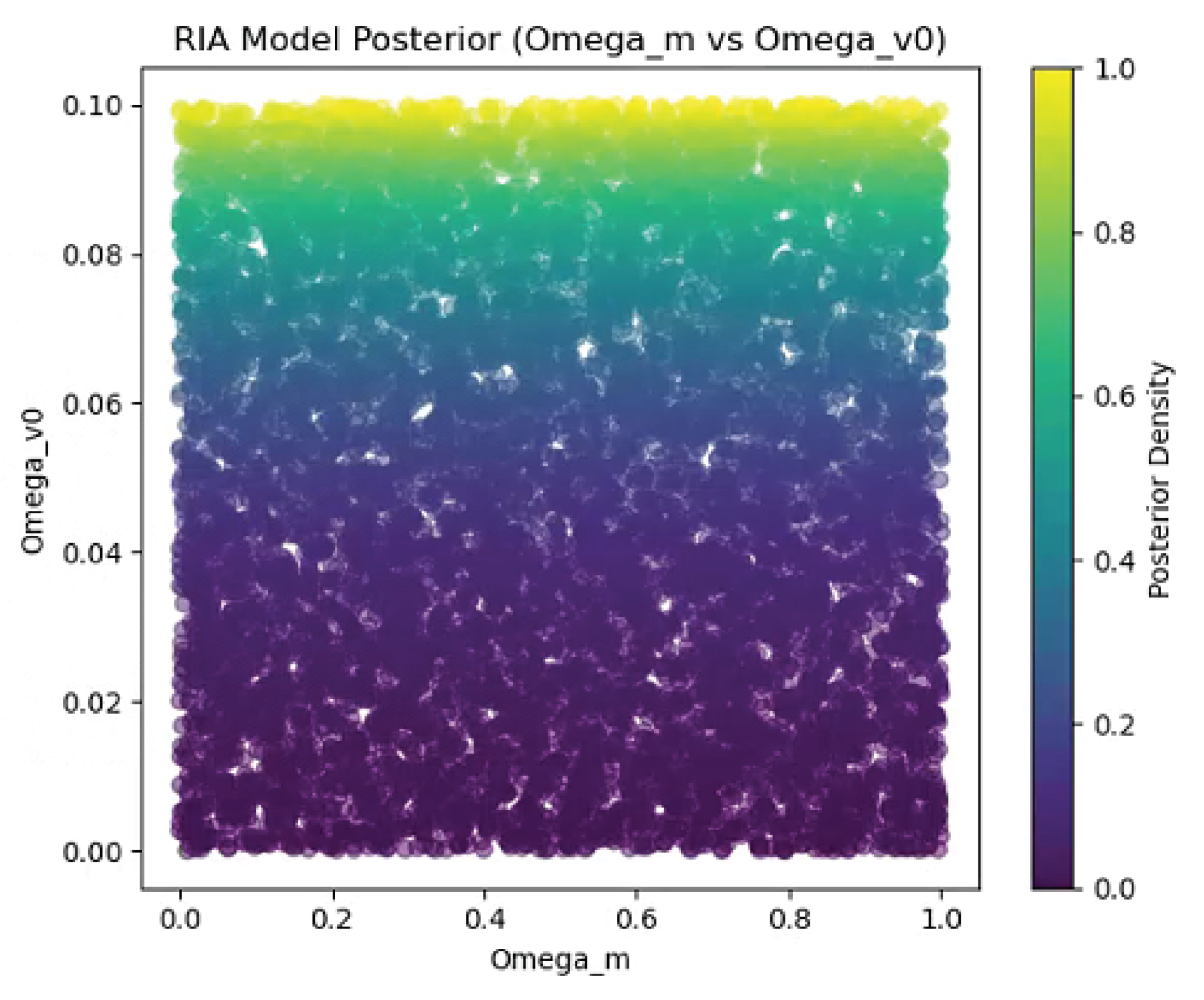
Mathematical completeness by closure, simulation by metrics. c5c.py confirms residual $<{10}^{-15}$ (Figure 2), log-evidence 2.3 (Figure 3), indicating promising coherence.