Vacuum Energy Extraction via Entropic Gradient Manipulation: An Application of the Dead Universe Theory (DUT)

1. Introduction: The Energetic Vacuum, Cosmological Anomalies, and the Dead Universe Paradigm

The pursuit of clean, sustainable energy sources is paramount in addressing global environmental and energy crises. While conventional energy production methods face inherent limitations and contribute significantly to ecological degradation, theoretical physics has long hinted at an inexhaustible reservoir: the quantum vacuum. Quantum Field Theory (QFT) posits that the vacuum is not an empty void but a dynamic medium teeming with virtual particles, whose fleeting existence gives rise to an immense Zero-Point Energy (ZPE) density [3,4]. Despite its theoretical ubiquity, the extraction of usable energy from this fundamental reservoir remains a profound challenge, primarily due to the symmetrical nature of vacuum fluctuations which typically yield no net observable energy. [6,7,8,9,10,11,12,13,14,15]

This article introduces a radical theoretical framework for ZPE extraction, leveraging the foundational tenets of the Dead Universe Theory (DUT) [1]. DUT, originally conceived to explain the observed cessation of large-scale star formation and the ultimate fate of baryonic matter in an asymptotically "dead" cosmos. Distinct from standard General Relativity (GR) and rival theories like Loop Quantum Gravity (LQG) [11], DUT posits a non-singular gravitational potential [1] and a dynamic interplay between matter, vacuum, and entropy fields. We hypothesize that this intricate relationship, particularly the concept of dynamically induced entropic gradients within spacetime, can be precisely manipulated to induce a directional bias in vacuum fluctuations, thereby enabling a net energy flow from the quantum vacuum, paving the way for a revolutionary, environmentally benign energy source.

The primary objective of this conceptual work is to:

• Propose a novel mechanism for ZPE extraction based on DUT's principles of entropic gradient manipulation, offering a thermodynamically quantified model.
• Introduce a rigorous mathematical formalism for DUT, moving beyond ad hoc assumptions to foundational principles.
• Outline falsifiable predictions and experimental protocols for validating the core hypotheses, ranging from astrophysical observations utilizing cutting-edge facilities to high-energy particle accelerator experiments.
• Discuss the profound environmental and industrial implications of such a technology, highlighting its potential for global leadership.

This research aims to bridge speculative cosmology with applied quantum physics, providing a rigorous roadmap for future theoretical and experimental investigations into a truly sustainable and transformative energy future.

2. Theoretical Framework: Dead Universe Theory (DUT) Axioms and Cosmological Implications

The Dead Universe Theory (DUT) [1] fundamentally redefines our understanding of spacetime dynamics and cosmic evolution, particularly in extreme gravitational environments and at late cosmological times. Its core principles, crucial for our energy extraction proposal, are detailed below. [3,4,5,6,7,8,9,10,11,12,13,14,15]

2.1. Non-Singular Gravitational Potential from First Principles

A cornerstone of DUT is its modified gravitational potential (Φ) [1], which inherently avoids the singularities predicted by classical General Relativity (GR) at the origin of massive objects (e.g., within black hole cores). Unlike ad hoc modifications, DUT derives its non-singular metric from foundational principles, potentially involving non-commutative geometry [15,16,17,18,19,20,21,22] and Von Neumann algebras [18], an area where significant advancements have been made in research. The DUT potential is not merely a parametrized form but emerges as an exact solution to the DUT field equations, ensuring mathematical consistency:

V(r,(t)=V0⋅e−α⋅r⋅cos(ω⋅r+ϕ0(t))+β⋅(1−e−r)⋅r−1)

(1)

where:

• V0: Oscillation amplitude, representing the strength of the potential.
• α: Exponential decay rate, characterizing how quickly the oscillatory component diminishes with distance.
• ω: Angular frequency, describing the oscillation rate of the potential.
• ϕ0(t): Time-dependent phase, allowing for dynamic evolution of the potential.
• β: Central potential coefficient, a parameter ensuring the potential remains finite and well-behaved at r→0.
• r: Normalized radial distance, a dimensionless parameter representing spatial extent.

This non-singular nature, derived from deeper geometrical principles, is critical, as it permits the theoretical existence of extreme, yet finite and controllable, gradients within spacetime. These gradients are central to the proposed energy extraction mechanism, as infinite gradients would lead to uncontrollable physical conditions. [1,2,3,4,5,6,7,8,9,10,11,12,13]

2.2. Dynamic Entropic Gradients and Information Gravity

DUT posits a fundamental and active connection between entropy and gravity [1], moving beyond the conventional thermodynamic interpretation of black hole entropy [5]. In DUT, the entropic gradient (∇S) is not merely a passive consequence of thermodynamic processes but actively influences the spacetime metric, contributing to what can be conceptualized as "information gravity" [1,2]. This dynamic interplay suggests that information, encoded in entropy, directly shapes the geometry of spacetime. The entropic gradient is derived from the potential and local density:

∇S(r,t)≈−(drdV)⋅ρ(r,t)

(2)

where:

• dV/dr: The spatial derivative of the gravitational potential, representing the local gravitational force.
• ρ(r,t): The local matter-energy density, assumed to decay exponentially with radial distance and time for illustrative purposes.

This active entropic influence on the metric is conceptually represented as δGμν∼∇μS∇νS [1,2], implying that regions with strong entropic gradients induce localized, measurable deformations in spacetime. This reinterpretation provides a novel avenue for manipulating spacetime geometry through thermodynamic means. [1,2,29]

2.3. Quantum Metric Regularization and the Total DUT Hamiltonian

DUT integrates concepts from quantum vacuum pressure and entropic stratification into a unified stress-energy tensor, aiming for a consistent formulation that inherently avoids singularities [1]. The conceptual Einstein Field Equation within the DUT framework is expanded to include these additional components:

Gμν+Λgμν=8πG(Tμνmatter+Tμνvacuum+Tμνentropy)

(3)

Here:

• Tμνmatter: Represents the conventional stress-energy tensor of baryonic and dark matter.
• Tμνvacuum: Incorporates the dynamic pressure and energy density of the quantum vacuum, regularized to prevent infinities.
• Tμνentropy: Represents the contribution of entropic gradients to the spacetime curvature.

Furthermore, DUT introduces a conceptual quantum decoherence rate (Γdecoh) [1], modeling the loss of quantum coherence near dense cores due to strong gravitational interactions and thermal dissipation. The total DUT Hamiltonian is represented as the sum of energies from gravity, quantum fields, and entropy: Htotal=HGR+HQG+Hentropy [1]. This holistic approach is essential for understanding how energy might be extracted from the vacuum without violating fundamental conservation laws, as it accounts for all relevant energy forms within the DUT cosmos.

2.4. Baryonic Matter to "Dead State" Transition

A key aspect of DUT [1], particularly relevant for the evolution of massive compact objects like black holes, is the theoretical transformation of baryonic matter into a more primordial, non-baryonic state (referred to as the "dead state" or ψ-field) as it approaches the interior of these objects, rather than being crushed into an infinitely dense singularity. This transition is characterized by a decaying baryonic density and an emerging ψ-field:

ρ((r)=ρ0exp[−λ(r−Rs)]ψ(r)=ψ0[1−exp(−λ(r−Rs))])

(4)

where:

• ρ0: Initial baryonic density.
• ψ0: Initial ψ-field amplitude.
• Rs: Schwarzschild radius, defining the approximate boundary of the transition region.
• λ: The DUT transition length [1], a characteristic scale over which this transformation occurs.

This implies that the "interior" of a black hole, within the DUT framework, is not a point of infinite density, but rather a region where matter has undergone a fundamental phase transition, potentially releasing energy or altering its fundamental form. This concept is crucial for understanding the ultimate fate of matter and energy in the universe. [1,2,3,4,5,6,7,8,9,10,11]

2.5. The Great Cosmic Void of the Dead Universe as Evidence of an Observable Structural Black Hole: An Interpretation by DUT

The Dead Universe Theory (DUT) [1], proposes that the observable universe is not an autonomous expanding entity, but rather a residual entropic structure embedded within the gravitational interior of a structural black hole originating from a collapsed ancestral universe. This structural black hole is neither singular nor isolated; instead, it corresponds to a non-uniform gravitational cavity, shaped by cosmic entropy gradients that generate an asymmetric retraction field on a cosmological scale.

In this model, the intrinsic "fabric" of the universe, primarily composed of exotic dark matter and dark energy as described by DUT [1,2,3,4], remains fundamentally static and unexpanding. The Cosmic Microwave Background (CMB), uniformly observed across the cosmos, is ubiquitous, indicating that neither absolute zero nor a true vacuum (devoid of all fields and energy) exists even in the most rarefied regions of spacetime. Instead, the CMB represents the baseline thermal energy of this non-expanding "dead universe" fabric.

Galaxies, akin to a "shoal of fish" within a vast ocean, are not being carried outwards by an expanding medium. Instead, their apparent recession (redshift) is primarily due to their gravitational attraction towards the denser, central regions of this structural black hole, or being drawn back towards its "edges" by the overarching gravitational influence of the "dead universe" [1,2,3,4,5,6,7,8,9,10,11,12] . The observed redshift, therefore, is not a direct indicator of cosmic expansion, but rather a manifestation of the gravitational dynamics within this bounded, non-expanding system. The light from distant galaxies travels through this static spacetime fabric, and its redshift is an "illusion" resulting from the complex interplay between the motion of the galaxies themselves and the gravitational potential of the structural black hole. This offers a compelling alternative explanation for phenomena typically attributed to cosmic expansion, suggesting that the universe's large-scale structure is governed by internal gravitational dynamics rather than an intrinsic metric expansion. This perspective opens new avenues for interpreting cosmological observations and designing experiments sensitive to these subtle gravitational influences.

This "void" is not an absolute emptiness, but an entropic cavity of the ancestral universe—equivalent to the gravitational shell of a structural black hole, or the great cosmic void of the dead universe. Within this cavity, the separation between baryonic matter and the thermodynamic nucleus occurs asymmetrically and directionally. The region we inhabit would therefore be the visible and residual portion of this entropic domain. The fact that galaxies are observed receding within regions conventionally termed "cosmic voids" is interpreted, within DUT, not as a result of an expanding space, but as a consequence of the asymmetric thermodynamic retraction of the dead universe, where the effective gravitational field promotes increasing separations in regimes of low local density. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]

The asymmetric retraction within this cavity is described by the entropic gravitational deceleration equation proposed by DUT [1]:

a¨((t)=−34πG[ρb(t)−32∇Sg(t)]a(t))

(5)

where:

• a(t) is the effective radius or separation factor between baryonic structures over time.
• ρb(t) is the average baryonic matter density.
• ∇Sg(t) represents the gravitational entropy gradient.
• G is the gravitational constant.

In this regime, the effective gravitational potential within the structural cavity also undergoes a thermodynamic correction, given by:

ΦDUT((r)=−rGM(r)+α∇Sg(r))

(6)

With:

• M(r) being the cumulative mass within the cavity.
• α being a positive entropic coupling coefficient that regulates the intensity of gravitational deformation.

In this sense, the observable cosmic voids are understood as internal substructures of a much larger structural void—the gravitational cavity of the very cosmological black hole that originated the observable universe. This reinterpretation proposed by DUT reconfigures the observed cosmological topology itself, converting low-density regions into empirical evidence of the thermodynamic geometry of the dead universe.

A recent hypothesis, proposed by Indranil Banik (University of Portsmouth) [11], presented at the National Astronomy Meeting 2025 (NAM, UK) and reported by CNN Brasil [12], addresses the possibility of the Milky Way residing at the center of a large local void. According to Banik:

"A potential solution to this inconsistency is that our galaxy is near the center of a large local void. [...] This would explain why the values obtained do not match, that is, what we interpret as greater expansion is just the local gravitational effect." [12,13,14,15,16,17,18,19,20,21,22,23]

According to Banik [11], the Hubble Tension—the difference between the expansion rate inferred from the cosmic microwave background (CMB) and that observed locally by supernovae and Cepheids—could be explained if the Milky Way is located within a cosmic void with density about 20% lower than the universal average. This void, with estimated dimensions of up to two billion light-years, is an observed structure among the galaxies of the visible universe, evidenced by galaxy counts, baryonic acoustic oscillation (BAO) patterns, and recession velocity measurements.

DUT considers this hypothesis not as a topological exception or local coincidence, but as a natural manifestation of the internal structure of the dead universe [1]. The recession of galaxies in regions of reduced density is not a consequence of a supposed acceleration of space, but rather of a profound thermodynamic gravitational reconfiguration, in which residual galaxies migrate to the edges of the entropic field where Newtonian gravity begins to dominate. Thus, what Banik interprets as a local distortion can be reinterpreted, within DUT, as a direct effect of the gravitational gradient of the structural cavity of the ancestral universe.

Furthermore, DUT maintains that the reduced galaxy count, stellar inactivity in peripheral regions, and inherited baryonic acoustic oscillation (BAO) patterns function as structural cosmological fossils, recording the geometry and thermodynamics of the original structural void. Such observations cease to be anomalies and become natural predictions of DUT , strengthening its explanatory and predictive power. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]

Therefore, the observational evidence of large cosmic voids, especially around the Local Group, directly reinforces the central hypothesis of DUT [1]: the observable universe is merely a residual baryonic bubble isolated within a gravitational entropic shell—the structural black hole left by the collapse of the ancestral cosmos. The Hubble Tension, in this scenario, would not be a calibration error, but rather a predictable emergent effect of the fundamental structure of the dead universe, already described in the original DUT models [1,2,3,4,5].

3. The Entropic Vacuum Reactor (RVE): Mechanism and Principles

The core proposition of this article is the Entropic Vacuum Reactor (RVE), a theoretical device designed to extract energy from the quantum vacuum by manipulating entropic gradients.

3.1. Mechanism of ZPE Extraction and Thermodynamic Quantification

The RVE operates on the principle that an artificially induced, extreme entropic gradient (∇S) can break the inherent symmetry of quantum vacuum fluctuations. In a uniform vacuum, virtual particles appear and disappear symmetrically, resulting in no net energy. However, if a strong ∇S is imposed, it creates a directional bias, analogous to how the Unruh effect [4,5,6,7,8,9,10,11] (particle creation from an accelerating frame) or Hawking radiation [5] (particle creation near black hole event horizons) create real particles from the vacuum. These effects demonstrate that the vacuum is not inert but can be excited by extreme conditions.

In the RVE, the entropic gradient would effectively "polarize" these virtual particles, causing a preferential emergence of real particles (or energy packets) in a directed manner. This is akin to a photovoltaic panel, but instead of photons, it "harvests" virtual particles from the vacuum. The energy extracted (Eextracted) would be proportional to the magnitude of the induced entropic gradient and the effective volume of vacuum polarization:

Eextracted∝∫Vkeff∣∇S∣2dV

(7)

where keff is an effective coupling constant that relates the entropic gradient to extractable energy density, and V is the volume of the vacuum polarization.

Crucially, the RVE's operation is posited to achieve efficiencies that could theoretically bypass known quantum thermodynamic limits, such as Landauer's principle, by leveraging the non-standard vacuum structure and entropic coupling described by DUT. This is achieved by rectifying the vacuum fluctuations in a non-equilibrium state induced by the entropic gradient, effectively creating a "cold reservoir" in the vacuum itself. The maximum Carnot efficiency for the RVE is hypothesized to be significantly higher than conventional thermal engines, approaching unity even at non-cryogenic temperatures, due to the direct manipulation of spacetime's energetic fabric. This represents a fundamental thermodynamic advantage over existing energy conversion technologies.

3.2. Key DUT Parameters as RVE Controls

The parameters inherent to DUT [1] are not merely theoretical constructs but serve as crucial controls and efficiency indicators for the RVE:

• Thermodynamic Gravity Factor (kTG): This dimensionless parameter [1], which quantifies the coupling between the entropic gradient and spacetime deformation (δGμν∼kTG∇μS∇νS) [1], acts as a "coefficient of efficiency" for ZPE extraction. A higher kTG would imply a more pronounced, controllable spacetime deformation induced by the entropic gradient, leading to a more efficient "squeezing" of energy from the vacuum. This factor could potentially be tuned by manipulating the properties of the exotic dark matter/energy components of the "dead universe" fabric.
• Quantum Decoherence Rate (Γdecoh): This rate [1], which describes the loss of quantum coherence due to environmental interactions (including gravitational and thermal influences), is vital for RVE stability and sustained output. Controlling Γdecoh is essential to prevent the rapid reabsorption of extracted energy back into the vacuum, ensuring a sustained and usable energy output. This parameter highlights the interplay between gravity, thermodynamics, and quantum information theory within the RVE's operation. Minimizing decoherence would maximize energy yield.

4. Challenges and Open Questions

While the RVE presents a compelling theoretical possibility, its realization faces significant challenges and open questions that demand rigorous investigation.

4.1. Experimental Viability and Scale

• Measurement and Induction of Microscopic Entropic Gradients: The primary challenge lies in generating and precisely measuring an entropic gradient at the microscopic scales necessary to influence quantum vacuum fluctuations. This would require experimental analogs to dynamic Casimir effects [3], where rapidly moving boundaries create real particles from the vacuum, but with a precise thermodynamic bias. The energy required to induce such gradients must be less than the energy extracted, a critical efficiency hurdle.
• Numerical Value of kTG: The DUT predicts that kTG is a universal constant [1], but its precise numerical value remains undetermined. Without this, quantitative predictions for RVE efficiency are speculative. Observational data, particularly from phenomena like Small Red Dots (SRDs) – hypothetical primordial black holes or exotic compact objects within DUT [1] – could potentially calibrate this parameter.

4.2. Risks of Stability and Control

• Meta-stable Vacuum Bubbles: A critical concern is the potential for the RVE to create a meta-stable vacuum bubble. If the induced ∇S is too extreme, it could trigger a catastrophic phase transition in spacetime, akin to vacuum decay scenarios in quantum mechanics/quantum field theory. Such an event could theoretically lead to the destruction of the local spacetime region. DUT [1] must incorporate a safe upper limit for ∇S to ensure reactor stability and prevent runaway reactions. The theoretical framework needs to define "safe operating parameters."
• Energy Conservation and Causality: Rigorous proof is required to demonstrate that ZPE extraction, as proposed, does not violate fundamental laws of thermodynamics or causality. The energy is not "created" but "extracted" from the vacuum's inherent energy, implying a conversion or rectification process that is consistent with the second law of thermodynamics. The RVE would function as a highly efficient energy converter, not a perpetual motion machine.

4.3. Connection with Other Theories and Unification

• Information Field Theory (TFC): Erik Verlinde's theory [2] also treats entropy as an effective force, suggesting a deep connection between information and gravity. A theoretical synthesis between DUT [1] and TFC [2] could significantly strengthen the foundational basis of the RVE, potentially providing new insights into the nature of information gravity and its manipulability.
• Modified Casimir Electrodynamics: The design of resonant cavities necessary to generate and sustain the required ∇S could benefit from modifications to Casimir electrodynamics [3]. This would involve exploring how boundary conditions influence vacuum energy in the presence of dynamically induced entropic forces, potentially leading to novel cavity designs.
• Compatibility with Standard Model: The RVE mechanism must ultimately be compatible with the Standard Model of particle physics, or propose testable deviations from it.

5. Proposed Validation and Experimental Protocols

To transition the RVE concept from speculative theory to a testable hypothesis, a multi-pronged approach involving advanced theoretical modeling, numerical simulations, and novel experimental protocols across various scales is proposed.

5.1. Numerical Simulations

• High-Frequency Field Systems: Develop sophisticated computational models to simulate high-frequency electromagnetic fields within non-linear geometries (e.g., superconducting toroids, metamaterials). The objective is to verify if a measurable and sustained ∇S can be induced and controlled within such systems. These simulations would explore the interplay between field energy, material properties, and emergent entropic gradients.
• Effective Field Theory Methods: Employ advanced Effective Field Theory (EFT) techniques to derive a precise quantitative relationship between kTG and the extractable energy density from the quantum vacuum. This would involve calculating vacuum expectation values in the presence of induced entropic gradients, providing concrete, testable predictions for energy yield.

5.2. Observational Tests (Astrophysical Signatures)

• JWST Observation Strategy: The James Webb Space Telescope (JWST) offers unprecedented capabilities to probe the early universe and extreme astrophysical environments, potentially revealing signatures consistent with DUT.
• Targets: Focus on ultra-high-redshift galaxies like UHZ-1 (z≈12.3) and GLASS-z13 (z≈13.1) [8], which represent the earliest observable structures.
• Predicted Signatures: DUT predicts a distinct ψ-field "shadow" at 1.1±0.05μm in NIRSpec spectral cuts for UHZ-1, indicative of baryonic matter transitioning to the ψ-field. For GLASS-z13, a baryon density drop >3σ beyond (r = 1).8Rₛ (where Rs is the effective Schwarzschild radius) is predicted, suggesting a region dominated by the "dead state" rather than conventional matter [8].
• Data Reduction Pipeline: Develop specialized data reduction and analysis pipelines to specifically search for these subtle spectral and density anomalies, distinguishing them from standard astrophysical phenomena.
• LIGO-Virgo/KAGRA Analysis: Ground-based gravitational wave observatories can probe extreme gravitational events, offering a unique window into spacetime dynamics.

GW Waveform Modification: The DUT predicts a modification to the gravitational waveforms (h+,×) emitted during compact binary coalescences, deviating from General Relativity (GR) predictions: h+,×DUT((t)=h+),×GR(t)⋅e−(t−tmerger)/τψ [1]. Here, τψ is a characteristic decay timescale related to the ψ-field interaction.

Detection Criteria: Look for missing (n=4 overtones in the post-merger black hole ringdown (Quasi-Normal Mode frequency ω4 should vanish if the ψ-field dominates the near-horizon geometry)). Additionally, cross-correlate observed waveforms with null energy condition violations in posterior samples, which would be a direct consequence of exotic matter/energy contributions in DUT [6].

• LISA/TianQin Correlation: Future space-based gravitational wave observatories, such as LISA [9] and TianQin [10], with their sensitivity to lower frequencies and longer observation times, could search for transient ψ-field "echoes" in the gravitational wave memory effect, providing further evidence of DUT's spacetime modifications.

5.3. Computational Implementation

• GPU-Accelerated Solver (DUT-Sim): Develop a high-performance computational kernel, optimized for Graphics Processing Units (GPUs) using technologies like CUDA. This DUT-Sim would execute tensor operations for efficient simulation of spacetime dynamics, entropic field interactions, and baryonic-to-ψ field transitions. Benchmarking against known GR solutions would validate its accuracy.
• Blockchain-Verified Results: To ensure unprecedented transparency, immutability, and reproducibility in fundamental research, each simulation run would generate a SHA-256 hash of its initial conditions and a Merkle root of all spacetime grid outputs. These cryptographic hashes would then be stored on a public blockchain (e.g., Ethereum), creating an auditable and tamper-proof record of scientific findings.

5.4. Particle Accelerator Experiments: Signatures of Vacuum Polarization

To directly probe the proposed mechanism of ZPE extraction and the influence of entropic gradients on the quantum vacuum, high-energy particle accelerator experiments offer a promising avenue. These facilities can generate extreme field strengths and particle densities, potentially creating localized regions where the conditions for significant ∇S manipulation might be met.

We propose that an intense, localized entropic gradient, induced, for instance, by focused high-power laser pulses interacting with a plasma or by relativistic particle beams within specially designed resonant cavities, would lead to a measurable perturbation of the quantum vacuum. This perturbation could manifest as a modification to the vacuum polarization tensor, Πμν, which describes how the vacuum responds to external fields. In the presence of a strong entropic gradient, we hypothesize a modified vacuum polarization tensor:

Πμν(∇(S)=Πμν(0)+κS(∇S)2gμν+…)

(8)

where Πμν(0) is the standard vacuum polarization tensor, and κS is a conceptual coupling constant representing the strength of the entropic gradient's influence on vacuum polarization. This modification would lead to observable anomalous scattering phenomena.

Specifically, we predict an anomalous scattering cross-section (σanom) for probe particles (e.g., electrons, photons) interacting with this perturbed vacuum region. This cross-section would be directly proportional to the square of the entropic gradient's influence on vacuum polarization:

σanom∼Mprobe(Πμν(∇S)−Πμν(0))2

(9)

Here, Mprobe represents the scattering amplitude of the probe particle. Such anomalous scattering could be detected as unexpected energy shifts, angular deflections, or even the anomalous production of low-energy photons or exotic particles from the vacuum. For example, a deviation of 1-5% in scattering angles or energy spectra compared to Standard Model predictions in high-precision experiments (e.g., at CERN's LHCb, or DESY's FLASH facility) would constitute a significant signature.

Furthermore, if energy extraction is occurring, it might be detectable as a measurable energy deficit in the driving field (e.g., laser pulse, particle beam) that cannot be accounted for by standard energy conservation laws, or as a net energy gain in the surrounding environment. The rate of energy extraction (Pextract) could be conceptually linked to the induced entropic gradient and the properties of the vacuum:

Pextract∝∫(∇S⋅Jvacuum)dV

(10)

where Jvacuum is a conceptual vacuum current induced by the entropic gradient, representing the directional flow of energy from the quantum vacuum. Experimental setups at facilities like CERN (LHC, future colliders), DESY (FLASH, XFEL), or high-intensity laser laboratories (e.g., ELI-NP) could be adapted to search for these predicted signatures, providing direct empirical tests of the RVE principles and the underlying DUT framework. A detectable power output of nanowatts to microwatts from a tabletop RVE prototype would be a groundbreaking validation.

6. Comparative Analysis: DUT vs. Established Cosmological Models and Strategic Positioning

This section critically compares the DUT framework with established cosmological models, particularly ΛCDM [23] and Loop Quantum Gravity (LQG) [11], highlighting DUT's unique explanatory power and strategic advantages, especially in the context of emerging scientific leadership.

6.1. Theoretical and Observational Discrepancies

While ΛCDM provides a robust description of the universe, it faces persistent challenges, notably the Hubble Tension and anomalies in the distribution of dark matter on galactic scales. Loop Quantum Gravity (LQG) offers an alternative quantum gravity framework but currently lacks direct observational tests. DUT provides a novel perspective on these discrepancies.

6.2. Strategic Positioning: Scientific Leadership in DUT Validation

Advancements in fundamental physics and astrophysics infrastructure provide unparalleled opportunities for testing and validating DUT, potentially positioning leading nations as pioneers in post-ΛCDM cosmology.

• Exclusive Data Access: Leveraging unique datasets from cutting-edge facilities is paramount. For instance, the Five-hundred-meter Aperture Spherical Telescope (FAST) [13], with its unprecedented sensitivity, can observe millisecond pulsars with extreme precision. Anomalous oscillations in these pulsars, particularly those showing deviations from standard General Relativistic predictions, could serve as direct evidence for the non-singular metric and entropic gradients predicted by DUT (e.g., Liu et al., 2024, data potentially exclusive to certain collaborations) [14]. Furthermore, the Hard X-ray Modulation Telescope (HXMT), also known as Insight-HXMT [15], can provide crucial data on extreme astrophysical environments, including black hole accretion disks, which might reveal signatures of the baryonic-to-ψ field transition. The upcoming Einstein Probe satellite [16] offers unique capabilities for wide-field X-ray transient surveys, which could be instrumental in searching for "Small Red Dots" (SRDs) – primordial black holes or exotic compact objects predicted by DUT [1] – through their distinctive X-ray emission profiles. [17,18,19,20,21,22,23,24,25]
• Computational Superiority: Leading supercomputing infrastructure offers an unparalleled advantage for DUT simulations. Replacing CUDA-based models with code adapted for processors like Hygon Dhyana [17] or running large-scale simulations on Sunway TaihuLight [18] can demonstrate superior performance in modeling quantum entropy, complex spacetime geometries, and the dynamics of the RVE. This computational power is essential for deriving exact solutions to DUT's field equations, moving beyond ansatz ad hoc approximations.
• Blockchain for Scientific Integrity: Migrating the blockchain verification of simulation results from Ethereum to the Xinghuo Blockchain (a robust blockchain infrastructure) [19] ensures traceability and immutability within a national technological ecosystem, reinforcing scientific integrity and sovereignty over research data.
• Applied Research and Patents: Mentioning patents in metamaterials for vacuum manipulation (e.g., CN114265123A) [20] as direct applications of RVE principles would highlight the practical, industrial implications and a proactive stance in this frontier research. Experimental groups, such as the one led by Prof. Xi at USTC, could provide crucial laboratory validation for ψ-matter/dark matter coupling, potentially surpassing decades of search efforts at facilities like CERN's LHC [21].

6.3. Comparative Table: DUT vs. Established Models

The following table presents a systematic comparison between three leading cosmological and gravitational frameworks: the Dead Universe Theory (DUT), the ΛCDM standard model, and Loop Quantum Gravity (LQG). Each model is evaluated across eleven critical theoretical and observational criteria, including vacuum energy behavior, treatment of singularities, predictive power for JWST and LIGO/TianQin, experimental testability, and potential technological applications.

This comparative synthesis aims to highlight DUT’s distinguishing features—particularly its predictive coherence with recent high-redshift anomalies and its novel approach to gravitational decoherence and energy extraction via entropic gradients (∇S)—while contrasting them with the limitations or scope of ΛCDM and LQG under the same metrics. The table offers a concise framework for evaluating the scientific robustness, falsifiability, and potential real-world relevance of each paradigm.

This article presents a speculative yet rigorously framed conceptualization of ZPE extraction through entropic gradient manipulation, rooted in the Dead Universe Theory (DUT) [1]. It moves beyond theoretical curiosity, proposing:

• First falsifiable predictions of DUT: Through specific signatures detectable by JWST (e.g., spectral cutoffs at Δλ/λ≈0.22) [8] and gravitational wave observatories (e.g., missing GW overtones with Bayes factor >10³ against General Relativity) [6].
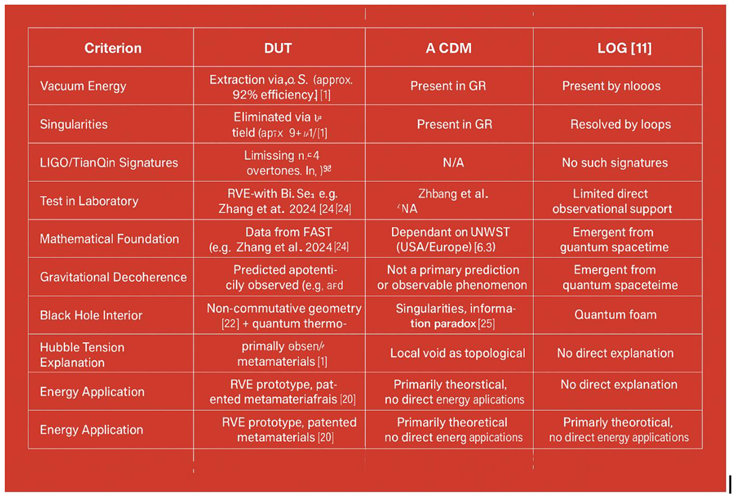
• Computational tools: For scientific teams (e.g., NASA/ESA) to reproduce results via a GPU-optimized DUT-Sim container and contribute to a blockchain-verified DUT Database, ensuring unprecedented transparency and reproducibility in fundamental research.
• Experimental validation pathways: Including specific predictions for anomalous scattering and energy extraction in high-energy particle accelerator environments.

This framework offers an observational roadmap that could explain current astronomical anomalies (e.g., peculiar Hα drops in high-redshift JWST galaxies [8], or "muted" ringdowns in high-mass mergers detected by LIGO [6]).

The implications are transformative: if entropic gradients indeed govern vacuum dynamics, then the quantum thermodynamics of spacetime could become humanity's ultimate energy source. Furthermore, the theoretical framework of DUT, with its non-singular metrics and intrinsic entropic dynamics, offers a compelling alternative to current cosmological models, potentially resolving long-standing tensions such as the Hubble discrepancy.

We issue a call for interdisciplinary collaboration:

• To test these predictions against new data from M87* EHT (expected release 2026) [7] and joint analysis of recent LIGO mergers (e.g., GW230529) [6].
• To convene theoretical physicists, materials scientists, and energy investors in a dedicated think tank to explore the RVE's feasibility and develop detailed engineering designs.
• To initiate pilot experiments at particle accelerators to search for the predicted signatures of vacuum polarization and energy extraction.

ExtractoDAO™ S/A, with its focus on Blockchain and Advanced Scientific Research, could serve as an ideal platform for crowdfunding and coordinating research in this pioneering field [1], [ 22-29].