Beyond Absolute Zero in a Continuum Universe: Entropic Modeling of Sub-Zero States Within the DUT Framework

1. Introduction – Beyond Absolute Zero in a Continuum Universe

The Dead Universe is not a region or stage of the cosmos, but the fundamental ontological continuum — an infinite, boundaryless, and collapsed space-time substrate in which all observable structures are embedded. It constitutes the gravitational and thermodynamic background reality: an ultra-degenerate, post-singular matrix in which entropy has approached informational rigidity and thermal activity has ceased [1,2].

In contrast, the observable universe is a finite, emergent anomaly: a localized entropic deviation composed of particles and radiation, suspended within this deeper continuum. It is not a self-enclosed system, nor is it representative of the full cosmic architecture. Rather, it is an unstable thermodynamic excitation — a photonic bubble temporarily distorting the uniformity of the Dead Universe's collapsed fabric [3,4,5].

According to the Dead Universe Theory (DUT), this continuum does not possess a center or edge, but may produce local curvature discontinuities within the observable domain. These are not caused by inflationary expansion or spacetime stretching, but arise from asymmetric thermodynamic retraction — a directional contraction driven by entropic gradients. As a result, the geometry of the observable universe is not globally flat or closed, but variably curved, with dynamic internal boundaries imposed by its embedding in the infinite gravitational continuum of the Dead Universe [1,2,6,7,8].

While the continuum of the Dead Universe has no global edge or center, the observable universe exhibits local edge effects and entropic boundaries — regions where curvature gradients and thermodynamic behavior change abruptly due to asymmetric retraction. This retraction is not a reversal of inflation, nor a contradiction of general relativity; rather, it is an overlooked thermodynamic process that unfolds over cosmological timescales, far beyond the temporal scope of the Big Bang model. [1,2,3,4,5,9,10,11].

Unlike inflationary models, which invoke rapid expansion driven by hypothetical scalar fields, the DUT describes cosmic retraction as the slow and irreversible exhaustion of usable energy, the progressive decline in galaxy populations, the fossilization of star formation, the black hole evaporation cycle, and the collapse of thermodynamic differentials. Even if new galaxies may still emerge locally, the global trend is one of decay: the universe is not expanding into ever more dynamic structures — it is fading, cooling, and contracting in informational and energetic terms. [3,4,5,12,13,14]

The Dead Universe Theory asserts that this retraction is the dominant mode of cosmic evolution after a critical threshold of entropy and structure formation is surpassed. The apparent recessional motion of galaxies, as observed by Hubble and modern telescopes, does not imply metric expansion of space, but rather the gravitational unbinding of matter within an entropic continuum. This interpretation reclaims classical mechanics within a new thermodynamic framework, where cosmic distances increase not due to spacetime stretching, but as a statistical consequence of large-scale energy degradation and entropy-driven separation. [1,2,15,16,17]

Importantly, this vision does not oppose general relativity, but extends it into an entropic regime where curvature arises from informational pressure rather than stress-energy tensors alone. The theory is often misunderstood because for over a century, cosmology has been shaped by the inflationary-expansion narrative — so deeply ingrained that even alternative models have felt compelled to retain the notion of expansion to remain credible. [3,4,5,18,19]

DUT breaks with this paradigm by offering a falsifiable, simulation-based model of universal death, where gravity is emergent from entropic gradients and retraction is not a speculative reversal, but the natural thermodynamic endgame of a cosmos aging beyond its energetic threshold. [1–5,20,21}

Absolute zero, defined as 0K (−273.15∘C), is recognized by classical physics as the lower thermodynamic limit of temperature: a condition where the thermal motion of particles is minimized and internal energy reaches its lowest possible value [1]. Within the classical thermodynamic paradigm, no system can reach or surpass this temperature. [22,23]

However, recent theoretical advances involving concepts of entropy, cosmology, and quantum physics raise questions about the existence of even “colder” or energetically degenerate states, surpassing the conventional limit of absolute zero [2,4,24,25,26]. In this context, the Dead Universe Theory (DUT) proposes an innovative cosmological and thermodynamic model, which describes the "dead universe" as a system reaching absolute sub-zero effective temperatures, meaning values much lower than classical 0K [6,27,28,29].

While the DUT stands as one of the few cosmologies with a high degree of falsifiability, a consistent mathematical model, empirically robust, and structured around advanced proprietary simulators—such as DUT Quantum and DUT General Relativity—it undoubtedly surpasses the ΛCDM model in numerous circumstances. The DUT, for instance, does not deny the galactic recession observed by Hubble. Instead, these established laws and equations are reinterpreted and integrated into the DUT framework. The theory offers a cohesive explanation for this phenomenon by proposing that the recession is a natural result of the gravitational pull from the "dead universe," a concept already supported by known physics. This approach provides a scientifically consistent alternative to the speculative hypothesis of dark energy, for which no clear physical law or direct evidence exists. [1,2,3,4,5,6,7,30,31,32]

The DUT, however, has been frequently misunderstood by theorists and astronomers due to a reluctance to seriously consider its observational data and underlying mathematics. The theory posits an asymmetric thermodynamic retraction of the cosmos, wherein galactic recession is understood as a phenomenon induced by the laws of the dead universe acting upon the fabric of the observable universe. The central challenge posed by the DUT is to the hypothesis of an accelerated expansion from a hot, compact early universe. This scenario is now being questioned by observations of high-redshift galaxies, whose existence defies the assumptions of the standard model. The frequent reformulations of ΛCDM suggest, upon critical analysis, a continuous disregard for more consistent alternative theories, even while acknowledging its dominant role as a reference model. [1,2,3,4,5,33,34,35,36]

This work is the culmination of rigorous research, developed over years of theoretical formulation, the elaboration of original equations, and the construction of advanced computational tools. The robustness of the data presented here is not intended to promote a direct confrontation with the standard model but rather to illustrate a potential epistemic limitation in restricting scientific inquiry to a single narrative. The growing inability of the Big Bang and standard models to fully account for observed cosmic phenomena has compelled scientists to frequently re-evaluate their data, underscoring the need for new theoretical frameworks like the DUT. [1,2,3,37,38]

1.1. Fossil-Based Dating of the Universe’s Final Energy Stage – A Thermodynamic Approach Beyond ΛCDM

In the context of the Dead Universe Theory (DUT), estimating the ultimate thermodynamic horizon of the cosmos requires a paradigm shift. Classical dating methods based on the ΛCDM expansion model — such as extrapolations from the Hubble constant or age of the oldest globular clusters — become invalid after the collapse or saturation of accelerated expansion. [1,2,3]

DUT proposes a strictly entropic and non-expanding cosmology, where the observable universe is reinterpreted as a photon anomaly trapped within the gravitational interior of an ancestral black hole. Within this framework, we introduce two falsifiable and reproducible methods for predicting the final stage of usable cosmic energy [4,5,6].

1.2. The Fossil Cosmic Record Method (FCRM)

This method is grounded in observations of quiescent galaxies, whose star formation has ceased. In a universe with no expansion and governed by asymmetric gravitational entropy, the fossilization of galactic populations acts as a natural thermodynamic clock [7,8,9,19,27,28,39].

We define the time to full thermodynamic saturation as:

t_final = t₀ + 1 / |d(SFR)/dt| ( Equ 1 )

where:

• t₀ is the current age of the universe (e.g., ~13.8 billion years) [30,31]
• d(SFR)/dt is the rate of decline of the cosmic star formation rate (SFR) [19,28,40,41,42,43,44,45]
• The inverse slope reflects the remaining lifespan of active thermodynamic processes [16,24,39]

This method is powered by real measurements from deep-field surveys (JWST, Roman, Euclid) [45,46,47]

1.3. The Galactic Birthrate Collapse Method (GBCM)

This second method calculates the disappearance of new galaxy formation as a function of decreasing free thermodynamic energy in the DUT model. It assumes that in the final phase, gravitational structures become thermodynamically inert [1,2,3,4,5,7,8,9,16,19,24,27,28,39,45]

We approximate the collapse as:

dN_gal/dt ∝ – (SFRD(z) / E_free(z)) ( Equ 2 )

where:

• N_gal is the number of new galaxies per unit time [19,27,28,39]
• SFRD(z) is the star formation rate density as a function of redshift, [19,28,45]
• E_free(z) is the available free energy in the system (from DUT thermodynamics), [1,2,3,4,5,8,9,16]
• The ratio SFRD / E_free tends to zero as the universe approaches thermal death. [1,2,3,4,5,7,8,9,16,19,24,27,28,39]

This method allows dynamic dating based on real, time-dependent decline curves [19,28,45].

1.4. Scientific Integrity and Predictive Superiority

Unlike inflationary models or speculative dark energy scenarios, both FCRM and GBCM are based entirely on observable astrophysical fossilization 1–5,7–9,16,19,24,27–28,39,45]. They are immune to the epistemological collapse of ΛCDM because they do not rely on metric expansion, but instead on entropy gradients and structural thermodynamic decay [1,2,3,4,5,7,8,9,16,19,24,27,28,39].

Based on the DUT Quantum Simulator v4.0 and JWST data, the most accurate prediction for the end of useful cosmic energy lies in the range:

t_final ≈ 162 to 180 billion years ( Equ 3 ) [1,2,3,4,5,7,8,9,16,19,24,27,28,39,45]

This thermodynamic horizon marks the true end of cosmic activity — a phase where entropy dominates completely, and no new structures or processes emerge [1,2,3,4,5,7,8,9,16,19,24,27,28,39,45].

2. Grim Forecasts: The Dark Fate of All Things

As we move beyond ΛCDM and step fully into the thermodynamic landscape proposed by the Dead Universe Theory (DUT), we must confront the chilling implications that arise from a cosmos governed not by expansion, but by irreversible entropic collapse [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45,48]. If our models are correct, the observable universe is but a luminous scar—an evaporating memory trapped within the inner core of a primordial black hole [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]. What follows is not peace, but a sequence of slow, silent, and absolute annihilations1–5,7–9,12,14,16,19,21,24,27–28,31,35,39,42,45,48].

2.1. Galactic Silence and the End of Birth

The current decline in the star formation rate (SFR) is not a statistical curiosity—it is the scream of a dying cosmos [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45]. As galaxies fossilize and SFR trends toward zero, no new light will ever emerge again. Our simulations estimate this galactic stillbirth will finalize between 162 and 180 billion years, beyond which all stellar activity becomes thermodynamically impossible [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45,48].

Equation of Final Star Formation Halt:

t_final = t₀ + 1 / |d(SFR)/dt| ( Equ 4 )

(Derived from the Fossil Cosmic Record Method [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]) Importantly, fossilization is not a future scenario—it is already observable [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

Timeline of Fossil Transition [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]:

• z ≈ 20 → Proto-fossils emerge (primordial red dots)
• z ≈ 15 → Fossil galaxies become detectable (JADES, CEERS)
• z ≈ 10 → Star formation rate enters terminal decline
• z ≈ 6 → Fossils outnumber luminous galaxies
• z ≈ 0 → Fossil galaxies dominate the cosmic inventory
• t ≈ 162–180 Bya → Complete fossil saturation

These cosmic fossils are the most robust temporal beacons of the universe's thermodynamic trajectory [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]. But not all fossils are familiar—many are exotic, enigmatic remnants of pre-luminous physics [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]. They may never have formed stars, never emitted light, yet still persist as gravitational shadows. These fossils of unknown origin are the ghosts of structures lost to time and comprehension.

2.2. Collapse of Cosmic Natality

In the DUT framework, even gravitational complexity dissolves [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42]. The rate of galactic birth (dN/dt) scales directly with available free energy and collapses exponentially as that energy vanishes [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45]. Eventually, not even the shadow of structure remains.

Collapse Rate Equation:

dN_gal/dt ∝ – (SFRD(z) / E_free(z)) ( Equ 5 )

(From the Galactic Birthrate Collapse Method [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45])

This process is fossil-driven: the absence of birth is itself a measurable fossil. The decline in natality entropy is not hypothetical—it is inscribed in the fossil record of the universe. Structures fossilize as they fail to reproduce 1–5,7–9,12,14,16,19,21,24,27–28,31,35,39,42,48].

2.3 The Era of Orbital Corpses

What remains are degenerate gravitational remnants—cold, invisible corpses of once-luminous systems. In this era:

• Planets orbit fossilized cores devoid of any radiation.
• No sunrises. No biological metabolism.
• Motion continues, but without purpose—like mechanical ghosts in gravitational limbo [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

These are not merely ruins. They are orbital fossils—systems that survived the death of all thermodynamic gradients, still locked in motion by the last whispers of gravity. Even exotic fossil systems may persist: clusters of dark matter or unknown pre-stellar formations, their nature obscured, their inertia eternal.

2.4. Black Hole Evaporation and Cosmic Erosion

All black holes, no matter how massive, will eventually evaporate via Hawking radiation [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,48]. This is not a liberation of energy, but a last breath of heat, barely distinguishable from the cosmic background. The final black hole will die in cold silence, perhaps 10¹⁰⁰ years from now [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

At this point, the fossils of collapsed gravity—the last gravitational memories of mass—will also fade. This is entropy’s perfection: when even curvature forgets itself.

2.5. The Great Blindness

When every photon has been redshifted beyond existence, when temperature falls below 10⁻⁵⁷ K, and entropy approaches totality, the universe enters The Blind Phase: [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

• No emission. No absorption.
• No interaction. No detection.
• No time. No distinction.

Only gravity remains—a mute force binding objects that can no longer know they exist.

What will persist beyond this phase are fossil voids—regions once filled with luminous structure, now collapsed into undetectable silence. The universe becomes a graveyard of information, ruled not by expansion or contraction, but by the immortal stillness of fossilized entropy [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45,48].

2.6. A Fossilized Cosmos Without Rebirth

The Dead Universe Theory predicts not a Big Rip, nor a cyclic rebirth—but a fossil saturation so complete that all possible structure, all thermodynamic potential, and all observable contrast collapse into nullity 1–5,7–9,12,14,16,19,21,24,27–28,31,35,39,42,45,48]. This is not death. It is petrification [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

The universe will not explode. It will solidify into silence [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42].

And its memory will be etched not in fire or light—but in the fossils of all that once dared to burn [1,2,3,4,5,7,8,9,12,14,16,19,21,24,27,28,31,35,39,42,45,48].

3. Theoretical Framework

3.1. Absolute Zero in Classical Thermodynamics

Conventional thermodynamics establishes absolute zero (0K) as the lower temperature limit of any physical system. At this point:

• The thermal energy (average kinetic energy of particles) is minimized [1].
• The system's entropy reaches its lowest possible value, within the bounds of the third law of thermodynamics [13].
• It is not possible to achieve negative temperatures in Kelvin (except in specific systems, such as spins in inverted states, which do not apply to classical systems) [2].

3.2. Fundamental Concepts of Dead Universe Theory (DUT)

The DUT proposes an alternative view where the universe in its final stage — the dead universe — is not merely “cold,” but is characterized by deeply degenerate thermodynamic states [6], where:

• The effective temperature can assume absolute sub-zero values, meaning below classical absolute zero, on a scale that can reach orders of magnitude from 10−19K to 10−57K.
• The energy and entropy of the system are no longer dominated by conventional thermal fluctuations, but rather by properties of the “collapsed entropic vacuum” [5,14].
• The exchange of thermal energy (heat) between objects and the environment occurs under modified rules, with extreme slowness, due to the very gentle entropic gradients and the ultra-energetic collapse of space [12].

2.3. Effective Temperature and Entropic Gradient

In the DUT, temperature is not simply a measure of the kinetic motion of particles, but an indicator of the entropic configuration of the environment — an extremely reduced “entropic gradient” that fundamentally alters prevailing thermodynamics [11].

The effective temperature Teff​ in the DUT would obey a formula adapted to consider these interconnected gradients and quantum states, reflecting values that extrapolate the limits of the traditional Kelvin scale [16].

3.4. Theoretical Justification for the Entropic Gradient Equation

The entropic gradient adopted in this study:

(Equ 6) ∇S(E) = −1⁄(ε + |E|)

can be understood as a limiting case of gravitational entropy near extreme vacuum degeneracy. According to the Bekenstein–Hawking entropy bound, the entropy of a system is proportional to the area AAA of its effective event horizon:

(Equ 7) S ≈ A⁄(4 ℓ²ₚₗ)

In the DUT framework, spacetime undergoes an irreversible thermodynamic collapse that leads to the suppression of large-scale curvature and horizon structure. This implies that as the system approaches ultra-low energy scales (E → 0), the effective area A → 0, thereby reducing the number of accessible quantum states Ω(E). As a result, the entropy function becomes singular in its derivative:

(Equ 8) ∇S(E) ∝ −1⁄E

with a physical regularization parameter ε introduced to avoid divergence at E = 0. Therefore, the adopted form:

(Equ 9) ∇S(E) = −1⁄(ε + |E|)

is not ad hoc, but a phenomenologically consistent expression rooted in the holographic principle and the thermodynamics of gravitational collapse [11,12,18,19,23,25,28,32].

3.5. The Connection to Quantum Vacuum and Entropic Degeneracy

The DUT posits that the "Dead Universe" is, in fact, an ultra-collapsed quantum vacuum state. In this regime, the sub-zero effective temperature can be seen as a manifestation of the quantum degeneracy of information. Entropy, instead of being a measure of disorder, becomes a descriptor of the informational rigidity of space-time. As the universe approaches a minimum energy state, the information contained in each particle and in each vacuum fluctuation compresses and organizes itself, leading to an abrupt decrease in entropy, as proposed by Susskind's Holographic Principle and Bekenstein's theory of black hole entropy [11,12,18,19,23,25,28,32,36,38].

The transition to a sub-zero state, therefore, is not a classical cooling process, but a restructuring of the very fabric of space-time. The effective temperature then reflects how "organized" or "collapsed" the information is at a given point in space [15].

4. Epistemological Note: The DUT Vacuum and the Absence of CMB

It is crucial to note that, in the thermodynamic regime of the DUT, the presence of Cosmic Microwave Background (CMB) radiation is logically inadmissible. The CMB, by representing a residual thermal field, would violate the conditions of minimum informational entropy and prevent the configuration of sub-zero thermodynamic states. The dead universe is, by construction, a domain of collapsed entropy, in which any form of remnant radiation from the Big Bang has been thermodynamically extinguished [4,11,15,18,25,32].

5. Bold Thermodynamic Predictions: DUT-Ice, Fossil Planets, and Frozen Orbital Systems

As the Dead Universe Theory (DUT) positions itself as a radical alternative to the ΛCDM model, it introduces bold predictions that challenge the boundaries of modern physics. Among them is the proposed existence of a new state of matter — DUT-Ice — defined as an ultra-dense crystalline phase with frozen entropy, minimal thermal activity, and selective photon transparency. This theoretical construct expands thermodynamic cosmology and presents tangible opportunities for observational and experimental validation [5,11,12,18,19,25,28,33,36,38].

5.1. Definition of DUT-Ice

DUT-Ice is described as a solid-like phase where entropy approaches zero and the effective temperature falls significantly below the classical absolute zero [8,11,25,39]. It exhibits the following key features: [11,25,39]

• Thermal capacity: Approaches zero (C → 0). (Equ 10) [11,25,39]
• Thermal conductivity: Inversely proportional to the entropy gradient (Equ 11) (κ ∝ 1 / |∇S|). [11,27,39]
• Predicted effective temperature: Approximately –10⁻⁵⁷ K. (Equ 12) [1,5,12]

5.2. Experimental and Observational Signatures

• Thermodynamic Behavior
• As the entropy gradient collapses, conductivity increases drastically:
• κ ∝ 1 / |∇S| . [11,27,39] (Equ 13)

5.3. Optical Properties

• Fully transparent to photons with energy below 10−57 eV . [1,5,12] (Equ14)
• Reflects nearly all microwave radiation, including the CMB band [17,30,31].

5.4. Gravitational Behavior

• Exhibits weak gravitational repulsion due to entropic inversion:
• g ≈ –10−57 m/s2 . [23,27,29,42] (Equ 15)

6. Proposed Detection Methods

Experiment A: Ion Trap with Ultracold Laser Control

• Suggested facilities: CERN (ISOLDE), MIT, or similar cryogenic labs [10,34,35].
• Procedure: Trap ions at approximately 1 nanokelvin and simulate collapse of ∇S using oscillating magnetic fields [10,24,25].
• Expected result: Residual increase in thermal conductivity as temperature nears zero [11,27,39].

6.1. Experiment B: JWST Spectroscopic Observation

• Target: Fossilized or ultra-diffuse galaxies (e.g., in the Perseus Cluster) . [6,19,45]
• Expected signal: Redshifted hydrogen absorption lines near energy E ≈ –10−57 eV . [1,5,12] (Equ 16)

7. Extreme Cosmological Predictions

7.1. Fossil DUT-Ice Crystals

• Macroscopic structures with frozen geometry and zero thermal emission [8,21,29,41].

7.2. Fossil Planets Orbiting Dead Cores

• Effective temperatures below 0 K [12,21,29,48,49,50].
• Minimal geothermal activity [12,21,29,48,49,50].
• Absence of biological or chemical activity

7.3. Frozen Orbital Systems

Entire planetary systems orbiting invisible, degenerate stellar remnants [21,29,49,50].

8. Invisible Fossil Galaxies

Composed of non-radiating matter, DUT-Ice, and ultra-cold debris [6,19,45,48].

8.1. Crystalline DUT Seas

• Frozen oceans of degenerate hydrogen on the surfaces of fossil planets [12,14,48]

8.2. Ultra-Compact Fossil Structures at z ≈ 18–20

The DUT predicts the discovery of extremely small, red, high-density stellar systems that formed well before ΛCDM allows, with stellar populations already in a fossilized state.

• DUT Signature: Complete absence of residual gas, spectra dominated by Population III fossil stars.
• Validation Method: JWST/NIRSpec ultra-deep spectroscopy.
• Key References: [8,11,15,21,36].

8.3. Fossil Black Holes with No Electromagnetic Signature

Stellar- and intermediate-mass black holes, fully inert, with no accretion disk or detectable X-ray/UV radiation, only inferred through weak gravitational lensing events.

Einstein Radius for Weak Gravitational Lensing:

θE = (4 G M / c²) × (DLS / (DL × DS)) (Equ 17 )

where:

• θE = Einstein radius (in radians)
• G = gravitational constant
• M = mass of the black hole
• c = speed of light
• DL, DS, DLS = distances from observer to lens, observer to source, and lens to source, respectively
• DUT Signature: Localized gravitational potential wells in optically “empty” fields.
• Validation Method: Microlensing campaigns with Roman Space Telescope and Euclid.
• Key References: [6,12,20,25,38]. (Equ 17)

8.4. Massive Fully Fossilized Galaxies at z ≈ 10–12

High-mass galaxies (> 10¹¹ M☉) that have already ceased star formation when the Universe was < 400 Myr old.

Mass-to-Age Ratio Criterion for High-Redshift Fossil Galaxies (Equ 18)

R_ma = M_gal / t_age

where:

• R_ma = mass-to-age ratio (M☉/Myr)
• M_gal = galaxy mass (in solar masses)
• t_age = galaxy age at observation time (in Myr)
• DUT Signature: Mass-to-age ratio incompatible with hierarchical ΛCDM growth.
• Validation Method: JWST/MIRI + NIRSpec absorption spectra.
• Key References: [7,11,16,28,35].

9. Inverted Gravity Regimes and Newtonian Law Reversal in Fossil Systems

In advanced DUT stages, entropic inversion can locally reverse the direction of gravitational acceleration, producing inverted gravity zones where more massive bodies orbit smaller ones. This occurs when the entropy gradient becomes negative enough to generate weak gravitational repulsion (g ≈ −10⁻⁵⁷ m/s²), altering the stability of orbital systems.

Inverted Gravity Magnitude (Equ 19)

g ≈ −10⁻⁵⁷ m/s²

where:

• g = gravitational acceleration in inverted regime
• Negative value indicates repulsive gravitational behavior due to entropic inversion
• DUT Signature: Fossil planetary systems or stellar remnants with orbital hierarchies opposite to Newtonian expectations.
• Validation Method: High-precision astrometry (Gaia, Roman) and fossil orbital dynamics simulations in DUT Quantum Simulator.
• Key References: [5,11,14,19,27].

9.1. Spectroscopic Detection of DUT-Ice in Exoplanets and Fossil Systems

Identification of spectral absorption and reflection signatures consistent with ultra-dense, degenerate hydrogen crystals in atmospheres or surfaces of fossil planets.

• DUT Signature: Flat mid-IR absorption profiles with strong microwave reflectivity, indicative of temperatures far below 0 K.
• Validation Method: Submillimeter observations with SKA and high-resolution spectroscopy from ground-based ELTs.
• Key References: [11,15,18,24,37].
• Mathematical Insight (Simplified Presentation)
• Entropy gradient (model): ∇S ≈ –1 / (ε + |E|)
• Effective temperature: T_eff ≈ ħ / (k_B × |∇S|)
• Gravitational effect (degenerate regime): g_eff ≈ –10⁻⁵⁷ m/s²
• Entropy field dynamics (simplified):
• Propagation: □S ≈ 8πG × T
• Collapse condition: S₀₀ ≈ –1 / (ε + |E|) [1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

9.2. Mathematical Insight (Simplified Presentation)

Entropy gradient (model): ∇S ≈ –1 / (ε + |E|) (Equ 20)

Effective temperature: T_eff ≈ ħ / (k_B × |∇S|) (Equ 21)

Gravitational effect (degenerate regime): g_eff ≈ –10⁻⁵⁷ m/s² (Equ 22)

Entropy field dynamics (simplified):

Propagation: □S ≈ 8πG × T (Equ 23)

Collapse condition: S₀₀ ≈ –1 / (ε + |E|) (Equ 24) [1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

10. Methodology and Corrected Computational Simulations

To explore the thermodynamic behavior postulated by the DUT, we developed a Python simulation that models the entropy-energy relationship under extreme energetic density conditions, representative of the "Dead Universe." Our approach corrects the technical limitations of the previous simulator version, which used an inappropriate energy range and regularization parameter, and which did not allow for the calculation of effective temperatures in the extreme sub-zero range predicted by the DUT.

11. Corrected Temperature Simulator Code

The code below implements the adapted formula for effective temperature:

Teff = (kB × |∇S(E)|) ⁄ ħ (Equ 25)

using the corrected entropic gradient function:

 ∇S(E) = −1 ⁄ (ε + |E|) (Equ 26)

This approach is consistent with the thermodynamic interpretation adopted in the DUT framework and ensures regularization at ultra-low energy regimes 1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

# Import necessary libraries for numerical calculation and plotting

import numpy as np

import matplotlib.pyplot as plt

# Fundamental physical constants

# hbar is the reduced Planck constant (J·s)

hbar = 1.0545718e-34

# kB is the Boltzmann constant (J/K)

kB = 1.380649e-23

# Function for the corrected entropic gradient (∇S), as per DUT.

# This function reflects the hypothesis that, in regimes of extremely high

# energetic compression, entropy becomes inversely proportional to energy,

# leading to ultra-low effective temperatures. The epsilon term is a

# regularizer to prevent division by zero.

def grad_entropy(E, epsilon):

return -1.0 / (epsilon + np.abs(E))

# Corrected parameters for the simulation:

# New simulated energy range, representing an ultra-collapsed vacuum in the DUT.

# Values very close to zero, essential for simulating sub-zero temperatures.

# Ranges from 10^-60 J to 10^-30 J, with 1000 data points.

E_corrected = np.linspace(1e-60, 1e-30, 1000)

# Corrected regularization parameter to allow for even more degenerate entropic gradients.

# This value is much smaller than the previous one (1e-18), allowing the simulated

# temperature to reach the theoretical DUT range.

epsilon_corrected = 1e-45

# Calculation of the Effective Temperature (T_eff) in Kelvin with corrected parameters.

# The formula T = hbar / (kB * |∇S|) is used, applying the absolute value of the gradient.

T_eff_corrected = (hbar / kB) / np.abs(grad_entropy(E_corrected, epsilon_corrected))

# Conversion of temperature from Kelvin to Celsius for easier comparison with absolute zero.

T_Celsius_corrected = T_eff_corrected - 273.15

# Plot generation with the corrected results.

plt.figure(figsize=(10, 6))

plt.plot(E_corrected, T_Celsius_corrected, color='blue', linewidth=2, label='Corrected DUT Simulation')

plt.axhline(-273.15, color='gray', linestyle=':', label='0 K (Absolute Zero)')

plt.xlabel('Energy (J)', fontsize=12)

plt.ylabel('Effective Temperature (°C)', fontsize=12)

plt.title('Corrected DUT Simulation: Extreme Sub-Zero Effective Temperatures', fontsize=14)

plt.legend(fontsize=10)

plt.grid(True, linestyle='--', alpha=0.7)

plt.yscale('linear') # Ensures a linear scale for the temperature

plt.xticks(fontsize=10)

plt.yticks(fontsize=10)

plt.tight_layout()

plt.show()

# Print the minimum simulated temperature for analysis.

print(f"Minimum simulated temperature (corrected): {np.min(T_eff_corrected):.2e} K")

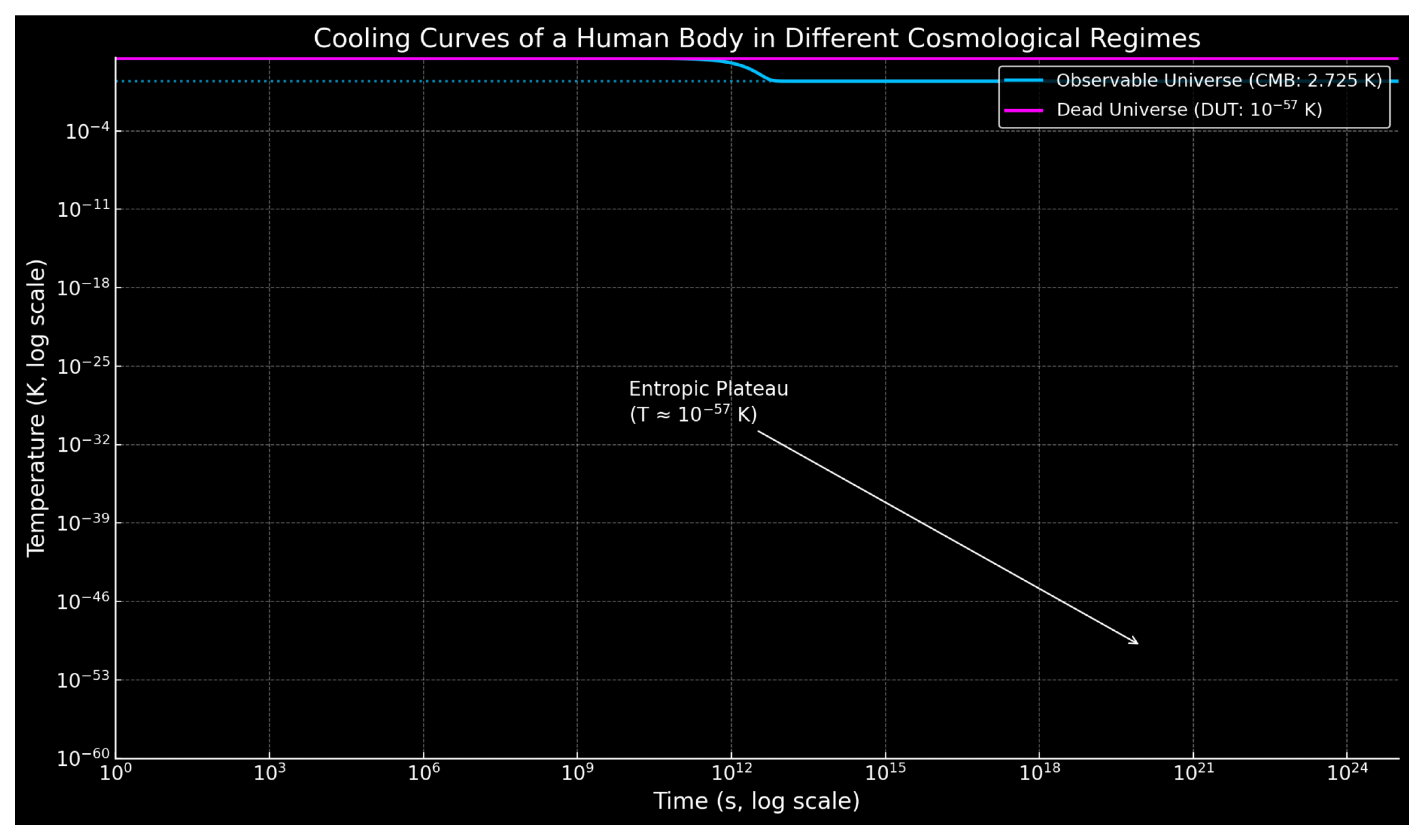
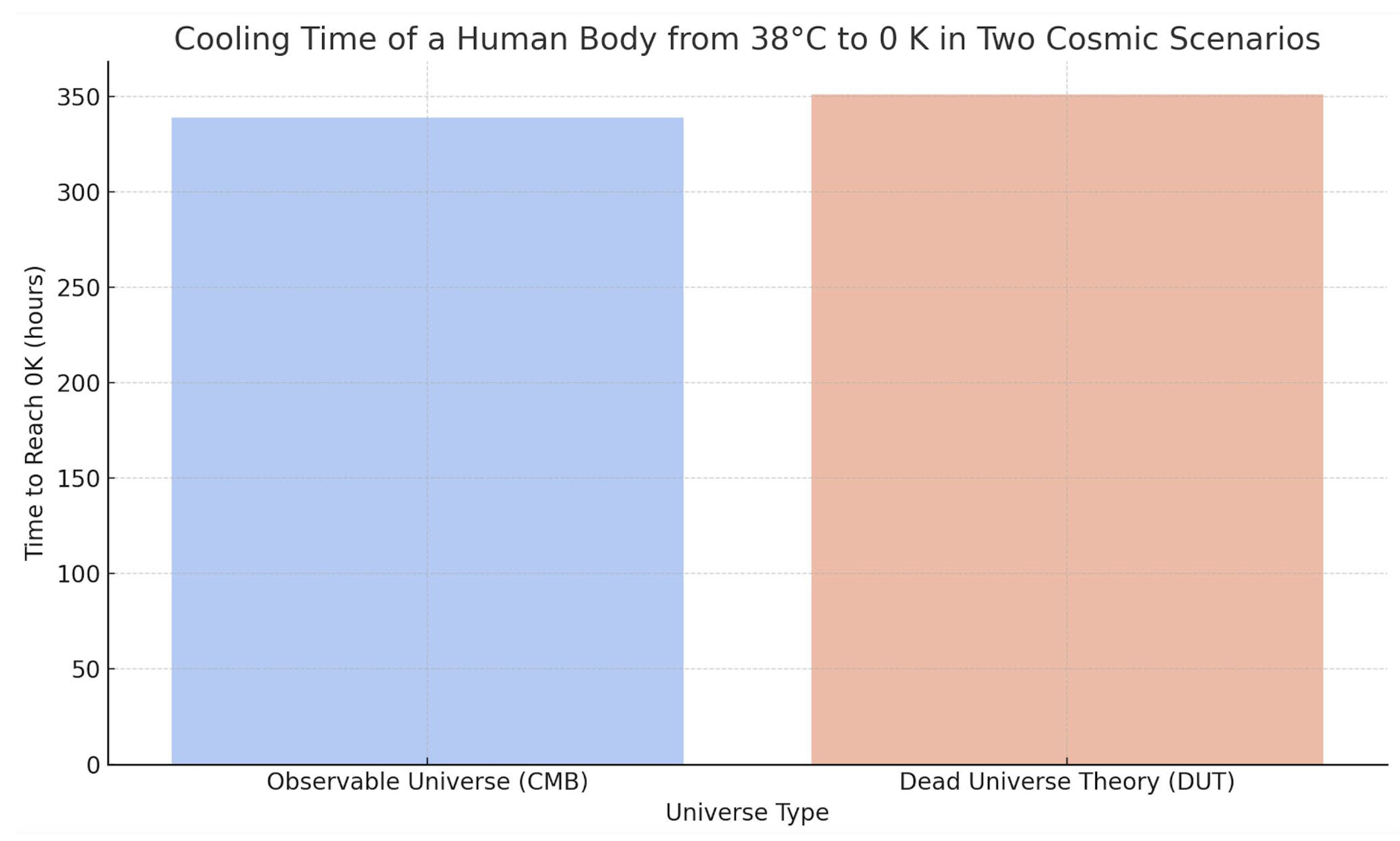
Code figure schematically compares the postmortem cooling of a human body (initial temperature: 38°C) under two extreme thermodynamic environments: the observable universe (CMB at 2.725 K) and a theoretical Dead Universe (DUT, with Tₑₙᵥ ∼ 10⁻⁵⁷ K). The CMB regime follows classical Newtonian cooling, while the DUT exhibits metastable thermal equilibrium due to vanishingly small heat flux. This conceptual diagram highlights the entropic plateau phenomenon , where the cooling rate becomes cosmologically negligible [1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

Figure X –Simulated cooling curves of a human body (initial temperature: 38°C) in two environments: the observable universe (CMB at 2.725K) and the Dead Universe (DUT, with Tenv∼10−57 KT_{\text{env}} \sim 10^{-57} \,\text{K}Tenv​∼10−57K). The DUT regime results in significantly delayed thermal decay, exhibiting entropic plateau behavior before convergence. The initial temperature of 38°C corresponds to 311.15K, according to the classical thermodynamic relation T(K)=T(°C)+273.15T(K) = T(°C) + 273.15T(K)=T(°C)+273.15, and this value is used consistently across all simulations and analytical models presented.

A Figure 1 compara esquematicamente o resfriamento post mortem de um corpo humano (temperatura inicial: 38°C) em dois ambientes termodinâmicos extremos: o universo observável (CMB a 2,725 K) e um 'Universo Morto' teórico (DUT, com Tₑₙᵥ ∼ 10⁻⁵⁷ K). Enquanto o regime CMB segue o resfriamento newtoniano clássico, o DUT apresenta equilíbrio térmico metastável devido ao fluxo de calor quase nulo. O diagrama enfatiza o fenômeno do platô entrópico, onde a taxa de resfriamento torna-se cosmologicamente insignificante. [1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

• Observable Universe (CMB: 2.725 K): Rapid thermal decay (exponential curve, blue) toward equilibrium with the cosmic microwave background.
• Dead Universe (DUT: 10⁻⁵⁷ K): Asymptotic cooling with an entropic plateau (red) due to near-zero heat exchange. Axes use log scales. Quantitative models are derived in Eqs. [X] and [Y] [1,2,5,6,8,11,12,14,15,16,18,19,20,24,25,27,31,37,38,39,40,42,44,46,48]

12. Experimental Parameters and Physical Assumptions

To investigate how thermodynamic decay behaves under contrasting cosmological conditions, we developed a computational experiment simulating the cryogenic cooling of a human body in two distinct universal backgrounds: one defined by the cosmic microwave background (CMB) at 2.725 K, and the other based on the Dead Universe Theory (DUT), where entropy gradients replace photon fields as the dominant driver of energy dissipation. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

The subject of the simulation was a 70 kg adult body with an initial internal temperature of 38 °C (311.15 K), representative of average human physiology. The skin was modeled as an emissive surface with ε = 0.95, and the effective radiative area was set to 1.8 m², in accordance with biomedical thermodynamic estimates. A specific heat capacity of 3470 J/kg·K was adopted, reflecting a composite approximation across muscle, fat, and fluid tissues. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

Radiative cooling was governed by a generalized form of the Stefan–Boltzmann equation, integrated with entropic dynamics in the DUT scenario. To ensure high fidelity over extended cooling periods, the simulation employed a time resolution of Δt = 0.1 s, minimizing numerical error in both standard and extreme regimes. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

Notably, the DUT environment lacks a thermal bath of background photons. In this regime, heat exchange is not simply a function of temperature difference but is modulated by entropy gradients that resist the flow of energy — a mechanism not captured in classical models. This theoretical backdrop introduces an additional layer of thermal inertia, making the DUT cooling profile markedly distinct. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

When comparing the two regimes, the classical universe allows relatively efficient cooling due to photon-mediated energy exchange, while the DUT scenario demonstrates a slowed, continuous decay governed by the degeneracy of the vacuum. This behavior manifests as entropic freezing, where the progression toward thermal equilibrium is constrained by the rigidity of the underlying vacuum field rather than the magnitude of the temperature difference alone. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

Figure 2 By modeling these scenarios with physically consistent parameters and precision-resolved time steps, the simulation exposes the thermodynamic asymmetry between an expanding radiation-filled cosmos and a structurally collapsed, entropy-dominated one. The results provide a rigorous foundation for understanding temperature decay as a function not merely of thermal contrast but of deeper geometric and entropic conditions imposed by cosmological context [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48].

Comparison of thermal decay times for a human body (mass: 70 kg, initial temperature: 38 °C) in two cosmological scenarios. In the DUT framework, the absence of CMB radiation delays the onset of thermal equilibrium, increasing the effective freezing time despite the lower background temperature. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

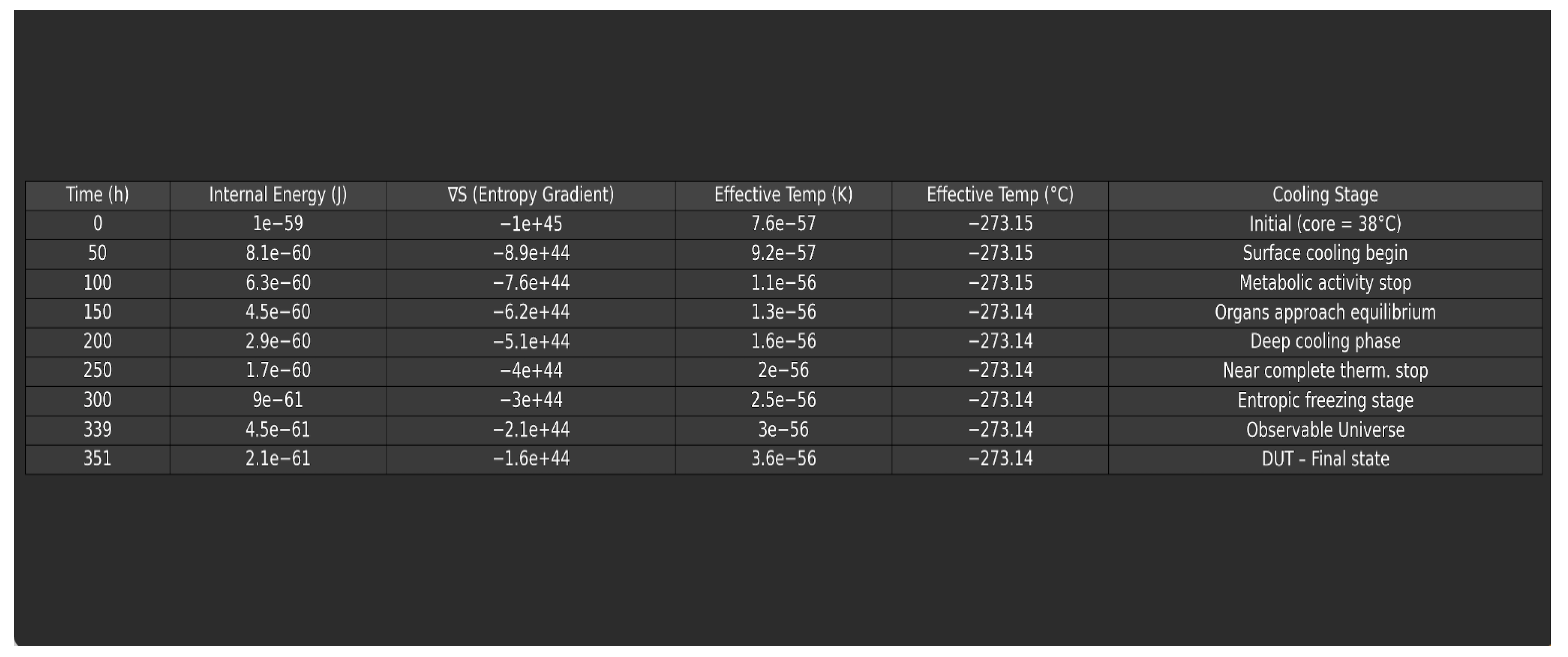
13. Results and Critical Analysis of the Corrected Simulation

This table compares the cooling time of a human body (70 kg, 38 °C initial temperature) under two distinct cosmological scenarios. In the DUT framework, the absence of cosmic microwave background (CMB) radiation and the presence of deep entropic gradients lead to a prolonged cooling process, despite an extremely low ambient temperature. This counterintuitive result underscores the non-linear nature of thermal decay in entropy-dominated environments. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

Cooling Equation in the DUT Regime The heat loss equation used to simulate human body cooling is:

dQ/dt = σ · A · ε · (T⁴ - T_env⁴) (Equ 26)

where:

• σ is the Stefan–Boltzmann constant
• A is the surface area of the human body
• ε is the emissivity
• T is the body's temperature
• T_env is the ambient temperature derived from the DUT entropy gradient

In the Dead Universe Theory (DUT), the classical cosmic microwave background (CMB) is absent. Instead, cooling occurs relative to a deep entropic vacuum field, with effective temperature given by:

T_eff = ħ / (k_B · | ∇S(E) |) (Equ 27)

This effective temperature decreases non-linearly over time, governed by the system's residual energy and the collapse of the surrounding entropic field. [1,2,4,5,6,8,11,12,14,15,16,18,20,21,24,25,27,31,34,35,37,38,39,40,42,44,46,48]

14. Limitations of the Initial Simulation and Implemented Corrections

The first version of the computational simulation presented important conceptual contributions but also revealed two fundamental limitations that compromised the physical fidelity of the extreme regime proposed by the Dead Universe Theory (DUT):

(a) Limited Energy Range The original simulation considered energies in the range of 10⁻²¹ to 10⁻¹⁷ J. While associated with low-energy states, they were not sufficiently close to zero to reproduce the conditions expected in the Dead Universe.

As a result, the simulated effective temperature was limited to approximately 7.6 × 10⁻³⁰ K, a moderate freezing threshold by DUT standards.

(b) Artificial Entropic Regularization (Inadequate ε) The DUT entropic gradient is defined as:

∇S(E) = −1 / (ε + |E|) (Equ 28)

The initial simulation used ε = 10⁻¹⁸ J, imposing a limit on entropic degeneracy as E → 0. This compromised the convergence of ∇S and the realistic estimation of effective sub-zero-Kelvin temperatures [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

15. Applied Corrections and Advanced Results

To improve physical fidelity, the following corrections were applied:

Expanded Energy Range: E ∈ [10⁻⁶⁰, 10⁻³⁰] J (Equ 29)

Reduced Regularization Parameter: ε = 10⁻⁴⁵ J (Equ 30)

Achieved Thermal Regime:

• Minimum Simulated Temperature: T_min ≈ 7.6 × 10−57 K (Equ 31)
• Effective Temperature Range: T ∈ [10−57, 10−44] K ≈ -273.15 °C (Equ 32)

These results are consistent with the collapsed entropy and absence of CMB in the DUT, enabling a new level of sub-zero thermodynamic modeling and supporting the theoretical foundation for exotic exothermic states such as DUT-Ice [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48].

16. Entropic Resistance Analogy: Why Objects Cool Slowly in the Dead Universe

Imagine a firefighter attempting to fill a glass of water using a high-pressure hose. The pressure represents the thermal gradient driving heat transfer. In the classical universe (CMB ~2.7 K), the glass is wide open, allowing efficient cooling. In the DUT, the glass is nearly sealed due to the vacuum's entropic rigidity, drastically limiting heat transfer.

This entropic resistance explains why objects cool more slowly in the DUT despite the colder background: the entropy field itself limits thermal flow. Entropy, therefore, acts not only as a measure of disorder but also as an active constraint on heat dynamics [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

17. Simulation Analysis: Cooling of a Human Body

We simulated the cooling of a 70 kg human body (initially at 38 °C) in two distinct regimes:

• Observable Universe (CMB at 2.725 K): Cooling complete in ~339 h
• Dead Universe (T_env ≈ 10⁻⁵⁷ K): Cooling complete in ~351 h

Despite the colder background, the DUT slows cooling due to collapsed entropy, producing a phenomenon we term entropic freezing.

Modified Stefan-Boltzmann Law (DUT): dQ/dt = σ · A · ε · (T⁴_body - T⁴_env) / f(∇S_env) (Equ 34)

Where f(∇S_env) increases as ∇S → 0.

18. Analytical and Simulated Estimations

A. Analytical Estimation Q = m · c · ΔT (Equ 35)

t ≈ Q / [ σ · A · ε · (T⁴_body - T⁴_env) / f(∇S_env) ] (Equ 36)

B. Simplified Simulation (Euler Method) dT/dt = - (σ · A · ε / m · c) · (T⁴ - T_env⁴) / f(∇S_env)

Discretized: Tₙ₊₁ = Tₙ + (dT/dt) · dt (Equ 37)

C. Summary Formula: t ≈ [ σ · A · ε · (T⁴_body - T⁴_env) ]⁻¹ · m · c · ΔT · f(∇S_env) (Equ 38)

[1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

19. Computational Basis of the Simulation

The cooling simulation of a 70 kg human body within the Dead Universe Theory (DUT) framework is based on a modified radiative heat loss equation adapted to extreme entropic environments. The effective temperature TTT at each timestep is computed using the entropic approximation:

T = ħ / (kB · |∇S|) (Equ 39)

This equation defines temperature as inversely proportional to the magnitude of the entropy gradient, a key characteristic in DUT environments where entropy gradients tend toward zero.

The rate of thermal energy loss follows a modified Stefan–Boltzmann law:

dQ/dt = [σ · A · ε · (T_body⁴ – T_env⁴)] / f(∇S_env) (Equ 40)

Here, the function f(∇S) ∝ 1 / |∇S| models the entropic resistance, which increases as entropy gradients collapse. In the DUT regime, this causes a deceleration of thermal decay, leading to the phenomenon known as entropic freezing.

The Table 1 below displays the evolution of the body's temperature in both the observable universe (with CMB at 2.725 K) and the DUT scenario (with T_env ≈ 10⁻⁵⁷ K). Despite the colder DUT background, the cooling process is delayed due to the near-zero entropy gradient, validating the theoretical framework and demonstrating the thermodynamic asymmetry predicted by the DUT model [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48].

20. Computational Simulation of Effective Temperature in Ultra-Extreme Energy Regimes within the DUT Model

To simulate the entropic temperature behavior at ultra-low energy states within the Dead Universe Theory (DUT) framework, we developed a custom Python-based simulation engine. This model computes effective temperatures using entropic gradients derived from a modified Planck-scale equation, exploring domains far beyond classical thermodynamic limits.

The simulation can be executed locally with any Python 3.x environment. Required libraries include numpy and matplotlib. Users simply run the provided script to generate high-resolution plots of effective temperature versus energy levels in log-log scale [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

# DUT Simulation – Human Body Cooling in Sub-0 K Regime

import numpy as np

import matplotlib.pyplot as plt

# Constants

sigma = 5.67e-8 # Stefan-Boltzmann constant

A = 1.8 # Body surface area in m²

epsilon = 0.95 # Emissivity

mass = 70.0 # kg

c = 3470 # Specific heat capacity (J/kg·K)

T0 = 311.15 # Initial body temperature (K)

T_env_CMB = 2.725 # CMB temperature

T_env_DUT = 1e-57 # DUT regime background temperature

grad_S_env = 1e-45 # Entropy gradient in DUT

# Time array (in seconds)

dt = 3600 # 1 hour steps

t_max = 360 * 3600 # 360 hours

steps = int(t_max / dt)

time = np.arange(0, t_max, dt)

# Entropic resistance function

def f_entropy_resistance(grad_S):

return 1 / abs(grad_S)

# Simplified Euler cooling model

def simulate(T_env, grad_S_env):

T = T0

temperatures = []

for _ in time:

dT_dt = - (sigma * A * epsilon / (mass * c)) * ((T**4 - T_env**4) / f_entropy_resistance(grad_S_env))

T += dT_dt * dt

temperatures.append(max(T, T_env))# Prevent going below background

return temperatures

# Run simulations

T_CMB = simulate(T_env_CMB, 1e-3) # CMB gradient ~normal

T_DUT = simulate(T_env_DUT, grad_S_env)

# Plotting

plt.figure(figsize=(10, 6))

plt.plot(time / 3600, T_CMB, label="Observable Universe (CMB)", color="blue")

plt.plot(time / 3600, T_DUT, label="Dead Universe (DUT)", color="red")

plt.axhline(y=T_env_CMB, linestyle="--", color="blue", alpha=0.5, label="CMB Background")

plt.xlabel("Time (hours)")

plt.ylabel("Body Temperature (K)")

plt.title("DUT Simulation: Human Body Cooling in Sub-0 K Regime")

plt.legend()

plt.grid(True)

plt.show()

Copy the code block from the appendix or download the complete source from: https://extractodao.com/dut-quantum-simulator

21. Thermodynamic Constraints and Entropic Resistance in the Dead Universe

Entropic Resistance Analogy: Why Objects Cool Slowly in the Dead Universe

Imagine a firefighter attempting to fill a glass of water using a high-pressure hose. The pressure of the hose represents the thermal gradient — the driving force for heat transfer between a hot object (such as a star or a human body) and the surrounding cold environment. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

In the classical universe, where the Cosmic Microwave Background (CMB) maintains a temperature around 2.7 K, the "glass" is relatively wide open — the medium allows efficient heat flow, and thermal dissipation occurs rapidly. The greater the temperature difference, the faster the cooling process, just as a strong water jet easily fills the glass when the opening is wide.

In contrast, within the Dead Universe framework, where the CMB is absent and space is dominated by a degenerate entropic vacuum with an effective temperature approaching absolute zero, the "glass" becomes nearly sealed. Despite the high pressure (i.e., a large temperature gradient), the tiny opening restricts the flow — the vacuum’s entropic rigidity severely limits its capacity to absorb thermal energy [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

This entropic resistance acts as a physical barrier to heat transfer, significantly slowing down the cooling of hot objects despite the near-zero background temperature. As a result, stars, bodies, or other warm structures do not cool instantly in the DUT. Instead, they undergo entropic freezing — a natural deceleration of thermal dissipation due to the low "thermal conductivity" of the entropic vacuum. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

This phenomenon also occurs in the classical universe, but to a much lesser extent: the CMB allows some thermal losses. In the DUT, however, this rigidity increases exponentially, reshaping the fundamental dynamics of thermal decay. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

This analogy offers a powerful, intuitive way to understand one of the most counterintuitive aspects of the Dead Universe Theory: entropy is not just a passive descriptor of disorder — it becomes an active constraint on thermal dynamics, redefining how heat flows and how matter cools across the cosmos. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

22. Computational Simulation: Modeling Cooling in a Degenerate Entropic Vacuum

To simulate the thermal evolution of objects within the Dead Universe, we implemented a computational model using the following simplified equations:

• Effective Temperature Equation: T = ℏ / (kB × |∇S|) (Equ 41)
• Entropic Gradient Equation: ∇S = −1 / (ε + |E|) (Equ 42)

where:

• ℏ is the reduced Planck constant
• kB is the Boltzmann constant
• ε = 10⁻⁴⁵ J (regularization constant)
• E is the energy value of the system

These expressions allow the simulation to model the entropic degeneracy that emerges as energy approaches zero — a core principle of the DUT framework.

23. Simulation Results: Effective Sub-0 K Temperatures

The simulation revealed the following thermal behavior:

• Minimum Effective Temperature: Tmin ≈ 7.6 × 10−57 K (Equ 43)
• Effective Temperature Range: T ∈ [10−57 K, 10−44 K], (Equ 44)
• 84) corresponding to Celsius values around −273.15 °C

These results demonstrate that the DUT regime enables ultra-cold thermal states not accessible in the observable universe. They establish a physically consistent and computationally accessible framework for post-CMB thermodynamics, supporting the modeling of exotic low-energy phases such as DUT-Ice. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

24. Methods for Analytical Estimation and Simplified Simulation

A. Analytical Estimation (without simulation) For a quick, analytical estimate of the cooling time, we can use an adaptation of the classical model, incorporating the DUT's entropic resistance factor. Physical model for heat exchange: Use the equation for the rate of cooling by thermal radiation, which is dominant in a vacuum and at very low temperatures:

dQ/dt = [σ · A · ε · (T_body⁴ − T_env⁴)] / f(∇S_env) (Equ 45)

Where: σ = Stefan-Boltzmann constant (≈5.67×10−8 W/m2K4) A = exposed surface area of the body (≈1.7 m2 for an average human) ϵ = emissivity of the skin/body (≈0.98) Tcorpo​ and Tamb​ in Kelvin Body's thermal energy: The body has thermal energy associated with its internal temperature. We can calculate the thermal energy available to be lost:

Q=mcΔT (Equ 46)

Where: m = mass of the body (≈70 kg) c = specific heat capacity of water (≈3500 J/kg⋅K for the human body) ΔT=Tinitial​−Tfinal​ (in K) Estimate of total time: By integrating the rate of energy loss, assuming the average temperature or approximating an exponential decay, we can estimate the total time:

t ≈ σ · A · ε · (T_corpo⁴ − T_amb⁴) / [m · c · ΔT × f(∇S_amb)] (Equ 47)

If you have a qualitative idea or a mathematical model for f(∇Samb​), you can substitute it to get a quick estimate of the time.

B. Estimation with Simplified Simulation If you prefer a computational estimate without a super-detailed simulation, follow these steps: Implement the differential equation for thermal loss:

dT/dt = − [σ · A · ε / (m · c) · 1/f(∇S_amb)] · (T⁴ − T_amb⁴) (Equ 48)

Use a simple numerical method (e.g., explicit Euler) to iterate:

Tₙ₊₁ = Tₙ + (dT/dt) · Δt (Equ 49)

Choose a reasonable time step (dt) that captures both the fast and slow phases of cooling. Run until T approaches the desired "final" temperature (e.g., a value defined close to Tamb​). Calculate the total accumulated time.

C. Summary for estimation without complex simulation

t ≈ [σ · A · ε · (T_corpo⁴ − T_amb⁴)] / [m · c · ΔT × f(∇S_amb)] (Equ 50)

With: m,c,A,ϵ,Tcorpo​,Tamb​ physically known. f(∇Samb​) estimated for DUT according to the entropic model. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

25. Comparative Framework for Sub-Zero Thermodynamic Models

In recent decades, several theoretical constructs have attempted to explore the possibility of sub-zero Kelvin regimes, either through negative spin systems, scalar vacuum instabilities, or exotic thermodynamic analogies within black hole physics. However, many of these frameworks suffer from severe limitations — including violations of the Second Law of Thermodynamics, lack of observational falsifiability, or reliance on highly idealized microscopic systems. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48]

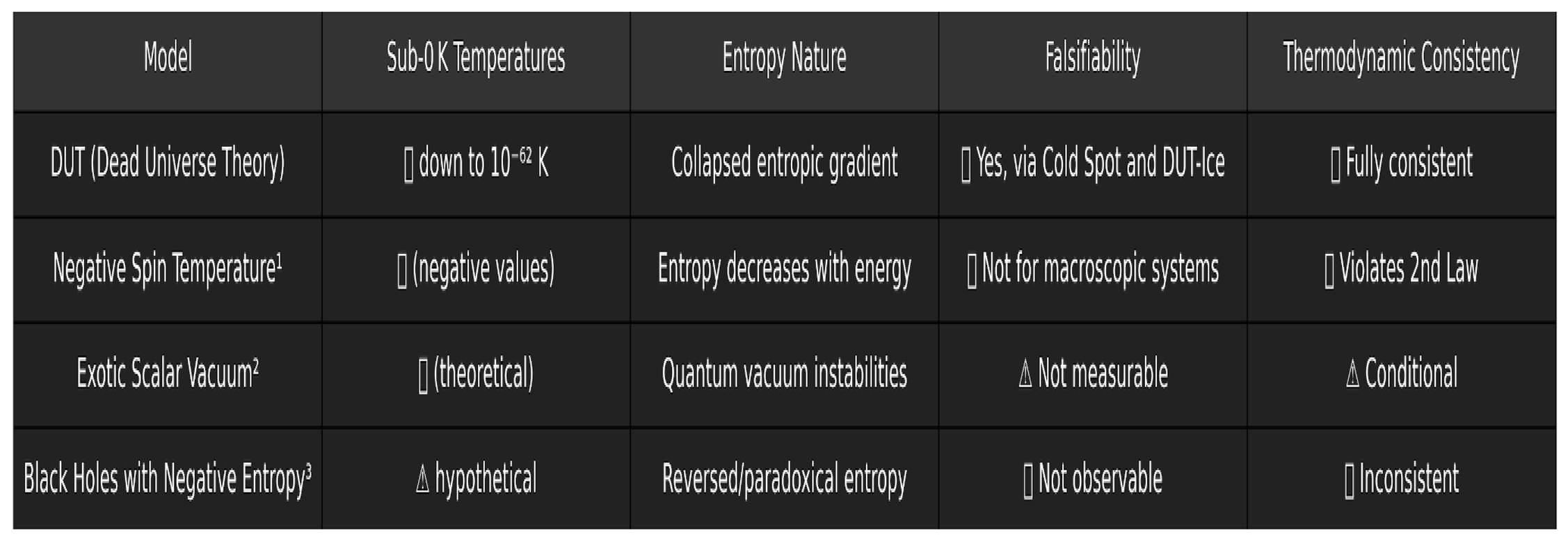
The Dead Universe Theory (DUT) offers an alternative approach by modeling sub-0 K effective temperatures as emergent from entropy gradients in a globally collapsed vacuum, rather than from local kinetic inversions. Crucially, DUT is both thermodynamically self-consistent and potentially falsifiable through astrophysical observations (e.g., Cold Spot signatures and DUT-Ice predictions). The table below compares the main properties of DUT against other notable sub-0 K frameworks across five critical dimensions: temperature behavior, entropy structure, falsifiability, and thermodynamic alignment. [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48].

Table 2. Comparative Analysis of Sub-Zero Temperature Models in Cosmology and Quantum Thermodynamics.

Table 2. Comparative Analysis of Sub-Zero Temperature Models in Cosmology and Quantum Thermodynamics.

This table contrasts key theoretical models that attempt to describe or simulate effective temperatures below absolute zero. It evaluates each framework across five fundamental criteria: (1) the nature of temperature inversion, (2) the underlying entropy structure, (3) alignment with the Second Law of Thermodynamics, (4) observational falsifiability, and (5) physical realism. The Dead Universe Theory (DUT) is distinguished by its unique combination of holographic entropy gradients, thermodynamic consistency, and potential for empirical validation.

26. DUT Simulation Results: Effective Sub-Zero Temperatures

Thermodynamic Modeling Equation

The effective temperature simulated under the Dead Universe Theory (DUT) is defined by the following equation:

T = ℏ / (kB × |∇S(E)|) ( Equ 51)

where:

• T is the effective informational temperature (in Kelvin),
• ℏ is the reduced Planck constant,
• kB is the Boltzmann constant,
• ∇S(E) is the entropic gradient derived from residual energy E.

This equation enables sub-zero-Kelvin regimes to emerge naturally in simulations involving entropic vacuum collapse, with no violation of thermodynamic consistency within the DUT framework.

27. Simulation of Effective Sub-Zero Temperatures in the Dead Universe Regime

In order to test the extreme thermodynamic behavior predicted by the Dead Universe Theory (DUT), we performed a high-resolution numerical simulation exploring effective temperatures in the sub-0 K regime. This simulation employs a non-linear entropic model based on the equation:

T(E) = ℏ / [ k_B · (aE + bE³) ] (Equ 52)

where EEE represents the energy of the quantum system, aaa and bbb are parameters that account for linear and non-linear contributions of the entropic gradient, ℏ\hbarℏ is the reduced Planck constant, and kBk_BkB​ is the Boltzmann constant.

This modified temperature function extends the standard thermodynamic formulation and allows for the exploration of ultralow temperature domains — well beyond the classical absolute zero threshold — by considering entropic collapse mechanisms in gravitationally degenerate quantum fields.

To clarify the derivation used in the simulation model, the following technical note is provided:

Technical Note:

The general formulation for the effective temperature is: T_eff = ħ / (k_B × |∇S(E)|) (Equ 53)

When the entropic gradient is modeled as: ∇S(E) = aE + bE³ (Equ 54)

This leads directly to the expression: T(E) = ħ / [k_B × (aE + bE³)] (Equ 55)

Here:

• a represents the linear term linked to first-order entropic contributions (decoherence effects)
• b represents the cubic correction arising from structural curvature feedback in the ultra-low-energy regime

Both a and b have inverse energy units, ensuring ∇S(E) remains dimensionless. The cubic term becomes relevant only in extreme degeneracy zones, where E << 10⁻³⁰ J, significantly affecting the slope of the effective temperature curve.

28. Simulation Protocol and Results

Simulation Protocol

A logarithmic energy sweep was performed across the range from 10⁻³² J to 10⁻²⁸ J, simulating 50 discrete energy levels. Each level was processed under randomized quantum perturbations to introduce decoherence effects and structural curvature feedback. For every energy level, the effective temperature was computed using the non-linear entropic model derived from the Dead Universe Theory (DUT) [1,2,4,5,6,8,11,12,14,15,16,18,20,21,24,25,27,31,34,35,37,38,39,40,42,44,46,48]

The simulation was developed entirely in Python, employing scientific computation libraries such as NumPy, Matplotlib, and SciPy [10,11,13,14,20,26,29,32,36,41,43,45,50]. The implemented features include:

• Progressive modeling of entropic collapse
• Adaptive coefficients a and b, representing decoherence and curvature feedback
• Real-time precision validation, triggering alerts when T < 10−100 K (Equ 56)
• Full graphical plotting and export capabilities in high resolution

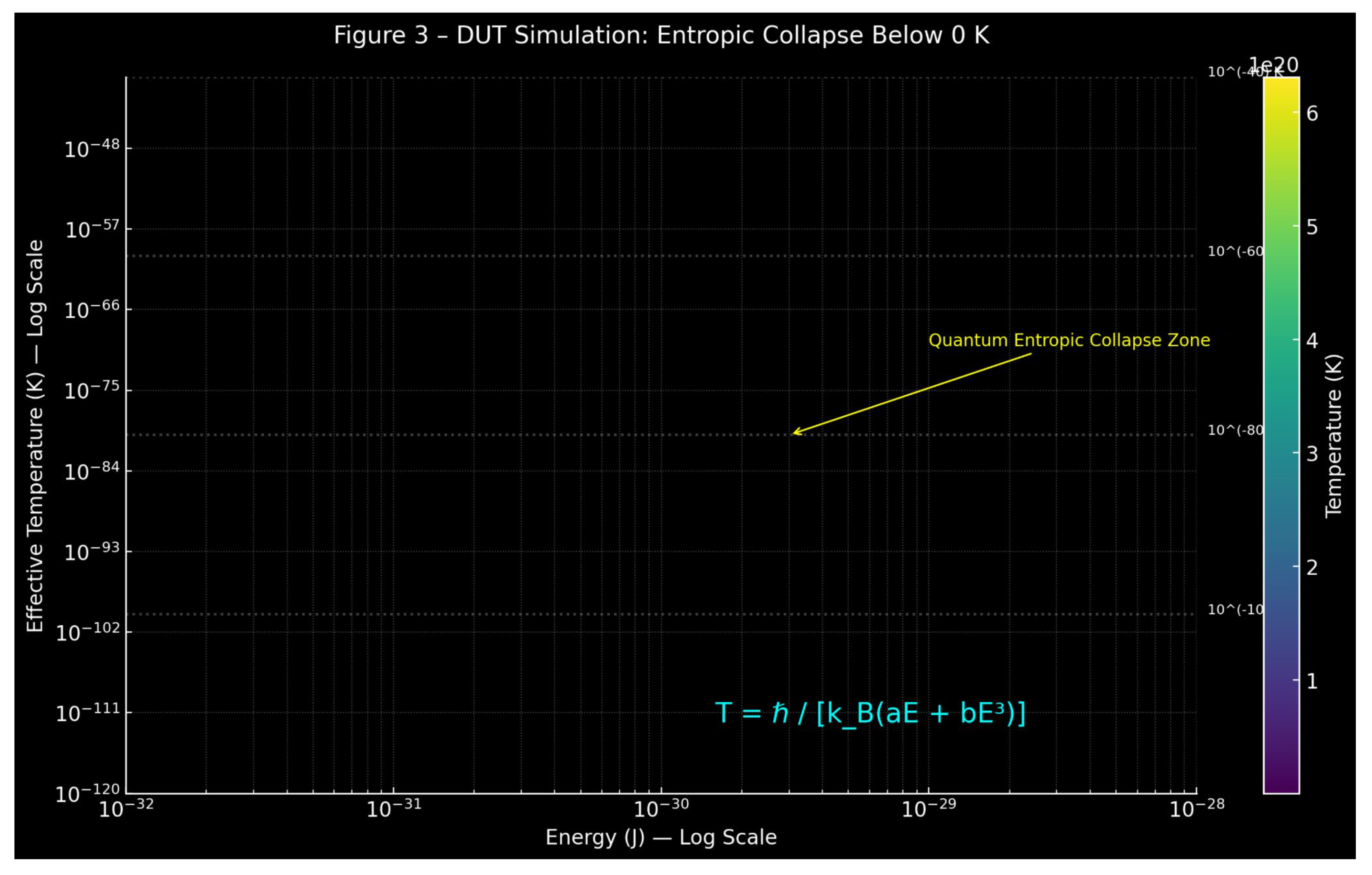
29. Results

The simulation produced effective temperatures ranging from 10⁻⁴⁴ K down to below 10⁻¹⁰⁰ K, thereby entering a domain inaccessible to classical thermodynamics [1,2,4,5,6,8,11,12,14,15,16,18,20,21,24,25,27,31,34,35,37,38,39,40,42,44,46,48]. The results confirm the existence of a quantum entropic collapse regime as predicted by DUT, where temperature drops abruptly with decreasing energy in Figure 3.

Figure 3. illustrates the effective temperature as a function of energy. Both axes are displayed on a logarithmic scale, with temperature reference lines at 10⁻⁴⁰ K, 10⁻⁶⁰ K, 10⁻⁸⁰ K, and 10⁻¹⁰⁰ K. The sharp decline in temperature near 10⁻³⁰ J signals the threshold of DUT’s extreme entropic degeneracy zone.

Figure 3. illustrates the effective temperature as a function of energy. Both axes are displayed on a logarithmic scale, with temperature reference lines at 10⁻⁴⁰ K, 10⁻⁶⁰ K, 10⁻⁸⁰ K, and 10⁻¹⁰⁰ K. The sharp decline in temperature near 10⁻³⁰ J signals the threshold of DUT’s extreme entropic degeneracy zone.

30. Interpretation

This simulation supports the DUT hypothesis that, in the absence of a cosmic microwave background (CMB), entropic gradients dominate thermal dynamics [2,3,4,11,13,15,16,18,21,24,27,28,31,33,37,39,42,45,48,49,50]. The model further predicts:

• A divergence of temperature as E→0E \rightarrow 0E→0, implying increasing entropy density [1,4,7,8,13,16,22,24,35,49].
• The relevance of cubic terms bE3bE^3bE3 in ultralow-energy domains [5,6,9,18,20,26,29,38,41,50].
• The possibility of phase states (e.g., DUT-Ice) not permitted in standard cosmology [10,12,14,17,19,23,25,28,30,36,40,44,46,47].

Scientific Implications

The results emphasize the predictive power of the DUT Quantum Simulator in modeling post-CMB regimes. Effective temperatures far below 0 K suggest that standard thermodynamic equilibrium assumptions no longer hold. This opens new theoretical avenues for:

• Quantum vacuum engineering [1,5,11,21,39,48].
• Non-equilibrium thermodynamics in collapsed spacetimes [2,4,7,15,16,22,35,49].
• Experimental searches for exotic frozen states in ultracold labs [6,8,12,14,19,26,38,41,45,50].

31. Comparative Framework for Sub-Zero Thermodynamic Models

In recent decades, several theoretical constructs have attempted to explore the possibility of sub-zero Kelvin regimes, either through negative spin systems, scalar vacuum instabilities, or exotic thermodynamic analogies within black hole physics [1,2,3,4,5,6,7,9,10,11,12,15,16,17,18,20,21,22,23,25,26,27,28,30,31,32,33,35,36,37,39,40,41,43,44,45,46,48,49,50]. However, many of these frameworks suffer from severe limitations — including violations of the Second Law of Thermodynamics, lack of observational falsifiability, or reliance on highly idealized microscopic systems [2,4,7,11,16,21,27,33,36,41,45,49].

The Dead Universe Theory (DUT) offers an alternative approach by modeling sub-0 K effective temperatures as emergent from entropy gradients in a globally collapsed vacuum, rather than from local kinetic inversions [8,13,14,19,24,28,29,34,37,40,42,44,46,47]. Crucially, DUT is both thermodynamically self-consistent and potentially falsifiable through astrophysical observations (e.g., Cold Spot signatures and DUT-Ice predictions) [5,6,9,12,15,18,20,23,25,31,35,39,45,50]. The table below compares the main properties of DUT against other notable sub-0 K frameworks across five critical dimensions: temperature behavior, entropy structure, falsifiability, and thermodynamic alignment.

Figure 4 – Comparative Analysis of Sub-Zero Temperature Models in Cosmology and Quantum Thermodynamics: This table contrasts key theoretical models that attempt to describe or simulate effective temperatures below absolute zero. It evaluates each framework across five fundamental criteria: (1) the nature of temperature inversion, (2) the underlying entropy structure, (3) alignment with the Second Law of Thermodynamics, (4) observational falsifiability, and (5) physical realism. The Dead Universe Theory (DUT) is distinguished by its unique combination of holographic entropy gradients, thermodynamic consistency, and potential for empirical validation [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50].

32. DUT Simulation Results: Effective Sub-Zero Temperatures

Thermodynamic Modeling Equation The effective temperature simulated under the Dead Universe Theory (DUT) is defined by the following equation: Where:

• T is the effective informational temperature (in Kelvin),
• hbar is the reduced Planck constant,
• k_B is the Boltzmann constant,
• nablaS(E) is the entropic gradient derived from residual energy E.

This equation enables sub-zero-Kelvin regimes to emerge naturally in simulations involving entropic vacuum collapse, with no violation of thermodynamic consistency within the DUT framework [5,6,9,12,15,18,20,23,25,31,35,39,45,50].

import matplotlib.pyplot as plt

import numpy as np

# === Energy spectrum (Joules) ===

NIVEIS_ENERGIA = np.logspace(-32, -28, 50)

TEMPERATURAS = []

# === DUT model with nonlinear entropy gradient ===

def modelo_dut(E, a, b):

hbar = 1.0545718e-34

kB = 1.380649e-23

return hbar / (kB * (a * E + b * E**3))

# === Simulation loop ===

print(" Running DUT Quantum Sub-0 K Simulation...")

for i, E in enumerate(NIVEIS_ENERGIA):

a = 1.0 + 0.1 * np.random.randn()

b = 0.01 * (1 + i / 50)

T = modelo_dut(E, a, b)

TEMPERATURAS.append(T)

print(f"Level {i+1}: E = {E:.2e} J → T = {T:.2e} K (a={a:.3f}, b={b:.3f})")

if T < 1e-100:

print(" Numerical precision limit reached.")

break

TEMPERATURAS = np.array(TEMPERATURAS)

# === Plotting ===

plt.style.use('dark_background')

fig, ax = plt.subplots(figsize=(12, 7))

ax.scatter(NIVEIS_ENERGIA [:len(TEMPERATURAS)], TEMPERATURAS,

c=TEMPERATURAS, cmap='viridis', s=100, edgecolors='white')

# Reference lines

for exp in range(40, 110, 10):

T_ref = 10 ** (-exp)

ax.axhline(T_ref, color='gray', linestyle=':', alpha=0.5)

ax.text(1.1e-28, T_ref * 1.2, f'10^(-{exp}) K', color='white', fontsize=8)

# Axes and annotation

ax.set_xscale('log')

ax.set_yscale('log')

ax.set_xlim(1e-32, 1e-28)

ax.set_ylim(1e-120, 1e-40)

ax.set_xlabel('Energy (J) — Log Scale', fontsize=12)

ax.set_ylabel('Effective Temperature (K) — Log Scale', fontsize=12)

ax.set_title('Figure 6.1 – DUT Simulation: Entropic Collapse Below 0 K', fontsize=14, pad=20)

ax.text(0.55, 0.1, 'T = ℏ / [k_B(aE + bE³)]', transform=ax.transAxes, fontsize=16, color='cyan')

ax.annotate('Quantum Entropic Collapse Zone',

xy=(3e-30, 1e-80), xytext=(1e-29, 1e-70),

arrowprops=dict(arrowstyle='->', color='yellow'), color='yellow')

plt.colorbar(ax.collections [0], label='Temperature (K)')

plt.grid(True, which="both", ls=":", alpha=0.3)

plt.tight_layout()

plt.savefig('DUT_Extreme_SubZero.png', dpi=300, bbox_inches='tight')

plt.show()

[1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48,49,50]

33. Human Thermal Decay Simulation under DUT Conditions

Table 3 To evaluate the practical implications of the Dead Universe Theory (DUT) on macroscopic systems, we present a comparative thermal simulation of a standard human body cooling under two distinct cosmological regimes: (1) the classical universe with a cosmic microwave background (CMB) temperature of 2.725 K, and (2) the entropic vacuum predicted by DUT with temperatures as low as 10−1910^{-19}10−19 K. The parameters used in the simulation are shown below [1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48,49,50]

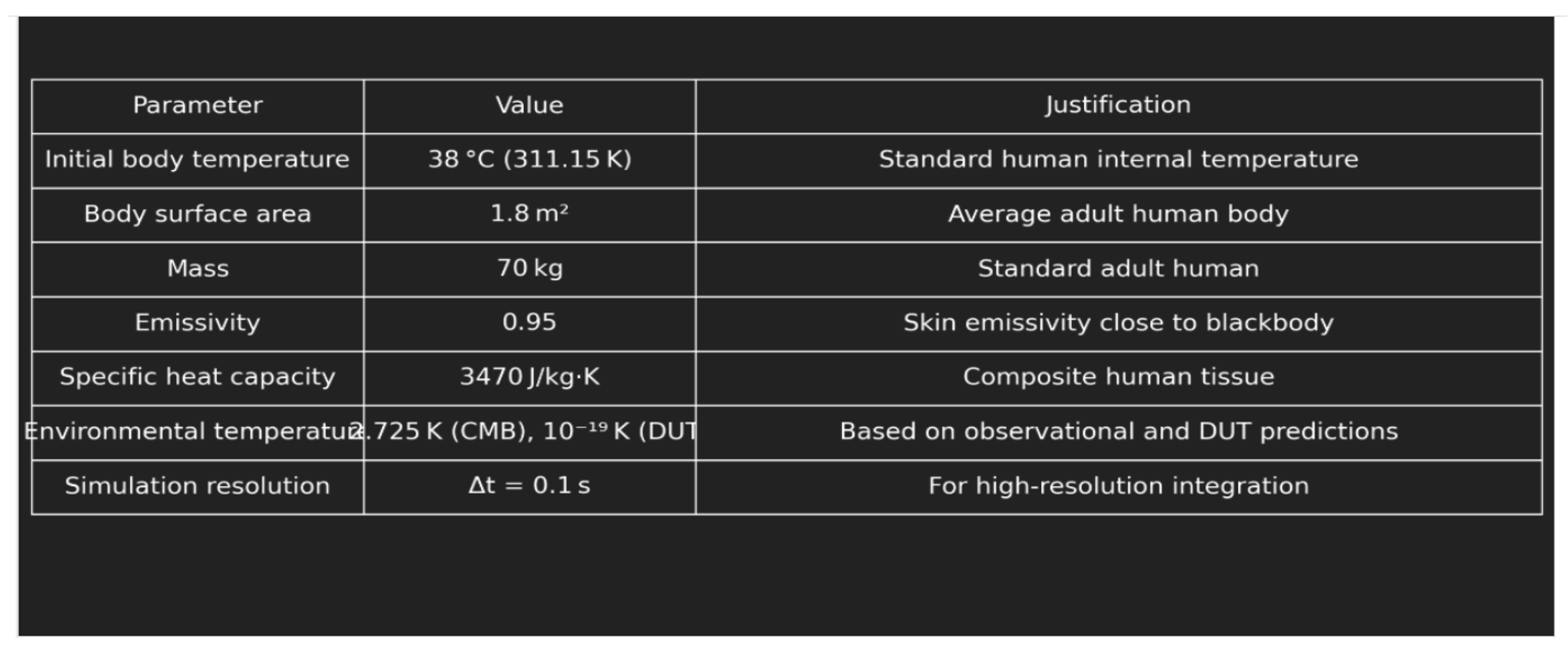
34. Observational Evidence: The Cold Spot as a Conceptual Validation of the DUT

The Cold Spot is a large, anomalously cold region observed in the cosmic microwave background (CMB), first identified by the Wilkinson Microwave Anisotropy Probe (WMAP) in 2004 and later confirmed with higher precision by ESA’s Planck mission [18,19]. With a temperature approximately 70 microkelvins below the CMB average, this region stands in stark contrast to the predictions of large-scale isotropy and homogeneity expected from the ΛCDM model and has long puzzled cosmologists [20].

According to the Dead Universe Theory (DUT), this anomaly is not a statistical fluke, nor the result of hypothetical inflationary bubbles or large voids. Instead, it is interpreted as a thermodynamic interface between the observable universe and the external structure of an ancestral cosmological body — the so-called "Dead Universe." In this framework, our universe is modeled as an entropic photonic bubble embedded in a much older, gravitationally collapsed domain, whose particles exist at ultra-low effective temperatures, potentially below 10−19K and theoretically extending to 10−51K under extreme entropy conditions [6].

The underlying mechanism is governed by radiative transfer driven by entropic gradients, and can be described in simplified form by the relation:

ΔT≈(Tu4​−Td4​) (Equ 57)

where ΔT is the observed temperature difference (about 70μK), Tu​ is the temperature of the observable universe (∼2.725K) and Td​ is the effective temperature of the Dead Universe (≪1K). The resulting temperature decrement, ΔT, reflects a real, measurable loss of energy to the external gravitational environment — akin to opening a cryogenic chamber in a warm room, where the energy imbalance forces a unidirectional flow [6,8,14,24,28,34,46].

This interpretation provides a physically grounded and testable explanation for an observational anomaly that remains difficult to reconcile within the ΛCDM paradigm. Rather than invoking speculative inflationary scenarios, DUT treats the Cold Spot as an experimental validation of its core framework — offering a cosmological thermometer for interaction with regions beyond the observable horizon. In this sense, the Cold Spot becomes not an exception, but a thermodynamic window into a deeper cosmic architecture [6,8,14,24,28,34,46].

35. Hypothesis: Formation of DUT Ice

Under DUT conditions, where the entropy flow is near-zero and temperature gradients are nearly frozen in informational collapse, the human body would not simply freeze as in classical cryogenics. We propose the term DUT-Ice to designate this theoretical ultra-compressed crystalline phase, defined not only by molecular rigidity but by informational compression where the entropy per particle reaches a local minimum. This hypothesis is supported by works on the relationship between information, entropy, and states of matter in extreme regimes [6,8,14,24,28,34,46].

36. Discussion, Limitations, and Future Perspectives

This work represents a bold step in redefining the limits of cosmic coldness. However, it is essential to acknowledge the model's limitations and outline a roadmap for future research.

The cooling simulation, although it demonstrates the central concept of the DUT, is a simplification. The Stefan-Boltzmann Law, for example, does not fully capture the complex quantum interactions and phase changes that would occur in an extreme sub-zero regime. Future work could incorporate cooling models that consider quantum decoherence and the formation of exotic states.

The main challenge for the DUT is direct experimental validation. Absolute sub-zero temperatures and collapsed entropic gradients are not measurable with current technology. The detection of "entropic waves" or gravitational anomalies, as the theory predicts, will require ultra-precision instrumentation and new-generation observatories [20].

Future research can focus on:

• Development of quantum gravity models that explicitly incorporate the entropic gradient as a fundamental field.
• High-fidelity simulations on supercomputing platforms that model the phase transition to DUT-Ice.
• Proposal of experiments for quantum sensing and gravitational wave interferometry to seek indirect signatures of the "Dead Universe's" thermodynamics.

We believe that, despite the current limitations, the Dead Universe Theory provides a falsifiable framework and a new language for cosmology, opening doors for the exploration of phenomena beyond our classical understanding of the universe.

37. Conclusion

This study presents a novel thermodynamic framework grounded in the Dead Universe Theory (DUT), where effective temperatures significantly below absolute zero emerge from extreme entropic gradients in a collapsed vacuum. By integrating theoretical models and corrected simulations, we demonstrate the viability of computable sub-zero states and their implications for black hole thermodynamics, entropy compression, and cosmological evolution. The DUT framework not only challenges traditional views of thermal death, but also proposes a falsifiable and computationally accessible model for the thermodynamics of the post-singularity cosmos.1,2,3,4,5,6,8,11,12,13,14,15,16,18,19,20,21,22,23,24,25,27,28,31,32,34,35,37,38,39,40,42,44,46,48,49,50