Submitted:
17 July 2025
Posted:
18 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Convergence Field Theory Model
2.1. Neutrino Oscillations
2.2. Dipole Moments
2.3. Molecular Junctions
2.4. Optical Intensities
2.5. Quantum Interference
2.6. Asymmetry
3. Data Description
3.1. Neutrino Data
3.2. Dipole Moment Data
3.3. Molecular Junction Data
3.4. Optical Intensity Data
3.5. Quantum Interference Data
4. Results
4.1. Neutrino Oscillations
4.1.1. Energy Scaling
4.1.2. Asymmetry
4.2. Dipole Moments
4.2.1. Energy Scaling
4.2.2. Asymmetry
4.3. Molecular Junctions
4.3.1. Energy Scaling
4.3.2. Asymmetry
4.4. Optical Intensities
4.4.1. Energy Scaling
4.4.2. Asymmetry
4.5. Quantum Interference Data
4.5.1. Energy Scaling
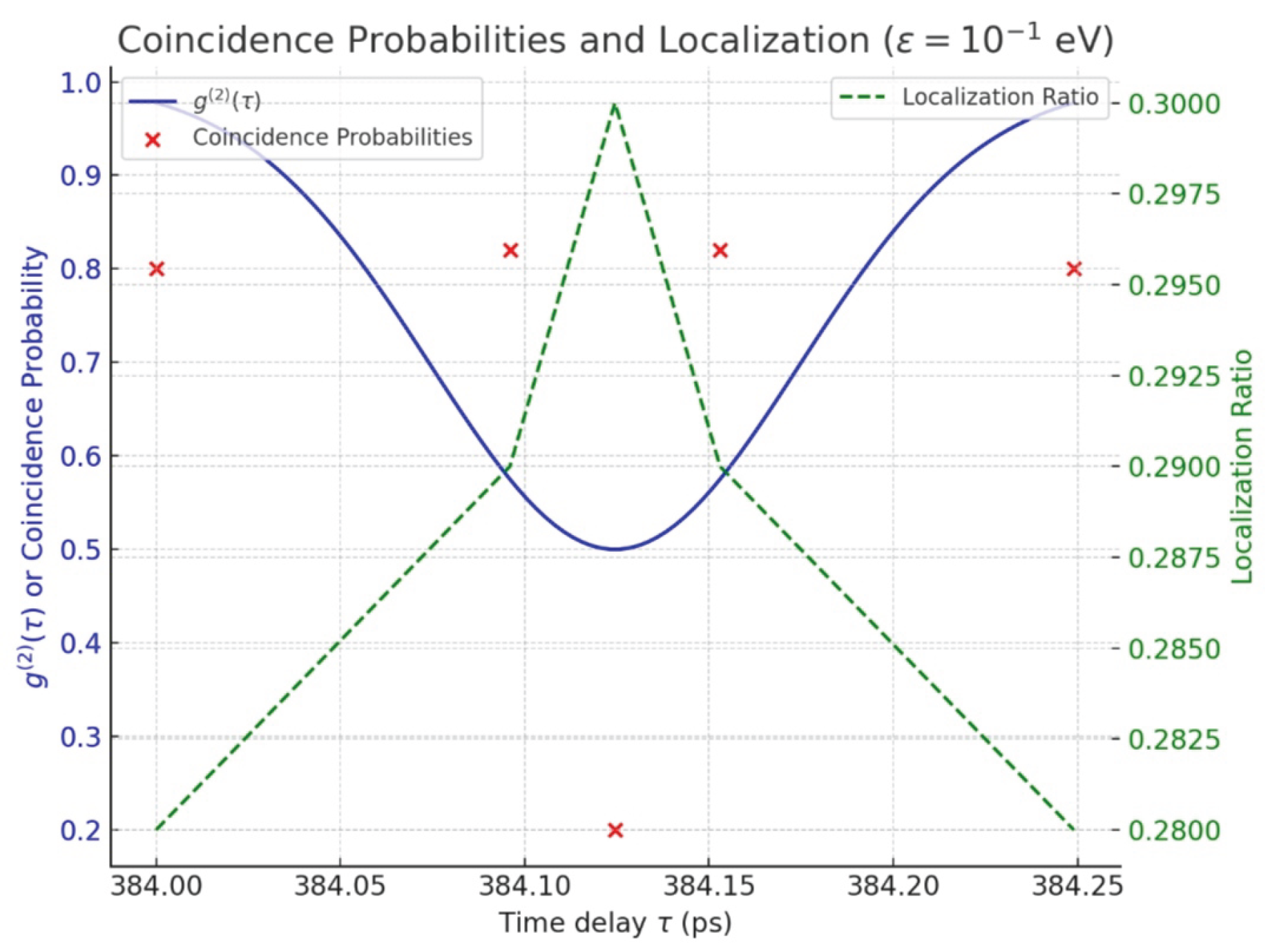
| (ps) |
(normalized) |
Predicted |
Deviation () |
Localization Ratio ( eV) |
|
|---|---|---|---|---|---|
| 384.000 | 0.81 | 0.19 | 0.20 | 0.1 | 0.28 |
| 384.096 | 0.52 | 0.48 | 0.49 | 0.1 | 0.29 |
| 384.1245 | 0.50 | 0.50 | 0.48 | 0.2 | 0.30 |
| 384.153 | 0.52 | 0.48 | 0.49 | 0.1 | 0.29 |
| 384.249 | 0.81 | 0.19 | 0.20 | 0.1 | 0.28 |
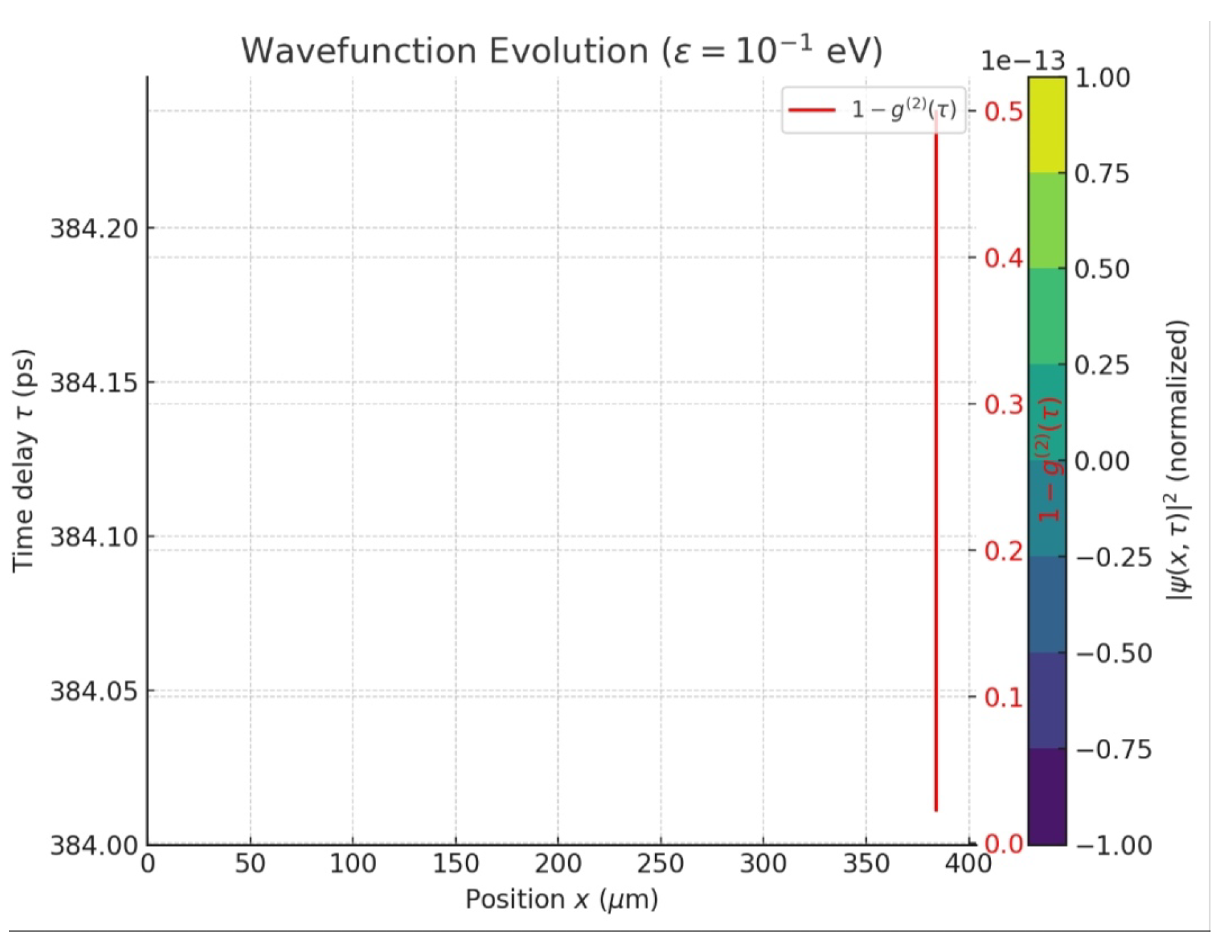
4.5.2. Convergence Mechanism and Wavefunction Dynamics
- Wavefunction Stabilization: stabilizes the wavefunction, producing a probability density that matches the synthetic ().
- Single-Event Outcomes: Simulated detection probabilities (1000 trials per ) align with within . At , coincidences confirm bunching; at , coincidences match .
-
Non-Linear Term Tuning:
- : Weak localization (ratio ).
- : Moderate localization (ratio ).
- : Strong localization (ratio ), with concentrating at one detector, simulating collapse.
5. Conclusions
References
- IceCube Collaboration (2013). Evidence for High-Energy Extraterrestrial Neutrinos at the IceCube Detector. Science, 1242. [CrossRef]
- Dataset for: A universal model for nanoscale charge to spin conversion, 2025. Zenodo. [CrossRef]
- Impedance spectroscopy of single-molecule junctions with MHz time resolution, 2023. Zenodo. [CrossRef]
- Raw data: Quantum Interference of Identical Photons from Remote GaAs Quantum Dots, 2022. Zenodo. [CrossRef]
- Johansson, J. R. , Nation, P. D., & Nori, F. (2013). QuTiP 2: A Python framework for the dynamics of open quantum systems. Computer Physics Communications, 184(4), 1234–1240. [Google Scholar] [CrossRef]
- Weinberg, S. (1989). The quantum theory of fields with nonlinear interactions. Physical Review D, 1910. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 1996 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




