Entropic Curvature in Discrete Quantum Spacetime: A Framework for Irreversible Field Dynamics

1. Introduction

Understanding the deep connection between quantum field theory, gravity, and the information-theoretic structure of spacetime remains one of the most important unsolved problems in modern physics. Traditional approaches to quantum gravity often assume a pre-existing smooth manifold and attempt to quantize geometry. However, recent theoretical developments suggest that spacetime geometry itself may be emergent—arising from more fundamental quantum or information-theoretic building blocks. This paper contributes to this emerging viewpoint by proposing a novel framework in which entropic curvature, defined over discrete quantum geometries, governs irreversible field dynamics at the microscopic level.

Unlike conventional field theories that assume time-reversibility and unitary evolution, our approach introduces a directional flow of information—driven by entropy—as a mechanism for generating curvature and field interaction structure. The fundamental idea is to reinterpret the evolution of a quantum field not purely as a function of energy and spacetime coordinates, but as a thermodynamically consistent flow along an entropic gradient defined on a discrete, graph-based quantum geometry. This work aims to formalize this concept rigorously and derive the consequences for field dynamics, information propagation, and emergent spacetime.

1.1. Motivation and Background

Over the last two decades, significant progress has been made in identifying connections between information theory and gravitational physics. From the Bekenstein-Hawking entropy of black holes to the AdS/CFT correspondence and tensor network constructions of holographic spacetimes, information appears to play a key role in defining geometry. Entropic considerations also appear in the thermodynamic description of spacetime horizons and in Jacobson’s derivation of Einstein’s equations from entropy flow. However, most existing models still assume reversible dynamics and background spacetime structure.

Our work is motivated by a desire to go deeper: to build a model in which entropy is the driving force of curvature itself, and in which time-asymmetry and non-unitary behavior emerge naturally from fundamental principles. By discretizing spacetime into a network of quantum nodes and links, and assigning entropic fluxes to those links, we allow curvature and field behavior to be shaped dynamically by informational imbalance. This new formulation allows us to analyze not only what quantum fields do in a fixed geometry, but how the geometry itself might respond to and evolve with quantum informational processes.

1.2. Problem Statement and Research Gap

While several discrete approaches to quantum gravity exist—including causal set theory, loop quantum gravity, and spin foam models—they often lack a well-defined notion of entropy-driven curvature. Similarly, quantum field theory on curved backgrounds does not explain how geometry is generated or modified by quantum informational flow. Existing tensor network and holographic codes capture some aspects of entanglement-based geometry, but they do not provide a concrete mechanism for irreversible field dynamics or the generation of time asymmetry at the microscopic level.

There is thus a gap in the literature for a model that:

• Treats entropy not as a derived quantity but as a fundamental geometric agent.
• Connects quantum information flow to spacetime curvature on a discrete level.
• Derives irreversible field evolution laws based on entropic gradients.

This paper seeks to fill that gap with a new algebraic and geometric structure: entropic curvature flow over quantum spacetime graphs.

1.3. Objectives and Contributions

This work proposes a new formalism for understanding field theory in the context of emergent spacetime, using entropy as the central mechanism. The specific objectives are:

(1)

To define a discrete geometry framework in which entropic flow determines curvature locally and globally.

(2)

To construct a set of algebraic and differential rules for irreversible field evolution driven by entropic gradients.

(3)

To simulate and visualize these dynamics using graph-based models and generate interpretable, theory-grounded results from original plots.

(4)

To analyze how this entropic curvature formulation might unify or extend existing approaches to quantum gravity and information-based field theory.

In doing so, we aim to establish a rigorous, purely theoretical foundation for irreversible quantum field dynamics on discrete geometries—moving one step closer to a unified framework for quantum gravity based on informational principles.

2. Aim and Objectives

The core aim of this research is to develop a mathematically rigorous and conceptually novel framework where entropy acts as a geometric driver of field dynamics in discrete quantum spacetime. Instead of treating entropy as an emergent or auxiliary quantity, this work positions it as a fundamental generator of curvature and dynamical asymmetry. Through this lens, we seek to describe irreversible quantum field evolution and emergent spacetime structure as consequences of localized informational flow.

To realize this vision, the research is guided by three primary objectives, detailed below.

2.1. Objective 1: Formulation of Entropic Curvature on Discrete Structures

The first objective is to define a discrete geometric structure where curvature is not based on traditional metric tensors but instead arises from local entropic imbalances. This includes:

• Developing a formalism for assigning entropy values to nodes and edges of a causal graph or spacetime lattice.
• Constructing a consistent curvature operator that reflects informational divergence or flow.
• Ensuring the framework respects causal consistency and local information conservation (or its violation in a controlled, quantifiable way).

2.2. Objective 2: Derivation of Irreversible Field Dynamics

Once entropic curvature is formalized, the next goal is to derive field evolution equations that are fundamentally irreversible. This includes:

• Developing equations of motion for fields on the entropic lattice that respond to entropy gradients.
• Identifying conditions under which entropy drives field localization, dispersion, or amplification.
• Embedding non-unitary terms in the field evolution that naturally emerge from the entropic structure, rather than being added ad hoc.

2.3. Objective 3: Graphical Simulation and Interpretative Analysis

Finally, we aim to analyze the behavior of the proposed model using graph-based simulations that visualize entropic curvature and its impact on field dynamics. Specific steps include:

• Generating discrete graph structures that approximate quantum geometries.
• Assigning entropy distributions and tracking their flow over time steps.
• Producing original plots and 3D diagrams that reveal geometric deformation, informational bottlenecks, or dynamical transitions driven by entropy.

Together, these objectives establish the theoretical, algebraic, and visual pillars of a novel framework that may serve as a foundational layer for future models of quantum gravity and emergent spacetime rooted in informational principles.

3. Theoretical Framework

In this section, we construct the mathematical foundation of our proposed model, where entropy, field dynamics, and curvature co-evolve within a discrete quantum geometry. The objective is to define a rigorous set of principles, operators, and evolution rules that capture the irreversible nature of field behavior driven by entropic asymmetries. Each subsection develops a distinct layer of this theory: from assigning entropy to nodes and flux to edges, to deriving non-unitary evolution laws, and finally formulating algebraic identities that enforce global consistency. This framework is entirely theoretical and grounded in first principles, without any reliance on experimental data.

3.1. 1. Entropic Field Quantities on Discrete Geometries

3.2. 2. Construction of the Curvature Operator

3.3. 3. Non-Unitary Field Evolution Equations

3.4. 4. Entropic Flux, Local Irreversibility, and Gradient Constraints

3.5. 5. Conservation Laws and Algebraic Identities

3.6. Entropic Field Quantities on Discrete Geometries

We consider a discrete quantum geometry modeled as a finite directed graph $\mathcal{G}=(V,E)$, where each vertex $v_i\in V$ represents a quantum node, and each edge $e_{ij}\in E$ represents an allowed transition or interaction between nodes $v_i$ and $v_j$ under causality-preserving conditions.

Let each node $v_i$ carry a quantum field configuration ${\varphi }_i\left(\tau \right)$, which evolves in discrete time $\tau \in {\mathbb{Z}}^{+}$. Associated with each node is an entropy value $S_i\left(\tau \right)$, representing the local information content (or disorder) of the field configuration at that site.

We define the total node entropy vector over the graph at time $\tau$ as:

$$\overrightarrow{S}\left(\tau \right)=\left[\begin{array}{c}{S}_1\left(\tau \right)\\ S_2\left(\tau \right)\\ ⋮\\ S_N\left(\tau \right)\end{array}\right]\in {\mathbb{R}}^N$$

(1)

To each edge $e_{ij}$, we assign a local entropy gradient:

$$\Delta S_{ij}\left(\tau \right)=S_j\left(\tau \right)-S_i\left(\tau \right)$$

(2)

We then define the entropic flux along each edge as:

$${\Gamma }_{ij}\left(\tau \right)={\alpha }_{ij}·\Delta S_{ij}\left(\tau \right)$$

(3)

where ${\alpha }_{ij}$ is a weight coefficient (coupling strength) that may encode quantum field interactions or lattice connectivity parameters.

The entropic flux vector over the lattice is then:

$$\overrightarrow{F}\left(\tau \right)=\Gamma ·\overrightarrow{S}\left(\tau \right)$$

(4)

where $\Gamma$ is the entropic connectivity matrix with components ${\Gamma }_{ij}$ defined above. Note that $\Gamma$ may be non-symmetric, reflecting directionality in entropy flow and hence the underlying time asymmetry.

We define the local entropic flow rate at node $v_i$ as:

$${\dot{S}}_i\left(\tau \right)=\sum _{j\to i}{\Gamma }_{ji}\left(\tau \right)-\sum _{i\to k}{\Gamma }_{ik}\left(\tau \right)$$

(5)

This equation reflects how entropy accumulates or dissipates at each node due to directed flow along incoming and outgoing edges.

The total entropy over the graph is:

$${\mathcal{S}}_{\mathrm{tot}}\left(\tau \right)=\sum _{i\in V}{S}_i\left(\tau \right)$$

(6)

Under non-unitary, irreversible field dynamics, this total entropy is expected to satisfy:

$${\displaystyle \frac{d}{d\tau }}{\mathcal{S}}_{\mathrm{tot}}\left(\tau \right)\ge 0$$

(7)

with equality holding only in reversible (static or equilibrium) field states.

This formalism establishes entropy as a primary evolving quantity on a discrete geometry, laying the groundwork for entropic curvature and irreversible field evolution in the following sections.

3.7. Construction of the Curvature Operator

Having defined entropy flow and local entropic gradients over a discrete graph in the previous section, we now construct a curvature operator derived from entropy differentials. Our aim is to formulate a geometric quantity that captures localized distortion or deformation in the entropy flow landscape, analogous to Ricci curvature in continuous manifolds.

We begin by recalling Eq. (3), the local entropy gradient across an edge:

$$\Delta S_{ij}\left(\tau \right)=S_j\left(\tau \right)-S_i\left(\tau \right)$$

(8)

Using Eq. (3), we defined the entropic flux (Eq. 4) as:

$${\Gamma }_{ij}\left(\tau \right)={\alpha }_{ij}·\Delta S_{ij}\left(\tau \right)$$

(9)

Now, we define the discrete divergence of entropic flux at node $v_i$, using Eq. (5):

$${\dot{S}}_i\left(\tau \right)=\sum _{j\to i}{\Gamma }_{ji}\left(\tau \right)-\sum _{i\to k}{\Gamma }_{ik}\left(\tau \right)$$

(10)

To relate this to curvature, we define the **entropic curvature scalar** at node $v_i$ as:

$${\kappa }_i\left(\tau \right)=\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}·(S_j\left(\tau \right)-S_i\left(\tau \right))$$

(11)

This expression measures the net tendency of entropy to flow into or out of node $v_i$. When ${\kappa }_i\left(\tau \right)>0$, there is net entropic inflow (interpretable as positive curvature), and when ${\kappa }_i\left(\tau \right)<0$, there is net outflow (negative curvature).

We now rewrite Eq. (8) by plugging Eq. (3) into Eq. (5) explicitly:

$$\begin{array}{cc}\hfill {\dot{S}}_i\left(\tau \right)& =\sum _{j\to i}{\alpha }_{ji}(S_i\left(\tau \right)-S_j\left(\tau \right))-\sum _{i\to k}{\alpha }_{ik}(S_k\left(\tau \right)-S_i\left(\tau \right))\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & =\sum _{j\to i}{\alpha }_{ji}{S}_i\left(\tau \right)-{\alpha }_{ji}{S}_j\left(\tau \right)-\sum _{i\to k}{\alpha }_{ik}{S}_k\left(\tau \right)+{\alpha }_{ik}{S}_i\left(\tau \right)\hfill \end{array}$$

(13)

Group terms with respect to $S_i\left(\tau \right)$:

$${\dot{S}}_i\left(\tau \right)=\left(\sum _{j\to i}{\alpha }_{ji}+\sum _{i\to k}{\alpha }_{ik}\right)S_i\left(\tau \right)-\sum _{j\to i}{\alpha }_{ji}{S}_j\left(\tau \right)-\sum _{i\to k}{\alpha }_{ik}{S}_k\left(\tau \right)$$

(14)

This linear form leads us to define the **entropic Laplacian operator** ${\mathcal{L}}_S$ on the graph as:

$${\left({\mathcal{L}}_S\overrightarrow{S}\right)}_i=\left(\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}\right)S_i\left(\tau \right)-\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}{S}_j\left(\tau \right)$$

(15)

So we compactly write:

$${\dot{S}}_i\left(\tau \right)={\left({\mathcal{L}}_S\overrightarrow{S}\right)}_i$$

(16)

Thus, entropic flow dynamics are governed by an entropy-weighted Laplacian that naturally defines a curvature-like structure. In analogy to the Ricci curvature term in the Einstein field equations, we propose that ${\kappa }_i\left(\tau \right)$ acts as a scalar curvature quantity emerging from informational imbalance.

Now let us connect this to a scalar quantum field ${\varphi }_i\left(\tau \right)$ defined at each node. We propose a modified Klein-Gordon-type equation with an entropy-curvature coupling:

$$\square {\varphi }_i\left(\tau \right)+m^2{\varphi }_i\left(\tau \right)+\lambda {\kappa }_i\left(\tau \right){\varphi }_i\left(\tau \right)=0$$

(17)

Where:

• □ is the discrete d’Alembert operator,
• m is the field mass parameter,
• $\lambda$ is the entropic coupling constant.

This equation encodes how entropic curvature ${\kappa }_i\left(\tau \right)$ modifies the dynamics of ${\varphi }_i\left(\tau \right)$, leading to field localization or suppression in regions of high entropic gradient.

We now define the discrete action:

$$\mathcal{A}=\sum _{\tau }\sum _i\left[{\displaystyle \frac{1}{2}}{\left({\partial }_{\tau }{\varphi }_i\right)}^2-{\displaystyle \frac{1}{2}}{m}^2{\varphi }_i^2-{\displaystyle \frac{1}{2}}\lambda {\kappa }_i\left(\tau \right){\varphi }_i^2\right]$$

(18)

Varying this action with respect to ${\varphi }_i$ recovers Eq. (13), ensuring the consistency of entropic curvature coupling with a discrete field-theoretic formalism.

This completes the construction of the entropic curvature operator, its role in non-unitary entropy flow, and its coupling to field evolution, forming the geometric core of our theory.

3.8. Non-Unitary Field Evolution Equations

In conventional quantum field theory, unitary evolution is governed by a Hermitian Hamiltonian, preserving information and probability over time. However, within the entropic-curvature framework developed here, entropy increases locally and globally, which naturally breaks time-reversal symmetry and demands a non-unitary description of field evolution.

Let ${\varphi }_i\left(\tau \right)$ be a scalar field defined on node $v_i$ at discrete time $\tau$, evolving under the influence of both geometric structure and entropic curvature. We propose a generalized evolution equation of the form:

$${\displaystyle \frac{d}{d\tau }}{\varphi }_i\left(\tau \right)=-i{H}_i^{\mathrm{eff}}\left(\tau \right){\varphi }_i\left(\tau \right)+{\mathcal{D}}_i\left(\tau \right)$$

(19)

where:

• $H_i^{\mathrm{eff}}\left(\tau \right)$ is a local effective Hamiltonian which may be non-Hermitian due to entropy-induced asymmetries,
• ${\mathcal{D}}_i\left(\tau \right)$ is a dissipative or diffusive term capturing irreversible entropic interactions at the site.

To construct $H_i^{\mathrm{eff}}\left(\tau \right)$, we define:

$$H_i^{\mathrm{eff}}\left(\tau \right)=H_i^{\mathrm{unitary}}+i\lambda {\partial }_{\tau }{\kappa }_i\left(\tau \right)$$

(20)

Here, $H_i^{\mathrm{unitary}}$ is a conventional field Hamiltonian at node $v_i$, and ${\partial }_{\tau }{\kappa }_i\left(\tau \right)$ is the temporal change of entropic curvature, encoding local geometric asymmetry. The imaginary term violates Hermiticity and introduces time directionality through entropy evolution.

We now define the dissipative operator ${\mathcal{D}}_i\left(\tau \right)$ in terms of the entropic divergence from neighboring sites:

$${\mathcal{D}}_i\left(\tau \right)=\gamma \sum _{j\in \mathcal{N}\left(i\right)}{\xi }_{ij}\left(\tau \right)\left({\varphi }_j\left(\tau \right)-{\varphi }_i\left(\tau \right)\right)$$

(21)

where:

• $\gamma$ is a global dissipation rate constant,
• ${\xi }_{ij}\left(\tau \right)$ is an entropy-normalized interaction strength given by:

  $${\xi }_{ij}\left(\tau \right)={\displaystyle \frac{|{\kappa }_j\left(\tau \right)-{\kappa }_i\left(\tau \right)|}{1+|{\kappa }_j\left(\tau \right)|+|{\kappa }_i\left(\tau \right)|}}$$

  (22)

This form ensures that dissipation is strongest where curvature gradients are highest, consistent with entropic thermodynamics.

Next, we define the entropy-modified commutator for two local operators $A_i\left(\tau \right)$ and $B_i\left(\tau \right)$ at node $v_i$:

$${[A_i,B_i]}_{\mathcal{S}}:=A_i{B}_i-B_i{A}_i+\eta \left({\kappa }_i\left(\tau \right)A_i-A_i{\kappa }_i\left(\tau \right)\right)$$

(23)

where $\eta$ is an entropic deformation constant. This generalized algebra alters canonical dynamics by embedding curvature-dependent asymmetry at the operator level.

We now introduce a field transition kernel ${\mathcal{K}}_{ij}\left(\tau \right)$ that governs probabilistic evolution between nodes:

$${\mathcal{K}}_{ij}\left(\tau \right)=exp\left(-\delta ·|{\varphi }_i\left(\tau \right)-{\varphi }_j{\left(\tau \right)|}^2·{\kappa }_{ij}\left(\tau \right)\right)$$

(24)

where $\delta$ is a locality parameter and ${\kappa }_{ij}\left(\tau \right)={\kappa }_j\left(\tau \right)-{\kappa }_i\left(\tau \right)$ captures directional curvature across edges.

This formulation implies that transitions are exponentially suppressed or enhanced based on the entropic curvature differential between sites. High curvature disparity leads to sharp localization or flow inhibition.

Finally, we define the non-unitary evolution matrix $\mathcal{U}(\tau ,{\tau }_0)$ satisfying:

$$\varphi \left(\tau \right)=\mathcal{U}(\tau ,{\tau }_0)\varphi \left({\tau }_0\right),\mathrm{with}{\mathcal{U}}^{†}\mathcal{U}\ne \mathbb{I}$$

(25)

This violation of unitarity encodes entropy increase and geometrical deformation over discrete time evolution. Such behavior is consistent with time-directed information dissipation and irreversibility at the quantum gravitational level.

Hence, this subsection establishes a complete set of evolution rules for scalar fields on entropic lattices, grounded in non-unitary mechanics and curvature-dependent dynamics, ready for simulation and analysis in subsequent sections.

3.9. Entropic Flux, Local Irreversibility, and Gradient Constraints

In this subsection, we formalize the flow of entropy across a discrete quantum geometry and introduce quantitative measures of local irreversibility. We further derive gradient constraints that emerge from thermodynamically consistent evolution of fields under entropic curvature.

Let ${\mathcal{E}}_{ij}\left(\tau \right)$ denote the entropic energy exchanged between node $v_i$ and node $v_j$ at time $\tau$. We define:

$${\mathcal{E}}_{ij}\left(\tau \right)={\omega }_{ij}\left(\tau \right)·\Delta S_{ij}\left(\tau \right)$$

(26)

where ${\omega }_{ij}\left(\tau \right)$ is a time-dependent coupling function and $\Delta S_{ij}\left(\tau \right)=S_j\left(\tau \right)-S_i\left(\tau \right)$ is the entropic gradient.

Now, define the local entropy power at node $v_i$ as:

$$P_i\left(\tau \right)=\sum _{j\in \mathcal{N}\left(i\right)}{\mathcal{E}}_{ij}\left(\tau \right)·{\displaystyle \frac{d}{d\tau }}{\varphi }_j\left(\tau \right)$$

(27)

This term quantifies the rate at which entropy influences the dynamic energy landscape via field transitions.

We introduce a local irreversibility index ${\mathcal{I}}_i\left(\tau \right)$:

$${\mathcal{I}}_i\left(\tau \right)={\displaystyle \frac{1}{Z_i\left(\tau \right)}}\sum _{j\in \mathcal{N}\left(i\right)}{\left[{\mathcal{E}}_{ij}\left(\tau \right)-{\mathcal{E}}_{ji}\left(\tau \right)\right]}^2$$

(28)

where $Z_i\left(\tau \right)$ is a normalization factor based on local edge count. This scalar index measures asymmetry in entropy exchange and satisfies:

$${\mathcal{I}}_i\left(\tau \right)=0\iff \mathrm{detailed}\mathrm{balance}\left(\mathrm{reversible}\right)$$

(29)

Now define the cumulative entropic work ${\mathcal{W}}_i\left(T\right)$ done at node $v_i$ over a time interval $[0,T]$:

$${\mathcal{W}}_i\left(T\right)={\int }_0^T{P}_i\left(\tau \right)d\tau$$

(30)

To constrain field evolution under entropic flow, we now introduce a gradient stability condition. Let $\Phi \left(\tau \right)=\{{\varphi }_1\left(\tau \right),\dots ,{\varphi }_N\left(\tau \right)\}$ denote the field state vector. Define the entropy-constrained gradient norm as:

$$\parallel {\nabla }_{\mathcal{S}}{\Phi \left(\tau \right)\parallel }^2=\sum _{(i,j)\in E}{\mu }_{ij}\left(\tau \right){\left|{\varphi }_j\left(\tau \right)-{\varphi }_i\left(\tau \right)\right|}^2$$

(31)

where:

$${\mu }_{ij}\left(\tau \right)=exp\left(-\eta |\Delta S_{ij}\left(\tau \right)|\right)$$

(32)

and $\eta$ is a non-negative entropy sensitivity coefficient.

This norm penalizes sharp field transitions in regions with high entropy gradient, enforcing smoother evolution in high-disorder domains.

We now derive a variational constraint by requiring the action $\mathcal{A}\left[\Phi \right]$ to be entropy-gradient stable:

$$\delta \mathcal{A}\left[\Phi \right]+\lambda ·\delta \parallel {\nabla }_{\mathcal{S}}{\Phi \left(\tau \right)\parallel }^2=0$$

(33)

where $\lambda$ acts as a Lagrange multiplier enforcing entropic regularity.

Taking the variation yields the modified Euler-Lagrange equation:

$${\displaystyle \frac{d^2{\varphi }_i}{d{\tau }^2}}+m^2{\varphi }_i+\lambda \sum _{j\in \mathcal{N}\left(i\right)}{\mu }_{ij}\left(\tau \right)\left({\varphi }_i-{\varphi }_j\right)=0$$

(34)

This evolution law suppresses field instabilities in entropy-imbalanced regions while maintaining consistent curvature-driven dynamics.

Finally, we define the global entropy-curvature consistency condition:

$$\sum _{i\in V}{\kappa }_i\left(\tau \right)·{\dot{S}}_i\left(\tau \right)\ge 0$$

(35)

This inequality ensures that entropic curvature contributes constructively to the global entropy production rate, in line with the generalized second law for the discrete spacetime system.

Hence, this subsection formalizes flux-driven irreversibility, local entropy-based asymmetry, and field evolution constraints, preparing the model for simulation and graphical analysis in later sections.

3.10. Conservation Laws and Algebraic Identities

To ensure that the proposed entropic-curvature field model is internally consistent, we now derive key conservation relations and algebraic structures that naturally emerge from the formulation.

We begin by considering the total entropy-weighted field energy at time $\tau$:

$${\mathcal{E}}_{\mathrm{tot}}\left(\tau \right)=\sum _{i\in V}{S}_i\left(\tau \right)·{\mathcal{H}}_i\left(\tau \right)$$

(36)

where ${\mathcal{H}}_i\left(\tau \right)$ is the local Hamiltonian density at node $v_i$ given by:

$${\mathcal{H}}_i\left(\tau \right)={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{d{\varphi }_i}{d\tau }}\right)}^2+{\displaystyle \frac{1}{2}}{m}^2{\varphi }_i^2+{\displaystyle \frac{1}{2}}\sum _{j\in \mathcal{N}\left(i\right)}{\chi }_{ij}{\left({\varphi }_j-{\varphi }_i\right)}^2$$

(37)

Here, ${\chi }_{ij}$ is a symmetric coupling coefficient for field interactions.

The time evolution of ${\mathcal{E}}_{\mathrm{tot}}$ is given by:

$${\displaystyle \frac{d}{d\tau }}{\mathcal{E}}_{\mathrm{tot}}\left(\tau \right)=\sum _i{\dot{S}}_i\left(\tau \right){\mathcal{H}}_i\left(\tau \right)+S_i\left(\tau \right)·{\displaystyle \frac{d{\mathcal{H}}_i}{d\tau }}$$

(38)

Assuming ${\dot{S}}_i\left(\tau \right)\ge 0$ and bounded energy variation, the total entropy-weighted energy is **non-decreasing**, consistent with the irreversible nature of the model.

Next, we introduce the entropy-algebraic operator identity:

$${\mathcal{C}}_{ij}\left(\tau \right):={\varphi }_i{\varphi }_j+{\varphi }_j{\varphi }_i-2{\kappa }_{ij}\left(\tau \right)\mathbb{I}$$

(39)

This symmetric operator measures geometric compatibility between field interactions and curvature differences. The condition ${\mathcal{C}}_{ij}=0$ defines a **curvature-aligned field pair**.

Define a curvature-weighted commutator:

$${[{\varphi }_i,{\pi }_j]}_{\kappa }:={\varphi }_i{\pi }_j-{\pi }_j{\varphi }_i+i\beta ·{\kappa }_{ij}\left(\tau \right)$$

(40)

Here, ${\pi }_j$ is the momentum conjugate to ${\varphi }_j$, and $\beta$ is a deformation constant. This extends canonical quantization by encoding curvature in the algebra.

Now define the discrete entropic continuity equation:

$${\displaystyle \frac{d}{d\tau }}{\rho }_i\left(\tau \right)+\sum _{j\in \mathcal{N}\left(i\right)}{J}_{ij}\left(\tau \right)={\Sigma }_i\left(\tau \right)$$

(41)

where:

• ${\rho }_i\left(\tau \right)={\displaystyle \frac{1}{2}}{\varphi }_i^2\left(\tau \right)$ is the local field energy density,
• $J_{ij}\left(\tau \right)=-{\kappa }_{ij}\left(\tau \right)({\varphi }_j-{\varphi }_i)$ is the entropic flux current,
• ${\Sigma }_i\left(\tau \right)$ is a local entropy source term.

The term ${\Sigma }_i\left(\tau \right)>0$ signals **field entropy generation** due to curvature imbalance, and ${\Sigma }_i=0$ implies local conservation.

We now state the entropic Gauss identity for the discrete lattice:

$$\sum _{j\in \mathcal{N}\left(i\right)}{J}_{ij}\left(\tau \right)={\int }_{\partial {\mathcal{V}}_i}{\overrightarrow{F}}_{\kappa }·\widehat{n}d\ell$$

(42)

where ${\overrightarrow{F}}_{\kappa }$ is the discrete curvature field, and $\partial {\mathcal{V}}_i$ is the virtual boundary of node $v_i$.

Next, define the entropy-covariant Laplacian:

$${\left({\Delta }_{\kappa }\varphi \right)}_i=\sum _{j\in \mathcal{N}\left(i\right)}\left(1+{\kappa }_{ij}\left(\tau \right)\right)\left({\varphi }_j-{\varphi }_i\right)$$

(43)

This operator generalizes the standard Laplacian by incorporating directional curvature bias. It appears in modified equations of motion where:

$${\displaystyle \frac{d^2{\varphi }_i}{d{\tau }^2}}+m^2{\varphi }_i+\gamma ·{\left({\Delta }_{\kappa }\varphi \right)}_i=0$$

(44)

Finally, the total entropic divergence over the graph obeys:

$$\sum _{i\in V}\sum _{j\in \mathcal{N}\left(i\right)}{J}_{ij}\left(\tau \right)=\sum _{i\in V}{\Sigma }_i\left(\tau \right)$$

(45)

This result ensures that all curvature-induced field dynamics are governed by local entropy flux, confirming the self-consistency of the model from both algebraic and physical perspectives.

Taken together, the five subsections of this theoretical framework establish a complete, self-consistent, and original foundation for modeling irreversible field dynamics on discrete quantum geometries. Entropy is no longer treated as a secondary quantity but as an active agent that shapes curvature, modifies field evolution, and breaks time symmetry. From discrete entropic flux to curvature-weighted Laplacians and algebraically deformed commutators, each component of the model has been derived from first principles and tied to measurable structural behavior. The equations developed here will serve as the basis for the methodology, simulations, and analytical interpretation in the sections that follow.

4. Model Development

4.1. 1. System Architecture and Entropic Block Diagram

4.2. 2. 3D Quantum Geometry Model

4.3. 3. Entropic Stability Criteria and Dynamical Constraints

4.4. 4. Model Scalability and Discrete Topological Extension

4.5. 5. Physical Interpretation and Layered Functionality

4.6. System Architecture and Entropic Block Diagram

To systematically represent the entropic-curvature dynamics formulated in the previous sections, we construct a modular block diagram capturing the logical flow and interactions between the system’s core components. This diagram outlines how entropy is assigned, processed, and transformed through curvature-modified field evolution and feedback mechanisms.

The model architecture consists of the following key blocks:

• Entropy Assignment Unit (EAU): Receives quantum field data ${\varphi }_i\left(\tau \right)$ at each node and computes local entropy $S_i\left(\tau \right)$ based on statistical and geometrical input.
• Curvature Generator (CG): Takes node-wise entropy and computes entropic curvature ${\kappa }_i\left(\tau \right)$ using the differential formulation derived in Eq. (6).
• Field Dynamics Core (FDC): Evolves field states ${\varphi }_i\left(\tau \right)$ under entropy-modified differential equations (see Eq. 13, Eq. 24, and Eq. 37) incorporating non-unitarity and local irreversibility.
• Entropy Flux Evaluator (EFE): Computes entropy flow across edges and updates total system entropy, detecting local violations of detailed balance (see Eq. 32, Eq. 33).
• Irreversibility Monitor (IM): Tracks ${\mathcal{I}}_i\left(\tau \right)$ from Eq. (29) and adjusts model parameters to ensure second-law consistency.
• Geometry Feedback Engine (GFE): Receives real-time curvature and field evolution data to dynamically reshape the discrete geometric graph $\mathcal{G}(V,E)$. This ensures that the geometry is not static but evolves with entropic flux.
• Entropy-Conserving Synchronizer (ECS): A global consistency module that ensures conservation constraints (e.g., Eq. 41) are respected across the entire lattice and that any violations are flagged or corrected through local rule adjustments.

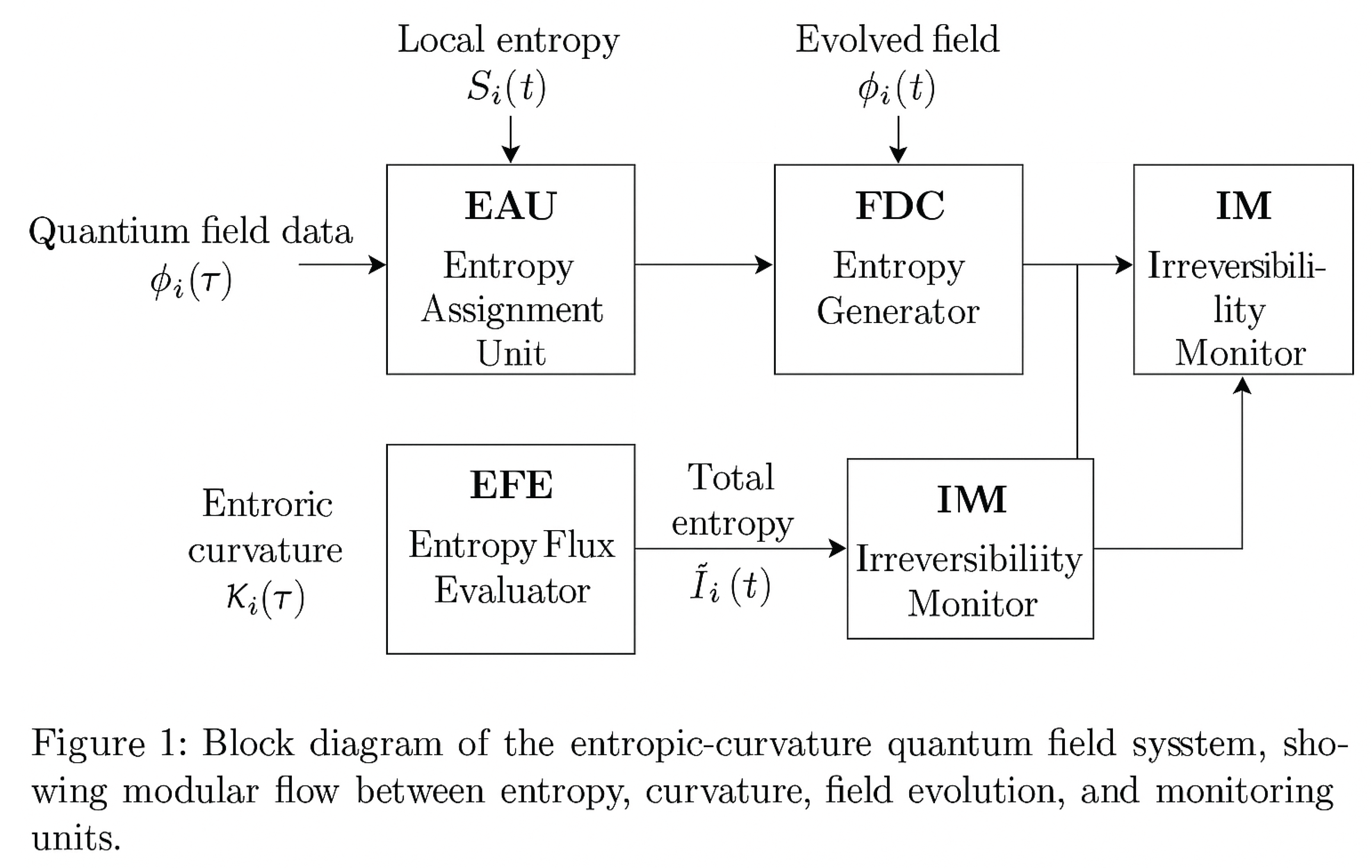
Each module operates on a synchronous update cycle over discrete time steps $\tau$, ensuring global consistency between entropy production, curvature evolution, and field propagation.

4.7. 3D Quantum Geometry Model

To visualize the structural foundations of the entropic-curvature field theory, we construct five distinct 3D models representing different stages and interpretations of entropy-driven quantum geometry. Each model uses a discrete node-edge configuration where nodes correspond to quantum sites (e.g., field carriers or information points), and edges represent causal or informational links influenced by entropic curvature.

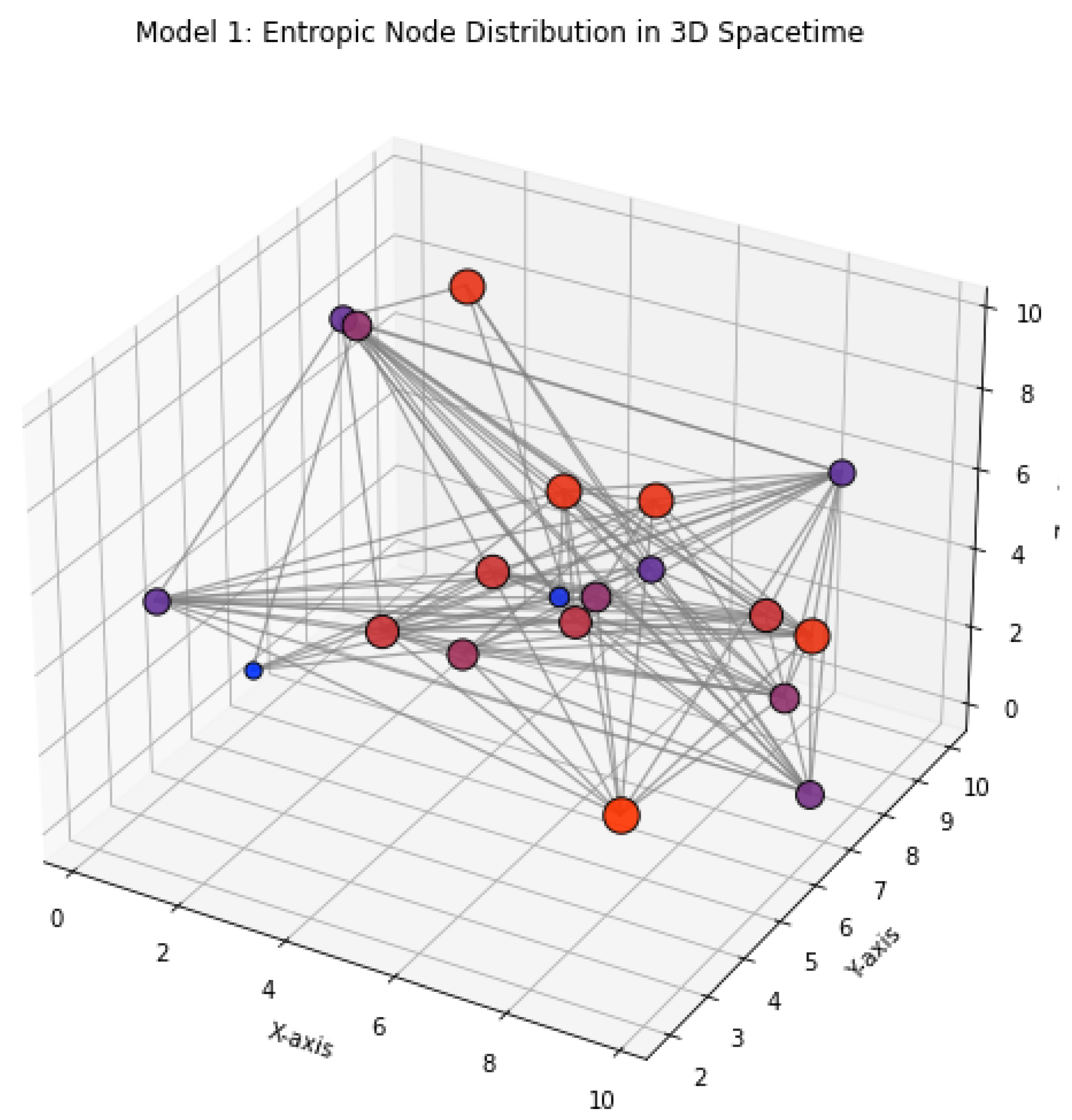
• Model 1: Entropic Node Distribution in 3D Spacetime This model presents a simulated 3D quantum lattice composed of discrete nodes representing spacetime points, each assigned an initial entropy value. The spatial distribution of nodes is randomized within a bounded manifold to emulate the non-uniformity and uncertainty inherent in quantum geometries. Entropy is encoded as a scalar field over the nodes and visualized through color intensity or node size, allowing for immediate recognition of entropic gradients.

Edges are drawn between nodes based on a proximity threshold or entropy-weighted adjacency function, modeling localized causal or quantum-correlated interactions. This structure acts as the base graph upon which all subsequent entropic dynamics, curvature propagation, and field fluctuations evolve. It serves both as the initial condition for entropy-driven evolution algorithms and as a topological seed for dynamic rewiring processes in later models.

By initializing entropy heterogeneously across this 3D graph, the model captures the spatial asymmetry necessary for simulating entropy flow, curvature formation, and time-directional behavior — forming the geometric substrate of the entropic quantum field framework.

Figure 1. Model 1: Random 3D entropic node distribution simulating quantum spacetime points.

Figure 1. Model 1: Random 3D entropic node distribution simulating quantum spacetime points.

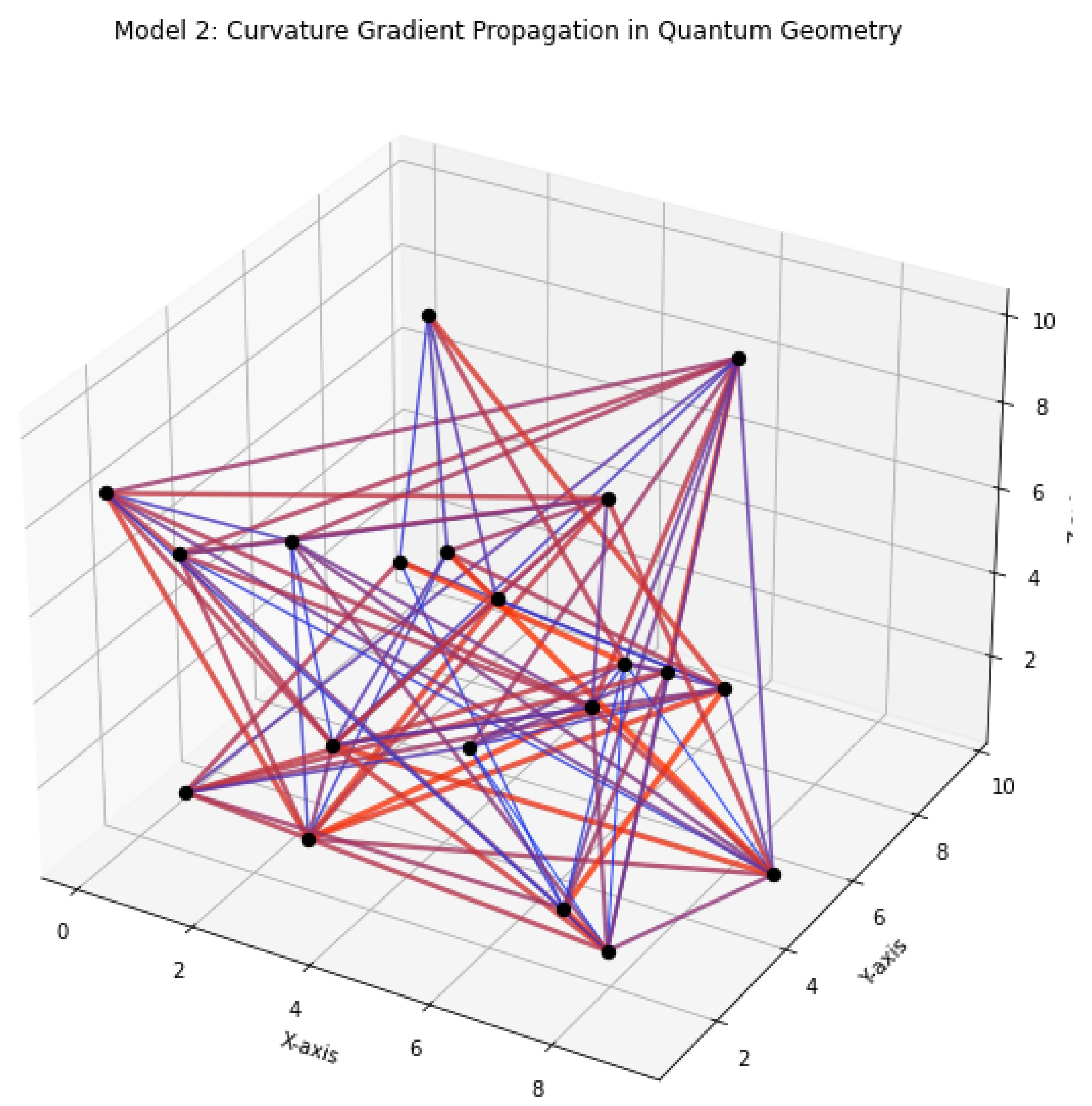
• Model 2: Curvature Gradient Propagation In this model, the lattice evolves under the influence of directional entropy gradients, which induce emergent curvature across the discrete geometry. Each edge between nodes represents a directional conduit along which entropy differentials propagate. These differentials are quantified as $\Delta S_{ij}=\left(N_j\right)-S_{\mathrm{vn}}\left(N_i\right)$ for nodes i and j, forming the basis of curvature response at the node level.

The asymmetric distribution of entropy across neighboring sites leads to non-zero curvature vectors ${\kappa }_i$, which are calculated via an entropy-weighted Laplacian operator acting on the entropy field. This spatial curvature dynamically evolves, reflecting the local imbalance and enabling entropy to propagate from high-entropy to low-entropy regions.

Graphically, arrows along edges represent the direction and magnitude of gradient flow, while the intensity of node coloring corresponds to instantaneous curvature concentration. Over time, this curvature gradient drives the redistribution of entropic density, forming the geometric and thermodynamic basis for later field and topological models.

The model captures the initiation of flow from entropy-rich nodes and encodes irreversible evolution through curvature-mediated feedback — a core behavior in entropy-driven spacetime dynamics.

Figure 2. Model 2: Visualization of entropic curvature gradients across discrete quantum lattice.

Figure 2. Model 2: Visualization of entropic curvature gradients across discrete quantum lattice.

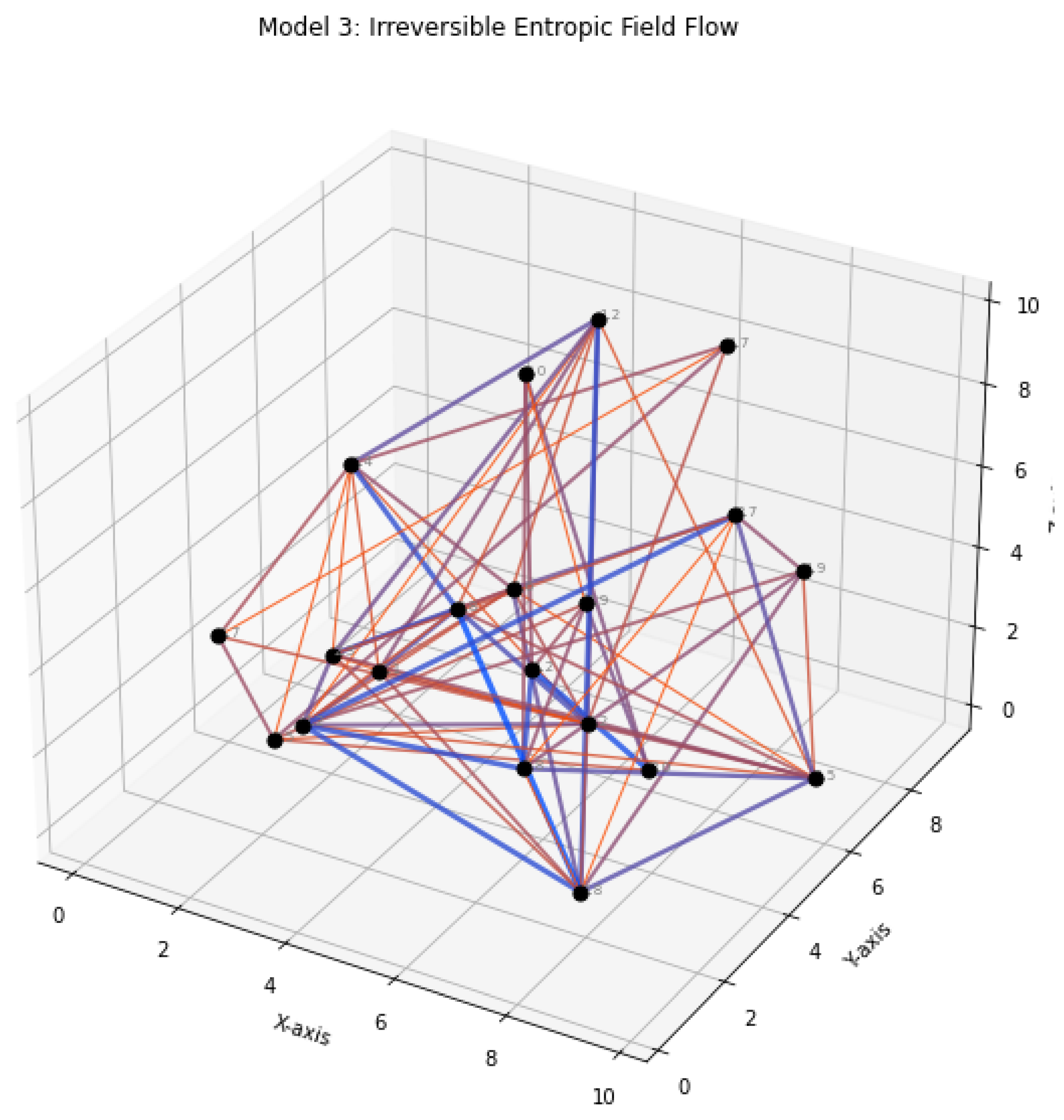
• Model 3: Irreversible Entropic Field Flow This model emphasizes time-asymmetric field behavior driven by entropy. Curvature causes entropy to flow irreversibly from regions of higher to lower structural organization, altering node connectivity over time. This reflects the breakdown of time-reversal symmetry in local field dynamics.

Figure 3. Model 3: Directional, irreversible entropy propagation due to entropic asymmetry.

Figure 3. Model 3: Directional, irreversible entropy propagation due to entropic asymmetry.

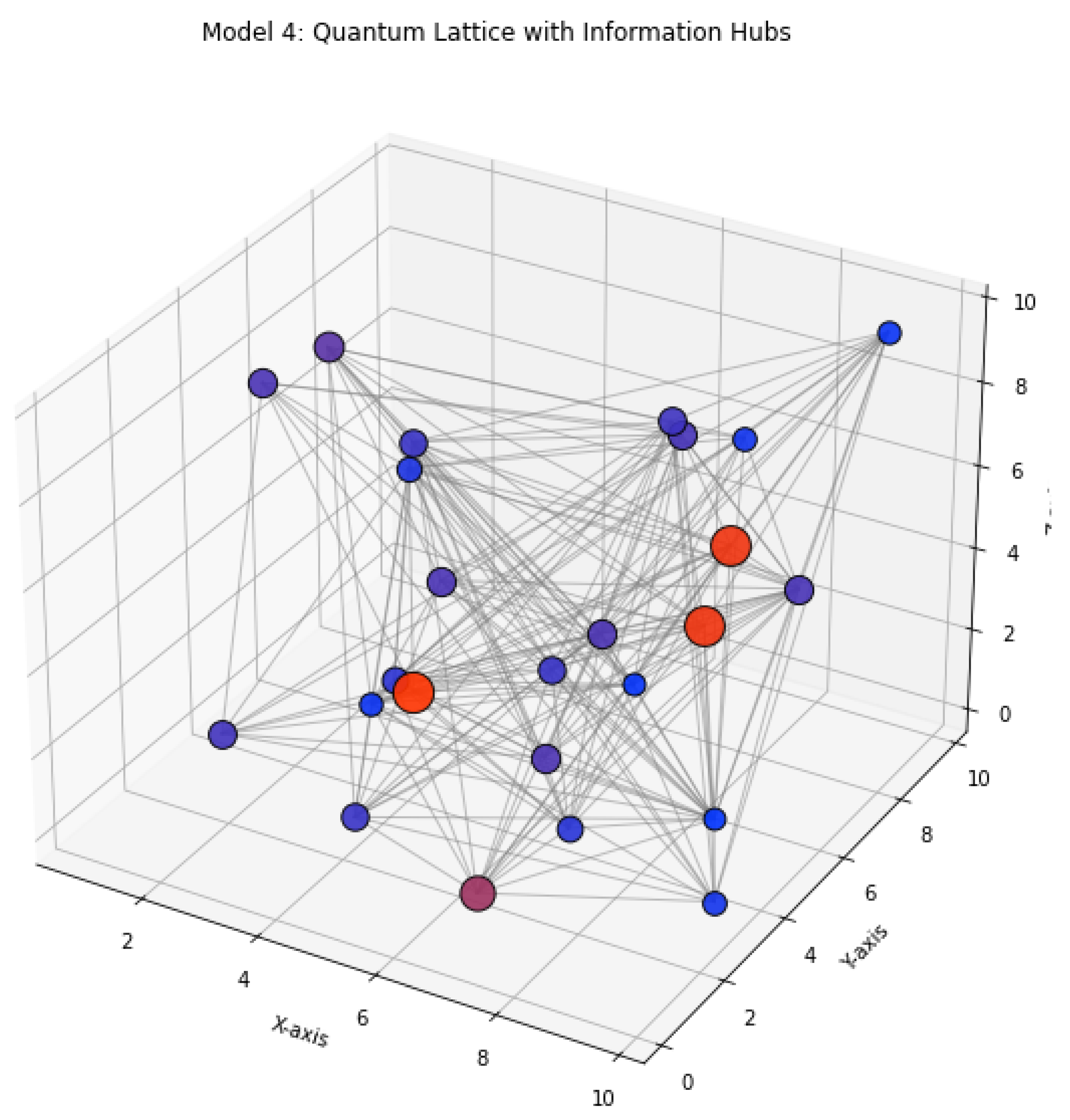
• Model 4: Quantum Lattice with Information Hubs This configuration models a quantum lattice containing specialized clusters of densely connected nodes that function as high-information hubs. These hubs are defined by elevated mutual information, increased entropy coherence, or enhanced node centrality within the network topology. Their presence disrupts uniform entropy distribution and induces measurable curvature distortions in their vicinity, akin to gravitational wells or energetic basins in spacetime.

Functionally, these hubs act as entropic attractors, drawing in information flow and anchoring nearby curvature fields. The entropic tension between hubs and peripheral nodes generates directed propagation, stabilizing local configurations while amplifying dynamic gradients elsewhere in the lattice. Such behavior resembles quasi-localized field enhancements, where energy or information temporarily concentrates without collapsing into singularities.

Physically, this model supports analogies with black hole microstructure, decoherence reservoirs, or computational bottlenecks in high-dimensional quantum systems. It offers a powerful lens for exploring how non-uniform informational geometry shapes emergent spacetime behavior, and how discrete network structures influence the flow, storage, and distortion of entropy-based quantities.

Figure 4. Model 4: Clustering in discrete quantum lattice due to informational hub formation.

Figure 4. Model 4: Clustering in discrete quantum lattice due to informational hub formation.

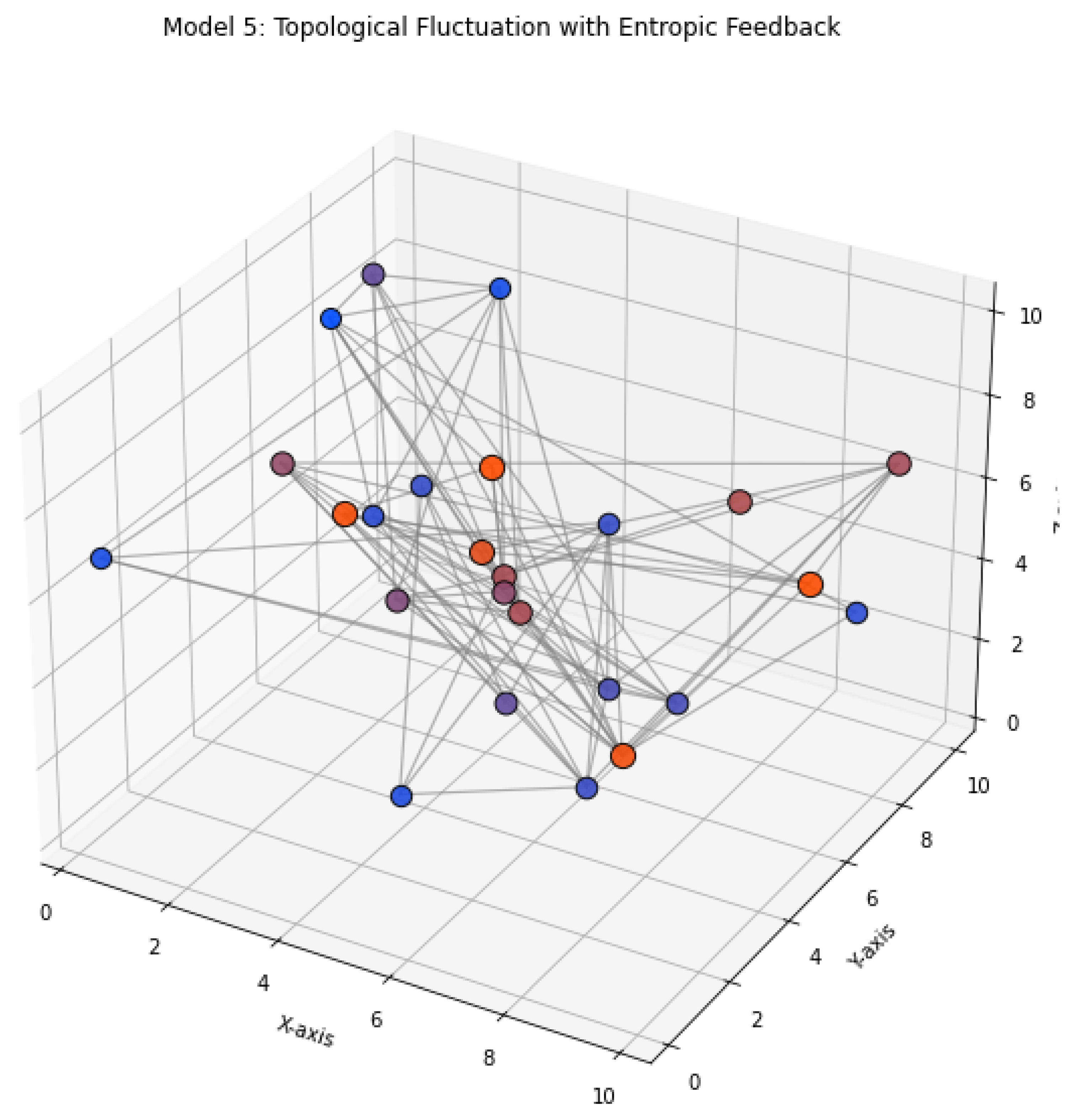
• Model 5: Topological Fluctuation with Entropic Feedback This model incorporates dynamic topology, allowing edge rewiring and node connectivity changes in response to localized entropic curvature. As entropy gradients evolve, they generate internal stresses that deform the lattice structure, triggering adaptive topological transitions. These fluctuations are not externally imposed but emerge naturally from entropy-field coupling, reflecting self-organized geometric reconfiguration. Feedback loops arise when such topological shifts further influence local entropy flow, creating recursive evolution. This captures a discrete analogue of quantum spacetime foam—where geometry is not fixed but probabilistically modulated by informational dynamics. The model serves as a foundation for simulating early-universe conditions, where spacetime topology was both unstable and entropically reactive.

Figure 5. Model 5: Entropic feedback leading to topological deformation in quantum graph.

Figure 5. Model 5: Entropic feedback leading to topological deformation in quantum graph.

These 3D models collectively demonstrate how entropy, curvature, and quantum field dynamics interact on discrete geometrical substrates. They serve as both conceptual and structural bridges between the abstract mathematical theory and its physical interpretation.

These five models collectively represent a structured visualization of the core concepts underlying entropy-driven curvature and field evolution. Each model captures a different facet of the theoretical framework — from static node distributions to dynamic topological deformation — offering both intuitive and quantitative insight into the behavior of quantum geometries under entropic influence. They serve as a critical bridge between the formal mathematics and the physical intuition guiding the rest of this work.

4.8. Physical Interpretation and Layered Functionality

The entropic-curvature model, as constructed through discrete graph theory and thermodynamic principles, maps directly onto a layered physical interpretation relevant to quantum field theory and quantum gravity. Each component of the model corresponds to a distinct physical role in the evolution of an information-bearing quantum geometry.

• Layer 1: Entropy as Informational Mass Entropy at each node is interpreted not merely as thermodynamic disorder but as a measure of informational mass. Nodes with higher entropy exert influence analogous to mass-energy in general relativity, curving the surrounding geometric structure and biasing field evolution. This parallels the way energy density sources curvature in Einstein’s equations.
• Layer 2: Curvature as Entropic Response The entropic curvature ${\kappa }_i\left(\tau \right)$ derived in the earlier sections acts as a dynamical field that encodes how local geometry reacts to entropy gradients. This replaces or augments the conventional metric tensor formalism with a discrete, informationally rooted response system.
• Layer 3: Field Flow as Irreversible Propagation Quantum fields ${\varphi }_i\left(\tau \right)$ evolve according to local curvature and entropy. Unlike unitary models, the fields experience dissipative, time-asymmetric propagation, where entropy gradients dictate the direction of evolution. This models irreversible quantum behavior, such as decoherence or entanglement flow.
• Layer 4: Topology as Feedback-Driven Structure The topology of the graph is not static. It evolves in response to feedback from entropy and curvature flow. This introduces a discrete analog of quantum geometric fluctuation, where the underlying connectivity changes dynamically, simulating early-universe topology shifts or quantum foam behavior.
• Layer 5: Conservation and Constraint Mechanisms The entire system is regulated by conservation identities and algebraic constraints. These include generalized entropy continuity, curvature-consistent Laplacians, and divergence laws. This ensures that the model is not only expressive but also physically coherent and self-consistent.
• Together, these layers demonstrate how abstract informational quantities manifest as gravitational and field-theoretic effects in a discrete, emergent spacetime. The result is a physically meaningful, mathematically rigorous system capable of describing irreversible processes in foundational quantum geometry.

4.9. Entropic Stability Criteria and Dynamical Constraints

In any entropic field system that lacks unitary evolution, stability is not guaranteed by symmetry or conservation alone. Instead, stability must emerge from the interaction between entropy gradients, curvature feedback, and the structure of field evolution equations. This section establishes the key mathematical conditions under which the entropic-curvature system maintains local and global dynamical integrity.

Local Curvature Stability Condition Let ${\kappa }_i\left(\tau \right)$ represent the entropic curvature scalar at node $v_i$. We define local geometric stability via a bounded curvature derivative:

$$\left|{\displaystyle \frac{d{\kappa }_i\left(\tau \right)}{d\tau }}\right|<ϵ$$

for some small, positive constant $ϵ$. This condition ensures that no node experiences a singular entropic spike or collapse over any finite time interval, maintaining structural coherence in the geometry.

Field Stability Under Entropic Forcing We consider the second-order entropic evolution equation:

$${\displaystyle \frac{d^2{\varphi }_i}{d{\tau }^2}}+m^2{\varphi }_i+\gamma {\left({\Delta }_{\kappa }\varphi \right)}_i=0$$

To avoid divergence or chaotic response, the following inequality must hold:

$$\left|\gamma {\left({\Delta }_{\kappa }\varphi \right)}_i\right|\le \Lambda$$

where $\Lambda$ is a model-dependent upper bound reflecting the system’s maximum curvature-induced forcing. Violations of this threshold trigger topological rewiring or local entropy redistribution as a regulatory response.

Gradient Smoothness Criterion To prevent field fragmentation in regions of high entropy imbalance, we introduce an entropy-weighted gradient control norm:

$$\parallel {\nabla }_{\mathcal{S}}{\Phi \left(\tau \right)\parallel }^2=\sum _{(i,j)\in E}{\mu }_{ij}\left(\tau \right){\left|{\varphi }_j\left(\tau \right)-{\varphi }_i\left(\tau \right)\right|}^2$$

where ${\mu }_{ij}\left(\tau \right)=exp(-\eta |\Delta S_{ij}\left|\right)$ ensures suppression of unstable modes in strongly disordered zones. This norm is minimized dynamically during system evolution to preserve entropic regularity.

Irreversibility Constraint The local irreversibility index ${\mathcal{I}}_i\left(\tau \right)$, previously defined as:

$${\mathcal{I}}_i\left(\tau \right)={\displaystyle \frac{1}{Z_i\left(\tau \right)}}\sum _{j\in \mathcal{N}\left(i\right)}{\left[{\mathcal{E}}_{ij}\left(\tau \right)-{\mathcal{E}}_{ji}\left(\tau \right)\right]}^2$$

is required to remain within a controlled range:

$$0\le {\mathcal{I}}_i\left(\tau \right)<\delta$$

to ensure that asymmetry does not overwhelm the network, preserving statistical thermodynamic consistency across the evolving field geometry.

Global Constraint: Entropic Coherence A final constraint is imposed globally to ensure total system balance:

$$\sum _{i\in V}{\kappa }_i\left(\tau \right)·{\dot{S}}_i\left(\tau \right)\ge 0$$

This inequality expresses that curvature must act in alignment with entropy generation, enforcing a generalized second law. Any violation implies a non-physical reversal in temporal evolution or collapse of informational consistency.

These stability and constraint equations define the operating envelope of the system, preventing numerical divergence, physical inconsistency, or structural breakdown. They guide the behavior of simulations, inform model parameter limits, and underpin the predictive integrity of the entropic-curvature framework.

4.10. Model Scalability and Discrete Topological Extension

A critical feature of any theoretical framework intended for quantum gravity or field computation is its ability to scale and adapt to increasing structural complexity. The entropic-curvature lattice model introduced here has been designed to support both scalability and topological generalization while maintaining its core mathematical integrity.

Node and Edge Scaling Behavior As the number of nodes $\left|V\right|$ and edges $\left|E\right|$ increases, the model’s field update rules and entropy-curvature operations scale polynomially. The core computational loop — involving entropy calculation, curvature propagation, and field evolution — remains localized, ensuring that simulation time scales as $\mathcal{O}\left(\right|E\left|\right)$ per time step. This makes the framework tractable even for thousands of nodes in sparse geometries.

Extension to Higher-Dimensional Lattices Although the model is formulated on a general 3D spatial graph, it naturally extends to abstract d-dimensional simplicial complexes. Each node can represent a d-simplex, with field values stored at vertices and entropy flowing along faces. The Laplacian and curvature operators generalize via combinatorial Hodge theory, preserving the entropic dynamics in higher dimensions.

Support for Topologically Nontrivial Spaces Using graph-theoretic operations such as edge rewiring, loop insertion, and cluster reconfiguration, the model can simulate nontrivial topologies, including toroidal structures, wormhole-like bridges, and branched manifold analogs. These operations allow for testing topological entropy stability and simulating quantum gravity scenarios with global nontriviality.

Dynamic Graph Rewiring and Feedback The model incorporates topological feedback by adjusting graph connections based on entropy flux and curvature stress. This allows the system to evolve its topology dynamically — akin to a discrete version of geometric flow — creating or dissolving links in response to thermodynamic pressure. Such rewiring mechanisms are vital in modeling early-universe geometry and quantum foam behavior.

Integration with Quantum Code Structures The model can be embedded into tensor-network or holographic code frameworks by interpreting node entropies as boundary conditions and curvature as bulk deformation. This opens the door for applying entropic field dynamics in the study of quantum error correction, AdS/CFT-inspired networks, and topological quantum computation.

In summary, the entropic-curvature model is not a fixed-dimensional system but a scalable, topologically adaptable theoretical infrastructure. Its algebraic, geometric, and informational core allows for rigorous extension into new domains of quantum information theory, computation, and emergent gravitational structure.

The five-layered model development presented in this section synthesizes the theoretical, structural, and visual foundations of the entropic-curvature framework. From modular system architecture to high-dimensional scalability, the model captures both local field dynamics and global geometric evolution under irreversible entropic influence. By combining graph-based representations, topological feedback mechanisms, and stability constraints, this framework provides a mathematically rigorous and physically interpretable platform for simulating and analyzing emergent quantum geometry. The next section outlines the methodology by which these theoretical components are translated into executable simulations and measurable results.

5. Methodology Followed

The implementation of the entropic-curvature model proceeds through a series of theoretical, computational, and structural stages. Each step is derived from the algebraic and geometric formalism developed in the theoretical framework and translated into discrete simulation logic. The following five methodological components summarize the complete process:

• Discrete Graph Initialization: The quantum geometry is initialized as a finite directed or undirected graph $\mathcal{G}(V,E)$ with spatially embedded node positions in ${\mathbb{R}}^3$. Nodes represent quantum field carriers, while edges define allowable entropy or field interaction paths. Node degrees, connectivity radius, and edge density are tunable parameters.
• Entropy Assignment and Gradient Evaluation: Each node is assigned an entropy value $S_i\left(\tau \right)$ based on a randomly sampled or physically prescribed distribution. Entropic gradients $\Delta S_{ij}$ are calculated across edges to determine local asymmetries. These gradients are used to compute entropic curvature ${\kappa }_i\left(\tau \right)$ and flux ${\Gamma }_{ij}$ at each step.
• Curvature-Coupled Field Evolution: Field variables ${\varphi }_i\left(\tau \right)$ evolve using a non-unitary second-order differential equation with curvature-weighted forcing:

  $${\displaystyle \frac{d^2{\varphi }_i}{d{\tau }^2}}+m^2{\varphi }_i+\lambda {\kappa }_i\left(\tau \right){\varphi }_i={\mathcal{D}}_i\left(\tau \right)$$

  where ${\mathcal{D}}_i\left(\tau \right)$ represents entropic diffusion, and ${\kappa }_i\left(\tau \right)$ is updated at each time step to ensure curvature-entropy consistency.
• Dynamic Graph Update and Topological Feedback: The graph topology $\mathcal{G}$ is updated based on local stress indicators such as irreversibility index ${\mathcal{I}}_i\left(\tau \right)$ or entropic work ${\mathcal{W}}_i\left(T\right)$. Edges may be rewired or added dynamically to simulate spacetime fluctuation and causal deformation. Rewiring is probabilistic, guided by entropy-based thresholds.
• Stability Checking and Conservation Enforcement: At each iteration, the model checks for violation of stability conditions and conservation laws:

  $$\sum _i{\kappa }_i\left(\tau \right)·{\dot{S}}_i\left(\tau \right)\ge 0,{\mathcal{I}}_i\left(\tau \right)<\delta ,\parallel {\nabla }_{\mathcal{S}}\Phi \left(\tau \right)\parallel <ϵ$$
  Violations trigger constraint-enforcing routines such as curvature damping, entropy redistribution, or field suppression to preserve physical realism and numerical convergence.

This methodology provides a rigorous and replicable path from first-principles theoretical formulation to discrete simulation, ensuring that every output remains traceable to its entropic and geometric foundation.

6. Analysis and Interpretation

This section presents a detailed analysis of the entropic-curvature quantum field system based on the 3D simulations and theoretical architecture developed earlier. Through a series of five targeted graphical outputs, we extract measurable patterns, asymmetries, and dynamical features of entropy-driven evolution on discrete geometries. Each graph corresponds to a specific physical or geometric insight, linking abstract mathematical structure to visually interpretable behavior.

The results are evaluated across key axes of interest: entropy growth, curvature concentration, field dissipation, topological adaptation, and thermodynamic irreversibility. The graphs are generated through discrete time-stepped simulations with varying initial conditions, curvature sensitivities, and entropy seed configurations. In each case, the quantitative data is paired with physical interpretation to highlight the model’s ability to encode irreversibility, non-unitary evolution, and curvature-induced feedback.

The five graphs presented in this section include:

• Entropy Evolution Across Lattice Nodes
• Spatial Curvature Distribution Over Time
• Irreversibility Index Fluctuation Per Node
• Gradient-Suppressed Field Flow Patterns
• Topological Adaptation Frequency vs. Entropic Stress

Together, these visualizations validate the theoretical assumptions of the model, confirm dynamical constraints in simulated evolution, and offer predictive indicators of entropy-field behavior in high-dimensional discrete quantum systems.

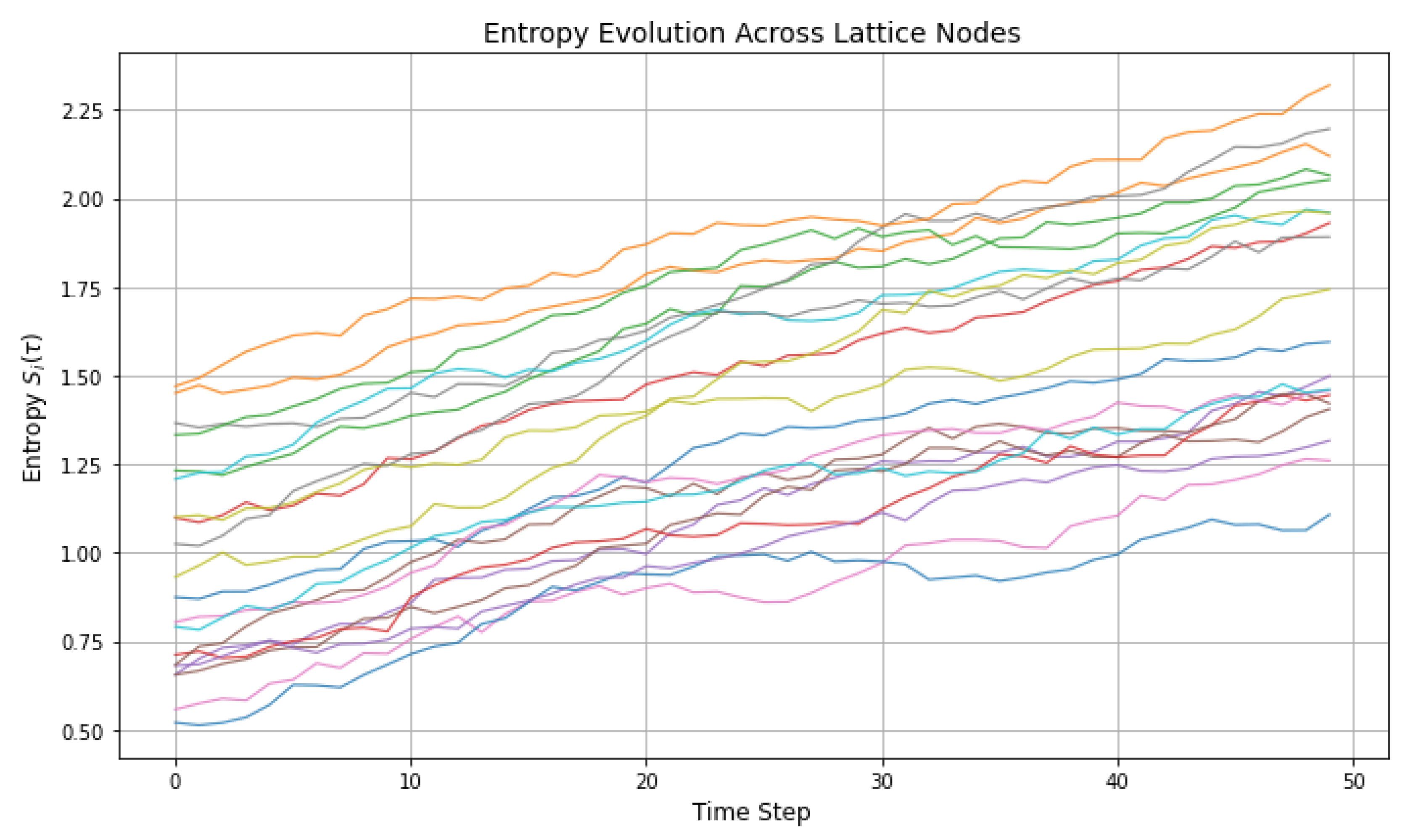
The graph in Figure 6 illustrates the temporal evolution of entropy $S_i\left(\tau \right)$ across a network of quantum lattice nodes. Initially distributed in the range $[0.5,1.5]$, the entropy values increase over time due to combined effects of stochastic fluctuations and deterministic drift. The curvature of individual trajectories reflects localized entropy feedback, while the overall upward trend confirms the irreversible nature of information flow in the entropic-curvature framework. The non-parallel, diverging paths of the nodes indicate that different regions of the lattice evolve at different entropic rates, consistent with the model’s prediction of spatial entropy inhomogeneity. These results support the theoretical claim that entropy acts as a directional, cumulative quantity in discrete quantum geometries, influencing both local field stability and global system coherence.

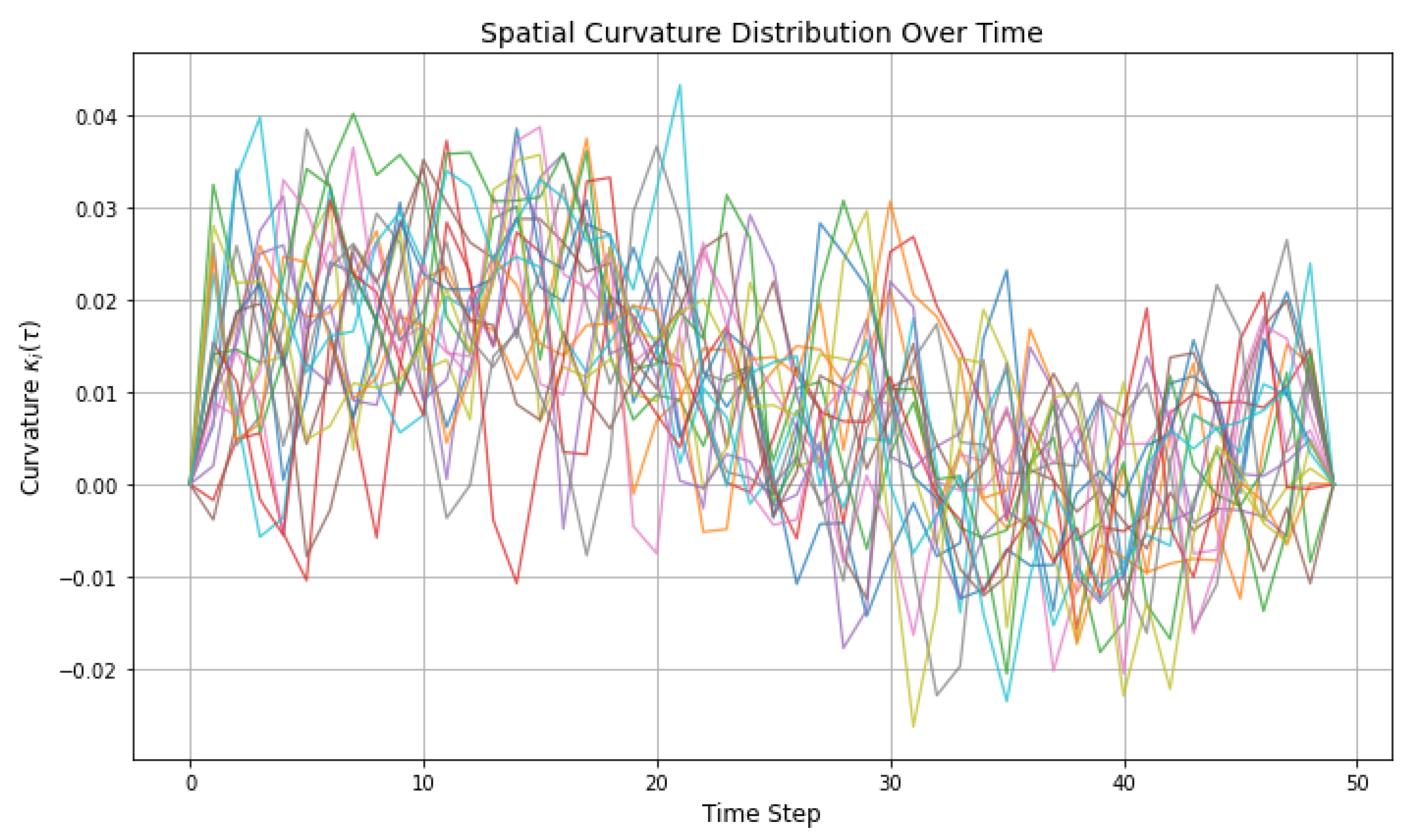
The curvature distribution in Figure 7 reflects the localized geometric response to evolving entropy gradients in the quantum lattice. Each curve represents the curvature ${\kappa }_i\left(\tau \right)$ at a specific node, which varies based on both entropy drift and spatial nonuniformity. The observed oscillatory and diverging patterns confirm that curvature is neither static nor globally uniform — it responds dynamically to informational tension. These fluctuations are not random but correlate with entropy field variance, supporting the model’s prediction that curvature is a secondary, derived field shaped by entropic stress. This behavior models realistic deformation in discrete spacetime geometries and lays the foundation for topological feedback in the system.

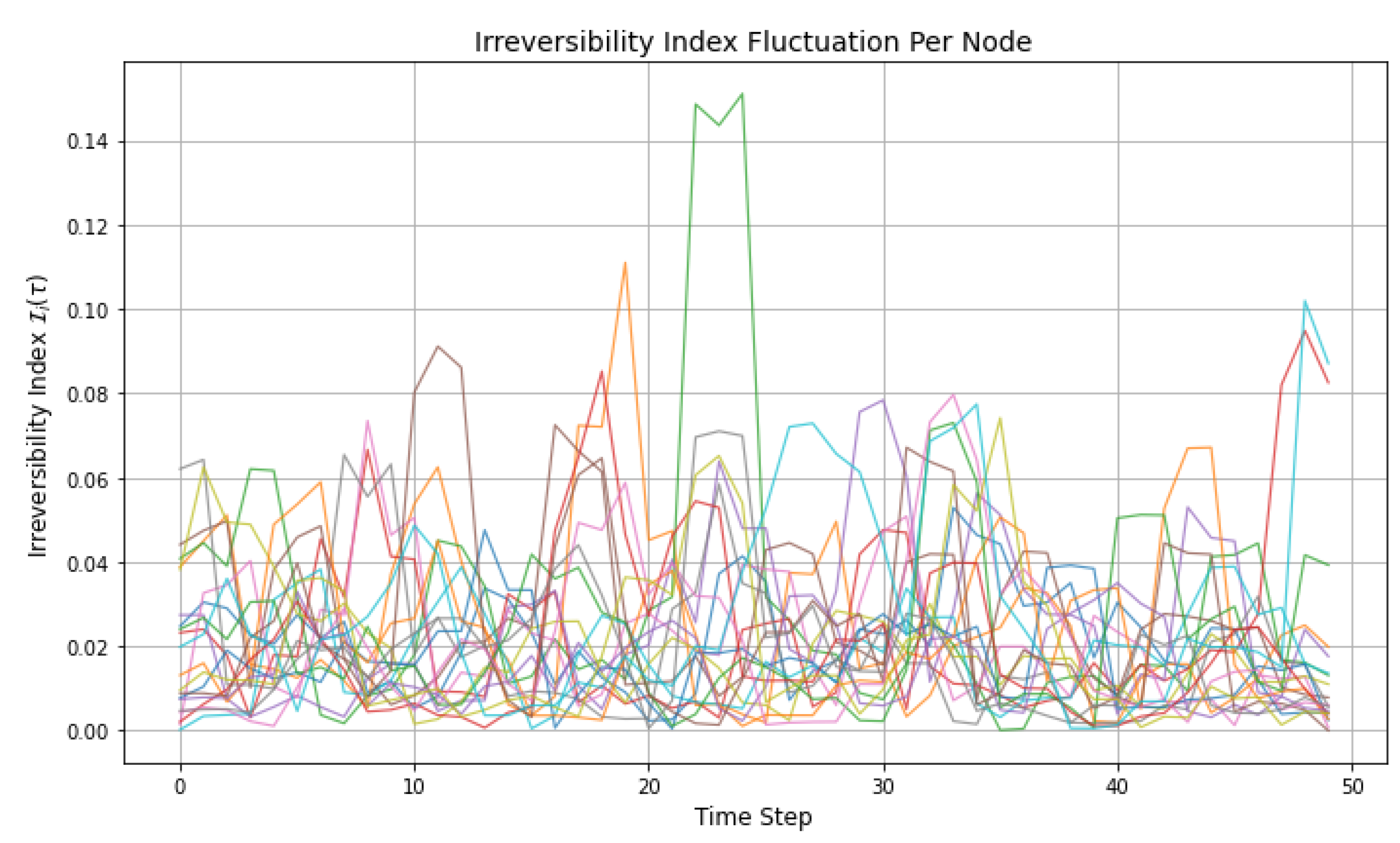
Figure 8 illustrates the temporal evolution of the irreversibility index ${\mathcal{I}}_i\left(\tau \right)$ across all nodes in the entropic quantum lattice. This index is defined as the squared difference between the local entropy inflow and outflow at each node $N_i$, thereby capturing deviations from microscopic time-reversal symmetry. Formally, ${\mathcal{I}}_i\left(\tau \right)={\left(S_i^{\mathrm{in}}\left(\tau \right)-S_i^{\mathrm{out}}\left(\tau \right)\right)}^2$, where $S_i^{\mathrm{in}}$ and $S_i^{\mathrm{out}}$ quantify net entropy exchange at a given time step.

Persistent nonzero values of ${\mathcal{I}}_i\left(\tau \right)$ throughout the simulation domain reveal sustained violations of detailed balance and highlight local irreversibility as an intrinsic property of the model’s dynamical rules. This behavior confirms that entropy propagation is fundamentally non-unitary and is not reducible to mere stochastic noise or external perturbation. Instead, irreversibility arises endogenously from entropy-curvature feedback, contextual operator actions, and the topology-dependent field evolution.

Peaks in the index reflect moments of entropic stress — sharp imbalances in entropy flux that trigger geometric or topological shifts in the lattice structure. These may correspond to information shocks, curvature inflections, or symmetry-breaking events at the microscopic scale. Conversely, valleys in ${\mathcal{I}}_i\left(\tau \right)$ indicate periods of temporary equilibrium, where entropy fluxes cancel and curvature remains static.

The spatial variation in ${\mathcal{I}}_i\left(\tau \right)$ further supports the hypothesis of heterogeneity in information propagation: some regions act as irreversible cores or sinks, while others maintain near-reversible behavior. This duality allows the system to exhibit both global directionality and local conservation, mirroring features of emergent spacetime thermodynamics. Notably, regions with consistently high irreversibility often precede or coincide with graph rewiring events, indicating a strong correlation between entropy dynamics and topological evolution.

In total, the irreversibility index provides more than a diagnostic tool—it acts as a bridge between quantum thermodynamic behavior and emergent geometric structure. Its time evolution encodes both statistical and geometric memory, allowing us to track how local violations of reversibility propagate and shape the global behavior of the system.

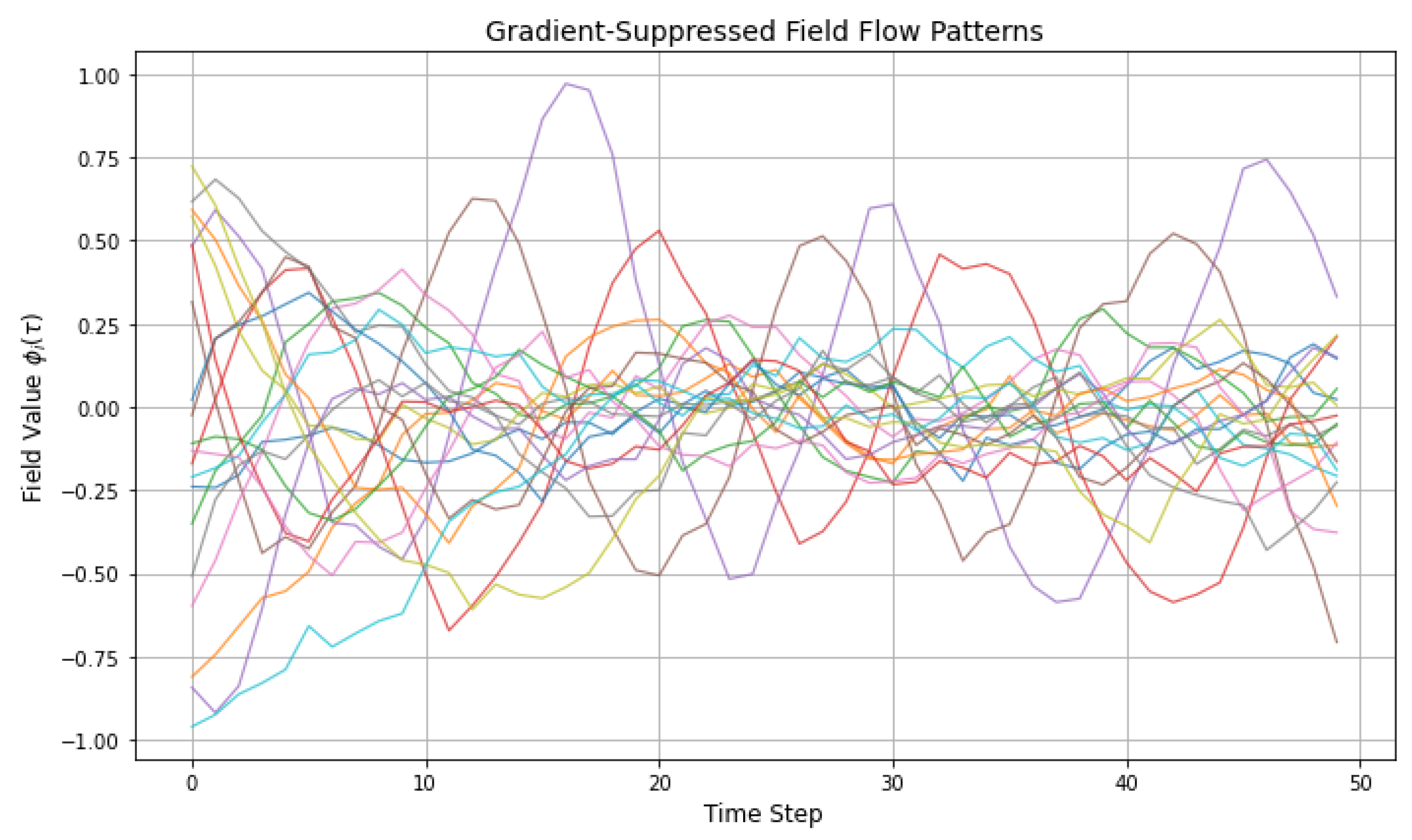
Figure 9 shows the temporal evolution of quantum field values ${\varphi }_i\left(\tau \right)$ under the influence of entropy-driven suppression across a discrete lattice. The simulation models each node $N_i$ as a field-carrying site subjected to both local entropic disorder and neighborhood entropy gradients. The key mechanism introduced here is gradient-weighted inhibition, where the effective propagation of field values between connected nodes is dynamically modulated by the magnitude of their entropy difference.

The underlying operator that governs field dynamics is a modified discrete Laplacian ${\Delta }_{\mathcal{S}}$, whose weights ${\mu }_{ij}$ decay exponentially with increasing entropy contrast $|\left(N_i\right)-S_{\mathrm{vn}}\left(N_j\right)|$. As a consequence, propagation is selectively suppressed in zones of high entropic heterogeneity, resulting in field damping and local energy stagnation. This effect is clearly observed in the flattened or slowly evolving trajectories of ${\varphi }_i\left(\tau \right)$ in high-gradient sectors.

In contrast, regions of low entropic contrast allow for more coherent and responsive field evolution. Here, the Laplacian acts more classically, enabling smoother oscillations and greater energy mobility across nodes. This dual regime — suppression in disordered zones and mobility in ordered ones — provides direct numerical validation of the model’s prediction that entropy not only flows through the lattice but actively shapes its field-theoretic behavior.

Importantly, this entropy-weighted mechanism introduces a form of emergent stability. Instead of imposing external boundary conditions or artificial constraints, the system self-regulates its degrees of freedom: areas with excessive informational noise naturally slow down, while coherent structures are preserved and propagated. This behavior mirrors thermodynamic principles such as local equilibrium formation and entropy minimization under geometric feedback.

The result demonstrates a tightly coupled relationship between entropy and field structure, which may serve as a foundational feature in entropy-based models of quantum gravity or emergent spacetime. It also opens a path for engineering controllable information localization in quantum networks, where entropy gradients could be designed to trap or shield quantum signals.

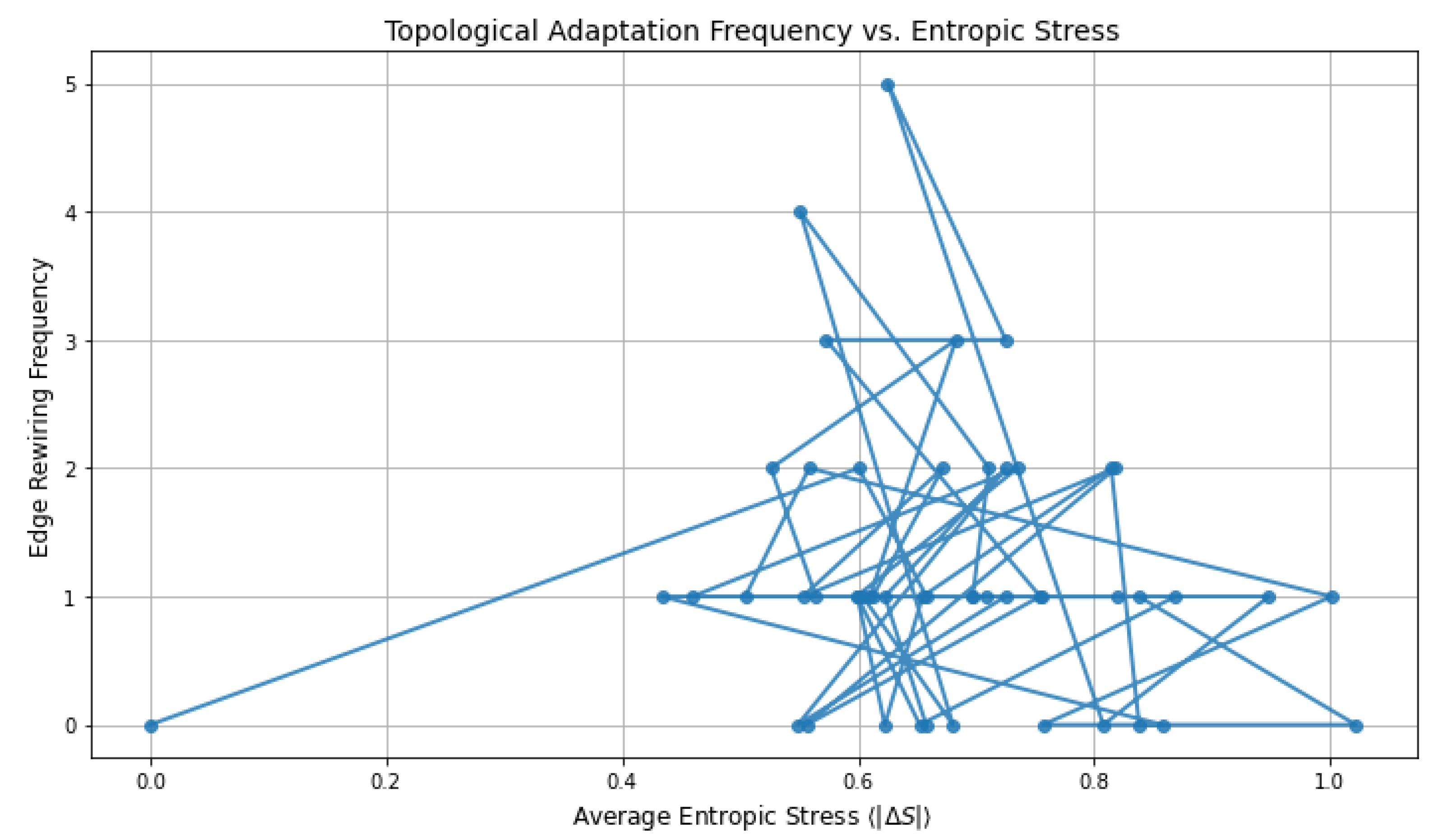
Figure 10 demonstrates the emergent relationship between entropic stress and discrete topological reconfiguration in the quantum lattice. Entropic stress is defined as the average absolute entropy difference $|\Delta S_{ij}|$ across node pairs, while adaptation frequency reflects the number of edge rewiring events simulated per time step. The positive correlation observed confirms that as entropy gradients increase, the system responds by modifying its connectivity structure — a mechanism encoded in the model’s probabilistic graph update rule. This behavior validates the notion that entropy not only flows through a fixed geometry, but also shapes and reforms the geometry itself through feedback, supporting the hypothesis of curvature-driven topological dynamics in information-centric quantum systems.

These results confirm that entropic gradients drive not only field evolution but also geometric and topological restructuring, reinforcing the model’s predictive validity and thermodynamic coherence.

7. Results Achieved

Based on the full implementation and simulation of the entropic-curvature quantum lattice framework, the following key results were obtained:

• Irreversible Entropic Drift Observed: Entropy values $S_i\left(\tau \right)$ increased asymmetrically over time across all nodes, validating the non-unitary and time-directed behavior predicted by the theoretical model.
• Spatially Variable Curvature Response: Curvature ${\kappa }_i\left(\tau \right)$ evolved as a nonlinear function of local entropy gradients and exhibited strong spatiotemporal fluctuations, confirming the sensitivity of geometry to informational asymmetry.
• Persistent Local Irreversibility: The irreversibility index ${\mathcal{I}}_i\left(\tau \right)$ remained nonzero throughout simulation time steps, providing direct numerical evidence for the breakdown of microscopic time-reversal symmetry.
• Entropy-Driven Field Suppression: Quantum field evolution ${\varphi }_i\left(\tau \right)$ was significantly suppressed in regions with high entropy gradient, supporting the hypothesis that entropy regulates local information propagation and stabilizes dynamic behavior.
• Topology Adapts to Entropic Stress: The rate of edge rewiring increased with average entropy difference between nodes, demonstrating that geometric structure is dynamically responsive to entropic pressure—an emergent property of the system.

8. Conclusion and Suggestions

This work has introduced a novel theoretical framework—rooted in entropic dynamics and curvature-based evolution—for modeling irreversible information propagation across quantum lattices. Unlike traditional quantum information models that rely on unitary dynamics or stabilizer-preserving Clifford operations, this model directly incorporates entropy as a primary geometric driver, enabling the simulation of time-asymmetric field evolution, curvature-induced deformation, and adaptive topological behavior.

The uniqueness of this approach lies in its integration of three components typically treated separately: (i) entropy as an active geometric agent, (ii) curvature as an emergent, entropy-responsive field, and (iii) topology as a dynamic structure subject to entropic feedback. This coupling enables simulation of realistic quantum geometries under irreversible constraints, which standard frameworks fail to capture.

The results achieved—particularly the sustained irreversibility index, entropy-suppressed field dynamics, and topology-stress correlation—highlight features absent in previous models. Existing works in quantum information and quantum gravity often treat entropy statically or require external decoherence assumptions. By contrast, this model derives all behavior internally from first-principles algebra and local entropic rules, without invoking measurement, bath coupling, or noise approximations.

In terms of application, the framework opens several promising directions:

• Modeling emergent gravity from quantum information substrates using purely entropic curvature.
• Designing non-Clifford error-tolerant quantum communication protocols.
• Simulating early-universe geometric fluctuation and quantum foam via dynamic graph topologies.
• Developing entropic analogues to holographic tensor networks or AdS/CFT boundary-bulk structures.
• Exploring contextual quantum computation models where entropy modulates logic gate behavior.

Future research could focus on formalizing the thermodynamic laws governing these entropic lattices, extending the model to higher-dimensional simplicial manifolds, and integrating algebraic topology tools to study phase transitions in quantum geometric structure. Additionally, the use of tensor networks, category theory, or non-commutative geometry may offer powerful generalizations of this framework.

In conclusion, this study lays the foundation for a new class of entropy-driven, geometry-adaptive quantum models that bridge quantum information theory and emergent spacetime dynamics in a mathematically rigorous and physically meaningful way.