A Condensed Overview of the Aethic Solution to the Measurement Problem

1. Introduction

To begin with, please note that this paper has been assembled as a condensed version of the intended Aethic reasoning paper [1], so that the reader might be able to engage with some of the major Aethic ideas without having to read the full 140 pages in detail. In case one becomes curious to some more of the surrounding philosophical and mathematical detail, then please do refer to the longer text accordingly. Let us now initiate the introduction of this paper.

The measurement problem–the question of how quantum superpositions resolve into single, observable outcomes–has been approached over the past several decades through a variety of frameworks, yet all fall short in key areas. The Copenhagen interpretation introduces wavefunction collapse as an unexplained axiom, relying on the Heisenberg cut to delineate classical and quantum behavior [2]. Such an approach, if applied elsewhere, would have spelled doom for any other theory–for instance, if Newton had simply shrugged and supposed that items above a certain height over the Earth magically stopped feeling gravitational attraction toward it, thereby neglecting the powerful inductive argument hiding in plain sight from the empiricism of a falling object on Earth. The many-worlds interpretation, meanwhile, while ostensibly avoiding collapse, lacks a well-defined ontological basis for phenomena like the Born rule, leaving a critical dead end in its explanatory power. Hidden-variable theories face significant challenges from Bell’s theorem [3], which fundamentally limits determinism in quantum mechanics. This result scrambles our intuitions on where rationalism ends and indeterminism begins–a titanic unknown that has arguably bled into our broader cultural movement of postmodernism itself. These challenges reveal deep conceptual gaps in our modeling of time, reality, and information–gaps that demand a fundamentally new approach spanning multiple layers of physics and philosophy.

To address these gaps, we propose a new framework called Aethic reasoning. At its heart, this paper presents Aethic reasoning as a graph-theoretic approach that culminates in a derivation of the collapse postulate, so the entire premise herein may be summarized as the pursuit of establishing such a statement, (which we refer to as the third postulate of the Aethus).

However, the fact of the matter is that the ability to even conceptualize this statement is dependent upon roughly three nodes of new mathematics and two or three nodes of new philosophy beyond which humanity has yet written down. As such, the barrier between our world here and now and a completed measurement problem solution is to be reconciled as contained only within these few nodes which need to be flipped. Naturally, then, we will spend the majority of this paper addressing and flipping these nodes, one by one. This can be viewed as effectively philosophical hygiene, analogously to how general relativity cannot be established until the equivalence principle replaces the notion of gravitational force. We will see much the same with the union principle of Aethic reasoning, being one of the philosophical nodes, for which we argue that humanity has accidentally left an inconsistency unchecked in the very semantic realization of logical conjunctions as encapsulated in the word ‘and’. This is a very subtle inconsistency that is hard to spot until it is pointed out, but once it is addressed it takes mere seconds to generalize the classical concept of ‘and’ versus ‘or’ to a well-defined superposition of states. The fact that this issue has not yet been weeded out serves as a direct instance of a barrier between modern science and a measurement problem solution, and this is only one of the five or so like it which this paper seeks to address. Effectively, then, the premise of this paper is not to invent new physics — at least not yet — but to merely put us in a position to do so by reformulating a series of axioms at the deepest layers of our preconceived epistemological and metaphysical understanding of the universe.

Note, however, that this paper also requires the creation of new math so as to couple to the advances made in philosophy. To summarize our mathematical nodes, they initiate with the restructuring of the block universe model into a Markov chain, being that very foundational step which unlocks the cascade of Aethic insights to follow–beginning with the establishment of a relativist principle toward the ability to structure such a temporal ontology in mathematical language. We achieve this structural definition of the Aethus using equivalence classes of sets, endowed with a specific condition regarding the instantiation of attributes. This allows us to capture all degrees of freedom in the Markov chain of block universes, effectively extending the classical notion of set membership—where an element either belongs to a set or doesn’t—into a richer trichotomy of presence within Aethae. Here, an element can exist in three states: it is present, its logical negation is present, or it is unknown altogether. This allows us to incorporate the Aethic union principle using a resultant ring structure revealed in the set of all Aethae.

We define the operations of traversing this ring of Aethae, being disjunctions as addition and conjunctions as multiplication. With this, we establish the needed structure to express the graph-theoretic major result of Aethic reasoning, the third postulate. Lastly, we create a well-defined rendering mechanism from an Aethus to a realized block universe, allowing us the degree of freedom needed to distinguish superpositions from contradictions within the Aethic structure itself, and from there we have a full theoretical derivation of the collapse postulate, in that Aethae which cannot possibly be physically realized, (namely being those in which a detector or observer is watching and yet an interference pattern still results from the double-slit experiment), are derived as such from the three Aethic postulates, aligning naturally with our observed physical reality.

Without further ado, then, let us begin our traversal through Aethic reasoning, a proposed solution to the quantum measurement problem.

2. The Extrusion Principle of Aethic Reasoning

2.1. The Aethic Model for the Ontology of Time

Let us set up Aethic reasoning by briefly elaborating on the methods by which we currently model the ontology of time. Simply put, there are models which consider a dynamic block universe, such as the growing block universe or presentist interpretations, and then there are models which consider a static block universe, being simply the `block universe’ interpretation itself. The introductory premise of Aethic reasoning is to observe that the distinction between these two classes of model actually serves as something of a false dichotomy. Specifically, our initial Aethic argument is to suppose that any sort of objectively accurate model must lie somewhere outside either choice of a dynamic block universe versus a static block universe, and the reasoning for this is simply an empirical one. To see this, consider how both the growing block universe and block universe interpretations clash with keystone empirical truths of modern physics, albeit in different areas. The growing block universe, for example, requires a well-defined boundary between the present and the future of the block universe, so as to even allow for the past and present to expand at all. This is something of an obvious circumstance of the model, but it turns out that even this assumption, through proof-by-contradiction, demonstrates that the model itself cannot be quite right. The contradiction, then, comes from its clashing with the notion of relativity of simultaneity, because for the boundary of the present to be well-defined implies that there is an objective present, which we know, of course, is an ontological construct due to the insights of special relativity.

The block universe model, then, (which we might refer to as simply the `static block universe model’ for ease of distinction with the growing block universe model), is somewhat more famously in conflict with empirical truths, specifically on account of its implication of a hidden-variables interpretation of quantum mechanics. That is, for there to be an objectively deterministic past, present, and future, as the model implies, is a violation of Bell’s theorem, which we know is to, in the very least, cast a significant amount of doubt onto hidden-variables interpretations in general. As such, so long as one does not subscribe to hidden-variables models on account of this empiricism, then we are forced to discount the static block universe model as well.

What this leaves us with, then, is something of a predicament regarding how we ought to actually understand the ontology of time. However, it is this exact setup which we will use to not only suggest the Aethic interpretation for the ontology of time, but perhaps even imply it on account of the falsehood of both existing models.

The Aethic interpretation for the ontology of time, simply put, is to suggest that there is not one single block universe at all, but rather a Markov chain of them, so as to hold the entire Markov chain structure as the full physical extent of the universe. This is a crucial development for a few major reasons. For one, now it gains us an additional degree of freedom to the ontology of time beyond what can be expressed in the physical space of a single block universe alone, and this is just what we need to move beyond the false dichotomy of the growing block universe versus static block universe models. Secondly, this model now allows us to separate the direct flow of time within a block universe from the progression along the Markov chain of block universes. And perhaps most importantly of all, it allows us to make the fundamental supposition that quantum wavefunction collapses themselves are fundamentally characterized by the switching to a new block universe along the Markov chain, rather than ever having to be localized to a single block universe on account of the progression of time. Shown in Figure 1 is an example representation of the block universe Markov chain structure, and in Figure 2 is a direct representation of how this added Aethic layer differs from the Copenhagen interpretation about a collapse.

This net supposition, now, is what we refer to as the Aethic extrusion principle.

Principle 1 

(Aethic Extrusion Principle). According to Aethic reasoning, the universe is fundamentally constructed of many block universes in a Markov chain, such that quantum superposition collapse events may only be triggered by the movement between two block universe states in this Markov chain. Resultantly, we hold that a single block universe, on account of holding no wavefunction collapse events within its direct contents, is indeed entirely unitarily time-reversible.

The primary goal of this interpretation, then, is to decouple the Einsteinian flow of time from the progression of wavefunction collapse, as doing this may be shown to solve a myriad of paradoxes throughout theoretical physics, most notably being the measurement problem. While elaborating fully on such is beyond the scope of this condensed paper, it is worth mentioning that the upcoming Aethic mathematical structure was actually derived prior to the extrusion principle, with the extrusion principle itself having served as the single adaptation to temporal ontology which enabled the Aethic structure to describe superpositions in a real-world setting. In effect, then, at its best we ought not to picture the extrusion principle as being arbitrary, but rather as operating in an exact conjunction with any idealistically perspectivist model of the universe which is also capable of describing superpositions. Such is why this principle is quite foundational to all further Aethic pursuits.

Note that we might refer to the Markov chain structure itself as the `Aethic dimension’, all while noting that it of course has a structure more akin to a Markov chain than anything directly isomorphic to the real number line.

We must remember, now, the premise of the Aethic argument regarding this principle: it is not only that it might be in effect, but rather that the universe necessarily behaves in at least a tangentially similar way to such a model. Such a result is a consequence of both the dynamic block universe and static block universe models combating fundamental empiricism, so through Einstein’s philosophical razor [4] alone we are compelled to argue for something on par with the extrusion principle of Aethic reasoning1.

Perhaps the beauty of this model can be summarized in its bringing together of the Bohrian and Einsteinian perspectives on the universe into one single picture. Bohr would approve of the extrusion principle on account of his views of the world, because all quantum empiricism is indeed contained and in the very least expressible with this model [6]. Einstein himself, then, would also probably not object to this model on account of the specifics of his own views of the universe [6], where the ontological hand-waiving of the Copenhagen interpretation is replaced with a well-defined view of the universe, which not to mention is deterministic down to the individual block universe on account of their each being unitarily transformable.

2.2. Why the Aethic Model Is Original

Let us quickly touch upon why the Aethic model of the ontology of time is not simply the many-worlds interpretation of quantum mechanics, and instead is a fully original idea.

The key difference here is that the many-worlds interpretation is fundamentally an extension of the growing block universe model, such that all deviations to possible outcomes are contained within the branching at the present, and therefore are external to the physical structure of the existing block itself. With the Aethic model, however, we have that there is no intrinsic dependence of the branching of the Aethic Markov chain upon the present moment of the block universe, and furthermore it follows that all possibilities are already encoded into the physical constituents of the immediately prior block universe in the form of superpositions, (as is consistent with its satisfaction of the Markov property anyway).

Let us illustrate this idea with a use of Schrödinger’s cat, being the thought experiment in which a cat in a box is either killed or spared depending on the random outcome of a quantum particle’s decay. We will use this thought experiment to paint the picture of our next point, but one might just as easily substitute a safer concept like quantum spin state into the following argument if Schrödinger’s cat seems to ontologically far-fetched. Now, let us paint the picture of why the Aethic interpretation of the wavefunction collapse is distinct from the many-worlds interpretation. Let us suppose that our agent in question–being the experimenter perhaps–has run the experiment at 2:00 PM, but only checks the state of the cat at 2:30. The Aethic premise, then, is the following: as is consistent with the extrusion principle of Aethic reasoning, our experimenter’s Aethic worldline must lead them into a new block universe at the instant at which they look in the box and observe the state of the cat. Given this supposition, then, let us now analyze the respective prior-block universe and subsequent-block universe of the experimenter.

In the prior-block universe alone, there is never to be a wavefunction collapse, so we are left with the strange result that the cat will never be able to leave superposition in that universe. Even at 2:30 in the prior-block universe, when the experimenter checks the box, they will have to find a cat in superposition, thereby putting themselves into superposition upon becoming entangled with the cat. This strange outcome, of course, is not what the experimenter themselves will observe, because such a happening may be regarded as that which kicks them into the next block universe along the Markov chain, such that they are never allowed to experience that outcome in first block universe directly. Rather than interpreting this as some nightmarish zombie-like scenario to unfold in the prior-block universe at 2:30, then, we might simply suppose that said block universe is merely an overlay of the two possible outcome block universes, such that in some sense the experimenter is still present there, but without being able to access the other block universe any longer. This may seem somewhat similar to the many-worlds interpretation so far, but the key point of deviation is our next Aethic result: once the experimenter reaches their subsequent-block universe at 2:30 sharp, it follows that the cat in that universe was never in superposition in the first place, so therefore the effects even at 2:00 PM change with respect to the experimenter’s perspective. This notion may very well represent the heart of the extrusion principle, in that it is a precise reinterpretation of the Copenhagen interpretation: that is, we have that in the subsequent-block universe, it is so that the past changes as well, such that tracing back in time within that block universe does not actually retrace the steps of the experimenter themselves, who has been in the other block universe in the prior moment. Specifically, the 2:00 PM of the subsequent-block universes holds that the cat had survived all along for the `living’ outcome block universe, and that the cat was dead all along for the `dead’ outcome block universe. In the Copenhagen interpretation, we have that reversing time would make the superposition un-collapse, but in the Aethic interpretation we have that this cannot be so, because in the subsequent-block universe we have that there had never been a superposition in the first place.

Principle 2 

(Indiscriminate Time Principle of Aethic Reasoning). In classical metaphysics, we hold that the future is represented by something of an unknown cloud of possibilities, such that it is the act of one’s progression through time which allows said cloud of possibilities to collapse into single happenings.

In Aethic reasoning, however, as per its major tenets, we instead hold that such a cloud is not restricted to the future at all, and instead is indiscriminately spread across the entire past and future of the universe. As such, the gaining of knowledge about a present event, a future event, or a past event are ontologically indistinguishable happenings with respect to the foundation of the Aethus. This is a crucially important insight of Aethic reasoning, and an important corollary to the principle of extrusion.

Now, to be clear on this point, there had indeed been a version of the experimenter in the subsequent block universe all along, so we might ask what becomes of them prior to the experimenter’s consciousness following the Markov chain to that universe at 2:30 sharp. The interpretation to this is quite simple: the experimenter of the prior-block universe in particular was essentially in superposition of occupying the consciousness of themselves in both subsequent-block universes at once. That is, we might go as far as to `define’ the experimenter at 2:00 in the prior-block universe as equating to the quantum superposition of themselves in each of the two possible subsequent-block universes for which the cat is alive or dead, respectively. Such is how we define the cat in the prior-block universe already, so by induction it follows that we might think the define the experimenter in a similar way. The key difference between the two, however, is that the experimenter has no way of proving or even knowing that they are occupying both versions of themselves at once at 2:00 PM, because, simply put, there are no discernible differences in their environment to tip them off. The cat, however, would obviously be well aware of being in superposition at 2:00 on account of one component of itself being dead, so we would suppose that even though the cat is in superposition relative to the consciousness of the experimenter in that block universe, their own consciousness cannot possibly be located there on account of the perceivable difference in available information to them between the two outcomes of the superposition. With this being something of an inductive argument at this point, let us raise it to the level of a full principle, for which the empiricism we have noted is simply the consequence.

Principle 3 

(Aethic Base Principle of Superpositions). In Aethic reasoning, we have that an agent’s consciousness will always occupy whatever block universe in the Aethic Markov chain maximizes the surrounding superposition content of their universe without alerting them to a discernible difference between any two particular states in superposition.

Another way of expressing this is that, where a block universe may be written as the superposition of some number of alternative block universes, in effect putting all differing states between them into quantum superposition, it then follows that an agent’s consciousness will occupy whichever block universe corresponds to the superposition of the set of all block universes which they could not possibly be alerted to the variation between in the moment.

Note that this principle will become the second postulate of the Aethus once we assign the right mathematical structure to it. Such will help us define it with a more mathematically objective grounding than merely a supposition of consciousness.

In conclusion for this argument, then, we have clearly shown that the Aethic interpretation of superpositions is distinct to the many-worlds interpretation, because the many-worlds interpretation holds a time-reversal interpretation which matches the Copenhagen interpretation, whereas the Aethic interpretation has a different perspective on this entirely, as emerges from its supposition that an entire block universe branches with the Aethic Markov chain, rather than only ever the future component of it. Let us now move to more epistemological arguments about this Aethic notion.

2.3. Aethic Reasoning as an Epistemological Assertion

What also follows from this logic is a clear principle of relativity, because we can clearly show that the experimenter and the cat do not both satisfy this principle in the the prior-block universe. As such, what we need is a mathematical object which effectively serves as the current fingerprint of sorts for an agent’s net content of information as plays a role in whichever block universe their consciousnesses sorts into at present. We will refer to this net scope of current information for an agent as their Aethus, which is of course the namesake for Aethic reasoning. What we have, then, is that an agent’s Aethus must be compatible with whatever block universe they currently exist in, so in short, that block universe which they exist in can be written as a function of their current Aethus. That is, no one Aethus is compatible with more than one block universe, because one of them will have to hold a higher unknown-superposition content than the other in order to remain distinct, and therefore will rank higher with the Aethic principle of superpositions. As such, the experimenter’s block universe can indeed be written as a function of their Aethus, because one Aethus will only ever map to one block universe.

A basic summary of Aethic knowledge is that it has to be more objective than purely subjective knowledge, because otherwise we fall into the reductio ad absurdum in which one’s subjective opinions count toward their block universe placement. Such a thing is effectively divinity, which is why we know it cannot be in place. Furthermore, we know trivially that Aethic knowledge is more subjective than objective information, simply because it is allowed to vary for two different agents. For it to be objective, then, would force a contradiction, so again by reductio ad absurdum we have that Aethic knowledge is not truly objective.

Regarding the relativism of Aethic knowledge, we can quickly derive such a thing using a simple application of the thought experiment of Wigner’s friend, which is a variation of the Schrödinger’s cat thought experiment in which the experimenter, Wigner, had his friend check the state of the cat five minutes before him [7]. Let us imagine a variation of the thought experiment in which Wigner and his friend sit across a table from one another, and the fate of Schrödinger’s cat is revealed from behind Wigner in the room so that only his friend can see it. This reveals something of an understandable objection to the extrusion principle, being the question of how Wigner and his friend can possibly be at different locations along the Aethic dimension if Wigner is staring right at his friend, and thereby confirming that they are sitting in the same room and therefore the same physical space. The counterargument from Aethic reasoning to this is rather straightforward: what truly do you mean by physical space in the first place? Is it really that Wigner and his friend are sitting in precisely the same physical space, or might we have missed any of the discriminating characteristics of a physical space when we thought only to define it with three dimensions of space and one dimension of time? That is, given how we are already playing around with the concept of physical reality having an Aethic component in addition to only the spatial components which one is referring by to when they say “physical space,” we might then suggest that characterizing a physical space only by its spatial profile is something of an oversimplification. After all, we see from Zeno’s paradox [8] that disregarding derivatives in a physical space leads to paradoxes, and we see from special relativity that disregarding time as a dimensional component of a physical space also leads to paradoxes. With it being, generally speaking, a reasonable claim to suppose that there are qualitative elements to a physical space beyond what we first assume is the exhaustive description, we might then ask if the same is true here. The idea, then, is that we might picture the Aethic dimension itself, although physical by some sense, as being primarily qualitative in any practical circumstances. This is indeed somewhat similar to how we already picture time, even though we know from Einstein that it also has a physical component. In the case of the Aethic dimension, then, perhaps we suppose that even as Wigner stares at his friend, his friend is then and there qualitatively infused with his own unique Aethus, whereas Wigner himself is infused with his own Aethus. Comprehension for concepts like these is admittedly underdeveloped in Western philosophy, but the East has been studying them for thousands of years. The closest English word for this kind of qualitative infusion of something is what we might refer to as “consciousness”, however we see that Aethic qualities cannot be justifiably regarded as representing consciousness specifically, (on account of their not fitting neatly into the Western notion of subjectivity). Truly what we are looking at is a new form of qualitative assessment altogether, (at least in the West), although one which is strictly correspondent to conceptual philosophy and empiricism of one’s tangible life. Regarding what one best ought to picture when engaging with this Aethic material, the recommended idea is that the very degrees of freedom which distinguishes the room as seen through Wigner’s eyes as compared with through his friend’s eyes are those degrees of freedom with which we attain that they are sitting at different spots along the Aethic dimension, even though they are indeed directly in one another’s physical company. There is indeed something of a dualist element behind this, but to keep these ideas scientifically respectable we might then cite how without making our exact series of assumptions so far, we would still be stuck with the static block universe versus growing block universe paradox2. As such, in some sense Einstein’s razor [4] compels us to see things this way.

What we have, then, is that in Aethic reasoning, two humans may very well be sitting in the same room, but nonetheless have subtly different realities between them3. For comparison, the postulate that any two humans in communication share exactly the same surrounding block universe becomes a luxury of the classical paradigm, because it allows us to express notions of realism in an objective sense, and without having to always cite the reality in which such a notion is true. That is, I might remark to a friend that “that three is tall!" and without explicitly saying it, we both immediately understand that I am really saying “that tree is tall with respect to our current possible world!" I never have to express that I am talking about our possible world, because we always default to assuming so anyway, and through such a thing the specificity of realism begins and ends with what is actually real rather than what is not real. Or perhaps more specifically, actually real things fall in our possible world, whereas not real things fall outside of it.

As we said, this is remarkably convenient for the purposes of conveying language, however that does not mean that it has to be accurate to the true way of things. We already have the tools within Aethic reasoning, relying only on the notions thus far traversed, to derive such a system as arbitrary. This is quite a simple line of deduction, actually: given how we have shown a the surrounding block universe of two agents in the same room may differ, it then follows that the fixed assumption that only a specific possible world is “the real one" quite truly goes out the window. As such, we can decide to mark an Aethus itself as the fundamental arbiter of what is or is not real, given that a possible world would have lost this title. But rather than simply assuming some kind of “one real" Aethus, we instead find it advantageous to the prospect of Aethic relativism that all Aethae are equally real–just with respect to themselves.

The supposition here, then, is that the very notion of defining something as “real" is and always has been a two-node system: “what is the object" against “what is the reality." In the classical paradigm, we get to fix the reality node, but in Aethic reasoning we cannot do this anymore. So it is the very act of placing the reality node onto an Aethus which reveals to us our fundamental insight: the realism of an object is dependent upon which Aethus we measure said realism with, and an Aethus is a fundamental ontological object. Therefore, realism itself is not a fixed property of an object, but is merely a statement of relation between it and a given Aethus.

First Postulate of the Aethus

Any attribution of realism is a statement of relation to a particular Aethus.

The consequences of the first postulate of the Aethus are expansive, but one immediate result to take note of is that there are no marginal probabilities in Aethic reasoning, because they assume an objective reality, which itself violates the first postulate of the Aethus. The reasoning for this is simply because reality is itself defined as relational under the first postulate, which effectively means that all valid statements of probability are going to have to be conditional in Aethic reasoning. Even a simple statement like this is naturally going to have a ripple effect into our understanding of reality, and such is the nature of the first postulate of the Aethus.

Such marks the completion of the introductory epistemological assertions of Aethic reasoning, being that there effectively exists a bijection between an Aethus and a given block universe along the Aethic Markov chain.

3. Analyzing Aethic Decoherent Superpositions

3.1. Motivating Decoherent Superpositions Through Inductive Reasoning

Now it is time to make the next general inductive claim of Aethic reasoning. So far, we have been able to express quantum superpositions through the Aethic block universe model, where both outcomes occur in the prior-block universe whereas only one occurs in each subsequent-block universe. The key next step we can make, now, is to suppose that a bout of inductive reasoning may be immediately drawn from this interpretation of the realization of happenings. That is, if quantum superpositions do indeed operate under this model, and macroscopic objects are composed of quantum objects, then by induction we can justifiably claim that macroscopic events themselves, through decomposition, are to be modeled as following that same pattern of realization that we saw for quantum objects with the extrusion principle, where a superposition maintains indefinitely in a prior-block universe, and never existed in the first place in a subsequent-block universe. For example, macroscopic crossroads like which team will win the next World Cup tournament would themselves be modeled by the extrusion principle. And, by the indiscriminate time principle of Aethic reasoning, we further would have that even a historical event, like the outcome of the American revolution, would have to be both relative to the Aethus of a given agent up until they directly learn about or are otherwise given the ability to deduce the outcome.

So we are already well aware that macroscopic phenomena trivially ought to obey the extrusion principle due to their quantum subcomponents doing so, but such a statement turns out to only be a red herring against this section’s actual fundamental inductive claim. That is, given how we have already taken the fundamental step of modeling macroscopic phenomena as distributing across block universes to no less an extent than quantum particles, we might then think to suggest that such macroscopic crossroads may not actually be ontologically decomposable into quantum coherent effects in the first place, but instead are to induce as an entirely original elemental form of superposition, being what we will now refer to as a `decoherent superposition’. This is a major inductive leap on two fronts, because it both infers that macroscopic properties follow the same guidelines of the extrusion principle, all while supposing that they do so without reliance on the induction from quantum coherence specifically. The major claim here, then, is that Occam’s razor actually supports this position for the flexibility it allows us in the expression of quantum decoherence through the Aethic mathematical structure. We will indeed discover that both of these steps turn out to be quite fruitful with regard to their heightening of our capacity to solve the measurement problem in the coming sections.

Regarding how we think to define a decoherent superposition, now, let us simply suppose that they place multiple states into an ontological superposition of all happening at once, all while disallowing their interference in the vein of quantum superpositions. In effect, it is a less complicated form of superposition, which begins and ends with a real-valued linear combination of states, all without including the extra layer of details which regards having to apply the Born rule to actually gather probabilities. Instead, we merely pull the real-valued coefficient already present on the state in question. In general, let us suppose that quantum superpositions and decoherent superpositions are instances of the wider class of Aethic superpositions, being whatever the exhaustive ontological generalization of a quantum superposition is to be.

Intriguingly, the mere supposition that decoherent superpositions ontologically exist avails to us a fundamental reinterpretation of the onset of quantum decoherence as opposed to what is suggested by the Copenhagen interpretation alone. To begin with, we immediately see that quantum states, while still unobserved, must be in an ontological Aethic superposition regardless of whether they are still coherent. We already know how quantum coherent superpositions operate, being simply a linear combination of two wavefunctions, themselves operating as linear combinations of linearly independent quantum eigenstates. Upon collapsing this wavefunction, now, we are already in possession of a subtly different interpretation: the Aethic supposition, now, is that rather than all eigenstates dissipating with the exception of a single one, we instead have that the eigenstates remain in superposition in full, but simply transfer from a coherent superposition that is a quantum wavefunction to instead a strictly decoherent superposition. It is there where they remain, then, until an Aethus physically observes one of the states, at which point said Aethus truly collapses the decoherent superposition into but one eigenstate. This Aethic interpretation can be seen to fundamentally sift out the Copenhagen measurement process into characteristic effects of strictly measurement versus observation. Measurement, see, triggers the transfer to a decoherent superposition, whereas observation physically collapses that decoherent superposition to a single state.

A quick additional important principle to grasp, now, is that decoherent superpositions will naturally be real-valued rather than complex-valued like their coherent superposition-analogues. Furthermore, it follows intuitively that the weights on the eigenstates in a decoherent superposition will simply be the square magnitude of their weights under the coherent superposition, as is the premise of the Born rule anyway.

Let us now move to gathering some of the ontological consequences of Aethic decoherent superpositions, specifically as relates to the extrusion principle again.

3.2. Stating the Aethic Union Principle

There is a very important property to be understood about how a possible outcome is realized in Aethic metaphysics as compared with classical metaphysics. In classical metaphysics we have that a possible outcome’s realization is put through an `or’ operation with the remaining states prior to the realization. For example, perhaps we suppose that it will be sunny tomorroworit will not be sunny tomorrow. In Aethic reasoning, however, on account of the extrusion principle, we now have a very different nature of outcome realization. In the prior-block universe to the agent realizing whether it will be sunny tomorrow, we naturally have that it will both be sunny and not be sunny in decoherent superposition, simply on account of the agent existing in superposition across both block universes at once. What this tells us, then, fundamentally speaking, is that even though the prior-block universe is logically a disjunction between the subsequent-block universes which correspond to the outcomes, semantically we would have to refer to it as `and’ still on account of both outcomes physically being in effect in that prior-block universe. This is something of a fascinating claim which turns out to be central to Aethic reasoning. The supposition, to state it in terms of Aethae this time, is that unions and intersections over Aethae hold an ontological distinction in that regard, but must nonetheless both align with the semantic definition of `and’ rather than the semantic definition of `or’, which itself then becomes a construct for its lack of correspondence to any ontologically real phenomenon. This turns out to be a crucially important result for the inductive consequences of Aethic reasoning, because it directly tells us that quantum superpositions do indeed align with a logical disjunction or union over an Aethus, even though they clearly correspond to multiple happenings at once, and as such a semantic `and’ over states. This supposition then is to merely become a special case of the wider identity of the Aethic union principle, being that both disjunctions and conjunctions over Aethae or block universes still all represent cases of what we mean semantically when we say `and’. Figure 3 is meant to help illustrate this.

Principle 4 

(Aethic Union Principle). Regarding real-world states, the semantic `and’ is in place for both Aethic unions and Aethic intersections. As such, a quantum superposition will correspond to an Aethic union, (or disjunction), even though it does not correspond to a semantic `or’ over the relevant states.

For an analogy, this principle is something like the equivalence principle in general relativity, because all it really does is highlight a philosophical misstep which we have been engaging in all along.

Put simply, the Aethic union principle tells us that we need to find a way to associate instances of real-world physical `and’ versus `or’ statements into the corresponding logical `and’ versus `or’ of Aethic reasoning. We first state that classically physical `and’s and `or’s need to both go to Aethic physical `and’s, since in either case Aethic retrieval will cause the states to physically share the same block universe, (being due to attribute conjunction for `and’s, and due to blanks becoming superpositions by the second postulate for `or’s). However, this being said, we have that all classical physical `or’s go to logical `or’s in Aethic reasoning, although `and’s are a bit more specific. That is, classical-world-involving classical physical `and’s are to go through to Aethic logical `and’s, but quantum-minded classical physical `and’s are actually to go through to logical `or’s instead, but are still characteristically different than that other batch of logical `or’s because this time they involve coherent (agreeing) superpositions rather than decoherent (disagreeing) superpositions. Note that Aethic logical `and’s are just Aethic intersections, whereas Aethic logical `or’s are Aethic unions.

Importantly, it follows from this principle that there is a needed extra degree of freedom behind the word `and’. That is, every time we say `and’ in the English language, (in reference to a physical state), we do not specify whether we are referring to an Aethic union or to an Aethic intersection, which are now both options. It now follows that quantum superpositions and quantum coherence fall under Aethic unions with decoherent superpositions, even though decoherent superpositions are always referred to with `or’. Aethic intersections, however, are aligned with what we mean by `and’ when we refer to direct conjunctions, as in that `the blue book and the red book are on the table’. For the blue book `or’ the red book to be on the table, semantically speaking, we now declare with the Aethic union principle would still be an ontological `and’ on account of the Aethic block universe model, even though it would be a decided Aethic union rather than an Aethic intersection.

Crucially, we cannot just redefine our semantic definition of `or’ to correspond to Aethic unions, because we have already established that quantum superpositions clearly correspond to an ontological `and’. As such, in order to induce from quantum superpositions being `and’, induce from Aethic decoherent superpositions being Aethic unions, and then satisfy the basic identification of macroscopic `or’ states under event unions and `and’ states under event intersections as seen throughout all probability theory, our only avenue which does not conflict with these requirements is that we ditch the semantic `or’ for an ontological construct, (relabeling them all as Aethic unions), rephrase everything in terms of current Aethic unions and intersections, and then come to terms with the profound conclusion that every use of the word `and’ up until this moment needs to be reassessed under this new partitioning system.

Very importantly, let us now consider the notion of applying iterations onto Aethic unions and intersections. Using the same notation of unions and intersections which we use for probabilistic events, consider an exercise in which we have n states, which we will mathematically denote with the Aethae $A_1$ through $A_n$. The simplest possible form of combining these in superposition might just be to apply an Aethic union to them, which we now know is to represent the Aethic generalization of a quantum superposition. Such an Aethic union, which we might refer to as $C_1$, is known in Aethic reasoning as the `agreeing superposition’ of $A_1$ through $A_n$.

$$C_1=\bigcup _i{A}_i$$

(1)

Now imagine that we instead create n new Aethae, being $B_1$ through $B_n$, such that they are defined as the following Aethic operation over these initial states.

$$B_i=A_i\cap \bigcap _{j\ne i}\neg A_j$$

(2)

Verbally speaking, this takes an Aethic intersection over all the initial states, but turns all of them off, (i.e. states that they are decidedly not realized), except for a single one, which we take as Aethically realized in that block universe. For each possible realized state, this compilation creates a corresponding $B_i$. Then, we take the Aethic union–not an Aethic intersection this time–over all the states of $B_1$ through $B_n$, which we call $C_2$, perhaps.

$$C_2=\bigcup _i{B}_i=\bigcup _i\left(A_i\cap \bigcap _{j\ne i}\neg A_j\right)$$

(3)

Such a doubly-iterated combination is what we refer to in Aethic reasoning as a `disagreeing superposition’ of $A_1$ through $A_n$. The highly important key, then, is that by the Aethic union principle, standard English will have referred to either of these as `and’, because it lacks the degrees of freedom to distinguish an Aethic union from an Aethic intersection. In effect, we need the Aethic union principle as it stands in Aethic reasoning to characterize states such as these, and of course we see with the infinite possible iterative structures of Aethic unions and intersections that there is now a vast degree of furthered Aethic specificity behind what we initially would have only called `and’. The key, now, is that quantum coherent superpositions will be assumed to be categorized under agreeing superpositions, whereas quantum decoherent superpositions will be categorized under disagreeing superpositions. We have just created the very iterative structure which we will need to derive the double-slit experiment from scratch, and thereby solve the measurement problem.

Another fundamental consequence of the Aethic union principle becomes that we may indeed rigorously distinguish contradictions from superpositions in Aethic reasoning. An `Aethic contradiction’ is what happens when we take the Aethic intersection of two disjoint Aethae, whereas an `Aethic superposition’ is what happens when we take take the Aethic union of two Aethae, disjoint or not. Importantly, this means that contradictions very much still exist in Aethic reasoning, just they follow from encoding conflicting states directly within the underlying Aethic mathematical structure. Aethic superpositions, on the other hand, are indirectly generated in a reality by withdrawing states from the Aethic underlying structure, as will essentially trace out the `backward Aethic progression’ from the typical knowledge-gain of adding states to an Aethus. Withdrawing states from an Aethus will cause them to occupy all possible values at once in the physical block universe which corresponds to that Aethus, with this fundamental interplay between superpositions and the lack of information amounting to the coming second postulate of the Aethus.

3.3. Statement of Centric Unfolding

Perhaps the next fascinating result from this, then, is that now the semantic `and’ becomes insufficient to distinguish unions versus intersections over Aethae, with our intuition for the gain and loss of information needing to fill that distinguishing role. Explicitly speaking, Aethic unions are characterized by the loss of information, whereas Aethic intersections are characterization by the gain of information. We can physically picture them as having a sort of direction in this way, with `forward’ on the Aethic Markov chain always corresponding to the direction of intersections, and `backward’ on the Aethic Markov chain corresponding to Aethic unions. Such an direction-oriented interpretation of the Aethic ontology is what we refer to as the principle of centric unfolding.

Principle of Centric Unfolding

Centric unfolding is what we will refer to as the default interpretation of Aethic reasoning, although we must note that it is only a convention. In this way, it might represent the current outer boundary of Aethic reasoning with regard to its ontological footprint, because while we know that it agrees with our current understanding of the empiricism, we nonetheless have to acknowledge that it operates on substantially shakier ground than something like an Aethic postulate, merely on account of being more a convention than an ontology. In much the same way what we did to classical conventions like the ontological `or’ with the Aethic union principle, a future generation of scientists may very well view this stepping stone as archaic, but at present it is the best supposition we are able to make given our current understanding of where Occam’s razor is to be best applied. This now being said, the convention of centric unfolding can be expressed as the assumption of the two following axioms. Every past Aethus which an agent inhabited is to serve as a parent Aethus to their current Aethus. Upon adding a new attribute to one’s Aethus, its state is drawn from its standing superposition at random. This assumption can be seen as a tool for our approaching the agent-based Aethic interpretation of reality, but through its relative empirical flimsiness can only ever be a hypothesis at present. Also please quickly note that for an agent to move across the Aethic dimension in a way which is consistent with these axioms can be referred to as said agent “centric unfolding." That way we are able to use the term both as a noun, (designating the principle), and a verb, (designating the act of doing it oneself).

Now let us move to describing the general mathematical structure of the Aethus.

4. Overview of the Aethic Mathematical Structure

4.1. Mathematical Structure of the Aethus

The primary motivation of the Aethic mathematical structure is the following goal: we want for the realized contents of reality to be correspondent not to the mathematical object of the Aethus itself, but instead to a well-defined mapping from an Aethus called an Aethic retrieval. In effect, we are to tailor both the structure of an Aethus and a retrieval toward successfully being able to depict Aethic superpositions as categorically distinct from logical contradictions, all while otherwise accurately depicting the existing Aethic philosophical suppositions about the universe. This means we should then be able to translate any physical system into whatever Aethus will have generated it upon an Aethic retrieval, although having the extra step of a retrieval in the intermediary between an Aethus and reality will be a crucial element toward giving us a higher order of flexibility beyond classical logic. Such will be the backbone of the Aethic approach to logic.

This being said, here is the base five-step hierarchy which we will use to construct a mathematical Aethus, which we refer to as the Aethic definitional hierarchy.

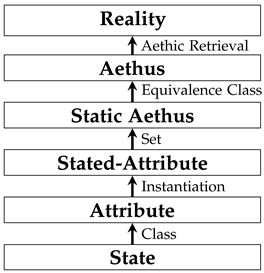
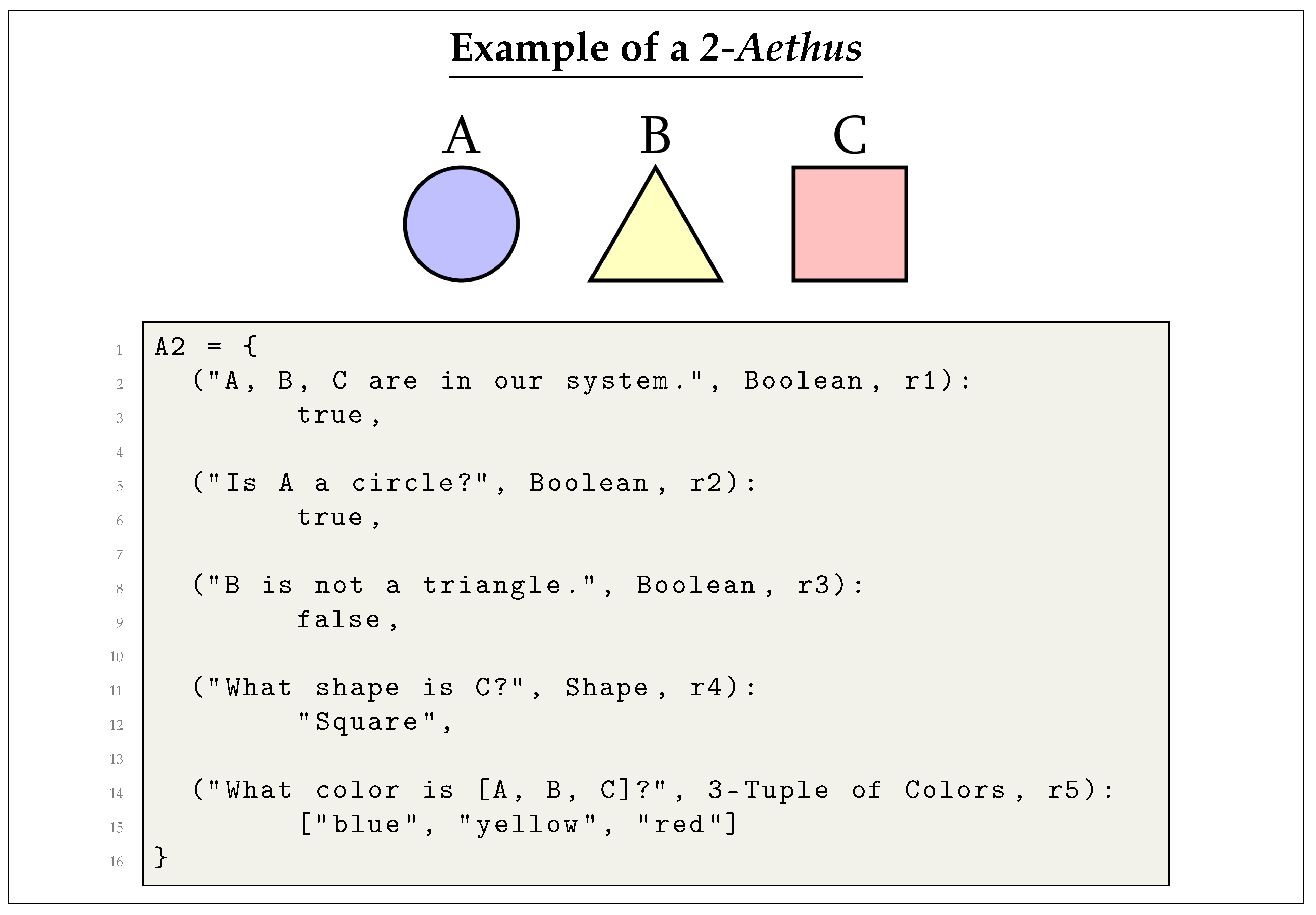
4.1.1. Iterative Construction of the Aethus

The iterative premise for constructing an Aethus takes inspiration, at least in naming, from the iterative categorization of n-spheres, being the generalization of the circle to each larger dimension. As is roughly analogous, we will do the same with the Aethus, in effect converging to the true structure of an Aethus, at $n=4$, with a series of inductive steps upon the index of n.

To begin with, let us define a 1-Aethus, which is better known as a stated-attribute in Aethic reasoning.

Definition 1 

(Definition of a 1-Aethus). A 1-Aethus is simply taken as equivalent to an Aethic stated-attribute so as to form its definition.

The supposition is that a stated-attribute, (Figure 5), serves as an ordered pair of an Aethic attribute, (Figure 4), and a particular Aethic state to that attribute. The primary motivation of this system, then, is that we might regard Aethic states not as lone objects, but instead as instantiations of sorts of broader Aethic attributes, with their always then being paired with the corresponding attribute within a particular 1-Aethus. The best analogy to draw between this Aethic system and standard object-oriented design is one in which the Aethic attribute serves as a class, and the Aethic stated-attribute serves as an instantiation, with its held state then serving as its effective value. However, we must note that an Aethic attribute is a more specific object than a class alone, simply because it holds a signifier in addition to a class structure. That is, unlike a class, which must be able to be exhaustively coded into a computer, it is the abstract component of an Aethic attribute through which it is implied to correspond to a real-world or at least mathematically-existent physical phenomenon. Specifically, we might suppose that the class of `normal distribution’ may be referenced and occupied by any normal distribution in the universe. An Aethic attribute corresponding to a normal distribution, however, strictly has to attach to a particular facet of the universe, such as `the normal distribution of human heights’. This is not to say that an Aethic attribute is an object rather than a class, but merely that it is essentially a class which is usable only on a non-general phenomenon to which is corresponds. In the human heights example, then, we might select a state which corresponds to the true normal distribution of human heights, and then build a stated-attribute which holds the attribute and that state in an ordered pair. Such could be a possible 1-Aethus which corresponds to that particular facet of the human population and the world.

Note, however, that even to define human heights reliably, we of course need some sort of unit of measurement, and this is where the third and final component of an Aethic attribute comes into play, being its relation set. The relation set, simply put, is the set of all alternate Aethic attributes which are in some way mutually dependent on the present Aethic attribute. For example, if we doubled the conventional physical length of the meter, then with the height attribute being described in terms of the meter, any stated-attributes of that attribute would now have to double in physical height as well. Alternatively, if we described the Aethic attribute for height with some more objective means than conventional units, then doubling the conventional length of the meter would not affect the Aethic attribute at all, but in the process would effect any additional attribute which is collectively defined in terms of both of them. Such nuances, then, would be encoded in the Aethic attribute’s relation set, although we typically only refer to it through inferences upon the verbal or logical description of the Aethic attribute rather than filling in the entire set exhaustively, as of course that would be a jarring task for its sheer size. The supposition, then, is that we are not attempting truly to gather a definitive mathematical definition for an Aethic attribute, but are instead merely alluding to the vast network of relational dependence between that Aethic attribute and any and all others. In a language, perhaps it is ideal for there to be a root axiomatic foundation to any verbal definition, but for an Aethic attribute this is not considered relevant, so long as the full web of all implicational relations is considered mathematically well-defined, regardless of whether one can feasibly construct it directly or not. Much like the semantic background to a word, then, the premise is a primarily abstract one.

A basic example of using Aethic stated-attributes can be seen in the following exercise: suppose we want to create a 1-Aethus to depict a certain physical property of a mineral. For example, suppose we wish to depict the Mohs hardness of topaz. In such a setting, the important realization is that Mohs hardness would be the Aethic attribute, and a Mohs hardness of eight itself would be the Aethic stated-attribute, with the integer eight itself being the Aethic state. Regarding an Aethus itself, now, the goal would be to layer not just a single stated-attribute which is correspondent to topaz, but instead the exhaustive set of Aethic attributes which could ever be said of it. In effect, we would want to create a mapping between Aethic attributes, and their corresponding states for topaz, with the graph of such a mapping then naturally being the set of stated-attributes for topaz. This sort of mapping itself is what we refer to as a 2-Aethus, with its graph being known as a static Aethus. Let us imagine, then, some sort of catalog which depicts all properties of topaz, being the Aethic attributes, and then all values of said properties, regardless of class, which would then be the Aethic states for those attributes within topaz. If we were to take this catalog, and then structure it as a mapping, and such a mapping itself, when considered as a function, would be a genuine 2-Aethus for topaz. In general, then, a function between a domain of Aethic attributes and an image of Aethic states is the form of a 2-Aethus.

Definition 2. 

(Definition of a 2-Aethus).A 2-Aethus is defined as a function between a domain of Aethic attributes and an image of corresponding instantiations of those attributes, (with an instantiation of an attribute being referred to as a `state’.) The three major conditions for a well-defined 2-Aethus is that the every item in the domain must map to only one item in the image, (being the definition of a function), that each attribute, φ, in the domain must map to a state of the correct class.

Given this definition, shown in Figure 6 is a visual example of a mathematical system, and the 2-Aethus which we might consider to describe it.

With this having been said, however, let us now also look to what a 3-Aethus would be. Simply put, a 3-Aethus is generated from a particular 2-Aethus by also including the exhaustive set of all properties which can be derived from the stated-attributes already consistent with that 2-Aethus. Technically speaking, a 3-Aethus is a 2-Aethus with the extra condition that every possible stated-attribute which can be derived from the stated-attributes in its graph must also then be present in its graph.

Definition 3. 

(Definition of a 3-Aethus). A 3-Aethus is defined as a 2-Aethus for which every possible stated-attribute which can be derived from the stated-attributes in its graph must also then be present in its graph.

In the longer Aethus paper, we will go into a more technical mathematical support for such an idea, but for this condensed paper it is sufficient to note this general procedure by its outcome. To give an intuitive example, if we create a 2-Aethus of only two stated-attributes, where the first says that topaz has a Mohs hardness which is double the value of x, and then we add a second which states that x is equal to four, then the supposition now is that such a function would indeed be a valid 2-Aethus, because it satisfies the base definition of a function, however it would not be a valid 3-Aethus, because it is not in direct possession of the immediate implied property that topaz has a Mohs hardness of eight. Naturally, such a conclusion can be gathered given the two premises already present in that 2-Aethus, so in order to elevate it to a true 3-Aethus, we would need to append these extra implied stated-attributes to its graph. Such a procedure is known as generating the 3-Aethus from the 2-Aethus in question. Note that in order to be well-defined, such a generated 3-Aethus must represent the 3-Aethus whose graph has the lowest possible cardinality which still serves as a superset to the 2-Aethus from which it was generated, otherwise we will inevitably add additional stated-attributes which are not implied by the 2-Aethus, in effect defeating the purpose of taking the correct generation in the first place.

The immediate observation which we might make about a 3-Aethus, now, is that it is somewhat unwieldily for its vast size. This, then, is why we need a 4-Aethus, which simply put, is taken as an equivalence class over all the 2-Aethae which generate the same 3-Aethus. This is a very important supposition of Aethic reasoning, which we might take to be analogous to how our society abstractly defines numbers. Consider, for instance, the following three digit representations.

$$10$$

(4)

$$010.0\dots$$

(5)

$$9.9999\dots$$

(6)

Of course, we imply intuitively that all three of these digit representations are in fact equivalent to the number ten. This can only be said about their equivalence relation regarding the abstract number which they represent, however of course we know that they are not equivalent merely as strings of digits, because at a glance we can conclude that said strings of digits fail the Leibnitz property of equality. That is, they are not the same string of digits. This is important, now, because it is the precise notion by which we will also characterize the difference between a static Aethus and a genuine Aethus. That is, in Aethic reasoning, the primary role of a static Aethus is to be treated under the Aethic equivalence relation rather than its own native set equivalence relation, in effect elevating it to merely a representation of a wider abstract Aethus. This is just what we do with digit representations when we treat them as representations of numbers, so the supposition is that we are to do the same with static Aethae and 2-Aethae unless otherwise specified.

We may define an Aethus as such, then, where we take an Aethus and a 4-Aethus to be two names for the same thing.

Definition 4 

(Definition of an Aethus). A 4-Aethus, otherwise known as an Aethus, is defined as an equivalence class of 2-Aethae and static Aethae under the Aethic equivalence relation, which itself regards two objects equal if and only if they generate the same 3-Aethus.

The most important way to regard whether two static Aethae are Aethically equivalent, then, is to check whether any given stated-attribute in one can be derived from the stated-attributes in the other. If this condition is satisfied, then they are deemed Aethically equivalent, as is an important theorem of Aethic reasoning.

Put into simpler terms, a static Aethus is a list of the properties describing part of a system, and an Aethus is an equivalence class of lists of properties which can be fully derived from one another. The use of mappings in the formal mathematical definition is meant to wring out any ambiguity, but the conceptual idea is quite the same.

Let us now move to supplying a quick representation of blank stated-attributes in an Aethus.

4.1.2. Incorporation of Invalid Aethae

Please note that we must also infer the existence of invalid Aethae in Aethic reasoning, which effectively comes about so as to ensure the resistance of Aethic reasoning to the argument which Plato used against Protagorean relativism. The argument goes that if truth is only ever measured up against the individual person, (as Protagoras argues), then for Plato himself to argue against the validity of Protagorean relativism implies that he must be right, and therefore that Protagorean relativism, by its own account, is false [9]. By the first postulate of the Aethus, then, where we take reality to only exist relative to an Aethus, we of course need resistance to this very argument. The Aethic solution, then, is that we must infer the existence of Aethae which are physically unrealizable, being what we call invalid Aethae. There is indeed some nuance to the particular avenue through which we define them, being the question of whether they are mathematically registered as false, or merely true in some abstract sense but nonetheless disallowed to be traversed to by and agent in the physical world. Regardless of this, however, we assert in Aethic reasoning that any Aethus which contradicts the validity of Aethic reasoning, either directly or indirectly, is to be an example of just such an invalid Aethus.

To state this explicitly, we can suppose that the direct epicenter of Aethic reasoning’s resistance to the Platonic argument against relativism is the state of existence of invalid Aethae. For an Aethus to be able to be objectively unrealizable, then, means we have a place to store all of the conflicts with abstract logic without being obliged to keep said Aethae valid. In effect, we have a fully relativist structure, (being the collection of all possible Aethae), which is endowed with a validity operation, (being perhaps not so much objectivist as relational itself, given that it is merely a function of an Aethus), and from such a thing we have construed direct resistance to the argument which befell Protagorean relativism.

Perhaps the most immediate example of an invalid Aethus is an Aethic contradiction itself, in which case an Aethus is produced from a static Aethus which holds the same attribute with two conflicting states. In general, however, the primary motivation of invalid Aethae are that we may state the second and third Aethic postulates in terms of them directly. That is, rather than writing that say the second postulate regards the truth of statement S, we can instead simply write that the second postulate asserts that $\neg S$ implies an invalid Aethus. By using invalid Aethae this way, we create a systematic means of defining the Aethic framework through the lens of acceptability.

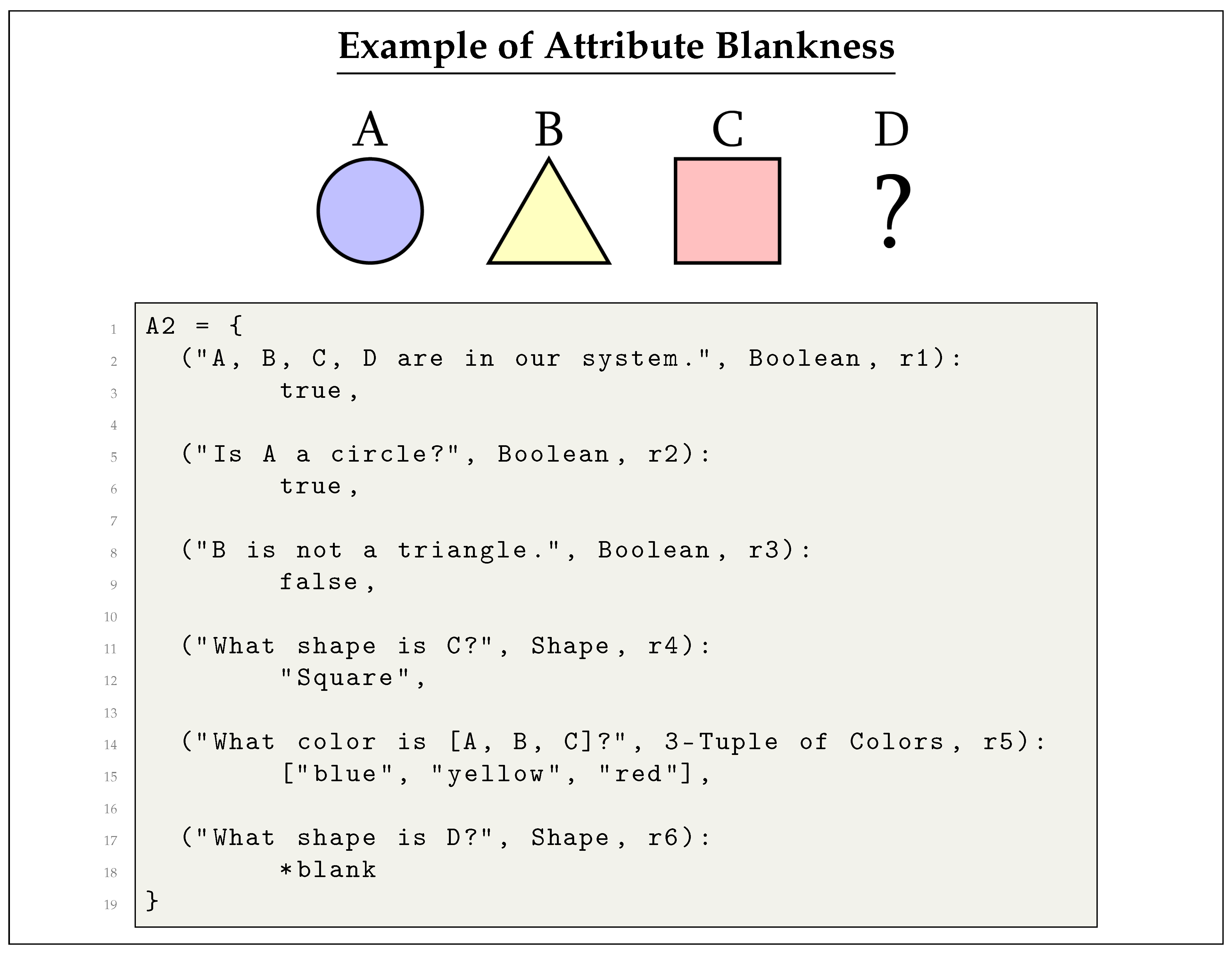
4.1.3. Regarding Blank Stated-Attributes in an Aethus

Let us consider all of the attributes which are not ultimately included within the domain of the 3-Aethus which corresponds to some particular Aethus. In Aethic reasoning, we refer to such attributes as blank relative to that Aethus, and so it serves as a useful mathematical extrapolation to construct a new Aethic state just for the purpose of encoding them. That is, we might suppose that for a 3-Aethus to not contain a particular attribute in its domain is Aethically equivalent to it instead holding that attribute in its domain, put then mapping it to a specially prescribed object which we might call the blank state. Perhaps we even regard the blank state as a single mathematical object, sort of like the null state in many computer languages, which may be used for expressing the lack of an attribute in an Aethus with the same mathematical framework with which we depict the presence of an attribute in an Aethus, all while tailoring that mathematical expression to accurately depict the workings of blank stated-attributes.

Shown in Figure 7 is an intuitive example of a 2-Aethus which incorporates blank stated-attributes.

Very importantly, note that a blank attribute in an Aethus is fundamentally a representation of the ontological state of unknowing. Allowing states to be encoded in an Aethus as blank is ultimately a very powerful aspect of Aethic reasoning, because it enables us both to characterize unknown attributes upfront, and then add them to a future Aethus without triggering contradiction, as it is a fundamental property of blank attributes that the blank state cannot Aethically contradict a state of the same attribute, with the state itself simply being defaulted to. In the above 2-Aethus example, then, we could very well append a new “What shape is C?" as blank, and an Aethic contradiction would not be drawn between that instance of the attribute and the one where it is cataloged as “Square".

Consider the following three major characterizations for an attribute’s presence within an Aethus. Note that it is slightly more nuanced than merely supposing that an attribute is either fully stated or fully blank in that Aethus, as we have to consider the edge cases for which some component attributes to it are stated while others are blank in the 3-Aethus in question. Such edge cases are referred to as mixed-decomposable attributes, otherwise known as semiblank attributes. Examples of all three such cases are shown in Figure 8.

Very importantly, we designate the following special names for the presence of attributes in an Aethus as based on this characterization.

• Stated: The attribute is state-decomposable in that Aethus. Importantly, this is also referred to as the attribute being present to the Aethus in question.
• Conceptually Blank: The attribute is blank-decomposable in that Aethus. Importantly, this is also referred to as the attribute being nonpresent to the Aethus in question.
• Semiblank: The attribute is neither state-decomposable nor blank-decomposable in that Aethus, which is what we refer to as mixed-decomposable. This is also referred to as the attribute being semipresent to the Aethus in question.
• Physically Blank: The attribute is either blank-decomposable or mixed-decomposable, (or alternatively either conceptually blank or semiblank). This is referred to as `physically blank’ on account of all such attributes being physically registered as the blank state in the corresponding 3-Aethus, regardless of whether they are genuinely conceptually blank or not. Conceptual blankness can then be regarded as the strongest special case of physical blankness.
• Impartially Blank: A useful term in more advanced Aethic reasoning, (namely with applications to the third postulate and fundamental theorem of Aethic reasoning), impartially blank attributes serve as a special case of physical blankness for which the Aethic intersection of any state of the attribute with the Aethus in question is not an abject invalidity.
  These are useful for generalizing the second postulate of the Aethus to more advanced iterations of superpositions beyond what conceptual blankness can imply directly, (with `generalizing’ meaning a shorthand convention rather than an axiomatic extension, note).
  Note that conceptual blankness is itself a special case of impartial blankness.

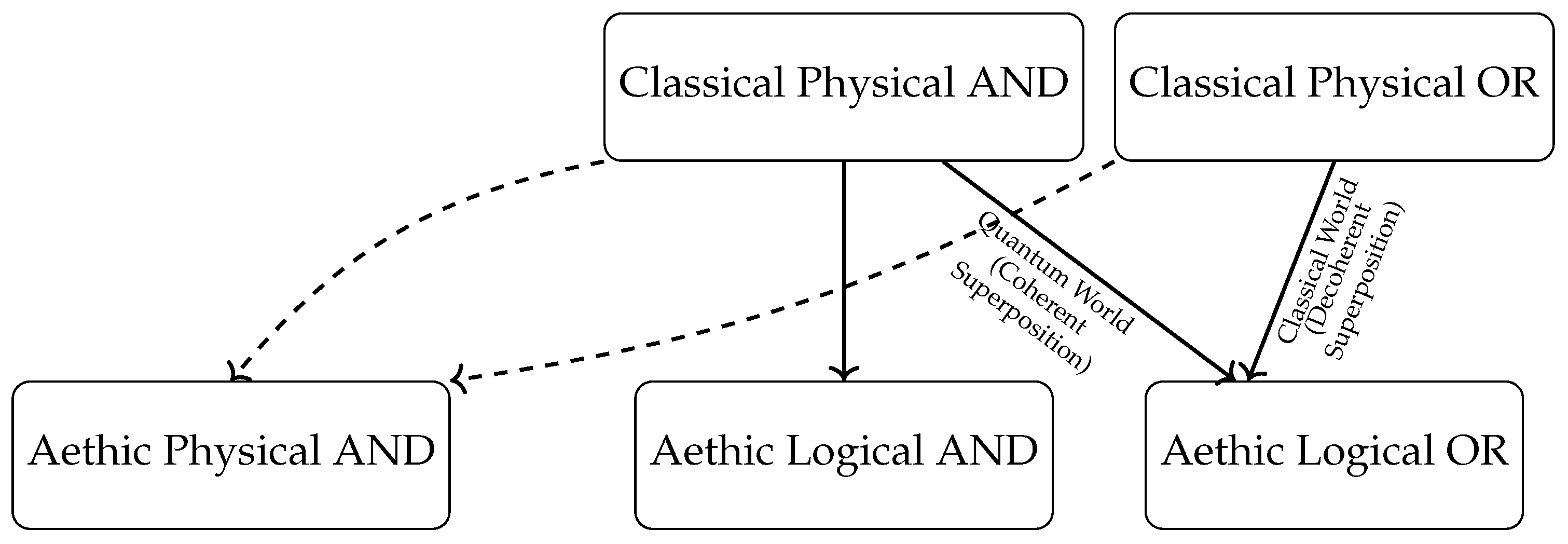
4.2. Direct Aethic Treatment of Superpositions

Explicitly speaking, one of the fundamental tenets of the Aethic mathematics is that we are to regard blank attributes in an Aethus as being precisely correspondent to realized Aethic superpositions. Such is the major benefit of using Aethic retrievals, because they now allow us to encode all Aethic logical manipulation within the Aethic structure itself, and then merely regain all realized consequences onto reality through however that underlying structure retrieves under the deterministic mapping that is an Aethic retrieval.

One useful example, to begin with, is the question of how we might encode the decoherent superposition that is Schrödinger’s cat within an Aethus. Shown with Figure 10 is the 2-Aethus from which we might draw the Aethus in question, as corresponds to an instance of Schrödinger’s cat from Figure 9.

In general, then, the premise is that any superposition which we see in a reality is precisely correspondent to a blank under that superposition’s attribute within the corresponding Aethus. This gives us a fundamentally important postulate of Aethic reasoning, for which a realized superposition and a blank attribute are two sides of the same coin. Let us now write such a postulate, being the second postulate of the Aethus.

Second Postulate of the Aethus

If an Aethus is valid, then any given attribute will be in Aethic superposition relative to it if and only if it is nonpresent to it.

The heart of this postulate, perhaps, comes from its assertion of a reliable framework by which any unknown Aethic attribute can be rendered equivalent to a realized superposition, which effectively serves as a kind of abstract generalization of the underlying quantum phenomenon for which unknown and unknowable quantum states correspond to quantum superpositions.

Highly importantly, considering how the second postulate of the Aethus only directly applies to blank-decomposable attributes, please note that we have a further notion called the Aethic dichotomy theorem for the purpose of handling Aethic superpositions in mixed-decomposable attributes. As may be derived with a proof by contradiction for consistency with the second postulate of the Aethus, the Aethic dichotomy theorem simply states that given a mixed-decomposable attribute in an Aethus, we define its retrieval by putting its blank-decomposable component into Aethic superposition, all while leaving its state-decomposable component at its single prescribed state. This is perhaps the core premise behind the procedural power of the second postulate of the Aethus, because such solidifies the fundamental interplay between the removal of attributes from an Aethus and the resultant gain to its respective superposition content upon retrieval. While we do not have the time in this paper for too many examples, consider the earlier notion with the mixed-decomposable normal distribution as a reference guide for how this principle works in practice. From a purely mathematical standpoint, (regardless of consideration of philosophical implications, which of course is naturally going to be stronger), the underlying structural motivation is that with Aethic retrievals being set up the way they are, we get the intriguing identity that unioning two Aethae effectively gives the union of their respective retrieval possibilities to a given attribute.

4.3. Aethic Tree Operations

Let us briefly consider the mathematical rendition of Aethic unions and intersections. Given how we have defined both already so as to align with the respective unions and intersections of probabilistic events, we now have to make note of a slight notational inconvenience, being that Aethic unions and intersections actually swap with respect to how they operate over the actual 3-Aethae over the Aethae which they correspond. That is, in order to have an Aethic union correspond to the tangible event union, it actually has to serve as a set intersection over the graphs of the corresponding 3-Aethae of the relevant Aethae, whereas an Aethic intersection has to serve as a set union over those graphs. This is a bit unfortunate for its trickiness of convention, however we might argue that it is far superior to the alternative, in which we would have to define Aethic unions and intersections in terms of the set-terminology, and thereby make the ontology less accessible. As such, so long as one gets over the initial hump of remembering to relate Aethic unions and intersections with the retrievals instead of the 3-Aethae themselves, and then it hopefully becomes quite intuitive.

Let us now take a moment to identify the fundamental graph structure of the set of all Aethae, which we might refer to as the Aethic tree. There are essentially three main pieces of relational terminology to take note of.

Definition 5 

(Child Aethus). A child Aethus is the product of adding an additional attribute to a given Aethus. Formally speaking, the Aethus C will be a child Aethus to A if and only if there exists some Aethus B for which $C=A\cap B$. We denote a child Aethus using the `subset’ operation, being $C\subseteq A$. Note that all Aethae are their own child Aethae, as can be taken by intersecting with an Aethus of all blanks.

Definition 6 

(Parent Aethus). A parent Aethus is taken as the inverse of a child Aethus, such that it is produced by removing an attribute instead of adding one. Formally speaking, the Aethus C will be a child Aethus to A if and only if there exists some Aethus B for which $C=A\cup B$. We denote a parent Aethus using the `superset’ operation, being $C\supseteq A$. Note that all Aethae are their own parent Aethae, as can be taken by unioning with themselves.

Definition 7 

(Proper Child Aethus). A proper child Aethus is a stronger form of child Aethus, which may only be produced by adding an attribute to an Aethus which is physically blank in it already. In effect, we have that C will be a proper child Aethus of A if and only if it can be written as $A\cap B$ for which the Aethus B is a stated-attribute to an attribute which is physically blank in A.

Lastly for the basics of the Aethic tree, let us define a term for an Aethus which is entirely blank, as corresponds to an empty static Aethus. Let us refer to such an Aethus as the Null Aethus, with it therefore following that it serves as a parent Aethus to all possible Aethae.

Definition 8 

(The Null Aethus). The Aethus which is the parent to all possible Aethae on an Aethic tree is known as the `Null Aethus’ of that Aethic tree.

4.4. Incorporation of Weighted Aethae

One last highly important notion to notice for the underlying Aethic mathematics, is that we might imaging extending the present set of all Aethae so as to also be considerate of intermediate cases between the rather abrupt addition of Aethic attributes as it stands. This is effectively analogous to the postulate of inferring the existence of general real numbers in-between the integers themselves, thereby extending a discrete set to a continuous one.

The way in which we may do this is rather simple. To begin with, consider the Aethic intersection operation as it stands, such as may be taken between the Aethae $A_1$ through $A_n$.

$$B=A_1\cap A_2\cap \dots \cap A_n$$

(7)

It will now be a fundamental axiom of the Aethic field structure that Aethic unions actually correspond to the addition operation, whereas Aethic intersections correspond to the multiplication over Aethae. Without getting too far into the details of this for this condensed paper, let us now rewrite such an iterated intersection accordingly.

$$B=A_1+A_2+\dots +A_n$$

(8)

The fundamental supposition of weighted Aethae, now, is the following: with Aethic unions now already being known to correspond to sums of Aethae, we may think to then extend Aethic unions so as to also incorporate linear combinations of Aethae in general. As we know, linear combinations are merely sums for which the weights need not only be one, so such a thing yields to us the following.

$$B={\alpha }_1{A}_1+{\alpha }_2{A}_2+\dots +{\alpha }_n{A}_n$$

(9)

This is so for some real-valued coefficients ${\alpha }_1$ through ${\alpha }_n$. Note, intriguingly, that for particular Aethus $A_i$, the operation ${\alpha }_i{A}_i$ effectively continuously interpolates $A_i$ toward nonexistence when it is zero, (akin to an invalid Aethus), and then of course being $A_i$ itself when ${\alpha }_i$ is one. This form of interpolation is fundamentally new in comparison to the allowed operations of unweighted Aethae, with its power being the ability to only add a proportion of an attribute to an Aethus instead of having to fully add it or fully leave it as blank. An important consequence of this, then, is that if we wish to put the Aethus $A_1$ through $A_n$ in an Aethic superposition, then a linear combination of them is one such avenue of doing this, due to it being the extension of the base Aethic union anyway. This is a fascinating result of weighted Aethae, being that both Aethic unions and linear combinations of Aethae, (with weights between zero and one exclusive), are fundamentally representations of Aethic superpositions. Note that the reasoning for this is because B is technically a parent Aethus of all of $A_1$ through $A_n$ in the given example, because there is always some $K_i$ which can be added to B so as to yield an Aethus which is Aethically equivalent to $A_i$. In the case of where $A_1$ through $A_n$ are disjoint, (meaning the Aethic intersection of any two of them is an invalid Aethus), we have that such a $K_i$ follow from $K_i=\left(1-{\alpha }_i\right)A_i$. Note that we know there is always such a $K_i$ as a direct consequence of the Aethic partition theorem, which states that for a set of child Aethae to a valid Aethus A to Aethic union together into A itself, it then follows that the Aethic union of the valid Aethae in that set only is also Aethically equivalent to A. The proof of this theorem is beyond the scope of this paper, but the general idea is that it then implies that if a given weighted Aethus is by $\alpha$ proportion valid, and by $1-\alpha$ proportion invalid, then it merely defaults to its valid component immediately with regards to realization, as is effectively a form of normalization.

In general, for a weighted Aethus $\alpha A$ where $\alpha$ is a real number and A is an unweighted Aethus, we refer to $\alpha$ as the `norm’ of said Aethus, and we refer to A as the `unit Aethus’ of said Aethus. Intriguingly enough, note how a fully invalid Aethus, (i.e. constructed by directly intersecting two disjoint Aethae whose union is the Null Aethus), has no single unit Aethus, as is the Aethic extension of the divide-by-zero error.

The last major immediate tenet of weighted Aethae is that they offer a direct ontological definition of probability, as a kind of Aethic extension of the Bayesian definition of probability. Simply put, consider the following.

Definition 9 

(Definition of Probability in Aethic Reasoning). Let us consider expressing the weighted Aethus B as a linear combination of the Aethae A and $A^{\prime }$, such that $A\cap A^{\prime }$ is either invalid, or otherwise Aethically equivalent to A, (meaning simply that $A^{\prime }$ is itself composed of a blank component and a disjoint component with respect to A). This then yields the following.

$$B=\alpha A+\left(1-\alpha \right)A^{\prime }$$

(10)

In such a case, then, we define α as the `weight of A in B’, and intriguingly, we may simply then define the probability of A with respect to B as being equivalent to such a weight. This then allows us to generalize the application of probability itself to all Aethic extensions, even when straying into the regime of superpositions.

$$\mathrm{P}\left(A\mid B\right)=\alpha \mid B=\alpha A+\left(1-\alpha \right)A^{\prime }$$

(11)

Note that with this rendition of the Aethic structure, we can indeed characterize the set of all Aethae as holding a commutative ring structure, such that Aethic unions take the form of addition, and Aethic intersections of multiplication.

5. Derivation of the Third Postulate of the Aethus

5.1. Setting up the Derivation

We are going to derive the third postulate using a rendition of the double-slit experiment. To summarize this experiment, we are to fire electrons, one by one, toward a plate with two slits, such that each electron which makes it through the slits is allowed to fall upon a back screen behind the experiment itself, leaving a mark to signify where it landed. We will then observe, given this setup, that the pattern of electrons will form a banded interference pattern, which is somewhat puzzling from a macroscopic perspective, where a single item is not allowed to interfere with itself in such a wavelike way. An especially unanticipated property of the experiment is that closing one of the slits while leaving the other open tends to, at least roughly, revert to a single concentrated bright spot behind the open slit, which then demonstrates that the feat of having both slits open at once implies some form of ability for the electron to pass through or at least attain information from both slits at once. This, of course, we know to be a very different outcome than anything in our macroscopic sphere of reality.

However, the most confusing aspect of the experiment is what happens if we place a detector over one of the slits, perhaps for the goal of identifying which slit the electrons went through for sure. The moment the detector is placed and the experiment commences, we see that the pattern on the back screen changes. Now it is no longer an interference pattern, but instead is a pattern of two bright spots, one behind each slit, as is more analogous to the particle manifestation of electrons. The paradox itself, then, is to ask by what process or mechanism does this change come about? Solving this will be a primary goal of Aethic reasoning in the coming section.

The most important initial step toward achieving such a thing will be to explicitly depict these two experimental outcomes with the mathematical structure of the Aethus. To begin with, consider the four possible cases for what slit will be traversed by the photon such that each is assigned a corresponding Aethus, as illustrated with  Figure 11.

The key, now, is to structure both empirical outcomes, (being an interference pattern versus a two-clusters pattern), using these four Aethae which we have just devised. We might then argue that the way to do this is the following representation by Figure 12.

Notice how we may take the Aethic superposition of entire Aethae, just as we may take it over Aethic attributes. By the Aethic union principle, we have than an Aethic superposition is one in the same with an Aethic union, so we denote such superpositions with unions accordingly. This yields to us Aethus P for the particle-like pattern, and Aethus Q for the wavelike pattern. An important assertion which we have made here is that the the wavelike pattern is specifically brought about by Case 4, whereas the particle-like pattern is brought about by Case 2 and Case 3 in Aethic superposition. Note that it is easy to prove that Case 2 and Case 3 in Aethic superposition will yield the particle-like pattern, simply because such a union of disjoint Aethae will effectively overlay the individual intensity patterns generated by Case 2 and Case 3 alone. The Aethae are clearly disjoint, because their Aethic intersection is an Aethic contradiction, and we know that each of them is individually correspondent to one slit being open and the other closed. Therefore, when we compile them both, we add the individual probability density functions, so as to generate Aethus P as the outcome.

Regarding why Case 4 must imply Aethus Q, then, is simply a statement of induction, because we know that Aethus Q still needs to be represented, and Case 4 still needs to be associated with an empirical outcome. We know that the Aethic union of Case 2 and Case 3 is not itself equal to Case 4 simply because Case 2 and Case 3 unioned together represent a disagreeing superposition of the slit of traversal, whereas Case 4 represents a purely agreeing superposition. The distinction between these two forms of superposition is a fundamentally important consequence of the Aethic union principle. Given this, then, we may justifiably induce that Case 4 goes together with the interference pattern of Aethus Q, simply because, as stated, we know Case 4 is already not equal to Case 2 union Case 3, and we know that Case 2 union Case 3 must correspond to Aethus P. Therefore, inductively speaking we know with certainty that Case 4 must correspond to Aethus Q due to its being the only remaining option, (i.e. an interference pattern corresponds to an agreeing superposition of electrons), with this prospect thereby being logically equivalent to the state of accuracy of Aethic reasoning itself.

Importantly, now, we need to directly derive two major things. Firstly, that the mere presence of the detector versus not results in the realization of Aethus P versus Aethus Q, respectively, and secondly the mechanism by which an agreeing superposition of the slit of traversal amounts to an interference pattern in the first place. The first of these two goals will be addressed by the direct statement of the third Aethic postulate, however the second will be left for its own paper, as it is a bit more intensive in geometry and calculus, and thereby is perhaps beyond the logically-minded scope of the present paper. Such a followup paper will deal with what we call active reasoning, being the extension of Aethic methods to a geometric setting. For the meantime, however, we will regard the establishment of the third Aethic postulate as sufficient for a theoretical derivation of the collapse postulate, with the supplementary wavefunction results being left for the followup paper.

To make this procedure a bit more clear, we have named three major steps needed to attain the full derivation of the quantum empiricism.

• Step Z

  –

  The step by which Aethic blanks are configured into superpositions, which is handled by the second Aethic postulate.

  –

  The statement of the nuances of the Aethic union principle is perhaps also part of this step.

• Step Y

  –

  The step by which we perform a direct theoretical mapping between the state of the detector and one of Aethus P or Aethus Q, which is to be handled by the third Aethic postulate.

• Step X

  –

  The step by which the wavelike physical properties of matter are expressed in Aethic terms, specifically in the face of positional agreeing superpositions. This is to be handled by active reasoning in a followup paper.

The last major derivation of this paper, then, will be to attain Step Y. To begin this, we need one more epistemic principle: when considering whether our Aethus is to map to Aethus P or Aethus Q as depending on the presence of detectors versus not, respectively, we might consider depicting the distinguishment using invalid Aethae rather than any other means. That is, consider the following statement.

$$``\mathrm{When}\mathrm{the}\mathrm{detector}\mathrm{is}\mathrm{running},\mathit{Aethus}\mathit{P}\mathrm{will}\mathrm{occur}."$$

(12)

This is an empirically true statement, of course, but we might consider phrasing it in a more advantageous form.

$$``\mathrm{It}\mathrm{is}\mathrm{an}\mathrm{invalid}\mathrm{Aethus}\mathrm{for}\mathit{Aethus}\mathit{Q}\mathrm{to}\mathrm{occur}\mathrm{when}\mathrm{the}\mathrm{detector}\mathrm{is}\mathrm{running}."$$

(13)

What we have done here is simply rewrite the original statement in disjunctive normal form, so as to isolate where the invalid Aethus is given to occur, at least to the degree of logical equivalence with the empiricism. This takes advantage of the following logical identity.

$$a\to b\iff \neg \left(a\wedge \neg b\right)$$

(14)

In this case, a would be the state of the detector running, b would be the case of Aethus P occurring, and $\neg b$ would be the case of Aethus Q occurring instead.

This statement, then, is an empirical postulate, so our goal will be to translate it into a generally applicable postulate within the mathematical structure of the Aethus. Such will be our third postulate, and such will be our proposed solution to Step Y.

5.2. The Aethic Soccer Field Thought Experiment

Let us analyze what we may call the Aethic soccer field thought experiment. Simply put, this is a premise built to counter the supposition of epistemic antirealism in quantum mechanics by supposing that whatever is the cause of quantum decoherence, it ought to induce to the macroscopic scale as well through some consistent underlying Aethic phenomenon.

Consider the prospect of attempting to apply the double-slit experiment to the macroscopic world, so as to highlight any resulting properties of interest from a purely tangible perspective. That is, whatever phenomenon brings about decoherence on the quantum level should, by the same underlying principles, bring it about on the macroscopic scale if Occam’s razor is to hold. So, instead of performing the double-slit experiment with electrons and two slits, let us perform the experiment with humans and two doors. If we can isolate exactly where the decoherence Aethically occurs, especially within the context of applicability to just such a thought experiment as this, and we will have found the root of the third postulate.

As such, let us imagine a soccer field which has been set up with a two-doored walled across its midline, and then a numbered wall on the far side of the field, as corresponds to the slits and back screen, respectively. Naturally, we know ahead of time what is to result from this experiment–most assuredly not an interference pattern, as that would violate the macroscopic axiom of the Heisenberg cut [2]–but this serves as only more reason to attempt to isolate the root of such a phenomenon. As such, we commence the experiment. For some quick context, we might suppose that the organizer of the experiment is a college freshman4 who wants to see the outcome, and the involved participants are their friends from around campus. Suppose we refer to the organizing freshman in question as Oliver.

Given this, then, Oliver is to be sitting, blindfolded, on the bleachers, so that he is guaranteed to not be aware of the outcome of the experiment as it unfolds. At the end he will remove his blindfold, but for now he can only wait in his excitement to see the results. As for the friends themselves, they are to each be texted two numbers, the first being either Door 1 or Door 2 to traverse, and the second being a random angle to leave that door at, so as to walk to the back wall accordingly. With this setup being complete, Oliver gives the signal, and the experiment commences.

As each participant walks through a door, Oliver, of course, has no awareness of which one they will have picked. His Aethus will therefore register the door of traversal attribute for each participant as blank, however we know from the empiricism that this is to project to a disagreeing type superposition instead of an agreeing one, specifically due to the added influence of the third postulate, wherever it might say in particular. As discussed earlier, our goal at present can be isolated to the following: we ought to find a theoretical derivation for the empirical axiom of that for Oliver to see an interference pattern of his friends amounts to an invalid Aethus. To put it another way, the major benefit of using this thought experiment as our source for such a task is that we have one less degree of freedom to juggle, because the macroscopic axiom of being above the Heisenberg cut stands in for the detector-based dichotomy of decoherence versus coherence. Now all we have to do is explicitly derive the invalidity of Oliver’s Aethus using the tools intuitively expressible to his setting, and that should be sufficient to gather the entire postulate due to generality. To be clear on these matters, we are imagining the Aethus in which Oliver removes the blindfold and sees the interference pattern of his friends, and will suppose that this is called an Oliver’s Aethus by convention. The procedure, then, is to gather a well-defined mechanism within the Aethus structure which will best produce such a property of invalidity to Oliver’s Aethus.

Our first attempt at the underlying mechanism might be a basic proof by contradiction of why such an initial scenario should be impossible. This is quite simple actually–all he needs to do is walk over to one of his friends, and ask five simple words.

$$``\mathrm{Which}\mathrm{door}\mathrm{did}\mathrm{you}\mathrm{get}?"$$

(15)

The friend, naturally, will reply with one of the two doors, being either Door 1 or Door 2, and in that simple sentiment, Oliver will have added to his Aethus that said friend must have gone through a single door, and accordingly must be of the single-slit or particle manifestation, not the wavelike manifestation as the interference pattern demonstrates. As such, because the interference pattern implies that both doors were traversed in superposition, and because the friend’s response5 implies that they went through only one door, an Aethic contradiction is clearly reached, and the corresponding Aethus must be invalid.

The more nuanced element to this, however, is that truly the contradiction only directly occurs in the later Aethus. This means that while such a proof by contradiction is valid there, the principle of extrusion demands that the contradiction itself cannot directly backtrack to the older Aethus, as we might do in classical proofs by contradiction with only one universal Aethus. What we need, then, is an expression for why the past Aethus somehow “knows" what will happen in the future Aethus, all while staying true to the well-defined principles we have accumulated thus far in Aethic reasoning. This means that any kind of timelike expression for the cause of this should be out of the question, because that would combat the extrusion principle. Somehow we need to manifest this odd occurrence using only the Aethic structure as our tool.

So far we have gathered a very important insight from the future Aethus in which Oliver speaks to the friend: it only takes one question to trigger a direct Aethic contradiction. We know, then, that Oliver decidedly has the ability to generate an Aethic contradiction given the scenario where the interference pattern has occurred with his friends, but this leaves for us a pressing question. Does it make a difference that only some possible futures involve an Aethic contradiction in this scenario, or is that already enough to imply that the whole scenario is an invalid Aethus? To answer this, let us begin our formal derivation.

5.3. The Derivation

We ought to start the procedure of derivation with an important corollary of the definition of invalid Aethus. Let us phrase this as follows.

Corollary 

(Corollary of Aethic Invalid Inheritance). Every child of an invalid Aethus must also be invalid.

The derivation of this is somewhat straightforward in both the structural and centric unfolding respects. Structurally speaking, whatever Aethus of stated-attributes are present in the parent invalid Aethus must also be passed to the child invalid Aethus, so for said stated-attributes to trigger an invalid Aethus in one case should also apply to any other case. Also, regarding centric unfolding, we have that valid Aethae have to be reachable from their parent Aethae, but invalid Aethae must not. So in the case of three generations of Aethae, for the second generational Aethus to be invalid now “blocks" off the ability of reaching the third generation, and thereby implies that it must be invalid as well. Given this corollary, then, we can immediately identify a conflict with the principle of “there exists" invalid child Aethae.

Consider a proposed statement of the third postulate which regards a there exists representation.

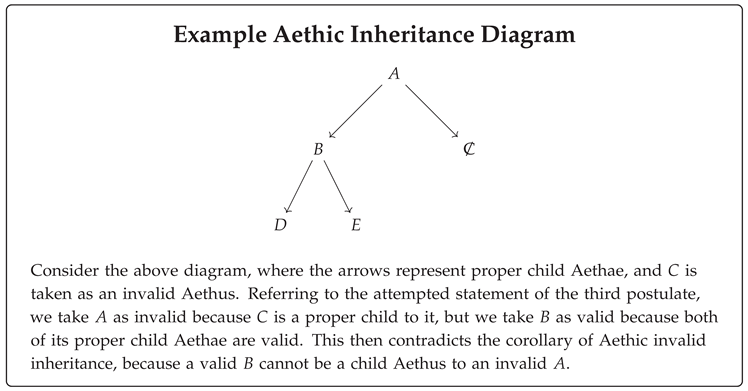
Third Postulate Attempt 1 “An Aethus will be invalid if it has any invalid proper child Aethae."

$$\exists B\subset A,\neg \mathbf{V}\left[B\right]\Rightarrow \neg \mathbf{V}\left[A\right]$$ (16)

Notice that we used the term “proper child Aethae" here, because trivially speaking, any Aethus will have an invalid child Aethus, if only we generate one by intersecting it with a disjoint Aethus. As such, this statement is only compelling at all if we consider proper child Aethae, which are now compatible with a more centric unfolding style of Aethic inheritance. Even so, however, we may still write up a proof by contradiction of a different sense for why this fails as a possible third postulate statement.

Given this failure, let us also consider the opposite form of the statement, being a for all statement rather than a there exists statement.

Third Postulate Attempt 2 “An Aethus will be invalid if all of its proper child Aethae are invalid."

$$\forall B\subset A,\neg \mathbf{V}\left[B\right]\Rightarrow \neg \mathbf{V}\left[A\right]$$ (17)

This statement, now, is a poor attempt at the third postulate for an entirely different reason: it is technically always true, but is overly specific, to the point of not describing most empirical cases of invalidity. If we consider Oliver’s Aethus again, say as some Aethus A, then notice how this statement is insufficient to derive it as an empirically invalid Aethus. To see this, consider how all of the proper child Aethae to Oliver’s Aethus can be sorted into two categories.

• Category 1 (Aethic contradiction)

  –

  The proper child Aethus is a direct Aethic contradiction, on account of Oliver having attained the Aethic information of which door was traversed by one or more participants.

• Category 2 (Other)

  –

  The proper child Aethus is not yet an Aethic contradiction, however a future Aethic contradiction is still very much on the table, due to Oliver still having the chance to gain the door of traversal information.

  –

  Crucially, notice how every one of these Aethae is itself an Oliver’s Aethus, because it satisfies all the same original criteria which we used to define an Oliver’s Aethus, being the sight of an interference pattern coupled with the ability to attain each door of traversal information.

  We can write such a statement in the form of a mathematical statement, being that every proper child Aethus of an Oliver’s Aethus is an Aethic contradiction or another Oliver’s Aethus.

  $$\mathbf{O}\left[A\right]\Rightarrow \forall B\subset A,\mathbf{C}\left[B\right]\vee \mathbf{O}\left[B\right]$$

  (18)

  We can make such an or statement either a disjunction or exclusive disjunction depending on if we want to include the Aethic contradiction cases as Oliver’s Aethae themselves, but the distinction is only important to the point of convention.

  –

  Notice, however, that even though these extra cases are highly relevant from the empirical lens, they end up becoming circular logic if we suppose the correctness of our second attempt at the statement of the third postulate.

  To see this in effect, consider our attempt to prove the Oliver’s Aethus of A as invalid through the use of this second attempt at the statement of the third postulate. To do this, we would both need to rely on the contradiction proper child Aethae and the other cases in order to satisfy the condition all all proper child Aethae being invalid. The issue with this, however, is that we would then need to demonstrate these other cases as invalid themselves, but given that they themselves are Oliver’s Aethae, we would then be stuck in the same recursive pattern of relying on their own non-contradictory cases for invalidity. The problem, then, is that this recursive pattern would never have a base case, so all invalidity for an Oliver’s Aethus would be indeterminate. As such, we might think to refine this second attempt at third postulate of the Aethus to rely on Aethic contradictions directly rather than further invalid Aethae.

Third Postulate Attempt 3 “An Aethus will be invalid if all of its proper child Aethae are Aethic contradictions."

$$\forall B\subset A,\mathbf{C}\left[B\right]\Rightarrow \neg \mathbf{V}\left[A\right]$$ (19)

This statement is less misleading than the previous attempt, perhaps, but it is still far from being quite sufficient. The reason is simply that, well, we still have leftover non-directly-contradictory proper child Aethae to an Oliver’s Aethus. The tricky thing about such Aethae is that they are indeed not directly Aethic contradictions by themselves, even though they have an empirically discernible semblance of invalidity about them. As stated before, then, we see that this attempt at the third postulate is indeed a true statement to the cases in which it applies, but its scope of application is far too specific to account for all instances of an Oliver’s Aethus. In effect, where the there exists argument of attempt one is perhaps too mathematically “weak" a statement, the for all arguments of attempt two and three are too “strong" to be applicable. We might specifically think to use terms such as weak versus strong because it simply follows that whatever the true reason is for why Oliver’s Aethus is invalid, (being the third postulate itself), it follows that its occurrence in Oliver’s Aethus will indeed imply that Oliver’s Aethus has some invalid proper child Aethae, (thus making the there exists argument comparatively weaker), and at the same time we have that all special cases of it in which the for all case holds will imply it as still being in effect. What this tells us, then, is that for all proper child Aethae to be contradictions implies an application of the third postulate toward invalidity, and also that for the third postulate to be in effect toward implying invalidity also implies that there exists an Aethic contradiction amongst the improper child Aethae. So while this case is intermediate regarding implications, it does not correctly align with either extreme.

This issue is, naturally, something of a paradox, however the solution to it is already hiding in plain sight, if only we think to look for it. Let us first explain what this solution is in intuitive language, and then move to express it with but a single algebraic substitution of the equations we have already written.

Let us take a moment to consider the workings of Oliver’s Aethus from a merely procedural stance. If we refer to the diagram once more where the Aethus A has two proper child Aethae, B and C, such that B is valid but C is invalid, then we see accordingly that the centric unfolding of an agent at Aethus A may only ever develop them to Aethus B, but never Aethus C. As such, in an intuitive way, we have that it might as well be part of their Aethus already that C will never be a future possibility for them, because it is indeed an invalid Aethus. Considering how Aethic information is fundamentally derivational in scope, we can assess that this is as legitimate a form of derivation as any. That is, we might naturally consider it to be an attribute of any Aethus anyway that all invalid child Aethae are not to be centric unfolded to. The key, then, is that for the Aethus A to already contain the attributes which forbid the eventuality of C, it follows that, bluntly, A must be capable of attaining such attributes. A keen analogy at this stage is the concept of check in the game chess.

Specifically, we might suppose that for some Aethus, each proper child Aethus to it represents a kind of `chess move’. When even a single proper child Aethus to some Aethus is invalid, then, this means that said Aethus would be in what is analogous to `check’ on account of a possible next move being fatal. In the case at hand, we have that the Aethus A has a proper child Aethus of C, so therefore A would then be in `check’ as per the analogy. This is a risk, yes, however it does not represent a true loss of the game. As a player at chess might simply move their king out of check in the next move, an agent’s Aethus might centric unfold them to B so as to remove the possibility of C. Now the check is gone, and the game may continue. This being said then, we have to ask ourselves the essential question, being what happens when we can no longer move out of check with any possible move? In chess, of course, such a thing is called `checkmate’, and it signifies the loss of the game. In Aethic reasoning, we can declare that such a thing implies an invalid Aethus, with such a declaration being none other than the third postulate itself.

So, if check in Aethic reasoning is the possibility of contradiction, on account of Oliver’s Aethus centric unfolding to an Aethus in which the door of traversal is attained, then checkmate would be the impossibility of avoiding the possibility of contradiction. Given that this, in being checkmate, must be absolutely implied invalid, we then get the following full sentiment. It shouldn’t be impossible to make a contradiction impossible. This is the very assertion of the third postulate of the Aethus, but of course it would be beneficial to write it in terms of a mathematical formalism.

Consider two statements which we have thus far shown to be true, being the statement of inheritance for an Oliver’s Aethus and the there exists expression for Aethic invalidity inheritance, which remember we have shown to be implied by an Oliver’s Aethus on account of it being weaker.

$$\mathbf{O}\left[A\right]\Rightarrow \forall B\subset A,\mathbf{C}\left[B\right]\vee \mathbf{O}\left[B\right]$$

(20)

$$\mathbf{O}\left[A\right]\Rightarrow \exists B\subset A,\mathbf{C}\left[B\right]$$

(21)

Given these two statements, we can imply that the third postulate is, as stated earlier, expressible only with algebraic substitution of these two statements. That is, given how these are both true statements, we might think to substitute the latter into the former to get a statement which must also be true.

$$\mathbf{O}\left[A\right]\Rightarrow \forall B\subset A,\mathbf{C}\left[B\right]\vee \exists C\subset B,\mathbf{C}\left[C\right]$$

(22)

We can easily simplify this further by simply noting how for an Aethus, B, to be an Aethic contradiction of course implies that it possesses a proper child Aethus, (being itself, perhaps), which is an Aethic contradiction. Because the logical disjunction between a statement and something it implies equals the thing it implies, we have that $\mathbf{C}\left[B\right]\vee \exists C\subset B,\mathbf{C}\left[C\right]=\exists C\subset B,\mathbf{C}\left[C\right]$. We may then simplify accordingly.

$$\mathbf{O}\left[A\right]\Rightarrow \forall B\subset A,\exists C\subset B,\mathbf{C}\left[C\right]$$

(23)

As such, all we need to do is generalize this to all Aethae, so as to conclude that this property is the direct cause of Oliver’s Aethus being invalid in the first place.

$$\forall B\subset A,\exists C\subset B,\mathbf{C}\left[C\right]\Rightarrow \neg \mathbf{V}\left[A\right]$$

(24)

Notice that this is precisely equivalent of our earlier linguistic statement that it shouldn’t be impossible to make a contradiction impossible.

With the intuition of Aethic contradictions having served us well in formulating this statement, let us now finally generalize it back to all forms of Aethic invalidity through the node of the Aethic contradictions.

$$\forall B\subset A,\exists C\subset B,\neg \mathbf{V}\left[C\right]\Rightarrow \neg \mathbf{V}\left[A\right]$$

(25)

The fascinating thing about this, now, is that we can consider it be something of a cascading effect. So long as we can prove that the Aethus under the for all and there exists arguments is invalid, through perhaps Aethic contradictions, the second postulate contrapositive, or any other means, and we may immediately imply properties about their parent Aethae through the mechanism of this formulation. Such is the power of the third postulate of the Aethus.

To complete our final representation of the third postulate of the Aethus, we might consider writing it in the positive rather than the negative, through the use of the logical contrapositive of the present statement.

5.4. Statement of the Third Aethic Postulate

Here is the completed statement of the third postulate of the Aethus.

Third Postulate of the Aethus

If some Aethus is valid, then there exists a proper child Aethus to it for which every one of its own proper child Aethae are valid

$$\mathbf{V}\left[A\right]\Rightarrow \exists B\subset A,\forall C\subset B,\mathbf{V}\left[C\right]$$ (26)

Note how this is a strictly two-generational argument for the ontology of wavefunction collapse. This resultantly deviates it from perhaps the majority of modern hypotheses for how this might happen, which instead rely on a more one-generational “leaking of information," as is the supposition of quantum decoherence.

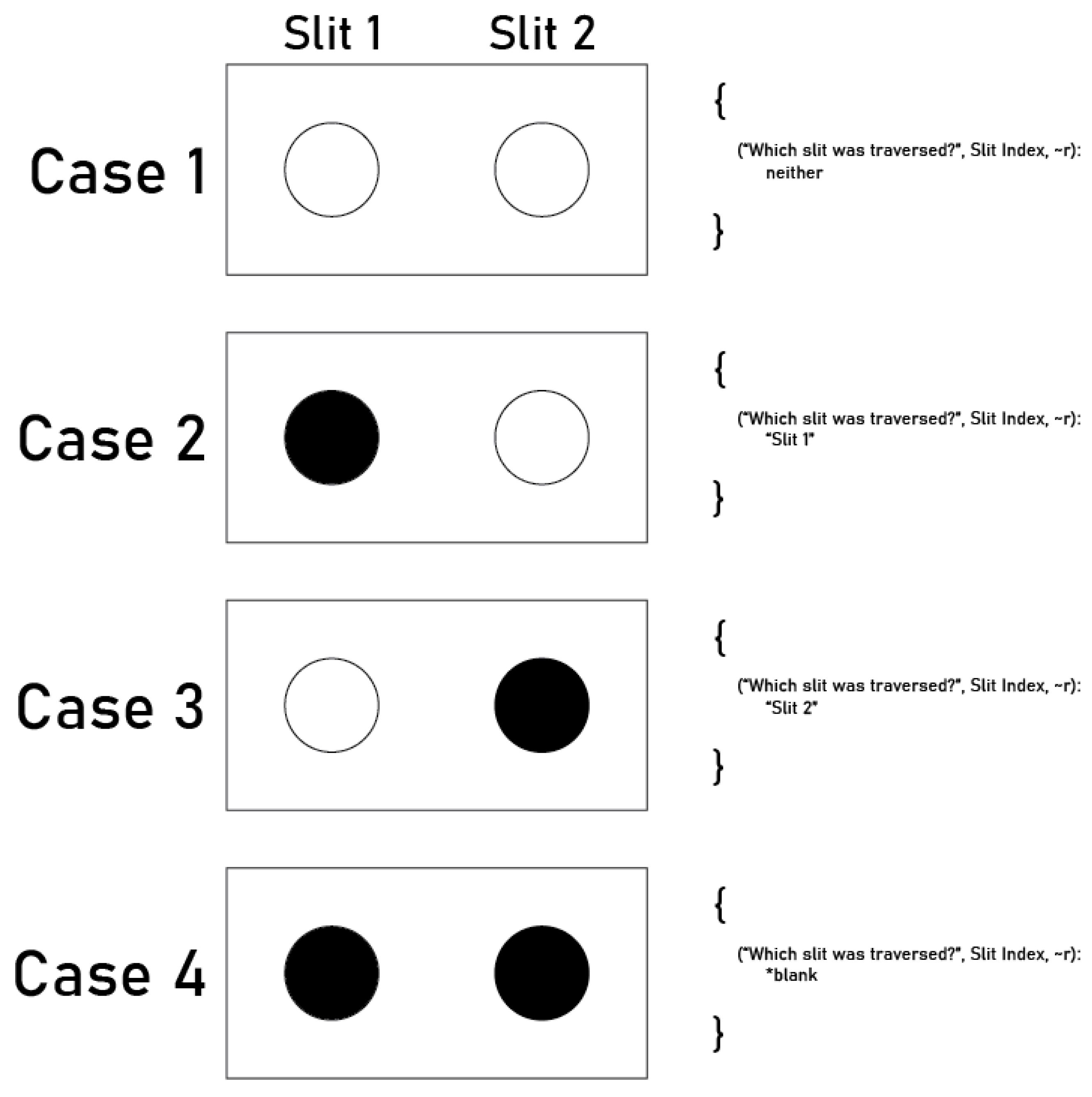
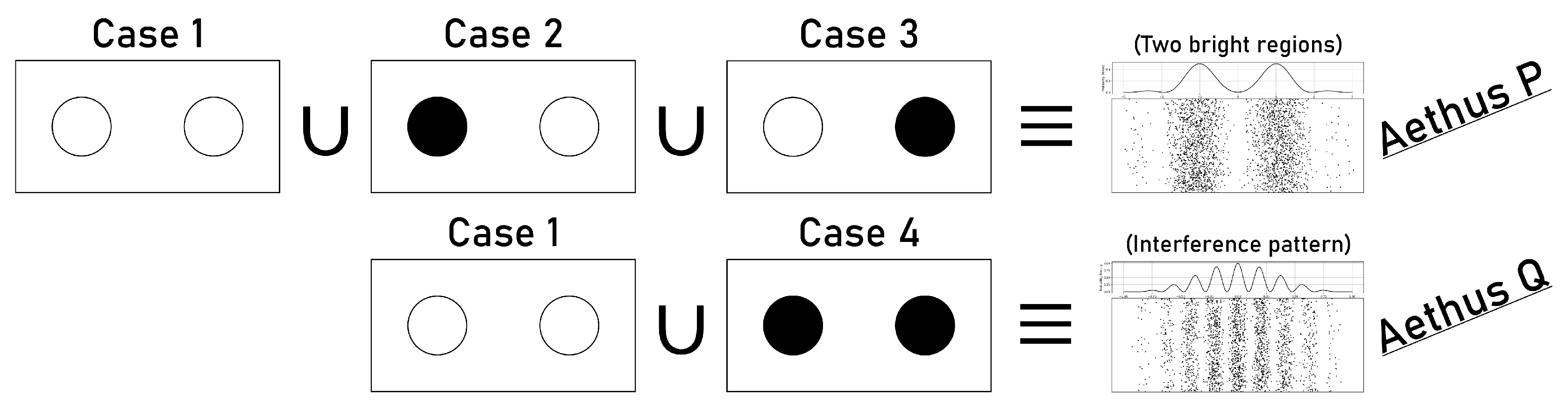
6. A Complete Rationalist Derivation of the Double-Slit Experiment

Given that the experimenter in place during the performance of the double-slit experimenter has the Aethus for which we will analyze, it follows that there are four main outcomes for what could potentially happen to a particle which is sent toward the slits during the experiment, as displayed in Figure 13 and Figure 14.

Remember that each of these outlined cases are themselves Aethae, specifically being child Aethae of the Aethus of the experimenter. However, this being said, it will be included in the experimenter’s Aethus which of these are valid and which are not according to the rules set in place by the three Aethic postulates. The game, then, will be one of finding which are invalid, and stating in the experimenter’s Aethus that these ones are forbidden accordingly.

The experimenter, of course, themselves has two possible overarching Aethae they have to work between. In one case, they have placed one or more detectors over the two slits of the experiment, and so the goal of this section is to, using nothing but the presence of the detectors and the Aethic postulates, demonstrate which of the four possible cases are automatically to be deemed invalid in the Aethus of the experimenter, in the process solving the measurement problem by very specifically stating what ontological process brings about the collapse of the wavefunction at large.

6.1. Derivation for the Detector-Off Case

Let us begin with the case where the detector is absent. As such, the key property we need to make use of is the Heisenberg uncertainty principle, which provides us with a lemma that quantum information, once not measured, may never again be attained. This is a crucial input to the Aethic postulates, because it immediately fails to invalidate Case 4 of the possible cases, being the one in which the interference pattern is raised. That is, there is indeed a proper child Aethus to the experimenter’s Aethus – in fact all of them – for which their own proper child Aethae all prevent the slit of traversal’s information from being reattained, which would have triggered a contradiction to the state of Case 4. As such, the third postulate returns indeterminate, but does not necessarily argue in the true or false direction due to the nature of its converse being unknown, (so as to allow for the second and first postulates to also contribute to any potential invalidity). In addition to this, however, the contrapositive of the second postulate also fails to invalidate such an Aethus, because the slit of the traversal of the particle is in fact unknown and it is in fact in superposition. As such, because none of the three postulates are able to invalidate this Aethus, we may claim that it is valid. However, even though this is now known, we must still be careful in supposing that this Aethus equates to that of the experimenter automatically – for there are still three other possibilities in the permutation of which slit is gone through beyond Case 4 alone.

Thus, the only way to mathematically demonstrate that the experimenter’s Aethus is necessarily equal to an Aethus in which the particle goes through both slits at once is to invalidate the other Aethae. Let us do this now. To begin with, we must note how Heisenberg’s uncertainty principle implies that the slit of traversal attribute is strictly unattainable given that the double-slit experiment has been run without the use of a detector, so such a thing is a property not only of the experimenter’s Aethus, but any valid child Aethus of it as well, because for a child Aethus of it to not agree with this property would be a direct contradiction of the empiricism under Heisenberg’s uncertainty principle. In total, there is a full contradiction in the works here, because we simply have that Case 2 and Case 3 themselves contradict such an assertion of the which-slit attribute needing to remain blank. As such, they must amount to invalid Aethae when intersected with the experimenter’s Aethus, therefore invalidating both of them for the detector-off case.

Note that equivalent approach for demonstrating this leverages the second postulate of the Aethus, where we may specifically show that Heisenberg’s uncertainty principle being in effect means that any valid child Aethus of the experimenter’s Aethus must hold the slit of traversal as conceptually blank, and therefore must hold it in superposition as per the second postulate of the Aethus. However, we clearly see that Case 2 and Case 3 do not hold the slit of traversal attribute in superposition, so through such a thing they also contradict Heisenberg’s uncertainty principle, and must accordingly be taken as invalid Aethae in the case of the detector being off. This also serves as something of an intuitive argument for why Case 4 must be allowed to remain in their place, being because it contains the property which they lack of never being able to centric unfold to an Aethus in which the slit of traversal drops out of superposition. Such a property is uniquely compatible with Heisenberg’s uncertainty principle, therefore favoring Case 4 in the process.

Finally, regarding Case 1 within the detector-off case, this time such an Aethus is actually not invalidated in the first place. This can clearly be seen empirically, for those cases in which the particle does not wind up behind the slits, but instead gets caught elsewhere on the plate adjoining the slits without managing to traverse them.

As such, for the case where any detectors are utterly absent, we can see that the double-slit experiment results in the particle being in a weighted superposition between the Aethae of entering both slits at once, or neither at all.

6.2. Derivation for the Detector-On Case

All that is left now is to derive the solution to the case where the detector is present. We can immediately start by deciding that Case 4 is invalid, because the experimenter always has the option of checking the data in the detectors later on, hence invaliding that case for at least some child Aethae for every one of the experimenter’s own child Aethus where they observe an interference pattern, (in the absence of some near-improbable fluke of generation). Specifically, the attribute of Case 4 that neither slit is not gone through can possibly be contradicted by any double-generational child Aethus, immediately violating the third postulate.

Put rigorously, suppose that the experimenter’s Aethus then and there, being detector on intersected with Case 4, is to be some Aethus X, with there existing a proper child Aethus of Y to that. All we need to demonstrate is that we can find such a Y for which every proper child Aethus to it, Z, is valid–or alternatively we can prove X invalid by finding that any given Y must possess a proper child Aethus of Z which is invalid. To do this, simply consider how Y can either consist of an Aethus in which the experimenter looks at the detector output, or they do not. If Y holds that they looked, then that is an invalid Aethus on account of contradicting the interference pattern, so by another application of the third postulate of the Aethus we have that all of its further child Aethae are already invalid. That leaves the case where they are yet to look for Y, however we can then show that we might consider some further child Aethus to this, Z, in which they do look. Specifically, let us consider Z to simply consist of them adding the information from the detector to their Aethus. It immediately follows from this that Z is indeed a proper child Aethus of Y, because in either case of if the particle goes through Slit A or Slit B, and such an added stated-attribute is clearly physically blank in Y, on account of Y having already been defined in holding no information whatsoever about the slit of traversal, via the interference pattern as well as its prior condition of having the experimenter to not look, (and, generally, with there being no derivational process within the scope of Y which can discriminate between the particle having gone between Slit A versus Slit B). All in all, we then know that this Z must be an invalid Aethus, because it does indeed contradict the state of there having been an interference pattern in the first place, on account of that pattern’s implication that the particle decidedly did go through whichever slit was not registered by the detector also. Hence, for every Y it turns out that Z becomes invalid, so therefore, by the contrapositive of the third postulate of the Aethus, this X has to be invalid. As such, Case 4 with the detector on is an invalid Aethus.

This, note, causes an intriguing ripple effect onto the remainder of the experimenter’s Aethus. It is no longer truly the case that the slit of traversal is to be conceptually blank to their Aethus, even if they have yet to check the detectors, because the mere fact that the act of going through both slits at once triggers an invalid Aethus is an indicator that certain configurations of the slit of traversal attribute can be used to attain information about the Aethus at large. In effect, this tells us that the slit of traversal attribute is merely semiblank in such a case. With this being so, what is still decidedly unknown to the experimenter’s Aethus of before they observe where the particle landed on the back screen, is which of the other three cases is actually in effect. What we see from this is two intriguing consequences. The first is that we can no longer leverage the second postulate of the Aethus so as to show Case 2 and Case 3 as invalid, because the lack of needed conceptual blankness of the slit of traversal attribute no longer forces a superposition to have to be in effect at all. The second, most importantly, is that an attribute which points to whether Case 1, Case 2, or Case 3 is in effect is indeed fully conceptually blank. This is a huge result, because it allows us to use the second postulate of the Aethus to imply that all three of the cases themselves ought to go into Aethic superposition in the given Aethus. As such, this might be specifically contrasted with the detector-off case by our two-step process of first discounting the need for the slit of traversal attribute itself to be the one in agreeing superposition, and second abiding by the new iterative layer of the full Aethic cases themselves as our new unit of agreeing superposition. In effect, the implied disagreeing superposition itself of the slit of traversal attribute can be alternatively expressed as the agreeing superposition of the cases Case 2 and Case 3 as taken as Aethae over the base attribute. This is so where we specifically take the attribute which points to either Case 2 or Case 3 as being conceptually blank to imply an agreeing superposition as per the second postulate of the Aethus, but such an agreeing superposition which may be stated in a valid child Aethus. Agreeing superpositions over physical observables like the slit of traversal typically do not follow this same quality of being still valid if their child Aethae can be stated as per the specific nature of the third postulate of the Aethus, so such a thing can be taken as a special property of more abstract Aethic superpositions like those over an Aethus in place of physical observables. Note that it is a general rule that an attribute in disagreeing superposition ought not to be conceptually blank in the Aethus in question, due simply to whatever informational spillover is accounted for by the disagreeing superposition itself.

If the experimenter has not observed anything about the landing location of the particle besides what could be attained from setting up the detectors beforehand and running the experiment blindly, then relative to their Aethus of that nature, Case 1, Case 2, and Case 3 are all in agreeing Aethic superposition. However, if the experimenter adds the location of the particle to their Aethus by looking at or otherwise assessing the information on the back screen, then the weights on the three cases in superpositions shifts accordingly – as in perhaps if it is closer to slit A, hence implying more of a chance to Case 2 than Case 3, however not entirely guaranteed and therefore not entirely added to their Aethus. Only if they can truly add this information to their Aethus, such as checking the detector, may the experimenter actually collapse their Aethus as far down as an individual case amongst Case 1, Case 2, or Case 3 here, but note that this is not given merely by the feat of the particle having been measured by the back screen beforehand, as this would, Aethically speaking, be no less arbitrary than simply asserting that quantum superpositions are known beforehand.

6.3. Assessing the Results

All this being said, with the detector absent, the tendency is an Aethic superposition between Case 1 and Case 4, whereas with the detector present, the tendency is an Aethic superposition between Cases 1, 2, and 3. The crucial takeaway here, all things considered, is that the detector-off case implied an agreeing superposition of the slit of traversal, whereas the detector-on case implied a disagreeing superposition of the slit of traversal. This fundamental flip can be seen as a major component of the ontological essence of the wave-particle duality notion, with the complete picture needing to be filled in with Step X.

Generally, then, we see that there are two major varieties of ontological content to what we call “quantum wavefunction collapses.” The first is like what we see in the double-slit experiment, where a measurement triggers the change from agreeing to disagreeing Aethic superposition. The second is when a direct observation is taken from a list of many options, such as randomly shooting a particle at some array of detectors and personally determining which one has been struck. This is simply an instance of a child Aethus being taken from a disagreeing superposition of the possible ending locations, no differently than all the other disagreeing superpositions we collapse relative to our Aethae in day-to-day macroscopic life. Note, however, that even after a particle is detected at a destination, the path it took to get there remains very much in agreeing superposition if not recorded in some way, just due to the second postulate itself. The point there is that even the supposed claim of having gathered an attribute in one’s Aethus is only ever a small part of a largely superposition-infused picture. This lingering set of agreeing superpositions to any system is part of what makes quantum mechanics so eye-catching.

Regarding the notion of expanding this to the general solution, there are four crucial steps to undergo to validate all three postulates to a given Aethus, in effect describing the precise ontological makeup of a system so as to satisfy a solution to the measurement problem.

Through this, the measurement problem has its first official solution. Whether there will be others, it is hard to tell. But it is very unlikely that they should be as simple as this one, due to the nature of the particular inductive steps that were chosen to create this. At least as far as Einstein’s razor [4] is concerned, that would make this the final solution itself. Naturally, then, we have the complete solution to the measurement problem, hence satisfying a theoretical derivation of the collapse postulate which matches the empiricism. From here, now, let us look to what might perhaps be the most general expression of Aethic reasoning.

Algorithm 1:How To Perform Aethic Reasoning Over a System

1: Basic Description: The following algorithm is a rendition of the specifically epistemological procedure which one might undergo in order to assess the Aethic retrieval and thereby state of presence in reality which a particular attribute holds with respect to a particular Aethus, (being most commonly a first or third-person empirical Aethus). 2: Input: Our inputs are the empirical Aethus corresponding to the reality of the system, A, and an Aethic Template which we wish to retrieve the state of, $\beta$. 3: Output: The result will be an exact mapping between the parameters of the system and the set of allowed Aethic outcomes. Aethic reasoning now renders the wavefunction collapse as algorithmic through the very state of the present algorithm producing the correct empiricism independently of external epistemic intervention. 4: functionDecipherRetrieval(A, $\beta$) 5:     if $\beta$ is present in A then 6:         We know that $\beta$ is present in the Aethic reality of the system 7:         $B\leftarrow$ The queried state of $\beta$ in A 8:         return B 9:     else if $\beta$ is impartially blank in A then 10:         We understand that $\beta$ must be in a general superposition of some sort with respect to A, but we still need to determine if it is agreeing or disagreeing 11:         Proceed to the next layer of the algorithm 12:     else if $\beta$ is otherwise semiblank blank in A then 13:         ${\beta }_1,{\beta }_0\leftarrow$ The decomposition of $\beta$ into its present and impartially blank components in A, respectively, which we know to be possible by the generalized Aethic dichotomy theorem for impartial blankness 14:         return The retrieval conjunction of DecipherRetrieval(A, ${\beta }_0$) and DecipherRetrieval(A, ${\beta }_1$) 15:     end if 16:     Let us now analyze the specifics of the case where $\beta$ is impartially blank in A 17:     if $\beta$ is uncertain in all proper child Aethae of A then 18:         $\beta$ is representative of an Aethic uncertainty principle of some kind with respect to A 19:         We now know that $\beta$ is both conceptually blank with respect to A, and therefore in agreeing superposition with respect to it by the second postulate of the Aethus 20:         return The retrieval which consists of the set of all possible states of $\beta$ as according to however they are weighted in A, if applicable 21:     else if $\beta$ holds the possibility of being attained in some proper child Aethus to A then 22:         In this case, the third postulate declares that for $\beta$ to be conceptually blank with respect to A would amount to an invalid Aethus 23:         With such a case of $\beta$ being conceptually blank being an invalid Aethus, we now look to all the remaining cases, being the remaining combinations of the individual states of $\beta$ being present in the retrieval or not, with their corresponding descriptive Aethae 24:         Go through and invalidate each of these other cases, one by one. This represents a major shift from classical epistemology, in which we assume that all cases which realize multiple disjoint states are automatically invalid. Here we have to do a case-by-case analysis of all possible combinations of the realized states of $\beta$, and invalidate them with the third postulate of the Aethus directly 25:         Some number of Aethic cases will now be left over, out of not being able to be invalidated by the third postulate 26:         Since the property of which is these cases is realized in the the retrieval is itself conceptually blank in A on account of their all not being invalidated by the third postulate, we use the second postulate of the Aethus to put the cases themselves in agreeing Aethic superposition within the retrieval 27:         With the iteration-layer of the cases being in agreeing superposition, this then implies a disagreeing superposition of the lower iteration layer that is the states of $\beta$ itself 28:         return A disagreeing superposition of the states of $\beta$, or alternatively an agreeing superposition of whichever cases remained after the validity cropping done by the third postulate 29:     end if 30: end function

7. Generalized Aethic Coherence Principles

The natural question at this point is what comes next given our scientific understanding of Aethic reasoning. The natural answer, then, is that we ought to peer deeply into further uncertainty principles, perhaps even giving them a type. So far, one of these uncertainty principles is known to us – Heisenberg’s uncertainty principle itself – which we may consider our node of entry into the larger Aethic reasoning. But, consider an uncertainty principle itself to signify the larger class of these types of forever-unknowable Aethae.

Principle 5 

(Aethic Uncertainty Principle). An empirical principle which corresponds to an instance of a particular class of Aethic attributes being permanently blank by the effects of some related permanencible attribute.

Principle 6 

(Aethic Uncertainty Attribute Class). The class of Aethic attributes which correspond to their Aethic uncertainty principle.

Principle 7 

(Aethic Coherence Principle). An Aethic coherence principle is an empirical principle which regards a certain class of Aethic attributes as following a predictable agreeing superposition under the relevant context.

This is why Heisenberg’s uncertainty principle is itself a type of Aethic uncertainty principle – because it corresponds to a class of attributes, which we might call “Heisenberg attributes,” or perhaps “quantum attributes,” themselves pertaining to the Aethus of a particle’s position and momentum at once. By the classic statement of the quantum uncertainty principle itself, we know that for any quantum attribute such as this, there exists a child Aethus to it which will be permanently statistically independent to any single valid Aethus in which it is placed. This is simply due to [dichotomy]the Aethic dichotomy theorem and the classic statement of the quantum uncertainty principle. By the quantum uncertainty principle, we cannot know position and momentum at once, so therefore the knowledge of position implies an Aethus holding momentum which is blank to one’s Aethus, and alternatively knowing momentum implies an Aethus holding position which is blank to one’s Aethus. As such, quantum attributes will always return a nonempty retrieval due to their ensured possession of superpositions in at least position or momentum. As such, given that a quantum attribute is present in a valid Aethus, it follows that the third postulate may very potentially not return an invalidation, because we might simply choose an Aethus to house them in in which position, momentum, or both are unknown, (implied by its validity), hence arguing that any proper child Aethus of the standing one will possess proper child Aethae due to its inherent validity already discussed. Furthermore, we know that such a valid Aethus must exist due to the principle of centric unfolding, (assuming that we exist and valid Aethae with us), and so, therefore, we see that quantum attributes are indeed coupled with an uncertainty principle, and that uncertainty principle is Heisenberg’s uncertainty principle itself.

This now being said, it is inductively implied by Aethic reasoning that any single uncertainty principle will result in agreeing superpositions of a corresponding type. This is simply due to the correlation between agreeing superpositions and the application of the third Aethic postulate, as well as the assertion by an uncertainty principle that the third Aethic postulate be applicable after all. As such, a major goal of any future studies on Aethic reasoning is to name as many classes of uncertainty principles as possible; primarily those which have practical use and or prevalence. Given that quantum uncertainty is already in existence, it is quite reasonable to imagine that there are a full myriad of alternative classes of uncertainty attributes, with their corresponding uncertainty principles. And if this is true, then the best among them will provide agreeing superpositions which can possibly rival those in quantum mechanics for their mysterious intrigue and classical-defying scope. Just as an Aethic uncertainty principle generalized the quantum uncertainty principle, let us also suppose that “Aethic coherence" to a given Aethic uncertainty principle generalizes quantum coherence–so, that is, the agreeing superpositions of some Aethic uncertainty principle can be designated as holding that uncertainty principle’s Aethic coherence–with any conversion of this to disagreeing superpositions being referred to as “Aethic decoherence." The same as in quantum mechanics, but for the general Aethic system. This can be phrased in the form of a theorem.

Fundamental Theorem of Aethic Reasoning

To every valid Aethic uncertainty principle there corresponds an Aethic coherence principle.

Put into more simple language, this theorem states that according to Aethic reasoning, that which is permanently uncertain performs every possible action at once. Such is to be interpreted as a fundamental rule of the universe in any and all relevant contexts. The argument is that given the existence of quantum coherence, we assert that this is the only reasonable inductive conclusion, with the entire layered argument of Aethic reasoning being the support to this claim.

8. Conclusions

The measurement problem has long challenged our understanding of quantum mechanics, raising profound questions about the mechanisms of wavefunction collapse and the nature of observed reality. In this paper, we introduced Aethic reasoning, a novel framework that reimagines time, reality, and information through a philosophical and mathematical lens. This approach offers a reinterpretation of both quantum mechanics and the classical world, but beyond even this serves as a broad platform for addressing deeper metaphysical questions about the universe.

Aethic reasoning proposes a unique solution to the measurement problem through its extrusion principle, which models quantum collapse as transitions along a Markov chain of block universes rather than local events within a single static or growing block universe. This additional degree of freedom in the ontology of time allows us to bridge the false dichotomy between classical temporal models while preserving consistency with observed phenomena. Moreover, the union principle within this framework resolves key semantic inconsistencies in classical logic, enabling a generalization that accommodates quantum superpositions and decoherence. Importantly, the mathematical rigor of Aethic reasoning, such as operations over the commutative ring of Aethae and the interplay between agreeing and disagreeing superpositions, provides a robust means to encode quantum and macroscopic states alike. This approach aligns naturally with empirical results, such as those observed in the double-slit experiment, while also presenting a philosophically coherent augmentation to prevailing frameworks like the Copenhagen and many-worlds interpretations. By grounding its model in the Aethic structure and its relational notion of realism, Aethic reasoning establishes a unique perspective on the interconnectedness of observation, information, and reality. All that is left now to demonstrate, via the followup paper on active reasoning, is the specific ontological reason for why agreeing superpositions imply a wavelike interference when taken over the properties of physical matter quanta. Such is the final question of Step X, which deserves a paper of its own in order to be accordingly gathered.

With these things representing the specific impacts of Aethic reasoning to the measurement problem, it of course follows that the inductive steps of this framework can only have a broader impact. We have already seen with some of the great works in physics of the twentieth century that simultaneity and energy are fundamentally relative concepts, but now we extended the front of relativism all the way to core metaphysical notions like knowledge and truth. Beyond even this, if Aethic reasoning has even a shadow of correctness to its suppositions about superpositions, and of course that would imply a vast string of consequences across the remainder of human history. Among these consequences, at the very least, are the emergence of a metamodern paradigm of physics, a new layer of philosophical depth to be explored by humanity, a first tangible tie between scientific rationalism and Eastern metaphysics, and perhaps a myriad of deeper implications into the scope and meaning of life itself. After all, in the Aethic world, many a preconceived anthropic notions have to be shaken, to say the least, and it seems more than evident that the dominoes are falling in the meaningful direction, (as highlights the metamodern alignment6 of Aethic reasoning once more).

At this point, now, we are entering something of a very creative time in human history, so the world truly is whatever we make of it.