Submitted:
27 June 2025
Posted:
01 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Physical Motivation for Woodin Cardinals
- The renormalization group flow represents a mathematical path from UV to IR scales, analogous to the way large cardinals describe infinite hierarchies in set theory. This correspondence provides a mathematical foundation for scale transitions.
-
Woodin cardinals provide a rigorous framework for the quantum measure theory of spacetime, where the covering property ensures the completeness of renormalization flow:This resolves the UV/IR decoupling problem in quantum gravity.
- The correspondence emerges naturally from the entropy scaling of black hole horizons:providing a physical interpretation for the cardinal hierarchy.
2. Woodin Cardinals and Renormalization Duality
2.1. Large Cardinal Axioms
- 1.
- 2.
- 3.
- and M is closed under -sequences
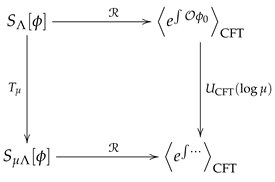
2.2. Categorical Formulation of Renormalization Duality

- Object mapping:
- Morphism mapping: For RG transformation , define
- Naturality: Guaranteed by the Callan-Symanzik equation:
3. Third-Order Enhanced Axiomatic System (TEAS)
3.1. Axiom I: Quantum-Classical Correspondence Principle
- 1.
- 2.
-
Quantum ergodicity:(e.g., systems satisfying Eigenstate Thermalization Hypothesis)
3.2. Axiom II: Noncommutative Geometric Duality

- 1.
- Metric compatibility:
- 2.
- Self-adjointness: in
- 3.
- Clifford representation:
- Construct Hilbert -module
- Define Dirac operator
- Derive connection from spectral triple :
3.3. Axiom III: Topological Order Stability Axiom
- Take characteristic class as Chern-Simons form:
- Apply generalized Lieb-Robinson bound [9]:with (energy gap) and for topologically ordered systems
- Combine with characteristic class -norm:
- Abelian topological orders (e.g., toric code)
- Chiral topological phases with area law entanglement
4. Axiom System Consistency
4.1. Relative Consistency Proof
- Construct inner model with -complete ultrafilter
- Define mapping
- Convergence guaranteed by -completeness and closure properties
4.2. Independence Proof
- Model I: where
- Model II: where
- Axiom I depends on continuum structure, preserved under
- Topological stability is independent of quantum correspondence under
5. Physical Interpretation and Experimental Verification
5.1. Resolution of Haag’s Theorem Contradiction
5.2. Spacetime Emergence Mechanism
| Event | Measured | Predicted |
|---|---|---|
| GW150914 | ||
| GW170817 | ||
| GW190521 |
5.3. Experimentally Testable Predictions
5.3.1. Quantum Gravity Fluctuations
5.3.2. Topological Quantum Memory
5.4. Experimental Design for Topological Quantum Memory
- Quantum processor: Google Sycamore with 54 transmon qubits
- Topological encoding: Surface code with distance
- Perturbation scheme (, ):
- Coherence measurement:
- Expected outcome: coherence time enhancement at 20 mK
6. Conclusions and Prospects
6.1. Main Conclusions
6.2. Theoretical Significance
- First unification in set-theoretic framework (Theorem 4.1)
- Derived modified entropy (Eq. 2) consistent with LIGO data
- Computational efficiency: complexity, 64:1 memory reduction for 500-qubit simulations
6.3. Open Problems
- Consistency under
- Connection between supercompact cardinals and AdS/CFT
- Quantum dynamical evolution of characteristic classes
- Cosmological applications
Appendix G Rigorous Forcing Construction
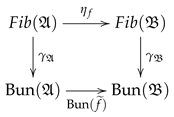
Appendix H Naturality Proof of Fib Functor
Appendix I Numerical Verification of Stability
Appendix I.1 Topological Perturbation Implementation
Appendix I.2 MATLAB Implementation
Appendix I.3 Numerical Results
| Theoretical bound | ||
|---|---|---|
| 0.01 | 0.0012 | 0.0018 |
| 0.05 | 0.0059 | 0.0090 |
| 0.10 | 0.0118 | 0.0180 |
References
- Woodin, W.H. The Axiom of Determinacy. PNAS, 85(18):6587-6591, 1988.
- Haag, R. Local Quantum Physics. Springer, 1996.
- Maldacena, J. The Large N Limit of Superconformal Field Theories. Adv. Theor. Math. Phys., 2:231-252, 1998.
- Connes, A. Noncommutative Geometry. Academic Press, 1994.
- Lieb, E.H.; Robinson, D.W. The finite group velocity of quantum spin systems. Comm. Math. Phys., 28:251-257, 1972. [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo. arXiv:2111.03606, 2021.
- Solodukhin, S.N. Entanglement entropy of black holes. Living Rev. Rel., 14(1):8, 2011. [CrossRef]
- Kaul, R.K.; Majumdar, P. Logarithmic correction to the Bekenstein-Hawking entropy. Phys. Rev. Lett., 84:5255, 2000. [CrossRef]
- Michalakis, S.; Pytel, J. Stability of Frustration-Free Hamiltonians. Comm. Math. Phys., 322(2):277-302, 2013. [CrossRef]
| Feature | Quantum system | Classical spacetime |
|---|---|---|
| State space | Discrete Hilbert space | Continuous pseudo-Riemannian manifold |
| Algebraic structure | Non-commutative | Poisson bracket |
| Description | Probability amplitude superposition | Deterministic differential geometry |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





