Why Can’t Large Galaxies Centered on Neutron Stars be Observed?

1. Neutron Star Observation Facts

The mass of a neutron star is generally between 1.35 and 2.1 times the mass of the sun, but its diameter is only about 10 kilometers. The significant characteristics of neutron stars are high density, high speed, strong magnetic field, and strong radiation. Many neutron stars exist in the form of pulsars and regularly emit electromagnetic waves outward. This phenomenon is because the rotation axis of the neutron stars does not coincide with their magnetic axis, causing their powerful magnetic field to continuously accelerate the charged particles, thus forming radiation. The most famous pulsars, such as those in the Crab Nebula, can send hundreds of signals per second.

In 1967, Joselene Bell, a graduate student at Professor Hueysh of Cambridge University, discovered the first pulsar. According to some scholars’ estimates, the total number of neutron stars in the Milky Way should be at least more than 200,000. As of August 2023, there have been more than 3,000 pulsars discovered by humans in the Milky Way. Currently, the world’s largest radio telescope is the 500-meter aperture spherical radio telescope (FAST) located in Guizhou, China. As of November 2024, the number of pulsars discovered by FAST has exceeded 1,000.

Neutron stars usually exist in isolation, with a small number of neutron stars forming a binary star system with other galaxies (companiment stars). These companion stars may be neutron stars, white dwarfs, or other types of celestial bodies. ‌At present, more than 60 pulsars have been found in the binary star system, and even fewer multi-star systems containing neutron stars. Currently, the typical galaxy of the multi-star system of neutron stars is PSR B1257+12, but there is no large celestial structure centered on neutron stars.

Currently, the binary and multi-star systems that astronomers have discovered are as follows:

PSR B1913+16 is a two-neutron star system discovered by Taylor and Hulls in 1974. It is the earliest two-neutron star system discovered by humans. The orbital period of PSRB1913+16 is actually changing. Over time, its orbit becomes smaller and smaller, but the amplitude of smaller size is very small, only 1cm a day. According to Einstein’s general theory of relativity, when two neutron stars circle each other, they generate gravitational waves, which take away the energy and angular momentum of the binary star system, and the last two celestial bodies will merge. Currently, “PSRB1913+16” is in the early stages of merger. Through long-term monitoring, Taylor and Hulls found that the amplitude of their orbital contraction was exactly consistent with the prediction of general relativity, and for this, the two scientists won the Nobel Prize in Physics in 1993.

PSR B1257+12[1] was discovered by astronomers Alexander Waltzson and Dale Frell in January 1992. It is located in Virgo, about 2300 light years from the earth. It has a diameter of only 20km, but its mass is 1.44 times the size of the sun. It rotates very quickly and can rotate every 6.22 milliseconds, that is, it can rotate 160 turns in a second. Its temperature is 5227℃ and is a neutron star with planets. Scientists initially discovered that there were three planets around the neutron star, and subsequent research further confirmed that the number of its satellites increased to 6. Named after A, B, C, D/, PSR B1257+12 A is at the closest position to the pulsar, with an average sun distance of 0.19 astronomical units, its mass is about twice the moon, a radius of about 2,200 kilometers, an orbital period of 25.262 days, and a surface temperature of about 1763K. PSR B1257+12 B is 0.36 astronomical units from the parent star, with a eccentricity of 0.0186, an orbital period of 66.5419 days, an orbital inclination angle of 53, a perihelion longitude of 250.4, a perihelion time of 2,449,768.1, a mass of 4.29 times the earth’s mass, a radius of about 10,500 kilometers, and a temperature of 1269~1293K. PSR B1257+12 C is 0.46 astronomical units from the parent star, with a temperature of 846~875℃, a centrifugal rate of 0.0252, an orbital period of 98.2114 days, an orbital inclination angle of 47, a perihelion longitude of 108.3, a perihelion time of 2,449,766.5, a mass of 3.91 times the earth’s mass, a radius of about 9,800 kilometers, and a temperature of 1119~1148K. The unproven PSR B1257+12 D (probably an asteroid, comet or dwarf planet, semi-major axis 2.8 AU, 186°C), estimated to be about 2.8 astronomical units, mass is about four-tenths of the earth, a radius of about 700 kilometers, and a surface temperature of about 459K. The mass of the sun: 1.989×10^30kg, the mass of the moon: 7.342×10^22kg, the mass of the earth: 5.972168×10^24kg, astronomical unit: 1.496×10^11m, the data summary of PSR B1257+12 is shown in Table 1.

PSR J0348+0432: On May 3, 2013, scientists discovered a neutron star in a binary galaxy, and its distance from the earth is 7,000 light-years. The PSRJ0348+0432 is about twice the mass of the Sun, and it is tightly wrapped in a sphere with a diameter of less than 13 miles or 20.92 kilometers, and rotates at a speed of 25 laps per second. The neutron star PSRJ0348+0432 has a white dwarf rotating around it. The white dwarf and the neutron star orbit each other, forming a binary galaxy, with a period of 144 minutes.

PSR J0952-0607: In 2017, this neutron star named PSR J0952-0607 was captured in the sextant galaxy about 3,000 light years from Earth. The latest observations show that the mass of this neutron star is about 2.35 times that of the sun, and it is the heaviest neutron star known. PSR J0952-0607 has a rotation speed of more than 700 times per second. PSR J0952-0607 is part of the venomous spider pulsar binary system. These binary star systems are composed of a companion star and a neutron star that will swallow the companion star. The swallowed matter is exactly why the neutron star rotates so high. Astronomers are now able to estimate the mass of PSR J0952-0607 through the residual matter of its companion star, whose companion star has been downgraded to a larger planet, about 20 Jupiters. The mass of a neutron star is between 0.17 and 2.35 times the mass of the sun.

On August 17, 2017, LIGO and Virgo gravitational wave detectors captured the gravitational wave signal GW170817 generated by the merger of two neutron stars for the first time.

In October 2017, the Swift Observatory in the United States observed a binary galaxy called Swift J0243.6 + 6124, which contains a neutron star that can eject “relativistic jets”.

On May 22, 2025, Chinese astronomers used the Sky Eye FAST to discover rare millisecond-level pulsars and a helium-nuclear companion star.

2022-09-27 The first static neutron star candidate J1123 discovered through time-domain optical observations determined by the Chinese research team. The J1123 binary star system consists of an M-type red dwarf and an optically invisible companion star. The binary star system is about one thousand light years away from the earth, with an orbital period of about 6.6 hours. The half-amplitude of the optical velocity of the M-type dwarf is about 257 kilometers per second, and the mass of its optically invisible companion star is about 1.24 times the mass of the sun. This companion star did not detect radio or ultraviolet signals, so it is more inclined to think of neutron stars.

Generally, neutron stars have particularly high density. neutron stars with a diameter of 10km have a mass greater than that of the sun. According to Newton’s law of universality, gravity is proportional to mass, so the gravity of neutron stars should be larger than that of the sun, and the gravitational range of neutron stars should be larger than that of the solar system. Planets with such a large .

gravitational range should form galaxies larger than that of the solar system. The fact that many years of observations is that no large galaxies centered on neutron stars are found.

2. Deflection Gravity Theory

“Graining, gravitational field and graviton - inference about the frequency of gravitational energy waves” [2] believes that the most basic unit of matter is nucleons (collective name of protons and neutrons). All nucleons emit gravitons. The energy carried by gravitons is the Planck constant h, and the value is 6.626×10^ (-34) J·s. Gravitators propagate in space with gravitational energy waves. Gravitational energy waves resonate with other nucleons, transmitting energy to form gravity. For planets, gravitons emitted by nucleons inside the planet interact with other nucleons inside the planet to form the cohesion of the planet. The gravitons emitted by nucleons near the outside of the planet are partially emitted outside the sphere and propagate in space with gravitational energy waves. The gravitational energy waves encounter nucleons from other planets and resonate with them to form gravitational force between the planets.

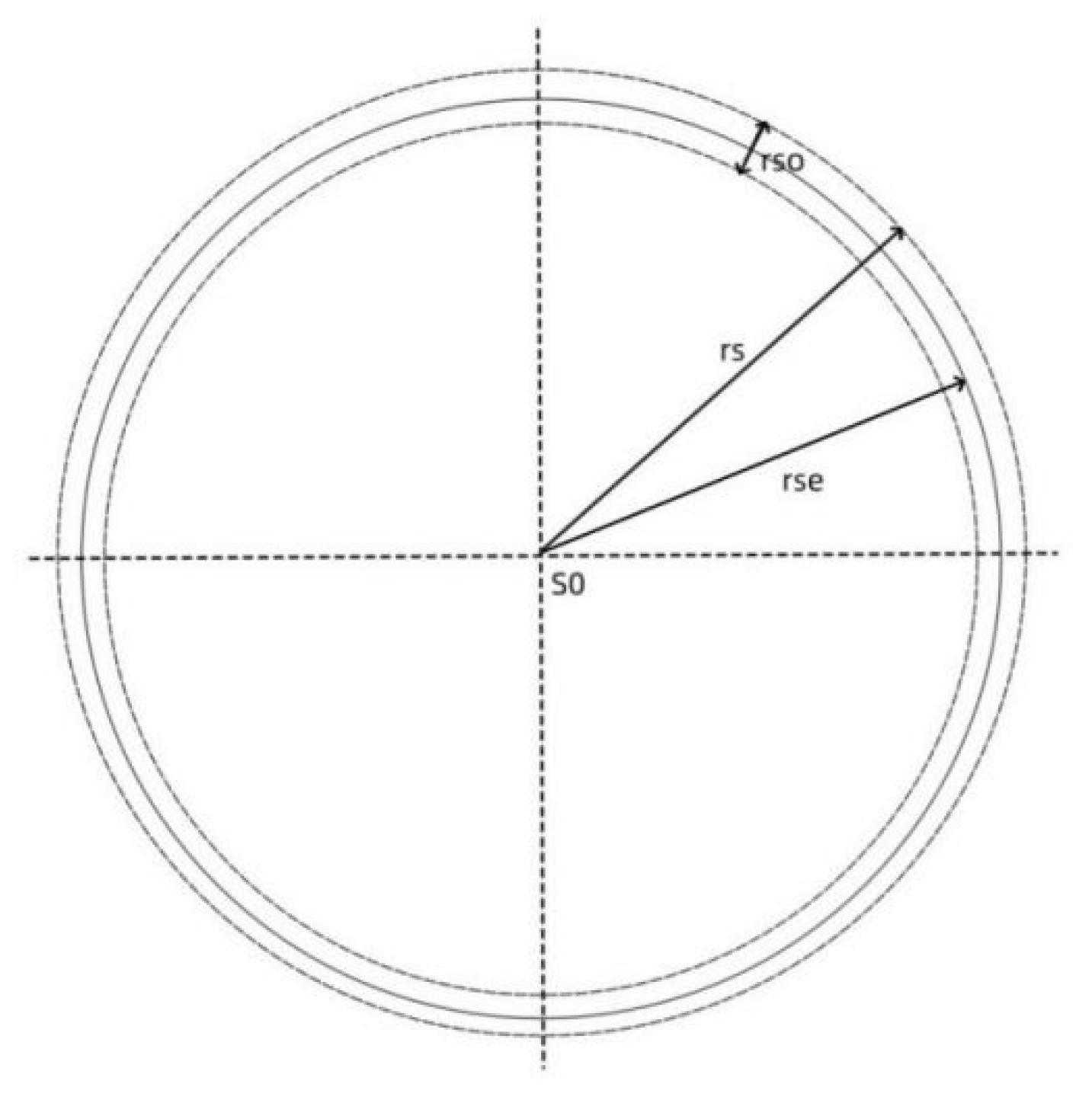
Figure 1 is a schematic diagram of the equivalent spherical surface of a planet launching gravitons. In the figure, rs is the planet’s radius, and rso is the thickness of the graviton shell sent by the planet to the outside of the ball. There should be a spherical layer rse in the middle. It can be considered that all gravitons on the planet are emitted by this spherical layer. If this spherical layer is used as a planet’s spherical layer, it should be considered that all the gravitons on the planet are emitted by this spherical layer.

The equivalent spherical layer of force emission, for general cases, can be considered to be in the middle of the planet’s graviton emission shell.

“On the nuclear force is the manifestation of gravity at the microscopic distance” [3] The article calculates the number of gravitons emitted by a single nucleon based on the binding energy of hydrogen. On the relationship between atomic structure and basic force” [4] The article, based on the analysis that the resonance of gravitational energy waves and nucleons conforms to the normal distribution, the number of gravitons emitted by a single nucleon per second is corrected as:

$$n_{ng}=2.227\times {10}^{22}$$

(1)

The ratio of gravitons passing through nucleons can be absorbed by nucleons is:

$$k_{ng}=0.378$$

(2)

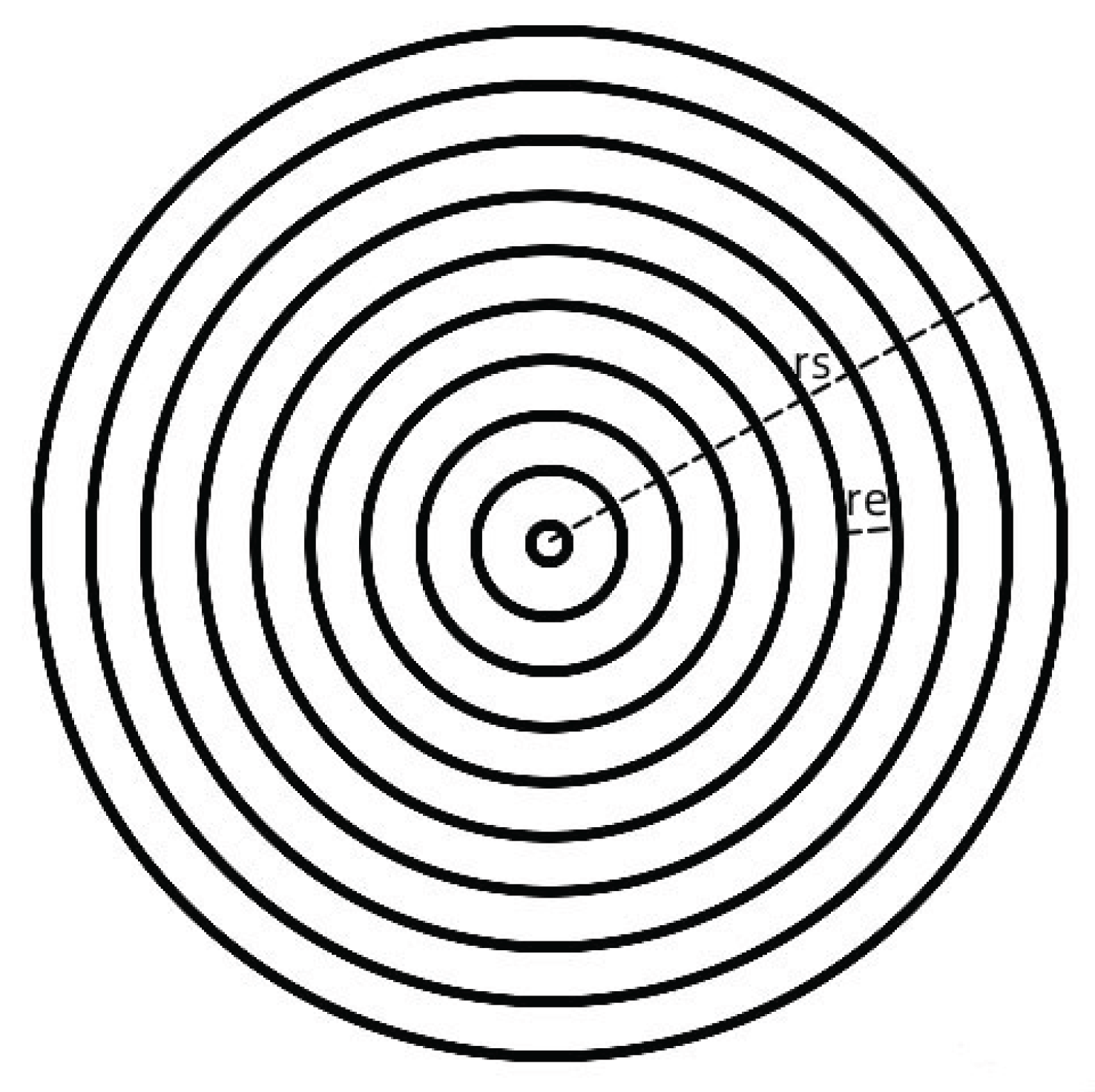
”The attempt to correct the universal gravitational formula from the proportion of the planet emitted to the outside of the ball - the ratio of the outside of the ball graviton in the deflection gravitational theory” [5] article calculates the number of gravitons sent to the outside of the ball. Figure 2 is a schematic diagram of the planet layering. In the figure, the mass of the planet is ms, the radius is rs, and the density is uniform.ρs, assuming the mass of a single nucleus is m0 and the radius is r0, assuming the equivalent radius of the volume occupied by a single nucleus in the planet is re, and then layer the planet according to the equivalent radius re, calculate the number of nucleons that can be distributed in each layer and the proportion of nucleon occlusion gravitons per layer, calculate the number of nucleon layers when the occlusion area is 4π, and then it can be calculated that the outer thickness of the sphere can emit gravitons outside the sphere is:

$$r_{so}={\displaystyle \frac{k_{s\rho }}{{\rho }_s}}={\displaystyle \frac{41540}{{\rho }_s}}$$

(3)

The number of gravitons sent by the planet to the outside of the ball is:

$$n_{go}=1.599\times {10}^{55}\left[r_s{}^2-2.679\times {10}^4{\displaystyle \frac{r_s}{{\rho }_s}}+2.876\times {10}^8{\displaystyle \frac{1}{{\rho }_s^2}}\right]$$

(4)

Where ρs is the density of the shell matter of the planet, ngo is the number of gravitons sent to the outside of the sphere by the planet, and rs is the radius of the planet.

When the planet is relatively large, the above formula is approximate:

$$n_{go}\approx {\mathrm{k}}_{\mathrm{gr}}{r}_s{}^2=1.599\times {10}^{55}{r}_s^2$$

(5)

Table 2. The number of extrasphere gravitons emitted by solar system planets.

Planet Name	ms (kg)	rs (m)	ρs (kg/m^3)	rso (m)	k	nso	nso （rs）	r0(m)
sun	1.99E+30	6.96E+08	10	4145.00	5.96E-06	7.75E+72	7.75E+72	8.00E-16
Mercury	3.30E+23	2.44E+06	5425	7.64	3.13E-06	9.52E+67	9.52E+67	m0(kg)
Venus	4.87E+24	6.05E+06	5242.3	7.91	1.31E-06	5.86E+68	5.86E+68	1.67E-27
Earth	5.97E+24	6.37E+06	2800	14.80	2.32E-06	6.49E+68	6.49E+68	nng
Mars	6.42E+23	3.39E+06	3934.1	10.54	3.11E-06	1.84E+68	1.84E+68	2.23E+22
Jupiter	1.90E+27	6.99E+07	1326.2	31.25	4.47E-07	7.81E+70	7.81E+70	ko
Saturn	5.68E+26	5.82E+07	687.1	60.33	1.04E-06	5.42E+70	5.42E+70	0.55
Uranus	8.68E+25	2.54E+07	1270.4	32.63	1.29E-06	1.03E+70	1.03E+70	kng
Neptune	1.02E+26	2.46E+07	1637.9	25.31	1.03E-06	9.69E+69	9.69E+69	0.378

Table 2. The number of extrasphere gravitons emitted by solar system planets.

Planet Name	ms (kg)	rs (m)	ρs (kg/m^3)	rso (m)	k	nso	nso （rs）	r0(m)
sun	1.99E+30	6.96E+08	10	4145.00	5.96E-06	7.75E+72	7.75E+72	8.00E-16
Mercury	3.30E+23	2.44E+06	5425	7.64	3.13E-06	9.52E+67	9.52E+67	m0(kg)
Venus	4.87E+24	6.05E+06	5242.3	7.91	1.31E-06	5.86E+68	5.86E+68	1.67E-27
Earth	5.97E+24	6.37E+06	2800	14.80	2.32E-06	6.49E+68	6.49E+68	nng
Mars	6.42E+23	3.39E+06	3934.1	10.54	3.11E-06	1.84E+68	1.84E+68	2.23E+22
Jupiter	1.90E+27	6.99E+07	1326.2	31.25	4.47E-07	7.81E+70	7.81E+70	ko
Saturn	5.68E+26	5.82E+07	687.1	60.33	1.04E-06	5.42E+70	5.42E+70	0.55
Uranus	8.68E+25	2.54E+07	1270.4	32.63	1.29E-06	1.03E+70	1.03E+70	kng
Neptune	1.02E+26	2.46E+07	1637.9	25.31	1.03E-06	9.69E+69	9.69E+69	0.378

Table 1 is a statistical table of the number of extraspheric gravitons emitted from the solar system planet. The first column in the table is the name of the planet, the second column is the mass of the planet, the third column is the radius of the planet, the fourth column is the thickness of the shell that the planet can send out of the ball, the sixth column is the ratio of the thickness of the shell that the planet can send out of the ball to the radius, it can be seen that this ratio is on the order of 10^-6, the seventh column is the number of gravitons sent out of the ball calculated based on the above equation (4), and the eighth column is the number of gravitons sent out of the ball calculated based on the above equation (5). It can be seen that the simplified formula has no effect on the calculation of the number of gravitons sent out of the ball, and the last column is several commonly used constants. From the above analysis, it can be seen that the thickness of the shell of the planet emitting gravitons outward is too small relative to the planet’s radius and can be ignored. Therefore, the equivalent shell radius of the planet’s emitting gravitons is approximately equal to the planet’s radius.

$$r_{se}=r_s-{\displaystyle \frac{1}{2}}{r}_{so}\approx r_s$$

(6)

If the energy transmitted by planet S per unit time to planet E is used as the gravity of planet S on planet E, then this gravity is the ratio of the area of ​​the sphere occupied by planet E from planet S distance R0 to the total number of gravitons emitted by planet S:

$$F_{se}={\displaystyle \frac{\pi r_e^2}{4\pi R_0^2}}{k}_{gr}{r}_s^{2}h=G_r{\displaystyle \frac{r_e^2{r}_s^2}{R_0^2}}$$

(7)

$$G_r={\displaystyle \frac{1}{4}}{k}_{gr}h$$

(8)

In the formula, Gr is the gravitational constant for calculating the gravity according to the planet’s radius. The modified gravitational formula above is related to the size of the planet and has no direct relationship with the planet’s mass. The radius of a planet actually represents the surface area of ​​the planet. Considering the equivalent radius of the gravity of the planet, under the same radius, the gravity of a neutron star will be slightly greater than that of an ordinary planet, but it will not be too different.

It is inferred from this that the gravity of the planet is proportional to the planet’s surface area. Although the density of neutron stars is very large, the volume is very small. Therefore, the internal density of neutron stars can be very large, but there are not many gravitational units emitted outside the ball, so the gravity of neutron stars is not very large, and the gravitational range of neutron stars is very limited. Therefore, it is impossible to form a large galaxy centered on neutron stars in the universe.

3. Conclusion

Generally, neutron stars have particularly high density. neutron stars with a diameter of 10km have a mass greater than that of the sun. According to Newton’s law of universality, gravity is proportional to mass, so the gravity of neutron stars should be larger than that of the sun, and the gravitational range of neutron stars should be larger than that of the solar system. Planets with such a large gravitational range should form galaxies larger than that of the solar system. The fact that many years of observations is that no large galaxies centered on neutron stars are found. The theory of deflection gravity believes that the most basic unit of matter mass is nucleons (collectively known as neutrons and protons). Each nucleon emits gravitons. Gravitational energy waves propagate in space. When gravitational energy waves encounter other nucleons and resonate with them to form gravity. For the planet, the gravitons emitted by the nucleons inside the planet interact with other nucleons inside the planet, forming cohesion inside the planet. Some of the gravitons emitted by the nucleons of the planet are emitted outside the ball, and these gravitons emitted outside the ball interact with other planet shell nucleons to form gravity between the planets. From this, the planet is layered and the number of gravitons sent out of each layer can be calculated. You can get the number of graviton layers (thickness) sent out of the planet and the total number of gravitons sent out of the ball. From the derivation calculation, we can see that the total number of gravitons sent out of the ball of the planet is proportional to the planet’s surface area. The total number of gravitons sent out of the ball of the planet is equivalent to the gravity of the planet, and the gravity of the planet is proportional to the planet’s surface area. Although the density of neutron stars is very large, the volume is very small. Therefore, the internal density of neutron stars can be very large, but there are not many gravitons emitted outside the sphere, so the gravity of neutron stars is not very large, and the gravitational range of neutron stars is also very limited. Therefore, it is impossible to form a large galaxy centered on neutron stars in the universe.