Estimation of the Coupling Constants for the Strong Interaction in the Framework of the Electromagnetic Bridge Theory

1. Introduction

This paper proposes a very particular approach to the problem of variability with the energy scale of the coupling constant of the strong interaction ${\alpha }_s\left(\mu \right)$. The approach, developed in the framework of Bridge Electromagnetic Theory (or in short Bridge Theory), has deep roots in Maxwellian electromagnetism [1] and suggests a clear framework of unification between electromagnetic and strong forces, introducing a possible general solution to the problem of the running coupling. The developed model allows to obtain a unified view of electromagnetic and strong interactions, paving the way for a unique theory based on the Bridge Theory (BT).

BT is a relativistic quantum theory of electromagnetic interactions between particles. Developed entirely on the basis of Maxwellian electromagnetism, BT has the advantage over many other theories of being completely self-consistent. In fact, the theory makes use of Maxwell's electromagnetism to explain typically quantum and relativistic phenomenologies, demonstrating that these two apparently incompatible aspects of the physical world have the same origin [2,3]. In this sense, it can be said that BT is a conceptual, phenomenological and formal bridge between different theories, able of justifying their synergistic use within the same phenomenological context.

The basic idea arose from the consideration that an electromagnetic interaction between two charged particles generally creates an electromagnetic dipole considered in the context of electromagnetism as point-like, therefore with a symmetrical electromagnetic field emitting a spherical wave.

If we make a leap in scale, their interaction at the nano level takes place with a non-zero collision parameter, therefore with a finite dipole moment that has an evolution over time. This implies that the dipole electromagnetic field has a cylindrical symmetry, so it has a Poynting vector that is not always radial with respect to the virtual centre of the dipole and due to the process of approaching and moving away of the two interacting particles, it lives only for a finite time determined by the collision parameters. Because of cylindrical symmetry, not all of the energy produced in the interaction can be emitted instantaneously, which is the case with spherical symmetry. A part of the energy and momentum associated with the transverse component of the Poynting vector is localized in the source zone and represents, quantitatively and formally, the quantum of energy exchanged in the interaction between the two particles. The effective duration of the interaction is $T=c/\lambda$ where $\lambda$ is the minimum distance reached by the two particles during the dipole formation, identical to the emission wavelength. This idea, proposed under form of conjecture [4] in 1989, was proved in 1990 with the explanation of the nature of the Sommerfeld and Planck constants [5,6], represents the starting point for the BT.

Compared to all other quantum theories in which quantization must be introduced as a fundamental principle, BT has the advantage of being self-quantized, i.e. given the particular way of interaction between charges and electric fields, it is possible to determine autonomously and without introducing extraneous constants, the electromagnetic coupling constant and from this to coherently obtain the value of the Planck action constant. The values obtained are in excellent agreement with those obtained experimentally but unlike what happens for standard theories these are not true constants, because they are subject to changes according to the constraints and external forces to which the interacting system is subjected, as in the case of the electron-proton capture process that gives rise to a hydrogen atom [7].

Formally, BT agrees with both formalism and the standard phenomenologies of relativity and quantum mechanics, only some basic phenomenologies disagree as they are consistent with the fundamental distinguishing elements of BT and that is why they can provide valuable experimental support to test the theory. In fact, in this framework, the interactions between charged particles follow a different phenomenology than usual which nevertheless leads to a result consistent with the experimental one.

In BT, an unusual way of conceiving interactions between charged particles has therefore been developed. In fact, interactions in a group of $n$ particles occur as superpositions of dipoles and not as multipolar interactions. Each dipole is formed by a possible combination of two of the $n$ particles, each of which forms a Dipole Electromagnetic Source (DEMS). The electromagnetic structure of each DEMS, if formed by pairs of particles, corresponds formally and quantitatively to a quantum of energy, therefore to an exchange photon that mediates the interaction between the two particles, otherwise, although having the same formal appearance of a quantum, the value of its constant of action can be very different from that of Planck's constant.

For example, for a pair of particles with one unit of electric charge, such as the interacting electron and proton, the action constant coincides with the value of Planck's constant but may be slightly different in the case of unconstrained free interaction and in the case of bound interaction as in a hydrogenoid atoms [8]. This result allows us to obtain an explanation consistent with Maxwellian electromagnetism of the reason for the value of the electromagnetic coupling constant of Sommerfeld which can take slightly different values depending on the type of experimental measurement system used.

The aim of this article is to demonstrate that the same phenomenology and the same principles applied to the electromagnetic interactions between integer electric charges, when applied to hadrons, provide results in excellent agreement with the experimental measurements of the strong coupling constants, providing a prediction of the coupling value as a function of the coupling energy, therefore as a function of the scale value, demonstrating that the strong interaction is not another force, but is a different way of manifesting itself from the electromagnetic force and that it is therefore unifiable in a single theoretical scheme.

To achieve our goal, we will first deal with the interaction between two particles with any electric charge. One will then apply the model to the direct electromagnetic interaction of a pair of electrons by obtaining the structure function and calculating its action, and then extend the model to single pairs of quarks and a pair of protons. One will calculate theoretically the low-energy, high-energy strong coupling constant assuming the production of up to three $Z^0$ bosons, then develop a method for the generalized calculation of the coupling constant at any energy level.

2. Electromagnetic Interaction of Two Charged Particles Mediated by DEMS

Following the principles of BT in Ref. [2], to generalize the formation model of a DEMS produced by the direct electromagnetic interaction of two charged particles, regardless of their actual charge value: $C_i={\chi }_{i}e$ and $C_j={\chi }_{j}e$, where $-1\le {\chi }_i\le 1$ and $-1\le {\chi }_j\le 1$ are dimensionless charges associated with a DEMS with an action value expressed in the Dirac form ${\hslash }_{ij}$, the DEMS produced localize an energy exchange

$$E_{ij}=2\pi {\displaystyle \frac{{\hslash }_{ij}c}{\lambda }}$$

(1)

with wavelength $\lambda$ equal to the minimum distance achieved by the two particles during their approach.

The value of the action written in Gaussian units

$${\hslash }_{ij}={\sigma }_{{\chi }_i{\chi }_j}{\displaystyle \frac{e^2}{c}}$$

(2)

depends on the value of the electromagnetic structure function of the DEMS

$${\sigma }_{{\chi }_i{\chi }_j}={\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left({\chi }_i,{\chi }_j,\rho ,\theta \right)d\theta }-{\displaystyle \frac{{\chi }_i{\chi }_j}{4\pi {\rho }^2}}$$

(3)

where the function in the integral at first term at R.s. of the Eq. (3)

$$\begin{array}{l}{\mathsf{\Theta }}_t\left({\chi }_i,{\chi }_j,\rho ,\theta \right)=16\sqrt{{\displaystyle \frac{{\chi }_i^2}{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{{\chi }_j^2}{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{2{\chi }_i{\chi }_j\left(4-{\rho }^2\right)}{\sqrt{{\left[{\left(4+{\rho }^2\right)}^2-16{\rho }^2{\cos }^2\theta \right]}^3}}}}\\ \cdot \left|{\displaystyle \frac{{\chi }_i\left(2+\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^3}}}+{\displaystyle \frac{{\chi }_j\left(2-\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^3}}}\right|\end{array}$$

(4)

is directly related to the structure of the electromagnetic field associated to the transversal component of the Poynting vector of the DEMS produced during the interaction, and the second term at R.s. of the Eq. (3), is related to the Coulombian term due to the electrostatic work of the two interacting particles. Therefore, considering the Eq. (3) and (4), the theoretical value of the structure function for an interaction between two charged particles, depends on the value of the dipole ratio $\rho =R/\lambda$ and by the value of the dimensionless charges $({\chi }_i,{\chi }_j)$that parametrize it.

The structure constant (3), describes the ability of the electromagnetic field of the DEMS to localize energy as a function of the dipole ratio and of the dimensionless charges value of the interacting particles. It easy to verify that only for pairs of particles Eq. (3) can be simplified in the form

$${\sigma }_{{\chi }_i{\overline{\chi }}_i}={\chi }_i^2\sigma$$

(5)

therefore, using Eq. (3) the electromagnetic coupling constant of two particles is ${\alpha }_{{\chi }_1{\chi }_2}={\sigma }_{{\chi }_1{\chi }_2}^{-1}$ and for pairs of charges using Eq. (5) becomes ${\alpha }_{\chi \overline{\chi }}={\displaystyle \frac{\alpha }{{\chi }^2}}$, where α represents the intensity of the interaction between two particles with unit of charge, i.e., $\alpha \equiv {\alpha }_{1,-1}$.

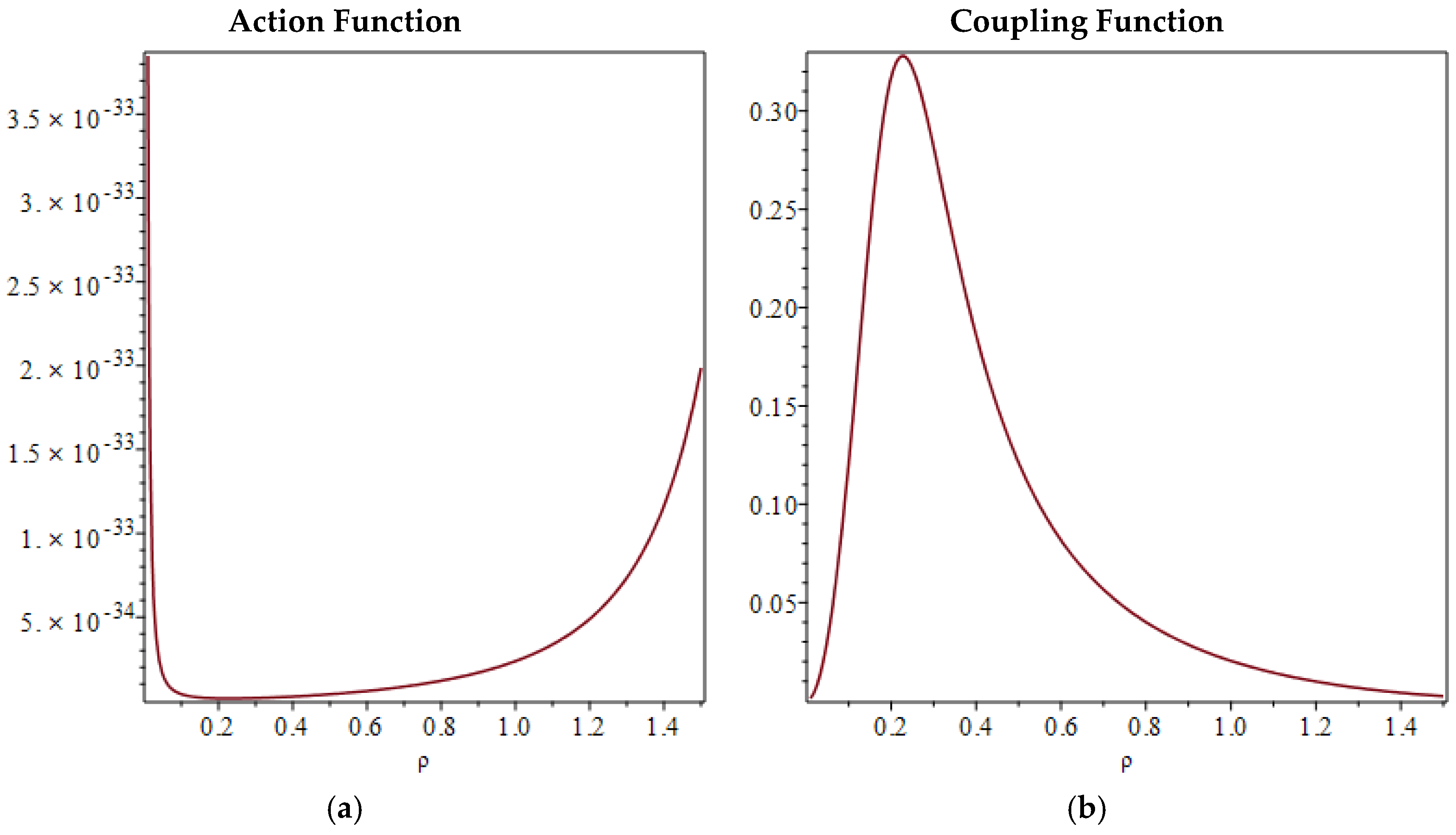
To exam the behaviour of the coupling constant α as a function of the dipole ratio, using Eq. (3) one defines the coupling function

$$\alpha ={\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}\right)}^{-1}$$

(6)

with which using the Eq. (2) in S.I. units one defines the action function

$$h=\left({\displaystyle \frac{2\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{8\pi {\rho }^2}}\right){\displaystyle \frac{e^2}{{\epsilon }_{0}c}}$$

(7)

Figure 1a-b show the behaviours of the Eq. (6) and (7). Since the type of interaction depends on the value of the dipole ratio, for $R\ge \lambda$, i.e. for $\rho \ge 1$, the interaction is electromagnetic, otherwise for $R<\lambda$, i.e. for$\rho <1$, the ability of the DEMS to store energy is reduced compared to the electromagnetic case but the interaction is much more intense.

One assumes that for $\rho <1$ the interaction is of strong type, while for $1\le \rho \le 3/2$, as already demonstrated in BT (see Ref. [2],[5]), the interaction is electromagnetic but it occurs in a quantised way. In this paper one wants study the range $\rho <1$ corresponding to the strong interaction.

Let us now analyse the case of electromagnetic interaction.

- Free interaction between a pair of charged particles with unitary integer charge.

Without external constrains acting on the DEMS, the dipole ratio has been calculated using a stochastic method giving the root-mean-squared length${\rho }_{free}=1.27555787491640$ (see Ref. [2],[6]) giving respectively structure constant, coupling constant and action constant:

$$\begin{array}{l}{\sigma }_{free}=137.036669830443\\ {\alpha }_{free}=7.29731685130200 {10}^{-3}\\ h_{free}=6.626102585 {10}^{-34} \mathrm{Js}\end{array}$$

Since the energy exchanged during an interaction between a pair electron-positron $E_{exc}=h_{free}c/\lambda$ depends by the minimum distance $\lambda$ achieved during their reciprocal motion, since the standard value of action $h$ is the value of the Planck’s constant $h_{free}>h=6.62607015 {10}^{-34} \mathrm{Js}$, it follows that the energy exchanged between an interacting electron-positron pair is slightly greater than expected $hc/\lambda$. As a result, the photons emitted in the process of annihilation of the pair have an energy slightly higher than that predicted using Planck's constant, indicating that the mass of the electrons is slightly higher than the real one. Conversely, for the creation of a pair by means of two gammas, the energy required to produce the electron-positron pair must be slightly greater than the calculated threshold value, as a small excess of electron mass with respect to the masses calculated using the standard value of Planck's constant must be taken into account.

- Electron-proton capture.

In the case of electron-proton capture (see Ref. [7]), the dipole ratio initially identical to that of the free case, undergoes a series of successive adjustments during the capture and stabilization phase. The value was calculated initially using the stochastic method as in the previous free case, then a number $N$ of recursive corrections were applied, each corresponding to an orbital readjustment at each revolution of the electron of the reciprocal distance electron-proton, until the equilibrium condition was reached in a stable hydrogen configuration.

The capture corresponds to a constrain acting on the two interacting particles on the fundamental level $n=1$ of the hydrogen: ${\rho }_{orb}=1.27555661859994$. In this case, the value of the coupling constant is closer to the experimentally measured value, consequently the action constant is also closer to the standard value:

$$\begin{array}{l}{\sigma }_{orb}=137.035950244954\\ {\alpha }_{orb}=7.29735517003008 {10}^{-3}\\ h_{orb}=6.626067788 {10}^{-34} \mathrm{Js}\end{array}$$

Considering that the experimental value of the Sommerfeld constant [9] ${\alpha }^{-1}={\sigma }_{\exp }=137.035999206(11)$ has a value internal to the interval $\left[{\sigma }_{orb} , {\sigma }_{free}\right]$ and that the theoretical value of the atomic structure constant $\sigma$ increases as a function of the quantum number $n$ associated to the orbital, reaching as its maximum value ${\sigma }_{free}$ and decreases as a function of the atomic number $Z$ (see Ref. [8]), the experimental value ${\sigma }_{\exp }$ could be considered compatible with atomic transitions involving the outermost orbital levels of matter with a high $Z$value, therefore, experimental measures involving different atomic transition will give different values of the structure constant.

Figure 1b plots the coupling function (6) in the range of dipole ratio values $0<\rho \le 1.5$. Consider that the characteristic electromagnetic interaction zone is limited to the range $1\le \rho \le 1.5$ of the dipole ratio. In Figure1a,b it can be seen that for a single interaction between a pair of integer charges the maximum value of the coupling constant $\alpha \approx 0.33$ is reached for the minimum action value ${\rho }_{\min }=0.22734330$.

3. Strong Interactions

Considering the low-energy electromagnetic interaction of a proton-antiproton pair, having the unit charge pair, the action function and the coupling function are exactly the same as those obtained for the electron-positron interaction, so the Eq. (6) and (7) describe their interaction.

Increasing the interaction energy reduces the dipole ratio, so that the quarks that make up the two particles also interact. Examining the structure function in Eq. (5) and considering the internal structure of the proton-antiproton in the form $(uud)-(\overline{u}\overline{u}\overline{d})$, is possible to consider the interaction of the two particles as formed by the contributes of three pairs quark-antiquark $\left(u\overline{u},u\overline{u},d\overline{d}\right)$, i.e. the structure function can be written indifferently as the interaction between two unitary charges obtaining ${\sigma }_{p\overline{p}}$ or:

$${\sigma }_{p\overline{p}}=2{\sigma }_{u\overline{u}}+{\sigma }_{d\overline{d}}$$

(8)

which sum gives the electromagnetic structure constant

$${\sigma }_{p\overline{p}}={\displaystyle \frac{8}{9}}\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}\right)+{\displaystyle \frac{1}{9}}\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}\right)={\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}$$

(9)

identical to that of a pair electron-antielectron ${\sigma }_{p\overline{p}}\equiv \sigma$.

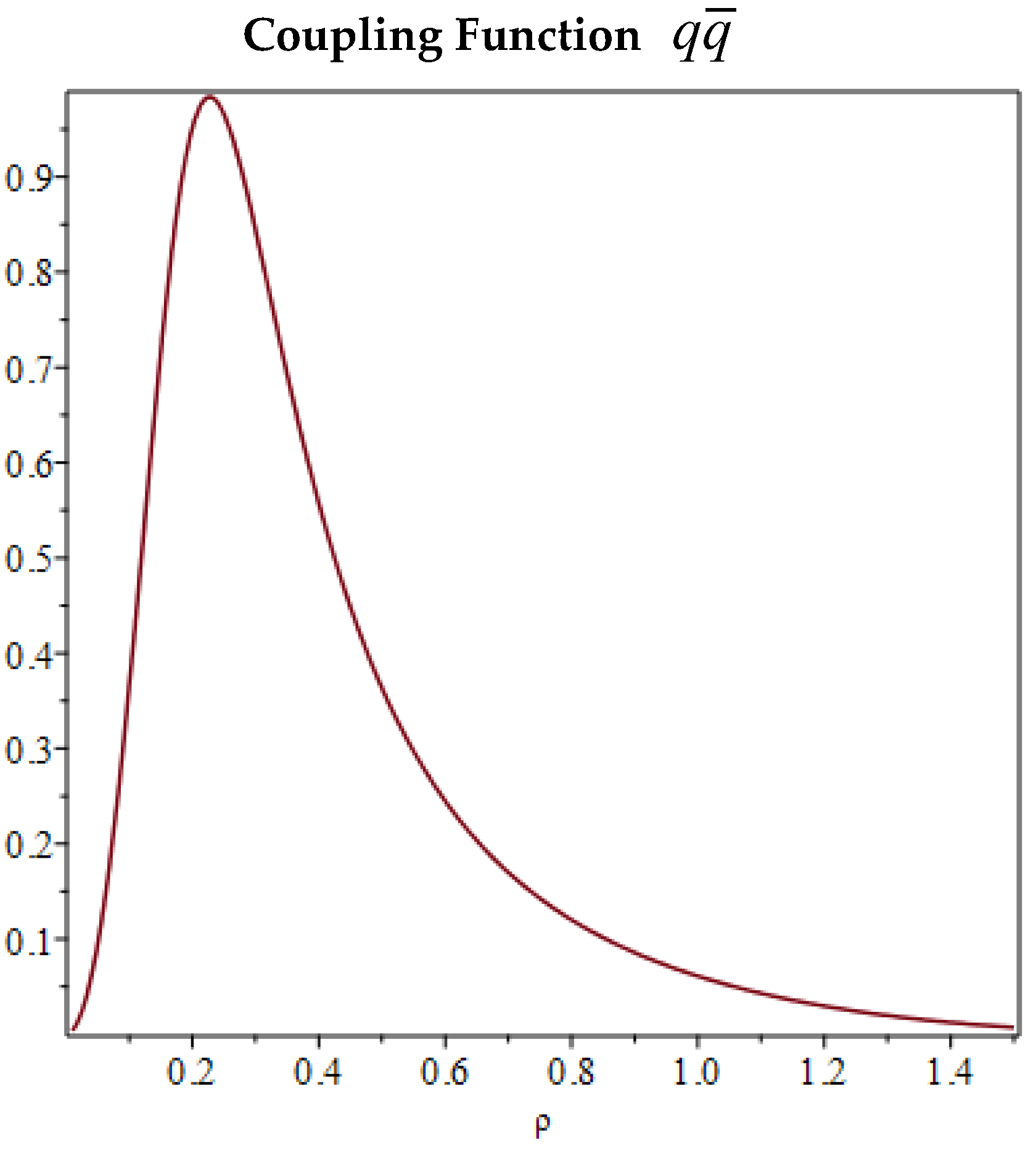
Considering the presence inside the protons of quarks in interaction, their field structures are intimately connected, so to consider the structural function of the DEMS produced by a single pair of quarks, given the additive property highlighted by Eq. (9), one considers the mean interaction constant constructed by dividing by three by the structure constant (9) of the proton-antiproton pair, obtaining by the quark-antiquark mean coupling constant

$${\alpha }_{q\overline{q}}={\displaystyle \frac{3}{\sigma }}={\left({\displaystyle \frac{4\pi }{9}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{12\pi {\rho }^2}}\right)}^{-1}$$

(10)

with maximum value of coupling in the minimum action point corresponding to a mean ratio ${\rho }_{min}$ .

3.1. Strong Coupling Constant ${\alpha }_s$ and Gluons

Considering a quark-antiquark interaction at very low energy in such a way that the action is minimal, the correlated coupling constant has maximum value

$${\alpha }_s=\max ({\alpha }_{q\overline{q}})={\left({\displaystyle \frac{4\pi }{9}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(1,-1,{\rho }_{\min },\theta \right)d\theta }+{\displaystyle \frac{1}{12\pi {\rho }_{\min }^2}}\right)}^{-1}=0.983898139$$

(11)

which value can be considered approximatively ${\alpha }_s\cong 1$ corresponding to the value of the strong coupling constant in Figure 2 at the minimum of action.

If one considers the DEMS formed between the two quarks of the pair, the localised energy is formally similar to that of the photon but with a much smaller constant of action

$$h_{q\overline{q}}^{\min }={\displaystyle \frac{e^2}{2{\epsilon }_0{\alpha }_{s}c}}=4.914408122 {10}^{-36} \mathrm{Js}$$

(12)

Thus, the average energy exchanged in a pair of quarks is equivalent to a quantum “Q” that differs from the photon only in the value of the action constant. We will call this mediator “gluon” by analogy with the standard phenomenology; its energy depends on the minimum interaction distance at which the quarks are located:

$$E_Q={\displaystyle \frac{h_{q\overline{q}}^{\min }c}{\lambda }}$$

(13)

Considering that two quarks are two charged particles that can also interact electromagnetically, for a pair of quarks placed at the same minimal interaction distance $\lambda$ the electromagnetic interaction produce a DEMS by locating a photon energy equal to that of the mass energy of the two interacting particles

$$E_{ph}={\displaystyle \frac{hc}{\lambda }}$$

(14)

By performing the ratio between the energies of Eq. (13) and (14) one obtains

$${\displaystyle \frac{E_Q}{E_{ph}}}={\displaystyle \frac{\alpha }{{\alpha }_s}}\cong {\displaystyle \frac{1}{137}}$$

(15)

The Eq. (15) highlight as the coupling value of the strong interaction ${\alpha }_s$ is 137 times greater than the electromagnetic coupling value, with an exchange of energy and momentum 137 times intense than the electromagnetic one, therefore, for the energy exchanged between a pair of quark, using Eq. (15) the exchanged energy of a gluon can be written as

$$E_Q={\alpha }_s^{-1}\alpha E_{ph}\cong \frac{1}{137}{E}_{ph}$$

(16)

Considering the collision of a pair of particles $\left(X,\overline{X}\right)$, the interaction forms a DEMS, therefore, one can consider the interaction occurring in two phases, the first produce the DEMS, the second from the DEMS are emitted the product in the form $Y=y_1+y_2+\mathrm{...}$ in these two phases the DEMS change in internal composition but not in energy

$$X\overline{X}\to DEMS\to Y$$

(17)

Considering that the DEMS has an energy in the centre of mass $E_{ph}$ equal to that of the interacting pair of particles, the energy of the DEMS can be considered formed by two contributes: the former due to the energy and momentum associated to the number $N=\left(\begin{array}{c}k\\ 2\end{array}\right)\left(n_{ph}+n_g\right)$ of energy exchanges $E_Q$ occurring during the interaction, where $k\ge 2$ is the number of the active virtual quarks at the energy of the DEMS $E_{ph}$, $n_{ph}$ is the number of photon exchanges between the integer interacting particles, $n_g$ is the number of gluons exchanged at the same distance of interaction between all pairs of quarks; the second corresponds to the total energy ${\epsilon }_Y$ of the rest mass of the emerging particles after the interaction, so it can be written

$$E_{ph}=N{E}_Q+{\epsilon }_Y$$

(18)

Using Eq. (16), the Eq. (18) becomes

$$E_{ph}=N{\alpha }_s^{-1}\alpha E_{ph}+{\epsilon }_Y$$

(19)

from which

$${\epsilon }_Y=E_{ph}(1-N{\alpha }_s^{-1}\alpha )$$

(20)

is the energy of the total rest mass of the emerging particles after the collision. Equation (20), known $E_{ph}$ and known ${\epsilon }_Y=\overline{m}{\epsilon }_0$, with ${\epsilon }_0$ rest mass energy of an intermediate boson $Z^0$ and $\overline{m}$ the mean multiplicity of the event produced during the collision, is able to predict the value of the strong coupling constant as a function of the energy scale defined by $E_{ph}$ (running coupling). From Eq. (20) one obtains:

$${\alpha }_s(E_{ph})=\left(\begin{array}{c}k\\ 2\end{array}\right){\displaystyle \frac{\left(n_{ph}+n_g\right)\alpha }{1-\frac{\overline{m}{\epsilon }_0}{E_{ph}}}}$$

(21)

To test the "running coupling" described in Eq. (21), we will use the standard energy scale used experimentally to measure the value of the strong coupling constant as the energy scale changes. To simplify the comprehension of the elements of the equation (21) in QCD terms, let formally $n_f=k$ equal to the number of activated quarks at the energy scale $\mu =E_{ph}$ and ${\epsilon }_0=E\left(M_Z\right)$ the mass of the boson $Z^0$; Eq. (21) can be rewritten as

$${\alpha }_s(\mu )=\left(\begin{array}{c}{n}_f\\ 2\end{array}\right){\displaystyle \frac{\left(n_{ph}+n_g\right)\alpha }{1-\frac{\overline{m}E(M_Z)}{\mu }}}$$

(22)

Considering the channels in Eq. (17), the following will be considered as DEMS:

$$X\overline{X}\to \left(\begin{array}{c}e\overline{e}\\ p\overline{p}\end{array}\right)$$

(23)

it is important to note that in this work all references to hadronic collisions explicitly refer to proton-antiproton interactions $\left(p\overline{p}\right)$ rather than proton-proton $\left(pp\right)$, in order to model the real dynamics of the quark-antiquark pair consistent with the DEMS framework in the context of BT. Therefore, the emission products of Eq. (17) are

$$Y=\left(\begin{array}{l}{y}_1\\ y_2\\ y_3\end{array}\right)=\left(\begin{array}{l}{Z}^0\\ Z^0{Z}^0\\ Z^0{Z}^0{Z}^0\end{array}\right)$$

(24)

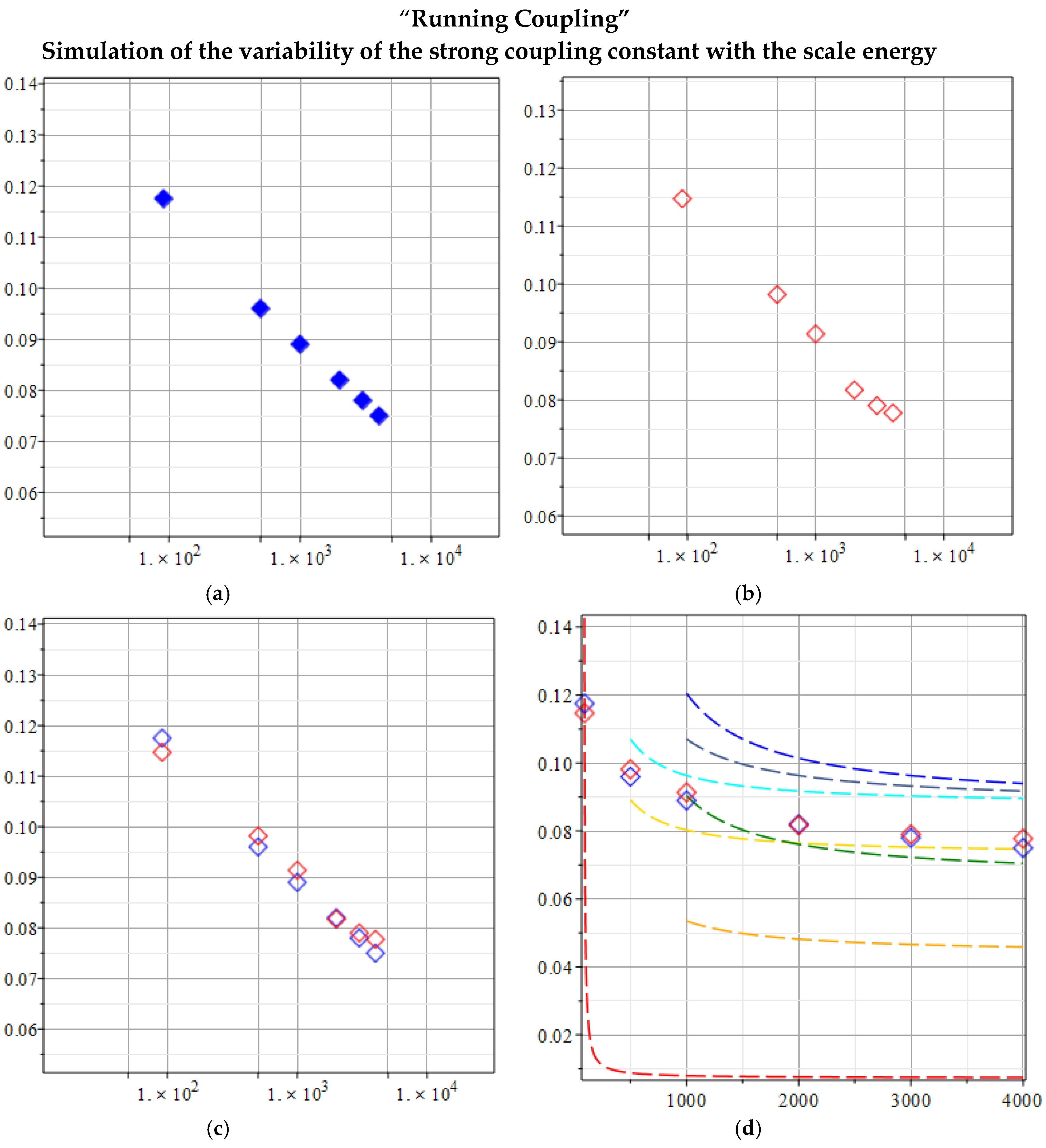
each associated with a family of coupling functions (22) defined by a set of numbers $\left(n_f,n_{ph},n_g,\overline{m}\right)$. Table 1 shows the results of the coupling constants obtained for each channel (24) as a function of the energy scale. The results obtained were averaged by homogeneity of the energy scale value. The same operation was carried out on the results obtained experimentally. Figure 3 shows the experimental results (a), the theoretical results (b), their superposition (c) and their relationship with the curves obtained from Eq. (22) before being mediated in (d). The extraordinary agreement between the theoretical and experimental results is evident. 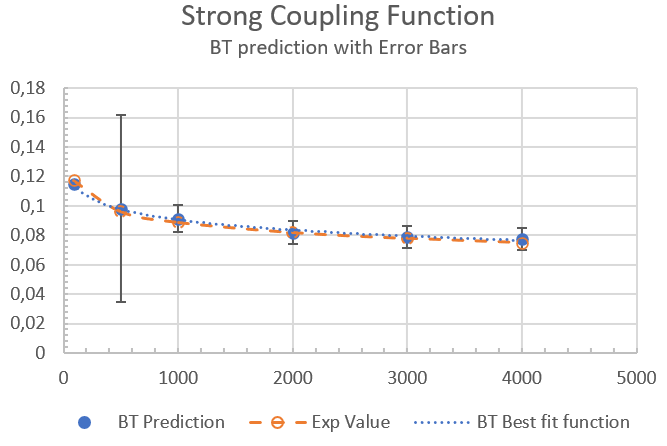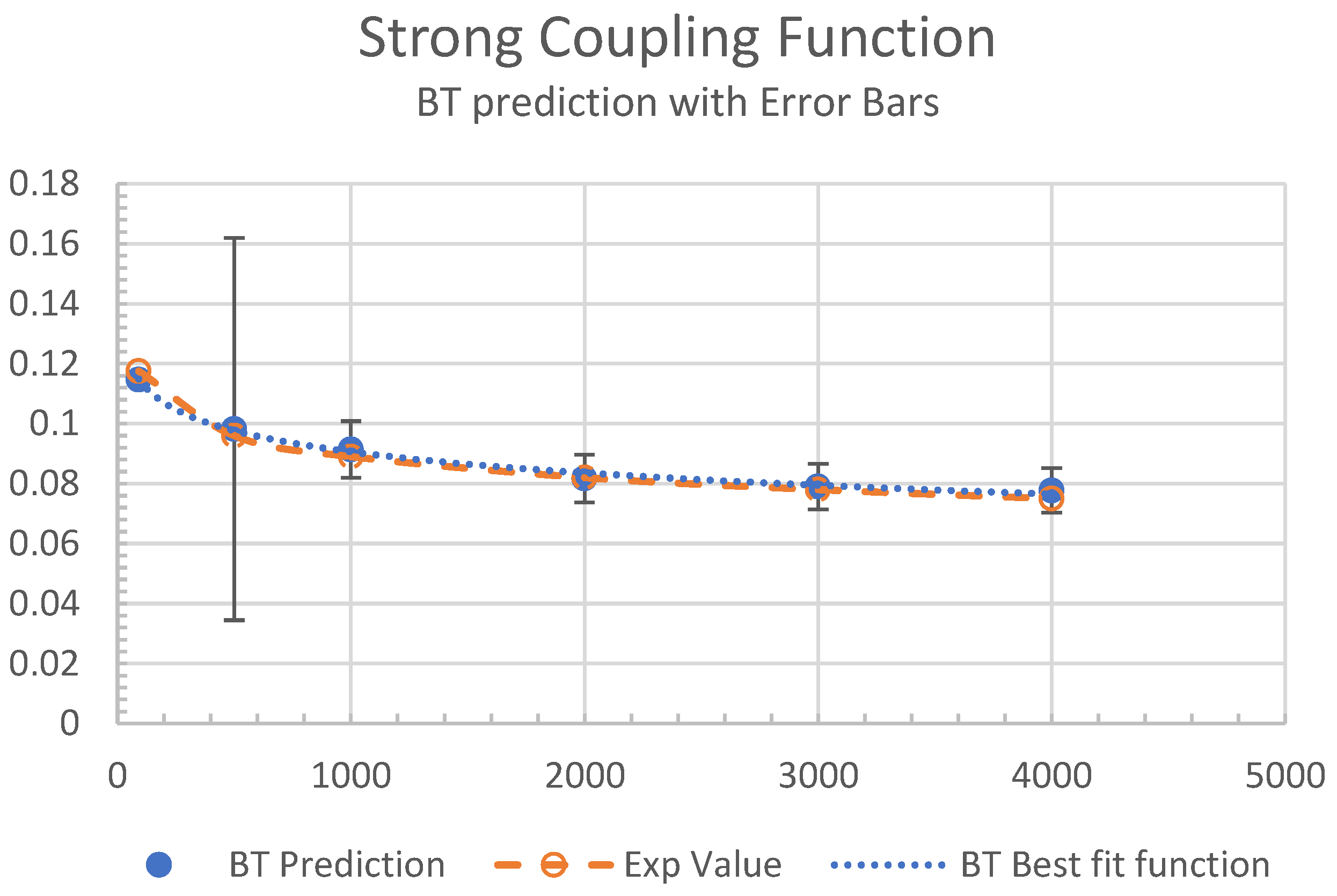Figure 4 shows the data of Figure 3c with the relative statistical errors due to the superimposition of measurements from curves of different origin.

Considering the best fit function of the theoretical data in Figure 3b, one obtains an enough precise function with$R^2=0.9941$ within the energy scale range 92.200 GeV – 4000 GeV

$${\overline{\alpha }}_s^{th}(\mu )=0.1607-0.01\ln \mu$$

(25)

the Eq. (25) is able to interpolate the strong coupling values on the running function. The curve (25) is shown in Figure 4. Its best correspondence with the best fit function obtained by the experimental data

$${\overline{\alpha }}_s^{\exp }(\mu )=0.1668-0.01\ln \mu$$

(26)

with $R^2=0.9962$, confirms the excellent correspondence of the theoretical strong coupling values with the experimental ones, allowing us to suggest an electromagnetic nature of the origin of the strong interaction at each energy scale value.

9. Discussion and Conclusions

The results reported here provide the first fully theoretical prediction of ${\alpha }_s\left(\mu \right)$ within a framework entirely distinct from QCD, yet achieving excellent agreement with experimental data across multiple energy scales. In fact, this work presents a theoretical prediction of the strong coupling constant ${\alpha }_s$ as a function of energy scale, developed entirely within the framework of Bridge Theory (BT). Applying the concept of electromagnetic dipole interaction (DEMS) between quarks, the running behaviour of ${\alpha }_s$emerges naturally from considerations on the field geometry of the DEMS and energetics, without invoking specific postulates of QCD.

The resulting coupling function, derived from the electromagnetic interaction geometry of quark pairs, exhibits a maximum value ${\alpha }_s\cong 1$ at low energy and decreases with increasing scale, reproducing the expected asymptotic freedom. Equation (22), formulated from first principles, enables the calculation of ${\alpha }_s$ for any energy scale by considering the number of active quarks and exchanged gluons and photons during the interaction of the particles. The theoretical predictions match remarkably well with experimental values across the 91–4000 GeV range, as demonstrated in Table 1 and Figure 3 and Figure 4.

This agreement is particularly striking given that no QCD formalism is used. Instead, the BT formalism interprets strong interactions as emergent from high-intensity electromagnetic couplings between fractional charges, localized through DEMS. The fit function obtained from the BT model closely mirrors the empirical best fit for ${\alpha }_s(\mu )$, confirming the predictive power of the approach.

These results support the hypothesis that the strong force may be an effective manifestation of electromagnetic interactions under specific geometric constraints, and that the coupling constant ${\alpha }_s$derives from the same fundamental action principles that govern electromagnetic interactions.

This reinterpretation opens a possible unification path between the strong and electromagnetic interactions without introducing new interaction types, suggesting that the distinction between forces may arise from the interaction scale and dipole structure rather than from fundamentally different fields.

Future investigations will aim to extend this analysis to other processes and energy regimes, and to derive the dynamics of confinement and hadronization within this unified framework.