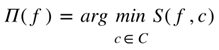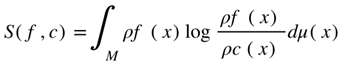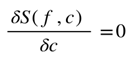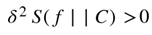Entropy-Guided Constraint Collapse: A Compact Framework for Field Stability and Structure

1. Constraint Manifold and Collapse Operator

Let F denote the space of physically admissible field configurations, typically smooth mappings f:M→R^n over a manifold M. We define a constraint manifold C⊂F as the subspace of configurations satisfying physically or geometrically consistent boundary or regularity conditions. These conditions are not externally imposed, but emerge via a generalized entropy functional S(f,c), with f∈F, c∈C.

We define a collapse operator

which selects, for a given unconstrained field f, a configuration c∈C that minimizes entropy mismatch. This operator enforces a collapse dynamic, interpreted as a resolution mechanism, by which unstable or off-shell field states are projected into stable, constraint-compatible forms.

One representative form of the entropy functional is

where ρf, ρc represent probability or energy densities associated with configurations f and c, and μ is a background measure on M. This formulation captures the information-theoretic deviation between arbitrary and admissible field states.

2. Entropy Topology and Morse Structure

The entropy functional defines a geometric landscape over the constraint manifold C, where variational stability is encoded in the curvature of S(f,c). Critical points of the collapse operator correspond to solutions satisfying

with stability governed by the second variation

This condition implies the existence of isolated minima, akin to Morse-type critical points, which act as structural attractors for the collapse dynamic. These attractors represent discrete, stable field configurations emerging from entropy-reducing evolution.

This behavior naturally induces a stratified topology over C, where solutions cluster into discrete layers according to their entropy depth. These strata may correspond to observable physical structures such as energy eigenstates, curvature configurations, or gauge-invariant solutions.

3. Sobolev-Type Admissibility

Rather than assuming smoothness or differentiability conditions a priori, this framework derives them as a consequence of entropy minimization. Such configurations with discontinuities or divergences result in S(f,c)→∞, making them inadmissible under the collapse operator. Only fields with sufficient regularity, bounded variation, or compact support can participate in the entropy-guided projection.

This behavior resembles Sobolev admissibility, where function classes are filtered by smoothness and integrability properties. The constraint manifold C⊂F thus inherits a naturally regularized functional topology, not from assumption, but from the entropy metric’s exclusion of non-convergent fields.

4. Summary and Outlook

This framework defines collapse as a variational projection onto entropy-minimizing constraint manifolds. Its key features include a collapse operator Π:F→C governing dynamic resolution through entropy minimization. Morse-type structure and stratification of admissible fields via second variation of the entropy functional. Emergent smoothness criteria analogous to Sobolev constraints, without external imposition. This formulation remains agnostic to specific field dynamics or symmetry assumptions. Instead, it proposes a geometric-informational mechanism by which structure and regularity emerge from constraint-enforced entropy flow. Future work will explore extensions to curved manifolds, gauge field emergence, and experimental implications in Casimir and interferometric systems.