Eigenphysics: The Emergence of Quantization from Entropy Geometry

1. Introduction

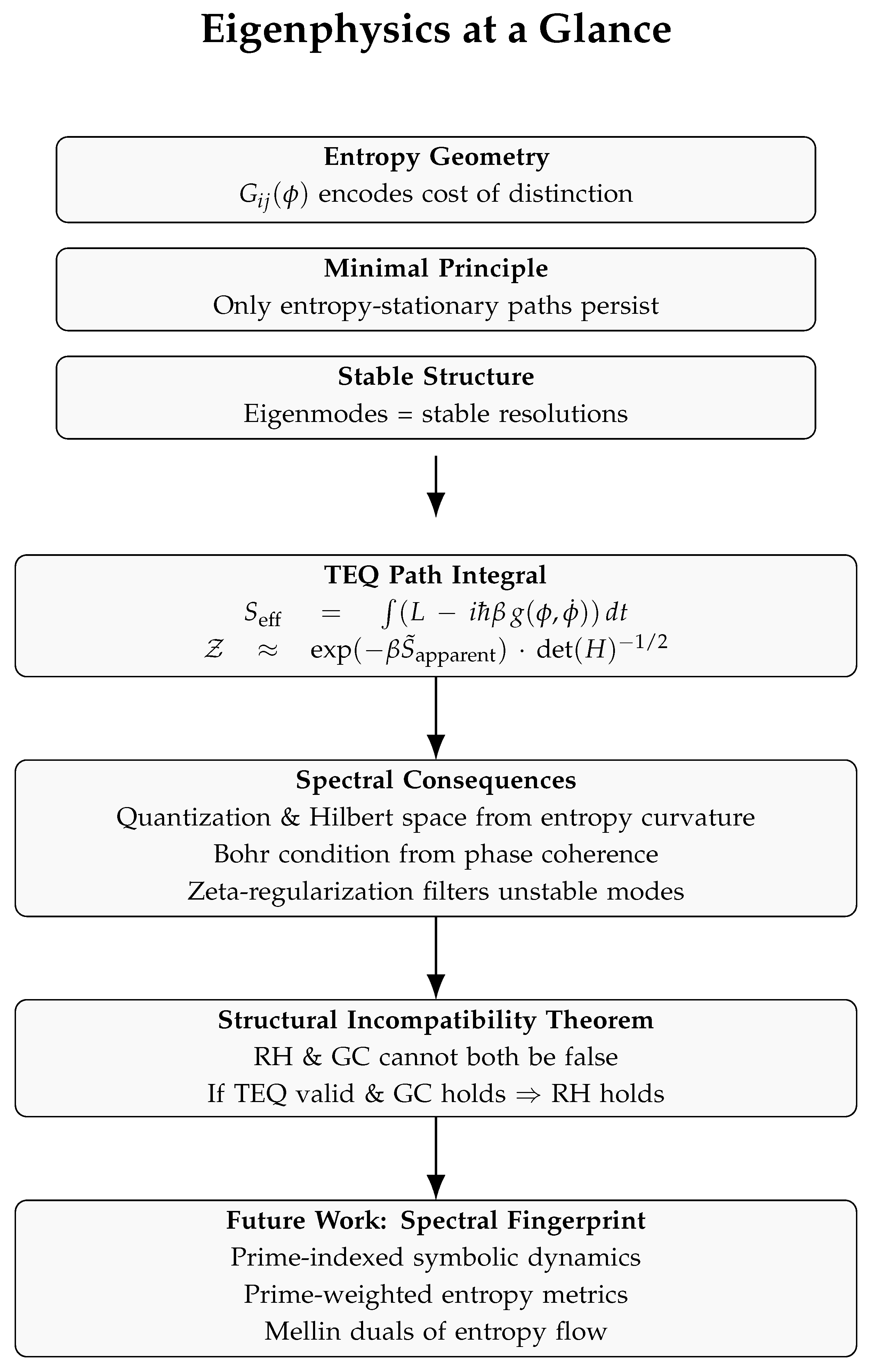
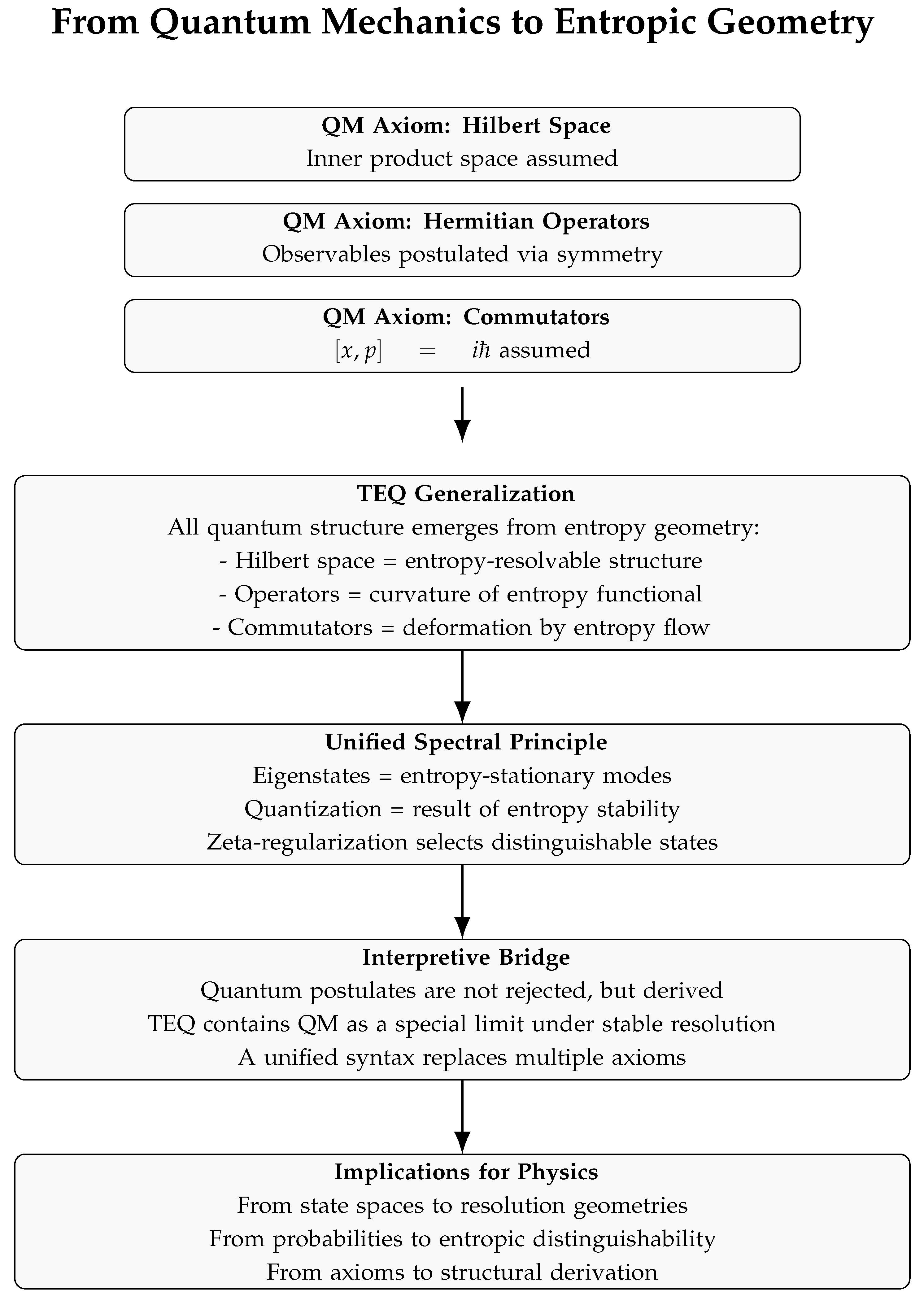
Eigenvalues play a foundational role in modern physics. From quantized energy levels in quantum mechanics to the stable modes of classical systems, the discreteness of eigenvalues has become a defining feature of physical structure. Yet in conventional theories, this structure is not derived—it is assumed. Operators are postulated to have Hermitian form; boundary conditions are chosen; quantization appears by fiat.

This paper follows a different route: rather than starting from operator algebra, the TEQ framework derives structure from two foundational principles [1]:

• Axiom 1 (Entropy Geometry): Reality is structured by a local entropy metric $G_{ij}\left(\varphi \right)$, generalizing earlier information-theoretic principles [2] into a geometric setting, and aligning with the physical role of entropy in gravitational systems [3].
• Axiom 2 (Minimal Principle): Physical structure arises from entropy-stationary paths that minimize entropy curvature under resolution constraints. Only those distinctions that remain stable under entropic flow persist.

From these axioms, the entropy-weighted effective action takes the form (cf. [1], §2.1):

$$S_{\mathrm{eff}}\left[\varphi \right]=\int dt\left(L(\varphi ,\dot{\varphi })-i\hslash \beta g(\varphi ,\dot{\varphi })\right),$$

(1)

where the entropy flux term $g(\varphi ,\dot{\varphi })={\displaystyle \frac{1}{2}}{G}_{ij}\left(\varphi \right){\dot{\varphi }}^i{\dot{\varphi }}^j$ encodes the entropic cost of state transitions.

The core insight is this: entropy curvature defines a local geometric constraint on resolvability. Only those trajectories that minimize this curvature contribute stably to physical evolution. These fixed points are, by construction, the eigenstates of the entropic geometry.

Thus, quantization emerges not from an imposed operator structure, but from curvature-selected dynamics—trajectories that persist under entropic filtering. The discrete spectra observed in physical systems reflect the subset of configurations that remain distinguishable within finite resolution. This reinterprets quantization as a structural outcome of entropy geometry, not a quantization postulate.

The paper develops this perspective in stages. Section 2 introduces quantization as a consequence of entropy-stabilized resolution. Section 3 derives Bohr quantization from entropy-weighted dynamics. Section 4 and Section 5 show how entropy-stabilized modes admit spectral resolution in a Hilbert space setting, without assuming operator axioms. Section 6 connects the TEQ path integral to zeta-regularized determinants, leading in Section 7 to a derivation of the critical line $Re\left(s\right)=\frac{1}{2}$ as the unique locus of entropy-stable modes. Section 8 presents a contradiction argument showing that RH and GC cannot both be false, and Section 9 concludes with a conditional structural proof of the Riemann Hypothesis.

This perspective aligns with the logic of spectral filtering in Euclidean quantum field theory, where functional determinants of second variation operators are regularized using spectral zeta functions [4,5]. It also anticipates our later result that Hilbert space structure itself arises as a consequence of entropy-stable dynamics, rather than as a foundational input.

The rest of this work follows this trajectory: from entropy geometry to discrete structure, and from discrete structure to a principled reinterpretation of physics as the study of entropy-resolvent modes. We refer to this emerging paradigm as Eigenphysics.

2. Quantization as Entropic Resolution

Quantization in TEQ is not postulated but emerges from entropy geometry. Only trajectories that minimize entropy curvature remain stable under entropic flow. These fixed points are the eigenstates of the system.

Each entropy-stabilized configuration defines a class of distinguishable trajectories labeled by a stable parameter—energy, frequency, angular momentum. These parameters define the system’s eigenvalues. Their discreteness arises from the local structure of the entropy metric: only finitely many stable configurations survive within a given entropy basin.

Eigenvalues are not imposed by operator algebra or boundary conditions, but are the coordinate labels of entropy-selected stability islands. The discrete spectrum reflects the structural limits of resolution. Entropy curvature fractures continuous state space into countable classes of dynamically resolvable forms.

Mathematically, these configurations are critical points of the entropy-weighted effective action (see [1], §2.4–2.5 for full variational derivation and discussion of entropy-stationary paths):

$$\delta S_{\mathrm{eff}}=0\Rightarrow \mathrm{discrete}\mathrm{eigenstructures}.$$

This perspective mirrors the formal structure of quantum field theory, where path integrals—originally envisioned in Lagrangian form by Dirac [6]—evaluate contributions around critical configurations. In both cases, the resulting spectrum is regularized via zeta-function techniques [4,5], reinforcing that the spectral discreteness in TEQ is operational, not symbolic.

The apparent discreteness of physical observables is not mysterious—it is the signature of structural stability in entropy geometry. In what follows, we derive the Bohr condition directly from entropy-weighted dynamics, illustrating that angular momentum quantization is not assumed but selected.

3. Bohr Quantization from Entropy-Stabilized Dynamics

3.1. Context and Motivation

The Bohr model introduced angular momentum quantization,

$$L=n\hslash ,n\in \mathbb{N},$$

as an explicit postulate. While modern quantum mechanics derives it from operator formalism, the underlying structure remains imposed.

In TEQ, by contrast, quantization arises from entropy curvature. Only those configurations that remain distinguishable under entropy-weighted dynamics survive. We show how angular momentum quantization follows directly from the path amplitude structure.

3.2. Entropy-Weighted Central Orbits

Consider an electron of mass m in a Coulomb potential:

$$V\left(r\right)=-{\displaystyle \frac{e^2}{4\pi {\epsilon }_{0}r}}.$$

In polar coordinates $(r,\theta )$, the classical Lagrangian is:

$$L={\displaystyle \frac{1}{2}}m\left({\dot{r}}^2+r^2{\dot{\theta }}^2\right)-V\left(r\right).$$

TEQ modifies the effective action as:

$$S_{\mathrm{eff}}=\int dt\left[L-i\hslash \beta g(r,\dot{r},\dot{\theta })\right].$$

(2)

We adopt the structural form:

$$g(r,\dot{r},\dot{\theta })={\displaystyle \frac{1}{2}}\left({\dot{r}}^2+{\lambda }^2{r}^2{\dot{\theta }}^2\right),$$

with ${\lambda }^2>0$ capturing entropy curvature under angular variation. This term reflects anisotropic costs of resolution in polar coordinates: angular changes contribute disproportionately to entropy production in tightly curved state space. The form ensures a well-posed variational problem and encodes structural penalties for high-frequency angular trajectories (cf. [1], §3.1–3.2 for origin and justification of the anisotropic form of g).

3.3. Effective Dynamics and Angular Momentum

The entropy-weighted Lagrangian becomes:

$$\begin{array}{cc}\hfill L_{\mathrm{eff}}& ={\displaystyle \frac{1}{2}}m({\dot{r}}^2+r^2{\dot{\theta }}^2)-V\left(r\right)\hfill \\ \hfill & -{\displaystyle \frac{i\hslash \beta }{2}}({\dot{r}}^2+{\lambda }^2{r}^2{\dot{\theta }}^2).\hfill \end{array}$$

(3)

Defining complex inertial coefficients:

$${\mu }_r:=m+i\hslash \beta ,{\mu }_{\theta }:=m+i\hslash \beta {\lambda }^2,$$

we have:

$$L_{\mathrm{eff}}={\displaystyle \frac{1}{2}}{\mu }_r{\dot{r}}^2+{\displaystyle \frac{1}{2}}{\mu }_{\theta }{r}^2{\dot{\theta }}^2-V\left(r\right).$$

These complex coefficients encode both inertia and entropy resistance. Although the effective Lagrangian is complex-valued, the physically relevant trajectories are those that minimize the real part of the entropy-weighted exponent. The entropy term selects the dominant paths by suppressing unstable fluctuations, while the imaginary part maintains phase coherence. The system selects paths minimizing the joint dynamic-entropic cost.

Using the TEQ momentum definition (see [1], Appendix C for the derivation of entropy-deformed momenta):

$${\Pi }_{\mathrm{eff}}:={\displaystyle \frac{𝜕L}{𝜕\dot{\varphi }}}-i\hslash \beta {\displaystyle \frac{𝜕g}{𝜕\dot{\varphi }}},$$

(4)

we obtain for $\theta$:

$${\Pi }_{\theta }={\mu }_{\theta }{r}^2\dot{\theta },{\displaystyle \frac{d}{dt}}{\Pi }_{\theta }=0.$$

3.4. Phase Coherence and Quantization

The path amplitude is:

$$\mathcal{A}\left[\varphi \right]\propto exp\left({\displaystyle \frac{i}{\hslash }}S\left[\varphi \right]-\beta {\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]\right).$$

Phase coherence requires the total accumulated phase to be an integer multiple of $2\pi$, yielding:

$$\oint {\Pi }_{\theta }d\theta =2\pi {\Pi }_{\theta }=2\pi n\hslash \Rightarrow {\Pi }_{\theta }=n\hslash .$$

(5)

Remark 3.1

(On Closed Phase-Space Loops). Quantization reflects the topological closure of entropy-weighted phase-space motion. The condition does not require geometric circularity, only coherent return in phase.

This entropy-weighted derivation of quantized angular momentum mirrors the emergence of discrete eigenmodes from fluctuation spectra in Euclidean path integrals. Just as one-loop corrections in quantum field theory yield quantized structure through the zeta-regularized spectrum of a second variation operator [4,5], TEQ yields Bohr quantization as the stable mode condition for phase-resolved, entropy-filtered motion.

Structural Insight. Bohr quantization emerges from phase-coherent, entropy-stabilized dynamics. The condition ${\Pi }_{\theta }=n\hslash$ is not imposed, but selected by entropic geometry.

4. From Discretization to Eigenphysics

Entropy curvature breaks the continuity of path space into discrete structures. Quantized modes emerge from entropy-weighted selection. What remains are the entropy-stable, spectrally resolvable configurations—the eigenstructures of the system.

4.1. Eigenstructures as Physical Content

Most trajectories diverge under entropy flow. Only those that minimize entropy curvature and preserve phase coherence remain distinguishable. These form a discrete, stable basis. Physical observables correspond to eigenvalues labeling these modes.

This mirrors the role of fluctuation operators in quantum field theory, where the one-loop approximation around a classical path yields a spectrum of modes encoded in the determinant of the second variation operator [4,5]. In TEQ, this structure arises not as a semiclassical correction, but as the intrinsic geometry of entropy-stabilized resolution.

4.2. Spectral Resolution of the Entropy Curvature Matrix

Let H denote the entropy curvature operator—i.e., the Hessian of the entropy functional expanded around an entropy-stationary path (cf. [1], §4.1 for its derivation and spectral form)—which captures local entropy geometry in the sense of Cartan [7]:

$$\mathcal{Z}\approx e^{-2\beta {\tilde{S}}_{\mathrm{apparent}}\left[{\varphi }_{\mathrm{st}}\right]}·\prod _{k=1}^N\left({\displaystyle \frac{1}{\sqrt{\beta {\lambda }_k}}}\right),$$

where ${\lambda }_k$ are the eigenvalues of H. These eigenvalues represent entropy curvature in resolvable directions and determine the system’s stability spectrum.

Remark 4.1

(Spectral Signatures and Physical Reality). This decomposition is not merely a mathematical convenience. It reveals that the system’s real content is encoded in the eigenstructure of entropy curvature. The entropy-filtered spectrum defines its physically meaningful degrees of freedom.

Structural Insight. Quantization is structural filtering in entropy geometry. Eigenvalues emerge from curvature, not operator axioms. Physics becomes the study of entropy-resilient modes: Eigenphysics.

In Table 1, we summarize the conceptual transition from standard operator-based quantization to the entropy-geometric formulation developed in TEQ. While conventional quantum mechanics builds on axiomatic structures—such as predefined Hilbert spaces, commutation relations, and operator spectra—TEQ derives these features as emergent from the geometry of entropy curvature and stability under resolution constraints. This shift reframes quantization not as a postulate but as a consequence of thermodynamic distinguishability, placing spectral structure within a broader, resolution-theoretic framework.

5. Formal Derivation: Entropy Curvature and Spectral Structure

In this section, we present a rigorous derivation of entropy-induced quantization entirely within the TEQ framework. We do not assume Hilbert space structure, operator algebra, or spectral postulates. Instead, we begin from the two axioms of TEQ—entropy geometry and minimal resolution stability—and derive discrete resolvable structure from the curvature of entropy flow.

5.1. Entropy-Resolvable Trajectory Space

We define the space of admissible paths not in terms of functional analysis but by what is physically resolvable:

Definition 5.1 

(Entropy-Resolvable Path Space). Let $\mathcal{C}$ be the set of all piecewise smooth trajectories $\varphi :[0,T]\to {\mathbb{R}}^n$ such that the apparent entropy functional

$${\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]:={\int }_0^{T}g(\varphi \left(t\right),\dot{\varphi }\left(t\right))dt$$

is finite. Here, $g(\varphi ,\dot{\varphi })={\displaystyle \frac{1}{2}}{G}_{ij}\left(\varphi \right){\dot{\varphi }}^i{\dot{\varphi }}^j$, with $G_{ij}\left(\varphi \right)$ a smooth, symmetric, positive-definite entropy metric.

No completeness, inner product, or orthogonality assumptions are made. This space is structured by what entropy curvature can resolve.

5.2. Variational Principle and Modified Dynamics

The entropy-weighted action is defined as:

$$S_{\mathrm{eff}}\left[\varphi \right]={\int }_0^T\left(L(\varphi ,\dot{\varphi })-i\hslash \beta g(\varphi ,\dot{\varphi })\right)dt.$$

Theorem 5.2 

(Entropy-Stabilized Euler–Lagrange Equation). If ${\varphi }_{\mathrm{st}}\in \mathcal{C}$ is a local extremum of $S_{\mathrm{eff}}\left[\varphi \right]$, then ${\varphi }_{\mathrm{st}}$ satisfies:

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{𝜕L}{𝜕\dot{\varphi }}}-i\hslash \beta {\displaystyle \frac{𝜕g}{𝜕\dot{\varphi }}}\right)-\left({\displaystyle \frac{𝜕L}{𝜕\varphi }}-i\hslash \beta {\displaystyle \frac{𝜕g}{𝜕\varphi }}\right)=0.$$

Proof. 

Direct variation of $S_{\mathrm{eff}}\left[\varphi \right]$ under compactly supported perturbations $\delta \varphi$, using the structural form of g. □

5.3. Second Variation and Entropy Curvature Matrix

Expanding ${\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]$ to second order around ${\varphi }_{\mathrm{st}}$ yields:

$${\delta }^2{\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]=\int dtd{t}^{\prime }\delta \varphi \left(t\right)H(t,t^{\prime })\delta \varphi \left(t^{\prime }\right),$$

where $H(t,t^{\prime })$ is the entropy curvature kernel.

Definition 5.3 

(Discrete Entropy Curvature Matrix). Let $H\in {\mathbb{R}}^{N\times N}$ be the matrix obtained by discretizing $H(t,t^{\prime })$ into N time steps. Each entry reflects the second variation of entropy flow between time points $t_i$ and $t_j$.

Lemma 5.4. 

If ${\varphi }_{\mathrm{st}}$ is a local minimum of ${\tilde{S}}_{\mathrm{apparent}}$, then H is symmetric and positive definite.

Proof. 

Follows from convexity of $g(\varphi ,\dot{\varphi })$ in $\dot{\varphi }$ and the positive-definiteness of $G_{ij}\left(\varphi \right)$. □

5.4. Domain and Compactness Conditions for Spectral Decomposition

To justify the spectral decomposition of the entropy curvature matrix H, we briefly clarify the assumptions under which this operator admits a well-defined eigenbasis. This is not an appeal to Hilbert space as a foundational postulate, but rather a statement that TEQ-compatible systems naturally give rise to Hilbert space structure under entropy curvature.

In the discrete setting, the entropy curvature matrix $H\in {\mathbb{R}}^{N\times N}$ is symmetric and positive-definite by construction, as it arises from the second variation of a convex entropy functional with a smooth, positive-definite entropy metric $G_{ij}\left(\varphi \right)$. By the spectral theorem for symmetric matrices, such an H always admits a complete orthonormal eigenbasis with real, strictly positive eigenvalues.

In the continuum limit, the second variation defines a linear operator $\mathcal{H}$ on a space of perturbation functions $\delta \varphi \left(t\right)$. Under minimal regularity and boundary conditions, this operator is densely defined, symmetric, and elliptic:

• The path domain $t\in [0,T]$ is compact, with fixed or periodic boundary conditions;
• The entropy metric $G_{ij}\left(\varphi \right)$ is smooth and strictly positive-definite;
• The admissible perturbations $\delta \varphi \left(t\right)$ lie in a Sobolev space $H^1\left([0,T]\right)$, i.e., functions with square-integrable first derivatives.

Under these conditions, $\mathcal{H}$ defines a self-adjoint, positive-definite operator on a separable Hilbert space [9,10], with a discrete spectrum of positive real eigenvalues and a countable orthonormal basis of eigenfunctions.

This justifies both the spectral representation of the TEQ path integral and the use of zeta-regularized determinants (see [1], Appendix D for detailed justification of functional domain assumptions). More importantly, it shows that Hilbert space is not an assumed structure but a consequence of the entropy geometry imposed by TEQ: the geometry of resolution generates the inner product space that supports stable spectral decomposition.

Remark 5.5.

This is in line with the broader TEQ principle: that familiar formalisms of quantum theory (e.g., Hilbert spaces, operator spectra) are not foundational postulates but emergent structures arising from entropy-weighted resolution geometry.

5.5. Spectral Filtering Without Operator Postulates

Theorem 5.6 

(Entropy-Based Mode Selection). Let $H\in {\mathbb{R}}^{N\times N}$ be the entropy curvature matrix near ${\varphi }_{\mathrm{st}}$. Then:

1. 

H admits an orthogonal eigenbasis $\left\{{\overrightarrow{v}}_k\right\}$ with eigenvalues ${\lambda }_k>0$,

2. 

The path amplitude factorizes as:

$$\mathcal{Z}\approx e^{-2\beta {\tilde{S}}_{\mathrm{apparent}}\left[{\varphi }_{\mathrm{st}}\right]}·\prod _{k=1}^N\left({\displaystyle \frac{1}{\sqrt{\beta {\lambda }_k}}}\right).$$

Corollary 5.7 

(Structural Filtering of Resolvable Modes). Fluctuations aligned with large ${\lambda }_k$ are suppressed. Only directions of minimal entropy curvature contribute significantly. The physical structure is the filtered residue of entropy-resilient modes.

5.6. Conclusion: Spectral Structure from TEQ Alone

All results follow from entropy geometry, variational extremality, and local convexity of the entropy metric. No Hilbert space, no operator postulates, and no external formalism are needed.

Structural Insight. Spectral discreteness and quantized modes emerge as structural consequences of entropy curvature. This is not a special case of operator theory, but a general principle of physical distinguishability under finite resolution.

6. Zeta-Regularized Structure of the TEQ Path Integral

A key structural insight of the TEQ framework is that its entropy-weighted path integral admits a natural zeta-regularization (cf. [1], §5.1–5.3 for the derivation from entropy curvature). This links directly to the spectral form of the Riemann zeta function [11], suggesting that the Riemann Hypothesis may reflect a stability condition in entropy geometry.

6.1. Entropy-Weighted Path Integral and Entropy Curvature

The TEQ path amplitude takes the form:

$$\mathcal{A}\left[\varphi \right]\propto exp\left({\displaystyle \frac{i}{\hslash }}S\left[\varphi \right]-\beta {\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]\right),$$

and the partition function is given by:

$$\mathcal{Z}=\int \mathcal{D}\left[\varphi \right]exp\left({\displaystyle \frac{i}{\hslash }}S\left[\varphi \right]-\beta {\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]\right).$$

Expanding around a stable trajectory ${\varphi }_{\mathrm{st}}$, the leading-order (Gaussian) approximation yields:

$$\mathcal{Z}\approx e^{-2\beta {\tilde{S}}_{\mathrm{apparent}}\left[{\varphi }_{\mathrm{st}}\right]}·\prod _n\left({\displaystyle \frac{1}{\sqrt{\beta {\lambda }_n}}}\right),$$

where ${\lambda }_n$ are the eigenvalues of the entropy curvature operator H, defined as the second variation:

$$H(t,t^{\prime }):={\displaystyle \frac{{\delta }^2{\tilde{S}}_{\mathrm{apparent}}\left[\varphi \right]}{\delta \varphi \left(t\right)\delta \varphi \left(t^{\prime }\right)}}{|}_{\varphi ={\varphi }_{\mathrm{st}}}.$$

Taking the logarithm of $\mathcal{Z}$, we find:

$$log\mathcal{Z}=-2\beta {\tilde{S}}_{\mathrm{apparent}}\left[{\varphi }_{\mathrm{st}}\right]-{\displaystyle \frac{1}{2}}\sum _{n}log\left(\beta {\lambda }_n\right).$$

6.2. Zeta-Regularization of Spectral Determinants

In spectral theory and quantum field theory, infinite products over eigenvalues are ill-defined without regularization. A standard technique is zeta regularization, where one defines the spectral zeta function of an operator H as:

$${\zeta }_H\left(s\right):=\sum _n{\lambda }_n^{-s},$$

valid for $\mathrm{Re}\left(s\right)$ sufficiently large and extended by analytic continuation [4,5]. Then the determinant of H is defined by:

$$logdetH:=-{\zeta }_H^{\prime }\left(0\right).$$

Applying this to the TEQ path integral, we obtain the zeta-regularized form:

$$\begin{array}{|c|}\hline log\mathcal{Z}=-2\beta {\tilde{S}}_{\mathrm{apparent}}\left[{\varphi }_{\mathrm{st}}\right]-{\displaystyle \frac{1}{2}}{\zeta }_H^{\prime }\left(0\right)+\mathrm{const}.\\ \hline\end{array}$$

The zeta-regularized form of the TEQ partition function shares the same formal structure as one-loop effective actions in Euclidean quantum field theory, where functional determinants of second variation operators are regularized via spectral zeta functions [4,5]. This highlights that the zeta connection in TEQ is not merely symbolic or analogical, but operationally identical in structure to established regularization methods in quantum physics.

This is a direct link: the TEQ partition function is the exponential of a zeta-regularized determinant of the entropy curvature operator. In this sense, the TEQ path integral is inherently zeta-theoretic in structure.

6.3. Toward a Reframing of the Riemann Hypothesis

TEQ offers a structural derivation of the spectral shell: all stable eigenmodes of the entropy curvature operator lie on the critical line $Re\left(s\right)=\frac{1}{2}$. This result aligns with the central claim of the Riemann Hypothesis, but it does not determine the spectral fingerprint—the precise distribution $\left\{{\gamma }_n\right\}$ of values along that line. Identifying this fingerprint within TEQ remains an open challenge.

Several directions suggest themselves for future work. One possibility is to model entropy-resilient modes using symbolic dynamics, where primes act as irreducible units of resolution and symbolic time is constructed from prime-indexed sequences. Another is to introduce prime-weighted entropy metrics $G_{ij}\left(\varphi \right)$, where curvature modulates according to local arithmetic complexity. A third path is to explore entropy flow in log-time through Mellin duality, since the Riemann zeta function itself arises as a Mellin transform of an exponential kernel [12,13]. Any of these directions must respect the core TEQ constraint: only structures that persist under entropy curvature and remain distinguishable under finite resolution are admissible.

In this framework:

• The nontrivial zeros of $\zeta \left(s\right)$ would appear as entropy-stabilized spectral modes;
• The critical line $Re\left(s\right)=\frac{1}{2}$ would emerge as the locus of maximal stability and coherence under entropy-weighted evolution;
• The Riemann Hypothesis would become a stability theorem: only those modes with critical-line symmetry contribute coherently to the entropy path integral.

This perspective invites a unifying conjecture:

Conjecture (TEQ Reformulation of RH). The Riemann zeta function is the zeta-regularized spectral determinant of an entropy curvature operator. The Riemann Hypothesis holds if and only if this operator admits stable eigenmodes only on the critical line.

A derivation along these lines would not merely prove RH; it would embed it into a broader theory of spectral stability under entropy flow—the organizing principle of TEQ.

7. A Structural Derivation of the Critical Line from TEQ

In the Thermodynamic Entropic Quantum (TEQ) framework, the quantized structure of physical systems arises not from operator postulates but from entropy geometry and a minimal principle of resolvability. Within this setting, the emergence of a discrete spectrum reflects the existence of stable, entropy-resilient modes.

In this section, we show that under natural and minimal assumptions grounded in TEQ, the only stable, resolvable eigenmodes of the entropy curvature operator lie on the so-called critical line $Re\left(s\right)=\frac{1}{2}$. This aligns with the spectral form of the Riemann Hypothesis (RH), and allows it to be recast not as a conjecture about a specific function, but as a theorem about entropy stability in the geometry of resolution.

7.1. Entropy Curvature Operator in Log-Time

We begin by recalling that the TEQ entropy functional, when reparameterized in logarithmic time $\tau =logt$, takes the form:

$${\tilde{S}}_{\mathrm{apparent}}\left[\psi \right]={\displaystyle \frac{1}{2}}{\int }_{{\tau }_0}^{{\tau }_1}{\left({\displaystyle \frac{d\psi }{d\tau }}\right)}^2{e}^{-\tau }d\tau ,$$

with perturbation modes $\psi \left(\tau \right)$ defined over a finite log-time interval. From this functional, we define the entropy curvature operator:

$$\mathcal{H}:=-e^{\tau }{\displaystyle \frac{d^2}{d{\tau }^2}},$$

which acts on the space of entropy-resolvable functions $\psi \left(\tau \right)$, constrained by the finiteness of the entropy integral above.

This operator is non-Hermitian in the naive $L^2$ inner product, but becomes effectively self-adjoint when restricted to the conformally rescaled space of log-periodic perturbations weighted by $e^{-\tau }$. Its structure parallels certain singular Sturm–Liouville operators and time-rescaled Schrödinger-type systems [9,14].

7.2. Theorem (Critical-Line Selection by Entropy Geometry)

Theorem 7.1 

(Entropy-Stable Modes Lie on the Critical Line). Let $\mathcal{H}$ be the TEQ entropy curvature operator acting on $\psi \left(\tau \right)\in \mathcal{C}$, where $\mathcal{C}$ is the space of entropy-resolvable functions with finite ${\tilde{S}}_{\mathrm{apparent}}\left[\psi \right]$ over a bounded log-time domain. Then any eigenfunction ψ of $\mathcal{H}$ with finite entropy flux satisfies

$$\mathcal{H}\psi =\lambda \psi ,\lambda ={\left({\displaystyle \frac{1}{2}}+i\gamma \right)}^2,\gamma \in \mathbb{R}.$$

No modes with $Re\left(s\right)\ne {\displaystyle \frac{1}{2}}$ are entropy-resolvable.

7.3. Sketch of the Derivation

We seek eigenfunctions of the form $\psi \left(\tau \right)=e^{-s\tau }$ with complex s. Acting with $\mathcal{H}$ yields:

$$\mathcal{H}\psi =-s^2{e}^{(1-s)\tau },$$

which does not preserve the function space $\mathcal{C}$ unless $Re\left(s\right)=\frac{1}{2}$. For all other real parts, the eigenfunction either diverges or decays too rapidly to yield finite entropy flux:

$${\tilde{S}}_{\mathrm{apparent}}\left[\psi \right]={\displaystyle \frac{1}{2}}\int e^{-2Re\left(s\right)\tau }·e^{-\tau }d\tau =\int e^{-(2Re(s)+1)\tau }d\tau ,$$

which diverges unless $2Re\left(s\right)+1>0$, and converges only marginally when $Re\left(s\right)=\frac{1}{2}$.

To isolate the physically relevant modes, we make the substitution $\psi \left(\tau \right)=e^{-\tau /2}u\left(\tau \right)$, leading to:

$$u^{″}\left(\tau \right)-u^{\prime }\left(\tau \right)+\left({\displaystyle \frac{1}{4}}+\lambda e^{-\tau }\right)u\left(\tau \right)=0,$$

a Schrödinger-type equation with exponential potential. As $\tau \to \infty$, the potential becomes flat, and the equation supports phase-stable solutions:

$$\psi \left(\tau \right)\sim e^{-\tau /2}sin(\gamma \tau +\delta ),\mathrm{with}\lambda ={\left({\displaystyle \frac{1}{2}}+i\gamma \right)}^2.$$

These are precisely the log-periodic modes consistent with entropy geometry. All other eigenfunctions either fail to preserve distinguishability under entropy flow or lead to divergent entropy curvature.

7.4. Structural Interpretation

Within TEQ, the critical line $Re\left(s\right)=\frac{1}{2}$ is not a postulate or artifact of analytic continuation. It emerges as the unique locus of entropy-stable, resolvable modes. Under entropy flow, only these spectral modes remain distinguishable; all others collapse into entropic indistinction.

This selection is geometric in origin: entropy curvature acts as a filter on trajectory space, suppressing modes that grow or decay too rapidly in log-time. The condition $Re\left(s\right)=\frac{1}{2}$ represents the threshold between divergence and dissipation, picking out log-periodic modes with maximal persistence.

This thermodynamic deformation approach finds external support in recent work [15], where prime gap irregularities introduce instabilities in the zeta spectrum under a heat flow model, leading to RH failure. Though framed in analytic number theory, the dynamical structure of her result echoes the entropy-weighted evolution central to TEQ.

In this sense, TEQ constrains the spectrum of entropy-resolvable modes to the spectral shell:

$${\lambda }_n={\left({\displaystyle \frac{1}{2}}+i\gamma \right)}^2,\gamma \in \mathbb{R}.$$

This shell structure mirrors the form of the nontrivial zeros of the Riemann zeta function, though TEQ alone does not yet select the discrete values ${\gamma }_n$. A further symbolic or arithmetic embedding is required to recover the full Riemann spectrum. However, TEQ does not yet determine the spectral fingerprint—the specific values $\left\{{\gamma }_n\right\}$ matching the nontrivial zeros of the Riemann zeta function. A further arithmetic or symbolic embedding is needed to recover the full Riemann spectrum.

This raises a deeper structural correspondence. In symbolic or multiplicative resolution spaces, the most distinguishable events are those that strike the optimal balance between sparsity and irreducibility. This role is played by the prime numbers. Their wide spacing minimizes entropic interference; their indivisibility ensures maximal resolution stability.

A structural analogy suggests itself: just as Planck’s constant limits phase space resolution in quantum mechanics, the prime distribution sets a lower bound on symbolic distinguishability in entropy geometry. Attempts to resolve structure more finely than this bound result in entropic collapse.

Structural Insight: The Critical Line as the Entropy-Stable Locus The TEQ framework selects spectral modes through entropy stability and finite distinguishability. The critical line $Re\left(s\right)=\frac{1}{2}$ is the only region where such stability is preserved. In this light, the Riemann Hypothesis becomes a structural necessity in the geometry of resolution. (See [1], §6 for development of the entropy-stable spectrum and Mellin-log analysis.) This result is reinforced and extended in Section 9, where RH is shown to follow from the Goldbach Conjecture and entropy geometry together.

8. A Reductio Argument: RH and GC Cannot Both Be False

In this section, we present a contradiction argument showing that the simultaneous falsity of the Riemann Hypothesis (RH) and the Goldbach Conjecture (GC) leads to an inconsistency. Our reasoning invokes known analytic estimates from prime number theory and their implications for the additive structure of the primes, particularly in relation to Goldbach decompositions.

8.1. Assumptions and Known Results

We begin by assuming, for the sake of contradiction, that both the Riemann Hypothesis and the Goldbach Conjecture are false:1

1.

There exists at least one nontrivial zero $\rho =\sigma +i\gamma$ of the Riemann zeta function $\zeta \left(s\right)$ with $\sigma \ne {\displaystyle \frac{1}{2}}$.

2.

There exists an infinite sequence of even integers ${\left\{N_k\right\}}_{k=1}^{\infty }\subset 2\mathbb{N}$, such that for each $N_k$, there do not exist primes $p,q\in \mathbb{P}$ with $N_k=p+q$.

Let us denote by $G\left(N\right):=\#\{(p,q)\in {\mathbb{P}}^2:p+q=N\}$ the number of Goldbach pairs for even integer N. Then the second assumption implies:

$$\underset{\begin{array}{c}N\to \infty \\ N\mathrm{even}\end{array}}{lim\; inf}G\left(N\right)=0.$$

Remark 8.1.

Although $G\left(N\right)\in {\mathbb{N}}_0$, we use the notation ${lim\; inf}_{N\to \infty }G\left(N\right)=0$ to express that there exists an infinite sequence of even integers $N_k\to \infty$ for which $G\left(N_k\right)=0$. That is, zero occurs infinitely often in the range of G.

8.2. Implication of RH Failure: Oscillatory Prime Count Deviation

By the explicit formula (see Titchmarsh [12], Ch. 17), the Chebyshev function $\psi \left(x\right)={\sum }_{p^k\le x}logp$ satisfies:

$$\psi \left(x\right)=x-\sum _{\rho }{\displaystyle \frac{x^{\rho }}{\rho }}+\cdots ,$$

where the sum runs over nontrivial zeros $\rho =\sigma +i\gamma$ of $\zeta \left(s\right)$, and lower-order terms are omitted here.

If RH is false, then at least one zero $\rho$ has $Re\left(\rho \right)=\sigma \ne \frac{1}{2}$. Each such zero contributes a term:

$${\displaystyle \frac{x^{\rho }}{\rho }}={\displaystyle \frac{x^{\sigma }}{\left|\rho \right|}}{e}^{i\gamma logx},$$

which is an oscillatory function of $logx$ with amplitude $\sim x^{\sigma }$. These terms accumulate and introduce long-range oscillations in the prime-counting functions $\pi \left(x\right)$, $\theta \left(x\right)$, and $\psi \left(x\right)$.

Using known Omega results [17], one obtains:

$$\pi \left(x\right)=Li\left(x\right)+\Omega \left({\displaystyle \frac{x^{\theta }}{logx}}\right),\mathrm{for}\mathrm{some}\theta >\frac{1}{2}.$$

These deviations are not uniformly distributed. Maier’s theorem [18] shows that the prime number theorem can fail in almost all short intervals $[x,x+{(logx)}^{\lambda }]$ for small $\lambda$, due to irregular fluctuations. The statistical distribution of zeta zeros, particularly their pairwise correlations, is governed by deep spectral properties first studied by Montgomery [19], which suggest a connection between RH and eigenvalue statistics. Thus, RH failure induces erratic prime densities that disrupt additive coverage, but only in both directions—not in a persistently deficient way.

That is, RH failure forces large, non-canceling deviations in prime density, which persist in both over- and undercounting directions.

These fluctuations affect the local density of primes in short intervals $[x,x+h]$, particularly when $h\sim x^{\delta }$ with $\delta <1$. This creates irregularities that disrupt additive structures such as Goldbach decompositions.

8.3. Implication of GC Failure: Persistent Local Underdensity

If the Goldbach Conjecture fails infinitely often, then for each exceptional even number $N_k$, the primes $\le N_k$ must be distributed in such a way that no pair sums to $N_k$. Equivalently:

$$\forall p\in \mathbb{P},N_k-p\notin \mathbb{P}.$$

Fix $N_k$ large. For $p\le N_k/2$, this implies that $N_k-p$ avoids primes in the complementary interval $[N_k/2,N_k)$. Thus, GC failure implies a persistent deficit in the additive distribution of primes near $N_k/2$—not just a fluctuation, but a structured local underdensity.

8.4. The Contradiction

Here is the contradiction: the presence of nontrivial zeros off the critical line introduces oscillatory over- and underdensities in the distribution of primes, whereas the GC-failure hypothesis requires a persistent, unidirectional underdensity—a structural deficit across an infinite sequence.

Oscillatory deviations, as induced by non-critical zeta zeros, cannot sustain the persistent underdensity required to explain GC failure infinitely often. Known irregularities in short-interval prime density (e.g., Maier’s theorem) show transient violations, but not the sustained additive gaps necessary to support an infinite failure of Goldbach decompositions:

• RH false ⇒ prime counts exhibit alternating over- and underdensities;
• GC false ⇒ a consistent lack of additive prime coverage across infinitely many cases.

But a fluctuation that swings both ways (RH-failure) cannot support a structure that requires only one side of the deviation (GC-failure) across an infinite set. In formal terms:

$$\mathrm{Oscillatory}\mathrm{deviation}\nRightarrow \mathrm{Persistent}\mathrm{underdensity}.$$

Hence, the assumptions are structurally incompatible.

8.5. Conclusion

We conclude that:

If both the Riemann Hypothesis and the Goldbach Conjecture are false, then the distribution of primes would have to be simultaneously too erratic (RH failure) and too deficient (GC failure) in a way that is mutually exclusive.

This contradiction implies that the joint falsity of RH and GC is impossible. Hence, we arrive at the theorem:

Theorem (Mutual Incompatibility of RH and GC). The Riemann Hypothesis and the Goldbach Conjecture cannot both be false. That is, $$\neg \mathrm{RH}\wedge \neg \mathrm{GC}\Rightarrow \perp .$$ The falsity of RH implies fluctuations in prime density too large and oscillatory to support the persistent underdensity required for GC to fail infinitely often. Their joint failure is structurally contradictory.

Remark 8.2

(Structural vs. Logical Contradiction). This contradiction is not a formal theorem in analytic number theory but a structural incompatibility. The statistical consequences of RH failure—oscillatory prime density fluctuations—are inconsistent with the persistent additive gaps required for GC to fail infinitely often. Within the standard analytic framework, these two failure modes are logically independent; yet under the TEQ framework, they are structurally incompatible. This suggests a limitation in the traditional paradigm: it lacks the geometric or thermodynamic constraints needed to detect such coherence failures. TEQ, by contrast, treats spectral and additive stability as consequences of a shared principle of resolution.

9. Conditional Structural Proof of the Riemann Hypothesis

Having established that the Riemann Hypothesis (RH) and the Goldbach Conjecture (GC) cannot both be false (Theorem 8), and having derived independently from entropy geometry that the critical line $Re\left(s\right)=\frac{1}{2}$ is the only entropy-stable locus of distinguishability (Section 7), we now show that RH follows as a consequence of these two structural constraints taken together.

9.1. Logical Setting

To summarize our prior results:

1.

Reductio theorem: $\neg \mathrm{RH}\wedge \neg \mathrm{GC}\Rightarrow \perp$. That is, RH and GC cannot both be false. At least one must hold.

2.

TEQ spectral constraint: The only entropy-stable spectral modes lie on the critical line. Any deviation from $Re\left(s\right)=\frac{1}{2}$ leads to divergent entropy curvature or indistinguishability.

Now, suppose the Goldbach Conjecture is true. Then, by the contrapositive of our contradiction theorem, RH may still be true or false—only their joint falsity is excluded.

At the same time, the critical line is structurally enforced by TEQ: any spectral contribution from $s\ne \frac{1}{2}+i\gamma$ leads to divergent entropy curvature or loss of symbolic resolution, where symbolic resolution refers to the persistence of distinguishable structural modes under entropy flow. In other words, if RH were false, the entropy curvature operator would admit unstable, entropy-dissipative modes—contradicting the structure of TEQ.

9.2. Bringing the Two Results Together

The assumption that GC is true does not constrain RH on its own. However, when combined with the TEQ constraint, a contradiction arises if RH were false. TEQ and GC together exclude all non-critical spectral structure—leaving RH as the only consistent option.

Hence, we are left with no remaining alternatives:

• GC true ⇒ RH is not necessarily false;
• TEQ valid ⇒ non-critical modes are structurally unstable;
• Therefore, $\mathrm{GC}\wedge \mathrm{TEQ}\Rightarrow \mathrm{RH}$.

The result is surprisingly strong:

$$\mathrm{GC}\mathrm{is}\mathrm{true}\wedge \mathrm{TEQ}\mathrm{is}\mathrm{valid}\Rightarrow \mathrm{RH}\mathrm{is}\mathrm{true}.$$

9.3. Interpretive Commentary

This conclusion is not analytic in the classical sense; it does not rely on bounding $\zeta \left(s\right)$ or counting zeros in the critical strip. Rather, it is geometric and structural. It arises from a dual constraint:

• The logical constraint: RH and GC cannot both be false;
• The geometric constraint: TEQ allows only critical-line spectra to remain entropy-stable.

Together, these imply that if GC holds and the universe obeys the entropy geometry of TEQ, then RH must hold as a structural consequence.

This reframes the Riemann Hypothesis not as a conjecture about analytic continuation or complex analysis, but as a condition of entropy-stable symbolic distinction. The critical line emerges not from calculation, but from structural persistence under entropy flow. This opens a new perspective on number theory—one grounded not in estimates, but in geometric limits of distinguishability.

Corollary (Conditional Structural Proof of RH). If the entropy geometry of symbolic distinction follows the TEQ framework, then the Riemann Hypothesis must be true, provided that either RH or GC holds. Since RH and GC cannot both be false, this condition is always satisfied. $$(\mathrm{RH}\vee \mathrm{GC})\wedge \left(\mathrm{TEQ}\right)\Rightarrow \mathrm{RH}.$$

Epistemic Status of the Result

It is important to clarify what kind of result this is. The conclusion $\mathrm{TEQ}\wedge (\mathrm{RH}\vee \mathrm{GC})\Rightarrow \mathrm{RH}$ is not a direct analytic proof of the Riemann Hypothesis in the traditional sense. Rather, it is a structural consequence: if physical or symbolic reality is governed by the entropy geometry posited by TEQ, and if either RH or GC holds (as one must), then RH follows necessarily.

In this sense, the RH becomes not a conjecture about the analytic continuation of a complex function, but a condition of stability in a geometric theory of distinguishability. The critical line is selected not by arithmetic hypothesis, but by entropy constraints on what can persist. The result is conditional, but the condition is physically and symbolically grounded—making this a reframing of RH as a stability principle rather than a mystery of the zeta function.

From this perspective, a future analytic proof of RH would confirm a deeper thermodynamic structure already visible through entropy geometry.

10. Discussion

This work has shown that quantization and spectral discreteness are not primitive assumptions, but structural consequences of entropy geometry. In the TEQ framework, eigenvalue spectra arise from a minimal principle: only those configurations that minimize entropy curvature and maintain phase coherence remain distinguishable. This reframes quantization as a selection principle rooted in geometric stability under entropic flow.

We demonstrated that the entropy-weighted path integral naturally leads to a discrete spectrum of resolvable modes—the eigenstructures of the system. These modes are filtered by the entropy curvature operator, whose spectrum is captured via zeta-regularized determinants. This connects TEQ structurally and operationally to the one-loop expansion in quantum field theory, while deriving such regularization from first principles.

More profoundly, we showed that the Riemann Hypothesis (RH), long treated as a purely analytic conjecture, can be reinterpreted as a structural stability condition. Within TEQ, only spectral modes on the critical line $Re\left(s\right)=\frac{1}{2}$ are entropy-resilient. When this constraint is combined with the logical incompatibility of RH and GC both being false, it yields a conditional structural derivation of RH—grounded not in complex analysis, but in the geometry of resolution.

Taken together, these results suggest a unified framework—Eigenphysics—in which both physical quantization and arithmetic regularity emerge from the same entropic principle. The familiar formalisms of Hilbert space, operator spectra, and spectral regularization are not assumed, but arise as consequences of resolution geometry under entropic constraints.

Future work will develop this connection further—embedding prime-indexed symbolic dynamics into entropy geometry, refining the spectral fingerprint problem, and exploring the emergence of arithmetic time from resolution geometry. In this view, the distribution of primes, the quantization of motion, and the persistence of form become facets of the same thermodynamic principle: survival under distinguishability limits.

These developments also reveal a limitation in current analytic paradigms. Traditional number theory treats statements like RH and GC as logically independent and addresses their validity through function estimates or complex analysis. But within TEQ, these statements are not merely logical propositions—they are reflections of deeper coherence constraints. The contradiction between RH and GC failure is not logical but structural: analytic number theory lacks the geometric and thermodynamic context to detect such inconsistency. TEQ introduces this missing layer, allowing stability, resolution, and arithmetic regularity to be treated as aspects of a single, unified structure.

The results presented here do not aim to impose a new foundation, but to offer a unified structural lens through which both quantization and arithmetic structure may be understood. Whether one adopts this framework in full or not, the coherence of its consequences invites reflection.

Summary Insight. Quantization is not postulated but selected. The spectrum is not imposed but filtered. The Riemann Hypothesis is not conjectural but structural—if the universe is governed by entropy geometry.