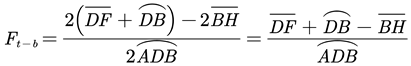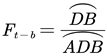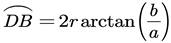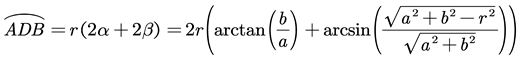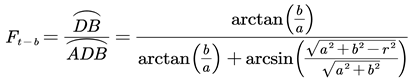High-Temperature Thermal Camouflage Device Considering Radiative Thermal Transfer from the Target

1. Introduction

Metamaterials offer us an approach to realize diverse artificial materials with counterintuitive properties that do not exist naturally. Thanks to the groundbreaking contributions of our predecessors, many significant achievements of metamaterials have been witnessed [1,2,3,4,5,6,7]. In recent years, thermal metamaterials [8,9] possessing extraordinary thermal control properties have made great progress in solving special thermodynamic problems, which offer the ability to manipulate the anisotropy of heat flow through structural design. This has led to the creation of thermal devices with various thermal functions, including thermal cloak and concentrator [10,11,12,13,14], multiphysics metamaterials [15,16], thermal sensor [17,18], thermal harvester [19], thermal information device [20,21].

Among them, thermal camouflage [22] is one of the novel functionalities that can be realized by the thermal metamaterials. In the past few years, a lot of thought-provoking design and processing methods were proposed to create metamaterials with the functionality of thermal camouflage. The strategy of thermal camouflage involves manipulating the temperature distribution surrounding the target to effectively conceal it within its background environment. Precise control over heat flow is achieved through the design of thermal metamaterials using the transformation thermotics method [10,11,12,14,15] or the scattering cancellation method [23]. Many studies [10,11,12,13,23] have shown successful thermal camouflage effect with devising the anisotropic thermal conductivity of thermal metamaterials to create equivalent thermal temperature profiles at certain regions. Despite achieving an equivalent exterior temperature profile, the target remains susceptible to detection through infrared (IR) cameras when observed from the normal direction (Z plane). This highlights that relying solely on in-plane heat conduction is insufficient for achieving comprehensive thermal camouflage. Therefore, alternative approaches must be investigated.

Recently, some studies [24,25,26] have achieved camouflage by adjusting the out-of-plane heat conduction. Li et al. [24] used two consecutive transformation thermotics to design a conductive structure without a priori knowledge of the background temperature. They further extended the 2D metamaterials-based thermal camouflage device into a 3D version prepared by 3D printing [25]. Zhang et al. [26] maintained the surface temperature of the device and background plate as the same from point to point through the method of scattering cancellation. They successfully designed various camouflage devices that cover a hidden target against a background plate, ensuring precise correspondence of surface temperatures between the camouflage device and the background plate in the projection domain. As a result, the covered object will be effectively concealed, appearing as if it is nonexistent. However, most previous works [24,25] have neglected the thermal characteristics of the target, focusing primarily on scenarios where the hidden target is a not heat source. As any target emits with nonzero temperature thermal radiation described by the Stefan-Boltzmann law, the thermal radiation energy is proportional to the fourth power of the temperature, i.e., $Q_r=\epsilon A\sigma T^4$. In particular, if the target experiences high temperatures, the dissipation of thermal radiation energy from the target will significantly impact the effectiveness of the thermal camouflage device. This will result in weakened or even compromised camouflage performance of the device. Thus, obviously, it is crucial to acknowledge and account for the target's role as a heat source, ensuring that thermal radiation is taken into account during the design of thermal camouflage devices. Unfortunately, up to now, there have been limited works [26,27] investigating the camouflage performance of the device, considering its target as a heat source. They primarily concentrate on the target as a low-temperature heat source, while overlooking the significance of the target's thermal radiation. However, due to the absence of theoretical design method, the high-temperature thermal camouflage device has never been reported.

Therefore, this work proposes a high-temperature thermal camouflage device that considers the influence of the radiative thermal transfer from the target, aiming to address the limitation of in this field. Theoretically, we precisely deduce the conditions for the realization of thermal camouflage performance. The theoretical principle is based on maintaining the synchronous heat transfer separately along the device and the background. Besides, we find unexpectedly that the performance of thermal camouflage can be further optimized by changing the structure of the thermal camouflage device. The results are validated by the numerical simulation. Furthermore, the effects of the geometry and location, the temperature, and the surface emissivity of the target on the performance of the thermal camouflage of the device are discussed, respectively.

2. Theoretical Analysis

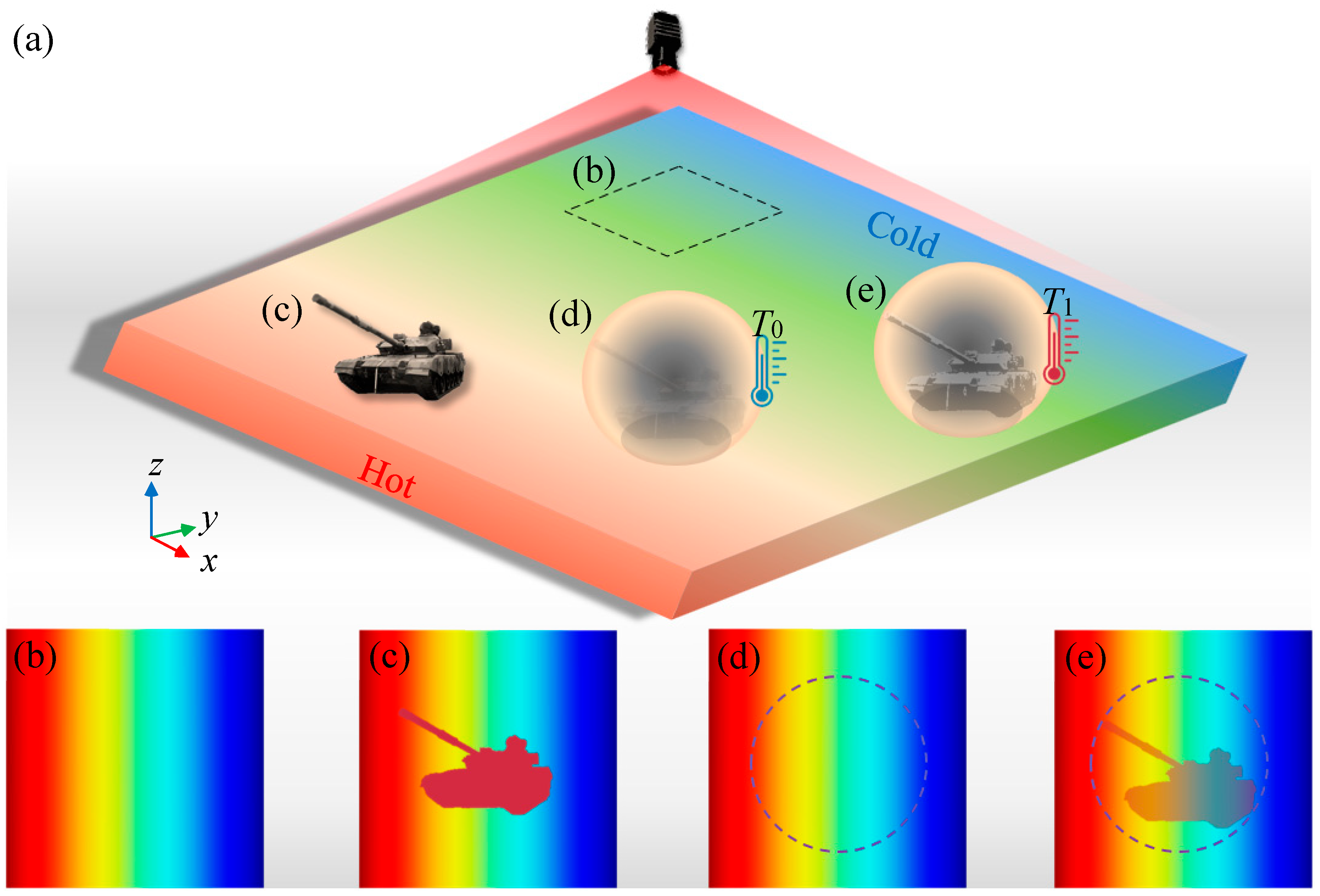
The realistic functional presentation of thermal camouflage can be explained by the illustration shown in Figure 1(a)-(e). There are four different cases shown in Figure 1(a). Firstly, as shown in Figure 1(b), when the scanning object of the Infrared Thermal Imager is only the bare background plate, all that is obtained is a thermal image of the basic background plate. In addition, when there are some targets are placed on the basic background plate, the thermal imagery will expose their abnormal information, as shown in Figure 1(c). Furthermore, as shown in Figure 1(d), when the target is a non-heat source, it exerts no thermal effect on the external environment. By employing a specialized device for target protection, the resulting thermal image closely resembles that of the basic background plate, effectively concealing any pertinent information regarding the target. In contrast, as depicted in Figure 1(e), when the target is a heat source, an increase in its temperature leads to heat transfer from the target to its external surroundings, thereby compromising the effectiveness of thermal camouflage and exposing crucial information about the target.

The heat conduction equation that considers the heat radiation was adopted to describe the heat transfer process in the radiative thermal camouflage device, which is expressed as:

$${\rho }_i{c}_i{\displaystyle \frac{\partial T_i}{\partial t}}=\nabla \cdot ({\kappa }_i\nabla T_i)+Q_{r,i}$$

(1)

where T and t denote surface temperature and time; $\rho$, $c$, and $\kappa$denote the density, specific heat capacity, and thermal conductivity of the object, respectively; $Q_r$denotes the net radiation heat transfer. The subscript $i$ can denote target ($i=t$), background ($i=b$) and camouflage device ($i=d$), respectively.

According to the law of Stefan-Boltzmann, the radiation heat exchange between the objects of the research (i.e. camouflage device and background) and the target in the closed cavity can be given by

$$Q_{r,i}=F_{t-i}{\epsilon }_t{A}_t\sigma （T_t^4-T_i^4）$$

(2)

where F denotes the configuration factor between different surfaces, $\epsilon$ and $A_t$ denote the surface emissivity and the surface area of the target, respectively; $\sigma$ is the Stefan-Boltzmann constant equal to 5.669 × 10-8W/(m²·K⁴).

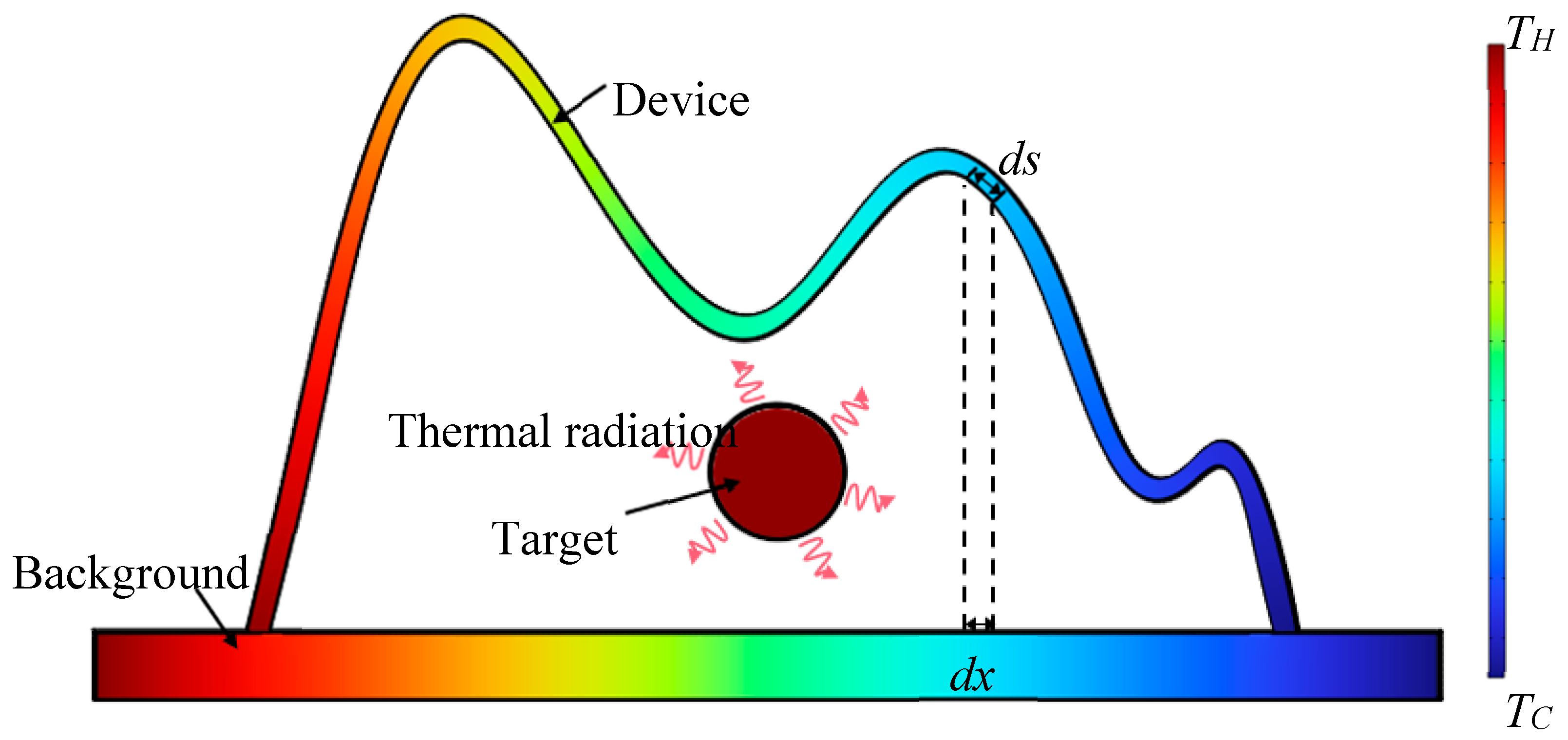
As shown in Figure 2, the left and right end of the background plate are set as $T_H$ and $T_C$ ($T_H>T_C$), respectively, resulting a temperature gradient. There is a target at high temperature put above the background radiating thermal energy all around. And the thermal camouflage device is represented by an arbitrary curve covering the background and the target. The theoretical principle used in this work is based on maintaining the synchronous heat transfer separately along the device and the background, when the temperatures of the device and the background are the same, the targets will be concealed. For an infinitesimal segment along the background plate, the path integral length of heat conduction is dx, while the counterpart along the camouflage device is the path integral of the device profile, $f(x)$, as $ds=\sqrt{1+f\text{'}{(x)}^2}dx$. According to the law of conservation of energy, after considering the radiation heat exchange between the target and the objects of the research, the thermal equilibrium equation in the case of two-dimension can be written as

$${\rho }_b{c}_b{\displaystyle \frac{\partial T_b}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}({\kappa }_b{\displaystyle \frac{\partial T_b}{\partial x}})+F_{t-b}{\epsilon }_t{A}_t\sigma （T_t^4-T_b^4）$$

(3)

$${\rho }_d{c}_d{\displaystyle \frac{\partial T_d}{\partial t}}={\displaystyle \frac{\partial }{\partial s}}({\kappa }_d{\displaystyle \frac{\partial T_d}{\partial s}})+F_{t-d}{\epsilon }_t{A}_t\sigma （T_t^4-T_d^4）$$

(4)

Eq. (3) and Eq. (4) can be further calculated as

$${\displaystyle \frac{\partial T_b}{\partial t}}={\alpha }_b{\displaystyle \frac{{\partial }^2{T}_b}{\partial x^2}}+{\displaystyle \frac{\partial {\alpha }_b}{\partial x}}{\displaystyle \frac{\partial T_b}{\partial x}}+{\displaystyle \frac{F_{t-b}{\epsilon }_t{A}_t\sigma （T_t^4-T_b^4）}{{\rho }_b{c}_b}}$$

(5)

$$\begin{array}{c}{\displaystyle \frac{\partial T_d}{\partial t}}={\alpha }_d{\displaystyle \frac{{\partial }^2{T}_d}{\partial s^2}}+{\displaystyle \frac{\partial {\alpha }_d}{\partial s}}{\displaystyle \frac{\partial T_d}{\partial s}}+{\displaystyle \frac{F_{t-d}{\epsilon }_t{A}_t\sigma （T_t^4-T_d^4）}{{\rho }_d{c}_d}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\displaystyle \frac{{\alpha }_d}{1+f\text{'}{(x)}^2}}{\displaystyle \frac{{\partial }^2{T}_d}{\partial x^2}}+{\displaystyle \frac{1}{1+f\text{'}{(x)}^2}}{\displaystyle \frac{\partial {\alpha }_d}{\partial x}}{\displaystyle \frac{\partial T_d}{\partial x}}+{\displaystyle \frac{F_{t-d}{\epsilon }_t{A}_t\sigma （T_t^4-T_d^4）}{{\rho }_d{c}_d}}\end{array}$$

(6)

where α denotes the thermal diffusion coefficient, as $\alpha ={\displaystyle \frac{\kappa }{\rho c}}$.

It can be inferred from Eq. (5) and Eq. (6) that the requirements $T_d(x,t)\equiv T_b(x,t)$, when x changes in the range of $\left[a,b\right]$ to be satisfied can only be achieved if the following Eq. (7) to Eq. (9) are satisfied simultaneously.

$${\alpha }_b={\displaystyle \frac{{\alpha }_d}{1+f\text{'}{(x)}^2}}$$

(7)

$${\displaystyle \frac{\partial {\alpha }_b}{\partial x}}={\displaystyle \frac{1}{1+f\text{'}{(x)}^2}}{\displaystyle \frac{\partial {\alpha }_d}{\partial x}}$$

(8)

$${\displaystyle \frac{F_{t-b}}{{\rho }_b{c}_b}}={\displaystyle \frac{F_{t-d}}{{\rho }_d{c}_d}}$$

(9)

Therefore, substituting Eq. (7) into Eq. (8) yields the following equation:

$${\displaystyle \frac{2f\text{'}(x)f\text{'}\text{'}(x)}{{(1+f\text{'}{(x)}^2)}^2}}{\alpha }_d=0$$

(10)

Due to ${\alpha }_d\ne 0$, the solution of Eq. (10) is valid only when $f\text{'}(x)f\text{'}\text{'}(x)=0$. When $f\text{'}(x)=0$, the thermal camouflage device is completely attached to the background plate, which does not conform to the theoretical model. Hence, the reasonable solution of Eq. (10) is $f\text{'}\text{'}(x)=0$, yields the following equation:

$$f\text{'}(x)=C=\tan \theta$$

(11)

where C denotes constant, $\theta$ denotes the angle between the thermal camouflage device and the background plate. Substituting Eq. (11) into Eq. (7) yields:

$${\displaystyle \frac{{\alpha }_d}{{\alpha }_b}}=1+{\tan }^2\theta$$

(12)

Besides, Eq. (12) can further become the following equation.

$${\displaystyle \frac{{\alpha }_d}{{\alpha }_b}}={\displaystyle \frac{\frac{{\kappa }_d}{{\rho }_d{c}_d}}{\frac{{\kappa }_b}{{\rho }_b{c}_b}}}={\displaystyle \frac{{\kappa }_d}{{\kappa }_b}}{\displaystyle \frac{{\rho }_b{c}_b}{{\rho }_d{c}_d}}=1+{\tan }^2\theta$$

(13)

Hence, substituting Eq. (9) into Eq. (13) can further yield:

$${\displaystyle \frac{{\kappa }_d}{{\kappa }_b}}{\displaystyle \frac{{\rho }_b{c}_b}{{\rho }_d{c}_d}}={\displaystyle \frac{{\kappa }_d}{{\kappa }_b}}{\displaystyle \frac{F_{t-b}}{F_{t-d}}}=1+{\tan }^2\theta$$

(14)

Namely

$${\displaystyle \frac{{\kappa }_d}{{\kappa }_b}}=(1+{\tan }^2\theta ){\displaystyle \frac{F_{t-d}}{F_{t-b}}}$$

(15)

In this paper, the configuration factor is a parameter that is only related to the geometric structure. Thus, Eq. (15) shows that as long as the thermal conductivity of device and background, also the configuration factor can be determined, we can calculate the angle $\theta$ from Eq. (15) to achieve the thermal camouflage that we expect. Since the camouflage device has to contact the background plate again to form an enclosed interior space, we can use the piecewise linear function with an angle $\theta$ to the X-axis to describe the profile of the device. Obviously, the resulting device is an isosceles triangle structure. So now the question is how to calculate the configuration factor.

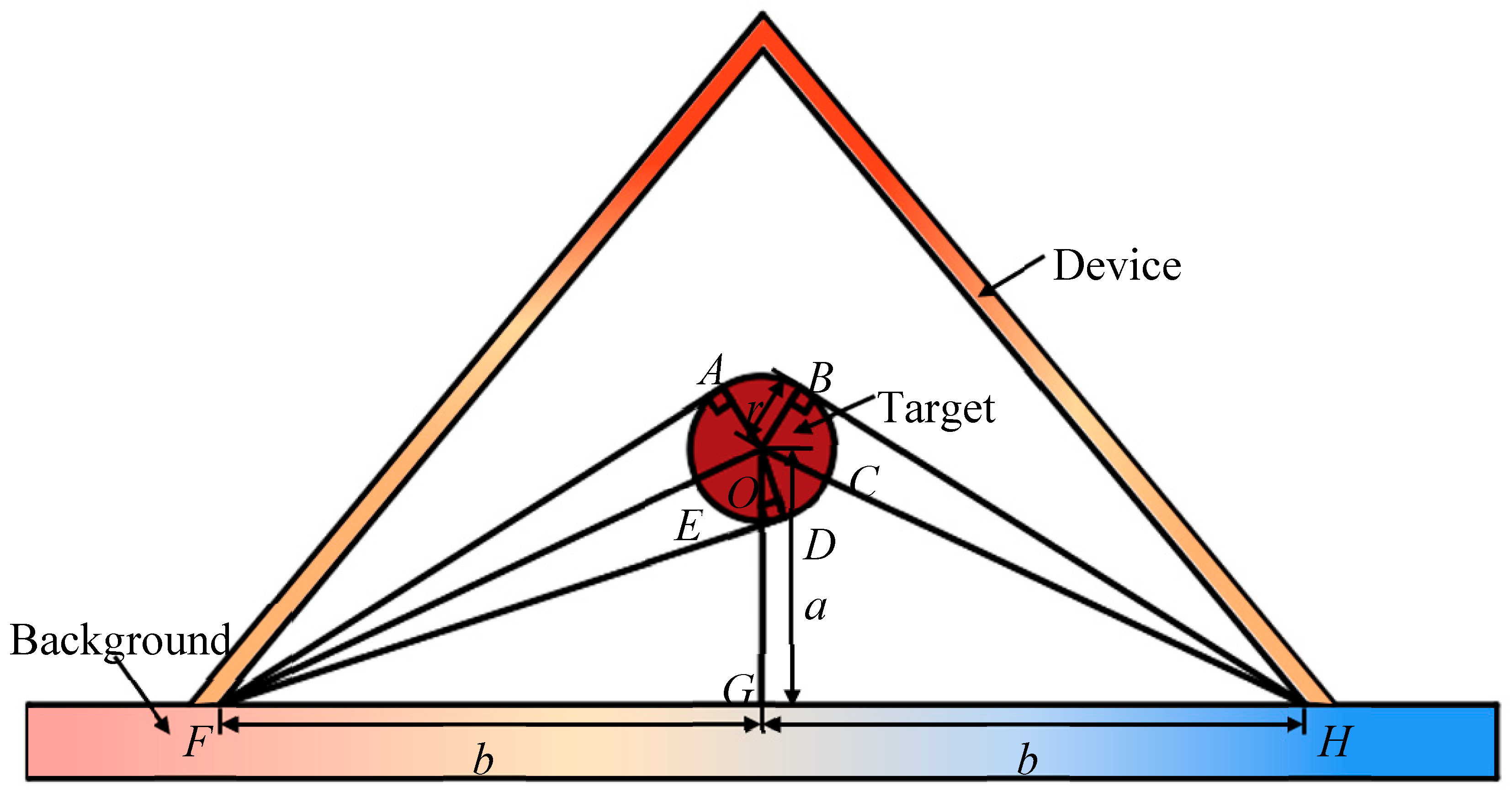
The schematic of the geometric relationships among the background, the device and the target are shown in Figure 3. Name $\angle FOG=\angle HOG=\alpha$, $\angle FOA=\angle FOD=\angle HOB=\beta$. According to the Hottel’s Cross-string Method, the configuration factor between the background and the target can be written as

(16)

Further, note that $\Delta ODF\cong \Delta OBH$,thus,

$$\overline{DF}=\overline{BH}$$

(17)

Substituting Eq. (17) into Eq. (16)results in

$$\angle FOD=\angle BOH$$

(18)

(19)

Besides, note that $\angle FOH=\angle BOD=2\alpha =2\arctan \left({\displaystyle \frac{b}{a}}\right)$, thus

(20)

In addition, according to the Law of Sines,

$$\sin \beta ={\displaystyle \frac{\overline{FD}}{\overline{FO}}}={\displaystyle \frac{\sqrt{a^2+b^2-r^2}}{\sqrt{a^2+b^2}}}$$

(21)

Therefore, we can derive

(22)

Thus, substituting Eq. (20) and Eq. (22) into Eq. (19) results in

(23)

Furthermore, for a closed cavity,

$$F_{t-d}+F_{t-b}=1$$

(24)

Consequently, substituting Eq. (23) and Eq. (24) into Eq. (15) results in

$${\displaystyle \frac{{\kappa }_d}{{\kappa }_b}}=(1+{\tan }^2\theta ){\displaystyle \frac{F_{t-d}}{F_{t-b}}}=(1+{\tan }^2\theta ){\displaystyle \frac{\arcsin \left(\frac{\sqrt{a^2+b^2-r^2}}{\sqrt{a^2+b^2}}\right)}{\arctan \left(\frac{b}{a}\right)}}$$

(25)

Therefore, with Eq. (25), once we know the material parameters and the geometric relationships of the three objects, we can design the thermal camouflage device with the triangle shapes at the inclination angle $\theta$.

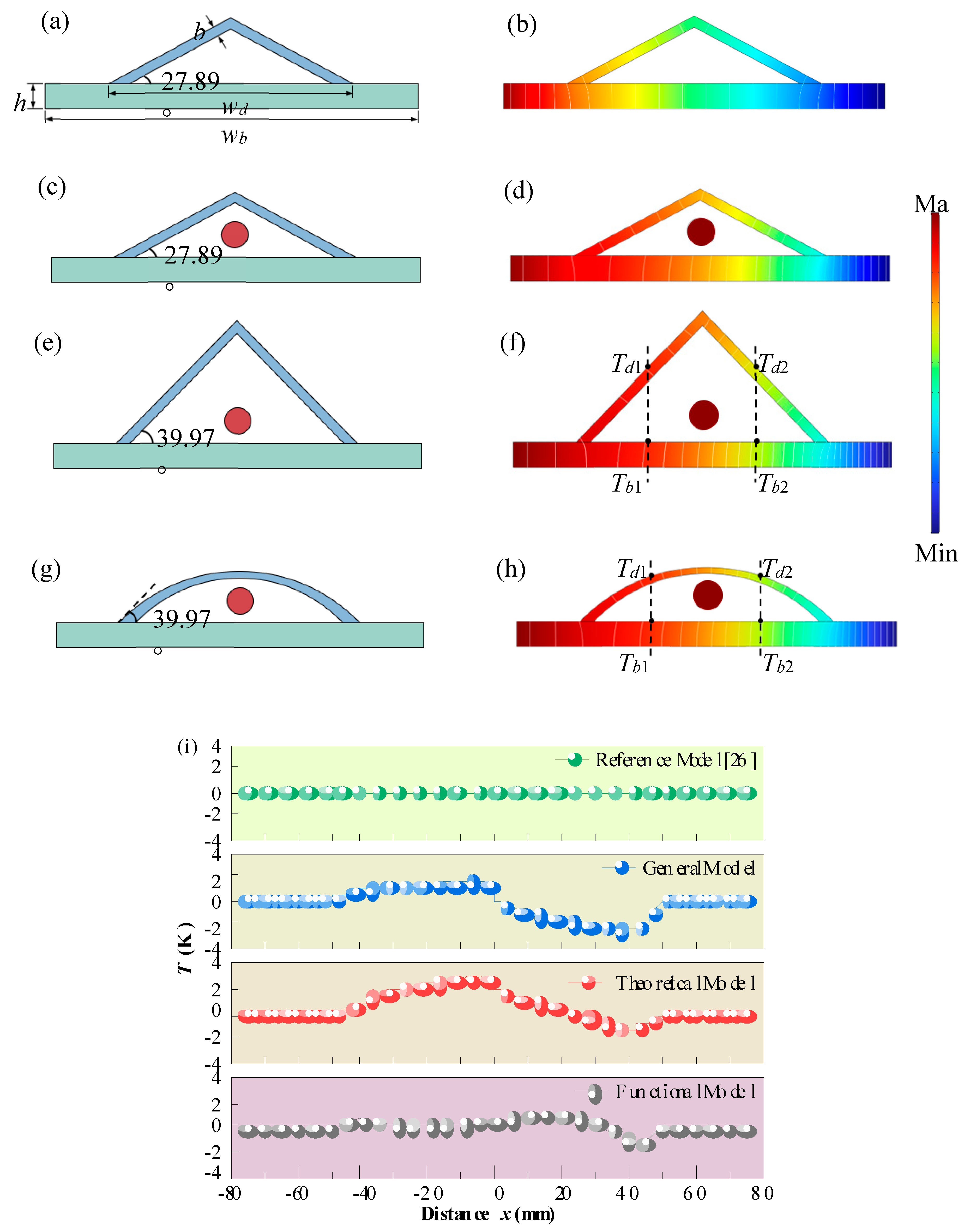
3. Results and Discussions

In order to verify the validity of the effectiveness of the thermal camouflage device which considers the influence of the radiative heat transfer of the target, the Reference Model, the General Model and the Theoretical Model are established. As shown in Figure 4(a), the Reference Model consists of an isosceles triangular camouflage device and a background plate, with a proposed inclination angle of $\theta$ = 27.89° by Zhang et al. [26], disregarding the thermal properties of the camouflaged targets. Besides, to investigate whether there is an impact on the thermal camouflage device from a target, we establish a General Model as shown in Figure 4(c). The General Model resembles the Reference Model but incorporates a circular target with a radius of 5 mm positioned at a vertical distance of 10 mm from the background plane. In addition, the Theoretical Model proposed in this paper is shown in Figure 4(e), which takes into account the thermal properties of the camouflaged target. It also features an isosceles triangular camouflage device, but with an inclination angle of $\theta$ = 39.97°. In both the General and Theoretical Models, the temperature and surface emissivity of this target are set as 1500 K and 0.8, respectively. Additionally, all models employ copper for constructing the thermal camouflage device while aluminum alloy 6063 is used for the background material, which possesses respective values for thermal conductivity (${\kappa }_d$= 398 W/(m·K), ${\kappa }_b$= 218 W/(m·K)), density (${\rho }_d$ = 8930 kg/m³, ${\rho }_b$ = 2690 kg/m³), specific heat capacity (cd = 386 J/(kg·K), cb = 900 J/(kg·K)), and the surface emissivity (${\epsilon }_d$ = 0.04, ${\epsilon }_b$= 0.095). As shown in Figure 4(a), the dimensions of the background are set as w_b = 150 mm, h = 10 mm, and w_d = 100 mm, and the thickness of the device is b = 4 mm.

Subsequently, we perform the numerical simulation with the commercial software COMSOL Multiphysics to validate their performance. We set a constant temperature on the left and right side as T_L = 400 K and T_R = 293.15 K, respectively. The remaining outer boundaries of the system are considered insulated, while the ambient temperature remains at 293.15K. The temperature distribution of the Reference Model, the General Model and the Theoretical Model are shown in Figure 4(b), Figure 4(d) and Figure 4(f), respectively. The performance of the thermal camouflage is quantified using the temperature deviation between the surface temperature of the device and the background $\Delta T(x)$ along the position distribution [$\Delta T(x)=T_b(x)-T_d(x)$]. As shown in Figure 4(i), the temperature deviation $\Delta T$ of the Reference Model identically equal to zero, meaning the surface temperature of the device and the background is exactly the same. The Reference Model is the control group for this simulation. Compared with the Reference Model, under the action of the thermal radiation heat transfer of the target, the diagram of the temperature deviation $\Delta T$ of the General Model has significantly changed, representing significant deviations and fluctuations. The sharp change of $\Delta T$ easily exposes the presence and contour of the target, this means that the camouflage performance of the thermal camouflage device by the General Model becomes weakened or even destroyed. Furthermore, considering the influence of radiative thermal transfer from the target in the Theoretical Model, it is evident that the temperature deviation $\Delta T$ is effectively mitigated within the anterior section of the device.

This abrupt jump in $\Delta T$ observed within the posterior section is greatly suppressed by the modified Theoretical Model (named the Functional Model), which incorporates tangent arcs on both sides of the original Theoretical Model (the triangle structure). The Functional Model, depicted as an arc structure in Figure 4(g), exhibits the temperature distribution shown in Figure 4(h). As shown in Figure 4(i), the temperature deviation $\Delta T$ of the Functional Model does not produce a sharp change at the coordinate x = 0, but remains closer to zero throughout the whole structure. This variation can be attributed to the influence of heat concentration on heat radiation transfer caused by the acute top angle of the triangular structure, which is eliminated by the smooth surface of the arc structure. The Functional Model demonstrates a maximum deviation value of 1.2 K, representing its smallest magnitude among all three models.

In addition, as depicted in Figure 4(f) and Figure 4(h), we extract and plot the surface temperature of specific points on both the background and the device over time at two different horizontal locations for the Theoretical Model [Figure 4(j)] and the Functional Model [Figure 4(k)], respectively. It is worth noting that $T_d$ and $T_b$ exhibit a similar trend over time, eventually reaching a steady state for both models. However, in the case of the Theoretical Model, there is a noticeable deviation between the curves of $T_d$ and $T_b$ over time. Specifically, there is a maximum difference of 6.4 K (2.8 K) between the curves of $T_{d1}$ and $T_{b1}$ ($T_{d2}$ and $T_{b2}$), indicating non-synchronous heat conduction through both the device and the background. Such deviations from synchronous heat transfer can be easily detected using an infrared thermal imager, thereby revealing not only its presence but also its location accurately. In contrast, for the Functional Model, there is excellent agreement between $T_d$ and $T_b$ throughout all stages of temperature change, further confirming its exceptional performance in synchronous heat transfer. In summary, except effectively matching steady-state temperature fields, it can be concluded that the Functional Model exhibits outstanding performance in terms of synchronous heat transfer over time.

along the position distribution for each model. The transient temperature field comparison of the certain points between the background and the device for (j) the Theoretical Model and (k) the Functional Model.

According to Eq (2), the radiation heat exchange between the camouflage device or background and the target $Q_{r,i}$ is related to the configuration factor between different surfaces F, the surface emissivity $\epsilon$, the surface area of the target A and the temperature of the target T. 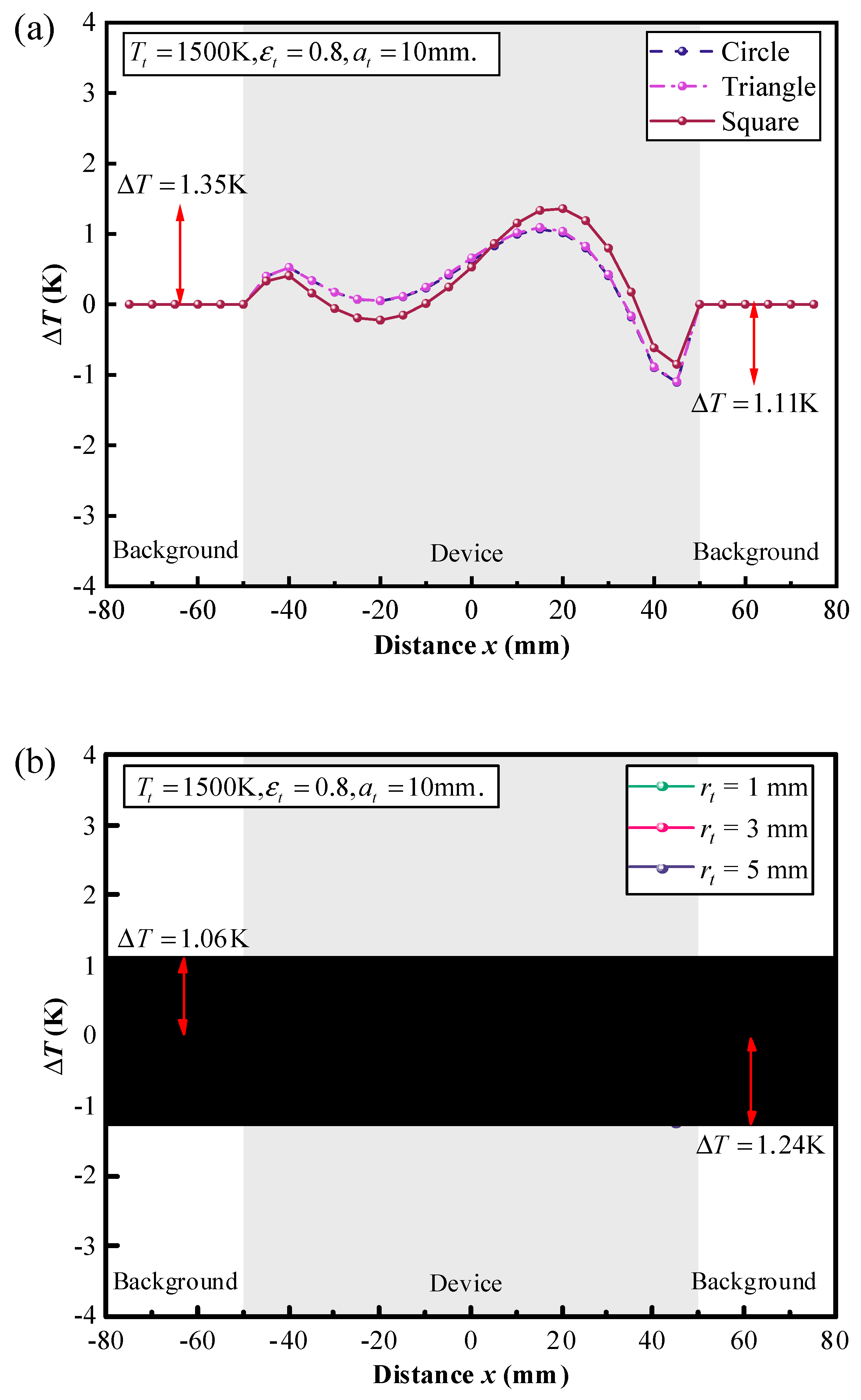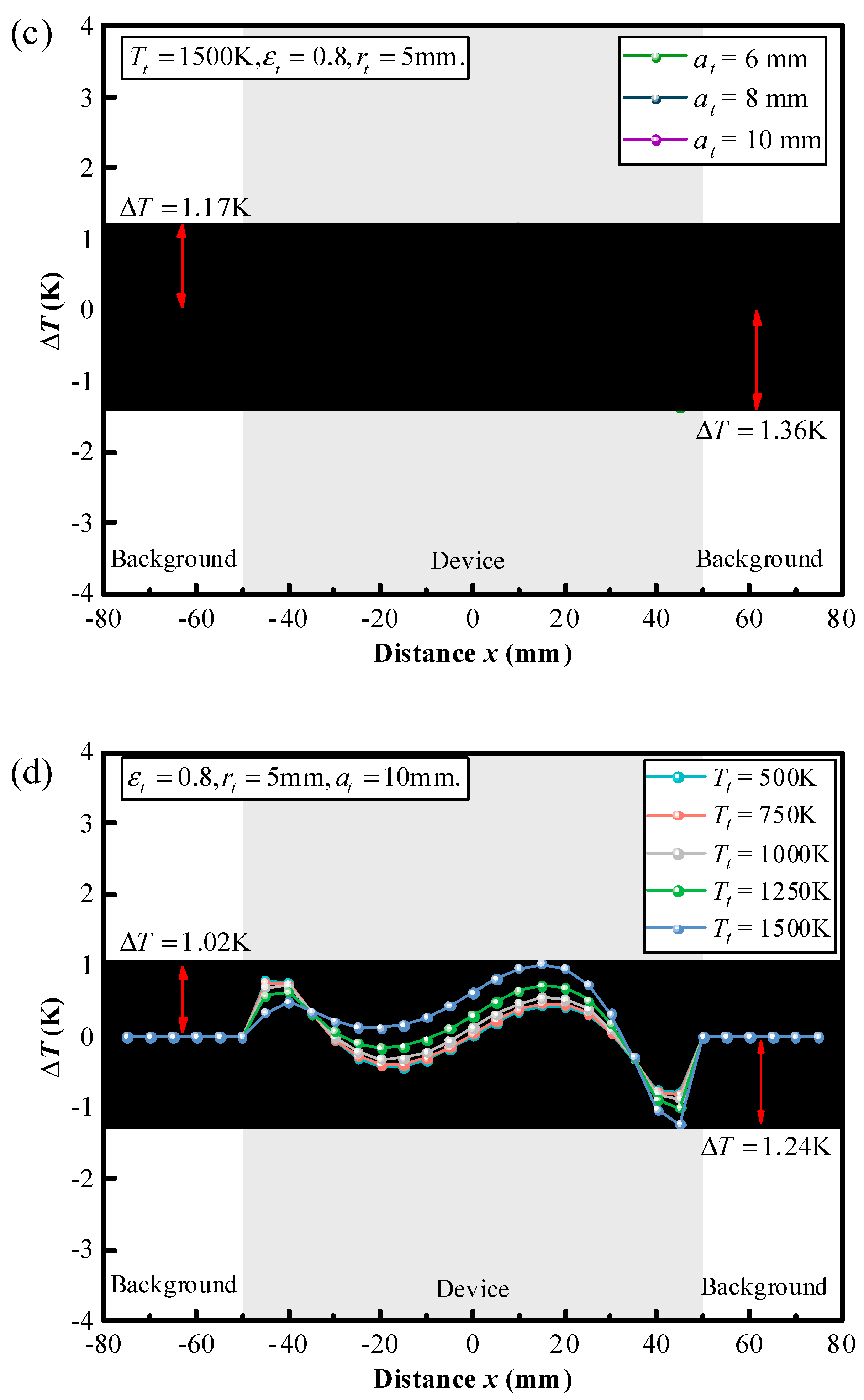Therefore, in order to further validate the thermal camouflage performance of the Functional Model, a comprehensive analysis is presented in Figure 5(a)-(e), encompassing various parameters such as target geometry and location, temperature and surface emissivity. To simplify the discussion, only one parameter is varied while keeping the other parameters fixed. In the following discussion, the boundary conditions remain unchanged.

The effect of the geometry and the location of the target on the thermal camouflage performance of the thermal camouflage device is studied, as depicted in Figure 5(a)-(c). Firstly, we systematically vary the shapes of the target, including a circle, triangle, and square, while maintaining a constant surface area. Subsequently, we maintain a circular shape for the target and adjust its surface area by altering the radii values to 1 mm, 3 mm, and 5 mm respectively. Finally, we employed a circular geometric target with a radius of 5 mm, and varied the position of the target within the cavity between camouflage and background by changing the y-coordinate of the target center by 6 mm, 8 mm, and 10 mm, respectively, while keeping the x-coordinate constant. By combining Figure 5(a)-(c), it can be found that no matter how to change the shape, the surface area or the position of the target, the temperature deviation $\Delta T$ agrees closer to zero all the time.

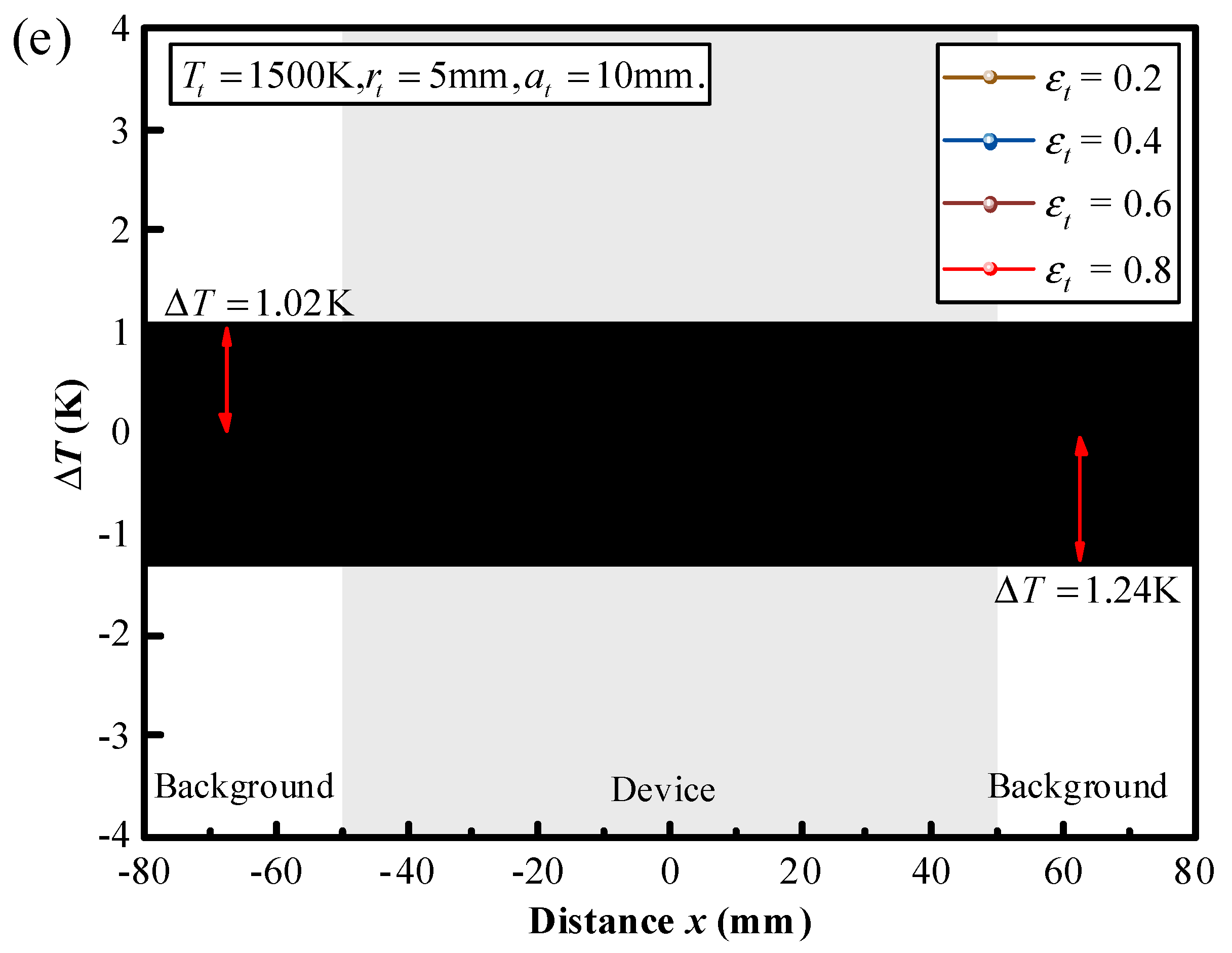
The effect of the temperature and surface emissivity of the target on the thermal camouflage performance of the thermal camouflage device are illustrated in Figure 5(d) and (e), respectively. From Figure 5(d) and (e), even with significant increases in target temperature and surface emissivity, the temperature deviation $\Delta T$ consistently approaches zero. These results demonstrate that the Functional Model maintains excellent thermal camouflage performance.

along the position distribution in the case of (a) the different shapes, (b) the different surface areas, (c) the different locations, (d) the different temperatures and (e) the different surface emissivity of the target.

4. Conclusions

In summary, quite different from the previous thermal camouflage metamaterials do not consider the thermal characteristics of the target, we proposed a high-temperature thermal camouflage device that considers the influence of radiative thermal transfer from the target. The theoretical principle of the device is based on simultaneous heat transfer between the device and the background at all times. The performance of the device is confirmed by numerical simulations. Specifically, the Functional Model (arc-shaped device) achieves near-zero temperature deviation (1.2 K) under steady-state conditions, outperforming the Theoretical Model (traditional triangular-shaped device). Additionally, the arc-shaped device based on the Functional Model demonstrates consistent thermal camouflage performance across various target geometries (circle, triangle, square), vertical positions (6-10 mm), temperatures (500-1500 K), and surface emissivities (0.2-0.8). Future integration of this design with existing frameworks may enable robust thermal camouflage systems for high-temperature environments. Moreover, this research has the potential to extend its applications to areas such as infrared stealth in optoelectronics, thermal diagnostics for high-power chips, and dynamic heat flux control in integrated circuits.