Quantum Substrate Dynamics (QSD): A Relativistic Field Model of Emergent Mass, Inertia and Gravity

1. Introduction

This work develops a coherence-based physical model in which mass, gravity, inertia, and time emerge from the internal dynamics of a conserved, Lorentz-invariant substrate field. Rather than treating geometry or particles as fundamental, Quantum Substrate Dynamics (QSD) models all known physical behavior as consequences of phase coherence, tension, and boundary interactions within a continuous field $\mathsf{\Psi }$.

The substrate is not composed of discrete particles nor embedded in spacetime—it is the coherence medium from which spacetime behavior and classical observables arise. Matter, fields, and radiation are interpreted as structured waveforms or phase transitions within this medium. Coherence saturation leads to mass formation, tension gradients manifest as gravitational effects, and inertial resistance results from the energetic cost of boundary reconfiguration.

QSD is motivated by the recognition that while modern physics successfully describes particle interactions and gravitational curvature, it offers limited insight into why these effects arise or how they might emerge from a deeper physical structure. This framework seeks to bridge that conceptual gap by introducing a substrate whose internal coherence dynamics give rise to the observed laws of physics, rather than assuming them axiomatically.

QSD does not seek to replace established physical theories, but rather to provide a unified physical substrate from which they emerge naturally. Under appropriate coherence and tension limits, the dynamics of the substrate reproduce:

• Newtonian mechanics as a linear coherence-drag regime in low-velocity, low-gradient systems;
• General Relativity as the macroscopic expression of coherence tension gradients, matching geodesic motion and Einstein field equations;
• Quantum Field Theory as a high-coherence limit with quantized excitation modes corresponding to persistent substrate geometries.

These recoveries are not merely imposed assumptions, but emerge as natural consequences of conservation principles and coherence dynamics governing the substrate field $\mathsf{\Psi }$. This compatibility ensures that QSD remains consistent with all verified experimental regimes while offering novel, testable extensions in domains involving coherence breakdown, scalar wave propagation, or inertial geometry-dependence.

Critically, QSD addresses conceptual and physical limitations that persist in mainstream frameworks. General Relativity (GR) lacks internal physical mechanisms for inertia or black hole structure; it models curvature outcomes but not the physical substrate that enforces them. Quantum Field Theory (QFT), meanwhile, treats the vacuum as an inert and featureless background, offering no structural explanation for mass localization, geometry-sensitive inertia, or neutrino flavor coherence. QSD fills these gaps by positing a conserved substrate whose internal coherence and tension gradients give rise to inertial drag, coherence-bound mass knots, and scalar emission during rapid phase reconfiguration—offering explicit mechanisms where GR and QFT rely on external postulates.

A central insight of this framework is that time is not a pre-existing background dimension but a phase-structured interval defined by the passage of scalar wavefronts. Motion, interaction, and radiation are governed by how the substrate reorients to conserve coherence under deformation. This approach reinterprets force postulates and geometric axioms with physically motivated coherence dynamics, while preserving Lorentz invariance and local symmetry.

The mathematical formulation builds on analogies from superfluid systems and nonlinear field theory, but generalizes them to a relativistic context. Known physical laws—including classical mechanics, gravitational behavior, and quantum field excitation—emerge as limiting cases of the substrate’s behavior under specific coherence conditions. This compatibility is not imposed; it is required by internal conservation of the substrate and the dynamics of its reconfiguration.

Quantum Substrate Dynamics presents a physically grounded reinterpretation of familiar concepts within a continuous, conserved field. It yields testable predictions in regimes where standard models remain incomplete, including scalar emissions during rapid coherence transitions, geometry-dependent inertia, and non-Doppler shifts across gravitational domains. The substrate field $\mathsf{\Psi }$ is not hypothetical scaffolding—it is proposed as the physical field from which all known behaviors arise.

The timing of this work does not reflect a shift in experimental data, but a shift in conceptual understanding. The model emerged when it became clear that mass, inertia, time, and quantization could all arise from coherence dynamics within a single conserved substrate—without invoking imposed discreteness, virtual intermediaries, or geometric axioms. While modern frameworks have achieved great predictive power, they often do so by modeling abstractions—virtual particles, statistical operators, and curvature-based constraints—that function effectively but lack physical grounding. These abstractions, powerful though they are, resemble the shadows of a deeper structure. Quantum Substrate Dynamics (QSD) is an attempt to illuminate the form that casts those shadows. It seeks not to overwrite known physics, but to reveal it as the natural outcome of deeper coherence-based dynamics. The goal is to offer a structural foundation beneath established models—one that remains compatible with known laws while enabling testable predictions that arise from the substrate’s internal logic.

Numerous theoretical approaches have attempted to reinterpret gravity, quantization, and spacetime structure as emergent phenomena. These include Sakharov’s proposal of vacuum-induced gravity [8], Verlinde’s entropic force model [12], and Padmanabhan’s equipartition-based view of spacetime [30]. Analog gravity models in superfluid systems by Unruh [13], Visser [10], and Volovik [9] have explored how horizon and curvature phenomena might arise in effective media. Ontological interpretations of quantum mechanics—such as Bohm’s hidden-variable theory [11], Madelung’s hydrodynamic formulation [15], and Hiley’s nonlocal process models [37]—have also laid conceptual groundwork for phase-structured theories.

Experimental work across coherence domains, including Bose–Einstein condensation [16,17,27,28], quantized vortex flow [5,6,7,21,22,23], and nanofluidics [24,25,26], provide indirect support for substrate-bound coherence structures. Astrophysical and high-energy timing anomalies observed in neutrino events [31,32,33], scalar-precursor models [29], and gravitational detection systems like LISA [34] offer potential observational contexts for falsifiability. Studies of inertial lag [35] and heat conduction in acceleration-sensitive media [36] further illustrate coherence-driven dynamical effects.

While these models and data points contribute meaningfully to the broader discourse on emergent and structured physics, the present formulation of Quantum Substrate Dynamics (QSD) is developed independently, from physical first principles. The cited works are included for conceptual awareness and contrast, not as theoretical foundations. QSD does not rely on thermodynamic, statistical, or analog metaphors; instead, it presents a Lorentz-invariant, coherence-based substrate model in which quantization, curvature, and time arise from internal phase constraints, reconfiguration resistance, and tension propagation dynamics.

2. Foundational Principles of Quantum Substrate Dynamics

To clarify the internal structure of Quantum Substrate Dynamics (QSD), we present the following set of foundational principles. These are not claimed as final laws of nature, but rather as physically motivated postulates that guide the behavior and implications of the theory. They provide a coherent substrate-based ontology from which the known laws of physics—classical, quantum, and relativistic—emerge as limiting cases.

• Substrate Ontology Principle
  At the foundation of all physical phenomena is a Lorentz-invariant quantum substrate—a continuous, conserved, coherence-bearing field. This substrate supports all matter, forces, radiation, and time as emergent behaviors of its internal structure. It is not composed of particles, nor embedded in spacetime—it is the source from which spacetime, mass, and energy arise. This is the sole ontological postulate of QSD; all subsequent physical behavior follows as emergent consequence.
  In this context, coherence refers to the degree of phase alignment and continuity within the substrate’s internal wave structure. High coherence allows stable, low-loss propagation of wave modes; disruptions or gradients in coherence give rise to forces, mass condensation, and radiation.
  The substrate is not generated from within itself, nor does QSD propose an origin mechanism. Its existence is posited as a foundational condition, parallel to how spacetime is treated in General Relativity or the quantum vacuum in QFT. Just as those frameworks do not explain why spacetime or field structure exists, QSD takes the substrate as the starting point for physical law.
• Lorentz Invariance of the Substrate Principle
  The substrate respects Lorentz symmetry. Uniform motion through it is undetectable; only acceleration, coherence disruption, or tension gradients reveal its presence. The observed speed of light c is not an intrinsic constant of spacetime, but emerges from local coherence properties of the substrate. While locally invariant and undetectable in uniform motion, its global value may shift subtly across regions of differing substrate tension—though this variation remains unmeasurable within any single local frame.
• Conservation of Substrate Principle
  The substrate is fundamentally conserved. It is neither created nor destroyed—only reconfigured through changes in coherence, phase, or tension. All energetic phenomena arise from the redistribution of the same continuous field.
• Substrate Equilibrium Principle
  The quantum substrate continuously reorients to restore local and global coherence equilibrium. It redistributes phase and internal tension to minimize distortion and maintain structural stability. This behavior governs all emergent physical dynamics.
• Coherence Lag Principle — A mass-phase structure undergoing acceleration must reconfigure the coherence flux across its boundary. When acceleration ceases, this flux does not instantaneously stabilize. A brief but physically real coherence lag phase follows, during which residual substrate reconfiguration continues. This lag resolves as the system transitions into flux equilibrium, manifesting as inertial settling or scalar relaxation phenomena. It accounts for experimentally observed nanosecond-scale delays in systems ranging from self-propelled particles[35] to heat flux fields[36], and provides a dynamic extension to the classical notion of motion transition.
• Substrate Coherence Principle
  All observable physical phenomena emerge from the coherence structure of the substrate. Coherence gradients, interference, saturation, and restoration drive the formation of mass, forces, time, and radiation.
• Minimal Deformation Principle
  When deformation is required to support mass-phase condensation or wave energy localization, the substrate displaces over the smallest possible region. This minimizes energy cost, confines tension gradients, and leaves distant regions undisturbed unless coherence continuity demands otherwise.
• Vacuum Equilibrium Principle
  What is conventionally called “vacuum” is, in QSD, the substrate in a locally balanced coherence state. This equilibrium condition supports quantum fluctuations and wave excitations without requiring spacetime curvature or matter. The vacuum is not empty—it is coherence-neutral. All field effects arise from deviations from this state.
• Substrate Energy Principle
  All energy in QSD arises from internal movements and reconfigurations of the conserved substrate. Energy is not a separate entity, but a manifestation of coherence displacement, tension propagation, or wavefront reorientation within the substrate field $\mathsf{\Psi }$. Kinetic, potential, thermal, and radiant energy correspond to specific modes of structured substrate motion or deformation. Rather than existing independently, energy reflects the dynamic state of the substrate as it shifts, compresses, or restores coherence in response to internal or boundary conditions.
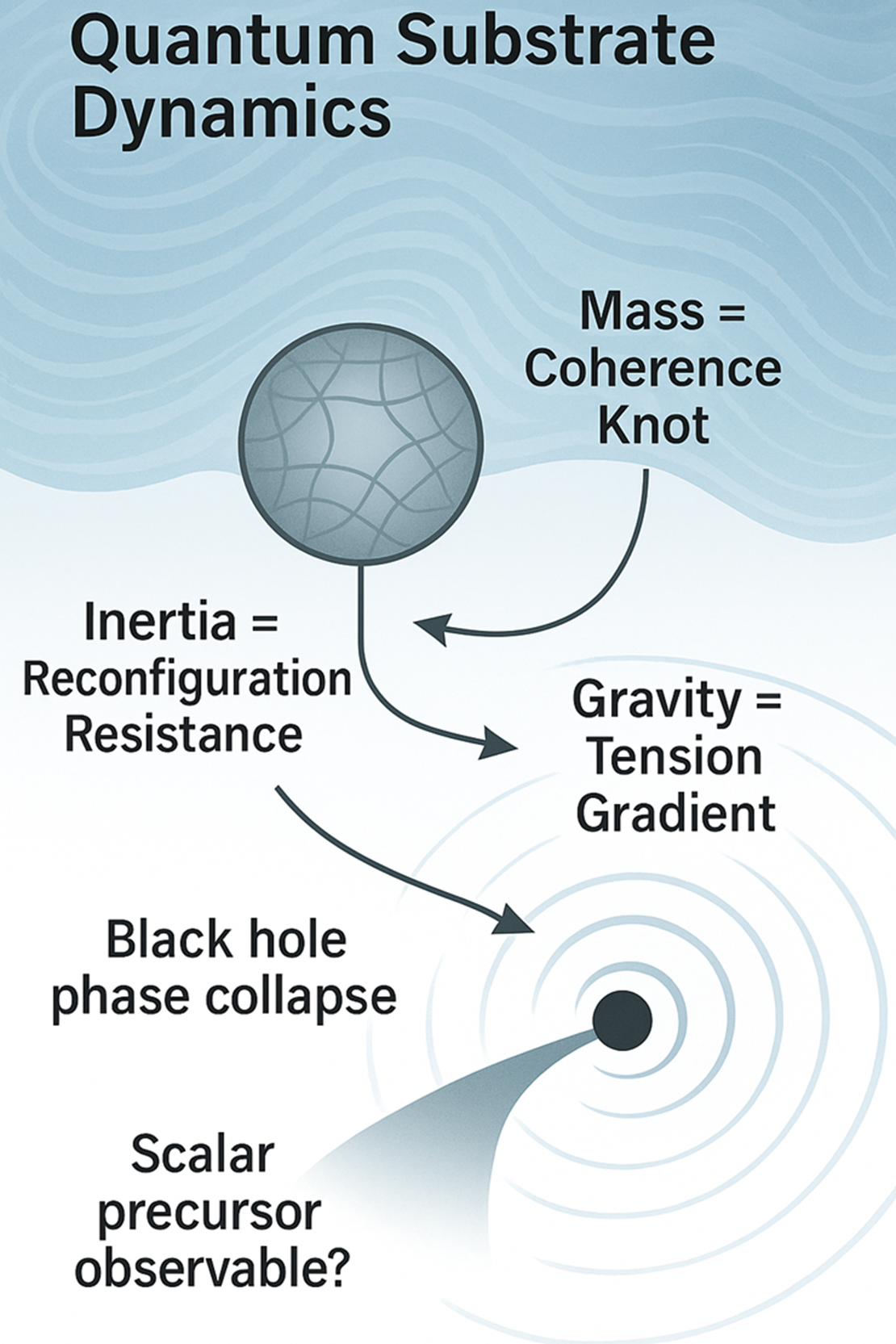
• Mass as a Coherence Phase Principle
  Mass is a localized, stable condensation of coherence—or a coherence knot—a phase state within the substrate where waveforms saturate and resist deformation. Mass is not substance, but structured tension.
• Embeddedness Principle
  Because mass-phase structures are localized coherence configurations within the quantum substrate, they are never isolated. Their existence and behavior are defined by continuous interaction with the surrounding field. All observable motion, inertia, and gravitational response emerge from this embedded condition. The substrate is not a passive background but an active coherence environment, shaping and responding to mass through flux continuity, tension gradients, and reconfiguration resistance. Embeddedness is a structural property of mass, not an external effect.
• Inertia as Coherence Reconfiguration Resistance (”Inertial Drag”)
  Inertia is the energetic cost of reconfiguring the substrate boundary as a mass-phase object accelerates. This resistance is shaped by internal geometry, coherence gradients, and scalar interactions.
• Emergent Quantization Principle
  Quantized mass states arise not from intrinsic discreteness, but from the stability conditions of substrate coherence. The quantum substrate supports a continuous spectrum of curvature configurations, but only certain geometries persist—those that resist reconfiguration. Observable particles correspond to these stable folds, while all other states dissipate as scalar or neutrino emissions or return to the wave phase undetected.
• Equivalence Principle (Reframed)
  Gravitational and inertial mass are identical because they both reflect the same coherence-boundary structure. Their equivalence arises naturally from substrate drag and tension geometry.
  Flux Transition Threshold.
  As part of this rebalancing behavior, there exists a specific substrate flux value $J_{\mathsf{\Psi }}^{\mathrm{eq}}$ at which reconfiguration resistance vanishes. This threshold marks the transition from active acceleration to stable uniform motion, identifying the point where coherence flux across the mass-phase boundary equalizes. Rather than treating uniform motion as force-free, this defines it as a resolved substrate interaction state. The flux threshold depends on internal structure and coherence resistance, offering a measurable and falsifiable inflection point in the dynamics of motion.
• Gravity as Tension Gradient Principle (Driven by Substrate Saturation)
  Gravity is a push force caused by coherence tension gradients. These gradients emerge when regions of high waveform complexity saturate the substrate, drawing in restorative pressure from the surrounding field. What appears as gravitational attraction is actually the substrate pushing inward toward regions of distortion. All forces in QSD arise from tension gradients and equilibrium restoration—not action at a distance.
• Transverse Wave Principle
  Electromagnetic waves are transverse coherence modes of the quantum substrate. Their propagation speed c arises from the local coherence tension and transverse elasticity of the substrate, and reflects the maximum stable velocity for transverse wavefronts within a coherence-neutral domain.
  These waves are not fundamental entities, but structured oscillatory states of the substrate’s internal phase geometry. Observable constants such as vacuum permittivity and permeability correspond to local substrate response parameters in the transverse mode regime.
  While c appears universal, its value is set by substrate properties and may vary across large-scale coherence gradients—though such variation remains unmeasurable within any single inertial frame, preserving Lorentz invariance locally.
  In this framework, electromagnetic behavior emerges from the same substrate mechanics as scalar and gravitational phenomena. EM fields are coherence structures, not separable forces, and their wave behavior is a specific manifestation of substrate phase continuity under transverse excitation.
  The observed emission spectrum of transverse waves, such as blackbody radiation, reflects not only temperature but the substrate’s local mass-phase structure, which governs which coherence modes couple to EM radiation and which offload through scalar or non-radiative channels.
• Scalar Wave Principle
  Scalar waves are longitudinal coherence-pressure excitations in the substrate. They propagate independently of charge and can travel through dense or shielded environments. These waves are emitted during rapid substrate reconfiguration. They are variations of the substrate, not in it.
• Gradient Frame Transition (GFT) Principle
  Transitions between large-scale substrate tension gradient domains produce observable dynamical effects. As mass-phase structures or wavefronts cross between macro-coherence fields, they may experience shifts in inertia, apparent gravitational response, or scalar drag. These transitions may also induce non-Doppler redshifts or blueshifts in propagating light due to phase discontinuities across coherence gradients.
  Coherence wavefronts—including light—must rephase across domain boundaries. This produces coherence shocks, which can yield measurable anomalies in spectral lines, pulse timing, or inertial balance. Such effects offer testable signals of underlying substrate structure and may explain observed gravitational or spectroscopic anomalies in astrophysical systems.
• Time as Scalar Propagation Interva Principlel
  Time is not a fundamental background dimension, but a measure of phase displacement. It emerges from the interval between scalar wavefronts propagating through the substrate.
• Coherence-Coupling Misinterpretation Principle
  While implicit in the preceding principles of time, coherence, and wave propagation, this principle is stated explicitly to address a subtle but critical interpretive point.
  Observed variations in clock rates and light speed under gravitational or inertial conditions reflect paired responses of the quantum substrate to local coherence tension—not deformations of a geometric manifold.
  In the QSD framework, both time dilation and the bending of light emerge from the same underlying substrate behavior: local modulation of scalar and transverse wave propagation due to coherence gradients. These are not independent changes in time and space, but co-manifestations of tension-induced phase response.
• Required Recovery and Field Behavior Principle
  Quantum Substrate Dynamics reproduces the known laws of physics under appropriate limits. Newtonian mechanics arises from coherence drag in low-velocity regimes; General Relativity emerges from macroscopic tension gradients; and Quantum Field Theory describes wave-phase excitations in high-coherence, weakly nonlinear domains.
  In this view, fields traditionally treated as independent—electromagnetic, scalar, gravitational, fermionic—are interpreted as distinct coherence modes of a single, conserved substrate. Their consistent propagation and coupling behavior suggest a common physical origin. QSD does not contradict quantum field theory, but reframes it as an effective description of deeper substrate coherence dynamics. This requirement dictates all known physics must appear as a limiting case of substrate behavior under specific coherence conditions.

3. Theoretical Framework

Quantum Substrate Dynamics (QSD) proposes a physically real, Lorentz-invariant quantum fluid substrate $\mathsf{\Psi }$ as the foundation from which all observed physical phenomena—mass, inertia, gravity, time, and field interactions—emerge. This section outlines the fundamental features of this substrate and its core behavioral regimes, providing the structural basis for the emergent physics developed in subsequent sections.

3.1. The Substrate Ontology Principle

At the core of Quantum Substrate Dynamics (QSD) is the assertion that all observable physical phenomena emerge from the behavior of a single, continuous, conserved medium: a Lorentz-invariant quantum substrate, denoted $\mathsf{\Psi }$. This substrate is not composed of particles nor embedded within spacetime—it is the fundamental physical entity from which spacetime, energy, matter, and radiation arise [see Appendix A.1].

Substrate Ontology Principle:

At the foundation of all physical phenomena is a Lorentz-invariant quantum substrate—a continuous, conserved, coherence-bearing field. This substrate supports all matter, forces, radiation, and time as emergent behaviors of its internal structure. It is not composed of particles, nor embedded in spacetime—it is the source from which spacetime, mass, and energy arise.

In this framework, the defining property of the substrate is its ability to support coherent wave structures. The term coherence refers to the degree of local phase alignment and continuity within the substrate’s internal oscillatory state. High coherence allows stable, low-loss propagation of wave modes across the substrate; disruptions, discontinuities, or gradients in coherence manifest as forces, mass condensation, radiation, and other physical effects.

3.1.1. Mathematical Representation of Coherence.

Let the substrate at point $\overrightarrow{r}$ and time t be described by a complex field:

$$\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)},$$

where $\rho$ is the local coherence amplitude, and $\theta$ is the local phase.

We define the local coherence measure $\mathcal{C}(\overrightarrow{r},t)$ over a finite volume V as:

$$\mathcal{C}(\overrightarrow{r},t)=\left|{\displaystyle \frac{1}{\left|V\right|}}{\int }_V{e}^{i\theta ({\overrightarrow{r}}^{\prime },t)}{d}^3{\overrightarrow{r}}^{\prime }\right|,$$

where $\mathcal{C}\in [0,1]$. A value near 1 indicates strong local phase alignment; lower values indicate dephasing, interference, or breakdown of coherence.

3.1.2. Physical Consequences.

• Mass: arises as regions of saturated coherence—stable, phase-aligned condensates of the substrate.
• Inertia: results from the energetic cost of deforming or accelerating a coherence-boundary region.
• Forces: emerge as the substrate reorients to minimize internal coherence gradients.
• Time: is defined by the propagation of scalar wavefronts through $\mathsf{\Psi }$, tied to substrate response time.
• Spacetime geometry: is a derived effect of substrate curvature and tension, not a primary manifold.

This principle serves as the ontological foundation of QSD. The rest of the framework explores how coherence structure and its dynamics produce classical fields, particles, relativistic behavior, and quantum effects from a single, conserved physical substrate.

3.2. The Conservation of Substrate Principle

A central tenet of Quantum Substrate Dynamics (QSD) is that the underlying physical medium—the quantum substrate $\mathsf{\Psi }$—is not created or destroyed. It is a conserved field, continuous in space and time, whose dynamic behaviors result entirely from internal reconfiguration. This conservation principle is foundational to the emergence of energy, force, mass, and field interactions.

Conservation of Substrate:

The substrate is fundamentally conserved. It is neither created nor destroyed—only reconfigured through changes in coherence, phase, or tension. All energetic phenomena arise from redistribution of the same continuous field.

This conservation law supersedes conservation of mass and energy as separate principles. In QSD, mass and energy are forms of structured coherence within the substrate; their interconversion—described, for example, by $E=m{c}^2$—is simply a shift in the substrate’s internal configuration, not a creation or annihilation event.

3.2.1. Mathematical Implication.

Let $\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}$ be the complex substrate field. Conservation implies that the total integrated coherence amplitude remains constant under all transformations:

$${\displaystyle \frac{d}{dt}}{\int }_{\mathsf{\Omega }}\rho {(\overrightarrow{r},t)}^2{d}^3\overrightarrow{r}=0.$$

This represents the preservation of substrate density across any domain $\mathsf{\Omega }$, even during energetic processes such as wave collapse, mass formation, or scalar emission.

3.2.2. Physical Interpretation.

• Energy release: Events like particle annihilation or nuclear reactions are not destruction of substance, but reconfiguration of tightly bound substrate coherence into freely propagating wave modes.
• Mass formation: Mass condensation involves local increase in coherence density and tension, drawn from surrounding wave-phase substrate.
• Scalar waves: Emitted scalar waves are phase-pressure responses of the substrate—not external agents—ensuring no net gain or loss of field substance.

This principle ensures the internal closure of QSD: all physical change occurs within a single conserved medium. It provides the structural integrity needed to unify classical and quantum behaviors under a continuous field model, replacing ontological gaps with fluidic coherence logic.

3.3. The Substrate Equilibrium Principle

The dynamical behavior of the quantum substrate $\mathsf{\Psi }$ is governed by its intrinsic drive toward equilibrium. The substrate acts continuously to restore local and global coherence, minimizing internal tension, distortion, and phase discontinuity. This tendency underlies the emergence of force, motion, field propagation, and energy exchange.

Substrate Equilibrium Principle:

The quantum substrate continuously reorients to restore local and global coherence equilibrium. It redistributes phase and internal tension to minimize distortion and maintain structural stability. This behavior governs all emergent physical dynamics.

This principle positions the substrate as an inherently self-organizing medium. Unlike classical fields, which passively evolve under external forces, the substrate actively reconfigures in response to coherence gradients. It behaves analogously to a superfluid or elastic medium—but one generalized to relativistic and quantum-coherent regimes.

3.3.1. Mathematical Characterization.

Let $\mathcal{C}(\overrightarrow{r},t)$ represent the local coherence as previously defined. The substrate evolves to minimize the spatial and temporal gradient energy associated with $\mathcal{C}$. A generalized coherence-tension functional may be written:

$${\mathcal{E}}_{\mathrm{coh}}=\int \left[{\gamma }_1{|\nabla \mathcal{C}|}^2+{\gamma }_2{\left({\displaystyle \frac{\partial \mathcal{C}}{\partial t}}\right)}^2\right]d^3\overrightarrow{r},$$

where ${\gamma }_1$ and ${\gamma }_2$ are substrate-dependent stiffness coefficients. The substrate dynamically evolves to minimize ${\mathcal{E}}_{\mathrm{coh}}$, driving reorientation and stabilization of the internal wave structure.

3.3.2. Physical Interpretation.

The drive toward equilibrium manifests across scales:

• In low-gradient regions, equilibrium leads to uniform wave-phase behavior and freely propagating excitations.
• Near mass-phase boundaries, tension gradients create restorative push-forces that resemble gravity and inertia.
• During high-gradient events (e.g., collapse, excitation, or decoherence), rapid reconfiguration releases energy in the form of scalar waves or other phase-stabilizing excitations. (For a detailed treatment of scalar emissions, coherence trench dynamics, and black hole merger frustration, see [29].)

This equilibrium-seeking behavior replaces the notion of static background fields with a dynamic substrate that actively reshapes its structure to minimize energetic imbalance. It is the source of all reactive phenomena in QSD—gravity, mass retention, inertial drag, and scalar emission—and frames the universe not as a fixed stage, but as a tension-driven coherence system.

Flux Transition Threshold.

As a corollary of this equilibrium behavior, there exists a specific substrate flux value $J_{\mathsf{\Psi }}^{\mathrm{eq}}$ at which reconfiguration resistance vanishes. This threshold marks the transition from acceleration to uniform motion and defines the moment at which inflow and outflow of substrate coherence flux across the mass-phase boundary equalize. Rather than treating uniform motion as the absence of force, this perspective reframes it as a stabilized substrate interaction state. The flux threshold is expected to depend on the internal geometry and CRI (Coherence Resistance Index) of the object, offering a potentially measurable inflection point in motion dynamics.

3.4. The Minimal Deformation Principle

While the quantum substrate actively seeks coherence equilibrium, it does so with remarkable economy. Rather than deforming broadly or diffusely, the substrate responds with strictly localized adjustments, displacing only where coherence demands are critical. This behavior underlies the localized nature of mass, forces, and field interactions observed in physical systems.

To model this behavior, we define a coherence-bearing field $\mathsf{\Psi }(\overrightarrow{r},t)$, and introduce an energy functional that characterizes the cost of deformation:

$$E_{\mathrm{deform}}\left[\mathsf{\Psi }\right]={\int }_{\mathsf{\Omega }}\left[{\sigma |\nabla \mathsf{\Psi }|}^2+\kappa {\left|{\nabla }^2\mathsf{\Psi }\right|}^2+V\left(\mathsf{\Psi }\right)\right]d^{3}x,$$

(1)

where:

• $\sigma$ is the local substrate tension coefficient,
• $\kappa$ is the substrate stiffness (resistance to curvature),
• $V\left(\mathsf{\Psi }\right)$ is a potential governing preferred coherence states (e.g., double-well or nonlinear saturation),
• $\mathsf{\Omega }$ is the spatial domain over which deformation occurs.

The principle of minimal deformation asserts that the substrate reconfigures in such a way that $E_{\mathrm{deform}}$ is minimized, and the domain $\mathsf{\Omega }$ over which the field departs from equilibrium is as small as possible, consistent with coherence continuity:

$$\delta E_{\mathrm{deform}}=0,\mathrm{subject}\mathrm{to}\mathsf{\Psi }\to {\mathsf{\Psi }}_0\mathrm{as}\left|\overrightarrow{r}\right|\to \infty .$$

(2)

This variational formulation implies that substrate distortions—such as those required to support mass-phase condensation or scalar wave passage—are confined to compact regions. The resulting coherence field behaves analogously to localized solitons or phase-locked droplets, preventing long-range substrate deflection except where coherence constraints require it.

The Minimal Deformation Principle thus explains why mass, inertia, and curvature effects are not smeared across space, but are sharply localized, enabling isolated particles and field interactions to emerge from continuous substrate dynamics.

3.5. The Substrate Coherence Principle

In Quantum Substrate Dynamics (QSD), coherence is the principal organizing property of the substrate. Every observable physical effect—mass, motion, time, force, radiation—arises from how coherence is structured, distorted, or restored within the quantum substrate $\mathsf{\Psi }$. This law unifies disparate phenomena under a single explanatory framework: the internal phase alignment of the substrate field.

Substrate Coherence Law:

All observable physical phenomena emerge from the coherence structure of the substrate. Coherence gradients, interference, saturation, and restoration drive the formation of mass, forces, time, and radiation.

Coherence is not a background property—it is the dynamic variable that determines the local and global behavior of the field. When coherence is high, waves propagate smoothly and stably. When coherence breaks down or saturates, mass forms, fields emerge, and wave modes become localized or disrupted.

3.5.1. Quantifying Coherence Effects.

Let $\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}$ describe the local substrate field. Then:

• The coherence amplitude $\rho (\overrightarrow{r},t)$ defines wave stability.
• The phase gradient $\nabla \theta (\overrightarrow{r},t)$ contributes to local flow and tension.
• The coherence scalar:

  $$\mathcal{C}(\overrightarrow{r},t)=\left|{\displaystyle \frac{1}{\left|V\right|}}{\int }_V{e}^{i\theta ({\overrightarrow{r}}^{\prime },t)}{d}^3{\overrightarrow{r}}^{\prime }\right|$$

  measures local phase alignment across a neighborhood V.

Spatial or temporal changes in these quantities create measurable physical outcomes.

3.5.2. Emergent Phenomena from Coherence Dynamics.

• Mass formation: occurs when local coherence saturates, locking wave-phase into a stable lattice.
• Forces: arise from coherence gradients, which push or reorient the substrate toward equilibrium.
• Time: is defined by the scalar wave propagation interval through coherent substrate regions.
• Radiation: is the outward propagation of localized coherence disturbances (wavefronts) across the field.

This law shifts the explanatory burden in physics from abstract interactions between fields to concrete phase-geometry within a single conserved substrate. Coherence is not just a wave property—it is the structural driver of reality in QSD.

Minimal Deformation Principle:

When deformation is required to support mass-phase condensation or wave energy localization, the substrate displaces over the smallest possible region. This minimizes energy cost, confines tension gradients, and leaves distant regions undisturbed unless coherence continuity demands otherwise.

This principle explains why mass and gravitational influence are spatially compact despite being coherence phenomena. The substrate resists wide-area reconfiguration, preferring to adjust minimally around high-coherence or high-tension structures, much like elastic media that localize stress around inclusions or defects.

3.5.3. Mathematical Formulation.

Let $\delta \mathsf{\Psi }(\overrightarrow{r},t)$ denote a perturbation to the substrate field due to an imposed coherence requirement. The deformation region $\mathsf{\Omega }$ is determined by minimizing the coherence energy functional under localization constraints:

$$\delta \mathcal{E}=\underset{\mathsf{\Omega }}{min}{\int }_{\mathsf{\Omega }}\left({|\nabla \mathsf{\Psi }|}^2+V_{\mathrm{coh}}\left(\mathsf{\Psi }\right)\right)d^3\overrightarrow{r},$$

subject to the boundary condition that coherence is preserved at the interface between mass-phase and wave-phase regions. The minimization of $\delta \mathcal{E}$ constrains deformation to the smallest spatial volume that can satisfy the required coherence transition.

3.5.4. Physical Consequences.

• Mass localization: Stable mass-phase structures do not broadly deform the substrate; their influence is contained near their coherence boundary.
• Force locality: Gravitational and inertial forces arise only near mass-phase regions where tension gradients form. Distant substrate regions remain unaffected unless continuity requires participation.
• Scalar emission localization: Energy released during substrate reconfiguration is radiated as localized scalar waves, not distributed broadly, preserving local-global coherence balance.

This principle ensures that the substrate’s coherence economy produces localized, efficient reconfiguration—supporting discrete structures and confined interactions without requiring global rearrangement. It explains why matter appears particulate and why field effects have finite range and fall off with distance. Together with the equilibrium principle, it defines the energy-efficient dynamics of the substrate.

3.6. The Vacuum Equilibrium Principle

In conventional physics, the vacuum is often conceptualized as empty space, or in quantum field theory, as a zero-point energy sea with fluctuating virtual particles. Quantum Substrate Dynamics (QSD) reinterprets these abstract notions with a physically real coherence medium in a balanced state—what QSD identifies as the true vacuum.

Vacuum Equilibrium Principle:

What is conventionally called “vacuum” is, in QSD, the substrate in a locally balanced coherence state. This equilibrium condition supports quantum fluctuations and wave excitations without requiring spacetime curvature or matter. The vacuum is not empty—it is coherence-neutral. All field effects arise from deviations from this state.

In this view, vacuum is not the absence of structure, but a dynamically neutral configuration of the substrate—characterized by uniform coherence amplitude and zero net phase gradient. It serves as the default background state from which deviations define forces, particles, and interactions.

3.6.1. Mathematical Characterization.

Let $\mathsf{\Psi }(\overrightarrow{r},t)={\rho }_0{e}^{i{\theta }_0}$ define the local substrate field in a vacuum region, where ${\rho }_0$ and ${\theta }_0$ are spatially uniform. Then:

$$\nabla \rho =0,\nabla \theta =0,{\displaystyle \frac{\partial \mathsf{\Psi }}{\partial t}}=0,$$

and the local coherence measure $\mathcal{C}(\overrightarrow{r},t)\approx 1$. This defines the coherence-neutral condition. Perturbations $\delta \mathsf{\Psi }$ from this state generate localized excitations (e.g., particles, waves, or curvature analogs).

3.6.2. Physical Implications.

• Quantum fluctuations: arise as micro-perturbations of phase or amplitude within the vacuum’s coherence field, not as random field insertions but as structured, bounded deviations.
• Wave propagation: coherent wave modes—including electromagnetic, scalar, and neutrino-like excitations—propagate stably through this medium when coherence remains high.
• Field emergence: all observable fields (EM, gravitational, etc.) are expressions of local departures from vacuum coherence. No separate background geometry is required.

This principle reframes the vacuum as a tangible, Lorentz-invariant coherence configuration—quiet but active, and always poised to support structure. By establishing vacuum as a neutral coherence state, QSD provides a coherent, falsifiable physical foundation for wave propagation, field theory, and cosmological structure without invoking abstract geometric space or infinite zero-point fields.

3.7. Substrate Energy Principle

In Quantum Substrate Dynamics (QSD), energy is not treated as a primitive quantity or external bookkeeping tool, but as a structural manifestation of internal substrate behavior. All forms of energy—kinetic, potential, thermal, radiant—are emergent expressions of how the conserved substrate field $\mathsf{\Psi }$ reconfigures in space and time under coherent phase displacement.

Energy as Substrate Reconfiguration

The substrate is a Lorentz-invariant coherence field whose internal tension and phase alignment determine the stability and evolution of physical systems. In this context, energy arises from localized or propagating disruptions of coherence. Specifically:

• Kinetic energy corresponds to the continuous reorientation of the substrate’s coherence field around a moving mass-phase object. The faster the motion, the greater the rate of phase reconfiguration at the object’s boundary, increasing substrate tension and internal wavefront disruption.
• Potential energy represents stored coherence tension due to substrate gradients. In a gravitational field, for example, a mass-phase structure placed in a region of higher substrate tension gradient possesses increased potential energy because its stable configuration requires greater rebalancing effort from the surrounding field.
• Thermal energy arises from incoherent or semi-coherent oscillations within the substrate near a mass-phase structure. These small-scale fluctuations represent persistent, high-frequency reconfigurations that fail to achieve long-range phase alignment, yet contribute net tension and offload pressure.
• Radiant energy (e.g., electromagnetic or scalar wave propagation) is the transport of phase disturbance through the substrate, either in transverse or longitudinal modes. These are coherence wavefronts detached from their source, preserving structured phase information across spacetime.

3.7.1. Substrate Dynamics and Energy Flow

Energy transfer in QSD is modeled not as the movement of a quantity, but as the ongoing deformation and restoration of substrate coherence. Wave-matter interactions, heating, radiation, and mass accretion are all described as shifts in the substrate’s local phase configuration and tension state. In this view, conservation of energy is a consequence of the conservation and continuity of the substrate field itself, rather than an imposed symmetry.

$$\mathcal{E}\sim {\int }_{\mathsf{\Omega }}\tau (\overrightarrow{r},t)·\nabla \theta (\overrightarrow{r},t)d^{3}r$$

(3)

Here, $\tau$ represents local coherence tension and $\nabla \theta$ the phase displacement gradient. This expression provides a generalized measure of energy as stored or propagating substrate strain across a finite region $\mathsf{\Omega }$.

Unified Interpretation

This principle repositions energy as a pattern of motion within the underlying physical substrate. Rather than being treated as an abstract scalar or a conserved accounting quantity, energy in QSD reflects the measurable, structural dynamics of a conserved medium. It exists only insofar as the substrate is being reconfigured—compressed, displaced, twisted, or excited. Once coherence is restored and all gradients equilibrate, energy vanishes as a distinguishable phenomenon, leaving behind only geometric structure or vacuum phase.

This framework restores energy to its physical roots—not as a separate essence, but as an emergent behavior of a continuous, conserved, and reconfigurable field. It completes the reinterpretation of classical physical quantities in substrate terms and unifies the behaviors of motion, force, temperature, radiation, and mass into a single fluid ontology.

3.8. Mass as a Coherence Phase Principle

In Quantum Substrate Dynamics (QSD), mass is not treated as an intrinsic property or indivisible particle substance. Instead, mass is a stable, localized phase state of the substrate—formed when coherence saturates and wave modes become locked into a persistent lattice. It is structured, not static; emergent, not fundamental.

Mass as a Coherence Phase:

Mass is a localized, stable condensation of coherence—or a coherence knot—a phase state within the substrate where waveforms saturate and resist deformation. Mass is not substance, but structured tension.

This interpretation replaces the notion of “massive particles” with the concept of coherence-bound solitonic regions—phase-stabilized bundles of wave energy that maintain their shape due to internal coherence reinforcement and external tension gradients. These regions exhibit long-lived stability, resist deformation, and behave as inertial structures.

3.8.1. Phase Locking and Stability.

Let the substrate field be written $\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}$. A mass-phase region is characterized by:

$${\displaystyle \frac{\partial \theta }{\partial t}}\approx 0,\nabla \theta \approx 0,\rho (\overrightarrow{r},t)\gg {\rho }_0,$$

where ${\rho }_0$ is the background wave-phase amplitude. These conditions reflect stationary internal phase, coherence saturation, and phase locking—conditions under which the substrate locally resists reconfiguration.

3.8.2. Energetic Implications.

The mass-phase stores energy in the form of coherence tension:

$$E_{\mathrm{mass}}\sim {\int }_V\left({\rho }^2+{|\nabla \rho |}^2+{\mathcal{U}}_{\mathrm{coh}}\left(\rho \right)\right)d^3\overrightarrow{r},$$

where ${\mathcal{U}}_{\mathrm{coh}}$ is a stabilizing potential that penalizes deviation from the lattice’s internal coherence profile. This integral reflects the energy density associated with amplitude locking, coherence curvature, and substrate stiffness. The inertial mass associated with this energy is thus:

$$m_{\mathrm{eff}}={\displaystyle \frac{1}{c^2}}{\int }_V\left({\rho }^2+{|\nabla \rho |}^2+{\mathcal{U}}_{\mathrm{coh}}\left(\rho \right)\right)d^3\overrightarrow{r}.$$

This expression grounds $E=m{c}^2$ not as a postulate, but as a derived result: the rest mass is proportional to the total stored coherence energy, and conversion to wave-phase radiation occurs when the mass-phase dissolves.

3.8.3. Connection to Observables.

This coherence model provides a path to empirical correspondence. For example, assuming a coherence knot localized within a sphere of radius equal to the Compton wavelength ${\lambda }_C$, one obtains energy magnitudes comparable to known particle rest masses when $\rho \sim 1/{\lambda }_C^{3/2}$. This supports the claim that coherence tension, not particle essence, sets mass.

3.8.4. Physical Consequences.

• Mass persistence: The structured coherence of a mass-phase region resists deformation and disruption, giving rise to inertial effects and long-term stability. Acceleration requires work against this boundary coherence.
• Mass-energy equivalence: The stored tension within a coherence lattice can be released as wave-phase energy. The relation $E=m{c}^2$ emerges as a reconfiguration identity: coherent energy transforms to traveling waves during annihilation or decay, not as annihilation of substance but as release of structure.
• Quantized states: Only certain lattice geometries remain stable under substrate tension—mass quantization arises from coherence persistence, not from intrinsic discreteness.
• Particle interpretation: What we call “particles” are coherence-phase solitons—localized, metastable, reconfigurable field structures shaped by substrate tension. Their properties emerge from geometry and coupling, not from substance.

3.8.5. Conceptual Summary

This principle reframes mass as a geometrical and dynamical feature of substrate coherence, not an ontological building block. Matter becomes a phase phenomenon—a configuration of coherent energy embedded in a deeper continuous field. It is persistent because it is locked; inertial because it resists reconfiguration; and energetic because it stores coherence tension.

3.9. Embeddedness Principle

Mass-phase structures in QSD are not free-floating or abstract point sources. They are localized coherence configurations within a conserved, relativistic substrate field. As such, they cannot exist, persist, or evolve independently of the substrate in which they are formed. This embeddedness is not a modeling assumption—it is a structural requirement.

Because mass arises from substrate saturation and phase alignment, it necessarily engages in continuous coherence flux exchange with the surrounding field. This flux mediates all observable phenomena associated with mass, including inertial resistance, gravitational response, and scalar wave interaction. A mass-phase object is therefore always a boundary condition on the substrate—a persistent deformation, maintained only through dynamic interaction.

This principle distinguishes QSD mass from classical or quantum point particles, which are typically treated as isolated entities with externally applied forces or fields. In contrast, QSD mass is a phase object defined by its immersion in—and tension against—the substrate. It cannot be separated from this context without dissolving the very structure that gives it physical identity.

Implications

• Inertia arises not from intrinsic mass, but from resistance to altering substrate flux through the embedded structure.
• Gravity is a local flux asymmetry—not a geometric property—arising from mass-phase deformation of the surrounding field.
• Scalar wave emission, flux threshold stabilization, and coherence lag all require the object to be embedded and interacting with its local coherence gradient.

Contrast with Classical Mass

In classical mechanics and general relativity, mass is often considered fundamental and isolated—either as a point source or curvature origin. In QSD, mass is emergent and interactive. It is only meaningful within the substrate, which defines its resistance, trajectory, and dynamical exchange. This redefinition of mass places the substrate, not empty spacetime, at the center of all physical behavior.

3.10. Inertia as Coherence Reconfiguration Resistance Principle (“Inertial Drag”)

In QSD, inertia is not a fundamental property of mass but a dynamical resistance that emerges from the substrate’s response to motion. Specifically, it arises from the energetic cost of reconfiguring the coherence structure surrounding a mass-phase object as it accelerates. This cost is not limited to an infinitesimal surface, but spans a finite transition region where coherence gradients reorient in response to displacement of the internal waveform structure.

Inertia as Coherence Drag:

Inertia is the energetic cost of reconfiguring the substrate’s coherence-gradient zone around a mass-phase object during acceleration. This resistance is shaped by internal waveform geometry, coherence tension gradients, and scalar coupling.

Acceleration requires the substrate to reconfigure the coherent envelope enclosing the mass-phase structure. The sharper the gradient and the more complex the internal structure, the more costly this reconfiguration becomes—giving rise to inertial resistance. In this model, "drag" is not dissipative friction, but a conservative deformation cost imposed by the substrate’s coherence continuity.

3.10.1. Quantitative Framework.

Let the substrate field be expressed as $\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}$, and let the mass-phase object be moving with velocity $\overrightarrow{v}\left(t\right)$. The coherence transition zone is defined as a shell ${\mathsf{\Omega }}_{\delta }\left(t\right)\subset {\mathbb{R}}^3$, bounded by a coherence density threshold $\rho \in [{\rho }_0,{\rho }_m]$, where coherence begins to depart from wave-phase uniformity but has not yet saturated into mass-phase rigidity.

The inertial reaction force is given by the rate of substrate energy reconfiguration in this gradient zone:

$$F_{\mathrm{inertial}}={\displaystyle \frac{d}{dt}}\left({\int }_{{\mathsf{\Omega }}_{\delta }\left(t\right)}{\mathcal{E}}_{\mathrm{grad}}(\overrightarrow{r},t)d^{3}r\right),$$

where ${\mathcal{E}}_{\mathrm{grad}}$ is the coherence deformation energy density, composed of:

$${\mathcal{E}}_{\mathrm{grad}}={\alpha |\nabla \rho |}^2+\beta {|\nabla \theta |}^2+\gamma \mathcal{K}(\rho ,\theta ),$$

with $\alpha ,\beta ,\gamma$ encoding substrate elasticity and phase responsiveness, and $\mathcal{K}$ representing geometric curvature or coherence torsion within the field. This formulation captures how the substrate energetically responds to preserving phase continuity across moving coherence structures.

3.10.2. Inertial Mass from Gradient Shell Reconfiguration.

For small accelerations and near-linear reconfigurations, the substrate response reduces to a familiar inertial form:

$$F=m_{\mathrm{eff}}\overrightarrow{a},\mathrm{with}{m}_{\mathrm{eff}}={\displaystyle \frac{1}{c^2}}{\int }_{{\mathsf{\Omega }}_{\delta }}\left({\alpha |\nabla \rho |}^2+\beta {|\nabla \theta |}^2+\gamma \mathcal{K}\right)d^{3}r.$$

Here, $m_{\mathrm{eff}}$ is the effective inertial mass, emerging from the field’s energetic resistance to realigning its coherence structure in the finite transition layer surrounding the mass-phase body.

3.10.3. Variational Formulation and Least Action.

The inertial response of a coherence structure can be equivalently described by a principle of least action applied to the substrate’s reconfiguration dynamics. Define an effective Lagrangian density ${\mathcal{L}}_{\mathrm{coh}}$ for the coherence field $\mathsf{\Psi }=\rho e^{i\theta }$ as:

$${\mathcal{L}}_{\mathrm{coh}}=-\left({\alpha |\nabla \rho |}^2+\beta {|\nabla \theta |}^2+\gamma \mathcal{K}\right),$$

where each term penalizes spatial deformation or curvature in the transition zone. The inertial path taken by an accelerating object minimizes the total reconfiguration action:

$$S={\int }_{{\mathsf{\Omega }}_{\delta }}{\mathcal{L}}_{\mathrm{coh}}{d}^{3}rdt.$$

The observed inertial force thus emerges as the substrate’s response to deviations from this minimal-action path—reflecting its resistance to disruptive phase deformation. In this framework, acceleration is constrained not by an external geometry, but by the substrate’s intrinsic coherence economy.

3.10.4. Dimensional Analysis of Inertial Drag in the Substrate

In the QSD framework, inertia arises from the energetic cost of reconfiguring the quantum substrate at the boundary of a mass-phase object undergoing acceleration. This resistance manifests as a form of inertial drag due to coherence displacement and substrate tension response.

To dimensionalize this concept, we consider the drag force as arising from resistance across the mass-phase boundary envelope of characteristic length scale L (e.g., radius of the coherent mass knot). Let ${\rho }_{\mathsf{\Psi }}$ denote the effective mass-equivalent density of the substrate (units $\mathrm{kg}/{\mathrm{m}}^3$), and let $a={\displaystyle \frac{dv}{dt}}$ represent the acceleration of the object. Then the inertial drag force can be approximated as:

$$F_{\mathrm{drag}}\sim {\rho }_{\mathsf{\Psi }}·L^2·a,$$

(4)

where $L^2$ represents the effective cross-sectional area over which coherence drag acts. This formulation ensures that $F_{\mathrm{drag}}$ carries the correct physical units of force ($\mathrm{kg}·\mathrm{m}/{\mathrm{s}}^2$).

The corresponding inertial energy cost for a displacement $\Delta x$ is:

$$E_{\mathrm{drag}}\sim F_{\mathrm{drag}}·\Delta x\sim {\rho }_{\mathsf{\Psi }}·L^2·a·\Delta x,$$

(5)

yielding units of energy ($\mathrm{Joules}$), consistent with the expected work done to overcome substrate resistance during reconfiguration.

This approach emphasizes that inertia in QSD is not a fixed intrinsic property, but a dynamic response of the substrate to deformation across coherence boundaries. Variations in ${\rho }_{\mathsf{\Psi }}$, boundary curvature, or substrate tension gradients could therefore produce geometry-dependent inertial behavior—a prediction distinct from classical and quantum field models.

3.10.5. Key Contributions to Inertial Resistance.

• Internal waveform geometry: Fine-grained or structured coherence topologies create more surface variation in the gradient zone, increasing reconfiguration energy.
• Coherence gradients: Steeper transitions between wave and mass phase (i.e., sharper phase boundaries) raise ${|\nabla \rho |}^2$ and ${|\nabla \theta |}^2$, amplifying drag response.
• Scalar coupling: At high accelerations or under nonlinear excitation, coherence disruption may radiate scalar waves, producing dissipative back-reaction and measurable phase lag.

3.10.6. Implications and Predictions.

• Variable inertia: Objects with the same rest mass but different internal coherence geometries (e.g., solid vs. nanoporous structures) may exhibit differing inertial resistance.
• Nonlinear acceleration response: Inertial drag is expected to become nonlinear at high acceleration gradients, possibly showing threshold discontinuities or emission-induced phase shifts.
• Experimental testability: Structure-sensitive inertia predicted by QSD could be probed using torsion balances, drop-tower experiments, or space-based interferometry to detect coherence-dependent inertial deviations.

3.10.7. Conceptual Summary.

This principle reframes inertia as an emergent property rooted in the energetic cost of reconfiguring substrate coherence. Resistance is not applied by "mass" as substance, but by the substrate’s need to maintain phase continuity and coherence alignment under displacement. The term “inertial drag” thus refers to the substrate’s dynamic opposition to coherence distortion—localized not to a surface, but to a finite region of gradient tension surrounding the mass-phase structure.

3.11. The Emergent Quantization Principle

In Quantum Substrate Dynamics (QSD), quantization is not assumed—it emerges naturally from the stability properties of coherence folding—or coherence knotting. The substrate supports a continuous range of curvature configurations, but only specific ones achieve the structural persistence necessary for observation. These stable configurations correspond to what we conventionally identify as quantized mass states.

Mass in QSD is defined as the localized resistance to substrate reconfiguration—a function of how tightly the substrate is curved, bound, and phase-locked. However, not all curvatures result in a viable mass-phase lattice. Most configurations either:

• fail to maintain structural coherence,
• radiate excess tension through scalar or neutrino emission,
• or dissolve back into the wave-phase substrate.

Only certain folds—those that minimize boundary drag and maintain coherence flux equilibrium—survive. These correspond to the “quantized” particles seen in experiment. The quantization is not due to fundamental discreteness, but rather to the energetic filtering of viable folds.

To represent this formally, we define a substrate folding potential landscape $V_{\mathrm{fold}}\left(\kappa \right)$, where $\kappa$ is the local coherence curvature:

$$V_{\mathrm{fold}}\left(\kappa \right)=\left\{\begin{array}{cc}\mathrm{Metastable}\mathrm{or}\mathrm{unstable}\hfill & \mathrm{if}\kappa \notin \left\{{\kappa }_n\right\}\hfill \\ \mathrm{Stable}\left(\mathrm{observable}\right)\hfill & \mathrm{if}\kappa ={\kappa }_n\hfill \end{array}\right.$$

Here, ${\kappa }_n$ are the discrete curvature configurations that produce persistent mass-phase structures. The evolution of a folding region follows:

$${\displaystyle \frac{d\kappa }{dt}}=-{\displaystyle \frac{\partial V_{\mathrm{fold}}}{\partial \kappa }}+S\left(t\right)$$

where $S\left(t\right)$ represents an external scalar compression source (e.g., a collapse front or shock wave). As the field compresses, it attempts to settle into one of the minima ${\kappa }_n$. If unsuccessful, the excess curvature is shed via scalar waves or emitted as neutrino-like off-spectrum coherence modes.

We define the effective mass as a functional over the folding surface $\Sigma$, capturing the drag, curvature, and scalar tension:

$$m_{\mathrm{eff}}={\int }_{\Sigma }{\mathcal{F}}_{\mathrm{fold}}[\mathsf{\Psi },\nabla \mathsf{\Psi },\varphi ,\nabla \varphi ]dA$$

where ${\mathcal{F}}_{\mathrm{fold}}$ quantifies the local resistance to deformation as a function of coherence density $\mathsf{\Psi }$, phase curvature, and scalar potential coupling $\varphi$. In regions where $m_{\mathrm{eff}}\approx n·m_0$ (for $n\in \mathbb{N}$), the fold stabilizes as an observable particle. Otherwise, the field relaxes back toward the wave phase.

This principle explains the apparent discreteness of mass in particle physics not as a mystery, but as a visibility condition. We do not see all possible coherence configurations—only the ones that remain locked in place long enough to produce measurable effects such as inertia, gravitational influence, or charge interaction.

Thus, in QSD, quantization is a signature of geometric survival. It reflects the substrate’s internal rule set for what can exist stably, not a limit on what can momentarily form.

3.12. Substrate Flux Equilibrium Principle

Within the Quantum Substrate Dynamics (QSD) framework, motion is not governed by external forces acting upon isolated bodies, but by the need to maintain internal flux balance through a coherence-bound mass-phase structure. A mass persists in uniform motion only so long as substrate inflow and outflow through its coherence envelope remain balanced. When coherence tension gradients appear, this flux becomes imbalanced—necessitating acceleration to restore equilibrium.

Substrate Flux Equilibrium Principle:

Mass-phase structures maintain continuous substrate flux through their coherence envelope. In a flat substrate, inflow and outflow remain balanced, enabling uniform motion. But when the substrate exhibits a tension gradient, conservation requires rebalancing this flux—demanding acceleration of the mass-phase structure along the gradient. Thus, even an object in uniform motion must accelerate to maintain flux continuity. Acceleration is not caused by external force, but by the substrate’s intrinsic requirement to preserve coherent, conserved flow through the mass lattice.

This principle reinterprets Newton’s Second Law not as a law of response to applied force, but as a kinematic consequence of coherence conservation. Acceleration arises from internal substrate dynamics, not from interaction with an external field.

3.12.1. Flux-Balance Model.

Let ${\mathsf{\Phi }}_{\mathrm{in}}$ and ${\mathsf{\Phi }}_{\mathrm{out}}$ represent the substrate flux entering and exiting a mass-phase object, defined over a coherence boundary $\partial V$:

$${\mathsf{\Phi }}_{\mathrm{in}}={\int }_{\partial V_{\mathrm{front}}}\rho \overrightarrow{v}·d\overrightarrow{A},{\mathsf{\Phi }}_{\mathrm{out}}={\int }_{\partial V_{\mathrm{rear}}}\rho \overrightarrow{v}·d\overrightarrow{A}.$$

In equilibrium (flat substrate), ${\mathsf{\Phi }}_{\mathrm{in}}={\mathsf{\Phi }}_{\mathrm{out}}$. When a tension gradient distorts substrate flow, conservation demands:

$${\displaystyle \frac{d{\overrightarrow{v}}_{\mathrm{mass}}}{dt}}\propto \nabla T\left(\rho \right),$$

where $T\left(\rho \right)$ is the local coherence tension, and ${\overrightarrow{v}}_{\mathrm{mass}}$ is the velocity of the mass-phase structure.

3.12.2. Physical Implications.

• Acceleration without force: Acceleration is the substrate’s way of resolving flux imbalance—reconfiguring the position of the mass-phase to restore coherent flow.
• Frame-dependent motion: Uniform motion is only maintained in locally flat coherence conditions; gradients demand motion adjustments to preserve flux balance.
• Inertia-flux connection: Inertia becomes the substrate’s resistance to rapid flux change, modulated by coherence geometry and internal boundary complexity.

3.12.3. Observational and Conceptual Shifts.

• Reframes Newton’s Second Law:$F=ma$ becomes a consequence of flux imbalance, not a primary law.
• Enables acceleration prediction: Direction and magnitude of acceleration can be derived from substrate coherence tension gradients.
• Clarifies interaction origin: Apparent forces are flow-maintaining corrections, not independent physical entities.

This principle reframes both inertia and gravity as conditions of coherent fluid flux conservation, fundamentally altering our understanding of motion, force, and the structure of space.

3.13. Coherence Lag Principle

When a mass-phase structure undergoes acceleration, it interacts with the quantum substrate via continuous reconfiguration of coherence flux across its boundary. This interaction generates inertial drag and stores localized tension in the substrate field. According to Quantum Substrate Dynamics (QSD), when acceleration ceases, this interaction does not instantaneously resolve.

Instead, a brief yet physically real phase persists in which the substrate completes its transition from a non-equilibrium, flux-reconfiguring state to a stable flux-neutral condition. We define this transient period as the coherence lag phase. During this interval, residual coherence tension—initiated by the prior acceleration—propagates through or dissipates across the mass-phase boundary, completing the final substrate realignment necessary for uniform motion.

This principle introduces a finite-timescale bridge between dynamic acceleration and inertial neutrality. It implies that uniform motion is not simply the absence of force, but a resolved and stable phase condition of coherence flux.

Predictive Formulation.

The coherence lag time ${\tau }_{\mathrm{lag}}$ may be approximated by the time required for substrate coherence flux to traverse and stabilize across the object:

$${\tau }_{\mathrm{lag}}={\alpha }_{\mathrm{CRI}}·{\displaystyle \frac{L_{\mathrm{eff}}}{v_{\mathsf{\Psi }}}}$$

(6)

Here:

• $L_{\mathrm{eff}}$ is the effective characteristic length across which the substrate must reconfigure,
• $v_{\mathsf{\Psi }}$ is the substrate’s scalar or coherence wave propagation speed,
• ${\alpha }_{\mathrm{CRI}}$ is a dimensionless coefficient that encodes the object’s internal coherence resistance (e.g., structural complexity, density, lattice configuration).

This relationship predicts that more structurally complex or higher-CRI materials will exhibit longer lag durations, potentially measurable as nanosecond-scale inertial settling following the cessation of thrust. This delay is testable and offers a novel diagnostic for internal mass-phase structure under QSD.

Empirical Anchors.

• In macroscopic systems, this coherence lag is exemplified by inertial delay in self-propelled particles, where velocity trails behind orientation during active motion [35].
• In field systems, finite response time in heat conduction under acceleration—contradicting the assumptions of instantaneous Fourier flux—is consistent with coherence flux relaxation [36].

Together, these data support the coherence lag principle as a universal substrate behavior, observable at both micro and macro scales, and consistent with QSD’s conservation-based field model.

3.14. Equivalence Principle (Reframed)

In classical and relativistic physics, the equivalence of inertial and gravitational mass is an empirical fact—an observed symmetry that underpins both Newtonian mechanics and General Relativity. Quantum Substrate Dynamics (QSD) offers a physical explanation for this equivalence by identifying a common origin: both gravitational and inertial behavior arise from the coherence-boundary structure of mass-phase objects within the substrate.

Equivalence Principle (Reframed):

Gravitational and inertial mass are identical because they both reflect the same coherence-boundary structure. Their equivalence arises naturally from substrate drag and tension geometry.

In QSD, mass is a phase-condensed coherence lattice (Sec. Section 3.8). When this lattice interacts with the surrounding wave-phase substrate, two behaviors emerge:

• Inertia: resistance to acceleration due to coherence-boundary reconfiguration,
• Gravity: substrate tension gradients that arise from coherence saturation.

Both effects originate from the same physical feature—the interface geometry and coherence complexity between the mass-phase object and the surrounding substrate.

3.14.1. Unified Drag and Tension Model.

Let $\mathcal{B}$ represent the boundary coherence geometry of a mass-phase object. Then:

$$m_{\mathrm{inertial}}\propto \left({\displaystyle \frac{\partial {\mathcal{E}}_{\mathrm{drag}}}{\partial a}}\right),m_{\mathrm{gravitational}}\propto \left(\nabla T\left(\mathcal{B}\right)\right),$$

where ${\mathcal{E}}_{\mathrm{drag}}$ is the coherence reconfiguration energy under acceleration, and $T\left(\mathcal{B}\right)$ is the coherence tension field surrounding the object. Since both expressions depend on the same coherence-boundary structure $\mathcal{B}$, the resulting inertial and gravitational mass values are naturally equivalent.

3.14.2. Physical Implications.

• No postulate required: The equivalence principle is not an assumed symmetry, but a derived outcome of how the substrate resists and transmits coherence deformation.
• Predictive capacity: Variations in internal structure or coherence coupling may subtly affect both inertial and gravitational response, offering measurable deviations from strict equivalence under extreme conditions.
• Unified interpretation: Inertia and gravity become two expressions of the same substrate response mechanism—one local (drag), the other extended (tension).

This coherence-based reformulation transforms the Equivalence Principle from an observational cornerstone into a structural prediction. In QSD, mass responds to motion and curvature not because of distinct mechanisms, but because of one substrate coherence geometry that governs both.

3.15. Gravity as Tension Gradient Principle

In Quantum Substrate Dynamics (QSD), gravity is not a fundamental force nor a geometric curvature of spacetime. Instead, it is an emergent behavior arising from the substrate’s internal coherence-tension gradients. These gradients form when mass-phase structures saturate the surrounding substrate, and the conserved medium reorients itself to restore coherence equilibrium.

Gravity as Tension Gradient (Driven by Substrate Saturation):

Gravity is a push force caused by coherence tension gradients. These gradients emerge when regions of high waveform complexity saturate the substrate, drawing in restorative pressure from the surrounding field.

Unlike the classical notion of attractive force, gravity in QSD arises from the substrate’s attempt to redistribute coherence in the most energy-efficient, localized way possible—consistent with the conservation of substrate. Because the substrate cannot be created or destroyed, it must reorganize under constraint, which results in the observed “gravitational” behavior.

3.15.1. Tension and Conservation.

Let $T\left(\overrightarrow{r}\right)$ represent the local coherence tension, and $\rho \left(\overrightarrow{r}\right)$ the coherence density. The conservation law requires:

$${\displaystyle \frac{d}{dt}}{\int }_{\mathsf{\Omega }}\rho {(\overrightarrow{r},t)}^2{d}^3\overrightarrow{r}=0,$$

meaning any increase in local saturation must be offset by reorientation or displacement of surrounding coherence. This drives gradients in $T\left(\rho \right)$, which manifest macroscopically as gravitational effects:

$${\overrightarrow{f}}_{\mathrm{gravity}}=-\nabla T\left(\rho \right).$$

3.15.2. Apparent Gravitational Phenomena.

• Push from flux conservation: In QSD, what appears as gravitational attraction is the result of coherence flux imbalance. As a mass-phase structure follows coherence toward a nearby tension minimum, the reaction to this flux imbalance imparts a push—driving the structure along the gradient. The force is local and directional, not remote.
• Apparent curvature: Trajectories of particles and wavefronts curve as they follow the gradient of least coherence distortion—mimicking general relativistic geodesics.
• Mass aggregation: Over time, this coherent flow reinforces mass concentrations, explaining gravitational stability and clustering without invoking attraction at a distance.

3.15.3. Subtle Variability of Gravitational Strength.

While Newton’s gravitational constant G is often treated as fixed, QSD predicts that its apparent value may shift slightly in regions where substrate coherence gradients vary across scales. A notable example is the Moon–Earth gravitational anomaly, where orbital dynamics suggest a subtle offset in effective G. In QSD, this effect arises not from dark matter or unknown fields, but from coherent substrate reorientation driven by internal structural features—most notably, angular momentum exchange within Earth’s core. As the core evolves, it modulates global coherence tension, altering how the substrate transmits gravitational effects across the Earth–Moon system.

3.15.4. Experimental Alignment and Predictions.

• Reproduces all weak-field tests of General Relativity (precession, lensing, redshift) via coherence-tension gradients.
• Predicts scalar wave precursors and coherence collapse effects in high-density collapse events (e.g., black holes, neutron stars).
• Offers an explanation for apparent gravitational constant variability in complex multi-body systems.

In QSD, gravity emerges from coherence flow, not curvature or force. The substrate responds to saturation and phase imbalance by pushing—not pulling—toward equilibrium. This viewpoint preserves empirical gravitational behavior while offering new insight into variability, structure, and wavefront phenomena in both terrestrial and astrophysical contexts.

3.16. Transverse Wave Principle

In Quantum Substrate Dynamics (QSD), electromagnetic (EM) waves are reinterpreted as structured transverse coherence excitations within the Lorentz-invariant substrate field $\mathsf{\Psi }$. These waves arise not from fundamental charge interactions, but from stable oscillations in the transverse geometry of the substrate’s phase-aligned structure[see Appendix A.3].

Waveform Structure and Propagation Speed

Let the substrate field be expressed locally as:

$$\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)},$$

(7)

where $\rho$ is the local coherence amplitude and $\theta$ is the phase. EM waves correspond to transverse oscillations in $\theta (\overrightarrow{r},t)$ that preserve coherence across wavefronts orthogonal to the propagation direction. These disturbances are phase-preserving, non-dissipative modes sustained by local substrate tension.

The observed speed of light c is interpreted in QSD as the natural propagation speed of transverse coherence waves in a locally balanced substrate region. It is determined by the substrate’s tension and compliance, analogous to wave speed in elastic media:

$$c=\sqrt{{\displaystyle \frac{{\tau }_T}{\mu }}},$$

(8)

where ${\tau }_T$ is the transverse coherence tension and $\mu$ is the effective inertia (coherence mass density) of the substrate in the transverse mode.

Relation to Classical Electromagnetism

In traditional electromagnetism, c is given by:

$$c={\displaystyle \frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}},$$

(9)

where ${\epsilon }_0$ and ${\mu }_0$ are the vacuum permittivity and permeability. In QSD, these are reinterpreted as emergent substrate properties, representing the response coefficients of the substrate to transverse excitation. That is,

$${\epsilon }_0\sim {\displaystyle \frac{1}{{\tau }_T}},{\mu }_0\sim \mu ,$$

(10)

linking classical EM constants to substrate mechanical parameters.

Local Invariance and Gradient Effects

While c remains invariant within any locally coherent domain—preserving Lorentz symmetry—the substrate’s tension and inertia may vary subtly across large-scale coherence gradients. This provides a mechanism for phenomena such as non-Doppler redshifts or gravitational lensing without invoking spacetime curvature.

Interpretation and Implications

• EM fields are not separate ontological entities, but phase modes of the substrate.
• Light propagation reflects substrate coherence, not empty-space invariance.
• Scalar and EM waves differ only in excitation geometry—longitudinal vs. transverse.
• The apparent universality of c is a consequence of the uniform substrate properties in low-curvature domains.

This reinterpretation aligns EM propagation with the same coherence-based framework that governs scalar waves, gravity, and mass. It completes the QSD view that all fields and particles are phase-structured excitations of a single, conserved, coherent substrate.

3.17. Scalar Wave Principle

Scalar waves occupy a central role in Quantum Substrate Dynamics (QSD) as a distinct class of excitations within the substrate. Unlike electromagnetic waves, scalar waves do not depend on charge, nor are they constrained by classical field theory frameworks. They are coherence-pressure excitations—longitudinal waves that directly reflect dynamic changes in the internal phase structure of the substrate [see Appendix A.4].

Scalar Waves:

Scalar waves are longitudinal coherence-pressure excitations in the substrate. They propagate independently of charge and can travel through dense or shielded environments. These waves are emitted during rapid substrate reconfiguration. They are variations of the substrate, not in it.

This distinction is critical: scalar waves are not conventional disturbances transmitted through the substrate like classical waves in a medium—they are substrate reconfigurations themselves. As such, they can pass through otherwise opaque or dense materials, coupling weakly with ordinary matter while transmitting energetic information.

3.17.1. Mathematical Form.

Let $\varphi (\overrightarrow{r},t)$ represent the scalar coherence displacement field. Its evolution follows a nonlinear wave equation of the form:

$${\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-v_s^2{\nabla }^2\varphi +{\displaystyle \frac{\partial V\left(\varphi \right)}{\partial \varphi }}={\beta }_s\nabla ·\overrightarrow{v},$$

where:

• $v_s$ is the scalar wave propagation speed,
• $V\left(\varphi \right)$ is an effective potential (e.g., double-well or sine-Gordon form),
• ${\beta }_s$ is a coupling coefficient to local compression or tension.

3.18. Dimensional Estimate of Scalar Wave Emission

In Quantum Substrate Dynamics, scalar waves are longitudinal excitations emitted during rapid reconfiguration events—such as collapse, merger, or deformation of mass-phase structures. These emissions are interpreted as coherence-pressure waves propagating through the substrate, and are expected to carry both energy and encoded structural information.

To estimate the physical dimensions of scalar wave output, we begin with the total energy released in a substrate reconfiguration event, $E_{\mathrm{scalar}}$, and relate it to the scalar wave power flux $\mathcal{P}$ through a surface area A over an emission duration $\Delta t$:

$$\mathcal{P}\sim {\displaystyle \frac{E_{\mathrm{scalar}}}{A·\Delta t}},$$

(11)

where $\mathcal{P}$ has units of $\mathrm{W}/{\mathrm{m}}^2$ and describes the energy flux per unit area carried by the scalar wavefront.

If the scalar wave propagates at velocity $v_{\mathrm{scalar}}$ (possibly near or exceeding c under certain substrate conditions), then its energy density $ϵ$ is given by:

$$ϵ\sim {\displaystyle \frac{\mathcal{P}}{v_{\mathrm{scalar}}}}\mathrm{with}\mathrm{units}\left[{\displaystyle \frac{\mathrm{J}}{{\mathrm{m}}^3}}\right],$$

(12)

representing the localized energy carried by the wave within the substrate.

Assuming a spherical emission front of radius R and constant energy density, the total scalar wave energy is:

$$E_{\mathrm{scalar}}\sim ϵ·{\displaystyle \frac{4}{3}}\pi R^3,$$

(13)

linking the coherence event scale R, the substrate energy density, and the observable scalar signal.

These expressions enable experimental scaling estimates and connect theoretical predictions to observables in gravitational wave detection or coherence-tension analogs. Scalar wave power, emission duration, and front velocity can be used to reconstruct expected strain amplitudes, spectral shifts, or precursor signals in candidate events such as black hole mergers or supernovae.

3.18.1. Emission Conditions.

Scalar waves are typically generated in the following conditions:

• Rapid coherence collapse, such as near black hole boundaries or supernova shock fronts,
• High-gradient reconfiguration events, e.g., lattice destruction or inertial thresholds,
• Nonlinear transitions across mass-phase or coherence-boundary domains.

3.18.2. Nucleation and Phase Creation.

Scalar waves are also predicted to accompany nucleation events—where new mass-phase regions emerge from the wave-phase substrate. These rapid, coherence-driven condensations create sharp boundary gradients, triggering scalar wave emission as the substrate reorients to maintain conservation. Such emissions are expected during early-universe symmetry breaking, hydrogen lattice formation, and even under controlled laboratory conditions involving abrupt material phase changes. [see Appendix Table A5]

3.18.3. Physical Properties.

• Charge-independent: Scalar waves do not require coupling to electric charge or current—they propagate directly as fluidic coherence shifts.
• Penetrating: They can travel through dense or shielded regions that block electromagnetic or neutrino radiation.
• Superluminal appearance: Because scalar coherence changes precede wavefront recombination, they may appear to arrive before conventional signals—but without violating causality, as they carry no encoded information faster than c.

3.18.4. Observational Relevance.

Scalar wave dynamics may offer explanations for several poorly understood astrophysical phenomena:

• Supernova precursor neutrino–photon gaps,
• Gravitational anomalies in high-density collapse zones,
• Coherence-related energy emissions in unexplained burst events.

In particular, scalar coherence fronts may play a role in the formation of stratified element shells observed around supernova remnants. These layers may reflect nucleation triggered by scalar wave compression, rather than solely by classical blast dynamics. The scalar field serves as both a coherence rebalancer and a nucleation initiator—contributing to material formation and structural patterning in post-collapse environments.

QSD treats scalar waves as a necessary and testable consequence of substrate coherence physics—emerging whenever the substrate reorients faster than coherence can redistribute smoothly. They are not speculative additions, but physical signatures of tension conservation in a dynamically reactive field.

3.19. Gradient Frame Transition (GFT) Principle

Quantum Substrate Dynamics (QSD) proposes that large-scale regions of the universe are structured by distinct coherence tension gradients—what may be considered macroscopic substrate frames. When mass-phase structures or wavefronts transition across these regions, they encounter discontinuities in coherence field alignment that must be resolved to preserve substrate conservation.

Gradient Frame Transition (GFT) Principle:

Transitions between large-scale substrate tension domains produce observable dynamical and spectroscopic effects. As mass-phase structures or wavefronts cross from one coherence frame to another, they experience rephasing discontinuities—leading to shifts in inertia, apparent gravitational behavior, scalar drag, or spectral anomalies. These transitions act as conservation-induced coherence shocks, analogous to bow shocks in classical fluid dynamics, where substrate continuity requires reconfiguration across macrogradient boundaries.

3.19.1. Coherence Shock at Domain Boundaries.

Let $T_1$ and $T_2$ represent the substrate tension fields of adjacent domains. A wavefront crossing this boundary must rephase:

$${\left[\mathsf{\Psi }\right]}_{\mathrm{boundary}}=0,{\left[\nabla \theta \right]}_{\mathrm{boundary}}\ne 0,$$

resulting in a coherence mismatch that induces shock-like behavior. Scalar emissions, light phase shifts, or inertial discontinuities may arise as the substrate rapidly restores equilibrium.

3.19.2. Predicted GFT Effects.

• Inertial anomalies: Shifts in effective mass or resistance during planetary flybys or orbital regime transitions.
• Spectral rephasing: Non-Doppler redshift or blueshift of light crossing field boundaries (e.g., at galactic voids or halo edges).
• Scalar bursts: Coherence-front corrections may emit transient scalar pulses analogous to coherence relaxation fronts.

3.19.3. Wave Conservation Across Gradient Frames.

Let a transverse wavefront cross from Region 1 to Region 2, with local substrate tensions $T_1$ and $T_2$, and coherence wave speeds $c_1$ and $c_2$ respectively. Conservation of substrate energy flux at the boundary requires:

$$T_1·A_1·c_1=T_2·A_2·c_2,$$

(14)

where $A_i$ is the amplitude (or envelope scale) of the wave in each region. Assuming energy continuity and field coherence, we may also express phase continuity as:

$${\theta }_1(x,t)\stackrel{\mathrm{boundary}}{\to }{\theta }_2(x,t+\delta t),$$

(15)

where $\delta t$ accounts for coherence slippage or tension delay, representing the effective shock compression or rarefaction across the gradient interface.

The observed frequency $\nu$ and wavelength $\lambda$ must satisfy a modified dispersion relation due to coherence shift:

$${\displaystyle \frac{{\nu }_2}{{\nu }_1}}={\displaystyle \frac{c_2}{c_1}},{\lambda }_2={\lambda }_1·{\displaystyle \frac{c_2}{c_1}}.$$

(16)

These expressions predict apparent redshift or blueshift in the absence of classical motion, purely from substrate field transition. Such rephasing effects define the observational signature of the GFT principle.

3.19.4. Conceptual Significance.

The GFT Principle reframes gravitational and inertial anomalies not as failures of existing theory, but as natural results of substrate coherence conservation under field transition. It establishes a new class of observables—coherence boundary shocks—that offer falsifiable signatures for QSD in both astrophysical and experimental contexts.

3.20. Time as Scalar Propagation Interval

In Quantum Substrate Dynamics (QSD), time is not an independent backdrop against which events unfold. Instead, it is an emergent measure of phase displacement within the substrate—specifically, the interval between coherent scalar wavefronts. As scalar waves propagate through the quantum fluid substrate $\mathsf{\Psi }$, they define the pacing of all physical processes.

Time as Scalar Propagation Interval:

Time is not a fundamental background dimension, but a measure of phase displacement. It emerges from the interval between scalar wavefronts propagating through the substrate.

This view reorients the traditional role of time. Rather than being absolute or geometrically woven into spacetime, time in QSD reflects the substrate’s internal state and coherence response. Where wavefronts are uniformly spaced, time progresses uniformly. Where coherence is compressed, distorted, or delayed, time dilates accordingly.

3.20.1. Scalar Timing Definition.

Let $\varphi (\overrightarrow{r},t)$ describe a scalar wavefront. Then the local proper time interval $\Delta \tau$ between successive wavefronts at a fixed position $\overrightarrow{r}$ can be defined as:

$$\Delta \tau \left(\overrightarrow{r}\right)=\left({\displaystyle \frac{1}{v_s}}\right)\Delta {\ell }_{\varphi },$$

where:

• $v_s$ is the scalar wave propagation speed,
• $\Delta {\ell }_{\varphi }$ is the coherence path length between scalar fronts,
• Local tension or coherence distortion modifies $\Delta {\ell }_{\varphi }$, thereby altering the experienced time interval.

3.20.2. Emergent Time Effects.

• Time dilation: In high-tension or coherence-saturated zones, scalar wavefront spacing stretches, producing slower local progression of time—analogous to gravitational time dilation.
• Relativity recovery: The invariance of scalar wavefront propagation across local Lorentz frames naturally reproduces time relativity effects without requiring a geometric time axis.
• Directional continuity: Because scalar wavefronts propagate forward, time inherits a consistent arrow—rooted in the relaxation of coherence tension gradients.

3.20.3. Conceptual Implications.

Time in QSD is not “added” to the theory—it is the byproduct of coherence reconfiguration dynamics. The regularity of time emerges only in highly ordered substrate regions; in nonlinear or high-gradient zones, scalar phase timing deviates—creating testable predictions about time anomalies in regions of strong gravity, rapid collapse, or coherence rupture.

This coherence-based definition restores physical meaning to time, grounding it in measurable wavefront intervals rather than abstract coordinates. Time becomes not what clocks measure, but what scalar wave coherence enforces.

3.21. The Coherence-Coupling Misinterpretation Principle

While this principle is implicit in the preceding foundations of time, coherence, and wave propagation, it is stated explicitly here to clarify a subtle but crucial interpretive distinction:

Observed variations in clock rates and light speed under gravitational or inertial conditions reflect paired responses of the quantum substrate to local coherence tension—not changes in a geometric manifold.

In the QSD framework, phenomena such as time dilation and gravitational lensing do not arise from curvature of spacetime itself, but from tension-induced modulation of scalar and transverse wave propagation. These two classes of effects—clock slowing and light path bending—are not independent but are co-manifestations of the same substrate response to local coherence gradients.

This pairing explains why, within any local frame, the speed of light and the rate of proper time always appear invariant: both are modulated together by the same physical substrate conditions. The phase evolution of scalar ticks (clocks) and the group velocity of transverse coherence (light) are synchronously governed by the local coherence-tension landscape of the substrate.

Interpretive Note: General Relativity (GR) accurately predicts and describes the empirical relationships between motion, gravity, and measured time, but does so without reference to a physical substrate. As a result, it interprets tension-induced delays and deflections as geometric curvature. QSD retains full compatibility with GR’s observational predictions, but reframes the cause as a substrate-based modulation of phase propagation. The apparent curvature of spacetime is thus an interpretive mirage—a geometric mapping of substrate coherence behavior.

3.22. Required Recovery and Field Behavior Principle

Quantum Substrate Dynamics (QSD) does not discard the frameworks of classical mechanics, general relativity, or quantum field theory. Instead, it explains them. Each established theory emerges as a limiting case of substrate behavior under specific coherence and tension conditions. The substrate’s structure places strict constraints on how energy, mass, and interaction can manifest—requiring consistency with known physics in the appropriate regimes.

Required Recovery and Field Behavior Principle:

Quantum Substrate Dynamics reproduces the known laws of physics under appropriate limits. Newtonian mechanics arises from coherence drag in low-velocity regimes; General Relativity emerges from macroscopic tension gradients; and Quantum Field Theory describes wave-phase excitations in high-coherence, weakly nonlinear domains.

In this framework, fields traditionally treated as distinct—electromagnetic, gravitational, scalar, fermionic—are reinterpreted as coherence modes of a single, conserved substrate. Their apparent independence arises from differences in wave structure, coherence symmetry, and boundary dynamics—but they all propagate within the same underlying fluid medium.

3.22.1. Field Unification through Coherence Modes.

The substrate supports a spectrum of modal excitations:

• Electromagnetic fields: Phase-coherent transverse waves with charge coupling,
• Gravitational phenomena: Large-scale coherence-tension gradients,
• Scalar waves: Longitudinal coherence-pressure disturbances,
• Fermionic modes: Localized coherence envelopes with rotational symmetry (spin).

These emerge not from separate fields, but from different configurations of a shared coherence medium.

3.22.2. Limiting Behavior and Compatibility.

• In the low-velocity, high-coherence limit, substrate drag behaves linearly, yielding Newtonian dynamics.
• In the macroscopic limit, coherence tension gradients mimic spacetime curvature as described in General Relativity.
• In the quantized, weakly nonlinear limit, the substrate supports discrete excitation spectra matching Quantum Field Theory.

This requirement dictates that all valid physics must emerge from substrate dynamics under appropriate conditions. Quantum Substrate Dynamics thus forms a physical foundation beneath existing theory, offering not contradiction, but cohesion.

Experimental and Theoretical Implications

Introducing a Quantum Reynolds Number provides explicit, quantitative predictions and experimental opportunities to test coherence-based inertia models directly:

• Measurable threshold transitions: Experiments can detect explicit critical thresholds for nonlinear coherence boundary effects, analogous to turbulence transitions in classical fluids or critical velocities in BEC systems.
• Tunable inertial effects: Manipulating coherence structure, internal geometry, or boundary conditions can alter effective Quantum Reynolds numbers, allowing experimental tuning or engineering of coherent inertial responses.
• Direct coherence-boundary observations: Measuring inertial resistance anomalies as functions of internal coherence structure, scalar-wave interactions, or coherence-boundary deformation rates validates QSD’s explicit coherence-based inertia predictions.

Thus, updating the classical fluid-drag analogy with explicit coherence-dependent terms and introducing a Quantum Reynolds Number significantly enriches the theoretical clarity, predictive power, and experimental testability of QSD’s coherence-boundary inertial framework. These quantified behaviors open the door to profound philosophical and experimental reinterpretations.

In summary, these conceptual impacts not only unify previously disparate phenomena within a single coherent field dynamics framework but also suggest novel experimental pathways and theoretical directions that can profoundly advance fundamental physics.

3.23. Superfluid Analogues and Zero-Resistance Phenomena

Quantum coherence in superfluid helium [5,6] and superconductors [7] demonstrates near-zero resistance to flow or current. QSD extends this principle to cosmological scales, suggesting that perfect coherence alignment at the substrate boundary could similarly minimize inertial resistance, producing an inertial decoupling state. This state, resembling frictionless fluid dynamics, theoretically eliminates coherence-boundary drag, providing a novel basis for understanding inertia and potentially enabling experimental and technological advancements (see detailed discussion in Appendix A.6).

3.24. Recovery of Newtonian Mechanics at Low Velocities

Quantum Substrate Dynamics (QSD) fundamentally interprets inertia as coherence-based fluid drag. Under low-speed and near-uniform coherence conditions, QSD naturally recovers classical Newtonian mechanics. In this regime, substrate coherence dynamics simplify significantly, allowing coherence-boundary interactions to directly yield Newton’s second law:

$${\oint }_{\mathrm{interface}}{\mathbf{F}}_{\mathrm{phase}}·d\mathbf{A}=m_{\mathrm{eff}}{\displaystyle \frac{d{\mathbf{v}}_{\mathrm{obj}}}{dt}},$$

(17)

where effective mass $m_{\mathrm{eff}}$ emerges explicitly from coherence-boundary geometry and interface energy (see Appendix A.7 for detailed derivation and implications). Thus, classical inertia emerges naturally as a special limit of deeper quantum fluid-coherence interactions.

4. Field Recovery and Compatibility

A core requirement for any new physical framework is that it must reproduce all established physical laws under appropriate limits. Quantum Substrate Dynamics (QSD) meets this requirement not as an imposed constraint, but as a natural consequence of substrate coherence mechanics. The classical, relativistic, and quantum frameworks emerge as special cases of substrate tension, coherence saturation, and phase alignment behavior.

4.1. Newtonian Mechanics as Low-Gradient Substrate Drag

In the low-velocity, weak-tension regime, QSD reduces to Newtonian mechanics through coherence-boundary drag. Let $m_{\mathrm{eff}}$ denote the effective inertial mass, arising from the energy required to reconfigure the coherence boundary of a mass-phase structure. The inertial force obeys:

$${\overrightarrow{F}}_{\mathrm{drag}}=m_{\mathrm{eff}}·\overrightarrow{a},\mathrm{where}{m}_{\mathrm{eff}}\propto {\int }_{\partial V}\rho {|\nabla \theta |}^{2}dA,$$

where $\partial V$ denotes the mass-phase interface, $\rho$ is coherence density, and $\theta$ is local substrate phase.

This reproduces Newton’s second law in the linear response regime, where $\rho$ and $\nabla \theta$ remain slowly varying and spatially symmetric.

4.2. General Relativity from Coherence Tension Gradients

Macroscopic substrate curvature emerges from coherence tension gradients. Let $T\left(\overrightarrow{r}\right)$ denote the local coherence tension field. The apparent gravitational acceleration becomes:

$$\overrightarrow{g}=-\nabla T\left(\overrightarrow{r}\right),$$

analogous to the Newtonian gravitational potential $\mathsf{\Phi }$, but derived from substrate saturation, not spacetime geometry. In the continuum limit, the Einstein field equation is recovered as:

$$G_{\mu \nu }={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }^{\left(\mathsf{\Psi }\right)},$$

where $T_{\mu \nu }^{\left(\mathsf{\Psi }\right)}$ is the stress-energy tensor constructed from coherence density, gradient tension, and scalar compression fields within $\mathsf{\Psi }$.

This interpretation replaces geometric curvature with fluidic reorientation, while preserving all observable predictions of GR in the weak-field, non-rotating regime.

4.3. Quantum Field Theory as High-Coherence Wave Behavior

In high-coherence, low-tension regions, the substrate supports quantized wave excitations analogous to QFT field modes. Let $\mathsf{\Phi }(\overrightarrow{r},t)$ describe a localized wave-packet solution within $\mathsf{\Psi }$. The substrate enforces discrete stable configurations governed by:

$${\mathcal{L}}_{\mathrm{QSD}}={\displaystyle \frac{1}{2}}{\left|{\partial }_{\mu }\mathsf{\Phi }\right|}^2-V_{\mathrm{coh}}\left(\mathsf{\Phi }\right),$$

where $V_{\mathrm{coh}}\left(\mathsf{\Phi }\right)$ is an effective potential arising from substrate phase saturation and coherence oscillation energy. Quantization of field modes follows from discrete resonance conditions within coherence-bound boundary envelopes, yielding particle-like behavior.

4.4. Substrate Mode Correspondence with Classical Fields

The various classical fields are reinterpreted in QSD as substrate mode types:

• Electromagnetic fields: Transverse coherence waves with vector phase polarization.
• Scalar fields: Longitudinal phase-pressure excitations (see Section 3.17).
• Gravitational fields: Macroscopic gradients in coherence tension.
• Fermionic fields: Coherence-knot excitations with internal spin phase geometry.

These field behaviors are not separate ontologies, but distinct modal regimes of a single, conserved substrate. Their propagation speed, interaction strength, and quantization arise from internal coherence geometry and local boundary conditions.

4.5. Requisite Field Compatibility

Thus, QSD recovers:

• Newtonian mechanics from linear drag behavior at low substrate gradients,
• General Relativity from macroscopic coherence tension gradients,
• Quantum Field Theory from stable excitation spectra in high-coherence, weakly nonlinear domains.

This recovery is not approximate—it is required by the internal conservation and coherence dynamics of the substrate itself. All known physics emerges as a limiting behavior of $\mathsf{\Psi }$ under specific coherence and saturation conditions.

5. Key Predictions and Falsifiability

A critical requirement for any proposed physical framework is that it must make predictions that are testable—and, if incorrect, falsifiable. Quantum Substrate Dynamics (QSD) meets this standard by generating distinct, observable effects that differ from conventional expectations under classical, relativistic, or quantum field models. These effects arise directly from the theory’s coherence-based substrate ontology and its conservation-driven dynamics.

5.1. Scalar Wave Precursors in Collapse Events

QSD predicts that rapid substrate reconfiguration—such as during core collapse supernovae or black hole formation—produces longitudinal scalar wave emissions. These scalar fronts propagate independently of charge and may precede both neutrino bursts and electromagnetic emissions. If detected, such precursors would provide strong evidence for coherence reconfiguration prior to light-speed-limited energy release. Candidate observational targets include timing anomalies in supernova neutrino–photon arrival sequences and coherence-aligned precursor pulses near compact object transitions.

5.2. Off-Spectrum Neutrinos as Coherence Reconfiguration Emissions

In Quantum Substrate Dynamics, neutrinos are interpreted as coherence envelope structures that arise when scalar-driven compression attempts—but fails—to stabilize a full mass-phase nucleation. These "aborted folds" form when the substrate reconfiguration does not reach a quantized equilibrium state. [see Appendix A6]

Instead of condensing into a stable mass-phase lattice, the partially folded waveform ejects from the system as a neutrino-like coherence packet. This offloading releases stored coherence tension and restores local substrate continuity.

Characteristics and Experimental Implications

• Each neutrino flavor corresponds to a distinct curvature envelope, determined by the degree of incomplete folding.
• QSD allows for a spectrum of such modes—potentially far more than the three known neutrino types.
• Many of these off-spectrum modes would interact only gravitationally or via coherence tension, rendering them undetectable by conventional weak-interaction methods.
• Sterile or anomalous neutrino detections in astrophysical timing or oscillation studies could be signatures of these failed-fold coherence emissions.
• Their energy spectrum may encode the gap between elemental nucleation thresholds, particularly during supernova shell formation.

This model reinterprets neutrinos not as standalone particles but as tension relief packets—natural byproducts of coherence field dynamics in extreme energy gradients.

5.3. Geometry-Dependent Inertial Anomalies

Unlike conventional physics, QSD predicts that two objects of identical mass but differing internal coherence structure (e.g., solid versus porous or nanostructured lattices) may exhibit measurable differences in inertial response. This arises from variation in coherence-boundary reconfiguration energy during acceleration. Precision torsion balance or drop experiments comparing structurally distinct test masses may reveal inertial asymmetries predicted by QSD. [see Appendix Table A5]

5.4. Gravitational Anomalies from Gradient Frame Transitions

QSD introduces the concept of gradient frame transitions (GFT)—boundaries between regions of differing substrate coherence tension. Objects or wavefronts traversing such boundaries may experience rephasing shocks, resulting in:

• Apparent changes in inertial or gravitational coupling,
• Non-Doppler redshifts or blueshifts,
• Scalar emission signatures at coherence boundaries.

This mechanism may account for known flyby anomalies, light propagation offsets across galactic voids, or unexplained spectral discontinuities.

5.5. Substrate-Origin Redshift Variations

In addition to GFT effects, QSD offers an alternative source of cosmological redshift: large-scale coherence tension gradients. Scalar wave-based time definition predicts that wavefront spacing can be modulated by substrate tension, causing redshift-like signatures even without recessional motion. Distinguishing such shifts from Doppler or expansion effects may allow independent testing of QSD in high-resolution spectral and timing data.

5.6. Energy Extraction During Coherence Collapse

QSD predicts that coherence collapse events—where phase-saturated substrate regions rapidly decompress or reorient—can emit scalar wave energy not accounted for by conventional particle radiation. These scalar waves carry coherence-pressure information and may represent a previously unobserved energy release channel.

A proposed mechanism involves quantized elemental nucleation and neutrino-mediated coherence offloading. During collapse, the substrate undergoes nucleation of condensed elements in discrete coherence layers, proceeding in a quantized order. Each nucleation phase temporarily saturates local coherence, prompting the emission of off-spectrum neutrino-like modes—interpreted in QSD as color-structured coherence envelopes ($\nu \left[0\right],\nu \left[1\right],\nu \left[2\right]$, etc.).

These neutrinos act as energy buffers, temporarily storing substrate tension until scalar coherence waves can propagate. The system alternates between nucleation layers and neutrino-color offloading cycles, gradually working outward toward lighter elemental shells. This flip-flop sequence dissipates excess substrate tension without violating conservation, and proceeds until the substrate reaches a new coherence equilibrium.

Observable consequences include:

• Scalar wave bursts or compression rings near collapse fronts,
• Anomalous neutrino emission profiles with flavor-state transitions tied to matter layering,
• Elemental shell stratification in supernova remnants, matching coherence phase boundaries.

Detection of coherence-structured neutrino emissions, especially in conjunction with scalar wave precursors and elemental layer stratification, would provide strong empirical support for this QSD mechanism of quantized energy release during coherence collapse.

Falsifiability Criteria

QSD can be falsified in multiple domains:

• Failure to observe scalar wave precursors in rapid collapse events, where coherence reconfiguration and pre-photonic energy release should dominate.
• Absence of inertial deviations in highly structured versus homogeneous materials, where internal coherence geometry is predicted to modulate boundary drag.
• Strict adherence to classical Doppler or relativistic redshift behavior across suspected Gradient Frame Transition (GFT) boundaries, with no coherence-related rephasing shifts.
• No evidence of coherence-origin energy release during high-tension transitions, such as quantized nucleation cascades or neutrino-envelope offloading in supernovae or analogous collapse systems.

These criteria do not rely on speculative new constants or undiscovered particles. Instead, they test QSD’s core proposition: that all physical behaviors arise from a conserved, coherence-structured substrate—whose internal dynamics become observable under specific structural, inertial, and spectral boundary conditions.

6. Experimental and Observational Opportunities

The coherence-based ontology of Quantum Substrate Dynamics (QSD) enables direct experimental and observational tests across a variety of physical regimes. Unlike speculative extensions of existing theories, QSD’s predictions manifest through accessible physical structures—coherence boundaries, tension gradients, and substrate reconfiguration—allowing validation or refutation using current or near-term technologies.

6.1. Geometry-Dependent Inertia Tests

QSD predicts that inertial response depends on the internal coherence geometry of a mass-phase object. Structured materials with high boundary complexity (e.g., nanostructured lattices, porous frameworks) should exhibit subtly different inertial behavior than homogeneous solids of equal mass.

Candidate methods:

• Precision torsion pendulum or interferometric drop tests comparing structured vs. unstructured masses.
• Oscillating platforms measuring phase lag or energy dissipation in response to driven acceleration.
• Space-based microgravity environments for isolating coherence-bound inertial drag effects.

6.2. Scalar Wave Detection and Collapse Precursors

QSD predicts scalar wave emissions from coherence collapse, nucleation fronts, and field transitions. These emissions are longitudinal, charge-independent, and potentially superluminal in appearance (without carrying information faster than c).

Observational strategies:

• Time-resolved neutrino–photon–scalar arrival sequences in supernovae, focusing on early-stage bursts.
• Laboratory coherence-breakdown experiments using high-tension lattice collapse (e.g., shocked crystal targets or piezoelectric deformation).
• Analysis of transient scalar-correlated signals near black hole boundaries or neutron star crust failures.

6.3. Gradient Frame Transition (GFT) Signature Surveys

The GFT Principle predicts spectral and inertial anomalies when objects or wavefronts cross between macroscopic substrate gradient domains.

Targets and methods:

• Analysis of gravitational flyby anomalies using spacecraft telemetry in regions near planetary coherence boundaries.
• High-resolution redshift surveys across galactic voids and cluster peripheries to detect coherence rephasing effects.
• Gravitational lensing comparisons between scalar-transparent and EM-transparent structures.

6.4. Neutrino Envelope Transitions in Nucleation Cascades

QSD reinterprets neutrino “flavor” as coherence-envelope curvature, predicting that quantized neutrino emissions should follow nucleation-phase energy saturation. Observations should reveal structured neutrino pulses tracking elemental shell formation during stellar collapse.

Opportunities:

• Long-baseline neutrino timing analyses correlated with elemental layering in supernova remnants.
• Lab-scale nucleation energy tests in dense matter under rapid compression or phase shift.

6.5. Optical Phase Shift Experiments in Structured Media

If scalar wave coupling occurs with changes in coherence tension, structured materials may exhibit observable optical or interferometric anomalies under deformation.

Approaches:

• Fabry–Pérot or Mach–Zehnder interferometry in materials under coherence gradient stress.
• Reflection or transmission anomalies near predicted scalar resonance thresholds.

Integration with Existing Instruments

Many of these tests can leverage existing observatories and experimental platforms:

• Neutrino observatories (IceCube, Super-Kamiokande) for flavor-phase signatures.
• Gravitational wave detectors (LIGO/Virgo/KAGRA) for pre-event scalar coupling or anomalous burst correlations.
• Deep-space probes and inertial guidance data from past flybys.
• Synchrotron beamlines or ultrafast optical setups for lattice collapse or structured mass oscillation.

By translating QSD’s substrate dynamics into concrete experimental conditions—coherence gradients, nucleation triggers, and inertial perturbations—these opportunities transform a theoretical field model into a testable physical framework.

7. Discussion

Quantum Substrate Dynamics (QSD) offers a structural reinterpretation of foundational physics, grounded not in new particles or dimensions but in the dynamics of a conserved, coherence-bearing substrate. While this approach departs from conventional field and geometric formulations, it remains consistent with known physical limits and extends them by resolving ambiguities that persist in modern frameworks.

7.1. Relation to General Relativity and Quantum Field Theory

QSD does not contradict General Relativity (GR) or Quantum Field Theory (QFT); it reframes their mathematical structures as emergent behaviors of an underlying coherence field. In GR, gravitational effects arise from spacetime curvature; in QSD, the same phenomena emerge from gradients in substrate tension. In QFT, quantized excitations exist in abstract fields; in QSD, they are localized resonance modes of a coherent substrate.

Both GR and QFT remain effective in their respective domains. QSD’s contribution is to provide a common physical origin for their behaviors—one in which local Lorentz invariance is preserved, but global properties (e.g., field tension or wave speed) arise from substrate conditions rather than assumed constants or geometric postulates.

QSD’s substrate ontology not only recasts the known interactions but also offers a reframing of long-standing open problems. The coherence-based model naturally mitigates the cosmological constant problem by treating vacuum energy as finite, structured tension rather than divergent zero-point fluctuations. Likewise, the emergence of mass from coherence knots sidesteps the need for Higgs-like field mechanisms to explain intrinsic particle mass. In areas such as dark matter and neutrino behavior, QSD provides a new interpretive lens: what appear as missing mass or flavor oscillations may instead reflect coherence structures with weak or delayed coupling to charge or radiation. This perspective encourages reinterpretation of existing experimental anomalies not by adding new entities, but by reconsidering what “presence” and “mass” mean in a coherence-governed field. Rather than discarding existing theories, QSD embeds them in a richer ontological substrate—preserving their predictions while revealing deeper physical origins.

7.2. Comparison with Emergent and Analog Gravity Models

QSD aligns conceptually with emergent gravity frameworks, such as Sakharov’s induced gravity and condensed-matter analog models, where spacetime and forces arise from microphysical substrates. However, QSD diverges by treating the substrate not as a metaphor or abstraction but as a real, conserved physical medium with measurable properties—coherence, tension, and phase continuity.

Unlike entropic or holographic approaches, QSD does not rely on statistical or informational constructs. It focuses on deterministic phase behavior within a continuous field, allowing for both local quantization and global field interactions without invoking inaccessible degrees of freedom.

7.3. Emergent Gravity Models: Comparative Analysis

While QSD aligns conceptually with emergent gravity frameworks, it departs significantly in both ontological basis and mechanistic structure. For instance, Sakharov’s induced gravity interprets gravitation as a residual elasticity of quantum vacuum fluctuations [8], while Verlinde’s entropic gravity models it as an emergent statistical force rooted in thermodynamic entropy gradients [12]. Padmanabhan’s holographic equipartition approach treats spacetime degrees of freedom as thermodynamically distributed microstates [30]. In contrast, QSD posits a physically real, Lorentz-invariant coherence substrate, where gravitational and inertial phenomena emerge from dynamic, local tension gradients and coherence-bound phase structures, rather than ensemble averages or information entropy.

Thus, QSD is neither entropic nor holographic in nature; it is phase-geometric and variationally grounded, deriving gravitational behavior from first-principles substrate dynamics. Importantly, it yields direct and falsifiable predictions—such as geometry-dependent inertia, coherence-induced redshift variations, and scalar wave precursors—that distinguish it both conceptually and experimentally from information-theoretic or statistical emergent gravity models.

7.4. Conceptual Clarifications: Mass, Inertia, and Time

QSD redefines several foundational concepts in terms of coherence behavior:

• Mass is not intrinsic substance, but a stable phase-condensed lattice within the substrate.
• Inertia arises from the energetic cost of reconfiguring the mass-phase boundary under acceleration.
• Time is not a geometric dimension but a phase interval between scalar wavefronts propagating through the substrate.

These interpretations eliminate the need to treat mass and inertia as unexplained primitives, or time as an external parameter. They also resolve the tension between quantum mechanics and relativity by embedding both within the behavior of a single conserved field.

While QSD provides a coherent framework spanning quantum, classical, and relativistic domains, it is not presented as a grand unified theory. It is a constrained, falsifiable physical model grounded in substrate conservation, coherence geometry, and observable dynamics. That it recovers known laws is not its ambition, but its necessity—any valid model must do the same.

QSD’s strength lies in its internal consistency, minimal assumptions, and ability to resolve open questions—such as the origin of inertia, the nature of neutrino oscillations, and coherence-based redshift—without contradicting empirical observations.

8. Future Scope and Limitations

This work presents a physically grounded reinterpretation of mass, inertia, gravity, and time through the internal coherence dynamics of a conserved substrate field. While the Quantum Substrate Dynamics (QSD) framework offers unified explanations and derives testable consequences, several aspects remain under development. The current formulation does not yet incorporate gauge symmetries or the standard model particle spectrum, and does not address electroweak or color charge as coherence modes—though such extensions are possible within a generalized field structure. Cosmological implications, such as early-universe phase transitions or vacuum saturation dynamics, are also deferred to future analysis. Furthermore, while scalar emissions and coherence drag effects are predicted, their simulation and detection will require high-resolution modeling and collaboration with experimental platforms. These limitations reflect not gaps in theory but the natural scope of a foundational paper: to establish physical principles, derive recoveries of known behavior, and propose falsifiable mechanisms. Future work will extend the formalism to nonlinear collapse, field interaction symmetries, and cosmological boundary conditions. This paper focuses on establishing foundational substrate principles, leaving symmetry derivations and field quantization to dedicated follow-up manuscripts.

9. Future Theoretical and Experimental Directions

Further development of QSD may include:

• Formal derivations of gauge symmetry from substrate phase structure,
• Nonlinear simulations of coherence collapse and scalar wave coupling,
• Integration with condensed matter experiments and scalar analog models,
• Cosmological modeling of coherence tension gradients and early-universe nucleation sequences.

Each of these directions remains grounded in the substrate’s coherence dynamics, offering pathways for both empirical exploration and mathematical expansion without speculative constructs.

Appendix A.1. Lagrangian Density of the Substrate Field

To formally describe the evolution of the quantum substrate field $\mathsf{\Psi }=\rho e^{i\theta }$, we construct a Lorentz-invariant Lagrangian that satisfies the foundational principles of Quantum Substrate Dynamics (QSD). This Lagrangian must:

• Preserve global coherence conservation (Principle III),
• Minimize spatial deformation and curvature under coherence stress (Principle VI),
• Support nonlinear condensation and stable mass-phase locking (Principle VIII),
• Reproduce scalar wave propagation and inertial resistance (Principles IX, XIV),
• Admit known field theories as limiting cases.

We begin by expanding the field $\mathsf{\Psi }$ into real amplitude and phase components:

$$\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}.$$

From this decomposition, the kinetic (gradient) contribution to the Lagrangian becomes:

$${\displaystyle \frac{1}{2}}{\partial }_{\mu }{\mathsf{\Psi }}^{*}{\partial }^{\mu }\mathsf{\Psi }={\displaystyle \frac{1}{2}}\left({\partial }_{\mu }\rho \right)\left({\partial }^{\mu }\rho \right)+{\displaystyle \frac{1}{2}}{\rho }^2\left({\partial }_{\mu }\theta \right)\left({\partial }^{\mu }\theta \right),$$

which separately tracks amplitude flow and phase evolution.

To enforce resistance to curvature and rapid deformation, we include a fourth-order stiffness term. To model phase-locked coherence states, we add a nonlinear saturation potential:

$$V\left(\rho \right)=\lambda {\left({\rho }^2-{\rho }_0^2\right)}^2,$$

where ${\rho }_0$ defines the coherence amplitude of a stable mass-phase region.

Combining all contributions, the full QSD Lagrangian density becomes:

$${\mathcal{L}}_{\mathrm{QSD}}={\displaystyle \frac{1}{2}}\left({\partial }_{\mu }\rho \right)\left({\partial }^{\mu }\rho \right)+{\displaystyle \frac{1}{2}}{\rho }^2\left({\partial }_{\mu }\theta \right)\left({\partial }^{\mu }\theta \right)-{\displaystyle \frac{\kappa }{2}}{\left({\nabla }^2\rho \right)}^2-\lambda {\left({\rho }^2-{\rho }_0^2\right)}^2.$$

(A1)

This expression contains all necessary structural dynamics for a coherence-driven field theory:

• The amplitude term ${\left({\partial }_{\mu }\rho \right)}^2$ governs scalar wave propagation,
• The phase term ${\rho }^2{\left({\partial }_{\mu }\theta \right)}^2$ models inertial drag and momentum flow,
• The curvature penalty ${\left({\nabla }^2\rho \right)}^2$ enforces local coherence economy,
• The nonlinear potential enables mass condensation and phase stability.

Limiting Case Reductions of the QSD Lagrangian

The QSD Lagrangian was derived from coherence conservation and deformation minimization—not reverse-engineered from existing theories. Nonetheless, it naturally reduces to several established models under constrained assumptions:

Table A1. Limiting case reductions of the QSD Lagrangian density ${\mathcal{L}}_{\mathrm{QSD}}$.

Limiting Case	Simplifying Assumptions	Resulting Lagrangian or Interpretation
Gross–Pitaevskii Equation (BECs)	Non-relativistic approximation, negligible curvature term $\kappa =0$, slow amplitude variation $\rho \approx \mathrm{const}$	Phase-dominant kinetic term ${\rho }^2{\left({\partial }_{\mu }\theta \right)}^2$ drives dynamics. Matches the GPE used in condensate evolution.
Ginzburg–Landau Equation (Superconductivity)	Static (time-independent) fields, real $\mathsf{\Psi }=\rho$, curvature resistance ignored	Reduces to: $\mathcal{L}={\displaystyle \frac{1}{2}}{(\nabla \rho )}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2$, the canonical Ginzburg–Landau free energy density.
Nonlinear Klein–Gordon / Higgs Field	Real scalar field $\mathsf{\Psi }=\rho$, relativistic treatment, curvature term dropped	Matches: $\mathcal{L}={\displaystyle \frac{1}{2}}{\left({\partial }_{\mu }\rho \right)}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2$, the standard symmetry-breaking scalar field Lagrangian.
Phase Field Models (Materials Science)	Replace ${\partial }_t^2\to {\partial }_t$ (dissipative dynamics), real field $\rho$, retain curvature penalty	Becomes the phase-field energy functional: $\mathcal{L}={\displaystyle \frac{1}{2}}{(\nabla \rho )}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2-{\displaystyle \frac{\kappa }{2}}{\left({\nabla }^2\rho \right)}^2$, used for boundary motion, domain wall formation, and pattern evolution.

Table A1. Limiting case reductions of the QSD Lagrangian density ${\mathcal{L}}_{\mathrm{QSD}}$.

Limiting Case	Simplifying Assumptions	Resulting Lagrangian or Interpretation
Gross–Pitaevskii Equation (BECs)	Non-relativistic approximation, negligible curvature term $\kappa =0$, slow amplitude variation $\rho \approx \mathrm{const}$	Phase-dominant kinetic term ${\rho }^2{\left({\partial }_{\mu }\theta \right)}^2$ drives dynamics. Matches the GPE used in condensate evolution.
Ginzburg–Landau Equation (Superconductivity)	Static (time-independent) fields, real $\mathsf{\Psi }=\rho$, curvature resistance ignored	Reduces to: $\mathcal{L}={\displaystyle \frac{1}{2}}{(\nabla \rho )}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2$, the canonical Ginzburg–Landau free energy density.
Nonlinear Klein–Gordon / Higgs Field	Real scalar field $\mathsf{\Psi }=\rho$, relativistic treatment, curvature term dropped	Matches: $\mathcal{L}={\displaystyle \frac{1}{2}}{\left({\partial }_{\mu }\rho \right)}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2$, the standard symmetry-breaking scalar field Lagrangian.
Phase Field Models (Materials Science)	Replace ${\partial }_t^2\to {\partial }_t$ (dissipative dynamics), real field $\rho$, retain curvature penalty	Becomes the phase-field energy functional: $\mathcal{L}={\displaystyle \frac{1}{2}}{(\nabla \rho )}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2-{\displaystyle \frac{\kappa }{2}}{\left({\nabla }^2\rho \right)}^2$, used for boundary motion, domain wall formation, and pattern evolution.

These reductions demonstrate that QSD serves as a unifying substrate-based framework from which prior nonlinear field models emerge as domain-specific limits. The Lagrangian thus provides both a physically grounded evolution law and a conceptual bridge across quantum, relativistic, and condensed matter physics.

Appendix A.1.1 Global Action and Field Evolution of the Substrate

Building on the local Lagrangian density, we construct the global field action that governs the full evolution of the quantum substrate field $\mathsf{\Psi }=\rho e^{i\theta }$. This global formulation satisfies the variational requirements of Quantum Substrate Dynamics (QSD) and embeds conservation, minimal deformation, and relativistic structure directly into its dynamical core.

This formulation must:

• Integrate the local Lagrangian density across all space and time to capture substrate evolution,
• Preserve Lorentz invariance in the full action functional,
• Generate the governing field equation via the principle of least action,
• Embed the substrate principles of coherence conservation and deformation economy.

Global Lagrangian and Action Functional

At any fixed time t, the total Lagrangian of the substrate is obtained by spatial integration of the local Lagrangian density:

$$L_{\mathrm{QSD}}\left(t\right)=\int {\mathcal{L}}_{\mathrm{QSD}}(\overrightarrow{r},t)d^{3}x.$$

To describe full substrate evolution over spacetime, we define the action:

$$S\left[\mathsf{\Psi }\right]=\int {\mathcal{L}}_{\mathrm{QSD}}(\overrightarrow{r},t)d^{4}x=\int {\mathcal{L}}_{\mathrm{QSD}}(\overrightarrow{r},t)d^{3}xdt,$$

where ${\mathcal{L}}_{\mathrm{QSD}}$ is as previously defined:

$${\mathcal{L}}_{\mathrm{QSD}}={\displaystyle \frac{1}{2}}{\left({\partial }_{\mu }\rho \right)}^2+{\displaystyle \frac{1}{2}}{\rho }^2{\left({\partial }_{\mu }\theta \right)}^2-{\displaystyle \frac{\kappa }{2}}{\left({\nabla }^2\rho \right)}^2-\lambda {({\rho }^2-{\rho }_0^2)}^2.$$

Applying the variational principle $\delta S=0$, subject to fixed boundary conditions, yields the governing equation of motion for the substrate field:

$${\displaystyle \frac{{\partial }^2\mathsf{\Psi }}{\partial t^2}}-\sigma {\nabla }^2\mathsf{\Psi }+\kappa {\nabla }^4\mathsf{\Psi }+2\lambda \left({\left|\mathsf{\Psi }\right|}^2-{\rho }_0^2\right)\mathsf{\Psi }=0.$$

This equation captures:

• Scalar wave propagation in low-tension domains,
• Inertial response and phase drag via the ${\rho }^2{\partial }_{\mu }\theta$ term,
• Localized coherence stabilization through the nonlinear potential,
• Structural resistance via higher-order stiffness (${\nabla }^4\mathsf{\Psi }$),
• Full Lorentz invariance and substrate conservation through Lagrangian derivation.

Limiting Case Reductions of the QSD Substrate Equation

The resulting substrate field equation was derived directly from physically grounded principles and not constructed to mimic known theories. Nonetheless, it recovers several classical models as special cases under domain-specific simplifications:

Table A2. Domain-specific reductions of the QSD substrate field equation under simplifying physical conditions.

Limiting Case	Assumptions Applied	Resulting Model
Gross–Pitaevskii Equation (BECs)	Non-relativistic limit (${\partial }_t^2\to i{\partial }_t$), slow amplitude variation, drop curvature ($\kappa =0$)	$i{\displaystyle \frac{\partial \psi }{\partial t}}=-{\displaystyle \frac{1}{2m}}{\nabla }^2\psi +\lambda {\left|\psi \right|}^2\psi$
Ginzburg–Landau Equation	Time-independence, real scalar field ($\mathsf{\Psi }=\rho$), curvature resistance ignored	$-{\nabla }^2\rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Nonlinear Klein–Gordon / Higgs Field	Real scalar field, relativistic treatment, drop curvature term	$\square \rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Phase Field Models	Replace ${\partial }_t^2\to {\partial }_t$, retain $\kappa >0$, real scalar field	${\displaystyle \frac{\partial \rho }{\partial t}}=-{\displaystyle \frac{\delta E\left[\rho \right]}{\delta \rho }}$
Dispersive Wave Equations	Drop nonlinear potential ($\lambda =0$), real scalar field, retain ${\nabla }^2$ and ${\nabla }^4$ terms	${\displaystyle \frac{{\partial }^2\rho }{\partial t^2}}-\sigma {\nabla }^2\rho +\kappa {\nabla }^4\rho =0$

Table A2. Domain-specific reductions of the QSD substrate field equation under simplifying physical conditions.

Limiting Case	Assumptions Applied	Resulting Model
Gross–Pitaevskii Equation (BECs)	Non-relativistic limit (${\partial }_t^2\to i{\partial }_t$), slow amplitude variation, drop curvature ($\kappa =0$)	$i{\displaystyle \frac{\partial \psi }{\partial t}}=-{\displaystyle \frac{1}{2m}}{\nabla }^2\psi +\lambda {\left|\psi \right|}^2\psi$
Ginzburg–Landau Equation	Time-independence, real scalar field ($\mathsf{\Psi }=\rho$), curvature resistance ignored	$-{\nabla }^2\rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Nonlinear Klein–Gordon / Higgs Field	Real scalar field, relativistic treatment, drop curvature term	$\square \rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Phase Field Models	Replace ${\partial }_t^2\to {\partial }_t$, retain $\kappa >0$, real scalar field	${\displaystyle \frac{\partial \rho }{\partial t}}=-{\displaystyle \frac{\delta E\left[\rho \right]}{\delta \rho }}$
Dispersive Wave Equations	Drop nonlinear potential ($\lambda =0$), real scalar field, retain ${\nabla }^2$ and ${\nabla }^4$ terms	${\displaystyle \frac{{\partial }^2\rho }{\partial t^2}}-\sigma {\nabla }^2\rho +\kappa {\nabla }^4\rho =0$

Interpretation and Role in QSD

This governing field equation forms the dynamic heart of QSD. It encodes not just motion, but the restructuring of spacetime itself as a manifestation of substrate coherence. It is from this action that gravity, inertia, scalar waves, and mass condensation all emerge—not as separate postulates, but as coherent responses to the substrate’s intrinsic principles.

This action-driven approach reinterprets geometric postulates with field evolution, placing coherence tension at the foundation of all observable dynamics. In this sense, QSD does not merely generalize known models—it structurally absorbs them into a unified substrate-based framework.

Appendix A.2. Governing Substrate Field Equation

To formally capture the dynamical behavior of the substrate field $\mathsf{\Psi }=\rho e^{i\theta }$, we derive its governing equation from first principles of Quantum Substrate Dynamics (QSD). This equation must:

• Conserve the total substrate coherence amplitude (Principle III),
• Minimize spatial deformation and curvature under coherence stress (Principle VI),
• Support nonlinear self-locking and phase-bound stability (Principle VIII),
• Enable scalar wave propagation and coherence collapse (Principles IX, XIV),
• Remain Lorentz-invariant and recover known physics in appropriate limits (Principle XVII).

We define a variational energy functional representing coherence tension, deformation, and phase saturation:

$$E_{\mathrm{deform}}\left[\mathsf{\Psi }\right]=\int \left[{\sigma |\nabla \mathsf{\Psi }|}^2+\kappa {\left|{\nabla }^2\mathsf{\Psi }\right|}^2+V\left(\mathsf{\Psi }\right)\right]d^{3}x,$$

(A2)

with physical terms interpreted as:

• $\sigma$: Substrate tension coefficient (resistance to gradient stress),
• $\kappa$: Substrate stiffness (resistance to curvature),
• $V\left(\mathsf{\Psi }\right)$: Nonlinear potential representing mass-phase saturation.

A coherence-locking potential with symmetric saturation points is given by:

$$V\left(\mathsf{\Psi }\right)=\lambda {\left({\left|\mathsf{\Psi }\right|}^2-{\rho }_0^2\right)}^2,$$

(A3)

where ${\rho }_0$ defines the target amplitude of a stable coherence phase.

Minimizing the deformation energy and applying relativistic field dynamics yields the full QSD evolution equation:

$${\displaystyle \frac{{\partial }^2\mathsf{\Psi }}{\partial t^2}}-\sigma {\nabla }^2\mathsf{\Psi }+\kappa {\nabla }^4\mathsf{\Psi }+2\lambda \left({\left|\mathsf{\Psi }\right|}^2-{\rho }_0^2\right)\mathsf{\Psi }=0.$$

(A4)

This substrate field equation describes how coherence gradients, curvature resistance, and phase saturation govern the emergence of matter-like structures, scalar excitations, and inertial response in QSD.

Limiting Case Reductions of the QSD Field Equation

The above equation was constructed from physically grounded coherence principles—not tuned to mimic known theories. However, it naturally reduces to several canonical field models under simplifying assumptions:

Table A3. Domain-specific reductions of the QSD substrate evolution equation under constrained physical regimes.

Limiting Case	Simplifying Assumptions	Resulting Equation or Interpretation
Gross–Pitaevskii Equation (BEC)	Non-relativistic limit ${\partial }_t^2\to i{\partial }_t$, small amplitude variation $\rho \approx \mathrm{const}$, drop curvature term ($\kappa =0$)	$i{\displaystyle \frac{\partial \psi }{\partial t}}=-{\displaystyle \frac{1}{2m}}{\nabla }^2\psi +\lambda {\left|\psi \right|}^2\psi$
Ginzburg–Landau Equation	Time-independence, real field $\mathsf{\Psi }=\rho$, no curvature resistance	$-{\nabla }^2\rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Nonlinear Klein–Gordon / Higgs Field	Real scalar field, relativistic dynamics, drop $\kappa$	$\square \rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Phase Field Evolution (Materials Science)	Replace ${\partial }_t^2\to {\partial }_t$, real scalar field, retain curvature penalty $\kappa >0$	${\displaystyle \frac{\partial \rho }{\partial t}}=-{\displaystyle \frac{\delta E\left[\rho \right]}{\delta \rho }}$
Dispersive Fluid Waves	Drop nonlinear potential ($\lambda =0$), real scalar field, retain ${\nabla }^2$ and ${\nabla }^4$ terms	${\displaystyle \frac{{\partial }^2\rho }{\partial t^2}}-\sigma {\nabla }^2\rho +\kappa {\nabla }^4\rho =0$

Table A3. Domain-specific reductions of the QSD substrate evolution equation under constrained physical regimes.

Limiting Case	Simplifying Assumptions	Resulting Equation or Interpretation
Gross–Pitaevskii Equation (BEC)	Non-relativistic limit ${\partial }_t^2\to i{\partial }_t$, small amplitude variation $\rho \approx \mathrm{const}$, drop curvature term ($\kappa =0$)	$i{\displaystyle \frac{\partial \psi }{\partial t}}=-{\displaystyle \frac{1}{2m}}{\nabla }^2\psi +\lambda {\left|\psi \right|}^2\psi$
Ginzburg–Landau Equation	Time-independence, real field $\mathsf{\Psi }=\rho$, no curvature resistance	$-{\nabla }^2\rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Nonlinear Klein–Gordon / Higgs Field	Real scalar field, relativistic dynamics, drop $\kappa$	$\square \rho +4\lambda ({\rho }^2-{\rho }_0^2)\rho =0$
Phase Field Evolution (Materials Science)	Replace ${\partial }_t^2\to {\partial }_t$, real scalar field, retain curvature penalty $\kappa >0$	${\displaystyle \frac{\partial \rho }{\partial t}}=-{\displaystyle \frac{\delta E\left[\rho \right]}{\delta \rho }}$
Dispersive Fluid Waves	Drop nonlinear potential ($\lambda =0$), real scalar field, retain ${\nabla }^2$ and ${\nabla }^4$ terms	${\displaystyle \frac{{\partial }^2\rho }{\partial t^2}}-\sigma {\nabla }^2\rho +\kappa {\nabla }^4\rho =0$

Interpretation and Role in QSD

This governing equation expresses not only the evolution of field structure but the active reconfiguration of coherence that defines matter, motion, and scalar energy flow. It unifies phenomena typically treated as independent—mass formation, field propagation, inertia, scalar radiation—under a single substrate field law.

From this formulation, we understand:

• Scalar and neutrino emissions arise from rapid local reconfiguration,
• Mass-phase knots emerge as stable minima of the substrate potential,
• Inertia arises from the cost of reconfiguring ${\rho }^2{\left({\partial }_{\mu }\theta \right)}^2$,
• Field theories like GL, GPE, KG, and phase models are special cases of substrate dynamics.

This equation is not just predictive—it is ontologically generative. It bridges quantum, relativistic, and continuum descriptions, all grounded in the conserved, coherence-structured fluid of QSD.

Appendix A.2.1 Unified Substrate Dynamics Equation

Quantum Substrate Dynamics (QSD) models the substrate field $\mathsf{\Psi }(\overrightarrow{r},t)$ with a hybrid formulation inspired by Navier–Stokes fluid dynamics and the Gross–Pitaevskii equation. The momentum balance equation is expressed as:

$$\rho \left({\displaystyle \frac{\partial \overrightarrow{v}}{\partial t}}+(\overrightarrow{v}·\nabla )\overrightarrow{v}\right)=-\nabla P+{\overrightarrow{F}}_{\mathrm{quantum}}+{\overrightarrow{F}}_{\mathrm{coherence}}+{\overrightarrow{F}}_{\mathrm{scalar}}+{\overrightarrow{F}}_{\mathrm{lattice}}+{\overrightarrow{F}}_{\mathrm{phase}},$$

(A5)

where:

• ${\overrightarrow{F}}_{\mathrm{quantum}}=-\nabla \left({\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\nabla }^2\left|\mathsf{\Phi }\right|}{\left|\mathsf{\Phi }\right|}}\right)$ is the quantum pressure,
• ${\overrightarrow{F}}_{\mathrm{coherence}}$ captures gradient tension from substrate deformation,
• ${\overrightarrow{F}}_{\mathrm{scalar}}=-{\alpha }_s\nabla \varphi$ represents feedback from scalar compression fields,
• ${\overrightarrow{F}}_{\mathrm{phase}}$ and ${\overrightarrow{F}}_{\mathrm{lattice}}$ describe boundary and internal lattice dynamics.

Appendix A.3. Transverse Phase Wave Equation in QSD

In Quantum Substrate Dynamics (QSD), transverse waves—such as electromagnetic radiation—emerge as oscillatory phase-shear excitations of the substrate. These waves propagate orthogonally to the direction of wavefront advance and are governed by local coherence tension and phase continuity. They represent a distinct coherence mode from scalar waves, which are longitudinal compressional excitations.

To explicitly model transverse wave behavior, we isolate the phase-dynamics portion of the QSD Lagrangian. Assuming the amplitude $\rho$ varies slowly or remains approximately constant over the region of interest, the relevant Lagrangian density becomes:

$${\mathcal{L}}_{\mathrm{trans}}={\displaystyle \frac{1}{2}}{\rho }^2\left({\partial }_{\mu }\theta \right)\left({\partial }^{\mu }\theta \right),$$

(A6)

where ${\rho }^2$ plays the role of an effective inertia or phase-permeability, and $\theta$ is the local phase field encoding transverse oscillations.

Euler–Lagrange Derivation

Taking the functional derivative of ${\mathcal{L}}_{\mathrm{trans}}$ with respect to $\theta$ and applying the Euler–Lagrange formalism yields:

$${\partial }_{\mu }\left({\rho }^2{\partial }^{\mu }\theta \right)=0.$$

(A7)

In component form, this becomes:

$${\displaystyle \frac{\partial }{\partial t}}\left({\rho }^2{\displaystyle \frac{\partial \theta }{\partial t}}\right)-\nabla ·\left({\rho }^2\nabla \theta \right)=0.$$

(A8)

This is the generalized transverse wave equation for phase evolution in a medium with spatially variable coherence density $\rho$. In the limit where $\rho$ is uniform, the equation reduces to the conventional wave equation for transverse phase oscillations:

$$\square \theta =0.$$

(A9)

Physical Interpretation in QSD

This transverse phase equation models electromagnetic-like wave behavior as structured shear within the substrate’s internal phase geometry. In QSD:

• Transverse waves are not fundamental fields but coherence structures,
• The propagation speed c arises from local substrate tension and phase elasticity,
• The wavefront travels orthogonal to $\nabla \theta$, with speed determined by $c^2\sim {\tau }_T/\rho$, where ${\tau }_T$ is the transverse coherence tension.

In regions of varying $\rho$, such as near mass-phase boundaries or within curved substrate zones, transverse wavefronts may bend, slow, or refract—reproducing the effects of lensing, time dilation, and waveguide behavior without invoking spacetime curvature.

Role in QSD Framework

The transverse phase wave equation:

$${\partial }_{\mu }\left({\rho }^2{\partial }^{\mu }\theta \right)=0$$

complements the scalar wave equation derived from the amplitude $\rho$. Together, they provide a dual-mode description of substrate wave phenomena:

• Scalar wave equation: describes longitudinal compressional dynamics tied to coherence-pressure release, such as neutrino emissions and supernova precursors.
• Transverse wave equation: governs phase-shear propagation, corresponding to electromagnetic radiation and transverse coherence modes.

These equations emerge from the same substrate Lagrangian and field formulation, reinforcing the QSD view that all fields—scalar, electromagnetic, gravitational—are coherence modes within a single, conserved, relativistic substrate.

This dual-mode structure unifies EM and scalar behavior not by analogy, but by shared origin in the field’s geometry. It also enables predictions for coherence-coupled interference, cross-mode conversion, and propagation anomalies in high-gradient regions such as black hole trenches, scalar emitters, or gradient transition domains.

Appendix A.4. Scalar Wave Equation Derivation

The scalar coherence displacement field $\varphi (\overrightarrow{r},t)$ obeys:

$${\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-v_s^2{\nabla }^2\varphi +{\displaystyle \frac{\partial V\left(\varphi \right)}{\partial \varphi }}={\beta }_s\nabla ·\overrightarrow{v},$$

(A10)

where $V\left(\varphi \right)$ is typically modeled as a double-well or sine-Gordon potential. The scalar field exerts feedback via:

$${\overrightarrow{F}}_{\mathrm{scalar}}=-{\alpha }_s\nabla \varphi .$$

(A11)

Appendix A.5. Quantitative Substrate Dynamics in SN 1987A-like Events

Appendix A.5.1. Motivation and Scope

To validate Quantum Substrate Dynamics (QSD) against observational data, we identify SN 1987A as a prototype event with timing, structure, and signal diversity suitable for testing the coherence slip hypothesis. This appendix develops a quantitative substrate model for scalar and neutrino emission during core failure and shows how the post-slip substrate geometry seeds the supernova outburst.

Appendix A.5.2. Scalar–Neutrino Delay Framework

Scalar coherence waves, traveling at or near c, should arrive measurably before neutrinos with small but finite mass. The delay is given by:

$$\Delta t\approx {\displaystyle \frac{D}{c}}·{\displaystyle \frac{m_{\nu }^2}{2E_{\nu }^2}}$$

(A12)

For SN 1987A ($D\approx 1.56\times {10}^{21}\mathrm{m}$), assuming $m_{\nu }=0.1\mathrm{eV}$ and $E_{\nu }=10\mathrm{MeV}$, we find:

$$\Delta t\approx 2.7\mathrm{seconds}$$

(A13)

This timescale provides a testable QSD signature: a scalar front preceding thermal neutrinos by seconds – consistent with early PMT activity in SN 1987A ( 2–3s pre-burst), which remains unclassified in GR-based interpretations.

Appendix A.5.3. Core Slip as Substrate Yielding

At peak internal coherence strain, the stellar core undergoes a geometric slip rather than a bounce. This is a localized substrate failure and reconfiguration:

$$\mathsf{\Psi }(\overrightarrow{r},t)=\rho (\overrightarrow{r},t)e^{i\theta (\overrightarrow{r},t)}$$

(A14)

Slip occurs when internal phase gradients approach a coherence failure threshold:

$$\nabla {\theta }_{\mathrm{core}}\to \nabla {\theta }_{\mathrm{crit}},\delta \rho /\rho \to \max$$

(A15)

This produces a scalar burst as stored gradient tension is released:

$$E_{\mathrm{scalar}}\sim \gamma {\int }_{\partial V}\left({\delta |\nabla \rho |}^2+\delta {|\nabla \theta |}^2\right)dA$$

(A16)

Exhaustion and Substrate Re-seeding

Following the slip, the core stabilizes temporarily in a lower-energy coherence configuration. This state is compact, low-tension, and unable to self-sustain fusion.

From the QSD view, this **exhausted coherence core** acts as a nucleation seed for nova outburst — the core has dumped enough scalar pressure to allow outer material to rebound and explode. It is **not** the bounce that causes the supernova — it is the scalar-driven offload that allows explosive release from outer layers.

Appendix A.5.4. Action Principle and Stability Transition

The core slip satisfies a coherence-conserving action minimization:

$$\delta S=\delta \int \mathcal{L}(\rho ,\theta ,\nabla \rho ,\nabla \theta )d^{4}x=0$$

(A17)

Before the slip, internal gradients make the system metastable. After the slip, the geometry lowers action by entering a smaller, stable coherence mode — like falling into a tighter basin in phase space.

Appendix A.5.5. Observational Signature Predictions

- A 2–3 s scalar–neutrino delay in future galactic supernovae - Low-count, early signals in pressure-sensitive detectors (e.g., Mont Blanc LSD) - Scalar emission setting up the geometry for delayed outburst (hours or more) - Spectral anomalies or anisotropies traceable to internal scalar offloading paths

Appendix A.5.6. Summary

QSD provides a natural, quantitatively predictive explanation for the timing sequence in SN 1987A-like events. The scalar emission is not optional — it is a geometric inevitability of coherence failure. The same slip that creates the early signal also reconfigures the core in a way that makes the later nova outburst possible.

Appendix A.6. Superfluid Analogues, Zero-Resistance, and Mathematical Framework

Appendix A.6.1. Conceptual Basis of Universal Coherence and Inertial Decoupling

In QSD, perfect coherence alignment at the interface between mass-phase and wave-phase regions eliminates coherence-boundary friction, analogous to zero-viscosity conditions in superfluid helium. Such idealized coherence conditions produce a state of inertial decoupling, effectively isolating mass-phase structures from substrate drag, potentially manifesting experimentally as a coherent shock bubble capable of frictionless propagation.

Appendix A.6.2. Madelung Representation and Zero-Resistance Conditions

Quantum fluid dynamics often employs the Madelung transform, representing the wavefunction in fluidic terms:

$$\mathsf{\Phi }(\mathbf{r},t)=\sqrt{\rho (\mathbf{r},t)}exp\left[i\theta (\mathbf{r},t)\right],$$

where $\rho (\mathbf{r},t)={\left|\mathsf{\Phi }(\mathbf{r},t)\right|}^2$ is coherence density, and $\theta (\mathbf{r},t)$ is coherence phase. The coherent velocity field is thus:

$$\mathbf{v}(\mathbf{r},t)={\displaystyle \frac{\hslash }{m_{*}}}\nabla \theta (\mathbf{r},t).$$

Key fluid coherence properties derived from this representation include:

• Irrotational Flow: Coherence-based velocity fields are irrotational ($\nabla \times \mathbf{v}=0$), reducing internal shear and vortex-induced drag, crucial for inertial decoupling.
• Boundary Coherence Matching: When an object’s velocity matches the substrate’s coherence velocity exactly, coherence-boundary friction vanishes:

  $${\mathbf{v}}_{\mathrm{obj}}\approx {\displaystyle \frac{\hslash }{m_{*}}}\nabla \theta .$$
• Quantum Pressure and Stability: Quantum pressure, emerging from coherence density gradients, prevents coherence collapse and maintains structural stability, allowing sustained zero-resistance conditions.

Appendix A.6.3. Broader Implications and Relevance

The zero-resistance conditions highlighted by the Madelung formulation imply:

• Cosmic-Scale Coherence: Extending zero-resistance phenomena observed in condensed matter systems to astrophysical and cosmological scales offers a coherent explanation for inertia and gravitational coupling.
• Technological Potential: Realizing inertial decoupling through engineered coherence states could inspire novel propulsion methods and inertial manipulation technologies, such as coherent boundary "shock bubbles" or vortex-mediated systems.
• Interdisciplinary Collaboration: Collaboration with quantum hydrodynamics specialists could significantly advance theoretical rigor, mathematical consistency, and empirical testing of QSD’s coherence-based hypotheses.

This expanded appendix content provides deeper theoretical context and mathematical rigor, serving as supplementary detail to the concise main-text summary.

Appendix A.7. Newtonian Recovery and Quantum Pressure

Appendix A.7.1. Derivation of Newtonian Limit from QSD

Consider a mass-phase object moving slowly in a nearly stationary, uniform quantum fluid substrate (coherence density ${\rho }_0\approx \mathrm{constant}$). The linearized quantum fluid momentum equation becomes:

$${\rho }_0{\displaystyle \frac{\partial \left(\delta \mathbf{v}\right)}{\partial t}}\approx -\nabla P-\nu {\nabla }^2\left(\delta \mathbf{v}\right)+{\mathbf{F}}_{\mathrm{phase}},$$

where effective coherence viscosity $\nu \approx 0$ under ideal conditions, leaving coherence-boundary interactions as primary inertial contributors. Integration over the coherence-boundary yields the classical Newtonian law:

$${\oint }_{\mathrm{interface}}{\mathbf{F}}_{\mathrm{phase}}·d\mathbf{A}\to m_{\mathrm{eff}}{\displaystyle \frac{d{\mathbf{v}}_{\mathrm{obj}}}{dt}},$$

where $m_{\mathrm{eff}}$ explicitly reflects coherence-boundary geometry and fluid-interface energy. This derivation reinforces the conceptual shift, viewing inertia not as intrinsic but emergent from coherence dynamics.

Appendix A.8. Binary Orbit QSD/GR Comparison

Figure A1. Side-by-side derivation of Newtonian gravity from GR and QSD.

Figure A1. Side-by-side derivation of Newtonian gravity from GR and QSD.

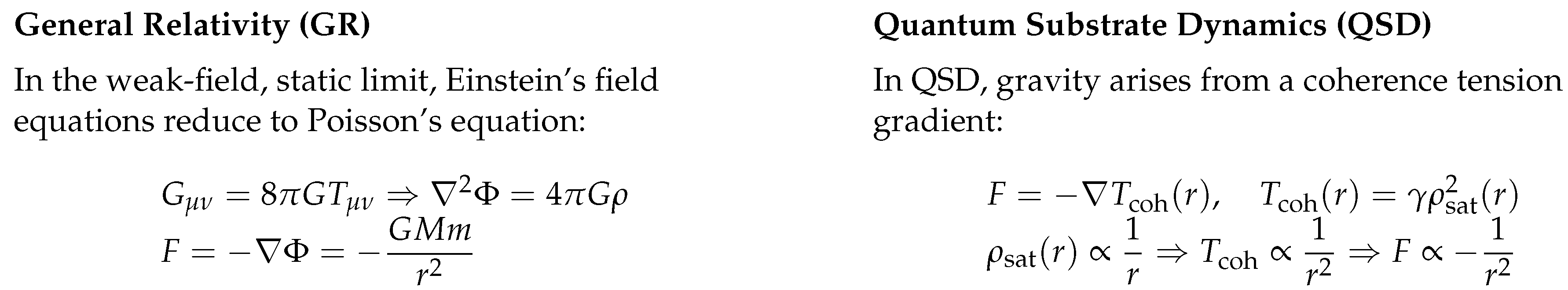
Appendix A.9. Coherence Wave Modes

Table A4. Comparison of Coherence Wave Modes in Quantum Substrate Dynamics (QSD)

Feature	Transverse Waves (EM)	Scalar Waves (Longitudinal)
Propagation Direction	Orthogonal to oscillation plane	Aligned with oscillation direction
Wave Type	Transverse coherence oscillation	Longitudinal compression/rarefaction
Physical Origin	Oscillatory tension in transverse coherence geometry	Pressure pulse in coherence density (phase pressure)
Emergent Speed	$c=\sqrt{{\tau }_T/\mu }$	$v_s=\sqrt{{\tau }_L/\mu }$, may differ from c
Charge Coupling	Strongly coupled to electric charge	Independent of charge; neutral mass-phase coupling
Propagation Medium	Requires coherent transverse tension	Supported in any compressible coherent substrate
Shielding Behavior	Blocked or absorbed by conductive materials	Can pass through dense or shielded environments
Analogous System	Electromagnetic waves in vacuum	Sound or pressure waves in fluids
Emission Source	Oscillatory boundary current or phase-excitation	Substrate reconfiguration or coherence collapse
Observational Role	Light, radio, gamma radiation	Neutrinos, scalar precursors, coherence shocks
Substrate Signature	Lateral phase tension modulation	Compression front with scalar pressure spike

Table A4. Comparison of Coherence Wave Modes in Quantum Substrate Dynamics (QSD)

Feature	Transverse Waves (EM)	Scalar Waves (Longitudinal)
Propagation Direction	Orthogonal to oscillation plane	Aligned with oscillation direction
Wave Type	Transverse coherence oscillation	Longitudinal compression/rarefaction
Physical Origin	Oscillatory tension in transverse coherence geometry	Pressure pulse in coherence density (phase pressure)
Emergent Speed	$c=\sqrt{{\tau }_T/\mu }$	$v_s=\sqrt{{\tau }_L/\mu }$, may differ from c
Charge Coupling	Strongly coupled to electric charge	Independent of charge; neutral mass-phase coupling
Propagation Medium	Requires coherent transverse tension	Supported in any compressible coherent substrate
Shielding Behavior	Blocked or absorbed by conductive materials	Can pass through dense or shielded environments
Analogous System	Electromagnetic waves in vacuum	Sound or pressure waves in fluids
Emission Source	Oscillatory boundary current or phase-excitation	Substrate reconfiguration or coherence collapse
Observational Role	Light, radio, gamma radiation	Neutrinos, scalar precursors, coherence shocks
Substrate Signature	Lateral phase tension modulation	Compression front with scalar pressure spike

Appendix A.10. Empirical Anomalies Addressed by QSD

While Quantum Substrate Dynamics (QSD) is constructed from first principles, its value is ultimately judged by its ability to illuminate unexplained phenomena. Several empirical anomalies—persistently observed yet poorly resolved within General Relativity, Newtonian gravity, or Quantum Field Theory—are naturally explained within the QSD framework. These include inertial deviations, coherence-induced element patterns, unexplained precursor signals, and post-merger echo dynamics.

Table A5 summarizes a selection of such anomalies and outlines how QSD interprets them as coherence-based substrate effects, offering a falsifiable and structurally motivated alternative to conventional models.

Table A5. QSD Engagement with Empirical Anomalies Unresolved by Conventional Theories

Anomaly	Conventional View	QSD Explanation
Flyby anomaly	Unexplained energy shifts in spacecraft during planetary flybys; not predicted by GR or Newtonian mechanics.	Arises from geometry-sensitive inertial drag due to coherence gradients in Earth’s substrate field. Inertial mass varies with coherence structure.
Off-pattern shell nucleation	Supernova remnants show element shells inconsistent with fusion energy deposition or standard hydrodynamics.	Mass-phase nucleation thresholds depend on scalar tension fronts, not just thermal expansion—yielding quantized element layers at coherence transition zones.
Scalar precursors	Some astrophysical events show signals preceding light or neutrinos; lacks explanation in GR or QFT.	QSD predicts scalar (longitudinal) coherence waves that propagate ahead of light as substrate compression fronts.
LIGO ringdown echoes	Residual oscillations after black hole mergers poorly matched by GR models; debated as noise.	Predicted as vibrational rebound or trench-mode relaxation of metastable dual-core coherence geometries following merger frustration.

Table A5. QSD Engagement with Empirical Anomalies Unresolved by Conventional Theories

Anomaly	Conventional View	QSD Explanation
Flyby anomaly	Unexplained energy shifts in spacecraft during planetary flybys; not predicted by GR or Newtonian mechanics.	Arises from geometry-sensitive inertial drag due to coherence gradients in Earth’s substrate field. Inertial mass varies with coherence structure.
Off-pattern shell nucleation	Supernova remnants show element shells inconsistent with fusion energy deposition or standard hydrodynamics.	Mass-phase nucleation thresholds depend on scalar tension fronts, not just thermal expansion—yielding quantized element layers at coherence transition zones.
Scalar precursors	Some astrophysical events show signals preceding light or neutrinos; lacks explanation in GR or QFT.	QSD predicts scalar (longitudinal) coherence waves that propagate ahead of light as substrate compression fronts.
LIGO ringdown echoes	Residual oscillations after black hole mergers poorly matched by GR models; debated as noise.	Predicted as vibrational rebound or trench-mode relaxation of metastable dual-core coherence geometries following merger frustration.

Appendix A.11. Falsification Scenarios and Test Designs

Table A6. QSD Predictions and Near-Term Experimental Tests

Prediction	Test Method	Competing Models	Distinguishing Signature
Scalar–neutrino delay (2–3 s)	Supernova timing with neutrino observatories [31,32,33]	GR/QFT	Early photomultiplier signal or scalar pulse preceding neutrinos
Variable inertia by geometry	Drop towers, torsion pendulums, microgravity platforms	None	Mass-equivalent samples with differing coherence topology exhibit inertial variation
Coherence trench burst behavior	Gravitational wave tail analysis via LISA [34]	GR	Scalar-mode ringdown echoes post-merger beyond tensor-only predictions
Substrate shear profile deviations	Flyby anomaly tracking, precision orbital dynamics	GR	Non-Keplerian deviations matching predicted substrate gradients

Table A6. QSD Predictions and Near-Term Experimental Tests

Prediction	Test Method	Competing Models	Distinguishing Signature
Scalar–neutrino delay (2–3 s)	Supernova timing with neutrino observatories [31,32,33]	GR/QFT	Early photomultiplier signal or scalar pulse preceding neutrinos
Variable inertia by geometry	Drop towers, torsion pendulums, microgravity platforms	None	Mass-equivalent samples with differing coherence topology exhibit inertial variation
Coherence trench burst behavior	Gravitational wave tail analysis via LISA [34]	GR	Scalar-mode ringdown echoes post-merger beyond tensor-only predictions
Substrate shear profile deviations	Flyby anomaly tracking, precision orbital dynamics	GR	Non-Keplerian deviations matching predicted substrate gradients