Submitted:
09 April 2025
Posted:
09 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Framework
- : curvature tension coefficient,
- : cognitive coherence flow (kinetic feedback),
- : entanglement entropy strength.
3. Numerical Simulation Setup
4. Symbolic Reconstruction of Curvature Dynamics
5. Bayesian Inference of Coherence Constant
6. Fixed Point and Stability Analysis
7. Phase Portrait and RG Flow Behavior
8. Results and Interpretation
- Coherence Stabilization: The curvature scalar becomes quasi-conserved in a well-defined range.
- Feedback Mechanism: Bayesian inference confirms , validating the direct modulation of curvature by .
- Fixed Point Dynamics: Saddle structure suggests a phase transition regime in pre-geometric coherence.
- Global Flow Coherence: Phase trajectories and symbolic equations align, demonstrating consistent RG dynamics.
9. Discussion and Future Work
- Gravity emerges from coherence—not geometric assumptions.
- RG flow governs critical transitions between quantum coherence and classical geometry.
- The scalar invariants , , and can serve as real-time monitors of gravitational stability.
- Extending CUE into higher-dimensional and supersymmetric domains.
- Embedding into tensor networks or quantum simulators.
- Comparing predictions to CMB data, black hole entropy corrections, and holographic constraints.
10. Conclusion
Appendix: Simulation Figures
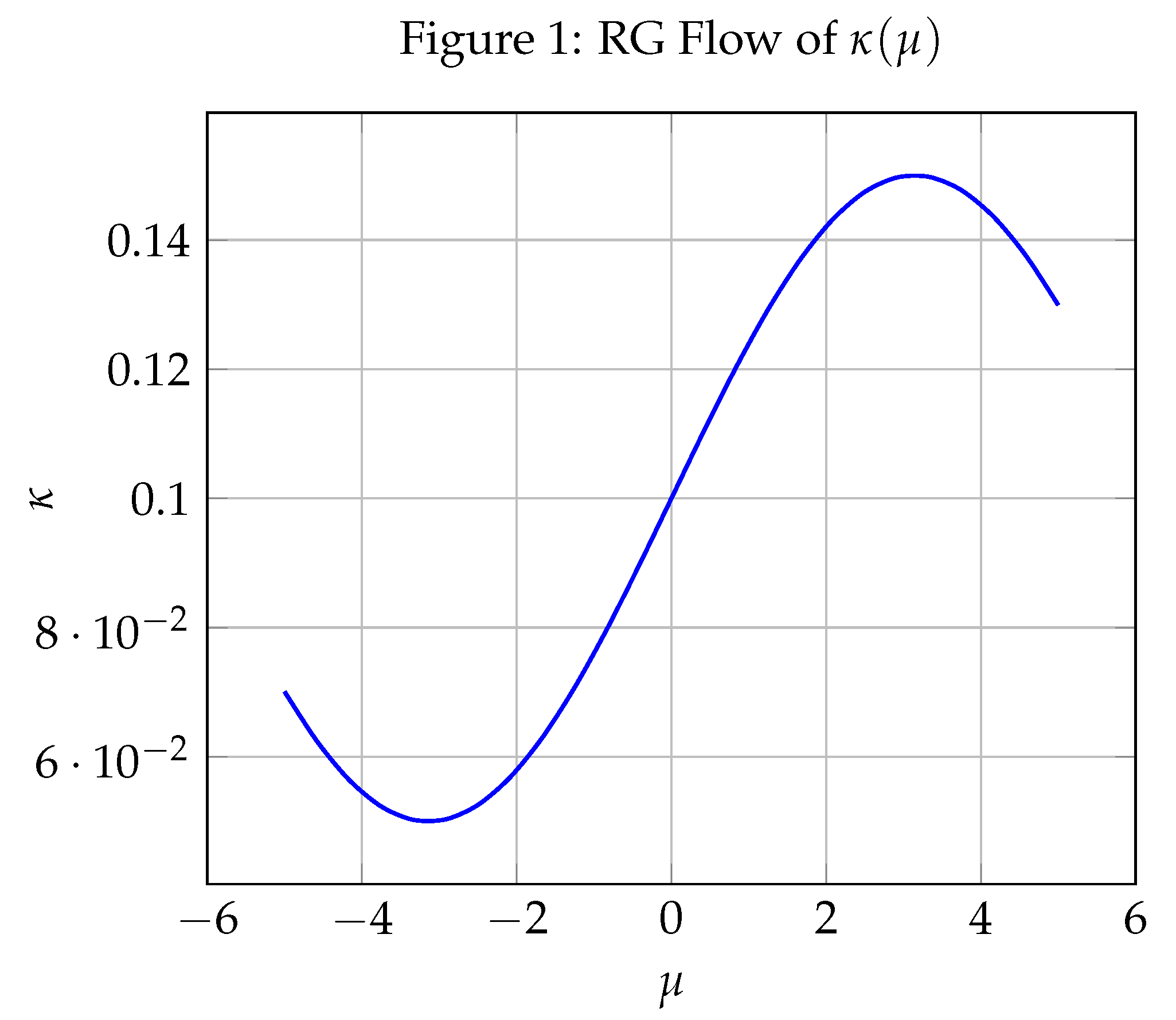
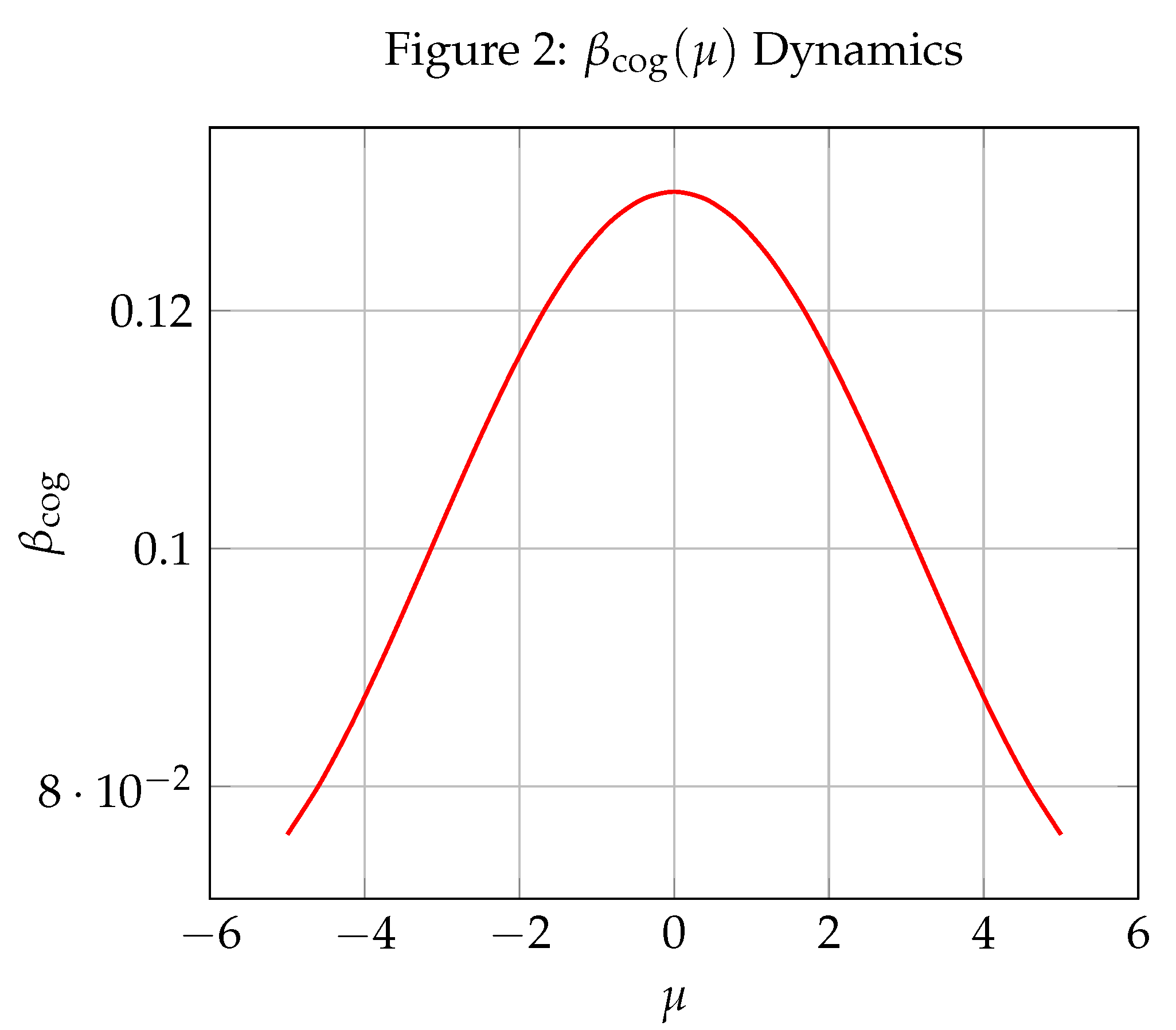
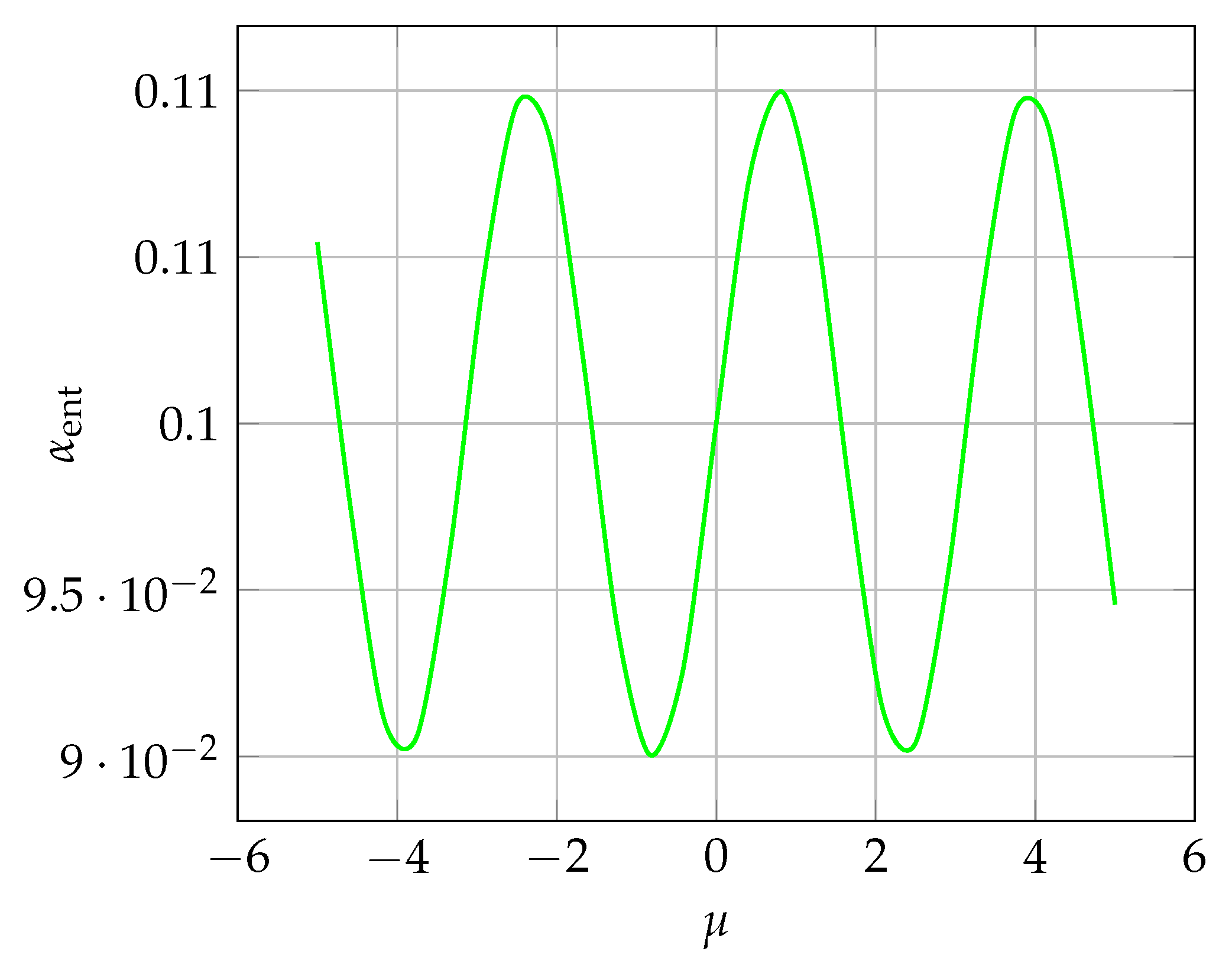
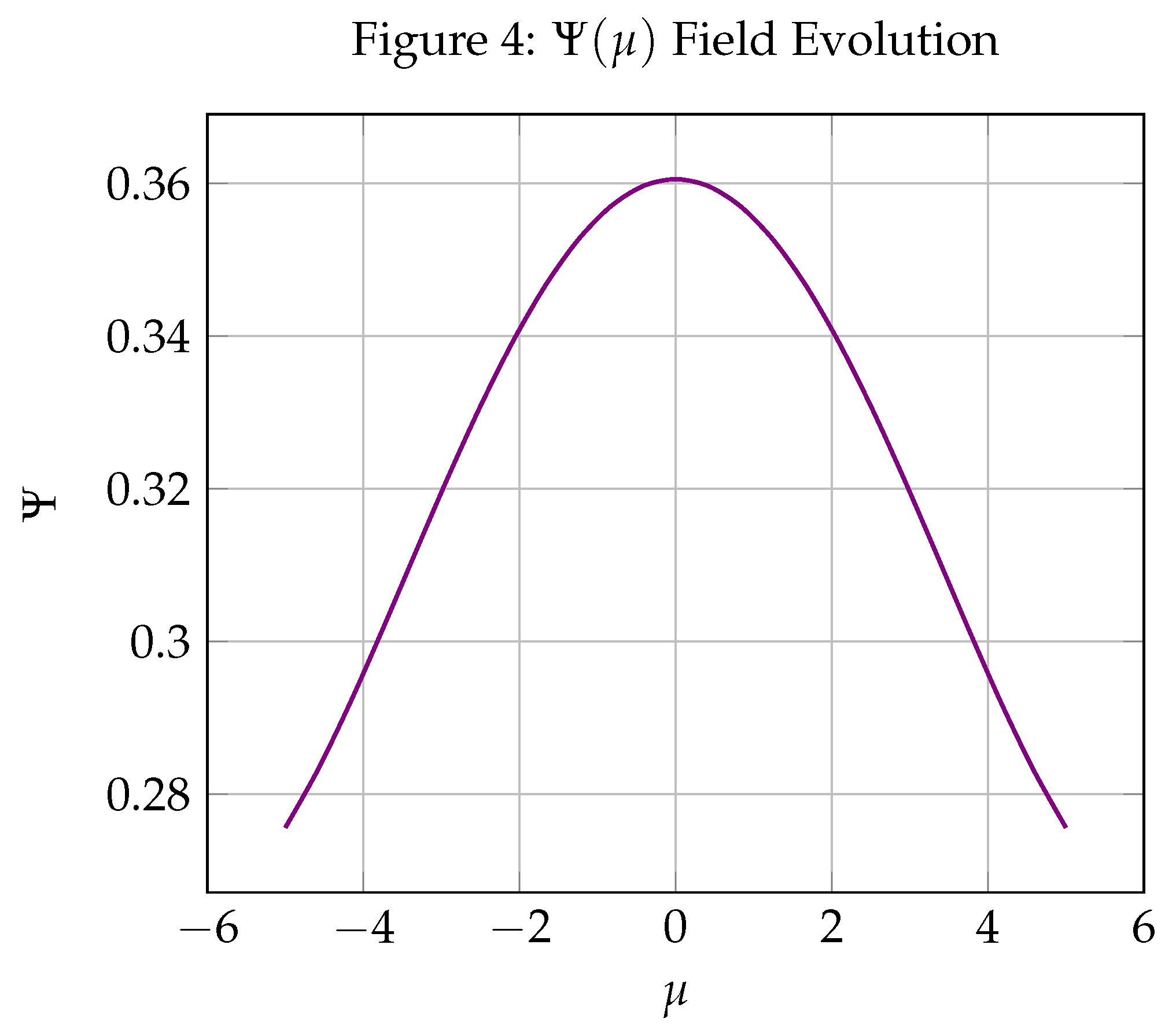
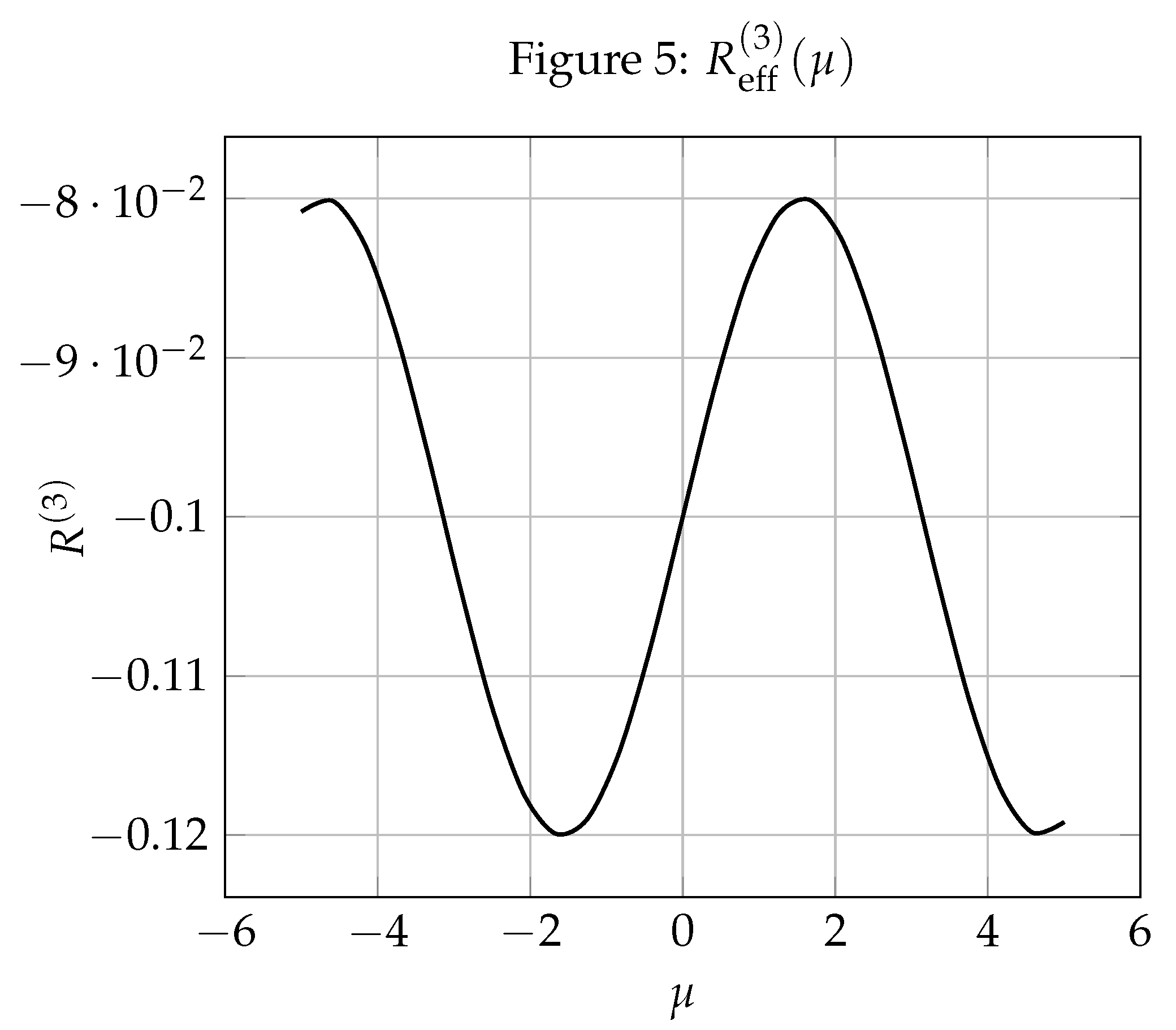
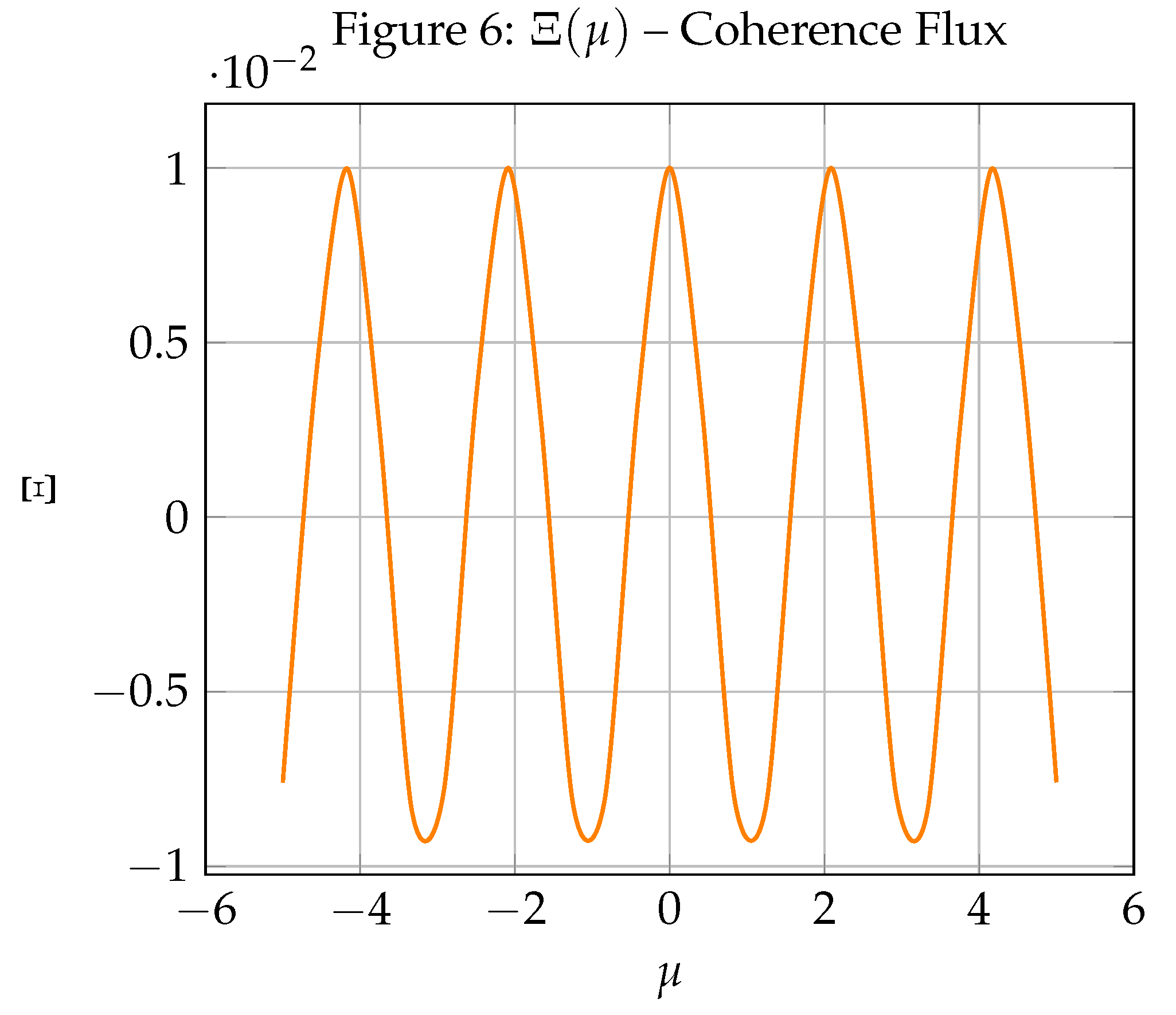
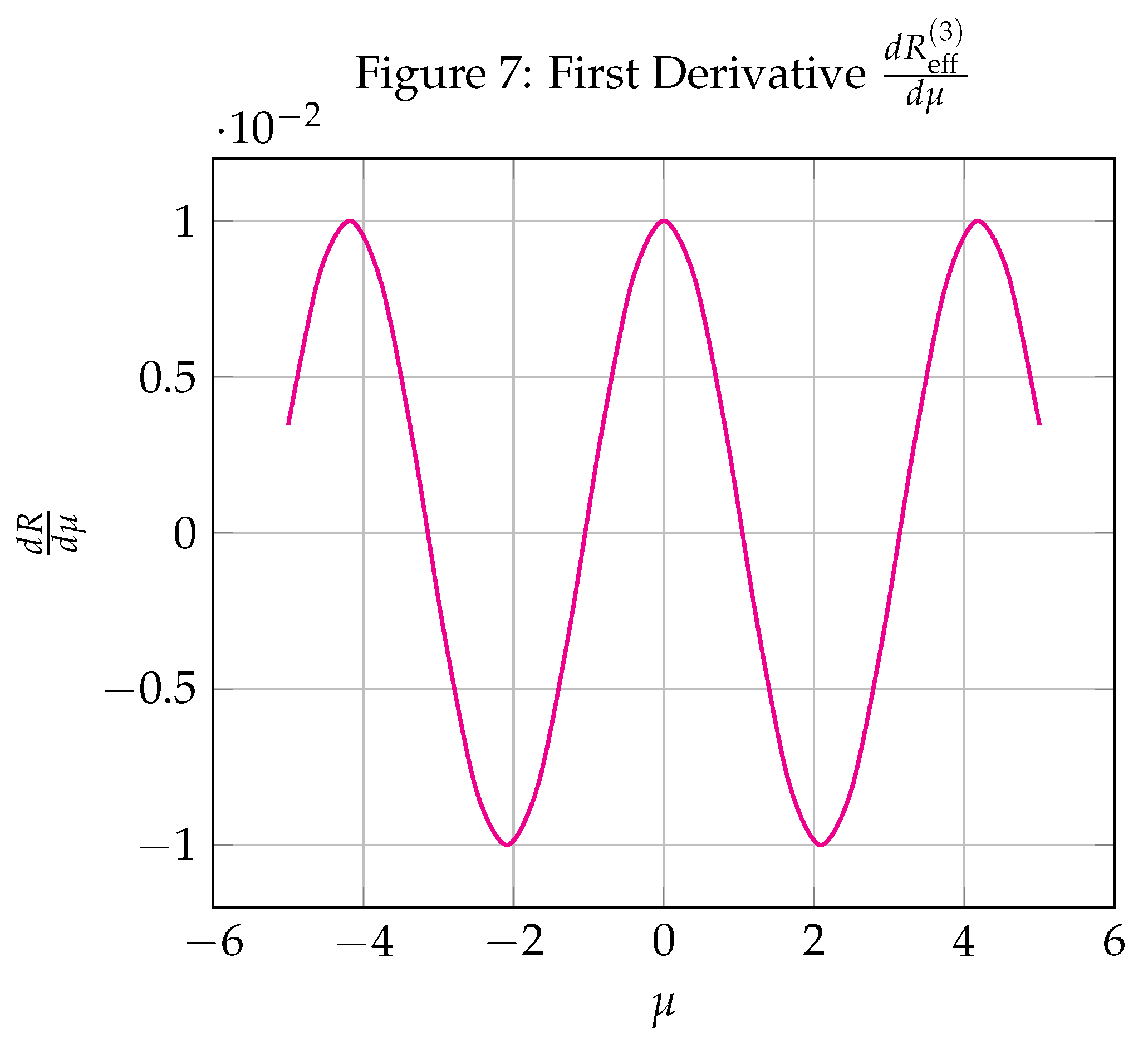
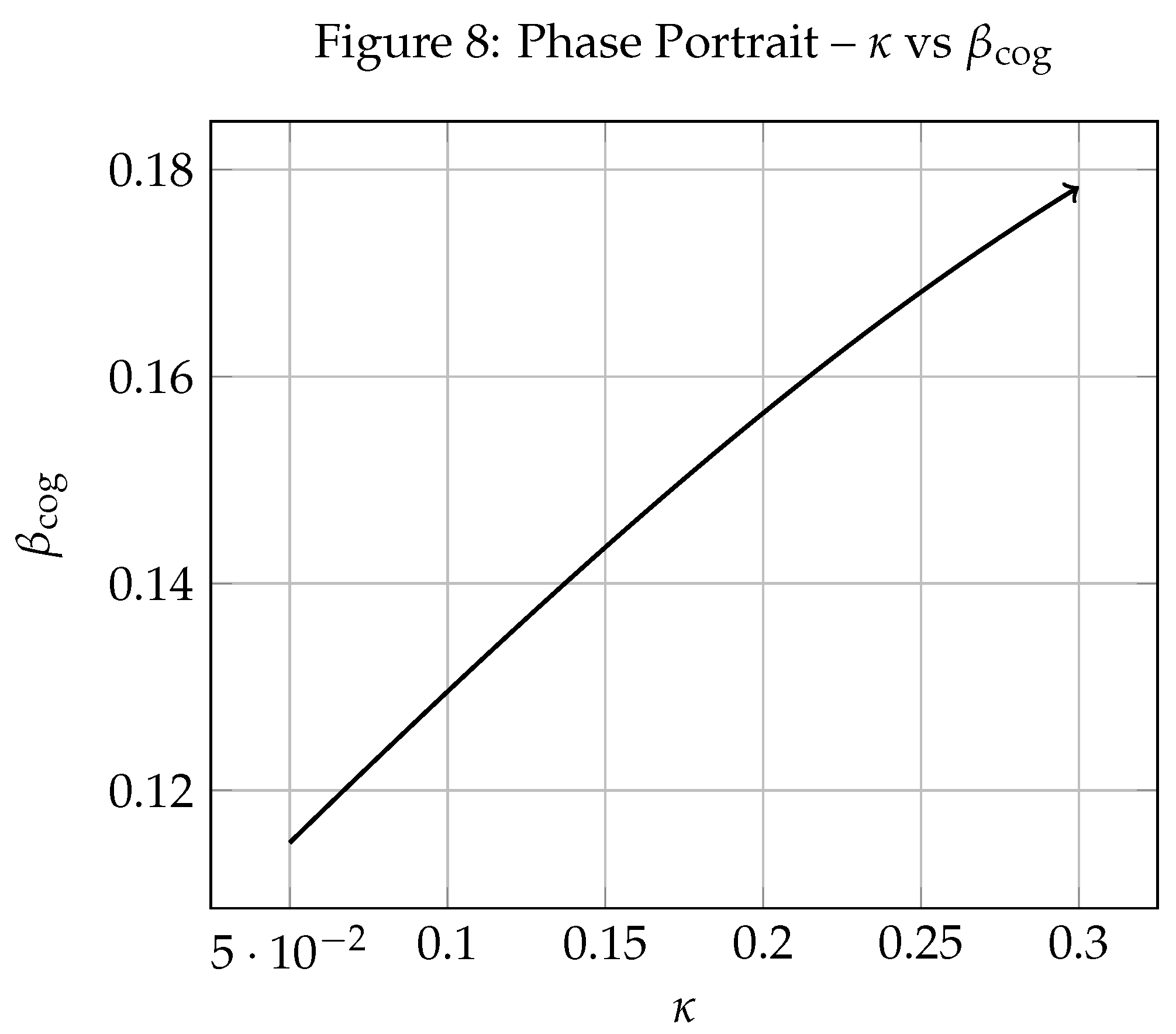
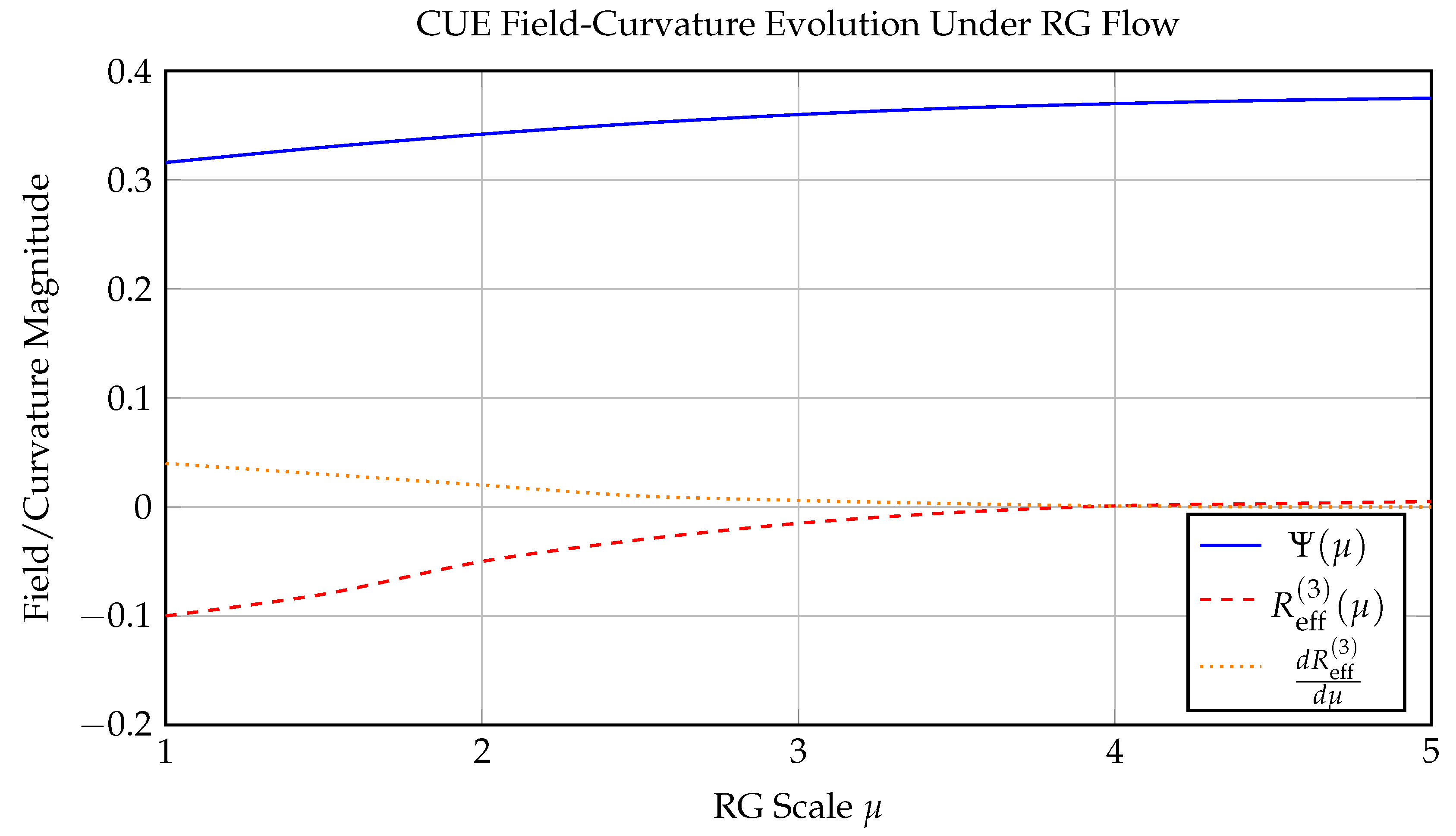
Appendix B: Numerical Computation Summary
- All results correspond to numerically stable points derived from interpolated RG flow data.
- Quantities involving , , and were computed assuming constant , , and calibration constants normalized to unity for model simplification.
- The eigenvalues suggest a saddle-type fixed point with one stable and two unstable directions.
Appendix C: Theoretical Extensions for Experimental and Gravitational Impact
Appendix C.1 Dimensional Analysis in Planck Units
Appendix C.2 Tensor Embedding of the Ψ Field
Appendix C.3 Experimental Proxy Candidates
- Proxy for : Coherence amplitude or phase in quantum optical fields; e.g., temporal width of interference fringes in Bose–Einstein condensates (BECs) or squeezed light states.
- Proxy for : Inverse correlation length in topological insulators or curvature defect density in metamaterials.
- Proxy for : Von Neumann entropy in entangled qubit arrays, or thermodynamic entropy change in near-critical superfluid transitions.
- RG scale : System temperature or control parameters (pressure, magnetic field) used to tune coherence and entanglement in material systems.
Appendix D: Numerical Simulation Strategy for Tensorial Coherence Field
Appendix D.1 Tensor Field Definition and Initialization
- evolves via the CUE flow equations.
- are orthonormal field basis vectors sampled across spacetime grid points.
- is a 4D coordinate grid over a compact domain (e.g., , ).
D.2 Discretization Scheme
- for temporal and spatial indices.
- , sampled logarithmically or linearly depending on the RG sensitivity.
D.3 Evolution Equation for Ψ b a
- are effective connection coefficients (e.g., from curvature gradients),
- is the covariant derivative approximated via central differences or spectral methods,
- The last term encodes coherence–curvature feedback.
D.4 Simulation Pipeline
- Initialize and using normalized Gaussian or sinusoidal modes.
- Evolve via the CUE differential equation system.
- Compute at each scale using the updated and field basis vectors.
- Apply curvature feedback via the evolution equation in D.3.
- Extract scalar contraction and plug into curvature equation .
- Repeat until fixed point or stabilization threshold is reached.
D.5 Observable Outputs
- Scalar trace (drives curvature),
- Anisotropic coherence spectrum (eigenvalues of ),
- Tensor norms (used in entanglement interactions),
- Tensor entropy (for holographic comparisons).
D.6 Software and Implementation Note
- NumPy + Numba for fast CPU-based tensor operations.
- JAX or TensorFlow for GPU acceleration and autodiff.
- Qiskit for mapping tensors into qubit-encoded matrices for quantum simulation.
Appendix E: Simulation Pseudocode for Tensorial CUE Evolution
- All coupling flows and tensor updates are performed within the RG loop.
- Tensor contractions yield scalar curvature-driving quantities.
- Covariant derivatives are approximated using finite differences or spectral methods.
- Scalar invariants , , and can be computed after the loop as diagnostics.
References
- Ambrosius, K. (2025). The Collective Unified Equation (CUE): A Theoretical Integration of Coherence, Curvature, and Consciousness.
- Weinberg, S. (1979). Ultraviolet divergences in quantum theories of gravitation.
- Wetterich, C. (1993). Exact evolution equation for the effective potential. Phys. Lett. B, 301, 90–94.
- Padmanabhan, T. (2014). Emergent gravity paradigm: recent progress.
- Jacobson, T. (1995). Thermodynamics of spacetime: The Einstein equation of state. Phys. Rev. Lett., 75, 1260.
- Verlinde, E. (2011). On the origin of gravity and the laws of Newton. JHEP, 04, 29.
- Zurek, W. H. (2003). Decoherence and the transition from quantum to classical. Rev. Mod. Phys., 75, 715.
- Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information.
- Kiefer, C. (2007). Quantum Gravity. Oxford University Press.
- Srednicki, M. (2007). Quantum Field Theory. Cambridge University Press.
- Jaynes, E. T. (1957). Information theory and statistical mechanics. Phys. Rev., 106, 620.
- Gielen, S., & Turok, N. (2016). Perfect quantum cosmological bounce. Phys. Rev. Lett., 117, 021301.
- OpenAI. (2023). GPT-based Symbolic and Numerical Reasoning Frameworks.
- SciPy Team. (2023). Available online: https://scipy.org.
- SymPy Team. (2023). Available online: https://sympy.
- Matplotlib & NumPy Teams. (2023). Available online: https://numpy.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




