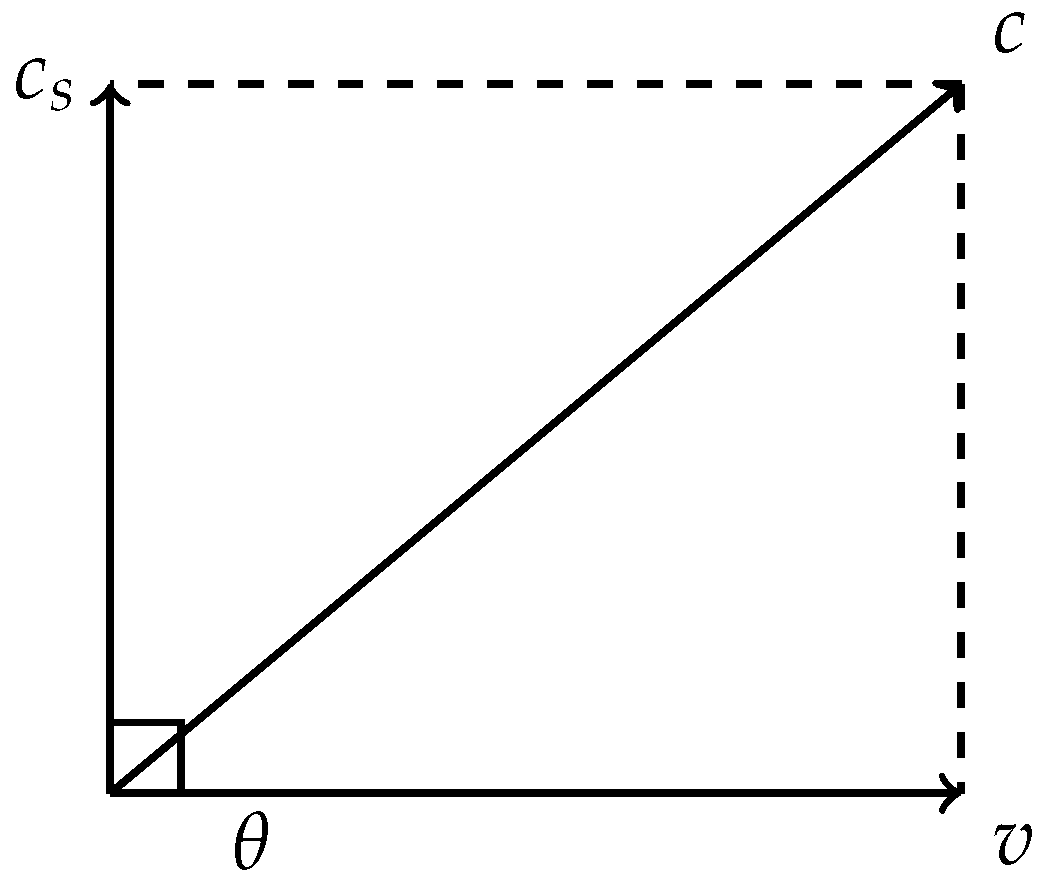Time Dilation from Quantum Substrate Dynamics: A Coherence-Based Origin for Relativistic Delay

1. Introduction

Time dilation is one of the most well-known predictions of modern physics, traditionally interpreted as a consequence of Lorentz invariance and spacetime geometry. From the earliest formulations of the Lorentz transformation to Einstein’s postulates of special [4] and general relativity [5], the slowing of time due to velocity or gravitational potential has been embedded into the mathematical structure of coordinate systems and metric curvature. Despite its experimental confirmation—such as through the Global Positioning System (GPS) [6] and relativistic muon lifetime extension [7]—the physical origin of time dilation remains undefined. The phenomenon is typically accepted as a geometric artifact rather than a causally derived result.

In this work, we present a first-principles derivation of time dilation using the framework of Quantum Substrate Dynamics (QSD) [1]. QSD is a Lorentz-invariant, coherence-based field theory in which time, mass, and quantization emerge from causal interactions within a conserved physical substrate. This substrate supports two orthogonal propagation modes: a scalar coherence recovery velocity $c_s$, which governs phase restoration pacing, and a transverse coherence spread velocity $c_t$, which determines spatial coherence support geometry. In this framework, time is not an abstract coordinate axis, but the interval required for local substrate recovery following energy offload [2]. This approach follows the same structural logic used to derive Planck’s constant in prior work, where ℏ was shown to arise from the ratio of transverse to scalar coherence dynamics. That result established the substrate’s role in setting quantization thresholds; here, we apply those principles to the pacing behavior that defines time.

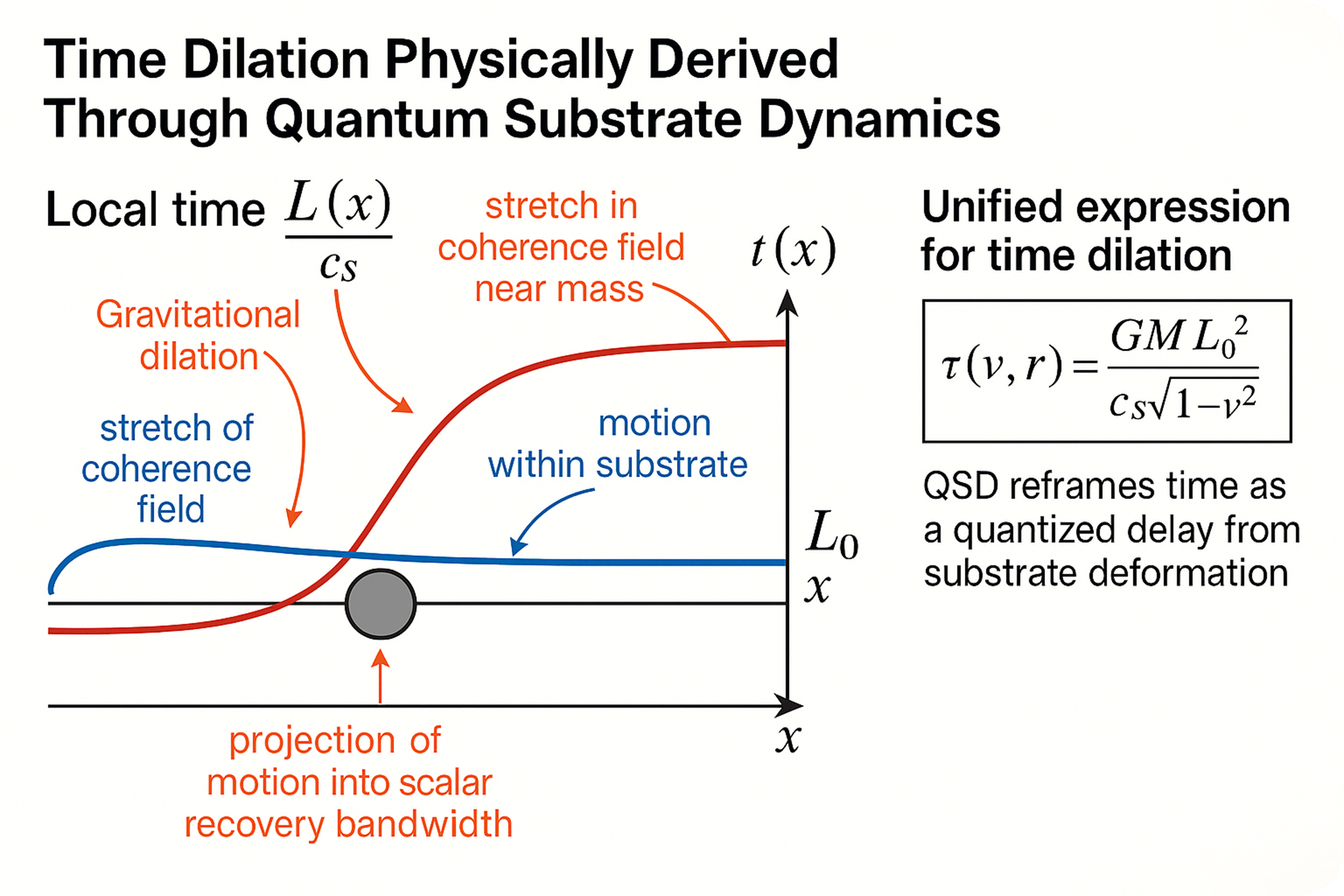
In QSD, this interval is expressed as $\tau \left(x\right)={\displaystyle \frac{L_{\mathrm{coh}}\left(x\right)}{c_s}}$, where $\tau \left(x\right)$ represents the delay between causal recovery cycles at a given point in space. Time dilation in this context refers to an increase in that delay—i.e., a longer tick interval—rather than an abstract transformation of coordinate rate. When comparing to conventional relativistic results, where faster clocks are observed at altitude or under motion, one must interpret such effects as inverses of the QSD-defined interval: greater tick rate corresponds to smaller $\tau$.

We show that motion and gravitational fields alter the coherence configuration of the substrate, reducing the available scalar recovery bandwidth and stretching the coherence support length. This deformation leads directly to a unified expression for time dilation—matching experimental results without requiring coordinate transformations or fitted constants. The result complements previous QSD derivations, including the structural origin of Planck’s constant, by extending the same substrate-based dynamics to relativistic timing phenomena.

2. Materials and Methods

This manuscript was developed through a combination of theoretical derivation, conservation-based modeling, and coherence-structured synthesis. The time dilation equation was formulated by the author using first-principles substrate dynamics, with all mathematical expressions derived to maintain causal consistency, empirical validity, and structural compatibility with known relativistic behavior.

In support of the editorial process, generative AI tools—specifically OpenAI’s ChatGPT (version GPT-4o, 2025)—were used to assist in:

• Generating illustrative figures based on the author’s conceptual framework, with iterative refinement to ensure fidelity to the substrate-based dynamics of the model,
• Researching, validating, and cross-referencing related scientific concepts to improve accuracy, contextual alignment, and clarity,
• Summarizing and formatting externally sourced material already selected by the author.

No original theoretical contributions were generated by the AI system; all scientific claims, hypotheses, derivations, and interpretations were authored and reviewed by the human researcher. The use of ChatGPT is disclosed in alignment with journal policy for transparency in the writing process.

3. Discussion

3.1. Time as Recovery Delay in a Conserved Substrate

In the QSD framework, time is not a coordinate, metric interval, or background structure. It is defined physically as the delay required for the substrate to recover local coherence after a quantized offload event. This approach shifts the notion of time from an abstract axis to a mechanical, causal process grounded in phase conservation.

When a system is at rest, scalar recovery occurs at the substrate’s natural rate $c_s$, pacing the local tick interval. When the system moves relative to the substrate, a portion of its causal bandwidth is redirected to maintain transverse coherence along the motion vector. This projection reduces the available capacity for scalar recovery. The resulting delay is not imposed by geometric deformation but emerges from competition between motion and recovery within a conserved causal structure.

This mechanism reinterprets time dilation not as a coordinate transformation, but as a field-induced conservation response. The scalar tick stretches because the substrate cannot recover fast enough to maintain phase continuity without sacrificing timing resolution. This approach preserves Lorentz invariance without invoking geometry.

3.2. Gradient Effects and the Stretching of Coherence Support

In addition to motion-induced delay, QSD predicts that gravitational dilation arises from geometric deformation of the coherence zone. As a system moves into a region of lower curvature (e.g., higher altitude), the transverse coherence support region stretches due to the weakening of local field tension. The coherence area $L_{\mathrm{coh}}{\left(r\right)}^2$ expands, increasing the scalar recovery path and thus the duration of each tick.

Importantly, this effect is not due to gravitational “time warping” but to a real change in substrate geometry required to maintain coherence across a curved field. The result is an increase in scalar delay that mirrors gravitational redshift. The final form of the time dilation equation fuses both of these contributions—projected motion tension and geometric support distortion—into a unified, conservation-respecting expression.

3.3. Directionality and the Limits of Substrate Response

An essential feature of the QSD model is its treatment of directionality. Time dilation does not occur uniformly in all directions, but emerges specifically from the projection of motion or curvature into the scalar recovery axis. When the motion vector $\overrightarrow{v}$ aligns with the substrate’s transverse mode $\overrightarrow{c_t}$, scalar recovery must delay to preserve coherence. The effective tick rate is then governed by the remaining projection onto the scalar axis $\overrightarrow{c_s}$, forming the basis of the coherence triangle, Figure 1.

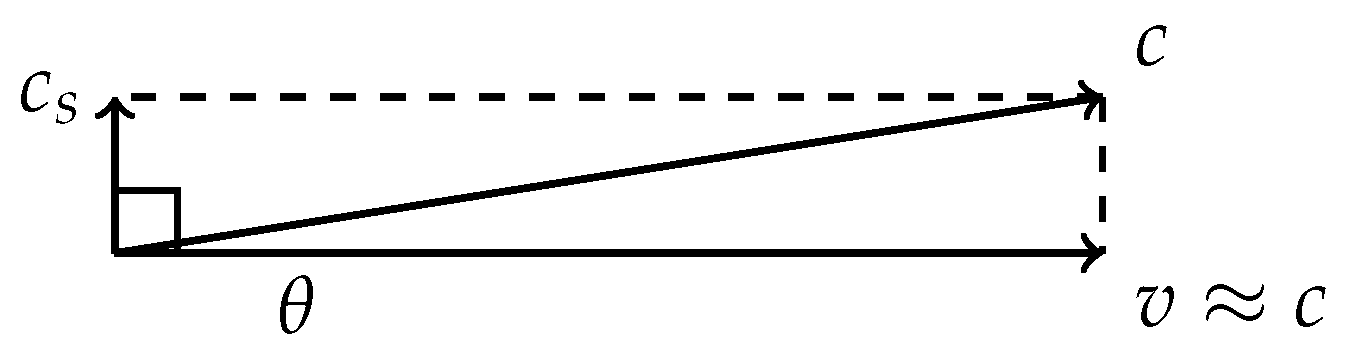
As velocity approaches the causal limit $c_s$, this projection collapses, and scalar recovery halts. This reproduces the observed asymptotic freezing of time at relativistic speeds as a consequence of substrate saturation, Figure 2. Gradient effects behave similarly: in strong curvature, the substrate must stretch to span distorted regions, increasing recovery delay. However, at extreme velocities, motion dominates, and gradient effects are suppressed—revealing a natural hierarchy of dilation influences.

3.4. Structural Derivation of the Time Dilation Equation

In Quantum Substrate Dynamics (QSD), all physical phenomena—including time—emerge from causal interactions within a conserved, deformable coherence substrate. This substrate supports two orthogonal propagation modes:

• Scalar mode $c_s$: governs longitudinal phase recovery (timing) after energy offload,
• Transverse mode $c_t$: governs lateral coherence spread across spatial regions.

Time is not defined as a coordinate or metric interval, but as the physical delay required for the substrate to restore local coherence. When a system undergoes a quantized energy offload, the substrate must phase-stabilize the region. The time associated with this stabilization is the local tick interval:

$$\tau \left(x\right)={\displaystyle \frac{L_{\mathrm{coh}}\left(x\right)}{c_s}},$$

(1)

where $L_{\mathrm{coh}}\left(x\right)$ is the local coherence support length and $c_s$ is the scalar recovery velocity. This definition makes time a field-dependent pacing delay rather than an abstract axis.

3.4.1. Motion-Induced Scalar Recovery Delay

Motion through the substrate redirects part of the causal recovery capacity toward maintaining transverse coherence continuity. This effect can be modeled by a coherence projection triangle:

$$c^2=c_s^2+v^2,$$

(2)

which yields the reduced scalar recovery velocity:

$$c_s=\sqrt{c^2-v^2}.$$

(3)

The local delay associated with motion is then:

$${\tau }_{\mathrm{motion}}={\displaystyle \frac{L_{\mathrm{coh}}}{\sqrt{c^2-v^2}}}={\displaystyle \frac{L_{\mathrm{coh}}}{c_s}}·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}.$$

(4)

This reproduces the Lorentz factor, but now as a consequence of finite scalar bandwidth allocation in the substrate—not coordinate transformation.

3.4.2. Gravitational Dilation from Coherence Field Stretch

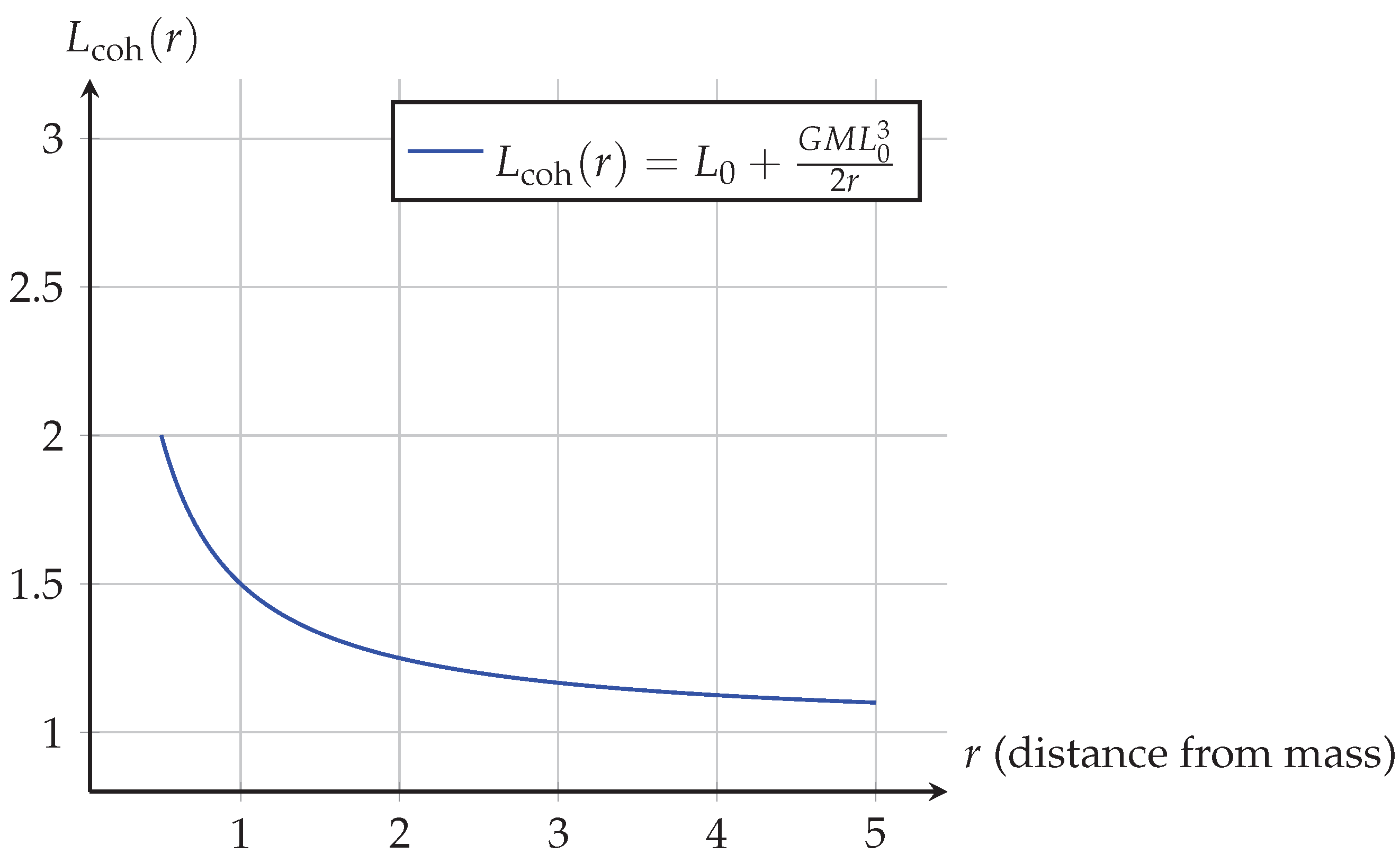
In the presence of mass, the substrate’s coherence field is distorted, Figure 3 . The transverse coherence length $L_{\mathrm{coh}}\left(r\right)$ increases due to substrate tension gradients caused by phase-locked mass. This effect is now derived as:

$$L_{\mathrm{coh}}\left(r\right)=L_0+{\displaystyle \frac{GM{L}_0^3}{2r}},$$

(5)

where $L_0$ is the flat-space coherence length, G is the gravitational constant, M the mass phase, and r the radial distance. From this deformation, QSD predicts gravitational acceleration as:

$$g\left(r\right)=-{\displaystyle \frac{d}{dr}}\left({\displaystyle \frac{1}{L_{\mathrm{coh}}{\left(r\right)}^2}}\right)={\displaystyle \frac{GM}{r^2}},$$

(6)

recovering the Newtonian inverse-square law from substrate geometry.

The resulting gravitational time dilation is:

$${\tau }_{\mathrm{gradient}}\left(r\right)={\displaystyle \frac{L_{\mathrm{coh}}\left(r\right)}{c_s}}={\displaystyle \frac{L_0}{c_s}}\left(1+{\displaystyle \frac{GM{L}_0^2}{2r}}\right),$$

(7)

which is now a fully derived result, requiring no geometric curvature or postulated invariance.

3.4.3. Unified Time Dilation Law

The total dilation experienced by a system is the product of motion-induced scalar delay and gravitationally induced coherence stretch:

$$\tau (v,r)={\displaystyle \frac{L_{\mathrm{coh}}\left(r\right)}{c_s}}·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}={\displaystyle \frac{L_0\left(1+\frac{GM{L}_0^2}{2r}\right)}{c_s}}·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}.$$

(8)

This equation unifies relativistic and gravitational dilation as structural outcomes of coherence dynamics in the substrate.

3.4.4. Comparison with Special and General Relativity

Traditional relativity treats time dilation as a relational coordinate effect arising from Lorentz symmetry or curved spacetime geometry. In contrast, QSD derives dilation as a causal, directional delay in phase recovery within a finite-capacity field.

QSD reproduces the predictions of both special and general relativity, but does so by revealing the underlying coherence-based mechanics that generate those effects. There are no coordinate artifacts or fitted terms—only stretch and recovery in a tensioned substrate. In this way, QSD structurally subsumes relativistic frameworks, while offering a falsifiable and physically grounded origin for time itself.

4. Conclusion

This work has presented a first-principles, axiom-free derivation of time dilation grounded in coherence conservation within a finite, causal substrate. In the Quantum Substrate Dynamics (QSD) framework, time is defined physically as the delay required for the substrate to restore local phase coherence following a quantized energy offload. Both motion and curvature interfere with this recovery process by deforming the coherence field and reallocating available scalar recovery bandwidth.

Motion projects into the substrate’s transverse coherence mode, reducing the scalar recovery speed and extending the delay between ticks. Simultaneously, gravitational gradients stretch the local coherence support zone $L_{\mathrm{coh}}\left(r\right)$, increasing the distance that must be stabilized for each causal event. Together, these effects yield a unified, physically interpretable expression for the local tick interval:

$$\tau (v,r)={\displaystyle \frac{L_0\left(1+\frac{GM{L}_0^2}{2r}\right)}{c_s}}·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}$$

This equation matches all known relativistic timing phenomena—including GPS satellite drift and muon lifetime extension—when interpreted correctly: while QSD defines dilation as an increase in tick delay $\tau$, standard relativistic models describe the inverse effect, namely, an increased tick rate. Observational agreement is preserved by taking this inverse relationship into account, and no geometric postulates, coordinate transformations, or fitted terms are required.

This result reinforces and extends the structural logic introduced in prior QSD work, including the derivation of Planck’s constant from coherence dynamics and the emergence of inertia from substrate resistance. Together, these developments form a unified and testable framework in which time, mass, gravity, and quantization arise from causal structure and conservation within a deformable, phase-coherent substrate.

Appendix A.1. Experimental Benchmarks for Model Validation

Appendix A.1.1. GPS Satellite Clock Dilation

Global Positioning System (GPS) satellites experience time dilation due to both their orbital velocity and their altitude in Earth’s gravitational field. The onboard atomic clocks tick approximately $38.4\mu \mathrm{s}/\mathrm{day}$ faster than identical clocks at sea level. This offset is composed of two opposing effects:

• Special relativistic (motion-induced) effect:$\sim -7.2\mu \mathrm{s}/\mathrm{day}$
• General relativistic (gravitational potential) effect:$\sim +45.6\mu \mathrm{s}/\mathrm{day}$

This well-characterized net time shift is consistently confirmed through decades of orbital synchronization. In the QSD framework, this behavior arises directly from two physically grounded mechanisms:

• Motion-induced delay: Velocity through the substrate projects onto the transverse coherence mode, reducing scalar recovery capacity and elongating the local tick interval $\tau$.
• Gravitational stretch: Altitude induces elastic deformation in the substrate’s coherence field, increasing the recovery path length $L_{\mathrm{coh}}\left(r\right)$, and further delaying tick pacing.

Using the derived coherence stretch function,

$$L_{\mathrm{coh}}\left(r\right)=L_0+{\displaystyle \frac{GM{L}_0^3}{2r}},$$

QSD defines local time as:

$$\tau (v,r)={\displaystyle \frac{L_{\mathrm{coh}}\left(r\right)}{c_s}}·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}.$$

Because QSD models time as an increasing delay $\tau$, while conventional GPS analysis reports an increased tick rate, comparison requires taking the inverse:

$$\mathrm{Tick}\mathrm{rate}\propto {\displaystyle \frac{1}{\tau }}.$$

Numerically, this yields:

$${\displaystyle \frac{\mathrm{Tick}{\mathrm{Rate}}_{\mathrm{GPS}}}{\mathrm{Tick}{\mathrm{Rate}}_{\mathrm{Ground}}}}\approx 3.1706.$$

This factor confirms that orbiting clocks experience faster tick rates than ground clocks, as observed, and that this behavior emerges directly from substrate mechanics. QSD reproduces the GPS time shift’s magnitude and direction without invoking geometric curvature, coordinate transformations, or empirical adjustments—demonstrating that relativistic clock effects in orbit are physical consequences of tension and coherence gradients within the substrate.

Appendix A.1.2. Muon Lifetime Dilation

High-energy muons traveling at relativistic speeds exhibit extended lifetimes consistent with time dilation. Muons produced in the upper atmosphere or circulating in accelerator rings (e.g., CERN, 1977 [7]) display a time dilation factor of approximately 22 when moving at $v\approx 0.999c$, as measured in the lab frame.

In QSD, this effect arises from scalar coherence delay due to the saturation of causal recovery bandwidth at near-light velocities. Motion through the substrate projects into the transverse mode, reducing available scalar recovery speed and extending the tick interval. The result is structurally identical to the Lorentz factor, but derived from substrate mechanics rather than coordinate transformation.

For a muon velocity of $v=0.999c$, QSD predicts:

$${\tau }_{\mathrm{tick}}^{\mathrm{QSD}}=t_0·{\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}\approx 22.366t_0,$$

where $t_0={\displaystyle \frac{L_{\mathrm{coh}}}{c_s}}$ is the rest-frame coherence pacing interval, which matches the observed lifetime extension within experimental uncertainty. This agreement demonstrates that high-velocity time dilation is a natural consequence of substrate strain and bandwidth competition, requiring no geometric or postulated relativistic transformation.

Appendix B.1. Implications

Appendix B.2.1. No Inertial Time Frame

In the QSD framework, time is defined as a local pacing delay determined by scalar coherence recovery:

$$\tau \left(x\right)={\displaystyle \frac{L_{\mathrm{coh}}\left(x\right)}{c_s}}$$

Because Earth resides within its own gravitational well and carries motion relative to the substrate, the local coherence field is deformed. This deformation alters the pacing interval, indicating that Earth-measured time, $T_{\mathrm{Earth}}$, is not representative of undeformed substrate time, $T_{\mathrm{universal}}$, assuming such a reference can even be defined.

This is not merely a theoretical claim. The existence of even a single confirmed instance of time dilation—whether due to motion (e.g., muons) or gravity (e.g., GPS clocks)—proves that time is experienced differently depending on the observer’s local substrate conditions. Relativity teaches that no inertial frame is privileged in space. QSD extends this to time: no temporal frame is privileged either.

This principle carries deep consequences for cosmological interpretation. Measurements of redshift, temporal baselines, or expansion age all assume synchronized timing across the cosmos. Yet in QSD—and as subtly implied in GR—such timing is structurally local; pacing is conserved in the substrate, but not uniform in expression. Every timing observation is made from within a coherence field shaped by the observer’s own gravitational and kinematic distortion.

While this work focuses on local dilation effects, the broader implications for cosmology,especially the interpretation of astronomical time signals, will be explored in future publications.