The Lorentzian Kernel as an Emergent Epistemic Envelope: Averaging, Resolution, and the Geometry of Distinguishability

1. Introduction

The Lorentzian (or Cauchy) kernel,

$$K\left(E\right)={\displaystyle \frac{E_0^2}{E_0^2+E^2}},$$

(1)

is a ubiquitous object in physics. It appears in quantum spectral line shapes, damped harmonic oscillators, signal filtering, and neural signal propagation. Often, it is introduced heuristically—as a consequence of finite lifetimes (via the uncertainty principle), as an ansatz for resonance behavior, or as a convenient low-pass filter in engineering contexts [4]. For a comprehensive review of line shape models and their empirical origins, see Demtröder [8]. For philosophical discussion of coarse-graining as an epistemic process, see Uffink’s “Compendium of the Foundations of Classical Statistical Physics” in the Philosophy of Physics volume [5].

Yet despite its universal presence, the Lorentzian kernel is rarely derived from first principles. It is typically treated as a dynamical approximation, not as a structural or epistemic consequence. (While entropy-based accounts of coarse-graining and profile broadening are well established in statistical mechanics and information theory [5,6,7], a direct structural derivation of the Lorentzian kernel as an epistemic envelope—emergent from entropy geometry—has not, to our knowledge, been given.)

Historically, the emergence of universal profiles like the Lorentzian has been viewed through the lens of coarse-graining and statistical modeling. In classical statistical mechanics, coarse-graining is seen as an epistemic procedure: microscopic states are averaged to obtain tractable macroscopic descriptions, as exemplified by Boltzmann’s kinetic theory [7]. In information theory, Shannon [6] formalized the limits of resolution as constraints on the transmission and recovery of information.

These perspectives treat uncertainty and profile broadening as artifacts of incomplete knowledge or environmental randomness. The standard interpretation of line shapes, for instance, attributes the Lorentzian to dynamical broadening—finite lifetimes or random fluctuations—rather than structural limits imposed by the geometry of resolution itself.

Other universal kernels, such as the exponential or Voigt profiles [8,9], are similarly employed as pragmatic models for decay and line broadening. However, their use remains primarily phenomenological, with limited attention paid to the deeper geometric or epistemological basis for their ubiquity.

By contrast, our approach derives the Lorentzian from entropy geometry directly, interpreting it as a universal form that arises when resolution becomes granular and further distinction is structurally prohibited.

In this work, we offer a different interpretation. We propose that the Lorentzian kernel emerges from the internal structure of entropy geometry itself, specifically within the TEQ (Total Entropic Quantity) framework [2]. We show that:

• Gaussian suppression of high-frequency paths, as dictated by entropy-weighted actions, leads to Lorentzian profiles when averaged over unresolved entropy scales (see Section 3 and Appendix A).
• The kernel in Eq. (1) is not merely a reflection of physical damping, but a boundary structure in entropy geometry—a marker of saturated distinguishability.

A recent minimalist derivation of the Lorentzian kernel from axiomatic principles [1] highlights its mathematical universality, but does not address its structural emergence from entropy-based constraints. By contrast, our approach derives the Lorentzian from entropy geometry directly, interpreting it as a universal form that arises when resolution becomes granular and further distinction is structurally prohibited.

We argue that the Lorentzian form should be understood as an epistemological envelope: it encodes how resolution fails when entropy curvature prohibits further refinement. It expresses a soft limit of knowability: the rate at which information fades, not due to randomness, but due to structural resolution constraints.

This interpretation leads to the central thesis:

The Lorentzian kernel is the epistemological exponent of uncertainty.

It arises wherever resolution is fundamentally granular and entropy geometry prevents further distinction. Rather than modeling stochastic decay, the Lorentzian encodes a deterministic epistemic horizon—a limit intrinsic to how structure is stabilized under entropy flow.

We elaborate this thesis by:

• Deriving Eq. (1) from an averaged Gaussian ensemble in Section 3,
• Interpreting the result as a transition from Gaussian to Lorentzian regimes in Section 4 and Section 5,
• Exploring the broader conceptual implications in epistemology, spectral theory, and information-limited systems.

We conclude that the Lorentzian kernel is not a physical artifact, but a universal boundary object in theories where entropy governs resolution (see also Figure 1 for a schematic comparison). The appendix provides a rigorous derivation of the kernel via superposition (Appendix A) and suggests generalizations to other uncertainty kernels.

2. Entropy Geometry and Entropic Path Weighting

The TEQ framework begins not from Hilbert space or canonical quantization, but from an entropy-weighted variational principle. A key structural object is the effective action:

$$S_{\mathrm{eff}}\left[\varphi \right]=\int dt\left(L(\varphi ,\dot{\varphi })-i\hslash \beta g(\varphi ,\dot{\varphi })\right),$$

(2)

where $L(\varphi ,\dot{\varphi })$ is the usual Lagrangian, $g(\varphi ,\dot{\varphi })$ is the entropy flux functional, and $\beta$ is a dimensionless inverse-resolution parameter related to the observer’s distinguishability scale. This structure is derived as a consequence of the Minimal Principle and entropy geometry, yielding both quantum dynamics and spacetime structure from a unified variational foundation (see [2], Sec. 2, App. A, and App. B).

The second term in Eq. (2) modulates the amplitude of each path based on its entropy cost: high-entropy (or low-resolution) paths are favored; highly curved or rapidly oscillating paths are suppressed.

Riemannian Entropy Geometry.

When entropy geometry is Riemannian, the entropy flux functional takes the quadratic form (see [2], App. B):

$$g(\varphi ,\dot{\varphi })={\displaystyle \frac{1}{2}}{G}_{ij}\left(\varphi \right){\dot{\varphi }}^i{\dot{\varphi }}^j,$$

(3)

where $G_{ij}\left(\varphi \right)$ is an emergent entropy-induced metric encoding local distinguishability. This expression parallels kinetic energy in classical mechanics, but here arises from the structure of entropy flow across configuration space.

Substituting Eq. (3) into the entropy-weighted path integral,

$$\mathcal{A}\left[\varphi \right]\propto exp\left(-\beta \int dt{G}_{ij}{\dot{\varphi }}^i{\dot{\varphi }}^j\right),$$

and expanding $\varphi \left(t\right)={\sum }_E{a}_E{e}^{iEt}$ shows that high-frequency components are exponentially suppressed. This yields the Gaussian kernel in frequency space,

$$G\left(E\right)=exp(-\gamma E^2),$$

(4)

which characterizes systems with continuous resolution and smoothly curved entropy geometry.

However, this Gaussian suppression is idealized: it assumes that the resolution structure is uniform and fine-grained. In physical systems where resolution is bounded or distinguishability saturates, such suppression must itself be corrected or averaged. In Section 3, we explore how these corrections give rise to Lorentzian profiles via superpositions over fluctuating entropy scales.

The shift from Eq. (4) to the Lorentzian form in Eq. (1) thus marks a structural transition: from ideal resolution to entropy-limited distinguishability. This transition will be interpreted not merely computationally, but epistemologically—as a deformation of resolvability under entropy curvature.

3. Emergence of the Lorentzian via Entropy Averaging

The Gaussian kernel (4) derived from a Riemannian entropy geometry reflects a sharp, symmetric suppression of off-peak contributions. However, in systems where resolution is not uniform—for instance, where entropy curvature varies or internal scales are unresolved—this suppression is not absolute. Instead, the effective kernel must account for fluctuations in resolution scale.

Let us denote by s an internal (unresolved) entropy-dependent scale parameter. Then, instead of a single Gaussian kernel with fixed width, we consider a statistical superposition over widths:

$$K\left(E\right)={\int }_0^{\infty }exp(-s^2{E}^2)\rho \left(s\right)ds,$$

(5)

where $\rho \left(s\right)$ is a probability density function over entropy fluctuation scales. Physically, s can be interpreted as a local standard deviation associated with microscopic resolution.

Choice of Distribution.

We choose

$$\rho \left(s\right)=s{e}^{-s^2{E}_0^2},$$

(6)

which is normalized and sharply peaked around $s\sim 1/E_0$. Substituting Eq. (6) into Eq. (5), and changing variables to $u=s^2$, yields

$$K\left(E\right)\propto {\int }_0^{\infty }{e}^{-u(E^2+E_0^2)}du={\displaystyle \frac{1}{E^2+E_0^2}},$$

(7)

which reproduces the Lorentzian kernel of Eq. (1) (see Appendix A for details).

The choice of $\rho \left(s\right)$ is structurally justified: the form $\rho \left(s\right)=2E_0^{2}s{e}^{-s^2{E}_0^2}$ defines a Rayleigh distribution for the resolution scale s, arising when local entropy fluctuations are isotropic and uncorrelated. The Rayleigh law is also the maximum entropy distribution for a positive variable with fixed mean square. This minimal statistical assumption yields the Lorentzian kernel, while alternative distributions with exponential cutoffs produce similar qualitative behavior.

This result shows that the Lorentzian kernel generically emerges wherever entropy curvature varies or fine-grained resolution is lost. In such regimes, the superposition of entropy-weighted Gaussian modes produces a Lorentzian envelope, a soft transition profile that reflects coarse-graining over unstable or indistinguishable microstates, structurally equivalent to integrating

Interpretive Summary.

Equation (7) shows that the Lorentzian is not a dynamical artifact, but a structural consequence of fluctuating entropy resolution. The substitution of a fixed Gaussian by a distributional average reflects the fact that in granular entropy geometry, suppression is no longer sharply localized—but spread, structurally, into long tails. This shift marks the beginning of epistemic saturation, to be interpreted further in Section 4 and Section 5.

4. From Gaussian to Lorentzian: A Transition in Knowability

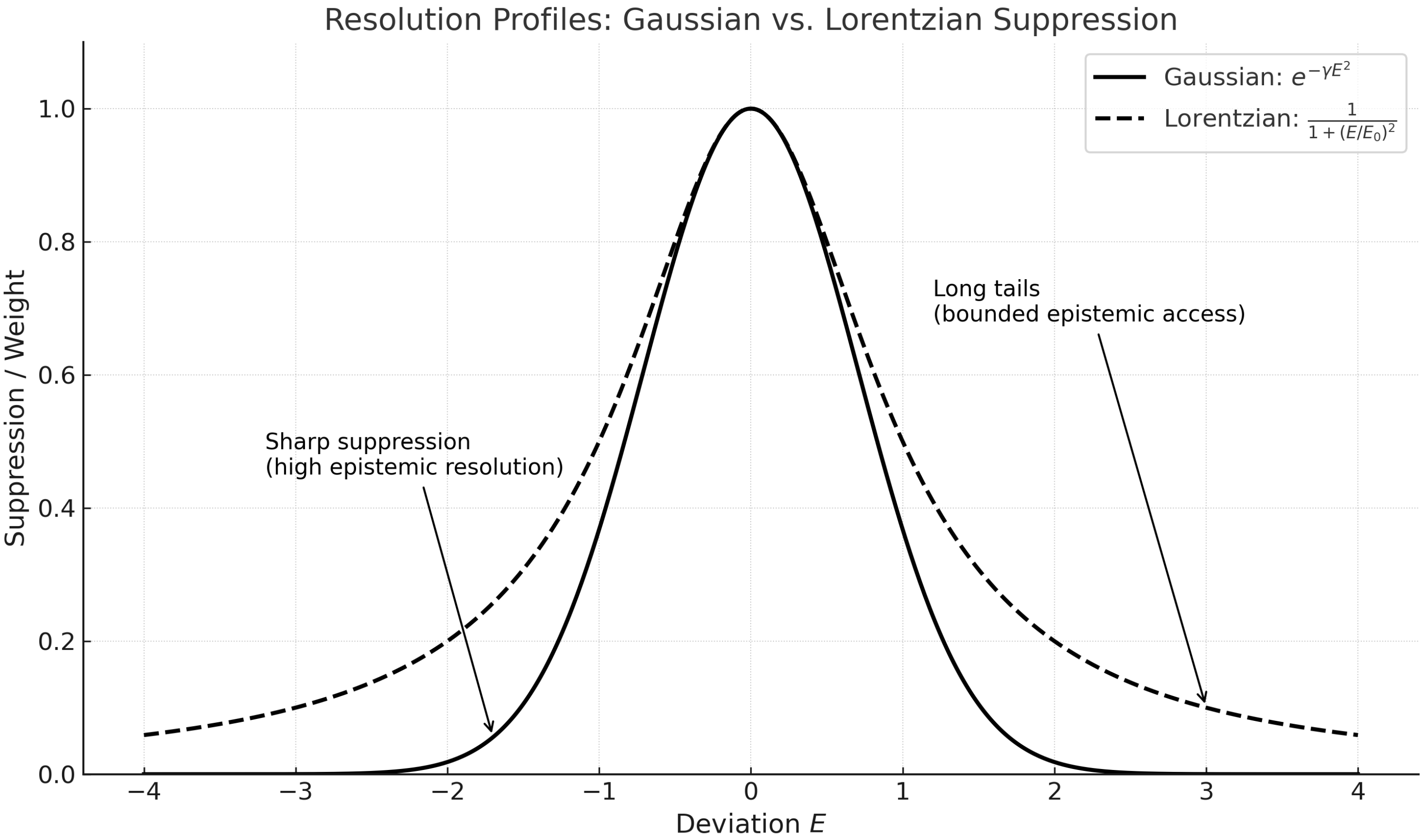
The structural difference between the Gaussian and Lorentzian kernels marks more than a shift in analytic form: it signals a transition in the geometry of discernability.

Gaussian Suppression: Localized Resolution

In the regime governed by continuous Riemannian entropy geometry (cf. Eq. (3)), suppression of path contributions is sharply localized. The resulting energy-space kernel,

$$G\left(E\right)=e^{-\gamma E^2},$$

decays rapidly and symmetrically, concentrating resolution tightly around $E=0$. This corresponds to a well-resolved regime: perturbations away from the mean are strongly penalized, and system behavior is localized both dynamically and spectrally.

Lorentzian Suppression: Spread Resolution and Soft Boundaries

By contrast, the Lorentzian kernel,

$$K\left(E\right)={\displaystyle \frac{1}{1+{(E/E_0)}^2}},$$

(8)

features slowly decaying tails and no sharply defined cutoff. It reflects a structure in which uncertainty does not simply grow with energy, but saturates: higher energy components are never completely excluded, but only gradually diminished. This corresponds to a regime of bounded distinguishability, where the resolution scale cannot be refined further, and distinctions blur into one another over soft boundaries.

The Epistemic Interpretation

This mathematical contrast encodes a deeper structural shift:

• The Gaussian kernel (4) describes a domain of high epistemic control—where the geometry supports precise localization, and entropy curvature allows stable distinctions.
• The Lorentzian kernel (8) emerges when that control fails: it describes the gradient of epistemic accessibility, not the mere presence of uncertainty.

In this sense, the Lorentzian is the universal envelope of soft resolution failure. It appears whenever entropy geometry no longer supports sharp distinctions, and where resolution—though still present—becomes structurally constrained.

Summary

The transition from Gaussian to Lorentzian form is not just analytical but geometric and epistemological. It reflects the saturation of distinguishability: a limit where structural information cannot be further refined. This transition, grounded in entropy curvature and resolution fluctuation, will be explored further in Section 5, where we interpret the Lorentzian as a boundary object in entropy geometry—the epistemological exponent of uncertainty.

In summary, the shift from a Gaussian to a Lorentzian profile signals more than a mathematical change: it marks the threshold where the ability to distinguish, predict, or control system behavior transitions from being limited by the system’s dynamics to being limited by the fundamental structure of resolution itself. The Gaussian regime reflects fine-grained, stable epistemic access; the Lorentzian regime encodes the onset of inherent indistinguishability, set not by noise or decay, but by the geometry of what can be resolved.

5. Granularity of Distinguishability

Figure 1 illustrates the contrasting profiles and epistemic interpretations of Gaussian versus Lorentzian suppression, visually summarizing the transition described above.

The preceding section revealed a structural transition from Gaussian to Lorentzian suppression profiles, corresponding to a shift from well-resolved to resolution-limited regimes. We now make this interpretation explicit by introducing the concept of granular distinguishability—a property of entropy geometry that bounds the scale at which structural resolution remains stable.

From Continuous to Granular Entropy Geometry

In an idealized Riemannian entropy geometry (cf. Eq. (3)), resolution is continuously scalable: the metric $G_{ij}\left(\varphi \right)$ allows, in principle, for arbitrarily fine discernment of trajectory curvature or energetic deviation.

However, in realistic systems:

• Entropy gradients may saturate at finite curvature.
• Resolution costs may diverge or flatten.
• The local entropy metric may break down into piecewise or non-smooth regions.

This behavior suggests a form of entropy geometry that is not smooth everywhere, but granular—supporting distinguishability only at discrete or bounded scales.

Structural Implications

When distinguishability is granular, the entropy-weighted suppression term in Eq. (2) no longer scales quadratically with E, and the Gaussian kernel (4) is no longer appropriate. Instead, superpositions over fluctuating resolution scales (see Eq. (5)) generate Lorentzian envelopes (Eq. (7)).

The result is structurally robust:

• Lorentzian profiles signal saturation in entropy curvature.
• Granularity acts as an effective coarse-graining over unresolved or indistinguishable states.
• This leads to suppression patterns with long tails and no sharp decay—mirroring what is empirically observed in many quantum and dissipative systems.

Geometric and Epistemic Interpretation

From a geometric point of view, the Lorentzian kernel encodes a “flattening” of entropy curvature: increasing energy deviation no longer corresponds to exponentially increasing suppression, but instead to a power-law decay of epistemic accessibility.

From an epistemological perspective, this expresses the fact that resolution is not unlimited: there exists a threshold beyond which further attempts at refinement do not yield new distinctions, but only diluted and unstable artifacts. As such, the Lorentzian is not just a spectral profile—it is a boundary marker between discernibility and structural blur.

Connection to Appendix A

The emergence of the Lorentzian kernel from Gaussian averaging (Appendix A) formalizes this intuition: the entropy-weighted path integral, when modulated by uncertainty in the resolution scale, produces a kernel that encodes not just physical damping, but fundamental limits to knowability. The tails of the Lorentzian are the tails of epistemic access—they do not vanish, but they do not resolve.

To recapitulate: once the geometry of entropy enforces a finite, granular scale of distinction, further refinement cannot yield additional knowledge. The Lorentzian kernel then stands as a boundary marker, a universal indicator of the point beyond which epistemic gain is structurally impossible, regardless of the dynamical details.

6. The Lorentzian as the Epistemological Exponent of Uncertainty

We are now in a position to articulate the central conceptual claim of this paper: that the Lorentzian kernel, derived structurally in Section 3 and interpreted geometrically in Section 5, functions as the universal envelope of epistemic limitation.

This has profound implications for the philosophy of physics, as the following remark clarifies:

A Structural Claim, Not a Metaphor

The statement

The Lorentzian kernel is the epistemological exponent of uncertainty

is not intended metaphorically. It asserts that the Lorentzian shape, Eq. (8)

$$K\left(E\right)={\displaystyle \frac{1}{1+{(E/E_0)}^2}}$$

emerges wherever information about system behavior is filtered through entropy geometry with bounded resolution. In this view, the kernel does not merely describe decay or noise; it expresses how uncertainty itself is structured when distinction becomes unstable.

Formal Roles of the Lorentzian

The Lorentzian kernel encodes:

• The rate at which epistemic access fades as deviation from a stable structure increases.
• The soft edge of resolution: unlike the Gaussian, which imposes sharp exclusion, the Lorentzian’s tails permit diminishing but persistent contribution.
• The epistemic horizon: it defines the observable bandwidth beyond which distinguishability dissolves into dispersion.

In information-theoretic terms, the Lorentzian may be interpreted as a saturation envelope of mutual information under entropy curvature constraints—where further energy or precision no longer enhances resolution, but only adds undistinguishable noise.

Comparison with the Gaussian Regime

As a contrast:

• The Gaussian kernel $G\left(E\right)=e^{-\gamma E^2}$ (Eq. ()) implies an exponential decay of uncertainty—a signature of systems where entropy geometry permits fine control.
• The Lorentzian kernel (Eq. (8)) implies a power-law decay—suggesting that uncertainty is no longer reducible, and that resolution granularity has structurally intervened.

This contrast corresponds to a shift from dynamically localized regimes to entropy-limited observational structure, as discussed in Section 4.

Implications for Measurement and Predictability

The Lorentzian profile expresses not merely the presence of noise, but a failure of resolution. Its tails represent modes that participate without being distinguished, and thus model situations where:

• Measurement ceases to resolve,
• Prediction becomes unstable,
• Quantization merges into decoherence or dissipation.

These are not stochastic failures, but structural ones—direct consequences of the entropy geometry’s bounded capacity to distinguish.

Epistemic Summary

We can now summarize the central structural insight of this paper:

The Lorentzian kernel is not a physical damping profile imposed by hand, but the emergent shape taken by irreducible uncertainty in entropy geometry. It marks the transition point where knowledge becomes indistinguishable from background.

This interpretation reframes the Lorentzian from a model of empirical phenomena to a structural object: a boundary kernel defined not by the dynamics of systems, but by the geometry of what can be resolved.

7. Applications and Broader Implications

The structural interpretation of the Lorentzian kernel as an epistemic envelope has direct implications across multiple domains. These applications not only illustrate the generality of the result, but also reveal how phenomena previously treated as empirical regularities may instead reflect fundamental limits of resolution imposed by entropy geometry.

7.1. Quantum Spectral Profiles

In quantum mechanics, the Lorentzian line shape arises in the context of finite-lifetime states—particularly in resonance phenomena and radiative decay. Conventionally, this form is derived from the Fourier transform of an exponentially decaying wavefunction:

$$\psi \left(t\right)\sim e^{-\mathrm{\Gamma }t}\Rightarrow \widehat{\psi }\left(E\right)\sim {\displaystyle \frac{1}{E^2+{\mathrm{\Gamma }}^2}},$$

with $\mathrm{\Gamma }$ interpreted as the decay rate.

However, under the TEQ framework, such decay can be understood not merely dynamically, but structurally: as a consequence of entropy-weighted suppression over unstable or short-lived resolution modes. The Lorentzian profile (Eq. (7)) thus reflects the boundary between coherent path stability and entropy-driven dispersion.

This view implies that Lorentzian broadening is not just a dynamical effect, but an emergent envelope of indistinguishability in systems where path resolution is bounded by entropy curvature (cf. Section 5).

7.2. Signal Processing and Neural Systems

Lorentzian filters are widely used in signal processing to attenuate high-frequency components while preserving phase structure. In neural systems, such filters appear as coarse-grained responses of biological signal transmission under delays, feedback, and thermal noise.

From the perspective developed here, this use of the Lorentzian reflects an implicit coarse-graining over fluctuating microstructure: delays, stochastic synaptic variations, and unresolved neural pathways contribute entropy-weighted fluctuations in signal resolution, leading to a Lorentzian envelope upon effective integration (cf. Section 3).

The presence of Lorentzian filters across both engineered and biological systems suggests that entropy-constrained resolution structures are not peripheral, but universal.

7.3. Blackbody Radiation and Spectral Envelopes

While Planck’s law governs the overall spectrum of blackbody radiation, detailed spectral features—particularly line broadening in atomic transitions—often display Lorentzian profiles. These are traditionally attributed to perturbative effects, including pressure broadening and natural linewidths.

TEQ provides a more unified account: the integration over unresolved entropy scales within radiative modes leads generically to Lorentzian-type decay when transition sharpness is limited by entropy geometry. This suggests that spectral profiles at high resolution may be better understood as entropy-induced envelopes, not solely as the result of isolated decay dynamics.

7.4. Information Flow and Computability

The Lorentzian kernel also applies to more abstract systems where information flow is structurally constrained. In observer-bound frameworks—such as those involving computational irreversibility, entropy-driven erasure, or bounded mutual information—the Lorentzian emerges as a marker of epistemic saturation.

For instance, in the observer-based Halting Problem reformulated under TEQ in [2], distinguishability between halting and non-halting behaviors becomes entropy-bounded. The Lorentzian kernel may then describe the gradient of observer certainty as resolution thresholds are crossed.

This bridges the Lorentzian’s role from physical systems to epistemic models—underscoring its universality as a structural feature of distinguishability-limited inference.

Summary

Across these domains, the appearance of Lorentzian forms is no longer a coincidence or convenience. Rather, it reflects the same underlying principle:

Wherever entropy geometry constrains resolution, the Lorentzian kernel emerges as the envelope of epistemic accessibility.

In this sense, the Lorentzian is not merely a physical or computational filter. It is the form taken by the soft failure of knowledge—where precision gives way to bounded discernment, and sharp distinctions dissolve into tails.

8. Conclusion

The Lorentzian kernel is one of the most frequently encountered forms in physics, yet it is also one of the least structurally explained. Traditionally, it has been treated as a pragmatic profile—used to model decay, resonance, or filtering effects. In this paper, we have offered a different view.

Starting from the entropy-weighted action of the TEQ framework (Eq. (2)), we showed that the Lorentzian kernel (Eq. (7)) arises generically from a superposition of Gaussian suppressions under fluctuating resolution scales (Section 3). This emergence is not contingent on dynamics per se, but follows from geometric constraints on distinguishability within entropy-curved configuration space (Section 5).

We argued that this form—traditionally associated with physical damping—can be reinterpreted as a structural boundary in the geometry of resolution. The Lorentzian kernel marks the regime where:

• Entropy curvature saturates,
• Distinction becomes unstable,
• And epistemic access fades—not sharply, but structurally.

This leads to the central thesis of the paper:

The Lorentzian kernel is the epistemological exponent of uncertainty: the structural signature of irreducible indistinguishability in entropy geometry.

It is the form taken by resolution failure—not due to noise, but due to the intrinsic limits of entropy-informed discernability. It appears wherever fine-grained distinctions cannot be sustained, and wherever geometry imposes a soft epistemic cutoff.

This result fits naturally within the broader aims of the TEQ (Total Entropic Quantity) program, which seeks to derive core structures of physics—including quantization, curvature, decoherence, and measurement—from first principles in entropy geometry. In that context, the Lorentzian kernel emerges not as a special case, but as a universal boundary form imposed by the geometry of resolution itself. It further illustrates how the TEQ framework recasts familiar physical profiles as structural consequences of entropy-stabilized motion and bounded distinguishability.

Outlook and Future Work

This reinterpretation opens several directions for further investigation:

• Generalization to other kernels: Are other filtering profiles (e.g., exponential, Voigt, sinc) similarly interpretable as emergent structures from more general entropy geometries? Classical line shapes such as the exponential (arising from Markovian decay) and the Voigt profile (a convolution of Gaussian and Lorentzian) [8,9] may themselves signal distinct structural regimes or transitions in entropy geometry. A unified geometric treatment could clarify when and why each kernel arises as an epistemic boundary.
• Formal epistemology: Can the Lorentzian be embedded in a rigorous entropy-based theory of observer-limited knowledge, perhaps drawing on information geometry and computability constraints?
• Experimental predictions: Are there measurable transitions between Gaussian and Lorentzian regimes in high-resolution spectroscopy, quantum coherence, or information-limited biological systems?
• Entropy curvature classification: What class of entropy metrics generate Lorentzian envelopes, and can this be used to classify physical systems by their resolution geometry?

Ultimately, we suggest that the Lorentzian kernel deserves to be seen not as an empirical afterthought, but as a boundary object—structurally emergent, universally applicable, and epistemologically profound.

Empirical leverage: TEQ’s reinterpretation of the Lorentzian kernel as an emergent epistemic boundary leads to testable predictions that differ from standard dynamical models. Specifically, the transition between Gaussian and Lorentzian regimes should manifest as a qualitative change in spectral line shapes, suppression thresholds, or noise tails—driven not by microscopic decay constants but by the geometry of entropy-induced resolution.

• High-resolution spectroscopy: In ultracold atom systems or optical cavities, systematic variation of environmental entropy (e.g., via tunable disorder, measurement back-action, or engineered indistinguishability) could induce a transition from sharp Gaussian to broad Lorentzian line shapes. Measurement of tail exponents and profile asymmetries can distinguish structural (entropy-driven) from purely dynamical broadening.
• Quantum coherence and decoherence: Experiments that probe decoherence under controlled entropy flow—such as engineered quantum circuits with variable path distinguishability—could reveal a crossover from exponential to power-law suppression, marking the onset of epistemic (not stochastic) resolution limits.
• Information-limited biological systems: In neural systems, one might observe a shift from narrow (Gaussian-like) to fat-tailed (Lorentzian-like) frequency responses as synaptic noise or unresolved pathway complexity increases, indicating a structural entropy constraint on signal propagation.
• Signal interference under bandwidth constraints: Physical or engineered systems where the effective entropy metric can be tuned (e.g., photonic lattices, coupled oscillators) may show a measurable crossover in filter behavior—diagnosable by tracking how suppression tails and cutoffs respond to controlled changes in distinguishability.

In all such contexts, TEQ predicts that Lorentzian behavior emerges not only where explicit damping exists, but whenever the system approaches the structural edge of resolvability. This provides a new, geometry-driven criterion for classifying spectral and filtering responses, and suggests concrete domains where standard dynamical models may fail to capture the underlying structural transition.