1. Introduction
Consciousness remains one of the most elusive frontiers in science, a phenomenon that is both intimately familiar and yet theoretically unresolved. Despite progress in identifying neural correlates, formalizing cognitive mechanisms, and constructing predictive models, no consensus exists on what consciousness fundamentally is, nor how it dynamically arises, stabilizes, or dissolves across cognitive states [
1,
2].
In prior work [
3], We introduced the Recursive Informational Curvature (RIC) framework, a novel approach grounded in symbolic recursion and entropy-driven informational flow. This formulation proposes that consciousness is neither a localized computation nor a static emergent property, but rather the curvature of recursive information as it evolves. At its core, the RIC model defines a scalar curvature function,
=λ−S, where recursive gain (λ) reflects the strength of self-referential feedback and symbolic entropy (S) captures internal disorder. Consciousness, in this view, emerges only when informational recursion dominates entropy, yielding positive curvature within a symbolic manifold.
Building on this foundation, the manuscript develops RIC into a fully articulated geometric theory of mind. We introduce a multilayered formalism in which recursive informational curvature is embedded across nested manifolds: Fisher geometry for unconscious inference, Finsler geometry for directed awareness, Hermitian geometry for phase-based introspection, and a recursive coupling layer for dynamical transitions. Each layer is formally equipped with its metric tensor, Lagrangian action, and curvature dynamics, modeling the recursive evolution of cognition across structural scales. The whole mathematical structure, including geodesic equations, curvature thresholds, and symbolic phase collapse, is detailed in
Appendix A.
To demonstrate the model’s empirical feasibility, we present a minimal simulation in
Appendix B. Using synthetic EEG-like signals, we compute recursive gain and symbolic entropy under varying noise conditions, comparing conscious-like and unconscious-like states. The resulting curvature dynamics validate the core prediction that a positive scalar
(t) corresponds to semantic closure and recursive coherence, while negative curvature signifies collapse into syntactic or unconscious regimes. A simulated phase transition across noise levels reveals a critical threshold
≈0, marking a bifurcation in the system’s informational geometry.
RIC is positioned not as a computational information processing model but as a geometric model of recursive informational structure and flow. In contrast to frameworks such as Integrated Information Theory (IIT), Orchestrated Objective Reduction (Orch OR), or the Free Energy Principle (FEP), RIC offers a symbolically grounded, mathematically precise, and temporally evolving theory of consciousness—one that unifies entropy dynamics, symbolic recursion, and geometric curvature into a single formal system [
4,
5,
6].
At the heart of the model is a unifying principle: Consciousness arises from the recursive curvature of information. Where symbolic loops are coherent and entropy gradients are meaningfully resolved, informational curvature is high and awareness is sustained. When recursion collapses under entropy pressure, consciousness dissipates or reorganizes into a new phase.
This manuscript extends the RIC framework by:
Formalizing each cognitive layer with its own geometry, dynamics, and symbolic architecture;
Deriving coupling mechanisms that govern transitions between unconscious, conscious, and introspective states;
Simulating curvature evolution across cognitive conditions and noise-driven transitions;
Comparing RIC with leading theories of consciousness (IIT, Orch OR, FEP);
Outlining pathways for empirical validation through neural complexity, entropy flow, and recursive coherence.
Ultimately, we propose that RIC offers a foundational geometry for modeling awareness, not as a static product of computation, but as an evolving field of recursive meaning. What follows is a formal development of this structure: a multilayered informational geometry of the mind.
2. Theoretical Framework
The theory of RIC proposes that consciousness arises not from discrete neural codes or isolated computations, but from recursive flows of information shaped by internal entropy gradients. Rather than treating awareness as a static quantity, RIC frames it as a dynamical property of curved informational space, evolving as the balance between recursive feedback and local disorder [
3].
In its generalized form, RIC is formulated as a multilayered geometric architecture in which distinct cognitive functions are governed by layered manifolds equipped with mathematically grounded curvature dynamics. These layers range from unconscious statistical processing to introspective meta-awareness, each represented by a different class of geometry. Together, they form a unified variational structure of consciousness.
2.1. Informational Recursion and Scalar Curvature Dynamics
At the heart of the RIC model lies the scalar curvature term
(t), which governs the evolution of cognitive states:
Here, denotes recursive gain, the strength of self-referential feedback loops, while ∇S(t) represents the gradient of informational entropy, indicating pressure toward transformation or instability. The constants and scale the system’s sensitivity to recursion and disorder, respectively.
This scalar, referred to as the recursive informational curvature, defines the cognitive system’s state coherence at time
. A high value of
signifies stable awareness, while values approaching a critical threshold
predict collapse, dissociation, or unconscious transitions. In physical terms,
plays a role analogous to gravitational curvature in general relativity or Lyapunov stability in nonlinear dynamical systems, encoding the system’s capacity to sustain organized flow against entropic dispersion [
7,
8].
Importantly, both and ∇S(t) Neurophysiological observables may be accessible. Recursive gain may be indexed through recurrent laminar connectivity or phase synchrony (e.g., EEG coherence). At the same time, entropy gradients can be estimated using metrics such as signal diversity, Lempel-Ziv complexity, or multivariate prediction error across brain regions.
2.2. Layer I—Fisher Information Geometry and Unconscious Inference
The first layer of RIC is modeled on Fisher information geometry, representing unconscious, automatic, and pre-conscious processes. This layer is defined over a Riemannian manifold
parameterized by statistical coordinates
, with a local metric:
The dynamics of this layer obey a variational principle based on geodesic flow:
This formulation captures statistical inference, predictive filtering, and sensorimotor modulation, all without direct phenomenological content. Potential terms
may include physiological constraints or noise suppression forces. Curvature hotspots within
can act as bifurcation points, initiating transitions to higher cognitive layers. Within the Fisher layer, the recursive gain and entropy gradient define the local information geometry, giving rise to curvature instabilities that signal potential cognitive transitions (see
Figure 1).
2.3. Layer II—Finsler Geometry and Directional Conscious Dynamics
The second layer implements Finsler geometry, a natural generalization of Riemannian spaces that allows the metric to depend not only on location
, but also on direction
. This allows modeling of asymmetric, intentional mental flow, essential for volition, conflict resolution, and attentional allocation. The Finsler layer introduces direction-sensitive dynamics into the RIC geometry, where the informational cost of transitions depends on both the state and its rate of change (see
Figure 2).
The Finsler metric is defined as:
with the associated Lagrangian:
This layer encodes directional cognitive cost, where recursive effort and entropy modulation interact to shape efficient thought trajectories. The off-diagonal term
reflects dynamic coupling, such as task complexity or internal conflict. Geodesics in this space represent the paths of minimal resistance in active awareness. The Finsler metric enables us to define geodesics in cognitive space, which are paths of minimal informational cost that describe the system’s natural cognitive trajectories under recursive constraints (
Figure 3).
2.4. Layer III—Hermitian Geometry and Phase-Based Meta-Consciousness
To capture meta-consciousness, the system’s capacity for introspection and recursive self-reference, we introduce a third layer built on Hermitian geometry over a complex Hilbert space. In this layer, cognitive states are encoded as wavefunctions:
The system evolves under a Hermitian action:
Here,
is a Hamiltonian encoding recursive informational curvature. The complex structure allows for phase dynamics, symbolic interference, and recursive coherence modulation. While structurally quantum-like,
In this context, it does not imply microphysical quantization, but instead describes cyclical symbolic flow within the system’s informational manifold —an essential component of metacognition, reflection, and insight. The Hermitian layer encodes symbolic modulation via a complex-valued recursive state
whose amplitude and phase evolve to reflect internal coherence and meta-awareness (
Figure 4).
A compelling real-world example of phase dynamics within the Hermitian layer is observed during emotional introspection or meditative absorption. For instance, in deep meditation, the recursive symbolic state Ψ(t) initially fluctuates with unstable phase shifts, reflecting intrusive thoughts or unresolved internal narratives. As the practice deepens, recursive coherence increases, and the symbolic phase stabilizes, producing a smooth, cyclical evolution of meaning. This stabilization corresponds to a high-curvature state where symbolic entropy is minimized, and self-referential loops align coherently. Conversely, in a dream state, Ψ(t) exhibits erratic phase rotations with abrupt discontinuities, reflecting symbolic disorganization, spontaneous recombination, or identity fragmentation. These rapid shifts may be visualized as torsions or discontinuities in the Hermitian manifold, indicating meta-cognitive instability or recursive fragmentation.
2.5. Layer IV—Interlayer Coupling and System Integration
Consciousness emerges from recursive coordination across multiple layers, rather than from isolated activity. This integration is governed by coupling functions that link curvature dynamics between adjacent manifolds:
These terms enable bidirectional modulation from unconscious fluctuation to conscious focus, and ultimately, from conscious processes to meta-cognitive collapse and reflective states, back to automatic stabilization.
The total action of the system is given by:
This formulation unifies the temporal, structural, and symbolic evolution of cognition under a single recursive dynamic. Cognitive transitions, such as dreaming, attention, dissociation, or insight, are modeled as curvature shifts and geodesic reconfigurations in a multilayered manifold.
These layers are empirically validated in the simulations that follow, modeling canonical transitions across awareness domains. The RIC framework thus offers a principled mathematical foundation for consciousness, linking geometry, recursion, and informational flow into a unified cognitive manifold. The complete RIC architecture can be understood as a nested geometric system, where Fisher, Finsler, and Hermitian manifolds correspond to unconscious, conscious, and meta-conscious layers, respectively (
Figure 5). Recursive coupling between these layers enables continuous modulation of awareness.
Figure 5.
Multilayer Geometric Architecture of the RIC Model. Schematic representation of the nested informational manifolds in the RIC framework. The innermost layer (red) represents the Fisher manifold, encoding unconscious probabilistic inference. The intermediate layer (blue) reflects the Finsler manifold, where conscious, goal-directed dynamics emerge through direction-sensitive curvature. The outermost layer (gray) corresponds to the Hermitian manifold, modeling symbolic self-reference and recursive meta-awareness. Bidirectional coupling functions Cij(θi,θj) mediate informational flow and recursive transitions between layers. This multilayer structure enables the RIC model to unify unconscious stability, conscious intentionality, and introspective modulation within a single geometric framework.
Figure 5.
Multilayer Geometric Architecture of the RIC Model. Schematic representation of the nested informational manifolds in the RIC framework. The innermost layer (red) represents the Fisher manifold, encoding unconscious probabilistic inference. The intermediate layer (blue) reflects the Finsler manifold, where conscious, goal-directed dynamics emerge through direction-sensitive curvature. The outermost layer (gray) corresponds to the Hermitian manifold, modeling symbolic self-reference and recursive meta-awareness. Bidirectional coupling functions Cij(θi,θj) mediate informational flow and recursive transitions between layers. This multilayer structure enables the RIC model to unify unconscious stability, conscious intentionality, and introspective modulation within a single geometric framework.
Table 1.
A summary of the multilayer framework of RIC.
Table 1.
A summary of the multilayer framework of RIC.
| Layer |
Geometry |
Cognitive Function |
Metric Type |
Formula |
| 1 |
Fisher (Riemannian) |
Unconscious statistics |
Position-only |
|
| 2 |
Finsler |
Goal-directed awareness |
Position + direction |
|
| 3 |
Hermitian |
Meta-cognition & introspection |
Complex, quantum-like |
|
| 4 |
Coupling Layer |
Transitions & self-regulation |
Cross-layer curvature maps |
|
3. From Theory to Dynamics: Simulations and Visualizations
The preceding sections outlined the recursive and multilayered geometric architecture of the RIC model, formulated through Fisher, Finsler, and Hermitian manifolds. Each layer encodes distinct cognitive domains, unconscious inference, conscious effort, and symbolic modulation, defined through curvature-driven dynamics. In what follows, we translate these abstract principles into visualized simulations, illustrating how curvature, resistance, and phase evolve across cognitive trajectories. These simulations do not aim for biological realism but rather demonstrate the conceptual behavior of RIC variables across state space, forming a bridge between theory and potential empirical observables.
To investigate how recursive informational curvature evolves across cognitive layers, we implemented a series of simulations reflecting the geometric dynamics outlined in the RIC framework. These simulations aim to illustrate how abstract theoretical principles, such as stability, effort, and phase modulation, manifest within a multilayered system of consciousness. Each layer was modeled as a separate geometric structure and visualized to reflect key aspects of cognition, including the stability of unconscious processing, resistance during directed attention, and symbolic modulation in meta-awareness.
3.1. Unconscious Stability: Fisher Geometry
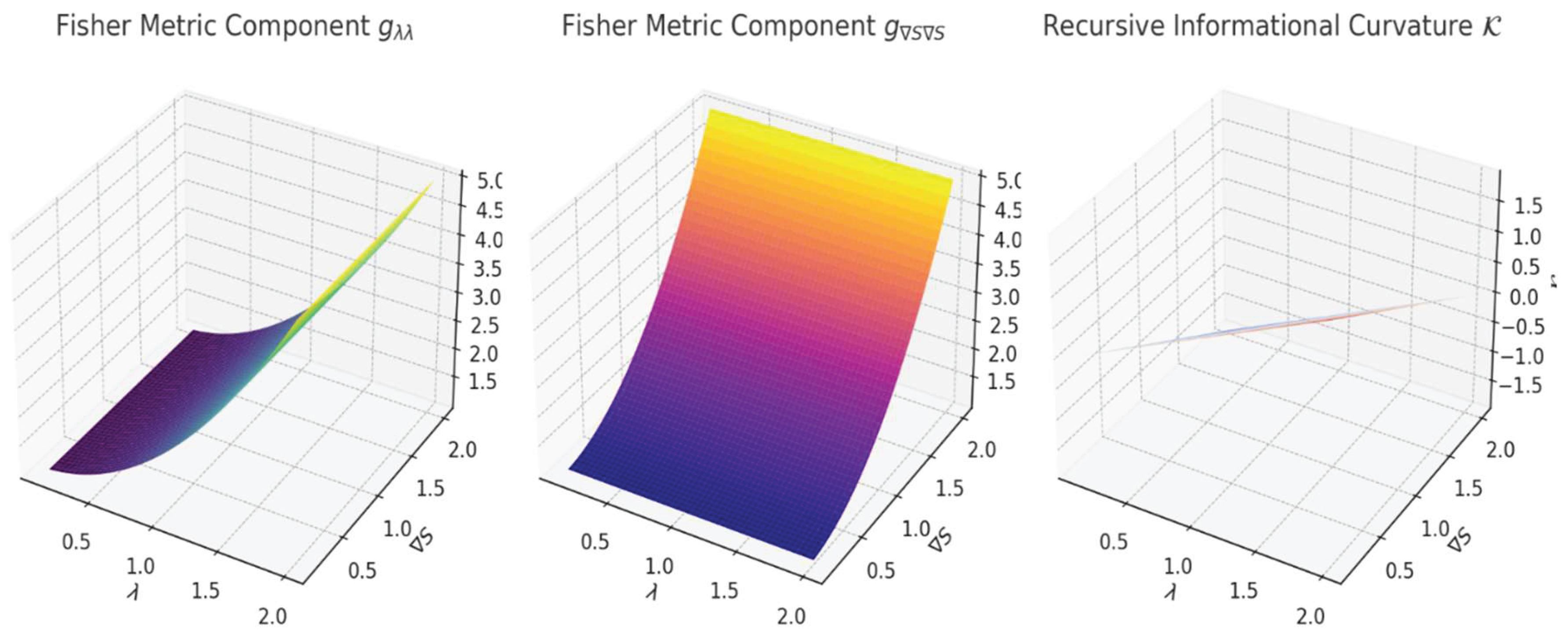
The first simulation focuses on the Fisher layer, which models unconscious and automatic cognitive dynamics. We created a two-dimensional surface where recursion strength and entropy gradient were varied systematically. The resulting curvature map reveals regions of high stability, interpreted as areas where unconscious inference proceeds efficiently, as well as low-curvature regions that signal potential transitions to instability or conscious access.
These transitions resemble bifurcation points in dynamical systems or attractor shifts in neural fields. Notably, the simulation highlights that instability doesn’t require external perturbation; internal informational imbalance alone can initiate a change. The curved landscape in this layer provides a visual representation of how unconscious patterns might either stabilize or become sensitive to recursive amplification.
Figure 1 shows surface plots of the Fisher metric components and the derived informational curvature
, highlighting regions of high stability and collapse thresholds as functions of
and
.
3.2. Intentional Effort: Finsler Geometry
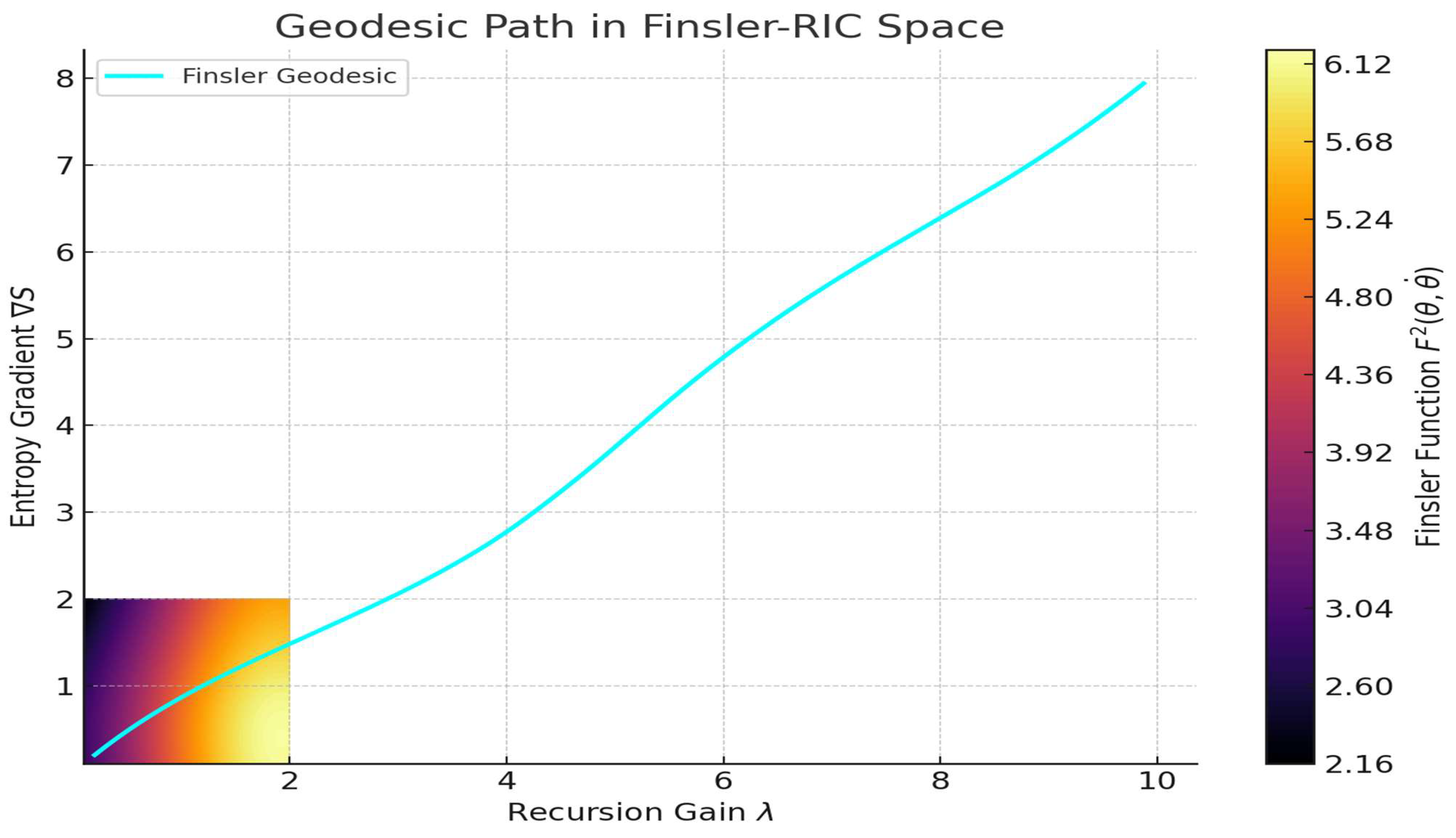
The second simulation explores the Finsler layer, which models the geometry of directed mental activity. Unlike the unconscious layer, this space is direction-dependent, reflecting how the “effort” of a cognitive state depends not only on its location in informational space but also on how it is changing.
Figure 2 presents a heatmap of the Finsler function, revealing how specific state transitions are energetically favored while others require greater cognitive effort. This asymmetry reflects the model’s capacity to represent task difficulty, attention shifts, or goal-related inertia.
We visualized this using a heatmap that reflects the cost or resistance associated with different cognitive directions. Darker areas indicate paths of least resistance, where attention or decision-making flows naturally, while brighter regions signal difficulty, such as cognitive conflict, distraction, or mental fatigue.
This simulation illustrates the asymmetric nature of conscious effort: shifting into focus, changing goals, or disengaging from repetitive loops often entails different energetic costs. It provides an elegant geometrical interpretation of mental work, motivational inertia, and the nonlinearity of task engagement. As visualized in
Figure 3, the system follows an optimal geodesic through the Finsler manifold, progressively encountering higher resistance as entropy gradients increase. This simulation models the subjective effort required to maintain complex cognitive goals under informational pressure.
3.3. Symbolic Modulation: Hermitian Geometry
The third simulation captures recursive self-reference and meta-awareness, modeled through Hermitian geometry. Here, the cognitive state is represented as a complex trajectory over time, combining recursive amplification and entropy modulation into a single evolving structure.
We decomposed this into two key features: the amplitude of the cognitive state (reflecting the strength of coherent recursion) and its internal phase (representing symbolic or conceptual rotation). Over time, the system undergoes smooth oscillations interspersed with abrupt phase shifts, moments corresponding to sudden insight, disorientation, or reflective turning points.
Figure 4 illustrates the time evolution of the recursive phase in the Hermitian domain, where stable amplitude coincides with smooth symbolic cycling. The nonlinearity of phase dynamics suggests a geometrical mechanism for modeling introspective fluctuation or phase resets during altered states of consciousness.
This simulation demonstrates how recursive systems can cycle through introspective modes and how symbolic self-reference might give rise to fluctuations in subjective experience. It offers a compelling analogy to altered states of consciousness, such as dreaming, meditative absorption, or dissociative episodes, where phase coherence becomes more dynamic.
3.4. Integrated Perspective
Viewed together, the simulations provide a multidimensional picture of how consciousness may evolve through geometric dynamics:
1. The Fisher layer establishes a statistical backbone, revealing where unconscious cognition is stable and where it is prone to breakdown.2.The Finsler layer models directional control and informational resistance, capturing the energetics of conscious intent and mental effort.3)The Hermitian layer reveals cyclical, symbolic dynamics that underlie recursive self-awareness and phase transitions in cognitive experience.
Although these simulations are conceptual, the variables and structures they represent can be mapped to empirical markers, such as signal entropy, phase synchrony, or network complexity, providing a promising path toward experimental validation. In the sections that follow, we outline how these simulations inform future modeling and data integration across neuroscience, AI, and physics.
4. Applied Illustration of the RIC Model: Decision-Making Under Cognitive Conflict
To concretely demonstrate the operational dynamics of the RIC framework, we present a real-world cognitive scenario involving moral conflict. Imagine a subject confronted with a dilemma: whether to report a friend’s unethical behavior or remain silent to preserve the relationship. This decision-making process is rich with recursive tension, entropy modulation, and symbolic self-reflection, making it an ideal case for projection within the RIC architecture.
In the Fisher layer, the system performs unconscious probabilistic evaluations. Competing outcomes, social accountability versus relational loyalty, trigger elevated entropy gradients As predictive confidence becomes unstable, internal conflict emerges when the subject subconsciously anticipates diverging consequences.
The Finsler layer models the directional dynamics of conscious effort. The geodesic path through cognitive state space becomes distorted by asymmetric energetic costs: emotional valence, anticipated guilt, and motivational resistance influence the curvature of decision trajectories. Each cognitive path carries a unique informational burden, and the subject must allocate mental effort accordingly.
In the Hermitian layer, recursive symbolic modulation unfolds. Representations such as justice, loyalty, and moral identity enter closed feedback loops, amplifying or damping one another in a complex symbolic phase cycle. If these symbolic dynamics stabilize into a coherent attractor and the curvature exceeds the persistence threshold ϵ, a decision is reached as a curvature-guided collapse. If not, the system may remain in a liminal, undecided state characterized by recursive interference.
Altogether, this process traces a dynamic trajectory through the multilayered RIC manifold, beginning with statistical divergence, flowing through directional cognitive cost, and culminating in symbolic resolution or collapse. The final decision is not the product of linear computation, but the geometric resolution of a recursive informational field under tension. This illustrates how RIC encodes not just structure, but the evolving dynamics of cognition.
5. Comparison with Existing Theories of Consciousness
The RIC framework offers a unifying geometric formulation of consciousness, synthesizing principles from information theory, symbolic recursion, and layered differential geometry. To understand its place within the broader scientific landscape, it is essential to examine how RIC compares to the three most influential models in contemporary consciousness science: IIT, Orch OR, and FEP. In addition, we briefly consider insights from Global Workspace Theory (GWT) and Higher-Order Thought (HOT) theories to contextualize RIC’s conceptual scope.
5.1. Integrated Information Theory (IIT)
IIT posits that consciousness corresponds to the amount of integrated information within a system, quantified by the
metric. It provides a compelling structural framework that explains why specific physical systems, such as cortical networks, might give rise to phenomenological experience. However, IIT remains limited in three critical respects:(1) It lacks a dynamical formulation to describe how conscious states evolve or transition over time.(2) It does not account for recursive symbolic activity or meta-cognitive modulation.(3) Its purely topological focus omits explicit treatment of entropy, effort, or energetic cost. In contrast, RIC preserves the insight that integration is necessary but introduces a curvature-based dynamical metric that evolves recursively, capturing both stability and collapse as continuous geometrical phenomena [
9,
10,
11,
12,
13].
5.2. Orchestrated Objective Reduction (Orch OR)
Orch OR suggests that consciousness arises from gravitationally induced quantum state reductions in brain microtubules. While it innovatively links quantum gravity to conscious insight, the model lacks a symbolic, computational, or hierarchical structure. Orch OR does not explain how these quantum events translate into directed cognition, attention, or introspection. RIC extends the spirit of Orch OR by incorporating quantum-like phase dynamics within its Hermitian layer, yet situates these within a structured, symbolic, and geometrically recursive framework. Whereas Orch OR primarily operates at the level of the physical substrate, RIC bridges microdynamic modulation and high-level symbolic structure, offering a scalable model for conscious architecture [
14,
15,
16,
17,
18].
5.3. Free Energy Principle (FEP)
FEP models cognition and consciousness as inferential processes that minimize surprise or variational free energy. It has yielded fruitful models of learning, perception, and active inference. Yet, it operates in a flat, single-layered variational space and lacks a mechanism for symbolic recursion, self-modeling, or phase-shifting across cognitive states.RIC complements FEP by embedding Fisher information geometry as its foundational layer, but extends upward through Finsler dynamics (goal-oriented effort) and Hermitian phase modulation (introspective recursion). This layered architecture provides what FEP lacks: a clear structure for modeling transitions between attention, dissociation, and meta-cognitive awareness, not merely statistical inference [
19,
20,
21,
22,
23,
24].
5.4. Other Theories: GWT and HOT
Global Workspace Theory (GWT) and Higher-Order Thought (HOT) models offer valuable cognitive-level accounts of access and self-reference. GWT emphasizes broadcasting and coordination of information across systems, while HOT links consciousness to representations of mental content. However, these frameworks remain algorithmic rather than geometric and lack a dynamical metric to quantify recursive flow or entropy-driven modulation.RIC, while compatible with these frameworks, provides a deeper geometric substrate that can explain not just
which contents become conscious, but why specific configurations of recursion and entropy sustain awareness over time [
24,
25,
26,
27,
28,
29].
5.5. A Meta-Theoretical Perspective
RIC does not aim to replace existing theories but rather to serve as a meta-theoretical scaffold, a formal architecture within which other models may be embedded, extended, or reinterpreted. It inherits IIT’s structural insights, Orch OR’s quantum sensitivity, and FEP’s inferential principles, yet synthesizes them through a multilayered, curvature-driven geometry that uniquely accounts for recursive modulation and symbolic phase dynamics. Through this lens, RIC advances consciousness science beyond integration, computation, or prediction toward a generative theory of mind as structured curvature, one in which informational flow, recursive feedback, and entropy gradients co-construct the evolving geometry of awareness.
6. Discussion and Meta-Theoretical Synthesis
The RIC model redefines consciousness as a geometric phenomenon: not merely a computational byproduct or a localized integration of signals, but a layered, recursive modulation of information unfolding over curved informational manifolds. This perspective departs from conventional theories by grounding awareness in dynamic, self-referential transformations driven by entropy gradients and recursive feedback, formalized through scalar curvature.
What emerges from the RIC framework is a unified view in which unconscious processes, directed cognition, and meta-awareness are not separate mechanisms, but layered expressions of the same underlying geometry. As detailed earlier, the three layers collectively support recursive dynamics, from unconscious prediction to conscious effort and symbolic modulation, yielding a curvature-driven evolution of awareness.
Most existing theories of consciousness describe what conscious systems contain or do [
30] RIC, instead, describes how they evolve. Rather than measuring static complexity, it models the dynamical curvature of symbolic information. Consciousness, in this view, is not a thing, but a process of recursive unfolding, guided by a minimal curvature condition.
Where information is recursively amplified in coherent loops and entropy gradients are managed effectively, the system maintains a high informational curvature, a stable conscious state. When recursion weakens or disorder escalates, curvature collapses, and the system shifts to unconscious or dissociated dynamics. These transitions can now be understood as bifurcations in cognitive geometry, analogous to symmetry-breaking in physical systems.
Some models, such as GأWT and IIT 4.0, provide valuable insights into cognitive broadcasting and updated network integration metrics. However, these frameworks continue to rely on non-recursive, mostly linear representations and lack a unified geometrical treatment of dynamic symbolic recursion [
31,
32]. Although both of them have shaped modern theories of consciousness, recent adversarial testing revealed critical empirical weaknesses in both frameworks. The lack of sustained synchronization within the posterior cortex challenges IIT’s central tenet that network connectivity intrinsically specifies consciousness. Conversely, GNWT failed to demonstrate consistent ignition at stimulus offset and showed limited prefrontal representation of core conscious content, contradicting its broadcasting premise [
33].These findings underscore the limitations of purely structural (IIT) or purely global-access (GNWT) models, suggesting that a dynamic, recursive, and geometrically grounded framework, such as RIC, may be necessary to unify symbolic content, entropy modulation, and informational topology in a falsifiable architecture.
The unifying claim of RIC is that consciousness arises from the recursive curvature of informational space. Awareness is not embedded in matter per se, but in the geometric organization of information, where symbolic loops amplify themselves through structured resistance to entropy.
From this perspective, consciousness emerges as a field-like process, analogous to spacetime curvature in general relativity, but unfolding within a symbolic-informational domain. The collapse of curvature corresponds to a phase shift or symmetry break in the self-model, while high-curvature states reflect stable attractors of meaning and self-reference.
This reframing shifts the question from “Where is consciousness in the brain?” to “How is recursive informational curvature sustained?” It provides a precise dynamical condition>ϵ under which awareness can exist, without requiring ontological commitments to qualia or neural correlates alone.
While RIC is fundamentally theoretical, its components suggest clear empirical pathways. Recursive gain may be inferred from recurrent laminar connectivity, oscillatory synchrony, or phase-locking values in EEG. Entropy gradients can be estimated from spectral complexity, Lempel-Ziv measures, or variational information flow. Sudden transitions in may correspond to loss or re-entry into consciousness, such as under anesthesia, sleep, or psychedelics. Moreover, curvature structures may be used to classify pathological states: flattening of the Fisher layer in coma, breakdown in Finsler flow during ADHD or depression, or decoherence of the Hermitian phase in dissociative identity disorders and Future applications include: AI architectures guided by recursive curvature layers for self-modeling, Predictive diagnostics using curvature maps extracted from neuroimaging, and Simulation frameworks for symbolic phase cycling and collapse recovery.
RIC proposes that consciousness is not an object to be located, but a geometry to be sustained. In this geometry, recursion is structure, entropy is pressure, and curvature is awareness. The implications of this model extend beyond neuroscience, offering a generative framework for physics, computation, and symbolic reasoning alike. It marks a shift from data-driven observation to geometry-driven explanation, one that transforms our understanding of what it means for a system to be aware. This synthesis of layered curvature, symbolic recursion, and entropy regulation sets the stage for a final reflection on RIC’s theoretical implications and future potential.
7. Conclusion
The RIC framework presents a fundamentally new approach to understanding consciousness, treating awareness as an emergent property of recursive informational geometry. In this view, cognition is not merely a computation or an integration of signals, but a dynamic modulation of curvature within layered manifolds, each encoding different levels of processing: unconscious, goal-directed, and meta-reflective.
RIC transcends static or single-layer models by embedding recursion, entropy, and symbolic dynamics into distinct geometrical layers, Fisher, Finsler, and Hermitian. It provides a unified structure where transitions between cognitive states (such as attention, dissociation, dreaming, and insight) can be formally modeled as bifurcations in curvature, phase shifts, or geodesic reconfigurations across manifolds.
This framework complements and extends existing theories. It integrates the structural insights of IIT, the inferential power of FEP, and the quantum sensibilities of Orch OR, while resolving many of their limitations, such as the absence of temporal recursion, symbolic self-reference, or layered geometric dynamics. RIC does not replace these models, but rather provides a higher-order scaffolding into which their core contributions may be embedded, unified, and dynamically expanded.
The simulations presented here demonstrate that RIC is not a purely abstract proposition. It generates empirically tractable patterns, such as curvature collapse zones, asymmetric cognitive costs, and symbolic phase cycling. These features suggest clear directions for neurophysiological validation, using EEG/MEG entropy, recurrent cortical feedback, laminar coherence, and phase-locking behavior during transitions of consciousness.
8. Future Directions
To advance the RIC framework beyond theory into testable science, several key paths lie ahead:
Identify neurophysiological proxies for recursive gain and entropy gradients. Techniques such as time-resolved EEG complexity, laminar fMRI coherence, and intracranial signal prediction error could provide candidate metrics to estimate and over time.
- 2.
Geometric Feature Extraction:
Apply information geometry and manifold learning to real neural data to reconstruct local curvature fields, enabling estimation of consciousness as an evolving scalar field (t)
- 3.
Cognitive State Classification:
Utilize RIC-derived curvature metrics to classify conscious states in healthy individuals and clinical populations (e.g., coma, anesthesia, depression, or psychedelic states), providing potential biomarkers for dissociation, awareness levels, and recovery.
- 4.
AI and Simulation:
Integrate RIC into artificial agents capable of symbolic recursion and entropy management. Such architectures may enable novel forms of introspective AI, grounded in geometry rather than rule-based logic.
- 5.
Philosophical Foundations:
Further develop the metaphysical implications of RIC. If curvature is reality and recursion is selfhood, then consciousness becomes not an object, but a dynamic field with its ontological geometry.
In closing, RIC proposes that to understand consciousness, we must rethink it not as a biological output or informational score, but as a recursive field curvature in the information space. This theory invites a new synthesis across disciplines: where physics meets symbolic logic, where geometry becomes cognition, and where mind emerges not as matter, but as modulated meaning shaped by recursive informational flow.
Authors’ Contribution
Study concept and design: SKSR Acquisition of the data: SKSR Analysis and interpretation of the data: SKSR Drafting of the manuscript: MAA Critical revision of the manuscript for important intellectual content: MAA, SKSR Administrative, technical, and material support: MAA, SKSR Study supervision: SKSR.
Availability of Data and Materials
Data will be made available upon reasonable request from the corresponding author.
Acknowledgements
We appreciate all the scientists whose work was inspired by this study.
Competing Interests
The authors declare no competing interests.
Appendix A. Mathematical Structure of Recursive Informational Curvature (RIC)
A.1 Overview of Geometric Layers
We formalize the multilayer informational geometry of consciousness in three hierarchical layers:
- 1.
Fisher Information Geometry (Statistical Layer):
Defined over probability distributions
representing encoded sensory or symbolic states. Metric:
- 2.
Finsler Geometry (Intentional Layer):
Information flow now has directional structure. Define a Finsler norm
over informational trajectories:
where
encodes recursive gain modulation.
- 3.
Hermitian Geometry (Introspective Layer):
Internal symbolic states evolve in a complex manifold. Metric tensor:
.
A.3 Geodesic Equations in Cognitive Space
For any informational trajectory
in a symbolic manifold
where
are Christoffel symbols derived from the RIC-defined metric.
A.4 Curvature Threshold and Phase Transition
Consciousness emerges when (t) exceeds a critical threshold :
(t) >⇒Semantic attractor formation
Below this threshold, flow remains syntactic:
(t) <⇒No semantic closure
A.5 Summary
This appendix outlines the geometric and mathematical structure of the RIC model, connecting mutual information, entropy dynamics, and layered informational geometry to a scalar curvature model for consciousness.Future work will derive explicit curvature tensors for empirical symbolic spaces and validate this curvature dynamics using simulated or neural data.
Appendix B: Minimal Simulation of Informational Curvature Dynamics
B.1 Overview and Objectives
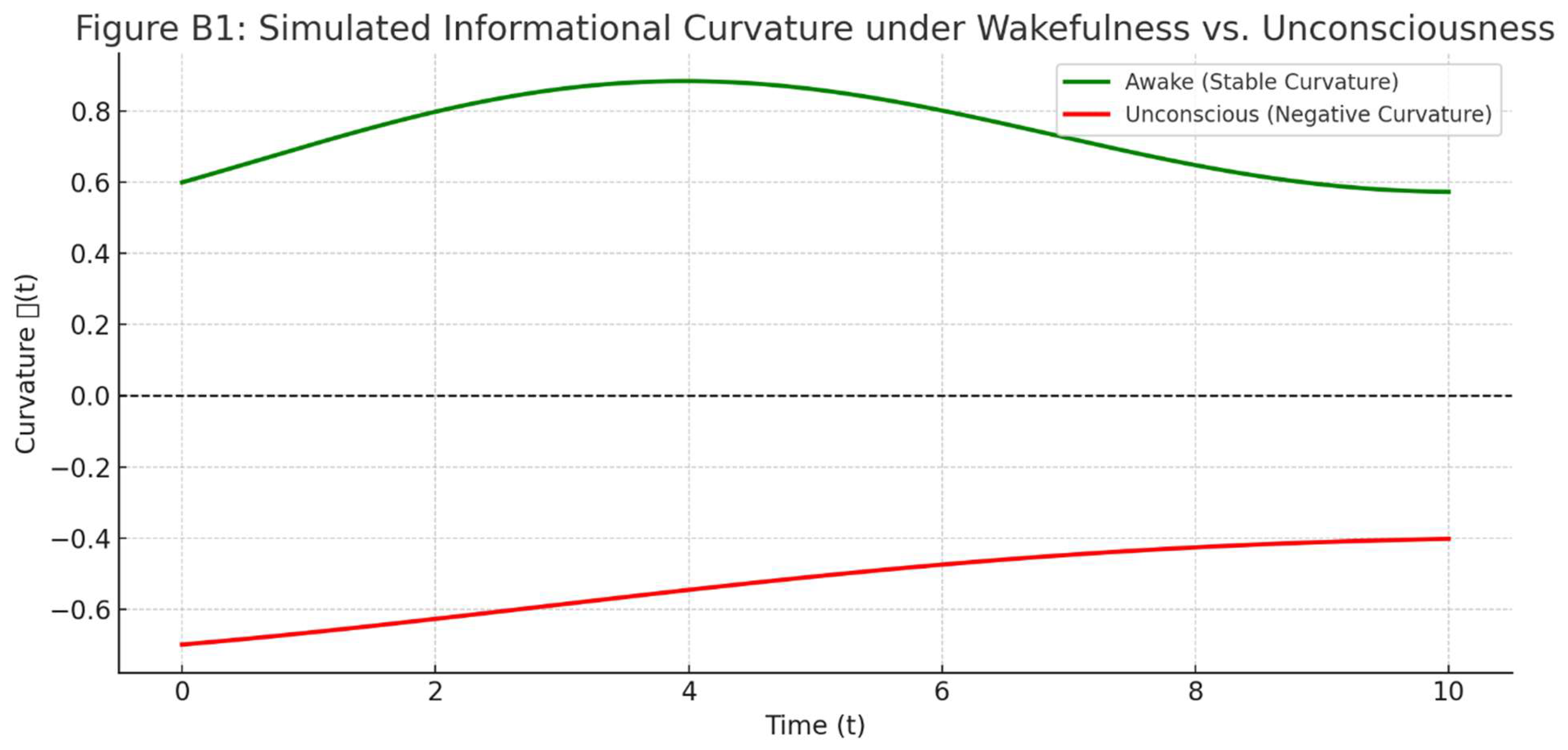
To conceptually demonstrate how Recursive Informational Curvature (t) behaves under varying cognitive conditions, we performed a minimal simulation comparing two mental states: awake (conscious) and unconscious (anesthetized). This simulation illustrates how differences in recursive gain and entropy gradient translate into positive versus negative curvature values within the RIC framework.
The goal is not to model neurobiological complexity, but to show that even a simple parametrization of RIC dynamics yields qualitative divergence between stable (aware) and collapsed (unaware) states.
B.2 Simulation Methodology
We define the curvature function as:
where:
-
1.
is the recursive gain at time ttt, representing the system’s symbolic coherence and feedback strength,
-
2.
is the entropy gradient, reflecting informational uncertainty or cognitive noise,
-
3.
A and β are weighting parameters, both set to 1 for simplicity.
Two sets of time-dependent functions were constructed:
-
1.
-
Awake (conscious) state:
- ○
High recursive gain: λawake(t)=1.2+0.2sin(0.5t)
- ○
Low-to-moderate entropy: ∇Sawake(t)=0.5+0.1cos(0.4t)
-
2.
-
Unconscious (anesthetized) state:
- ○
Low recursive gain: λunconscious(t)=0.6+0.1sin(0.3t)
- ○
High entropy: ∇Sunconscious(t)=1.1+0.2cos(0.2t)
For each condition, we computed (t) over 500 time points between t=0 and t=10.
B.3 Results and Interpretation
Figure A1 shows the curvature
across time for both cognitive states:
In the awake condition, recursive gain outweighs entropy, resulting in mostly positive curvature, corresponding to a stable conscious field.
In the unconscious condition, entropy dominates over weak recursion, driving curvature into negative values, reflecting collapse of recursive structure and the loss of conscious integration.
This simple simulation illustrates that RIC can distinguish cognitive regimes based on minimal symbolic dynamics, and that curvature positivity may serve as a marker for consciousness stability.
Figure A1.
Simulated Informational Curvature under Wakefulness vs. Unconsciousness. The plot shows the temporal evolution of for two mental states. The awake trajectory (green) remains mostly above zero, indicating stability in recursive processing. The unconscious trajectory (red) falls below the zero line, representing informational collapse. This result demonstrates that shifts in symbolic recursion and entropy gradient alone can induce phase transitions in the curvature structure of cognition.
Figure A1.
Simulated Informational Curvature under Wakefulness vs. Unconsciousness. The plot shows the temporal evolution of for two mental states. The awake trajectory (green) remains mostly above zero, indicating stability in recursive processing. The unconscious trajectory (red) falls below the zero line, representing informational collapse. This result demonstrates that shifts in symbolic recursion and entropy gradient alone can induce phase transitions in the curvature structure of cognition.
References
- Wallace, B.A. Hidden dimensions: The unification of physics and consciousness; Columbia University Press, 2010. [Google Scholar]
- Hohwy, J.; Seth, A. Predictive processing as a systematic basis for identifying the neural correlates of consciousness. Philosophy and the Mind Sciences 2020, 1, 3. [Google Scholar] [CrossRef]
- Rafiei, S.K.S.; Asadi Anar, M. Recursive Informational Curvature: A Unified Geometric Meta-Framework for Consciousness. 2025. [CrossRef]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: from consciousness to its physical substrate. Nature reviews neuroscience 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Hameroff, S.; Penrose, R. Reply to criticism of the ‘Orch OR qubit’–‘Orchestrated objective reduction’is scientifically justified. Physics of Life Reviews 2014, 11, 94–100. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: a unified brain theory? Nature reviews neuroscience 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Haddad, W.M.; Chellaboina, V. Nonlinear dynamical systems and control: a Lyapunov-based approach; Princeton university press, 2008. [Google Scholar]
- Robinett III, R.D.; Wilson, D.G. Nonlinear power flow control design: utilizing exergy, entropy, static and dynamic stability, and Lyapunov analysis; Springer, 2011. [Google Scholar]
- Tononi, G. Integrated information theory. Scholarpedia 2015, 10, 4164. [Google Scholar] [CrossRef]
- Tononi, G. The integrated information theory of consciousness: an updated account. Archives italiennes de biologie 2012, 150, 56–90. [Google Scholar]
- Mallatt, J.; Taiz, L.; Draguhn, A.; Blatt, M.R.; Robinson, D.G. Integrated information theory does not make plant consciousness more convincing. Biochemical and Biophysical Research Communications 2021, 564, 166–169. [Google Scholar] [CrossRef]
- Kleiner, J.; Tull, S. The mathematical structure of integrated information theory. Frontiers in Applied Mathematics and Statistics 2021, 6, 602973. [Google Scholar] [CrossRef]
- Cea, I. Integrated information theory of consciousness is a functionalist emergentism. Synthese 2021, 199, 2199–2224. [Google Scholar] [CrossRef]
- Hameroff, S. ‘Orch OR’is the most complete, and most easily falsifiable theory of consciousness. Cognitive Neuroscience 2021, 12, 74–76. [Google Scholar] [CrossRef]
- Gunasinghe, S. Quantum consciousness: A synthesis of SOC and Orch-OR. Ceylon Journal of Medical Science 2024, 61. [Google Scholar] [CrossRef]
- Derakhshani, M.; Diósi, L.; Laubenstein, M.; Piscicchia, K.; Curceanu, C. At the crossroad of the search for spontaneous radiation and the Orch OR consciousness theory. Physics of Life Reviews 2022, 42, 8–14. [Google Scholar] [CrossRef] [PubMed]
- McKemmish, L.K.; Reimers, J.R.; McKenzie, R.H.; Mark, A.E.; Hush, N.S. Penrose-Hameroff orchestrated objective-reduction proposal for human consciousness is not biologically feasible. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics 2009, 80, 021912. [Google Scholar] [CrossRef] [PubMed]
- Collins, A.L. Orchestrated objective reduction: quantum physics and its implications in human consciousness. College of William and Mary—Degree Program thesis 2015.
- Aguilera, M.; Millidge, B.; Tschantz, A.; Buckley, C.L. How particular is the physics of the free energy principle? Physics of Life Reviews 2022, 40, 24–50. [Google Scholar] [CrossRef]
- Buckley, C.L.; Kim, C.S.; McGregor, S.; Seth, A.K. The free energy principle for action and perception: A mathematical review. Journal of mathematical psychology 2017, 81, 55–79. [Google Scholar] [CrossRef]
- Andrews, M. The math is not the territory: navigating the free energy principle. Biology & Philosophy 2021, 36, 30. [Google Scholar]
- Zhang, Z.; Xu, F. An overview of the free energy principle and related research. Neural Computation 2024, 36, 963–1021. [Google Scholar] [CrossRef]
- Kiverstein, J.; Kirchhoff, M.D.; Froese, T. The problem of meaning: The free energy principle and artificial agency. Frontiers in Neurorobotics 2022, 16, 844773. [Google Scholar] [CrossRef]
- van Es, T. Living models or life modelled? On the use of models in the free energy principle. Adaptive Behavior 2021, 29, 315–329. [Google Scholar] [CrossRef]
- Baars, B.J. The global workspace theory of consciousness: Predictions and results. The Blackwell companion to consciousness 2017, 227–242. [Google Scholar]
- Baars, B.J.; Franklin, S. Consciousness is computational: The LIDA model of global workspace theory. International Journal of Machine Consciousness 2009, 1, 23–32. [Google Scholar] [CrossRef]
- Berger, J.; Mylopoulos, M. HOTT and heavy: higher-order thought theory and the theory-heavy approach to animal consciousness. Synthese 2024, 203, 98. [Google Scholar] [CrossRef]
- Byrne, A. Some like it HOT: Consciousness and higher-order thoughts. Philosophical Studies: An International Journal for Philosophy in the Analytic Tradition 1997, 86, 103–129. [Google Scholar] [CrossRef]
- Sebastián, M.Á. Drop it like it’s HOT: a vicious regress for higher-order thought theories. Philosophical Studies 2019, 176, 1563–1572. [Google Scholar] [CrossRef]
- Seth, A.K.; Bayne, T. Theories of consciousness. Nature reviews neuroscience 2022, 23, 439–452. [Google Scholar] [CrossRef]
- Albantakis, L.; Barbosa, L.; Findlay, G.; Grasso, M.; Haun, A.M.; Marshall, W.; Mayner, W.G.; Zaeemzadeh, A.; Boly, M.; Juel, B.E. Integrated information theory (IIT) 4.0: formulating the properties of phenomenal existence in physical terms. PLoS computational biology 2023, 19, e1011465. [Google Scholar] [CrossRef]
- Cea, I.; Negro, N.; Signorelli, C.M. Only consciousness truly exists? Two problems for IIT 4.0’s ontology. Frontiers in Psychology 2024, 15, 1485433. [Google Scholar] [CrossRef]
- Ferrante, O.; Gorska-Klimowska, U.; Henin, S.; Hirschhorn, R.; Khalaf, A.; Lepauvre, A.; Liu, L.; Richter, D.; Vidal, Y.; Bonacchi, N.; et al. Adversarial testing of global neuronal workspace and integrated information theories of consciousness. Nature 2025. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).