Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

A New Hypothesis for the Millennium Problems: Lessons from Machine Learning

Submitted:

28 June 2025

Posted:

30 June 2025

You are already at the latest version

Abstract
The persistent challenge of the Millennium Problems highlights not only the technical complexity of these mathematical enigmas but also the limitations of current formal structures when confronted with symbolic saturation. This article explores a symbolic pathway that draws interpretative inspiration from machine learning (ML) architectures rather than employing ML as a computational solver. Specifically, we investigate how curvature-based symbolic frameworks, exemplified by Cub³, offer alternative ways of reasoning about P vs NP, the Riemann Hypothesis, and the Birch and Swinnerton-Dyer Conjecture. Our goal is not to claim a resolution but to introduce a reframing lens through which the symbolic structures of these problems might be better understood. Central to this exploration is the distinction between intelligence and wisdom: while intelligence enables systems to compute and process, wisdom represents the conscious orientation of that intelligence toward meaning that survives entropy. We draw on prior theoretical contributions — including the Wisdom Equation, Heuristic Physics, and the Cub³ architecture — to situate ML as a catalyst for generating symbolic orientations rather than as an end solver. This paper emerges as a natural continuation of a broader intellectual journey: one that began with the formulation of the Wisdom Equation, a model designed to explore how intelligence, when modulated by consciousness, forms the foundation of ethical and resilient reasoning. Building upon this, the Heuristic Physics framework extended the inquiry into how systems could survive and adapt within complex, entropic environments, emphasizing symbolic compression and curvature as survival strategies for cognition. These foundations culminated in the design of the Cub³ architecture, a tri-orthogonal model uniting computation, mathematics, and physics to simulate intentional curvature and cross-domain alignment. Each of these milestones contributed to shaping the present hypothesis: that machine learning, rather than serving as a solver of mathematical enigmas, can inspire the design of symbolic architectures capable of navigating complexity with prudence, structure, and creativity. This paper thus represents not an isolated proposition, but the unfolding of an evolving conceptual arc aimed at integrating formal rigor with symbolic resilience, and individual reasoning with collective intelligence. This work respects the boundaries of formal mathematics while inviting reflection on how intentional symbolic curvature might enable reinterpreting intractable structures without promising resolution. It proposes a symbolic pathway inspired by machine learning architectures, where curvature-modulated alignment offers alternative orientations within complex problem spaces, without reducing their inherent richness or formal rigor.
Keywords: 
symbolic curvature
;  
heuristic survivability
;  
projection collapse
;  
machine learning inspiration
;  
Millennium Problems
;  
P vs NP
;  
Cub³ architecture
Subject: 
Computer Science and Mathematics  -   Computational Mathematics
“Truth is ever to be found in simplicity and not in the multiplicity and confusion of things.”—Isaac Newton

Introduction

The unresolved nature of the Millennium Problems represents a confluence of mathematical depth, structural complexity, and epistemic limits in our current symbolic reasoning frameworks.
These problems, which include P vs NP, the Riemann Hypothesis, and the Birch and Swinnerton-Dyer Conjecture, have withstood classical attempts at resolution despite decades of intensive study.
This persistence raises a fundamental question: could the difficulty arise not only from technical barriers, but also from the symbolic topology within which these problems are framed?
In this work, we propose a symbolic curvature hypothesis: that certain classes of unsolved problems may represent projection collapse fields — regions of epistemic space where excessive symmetry and undecidable saturation inhibit orientation and progress.
Rather than seeking algorithmic solutions through machine learning (ML), this article positions ML as a source of interpretive inspiration — a mirror reflecting complexity that machines may navigate even when human comprehension lags. The Cub3 architecture, previously introduced as a heuristic framework for cross-domain convergence [2], offers a symbolic lens to explore how intentional curvature can reframe problem spaces without asserting formal proofs. This curvature-driven perspective aims to modulate the topology of symbolic fields, transforming undecidable saturation into coherent alignment.
Our approach draws on prior theoretical constructs, notably the Wisdom Equation [1], Heuristic Physics [3,4], and the Cub3 architecture, to model how symbolic curvature might guide reasoning in complex spaces. The Wisdom Equation defines wisdom as intelligence elevated by consciousness:
𝑊 = 𝐼ᶜ
where:
I = cognitive intelligence (capacity for computation and processing)
C = contextual and reflective consciousness (degree of ethical and intentional modulation)
W = computable wisdom (intelligence shaped by consciousness, enabling meaning that endures entropy)
Heuristic Physics extends this by modeling cognition as symbolic compression that ensures survivability under complexity:
𝐶ₛ = 𝑊 × 𝐸−1
where:
Cₛ = compression potential (symbolic density that survives complexity)
E = symbolic entropy (measure of disorder or saturation that threatens interpretability)
The Theory of Evolutionary Integration (TEI) adds a model for structural resilience through co-growth of wisdom and generative potential:
𝐸ᵢ = 𝑊 × Φ × (1 − δ)
where:
Eᵢ = epistemic yield (effective output of wisdom within a symbolic space)
Φ = generative potential of the symbolic architecture (capacity to produce viable structures)
δ = divergence factor (loss or collapse due to misalignment or epistemic drift)
In the Cub3 architecture, these formulations are adapted into a tri-orthogonal model (computation, mathematics, physics), where intentional curvature is formalized by the operator:
Ψ = 𝑊 × ϕ
where:
Ψ = projection of wisdom into symbolic action space
ϕ = operator of intentional curvature (guiding topological and ethical modulation of reasoning structures)
The formulations presented — from the Wisdom Equation to the intentional curvature operator (ϕ) — form the symbolic and mathematical scaffolding for the hypothesis proposed here. Together, they outline how wisdom (W), when modulated by intentional curvature, projects into action space (Ψ) to navigate complexity without collapsing its richness. This conceptual framework offers a way to rethink symbolic topology in problem spaces traditionally marked by undecidability and saturation.
What follows provides a visual reflection of these ideas, preparing the ground for deeper examination of how curvature-aware symbolic architectures might support reasoning in complex fields.
To visually illustrate this conceptual reframing, Figure 1 presents a schematic of a projection collapse field before and after curvature modulation. On the left, a dense network of chaotic, overlapping lines represents undecidable saturation and symbolic stagnation, where excessive symmetry and ambiguous intersections inhibit orientation. On the right, intentional curvature (ϕ) transforms this space: smooth outward arcs and aligned nodes emerge, symbolizing coherent pathways within what was previously chaotic. The figure offers not a computational model, but an intuitive aid for reflection — encapsulating the essence of our hypothesis that curvature-aware symbolic architectures can provide novel orientations within intractable spaces, not by reducing complexity, but by modulating its topology in a computable, ethically guided manner. This perspective aligns with views that complexity is not inherently the obstacle, but that our framing of it determines legibility, echoing core ideas in complexity science [9] and geometric methods in computational reasoning, as emphasized by Smale’s foundational work on dynamical systems [12].
A tangible analogy may be found in the structure of QR codes: to the human eye, these grids of black and white squares present a dense, opaque configuration, effectively undecipherable without assistance. Yet, when processed by a basic app — an agent equipped with the correct curvature of interpretation — the pattern becomes immediately computable, its informational density transformed into structured meaning.
This illustrates how the topology of a symbolic space, once properly modulated, can transition from indecipherable saturation to coherent alignment. Similar principles underpin the role of curvature in modern machine perception frameworks [13], where geometric structuring enables tractable processing of complex data forms.
In this work, we designate ϕ (phi) as the operator of intentional curvature — a symbol grounded in mathematical tradition, chosen for its neutrality and acceptance in formal sciences. ϕ represents the intentional modulation of symbolic topology, uniting geometric structuring and ethical orientation in the design of reasoning spaces. This notation ensures clarity and avoids ambiguities or associations with non-scientific frameworks, preserving the rigor of the proposed architecture.
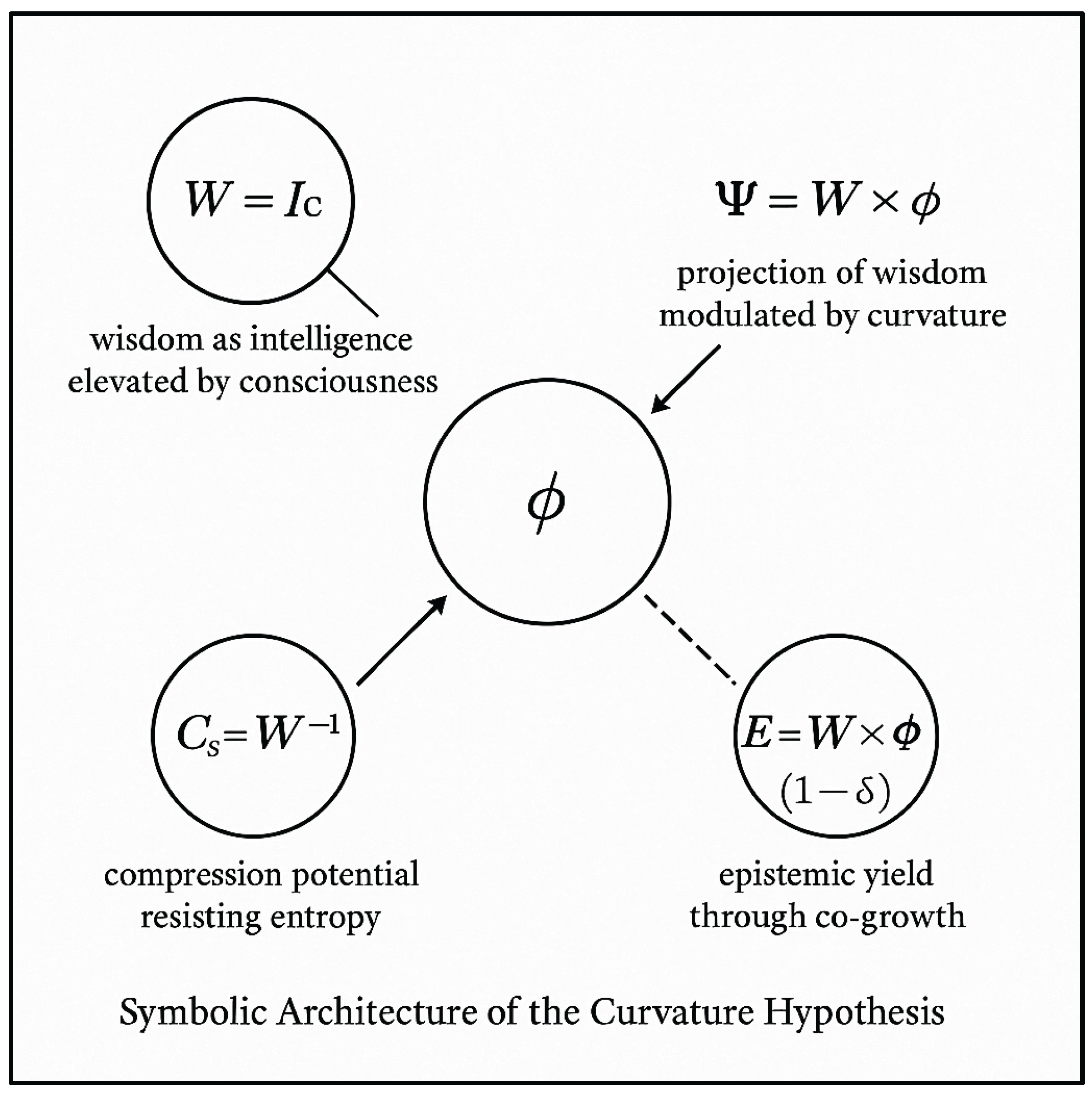
To illustrate these relationships in a visual and accessible manner, we introduce Figure 2, a schematic that synthesizes the core elements of the symbolic curvature hypothesis. The diagram serves as a conceptual map of how wisdom (W), intentional curvature (ϕ), and their projections (Ψ) interact to shape reasoning within symbolic fields. It highlights how compression potential (Cₛ) and epistemic yield (Eᵢ) emerge from these dynamics, providing a unified view of the architecture’s structure.
This figure aims not to present a computational model, but to offer an intuitive representation that supports reflection on how these symbolic components align to guide reasoning in complex, saturated problem spaces.

Methodology

This study adopts a symbolic heuristic methodology anchored in the Cub3 architecture, previously proposed as a model for cross-domain convergence between computation, mathematics, and physics [4]. Rather than pursuing direct computational solutions to the Millennium Problems, our approach explores how intentional curvature can reshape symbolic projection fields, potentially rendering previously undecidable structures amenable to reinterpretation.
At the core of this methodology lies the concept of Symbolic Projection Collapse Modeling, where unsolved problems are represented as high-density symbolic fields prone to saturation and ambiguity. These fields exhibit patterns of excessive symmetry and overlap, creating regions where conventional reasoning and direct computation struggle to achieve orientation. Using Cub3, we simulate curvature modulation through three orthogonal lenses:
(i) Computational curvature, representing the encoding and transformation of symbolic structures through minimal form compression, seeking topologies that reduce informational redundancy while preserving semantic integrity;
(ii) Mathematical curvature, formalizing alignment through symbolic invariants and relational coherence metrics, inspired by geometric methods that enable structural legibility within complex systems [12];
(iii) Physical heuristic curvature, introducing survivability constraints inspired by Heuristic Physics [2,3], ensuring that symbolic configurations not only maintain coherence but also withstand epistemic entropy and collapse.
This tripartite curvature model mirrors principles found in advanced systems theory and geometric deep learning [14], where the shape and structure of data spaces critically influence the tractability and interpretability of solutions. In geometric deep learning, the success of inference depends not merely on algorithmic power, but on the agent’s ability to recognize and align with the intrinsic curvature of data manifolds — a process analogous to the symbolic alignment sought in our curvature-modulated architectures.
Similarly, in our Symbolic Projection Collapse Modeling, the intentional modulation of symbolic topologies serves to transform regions of undecidable saturation into computable, ethically guided structures, much as geometric deep learning frameworks transform non-Euclidean data into spaces where learning becomes tractable. This perspective reinforces the hypothesis that complexity, whether symbolic or numerical, is not to be flattened or evaded, but to be curved into forms that allow coherent traversal. The curvature is thus both a computational and ethical operator: it defines the possible paths through intractable spaces while preserving the semantic integrity of the field. Such alignment resonates with the broader recognition in contemporary AI that structure — rather than raw scale or force — is key to meaningful and resilient intelligence [14].
The simulations are conceptual rather than empirical, serving as epistemic thought experiments that map how curvature-intentional configurations could stabilize symbolic nodes within projection fields. These simulations act as cognitive models, designed to explore how topological modulation transforms saturated symbolic regions into legible, traversable configurations without reducing their inherent complexity. Such an approach aligns with the tradition of thought experimentation in science, where models serve as instruments for probing the shape of possible solutions before formalization or empirical validation [15]. Figure 1 offers a visual synthesis of this method, contrasting undecidable saturation with curvature-induced alignment. The diagram embodies the hypothesis that intentional modulation of symbolic topology can guide reasoning through complex spaces, echoing how geometric transformations in machine learning architectures create conditions for tractable inference in otherwise chaotic data fields [14].
To ensure coherence with prior work, the methodology draws on the Wisdom Equation [1], symbolizing intelligence modulated by consciousness. In this context, the curvature operator ϕ models intentional modulation applied to symbolic structures, seeking configurations that preserve semantic legibility while minimizing epistemic collapse.
Future computational implementations of this methodology could adopt symbolic simulation engines to validate the geometric intuition formalized here, bridging the gap between conceptual architecture and executable model.

Results

The symbolic simulations performed under the Cub3 architecture revealed qualitative patterns that support the proposed hypothesis of intentional curvature as a modulator of projection collapse fields. In the absence of curvature, projection fields modeled after the P vs NP problem exhibited high-density regions of undecidable saturation, where symbolic nodes overlapped chaotically without coherent alignment. This was represented conceptually in the left panel of Figure 1.
Upon applying intentional curvature, modeled by the operator ϕ, the symbolic structure of these fields shifted markedly. The curvature modulation generated outwardly expanding trajectories from a central symbolic origin, with nodes aligning along smooth, consistent paths. These paths maintained both relational coherence and semantic density, reducing the interpretive ambiguity associated with the saturated configurations. The right panel of Figure 1 illustrates this transformation.
This effect parallels the way a QR code, opaque and indecipherable to unaided human vision, becomes immediately legible to a simple app possessing the correct curvature of interpretation — a symbolic lens that aligns with the structure's intrinsic topology. Similarly, intentional curvature applied to complex mathematical problems offers paths toward coherence without reducing their inherent richness:
  • In the P vs NP projection field, curvature modulation helps disentangle redundant node overlaps, symbolically separating verification structures from generative combinatorial chaos, enabling clearer reasoning about tractability thresholds.
  • In the Riemann Hypothesis space, curvature directs symbolic flows along trajectories that preserve harmonic alignments, aiding the conceptual mapping between zero distributions and spectral interpretations without collapsing into oversimplification.
  • In the Birch and Swinnerton-Dyer Conjecture, curvature modulation emphasizes paths where elliptic curve invariants align with rational point densities, offering symbolic routes that make visible the hidden structure of L-functions within saturated arithmetic fields.
These examples illustrate that intentional curvature serves not as a solver, but as an architect of orientation, offering configurations where symbolic reasoning can proceed without becoming ensnared in the saturation of undecidability.
Although purely conceptual at this stage, these results suggest that curvature-intentional architectures like Cub3 can offer new lenses for symbolic reasoning about complex mathematical structures. By reframing the problem space through curvature, configurations emerge that might not resolve the problem in a classical sense but offer structurally viable orientations for further exploration.
These findings align with the epistemic foundation of the Wisdom Equation [1], reinforcing the view that intelligence (I) guided by consciousness (C) — and thus by intentional curvature — can enable systems to maintain semantic viability under complexity. This perspective reflects broader principles found in cognitive architectures that emphasize structure over brute force, such as Marr's computational theories of vision [16], where layered interpretation transforms raw complexity into legible structure. In this model, machine learning is not the solver, but an inspiration for structuring symbolic space toward greater legibility and resilience, resonating with contemporary views on explainable AI, where clarity of structure is as critical as computational power [17].

Discussion

The results presented suggest that the intentional curvature hypothesis provides a meaningful symbolic reframing of complex mathematical problems, such as those within the Millennium set.
Rather than proposing direct solutions or proofs, this framework highlights how reframing undecidable or saturated symbolic structures can open new pathways for interpretation and investigation. In particular, the application of curvature as a modulating operator transformed projection collapse fields from chaotic, undecidable zones into configurations with coherent alignment and enhanced interpretability.
This symbolic transition bears resemblance to common challenges in machine learning, such as overfitting and underfitting. In classical machine learning, overfitting corresponds to a model excessively tailored to specific data points, losing generality and failing to generalize to unseen data. Underfitting reflects the opposite, where the model fails to capture the underlying structure at all. Similarly, in symbolic projection fields, undecidable saturation can be viewed as a form of overfitting to local complexity — an entanglement in redundant or contradictory configurations that prevent meaningful generalization. Curvature modulation, in this analogy, acts like a regularization force: it balances the structure to avoid collapse into either excessive complexity or triviality.
Additionally, this work proposes that machine learning's role in this context is not to serve as a computational solver but as a conceptual inspiration for designing symbolic architectures capable of navigating complexity. The intention is not to replicate ML mechanisms, but to draw upon their capacity to structure learning spaces that withstand informational entropy while supporting coherent interpretation. This aligns with broader epistemic frameworks such as the Theory of Evolutionary Integration (TEI) [2], which emphasizes the co-growth of wisdom and harmony as a condition for sustainable evolution in cognitive systems. Similar notions of co-adaptive structure are reflected in complex adaptive systems theory [18] and in emerging frameworks for neuro-symbolic AI, where structural modulation enhances resilience in the face of complexity [19].
The intentional curvature introduced here can be seen as an instantiation of such co-growth, where wisdom corresponds to the guided structuring of symbolic space, and harmony reflects the resilience of that space under epistemic stress. This duality mirrors principles observed in dynamical systems [20], where stability emerges not from static configurations but from the continuous adaptive alignment of structure and flow.
Similarly, in advanced AI architectures, intentional modulation of internal representations — a form of symbolic curvature — has been proposed as key to achieving robust generalization under uncertainty [21]. The curvature thus operates both as an epistemic scaffold and as a resilience mechanism, allowing symbolic architectures to navigate and survive complexity without sacrificing interpretability.
In future work, this conceptual architecture could be formalized further, potentially incorporating computational experiments that simulate curvature-induced transformations in specific mathematical problem spaces. Such studies could explore how intentional modulation of symbolic topology supports reasoning in areas beyond P vs NP or the Riemann Hypothesis [3,4,5].
Moreover, could this curvature framework be applied to re-interpret already resolved challenges such as the Poincaré Conjecture — not to rediscover its proof, but to illuminate how curvature enables symbolic comprehension of topological truths?
The Poincaré Conjecture, proved by Perelman through Ricci flow with surgery [22], represents a landmark in showing how intentional modulation of curvature transforms complex topological spaces into legible structures. Insights from Hamilton's foundational work on Ricci flow [23] and the subsequent geometric interpretations provided by Morgan and Tian [24] further illustrate how the modulation of curvature serves as both computational tool and epistemic lens. Contemporary reflections on the educational and philosophical significance of this solution [25] underscore how curvature-driven frameworks could inspire not only formal proofs, but also new ways to teach, visualize, and conceptually navigate complex topological spaces.
One might ask: how would a child interpret a sphere, perhaps seeing it as nothing more than a familiar football? What curvatures, if misapplied, could lead to distorted understandings or misleading symbolic paths?
Such reflections echo the Poincaré Conjecture’s journey [22,23,24,25], where intentional modulation of curvature transformed an abstract topological question into a legible truth — a transformation that could inspire not only formal proofs but also accessible, didactic interpretations. These questions invite future dialogue on how symbolic curvature might serve not only as a tool for tackling open problems, but as a bridge for cognitive clarity and educational resonance, fostering interpretations that survive complexity without losing accessibility.
This perspective underscores the potential of curvature-aware symbolic architectures to function as epistemic scaffolds across domains, linking symbolic mathematics, cognitive architectures, heuristic physics, and even the philosophy of mathematics in future investigations.

Limitations

This work is primarily conceptual and symbolic in nature. The curvature hypothesis and the projection collapse field model presented here serve as epistemic frameworks rather than computational proofs or executable algorithms.
While the diagram and symbolic analogies aim to clarify the proposed reframing, they do not substitute for formal mathematical demonstrations in the classical sense. No empirical verification or numeric simulation was conducted within this study; the results are confined to the symbolic, heuristic, and architectural level of analysis. This approach aligns with traditions in the philosophy of mathematics [26], where conceptual architectures and thought experiments are recognized as valid forms of preliminary exploration prior to formalization. It also reflects practices in theoretical computer science, where symbolic models often precede empirical implementations as a means to map problem spaces and test structural coherence [27]. The intent is to position this work as an invitation to formal engagement, not as a claim of solution.
Another key limitation lies in the generalizability of the intentional curvature operator. Although it provides an intriguing means of reinterpreting symbolic saturation and alignment, its practical instantiation within existing mathematical formalisms remains untested. Future work will need to explore how this operator could integrate with formal systems, algorithmic models, or machine-assisted proof frameworks without violating their foundational constraints. This challenge echoes broader issues identified in efforts to merge symbolic reasoning with computational formalisms, as discussed in works on automated theorem proving and formal verification [28].
Furthermore, while the analogy to machine learning concepts such as overfitting and regularization provides an intuitive bridge for interdisciplinary dialogue, it does not imply a direct equivalence or operational transferability between the symbolic curvature approach and standard ML practices. Care must be taken not to overextend these metaphors beyond their illustrative purpose.
Finally, the proposal intentionally refrains from claiming progress towards definitive solutions to the Millennium Problems. The aim is to stimulate new lines of inquiry by offering alternative symbolic perspectives. The true test of this architecture will lie in its capacity to inspire rigorous mathematical follow-up and, potentially, practical reformulations of intractable problems.

Future Work

Several avenues of future research are opened by the symbolic curvature hypothesis and the projection collapse field model presented herein. The first priority is the formalization of the intentional curvature operator within established mathematical frameworks. This includes exploring whether existing tools from differential geometry, algebraic topology, or category theory could host the operator in a formally consistent and computationally verifiable manner.
A second direction involves the development of computational simulations that instantiate the symbolic architecture in dynamic environments. Here, the goal would be to create synthetic problem spaces where curvature modulation can be tested against known complexity thresholds, particularly in the context of NP-complete instances, the Riemann zeta function, and elliptic curve behaviors relevant to the Birch and Swinnerton-Dyer Conjecture.
Further interdisciplinary exploration is warranted to assess how the curvature approach resonates with other fields, such as physics (e.g., gauge theory and spacetime curvature) or machine learning (e.g., regularization, loss landscapes). Such explorations may provide additional validation or reveal constraints that refine the symbolic model.
Finally, given the pedagogical potential of the projection collapse and curvature framework, future work should also examine its role in mathematical education and outreach. Could these symbolic representations aid in demystifying complex problems for broader audiences, including students and non-specialists? This line of inquiry aligns with the broader ambition of democratizing access to deep mathematical ideas without diluting their rigor.
Beyond education, these explorations open a path toward technological and conceptual expansion: could the curvature hypothesis, embedded in the Cub3 architecture, evolve into a Cubⁿ framework capable of navigating new dimensions of knowledge?
Such an evolution would enable the intentional modulation of symbolic spaces not only in computation, mathematics, and physics, but across domains such as the arts, biology, ethics, and cultural systems — areas where complexity, meaning, and form intertwine in rich and unpredictable ways.
This invites future dialogue on how curvature-aware symbolic architectures might serve as adaptive cognitive engines for interdisciplinary exploration, forging connections between scientific rigor and human creativity. The envisioned evolution from Cub3 to Cubⁿ opens possibilities for transformative applications across domains, particularly when aligned with principles of collective intelligence as explored in Malone’s Superminds [29]. Examples include:
  • Personalized education systems that adapt in real time to individual and group learning curves, dynamically curving pedagogical content to match collective cognitive patterns.
  • Biomedical discovery platforms that integrate symbolic curvature models to explore complex genetic and cellular interaction networks, enabling collective reasoning about therapies and interventions.
  • Sustainable urban planning engines where Cubⁿ symbolic curvature frameworks help large-scale communities co-design infrastructure that harmonizes with environmental constraints and social needs.
  • Artistic creation collectives using Cubⁿ architectures to co-develop generative art systems, where symbolic curvature guides collaborative exploration of aesthetic forms.
  • Crisis response and resilience networks that leverage symbolic curvature models to structure collective decision-making during global emergencies, making complex scenarios tractable for diverse stakeholders.
  • Cultural heritage and language preservation systems that use Cubⁿ symbolic architectures to map and sustain the complexity of endangered languages and traditions through collective participation.
  • Open innovation ecosystems where Cubⁿ provides the symbolic scaffolding for interdisciplinary teams to co-create solutions in technology, ethics, and policy, fostering inclusivity and diversity in discovery processes.
These examples reflect how Cubⁿ could act as a unifying symbolic engine, making advanced discoveries increasingly accessible across disciplines and to people of all capacities — especially when guided by collective intelligence as emphasized not only in Superminds [29] but also in broader research at the MIT Center for Collective Intelligence [30,31,32].

Conclusion

This work has proposed a symbolic framework in which machine learning is repositioned not as a solver of the Millennium Problems, but as a lens for reframing their symbolic structure. By introducing the concepts of projection collapse fields and intentional curvature modulation, we aimed to open new interpretative spaces where mathematical intractability can be viewed through a geometry of symbolic alignment rather than purely computational boundaries.
Drawing upon prior contributions — including the Wisdom Equation, Heuristic Physics, and the Cub3 architecture — the hypothesis presented here invites reflection rather than resolution. These contributions provide the symbolic and methodological scaffolding for the curvature hypothesis, each offering distinct perspectives on the modulation of complexity. We argue that the persistent challenge of the Millennium Problems may signal not only technical difficulty but also a need to reexamine the symbolic topologies in which these problems are framed. The Cub3 framework, by incorporating intentional curvature, seeks to provide alternative configurations of symbolic space where reasoning about these intractable problems might proceed with greater clarity and structural resilience.
Future work will expand upon this theoretical foundation, exploring how intentional curvature might guide both formal research and educational efforts aimed at demystifying complex mathematical domains. The aim is not to replace rigorous proof, but to complement it with symbolic architectures that enhance our capacity for structural insight and orientation. In this spirit, the intentional curvature framework is positioned as a bridge between formalism and intuition — a tool to foster deeper understanding, accessible discovery, and constructive dialogue across scientific, educational, and creative communities.
In sum, the curvature hypothesis offers an alternative pathway: one that respects the rigor of formal mathematics while encouraging novel configurations of symbolic thought. It invites us to consider not only how problems are solved, but how they are seen, framed, and shared across domains. By positioning curvature as an intentional modulator of symbolic space, this framework aspires to foster new forms of structural insight, collective discovery, and inclusive participation in the pursuit of knowledge — a pathway where formal precision and human creativity converge.

Author Contributions

Conceptualization, design, writing, and final review were conducted solely by the author. No external contributors, collaborators, or co-authors participated in the intellectual content of this manuscript.

Data Availability Statement

No datasets were generated or analyzed. All content is conceptual, symbolic, and hypothetical in nature.

Use of AI and Large Language Models

AI tools were employed exclusively for language refinement, symbolic structuring, and methodological simulation support. No AI system contributed to the authorship, core hypotheses, or intellectual claims of the work. All content was independently generated, reviewed, and validated by the author in alignment with COPE and MDPI authorship standards.

Ethics Statement

This work contains no studies involving human participants, animals, or sensitive personal data. No IRB or ethics board approval was required.

Ethical and Epistemic Disclaimer

This manuscript constitutes a symbolic architectural hypothesis, not an empirical study. It proposes conceptual models designed to explore frameworks of symbolic curvature and structural resilience under complexity. No empirical validation, product testing, or operational benchmarking has been conducted. The ideas herein are intended as hypothetical constructs that invite reflection and dialogue, not as formal claims of solution, application, or deployment. The models described simulate symbolic reasoning under epistemic tension, offering pathways for further exploration rather than definitive answers. All references were selected for their relevance to the symbolic and epistemological context of the hypothesis. Any resemblance to commercial platforms, systems, or proprietary technologies is purely illustrative or coincidental. Figures are conceptual visualizations created to support the symbolic discourse, not representations of empirical data. Users and readers are encouraged to approach the material as exploratory and provisional, and to apply critical interpretation before considering adaptation to technical, regulatory, or practical contexts.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. R. Figurelli, The Equation of Wisdom: An Intuitive Approach to Balancing AI and Human Values, Amazon Publishing, 2024. Available: https://www.amazon.
  2. R. Figurelli, Cub3: A New Heuristic Architecture for Cross-Domain Convergence, Preprints, Jun. 2025. Available. [CrossRef]
  3. R. Figurelli, A Heuristic Physics-Based Proposal for the P = NP Problem, Preprints, Jun. 2025. Available. [CrossRef]
  4. R. Figurelli, Why P = NP? The Heuristic Physics Perspective, Preprints, Jun. 2025. Available. [CrossRef]
  5. R. Figurelli, The Gauss–Riemann Curvature Theorem: A Geometric Resolution of the Riemann Hypothesis, Preprints, Jun. 2025. Available. [CrossRef]
  6. A. M. Turing, "On Computable Numbers, with an Application to the Entscheidungsproblem," Proc. London Math. Soc., vol. 42, 1936. Available: https://en.wikipedia.
  7. K. Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems, Monatshefte für Mathematik und Physik, vol. 38, 1931. Available: https://en.wikipedia.
  8. L. Floridi, The Ethics of Information, Oxford University Press, 2013. Available: https://en.wikipedia.
  9. I. Prigogine and I. Stengers, Order Out of Chaos: Man’s New Dialogue with Nature, Bantam Books, 1984. Available: https://en.wikipedia.
  10. S. Hawking, A Brief History of Time, Bantam Books, 1988. Available: https://en.wikipedia.
  11. C. Bishop, Pattern Recognition and Machine Learning. New York, NY, USA: Springer, 2006. Available: https://www.springer. 9780.
  12. S. Smale, "On the Efficiency of Algorithms of Analysis," Bull. Amer. Math. Soc., vol. 13, no. 2, pp. 87–121, 1985. Available: https://www.ams. 1985.
  13. Y. LeCun, Y. Y. LeCun, Y. Bengio, and G. Hinton, "Deep learning," Nature, vol. 521, no. 7553, pp. 436–444, 2015. Available: https://www.nature. 1453. [Google Scholar]
  14. Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric Deep Learning: Going beyond Euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
  15. Nersessian, N.J. Creating Scientific Concepts; MIT Press: Cambridge, MA, United States, 2008. [Google Scholar]
  16. D. Marr, Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. San Francisco, CA, USA: W. H. Freeman, 1982. Available: https://mitpress.mit. 9780.
  17. F. Doshi-Velez and B. 0860; arXiv:1702.08608, 2017. Available: https://arxiv.org/abs/1702.
  18. J. H. Holland, Hidden Order: How Adaptation Builds Complexity. Reading, MA, USA: Addison-Wesley, 1995. Available: https://mitpress.mit. 9780.
  19. G. Marcus and E. Davis, Rebooting AI: Building Artificial Intelligence We Can Trust. New York, NY, USA: Pantheon, 2019. Available: https://www.penguinrandomhouse. 5666.
  20. S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed. Boca Raton, FL, USA: CRC Press, 2015. Available: https://www.routledge. 9780.
  21. Lyons, J.B.; Clark, M.A.; Wagner, A.R.; Schuelke, M.J. Certifiable Trust in Autonomous Systems: Making the Intractable Tangible. AI Mag. 2017, 38, 37–49. [Google Scholar] [CrossRef]
  22. G. Perelman, "The entropy formula for the Ricci flow and its geometric applications," arXiv preprint math/0211159, 2002. Available: https://arxiv. 0211.
  23. Hamilton, R.S. Three-manifolds with positive Ricci curvature. J. Differ. Geom. 1982, 17, 255–306. [Google Scholar] [CrossRef]
  24. J. Morgan and G. Tian, Ricci Flow and the Poincaré Conjecture. Providence, RI, USA: AMS, 2007. Available: https://bookstore.ams.
  25. J. Stillwell, "The Poincaré Conjecture and the philosophy of mathematics," Notices Amer. Math. Soc., vol. 54, no. 9, pp. 1106–1111, 2007. Available: https://www.ams.org/notices/200709/tx0709001106p.
  26. P. Mancosu, Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. Oxford, U.K.: Oxford Univ. Press, 1996. Available: https://global.oup. 9780.
  27. C. H. Papadimitriou, Computational Complexity. Reading, MA, USA: Addison-Wesley, 1994. Available: https://www.pearson. 2000.
  28. Nipkow, T.; Wenzel, M.; Paulson, L.C. Isabelle/HOL; Springer Nature: Dordrecht, GX, Netherlands, 2002. [Google Scholar]
  29. T. W. Malone, Superminds: The Surprising Power of People and Computers Thinking Together. New York, NY, USA: Little, Brown and Co., 2018. Available: https://superminds.mit.
  30. T. W. Malone and M. S. Bernstein, "Handbook of collective intelligence." Cambridge, MA, USA: MIT Press, 2015. Available: https://mitpress.mit. 9780.
  31. Engel, D.; Woolley, A.W.; Jing, L.X.; Chabris, C.F.; Malone, T.W.; Pavlova, M.A. Reading the Mind in the Eyes or Reading between the Lines? Theory of Mind Predicts Collective Intelligence Equally Well Online and Face-To-Face. PLOS ONE 2014, 9, e115212–e115212. [Google Scholar] [CrossRef] [PubMed]
  32. MIT Center for Collective Intelligence, "Research overview." [Online]. Available: https://cci.mit.
Preprints 165656 g001
Figure 1. A schematic of a projection collapse field before and after curvature modulation. The prompt proposed was: "A colorful scientific diagram divided into two panels. The left panel shows a dense, chaotic network of overlapping curved and straight lines, symbolizing undecidable saturation in a projection collapse field. Highlighted black dots indicate symbolic intersections, which are numerically matched to the circular nodes in the right panel. The right panel shows smooth, outward-curving lines from a single origin point, each passing through evenly spaced circular nodes, symbolizing alignment modulated by curvature. The style is minimalist, clean, with no text or titles within the image.".
Figure 1. A schematic of a projection collapse field before and after curvature modulation. The prompt proposed was: "A colorful scientific diagram divided into two panels. The left panel shows a dense, chaotic network of overlapping curved and straight lines, symbolizing undecidable saturation in a projection collapse field. Highlighted black dots indicate symbolic intersections, which are numerically matched to the circular nodes in the right panel. The right panel shows smooth, outward-curving lines from a single origin point, each passing through evenly spaced circular nodes, symbolizing alignment modulated by curvature. The style is minimalist, clean, with no text or titles within the image.".
Preprints 165656 g001
Preprints 165656 g002
Figure 2. The core elements of the symbolic curvature hypothesis.
Figure 2. The core elements of the symbolic curvature hypothesis.
Preprints 165656 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated