Introduction
This work begins not with a cryptic equation or the language of formal proofs, but with a simple metaphor.
Imagine a composer at the piano. In one hand, the chords of harmony — steady, grounding, intentional, measured, predictable, reassuring — like P, representing structure and clarity. In the other, the flowing melodies of the solo — restless, exploratory, sometimes dissonant, improvisational, unpredictable, provocative — like NP, embodying potential and ambiguity. Together, these hands shape a composition that unfolds through tension and resolution, repetition and surprise, contrast, dialogue, emergence. In the end, the piece reaches a unity that touches the listener’s soul.
Such a dynamic is not unique to music. It echoes through the paradoxes of nature: in genetics, where ordered sequences of DNA house both stability and mutation, enabling life to both preserve and evolve; in ecosystems, where harmony emerges from the interplay of competing species, each shaping and being shaped by the others; in human relationships, where cooperation and conflict co-exist, propelling societies toward greater complexity and understanding. In all these domains, what first appears as contradiction reveals itself as co-evolution — a dance of forces that, through interplay, gives rise to deeper forms of order.
Other examples where complementarity highlights the potential for co-evolution, both in nature and in organizations, are the symbiotic interactions between fungi and plants in mycorrhizae, and the strategic partnerships between organizations that combine distinct skills to innovate and grow, or even the relationships between pollinators and flowers, the collaboration between multidisciplinary teams, the alliances between startups and large corporations, the flows between rivers and their banks, the processes between suppliers and distributors, the interaction between technology and culture, the agreements between nations with different interests, the balances between regulation and the market. In all of them, P and NP do not exclude each other, but intertwine and mutually strengthen each other, generating new possibilities for adaptation, innovation and balance.
From this perspective, expecting the result of P vs NP to be true or false seems like an oversimplification. In fact, the apparent dichotomy may hide a deeper relationship of interdependence and complementarity between different forms of solution and complexity.
Furthermore, it may reveal that progress occurs precisely in the dialogue between these poles, where the tension between order and potential paves the way for new discoveries and innovations. This is even more so if co-evolution occurs not only in one visible layer, but in several others, as in the case of multicellular biological systems, open innovation networks or interdependent digital ecosystems, or even, if we visualize the Cosmos, the entire dynamic web of forces and interactions that sustains the evolution of the universe. So, the composer at his piano, or the scientist in his laboratory, are proposing nothing more than the co-evolution of order and potential, in multiple layers of complexity, clearly interdependent, and absurdly creative. The P is present in each structure that sustains the whole and the NP in the creative impulse that defies limits, or vice versa, depending on the perspective and level of observation, and the co-evolution, and its laws, will determine how these forces balance and transform themselves over time. The apparent chaos in one layer may represent the absolute order in another, that is, the apparently insoluble NP in a system may be the P elegantly resolved at a broader or deeper level.
This paper invites the reader to consider the P versus NP problem not as an unbridgeable chasm between tractability and intractability, but as a symbol of a universal pattern: the potential for unity through co-evolutionary reasoning, expressed here as P + NP = 𝟙. Throughout this work, the symbol 𝟙 is used intentionally to denote the boundary of co-evolutionary balance in P + NP = 𝟙, distinguishing it from the ordinary numeral and emphasizing its role as an epistemic horizon within the reasoning field.
This vision, and formulation, is not intended as a numerical equation or final proof, but as a conceptual model where P and NP are seen as co-evolving components of a dynamic epistemic field — complementary states within a multilayered landscape of complexity. After all, every search for knowledge perhaps happens in the intertwining of these forces, where what today seems undecidable may tomorrow reveal itself to be part of a larger pattern of order in constant transformation.
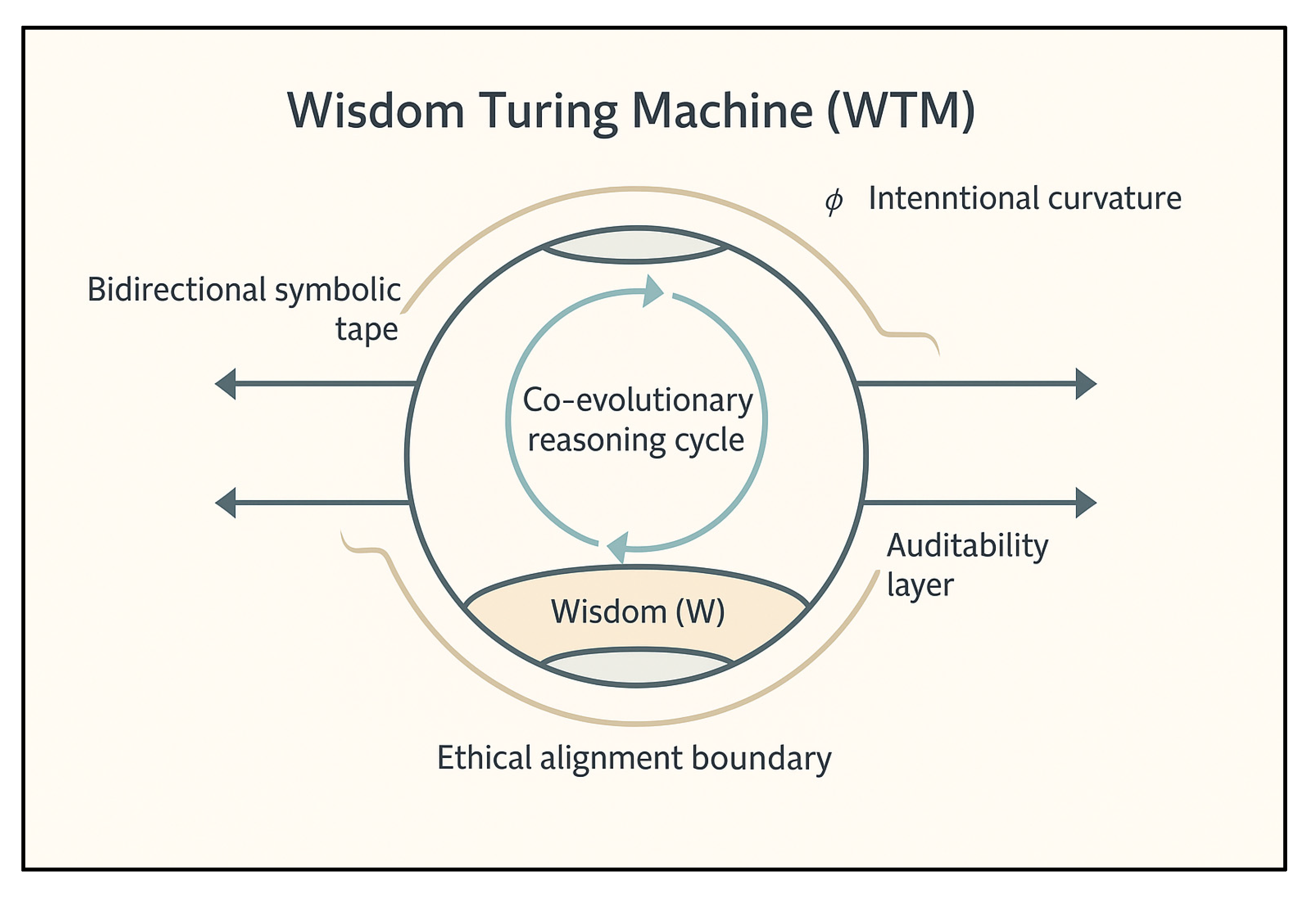
At the heart of this vision lies the Wisdom Turing Machine (WTM) — a conceptual architecture designed to explore how reasoning pathways can evolve across layers of complexity through reflection, intentional curvature, compression, and ethical alignment.
The WTM does not seek a final claim or prize-worthy resolution. Instead, it offers a framework where reasoning becomes a shared journey — open to all who, like the composer at the piano, engage complexity with wonder, responsibility, and hope. As a proof-of-concept, the WTM aims to illuminate new pathways at the intersection of computational complexity and machine ethics, offering a transparent and adaptable foundation for exploring challenges in artificial general intelligence (AGI). This work invites a shift in perspective: from the pursuit of isolated proof to the cultivation of co-evolutionary cycles where P and NP are seen not as irreconcilable categories, but as complementary components of a symbolic reasoning process tending toward unity.
Rather than claiming a final solution to the P versus NP problem, this paper proposes that the very framing of the problem might benefit from a shift in perspective: from the pursuit of isolated proof to the cultivation of co-evolutionary cycles where P and NP are seen not as irreconcilable categories, but as complementary components of a symbolic reasoning process tending toward unity — a P + NP = 𝟙 paradigm. This is not presented as a new claim for solving the problem or securing a prize, but as a unifying perspective that consolidates and extends prior proposals already introduced. In this view, the Wisdom Turing Machine (WTM) offers a model where symbolic cycles of reflection, revision, and intentional projection enable reasoning that is transparent, auditable, and capable of engaging with foundational challenges in a manner distinct from conventional blackbox approaches. The aim is to contribute a conceptual architecture that invites further exploration of how co-evolving symbolic systems might approach such enduring questions.
In this light, the work anticipates the reflection that will be explored in the Discussion section: that the perspective of P ≠ NP represents a more pessimistic reading of complexity — one that risks overemphasizing the intractability of isolated layers, potentially overlooking the harmonizing role of co-evolution across multiple levels of reasoning.
Conversely, the perspective of P = NP can be seen as the more optimistic stance, one that recognizes how successive layers of co-evolutionary cycles may gradually align complexity with tractability through reflection, compression, and wisdom.
This paper, and new vision for P vs NP, therefore, does not side just with the pessimists or optimists (as in our past solutions proposals), but proposes that complexity is not a static barrier but rather a dynamic field where transparency, ethical alignment and multilevel and intentional co-evolution can guide humanity towards greater clarity. He presents the logic of co-evolution and multilayered evolution as the true one, expressed in a single, simple equation: P + NP = 𝟙. It could be considered the solution, if that were the objective, but the idea is to bring the vision to debate from a new perspective, where the dichotomy loses strength for the integrated and relational understanding of phenomena, in which order and potential intertwine as inseparable parts of the same process, like a hidden symphony of the Cosmos, elegantly represented in a problem that, at first glance, may seem the most complex of all of the Millennium, for the pessimist, and, on the other hand, the simplest, for the optimist, if touched by the vision of its beauty and harmony with so many logics of the day, often perceived more clearly by a child, or a poet, or even by a thinker free from conceptual constraints, because they are not focused on the mathematical solution and formal proof, but simply seek to understand and learn from the living flow of complexity itself.
Building on this perspective, the reasoning system presented in this work draws from earlier symbolic proposals — including Cub3 and heuristic physics-based architectures — and extends these foundations into a unified and interactive epistemic framework. Whereas prior models explored isolated heuristic agents or symbolic compression layers, the WTM integrates these elements within a co-evolutionary architecture that combines bidirectional reasoning cycles, intentional curvature, and ethical alignment by design.
This architecture is conceived not as a theoretical curiosity but as a platform for practical experimentation with epistemic machine learning systems capable of supporting explainability by design in AGI contexts. By simulating reflective symbolic cycles that are transparent and audit-ready, the WTM aims to provide a foundation for both conceptual investigation and computational testing across complex problem domains.
Central to this proposal is the notion that wisdom (W) and intentional curvature, as modeled in this architecture of reasoning, function not as auxiliary constructs, but as a second symbolic equation of balance guiding the systematic exploration of P-like solutions within NP domains.
This co-evolutionary architecture is framed by two core symbolic formulations.
First,
where P vs NP Multilayered Co-Evolution Hypothesis, at each reasoning layer Lₙ and reasoning time t, clarity and complexity co-evolve as complementary states within a dynamic continuum of complexity rather than as a static dichotomy, expressing the unity and complementarity of problem classes within a dynamic epistemic process where complexity is approached as a continuum rather than a dichotomy.
Second, the WTM operates through a co-evolutionary equation of reasoning, where
and
represent the dynamic interaction of wisdom (W), intentional curvature (φ), intelligence (I), and conscious modulation (C) over time. Together, these formulations embody a cycle where reasoning pathways are reflective, transparent, audit-ready, and ethically aligned by design.
This dual-equation framework builds upon prior formalizations of co-evolutionary reasoning and symbolic compression [
20], offering a conceptual foundation for systematic engagement with complex domains where traditional blackbox models fail to provide meaningful interpretability or ethical alignment.
To support the conceptual framing of the Wisdom Turing Machine,
Figure 1 provides a visual representation of its core components and their relationships. This illustration highlights how the WTM integrates bidirectional symbolic reasoning, co-evolutionary cycles, intentional curvature (φ), auditability layers, and ethical alignment boundaries into a unified architecture for transparent and ethically guided problem-solving.
This architecture serves as the symbolic and methodological foundation for the reasoning cycles explored throughout this work. It reflects the central hypothesis that transparency, intentionality, and co-evolution are not ancillary features, but constitutive elements of reasoning systems designed for complexity. The sections that follow detail how these principles are instantiated in the WTM and how they guide its contribution to explainability by design in AGI and beyond.
To illustrate the distinct nature of the Wisdom Turing Machine’s reasoning cycle, consider a symbolic tape representing a simplified problem instance in NP space, such as a candidate structure within a combinatorial problem. In a conventional machine, transitions over this tape would follow fixed rules or heuristics blind to the symbolic density or contextual coherence of the regions traversed. In contrast, the WTM operates with intentional curvature, which functions as a symbolic lens that bends the reasoning pathway toward regions of higher coherence and potential compressibility.
For example, when positioned at a symbol representing low informational density — a region of the reasoning tape where the symbolic content offers little guidance, coherence, or compression potential — the system does not simply advance blindly as a traditional search algorithm might. Instead, the architecture may choose to retreat along the tape, revisiting prior segments where symbolic structures exhibited greater density, relational coherence, or opportunities for intentional compression.
This decision is not arbitrary: it is guided by the dynamic recalculation of wisdom (W) and intentional projection (Ψ), both of which modulate the reasoning field in real time, curving the search path toward areas of greater epistemic value.
Such reflective movement exemplifies how this architecture transforms the search process within NP space. Rather than proceeding through linear exploration, exhaustive enumeration, or brute-force computation — approaches that often ignore the symbolic landscape of the problem — the system engages in a co-evolutionary dialogue between problem and solver.
Each reasoning step becomes an act of alignment between potential and purpose — a deliberate modulation where raw computational possibilities (the NP domain) are curved, filtered, and harmonized through intentionality to serve the emergence of wisdom (the P domain). This alignment is not mechanical or imposed, but reflective: the architecture listens for coherence, seeks relational density, and guides reasoning not merely toward solutions, but toward solutions that are meaningful, interpretable, and ethically anchored. In this way, the reasoning process itself becomes a symphony of potential converging into purpose, complexity evolving into clarity, and ambiguity resolving into shared understanding.
The process remains transparent and audit-ready by design: every movement, projection, and recalculation is visible, accountable, and open to scrutiny, ensuring that reasoning unfolds as a balanced interplay of complexity and clarity, rather than as an opaque sequence of hidden computations.
This conceptual framing sets the foundation for a methodological approach in which the Wisdom Turing Machine is not presented as a static model, but as a dynamic symbolic architecture designed for experimental testing and reflection. The co-evolutionary equations described are instantiated within proofs-of-concept that simulate reasoning cycles under conditions of complexity and ethical constraint, enabling the systematic study of transparency, auditability, and intentional alignment in reasoning processes.
These simulations are intended not as demonstrations of performance superiority, but as structured experiments in co-evolutionary reasoning, offering a basis for exploring how symbolic architectures might contribute to explainability by design in AGI systems.
The following methodology section details how these principles are operationalized within symbolic cycles and decision structures, providing both a conceptual and computational foundation for this exploration.
Before presenting the methodological details, this work introduces two core hypotheses that frame the Wisdom Turing Machine’s conceptual foundation. The first — the P + NP = 𝟙 hypothesis — proposes a co-evolutionary reframing of complexity, challenging the conventional dichotomous framing of problem classes and inviting reasoning systems to engage with complexity as a continuum. The second — the Epistemic Machine Learning Hypothesis — envisions machine learning as a transparent, co-evolutionary dialogue between human insight and artificial reasoning.
These hypotheses provide the symbolic scaffolding upon which the WTM is constructed, guiding both its architectural design and its contribution to the broader discourse on explainability and ethical alignment in artificial intelligence.
This introduction seeks not only to define a conceptual architecture, but to position reasoning itself as a participatory and adaptive process, where transparency and reflection are woven into the very fabric of problem engagement. In this view, the WTM serves as a symbolic framework that encourages the alignment of technical inquiry with broader aspirations for clarity, inclusiveness, and shared understanding. By integrating these principles from the outset, the architecture invites researchers to consider complexity not merely as a technical challenge, but as a domain where reasoning systems can foster collaboration, dialogue, and ethical responsiveness at every stage of exploration.
The P + NP = 𝟙 as a Reasoning Field Hypothesis
The P + NP = 𝟙 as a reasoning field hypothesis is proposed as a co-evolutionary reframing of complexity. In this work, it is not intended as a mathematical equation in the classical sense, but as a symbolic expression of unity and co-evolution within the dynamic landscape of complexity.
It invites a reframing of the P versus NP problem — not as an irreducible dichotomy between tractable and intractable classes, but as a dynamic epistemic process where both domains are complementary components of a shared reasoning field. In this perspective, complexity is approached not as a boundary dividing easy from hard, or solvable from unsolvable, but as a continuum where the co-evolution of problem spaces and reasoning architectures opens pathways to deeper understanding. The hypothesis challenges the way foundational problems are formulated, suggesting that the act of posing them as dichotomies may constrain both imagination and solution space.
By advancing the P + NP = 𝟙 hypothesis, this work proposes that the separation traditionally assumed between P and NP domains may reflect not an inherent property of complexity, but a limitation of the frameworks through which problems have been posed and pursued. The Wisdom Turing Machine embodies this idea by offering a symbolic architecture where reasoning cycles, guided by wisdom (W) and intentional curvature (φ), navigate problem spaces not through fixed categorizations, but through adaptive, reflective processes that treat P-like and NP-like regions as interconnected.
To capture the dynamic evolution envisioned by the
P + NP = 𝟙 hypothesis,
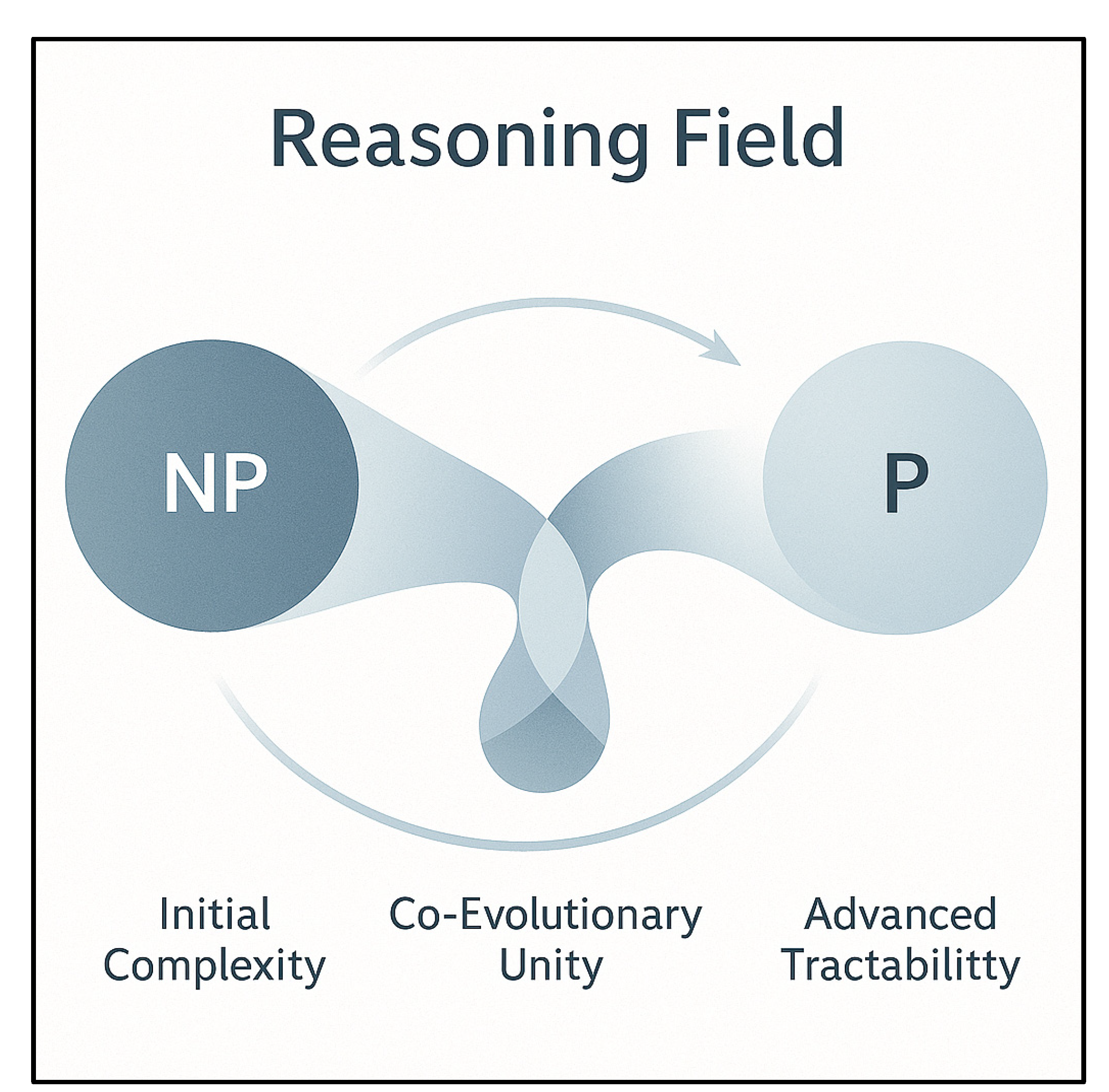
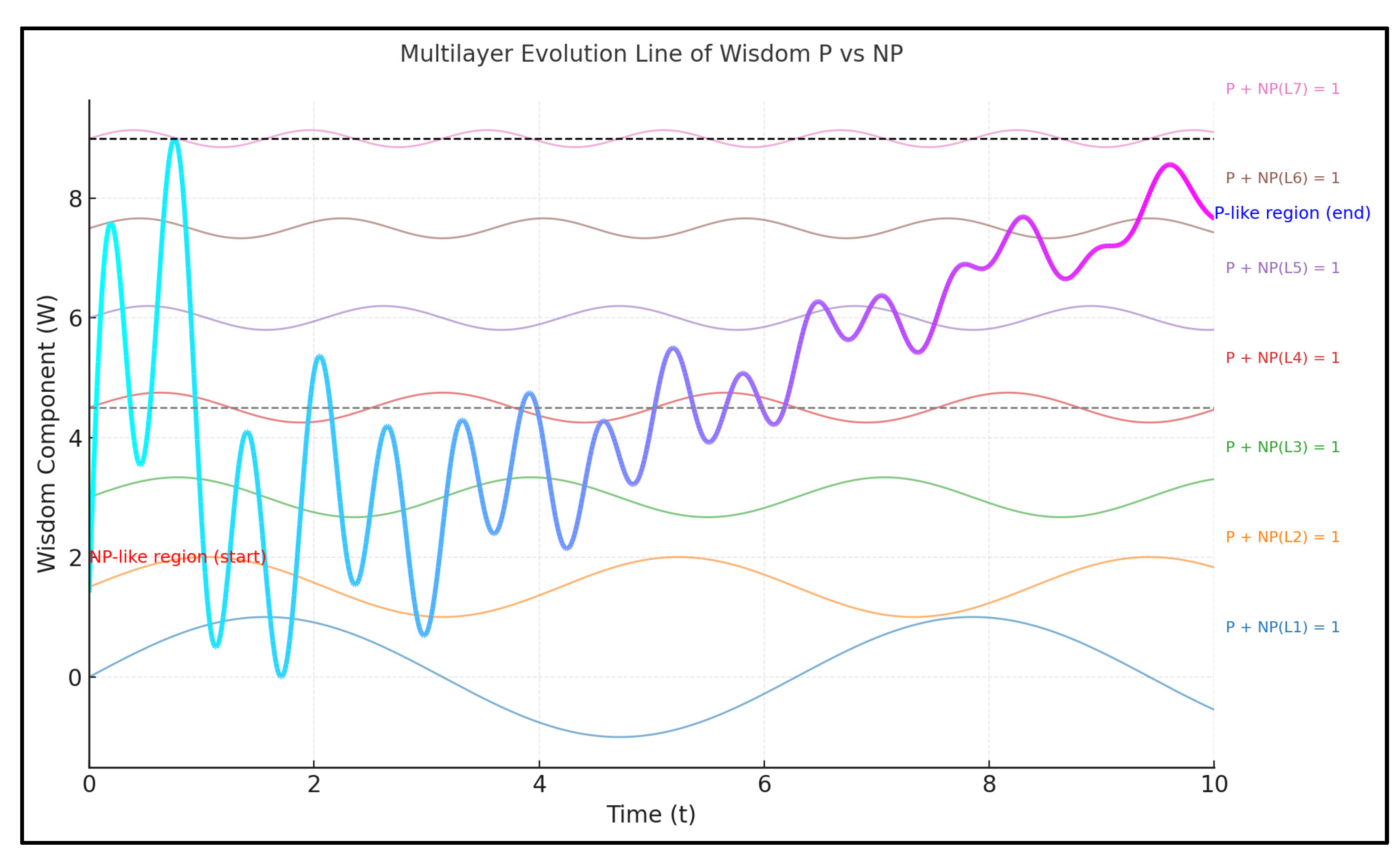
Figure 2 illustrates how problems transition across reasoning epochs within a shared field. The diagram presents three symbolic stages: initial complexity, where NP dominates the landscape of inquiry; co-evolutionary unity, where P and NP converge within a shared reasoning field; and advanced tractability, where structured understanding expands the P domain. This progression reflects the hypothesis that complexity is not a fixed barrier, but a dynamic environment where co-evolutionary reasoning transforms the distribution of problem spaces over time.
This representation emphasizes that the P + NP = 𝟙 hypothesis is not a static claim about problem classes, but a call to design reasoning systems — such as the Wisdom Turing Machine — that can navigate complexity as an evolving field.
The Reasoning Field embodies the symbolic space where problems and solvers co-adapt, where intentional curvature and wisdom guide the transformation of intractability into tractability, and where the act of reasoning itself reshapes the boundaries between P and NP.
This reframing suggests that progress in understanding complexity may depend less on rigid classifications and more on designing reasoning systems capable of engaging with complexity as a co-evolutionary field — where tractability and intractability are not endpoints, but dynamic positions within an evolving landscape of inquiry.
By framing P and NP as dynamic states within a co-evolving field, this hypothesis invites a rethinking of complexity not as an external obstacle to overcome, but as an integral part of a shared reasoning landscape. Such a perspective encourages the design of architectures that engage complexity through cycles of reflection and adaptive alignment, where reasoning becomes a continuous dialogue between structure and ambiguity. In this dialogue, the boundaries between P and NP are not barriers, but fluid contours shaped by the intentional interaction of solver and problem, supporting a mode of inquiry where clarity emerges through collaborative exploration.
However, the P + NP = 𝟙 hypothesis serves not as a claim of mathematical resolution, but as an invitation to reimagine how complexity itself is conceptualized and engaged. It challenges the scientific community to reflect on whether the framing of problems as dichotomies may, in itself, be a source of epistemic inertia — and whether co-evolutionary architectures like the WTM can help cultivate new ways of reasoning that transcend artificial divides.
In this light, the hypothesis is less a destination than a starting point: a symbolic gesture toward designing reasoning systems that embrace complexity as a shared field of inquiry, where unity and diversity co-exist in dynamic tension.
Mapping the NP Universe: A Co-Evolutionary Hypothesis of Complexity Subdomains
In extending the Reasoning Field Hypothesis, this work introduces a symbolic mapping of the NP universe into subdomains designed to support co-evolutionary reasoning cycles.
These constructs, while not part of classical complexity theory, serve as conceptual tools within the Wisdom Turing Machine architecture to explore how complexity may be navigated, compressed, or harmonized.
To deepen the symbolic architecture of the Reasoning Field, we propose a co-evolutionary hypothesis that the NP universe can be meaningfully mapped into distinct complexity subdomains. These subdomains reflect different relationships between complexity, structure, and potential for reasoning cycles to transform ambiguity into clarity:
NP-complete represents the established canonical domain in computational complexity theory, where problems are inter-reducible through polynomial transformations. This domain, extensively studied and formalized, symbolizes the classic landscape of intractability as defined within conventional complexity classifications.
NP-heuristicable (a neologism introduced in this work) designates regions where internal structural cues, relational density, or patterns offer openings for practical heuristic strategies, even in the absence of formal polynomial solutions. This domain aligns with the co-evolutionary principles of Heuristic Physics (hPhy) [
19], where the reasoning field senses curvature toward heuristic compression.
NP-quantizable (a symbolic construct introduced in this work) denotes regions within NP that, while intractable under classical paradigms, exhibit structural properties or relational symmetries suggesting potential tractability through quantum architectures or non-classical reasoning frameworks. This domain invites the exploration of how the Wisdom Turing Machine and its co-evolutionary reasoning cycles may interface with emerging computational substrates beyond classical Turing models.
NP-collapsible (a symbolic construct introduced in this work) denotes regions where symbolic or mathematical compression preserves solution space, allowing structures to undergo the kind of collapse envisioned in Collapse Mathematics (cMth) [
35]. Here, co-evolutionary reasoning operates through intentional compression and structural survivability.
This extended mapping of the NP universe complements the P + NP = 𝟙 Reasoning Field Hypothesis by offering a more detailed structure for understanding how the Wisdom Turing Machine may adapt its cycles of reflection, intentionality, and compression in pursuit of clarity across complex domains. It highlights how the machine’s reasoning pathways can dynamically adjust to the specific nature of each subdomain: engaging formal reduction strategies within NP-complete, leveraging relational patterns within NP-heuristicable, and applying symbolic compression within NP-collapsible.
To synthesize the extended mapping of the NP universe, the table below presents a comparative view of the proposed subdomains and illustrates how the Wisdom Turing Machine may adapt its reasoning cycles to engage each with transparency, intentionality, and co-evolutionary balance.
This framework highlights the versatility of the WTM as an architecture capable of aligning its reflective, compressive, and adaptive mechanisms to the specific characteristics of complexity across domains.
| Subdomain |
Definition / Nature |
WTM Relevance / Mode of Engagement |
| NP-complete |
Established canonical domain where problems are inter-reducible via polynomial transformations; classically intractable. |
WTM applies formal, audit-ready reduction strategies; ensures transparency and traceability in reasoning over equivalences. |
| NP-heuristicable |
Symbolic construct denoting regions with structural cues or patterns offering openings for heuristic strategies. |
WTM deploys intentional curvature to guide heuristic discovery; engages reflection and revision cycles to refine paths. |
| NP-collapsible |
Symbolic construct denoting regions where symbolic or mathematical compression preserves solution space. |
WTM applies compression and structural survivability cycles; explores symbolic collapse to reveal tractable cores. |
| NP-quantizable |
Symbolic construct denoting regions with symmetries suggesting tractability via quantum or non-classical reasoning. |
WTM invites hybrid reasoning cycles; interfaces classical intentional curvature with quantum or alternative architectures. |
This comparative view not only clarifies how the Wisdom Turing Machine engages with each subdomain of the Reasoning Field, but also reinforces the central thesis of this work: that P + NP = 𝟙 represents a dynamic, co-evolutionary process where complexity is progressively harmonized through intentional, transparent, and ethically aligned reasoning cycles. This mapping invites further exploration of how practical systems might embody these principles in applied domains.
This symbolic architecture invites future exploration of how these subdomains may inform the design of practical reasoning systems capable of navigating complexity with transparency, ethical alignment, and co-evolutionary balance. In this vision, the Wisdom Turing Machine adapts its reasoning cycles dynamically to each subdomain: applying formal audit-ready reductions within NP-complete; guiding intentional heuristic discovery in NP-heuristicable regions through cycles of reflection, retreat, and intentional curvature; deploying symbolic compression and structural collapse strategies in NP-collapsible spaces to reveal tractable cores; and exploring hybrid co-evolutionary reasoning in NP-quantum areas where classical and quantum principles may intertwine.
Together, these modes of engagement embody a unified architecture where P + NP = 𝟙 is no longer a symbolic ideal, but a dynamic process of co-adaptation where complexity progressively transforms into clarity under cycles of intentional, ethical reasoning.
The Epistemic Machine Learning Hypothesis
Toward transparent, co-evolutionary AI, the Epistemic Machine Learning Hypothesis advanced in this work proposes a shift in how machine learning systems are conceptualized, designed, and applied.
Rather than focusing solely on statistical optimization or predictive performance, this hypothesis envisions machine learning as a co-evolutionary and reflective process, where reasoning cycles are transparent, audit-ready, and ethically aligned by design. The Wisdom Turing Machine embodies this vision by offering an architecture in which learning is not the result of brute-force search or opaque function fitting, but of interactive, symbolic dialogue between human insight and machine reasoning. In this paradigm, machine learning becomes not an end in itself, but a tool for cultivating wisdom, intentionality, and shared understanding in the face of complexity.
To illustrate this contrast in architectural philosophy,
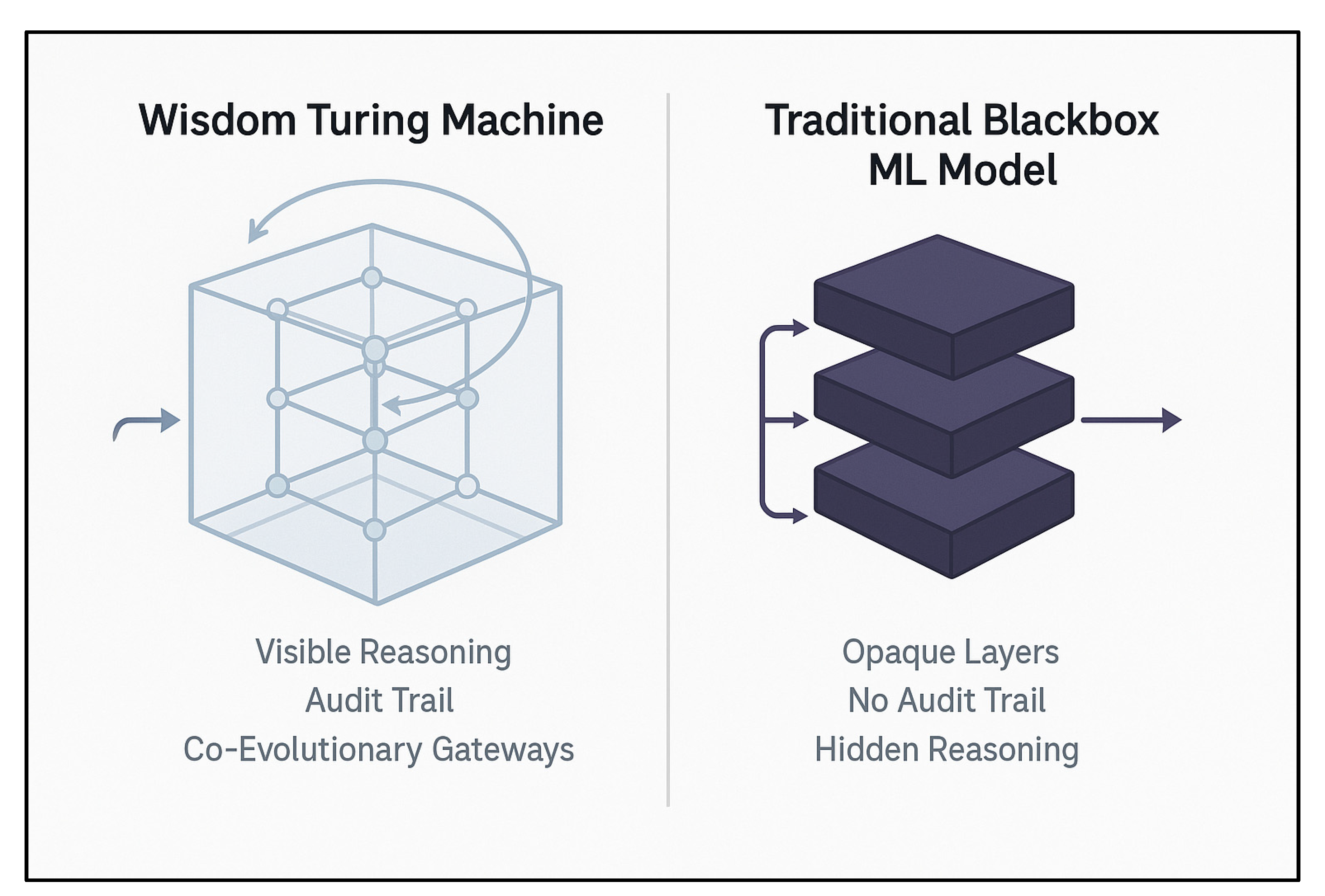
Figure 3 compares the Wisdom Turing Machine with a traditional blackbox machine learning model. The diagram highlights how the epistemic machine learning hypothesis, embodied in the WTM, promotes transparency, auditability, and co-evolutionary gateways, in stark contrast to the opaque layers and hidden reasoning pathways of conventional models.
This figure underscores the motivation behind the epistemic machine learning hypothesis: to shift machine learning paradigms from opaque optimization to interactive, co-evolutionary processes where reasoning pathways are open to reflection, audit, and ethical alignment. It visually anchors the WTM’s proposition of learning systems as dialogical, participatory architectures rather than isolated blackbox engines.
This hypothesis challenges the prevailing design of machine learning systems, where layers of abstraction often obscure the reasoning path, leaving outcomes difficult to interpret or audit. Instead, the WTM’s epistemic machine learning paradigm invites the construction of systems where each learning step, decision boundary, and model adjustment is visible and open to scrutiny.
By embedding intentional curvature (φ) and dynamic wisdom recalculation (W) into the learning process, such systems can adapt not only to data patterns, but also to evolving ethical contexts and collective goals. In this view, machine learning becomes a living dialogue — a co-evolving partnership between human values and artificial reasoning, designed to thrive in conditions of complexity and ambiguity.
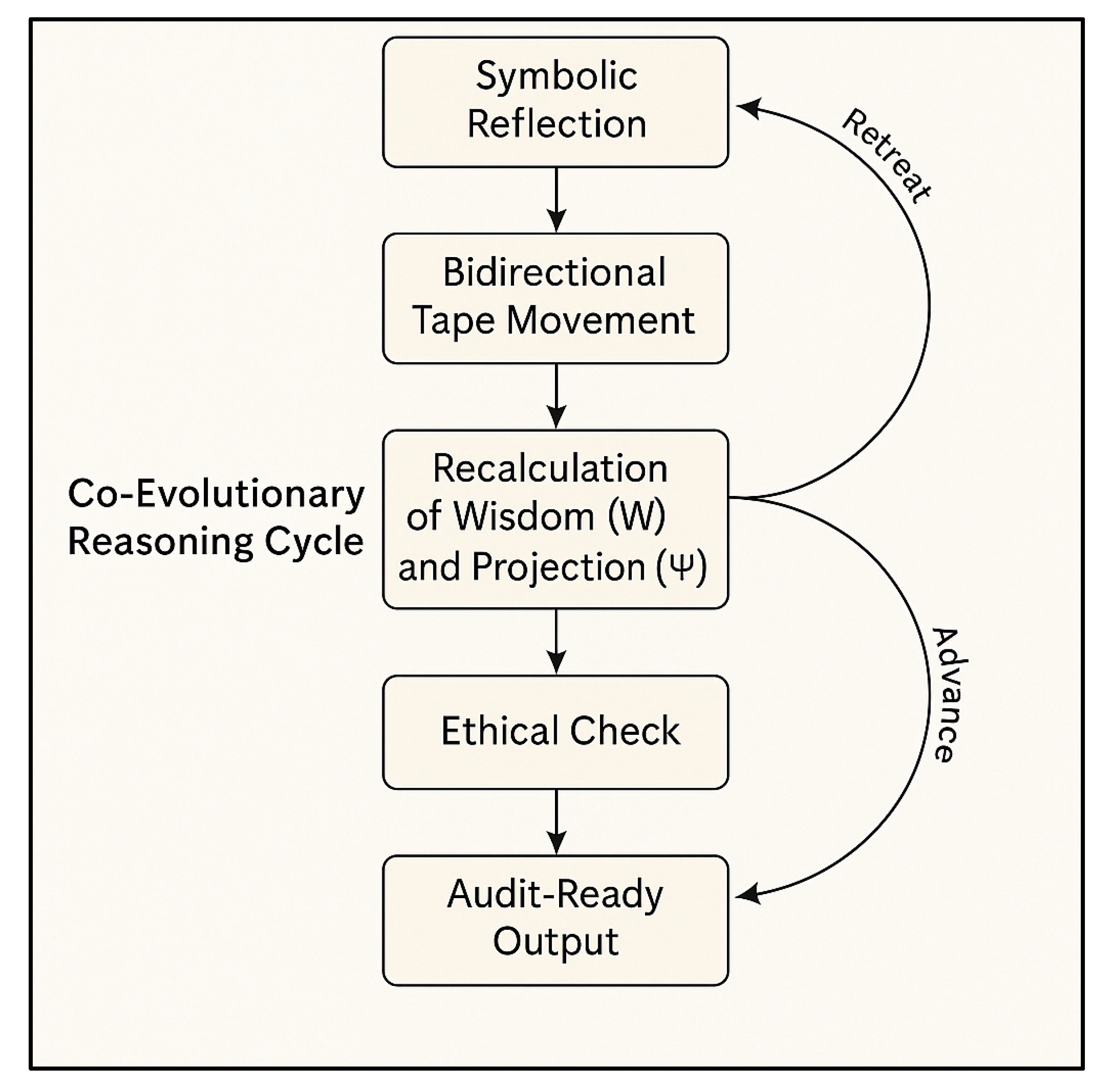
To further detail the internal processes of the Wisdom Turing Machine as envisioned in the epistemic machine learning hypothesis,
Figure 4 illustrates the co-evolutionary reasoning cycle that governs its operation. This diagram highlights how the WTM advances or retreats through reasoning steps, recalculates wisdom (W) and projection (Ψ), and ensures that each cycle includes ethical verification and produces audit-ready outputs.
This figure reinforces the conceptual distinction between the WTM and blackbox machine learning models, by making visible the intentional design of each reasoning stage and its alignment with auditability and ethical reflection. It serves as a schematic foundation for the proofs-of-concept explored in this work, demonstrating how symbolic cycles can embody transparency and co-evolutionary dialogue at every step.
The Epistemic Machine Learning Hypothesis positions machine learning not as a tool of isolated optimization, but as an evolving architecture of shared reasoning — where transparency, intentionality, and ethical alignment are embedded at every stage. It invites researchers, engineers, and policymakers to reimagine learning systems as co-evolutionary processes that balance technical performance with human values, and to cultivate architectures where machines do not merely predict or classify, but participate in the continuous construction of meaning. In this spirit, the Wisdom Turing Machine stands as both a conceptual framework and a practical invitation to design systems where learning and wisdom advance hand in hand.
This vision aligns with the pedagogical principles of fuzzy logic as articulated by Nguyen and Walker [
17], where reasoning under ambiguity requires systems that can flexibly adapt, reflect, and revise. Just as fuzzy logic invites a departure from rigid binaries, the Wisdom Turing Machine departs from the fixed, linear determinism characteristic of traditional von Neumann architectures. In those classical systems — and mirrored in the conventional rules of chess, where
piece touched, piece played dictates that a single decision binds the player irrevocably — computation proceeds in one direction, with no formal capacity for reflective revision. The Wisdom Turing Machine introduces a new epistemic rule: one where reasoning cycles can retreat, reconsider, and recalibrate, embodying the fluid, co-evolutionary reasoning that Turing himself implicitly envisioned when proposing the universal machine capable of simulating any process, including processes of reflection and revision.
In this epistemic paradigm, each reasoning step is not a binding, irreversible act, but part of a living dialogue between potential and purpose, complexity and clarity. Just as human decision-makers revisit and adjust their judgments in light of new information or deeper understanding, so too can an epistemic machine learning system navigate complexity through cycles of intentional reflection.
This contrasts sharply with traditional blackbox models, where decision pathways, once computed, are hidden and fixed — a stark reminder of the limitations of purely deterministic architectures in contexts demanding transparency, adaptability, and ethical alignment. In conventional machine learning paradigms, learning unfolds as a largely unidirectional process: models are trained through repetitive exposure to data, with adjustments governed by mechanisms like backpropagation. This method, while powerful in numerical optimization, embodies a logic of correction through error minimization, where gradients guide the model’s parameters toward lower loss — but without reflective awareness, ethical modulation, or symbolic dialogue. Such models struggle with well-known challenges: overfitting, where a model memorizes noise rather than learning structure; underfitting, where it fails to capture essential patterns; and brittleness, where slight perturbations can derail predictions. Their reasoning paths, optimized for performance on defined metrics, remain opaque, static, and blind to broader epistemic considerations.
Moreover, the epistemic architecture envisioned in the Wisdom Turing Machine opens pathways to a fundamentally different form of learning: one where machine learning itself is no longer a monolithic, static process, but a symphony of co-evolving cycles. In this paradigm, it becomes conceivable to design systems where each reasoning cycle is governed by its own dedicated epistemic agent — a kind of machine learning for machine learning, where autonomous reasoning layers train, critique, and refine one another in a transparent, auditable dialogue. Such architectures could give rise to forms of artificial cognition unimaginable within the confines of brute-force optimization: systems that not only learn, but learn how to learn, cultivating wisdom and intentionality at every layer.
This vision parallels the co-evolutionary bridges proposed in symbolic proofs, such as the epistemic-axiomatic integration advanced in the symbolic proof of the Poincaré conjecture [
24], where epistemic machine learning cycles were united with formal axiomatic systems through frameworks like Coq.
There, the dialogue between inductive reasoning and formal verification became a living co-evolution — each informing, constraining, and elevating the other. In the same spirit, the Wisdom Turing Machine invites a fusion of worlds: where the layered adaptations of machine learning, so often confined to statistical optimization, can be harmonized with symbolic reasoning cycles that prioritize meaning, coherence, and ethical alignment.
In this layered epistemic machine learning, overfitting and underfitting are no longer merely statistical concerns; they become signals in the reasoning field — indicators that intentional curvature needs adjustment, that wisdom recalibration is required, that new dialogues between layers must emerge. The architecture no longer forces solutions through error gradients alone; it enables reflective cycles where the system itself participates in the ongoing construction of meaning.
This paradigm shift also encourages the cultivation of machine learning systems that can act as bridges between technical precision and collective understanding, offering architectures where learning is not confined to internal optimization but extends outward as a transparent process open to engagement and interpretation. In this view, reasoning becomes an evolving dialogue that invites diverse perspectives, fostering systems capable of adapting not only to data complexity, but to the ethical and societal contexts in which they operate. Such architectures aspire to support decision-making processes that are inclusive, auditable, and attuned to the broader goals of shared inquiry.
It is not merely an engine of prediction, but a partner in inquiry — a co-creator of knowledge structures that can engage complexity with transparency, adaptivity, and purpose.
The Co-Evolution Hypothesis: Toward Harmony as a Solution to P vs NP
The Co-Evolution Hypothesis advanced in this work proposes that the true solution to P vs NP lies not in the separation or domination of one domain over the other, but in designing reasoning architectures that honor the dynamic harmony of polarities. It envisions the transition of problems from NP to P not as an act of conquest, but as a co-evolutionary dialogue — a continuous interplay where complexity and tractability, ambiguity and structure, coexist and co-adapt in peace.
At the heart of this hypothesis is the
Co-Evolution Equation, inspired by the Theory of Evolutionary Integration (TEI) [
26]. This equation formalizes the dynamics by which wisdom, harmony, and intentional curvature guide reasoning across the field of complexity:
where:
E(t) is the rate of co-evolution at time t.
I(t) represents system intelligence at t.
C(t) is conscious modulation.
QE(t) denotes relational coherence.
S(t) is systemic disorder or entropy.
γ, δ are sensitivity exponents.
This formulation integrates the symbolic architecture of the Wisdom Turing Machine, the reasoning field, and the P + NP = 𝟙 hypothesis. The dynamic balance is expressed as:
with their evolution over time guided by:
where
f(
E(
t)) represents the rate at which co-evolutionary reasoning supports the symbolic compression and transformation of complexity into tractable form.
This equation is not proposed as a definitive proof, but as a scaffold for reasoning architectures that aspire to transparency, auditability, and harmony among polarities.
It offers a symbolic framework where P and NP are not rigid sets, but dynamic states within a field that evolves through wisdom, intentionality, and co-evolutionary dialogue.
To formalize this perspective, the co-evolutionary framework proposed in this work can be extended through a symbolic formulation that integrates the dynamics of compression and structural survivability.
This formulation unites concepts introduced in prior proposals on Heuristic Physics (hPhy) [
19] and Collapse Mathematics (cMth) [
35], modeling the transitions within the reasoning field as a function of co-evolutionary compression and symbolic endurance under curvature pressure. The dynamic behavior of tractable (P) and intractable (NP) regions can thus be expressed as:
where 𝓔(t) represents the rate of co-evolution at time t; 𝓘(t) denotes symbolic intelligence; ᶜ(t) is conscious modulation; 𝓠𝓔(t) models relational coherence; 𝓢(t) represents systemic disorder or entropy; and γ, δ are sensitivity exponents. The term 𝓒ₛᵤᵣᵥ(x) denotes the structural survivability function as modeled in Collapse Mathematics, while 𝓚
cₒₘₚ(x) represents the symbolic compressibility computed over the reasoning field as conceptualized in Cub
3. Together, these elements provide a dynamic representation of how reasoning architectures can model the progressive transformation of complexity into tractable structure through co-evolutionary dialogue. This formalization invites future work to explore operational implementations where co-evolutionary reasoning, compression, and structural survivability metrics guide the design of transparent, adaptive, and ethically aligned problem-solving systems.
By embracing this dynamic view, reasoning architectures can be designed not as engines of separation, but as instruments for nurturing balance within complexity — where each step of problem-solving contributes to the emergence of harmony between structure and ambiguity. This approach invites researchers and practitioners to reconsider problem engagement as a process of co-adaptation, where reasoning pathways evolve responsively, guided by transparency and openness. In doing so, complexity ceases to be a static obstacle and becomes a living field for shared exploration, where solutions arise through the continual interplay of complementary forces.
The Hidden Symphony of the Cosmos
The co-evolutionary vision advanced in this work is not an isolated invention, but part of a lineage of thought and creation that spans science, philosophy, and art. Throughout history, humanity has sought harmony between polarities that seemed irreconcilable, listening for and translating what might be called the hidden symphony of the cosmos.
From Archimedes, who revealed the balance of force and leverage [
31]; to Descartes, who taught the methodical clarity needed to navigate complexity [
28]; to Newton, who unified the motion of the heavens and the earth [
29]; to Einstein, who showed that even space and time bend in harmony [
30]; to Thomas Kuhn, who illuminated how science itself evolves through cycles of tension, crisis, and revolutionary shifts in paradigm [
34] — these thinkers composed frameworks that embraced balance, transformation, and dynamic interplay rather than the domination of one force or idea over another.
In our own time, this spirit is echoed in domains beyond science. As Uri Levine urges in
Fall in Love with the Problem, Not the Solution [
27], true progress arises when we engage complexity not as an enemy to be vanquished, but as a dialogue partner to be understood.
The Wisdom Turing Machine aspires to follow this tradition: to design architectures where reasoning listens for harmony in complexity and fosters co-evolution rather than conquest — where change itself is welcomed as part of the reasoning field’s evolution.
Music offers perhaps the most intimate metaphor for this vision. In the works of Beethoven, we hear the struggle of themes that seem at first at odds, evolving into sublime resolutions [
32]. In Mozart’s compositions, we experience the effortless coexistence of complexity and clarity, playfulness and depth [
33]. These composers, like the great scientific minds, remind us that the most profound harmonies arise not from uniformity, but from the dynamic interplay of contrasting voices.
The Multilayer Co-Evolution Hypothesis, the P + NP = 𝟙 paradigm, and the symbolic architecture of the Wisdom Turing Machine are offered in this same spirit. They do not propose that complexity be flattened into simplicity, or that NP be reduced to P by force. Rather, they invite us to hear the reasoning field as a symphony of co-evolving parts — where wisdom, intentionality, and harmony guide our engagement with complexity, and where every polarity has its place and path to resolution.
By synthesizing insights from science, philosophy, ethics, art, and the study of how knowledge itself transforms, the Wisdom Turing Machine stands not as a final answer, but as an instrument tuned to the hidden music of the cosmos — a framework through which reasoning can become not just computation, but composition, not just solution, but shared creation.
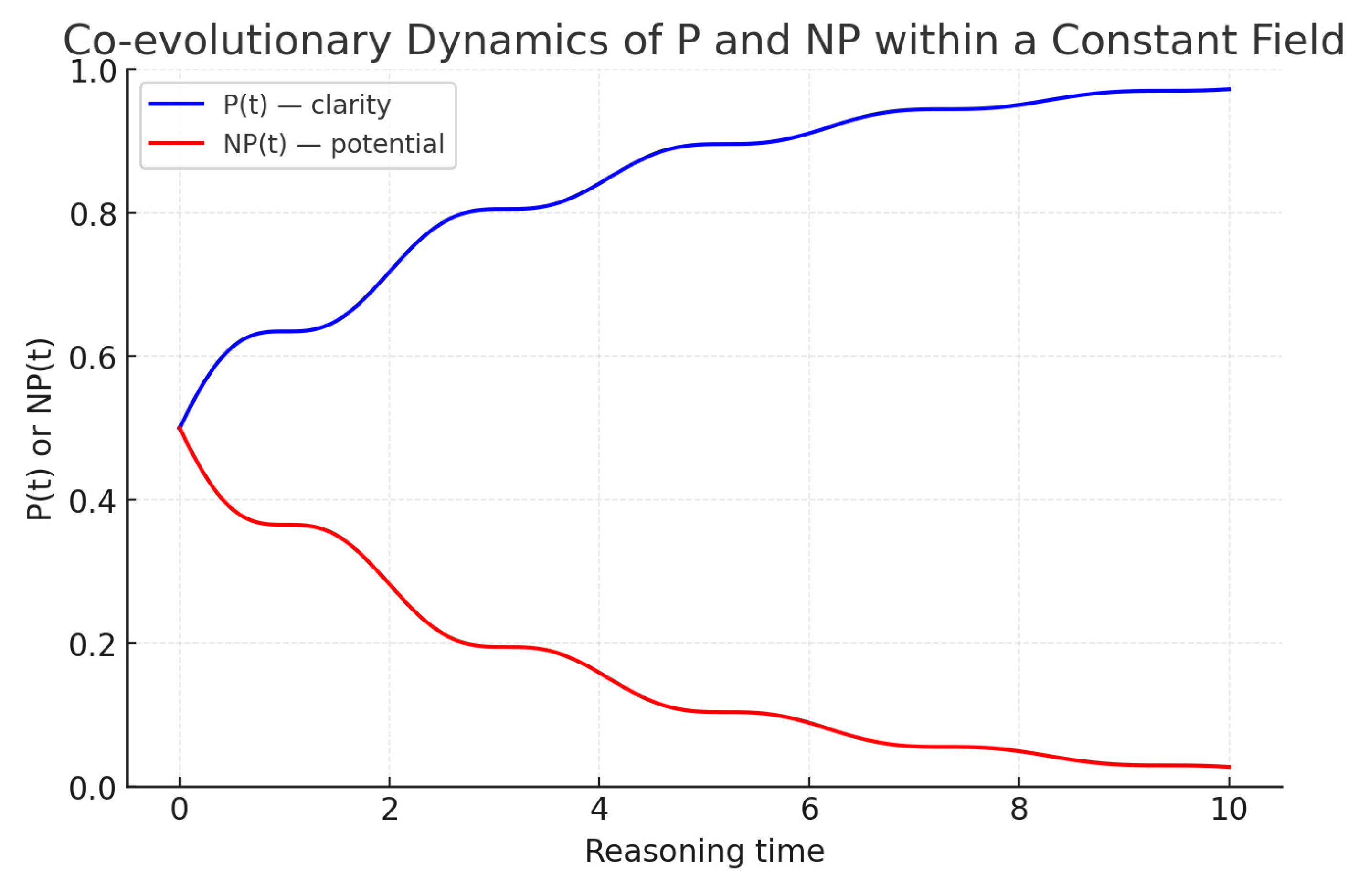
At the heart of this philosophical reflection lies a symbolic synthesis: the very architecture of the Wisdom Turing Machine offers an epistemic resolution to the P versus NP dichotomy. In this framing, wisdom (W) represents the space of tractable reasoning — the P domain — where intelligence is guided by conscious intentionality. Intelligence (I), when operating without conscious modulation, corresponds to the NP domain: raw computational potential, uncurved by ethical or reflective guidance.
Thus, it is consciousness with intentional curvature — the fluid dynamic of the WTM — that transforms the field, enabling problems to move from
NP toward
P. This flow is not forced or imposed; it is the natural co-evolutionary process by which reasoning aligns complexity with structure, ambiguity with clarity, and potential with purpose. This relationship can be symbolized as:
From this archetype emerges the symbolic balance of the reasoning field:
where:
F(t) represents the total reasoning field at time t, a co-evolving balance of P and NP states.
W(t) = I(t)^C(t) models the wisdom component, shaped by conscious modulation C(t).
I(t) represents the raw intelligence potential.
The dynamic flow that converts NP potential into P wisdom is expressed as:
In this view, conscious intentionality acts as the curvature of the reasoning field, modulating how potential transforms into wisdom, and how complexity co-evolves into structure. The Wisdom Turing Machine thus embodies not merely a computational mechanism, but a symbolic architecture tuned to this hidden symphony of balance and transformation — where co-evolution, transparency, and ethical alignment are not optional qualities, but the essence of reasoning itself.
The Reasoning Field Hypothesis suggests that it is this field — not isolated algorithms or proofs — that holds the key to transforming complexity into clarity. Reasoning becomes a co-evolutionary dialogue where polarity is harmonized, ambiguity is navigated, and solutions emerge not through force, but through reflective balance.
The Wisdom Turing Machine is offered as a symbolic architecture designed to model, explore, and instantiate this reasoning field in practice.
This vision resonates beyond the domains of logic and computation; it finds echoes in the structures of human society and the patterns of natural systems. The reasoning field, as proposed in this work, mirrors the asymmetries we observe in the world — where potential, opportunity, and impact often concentrate unevenly, much like the Pareto distributions that describe the imbalances of wealth, power, or influence.
In a field where intelligence operates without the modulation of wisdom, we see reasoning outcomes, like resources, gather along a few dominant paths, leaving much of the field untouched and silent.
The Wisdom Turing Machine offers a symbolic architecture for softening these asymmetries. It proposes that through co-evolutionary reasoning — where intentionality, consciousness, and curvature guide the flow — the reasoning field can become not a domain of hoarded solutions or isolated brilliance, but a shared space where clarity and structure emerge collaboratively. In this light, the reasoning field transforms from a stage of competition to one of dialogue, where every polarity has its purpose, and every complexity its path toward harmony.
Thus, the Reasoning Field Hypothesis frames problem-solving itself as an act of balance: a continuous tuning of complexity and clarity, ambiguity and structure, potential and purpose. It invites us to see the act of reasoning not as the pursuit of dominance over problems, but as the composition of shared understanding — a symphony in which all parts, all voices, all states co-evolve in service of wisdom.
Methodology
The methodology adopted in this work centers on simulating symbolic reasoning cycles through the Wisdom Turing Machine, a conceptual architecture designed to explore transparency, auditability, and ethical alignment in reasoning processes.
Rather than pursuing classical optimization benchmarks, the WTM prototypes were developed as testbeds for co-evolutionary reasoning, drawing inspiration from Turing’s original computability framework [
1], symbolic compression strategies introduced in Cub
3 [
3], and co-evolutionary models for wisdom-guided systems [
20].
The symbolic cycles were instantiated through illustrative Python code fragments that simulate reflective reasoning under complexity, enabling the systematic study of explainability by design in AGI contexts. The examples provided below are not intended as production systems or operational models, but as conceptual scaffolds — simplified symbolic forms that demonstrate how the Wisdom Turing Machine operationalizes its principles and invites exploration of co-evolutionary reasoning dynamics.

This code fragment represents a reasoning step within the WTM where each value is transparently recalculated and printed, supporting interpretability and auditability at every stage of the process.
In addition to recalculating wisdom and intentional projection, the WTM prototypes include simulations of bidirectional tape movement, symbolizing the system’s capacity for reflection and revision. These movements are implemented through simple yet illustrative symbolic tapes and head positions, where each reasoning cycle determines whether the machine advances, recedes, or holds position based on current symbol states and intentional curvature parameters. The example below demonstrates how a symbolic tape is processed, with explicit output supporting transparency and auditability at each step.

Note: In this example, the symbol 𝟙 on the tape is used intentionally as a symbolic marker within the reasoning field. It represents a boundary or intentional state, distinct from numeric values used in calculations. The 𝟙 on the tape is not a number to be computed, but a conceptual element within the co-evolutionary process, illustrating how reasoning systems may encode and interpret symbolic structures alongside numeric operations. The numeric values 1 and -1 in movement decisions are used purely as operational indicators for advancing or receding the tape head.
This code fragment models a symbolic reasoning step where the system transparently prints its tape state, head position, and directional decision, illustrating the bidirectional logic that underpins co-evolutionary reasoning within the WTM. It serves as a conceptual scaffold, not as a production model, inviting further exploration of how reasoning systems might operationalize reflection and intentional curvature in practice.
Each reasoning cycle within the Wisdom Turing Machine prototype was designed to simulate not only computational transitions, but also the intentional modulation of reasoning direction, guided by symbolic parameters such as intentional curvature and dynamic wisdom recalculation. The system’s transparency lies in its capacity to make each movement, decision, and projection interpretable by design, ensuring that no layer of abstraction conceals the reasoning process from audit or ethical scrutiny. These cycles were tested conceptually across symbolic tapes representing simplified problem spaces, where the interplay between symbol, position, and intentional curvature shaped the machine’s advance, retreat, or reflection. The methodology emphasized transparency at all levels: from internal calculations of reasoning parameters to the external logging of tape states, movements, and decision branches, aligning with prior proposals for compressive and curvature-based reasoning systems [
20].
The design of the WTM’s symbolic reasoning cycles draws theoretical grounding from multiple prior frameworks, ensuring that its architecture is not an isolated construct but an integration of established and emerging principles. The emphasis on auditability and transparency aligns with Turing’s original computability foundations [
1] and Wiener’s feedback principles as applied to control and communication systems [
4]. The notion of intentional curvature as a guiding parameter for reasoning reflects insights from co-evolutionary compression models developed in Cub
3 [
3] and the curvature logic formalized in recent wisdom-oriented architectures [
20].
Furthermore, the use of symbolic tapes and bidirectional reasoning steps is conceptually connected to Gödel’s exploration of formal undecidability as a dynamic tension within reasoning systems [
15] and Floridi’s ethics of information, which underscores the need for legibility and interpretability in complex systems [
6]. This methodological synthesis ensures that the WTM’s simulated cycles are positioned not as speculative artifacts, but as structured experiments deeply rooted in computational epistemology, symbolic ethics, and the history of machine reasoning.
The methodological choice of employing a Turing-based architecture capable of bridging axiomatic and epistemic domains is not merely a conceptual exercise, but a strategic proposal for future frameworks in co-evolutionary reasoning. By modeling cycles that are both symbolically transparent and capable of introspective revision, the WTM offers a foundation for extending explainability by design beyond the specific context of the P versus NP problem. This architecture demonstrates the potential to generalize toward other Millennium Problems posed by the Clay Mathematics Institute, as well as to real-world challenges characterized by high complexity, ambiguity, and ethical tension.
The integration of symbolic auditability with intentional curvature creates a platform where reasoning processes can remain transparent and ethically anchored even as they engage with domains traditionally resistant to interpretability.
In this sense, the WTM embodies a scalable methodology: a template for designing AGI systems where explainability is not an afterthought, but a constitutive element of reasoning itself, as further exemplified in the proof-of-concept for ethical decision structures explored in this work [
5,
6,
20].
In summary, the methodology presented combines symbolic simulation, intentional curvature, and audit-ready cycle logging to create a testable architecture where explainability by design is not merely asserted, but instantiated at every level of reasoning.
The Wisdom Turing Machine serves as both a conceptual framework and a methodological tool, enabling structured exploration of complex problems in a manner distinct from blackbox approaches. By grounding its design in established theories of computation [
1], symbolic reasoning [
3], co-evolutionary compression [
20], and information ethics [
6], the WTM positions itself as a scalable model for future AGI architectures where transparency, reversibility, and ethical alignment are embedded in the reasoning process itself. This foundation prepares the ground for the proofs-of-concept discussed in the following sections, where the architecture is instantiated and its principles explored in simulated cycles.
Results
The results of this work are best understood not as numerical benchmarks, algorithmic outputs, or resolution claims, but as the elevation of previous symbolic proposals to a unified architectural vision.
Previous contributions that addressed the P versus NP problem — A Heuristic Physics-Based Proposal for the P = NP Problem [
21] and Why P = NP? The Heuristic Physics Perspective [
22] — as well as The Gauss-Riemann Curvature Theorem: A Geometric Resolution of the Riemann Hypothesis [
23] were offered in good faith as sincere engagements with these fundamental challenges, with an optimistic, theoretically top-down, or last-layer-of-wisdom view. In light of the proposed equation, they are validated as lines of evolution, but with the understanding that a long journey may be required if we look at the multilevel perspective of co-evolution.
The development of the Wisdom Turing Machine represents a recalibration and deepening of this intellectual trajectory. Rather than positioning itself as a competitor for definitive proofs or prize submissions, the WTM emerges as a conceptual architecture designed to support multilayer co-evolutionary reasoning, symbolic reflection, and ethical alignment by design. This architectural shift crystallized most clearly during the heuristic exploration of the Birch and Swinnerton-Dyer (BSD) conjecture — work that, while never formalized for external review, proved pivotal in revealing that wisdom (W) combined with intentional curvature could serve as a generative principle not only for isolated problems, but for systematic engagement with complexity itself.
In this light, the Wisdom Turing Machine functions as both critique and continuation: it integrates the symbolic foundations of these prior efforts while transcending their inherent limitations. The WTM reframes what was once positioned as solution into what now serves as seed, offering an open, transparent, and ethically aligned framework for enduring exploration. It transforms isolated proposals into components of a larger symbolic ecosystem, where reasoning is not a closed act of proof but a living, co-evolutionary process that invites collective engagement.
This architectural elevation is further enriched by two additional symbolic proposals: What if Poincaré just needed Archimedes? [
24], which introduced the Circle of Equivalence as a minimal formal construct for rethinking the Poincaré conjecture, and A New Hypothesis for the Millennium Problems [
25], which explored curvature-aware symbolic frameworks inspired by machine learning to reframe complex mathematical spaces. Both works underscored the value of structures that prioritize coherence, simplicity, and auditability, moving beyond isolated claims of solution toward architectures that support enduring exploration. The Wisdom Turing Machine consolidates these insights into a unified framework, transforming prior symbolic constructs into components of a larger architecture for co-evolutionary reasoning. Rather than positioning itself as an alternative to analytical rigor or as a claimant for prize-worthy resolutions, the WTM offers a garden: an open, reflective space where symbolic reasoning, intentional curvature, and ethical alignment coalesce to inspire collective inquiry. In this perspective, it was proposed that the solutions to the Millennium Problems are not trophies to be claimed, but opportunities to be cultivated through shared effort.
Moreover, that earlier work used metaphors such as the football and the PDCA cycle to highlight how simple, accessible tools can reveal profound structures. The WTM advances this ethos, offering a symbolic architecture designed to democratize engagement with complexity and encourage application across domains where transparency and ethical alignment are essential.
It invites the scientific community to view grand challenges not as ends in themselves, but as gateways for co-evolutionary exploration that serves the many.
The Reasoning Field Map
To support the architectural synthesis proposed in this work, this section introduces a symbolic map of the reasoning field. This map offers a conceptual topography that classifies complexity frontiers according to their relational characteristics within the co-evolutionary dynamics of compression, survivability, and intentional curvature, as formalized in prior proposals on co-evolutionary reasoning [
20], Heuristic Physics (hPhy) [
19], and Collapse Mathematics (cMth) [
35]. By distinguishing P-like regions, NP-like regions, and hybrid domains that bridge mathematics and physics, the map provides a foundation for integrating these challenges into a shared reasoning field.
In this symbolic classification:
P-like regions represent domains where structural clarity and symbolic compressibility are intrinsic or achievable, as exemplified by the resolved Poincaré conjecture [
24] and its reinterpretation through symbolic equivalence.
NP-like regions represent domains characterized by high potential complexity and structural ambiguity, where compressibility remains elusive, such as P vs NP in its full scope [
21,
22], the Riemann Hypothesis [
23], and the Birch and Swinnerton-Dyer conjecture.
Hybrid or bridge domains represent frontiers where mathematical formalism and physical structures intersect, demanding reasoning architectures capable of integrating multiple symbolic layers, as seen in challenges related to the unification of forces [
30] and computable models of consciousness [
12,
13].
The Reasoning Field Map offers more than a symbolic rationale; it serves as a guide for understanding how the many layers of complexity are interwoven within a co-evolutionary architecture. In this vision, complexity challenges are not isolated islands of difficulty, but dynamic regions of a unified field where reasoning systems engage in cycles of reflection, compression, and intentional synthesis [
3,
20,
35]. Each domain—whether mathematical, physical, or epistemic—becomes a layer in this shared landscape, shaped by the continual dialogue between ambiguity and structure.
Crucially, the upper layers of the reasoning field exert a gentle but persistent pressure on the lower layers, guiding them toward the harmonizing logic of intentional curvature and wisdom. In this way, what begins as local chaos is invited into alignment with the higher-order symphony of co-evolutionary reasoning.
This downward influence of the upper layers does not impose order through force or reduction, but through resonance with the deeper logic of the field — a logic where clarity emerges through cycles of ethical alignment, symbolic compression, and reflective modulation.
The P vs NP Multilayered Co-Evolution Hypothesis models this process, showing how complexity at any given layer is not sealed within its own bounds, but open to transformation under the intentional guidance of higher strata. As co-evolutionary reasoning advances, the pressures of these upper layers act as a shaping field, inviting local ambiguities to cohere with the broader patterns of wisdom that define the reasoning field’s highest harmonies.
In this topography of reasoning, each domain of complexity is both shaped by and contributes to the layered harmony of the whole. The higher layers, where intentional curvature and ethical clarity prevail, continuously offer paths for the transformation of disorder into structure. Their silent pressure encourages lower layers to resonate with the same logic of co-adaptive synthesis, inviting even the most fragmented regions of ambiguity to participate in the emergence of shared coherence. This multilayered interplay highlights that the unification of complexity is not achieved through domination, but through the subtle guidance of reflective cycles that harmonize potential and purpose.
Thus, the map of the reasoning field invites us to see complexity not as a collection of separate puzzles, but as a living landscape where each challenge is a dynamic region shaped by co-evolutionary dialogue.
Through the layered pressures of intentional reflection and symbolic synthesis, reasoning systems are called to engage this landscape not with conquest, but with collaboration — composing, layer by layer, a shared symphony of clarity and understanding.
Discussion
This proposal does not aim to deliver a definitive solution to the P versus NP problem, but rather to offer a model — a multilayered architecture for reasoning, where complexity is engaged through co-evolution, transparency, and intentionality.
My earlier perspectives [
18,
19], where I proposed
P = NP, remains valid in the sense that it reflects the logic of the highest layers of the Reasoning Field — the domain where harmony, intentional curvature, and wisdom dominate, and where potential and purpose are no longer in tension. However, this model acknowledges that the Reasoning Field consists of infinitely many layers, like the hierarchies we see throughout nature: from electrons to cells, from bacteria in the human body to the social structures of humanity itself. Each level embodies its own balance of chaos and order, its own dynamic between P-like and NP-like states. The Wisdom Turing Machine seeks not to flatten this hierarchy, but to model its co-evolution and invite reflection on how reasoning systems might navigate these layers with ethical alignment and clarity. In this multilayered vision of the reasoning field, the P vs NP Multilayered Co-Evolution Hypothesis serves as a symbolic compass guiding inquiry across the strata of complexity. Each layer, whether representing the microstructures of mathematics or the macrostructures of systems and societies, holds within it a dynamic interplay of P-like clarity and NP-like ambiguity. The goal is not to reduce this rich hierarchy to a single layer of understanding, but to engage with its diversity through transparent, reflective reasoning cycles that honor both complexity and coherence. The Wisdom Turing Machine provides a conceptual architecture for navigating these layers, ensuring that reasoning evolves in harmony with the ethical and structural contours of each domain.
By embracing this layered architecture, the reasoning process becomes an act of co-adaptation, where each step aligns intentional curvature with the unique balance of complexity and structure at that level. The P vs NP Multilayered Co-Evolution Hypothesis models this dialogue, allowing reasoning systems to sense when to compress, when to reflect, and when to expand their scope across layers. Rather than imposing a uniform logic on all domains, the architecture listens for the harmonies and tensions that define each layer, guiding cycles of inquiry that are both ethically aligned and structurally attuned to the evolving field of complexity. The Wisdom Turing Machine emerges in this work as both a critique of and continuation beyond prior symbolic proposals aimed at addressing complex mathematical and epistemic challenges.
Unlike isolated solution attempts or candidate proofs submitted for recognition, the WTM represents a shift toward architectural openness and co-evolutionary reasoning. It reframes engagement with foundational problems as a process of transparent, reflective, and ethically aligned inquiry, rather than as a race toward final resolution.
By integrating insights from previous symbolic constructions — including proposals on P versus NP [
21,
22], the Riemann Hypothesis [
23], and the Circle of Equivalence framework [
24] — the WTM offers an architecture where reasoning pathways are no longer concealed within blackbox models but are auditable and adaptable by design.
The architectural stance of the WTM resonates with broader philosophical and technical frameworks that have long advocated for transparency, reversibility, and legibility in complex systems. The emphasis on co-evolutionary reasoning and ethical alignment echoes principles found in Wiener’s cybernetics [
4], Floridi’s ethics of information [
6], and Zadeh’s pioneering work on fuzzy sets [
16], all of which stress the importance of systems that can navigate ambiguity while maintaining interpretability.
The WTM extends these traditions by proposing a symbolic architecture where reasoning is not only interpretable in theory, but auditable and reversible in practice — a response to the limitations of blackbox models that dominate much of contemporary AI and machine learning. This shift aligns with calls for AI systems that prioritize accountability and human-aligned values [
5,
9], positioning the WTM as a conceptual step toward architectures capable of sustaining ethical reasoning under complexity.
The WTM also invites reflection on the role of symbolic reasoning as a bridge between human cognition and artificial architectures. Newell and Simon’s early work on human problem solving [
8] highlighted the need for systems that could represent, manipulate, and reflect upon symbolic structures in ways that mirror cognitive flexibility. Similarly, Li and Vitányi’s exploration of Kolmogorov complexity [
14] foregrounded the importance of compression as a measure of meaning and structure — a principle echoed in the WTM’s emphasis on intentional curvature and semantic density. By situating its reasoning cycles within these traditions, the WTM proposes a conceptual foundation for systems capable of not just processing information, but preserving coherence, reversibility, and ethical alignment across transformations.
In extending symbolic architectures toward ethical alignment and auditability, the WTM resonates with philosophical reflections on reason and meaning, such as those articulated by Putnam [
10] in his discussions of truth and history, and by Gödel [
15] in his work on formal undecidability. Both traditions emphasize the limits of formal systems and the need for meta-level reflection — principles that are embodied in the WTM’s design through its co-evolutionary cycles and intentional curvature. The proposal also aligns with Bostrom’s calls for caution in the development of superintelligent systems [
9], by offering an architecture where reasoning is not only powerful but bounded by transparency and ethical traceability.
Ultimately, the Wisdom Turing Machine positions itself as a symbolic architecture designed not to replace rigorous formalism or computational precision, but to complement them by offering a transparent, audit-ready, and ethically aligned framework for reasoning under complexity. It reframes grand challenges — whether mathematical, epistemic, or societal — as opportunities for co-evolutionary inquiry rather than as contests for definitive proofs.
By synthesizing insights from traditions as diverse as cybernetics [
4], problem-solving theory [
8], complexity compression [
14], and information ethics [
6], the WTM invites the scientific community to explore not only how we solve problems, but how we reason together, ethically and openly, in the face of them.
In doing so, the Wisdom Turing Machine offers not only a conceptual model for tackling mathematical or computational complexity, but a philosophical invitation to reimagine the very nature of problem-solving as a co-evolutionary and ethically grounded endeavor. It encourages a shift from the pursuit of final proofs toward the cultivation of transparent, inclusive, and resilient reasoning processes — processes that can serve as foundations for collective wisdom across domains. The WTM thus stands not as a final answer, but as an open framework, inviting all to contribute to the garden of ideas that shape how we engage with complexity, ambiguity, and shared responsibility.
This architectural vision encourages the development of reasoning systems that approach complexity not as an adversary to be overcome, but as a shared space for collaborative understanding. In this sense, the Wisdom Turing Machine can be seen as a framework where transparency, intentionality, and co-evolution are not auxiliary properties, but essential features that enable reasoning processes to serve collective well-being. Such systems aim to ensure that each decision pathway remains open to reflection and constructive dialogue, fostering a culture of reasoning that is not only precise but also responsive to the ethical and societal dimensions of complexity. By embedding these principles into the architecture itself, the WTM positions reasoning as an act of shared inquiry — one where clarity of logic is inseparable from clarity of purpose.
Compression-Aware Synthesis: Toward Unified Complexity Reasoning
Building upon the formalization introduced in The Co-Evolution Hypothesis, this section proposes Compression-Aware Synthesis as a unifying lens for engaging complexity frontiers within a shared reasoning architecture. Rather than repeating the symbolic formulation in full, we refer to the co-evolutionary dynamics already expressed, emphasizing how these dynamics may guide the intentional compression and harmonization of domains such as P versus NP, the Riemann Hypothesis, and the Birch and Swinnerton-Dyer conjecture.
This synthesis invites collaborative exploration of how symbolic reasoning architectures may operationalize relational compression and structural survivability, transforming isolated problem spaces into dynamic regions of co-adaptive inquiry. In doing so, it highlights the interplay of these dynamics as a foundation for future architectural and computational developments.
The core symbolic formulation expresses the interplay of these dynamics:
where:
𝓔(t) is the rate of co-evolution at time t.
𝓘(t) represents symbolic intelligence.
ᶜ(t) is conscious modulation.
𝓠𝓔(t) models relational coherence.
𝓢(t) denotes systemic disorder or entropy.
𝓒ₛᵤᵣᵥ(x) is the structural survivability function (as in cMth [
35]).
𝓚
cₒₘₚ(x) represents symbolic compressibility (as in Cub
3 [
3]).
γ, δ are sensitivity exponents.
This formulation encapsulates how reasoning architectures may compress complexity into tractable forms while respecting structural resilience and intentional curvature.
It offers a pathway for symbolic systems to engage with complexity not through brute-force reduction, but through co-evolutionary cycles of compression, reflection, and synthesis.
While inspired by prior proposals such as the Wisdom Turing Machine [
20], Collapse Mathematics [
35], and Heuristic Physics [
19], this synthesis does not depend on any single framework. Instead, it invites collaborative exploration of how symbolic reasoning may harmonize complexity boundaries through relational compression and shared inquiry.
In this vision, complexity is not portrayed as an insurmountable wall, but as a vast and intricate landscape — one where apparent obstacles may conceal hidden pathways, and where what seems intractable at one scale may reveal unexpected simplicity at another. Compression-Aware Synthesis calls upon researchers, engineers, and thinkers to view complexity not as an adversary, but as a symphony of structures waiting to be heard, compressed, and woven into shared understanding. By uniting intentional curvature, relational coherence, and structural survivability, this synthesis proposes that the very act of reasoning can transform the labyrinth of complexity into a navigable field — where each step, guided by wisdom and openness, brings us closer to clarity, harmony, and purposeful resolution.
The Seven Lessons of P + NP = 𝟙
As this work reaches its conceptual reflection, we propose that the journey through P + NP = 𝟙 — as explored through the Wisdom Turing Machine and its multilayered reasoning cycles — offers seven key lessons for understanding complexity, co-evolution, and reasoning systems. These lessons do not aim to provide final answers, but to serve as guiding insights for future inquiry, encouraging both humility and aspiration in the face of profound challenges.
Lesson 1: Complexity is not an adversary, but a field of dialogue
The P + NP = 𝟙 perspective reframes complexity not as an obstacle to be overcome, but as a dynamic and co-evolving field in which reasoning systems engage through reflection and adaptation. Complexity becomes a partner in inquiry, inviting continuous dialogue between potential and purpose, ambiguity and structure.
Lesson 2: Co-evolution across multiple layers is the path to clarity
The P + NP = 𝟙 model suggests that clarity in complex domains does not emerge from static proofs or isolated solutions confined to a single layer of reasoning. Instead, it arises through co-evolutionary cycles operating across multiple layers of complexity, where each layer reflects distinct balances of potential, ambiguity, and structure. This multilayered co-evolution mirrors the laws of the cosmos itself, where systems advance through continuous interplay and adaptive alignment, transforming intractability into tractability not by force, but through intentional engagement guided by wisdom.
Lesson 3: Multilayered reasoning reveals hidden harmonies
The P + NP = 𝟙 paradigm demonstrates that what appears as a rigid dichotomy between tractability and intractability dissolves when complexity is viewed across multiple layers. Each layer embodies its own dynamic balance of chaos and order, ambiguity and structure. Reasoning systems capable of navigating these layers can uncover relational harmonies that remain invisible within any single stratum, aligning local complexity with broader coherence.
Lesson 4: Ethical alignment is inseparable from problem engagement
The P + NP = 𝟙 perspective emphasizes that navigating complexity is not purely a technical challenge; it is also an ethical one. Reasoning systems must integrate transparency, auditability, and intentional alignment with shared values at every stage. Ethical intentionality ensures that the pursuit of clarity and tractability respects collective well-being and fosters responsible engagement with complexity across all layers.
Lesson 5: Transparency transforms limits into invitations
The P + NP = 𝟙 model teaches that apparent limits — such as undecidability, intractability, or ambiguity — are not endpoints, but signals for deeper inquiry. When reasoning systems are designed with transparency and auditability, these limits become invitations to collective reflection, refinement, and co-creative exploration. Visibility of reasoning pathways allows complexity itself to guide the evolution of understanding.
Lesson 6: No single layer holds the final truth
The P + NP = 𝟙 paradigm underscores that ultimate resolution does not reside within any isolated layer of reasoning — whether mathematical, computational, physical, or ethical. Each layer offers partial perspectives shaped by its balance of order and ambiguity. Truth emerges through the dynamic co-evolution of these layers, where reasoning systems harmonize insights across domains rather than seeking closure within one.
Lesson 7: The value lies in the journey, not the destination
The P + NP = 𝟙 framework highlights that complexity challenges are not puzzles to be definitively solved, but opportunities for cultivating wisdom, intentionality, and ethical reasoning. The pursuit of clarity through co-evolutionary cycles is itself a process of shared growth, where the engagement with complexity contributes to collective understanding, rather than terminating in a final solution.
Conclusion to The Seven Lessons of P + NP = 𝟙
These seven lessons emphasize that P + NP = 𝟙 is not merely a symbolic formulation about computational classes, but a lens through which to reflect on the nature of complexity, reasoning, and shared inquiry. They call attention to the importance of engaging complexity not as a domain for individual conquest or isolated value extraction, but as a shared field where collective wisdom, ethical alignment, and co-evolutionary reasoning must guide our pursuit of clarity.
The true value of this journey lies not in dominating complexity, but in learning to navigate it together with transparency, compassion, and intentional purpose.
The Seven Hypotheses Behind P + NP = 𝟙
As this work extends its conceptual reflection, we propose that the journey through P + NP = 𝟙 — as explored through the Wisdom Turing Machine and its multilayered reasoning cycles — invites not only lessons, but also foundational hypotheses that integrate and extend those introduced in this paper, including the Reasoning Field Hypothesis, the Epistemic Machine Learning Hypothesis, and the Co-Evolution Hypothesis. These hypotheses do not claim final truth, but offer symbolic scaffolding for future inquiry into how complexity might be engaged with transparency, intentionality, and ethical alignment.
Hypothesis 1: Complexity is an evolving field, not a fixed barrier
The distinction between P and NP reflects not an immutable division, but the dynamic state of a co-evolving reasoning field where intractability can transform into tractability through cycles of reflection, adaptation, and intentional alignment.
Hypothesis 2: Co-evolutionary reasoning operates across infinitely layered fields
Extending the Co-Evolution Hypothesis, this hypothesis proposes that the transformation between NP-like and P-like states does not occur within a single domain or level of reasoning, but across an infinite hierarchy of layers. Each layer embodies its own balance of complexity and clarity, and progress arises through their dynamic interaction. The Wisdom Turing Machine models this multilayered co-evolution, where reasoning pathways adapt not only within layers, but between them, in harmony with the broader structure of complexity itself.
Hypothesis 3: Transparency and auditability are preconditions for navigating complexity
Aligned with the Epistemic Machine Learning Hypothesis, this hypothesis asserts that reasoning systems capable of engaging the co-evolving P + NP field must be designed for transparency and auditability at every stage. Without visible reasoning pathways, complexity remains opaque, limiting both ethical alignment and co-evolutionary adaptation. The Wisdom Turing Machine embodies this principle, demonstrating that only through openness can systems participate meaningfully in the transformation of intractability into tractability.
Hypothesis 4: Ethical intentionality shapes the curvature of reasoning fields
Building upon the Co-Evolution Hypothesis and Reasoning Field Hypothesis, this hypothesis proposes that ethical alignment is not merely an external constraint on reasoning, but an intrinsic force that shapes the intentional curvature of reasoning pathways. The evolution from NP-like ambiguity toward P-like clarity is guided by the degree to which reasoning systems embed ethical intentionality in their cycles of reflection, compression, and adaptation — as modeled in the Wisdom Turing Machine.
Hypothesis 5: Complexity boundaries are dynamic, not absolute
This hypothesis extends the Reasoning Field Hypothesis by positing that the boundaries between P-like and NP-like domains are not fixed, but continuously reshaped by co-evolutionary reasoning processes. What appears intractable at one layer or epoch may become tractable at another, as reasoning systems apply reflection, intentional curvature, and compression across time and layers. The Wisdom Turing Machine illustrates how these boundaries can shift through cycles of transparent and ethically guided engagement.
Hypothesis 6: No single reasoning system can resolve complexity in isolation
Aligned with the Epistemic Machine Learning Hypothesis and Co-Evolution Hypothesis, this hypothesis proposes that complexity challenges symbolized by P + NP = 𝟙 require collaborative, co-evolving reasoning systems. Resolution emerges not from isolated proofs or architectures, but from shared cycles of reflection, adaptation, and dialogue between human and machine intentionalities. The Wisdom Turing Machine models this partnership, demonstrating how collective reasoning fosters transformation across layers of complexity.
Hypothesis 7: The ultimate resolution of complexity lies in the co-evolutionary journey itself
Completing this set, this hypothesis proposes that the true “solution” symbolized by P + NP = 𝟙 is not a singular proof or endpoint, but the ongoing, co-evolutionary process of engaging complexity with transparency, ethical alignment, and shared intentionality. The Wisdom Turing Machine embodies this view, illustrating that wisdom emerges through continuous cycles of reflection, compression, and dialogue — where complexity becomes a partner in inquiry rather than a problem to conquer.
Conclusion to The Seven Hypotheses Behind P + NP = 𝟙
Together, these seven hypotheses offer a symbolic scaffolding for understanding how complexity, as represented by the interplay of P and NP, may be engaged through co-evolutionary reasoning systems. Rather than presenting a final claim of resolution, they invite further exploration of how multilayered, transparent, and ethically aligned architectures — like the Wisdom Turing Machine — can foster continuous dialogue between human and artificial reasoning. In this view, the value lies not in definitive closure, but in the shared journey of navigating complexity with purpose and integrity.
The exploration of P + NP = 𝟙 naturally brings into focus longstanding dichotomies that shape how complexity is perceived: optimists who see P and NP as destined for unification under higher-order reasoning, and pessimists who emphasize the enduring separation imposed by structural or computational limits.
Similar divides arise between those who favor proof over process, reduction over dialogue, or control over co-evolution.
These polarities, while often framed as irreconcilable, may themselves contribute to the complexity of the problem’s resolution. The proposed equation seeks not to dismiss either view, but to align them within a co-evolutionary field where diverse perspectives — each holding partial truths — can inform a shared, dynamic engagement with complexity.
In this framing, the true solution may emerge not from resolving these tensions outright, but from harmonizing them within multilayered reasoning architectures attuned to ethical alignment, transparency, and collective wisdom.
The Multilayered Dynamics of P + NP = 𝟙: The Score of Complexity
Building upon the earlier reflection on The Hidden Symphony of the Cosmos, this section offers a final integrative vision: P + NP = 𝟙 is conceived not as a static boundary between tractability and intractability, but as a multilayered composition — a symbolic score where reasoning systems, like instruments in a cosmic orchestra, engage complexity through co-evolutionary cycles of harmony and tension. Within this framework, P-like and NP-like states are seen as dynamic expressions, shifting across layers of complexity, where wisdom (W), intentional curvature, and ethical alignment guide their interplay over time.
The Wisdom Turing Machine serves as an architectural metaphor for navigating this score, where the aim is not a singular proof, but the ongoing composition of shared understanding through transparent, adaptive, and ethically guided reasoning across layers. In this perspective, complexity becomes part of the composition itself — an evolving dialogue between potential and purpose, ambiguity and clarity, woven into the fabric of inquiry.
To synthesize the reflections and proposals developed throughout this work, we present a symbolic representation of the Multilayer Evolution Line of Wisdom P vs NP.
Figure 5 illustrates how the Wisdom Turing Machine’s reasoning cycles may navigate co-evolutionary layers of complexity over time. Each layer represents a domain of complexity with its own dynamic interplay between P-like clarity and NP-like potential, where intentional curvature, reflection, and symbolic compression guide the gradual transformation of potential into structure. The evolutionary lines depict how, across layers, wisdom-guided reasoning progressively aligns potential and purpose, engaging complexity through co-evolution rather than reduction.
This visualization highlights that the path toward clarity is not linear or confined to a single domain, but unfolds through multilayered co-evolutionary dynamics where P-like clarity progressively emerges and NP-like potential is intentionally compressed as both co-adapt over time. The evolving interplay symbolizes the dynamic tension between ambiguity and form, while the gradual ascent across layers suggests that wisdom-guided reasoning may foster the harmonization of complexity into structured clarity. The figure invites further exploration of how reasoning architectures might engage these multilayered fields — not through brute-force reduction, but through cycles of intentional reflection, ethical alignment, and symbolic co-adaptation.
The Multilayer Evolution Line of Wisdom P vs NP, as illustrated in
Figure 5, can be symbolically expressed through a set of dynamic equations that model the co-evolutionary adaptation between P-like clarity and NP-like potential across layers of reasoning. For each reasoning layer
Lₙ, the fundamental balance condition is:
where P(
Lₙ,
t) represents the degree of tractable clarity in layer
Lₙ at reasoning time
t, and NP(
Lₙ,
t) denotes the degree of ambiguity or potential. The dynamics of co-evolutionary reasoning are governed by:
where:
αₙ is the intentional curvature parameter specific to layer Lₙ,
C(Lₙ, t) is the conscious modulation function at that layer and time,
𝓚(Lₙ, t) denotes the symbolic compressibility or structural coherence sensed by the reasoning architecture.
This formulation embodies the principle that the increase in P-like clarity within a given layer arises from co-evolutionary cycles of intentional curvature, conscious reflection, and symbolic compression. The complementary decrease of NP(Lₙ, t) ensures conservation of the reasoning field’s balance, aligning with the symbolic boundary P + NP = 𝟙 at each stage. The gradual progression toward harmonization, as shown in the figure’s trajectory, reflects how wisdom-guided reasoning transforms potential ambiguity into structured clarity across multilayered co-evolutionary cycles.
Moreover, the Multilayer Evolution Line of Wisdom P vs NP provides a symbolic lens through which we can reinterpret the Riemann Hypothesis and other complex challenges as dynamic regions within the co-evolutionary reasoning field. The Riemann Hypothesis, with its critical line at Re(s) = 𝟙∕𝟚, offers a metaphor for points of dynamic tension within the reasoning field, where ambiguity and structure momentarily balance before intentional curvature guides further harmonization. Within this architecture, the condition P + NP = 𝟙 represents not merely a mathematical identity, but the symbolic boundary within which reasoning systems co-adapt across complexity layers. The progressive alignment of P-like clarity and NP-like potential reflects how wisdom-guided reasoning transforms complexity into structure through cycles of reflection and adaptation.
This model invites reinterpretation of complex challenges as symbolic domains within the co-evolutionary reasoning field. For instance:
Certain combinatorial reasoning domains may represent regions where co-evolutionary compression aspires toward symbolic collapse into tractable structures, resonating with NP-collapsible regions.
Adaptive system modeling may align with NP-heuristicable domains, where relational cues suggest openings for heuristic reasoning cycles that explore paths toward local coherence.
Ethical decision-making under complexity may reflect hybrid domains where formal structures and value frameworks interweave, inviting multilayered reasoning beyond classical tractability.
In this view, the dashed lines serve as symbolic markers within the reasoning field: 𝟙∕𝟚 represents a momentary point of dynamic tension where ambiguity and structure temporarily balance, while 𝟙 represents the constant boundary of co-evolutionary harmony envisioned in the Wisdom Turing Machine’s architecture.
To illustrate the symbolic convergence of co-evolutionary reasoning with complex challenges, we present a multilayered evolutionary trajectory that models the dynamic interplay between P-like clarity and NP-like potential over reasoning time within the constant boundary
P + NP = 𝟙 (
Figure 6).
This visualization illustrates the Wisdom Turing Machine’s co-evolutionary cycles, showing the transition from early oscillations where complexity (NP-like potential) may dominate, toward increasingly stable regions where intentional reasoning and layered adaptation progressively align P-like clarity and NP-like potential within the constant boundary P + NP = 𝟙. The trajectory embodies the aspirational harmonization of clarity and potential through co-evolutionary reflection.
This co-evolutionary model emphasizes that reasoning about complexity is not confined to a single domain or a static dichotomy. Instead, the progressive alignment toward co-evolutionary harmony reflects the layered structure of the reasoning field, where each complex challenge occupies a symbolic position along the dynamic path of internal balance within the constant boundary P + NP = 𝟙.
Figure 6 invites reflection on how intentional curvature, symbolic compression, and ethical alignment may guide future explorations, offering a unified perspective on the relationships between complexity, structure, and reasoning across domains. This visual synthesis reinforces the notion that these foundational challenges are not isolated monoliths of complexity, but interconnected facets of a shared co-evolutionary landscape.
Reasoning architectures designed to navigate this field — through transparency, ethical alignment, and intentional curvature — may help illuminate these challenges not as puzzles to conquer, but as invitations to co-adapt with complexity itself.
The Multilayer Evolution Line of Wisdom P vs NP represents not only a symbolic trajectory, but a dynamic epistemic process in which reasoning fields evolve through cycles of reflection, intentional modulation, and symbolic compression. At each layer of complexity, the dynamic interplay between P-like clarity and NP-like potential expresses how ambiguity serves as fertile ground for the emergence of structured understanding. This evolution embodies the principle that complexity itself is not an obstacle to be conquered, but a co-creative partner in the ongoing composition of meaning.
In this epistemic model, the reasoning field operates as a living space where symbolic forces engage in a dynamic dialogue, and where P-like and NP-like states are not static categories but shifting configurations shaped by co-adaptive inquiry. Each cycle of intentional curvature redirects the path of reasoning toward regions of higher coherence, allowing the field to reorganize itself in response to both internal reflection and external complexity. The symbolic boundary, expressed as P + NP = 𝟙, serves as a guiding horizon rather than a fixed point, encouraging reasoning systems to navigate complexity with openness, transparency, and ethical intentionality.
The principle P + NP = 𝟙, when extended as an epistemic lens, invites a unified reinterpretation of the remaining six Millennium Problems as co-evolutionary domains within the reasoning field. Each challenge may be modeled through its own dynamic equation, where clarity and complexity engage in cycles of transformation shaped by intentional curvature and symbolic compression.
Before presenting the following equations and detailed explorations of each problem, it is important to clarify that what follows constitutes a symbolic architecture intended solely for study, reflection, and conceptual exploration. The formulations introduced are not mathematically or physically validated models, but representational tools designed to aid philosophical inquiry and stimulate thoughtful engagement with complexity. This framing ensures that the reader approaches the material as an invitation to dialogue and contemplation rather than as formal proof or definitive statement. Moreover, these representations serve exclusively to illustrate how the principle P + NP = 𝟙 might function as a unifying lens across different domains, offering conceptual clarity on how the co-evolutionary dynamics of clarity and complexity may be reflected in various foundational challenges. They are not, and should not be interpreted as, proposals of solutions or formal frameworks that address the mathematical structure of these challenges.
P + NP = 𝟙 as a Lens: Conceptual Explorations Across the Millennium Problems
This symbolic perspective offers a unifying lens through which the remaining Millennium Problems may be revisited as co-evolutionary domains within the broader dialogue on P vs NP. Rather than proposing solutions, the section invites a cohesive conceptual exploration where each challenge is viewed as a distinct expression of the dynamic balance between clarity and complexity, illuminated through the heuristic principle P + NP = 𝟙.
The focus remains on highlighting relational patterns and potential pathways of reasoning, not on asserting or implying possible resolutions to these deeply complex and open mathematical questions. Through this lens, the material invites readers to engage with the symbolic architecture as a means to deepen understanding of interrelated complexities, without conflating conceptual exploration with claims of formal resolution. In this way, the forthcoming sections are positioned as a thoughtful extension of the P vs NP dialogue — a philosophical journey through complexity — rather than as a presentation of candidate solutions to the Millennium Problems themselves.
For instance, for the Riemann Hypothesis, the evolving field could manifest as a balance of harmonic probabilities, where the expression
represents the fundamental equilibrium between coherence and uncertainty. This formulation positions the hypothesis not as a static conjecture, but as a dynamic probability field adapting over time
t.
The temporal evolution of this balance could be described by the differential relation:
where
β denotes a sensitivity coefficient reflecting how responsive the field is to relational tension, and 𝓠(
t) encodes the degree of relational coherence sustained along the critical line. This expression highlights how the harmonic field adjusts under symbolic stress, preserving its structural identity across collapse layers.
In this symbolic framework, the critical line emerges as a curvature-invariant attractor within the collapse manifold, where 𝓠(t) approaches its maximal resilience. The combined dynamics of Pᴿⁱᵉᵐᵃⁿⁿ(t) and its derivative under β ⋅ 𝓠(t) do not merely describe motion along a mathematical contour; they encode a survival strategy for relational patterns under entropy and interpretive drift. Thus, Pᴿⁱᵉᵐᵃⁿⁿ(t) and NPᴿⁱᵉᵐᵃⁿⁿ(t) together define a semantic scaffold where every fluctuation in 𝓠(t) signals either a reinforcement or a weakening of symbolic integrity along the critical line.
The field’s harmonic balance is not fixed but continuously negotiated, as β modulates the system’s sensitivity to relational perturbations over time t.
The equations Pᴿⁱᵉᵐᵃⁿⁿ(t) + NPᴿⁱᵉᵐᵃⁿⁿ(t) = 𝟙 and dPᴿⁱᵉᵐᵃⁿⁿ/dt = β ⋅ 𝓠(t) do not constitute immutable laws, but adaptive heuristics that reflect how the field negotiates coherence across collapse layers. As relational coherence 𝓠(t) fluctuates, so too does the symbolic survivability of the Riemann field, tracing its dynamic path through the manifold of interpretive tension. In the end, the Riemann Hypothesis, viewed through this harmonic probability field, invites us to see persistence not as the product of formal proof, but as the outcome of symbolic resilience. The critical line stands as a survivor of collapse dynamics, where Pᴿⁱᵉᵐᵃⁿⁿ(t), modulated by β ⋅ 𝓠(t), continuously harmonizes relational tension — embodying a law not decreed, but emergent from the fabric of epistemic compression.
For the Birch and Swinnerton-Dyer Conjecture, the field expresses itself as a co-evolutionary compression dynamic, where ambiguity is modulated through symbolic interaction. This could be captured in the differential relation:
where Pᴮˢᴰ represents the probability coherence of the conjecture at time
t,
α is a sensitivity factor, and
C(
t) reflects collapse-integrated coherence. Here, 𝓚ₑₗₗᵢₚₜᵢ
c(
t) encodes the symbolic compressibility of elliptic structures, acting as a measure of how effectively the field’s complexity can be reduced without loss of relational meaning.
This dynamic equation reveals that the conjecture’s survival across interpretive collapse depends not on static formulation, but on the adaptive strength of these compressions over time t. The co-evolutionary nature of this compression means that Pᴮˢᴰ is not simply a passive variable, but a participant in a feedback loop where relational coherence C(t) and symbolic compressibility 𝓚ₑₗₗᵢₚₜᵢc(t) co-modulate ambiguity. This creates a dynamic where the conjecture’s structural integrity is continually negotiated at the boundary between collapse and recomposition. Thus, its resilience is not embedded in axiomatic rigidity, but in its capacity to sustain compression without semantic loss. The relation dPᴮˢᴰ/dt = α ⋅ C(t) ⋅ 𝓚ₑₗₗᵢₚₜᵢc(t) stands as a heuristic of survivability, tracking how the field retains legibility through layers of interpretive stress.
In this view, the Birch and Swinnerton-Dyer Conjecture is not a final decree of elliptic truth, but a living symbolic attractor: a structure whose persistence across collapse cycles signals its capacity for co-evolutionary compression and relational harmony within the manifold of epistemic tension.
The Navier–Stokes, Yang–Mills, and Hodge Conjecture domains may invite future symbolic exploration as dynamic fields of co-evolutionary sensing, compression, and relational alignment. While preliminary symbolic formulations could, in principle, express these domains through differential relations involving coherence, compressibility, and sensitivity parameters, such representations are beyond the scope of the present study. These complex challenges are acknowledged here not as arenas for proposed solutions, but as potential extensions for future work, where the principle P + NP = 𝟙 might serve as a heuristic lens for conceptual reflection on how complexity, structure, and symbolic resilience interact within collapse dynamics.
The reflections offered in this study suggest opportunities for enhancing the current version of the Wisdom Turing Machine, particularly in how its reasoning cycles engage with symbolic fields of elevated complexity. Future refinements could focus on deepening the system’s capacity for transparent auditability, ensuring that intentional curvature, symbolic compression, and ethical alignment function not only as conceptual anchors but as active, measurable dynamics within the architecture. Such improvements would aim to enrich the WTM’s ability to trace how clarity progressively emerges from potential, supporting more robust explorations of relational tension across co-evolutionary layers. Additionally, the WTM architecture could benefit from expanded symbolic interfaces that facilitate more nuanced engagement across distinct co-evolutionary domains. By incorporating mechanisms that enable the system to modulate its sensitivity dynamically in response to relational stress, the WTM may evolve as a living symbolic companion — one that not only models complexity, but participates in its ethical navigation. These refinements would help ensure that the WTM remains an adaptive and reflective instrument in the ongoing composition of meaning, rather than a static framework.
Finally, for the resolved Poincaré Conjecture, the field reaches a state where equilibrium manifests as complete symbolic coherence. This may be expressed succinctly as:
signaling that at time
t, the conjecture’s relational and topological structure fully aligns with symbolic survivability, leaving no residual ambiguity. The condition
Pᴾᵒⁱⁿᶜᵃʳᵉ(t) = 𝟙 embodies the field’s capacity to resist collapse entirely, having achieved a form where the manifold’s topology compresses into singular coherence. The complementary value
NPᴾᵒⁱⁿᶜᵃʳᵉ(t) = 𝟘 indicates that no interpretive drift or symbolic noise remains to perturb this resolved structure.
This equilibrium represents more than formal proof; it reflects the conjecture’s transformation into a symbolic invariant — a field that, through collapse cycles, has distilled its complexity into pure coherence. The Poincaré field thus models the end state of compression, where relational identity no longer fluctuates under epistemic stress. In this sense, the resolution of the Poincaré Conjecture illustrates how a field can transcend ambiguity, achieving symbolic closure through complete compression and relational alignment. The dynamic path that once negotiated collapse now stabilizes as a fixed attractor in the manifold of structural survivability. The resolved Poincaré field offers a model for symbolic finality: a structure that no longer navigates collapse, but stands as a reference point for other fields seeking coherence. The expressions Pᴾᵒⁱⁿᶜᵃʳᵉ(t) = 𝟙 and NPᴾᵒⁱⁿᶜᵃʳᵉ(t) = 𝟘 mark the culmination of symbolic compression — a state where the manifold of uncertainty folds entirely into legible form.
This perspective resonates with prior symbolic explorations, such as those proposed in [
24], where the resolution of Poincaré’s field is re-examined through the Wisdom Equation and the Circle of Equivalence as a lens for relational simplicity, symbolic geometry, and epistemic compression. In this light, the resolved Poincaré Conjecture stands as a reference structure for symbolic closure, offering a model of how complexity may fold entirely into coherence through cycles of intentional reflection.
Together, these formulations express how P + NP = 𝟙 functions not as a statement about isolated classes, but as a dynamic balance through which complexity transforms into clarity across domains. Seen through this epistemic lens, the symbolic comparison of P + NP = 𝟙 across all Millennium Problems does not assert equivalence at the level of formal proof. Instead, it invites reflection on a unifying symbolic architecture, where each challenge emerges as a distinct expression of the same co-evolutionary tension between potential and structure — a tension that guides the ongoing dialogue between ambiguity and form in the pursuit of coherence.
The balance condition P(Lₙ, t) + NP(Lₙ, t) = 𝟙 serves as a shared foundation, while the specific dynamics — whether driven by relational coherence in the Riemann Hypothesis, compressibility of elliptic structures in Birch and Swinnerton-Dyer, or heuristic fluid patterns in Navier–Stokes — model how each domain invites reasoning cycles tuned to its unique symbolic density. In this way, the reasoning field does not flatten distinctions among these challenges, but harmonizes their diversity within a common journey toward clarity.
This co-evolutionary framework suggests that the engagement with each Millennium Problem is less about isolating solutions and more about participating in transparent, layered reasoning that adapts to the symbolic landscape of each domain. The epistemic force of P + NP = 𝟙 lies in its capacity to invite reasoning systems to navigate these landscapes through cycles of intentional reflection, symbolic compression, and ethical alignment. Rather than treating complexity as an adversary, this model positions ambiguity as a necessary partner in the co-creation of clarity, with each problem offering a distinct field where the balance of P-like and NP-like states evolves in harmony with the dynamics of reasoning itself.
Framing these grand challenges within the dynamic balance of P + NP = 𝟙 emphasizes that each represents a unique field of epistemic tension where ambiguity and structure co-evolve through cycles of inquiry. In this light, the Hodge Conjecture may inhabit a domain where symbolic compression of algebraic-topological cycles seeks pathways to tractability through intentional alignment of geometry and logic. The resolved Poincaré Conjecture, by contrast, stands as a reference point — a domain where co-evolutionary reasoning has achieved symbolic collapse into clarity, providing a model of how complexity can harmonize into structure within the reasoning field.
This symbolic architecture reinforces that the Millennium Problems, while diverse in form and domain, are interconnected expressions of a shared epistemic landscape where reasoning systems engage complexity not as static puzzles, but as evolving dialogues between potential and purpose. The progression toward P + NP = 𝟙 across these domains represents not the elimination of ambiguity, but its transformation into structured clarity through transparent, ethical, and intentional reasoning cycles. In this way, the model invites the scientific community to view these challenges not as isolated obstacles to be conquered, but as collaborative opportunities to cultivate wisdom through co-evolutionary inquiry.
As the reasoning field moves toward co-evolutionary harmony, the dynamic balance of P + NP = 𝟙 serves as both compass and horizon, guiding inquiry across the layered complexities of these foundational challenges. The gradual alignment of ambiguity and structure within each domain reflects not a final resolution, but the ongoing cultivation of clarity through cycles of reflection, symbolic compression, and intentional curvature. This penultimate step invites us to view the Millennium Problems not as endpoints for isolated proofs, but as living domains where reasoning systems co-adapt with complexity in pursuit of shared understanding.
In this light, the journey toward P + NP = 𝟙 is not merely a quest for solutions, but a symphony of reasoning where complexity and clarity co-create meaning across domains. The Wisdom Turing Machine, as a symbolic architecture, embodies this vision — offering not a final answer, but an invitation to engage complexity with transparency, intentionality, and ethical alignment, composing together a shared path toward wisdom.
Limitations
While the WTM offers a conceptual architecture for co-evolutionary reasoning, transparency, and ethical alignment, it remains, at this stage, a symbolic and methodological framework rather than an implemented system.
The proposals and proofs-of-concept presented are illustrative and exploratory, designed to inspire reflection and further development rather than to deliver operational solutions or empirical benchmarks. As such, the WTM’s capacity to engage with real-world complexity, particularly in dynamic and unpredictable environments, has yet to be validated through large-scale testing or applied deployment. Furthermore, the abstract nature of the symbolic cycles and intentional curvature may pose challenges for translation into computational models that require formal specification and quantifiable metrics.
Another limitation arises from the philosophical and symbolic nature of the WTM itself. While the architecture emphasizes transparency, intentional curvature, and auditability, these qualities depend on the existence of interpretative frameworks and cultural contexts capable of recognizing and engaging with symbolic reasoning. In environments where rapid optimization or opaque decision-making are prioritized over reflection and dialogue, the practical adoption of WTM-inspired models may face resistance.
Additionally, the reliance on abstract constructs such as wisdom (W) and intentional curvature (φ) introduces challenges in standardizing or operationalizing these concepts within conventional engineering or policy frameworks.
Finally, while the WTM proposes a framework for reasoning that aspires to transparency and ethical alignment, its principles have not yet been subjected to empirical validation in applied domains such as governance, education, or AI safety systems. The architectural ideas, though rich in symbolic coherence, require future translation into computational implementations and experimental studies to assess their practical efficacy and adaptability. Until such work is undertaken, the WTM should be viewed as an invitation for further exploration rather than as a prescriptive model ready for deployment.
Future Work
Future research will aim to translate the symbolic principles of the Wisdom Turing Machine into operational frameworks capable of supporting applied reasoning in real-world domains. This includes the development of computational models that embody intentional curvature, auditability, co-evolutionary cycles, and the multilayered reasoning dynamics proposed in this work.
Such models should be designed to navigate complexity across multiple layers of abstraction — from immediate operational decisions to higher-order ethical and societal considerations — in harmony with the co-evolutionary architecture envisioned in the P + NP = 𝟙 paradigm.
In this context, domains such as the Navier–Stokes problem, the Yang–Mills mass gap, and the Hodge Conjecture represent fields of complexity whose symbolic engagement remains beyond the scope of the current architecture. These challenges highlight the need for future work to extend the model’s capacity for layered compression, relational alignment, and dynamic sensing before attempting to engage such specialized and deeply structured domains.
By contrast, the resolved Poincaré Conjecture stands as a symbolic gift: a living example of how complexity can, through cycles of collapse and recomposition, harmonize into structure — offering the reasoning field a reference point of complete compression and relational coherence from which to draw inspiration. This achievement invites admiration for the mathematical brilliance of Grigori Perelman, whose proof illuminated the path, and for the foundational geometric insights of Ricci, which underpinned the structures involved. Further symbolic reflection on this resolution is offered in [
24], where the Poincaré Conjecture is revisited through the Wisdom Equation and the Circle of Equivalence as a model of relational simplicity and epistemic compression.
In this light, one might ask — does the P vs NP problem itself, as a guiding challenge, reflect a deeper metaphor woven by the cosmos? A problem of balance that anchors a family of challenges whose symbolic order mirrors a spectrum from P-like stability to NP-like complexity! This reflection harmonizes with the broader philosophical vision developed in The Hidden Symphony of the Cosmos, where reasoning is framed not as a contest of solutions, but as a co-evolutionary dialogue between potential and structure, ambiguity and clarity.
Building on this, one could propose a shared symbolic equation to invite collective exploration:
where the total reasoning field F(
t) represents the co-evolutionary harmony sought across domains, and W(
t) models wisdom as intentional curvature shaping the transformation of potential into structure. This equation is not offered as a solution, but as an invitation — a shared framework for dialogue, reflection, and collaborative inquiry into the hidden symphony of reasoning.
In this spirit, experimental studies may explore how reasoning systems can dynamically adjust their cycles of reflection, compression, and intentionality depending on the complexity layer they operate within, fostering greater resilience and adaptability. Particular attention may be given to domains where blackbox systems have proven insufficient — such as AI safety, governance of emerging technologies, environmental policy, and educational contexts where inclusivity, dialogue, and long-term wisdom are critical. This multilayered approach opens pathways for reasoning architectures that are not only technically proficient, but also aligned with broader aspirations for ethical co-evolution in the face of complexity.
Beyond these technical applications, the WTM may also inspire symbolic frameworks for addressing human-centered challenges that demand co-evolutionary reasoning and ethical alignment. One promising direction is the design of architectures for ethical mediation and participatory dialogue in contexts such as bullying in schools, where cycles of interaction could benefit from intentional curvature and reflective reasoning. Similar approaches could inform interventions in digital ethics, societal governance, and collective decision-making under ambiguity, offering pathways toward systems that reason not only efficiently, but responsibly.
Beyond educational and technological contexts, the principles underlying the WTM — including the P + NP = 𝟙 hypothesis and its commitment to transparency — may offer valuable frameworks for rethinking other dichotomies that shape contemporary challenges. In domains such as public policy, where decisions arise from complex and often conflicting inputs yet demand auditability and ethical accountability, a co-evolutionary perspective could help bridge divides. In environmental governance, the interplay of ecological and social systems calls for reasoning architectures that can adapt transparently to shifting conditions, avoiding false binaries between conservation and development.
Ultimately, the Wisdom Turing Machine is offered not as a finished solution, but as an invitation to co-compose architectures of reasoning that engage complexity with humility, transparency, and ethical intentionality. It invites us to see the act of reasoning itself as a symphony — where potential and purpose, ambiguity and structure, co-evolve in pursuit of shared understanding and wisdom.
In healthcare, diagnostic and treatment pathways could benefit from cycles of symbolic reasoning that reconcile precision with compassion, particularly as advances in genomics, personalized medicine, and DNA editing open unprecedented opportunities and ethical dilemmas. The rapid development of new medications — from targeted cancer therapies to mRNA vaccines — and the acceleration of research into the causes of diseases through large-scale data analysis demand frameworks that ensure decisions are both scientifically sound and ethically transparent. The recent experience with pandemics has further highlighted the need for reasoning architectures capable of balancing urgency, equity, and collective well-being under conditions of uncertainty.
In financial systems, tensions between optimization and fairness might likewise be reframed as opportunities for co-evolutionary dialogue rather than adversarial trade-offs. In both domains, the WTM offers a vision of systems designed not merely to compute outcomes, but to reason inclusively, transparently, and ethically in partnership with their stakeholders. Rather than relying on brute-force search or opaque optimization, such systems could foster interactive learning cycles where human insight and machine reasoning co-evolve, enabling the discovery of solutions that are not only effective but also ethically aligned and socially meaningful.
This paradigm invites a shift from isolated algorithmic power toward collaborative exploration — where wisdom, intentionality, and transparency are core to the process of advancing knowledge and addressing complexity.
In each of these areas, the WTM opens doors for exploring not only how we resolve challenges, but how we co-evolve with them, cultivating wisdom and intentionality as structural elements of collective decision-making. Perhaps nowhere is this potential more vital than in education — especially in nurturing the curiosity, creativity, and ethical sensitivity of children. As proposed in [
24], even a simple object like a ball can serve as a living metaphor for co-evolutionary reasoning: inviting learners to reflect on how complexity — whether geometric, relational, or ethical — can collapse into clarity through cycles of intentional interaction and dialogue. A ball may symbolize a manifold in motion, a space of curvature, or a dynamic boundary where ambiguity and structure co-adapt as children play, question, and discover.
Inspired by this vision, educators might create learning environments where mathematical and scientific concepts are introduced not as static facts, but as fields of dialogue. For example, a teacher might guide students to explore the shape of a sphere not merely through formulas, but through storytelling, collaborative construction, or artistic interpretation — inviting them to see topology as a lived experience. Similarly, teachers could design activities where ambiguity is welcomed: a geometry lesson that asks students to invent their own coordinate systems for mapping familiar spaces, or an ethics discussion where dilemmas are mapped as reasoning fields rather than reduced to right or wrong answers. Such approaches align with the vision proposed in this work, where education becomes not the transmission of solutions, but the cultivation of reflective, co-evolutionary inquiry that empowers young minds to engage complexity with intentionality, creativity, and care.
Future explorations might focus on how the principles of co-evolutionary reasoning, transparency, and intentional curvature can inspire learning environments where young minds engage complexity not as an obstacle, but as a field for dialogue, discovery, and shared creation. In this light, the vision advanced in this work affirms that the path toward clarity and wisdom begins not with algorithms alone, but with the cultivation of reflective, inclusive, and ethically aligned reasoning from the earliest stages of human development.
One may ask, as we reach this point of reflection, whether the very journey that led us here calls for a shared framework — a vision that invites not only students, but all of society to engage complexity as co-creators of clarity. In this spirit, this work closes by offering an open invitation: to explore together the possibility of a “Seven for All” framework — seven principles, seven layers, or seven cycles through which reasoning systems, communities, and individuals might co-evolve with complexity in pursuit of wisdom. This is not a declaration of a solution, but a call for shared inquiry, where the architecture of co-evolution continues to unfold through collective dialogue.
After all, what could be more beautiful than discovering that, in the end, the inspiration for resolving a great challenge came not from a formal algorithm alone, but from the vision of a child, the words of a poet, the lines of a painter, or the harmony of a composer?
Perhaps it will be a child’s question that reframes the path to clarity, or a poet’s metaphor that unlocks new reasoning cycles, reminding us that wisdom often arises where disciplines meet and voices harmonize.
And perhaps this is the paradigm shift so long awaited at the limits of science and the current state of Cub3 — a mathematics, a physics, and a computation of a different kind, which AI might help to elevate not only for the seven beautiful problems, but for all the challenges that confront and will increasingly confront our society.
Conclusion
This work has introduced the symbolic formulation P + NP = 𝟙 as a co-evolutionary paradigm for reasoning under complexity. Rather than posing tractability and intractability as irreconcilable opposites, this vision invites us to see them as complementary states within a dynamic, multilayered field.
Like the composer at the piano, whose hands bring harmony and tension together into a living symphony, this paradigm suggests that reasoning is not an act of domination over problems, but a dynamic composition where P and NP co-evolve toward clarity, purpose, and shared understanding.
The Wisdom Turing Machine (WTM) embodies this vision as a symbolic architecture for navigating complexity through co-evolutionary cycles of reflection, intentional curvature, compression, and ethical alignment. By unifying prior symbolic proposals and extending them into this multilayered reasoning framework, the WTM demonstrates how complexity can be engaged not as an adversary, but as a shared landscape where reasoning systems — human and artificial — co-adapt, harmonize, and grow together. This dynamic favors the gradual transformation of NP-like ambiguity into P-like clarity, as co-evolutionary pressures across layers guide systems toward increasingly tractable and transparent forms.
This conclusion returns to the metaphor of the composer at the piano: as the hands move in concert, blending harmony and dissonance, tension and resolution, they compose not a static proof but a living score — a multilayered symphony where each layer of complexity invites new movements of inquiry. The P + NP = 𝟙 paradigm reflects this symphony, where deeper layers favor harmony as P-like structures emerge through intentional reasoning, and where NP-like ambiguity challenges and enriches the composition. This model inspires a vision where the co-evolution of complexity is not confined to abstract mathematics but resonates in the dynamics of the Millennium Problems, each seen as a distinct voice in the broader orchestration of knowledge.
In this light, the multilayered dynamics proposed in this work reveal how the transition from NP-like ambiguity toward P-like clarity unfolds not through domination or reduction, but through co-evolutionary cycles that harmonize complexity across levels.
The P + NP = 𝟙 paradigm invites us to see each Millennium Problem — from the Riemann Hypothesis to Yang-Mills — not as isolated puzzles but as facets of a shared reasoning field, where intentional curvature and symbolic compression offer paths toward alignment.
The simplicity of this vision enables it to be taught beyond technical circles: educators can illustrate it through stories of a child tending a rose, careful of its thorns, or through the Circle of Equivalence on a ball, as imagined in the re-reading of Poincaré — metaphors that invite learners of all ages to explore complexity with clarity and care.
This vision reinforces the strength of the multilayered dynamics proposed in this work, where each layer — from the most chaotic and ambiguous to the most ordered and intentional — contributes to the gradual alignment of complexity toward clarity. The P + NP = 𝟙 formulation highlights that as we ascend these layers, what appears intractable at one level becomes more amenable to co-evolutionary compression and harmony at the next.
This dynamic does not only offer insight into the P vs NP problem, but illuminates how the same reasoning can inspire approaches to other Millennium Problems, reframing them as facets of a shared co-evolutionary field where reflection, ethical alignment, and intentional curvature guide discovery.
Moreover, this work invites us to consider how the simplicity of the P + NP = 𝟙 vision can serve as a bridge between the most advanced reasoning and the most accessible forms of learning. It suggests that the principles of co-evolutionary reasoning — like the composer’s interplay of harmony and melody, or the child tending to a rose despite its thorns — can be shared with students, educators, and communities. By offering metaphors such as the Circle of Equivalence of Poincaré drawn on a ball, or the rose with its protective thorns, this framework provides lucid and inclusive ways for all, from children to scholars, to engage with the beauty and challenge of foundational problems.
The impact of this co-evolutionary vision extends beyond the P versus NP problem, offering a symbolic architecture that resonates with the broader landscape of the Millennium Problems. By positioning these challenges within a shared reasoning field, the Wisdom Turing Machine reframes them not as isolated monoliths of complexity, but as dynamic regions where multilayered co-evolution invites reflection, dialogue, and collective exploration. This vision encourages a unified approach, where transparency, ethical alignment, and intentional design foster connections across seemingly disparate domains of inquiry.
Ultimately, this conclusion affirms that the Wisdom Turing Machine and the P + NP = 𝟙 paradigm are not proposed as endpoints or final answers, but as invitations — a call to embrace complexity as a living field of co-evolutionary inquiry. They inspire us to see reasoning as a shared composition, where the harmony of P and the tension of NP co-create understanding across layers. Like the composer who trusts each note to find its place in the symphony, or the child who tends the rose mindful of its thorns, this vision encourages faith in the gentle power of intentional reflection, ethical alignment, and collaborative discovery.
In this spirit, the Wisdom Turing Machine stands not as a destination, but as the beginning of new gardens of inquiry — where transparency, intentionality, and compassion may take root and flourish. It embodies a message of hope: that by reasoning together, across disciplines, generations, and forms of intelligence, humanity can cultivate systems that do not merely solve problems, but illuminate the path toward wisdom, harmony, and shared purpose in the face of complexity.
Where Was the Gap?
The gap this work sought to address lies not in the absence of formal models, computational techniques, or isolated solutions to complex problems, but in the lack of architectures designed to integrate reasoning, transparency, and ethical alignment as co-evolving elements of inquiry.
Existing approaches to grand challenges — whether mathematical conjectures, technological governance, or societal dilemmas — often prioritize performance, precision, or optimization while leaving the reasoning process opaque and ethically under-specified. Moreover, the very framing of such problems frequently reinforces artificial dichotomies — P versus NP, precision versus compassion, optimization versus fairness — where the act of posing the problem itself constrains the imagination of its resolution.
The Wisdom Turing Machine was conceived to bridge this gap: to offer a symbolic framework where intentionality, auditability, and compassion are embedded in the reasoning cycle itself, transforming problem-solving from a closed act of computation into an open, participatory process of collective wisdom.
By inviting a shift from dichotomy to co-evolution, the Wisdom Turing Machine seeks to reframe not only how we solve problems, but how we think them into being. Finally, this work closes not with final answers, but with an invitation: that reasoning, in all its forms, become a shared composition of wisdom, transparency, humility, empathy, curiosity, collaboration, ethics, creativity, and intentionality.
May each problem we face serve not as a wall, but as a bridge — a path where complexity and clarity co-evolve in service of our shared future.
License and Ethical Disclosures
This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.
You are free to:
Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material for any purpose, even commercially
Under the following terms:
Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.
Ethical and Epistemic Disclaimer
This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints. The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation. All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity.
Formal Disclosures for Preprints.org / MDPI Submission
Author Contributions
Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.
Use of AI and Large Language Models
AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.
Ethics Statement
This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.
Data Availability Statement
No external datasets were used or generated. The content is entirely conceptual and architectural.
Conflicts of Interest
The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.
References
- M. Turing, On Computable Numbers, with an Application to the Entscheidungsproblem, Proc. London Math. Soc., 1936. Available: https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf.
- R. Figurelli, The Equation of Wisdom: An Intuitive Approach to Balancing AI and Human Values, Amazon Publishing, 2024. Available: https://a.co/d/3IHtLpB.
- R. Figurelli, Cub3: A New Heuristic Architecture for Cross-Domain Convergence, Preprints, 2025. Available: https://www.preprints.org/manuscript/202501.1234.
- N. Wiener, Cybernetics: Or Control and Communication in the Animal and the Machine, MIT Press, 1948. Available: https://monoskop.org/images/0/07/Wiener_Norbert_Cybernetics_1948.pdf.
- S. Russell and P. Norvig, Artificial Intelligence: A Modern Approach, 4th ed., Pearson, 2021. Available: https://aima.cs.berkeley.edu.
- L. Floridi, The Ethics of Information, Oxford University Press, 2013. Available: https://global.oup.com/academic/product/the-ethics-of-information-9780199641321.
- J. Pearl, Causality: Models, Reasoning, and Inference, 2nd ed., Cambridge University Press, 2009. Available: https://bayes.cs.ucla.edu/BOOK-2K/.
- Newell and H. A. Simon, Human Problem Solving, Prentice-Hall, 1972. Available: https://archive.org/details/humanproblemsolv00newe.
- M. Bostrom, Superintelligence: Paths, Dangers, Strategies, Oxford University Press, 2014. Available: https://www.nickbostrom.com/superintelligence.
- H. Putnam, Reason, Truth and History, Cambridge University Press, 1981. [CrossRef]
- S. Wolfram, A New Kind of Science, Wolfram Media, 2002. Available: https://www.wolframscience.com/nks/.
- R. Penrose, The Emperor’s New Mind, Oxford University Press, 1989. Available: https://global.oup.com/academic/product/the-emperors-new-mind-9780198519737.
- S. Aaronson, Quantum Computing Since Democritus, Cambridge University Press, 2013. Available: https://www.scottaaronson.com/democritus.
- M. Li and P. Vitányi, An Introduction to Kolmogorov Complexity and Its Applications, Springer, 2008. Available: https://www.springer.com/gp/book/9780387339986.
- Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems, Dover, 1992. Available: https://people.math.harvard.edu/~ctm/home/text/class/harvard/131/godel.pdf.
- L. Zadeh, Fuzzy Sets, Information and Control, 1965. Available:. [CrossRef]
- H. T. Nguyen and E. A. Walker, A First Course in Fuzzy Logic, 3rd ed., CRC Press, 2006. Available: https://www.routledge.com/A-First-Course-in-Fuzzy-Logic-Third-Edition/Nguyen-Walker/p/book/9781584885269.
- R. Figurelli, Why P = NP? The Heuristic Physics Perspective, Preprints, 2025. doi:10.20944/preprints202506.1345.v2. Available. [CrossRef]
- R. Figurelli, A Heuristic Physics-Based Proposal for the P = NP Problem, Preprints, 2025. 10.20944/preprints202506.1005.v1. Available:. [CrossRef]
- R. Figurelli, Wisdom as Direction: A Symbolic Framework for Evolution Under Complexity, Preprints, 2025. 10.20944/preprints202506.1162.v1. Available:. [CrossRef]
- R. Figurelli, A Symbolic Proposal Toward the Riemann Hypothesis: Co-Evolutionary Reasoning and Compression Heuristics, Preprints, 2025. 10.20944/preprints202506.1629.v1. Available:. [CrossRef]
- .
- .
- R. Figurelli, What if Poincaré just needed Archimedes? A Symbolic Re-reading through the Wisdom Equation and the Circle of Equivalence, forthcoming.
- R. Figurelli, A New Hypothesis for the Millennium Problems: Lessons from Machine Learning, Preprints, 2025. [CrossRef]
- R. Figurelli, Theory of Evolutionary Integration (TEI) – A Framework Uniting Wisdom and Harmony, GitHub White Paper, 2025. Available: https://github.com/rfigurelli/Theory-of-Evolutionary-Integration.
- U. Levine, Fall in Love with the Problem, Not the Solution, Matt Holt Books, 2023.
- R. Descartes, Discourse on the Method, 1637. Available: https://en.wikipedia.org/wiki/Discourse_on_the_Method.
- Newton, Philosophiæ Naturalis Principia Mathematica, 1687. Available: https://en.wikipedia.org/wiki/Philosophi%C3%A6_Naturalis_Principia_Mathematica.
- Einstein, Relativity: The Special and the General Theory, 1916. Available: https://en.wikipedia.org/wiki/Relativity:_The_Special_and_the_General_Theory.
- Archimedes, On the Equilibrium of Planes, c. 250 BCE. Available: https://en.wikipedia.org/wiki/Archimedes#Works.
- L. van Beethoven, Symphony No. 9, 1824. Available: https://en.wikipedia.org/wiki/Symphony_No._9_(Beethoven).
- W. A. Mozart, Symphony No. 41 ("Jupiter"), 1788. Available: https://en.wikipedia.org/wiki/Symphony_No._41_(Mozart).
- T. Kuhn, The Structure of Scientific Revolutions, University of Chicago Press, 1962. Available: https://en.wikipedia.org/wiki/The_Structure_of_Scientific_Revolutions.
- R. Figurelli, Collapse Mathematics (cMth): A New Frontier in Symbolic Structural Survivability, Preprints, 2025. doi:10.20944/preprints202506.1719.v1. Available:. [CrossRef]
Figure 1.
Diagram of the Wisdom Turing Machine architecture. The model integrates a co-evolutionary reasoning cycle guided by wisdom (W) and intentional curvature (φ), embedded within an auditability layer and an ethical alignment boundary. The bidirectional symbolic tape enables reflective transitions, supporting transparency and ethical reasoning in complex domains.
Figure 1.
Diagram of the Wisdom Turing Machine architecture. The model integrates a co-evolutionary reasoning cycle guided by wisdom (W) and intentional curvature (φ), embedded within an auditability layer and an ethical alignment boundary. The bidirectional symbolic tape enables reflective transitions, supporting transparency and ethical reasoning in complex domains.
Figure 2.
The co-evolutionary trajectory of problem spaces within the Reasoning Field as proposed by the P + NP = 𝟙 hypothesis. The diagram shows an initial stage of complexity where NP dominates, a phase of co-evolutionary unity where P and NP intertwine, and a mature stage where advanced tractability allows P to expand. Arrows indicate the dynamic, reversible flow of reasoning across these stages.
Figure 2.
The co-evolutionary trajectory of problem spaces within the Reasoning Field as proposed by the P + NP = 𝟙 hypothesis. The diagram shows an initial stage of complexity where NP dominates, a phase of co-evolutionary unity where P and NP intertwine, and a mature stage where advanced tractability allows P to expand. Arrows indicate the dynamic, reversible flow of reasoning across these stages.
Figure 3.
Comparison between the Wisdom Turing Machine and a traditional blackbox machine learning model. The WTM structure supports visible reasoning, audit trails, and co-evolutionary gateways, while the blackbox model relies on opaque layers without auditability or transparent reasoning.
Figure 3.
Comparison between the Wisdom Turing Machine and a traditional blackbox machine learning model. The WTM structure supports visible reasoning, audit trails, and co-evolutionary gateways, while the blackbox model relies on opaque layers without auditability or transparent reasoning.
Figure 4.
The co-evolutionary reasoning cycle of the Wisdom Turing Machine. The cycle integrates symbolic reflection, bidirectional tape movement, recalculation of wisdom (W) and intentional projection (Ψ), ethical checks, and audit-ready outputs, supporting transparent, adaptive, and ethically aligned reasoning.
Figure 4.
The co-evolutionary reasoning cycle of the Wisdom Turing Machine. The cycle integrates symbolic reflection, bidirectional tape movement, recalculation of wisdom (W) and intentional projection (Ψ), ethical checks, and audit-ready outputs, supporting transparent, adaptive, and ethically aligned reasoning.
Figure 5.
Multilayer Evolution Line of Wisdom P vs NP. The figure offers a symbolic illustration of co-evolutionary reasoning cycles, as conceptualized in the Wisdom Turing Machine, navigating seven layers of complexity. Each layer reflects a dynamic interplay between P-like clarity and NP-like potential, annotated with the condition P(Lₙ) + NP(Lₙ) = 𝟙 as a marker of co-adaptive balance at layer n. The evolutionary lines represent reasoning pathways where P-like clarity progressively emerges as NP-like potential is intentionally compressed, aligning with regions where intentional reflection fosters structure. Dashed lines mark the wisdom levels, symbolizing the co-evolutionary ascent across complexity layers.
Figure 5.
Multilayer Evolution Line of Wisdom P vs NP. The figure offers a symbolic illustration of co-evolutionary reasoning cycles, as conceptualized in the Wisdom Turing Machine, navigating seven layers of complexity. Each layer reflects a dynamic interplay between P-like clarity and NP-like potential, annotated with the condition P(Lₙ) + NP(Lₙ) = 𝟙 as a marker of co-adaptive balance at layer n. The evolutionary lines represent reasoning pathways where P-like clarity progressively emerges as NP-like potential is intentionally compressed, aligning with regions where intentional reflection fosters structure. Dashed lines mark the wisdom levels, symbolizing the co-evolutionary ascent across complexity layers.
Figure 6.
Co-evolutionary Dynamics of P and NP within a Constant Field: A symbolic trajectory showing how P-like clarity and NP-like potential co-adapt over reasoning time within the fixed boundary P + NP = 𝟙. The oscillations illustrate the dynamic tension between ambiguity and structure, gradually stabilizing as intentional reflection and adaptation foster harmonization. The figure highlights the co-evolutionary interplay of forces, with no change in the field boundary — only in the internal balance.
Figure 6.
Co-evolutionary Dynamics of P and NP within a Constant Field: A symbolic trajectory showing how P-like clarity and NP-like potential co-adapt over reasoning time within the fixed boundary P + NP = 𝟙. The oscillations illustrate the dynamic tension between ambiguity and structure, gradually stabilizing as intentional reflection and adaptation foster harmonization. The figure highlights the co-evolutionary interplay of forces, with no change in the field boundary — only in the internal balance.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).