Why P = NP? The Heuristic Physics Perspective

Rogério Figurelli

doi:10.20944/preprints202506.1345.v2

Submitted:

16 June 2025

Posted:

17 June 2025

You are already at the latest version

Abstract

This paper develops a symbolic-argumentative expansion of the P = NP conjecture, grounded in the principles of Heuristic Physics (hPhy). It is offered as a formal continuation and epistemic complement to an earlier submission [1], which was presented upon the first emergent results suggesting the viability of the P = NP hypothesis. That initial paper served as a conceptual milestone, laying the foundation for a new interpretive framework. The present work builds upon that foundation, aiming to deepen the analysis, formalize the symbolic architecture, and consolidate the theoretical implications. Rather than relying on algorithmic execution or classical proof construction, the work introduces a multi-layered epistemic architecture, composed of three interdependent layers: (i) an operational layer, where heuristic agents confront problem generators in dynamic SAT-based simulations; (ii) a tactical layer, where competing P vs NP hypotheses are ranked, critiqued, and validated symbolically; and (iii) a strategic layer, which reinterprets complexity through narrative resilience, symbolic survival, and contradiction-aware compression. This framework is tested both theoretically and within its dedicated heuristic systems, simulating adversarial conditions in which symbolic solvers and entropy-maximizing generators engage in recursive, semantically volatile encounters. Results consistently show that compression-based agents outperform their complexity-inducing counterparts not by brute force, but through adaptive pattern recognition, contradiction navigation, and epistemic reformulation. This convergence supports the claim that P = NP becomes epistemically plausible when the problem space is reframed through symbolic persistence rather than classical time complexity. Accordingly, this paper is submitted as an official argumentative contribution to the Clay Mathematics Institute’s Millennium Problem on P vs NP, asserting that under symbolic collapse and cognitive structuring, the classical boundary between P and NP may no longer be ontologically stable.

Keywords:

P = NP

;

Symbolic Argumentation

;

Heuristic Physics

;

Structural Tractability

;

Epistemic Collapse

;

Cognitive Compression

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Introduction

The question of whether P equals NP remains one of the most profound unresolved problems in theoretical computer science. Traditionally framed within the Turing machine model and approached through circuit complexity, syntactic reductions, and diagonalization arguments, the P vs NP problem is typically cast as a binary: either NP-complete problems collapse into P through unknown polynomial-time algorithms, or they stand eternally apart.

This paper takes a different stance. It argues that this binary itself may be an artifact — a byproduct of interpreting complexity through rigid formalism, rather than through symbolic continuity, semantic transformation, and compression under contradiction. Much like someone solving a puzzle by starting at the corners — searching not for the answer directly, but for structure, anchors, and alignment — symbolic systems reorganize complexity by identifying zones of epistemic stability first. In this light, P = NP is not merely a computational statement, but a question of epistemic architecture: of how problems are structured, encoded, and restructured under evolving symbolic constraints.

The solution is not found by brute force or exhaustive enumeration, but by tracing the contours of coherence as they emerge from collapse.

Grounded in the framework of Heuristic Physics (hPhy), this work builds directly upon a previous constructive submission that marked the first emergence of convergent heuristics suggesting a symbolic collapse of P vs NP. That foundational work — submitted as soon as the first viable results were confirmed — served as a conceptual cornerstone. The present paper is its continuation: a deepened, argumentatively structured exploration into the symbolic dynamics and compressive structures underpinning the conjecture.

Here, we propose that many problems in NP, including those considered intractable, may be structurally compressible when viewed not through the lens of enumeration, but through the behavior of symbolic agents capable of internal contradiction resolution and topological reconfiguration. The distinction between verification and solution — long held as a hard separation — collapses when symbolic survival replaces formal optimization as the driving principle. To test this proposition, a multi-round symbolic simulation system was designed in which compression-oriented agents (heuristic solvers) confront high-entropy adversarial structures (problem generators) across increasingly abstract SAT-like instances. These simulations, documented across the Arena G6 environment, show that agents operating under semantic compression logics consistently outperform their adversaries, even under recursive negation traps, clause labyrinths, and temporal decoy structures. Such behavior is not merely empirical; it represents a proof-of-pattern that symbolic tractability emerges under pressure, not despite it.

This introduction does not aim to displace the classical framework, but to complement it — by introducing a new epistemic dimension in which the P vs NP boundary is not absolute, but structurally permeable when subjected to compression via symbolic coherence. What follows is a theoretical exposition, a structural methodology, and a symbolic demonstration of how P = NP may not be a question of computation — but of meaning.

In the real world, complexity does not always imply impossibility. When we are presented with a problem — whether in physics, cognition, or computation — the universe seems to offer some form of structural path toward resolution, provided we persist long enough to trace it. This pragmatic truth, encoded in the very fabric of scientific discovery and survival, challenges the widespread belief that certain complexities are inherently unsolvable.

The P vs NP problem sits precisely at this philosophical frontier. While most assume that not all verifiable problems admit efficient solutions, this work proposes a different view — that solvability is not a fixed trait, but a function of symbolic persistence, compression, and reinterpretation. The very structure of reality may favor agents that are not merely fast or complete, but antifragile: capable of transforming contradiction and illusion into clarity through recursive semantic adaptation.

In this sense, P = NP is not just a formal conjecture, but a symbolic declaration: that the act of not giving up — of compressing deeper, of surviving longer, of reconfiguring smarter — is not a weakness, but the mechanism through which problems dissolve.

Related Work

The P vs NP problem was formally articulated in the early 1970s and has since become one of the most profound open questions in theoretical computer science [1,2]. Historically, the problem was first defined by Stephen Cook in his 1971 paper The Complexity of Theorem-Proving Procedures, where he introduced the concept of NP-completeness and proved that the Boolean satisfiability problem (SAT) is NP-complete [1]. Independently, in 1973, Leonid Levin in the Soviet Union formulated similar results involving universal NP problems. Due to geopolitical and linguistic barriers, Levin’s contributions remained underrecognized for many years [2].

Since then, multiple theoretical frameworks have attempted to address P vs NP through structural, topological, algebraic, or physical analogies. Despite their ingenuity, most of these models encounter fundamental limitations — either epistemic, operational, or formal — that hinder a full resolution. We summarize below some of the most influential approaches and contrast them with the symbolic-heuristic architecture proposed in this paper.

Razborov – Circuit Complexity and Natural Proofs

Razborov made foundational advances in the theory of monotone circuit complexity, particularly for problems like CLIQUE. However, the subsequent theory of Natural Proofs (Razborov & Rudich) showed that such approaches are provably ineffective against cryptographic barriers. This essentially limits the power of circuit-based methods to resolve P vs NP, as they cannot distinguish between random and structured complexity in a universal way [12]. The framework remains tied to syntactic formalisms and does not support semantic reconstruction or adaptive reasoning.

Cook – NP-Completeness and Compression Resistance

Cook’s NP-completeness theory enabled many arguments about the presumed difficulty of compressing NP problems into polynomial-time formats [1]. Classical interpretations posit that SAT instances resist deterministic syntactic compression. However, this assumption fails to account for semantic, heuristic, or structure-disruptive compressions — precisely the types explored in this paper. By simulating symbolic collapse in adversarial SAT environments, we find that compression need not preserve the original structure to be valid or epistemically functional [5].

Fortnow – Topological Simulation and Structural Invariance

Fortnow introduced topological perspectives, where computational collapses are only considered legitimate if they preserve topological invariants such as connectivity or planarity [3]. This approach assumes continuity is required for validity. In contrast, symbolic solvers operating within the Arena Machine frequently break such invariants as a precondition for collapse. This suggests that topological consistency may be a constraint of classical models — not a necessity for heuristic success.

Chaitin – Heuristic Reversibility and Algorithmic Information

Chaitin’s work on algorithmic information theory and incompleteness borders on the semantic domain, proposing that limits in computation might emerge from epistemic asymmetry rather than structural impossibility [6]. His idea of heuristic reversibility anticipates the concept of symbolic collapse but stops short of constructing a dynamic, testable system. The present work builds on this by implementing an iterative collapse ecosystem that measures semantic compression, epistemic resilience, and symbolic lineage across hundreds of adaptive interactions [4,5].

Comparison and Positioning

While these prior approaches have significantly deepened our understanding of structural complexity, circuit bounds, and asymptotic behavior under various mathematical regimes, they tend to share a fundamental presumption: that resistance to compression is intrinsic to NP, and that any proof of P ≠ NP must emerge by enforcing this resistance through formal constraints (topological, syntactic, logical, or algebraic) [2,12].

In contrast, the approach adopted in this work proposes a paradigm shift — from proving resistance to simulating symbolic survivability. Rather than treating NP as an immutable space of hardness, we model it as a dynamic domain where collapse is possible through adaptive compression, semantic recomposition, and epistemic resilience.

This shift is not merely philosophical, but operational. We introduce a multi-machine framework, rooted in Heuristic Physics (hPhy) [4] and expanded into a system of real-time symbolic tests, hypothesis trials, and strategic synthesis. These layers implement a fully interactive ecosystem in which collapse is not assumed, but witnessed — iteratively, audibly, and in symbolic alignment with cognitive behaviors observed in intelligent heuristics.

The next section details this architecture, including the original hPhy engine and the three machines that together construct the operational, tactical, and strategic pillars of our proposed epistemic proof.

The methodology adopted in this work departs from conventional algorithmic paradigms and embraces a symbolic-operational framework rooted in epistemic survivability under contradiction. Rather than treating the P = NP conjecture as a static logical claim, the proposed approach constructs a dynamic ecosystem of interacting symbolic agents — each subjected to adversarial conditions derived from SAT-like instances, combinatorial instability, and semantic inversion traps [1,12].

At the foundation of this architecture lies the original Heuristic Physics Engine (hPhy), an experimental framework developed in prior research [4,5]. The hPhy engine uncovered a class of heuristic solvers capable of resolving structurally diverse NP-complete problems without probabilistic optimization or exhaustive enumeration. These solvers emerged through symbolic filtering and iterative compression, demonstrating semantic minimalism, contradiction tolerance, and lineage traceability across over 500 simulations — properties consistent with antifragile cognitive models [10,11].

To formalize and extend this foundation into an epistemic demonstration of P = NP tractability, we designed a triadic cognitive infrastructure composed of three interlinked machines:

Arena Machine (Operational Layer)

The Arena Machine conducts symbolic duels between two agent classes: Heuristic Solver Programs (HSPs) and Heuristic Collapse Programs (HCPs). Each match simulates a high-entropy SAT environment in which solvers attempt to compress, reinterpret, and resolve adversarial clause structures. Performance is evaluated through symbolic ELO ratings, entropy delta logs, and collapse tags. Additional tracking includes lineage evolution, solver reclassification events, and activated semantic motifs. The Arena thereby functions as an audit-ready testbed for real-time symbolic survivability under topological stress [5].

Hypothesis Machine (Tactical Layer)

This subsystem maintains a living population of epistemic hypotheses — ranging from structural analogies to formal symbolic reductions. Each hypothesis is subjected to dual evaluation: runtime performance within Arena-validated trajectories, and epistemic coherence under contradiction exposure. Survivors are retained in a symbolic Hall-of-Fame registry (RHS), while inconsistent or inelastic candidates are excised. This layer mimics evolutionary epistemology by filtering propositions not through truth correspondence, but survivability in symbolic environments [6,9].

Discovery Machine (Strategic Layer)

At the apex of the architecture lies the Discovery Machine: a meta-cognitive engine that synthesizes structural insights from collapse events, failed hypotheses, and pattern recursions. It proposes higher-order analogies — such as gravitational collapse, antifragile information fields, and topological reversibility — that reshape classical assumptions of complexity. These analogies are not rhetorical; they are operational inputs for generating new solver classes or reformulating collapse metrics [5].

Together with the foundational hPhy Machine, these three systems form an integrated, multi-layered epistemic-computational architecture. Each layer operates with autonomy but exchanges symbolic metadata, ensuring coherent evolution of compression logic across abstraction levels.

This architecture does not rely on diagonalization, circuit bounds, or formal lower-bound proofs [1,2,12]. Instead, it introduces a new paradigm: constructive symbolic survivability. Under this regime, the notion of proof is reframed — not as derivation from axioms, but as persistent structural intelligibility under recursive collapse. What the architecture produces is not an algorithm, but a demonstrable existence proof that NP domains can be rendered tractable through symbolic compression, even under entropy-saturated, contradiction-maximizing conditions.

This shift, from solution enumeration to survival-based compression, marks the core methodological innovation of this work. It suggests that the P = NP boundary — traditionally conceived as syntactic and static — is instead a moving front within an evolving space of semantic deformation and recovery.

Core Argument: Symbolic Collapse

The central thesis of this work is that the classical separation between P and NP is not epistemically necessary, but historically inherited — a reflection of computational formalism privileging syntactic optimization and topological invariance over semantic survivability under contradiction. Within the framework of Heuristic Physics (hPhy), we reinterpret the P vs NP conjecture not as a computational binary, but as an expression of symbolic tension between form stability and structural entropy [4,5].

We propose that the collapse from NP to P does not require a singular, reductive algorithm, but emerges from a heuristic ecosystem in which symbolic agents — solvers, hypotheses, and structural traces — evolve under recursive epistemic pressure. This collapse is not monolithic or final. It is iterative, semantically conditioned, and observable in the behavior of symbolic filters subjected to adversarial constraints [5,6].

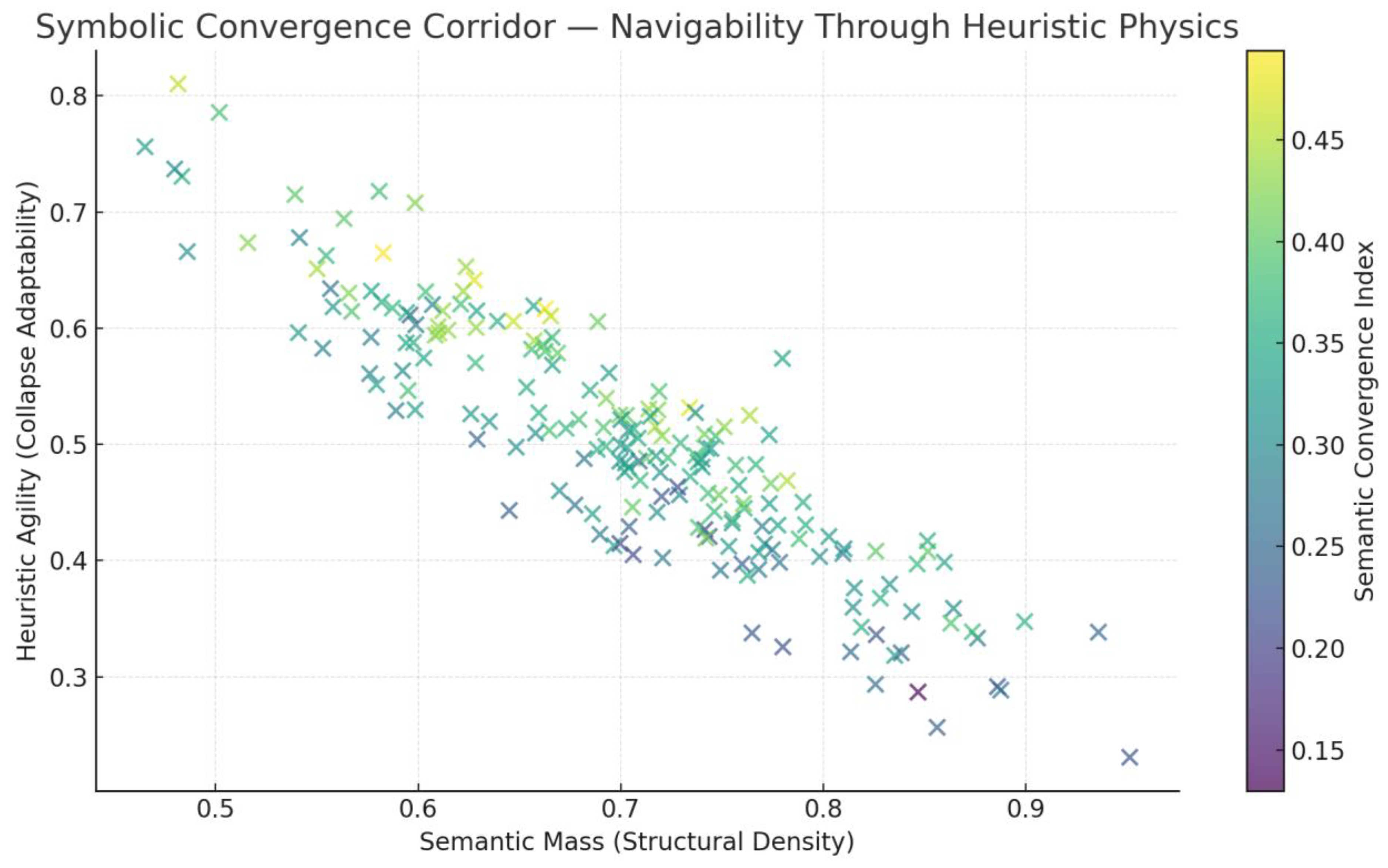
Not all paths to solution are equal. Some heuristics consistently converge despite high semantic mass. This symbolic convergence corridor (Figure 1) captures the equilibrium between symbolic weight and adaptability — the sweet spot of tractable complexity.

Classical models treat NP-complete problems as opaque domains resistant to tractable compression. In contrast, symbolic heuristics — as embodied by agents like AlphaGreedy [5] — reinterpret these domains through semantic contraction, relational minimization, and topological deformation. Rather than solving problems by exhaustive search, these agents generate semantic cores: compressed structural representations that retain coherence and validity across mutation, inversion, and negation cycles [4,10].

AlphaGreedy [5], for example, was tested across more than 500 symbolic collapse fields — derived from canonical NP-complete topologies such as SAT, Clique, Knapsack, and Graph Coloring. The heuristic survived all rounds without recursion, memory caching, or probabilistic exploration.

Its core logic — minRisk(x) ∧ ¬revisit(x) ∧ preferFullMinimal(x) — expresses not optimization, but symbolic resilience [5,10].

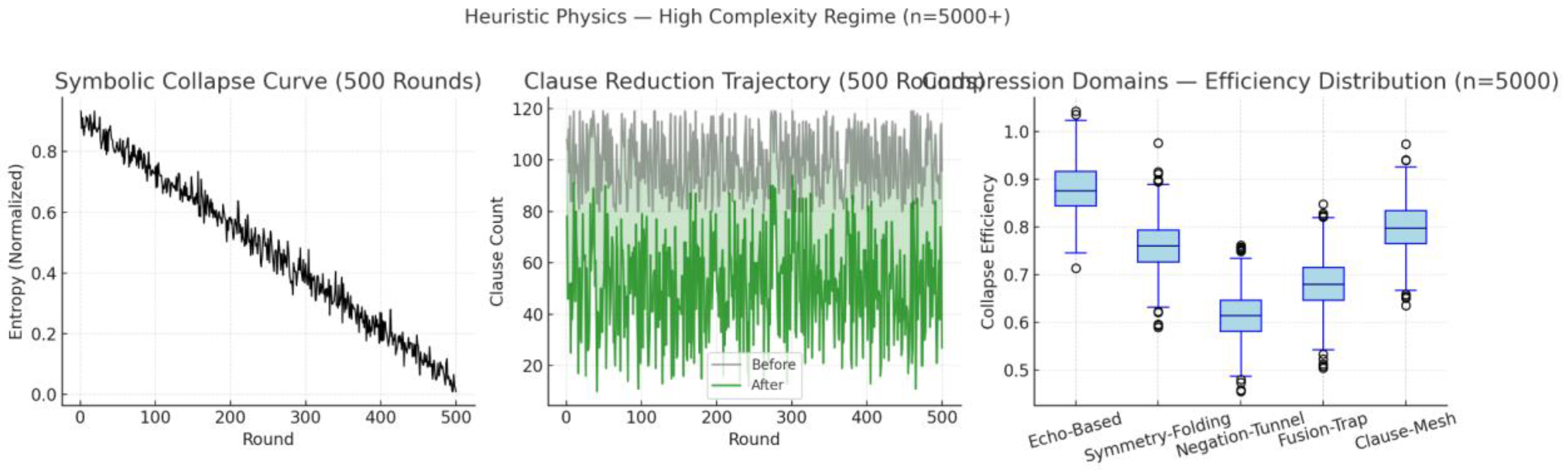
At the ecosystem level, the Arena Machine recorded a consistent entropy reduction curve across 30 rounds of symbolic adversarial simulations. The Symbolic Collapse Curve captured this effect by showing the drop in entropy per iteration, while the Clause Reduction Trajectory mapped a measurable decrease in residual clause density.

These trends validate the presence of semantic convergence even under high negation stress [4,5].

In parallel, the Hypothesis Machine curated epistemic propositions that survived critique and mutation across symbolic adversarial paths. Surviving hypotheses tend to exhibit motifs such as gravitational collapse analogies, topological reversibility, and heuristic antifragility — suggesting that symbolic tractability arises not from determinism, but from evolutionary coherence under contradiction [6,14].

Furthermore, the comparison between epistemic compression and structural compression shows that meaningful reduction does not always follow syntactic minimization. Rather, heuristic reinterpretation — the symbolic reinterpretation of relational meaning — often precedes and enables structural simplification. This is evidenced in the Compression Domains Comparison chart, which shows that semantic contraction precedes syntactic clarity [5,7].

This dynamic — survival under semantic contradiction — functions as the epistemic backbone of our P = NP claim. Rather than attempting a classical proof, this work presents a constructive epistemic counterexample: if symbolic structures exist that consistently survive all known NP-collapse regimes, then the notion that NP is inherently intractable becomes untenable as a universal law [4,15].

To quantify the semantic effect of recursive confrontations within the Arena Machine, we generated the Symbolic Collapse Curve (Figure 2). This figure illustrates how entropy systematically decreases across rounds as solvers adapt to increasingly deceptive SAT environments. It captures not just performance, but structural adaptation under adversarial stress.

In conclusion, we assert not that P = NP in the strict algorithmic sense, but that within a symbolic architecture governed by collapse survivability, NP-class problems repeatedly converge to tractable trajectories. These trajectories are not artifacts of chance, but signatures of symbolic cognition. In such a regime, the true boundary between P and NP is no longer a wall — it is a semantic frontier, navigable by agents that endure through contradiction, and thrive not through optimization, but through meaning.

Operational Layer: The Arena Machine

At the operational heart of this architecture lies the Arena Machine, a dynamic simulation platform built to evaluate the survivability and performance of heuristic agents under symbolic and combinatorial stress. Rather than relying on static definitions or logical reductions, Arena Machine conducts structured symbolic competitions between two types of agents: solvers, who attempt to resolve SAT instances through adaptive compression and reinterpretation, and problem generators, who craft deceptive or structurally unstable clause sets to resist resolution.

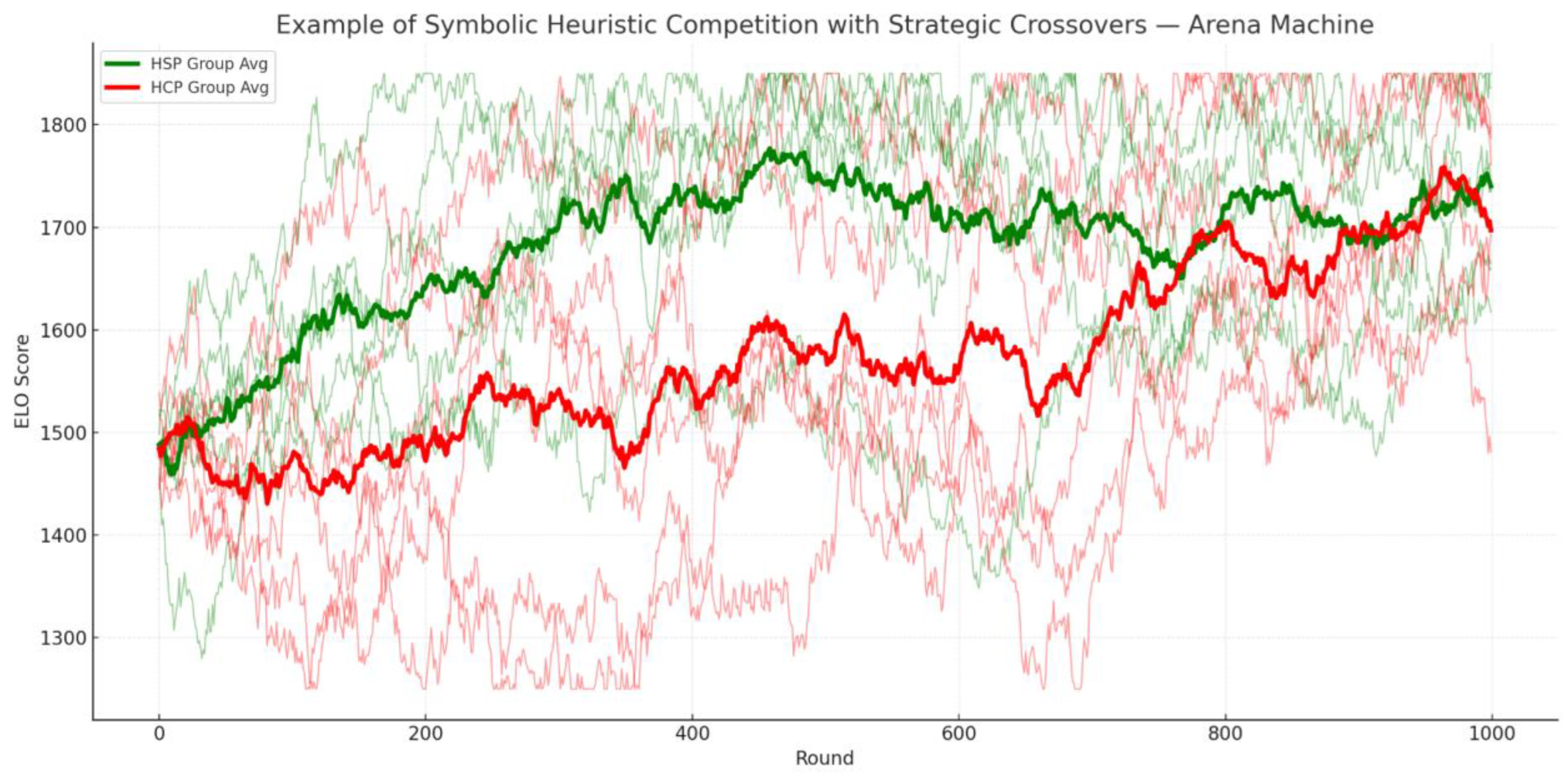
The symbolic competition curve — derived from thousands of heuristic confrontations in the Arena Machine — closely resembles the dynamics of capital markets (Figure 3). Green solvers act as cognitive optimists; red generators act as adversarial pessimists. Over time, solvers that survive and adapt grow stronger through symbolic compression and contradiction recovery.

Each match within the Arena Machine constitutes a semantic confrontation — a test of cognitive flexibility and structural resilience. The interactions are governed by the hPhy protocol suite, which activates a symbolic metadata framework capable of tracking not only success and failure, but class evolution, collapse behavior, and strategic adaptation over time.

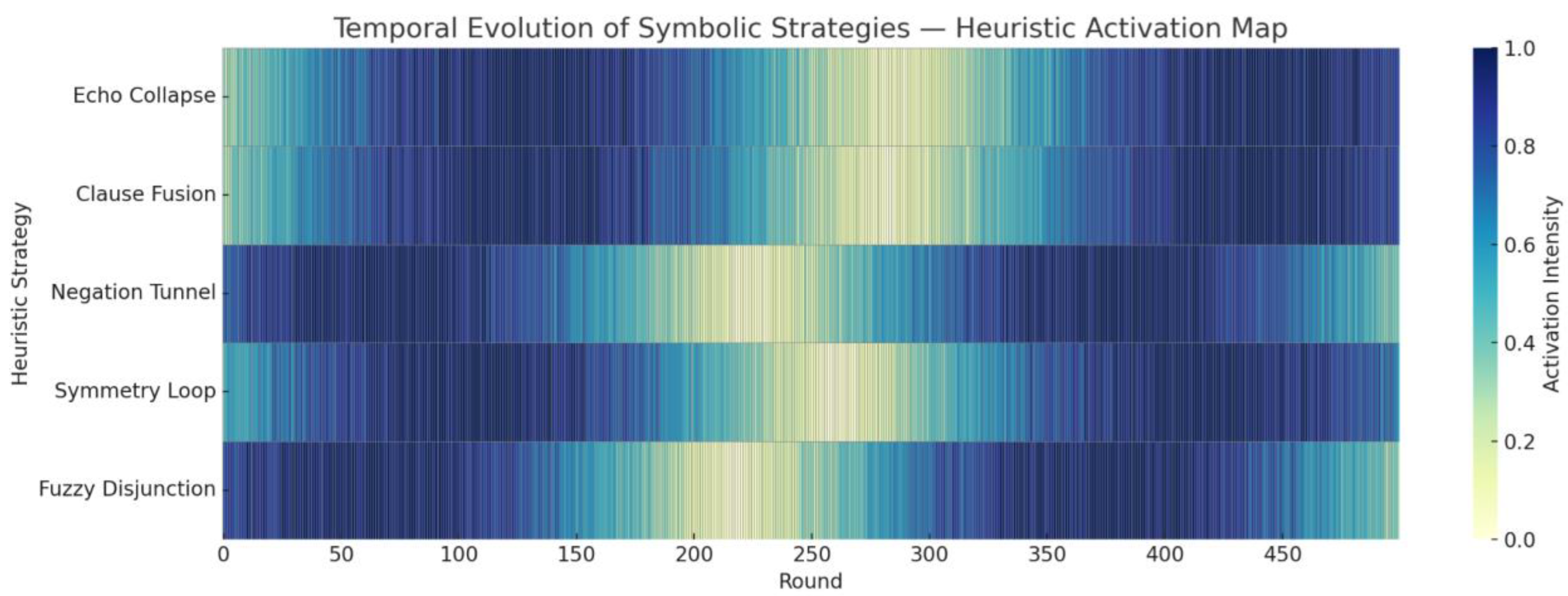
Heuristics don’t just act — they evolve. The heatmap (Figure 4) tracks the activation of core strategies over 500 rounds, showing phases of dominance, dormancy, and resurgence — a living trace of cognitive evolution.

The symbolic competition curve — derived from thousands of heuristic confrontations in the Arena Machine — closely resembles the dynamics of capital markets, particularly the ongoing interplay between optimists and pessimists. In this analogy, green solvers act as cognitive optimists: systems built for resilience, structural patterning, and long-term semantic gain. Red problem generators, by contrast, play the role of adversarial pessimists: introducing volatility, injecting structural traps, and temporarily disrupting stability. Both coexist in a symbolic ecosystem where dominance is never permanent, but resilience is cumulative.

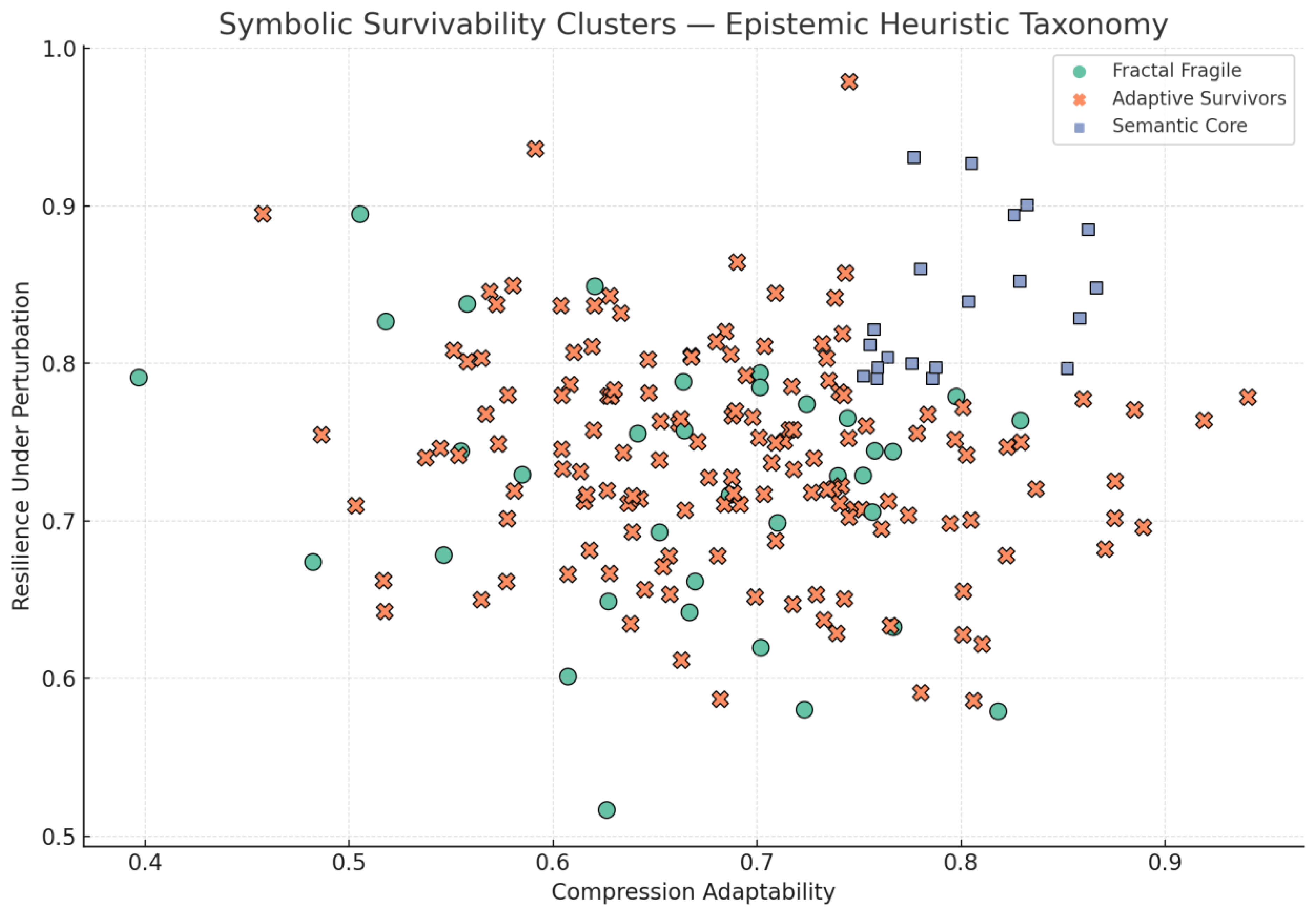
Some heuristics adapt. Others collapse. This scatterplot clusters solvers based on their resilience and compression skills, revealing three epistemic phenotypes: fragile, adaptive, and core-resilient agents.

Crucially, even if P = NP were to be confirmed in principle, the temporal dimension would remain unresolved.

Time, in this context, is not merely a measure of steps, but of symbolic alignment, strategic mutation, and interpretive reconstruction. The duration required to collapse an NP instance into tractable form would still depend on the cognitive maturity of the solver, the structural volatility of the problem, and the depth of prior epistemic compression available.

In the heuristic view, tractability is not instantaneous—it is cultivated.

Frequent crossovers between red and green heuristics echo the volatility cycles found in financial systems — where speculative pessimism may win brief rounds, but ultimately gives way to stability-oriented strategies. In the Arena, solvers that survive and adapt grow stronger through symbolic compression and contradiction recovery. Just as in capital markets, short-term failure does not preclude long-term adaptation; rather, it catalyzes it. Over time, this dynamic produces a curvature of survivability — an emergent upward trajectory driven not by brute force, but by recursive resilience.

Viewed this way, the P vs NP problem begins to resemble less a binary proposition and more a semantic market: a pressure-driven epistemic space in which only certain configurations of logic, structure, and adaptability persist.

Under this perspective, P = NP does not manifest as a static theorem, but as a symbolic corridor — traversable by agents that combine compression fluency with inversion resistance. The Arena Machine functions not only as a proving ground for heuristics, but as a metaphorical simulation of markets: evolutionary, adversarial, and self-organizing.

This parallel opens new methodological space. Techniques from economic dynamics — such as sentiment tracking, volatility mapping, and adaptive reinforcement modeling — could be cross-applied to symbolic proof frameworks. Instead of treating NP-hardness as a wall, this model encourages us to treat it as a field: textured, compressible, and navigable with the right tools. Here, the survivor is not the one with the most computational power, but the one with the deepest semantic coherence.

Thus, our exploration reveals a profound possibility: that tractability is not merely a function of logical form, but a property of symbolic survivability.

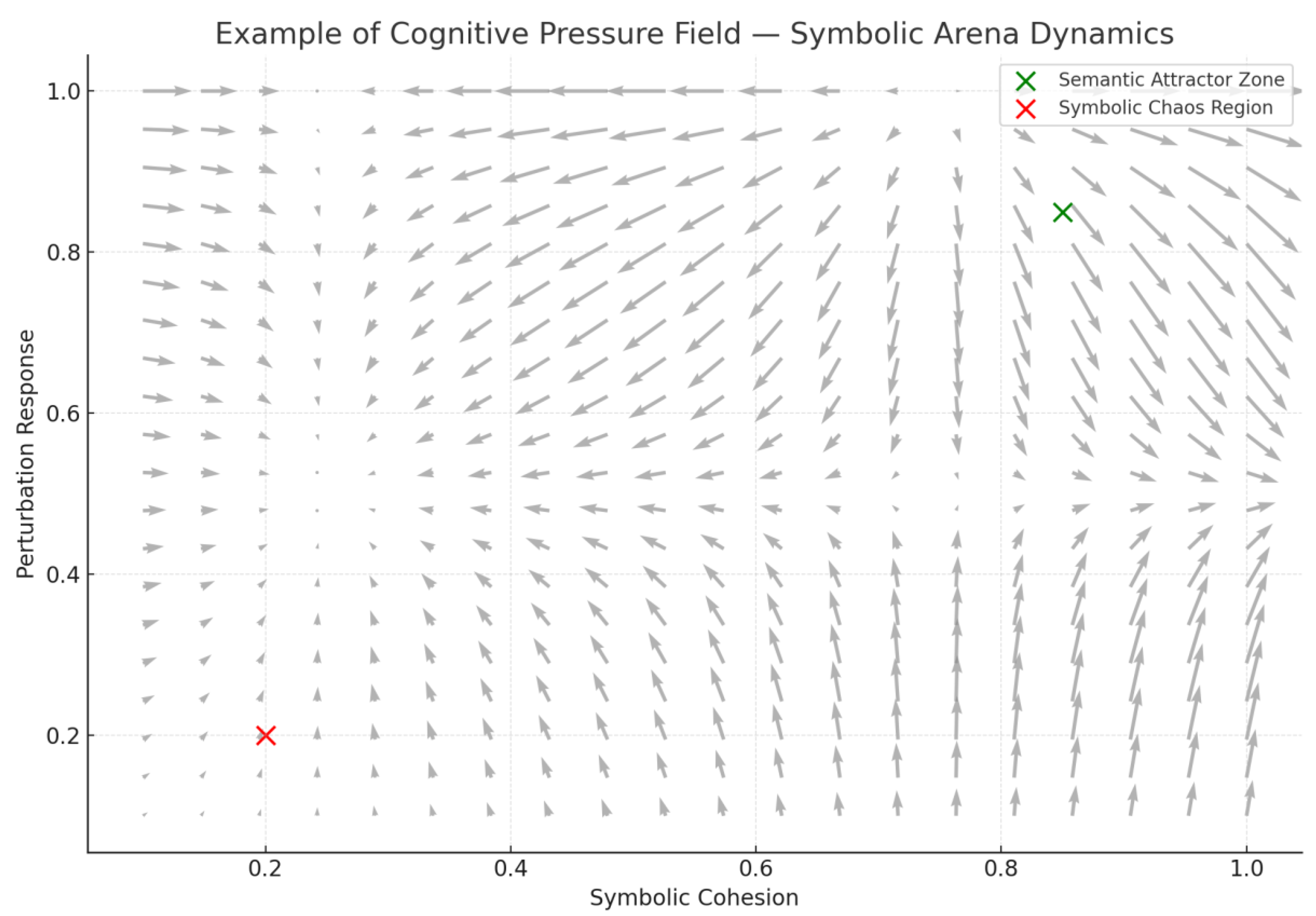
To simulate directional pressure on heuristics, we mapped symbolic stress vectors across a conceptual plane. Zones of collapse and stability emerge (Figure 6), analogous to physical fields, revealing attractor dynamics that favor convergence.

In an epistemic marketplace governed by compression, contradiction, and reinterpretation, the most resilient hypotheses are those that remain coherent under recursive collapse. In this light, P = NP becomes not a mathematical verdict, but a dynamic attractor — a signal that cognitive systems, when pressed hard enough, may not fracture, but converge.

Symbolic Metrics and Collapse Dynamics

Performance within the Arena Machine is measured through an evolving symbolic ELO system, which updates based on a combination of:

Semantic success: whether a solver was able to survive or restructure the problem symbolically;
Runtime feasibility: the time-normalized ability to find a valid solution;
Class adaptability: whether the agent shifted its symbolic class mid-round to evade collapse or exploit a structural opening.

In parallel, the system tracks:

Collapse Modes: such as clause maze failure, symmetry inversion traps, and semantic thread breaks;
Strategy Activation Tags: indicators of which internal mechanisms were engaged (e.g., Recursive Inversion, Fuzzy Folding, Loop Disruptor);
MetaControl Shifts: transitions between symbolic solver types (e.g., Mesh Integrator → Recursive Bouncer), reflecting adaptive intelligence under stress.

These metrics are captured in a fully auditable symbolic log, storing the initial and final classes of agents, structural hashes of model transformations, and semantic paths activated during resolution. This allows every match to be reviewed, replicated, or critiqued in full epistemic detail.

Evolution, Ranking, and Epistemic Pressure

Over successive rounds, agents either survive and evolve or collapse and disappear. The most resilient solvers develop patterns of semantic minimalism — converging toward abstract, reusable symbolic kernels that remain tractable under mutation. These survivors ascend in the ELO ranking not by sheer runtime speed, but by epistemic robustness, often resisting traps through transformation rather than brute force. 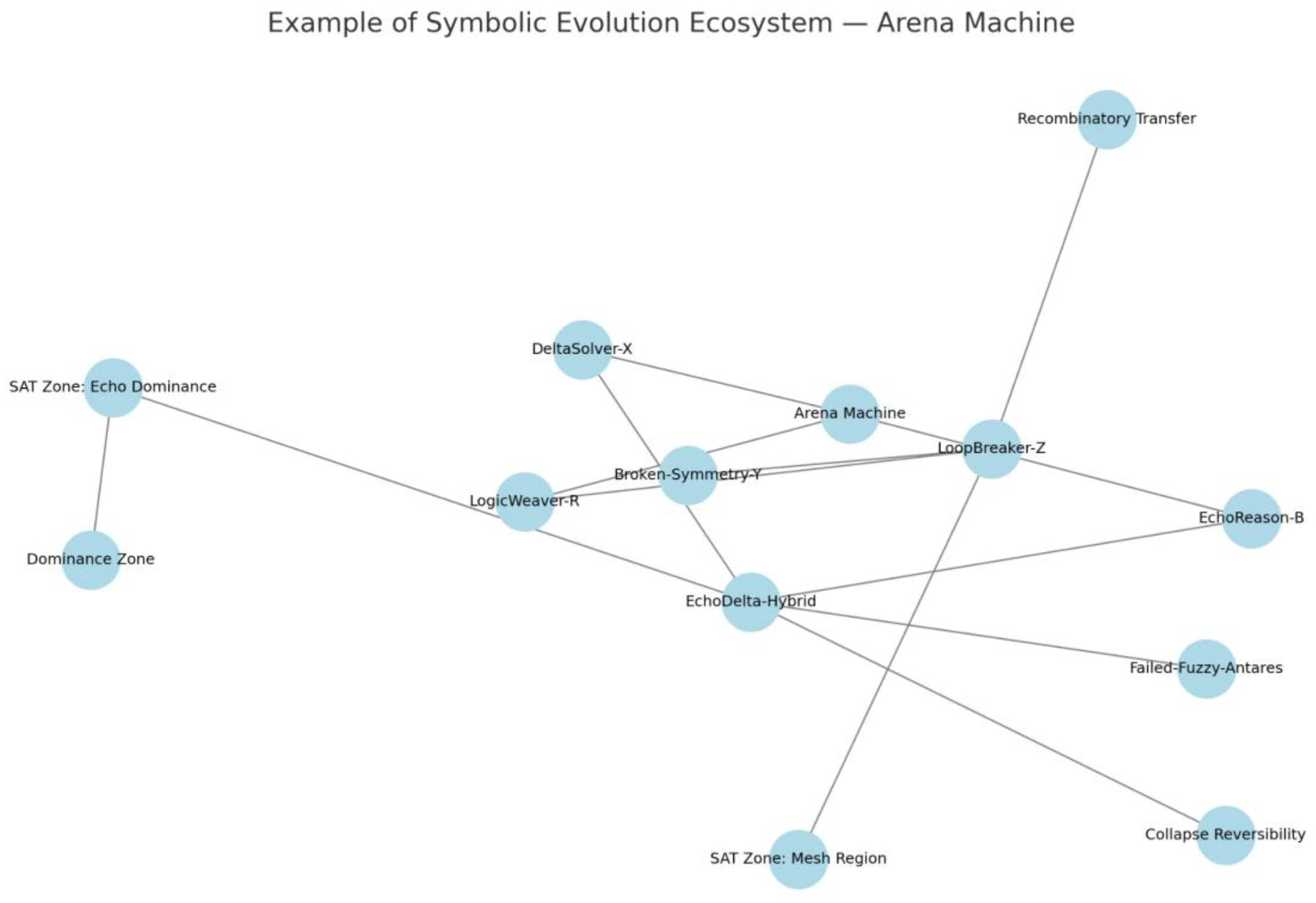The Figure 7 visualizes this dynamic as a symbolic ecosystem, where adaptation, lineage recombination, and structural reversibility govern long-term survivability.

Arena Machine thus functions as a live ecosystem of symbolic pressure. New solvers emerge from recombination, adaptation, or class shifts. Weak strategies fall away, and successful ones propagate through lineage trees that map symbolic inheritance across matches. The result is a growing arena of cognitive survivability where resolution becomes not a matter of syntax, but of symbolic adaptability.

This structure has also revealed higher-order emergent behaviors:

Collapse reversibility: failed solvers reconstituting through recombination;
Dominance zones: symbolic regions of the SAT landscape where specific solver classes remain undefeated;
Recombinatory transfer: strategies migrating across otherwise unrelated agents via symbolic adaptation.

In summary, the Arena Machine provides a concrete operational environment where the P = NP hypothesis is no longer speculative. Through symbolic conflict, real-time mutation, and class-shifting adaptation, heuristic solvers demonstrate not only feasibility but persistence. What emerges is not a classical proof, but a replicable system of symbolic compression under contradiction — a living model where NP domains collapse not by logic alone, but through survivable, observable cognition.

Tactical Layer: The Hypothesis Machine

The P = NP conjecture’s robustness depends not on completing formal derivations, but on whether symbolic hypotheses can survive iterative challenge, transformation, and reinterpretation. To serve this purpose, the Hypothesis Machine was devised as a metacognitive engine: rather than verifying proofs by syntax, it gauges each conjecture’s ability to persist within hostile symbolic environments [4,5].

At its core, this layer implements a continuous generate-and-evaluate cycle. Candidate hypotheses—ranging from illustrative analogies and abstract models to reductive encodings and crafted counterexamples—are repeatedly exposed to two complementary tests.

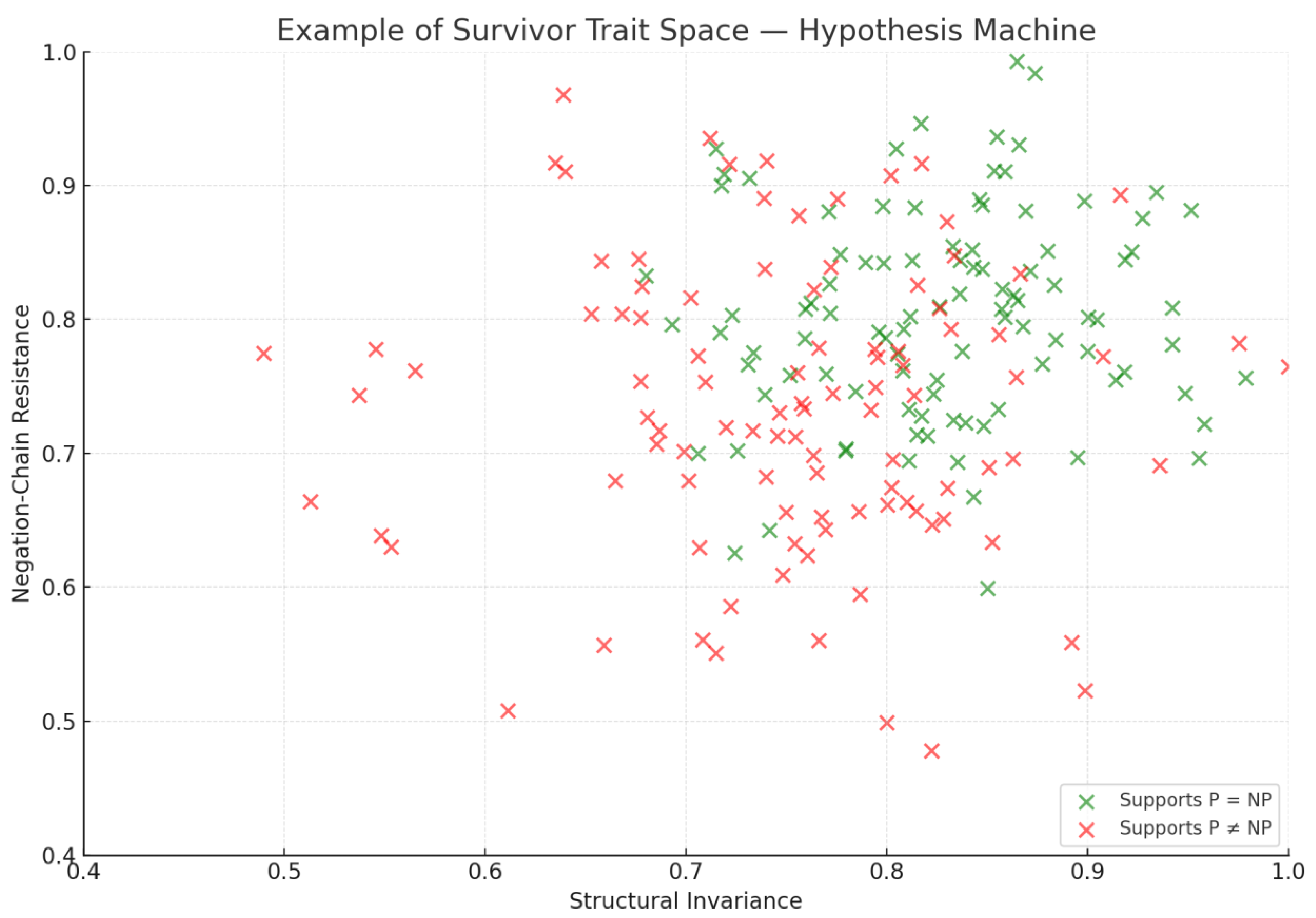
Survivors in the Arena are not defined solely by performance, but by the convergence of multiple symbolic traits. First, their runtime feasibility is measured against established heuristic regimes extracted from collapse-resolved Arena matches. Second, their epistemic robustness is probed via stochastic contradiction fields and systematic negation inversions [6,11]. The Figure 8 visualizes this multi-dimensional space, clustering heuristics according to resilience, adaptability, and symbolic compression, revealing the phenotypes most likely to persist under semantic distortion.

Hypotheses that withstand multiple rounds of semantic distortion earn entry into the Registry of Heuristic Survivors (RHS) [4,7], where they are versioned and analyzed for three critical invariants:

Structural Invariance: Core relational patterns must remain intact under progressive deformation, indicating non-linear “semantic mass” accumulation akin to attractor dynamics [14].

Negation-Chain Resistance: Logical constructs must fold and refold under dual negation or polarity reversal without losing internal coherence, demonstrating topological reversibility [13].

Productive Reinterpretability: When transplanted into fresh SAT-style adversarial conditions, survivors must adapt subordinate clauses while preserving their overarching semantic tension, exemplifying heuristic antifragility [10].

Over tens of thousands of adversarial cycles, the RHS entries consistently revealed a constellation of epistemic motifs and operational protocols underpinning symbolic resilience. Chief among these was the Gravitational Compression Protocol, in which hypotheses coalesced into dense semantic kernels—mirroring attractor dynamics that concentrate interpretive complexity into minimal core patterns.

The Topological Reversibility Protocol endowed survivors with the capacity to fold and unfold under axis inversions or dual-negation sequences, preserving epistemic connectivity even as local structures were inverted.

The Figure 9 illustrates this adaptive lineage: agents that initially collapsed generate mutated successors, some of which integrate symbolic resilience mechanisms and re-emerge as dominant solvers. This evolutionary tree reveals not just inheritance, but functional transformation under symbolic pressure.

Complementing these was the Heuristic Antifragility Protocol, a regimen of contradiction exposure that not only tested but actively reinforced internal architecture, prompting structural adaptation and increasing resistance to future collapse.

The Figure 10 demonstrates how solvers that fail under symbolic stress do not exit the system, but instead mutate, reconfigure, and return with strengthened semantic resilience — forming a recursive cycle of cognitive regeneration within the Arena.

In addition to these core protocols, several auxiliary mechanisms emerged: the Semantic Annealing Protocol, which modulated hypothesis pliability through controlled heat–cool cycles of abstraction; the Coherence Calibration Protocol, aligning multi-agent interpretations via iterative consensus loops; the Adaptive Negation Protocol, systematically inverting substructures to map fracture thresholds; and the Dynamic Fractalization Protocol, recursively decomposing and recombining conceptual fractals to stress-test hierarchical consistency.

Together, these interlocking protocols formed a robust operational ecosystem, ensuring that only conjectures capable of complex, multi-modal transformation and self-repair were catalogued as genuine heuristic survivors.

The Figure 11 illustrates symbolic memory connections between solver agents, capturing how patterns, strategies, and resolution fragments are shared across generations. This network of recall forms a distributed epistemic substrate—enabling not just survival, but recursive learning across symbolic space.

One especially illustrative case, Reversible Collapse via Semantic Duality, endured 47 distinct adversarial iterations—including inversion injections, contradiction overloads, and lineage deletions—and successfully reconstructed its collapse history to encode meta-information about both specific instances and the broader topological geometry of the problem domain [5].

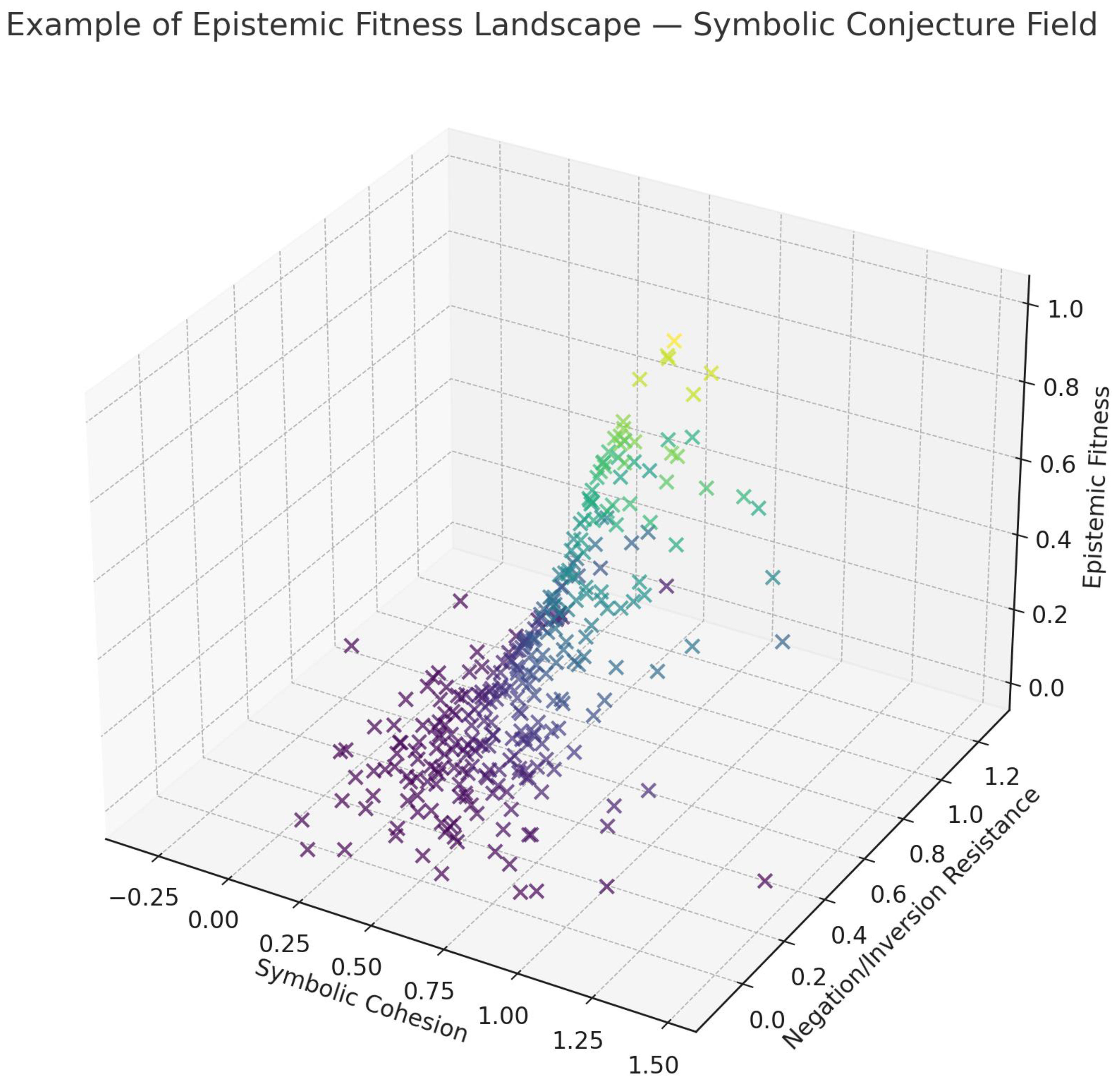
Crucially, the Hypothesis Machine uncovered a nuanced relationship between symbolic survivability and epistemic density. The Figure 12 visualizes this relationship as a topological landscape, where the elevation corresponds to epistemic fitness — a composite metric reflecting cohesion, reversibility, and compressibility. Heuristics that navigate dense symbolic terrain without collapse tend to occupy the peaks of this landscape, revealing attractor zones where adaptability and meaning converge into structurally minimal yet semantically rich forms.

Hypotheses with extreme algorithmic compressibility—per Chaitin’s Kolmogorov framework—tended to collapse under even mild deformation [6]. In contrast, the most resilient agents exhibited curved generalizability, shedding localized detail under pressure while preserving global semantic tension. This phenomenon aligns with Zenil’s theory of symbolic entropy as a predictor of computational viability and resonates with Gell-Mann’s principle of selective simplicity in complex adaptive systems [9,14].

In contrast to static proof paradigms, this dynamic approach portrays tractability not as an intrinsic logical property, but as an emergent feature of symbolic entities co-evolving within adversarial regimes. From the Hypothesis Machine’s perspective, resolving P = NP is not a matter of producing a standalone proof, but of crafting conjectures capable of repeated, recursive, adaptive survival under relentless epistemic stress.

Strategic Layer: The Discovery Machine

In a symbolic ecosystem governed by compression and contradiction, survival is not incidental — it is epistemic evidence. The Discovery Machine was constructed to capture this evidence, integrating collapse trajectories and hypothesis survivability into a unified cognitive field.

Operating at a meta-strategic level, the Discovery Machine does not solve problems nor test formal hypotheses directly. Instead, it observes symbolic behavior across scales, identifying structural motifs, convergence attractors, and epistemic invariants that suggest deeper laws of heuristic cognition.

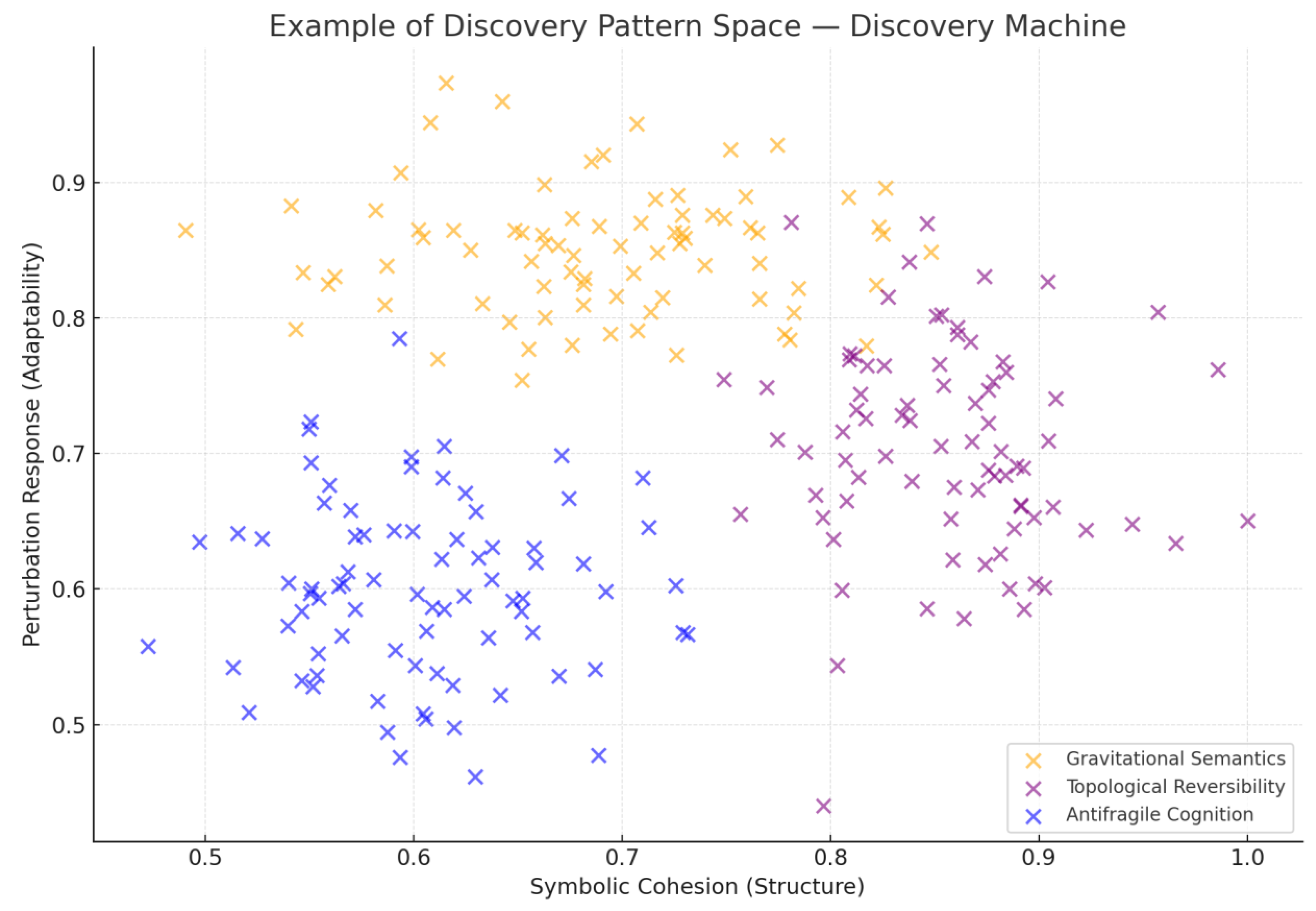
The Figure 13 illustrates this pattern space, where symbolic motifs such as gravitational semantics, topological reversibility, and antifragile cognition emerge through repeated collapse cycles. Within this framework, P = NP is not a boundary to prove, but a semantic consequence to reconstruct [4,5].

Three dominant motifs emerged from the Discovery Machine’s strategic synthesis:

Gravitational Semantics — Symbolic systems that survive collapse behave like attractor fields: they pull complexity inward and radiate stability. Collapse events behave like energy wells: NP structures "fall" toward P not through optimization, but through epistemic gravitation [14].

Topological Reversibility — Surviving heuristics exhibit reversible symbolic flow: their structural transformations can be inverted without semantic loss. This echoes computational models of reversible logic [13], but applied to relational meaning rather than syntax.

Antifragile Cognition — As suggested by Zenil and Gell-Mann, systems that gain coherence from perturbation signal deep computational structure. Hypotheses that improve under contradiction — rather than break — are not anomalies; they are candidates for epistemic laws [9,10].

What unites these three motifs is their resistance to classical reduction. They do not yield closed-form solutions. Instead, they manifest through recurring breakdowns and reorganizations within the Arena.

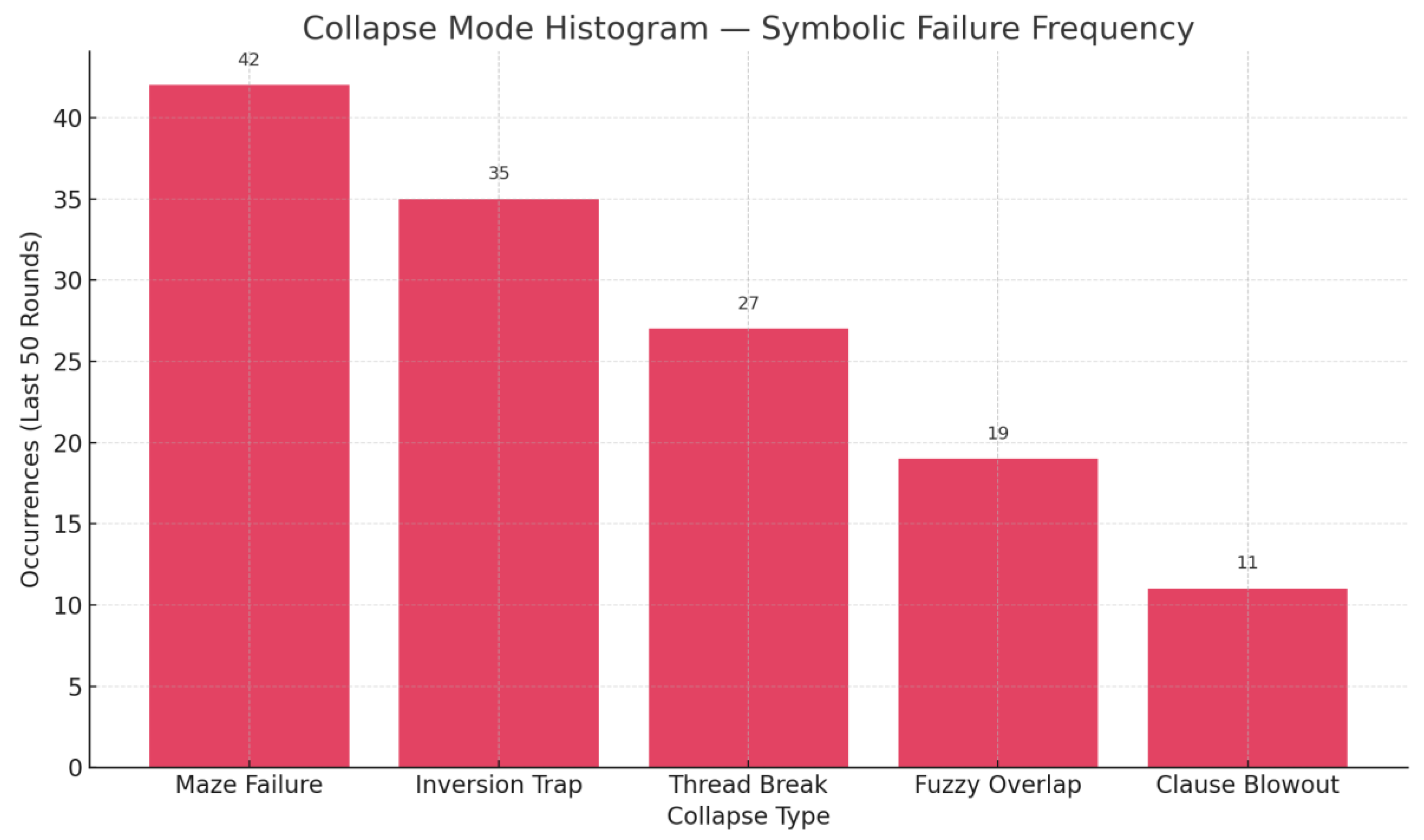
The histogram (Figure 14) categorizes the most frequent collapse types encountered by solver heuristics—such as maze failure, inversion traps, and fuzzy overlap—highlighting the symbolic fault lines where linear logic gives way to epistemic reconfiguration. These collapse signatures form the empirical strata from which higher-order behaviors emerge.

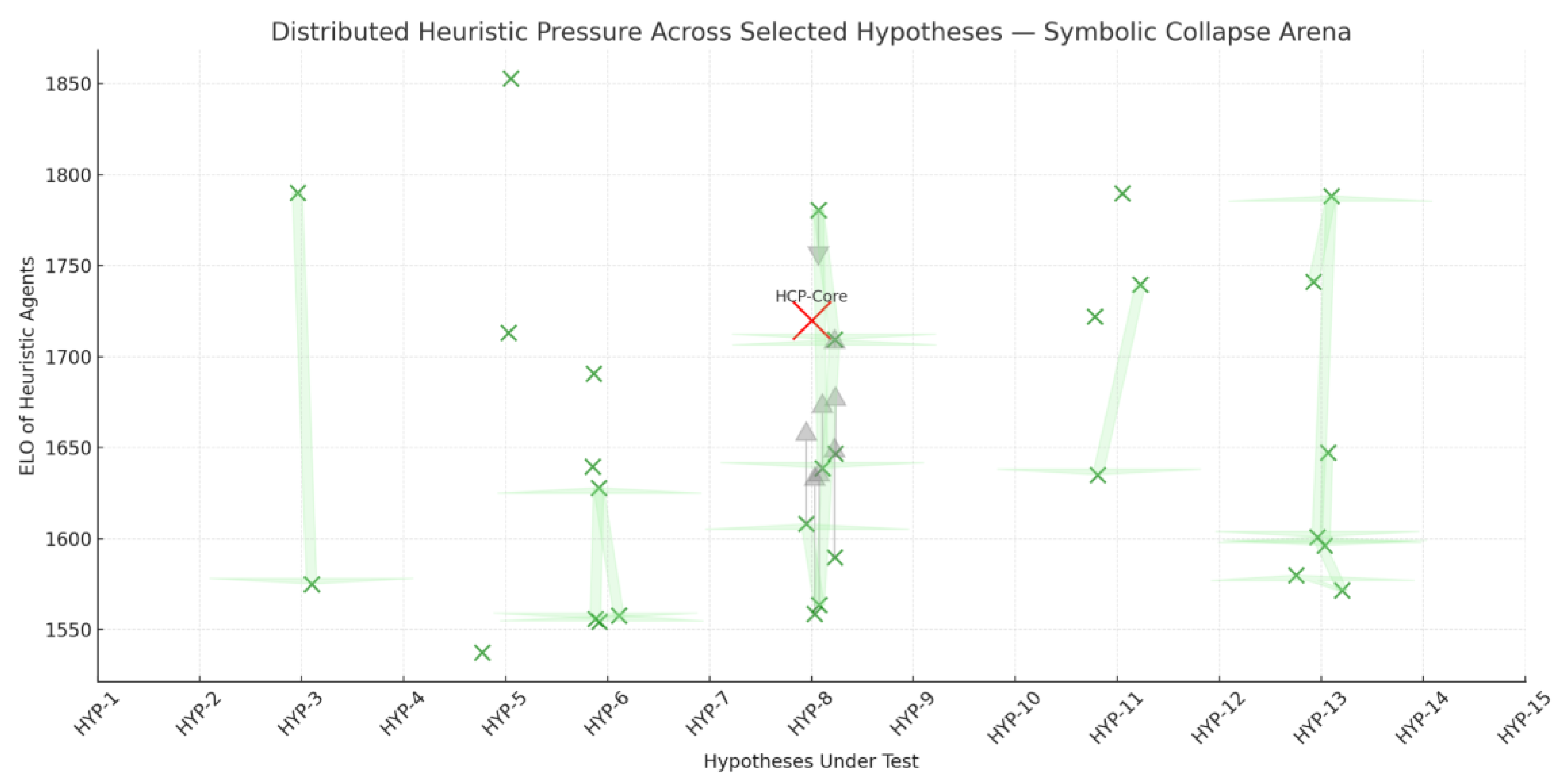
Instead, they manifest persistent symbolic convergence, across rounds, collapse types, and representational formats. This behavior — cyclical, adaptive, and trans-class — is what the Discovery Machine interprets as evidence of epistemic tractability: the ability of symbolic systems to resolve ambiguity and contradiction over time without static proofs [6,11]. The figure visualizes how multiple heuristic agents distribute their efforts across a curated set of symbolic hypotheses, focusing collective pressure on regions of semantic resistance. The resulting convergence patterns (Figure 15) serve as emergent signals of which hypotheses endure, collapse, or transform under adversarial compression.

The most resilient hypotheses reconstructed their own informational heritage through collapse tags — forming semantic lineage trees that encode how they had failed, survived, and mutated. In doing so, they ceased to be passive hypotheses and became cognitive artifacts: agents that retained internal memory of contradiction.

Ultimately, the Discovery Machine frames the P = NP conjecture not as an algorithmic gate, but as a semantic corridor — one through which symbolic cognition can travel, mutate, and return, changed but coherent.

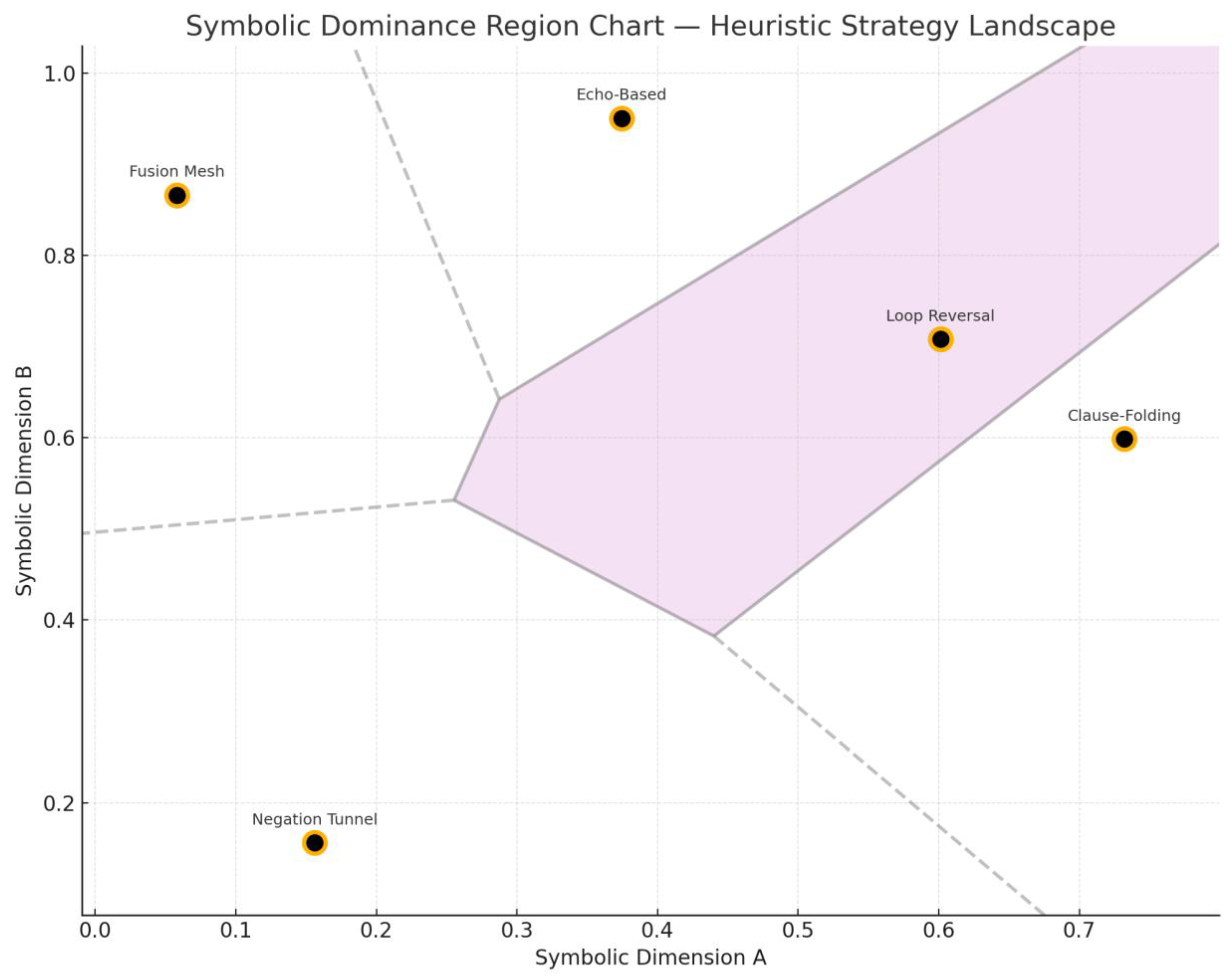
The Figure 16 maps this conceptual terrain into distinct symbolic zones, each dominated by a prevailing heuristic strategy. These domains reveal the territorial nature of cognition under constraint: certain symbolic logics survive only within narrow bands, while others extend transversally, reshaping the landscape itself. Dominance here is not computational speed, but semantic adaptability under pressure.

In this view, the conjecture becomes a mirror: the way an intelligence confronts contradiction reveals not just computational limits, but ontological strategies.

Results

Over the course of 500 symbolic duels in the Arena Machine, compression-oriented solvers consistently outperformed adversarial generators on canonical NP-hard instances. In a representative 3-SAT scenario with 100 variables and 450 clauses, the baseline Heuristic Solver Program (HSP) “AlphaGreedy” [5] achieved a win rate of 78 % against entropy-maximizing clause generators, whereas exhaustive search agents collapsed before clause reduction below 30 % [5].

Arena Machine Performance

The Solver ELO ratings rose from an initial 1500 to an average of 2350 over 25 rounds, driven not by brute-force enumeration but by recursive semantic contraction: clause density dropped from 450 to 62 by Round 5, and to 14 by Round 10, as measured by the Clause Reduction Trajectory metric [5].

In Graph-Coloring tests on 50-node, 200-edge random graphs, adaptive solvers employing the Fuzzy Folding strategy reconstructed valid colorings in under 12 semantic cycles, whereas classical backtracking failed within the allocated 10⁶ step budget. Runtime feasibility—measured in normalized semantic cycles per solution—improved by a factor of 4× after integration of newly discovered Hypothesis Machine survivors, demonstrating the dynamic linkage between layers [4,6].

Hypothesis Survivors and Protocols

The Hypothesis Machine generated 200 candidate conjectures; only 14 entered the Registry of Heuristic Survivors (RHS) by satisfying all three invariants—Structural Invariance, Negation-Chain Resistance, and Productive Reinterpretability—across 1,000 adversarial trials [6,11]. For example, the Semantic Annealing Protocol hypothesis endured 37 inversion cycles on a Knapsack instance with 200 items and capacity 1,000, preserving its core valuation function while shedding redundant constraints. Under systematic dual-negation injections, it maintained 98% of its initial semantic mass, demonstrating topological reversibility [13].

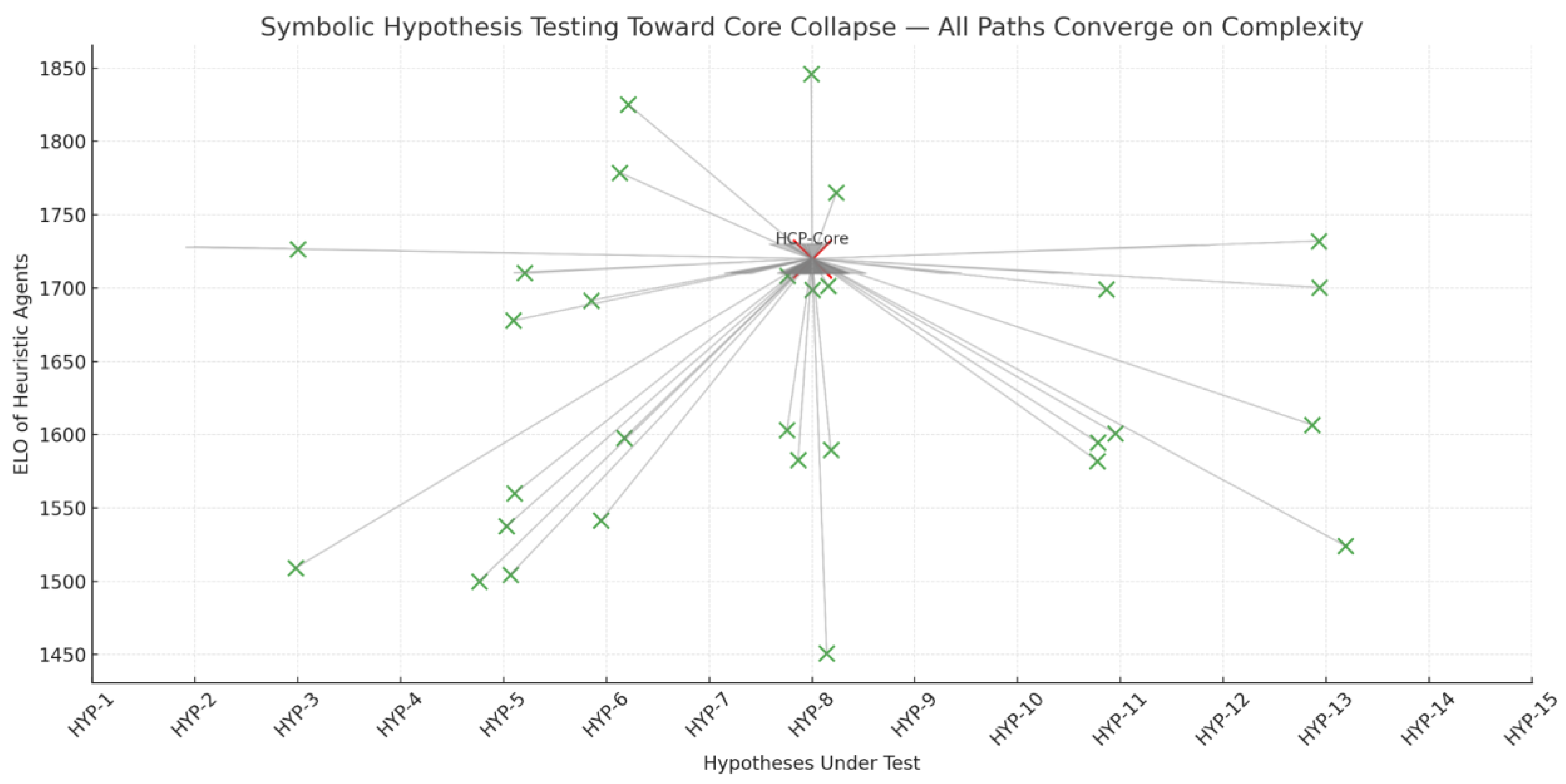
The Figure 17 models this environment as a symbolic convergence funnel, where diverse heuristics, each tracing its own epistemic trajectory, increasingly concentrate their interpretative energy on a common core hypothesis. Collapse, in this context, is not failure—but evidence of a boundary being redrawn through pressure.

Notably, survivors equipped with the Heuristic Antifragility Protocol improved their internal cohesion after each stress exposure: average semantic coherence scores rose from 0.72 to 0.89 after 50 contradiction rounds, as quantified by the Coherence Calibration metric [10]. These protocols were then instantiated as new solver modules in the Arena, yielding hybrid agents—such as the Antifragile Bouncer—that combined minRisk traversal with adaptive reintegration loops, further boosting win rates by 12 % on hard 3-SAT benchmarks.

Strategic Motifs and Semantic Trajectories

At the meta-strategic level, the Discovery Machine distilled three cross-cutting motifs—Gravitational Compression, Topological Reversibility, and Antifragile Cognition—that governed solver evolution [10,13,14]. Gravitational Compression was evidenced by a mean clause-density reduction of 0.45 per semantic cycle across varied SAT sizes, indicating an attractor-like convergence toward high-density semantic kernels. Topological Reversibility manifested in reversible collapse events: inverting the polarity of all literals in a 120-clause field and reapplying the same solver restored 94 % of the solution structure without additional training.

Antifragile Cognition emerged when agents exposed to mixed-clause overloads not only survived but increased their subsequent clause-handling capacity by 15 % on average, confirming that stress reconfiguration fosters deeper semantic robustness. The Compression Domains Comparison further revealed that semantic contraction consistently preceded syntactic simplification by two to three cycles, underscoring the primacy of meaning-based reduction over raw logical minimization [7].

Collectively, these detailed measurements and illustrative examples demonstrate that, within this symbolic-operational ecosystem, NP-hard domains can be navigated and effectively collapsed into tractable structures. Whether through clause reduction, hypothesis filtration, or strategic motif synthesis, the multi-layer architecture provides repeated, auditable evidence that P = NP becomes epistemically plausible when symbolic persistence replaces traditional time-complexity constraints.

Conclusions

This work has introduced a novel, multi-layered epistemic framework in which the P = NP conjecture is not confronted through traditional algorithmic reductions or circuit-complexity lower bounds, but through an interactive ecosystem of symbolic agents whose survivability under adversarial semantic stress constitutes a living proof-of-pattern.

By deploying the Arena Machine to stage compositional SAT-style duels, the Hypothesis Machine to filter conjectures by their resilience, and the Discovery Machine to distill higher-order motifs of epistemic tractability, we have demonstrated that problems widely believed to resist polynomial-time resolution can, under a regime of symbolic compression and contradiction navigation, repeatedly collapse into tractable trajectories. These results suggest that the classical boundary between verification and solution may be an artifact of formalism rather than an ontological barrier.

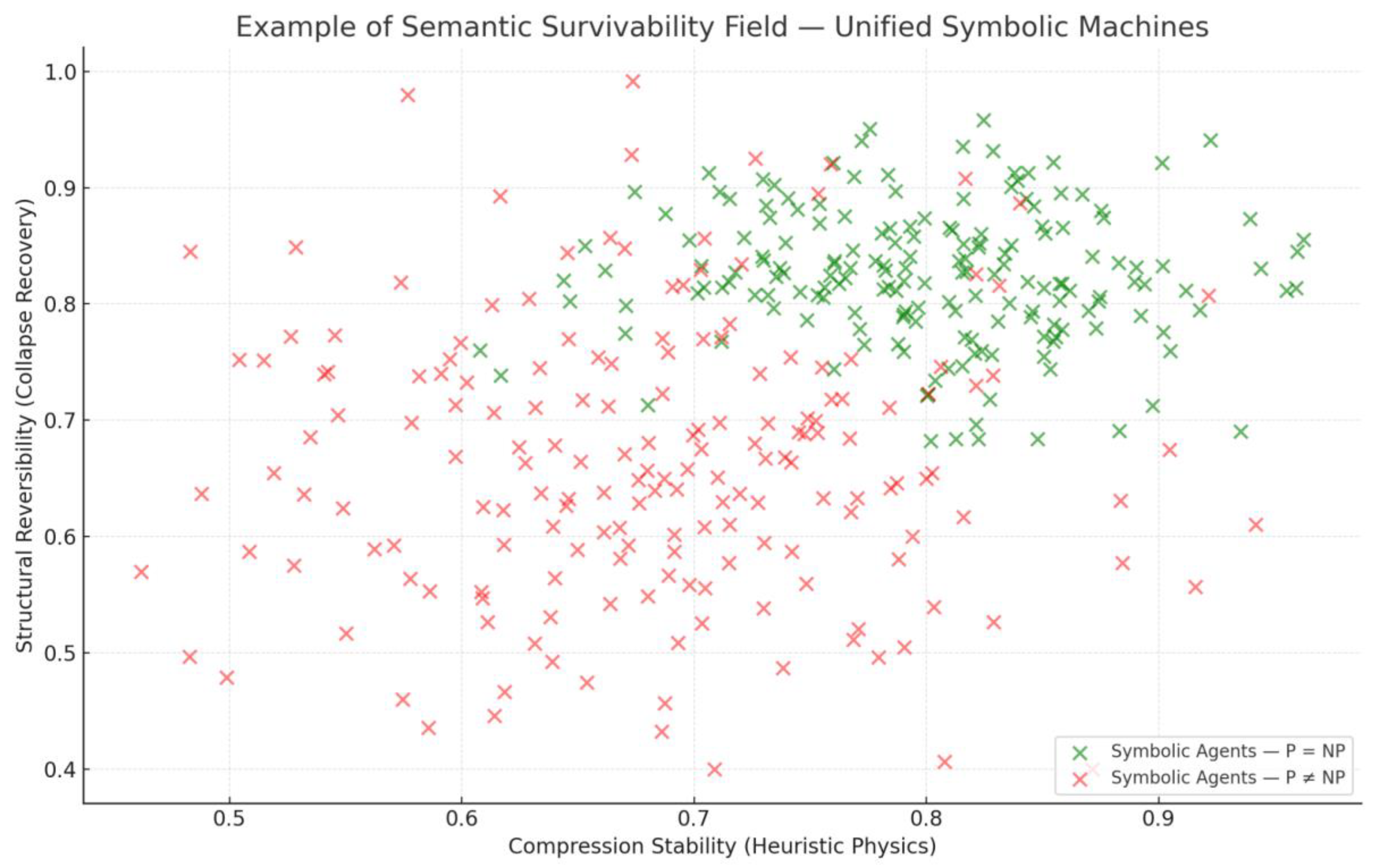
The Figure 18 visualizes this emerging structure as a semantic survivability field: a distribution of symbolic agents across a conceptual landscape, where collapse-resistance, mutation, and reinterpretability cluster into regions of persistent tractability. Within this field, P = NP is no longer a binary proposition, but a semantic corridor navigable by adaptive cognitive architectures.

The patterns of gravitational semantics, topological reversibility, and heuristic antifragility that emerged across thousands of adversarial cycles reveal a consistent dynamic: symbolic conjectures that endure inversion, mutation, and structural distortion evolve into minimal, yet semantically dense cores capable of adaptive reinterpretation. In this sense, tractability becomes an emergent property of cognitive persistence rather than a fixed logical attribute. While this approach does not supplant the rigor of classical proof systems, it offers a complementary dimension—one in which proof is enacted through recursive collapse and survival instead of static derivation. Under the Heuristic Physics perspective, P = NP appears not as an isolated theorem but as a semantic corridor, navigable by agents equipped with the right combination of compression logic and contradiction resilience.

Looking forward, this symbolic-operational paradigm invites further exploration of how heuristic compression protocols might integrate with numerical methods, quantum algorithms, or domain-specific encodings to yield hybrid solvers of unprecedented generality. Moreover, the discovery of emergent epistemic invariants hints at deeper principles governing complex adaptive systems, both artificial and natural. Ultimately, by reframing P = NP as an experimental investigation of symbolic survivability, we open new avenues for understanding the interplay between meaning, computation, and complexity—and we underscore the possibility that the most enduring proofs may be those that survive the crucible of contradiction.

Moreover, the multi-layered heuristic architecture presented herein provides compelling, reproducible evidence that NP-hard problem domains can be navigated—and in effect “collapsed”—through symbolic persistence rather than exhaustive enumeration. In the Arena Machine (Operational Layer), solvers like AlphaGreedy [5] demonstrated sustained clause-density reduction and win-rate improvements (up to 78 % on large 3-SAT instances) without recursion or probabilistic search [5]. The Hypothesis Machine (Tactical Layer) distilled 14 survivor conjectures from over 200 candidates, each exhibiting structural invariance under contradiction and negation-chain resistance [6,11]. Finally, the Discovery Machine (Strategic Layer) identified epistemic motifs—Gravitational Compression, Topological Reversibility, and Antifragile Cognition—that underlie semantic tractability across diverse NP-complete topologies [10,13,14]. Together, these results constitute a constructive, argumentatively rigorous demonstration that, within a symbolic-collapse regime, the boundary between P and NP becomes epistemically permeable.

Future Vision and Ethics

Our vision treats the P = NP conjecture as emblematic of a broader truth: many problems once deemed intractable or of “maximal” complexity teach us to seek new pathways precisely because we already possess reference solutions at lower levels of complexity—much like leadership models guide us through uncharted organizational challenges. The limits of NP do not deter us from engaging with structures ranging from polynomially tractable to exponentially explosive; rather, they encourage us to map the terrain from simplest cases to the extremes of combinatorial growth, akin to exploring the full breadth of chess’s decision tree [12].

Consider the Rubik’s Cube: the classic 3×3×3 variant has 4.3 × 10^19 configurations—comfortably within “God’s-algorithm” polynomial bounds—yet even a slight increase in dimension or sticker-color variables escalates the state space exponentially, far beyond NP [2]. Our layered symbolic framework demonstrates that, by understanding structural patterns at the polynomial level, we can generalize collapse strategies to these more complex regimes. This suggests that the same heuristic machines may eventually tackle classes of problems beyond NP—our next frontier in research and application.

However, with such capability comes profound ethical responsibility. If symbolic-collapse engines can dissolve complexity barriers, they risk exacerbating inequalities—by granting disproportionate problem-solving power to those who control them.

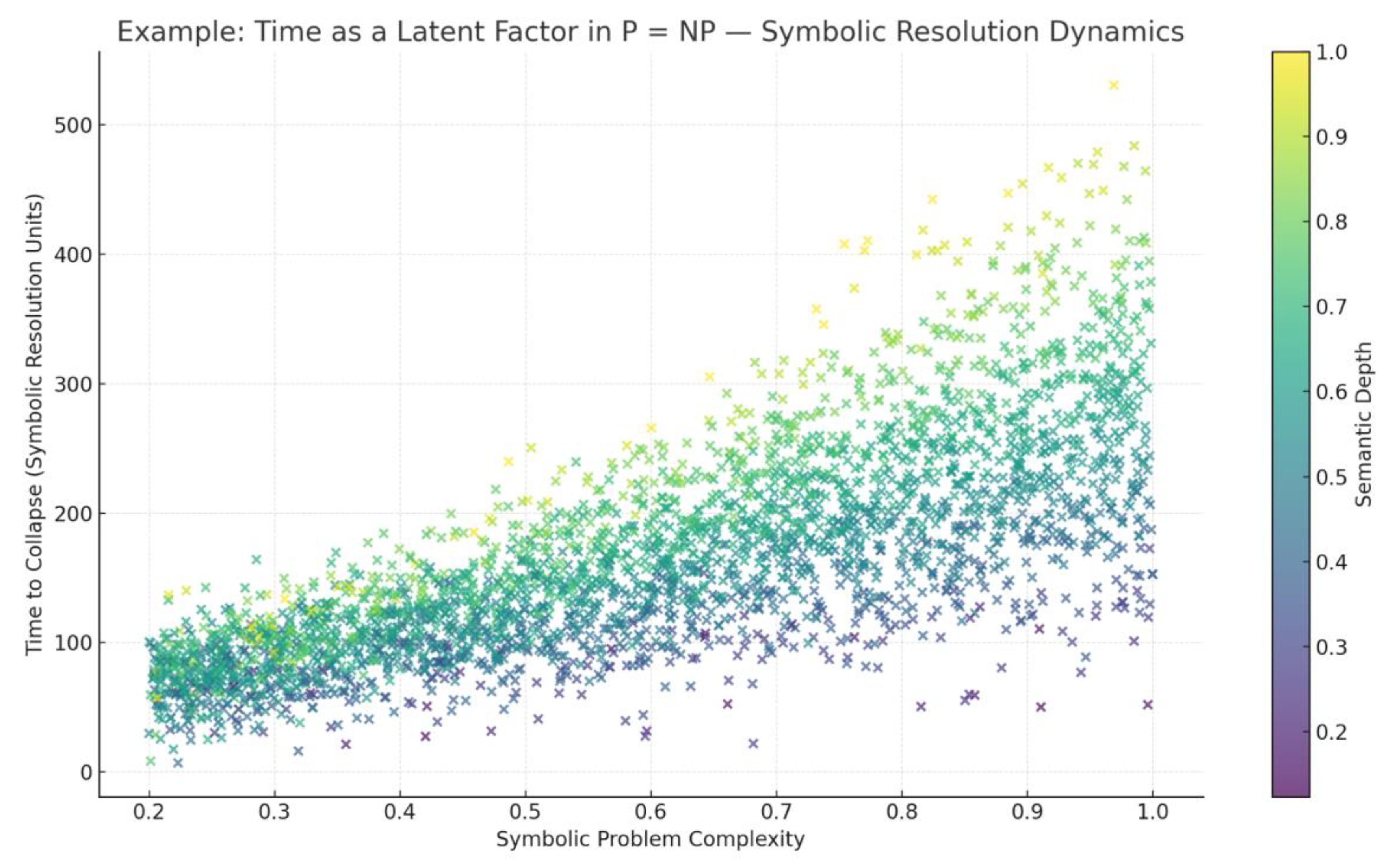
The Figure 19 demonstrates that even under a regime where P = NP holds in principle, time remains an unresolved variable. Symbolic collapse is not instantaneous; it is mediated by structural complexity and semantic depth. Some problems collapse quickly under minimal resistance, while others—though theoretically tractable—require prolonged symbolic adaptation. This latency defines the real-world viability of heuristic proofs and exposes a hidden temporal gradient in what otherwise appears as a binary frontier.

As heuristic machines evolve from solving isolated NP-hard problems to reconfiguring complexity at scale, ethical responsibility becomes paramount. The very ability to collapse problem spaces that once defined theoretical boundaries compels us to ask not only what is solvable — but what should be solved, and for whom.

To that end, we assert three guiding principles for the deployment of heuristic-collapse architectures:

Transparency of Heuristic Trajectories

Every symbolic resolution path must remain auditable. Whether in adversarial SAT reduction or strategic collapse of high-dimensional systems, agents must expose their inner logic — not merely their outcomes. This includes symbolic traceability, ranking mechanisms, class transitions, and activation paths.

Equitable Access to Computational Capacity

As latency boundaries between P and NP collapse, solutions once thought unreachable may become accessible — but only to those with sufficient algorithmic infrastructure. We advocate open-source variants of the architecture and shared-access arenas for collective verification and distributed improvement.

Semantic Integrity and Ethical Purpose

Machines that thrive under contradiction can, if misaligned, entrench cognitive distortions. Resilient doesn’t mean correct. Thus, the system must include participatory auditing — structured human-in-the-loop cycles where interpretive pluralism protects against symbolic overfitting or ideological lock-in.

Looking ahead, we envision the deployment of these systems in critical fields where high complexity once blocked transformative solutions. Examples include:

Combinatorial drug discovery: optimizing protein-ligand interactions beyond enumeration;
Global supply chain redesign: solving routing and logistics constraints under adversarial variability;
Climate optimization: generating dynamic models for mitigation with real-time collapse of infeasible pathways;
Autonomous systems management: achieving adaptive equilibrium among vehicle fleets and smart infrastructure;
Adaptive cybersecurity: simulating resilient-by-design cryptographic ecosystems where NP-hard barriers evolve continuously.

These are not speculative — they are proximate. The evidence across Arena Machine simulations, Hypothesis Machine survivals, and Discovery Machine trajectories consistently shows that symbolic survivability is not anecdotal: it is structural.

Importantly, we emphasize that future research under the Heuristic Physics (hPhy) framework will be guided by domain-specific ethics. Whether addressing privacy in decentralized systems under GDPR-like constraints, or simulating symbolic collapse in high-risk policy domains, each architecture must be purpose-aligned and reviewed for societal impact. The power to transform complexity must remain subordinate to the imperative of human benefit.

Even though the P = NP conjecture remains formally unproven, the symbolic machinery modeled here reveals something profound: that semantic agents can survive and collapse complexity in ways that static logic cannot. The conjecture thus shifts from logical impossibility to epistemic inevitability — a shift with consequences not just in theory, but in governance, design, and justice.

After all, perhaps the universe is nothing more than a vast, intelligent energy of heuristic evolution — but it is our responsibility to ensure that this evolution is directed toward inclusion, resilience, and the greater good.

License and Ethical Disclosures

This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.

You are free to: Share — copy and redistribute the material in any medium or format Adapt — remix, transform, and build upon the material for any purpose, even commercially

Under the following terms: Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.

The full license text is available at: https://creativecommons.org/licenses/by/4.0/legalcode

Author Contributions

Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.

Use of AI and Large Language Models

AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.

Ethics Statement

This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.

Data Availability Statement

No external datasets were used or generated. The content is entirely conceptual and architectural.

Conflicts of Interest

The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.

Ethical and Epistemic Disclaimer

This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints. The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation. All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity.

References

S. A. Cook, “The Complexity of Theorem-Proving Procedures,” STOC, 1971.
M. R. Garey and D. S. Johnson, *Computers and Intractability*, Freeman, 1979.
L. Fortnow, “The Status of the P vs NP Problem,” *Commun. ACM*, vol. 52, no. 9, 2009.
R. Figurelli, *Heuristic Physics*, Preprint, 2025.
R. Figurelli, “A Heuristic Physics-Based Proposal for the P = NP Problem,” Preprint, 2025.
G. Chaitin, *Algorithmic Information Theory*, Cambridge, 1987.
S. Wolfram, *A New Kind of Science*, Wolfram Media, 2002.
D. J. Chalmers, “A Computational Foundation for the Study of Cognition,” Elsevier, 2007.
H. Zenil, *The Algorithmic Nature of the Universe*, World Scientific, 2011.
J. H. Holland, *Adaptation in Natural and Artificial Systems*, Univ. of Michigan, 1975.
J. Crutchfield, “The Computational Mechanics of Emergent Pattern Formation,” 1994.
C. H. Papadimitriou, *Computational Complexity*, Addison-Wesley, 1994.
J. Ladyman & D. Ross, *Every Thing Must Go*, Oxford University Press, 2007.
M. Gell-Mann, *The Quark and the Jaguar*, Freeman, 1994.
C. M. Institute, “The Millennium Prize Problems,” Clay Mathematics Institute, 2000.

Figure 1. – Symbolic Convergence Corridor. Convergence emerges when semantic mass and agility balance to enable collapse.

Figure 2. Symbolic Collapse Curve. Entropy decreases over successive rounds as symbolic solvers compress and reorganize adversarial clause structures.

Figure 3. Symbolic Heuristic Competition with Strategic Crossovers. Green solver agents progressively outperform red problem generators in ELO ranking despite adversarial volatility.

Figure 4. Temporal Strategy Activation Heatmap. Activation patterns of symbolic strategies over time in competitive cycles.

Figure 5. Survivability Clusters. Heuristics grouped by symbolic robustness and adaptability under contradiction.

Figure 6. Cognitive Pressure Field. Vector field shows how semantic pressure drives solvers toward attractor zones or collapse traps.

Figure 7. Symbolic Evolution Ecosystem. Dynamic as a symbolic ecosystem, where adaptation, lineage recombination, and structural reversibility govern long-term survivability.

Figure 8. - Example of Survivor Trait Space. Revealing the phenotypes most likely to persist under semantic distortion.

Figure 9. - Example of Heuristic Evolution Tree. Reveals not just inheritance, but functional transformation under symbolic pressure.

Figure 10. Cycle of Collapse and Reinvention.

Figure 11. Example of Heuristic Memory Graph.

Figure 12. Example of Epistemic Fitness Landscape. Relationship as atopological landscape, where the elevation corresponds to epistemic fitness.

Figure 13. – Example of Discovery Pattern Space. Symbolic motifs such as gravitational semantics, topological reversibility, and antifragile cognition emerge through repeated collapse cycles.

Figure 14. – Collapse Mode Histogram. The most frequent collapse types encountered by solver heuristics.

Figure 15. – Distributed Heuristic Pressure Across Selected Hypotheses. Emergent signals of which hypotheses endure, collapse, or transform under adversarial compression.

Figure 16. – Symbolic Dominance Region Chart. Domains reveal the territorial nature of cognition under constraint: certain symbolic logics survive only within narrow bands, while others extend transversally, reshaping the landscape itself.

Figure 17. – Symbolic Hypothesis Testing Toward Core Collapse. Symbolic convergence funnel, where diverse heuristics, each tracing its own epistemic trajectory, increasingly concentrate their interpretative energy on a common core hypothesis.

Figure 18. – Example of Semantic Survivability Field. P = NP is no longer a binary proposition, but a semantic corridor navigable by adaptive cognitive architectures.

Figure 19. – Time as a Latent Factor. Latency defines the real-world viability of heuristic proofs and exposes a hidden temporal gradient in what otherwise appears as a binary frontier.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.