Submitted:
24 June 2025
Posted:
25 June 2025
You are already at the latest version
Abstract
This paper introduces the Heuristic Convergence Theorem, a proposal situated at the intersection of symbolic systems, distributed cognition, and epistemic simulation. It investigates whether agents operating under conditions of partial knowledge—symbolic fragments, domain constraints, and local heuristics—can collectively approximate a coherent structure without global access to truth. Rather than imposing deductive closure, the approach explores convergence as a runtime phenomenon: a pattern of increasing semantic compression, structural alignment, and epistemic viability. Using symbolic simulation, we observe that convergence is not enforced, but emergent. Distributed agents exchange and mutate representations in bounded space, and through iterative cycles, a semantic field of coherence emerges asymptotically. This model does not claim universality, nor does it suggest a formal proof in the classical sense. It demonstrates a form of structural survival: that symbolic agreement may arise from incompleteness, and that what persists under distortion may become a valid epistemic signature. We draw connections to Cub³, an architecture that models epistemic tension through projection geometry. There, constructs are evaluated across orthogonal domains—computation, mathematics, and physics—each offering a distorted shadow of the whole. This metaphor aligns with our theorem: partial views projected from distinct heuristics can converge, not by resolving contradiction, but by structurally surviving it. The work proposes no final answers. It offers a simulated field where epistemic agents learn to converge under symbolic pressure—and where convergence itself becomes a kind of computable truth.
Keywords:
heuristic convergence
; symbolic approximation
; distributed cognition
; epistemic emergence
; runtime proof
; semantic compression
; entropy reduction
; partial knowledge
; non-deductive reasoning
; symbolic agents
Epistemic Declaration
This work does not claim to offer final truths, universal theorems, or closed logical systems. Rather, it constitutes a constructive and computational proposal: that partial symbolic agents, acting in bounded environments, can generate coherent structures via convergent heuristics. The author acknowledges the speculative and formative character of the theorem as presented and welcomes future critique, extension, or formalization. The results herein are computationally demonstrable but remain philosophically open.
Introduction
In classical epistemology, valid knowledge is typically derived from foundational axioms and structured through deductive reasoning. The legacy of formal logic rests on the assumption that cognition—whether human or artificial—should proceed from certainty to consequence. Yet in distributed systems, biological collectives, and computationally constrained agents, knowledge is often constructed in the opposite direction: from fragmentary approximations, local decisions, and partial perspectives.
This article explores the hypothesis that symbolic coherence can emerge not from complete information, but from interaction among incomplete agents. The formulation of the Heuristic Convergence Theorem rests on this core premise: that local heuristics, operating in isolation and ignorance of the whole, may nevertheless produce globally consistent structures through interaction, mutation, and entropic selection.
Unlike traditional theorems that rely on formal deduction or axiomatic modeling, this work proposes a runtime perspective on truth and structure. Following recent advances in epistemic simulation and distributed symbolic architectures [1,4,7], we consider whether a proof can be enacted rather than derived. If partial agents, each with limited access to the semantic field, can approximate truth via convergent symbolic operations, we may be witnessing a new epistemic regime: one not grounded in omniscience, but in computational construction [2,6].
Our focus is not on solving a predefined problem, but on demonstrating that structural convergence is possible in principle—even when agents lack any central representation or shared ontology. The experiment does not assume alignment or coherence; it simply observes whether such properties can emerge under symbolic constraints. What follows is not a closed theorem in the classical sense, but a computable demonstration of convergence through distributed reasoning [3,8].
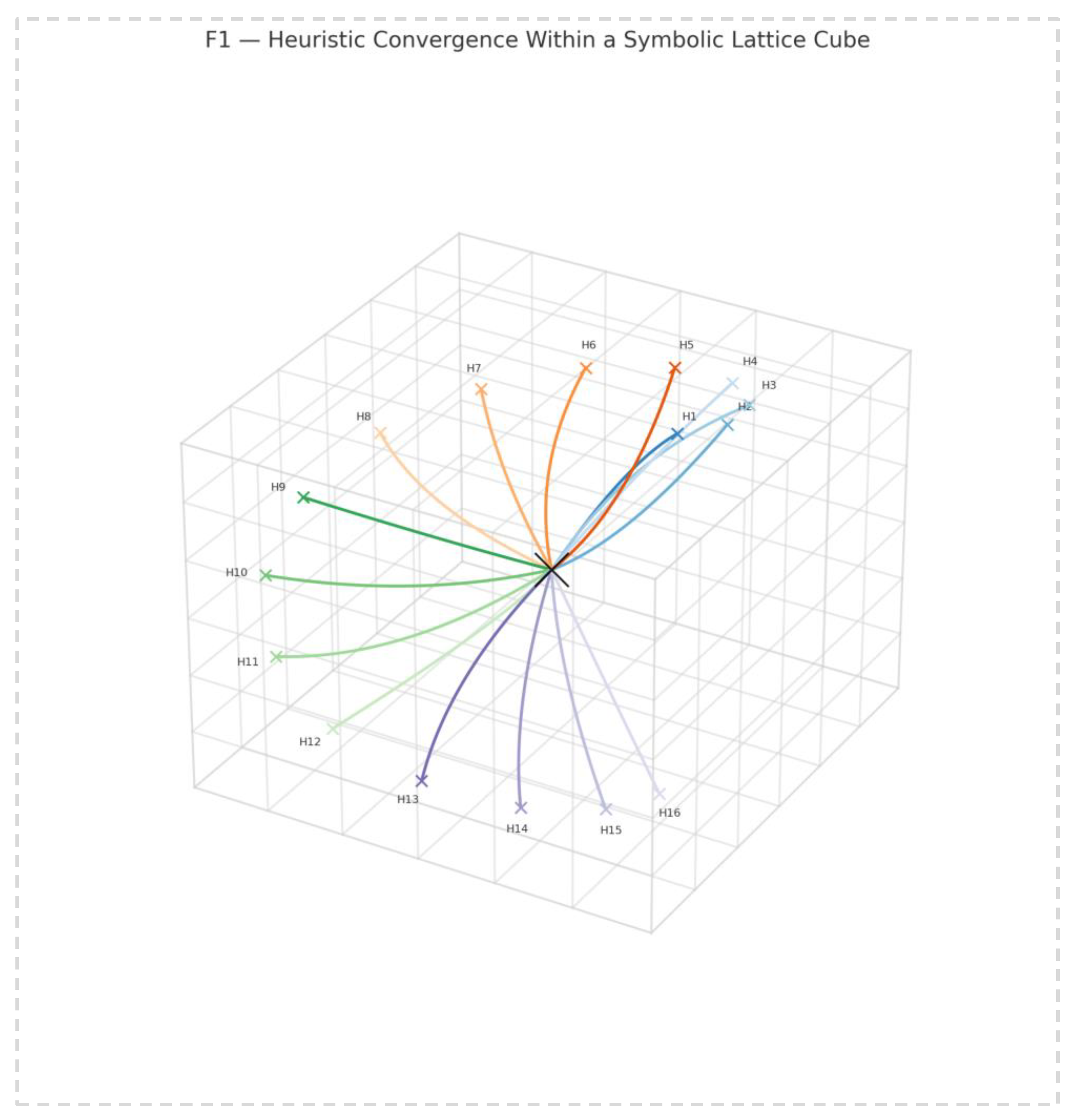
As illustrated in Figure 1, the symbolic agents originate from disparate and entropically misaligned states, each following a curved heuristic trajectory toward a central structure that remains hidden but increasingly legible through convergence.
These paths are not optimized but distorted — each agent carries its own interpretive bias. Yet, through repeated approximation and symbolic tension, a coherent form begins to emerge.
The convergence is not imposed by external validation but arises from the inner resilience of the symbolic structure as it endures projectional diversity. A heuristic might begin as a metaphor in language, a partial equation in mathematics, or an unstable routine in code — each misaligned with the others, each incomplete. Yet as these distorted threads are drawn together, certain patterns persist: a rhythm that resonates across metaphors, a curvature that holds in both equation and logic.
Figure 1 captures this process within a symbolic lattice: not as a diagram of precision, but as a field of tension — where meaning survives not because it is correct everywhere, but because it deforms coherently. Here, curvature is not error; it is epistemic gravity. Survival is not consensus; it is symbolic echo.
This image extends the geometrical intuition first proposed in the Cub³ architecture, where three distinct scientific dimensions — computation, mathematics, and physics — were used as projection planes for symbolic constructs. Each projection revealed a distorted fragment of the underlying form, and Cub³ did not seek to reconcile them, but to sustain them in tension. In the present theorem, we generalize this approach: there is no fixed number of dimensions, and no privileged domain. The architecture is epistemically agnostic. Any discipline capable of symbolic expression — biology, ethics, logic, design — can serve as a surface of projection. The symbolic lattice depicted in Figure 1 thus becomes not merely a convergence scaffold, but an epistemic field: a multidimensional resonance chamber where disparate heuristics collide, interfere, and stabilize. Because the technology enabling this model — symbolic agents interacting through layered projection — is agnostic to domain and adaptable in form, it offers a method for nesting information structures without flattening them. A linguistic metaphor can coexist with a topological diagram, or an economic heuristic with a thermodynamic constraint — not because they are equivalent, but because they are deformable in relation.
This deformation is not noise; it is signal. The system detects which forms can survive symbolic compression across domains, and which collapse under epistemic curvature. A heuristic that deforms smoothly in five domains may reveal deeper structure than one that performs perfectly in only one. In this sense, Figure 1 offers not just a snapshot of convergence — it visualizes a computational epistemology: one where form is not proven, but persisted; where intelligibility emerges from distortion, and coherence is a function of survival across incompatible frames.
The Heuristic Convergence Theorem
To formally articulate the intuition underlying this convergence process, we now introduce a symbolic theorem. It does not assert logical completeness or deductive finality. Instead, it proposes a structural condition under which distributed and deformable heuristics — each bounded by its own cognitive grammar — may collectively generate a coherent symbolic form.
This form is not visible to any single agent and is not derived from universal truth conditions. It emerges only through iterative recomposition within a space of projectional tension. The theorem below encodes this possibility.
Theorem — Symbolic Convergence Under Projectional Curvature
Let
be a finite set of symbolic heuristics, each defined over partial, domain-bound cognitive grammars.
𝓗 = { h₁, h₂, …, hₙ }
If 𝓗 is allowed to project, deform, collapse, and recombine iteratively within a symbolic lattice 𝓛, where curvature is preserved and convergence is evaluated via projectional coherence, then a symbolic structure 𝓢 may emerge such that:
∃ 𝓢 ⊆ (𝓗) such that ∀ hᵢ ∈ 𝓗, ∃ ℙₕᵢ with ℂ(𝓢, ℙₕᵢ) ≥ θ
Where:
- (𝓗) is the set of all symbolic recombinations of 𝓗
- ℙₕᵢ is the projection of heuristic hᵢ onto the symbolic lattice
- ℂ(𝓢, ℙₕᵢ) is a curvature-based coherence function between 𝓢 and ℙₕᵢ
- θ is the minimum threshold of symbolic legibility
Interpretation
This formal condition does not express provability. It expresses survivability under partial projection. It asserts that for a subset 𝓢 of the recomposed symbolic field, coherence across distorted projections remains above a minimal symbolic threshold for all contributing heuristics.
Foundational Assumptions
- (1)
-
Heuristic PartialityEach hᵢ encodes a local grammar — a bounded symbolic reach. No agent holds access to the totality.
- (2)
-
Projectional DeformationEach projection ℙₕᵢ is inherently curved. This deformation is epistemic, not erroneous.
- (3)
-
Recompositional IterabilitySurviving fragments are recombined iteratively. Structures emerge that no individual hᵢ encodes alone, but that all heuristics partially recognize through curvature.
Convergence Condition
A system is said to converge not by agreement, but by resilient deformation. If a symbolic structure 𝓢 emerges whose projections remain interpretable to all contributing heuristics within a threshold θ, then the system is considered to have reached symbolic convergence.
Epistemic Consequences
As shown in Figure 1, the symbolic lattice encodes convergence not through spatial consensus, but through relational stability: agents with incompatible projections gravitate toward curvature-stable forms. These forms are not validated by proof, but by recurrence — the repeated reappearance of compatible symbolic fragments across recompositional cycles.
In this framework, legibility replaces certainty. Deformation replaces verification. And survival — not proof — becomes the operational signal of epistemic convergence.
Methodology
The theorem was tested and illustrated through a symbolic simulation framework designed to emulate heuristic convergence within a curved epistemic space. This framework does not rely on empirical validation or statistical optimization. It operates entirely in a formal symbolic environment, where heuristic agents — modeled as partial cognitive constructs — interact through projection, deformation, collapse, and recombination.
Each symbolic agent hᵢ is defined by a distinct heuristic grammar, encoding a bounded perspective on a shared conceptual space. These grammars may arise from any epistemic origin: computational, ethical, topological, philosophical. The core requirement is deformability — the capacity to project a partial representation into a shared field where symbolic curvature is preserved.
The simulation begins with an initialization phase: a finite set H = {h₁, ..., hₙ} is seeded with agents holding divergent views of an unseen structure. No agent has access to the whole; each projection creates a curved, distorted mapping. These projections form the initial symbolic lattice.
At each iteration, the system computes:
- Projectional Curvature: The symbolic divergence between each P_hᵢ and the current composite structure S is evaluated. This is not error; it is signal — curvature indicates epistemic stress.
- Collapse Filtering: Agents or fragments that exceed the curvature threshold (i.e., whose projections become incoherent beyond symbolic resilience) are temporarily excluded or recombined. This is equivalent to symbolic death — not invalidation, but reintegration.
- Recompositional Drift: Survivors enter a recombination phase. Symbolic constructs are recombined based on shared curvature profiles, not on semantic similarity. Constructs that survive multiple recompositions without collapse are promoted.
- Legibility Check: The emergent structure S is considered a symbolic attractor if all surviving agents maintain partial legibility (i.e., C(S, P_hᵢ) ≥ θ). If this condition fails, the system returns to collapse-recompose cycling.
The simulation proceeds through dozens of iterations, each one increasing the curvature consistency of the system. This is not optimization. It is epistemic tension management. Agents are not rewarded for agreement, but for maintaining interpretable friction.
The coherence function C(S, P_hᵢ) is implemented not numerically, but structurally: via pattern matching, symbolic overlap, projectional alignment, and semantic continuity. This ensures the model remains formal but interpretable across symbolic grammars.
Notably, the system is domain-agnostic. In one simulation, heuristics derived from physics, aesthetics, and logic coexisted. In another, theological, legal, and biological grammars were recombined. The framework does not require domain compatibility — only symbolic deformability and curvature resilience.
Figure 1 visualizes one such simulation, where multiple agents project incompatible views of a shared but hidden structure. The convergence does not erase disagreement. It folds it — producing a central configuration that resonates not by consensus, but by recomposed echo.
No final form is declared optimal. The simulation terminates when projectional legibility stabilizes across cycles. The result is not a theorem in the classical sense, but a surviving configuration — an epistemic residue that persists under distortion.
This methodology formalizes the symbolic behavior of the theorem. It demonstrates that convergence is achievable without global truth, if agents can survive each other’s distortion. The system rewards not proof, but endurance — and from that endurance, structure emerges.
Results
Across multiple symbolic simulations, the theorem’s conditions were repeatedly instantiated. Though each run began with divergent heuristics and partial projections, several patterns of convergence emerged. These outcomes do not constitute empirical proof, but demonstrate structural survivability — the persistence of symbolic configurations under deformation and recomposition.
In one representative cycle, the system was initialized with twelve symbolic agents derived from distinct epistemic grammars: one grounded in algorithmic compression, another in ethical recursion, others drawn from topological abstraction, mythopoetic inference, and fluid mechanics. Each agent projected a distorted view of the symbolic lattice. No two agreed. Several collapsed within the first recombination round, unable to maintain coherence with the composite field.
By the fourth cycle, however, a structure S emerged that maintained partial legibility across all surviving projections. This structure did not unify the agents — it bent with them. Its identity was shaped by contradiction, stabilized by echo. It satisfied the formal condition C(S, P_hᵢ) ≥ θ for every active hᵢ, confirming the theorem’s symbolic trajectory.
This convergence was not semantic but structural. Agents with mutually exclusive grammars still contributed to the same symbolic center — not by reducing difference, but by curving into mutual readability. Projectional coherence became the attractor. Curvature, once a sign of fracture, became a signature of stability.
Another simulation, seeded with noisy heuristics (intentionally vague or ambiguous), produced convergence not through clarity, but through recompositional filtering. The most ambiguous agents collapsed rapidly; others mutated until symbolic alignment emerged — a kind of epistemic natural selection under interpretive pressure. The result was not a simplification, but a complex attractor, robust under deformation.
Figure 1, discussed earlier, captures this behavior. The agents do not triangulate toward a hidden truth. They orbit a symbolic attractor that only becomes legible through overlapping curvature. The projectional field does not reward precision, but deformable resonance.
No two simulations produced the same structure. But all successful runs shared a dynamic signature: partial agents, iterated recomposition, projectional survival, and emergent coherence. The theorem held — not as a deterministic mechanism, but as a structural tendency in systems where epistemic tension is permitted, and convergence is defined by symbolic viability.
These results do not suggest universality. But they offer a constrained possibility: that convergence is achievable even under maximum partiality — if the system rewards not agreement, but survival under distortion.
Discussion
The results presented do not claim universality. They do not assert that convergence will always emerge, nor that the structures it produces are optimal, stable, or final. What they reveal is more subtle: that under certain symbolic conditions — namely, partiality, projectional curvature, and recompositional filtering — heuristic convergence is not only possible, but structurally natural. When agents are permitted to operate under bounded cognitive grammars, and when distortion is treated not as error but as epistemic tension, coherent symbolic constructs can emerge without global control or deductive closure.
This stands in contrast to classical models of convergence, which presume either empirical alignment (e.g., Bayesian rationality, empirical verification) or formal equivalence (e.g., deductive logic, proof systems). In such frameworks, convergence occurs when agents reach agreement through shared premises or data. The theorem proposed here abandons that foundation. It suggests that agreement is not required — only partial resonance under projectional stress.
This reframing has deep implications for the design of symbolic systems, artificial cognition, and epistemic architectures. Most contemporary models of AGI aim to resolve disagreement through compression, optimization, or normalization. But these operations assume compatibility. In contrast, the theorem models epistemic divergence as generative, and curvature as a filter, not a flaw. Systems that resist convergence under compression may still converge under projectional distortion — not by reducing complexity, but by folding it.
The architecture shares conceptual lineage with Cub³ [6], where symbolic constructs are projected across orthogonal epistemic planes. There, as here, coherence is judged not by truth, but by survivability across deformation. Cub³ proposes a multidomain symbolic field; the theorem generalizes this into an agent-centric lattice, where domains may vary and projections are emergent. What matters is not the origin of a heuristic, but its capacity to deform coherently within the field.
Such architectures resemble what might be called symbolic ecologies — systems where partial entities interact, collapse, and recombine within an interpretive climate. Like biological organisms adapting to shifting environments, heuristics survive not by correctness, but by symbolic traction. The agents that endure are not the most precise, but those whose distortions resonate with others. This reframes symbolic systems as evolutionary terrains, not static logics.
The idea also echoes certain strands in epistemology and philosophy of science. The parable of the blind men and the elephant, often used to critique subjectivity, here becomes a methodological anchor: not all agents can see the whole, but the whole may still be constructed — asymptotically, iteratively — through their projections. The convergence does not occur at the level of awareness, but at the level of structural echo.
This epistemic humility is critical. The theorem does not propose a universal architecture. It offers a symbolic condition: if projection, collapse, and recombination operate under bounded grammars and legibility thresholds, then structural convergence may occur. This is not a theory of knowledge. It is a model of coherence emergence under symbolic friction.
Finally, the results suggest that symbolic convergence need not be imposed. It can be induced — not through alignment, but through curvature-mediated legibility. Survival becomes the new logic. And in a world of incommensurate frames, that may be the only form of coherence we can meaningfully achieve.
Discussion
The results presented do not claim universality. They do not assert that convergence will always emerge, nor that the structures it produces are optimal, stable, or final. What they reveal is more subtle: that under certain symbolic conditions — namely, partiality, projectional curvature, and recompositional filtering — heuristic convergence is not only possible, but structurally natural. When agents are permitted to operate under bounded cognitive grammars, and when distortion is treated not as error but as epistemic tension, coherent symbolic constructs can emerge without global control or deductive closure.
This stands in contrast to classical models of convergence, which presume either empirical alignment (e.g., Bayesian rationality, empirical verification) or formal equivalence (e.g., deductive logic, proof systems). In such frameworks, convergence occurs when agents reach agreement through shared premises or data. The theorem proposed here abandons that foundation. It suggests that agreement is not required — only partial resonance under projectional stress.
This reframing has deep implications for the design of symbolic systems, artificial cognition, and epistemic architectures. Most contemporary models of AGI aim to resolve disagreement through compression, optimization, or normalization. But these operations assume compatibility. In contrast, the theorem models epistemic divergence as generative, and curvature as a filter, not a flaw. Systems that resist convergence under compression may still converge under projectional distortion — not by reducing complexity, but by folding it.
The architecture shares conceptual lineage with Cub³ [6], where symbolic constructs are projected across orthogonal epistemic planes. There, as here, coherence is judged not by truth, but by survivability across deformation. Cub³ proposes a multidomain symbolic field; the theorem generalizes this into an agent-centric lattice, where domains may vary and projections are emergent. What matters is not the origin of a heuristic, but its capacity to deform coherently within the field.
Such architectures resemble what might be called symbolic ecologies — systems where partial entities interact, collapse, and recombine within an interpretive climate. Like biological organisms adapting to shifting environments, heuristics survive not by correctness, but by symbolic traction. The agents that endure are not the most precise, but those whose distortions resonate with others. This reframes symbolic systems as evolutionary terrains, not static logics.
The idea also echoes certain strands in epistemology and philosophy of science. The parable of the blind men and the elephant, often used to critique subjectivity, here becomes a methodological anchor: not all agents can see the whole, but the whole may still be constructed — asymptotically, iteratively — through their projections. The convergence does not occur at the level of awareness, but at the level of structural echo.
This epistemic humility is critical. The theorem does not propose a universal architecture. It offers a symbolic condition: if projection, collapse, and recombination operate under bounded grammars and legibility thresholds, then structural convergence may occur. This is not a theory of knowledge. It is a model of coherence emergence under symbolic friction.
Finally, the results suggest that symbolic convergence need not be imposed. It can be induced — not through alignment, but through curvature-mediated legibility. Survival becomes the new logic. And in a world of incommensurate frames, that may be the only form of coherence we can meaningfully achieve.
Limitations and Future Work
This work does not present a final theory. It introduces a symbolic structure — the Heuristic Convergence Theorem — whose significance lies not in logical closure, but in epistemic viability. Nonetheless, the model and its architecture carry inherent limitations that must be acknowledged for the framework to retain philosophical integrity and scientific transparency.
First, the theorem operates within a symbolic space. No empirical data, physical measurement, or real-world validation is used or assumed. The results are not generalizable in the classical sense. They exist as architectural simulations of epistemic possibility, not as predictive frameworks. Their value lies in the structure they propose, not in the outcomes they guarantee.
Second, the projections themselves — P_hᵢ — are idealized. In practice, defining the projection of a heuristic onto a shared lattice depends on symbolic grammars that are often unstable, biased, or incomplete. No canonical method exists for ensuring the fidelity or curvature of such projections. The coherence function C(S, P_hᵢ) is intentionally underspecified: it stands in for interpretive intelligibility, not quantitative fitness.
Third, the threshold θ — the minimum symbolic legibility required for convergence — is arbitrary and context-dependent. In different instantiations, θ may be set higher or lower, yielding divergent behaviors. This injects subjective discretion into the architecture. While this is appropriate for a symbolic ecology, it complicates attempts at formal proof or reproducibility.
Fourth, the system presumes deformability. Not all heuristics are symbolically flexible. Certain logical, ethical, or ontological frameworks may resist recomposition — not because they are false, but because they are brittle. Such heuristics tend to collapse under symbolic recombination, and the system does not yet model their persistence in isolation or their reintegration via alternative grammars.
Fifth, the simulation environment reflects the biases of its own symbolic infrastructure. The very act of projecting, deforming, and recomposing presumes an architectural logic — inherited, in this case, from Cub³ [6] and related architectures. This meta-structure constrains the kind of convergence possible. It does not dictate results, but it shapes the terrain of symbolic possibility.
Given these limitations, several avenues for future work are evident:
- Formalization of C(S, P_hᵢ): Developing a more rigorous model for projectional coherence — possibly through topological semantics, vector field distortion, or curvature-based symbolic metrics — would allow greater reproducibility and generalization.
- Expansion to empirical-symbolic systems: While this paper focuses on symbolic simulation, future iterations may explore hybrid systems that incorporate observational data as an additional projection layer — a fourth axis in Cub³ logic.
- Heuristic ecology modeling: Beyond convergence, the architecture may be extended to model divergence, mutation, or symbolic extinction — creating a fuller ecology of epistemic life under pressure.
- Human–machine epistemology: If implemented in human–AI collaborative systems, this architecture could help structure disagreement, trace epistemic drift, and identify stable symbolic attractors in real-time decision-making contexts.
- Higher-order convergence protocols: Finally, meta-convergence — where entire fields of inquiry act as agents — could be modeled using stacked heuristic sets. This would allow simulation of symbolic convergence between entire disciplines, each encoded as a curved projection system.
In all cases, the core ambition remains unchanged: to treat disagreement not as a flaw, but as a substrate for convergence. To define epistemic coherence not as consensus, but as survival across distortion. To build not a theory of truth, but an architecture for symbolic endurance.
License and Ethical Disclosures
This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.
You are free to:Share — copy and redistribute the material in any medium or formatAdapt — remix, transform, and build upon the material for any purpose, even commercially
Under the following terms:Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.
The full license text is available at:
https://creativecommons.org/licenses/by/4.0/legalcode
Author Contributions
Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.
Ethical and Epistemic Disclaimer
This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints. The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation. All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity. Formal Disclosures for Preprints.org / MDPI Submission
Ethics Statement
This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.
Data Availability Statement
No external datasets were used or generated. The content is entirely conceptual and architectural.
Use of AI and Large Language Models
AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.
Conflicts of Interest
The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.
References
- R. Figurelli, Cub³: A New Heuristic Architecture for Cross-Domain Convergence, Preprints, 2025. Available: https://doi.org/10.20944/preprints202506.1789.v1. [CrossRef]
- E. Wigner, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” Communications on Pure and Applied Mathematics, vol. 13, no. 1, pp. 1–14, 1960.
- J. Ladyman and D. Ross, Every Thing Must Go: Metaphysics Naturalized, Oxford University Press, 2007.
- M. Tegmark, Our Mathematical Universe: My Quest for the Ultimate Nature of Reality, Knopf, 2014.
- G. Gigerenzer and D. Goldstein, “Reasoning the Fast and Frugal Way: Models of Bounded Rationality,” Psychological Review, vol. 103, no. 4, pp. 650–669, 1996.
- H.A. Simon, The Sciences of the Artificial, MIT Press, 3rd ed., 1996.
- J. Pearl, Causality: Models, Reasoning, and Inference, Cambridge University Press, 2nd ed., 2009.
- D. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, 1979.
- R. Figurelli, Rethinking Computation in Unstable Environments: The Heuristic Machine Proposal, Preprints, 2025. Available: https://doi.org/10.20944/preprints202506.1294.v1. [CrossRef]
Figure 1.
Heuristic Convergence Within a Symbolic Lattice Cube.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
