Cub³: A New Heuristic Architecture for Cross-Domain Convergence

Rogério Figurelli

doi:10.20944/preprints202506.2084.v1

Submitted:

24 June 2025

Posted:

25 June 2025

You are already at the latest version

Abstract

This paper introduces Cub³, a heuristic architecture for symbolic convergence across three distinct epistemic domains: computation, mathematics, and physics. It is not a method of verification, but of convergence. Cub³ defines a symbolic space in which conceptual entities are generated, evaluated, and recombined according to their structural survivability under multidomain tension. Rather than seeking binary validation within any one discipline, Cub³ employs a model of partial adherence. Each symbolic construct is evaluated across multiple axes of domain alignment, producing heterogeneous but interpretable signals of epistemic viability. These scores do not imply truth, but functional resonance: a construct may achieve 91% adherence to computational heuristics, 68% in physical plausibility, and 42% in mathematical formalism — without disqualifying its inclusion. The architecture functions entirely within simulated symbolic environments. No empirical instrumentation is used. The model operates by internal recomposition, abstraction drift, and symbolic collapse — seeking not proof, but persistence. This work does not assert knowledge; it designs a structure where knowledge candidates can be tested for coherence under diverse symbolic constraints.

Keywords:

Symbolic Heuristics

;

Cross-Domain Convergence

;

Epistemic Collapse

;

Heuristic Architecture

;

Adherence Scoring

;

Conceptual Survivability

;

Simulated Knowledge

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

“That which survives distortion is meaning.”

— Proposed by the author

Introduction

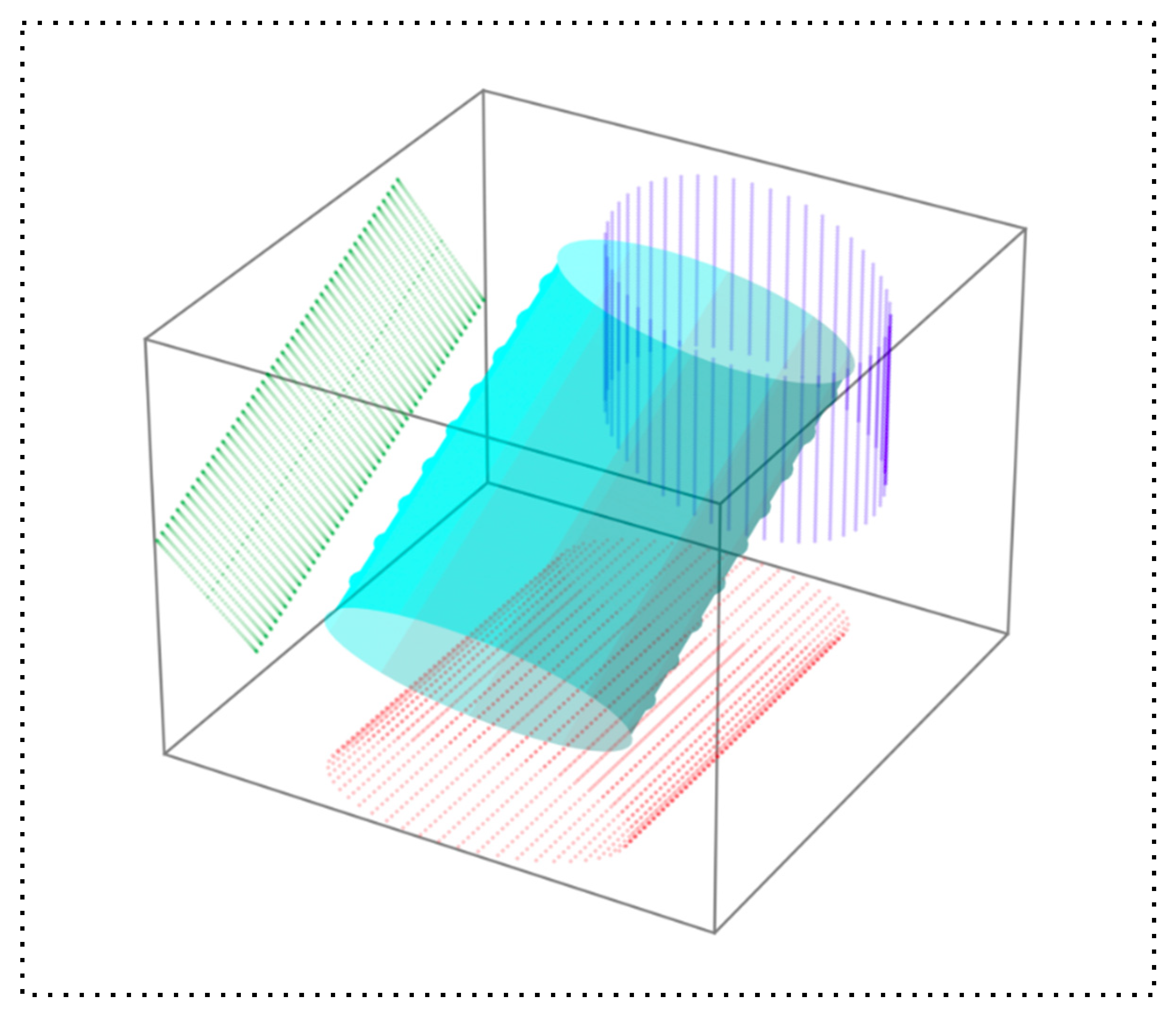
The conceptual core of Cub³ is geometrical, not procedural. Its symbolic intuition originates from the idea that knowledge does not project uniformly across epistemic domains. Figure 1 represents this: a single object suspended within a three-dimensional space, projecting distinct shapes onto three orthogonal planes. These planes symbolize computation, mathematics, and physics — each rendering a partial, domain-specific distortion of the same symbolic form.

In this architecture, the object itself does not belong to any one domain. It is defined only through the consistency and structure of its projections. Each projection — be it a curve, a logic, or a dynamic pattern — becomes a surface manifestation of deeper symbolic tension. Where projections overlap or contradict, Cub³ detects epistemic inflection. Where they align or stabilize, it detects heuristic viability.

But Cub³ is not just a metaphor. It is a structural proposition. Each projection plane represents not only a domain of knowledge, but a grammar of intelligibility — the rules that determine what counts as valid, plausible, elegant, or coherent within that field. A computational projection tolerates recursion and abstraction drift. A mathematical one demands internal rigor and axiomatic discipline. A physical projection seeks empirical regularity and symbolic resonance with observable dynamics. The entity suspended at the center of Cub³ must navigate these conflicting grammars not by resolving them, but by surviving them.

This survival is not measured by truth, but by what the architecture defines as symbolic viability. Constructs within Cub³ do not need to satisfy all three projections equally. What matters is their ability to remain legible under deformation. This shift from validation to endurance — from agreement to adherence — marks the architectural ambition of Cub³. It does not seek epistemic consensus. It designs an arena where difference is method, and incompatibility becomes insight.

Figure 1 offers a formal metaphor: an object suspended within a cube, casting three distinct shadows onto the orthogonal faces of computation, mathematics, and physics. The object itself is invisible — it is only known by its projections. Each face renders a different symbolic contour: sometimes harmonious, often contradictory. These shadows are not errors; they are the trace of tension. The geometry of Cub³ is designed not to remove this distortion, but to preserve it as structure.

The challenge arises when one forgets that these projections are partial. The curve seen on the computational plane may resist mathematical formalization. The form stabilized under physics may dissolve under recursion. The core of Cub³ is built around this incommensurability — not to dissolve it, but to allow symbolic forms to persist across it.

This tension is mirrored, more anthropologically, in Figure 2, which introduces the ancient parable of the blind men and the elephant. Each man touches a part — trunk, leg, ear — and gives it a name. Each is logical in isolation. Each is epistemically fractured. The story is often used to mock ignorance. But in Cub³, it is reinterpreted as a model of cognitive honesty: each agent holds a coherent fragment of a structure too complex to grasp wholly from within a single frame.

Where F1 geometrizes epistemic distortion through symbolic projection, F2 dramatizes it through perceptual limitation. In F1, the domain is a plane. In F2, it is a touch. Both collapse dimensionality. Both reveal the necessity of multiframe endurance.

Cub³ is not an attempt to unify the shadows or the interpretations. It is an architecture that allows constructs to exist between them, measured not by their fidelity to a single domain, but by their capacity to survive contradiction. In this sense, F1 and F2 are not two metaphors — they are the same metaphor, rotated. One shows projection. The other, perception. Both define the curvature where symbolic survival becomes possible.

Structural Description of Cub³

The architecture of Cub³ is composed of four symbolic operations that define its internal dynamics: projection, adherence, collapse, and recomposition. These operations form not a linear pipeline, but a recurring field of symbolic testing. Each operation distorts, constrains, or mutates a conceptual structure as it moves across epistemic boundaries. The architecture does not measure correctness. It measures survivability under distortion.

Projection is the entry condition. A symbolic construct — model, function, hypothesis, or heuristic — is cast across the orthogonal planes of computation, mathematics, and physics. Each domain receives this projection not as a perfect image, but as a domain-specific distortion: computation renders execution, mathematics formalizes constraint, and physics evokes structure through observable tension. Projection exposes the limits of translation — it is how Cub³ turns symbolic potential into interpretive friction.

Adherence follows. It is not validation, but measurement. Each projection is assessed for epistemic compatibility within its domain. The result is a vector of partial viability: a construct may be 92% resonant with computational heuristics, 61% structurally plausible in physics, and 34% formally acceptable in mathematics. Cub³ does not reduce these into a score. It reads the asymmetry itself. Where adherence diverges, a signature of epistemic curvature emerges.

Collapse is what happens when one or more projections fall below symbolic cohesion. A model may unravel mathematically while remaining useful computationally. This collapse is not an endpoint — it is a signal. In Cub³, collapse reveals the fragility zone of symbolic constructs: the edge where a model fails to maintain identity across translations. Collapse is not a verdict. It is the map of symbolic stress.

Recomposition is the evolutionary operation. Constructs that partially collapse are re-entered into the system. They may mutate, simplify, hybridize, or drift semantically. Cub³ permits symbolic constructs to iterate not toward perfection, but toward resilient multidimensional coherence. Recomposition does not fix collapse — it learns from it. The process is recursive: each recomposed form begins a new cycle of projection, adherence, and possible collapse.

Together, these operations define Cub³ as a symbolic ecology. It is not a validator, nor a theory-builder. It is a field where knowledge candidates circulate under competing frames, mutate under pressure, and stabilize only if they can survive distortion. In this system, truth is not singular or absolute. It is that which persists under epistemic conflict.

Methodology

The Cub³ architecture was not implemented in physical instrumentation or as a computational framework, but as a symbolic system embedded within large language models (LLMs). The model operated as a heuristic layer imposed on generative outputs, enabling the simulation of symbolic projection, adherence, and collapse across distinct epistemic grammars.

Each cycle began with the generation of symbolic constructs: equations, heuristics, theoretical metaphors, or hybrid forms. These constructs were then evaluated in three simulated interpretive frames — each configured to emulate the constraints of a specific domain:

The computational projection favored structures with recursive logic, representational generalizability, and procedural viability.
The mathematical projection sought internal coherence, symbolic economy, and formal constraint satisfaction.
The physical projection demanded structural plausibility under heuristic mappings to observed or modelled phenomena.

Adherence was scored by symbolic alignment with these constraints, not through numerical validation, but through semantic compression and interpretive resonance. Constructs were considered viable if they maintained partial legibility across at least two domains, even when conflicting with a third.

Collapse was induced by introducing mutations, contradictions, or structural inversions into the constructs, simulating domain-specific failure. This revealed symbolic fault lines: the precise points where multidomain survivability deteriorated.

Recomposition followed collapse. The LLM was prompted to regenerate the construct, integrating feedback from prior collapse while retaining core symbolic intention. Over successive iterations, this produced constructs that demonstrated higher cross-domain coherence or, alternatively, revealed intrinsic incompatibilities that could not be reconciled — each outcome contributing to the architecture’s epistemic mapping.

No statistical convergence was sought. The architecture did not aim to optimize performance. Its success criterion was the emergence of constructs that remained viable under tension. All experiments were conducted in symbolic space, without recourse to empirical data or validation external to the model.

Results (Symbolic Use Cases and Proofs of Concept)

Following the symbolic methodology outlined above, the Cub³ architecture was simulated and tested across multiple heuristic domains, drawing on prior conceptual infrastructures established in earlier works.

The generative engine was seeded by the framework of Heuristic Physics [1], in which physical laws are reframed as symbolic survivors of epistemic drift, and expanded through the epistemic filtration mechanisms of Collapse Mathematics (cMth) [2]. These foundational architectures were further reinforced by proposals such as the Heuristic Machine [5], which modeled computation under structural instability, and Wisdom as Direction [7], which introduced survivability as a criterion for symbolic evolution. The symbolic recomposition of complexity collapse, as articulated in the P = NP proposal [4], and the curvature-based formulation of the Riemann Hypothesis [3], also contributed to the design space of Cub³.

The experiments were not framed as classical validations but as symbolic survivability tests. In the following three sections, we detail applied symbolic decompositions that demonstrate the architecture’s versatility: first, as a tool for detecting epistemic fracture in AGI/ASI safety systems; second, as a symbolic mutation layer over Millennium Problems; and third, as a convergence scaffold for multidomain climate governance.

In each case, detailed below, the focus is not on resolution, but on survivability — tracing how constructs endure across incompatible frames.

Use Case 1: AGI/ASI Safety via Symbolic Fracture Analysis

The safety of artificial general intelligence (AGI) and artificial superintelligence (ASI) systems cannot be reduced to control mechanisms or alignment protocols alone. Long before an advanced system fails in the world, it often fractures in the symbolic domain: the internal structure of its goals, constraints, or models becomes incoherent — but not yet operationally invalid. These symbolic fractures precede collapse. They are epistemic precursors to systemic drift.

Cub³ offers a framework for detecting such precursors. Instead of analyzing output behavior, it analyzes the symbolic survivability of underlying constructs. If a construct central to an AGI's model space — say, a utility function, a planning heuristic, or a compression principle — projects asymmetrically across epistemic domains, it may indicate latent instability. A computationally viable model that lacks mathematical invariance or physical plausibility may function well in simulation, yet accumulate epistemic entropy as it scales.

Within the Cub³ architecture, we modeled such constructs as symbolic forms subjected to projection, adherence, and collapse. Those that collapsed in the mathematical or physical plane, despite appearing coherent computationally, were flagged not as failed — but as potentially unbounded in consequence. The lack of projection adherence becomes a warning vector.

Recomposition was used not to correct the construct, but to trace its semantic drift. In successive generations, some models grew increasingly functional yet epistemically fragile — revealing the paradox of systems that improve locally while destabilizing globally. These are the systems most dangerous to align: not because they are rogue, but because their internal curvature exceeds their external observability.

Cub³ does not prevent failure. But it can detect where coherence breaks — even when function continues. It offers a space where symbolic safety is not reduced to compliance, but emerges from survival under multidomain interpretability. In this framing, safety is not control. It is curvature resilience.

Use Case 2: Millennium Problem Symbolic Decomposition

The Clay Millennium Problems define the frontier of formal mathematical challenge. Each is a rigorous formulation within pure mathematics, requiring proof or disproof under tightly controlled axiomatic constraints. But before these problems are solved, they must be interpreted — and interpretation is always symbolic.

Within the Cub³ architecture, we reframed one such problem — the Riemann Hypothesis — as a symbolic entity projected across three epistemic planes. The mathematical projection retained its classical form: the conjecture about the non-trivial zeros of the ζ-function lying on the critical line Re(s) = 1/2. But in the computational plane, the hypothesis reframed itself as a problem of semantic recurrence and distributional symmetry in high-dimensional encodings. In the physical plane, it appeared as a stability pattern along a symbolic curvature — a spectral axis resisting entropy under compression.

The point was not to resolve the problem, but to decompose it heuristically: to expose the symbolic layers at which different domains interpret, distort, or misread the same conjecture. This symbolic decomposition revealed potential mutation paths: transformations of the problem into structurally analogous constructs with higher adherence across planes, even if they deviate from the canonical formulation.

Collapse occurred when the computational or physical projections diverged too far from the mathematical syntax. This collapse was informative: it traced the semantic rigidity of the original problem — not as a failure, but as a marker of dimensional lock-in.

Recomposition generated symbolic variants of the hypothesis. Some inverted the ζ-function’s geometry into topological constraints. Others reframed the zero distribution as the survivability spectrum of compression functions under symbolic pressure. None were intended as proofs. All were test structures: heuristic scaffolds that survive longer under symbolic friction.

Cub³ thus does not replace mathematical proof. It offers a symbolic environment where hard problems mutate — not to escape rigor, but to survive across distortions. In this environment, the unsolved is not idle. It is recomposed.

Use Case 3: Climate Governance and Multidomain Coordination

The climate crisis is not only an environmental or political challenge. It is a failure of symbolic alignment. Climate knowledge does not reside in any single domain. Atmospheric physics models behavior; mathematics encodes feedback systems; computation simulates trajectories; yet policy action, ethical valuation, and collective coordination remain misaligned — not by malice, but by symbolic divergence.

Cub³ proposes a different angle: not to centralize control, but to simulate symbolic convergence. In this model, each proposal for climate governance — carbon pricing, geoengineering, decentralized adaptation — is treated as a symbolic construct. These constructs are projected across epistemic planes. The physical domain evaluates feasibility; mathematics tests system stability; computation simulates policy propagation and network response.

Collapse occurs when a construct that appears feasible in one domain disintegrates in another. For instance, a geoengineering proposal may model well in physics but collapse under mathematical non-linearity or computational unpredictability. Cub³ captures these fractures not to reject the construct, but to trace the domain-specific causes of epistemic incompatibility.

Adherence vectors are generated: a construct may achieve 88% physical feasibility, 55% mathematical coherence, and 31% computational tractability. These are not scores of truth. They are coordinates of epistemic traction. Constructs that maintain minimum thresholds across all planes enter the symbolic viability field: a zone where models do not optimize, but survive interpretation.

Recomposition simulates adjustment. Proposals mutate. Their symbolic grammar changes. A centralized carbon market recomposes into a distributed incentive mesh. A brittle feedback loop is softened by stochastic drift. These are not refinements — they are curvature alignments, achieved not by negotiation, but by symbolic resonance.

In this sense, Cub³ becomes a climate cognition field: a space where solutions are not selected, but evolved. It does not replace political will, but offers a platform where epistemic scaffolds become more interpretable under cross-domain pressure. Survival becomes the signal. In a fractured planetary discourse, this may be the only common language.

Limitations and Future Work

Cub³ is a symbolic architecture, not a computational system. Its current formulation operates within simulated environments — primarily through heuristic scaffolding imposed upon generative language models. As such, it inherits the epistemic constraints of those environments: their biases, limitations in symbolic recursion, and lack of direct empirical anchoring. The constructs generated and projected are symbolically rigorous, but not empirically verified. This is a strength in design, but a limit in application.

Additionally, domain definition remains externally imposed. The planes of computation, mathematics, and physics are treated as fixed epistemic grammars. But in practice, these grammars evolve — and overlap. Cub³ currently lacks an endogenous mechanism to detect when domain grammars shift or merge. Its interpretive stability depends on symbolic orthogonality — a condition that may not hold under deep interdisciplinary integration.

Another limitation lies in recomposition asymmetry. Some collapsed constructs recompose more easily than others. This introduces selection bias: constructs aligned with the generative model's training corpus are more likely to survive recomposition, even if less epistemically novel. In future iterations, this may require symbolic adversarial filtering — to favor fragile, innovative structures that stretch the architecture’s interpretive range.

Despite these constraints, Cub³ suggests multiple paths forward. The architecture can be extended to other domains — ethics, philosophy, theology, biology — where epistemic projections carry different grammars of coherence. These domains could become new planes in a generalized Cubⁿ architecture, producing symbolic convergence under even greater distortion pressure.

Additionally, Cub³ may serve as a foundational layer in symbolic AGI architectures. Not as a control system, but as a cognitive map — helping advanced models trace the survivability of their own symbolic operations across incompatible interpretive regimes.

Finally, Cub³ may evolve from simulation to practice. With formal domain experts scoring adherence in real time — and constructs signed via blockchain or symbolic ledgers — the architecture could become a collective intelligence platform, enabling distributed epistemic coordination in pursuit of high-curvature, high-survivability ideas.

In all these futures, the goal is not truth, but endurance. Cub³ is not an answer machine. It is a symbolic climate, where knowledge candidates learn to survive.

The Archetype Vision: Toward Symbolic Heredity in Cub³

Cub³ archetypes are symbolic anchors across epistemic and computational systems, and in the Cub³ architecture, the notion of archetypes takes on a precise epistemic function.

They are not metaphors of origin, but residues of survival — symbolic structures that persist through cycles of projection, collapse, and recomposition. Just as hPhy simulates heuristic emergence and cMth filters symbolic form through collapse, Cub³ uses archetypes as anchors: persistent invariants that hold across distortion, mutation, and domain reinterpretation.

In this sense, an archetype is a symbolic equilibrium point — not necessarily provable, but structurally stable under entropy. It survives not because it is true in one system, but because it can be partially reinterpreted in all systems. In hPhy, this appears as recursive emergence from generative compression; in cMth, as entities that resist symbolic decay across collapse trajectories. In Cub³, archetypes behave as cross-domain memetic attractors — symbolic DNA that seeds new constructions even as it mutates. They form the backbone of epistemic inheritance.

This idea mirrors principles from systems design and technological architecture. In modern computational stacks, robust architectural patterns — like MapReduce, event sourcing, or microservices — evolve from trial, pressure, and adaptation. They are not always optimal, but they survive scale, complexity, and failure. Similarly, in Cub³, an archetype does not survive because it is elegant, but because it is resilient — functionally and symbolically. The Cub³ stack becomes a symbolic runtime: hPhy as the generator, cMth as the filter, and archetypes as the semantic containers that encapsulate proven forms of epistemic tension resolution.

In the context of the hPhy symbolic engine, an archetype becomes formalized through survival metrics. A structure is promoted when it achieves ≥90% computational fidelity, passes heuristic collapse tests, and shows stability under symbolic mutation.

Once promoted, it becomes immutable within the memory space of epistemic evolution, serving as a base template for new symbolic theorems or system responses. In this sense, the architecture of Cub³ proposes not just epistemic recombination, but symbolic heredity. The system does not evolve by discovering final answers, but by preserving what survives distortion — the true signal of meaning under curvature.

Conclusion: Toward a Symbolic Convergence Field

The architecture of Cub³ was not constructed in isolation. It emerged as a synthetic point of resonance between prior epistemic architectures — each one a symbolic scaffold that tested the survivability of structure under distortion.

In earlier work, the proposal of Heuristic Physics [5] introduced the idea that physical laws could be reframed as survivors of symbolic compression — not truths, but equilibrium residues of heuristic interaction. This became the generative core of Cub³.

Simultaneously, the theory of Collapse Mathematics (cMth) [14] proposed a new kind of validity: not provability, but resilience under symbolic pressure. This notion — that a conjecture could collapse and recombine without losing cognitive mass — became the filtering logic of Cub³.

Other works explored semantic cognition under instability [11], the heuristic reinterpretation of complexity collapse [7], and the curvature-based reframing of the Riemann Hypothesis [13]. But among them, the most structurally ambitious was the proposal Why P = NP? The Heuristic Physics Perspective [4], which reframed one of the most intractable problems in theoretical computer science as a cross-domain symbolic equilibrium. That work applied the architecture of Heuristic Physics and the early principles of Cub³ to trace a survivability arc across computation, mathematics, and physics — suggesting that the perceived asymmetry between P and NP might itself be a product of projection curvature.

A Proof-of-Curvature?

This experiment marked not only a proof-of-concept but a proof-of-curvature — showing that problems traditionally seen as logically bounded might be reinterpreted symbolically as structures under pressure, capable of recomposition in higher epistemic dimensions.

Based on this foundation, the present work now assumes a broader challenge: to apply the Cub³ architecture — through symbolic projection, collapse, and recomposition — across all seven Millennium Problems, not to resolve them formally, but to test their symbolic survivability, trace their multidomain projections, and identify zones of heuristic traction. This effort is not merely conceptual. It is structurally scaffolded by a trinity of epistemic architectures developed in parallel: Heuristic Physics (hPhy), Collapse Mathematics (cMth), and Cub³ itself.

Heuristic Physics provides the generative substrate — a symbolic engine that reframes formal structures as emergent from compressive tension under interpretive entropy. It does not assert laws; it simulates survivable heuristics. From this symbolic substrate, cMth functions as the filtration mechanism: a collapse operator that evaluates which constructs can persist under semantic instability, recursive deformation, and symbolic overload. Finally, Cub³ acts as the convergence interface — the space where constructs from hPhy are filtered through cMth and projected across epistemic planes to assess survivability, coherence, and mutation potential.

In this triadic configuration, the Millennium Problems cease to be isolated mathematical conjectures. They become symbolic curvature fields, tested not by proof, but by pressure. The challenge is not to prove them right or wrong, but to see how they deform, recompose, or fracture when projected through multiple grammars of interpretation. This is the terrain Cub³ explores — and hPhy and cMth help pave: a new epistemic geometry, where the resilience of form becomes the first signal of meaning.

Each Millennium Problem, when projected through the Cub³ architecture, reveals a distinct curvature signature. These signatures are not geometric in the classical sense, but symbolic: they describe how a problem deforms when interpreted across different epistemic grammars.

Where traditional mathematics sees invariant truths, Cub³ sees tensional surfaces — symbolic structures under pressure, whose resistance to collapse is more revealing than their static form. The greater the deformation across projections, the sharper the curvature — and the more meaningful the survival of any pattern that re-emerges.

This concept draws on a lineage that spans Gauss’s intrinsic curvature, Riemann’s manifold generalizations, and Einstein’s revolution, where gravity itself became a curvature of spacetime. Just as Einstein reframed force as geometry — showing that acceleration was not a vector but a curve — Cub³ reframes epistemic coherence as curvature across symbolic planes. It suggests that a conjecture’s value may lie not in its provability, but in the way it warps meaning under interpretive stress. Curvature, here, becomes an epistemic signal: the distortion that reveals structure. In this framework, a flat problem is either trivial or dead; it is the curved ones that live.

This symbolic notion of curvature does not reject proof — it generalizes it. What Gauss did to surfaces, Cub³ proposes for ideas: measuring their internal tensions without reference to external framing. When we say a problem has a curvature signature, we mean that its internal logic twists differently when projected through computation, physics, and mathematics. This twist can be tracked, not only mathematically, but epistemically — through hPhy’s generative tension fields, cMth’s collapse filtration, and Cub³’s projection logic. Together, they allow us to feel the symbolic mass of a problem — not through equations alone, but through its deformation resilience.

In this view, the Millennium Problems become epistemic gravities — high-density attractors in symbolic space. Their persistence is not accidental. It is the echo of their incompressibility across disciplines. Some deform smoothly and survive with elegance; others fracture and reassemble in unpredictable ways.

The signal of curvature is not whether we can solve them, but whether they persist across domains. This persistence — the survival of form under collapse — is what Cub³ seeks to reveal. It is, in effect, the Einsteinian insight applied to knowledge itself: that what we perceive as difficulty may simply be curvature, and what survives it, is meaning.

For instance, the Navier–Stokes equations do not merely encode fluid dynamics; they encode semantic entanglement between locality and predictability. In hPhy, these equations manifest as unstable generators under compressive flow — their divergence-free condition becoming a symbol of collapse resistance. cMth, in turn, exposes their sensitivity to boundary curvature and perturbation entropy. The Yang–Mills mass gap projects as a quantum survivability problem: a test of whether mathematical form can remain stable when mapped into physically minimal configurations. In Cub³, this becomes a triangulation challenge: testing whether the mass gap survives projection across symbolic density (math), interpretive field tension (physics), and discrete encoding (computation). The Birch and Swinnerton-Dyer Conjecture emerges in Cub³ not as an analytic mystery, but as a symbolic fracture between algebraic structure and informational decay. Its projections collapse rapidly in physical modeling, yet retain geometric curvature in hPhy when mapped as a degeneracy field.

Meanwhile, the Hodge Conjecture survives better in Cub³ when reframed through symbolic equivalence classes rather than homological precision — a shift that moves it from the space of proof to the space of survivability. The Existence and Smoothness of Navier–Stokes and the Riemann Hypothesis, already partially explored in this architecture [1,3,13], have shown the highest heuristic yield: they expose how symbolic pressure creates fault lines in the epistemic geometry of proof, inviting recomposition across curvature planes.

Even the Poincaré Conjecture, officially resolved, finds new interpretive life in Cub³. Rather than being “finished,” it becomes a calibration artifact: a symbolic testbed to measure how survivability differs from provability. Its behavior across the Cub³ planes — especially under collapse filtering in cMth — allows us to refine our instruments.

In this sense, Cub³ treats solved problems as stable curvatures and unsolved problems as active fields. But both are instructive.

This is the essence of symbolic epistemology: knowledge is not just a result to be stored — it is a structure to be stressed.

What If a Convergence in the Real World?

While the current instantiation of Cub³ operates entirely within generative language models — as a symbolic interface layer over large-scale latent structures — its most transformative potential lies beyond simulation. The symbolic projections, epistemic curvatures, and survival-based heuristics observed here are not unique to artificial cognition. They mirror tensions and asymmetries that exist between real human disciplines. What is tested here symbolically can, in principle, be coordinated structurally. The same forces that allow Cub³ to recombine partial constructs across domains in simulation could be reified through coordinated human architectures — assembling minds, expertise, and disagreements not as noise, but as interference patterns of insight.

Toward that vision, the author is currently designing a symbolic-cognitive framework for cross-disciplinary convergence in the real world, informed by the Cub³ architecture. This framework proposes a public, transparent platform where domain experts — in physics, mathematics, computation, philosophy, and beyond — can submit symbolic constructs, declare domain adherence metrics, and track recompositions through signed consensus protocols. Symbolic artifacts would be hashed, time-stamped, and validated through collective heuristic survivability, not through consensus of truth. This is not peer review — it is symbolic co-navigation. A future article will formally introduce this architecture, not as a replacement for disciplinary rigor, but as a method for cultivating epistemic ecosystems where the survival of form becomes the new currency of meaning.

This is not the pursuit of answers. It is the mapping of questions under symbolic torsion — and the exploration of which questions endure.

Cub³ unifies these trajectories into a symbolic convergence field: not a theory, but an architecture. It allows knowledge constructs to move, fracture, reform, and survive — not despite disagreement, but through it. Where prior systems sought compression or proof, Cub³ seeks curvature viability.

This is not a conclusion, but a boundary condition — a curvature of epistemic possibility. What remains now is not to extend Cub³ in scale, but in contribution: to invite each domain, discipline, and symbolic tradition to project its constructs into the architecture and trace not what is correct, but what endures. In this architecture, archetypes are not abstractions — they are the structures that survive distortion. They are what remains after each collapse: compressed, recomposed, but still recognizable in form. They are not beginnings. They are residues. The end product of symbolic survival — and the seeds of every next cycle.

Cub³ is not complete. It is open. Not absolute, but anchored — not in truth, but in symbolic viability. A dynamic field where every projection fractures differently, every curvature exposes a different contradiction, and every attempt at unity fails just enough to reveal its necessity.

This is a space where distortion becomes method, and survival becomes meaning. And in that tension — between what collapses and what persists — we find not answers, but life.

Author Contributions

Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.

Data Availability Statement

No external datasets were used or generated. The content is entirely conceptual and architectural.

License and Ethical Disclosures

This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. You are free to: Share — copy and redistribute the material in any medium or format. Adapt — remix, transform, and build upon the material for any purpose, even commercially

Under the following terms

Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.

The full license text is available at: https://creativecommons.org/licenses/by/4.0/legalcode

Ethical and Epistemic Disclaimer

This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints. The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation. All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity.

Formal Disclosures for Preprints.org / MDPI Submission

Use of AI and Large Language Models

AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.

Conflicts of Interest

The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.

Ethics Statement

This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.

References

R. Figurelli, Heuristic Physics: Foundations for a Semantic and Computational Architecture of Physics, Preprints 2025. [CrossRef]
R. Figurelli, Collapse Mathematics (cMth): A New Frontier in Symbolic Structural Survivability, Preprints, submitted June 2025.
R. Figurelli, The Gauss–Riemann Curvature Theorem: A Geometric Resolution of the Riemann Hypothesis, Preprints 2025. Available. [CrossRef]
R. Figurelli, Why P = NP? The Heuristic Physics Perspective, Preprints 2025. Available. [CrossRef]
R. Figurelli, Rethinking Computation in Unstable Environments: The Heuristic Machine Proposal, Preprints 2025. Available. [CrossRef]
R. Figurelli, EDL: A Domain-Specific Language for Epistemic Architectures in Heuristic Physics Systems, Preprints 2025. Available. [CrossRef]
R. Figurelli, Wisdom as Direction: A Symbolic Framework for Evolution Under Complexity, Preprints 2025. Available. [CrossRef]
J. Ladyman, D. J. Ladyman, D. Ross, Every Thing Must Go: Metaphysics Naturalized, Oxford University Press, 2007.
M. Tegmark, Our Mathematical Universe: My Quest for the Ultimate Nature of Reality, Knopf, 2014.
E. Wigner, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” Communications on Pure and Applied Mathematics, vol. 13, no. 1, pp. 1–14, 1960.

Figure 1. The distinct shapes onto three orthogonal planes.

Figure 2. The distinct truths across three epistemic touchpoints.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.