1. Introduction
At the dawn of the 20th century, physics found itself confronted by phenomena that defied classical explanation. The ultraviolet catastrophe of blackbody radiation and the photoelectric e!ect revealed that energy exchange comes in discrete quanta, shattering the classical wave theory of light. Planck’s postulate of energy quanta (1900)[
1] and Einstein’s explanation of the photoelectric e!ect (1905)[
2] introduced the radical idea that light can behave as particles, each carrying a quantum of energy
LM. By 1913, Bohr’s model of the atom invoked quantized electron orbits to explain atomic spectra,
further cementing the quantum paradigm. In 1922, the Stern–Gerlach experiment provided direct evidence of quantized atomic angular momentum (spin) by deflecting silver atoms into discrete beams[
3]. Evidence continued to mount: in 1914, Millikan’s meticulous experiments confirmed Einstein’s photoelectric equation to high precision[
4], and in 1923 Compton showed that X-rays scatter from electrons with particle-like momentum exchange[
5]. Quantum theory was no longer optional – it had become essential to make sense of nature.
Yet accepting quantization was only the beginning. Quantum mechanics, formulated in the mid-1920s by Schrödinger, Heisenberg, and others, departed starkly from classical intuitions. Its mathematical framework – wavefunctions, superposition, and a probabilistic interpretation of measurement outcomes – raised deep questions: Do quantum waves represent physical reality or just knowledge? When does a quantum possibility become a single outcome? Early debates raged between giants of the field. Niels Bohr and the Copenhagen interpretation emphasized that physical properties are undefined until measured – an unsettling break from realism – while Albert Einstein and others resisted, famously quipping that “God does not play dice” with the universe. Einstein sought a more complete description of reality, one that would remove the apparent randomness and instantaneity of quantum measurement.
From the beginning, then, interpretation was intertwined with experiment. Each time experi- menters probed a new corner of the quantum world, surprises forced reexamination of foundational assumptions. The double-slit interference experiment, for example, showed single electrons and photons behaving as waves until observed, embodying Bohr’s principle of complementarity. In 1927, Davisson and Germer observed electrons di!racting o! a crystal[
6], confirming de Broglie’s hypothesis that matter has waves. A few years later, at the 1927 Solvay Conference, Einstein proposed thought experiments to expose quantum oddities, which Bohr answered by invoking uncertainty and the disturbance of measurement. Alternative viewpoints also emerged: Louis de Broglie proposed in 1927 that each quantum particle is accompanied by a pilot wave guiding it along deterministic trajectories. This pilot-wave theory held onto realism and determinism, but it gained little traction at the time, as it made identical predictions to orthodox quantum mechanics in most situations and thus lacked distinguishing experimental evidence.
Over subsequent decades, as quantum theory triumphed in explaining atoms, nuclei, and solids, the Copenhagen view became the orthodox doctrine. Interpretation questions were often set aside as physicists focused on practical calculations. However, dissent never vanished. Einstein, with Podolsky and Rosen, would articulate a powerful critique in 1935[
7], arguing that quantum mechanics might be incomplete. Schrödinger, in the same year, devised his famous cat paradox to illustrate the absurdity of naively taking the theory to macroscopic scales. These challenges laid the groundwork for future experiments: real tests to determine whether the quantum world truly defies local realism and objective definiteness, or whether hidden explanations might exist.
In this review, we chronicle a series of pivotal experiments that have shaped the ongoing evolution of quantum interpretation. We proceed chronologically through the quantum epoch. Section II covers the early experiments that established the need for a quantum theory, from black- body radiation to Compton scattering and beyond. Section III examines experiments demonstrating wave-particle duality and the crucial role of observation, such as electron di!raction and interfer- ence. In Section IV, we discuss the challenge posed by entanglement and nonlocality through the Einstein-Podolsky-Rosen paradox and Bell’s theorem, and we review the landmark tests of Bell in- equalities that fundamentally altered our understanding of locality. Section V delves into Wheeler’s delayed-choice and the quantum eraser experiments, which probe the interplay of measurement and reality in time. Multi-particle interference phenomena and tests of hidden variable theories beyond Bell’s theorem are surveyed in Section VI. Section VII explores experiments pushing quantum phe- nomena to macroscopic scales and testing quantum realism – including studies of decoherence, the Leggett-Garg inequality, and the implications of Wigner’s friend scenarios. Finally, in Section VIII, we reflect on how these experiments have shaped current understanding and the interpretation of quantum mechanics.
2. Early Quantum Experiments and the Need for a New Theory
The first hints of a breakdown in classical physics came from thermal radiation. Experiments in the late 19th century showed that the spectrum of radiation emitted by a hot object (a blackbody) has a peak and falls o! at short wavelengths, contradicting the prediction of classical Rayleigh-Jeans theory which diverges in the ultraviolet (the “ultraviolet catastrophe”). In 1900, Max Planck found a formula that fit the blackbody spectrum perfectly by making a bold assumption: electromagnetic energy could only be emitted or absorbed in discrete packets, or quanta, of energy
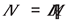
. Planck himself viewed this quantization as a mathematical trick, but in 1905 Einstein took the idea seriously to explain the photoelectric e!ect – the emission of electrons from a metal when light shines on it. Classical wave theory predicted that light of any frequency, if intense enough, should eventually eject electrons, and that higher intensity would yield higher electron energies. But experiments (notably by Philipp Lenard in 1902) revealed a di!erent behavior: electrons were only emitted if the light frequency exceeded a threshold, regardless of intensity, and the kinetic energy of emitted electrons depended on frequency, not intensity. Einstein proposed that light itself exists as quanta (later called photons), each with energy
LM, that could knock an electron out of the metal in a one-to-one collision[
2]. This explained why below a certain frequency no electrons emerge (photons lack the requisite energy) and why increasing the light intensity (more photons) increases the number of electrons but not their individual energies.
Einstein’s light-quantum hypothesis was radical, but it received striking experimental support.
Robert Millikan, initially skeptical of Einstein’s idea, undertook meticulous measurements of the photoelectric e!ect over several years. By 1914 he had verified Einstein’s linear relationship between the frequency of incident light and the maximum kinetic energy of ejected electrons, thereby determining an accurate value of Planck’s constant
L from the slope[
4]. Millikan’s results, published in 1916, left no doubt that the energy of light is packaged in quanta, vindicating Einstein’s theory (and earning Einstein the 1921 Nobel Prize in Physics for the photoelectric law).
Meanwhile, evidence of quantization was mounting in other areas. Niels Bohr’s atomic model (1913) successfully explained the discrete frequencies of spectral lines by assuming electrons in atoms occupy quantized orbits, emitting or absorbing photons when jumping between orbits. In 1914, James Franck and Gustav Hertz demonstrated directly that electrons lose specific, quantized amounts of energy when colliding with mercury atoms, corresponding to atomic transitions (an experimental vindication of Bohr’s quantized orbits)
1. Another puzzle was the specific heat of solids, which classical theory overestimated at low temperatures; in 1907 Einstein showed that assuming quantized vibrations of atoms (phonons) could resolve this discrepancy. Everywhere they looked, physicists found nature’s smooth continuum breaking into quantum chunks.
Perhaps the clearest early demonstration of quantization in a new domain was the Stern–Gerlach experiment of 1922. Otto Stern and Walther Gerlach sent a beam of silver atoms through a nonuniform magnetic field and observed that the beam split into two discrete spots on a detector screen[
3]. According to classical physics, the magnetic moments of the atoms (due to their electrons’ angular momentum) should be randomly distributed and produce a continuous smear on the screen. Instead, the atoms were deflected into either of two discrete angles, implying that their angular momentum was quantized. This experiment revealed the quantization of intrinsic angular momentum (what was later understood as electron “spin”) and provided concrete evidence that quantum-mechanical properties come in discrete units.
Further confirmation of the quantum idea came from X-ray scattering. In 1923, Arthur Compton aimed a beam of X-rays at carbon and found that the scattered X-rays had a longer wavelength (lower energy) than the incident radiation, with the wavelength shift depending on the scattering angle. This “Compton e!ect” could not be explained by classical wave theory, but Compton showed it was perfectly explained by treating the X-rays as particles (photons) that collide elastically with electrons, transferring energy and momentum[
5]. The photon concept successfully predicted the magnitude of the wavelength shift by invoking conservation of energy and momentum between a photon and an electron, analogous to two billiard balls colliding. Compton’s experiment thus provided direct evidence of photons carrying momentum
O = L/P, reinforcing the view that electromagnetic radiation has a dual particle-like nature.
By the mid-1920s, a compelling tapestry of experimental evidence had established that energy and even fundamental properties like atomic orientation are quantized. The successes of quantum ideas in explaining blackbody radiation, photoelectric emission, atomic spectra, and particle-like X-ray scattering made it clear that classical physics was incomplete. These findings set the stage for the formulation of a full quantum mechanics in 1925–1926 by Heisenberg, Schrödinger, and others. However, as the new theory took shape, it brought with it strange new conceptual challenges – wave-particle duality, uncertainty, and an inherent role of the observer – that would spark intense debates about what quantum mechanics really means.
3. Wave–Particle Duality and Observation
From the earliest days of quantum theory, it became clear that quantum objects possess a dual nature – exhibiting properties of both particles and waves. Which aspect is seen depends on how one looks. This wave–particle duality was vividly demonstrated by a series of interference experiments. Thomas Young had shown in 1801 that light produces interference fringes, evidence of a wave. In 1909, Geo!rey Taylor performed the double-slit experiment with extremely faint light, so that only one photon at a time passed through the slits. Remarkably, an interference pattern still emerged on the photographic plate after a long exposure[
8]. Each photon seemed to interfere with itself, suggesting it traveled through both slits as a wave – yet each photon was detected as an individual localized particle. This paradoxical behavior lies at the heart of quantum physics.
After Louis de Broglie proposed in 1924 that matter particles have waves associated with them, the wave nature of electrons was soon confirmed in the laboratory. In 1927, Clinton Davisson and Lester Germer observed that a beam of electrons reflected from a nickel crystal exhibited a di!raction pattern, exactly as X-rays (a wave) do[
6]. Independently, George Thomson (son of J. J. Thomson) obtained similar electron di!raction results the same year, emphatically verifying de Broglie’s hypothesis. A few decades later, in 1961, Claus Jönsson sent electrons through two closely spaced slits and observed interference fringes on a screen[
9] – a direct analog of Young’s double- slit with electrons instead of light. The electrons arrived at the detector one by one, as point-like impacts, yet the accumulation of many electrons recreated the classic interference pattern. Later experiments, such as those by Tonomura and colleagues in 1989, even recorded the build-up of an interference pattern electron-by-electron on film[
10], beautifully visualizing the wave–particle duality. Together, these experiments proved that electrons (and by extension all matter) can behave as coherent waves, producing interference, as well as individual particles.
The role of observation in determining how a quantum system behaves was dramatically high- lighted by these studies. If an experimental setup is arranged to observe interference (and does not reveal which path a particle takes), then wavelike behavior appears. However, the moment one attempts to gain which-way information – to detect through which slit an electron or photon goes – the interference pattern disappears. This is not merely a conjecture but has been confirmed whenever a measurement forces a choice of path. The act of measurement fundamentally disturbs the system, collapsing the delocalized wave into a definite particle path. Bohr elevated this insight to the principle of complementarity: the particle and wave aspects of a quantum system are mutually exclusive yet complementary, and both are needed for a complete description. In practice, a given experiment can show either interference (wave behavior) or definite particle trajectories, but never both at the same time.
This measurement e!ect is consistent with Heisenberg’s uncertainty principle, formulated in 1927. To determine which slit a particle goes through, one must interact with it (for instance, illuminating the slits to see the particle), unavoidably imparting a random momentum kick that scrambles the interference pattern
2. Thus, the appearance or disappearance of interference can be seen as a quantitative consequence of the uncertainty principle: precise knowledge of the path (position) trades away knowledge of the interference phase (momentum). Quantum theory encapsulates this in the idea that the wavefunction, which encodes superposed possibilities, is reduced (“collapsed”) to a single outcome when observed.
By the 1930s, experiments and thought-experiments on wave–particle duality had convinced most physicists of the correctness of the Copenhagen interpretation’s stance: one cannot speak of a quantum particle having a well-defined trajectory and an interference pattern simultaneously. The behavior observed depends on what the experiment is set up to measure. As we will see in later sections, this principle of measurement a!ecting reality would be tested in even more subtle ways by the quantum experiments of the late 20th century.
4. Entanglement and Nonlocality: EPR, Bell, and Experiments
In 1935, Einstein, Podolsky, and Rosen (EPR) published a bombshell paper arguing that quantum mechanics, as formulated, might be an incomplete theory[
7]. They considered a pair of particles prepared in a single quantum state such that their properties (for example, position and momentum, or spin components) are perfectly correlated. According to quantum mechanics, neither particle has a definite value for these properties before measurement – only a joint, entangled state. Yet if one measures one particle and instantaneously knows the corresponding property of the other (via the correlation), it seems the second particle’s wavefunction must have collapsed to a definite value at the same moment, no matter how far apart they are. To EPR, this “spooky action at a distance” implied that either information travels instantaneously (violating relativity), or that the particles carried pre-existing values (“elements of reality”) determining the outcomes. Since quantum theory provides no such definite values prior to measurement, EPR suggested the theory might be incomplete, and a more fundamental (perhaps local realist) theory could exist beneath it. Niels Bohr responded vigorously, defending the completeness of quantum mechanics and arguing that EPR’s notions of reality and locality were too classical. But the debate remained philosophical until 1964, when John Bell made a profound breakthrough. Bell discovered that the EPR argument could be put to experimental test[
11]. He derived an inequality – now called Bell’s inequality – that any local realistic theory (one wherein each particle has predetermined properties and no influence travels faster than light) must satisfy. Quantum mechanics, by contrast, predicts that entangled particles can violate this inequality under certain measurement settings. Bell’s theorem thus showed that no theory of nature that obeys locality and realism can reproduce all the predictions of quantum physics. If experiments violated Bell’s inequality, it would confirm the nonlocal character of quantum entanglement and force us to abandon local realism.
The first tests of Bell’s inequality were performed in the 1970s and early 1980s. In 1972, John Clauser and Stuart Freedman tested entangled photon polarization and found results consistent with quantum mechanics and in clear violation of the Bell inequality[
12]. Due to experimental limitations, their test had loopholes – conceivable escape routes for a local realist explanation. A decade later, in 1982, Alain Aspect and collaborators carried out a more stringent test using entan- gled photon pairs, with rapid switching of detector settings during flight to enforce locality. They too observed a strong violation of the inequality[
13]. Over the subsequent decades, experiments closed one loophole after another – improving detector efficiency, widening separation distances, using fast random setting choices – and the violations persisted. In 2015, a series of “loophole- free” experiments (using entangled electrons and high-efficiency detectors) finally simultaneously closed all remaining loopholes, definitively vindicating quantum mechanics at the expense of local hidden-variable theories[
14]. The empirical verdict was clear: nature is irreducibly nonlocal, in the sense that entangled particles coordinate their outcomes in ways that no exchange of signals (limited by the speed of light) could explain.
These remarkable experiments confirmed that entanglement is a real, physical phenomenon and not just a failure of imagination in the theory. In doing so, they vindicated the quantum view that the properties of particles are not pre-existing but are brought into being by measurement – even when those measurements are space-like separated. Any theory that hopes to reproduce quantum outcomes must abandon the principle of locality, as demonstrated by Bell’s theorem and its experimental confirmation. Notably, the idea of nonlocal hidden variables is realized in the de Broglie–Bohm pilot-wave theory (which is deterministic but overtly nonlocal), showing that determinism is not completely dead – but locality is. The triumph of entanglement experiments was recognized by the Nobel Prize in Physics 2022, awarded to Aspect, Clauser, and Zeilinger for their pioneering work. Today, entanglement not only underpins our understanding of quantum foundations, but also forms the basis of emerging technologies like quantum cryptography and quantum computing, further testament to its fundamental significance.
5. Delayed-Choice Experiments and Quantum Erasers
One of the most mind-bending questions raised by wave–particle duality is whether a quantum object’s behavior can be decided after it has entered an apparatus. In 1978, physicist John Wheeler proposed a “delayed-choice” thought experiment to probe this question[
15]. Wheeler imagined a single photon traveling through a two-path interferometer (like a Mach-Zehnder interferometer or double-slit setup) where the experimenter could choose at the last instant whether to fully close the interferometer (allowing interference) or to remove the second path beam splitter (forcing the photon to behave as if it went only one path). If the choice is made after the photon has already entered the setup, does the photon “know” whether to go through both paths (as a wave) or just one (as a particle)?
Quantum mechanics predicts that even if the choice is delayed, the photon’s behavior will still conform to the experimental arrangement – as if its prior state had no definite reality until the measurement context is decided. In the 2000s, delayed-choice experiments were realized in practice. In 2007, Vincent Jacques and colleagues performed Wheeler’s delayed-choice experiment with single photons in an interferometer, using a fast electro-optic shutter to change the setup at the last moment[
16]. The results showed that interference appears or disappears in accordance with the choice made, even though that choice is made after the photon has entered the interferometer. There is no way to ascribe a definite “wave” or “particle” behavior to the photon independent of the measurement context – the outcome is decided only when the experiment is run to completion. Closely related to delayed choice is the quantum eraser concept. In 1982, Marlan Scully and Kai Drühl proposed a thought experiment in which one could first acquire which-path information of a quantum particle and then “erase” that information, e!ectively restoring interference as if one had never observed the path[
17]. This idea was experimentally demonstrated by Yoon-Ho Kim and collaborators in 2000[
18]. In their quantum eraser experiment, a pair of entangled photons was used: one photon of the pair went through a double-slit (with a device marking its path), and the other photon (the “idler”) carried away the which-path information. By later making an appropriate measurement on the idler photon, the which-path information of its partner could be erased – and interference fringes were recovered in the sub-ensemble of partner photons conditioned on erasing the information. Astonishingly, the pattern emerges even though the “erasure” measurement was made at a time after the signal photons had already hit the detector.
These delayed-choice and eraser experiments do not actually send information backward in time or violate causality; rather, they illustrate that until all relevant observations are taken into account, we cannot say a quantum system has one behavior or another. The experimental choices and outcomes can be combined only at the end (for instance, by correlating the recorded signal photons with the later idler measurements in the quantum eraser) to reveal the interference. What these experiments underscore is the profound contextuality of quantum phenomena: the act of measurement – even when logically separated in time from the particle’s travel – determines the outcome, and quantum mechanics remains perfectly consistent when all is said and done. In short, the “delayed” choice of measurement simply underlines that a quantum system’s behavior is not set in stone until the measurement context is fully specified.
6. Beyond Bell’s Theorem: GHZ, Hardy, and Other No-Go Tests
Bell’s theorem was not the final word on testing the foundations of quantum mechanics. Researchers devised even more stringent theoretical scenarios and corresponding experiments that could expose conflicts with any hidden-variable theory, even those not constrained by Bell’s original assumptions. One famous example is the Greenberger–Horne–Zeilinger (GHZ) argument, proposed in 1989[
19]. The GHZ scenario involves three entangled particles and yields a definite logical contradiction between the predictions of quantum mechanics and the expectations of any local realistic theory – all without using inequalities or statistical arguments. In essence, the GHZ state produces correlated measurement outcomes that cannot be explained by assigning consistent pre-existing values to the particles. When the first experimental tests of three-particle entanglement were performed by Jian- Wei Pan and colleagues in 2000[
20], the results agreed exactly with quantum predictions, providing an even stronger refutation of local realism in the multi-particle regime.
Another approach beyond Bell’s original work was introduced by Lucien Hardy in 1992. Hardy found a paradoxical two-particle entanglement setup in which quantum mechanics predicts a small but nonzero probability of a joint outcome that is logically impossible under any local hidden-variable explanation[
21]. Unlike Bell’s inequality, which is violated by a statistical margin, Hardy’s paradox presents a qualitative contradiction: if certain outcomes are observed, it directly implies the failure of local realism (though the occurrence of these outcomes has low probability). In 1992, Hardy suggested this as a concept, and by 1997 he showed that an ideal entangled state could reach up to a 9% probability of demonstrating the paradox. In practice, experimental verification had to contend with less-than-ideal states. In 2005, an experiment by Toby Irvine and colleagues realized a photonic version of Hardy’s test, observing the paradoxical events in proportions consistent with quantum theory[
22]. Hardy’s paradox thus provided further evidence that no local hidden-variable explanation can mimic quantum entanglement, even in setups that di!er from the usual Bell inequality approach.
Researchers also explored whether relaxing the assumption of locality could save realism. A theoretical framework by Anthony Leggett in 2003 considered “nonlocal hidden-variable” models wherein entangled particles might influence each other (so nonlocality is allowed) but still have definite individual properties that obey certain constraints (for example, each photon’s polarization is assumed to have a definite value along any axis, albeit the pair’s outputs may be correlated in a nonlocal way)[
23]. Surprisingly, even these more permissive models make predictions (embodied in Leggett’s inequality) that di!er from standard quantum mechanics. In 2007, experimental tests by Stefanie Gröblacher et al. measured polarization correlations in entangled photon pairs to directly test Leggett’s nonlocal realist inequality. The quantum predictions were confirmed, and Leggett’s hypothetical models were decisively falsified[
24]. In other words, allowing entanglement to be nonlocal but insisting on objective individual properties still could not reproduce the quantum results. Reality, as far as experiments have shown, does not adhere to the intuitive classical idea of particles carrying their own definite values for all properties – even if one permits faster-than-light connections.
Through these multi-particle interference experiments and extended theoretical tests, physicists have progressively tightened the net around possible alternatives to quantum mechanics. Every empirical violation of a would-be hidden-variable inequality further solidified the view that quantum entanglement has no parallel in classical physics – it is sui generis. The only loopholes left for a hidden-variable proponent are extremely contrived options (such as superdeterminism, which assumes measurement settings are themselves pre-determined in correlation with hidden variables in just the right way) that many consider philosophically unpalatable. By the end of the 2000s, thanks to GHZ states, Hardy’s paradox, and Leggett-type inequalities, the evidence overwhelmingly supported the orthodox quantum description: correlations have no explanation in any theory that preserves a classical picture of independent elements of reality. Quantum mechanics stood, and still stands, as the only theory that fully accounts for these experimental facts.
7. Quantum Phenomena at Macroscopic Scales and the Ob- server’s Role
While most entanglement and interference tests involve microscopic systems, a key question is whether quantum principles hold unscathed as we move toward the macroscopic realm of everyday objects. Do wavefunctions “collapse” spontaneously beyond a certain scale, or can superpositions persist if environmental decoherence is suppressed? A suite of experiments over the past few decades suggests that quantum weirdness does extend surprisingly far toward the macroscopic. In 1999, Markus Arndt and collaborators sent C
60 fullerene molecules (each containing 60 carbon atoms) through a double-slit and observed a clear interference pattern[
27]. Each C
60 molecule has a mass of about 1.2 → 10↑24 kg – vastly larger than an electron – yet it exhibited wave-like delocalization. Subsequent experiments pushed this boundary further: by 2019, interference had been demonstrated for organic molecules with over 2,000 atoms (mass
> 25
, 000 amu) in a high-vacuum interferometer[
30]. No fundamental breakdown of quantum superposition has been observed, only practical limitations (molecules become harder to keep coherent). These results place stringent limits on hypothetical “spontaneous collapse” theories, which posit that wavefunctions might randomly collapse for large systems.
Another approach to probing the quantum-classical boundary is through time-domain tests of “macrorealism” – the notion that a system at macroscopic scales exists in a definite state at all times, and that measurements can simply reveal those pre-existing states without a!ecting them. In 1985, Anthony Leggett and Anupam Garg formulated an inequality (analogous to Bell’s inequality) that any macrorealistic theory should obey[
25]. Quantum mechanics, by contrast, permits coherent superpositions that violate this Leggett–Garg inequality. Multiple experiments have tested this idea by examining quantum coherence in circuits and other mesoscopic devices over time. In 2010, for instance, a team led by Anindya Palacios-Laloy performed a Leggett–Garg test using a superconducting quantum circuit (a “macroscopic qubit”) and weak measurements that minimally disturbed the system[
26]. The observed correlations violated the Leggett–Garg inequality, indicating that the qubit did
not behave as if it had a single pre-existing state at all times between measurements. Instead, the quantum superposition persisted, even for this circuit involving billions of electrons. Such experiments reinforce that there is no obvious point where a quantum system “switches over” to classical behavior – quantum coherence can extend to systems large enough to be nearly macroscopic, so long as they are sufficiently isolated from environmental noise.
To understand why we don’t see Schrödinger’s cats in everyday life, physicists have studied the process of decoherence – the rapid entanglement of a system with its environment, which destroys interference. A milestone experiment in 1996 by Michel Brune and colleagues managed to observe the gradual decoherence of a “Schrödinger’s cat” state in the laboratory[
28]. In their setup, a single Rydberg atom was used to prepare a coherent superposition of two opposite-phase states of a microwave field in a superconducting cavity (a mesoscopic superposition of a few photons). As these field states interacted with resonant atoms (playing the role of an environment), the coherence between the two components decayed over time. By carefully measuring the field after various delay times, Brune
et al. were able to track the continuous transition from a pure quantum superposition to an incoherent mixture – essentially watching the collapse of the “cat” state due to controlled decoherence. This experiment gave direct insight into how classical reality emerges from quantum possibilities when a system is no longer isolated.
Another fundamental question is whether quantum mechanics remains universally valid when applied to observers themselves. Eugene Wigner famously pondered this with his “Wigner’s friend” thought experiment: if a friend in a sealed lab observes a quantum event, collapsing its wavefunction, can an outside observer still describe the entire lab (friend included) as being in a superposition of di!erent outcomes? In 2019, a striking experiment by Massimiliano Proietti
et al. took a step toward probing this scenario[
29]. The experiment e!ectively realized a two-observer situation using entangled photons: one pair of “observers” (measuring devices acting as proxies for friends) made polarization measurements inside two separate labs, while another pair of observers outside the labs measured correlations between the results. The results showed that all observers, each applying quantum mechanics to their own perspective, obtained outcomes consistent with quantum predictions – even though the assumptions of objective, observer-independent facts would lead to a contradiction. In essence, the experiment suggests that two di!erent observers can irreconcilably disagree on what happened to a quantum system, within the bounds of quantum uncertainty, and both be correct from their own viewpoints.
Although interpreting such “observer-dependent” outcomes is subtle and remains controversial, these studies highlight that quantum measurement and the nature of reality are still not fully resolved issues. What is clear is that every experiment to date – from the smallest particles to mesoscopic fields and molecular interferometers – has upheld the quantum mechanical framework. No definite scale of “collapse” or failure of superposition has been found. Quantum mechanics appears to apply universally, but it forces us to rethink intuitions about realism and objectivity when observers are involved. As experimental capabilities continue to improve, pushing quantum tests to larger scales and more complex systems (even towards living organisms or quantum gravity regimes), we may yet learn whether there is a boundary to the quantum world or whether, as current evidence indicates, the only boundaries are those imposed by practical decoherence.
8. Conclusion and Outlook
From the early 20th-century puzzles that launched quantum theory, to the precision tests of entan- glement and macroscopic quantum phenomena today, experiments have continuously driven and refined our interpretation of quantum mechanics. We have seen how each landmark experiment forced physicists to let go of cherished classical intuitions – whether it was the idea of light as a continuous wave, the notion of local causality, or the belief that macroscopic objects have defini- tively real properties independent of observation. Quantum mechanics, buttressed by all these experimental victories, demands a radical worldview: one in which probability and superposition are fundamental, objects do not have definite attributes until measured, and distant events can be eerily correlated beyond any classical explanation.
These experiments have not only confirmed the quantum formalism with astonishing accuracy, but also ruled out broad classes of alternative theories. The dream of local hidden variables died with the violation of Bell’s inequalities. The hope that some subtle “macro-realism” might save classical intuition faded with tests of Leggett–Garg inequalities and demonstrations of long-lived quantum coherence in mesoscopic systems. Even proposals that modify quantum mechanics – such as spontaneous collapse models – have been pushed into increasingly implausible corners by molecular interference experiments that show no sign of such collapse. In short, any theory that looks too much like our classical worldview has been very hard to keep alive in the face of experimental facts.
And yet, the meaning of quantum mechanics is not fully settled. The experimental evidence has eliminated certain interpretative possibilities (like naive local realism), but it still permits a range of interpretations that are all consistent with current data. The Copenhagen interpretation – pragmatic and instrumentalist – continues to be used successfully by working physicists, essentially asserting that quantum mechanics is complete and one should not ask “unphysical” questions about reality between measurements. The de Broglie–Bohm pilot-wave theory retains a realist picture with particles guided by a nonlocal wave, and it survives empirically by design (at the cost of explicit nonlocality, which experiments show is necessary). The many-worlds interpretation (Everett’s theory) sidesteps collapse altogether, suggesting that all outcomes occur in branching universes – a view that is hard to confirm or refute experimentally but which remains consistent with the violation of Bell’s inequality and other tests, since it too forsakes any Einsteinian locality in a single world. Newer approaches like QBism or relational quantum mechanics question the very objectivity of quantum outcomes, resonating with scenarios like the Wigner’s friend experiment where di!erent observers can have di!erent accounts of events. None of these interpretations conflict with any experiment performed so far; they mainly diverge in what they regard as “real” or in the philosophical baggage they carry. Future experiments – perhaps probing quantum gravity, or producing even larger superpositions, or testing novel realms – might one day provide clues favoring one interpretation over another, but for now, the experimental facts have only solidified the strange baseline that any viable interpretation must accept.
The journey through these historical and contemporary experiments shows science at its best: confronting perplexing questions about reality with clever experimentation, and letting nature inform our worldview. Quantum mechanics emerged from experiments and has been continually challenged by them, only to emerge stronger and stranger each time. Over more than a century, we have gone from doubting the reality of atoms to manipulating single atoms at will; from debating whether God plays dice to generating genuine randomness for quantum cryptography; from pondering spooky action at a distance to harnessing entanglement in quantum networks. Each experiment that “changed interpretation” has in fact deepened our appreciation of the quantum world’s richness. As the field moves forward, quantum experiments will keep testing the limits of the theory – and whatever new phenomena we find, they will further shape our understanding, ensuring that the dialogue between experiment and interpretation remains as lively as ever.
References
- M. Planck, Über das Gesetz der Energieverteilung im Normalspektrum, Ann. Phys. 309, 553, (1901).
- Einstein, On a heuristic point of view concerning the production and transformation of light, Ann. Phys. 17, 132 (1905).
- W. Gerlach and O. Stern, Der experimentelle Nachweis der Richtungsquantelung im Magnet- feld, Z. Phys. 9, 349 (1922).
- R. A. Millikan, A Direct Photoelectric Determination of Planck’s “L”, Phys. Rev. 7, 355 (1916).
- H. Compton, A Quantum Theory of the Scattering of X-rays by Light Elements, Phys. Rev. 21, 483 (1923).
- Davisson and L. H. Germer, Di!raction of electrons by a crystal of nickel, Phys. Rev. 30, 705 (1927).
- Einstein, B. Podolsky, and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Phys. Rev. 47, 777 (1935).
- G. I. Taylor, Interference Fringes with Feeble Light, Proc. Cambridge Phil. Soc. 15, 114 (1909).
- Jönsson, Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten, Z. Phys. 161, 454 (1961).
- Tonomura, J. Endo, T. Matsuda, T. Kawasaki, and H. Ezawa, Demonstration of single- electron buildup of an interference pattern, Am. J. Phys. 57, 117 (1989). [CrossRef]
- J. S. Bell, On the Einstein Podolsky Rosen paradox, Physics 1, 195 (1964).
- S. J. Freedman and J. F. Clauser, Experimental test of local hidden-variable theories, Phys. Rev. Lett. 28, 938 (1972). [CrossRef]
- Aspect, P. Grangier, and G. Roger, Experimental Realization of Einstein-Podolsky-Rosen- Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities, Phys. Rev. Lett. 49, 91 (1982).
- Hensen et al., Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres, Nature 526, 682 (2015).
- J. A. Wheeler, The “Past” and the “Delayed-Choice” Double-Slit Experiment, in Mathemat- ical Foundations of Quantum Theory, edited by A. R. Marlow (Academic, 1978), p. 9.
- V. Jacques et al., Experimental realization of Wheeler’s delayed-choice Gedankenexperiment, Science 315, 966 (2007).
- M. O. Scully and K. Drühl, Quantum eraser: A proposed photon correlation experiment concerning observation and “delayed choice” in quantum mechanics, Phys. Rev. A 25, 2208 (1982). [CrossRef]
- Y.-H. Kim, R. Yu, S. P. Kulik, Y. Shih, and M. O. Scully, Delayed choice quantum eraser, Phys. Rev. Lett. 84, 1 (2000).
- M. Greenberger, M. A. Horne, and A. Zeilinger, Going beyond Bell’s theorem, in Bell’s Theorem, Quantum Theory, and Conceptions of the Universe, edited by M. Kafatos (Kluwer, 1989), p. 69.
- J.-W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter, and A. Zeilinger, Experimental test of quantum nonlocality in three-photon GHZ entanglement, Nature 403, 515 (2000).
- L. Hardy, Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories, Phys. Rev. Lett. 68, 2981 (1992). [CrossRef]
- W. T. M. Irvine, J. F. Hodelin, C. Simon, and D. Bouwmeester, Realization of Hardy’s thought experiment with photons, Phys. Rev. Lett. 95, 030401 (2005). [CrossRef]
- J. Leggett, Nonlocal hidden-variable theories and quantum mechanics: An incompatibility theorem, Found. Phys. 33, 1469 (2003).
- S. Gröblacher et al., An experimental test of non-local realism, Nature 446, 871 (2007). [CrossRef]
- J. Leggett and A. Garg, Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks?, Phys. Rev. Lett. 54, 857 (1985).
- Palacios-Laloy et al., Experimental violation of a Bell’s inequality in time with weak measurement, Nature Phys. 6, 442 (2010).
- M. Arndt et al., Wave–particle duality of C60 molecules, Nature 401, 680 (1999).
- M. Brune et al., Observing the progressive decoherence of the “meter” in a quantum mea- surement, Phys. Rev. Lett. 77, 4887 (1996).
- M. Proietti et al., Experimental test of local observer independence, Sci. Adv. 5, eaaw9832 (2019). [CrossRef]
- Y. Y. Fein et al., Quantum superposition of molecules beyond 25 kDa, Nat. Phys. 15, 1242 (2019). [CrossRef]
Notes
| 1 |
Franck and Hertz reported that electrons accelerated through a vapor of mercury would only lose kinetic energy in specific quanta, causing a drop in current at certain voltages – evidence that atoms can only absorb fixed energy amounts. Their experiment provided one of the earliest direct confirmations of discrete quantum energy levels. |
| 2 |
Heisenberg illustrated this with his Q-ray microscope thought experiment, showing that any attempt to pinpoint an electron’s path with high-energy light would scatter the electron and disturb its momentum enough to destroy interference. |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
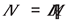 . Planck himself viewed this quantization as a mathematical trick, but in 1905 Einstein took the idea seriously to explain the photoelectric e!ect – the emission of electrons from a metal when light shines on it. Classical wave theory predicted that light of any frequency, if intense enough, should eventually eject electrons, and that higher intensity would yield higher electron energies. But experiments (notably by Philipp Lenard in 1902) revealed a di!erent behavior: electrons were only emitted if the light frequency exceeded a threshold, regardless of intensity, and the kinetic energy of emitted electrons depended on frequency, not intensity. Einstein proposed that light itself exists as quanta (later called photons), each with energy LM, that could knock an electron out of the metal in a one-to-one collision[2]. This explained why below a certain frequency no electrons emerge (photons lack the requisite energy) and why increasing the light intensity (more photons) increases the number of electrons but not their individual energies.
. Planck himself viewed this quantization as a mathematical trick, but in 1905 Einstein took the idea seriously to explain the photoelectric e!ect – the emission of electrons from a metal when light shines on it. Classical wave theory predicted that light of any frequency, if intense enough, should eventually eject electrons, and that higher intensity would yield higher electron energies. But experiments (notably by Philipp Lenard in 1902) revealed a di!erent behavior: electrons were only emitted if the light frequency exceeded a threshold, regardless of intensity, and the kinetic energy of emitted electrons depended on frequency, not intensity. Einstein proposed that light itself exists as quanta (later called photons), each with energy LM, that could knock an electron out of the metal in a one-to-one collision[2]. This explained why below a certain frequency no electrons emerge (photons lack the requisite energy) and why increasing the light intensity (more photons) increases the number of electrons but not their individual energies.



