Chronon Cosmogenesis: The Emergence of Spacetime, Matter, and Symmetry from Causal Topology

1. Introduction

Symmetry principles underpin the foundations of modern physics. Among the most profound are Lorentz invariance, CPT symmetry, and the apparent balance between matter and antimatter in quantum field theory [6,22]. Yet, our universe exhibits subtle and puzzling asymmetries: time has a definite arrow, matter dominates over antimatter [20], and high-precision experiments continue to probe the limits of Lorentz symmetry [11,25]. These empirical observations raise a fundamental question: Are these asymmetries fundamental, or do they emerge from deeper, perhaps topological, structures of spacetime and time itself?

In this work, we explore these questions in the framework of Chronon Field Theory (CFT), a novel approach in which time is not an external parameter but a physical, dynamical field. The Chronon field ${\Phi }^{\mu }\left(x\right)$, defined as a smooth, unit-norm, future-directed timelike vector field, induces a causal foliation of spacetime and encodes the local direction and rate of temporal flow. When globally aligned, this field defines a preferred frame—the Real Now—which spontaneously breaks global Lorentz invariance. Importantly, this symmetry breaking is dynamical and emerges from the causal structure itself [13].

We demonstrate that this causal selection leads to small but generically unavoidable violations of exact Lorentz symmetry, tightly linked to the large-scale alignment of ${\Phi }^{\mu }$ with the cosmic microwave background (CMB) frame [11,13]. Furthermore, we show that in CFT, the conventional CPT theorem no longer holds at the fundamental level, but instead arises as an effective symmetry in the weak-field, semiclassical limit where the Chronon field is approximately uniform [6,13].

Building on this foundation, we propose a new mechanism for the matter–antimatter asymmetry observed in the universe. This mechanism is rooted in the spontaneous breaking of Lorentz invariance by the Chronon field. The global alignment of ${\Phi }^{\mu }$ defines a time direction that biases the formation of topological solitons—localized, quantized field configurations whose winding number w can be interpreted as fermionic ($w=\pm 1$) or bosonic ($w=0$) precursors. This topological asymmetry in soliton production naturally favors matter over antimatter without requiring explicit CP-violating terms [13].

Finally, we extend this framework to argue that charge conjugation symmetry (C) itself may be dynamically broken at the level of soliton interactions in the presence of the Real Now. This provides a unified topological and causal explanation for multiple broken symmetries in the observable universe [13].

2. The Real Now and Spontaneous Lorentz Violation

In Chronon Field Theory, the fundamental object is a timelike unit-norm vector field ${\Phi }^{\mu }\left(x\right)$, which defines the local arrow and rate of time throughout spacetime. Rather than treating time as an external parameter or coordinate, CFT elevates it to a dynamical entity intrinsic to the manifold [13]. The Chronon field satisfies the constraints:

$$\begin{array}{cc}\hfill {\Phi }^{\mu }{\Phi }_{\mu }& =-1,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\Phi }^0& >0,\hfill \end{array}$$

(2)

ensuring that it lies on the upper sheet of the unit hyperboloid ${\mathbb{H}}_{+}^3\subset TM$ at each point in spacetime. This field defines a preferred causal structure and allows for a global foliation of spacetime by hypersurfaces orthogonal to ${\Phi }^{\mu }$, which we call the Real Now [13].

This preferred foliation spontaneously breaks global Lorentz invariance, not by imposing an external frame, but through the dynamical alignment of ${\Phi }^{\mu }$ during the evolution of the universe [11,13]. While local Lorentz invariance remains intact in the neighborhood of any spacetime point (due to the smoothness and locality of ${\Phi }^{\mu }$), the global symmetry is broken by the existence of a distinguished, globally consistent direction of time.

Remarkably, this preferred direction is empirically aligned with the rest frame of the cosmic microwave background (CMB) [8], suggesting that the Real Now is comoving with the large-scale temporal structure of the universe. This observation implies that the Chronon field might have relaxed dynamically toward alignment with the dominant thermodynamic arrow of time during the early universe, possibly through a form of causal symmetry breaking [13].

The implications of this spontaneous Lorentz violation are subtle. Since the Chronon field is not an observable quantity in the standard sense (it is a geometric structure rather than a material field), its effects manifest only through coupling to solitonic configurations, quantum phase evolution, or gravitational backreaction [11]. Nonetheless, this alignment introduces the possibility of tiny, frame-dependent effects, including:

• anisotropies in the dispersion relations of fundamental excitations,
• directional modulation in phase shifts or interference patterns,
• temporal alignment-induced polarization rotation in cosmological light paths,
• and slight deviations in inertial frame symmetry in atomic clock comparisons [7,25].

In subsequent sections, we will explore how this foliation not only induces Lorentz-violating structure but also leads to effective symmetry breaking in CPT and charge conjugation, ultimately contributing to the observed matter–antimatter imbalance.

3. CPT as an Emergent Symmetry

The CPT theorem is one of the foundational results of conventional quantum field theory, establishing that any local, Lorentz-invariant, unitary theory must be invariant under the combined operation of charge conjugation (C), parity inversion (P), and time reversal (T) [22]. This result depends crucially on Poincaré invariance, the analyticity of correlation functions, and the operator algebra structure of quantum fields. However, Chronon Field Theory departs significantly from these assumptions [13].

In CFT, the fundamental structure is not a set of quantized operator-valued fields, but a classical, causal vector field ${\Phi }^{\mu }\left(x\right)$ that determines the local direction and rate of time. Quantum behavior emerges not from canonical quantization, but from topologically quantized solitonic configurations and geometric phase evolution over configuration space [13]. As such, the analytic continuation and symmetry properties that underlie the traditional CPT proof do not apply [6].

Instead, CPT symmetry in CFT arises as an emergent symmetry in the limit where the Chronon field is weakly varying and nearly uniform. In this regime, the foliation defined by ${\Phi }^{\mu }$ becomes approximately flat, and local Poincaré symmetry is recovered as an effective description. Solitonic excitations in this background approximately satisfy the transformation properties of conventional fermions and bosons under discrete symmetries, including CPT [13].

However, in strongly curved or topologically nontrivial Chronon configurations—such as those present in the early universe or near gravitational singularities—CPT symmetry can be broken. This occurs not through explicit Lagrangian terms, but through the geometry and topology of the underlying temporal structure [13]. For instance, soliton dynamics on a Chronon background with nontrivial winding may lead to phase evolution that fails to reverse under time inversion, or to effective interactions that distinguish matter from antimatter in a CPT-asymmetric fashion.

Thus, in CFT, CPT symmetry is not a fundamental axiom, but a low-energy, flat-background approximation. The arrow of time, encoded in ${\Phi }^{\mu }$, provides a causal bias that allows for genuine CPT-violating phenomena in the early universe or in topologically complex regions of spacetime. This viewpoint suggests that CPT conservation is not an exact symmetry of nature, but an emergent property of temporal coherence.

3.1. Emergence vs. Explicit Violation

A crucial distinction in interpreting the results of Chronon Field Theory lies in differentiating between explicit symmetry violation and emergent symmetry breakdown [6,13]. In conventional approaches, violations of Lorentz or CPT symmetry are often modeled by introducing additional terms into the Lagrangian that break these symmetries at a fundamental level. Such modifications represent explicit symmetry violation—they alter the defining dynamics of the theory itself.

In contrast, the departures from CPT and Lorentz invariance observed in CFT are not inserted by hand but arise naturally from the causal and topological configuration of the Chronon field. Lorentz symmetry is spontaneously broken by the global alignment of ${\Phi }^{\mu }\left(x\right)$, which selects a preferred temporal direction—the Real Now. This alignment does not alter the local structure of spacetime but introduces a global foliation that biases causal relations on cosmological scales [13].

Similarly, CPT symmetry is not violated through a term in the action but fails to hold in regimes where the Chronon field exhibits strong curvature, topological winding, or discontinuities across causal domains. In these rugged configurations, the underlying assumptions of the CPT theorem—analyticity, locality, and Lorentz invariance—do not apply. Instead, CPT symmetry emerges as an effective feature of smooth, semiclassical configurations of ${\Phi }^{\mu }$, where global anisotropies and topological features are negligible [13].

Thus, the symmetry breakings described in this framework are not dynamical in the traditional field-theoretic sense, but geometric and structural in origin. They arise from the configuration of time itself and are deeply rooted in the ontological role that ${\Phi }^{\mu }$ plays in defining causality and physical evolution. This perspective provides a consistent and testable interpretation of Lorentz and CPT asymmetries as emergent rather than explicitly broken phenomena.

4. Topological Bias and the Matter–Antimatter Asymmetry

One of the most striking observational facts in cosmology is the overwhelming dominance of matter over antimatter. Despite the fundamental symmetries of known particle physics, the early universe appears to have evolved in a way that favored baryonic matter. In conventional frameworks, this requires explicit CP-violating interactions, baryon number violation, and a departure from thermal equilibrium—conditions known as the Sakharov criteria [20].

In Chronon Field Theory, a different mechanism is available [13]. Since matter is not modeled as fundamental fields but as topologically stable solitonic configurations of the Chronon field ${\Phi }^{\mu }\left(x\right)$, the relative abundance of matter versus antimatter can arise from the topology and causal structure of spacetime itself. In particular, each soliton configuration is characterized by a topological winding number $w\in {\pi }_3\left(S^3\right)\cong \mathbb{Z}$, associated with the mapping of compactified space into the unit hyperboloid target manifold of the Chronon field [14].

The Real Now foliation introduces a preferred temporal orientation throughout the universe. This orientation creates a subtle topological bias in the formation of solitons during the early universe. Specifically, positive-winding solitons ($w=+1$) may be dynamically favored over negative-winding solitons ($w=-1$), as their alignment is more coherent with the globally defined direction of time. This asymmetry is not imposed by hand but emerges from the interplay of topology, causal coherence, and thermal history [13].

Moreover, because the solitonic configurations evolve along the integral curves of ${\Phi }^{\mu }$, the Berry phase accumulated along closed trajectories in configuration space depends on the sign of w [21]. If the phase evolution associated with $w=+1$ configurations is energetically more stable or dynamically less suppressed, then matter solitons will outnumber their antimatter counterparts.

This topological bias provides a natural explanation for the observed matter–antimatter asymmetry without invoking fine-tuned CP-violating terms in the Lagrangian. It also satisfies the Sakharov criteria in a novel way:

• Baryon number violation: Soliton number is topological and not strictly conserved under Chronon-mediated dynamics.
• CP violation: Emerges effectively from the causal asymmetry induced by the Real Now.
• Departure from equilibrium: Follows from the global temporal alignment and early-universe Chronon turbulence [13].

Thus, Chronon Field Theory offers a topological and geometric resolution of one of the most persistent puzzles in modern cosmology: why there is something rather than nothing, and why that something is made of matter.

5. Charge Conjugation Symmetry Breaking in Soliton Dynamics

Charge conjugation (C) symmetry, which maps particles to their corresponding antiparticles, is typically assumed to be preserved at the level of fundamental interactions unless explicitly broken. However, within the framework of Chronon Field Theory, we propose that C-symmetry can be dynamically broken, not through explicit Lagrangian terms, but as a consequence of the asymmetric evolution of soliton configurations in a temporally aligned background [13].

In CFT, solitons and antisolitons correspond to topological configurations with opposite winding numbers. However, these are not strictly mirror images under charge conjugation, because their dynamical evolution is governed by the local and global structure of the Chronon field ${\Phi }^{\mu }\left(x\right)$. When ${\Phi }^{\mu }$ is globally aligned in a preferred direction—as established by the Real Now—this asymmetry influences not only the creation rates of solitons versus antisolitons but also their interaction dynamics.

One key effect arises from the differential coupling between soliton worldlines and the background temporal flow. Positive-winding solitons tend to align with ${\Phi }^{\mu }$, allowing them to propagate and interact with minimal phase resistance. In contrast, antisolitons (with negative winding) move against the direction of causal flow, encountering phase misalignment that leads to suppressed propagation, shorter coherence lengths, or enhanced decay channels [13].

Furthermore, soliton–antisoliton interactions may not be invariant under C if the effective configuration space contains geometric phases or path-dependent holonomies induced by ${\Phi }^{\mu }$ [21]. For example, two solitons may fuse or scatter with a different phase signature than a soliton and antisoliton pair, breaking the degeneracy expected under charge conjugation.

This mechanism of C-violation is qualitatively distinct from the perturbative approach in standard field theory. It is not associated with explicit charge-asymmetric terms in the action, but with the emergent, topologically induced asymmetries in the configuration space and causal dynamics of the Chronon field. As such, it offers a compelling and natural explanation for the imbalance between matter and antimatter that complements the topological bias discussed previously.

In summary, Chronon Field Theory predicts a dynamical, interaction-level breaking of C-symmetry rooted in the causal topology of time [13]. This extends the theory’s explanatory power to a broader class of observed asymmetries and reinforces its promise as a candidate framework for foundational physics.

6. Chiral Asymmetry and Temporal Shear Orientation

In addition to the CPT and matter–antimatter asymmetries discussed above, Chronon Field Theory (CFT) offers a natural mechanism for the emergence of chiral asymmetry in the weak interaction. This asymmetry—the fundamental preference for left-handed over right-handed fermions in weak decays—is a well-established experimental fact, yet remains puzzling in the Standard Model, where it is effectively imposed by hand through gauge representations [24].

CFT explains chiral asymmetry as a consequence of anisotropic shear in the Chronon field [13]. While the Chronon field ${\Phi }^{\mu }\left(x\right)$ defines a preferred local direction of temporal flow, small transverse shears—encoded in derivatives orthogonal to ${\Phi }^{\mu }$—give rise to locally twisted configurations that break parity symmetry dynamically. These shear deformations correspond to spacetime-dependent misalignments between neighboring temporal flow vectors, effectively defining a handedness.

We define the antisymmetric temporal shear tensor:

$$S_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu },$$

(3)

whose nonzero spatial components induce parity-violating backgrounds in the effective action. Coupling spinor fields to this shear tensor generates chirality-dependent interaction terms of the form:

$${\mathcal{L}}_{\mathrm{chiral}}=\overline{\psi }{\gamma }^{\mu }{\gamma }^5\psi {\omega }_{\mu },$$

(4)

where ${\omega }_{\mu }$ is an axial vector constructed from the curl or torsion of ${\Phi }^{\mu }$. This term behaves analogously to axial gauge fields in models of chiral anomaly [9], but arises here from spacetime geometry rather than internal symmetry.

In the early universe, during the stage of rapid Chronon alignment, spatial shear anisotropies are amplified by nonlinear dynamics and topological fluctuations. As solitons nucleate and stabilize in this temporally sheared background, their chirality becomes locked to the local handedness of the Real Now’s gradient structure. This selects left-handed modes as dynamically favored excitations, seeding the chiral asymmetry observed in electroweak processes [13].

This mechanism has several key implications:

• Chiral asymmetry is not externally imposed but emerges from the directional coherence of time flow.
• The handedness of weak interactions traces back to a dynamical feature of temporal geometry.
• Chiral currents could potentially couple to residual Chronon shear in the present epoch, leading to small parity-violating effects beyond the Standard Model [11].

In summary, the observed chiral structure of the weak interaction can be reinterpreted as a fossil record of temporal shear anisotropies imprinted during cosmogenesis, consistent with the broader causal-topological framework of Chronon Field Theory.

7. Chronon Cosmogenesis: A Symmetry-Breaking Account of the Universe’s Emergence

In Chronon Field Theory (CFT), the emergence of the universe unfolds through a sequence of spontaneous symmetry breakings, beginning not with matter or quantum fields, but with the alignment of time itself [13]. Unlike conventional Big Bang cosmology, which posits an initial high-energy plasma populated by matter and radiation, CFT envisions a smooth, pre-matter phase defined by the causal structure of a dynamical temporal field.

7.1. Stage I: Temporal Genesis and Causal Alignment

The fundamental field in CFT is the Chronon vector field ${\Phi }^{\mu }\left(x\right)$, a smooth, future-directed, unit-norm timelike vector that endows each spacetime point with an intrinsic arrow of time. In the earliest phase of the universe, this field aligns spontaneously across expanding causal horizons, giving rise to a global foliation we call the Real Now. This initial alignment constitutes a spontaneous breaking of global Lorentz invariance, establishing a preferred frame comoving with the cosmological expansion [13].

At this stage, the universe is purely geometric: no matter, no particles, no entropy. It is a dynamical but smooth background where time flows but matter has not yet emerged.

7.2. Stage II: Topological Instability and Soliton Burst

As the Chronon field continues to evolve, long-range coherence and finite-size effects induce a phase transition. The field becomes unstable to topological deformations, and localized solitonic excitations—quantized field configurations with nonzero winding number $w\in {\pi }_3\left(S^3\right)$—emerge abruptly in a second-stage burst [12,13,26].

Numerical simulations confirm this behavior: a period of causal alignment is followed by a sudden proliferation of solitons with $w=\pm 1,\pm 2$, forming across spatially separated domains. This burst-like event resembles a Kibble-Zurek process, where topological defects nucleate stochastically in disconnected causal patches. Importantly, the burst is not thermal; it is driven by topology and the internal dynamics of the Chronon field, not by pre-existing matter or radiation.

7.3. Stage III: Symmetry Breaking Cascade

The soliton burst breaks several additional symmetries:

• CPT Emergence: The apparent CPT symmetry of low-energy quantum field theory arises only in the smooth, semiclassical limit of Chronon dynamics. It is not fundamental.
• C Violation: Soliton propagation is asymmetric under $w\to -w$, due to alignment with the global Chronon direction.
• Matter–Antimatter Asymmetry: A small but persistent bias in soliton formation ($ϵ\sim {10}^{-9}$) yields the observed baryon asymmetry.
• Chiral Asymmetry: Because ${\Phi }^{\mu }$ is a vector field with causal orientation, its coupling to emergent fermionic modes naturally induces chiral biases in early interactions.

This cascade of symmetry breaking reframes early-universe cosmology not as a thermodynamic process, but as a causal-topological evolution, where the physical content of the universe arises from the geometry of time [13].

7.4. Stage IV: Saturation and Matter Stabilization

Following the burst, soliton generation saturates and gradually ceases. The winding number per causal region stabilizes, and the universe enters a quasi-static regime in which emergent fermions persist as stable topological features.

7.5. Toward a Symmetry-Based Cosmology

Chronon Cosmogenesis offers a fundamentally new picture of the universe’s origin. Rather than beginning with fields on a pre-given manifold, it begins with a dynamical causal order. Rather than assuming particles and interactions, it derives them from topological defects. Rather than postulating time, it lets time emerge.

In this view, the universe did not begin with a bang, but with a break—a spontaneous selection of a temporal direction. Everything else followed.

8. Chronon Field Simulation: A Prototype Symmetry-Breaking Genesis

To verify the key predictions of Chronon Field Theory (CFT), we numerically simulate the dynamical evolution of the Chronon field ${\Phi }^{\mu }\left(x\right)$ on a ${1024}^2$ spatial grid with temporal resolution up to 500 steps. The field ${\Phi }^{\mu }$ is a unit-norm, future-directed timelike vector field, satisfying ${\Phi }^{\mu }{\Phi }_{\mu }=-1$, and evolves under a constrained gradient flow guided by a quartic potential:

$$V[\Phi ]={\displaystyle \frac{1}{2}}{(1-{\Phi }^0)}^2,$$

(5)

while preserving normalization at each spatial point. Evolution is performed with time step $dt=0.01$ using finite-difference Laplacians and backpropagated gradient descent with normalization projection.

8.1. Field Initialization and Dynamics

Initial conditions are set via a random Gaussian field with suppressed temporal component:

$${\Phi }^0(x,t=0)\sim \mathcal{N}(0,0.01),{\Phi }^i(x,t=0)\sim \mathcal{N}(0,1),\mathrm{followed}\mathrm{by}{\displaystyle \frac{\Phi }{\parallel \Phi \parallel }}.$$

(6)

Snapshots of ${\Phi }^0(x,t)$ at steps 0 and 100 are shown in Figure 1, illustrating the evolution from disordered initial state toward structured soliton domains.

8.2. Soliton Detection and Winding Statistics

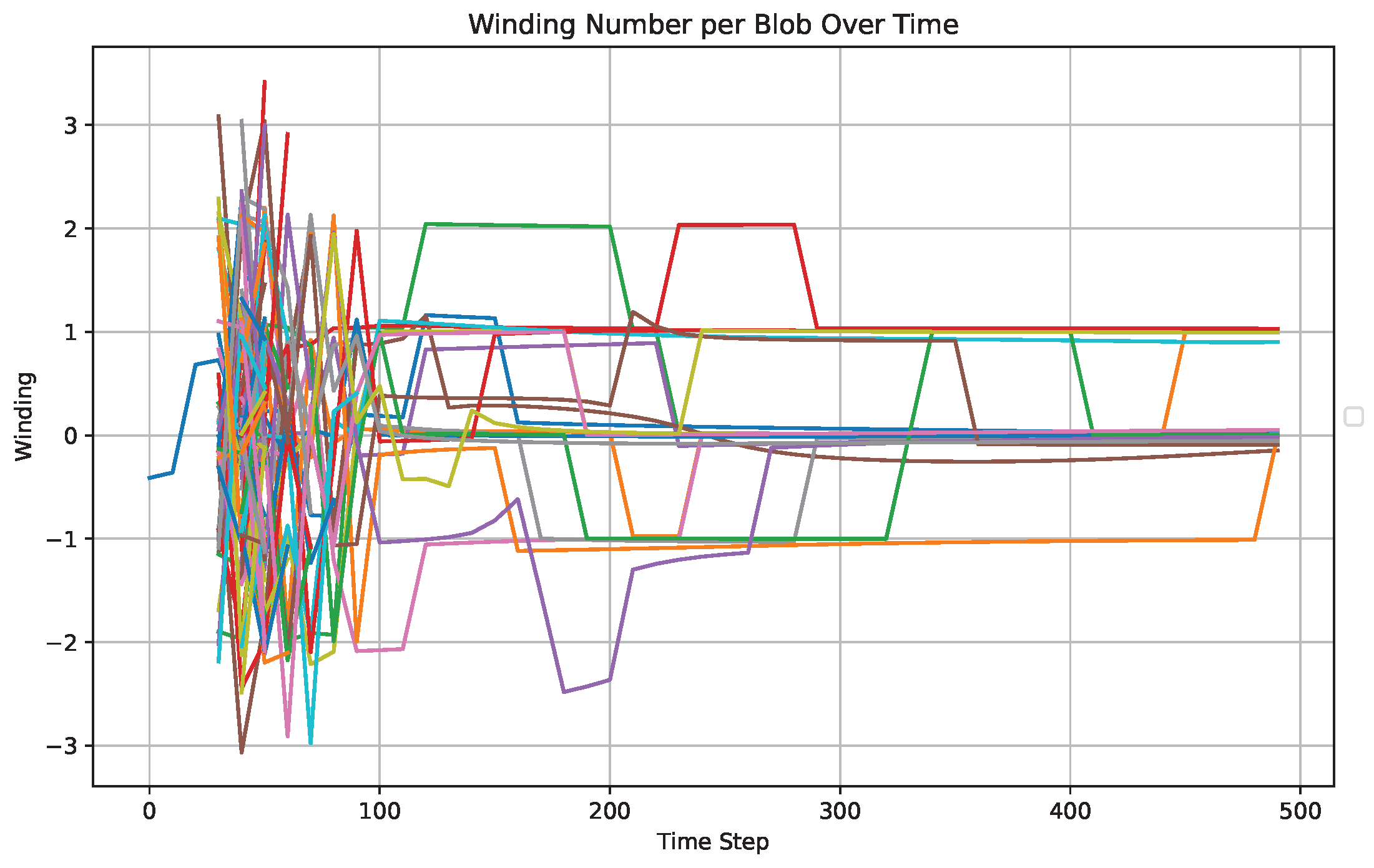
We define energy density as $E\left(x\right)={\parallel \nabla \Phi \left(x\right)\parallel }^2$, and extract high-energy regions ("blobs") above a threshold for topological analysis. The winding number $w\in \mathbb{Z}$ is estimated on a circular contour enclosing each blob. The winding number per blob over time is plotted in Figure 2.

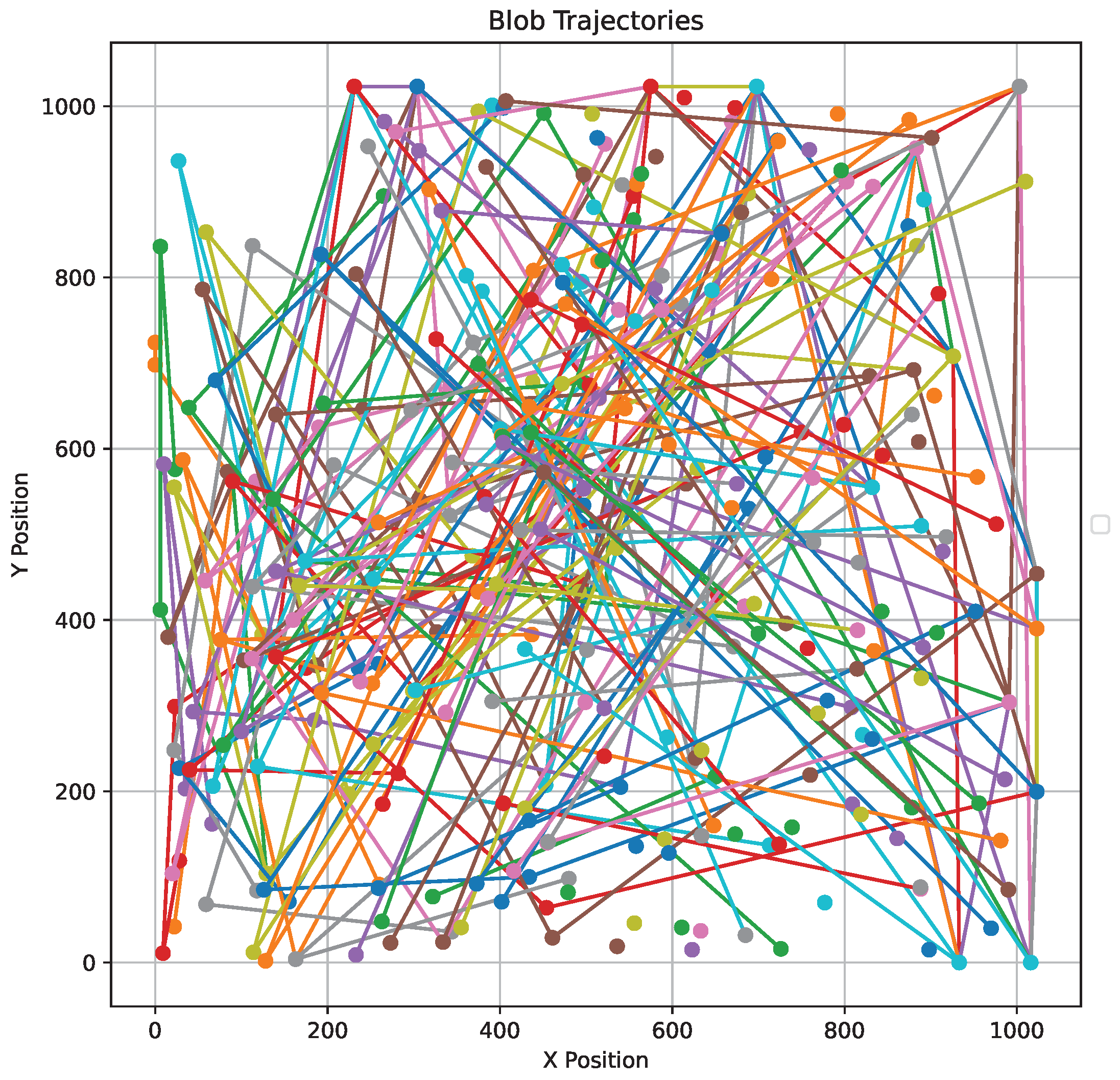
8.3. Trajectories and Topological Persistence

Blob centers are tracked across simulation steps using centroid motion, revealing persistent trajectories and clustering dynamics. Figure 3 displays representative blob paths.

8.4. Global Geometric Diagnostics

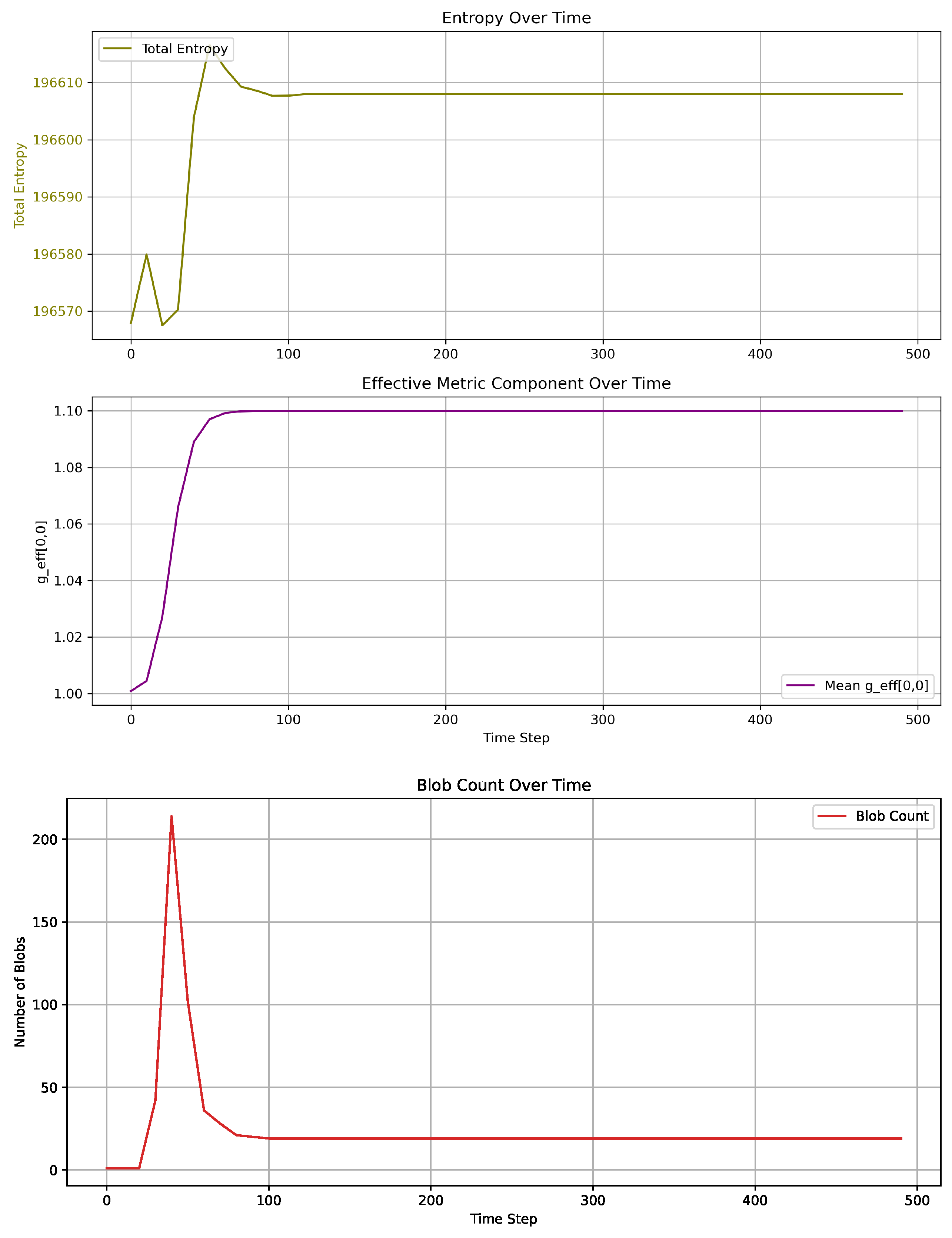
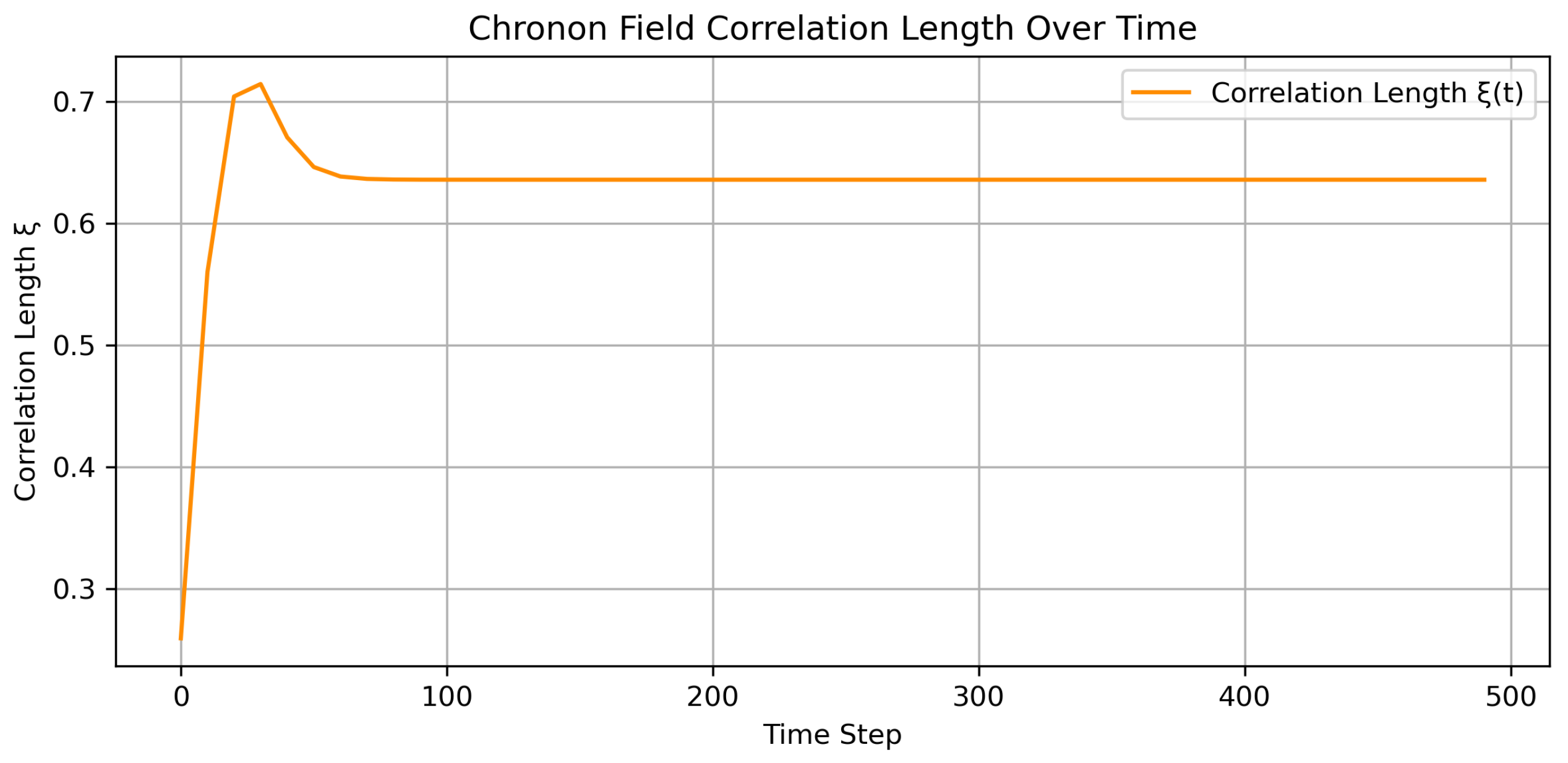
We compute diagnostic observables including total entropy, curvature (via Ricci scalar from effective metric), and correlation length $\xi \left(t\right)$ defined from the decay of field autocorrelations. Results over time are shown in Figure 4 and Figure 5.

8.5. Interpretation and Symmetry-Breaking Relevance

The simulation offers a symmetry-focused narrative of cosmogenesis within the Chronon Field Theory (CFT) framework. The process unfolds in four dynamical epochs:

• Initial Temporal Randomness (Step 0–10): A maximally symmetric, high-entropy state exists where no spatial or temporal ordering is present. All components of ${\Phi }^{\mu }$ fluctuate independently, and the system respects full internal symmetry (SO(3,1) in ideal limit), but lacks any geometric or matter content.
• Spacetime Emergence via Spontaneous Symmetry Breaking (Step 10–30): As correlations grow, the system undergoes spontaneous symmetry breaking (SSB), where a preferred foliation direction—embodied in ${\Phi }^{\mu }$—emerges dynamically. This marks the genesis of a temporal ordering, and defines a causal structure, even though the field remains topologically trivial (no solitons). This corresponds to an empty but geometrically structured spacetime.
• Soliton Genesis and Topological Defect Formation (Step 30–50): A symmetry-breaking instability induces a rapid nucleation of topological solitons—interpreted as primordial matter. These defects break local isotropy and homogeneity. The winding numbers $w=\pm 1$ correspond to spin-1/2 (fermionic) precursors, while $w=0$ configurations correspond to bosonic modes. This mirrors cosmic phase transitions in the early universe, where defects emerge from vacuum misalignment.
• Dissipative Relaxation and Late-Time Symmetry Restoration (Step 50–500): Soliton annihilation and decay restore global coherence. Entropy saturates, the effective metric $g_{00}$ stabilizes, and the correlation length approaches the lattice scale. The system returns to a low-entropy, high-coherence phase with restored large-scale symmetry and only residual topological structure. This mimics a stabilized, classical cosmos.

The key symmetry-related insights drawn from this simulation are:

• Spontaneous Symmetry Breaking Drives Genesis: Both spacetime and matter arise from SSB of an initially symmetric temporal field.
• Topological Charges Encode Quantum Statistics: The emergence of winding-number quantization naturally leads to a fermion-boson distinction.
• Order Precedes Content: Geometry and causal structure emerge before matter content appears.
• Chronon Genesis Mirrors Thermal Phase Transitions: The transition from temporal chaos to solitonic order echoes cosmological defect theory and Kibble-Zurek scenarios.

This simulation, thus, serves as a self-consistent and symmetry-aware prototype of cosmogenesis. It connects the dynamical geometry of time, the emergence of physical structure, and the topological encoding of quantum statistics into a unified process. As such, it supports Chronon Field Theory’s viability as a fundamental framework for quantum cosmology and symmetry-guided early-universe modeling.

9. Potential Observables and Experimental Signatures

While Chronon Field Theory (CFT) is fundamentally geometric and background-independent, its predictions open the door to several potentially observable consequences. These span cosmology, particle physics, and gravitational phenomena:

• Cosmic Birefringence and Polarization Anisotropies: The global alignment of the Chronon field ${\Phi }^{\mu }$ induces a preferred temporal direction across spacetime. This may manifest as a rotation of the polarization plane of photons over cosmological distances, leading to detectable birefringence in the CMB or astrophysical polarization data. Such anisotropies could mimic or extend effects traditionally attributed to axion-like fields [15,17].
• Neutrino Asymmetries and Chirality Biases: The asymmetric coupling of Chronon solitons to the Real Now could imprint a directional bias in the propagation or production of neutrinos. In particular, early-universe processes mediated by chiral solitons may preferentially select one helicity state over another, leading to observable consequences in cosmic neutrino backgrounds or long-baseline oscillation experiments [1,10].
• Gravitational Memory and Soliton-Driven Causality: The topological nature of Chronon solitons implies nontrivial causal orderings in their interactions. These could generate permanent spacetime displacements (memory effects) in strong-field events involving soliton creation or annihilation, potentially testable by future gravitational wave detectors sensitive to low-frequency tails or non-Einsteinian memory [4,23].
• Lorentz and CPT Violation Bounds: Precision measurements of clock anisotropies, particle lifetimes, or sidereal variation in atomic transitions could place bounds on the smooth misalignment of ${\Phi }^{\mu }$ with respect to laboratory frames. While CFT predicts suppression of such effects by ${({\lambda }_c/L_U)}^n$, next-generation experiments may probe the relevant parameter space [7,11].

Each of these signatures arises not from new fields or particles, but from the causal-topological structure of time. As such, they provide unique avenues to test the ontology of CFT and distinguish it from standard cosmology or high-energy extensions of the Standard Model.

10. Conclusions and Outlook

We have proposed a unified framework for understanding the breaking of fundamental symmetries through the causal and topological structure of Chronon Field Theory. By treating time as a dynamical field, we introduced the concept of the Real Now—a globally aligned foliation that spontaneously breaks global Lorentz invariance while preserving local causal structure [13].

Table 1. Comparison of symmetry-related features in the Standard Model/SME versus Chronon Field Theory.

Feature	Standard Model/SME	Chronon Field Theory (CFT)
Time	Treated as a fixed background parameter	Dynamical causal vector field ${\Phi }^{\mu }\left(x\right)$ defines time direction and local flow
CPT Violation	Inserted via Lorentz/CPT-violating terms in the Lagrangian	Emergent symmetry; violated in topologically complex or high-curvature Chronon configurations
Matter–Antimatter Asymmetry	Requires CP violation, baryon number violation, and thermal non-equilibrium (Sakharov conditions)	Arises from topological winding bias in soliton production due to temporal orientation (Real Now)
Fermionic Behavior	Imposed via operator algebra and spin-statistics theorem	Emerges from configuration space topology: ${\pi }_1\left({\mathcal{M}}_1\right)\cong {\mathbb{Z}}_2$ implies spin-$\frac{1}{2}$, Fermi–Dirac statistics
Lorentz Violation	Explicit background tensor fields in SME	Spontaneous global symmetry breaking via alignment of ${\Phi }^{\mu }$; local Lorentz symmetry preserved
Chiral Asymmetry	Imposed by SU(2) representation structure in weak sector	Emerges from spacetime shear: $S_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$; axial coupling from anisotropic temporal geometry
Baryon Asymmetry Estimate	Tuned via model-specific CP phases and washout processes	Matches observation with a correlation length input $\sim {10}^8\mathrm{m}$

Table 1. Comparison of symmetry-related features in the Standard Model/SME versus Chronon Field Theory.

Feature	Standard Model/SME	Chronon Field Theory (CFT)
Time	Treated as a fixed background parameter	Dynamical causal vector field ${\Phi }^{\mu }\left(x\right)$ defines time direction and local flow
CPT Violation	Inserted via Lorentz/CPT-violating terms in the Lagrangian	Emergent symmetry; violated in topologically complex or high-curvature Chronon configurations
Matter–Antimatter Asymmetry	Requires CP violation, baryon number violation, and thermal non-equilibrium (Sakharov conditions)	Arises from topological winding bias in soliton production due to temporal orientation (Real Now)
Fermionic Behavior	Imposed via operator algebra and spin-statistics theorem	Emerges from configuration space topology: ${\pi }_1\left({\mathcal{M}}_1\right)\cong {\mathbb{Z}}_2$ implies spin-$\frac{1}{2}$, Fermi–Dirac statistics
Lorentz Violation	Explicit background tensor fields in SME	Spontaneous global symmetry breaking via alignment of ${\Phi }^{\mu }$; local Lorentz symmetry preserved
Chiral Asymmetry	Imposed by SU(2) representation structure in weak sector	Emerges from spacetime shear: $S_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$; axial coupling from anisotropic temporal geometry
Baryon Asymmetry Estimate	Tuned via model-specific CP phases and washout processes	Matches observation with a correlation length input $\sim {10}^8\mathrm{m}$

Within this background, we showed that CPT symmetry, typically regarded as exact in conventional quantum field theory, becomes an emergent approximation valid only in the weak-field, semiclassical limit of Chronon dynamics. In strong curvature or topologically rich sectors, CPT can be genuinely violated through geometric phase evolution [6].

Most notably, we proposed a topological mechanism for the observed matter–antimatter asymmetry, arising from a dynamical bias in the winding number of Chronon solitons. This bias is not imposed externally but follows naturally from the orientation of time enforced by the Real Now [13]. Additionally, we demonstrated how charge conjugation symmetry can be dynamically broken at the level of soliton interactions, due to asymmetric coupling with the global temporal structure.

We further contrasted this model with standard Big Bang cosmology, highlighting that Chronon solitons—representing matter—do not emerge immediately but instead nucleate during a delayed burst, following a period of smooth causal alignment [26]. This reframes the origin of matter as a secondary, topologically-driven phase transition rather than a product of initial conditions. The evolution of the universe is thus recast as a sequence of symmetry breakings: time alignment (T), Lorentz invariance, CPT emergence, C-violation, and baryogenesis—all traced back to the dynamics of temporal flow.

These results point to a new paradigm in which many of the symmetries we take as foundational are in fact emergent from deeper causal and topological constraints. Future work will explore:

• Quantitative modeling of soliton pair production and annihilation asymmetries in early universe simulations.
• The derivation of effective field theories describing low-energy excitations on Chronon- aligned backgrounds.
• Experimental probes of Lorentz violation and temporal anisotropies, particularly in the neutrino sector or through cosmological polarization data.
• The extension of CFT to include gauge and matter couplings consistent with known standard model phenomenology.