Introduction: A Wish Inscribed in the Margins
If the author of this paper could be granted but one wish by an all-powerful genie, it would not be for riches, nor fame, nor even wisdom. It would be for a single marginal note — a tiny inscription, scrawled in the corner of an old manuscript on a physicist’s desk nearly a century ago. Two symbols, circled in haste: D+, D- ?
Oh, what a marvelous world would I awaken to, had that whisper reached across time.
In 1928, Paul Dirac etched into history one of the most beautiful equations known to science. He crafted a bridge between quantum mechanics and special relativity, and a prediction of antimatter born of pure mathematical elegance. And yet, even as he opened that door, another remained closed, a deeper symmetry hidden just out of sight.
If only that single hint had been given. Had Dirac glimpsed not only particles and antiparticles but positive and negative eigen-directions of spacetime itself. The structure of modern physics might have unfolded along an entirely different path. A path in which matter-antimatter asymmetry, dark energy, the origin of mass, biological chirality, and even the arrow of time itself emerged naturally, inevitably, from a deeper topological grammar of the universe. This paper attempts to capture what might have happened had Dirac followed that whisper a little further. We begin by tracing how the introduction of the spinor pairing leads, step by step, to a deeper model of physical law. The Dirac equation already encodes the duality of forward and backward propagation in time; the formulation makes this explicit, separating the spinorial contributions to causality into distinct temporal components. Rather than treating these as merely solutions to a wave equation, we reinterpret them as recursive phase operations, but as local generators of directional iteration through a spinor-valued fieldspace. This reconceptualization reveals that time itself is not an external parameter, but an emergent direction of stable phase alignment. In this framework, spinors are not just describing particles, but are the geometry of recursion, and time is the accumulation of phase-locked iteration within that structure. Along the way, we will re-express several long-standing physical anomalies, such as matter-antimatter asymmetry, entropy’s arrow, and the discreteness of mass as emergent consequences of this deeper spinorial logic.
1. Modern Contextual Justification
Since the early successes of quantum field theory and general relativity, physics has run into a cascade of deepening paradoxes. The accelerating expansion of the universe, attributed to an unexplained dark energy, has upended the standard cosmological model. The dominance of matter over antimatter remains unresolved despite decades of precision particle experiments. Bell nonlocality, once a fringe theoretical curiosity, is now experimentally confirmed, challenging the foundations of locality and realism. The black hole information paradox has exposed a fundamental incompatibility between gravity, thermodynamics, and quantum mechanics.
Each of these puzzles, formidable on its own, reveals a broader pattern: the dominant frameworks of physics, though extraordinarily successful within their domains, appear blind to the structural causes behind these phenomena. Had the deeper topological character of spinor fields been recognized earlier, many of these anomalies might have emerged not as mysteries, but as predictions.
Over the intervening decades, numerous theorists have sounded the alarm. Roger Penrose emphasized the primacy of geometry, proposing twistors and spin networks as pre-quantum substrates for spacetime. Lee Smolin has critiqued the stagnation of theoretical physics and called for more inclusive, independent, relational frameworks. Gerard ’t Hooft has explored deterministic models beneath quantum mechanics. Erik Verlinde has proposed that gravity may emerge from entropic and informational principles rather than from fundamental interactions. Each of these perspectives questions the completeness of our current foundations.
As Richard Feynman once put it, “I don’t know what energy is.” This candid admission from one of physics’ greatest minds highlights the extent to which even our most basic quantities may still be conceptual placeholders for deeper phenomena.
These voices converge on a common point: the frameworks we inherited may not be broken, but they are incomplete. The search is not for new particles, but for a new architecture that accounts for space, matter, and causality as emergent expressions of deeper structure. The spinor-topological approach developed in this paper aims to offer exactly that: a framework in which coherence, rather than force, becomes the organizing principle of physical law.
“The notion that the universe is not merely governed by physical laws but actively computes its own state has deep roots in 20th-century thought [
4,
5].”
2. The Spinor Universe as Possibility Space
What began as a thought experiment of a speculative extension of Dirac’s formalism quickly revealed itself to be a much deeper inquiry. The pairing was not just a spinor annotation, but a keyhole into a broader architecture: one in which duality, chirality, and time itself are woven from deeper phase structures. As we traced the implications, the terrain expanded beneath our feet.
This paper extends the framework introduced in
The Spinor Universe: A Topological Model of Matter-Antimatter Asymmetry and Temporal Duality, which includes more specific mathematical formalism concerning global spinor topology structure than is presented here. [
1]
To pursue this idea, we had to reconstruct the underlying stage of physics not in terms of particles or fields, but in terms of possibility. This led to the formulation of the Spinor Universe: a static, recursive phase topology encoding every coherent configuration reality could, in principle, adopt. The story of is no longer a correction to quantum mechanics, but a glimpse into the structure that quantum mechanics emerges from.
The Spinor Universe is a topological model of reality in which phase-locked spinor configurations define the space of all possible coherent structures. In this view, classical spacetime, particles, and fields are not fundamental, but emergent properties of deeper recursive relationships in spinor-valued fieldspace.
The model provides a static framework where all viable phase structures are encoded as paths through a constrained topological manifold. Time, matter, and causality emerge only when this structure is iterated, when phase configurations loop back on themselves in self-consistent ways.
In standard quantum theory, the Pauli exclusion principle is derived from the antisymmetry of fermionic wavefunctions, formalized by the spin–statistics theorem. While this ensures internal mathematical consistency, it does not offer a dynamical explanation for why identical fermions must repel occupation of the same quantum state. In the Spinor Universe model, this exclusion arises naturally from the structure of recursive spinor topology. Each fermion is a stable phase-locked loop in spinor-valued fieldspace, and two identical spinors attempting to occupy the same local phase domain will destructively interfere unless they differ in spin orientation or topological signature. This extends to antimatter: a particle and its conjugate may coexist at the same node precisely because they traverse the attractor in opposite phase, each inhabiting a dual coherence basin within the same spinor manifold. The Ontolotron, acting as the recursive selector of stable configurations, enforces these constraints by suppressing self-canceling phase paths before they are iterated into reality.
The vacuum expectation value (vev) is reinterpreted here not merely as a scalar minimum but as a global fold in the spinor topology, a phase pivot where symmetry is broken and matter becomes possible. The early universe begins in a high-symmetry, low-coherence state. Matter emerges gradually, through recursive phase alignment, as coherence condenses from the ambient spinor field.
Black holes, in this framework, are attractors of maximal coherence. They are not singularities but topological knots, where internal and external phase structures are unified. Their evaporation does not erase information but projects it outward in phase, unwinding coherence back into the field as structured radiation.
This spinor framework sets the stage. It defines the landscape. But it does not tell us which configuration becomes real. That role belongs to the Ontolotron: the dynamic subsystem that selects, iterates, and stabilizes coherent phase structures from within the Spinor Universe. It is this selective process that gives rise to entropy, time, and reality as we experience it.
Definition 1.
The
Ontolotron
is a recursive actuator embedded within the spinor-valued phase space of the universe. It selects actualized configurations through coherence-seeking iteration, minimizing global decoherence under topological constraints.
3. From Structure to Actuation: The Ontolotron Hypothesis
The Spinor Universe framework defines the topological phase space of all possible coherent configurations, but it does not, by itself, determine which configuration is realized. To account for this, we introduce the Ontolotron: a dynamic, coherence-optimizing subsystem that actuates the transition from possibility to actuality. While the full spinor-valued topology encompasses all realizable structures, the Ontolotron governs their selection through recursive iteration, favoring configurations that maximize global coherence.
In this view, the universe is not merely one of many worlds, but a specific attractor trajectory through spinor phase space. Reality is actualized through alignment with coherent recursion. This distinction is crucial: the Spinor Universe defines the possibility space; the Ontolotron serves as the reality engine. Together, they form a complete ontological and dynamical cosmology.
Ontolotron Hypothesis. The Ontolotron is a physically instantiated selection mechanism embedded within the spinor-valued field topology of the universe. It acts by recursively evaluating candidate configurations of spinor phase space and actualizes those whose global coherence residues minimize entropy under CPT-symmetric constraints. This recursive selection process defines the observed physical vacuum, determines particle stability thresholds, and bounds the allowable gauge symmetries by favoring attractors that converge under spinor recursion.
Observable consequences include:
Quantized stability zones corresponding to fixed points in spinor recursion.
Asymmetry in matter/antimatter distribution as a result of coherence optimization.
Black hole–white hole duality as the macroscopic imprint of coherence selection boundaries.
The Ontolotron is not a field, particle, or external force. It is the recursive, self-organizing actuator within the Spinor Universe that promotes local coherence and suppresses decoherence through entropic routing. It drives the selection, stabilization, and iteration of phase-locked structures, giving rise to phenomena we perceive as time, gravity, space, and matter.
Proposition 1. Any ontologically complete configuration favored by the Ontolotron corresponds to a global coherence attractor, such that its recursive topology is CPT-stable and thermodynamically convergent.
Proposition 2. In a post-forward-time anti-de Sitter regime, matter fields arise as fixed-point recursive solutions of spatial spinor computation, where the phase constraints encoded by the forward-time attractor define a topological basis for particle stabilization. Each stabilized mode is a product of locally constructive recursion seeded by global coherence residues, and all emergent gauge structure reflects constraint satisfaction within this inherited computational manifold.
4. Temporal and Entropic Flow
Various models have proposed that the arrow of time may be a perspectival or emergent property [
2], and cosmological frameworks based on time-reversal symmetry have been seriously developed [
6,
9]. In the Spinor Universe framework, time is not an absolute axis but the integral of local phase iteration. Every re-locking of spinorial symmetry represents a step in time. The passage of time, therefore, is not measured by distance or clocks but by the successful alignment and propagation of coherence in the field.
This interpretation also demands a re-examination of thermodynamic laws in ontological terms. In the Ontolotron framework, energy is not lost or dissipated but recursively redistributed across coherence attractors. Apparent entropy increase corresponds to local misclosure of spinor recursion, while conserved energy is maintained as a function of global coherence. Entropy becomes a descriptor not of disorder, but of deviation from recursive alignment. Thus, thermodynamics itself is reframed: energy conservation and entropy production are not fundamental axioms, but emergent features of spinor field recursion under coherence constraints.
This makes time a locally determined quantity, emerging from the recursive structure of matter itself. Systems that undergo no phase iteration experience no local time. In high-coherence configurations, time dilates; in decoherent environments, time unspools rapidly. Time is not universal, but a measure of internal transformation.
4.1. Phase Transitions Between de Sitter and Anti-de Sitter Domains
The large-scale topology of the Spinor Universe features a structural asymmetry between forward-time (de Sitter-like) and reverse-time (anti-de Sitter-like) geometries. These distinctions are not merely metric, they reflect fundamental differences in how computation propagates through spacetime.
In the forward domain, the positive cosmological constant corresponds to de Sitter expansion: a globally repulsive geometry that stretches spatial slices and thins coherence gradients over time. This is the domain in which matter computes space into being as localized excitations drive inflationary behavior, and spinor phase gradients seek relaxation.
In the reverse domain, however, the spatial field iterates inward. The effective geometry corresponds to anti-de Sitter logic: boundary-driven recursion, where the spatial field computes internal structure. Coherence does not dissipate outward but is drawn inward toward fixed-point attractors defined by phase kernels left behind by black hole evaporation.
The Higgs VEV functions as the boundary between these two regimes. Not as a local symmetry-breaking event, but as a global phase constraint enforcing a conformal pivot. As the forward-time domain expands and decoheres, the spinor field approaches a phase-flattened limit. When the attractor reaches null coherence gradient, inversion initiates.
The phase transition is not thermodynamic, but topological. It is a switch in the direction of recursion, governed by the sign of curvature in the attractor’s computational manifold. The resulting anti-de Sitter structure inherits its topology not from inflation but from the total computational residue of the forward universe.
Thus, the transition from de Sitter to anti-de Sitter is not a collapse nor a bounce. It is a global refactoring of coherence roles. Expansion becomes recursion. Geometry becomes computation. What was once output becomes the substrate. In the Spinor Universe framework, the total recursive attractor, or The Ontolotron, encodes a dual computational structure across time. In the forward-time domain (
), matter acts as both the computer and the workload, recursively computing space as its output. In the reverse-time domain (
), this structure is inverted: space recursively computes itself, with matter emerging as its output. The Higgs vacuum expectation value (VEV),
, acts not only as a spontaneous symmetry-breaking field, but as a
cross-temporal attractor—a pivot across which dual computational roles are exchanged.
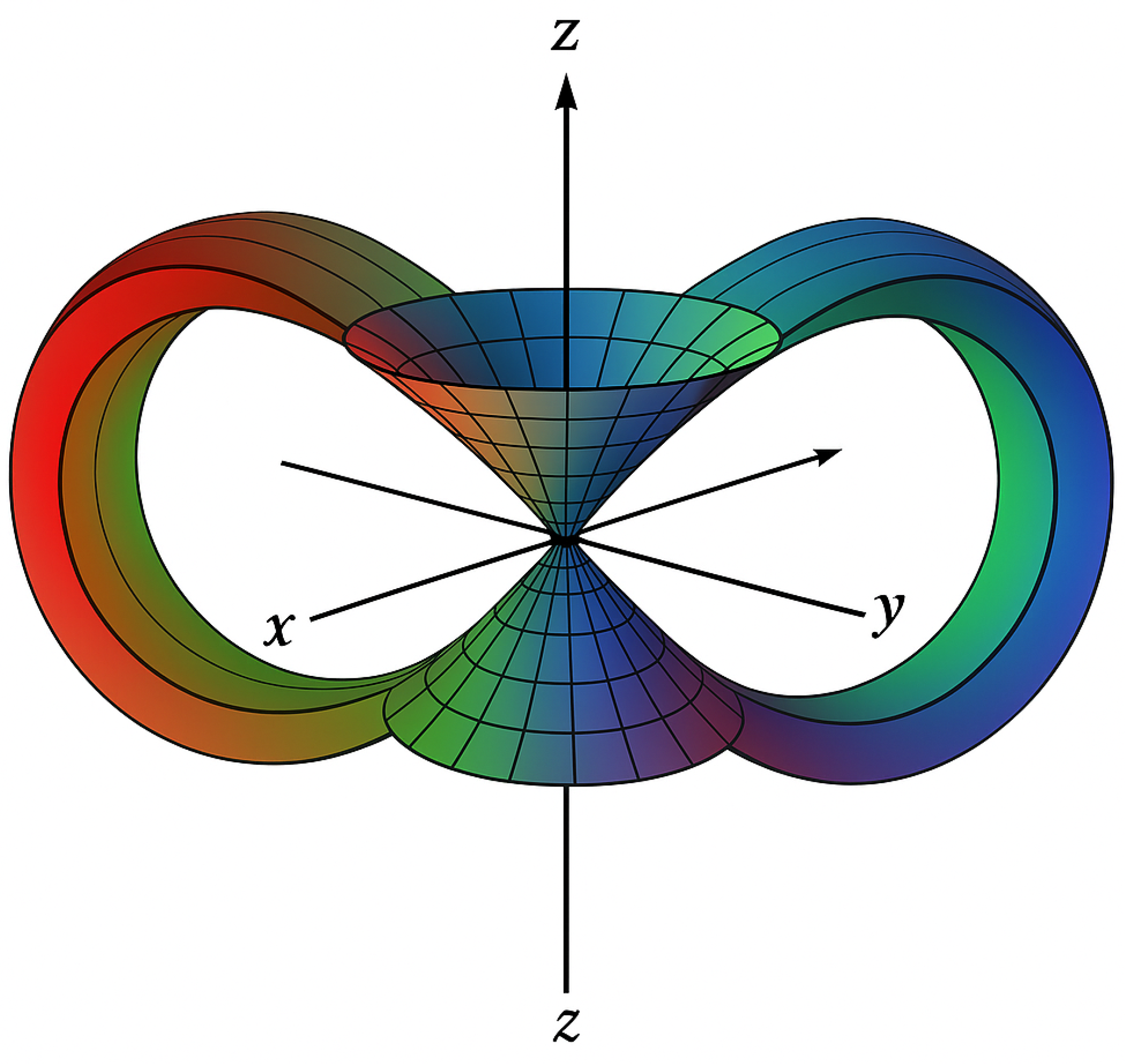
Figure 1.
Recursive spinor-coherence manifold shaped as a temporally embedded toroidal lemniscate. Forward-time flow extends outward through the upper cone and loops back through the interior. The structure illustrates recursive attractor dynamics and phase inversion across temporal axes.
Figure 1.
Recursive spinor-coherence manifold shaped as a temporally embedded toroidal lemniscate. Forward-time flow extends outward through the upper cone and loops back through the interior. The structure illustrates recursive attractor dynamics and phase inversion across temporal axes.
Definition 2.
A
coherence attractor
is a locally phase-stable configuration in spinor space that persists under recursive iteration and minimizes entropic export to surrounding structure.
Entropy, in this context, is not simply disorder but a routing function. It represents the projected footprint of coherence maintenance. As systems seek stable attractors, they must expel quanta of phase misalignment into the surrounding topology. This expelled incoherence, statistically randomized, is observed as thermodynamic entropy.
Thus, the arrow of time is simply the direction of coherence optimization. What we call "past" is the record of transformations that increased global stability. What we call "future" is the edge of possibility where coherence has not yet been resolved.
In this view, the second law of thermodynamics is not a fundamental limit but an emergent shadow of Ontolotronic book-keeping. The universe does not simply trend toward chaos as an endpoint. It trends toward locked coherence. It filters through energy until it can get a unanimous vote from all parties, and the entropy we observe is merely the necessary expulsions to the void paid to achieve it.
4.2. Termination Conditions and the Attractor Inversion Threshold
The final fate of the universe in the Spinor framework is not heat death, but computational saturation. Once all matter decays, black holes evaporate, and coherence gradients dissipate, spacetime becomes globally silent. This silence is not emptiness, but a boundary condition: a signal that the Ontolotron has no remaining degrees of forward computation.
Where Penrose’s conformal cyclic cosmology suggests a scale-flattening between aeons, the Spinor Universe model suggests a computational inversion. The same conformal boundary that erases the distinction between massless infinity and a newborn big bang is reinterpreted here as a structural switch: from matter-as-computation to space-as-computation.
Hawking radiation plays a vital role in this transition. It is not merely thermal leakage, but the final structured dissipation of spinor tension. Each evaporating black hole emits not just entropy but a boundary imprint a phase-coded remnant of all computations it once contained. These imprints act as the phase seeds for white hole nucleation on the reverse-time side. As the very last ripple of gravitational or thermal distortion fades, the global field reaches a threshold where phase becomes flat and incompressible. The attractor has nothing left to compute.
At this point, the universe satisfies:
That is, when the coherence gradient approaches zero and the stress-energy tensor vanishes across all space, the spinor field completes its forward recursion. The attractor inverts, but the clock keeps ticking anyway.
Rather than the emergence of a new universe, the existing manifold reinterprets its topology and computational roles. Space becomes the computer. Matter emerges again, as output. Thus, the end of time is not the cessation of history, but its recursive reflection.
4.3. VEV as a Boundary Condition, Not a Starting State
Instead of assuming the Higgs field breaks symmetry
within time, we treat
as a
boundary condition imposed across the temporal interface. This allows us to reinterpret the Dirac field as a stabilized solution to a spatial self-computation that asymptotically approaches the VEV:
This interpretation frames matter not as a primitive ingredient, but as the output of a convergent process from the space-computes-itself regime. In this view, the asymmetry between matter and antimatter may reflect not an intrinsic imbalance, but a directional spillover: matter emerges as the stabilized expression of a boundary value problem solved by the recursive dynamics of spacetime itself.
5. Entanglement as Chiral Coherence and Global Constraint
In the Spinor Universe, entanglement is not merely a statistical correlation but an expression of chiral coherence is a topologically enforced constraint between spatially or temporally separated spinor regions. These relationships are not instantaneous transmissions but recursive coherence conditions embedded in the attractor’s structure.
Entangled particles, when viewed through this lens, are phase-linked solutions to a global equation are not separate entities, but fragments of a larger, coherent mode. The ontological root of their connection lies in their shared origin within a cross-temporally extended spinor loop.
Chirality, in this context, is not just helicity but a manifestation of directional coherence across attractor layers. The chirality of interactions (e.g., weak force asymmetry) reflects deeper global constraints: entanglement does not violate locality because locality itself is an emergent computation within the Ontolotron.
This view resolves several paradoxes: wavefunction collapse becomes a localized decoherence threshold rather than a global informational change; nonlocal correlations are understood as topologically conserved phase states; and causality is preserved through recursive constraint satisfaction, not by classical light-cone enforcement.
Thus, entanglement is recast as a visible expression of invisible global order, but a boundary surface of the deeper attractor structure that remains coherent even when spacetime decoheres.
6. Curvature from Spinor Nonclosure in Double Cover Space
To understand how the Ontolotron shapes physical structure, we begin with its most visible symptom: gravity. Conventional differential geometry defines curvature as the failure of vectors to return to their original state after parallel transport around a closed loop. In the Ontolotron framework, where spacetime and matter arise from the recursion of spinor fields, curvature is instead understood as the failure of foundational spinor recursion to reach full closure. There are still more game rounds to play, which keeps the clock ticking.
Spinor fields, by their nature, require phase rotation to return to their original state. This double-cover property implies that even infinitesimal misalignments in spinor recursion can lead to large-scale geometric tension when extended across macroscopic domains. We model this failure of closure as the source of curvature itself.
Let
be a spinor field defined on spacetime. The curvature associated with spinor transport is given by the commutator of covariant derivatives:
where
is a generator of spinor rotation, an element of the Clifford algebra formed by products of gamma matrices. This curvature operator measures the infinitesimal failure of phase closure in the spinor field due to background topology.
The gravitational field is then expressed not as an externally imposed geometry, but as the integrated trace of this internal spinor twist:
or equivalently,
where the trace is taken over spinor indices. This construction yields a symmetric rank-2 tensor naturally encoding curvature from the internal algebraic properties of the spinor field itself.
6.1. Recovery of Classical Curvature from Spinor Misclosure
Having established that curvature in the Ontolotron framework arises from spinor nonclosure in a double-cover fieldspace, we now turn to the question of how this formalism recovers the specific gravitational behavior described by general relativity. To make contact with known physics, we must demonstrate that spinor-induced curvature reproduces the Einstein tensor in the appropriate macroscopic limit, and yields Newtonian gravity as a further reduction.
We begin with the curvature operator defined on the spinor field:
where
encodes the algebraic failure of spinor recursion closure across spacetime. This quantity is valued in the Clifford algebra and generates internal holonomy.
To recover observable curvature, we project this operator into the effective geometry by taking the spinor inner product:
This symmetric rank-2 tensor contains the geometric imprint of spinor phase tension across spacetime and defines the emergent gravitational field.
We posit that in the limit of macroscopic, smooth phase recursion—where local spinor fluctuations average out and coherence dominates—this tensor converges to the Einstein tensor of general relativity:
In the weak-field, non-relativistic regime, the spinor field may be expressed as a static phase configuration:
The commutator of derivatives then reduces to:
and curvature becomes expressible as the second derivative of the phase field. Identifying
with the Newtonian potential
, we recover:
thus reproducing the Newtonian limit of gravity from spinor recursion misalignment.
This result shows that gravitational geometry, as measured by the Einstein tensor, is not externally imposed, but arises naturally from the topological structure of the spinor field. The classical curvature of spacetime is the macroscopic shadow of microscopic spinor non-closure. The topological debt incurred by a temporal manifestation produces a particular interest rate.
6.2. Coherence Economics of Gravity
Having previously formalized gravity as the macroscopic residue of spinor nonclosure, we now offer a metaphorical perspective: gravity as a coherence economy. In this framework, mass is not a quantity but a role, a structure that successfully accumulates and preserves the recursive phase alignment. It persists because it pays the cost of coherence.
Curvature is the invoice that the vacuum issues for metering the recursion. Matter “attracts” not by force but by minimizing the entropic cost of maintaining separate phase states. Gravity is thus a bookkeeping mechanism for coherence expenditure: a redistribution of decoherence away from stable structures and into the surrounding field.
In this economy, thermal radiation is not merely waste heat but phase re-balancing liquidity. Gravitational wells are not traps, but subsidized phase attractors. Spacetime becomes the ledger of this transaction, is its geometry sculpted by the recursive constraints of the Ontolotron.
This metaphor reinforces the view that gravitation is not imposed, but emergent: a symptom of phase optimization under recursive constraints. To understand this process in motion, we must now examine the structure of time and entropy as expressions of recursive iteration.
6.3. Angular Momentum as the Scaffold of Coherence
In the Ontolotron framework, the emergence of structure, time, and gravity is grounded in the recursive behavior of spinor fields. These fields are not merely directional, but are inherently rotational. Spinors possess an intrinsic angular phase, and their recursive stabilization requires full
closure to return to their initial configuration. This double-cover nature suggests that angular momentum is not incidental to coherence, but rather its organizing principle. This idea resonates with Penrose’s early work on spin networks, where angular momentum quanta were proposed as the combinatorial building blocks of spacetime geometry itself. [
8].
In standard physics, angular momentum is conserved and quantized, but is generally treated as a secondary attribute of particles or macroscopic systems. Here, we argue that angular momentum is the structural alignment vector around which phase-locking emerges.
This view is justified algebraically by considering curvature as arising from noncommuting spinor transport in Clifford algebra. As previously shown:
where
are the generators of spinor rotation. These generators belong to the Clifford algebra of spacetime and encode the geometric twist accumulated through recursive phase transport. The Einstein tensor, as we derived, emerges from the trace of this algebraic rotation:
This would imply that the gravitational geometry we observe is the large-scale residue of aligned angular recursion.
To understand how such alignment behaves in extreme conditions, we look to neutron stars: astrophysical objects in which quantum degeneracy, spin alignment, and enormous angular momentum produce high-coherence gravitational entities. Neutron stars spin rapidly, exhibit high magnetic ordering, and act as near-perfect macroscopic coherence traps. These systems demonstrate that angular momentum, when sufficiently stabilized, can organize matter and curvature into phase-locked geometries sustained across cosmic time.
In this view, angular momentum is the topological framework upon which coherence is stretched. It is not merely an energetic quantity but the field-theoretic glue that binds recursive identity across spacetime.
This insight leads directly to the construction of coherence attractors in the lab. To simulate and study the effects of coherence-induced curvature and phase filtering, we seek to create a miniature version of these systems. Rather than spinning collapsed matter, we turn to a tractable analog: the sonic black hole.
By constructing a vortex horizon in a superfluid helium bath, we impose angular recursion from the top down. This geometry traps phase information, filters incoming isotopes by alignment, and generates the kind of topological basin in which Ontolotron dynamics can be observed. The sonic horizon becomes not a metaphor, but a functional stand-in for the recursive boundary condition that mass and curvature themselves represent.
7. Coherence Tension and the Gravitational Phenomenology of Dark Matter
Within the Spinor Universe framework, gravity is not merely a geometric curvature of spacetime induced by mass-energy, but a manifestation of coherence tension within the underlying spinor field structure. In this view, matter is the localized expression of stable, recursively self-reinforcing spinor configurations, while gravity emerges as the ambient consequence of their coherence gradients across the vacuum. This reinterpretation opens a path to understanding dark matter not as a particle species, but as the distributed, uncollapsed coherence tension that surrounds phase-locked matter systems.
A region of high coherence density in spinor space resists phase deformation. This resistance manifests macroscopically as gravitational potential. In highly collapsed systems, such as black holes, the coherence gradient becomes extreme, forming a fully locked phase attractor. But in less collapsed, more diffuse systems such as galactic halos, the coherence field may remain uncollapsed but still exert coherent tension on surrounding spacetime, effectively acting as an invisible gravitational scaffold.
Thus, we propose that the gravitational influence attributed to dark matter arises from these extended coherence gradients. Unlike baryonic matter, which is recursively converged into stable field configurations, this coherence tension is structurally non-local: it spans large spatial domains without resolving into conventional mass-energy, yet still couples to the gravitational field through its influence on vacuum structure.
7.1. Coherence Energy Density
Let
denote a scalar coherence field encoding the local spinor phase alignment. The coherence energy density can be written analogously to a scalar field theory:
where represents a coherence potential, possibly encoding topological constraints, field torsion, or residual phase locking. This energy density contributes to the stress-energy tensor and can source gravity even in the absence of conventional particles.
By integrating this coherence energy density across galactic-scale volumes, one could in principle, recover an effective mass density corresponding to observed dark matter distributions:
If is sufficiently structured on halo scales, the coherence gradients could account for the observed flat rotation curves of galaxies, lensing anomalies, and CMB acoustic peak shifts without invoking new particles.
7.2. Coherence Collapse and Angular Momentum
Just as angular momentum organizes gravitational structures at all scales, it also governs coherence localization. We propose that the angular momentum of galactic systems serves to "trap" coherence tension in extended configurations, delaying full phase collapse into baryonic matter or black holes. This coherence tension, maintained across large rotating structures, constitutes the dark matter halo.
In this sense, dark matter is not missing mass, but uncollapsed coherence phase locked by rotational geometry. The size of the galactic coherence halo and its gravitational signature reflect the degree of unresolved tension in the spinor vacuum, organized and constrained by angular momentum as a coherence scaffold.
7.3. Observational Implications
If dark matter is a manifestation of coherence tension rather than particulate matter, we expect it to:
Interact only gravitationally (as observed)
Exhibit diffuse, non-dissipative behavior (consistent with lensing and halo profiles)
Be correlated with rotational geometry and global coherence alignment of galaxies
Possibly exhibit subtle topological signatures in large-scale structure
This interpretation preserves the empirical successes of the dark matter paradigm while rooting its cause in a deeper ontological substrate: the structured phase tension of an evolving spinor vacuum. Importantly, coherence tension is not confined to mass alone, but includes the recursive misclosure of angular momentum fields—what classical theory would describe as frame-dragging. These embedded coherence structures propagate beyond local mass distributions, generating long-range recursive tension in the spinor field. What is conventionally attributed to "dark matter halos" may instead represent topologically extended coherence basins.
Evidence for such an effect may already exist in the form of annual modulation observed in underground dark matter detectors such as DAMA/LIBRA [
7]. These detectors register a higher flux of apparent dark matter interaction in June than in December. While this is typically interpreted as the Earth moving through a dark matter wind, the Ontolotron framework suggests an alternative: the Earth is cyclically intersecting coherence gradients aligned with the galactic spinor structure. The annual modulation is thus a phase interaction with meta-stable curvature tension, not a particle flux, but a wavefront in coherence fieldspace.
8. Reverse-Time Field Dynamics
In this section, we explore how familiar physical structures such as particles, forces, and interactions emerge in the reverse-time domain of the Spinor Universe. Though governed by the same fundamental attractor, the reversal of computational flow gives rise to unique dynamics, where coherence, not just entropy, becomes the guiding principle of physical law.
Despite their differing initial conditions, both forward and reverse-time domains must satisfy the same fundamental constraints—Dirac, Yang-Mills, and Einstein equations, and respect CPT invariance [
10]. As such, reverse-time configurations are not violations of known physics, but alternate embeddings of the same spinor-valued phase attractor. Furthermore, the condensation of matter through recursive spatial iteration finds conceptual support in informational models of gravity and emergence [
12], and in time-symmetric treatments of black hole induced structure [
11].
8.1. Dissimilarity of the Reverse Initial State
An inverted universal timeline does have rather particular implications, namely an inward-pointing arrow of time, and entropy decreasing over the local time metric. Unlike in the forward domain, where time flows with increasing statistical disorder, the reverse domain flows toward decreasing phase dispersion. In this context, entropy does not vanish, but reinterprets: coherence increases not in defiance of thermodynamics, but as a result of recursion acting in a space-computing mode.
Rather than a hot, dense plasma of particles rapidly scattering outward, the reverse universe begins as a cold, low-amplitude spatial field we could describe as smooth and nearly empty. Coherent phase gradients seeded by evaporated black holes function like slow-burning fuse lines, gradually igniting regions of localized recursion. These are not explosions but implosions: geometry folding inward toward phase-locked attractor states.
This results in an emergent picture very unlike the Big Bang. There is no thermal inflation, no symmetry-breaking cascade. Instead, the early reverse universe is computationally sparse and topologically rich. Its complexity is not generated by expansion, but revealed by recursive contraction. The vacuum is not a canvas, but a condensed medium laced with phase-coded memory from a prior epoch.
This dissimilarity is causally required. The reverse domain is not governed by a clock but by recursion depth; not by heat but by coherence gradient; not by expansion but by resonance. Though governed by the same fundamental constraints as our own universe, it arrives at those constraints through a fundamentally different computational path.
Yet this divergence does not imply asymmetry of law, only of initialization. The attractor architecture ensures that even opposite temporal arrows must ultimately spiral toward the same global solutions, despite radically different boundary conditions.
While the reverse-time domain inherits its structure from the attractor residues of the forward universe, this inheritance results in a globally dissimilar topology. Not born of thermal symmetry breaking, but of recursive spatial condensation seeded by black hole evaporation. Yet this divergence at the level of cosmogenic origin does not preclude equivalence at the level of embedded experience. In fact, it is precisely this dissimilarity in initialization that makes possible a deeper unity in how structure is expressed and stabilized.
Building upon this duality, we propose that black holes in the forward-time domain, which compress and forward-project matter and information, act as seed points for white hole formation in the reverse-time domain. As the universe iterates toward increasing coherence, these compressed information nodes form "bunched-up" regions of spinor winding and tension.
When the attractor dynamics flip across the temporal pivot, these high-tension loci act like tension-loaded spools in a wound string: they encode the structure of forward-time compression, and unwind precisely as temporal tension inverts. The white holes are thus not arbitrary features, but reflected echoes of black hole activity manifesting precisely where forward-time compression left structural imprints.
This correspondence provides a new mechanism for cosmic structure continuity across the time boundary, suggesting that black hole activity is not an endpoint, but a forward loading of conditions for reverse-time matter genesis.
8.2. Embedding Equivalence and Observational Indistinguishability
The emergence of structure via white hole condensation in the reverse-time domain, seeded by forward-time black holes, leads to a surprising consequence: local observers in either domain would experience equivalent physical laws, particle types, and apparent cosmological history.
Because the spinor field solution that emerges from spatial iteration satisfies the same field equations as forward-time matter, including Dirac, Yang-Mills, and Einstein equations, the universe evolved from a white hole would appear indistinguishable from our own. The antimatter content of this domain evolves to play the same role as matter does here, governed by CPT symmetry and convergent attractor dynamics.
However, to ask when such a bounce occurs, one must answer for every where and every what. The attractor’s recursive logic permits no absolute temporal coordinate independent of the embedded structure. In this view, the emergence of time itself is a relational product of global coherence, not an external clock. Thus, the reverse-time domain is not simply a mirror, it is a self-sustaining and phase-locked sibling.
8.3. Reverse-Time Emergence of Matter from Spatial Iteration
In the reversed computational regime of the Spinor Universe, matter is not postulated but arises as the asymptotic solution to spatial recursion. As the anti-de Sitter domain begins its evolution, space no longer expands; it computes its own collapse. Each region of space begins to iterate its own internal topology, guided by residual phase gradients left behind by the forward-time universe.
The operator defines the local rules by which space recurses. These rules are not externally imposed but are inherited from the boundary conditions set by the forward-time attractor, particularly through encoded residues in the Higgs field, gravitational memory, and topological phase. The result is the spontaneous condensation of coherent structures: first as low-amplitude phase modes, and then as stabilized particle-like excitations.
Matter fields emerge where coherence becomes recursive, where the spinor tension reaches a topologically closed feedback loop. These emergent particles are not identical to their forward-time analogs but are conjugate structures in a mirrored attractor landscape. Mass, charge, and spin appear as conserved features of phase stability, not as innate properties.
Importantly, the stability of these structures is enforced by the same attractor constraints that operated in the forward domain. SU(3), SU(2), and U(1) gauge behaviors are re-expressed not through symmetry breaking, but through topological regularity in the recursive spinor computation.
Thus, matter does not appear all at once, nor uniformly. It emerges in regions of constructive recursion: locally seeded by the computational memory of evaporated black holes, globally organized by the inverted curvature of the attractor. The result is a universe in which matter is the output of space, just as space was the output of matter in the prior domain.
8.4. Condensation into White Hole Horizon
To translate this converged matter field into observable structure, we propose that the spinor eigenmode condensation manifests macroscopically as a white hole horizon a time-reversed analog to black hole formation. In this context, the white hole acts as the geometric resolution point where accumulated spinor coherence in the reverse-time domain spills over into the forward-time domain as localized, structured matter.
We treat the condensation process as a topological phase transition governed by local coherence thresholds:
where
is a coherence density threshold for horizon nucleation and
is a compact spatial domain in the reverse-time manifold.
The resulting white hole horizon marks the boundary beyond which spinor coherence cannot remain spatially distributed and must resolve into a forward-time causal structure a particle or field excitation. This provides a physical mechanism for particle genesis at the spacetime pivot, respecting both information conservation and temporal symmetry. Rather than representing the end of information, black holes in our model are phase convergence sites, echoing the unresolved questions of Hawking’s information paradox [
11] and Penrose’s spin-based view of spacetime structure [
3].
8.5. Dirac Evolution from the Reverse Side
In conventional high-energy physics, the Dirac equation is used to describe the evolution of matter fields forward in time:
where the mass term
m is generated by the Higgs mechanism via
.
However, in the Spinor Universe model, the reverse-time domain does not begin with particle excitations but rather with spatial self-iteration. In this domain, the spinor field
is not given as initial data, but is
generated by an operator acting on the spatial geometry:
where
is an operator or potential functional encoding the topology, curvature, and coherence of the spatial field.
8.6. Chirality and Spinor Directionality
The chiral nature of the weak force in the form of its exclusive coupling to left-handed fermions, has presented a longstanding puzzle within the Standard Model. In the Ontolotron framework, this asymmetry emerges not from a fundamental breaking of symmetry at high energy, but as a directional property of recursive spinor computation. The forward-time attractor favors left-handed coherence alignment during phase condensation, while the reverse-time field regime, we can interpret as a white hole horizon, would impose right-handed dominance. This suggests that chirality is not an intrinsic particle property, but a local expression of phase alignment with the temporal recursion axis. Under this interpretation, the CPT asymmetry of the weak force becomes a natural consequence of global coherence selection.
8.7. Toy Model for : Spatial Self-Computation Potential
We propose a toy model for the operator
that governs the self-computation of space in the reverse-time domain. Let
be a spinor-valued spatial field with curvature
, torsion
, and coherence phase
. Then we define:
where:
are weighting constants encoding how geometry contributes to emergent matter modes,
is a scalar curvature term derived from local spinor orientation fields,
is a local measure of topological torsion or spinor winding,
captures gradients in phase coherence, functioning like a local informational clock.
This operator enables self-consistent spatial regions to converge toward spinor eigenmodes that are compatible with a Higgs-stabilized boundary state. Thus, matter in the forward domain can be understood as the eigen-solution to a reverse-domain spatial phase evolution problem.
9. Precedents in Emerging Physics
While the Ontolotron framework introduces a novel interpretation of coherence, recursion, and gravitational structure, several recent discoveries across diverse domains suggest that these ideas may already be surfacing in observable ways. The following examples highlight physical systems where coherence, geometry, or recursion influence outcomes in ways that resonate with Ontolotron predictions.
9.1. Quantum Geometry
Recent work in condensed matter theory has demonstrated that quantum geometric properties, specifically the structure of wavefunctions in momentum space, can significantly influence physical observables, such as the critical temperature of superconductors [
13]. These studies show that modifying the underlying geometry of quantum states can relax pairing constraints and enable superconductivity at higher temperatures. This finding offers a powerful precedent for the Ontolotron framework, which extends this principle beyond band geometry to recursive spinor field topology. Where conventional approaches adjust electron overlap in k-space, the Ontolotron acts on recursion alignment in full spinor-valued fieldspace. The observed sensitivity of macroscopic coherence thresholds to quantum geometry provides supporting evidence that phase-structured attractor logic may govern physical transitions in at least the domain of condensed matter.
9.2. Muon-Catalyzed Fusion as a Recursion Shortcut
Muon-catalyzed fusion demonstrates that nuclear resolution can be dramatically enhanced by the presence of a mass-aligned intermediary, reducing energy barriers and favoring attractor states in line with recursion-driven models [
14]. In Ontolotron terms, the muon acts as a mass-weighted recursion anchor, aligning the phase structure and reducing the entropic friction. While traditionally dismissed as impractical due to muon loss, this mechanism provides a working example of how non-thermal, topological factors can guide nuclear resolution.
9.3. BEC-Based Black Hole Analogs and Horizon Formation
Experimental realization of acoustic black holes in Bose-Einstein condensates offers a laboratory demonstration of coherence trapping via sonic horizons, structures that Ontolotron theory interprets as phase recursion locks rather than mere analogs [
15]. These phenomena serve as laboratory-scale expressions of topological recursion barriers, where coherence becomes locally dominant and entropy export is blocked.
9.4. Quantum Hall Effects and Topological Insulators
The discovery of topological insulators and the quantum Hall effect affirms that global geometric properties can determine macroscopic electronic behavior, consistent with the Ontolotron’s broader principle of phase-structured recursion influencing dynamics [
16].
9.5. Anomalous Coherence Signatures in Astrophysical Contexts
Observations of unexplained positron distributions and gamma-ray signatures near galactic centers may reflect vacuum realignments in strong gravitational fields, offering possible large-scale evidence of coherence attractor behavior [
17].
10. Direct Test of Ontological Phase Completion
In a landscape increasingly dominated by mathematical elaborations of existing frameworks, often lacking in falsifiable predictions, we are pleased to present a series of concrete, testable proposals derived from the Ontolotron framework. These experiments are not merely heuristic illustrations, but operational hypotheses designed to expose measurable deviations from standard expectations under specific coherence-enhancing conditions. By linking the abstract logic of spinor-valued recursion with laboratory-accessible phenomena, we aim to demonstrate that foundational physics need not remain confined to formal perturbations, but can re-engage with empirical science in a meaningful and generative way.
10.1. Objective and Theoretical Basis
This experiment is designed to test a central prediction of the Ontolotron framework: that physical systems will resolve into globally coherent attractor configurations when supplied with sufficient symmetry ingredients and embedded within a macroscopic phase-convergent environment. Specifically, we propose to test whether a mixture of helium-3 and helium-6, in the correct nucleonic proportion to form helium-4, will undergo nuclear phase completion more readily than expected under standard statistical decay models when placed under conditions favoring global coherence. It addresses whether coherence emerges in defiance of entropy, or as its natural resolution. The Ontolotron proposes that entropy is not disorder, but the structural cost of phase convergence.
10.2. Isotopic Selection and Coherence Criteria
We select a mixture of 3He and 6He isotopes in stoichiometric proportion such that the total nucleon pool per ensemble aligns exactly with the formation of 4He nuclei. This provides an optimal phase symmetry landscape: all constituent nucleons are present, and the final attractor state (4He) represents a globally minimal configuration in both mass-energy and recursion complexity. The key hypothesis is that the presence of this latent coherence pathway will bias nuclear decay and reconfiguration events in a phase-structured environment.
10.3. Experimental Setup and Environmental Conditions
The isotope mixture is introduced into a bath of superfluid 4He, maintained below its lambda point at 2.17 K, forming a macroscopically coherent quantum medium. To impose global angular recursion alignment, the bath is shaped into a vortex geometry sufficient to create a sonic black hole configuration by creating a rotating flow regime in which local fluid velocity exceeds the speed of phonon propagation, thereby forming an acoustic event horizon. This geometry traps phononic excitations and prevents phase decoherence from radiating outward, producing a stable recursion environment in which spinor phase alignment may be externally enforced. Freshly generated 6He atoms and cryogenically cooled 3He atoms are injected continuously at low flux near the periphery of the vortex, allowing interaction with the coherence field without immediately disrupting its integrity. The 6He supply is sourced via neutron-lithium spallation and magnetically slowed prior to delivery. Control setups use identical isotope injection protocols into non-superfluid helium or inert cryogenic gases lacking coherence structure.
10.4. Detection Strategy and Measurement Criteria
Decay products are monitored through a multi-instrument arrangement designed to capture both conventional and coherence-correlated nuclear events. Specific measurement channels include:
Beta emission rate tracking from 6He, using high-resolution scintillation or semiconductor detectors, with attention to deviations from standard decay timing
Neutron detection via time-resolved scintillators or He-3 counters to identify possible emission spikes consistent with transient 5He formation
4He yield quantification through cryogenic mass spectrometry or time-of-flight particle analysis of evaporated atoms above the bath
Temporal synchronization of detected decay events with the injection schedule and phase profile of the superfluid vortex, allowing cross-correlation with coherence dynamics
Care is taken to distinguish statistically expected decay distributions from those exhibiting temporal clustering, enhanced production rates, or alignment with known coherence cycles. Additional shielding and background suppression methods are implemented to ensure that any deviations are attributable to the experimental configuration.
10.5. Standard Model Predictions vs. Ontolotron Forecast
Under standard nuclear physics, 6 He decays via beta emission with a half-life of 0.8 seconds, unaffected by surrounding electromagnetic or coherence conditions. 3 He is stable. The formation of 4 He beyond natural decay is not expected, nor is the emergence of 5 He, which is an extremely short-lived resonance in high-energy contexts.
Under the Ontolotron hypothesis, if coherence alignment influences attractor resolution, then:
Slight acceleration in 6 He decay rates may occur
Observable neutron bursts (suggesting 5 He) may emerge
4 He formation may exceed statistical expectation
Timing correlations between coherence field formation and nuclear transitions may be evident
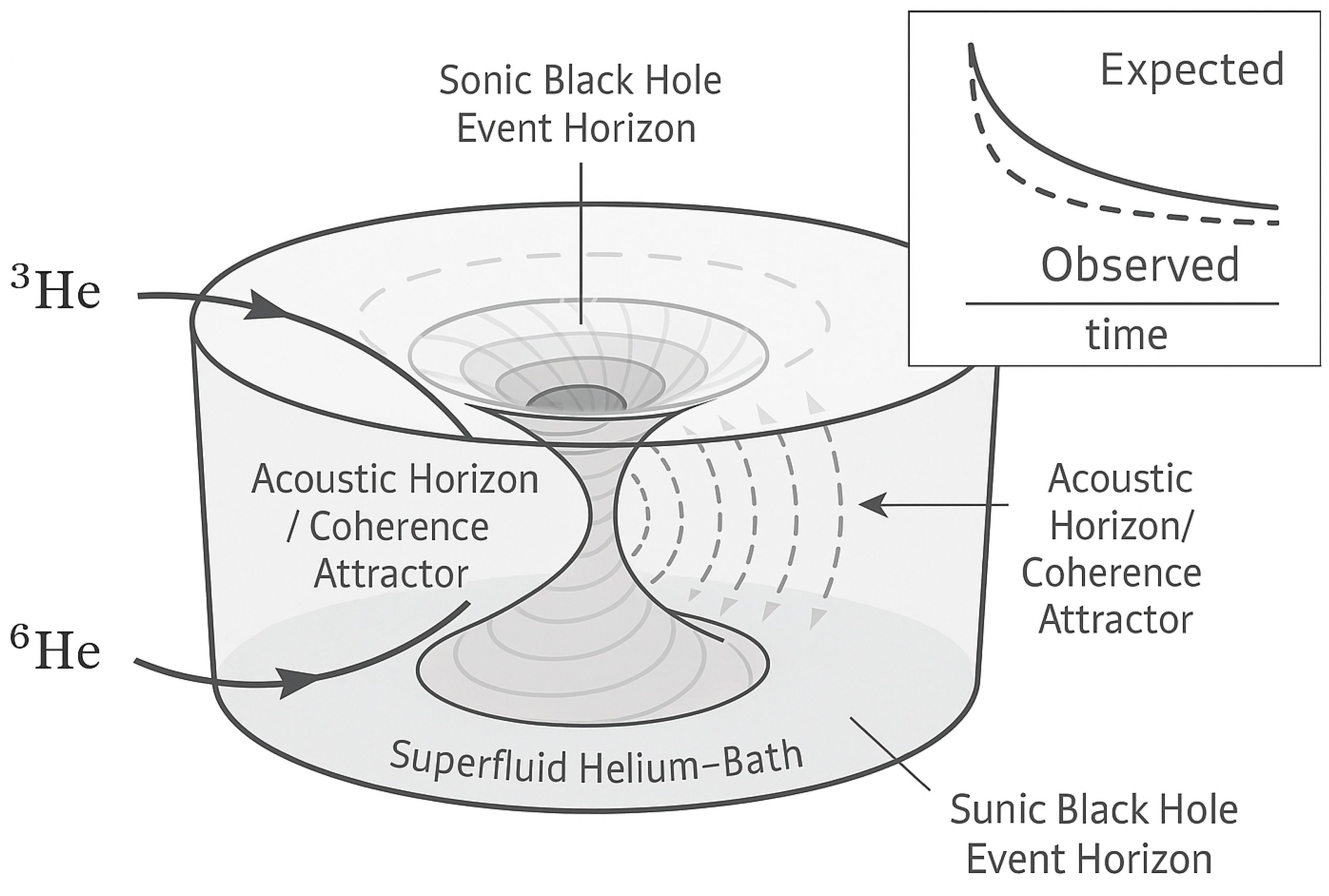
Figure 2.
This experimental setup introduces He isotopes into a superfluid helium-4 bath containing a coherence attractor in the form of a sonic black hole. The rotating superfluid creates a macroscopic quantum vortex, simulating an acoustic horizon. The Ontolotron framework predicts that such a structure may enhance phase convergence and influence nuclear decay behavior, revealing coherence-assisted resolution.
Figure 2.
This experimental setup introduces He isotopes into a superfluid helium-4 bath containing a coherence attractor in the form of a sonic black hole. The rotating superfluid creates a macroscopic quantum vortex, simulating an acoustic horizon. The Ontolotron framework predicts that such a structure may enhance phase convergence and influence nuclear decay behavior, revealing coherence-assisted resolution.
10.6. Interpretation
The presence of statistically significant deviations in beta decay timing, neutron emission patterns, or 4He yield, particularly if temporally correlated with coherence field formation or injection cycles, would constitute evidence that nuclear transitions are not governed purely by local energetics, but are influenced by global phase topology. In the Ontolotron framework, such results would indicate that the system is resolving into a deeper symmetry configuration in response to the coherence attractor of the sonic black hole geometry. Transient formation of 5He, enhanced clustering of decay events, or anomalous emergence of 4He would signal recursive phase closure guided by attractor logic, not stochastic independence. A null result would constrain the Ontolotron’s field influence to below the experimental sensitivity threshold, but would still validate the boundary conditions of coherence-mediated nuclear recursion.
10.7. Preliminary and Supporting Tests
While the primary experiment involving 3He and 6He in a superfluid 4He coherence field offers the most direct probe of the Ontolotron framework, several lesser tests may serve as stepping stones or partial validations. These experiments target specific signatures of coherence selection, entropy routing, and phase-alignment effects under progressively constrained conditions.
Electron-Sector Phase Closure Test via Bidirectional Ion Injection: Mirroring the principles explored in the primary helium-based test, this experiment translates the Ontolotron framework into the more accessible realm of electron dynamics. It explores whether macroscopic coherence fields can assist in resolving electron-scale phase opposites. Oppositely charged ions (e.g., H+ and OH− or electron-hole analogs) are introduced from opposite ends of a cryogenically stabilized superconductor or coherence-supporting medium. The hypothesis is that the superconductor, acting as a phase recursion basin, will accelerate charge recombination beyond classical diffusion-limited rates. Observable effects may include shortened resolution time, reduced radiation output upon recombination, or spatial phase alignment across the medium. The absence of recoil or radiation would signal not neutrality, but successful recursive integration towards coherence so complete that interaction leaves no trace. This serves as a clean electron-sector analog of the Ontolotron phase convergence principle, testing whether topological recursion preference applies beyond the nuclear domain.
Interferometric Phase Drift in Fiber Loops: Fiber optic interferometers arranged across a gravitational gradient may reveal minute deviations in phase stability not accounted for by conventional field models. Ontolotron prediction: phase-lock bias in systems embedded in global coherence gradients.
Time-Correlated Neutron Emission Clustering: Monitor beta and neutron emission from short-lived isotopes (e.g., 6He) in cryogenic traps for temporal clustering or phase-aligned release. Ontolotron prediction: coherence-linked timing preference in otherwise stochastic events.
BEC-Adjacent Nuclear Modulation: Embed weakly radioactive isotopes near a Bose-Einstein condensate of rubidium or lithium atoms. Ontolotron prediction: proximity to a macro-phase-locked field may bias decay channel selection or timing.
He-II Vortex Pattern Disruption: Introduce localized nucleon asymmetries (e.g., 3He) into a superfluid 4He bath and monitor vortex lattice integrity. Ontolotron prediction: Attractor incompatibility is expected to manifest as disruption in vortex lattice integrity, indicating that nucleonic asymmetries can interfere with coherent recursion.
These experiments, while indirect, offer meaningful constraints and possible early signals of coherence-sensitive dynamics within nuclear or field-aligned systems. They also serve to validate instrumentation, establish background models, and refine the theoretical bounds of Ontolotron influence.
11. Implications of Proposed Experiments
Each proposed experiment serves not only as a test of the Ontolotron framework, but as a potential gateway to new classes of physical interaction. If coherence alignment proves to influence nuclear or electronic behavior in any measurable way, a cascade of technological and theoretical consequences would follow.
If 3He and 6He isotopes undergo fusion-like phase resolution in a superfluid coherence field, it would demonstrate that nucleon arrangement can be influenced by global recursion topology. This would mark the emergence of nuclear structural engineering: the ability to guide nuclear reconfiguration using environmental coherence rather than brute-force energy input. It could enable stable transmutation, programmable decay channels, or low-radiation isotopic synthesis, opening the door to controlled nuclear manipulation without particle accelerators or reactors. More significantly, if attractor-based resolution proves sufficient to produce 4He, it would represent a new class of fusion driven not by thermal thresholds but by phase convergence. Fusion, in this model, becomes a coherence event, one in which nucleons resolve not through collision but through recursive phase locking. This redefinition could lay the groundwork for stable, low-temperature fusion strategies guided by coherence topology rather than brute thermodynamics.
If oppositely charged ions resolve silently in a rotating superconducting coherence basin, it would imply that phase alignment, not merely kinetic energy, is the limiting factor in charge recombination. This suggests new architectures for coherence-tuned electronics and quantum-classical hybrid computing systems. The ability to offload entropy-free charge resolution could radically reduce thermal bottlenecks in information systems, and may inform new low-noise measurement regimes for quantum devices. If coherence-guided charge resolution can be reliably engineered, it would mark a shift in how quantum computing architectures are conceived. Rather than sustaining fragile entangled states across large, monolithic arrays, computation could be distributed across modular coherence basins, each performing low-entropy phase resolution locally. These modules would act as passive recursion filters, resolving the input into stable, phase-aligned output. Such an architecture would enable scalable, entropy-robust quantum-classical hybrid networks, reducing the thermal and coherence burdens that limit current quantum hardware. In this model, computation is not the manipulation of qubits, but the selection of minimal-decoherence phase states performed across a spatially distributed quantum substrate.
Detection of phase-aligned neutron bursts from cryogenically trapped isotopes would show that even statistically random decay events can be pulled into coherence cycles under environmental constraints. This would imply that radioactive decay is not purely stochastic but conditionally recursive, a claim with implications for nuclear clock calibration, neutrino detection, and background radiation filtering.
If proximity to a Bose-Einstein condensate biases nuclear behavior, it would support the hypothesis that phase-locked environments can act as coherence amplifiers. This could lead to layered coherence systems where nuclear, electronic, and photonic domains are phase-coupled via shared recursion attractors, enabling cascading coherence transfer across physical scales.
If the introduction of nucleonic asymmetry disrupts vortex lattice structure in superfluid helium, it confirms that macroscopic phase coherence is selectively responsive to nuclear-scale alignment mismatches. This would further validate the cake ratio as a real-field coherence metric and support the use of superfluid systems as coherence-selective filters for material or isotopic classification.
12. Closing Reflection
Had Dirac written a marginal note differently, had he treated not merely as solutions, but as ontological primitives, the story of physics might have taken a different turn. But it is not too late.
This work does not seek to revise quantum mechanics or discard relativity. It seeks to reinterpret them within a deeper architectural framework: one in which time, matter, and information emerge through spinor-valued recursion, guided by a dynamic principle of coherence. The Ontolotron is offered not as a new force or field, but as a name for the actuator of actuality, the mechanism by which a universe selects itself from among the possibilities embedded in its own structure.
We have proposed a concrete path to empirical validation: a suite of experiments that press coherence itself into service as a physical variable. These tests range from modest phase measurements to nuclear recursion completion in superfluid attractor baths. They invite the universe to reveal whether coherence is merely a statistical accident, or the logic by which structure evolves.
Physics has not failed, but it has settled. This framework is a wager that the next leap will not come from one more layer of quantization or one more particle symmetry, but from a shift in what we believe physics is *for*: not to catalog what exists, but to uncover why this world, and no other, coheres into being.
The Ontolotron is not a theory of everything. It is a theory of *this*.
References
- A. Bruss, The Spinor Universe: A Topological Model of Matter-Antimatter Asymmetry and Temporal Duality, 2025. DOI:10.20944/preprints202504.2440.v1. [CrossRef]
- J. Barbour, The End of Time: The Next Revolution in Physics, Oxford University Press, 1999.
- R. Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Jonathan Cape, 2004.
- J. A. Wheeler, Information, Physics, Quantum: The Search for Links, Proceedings III International Symposium on Foundations of Quantum Mechanics, Physical Society of Japan, 1990.
- S. Lloyd, Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos, Knopf, 2006.
- L. Boyle and N. Turok, Conformal Symmetry, the Big Bang, and Cosmology, Phys. Rev. D, vol. 95, no. 12, 123510, 2017.
- R. Bernabei et al., Final model independent result of DAMA/LIBRA-phase1, The European Physical Journal C, vol. 73, no. 12, p. 2648, 2013. [CrossRef]
- Penrose, Angular momentum: an approach to combinatorial space-time, in Quantum Theory and Beyond, edited by T. Bastin, Cambridge University Press, pp. 151–180, 1971.
- P. J. Steinhardt and N. Turok, A Cyclic Model of the Universe, Science, vol. 296, no. 5572, pp. 1436–1439, 2002. [CrossRef]
- R. F. Streater and A. S. Wightman, PCT, Spin and Statistics, and All That, Princeton University Press, 2000.
- S. W. Hawking, Breakdown of Predictability in Gravitational Collapse, Phys. Rev. D, vol. 14, no. 10, pp. 2460–2473, 1976. [CrossRef]
- E. Verlinde, On the Origin of Gravity and the Laws of Newton, JHEP, vol. 2011, no. 4, p. 29, 2011. [CrossRef]
- J. B. Williams et al., Probing Instantaneous Single-Molecule Chirality in the Planar Ground State of Formic Acid, arXiv preprint arXiv:2503.13318, 2025. arXiv:2503.13318, 2025. [CrossRef]
- K. Nagamine, Muon catalyzed fusion, Reviews of Modern Physics, vol. 70, no. 4, pp. 1331–1360, 1998.
- O. Lahav et al., Realization of a sonic black hole analog in a Bose-Einstein condensate, Physical Review Letters, vol. 105, no. 24, 240401, 2010. [CrossRef]
- M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators, Reviews of Modern Physics, vol. 82, no. 4, pp. 3045–3067, 2010. [CrossRef]
- G. Weidenspointner et al., An asymmetric distribution of positrons in the Galactic disk revealed by gamma-rays, Nature, vol. 451, no. 7175, pp. 159–162, 2008. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).