Entropy-divergent Photon Tunneling For Time-asymmetric Information Retrieval

1. Introduction

Photons, as massless particles, follow null geodesics in general relativity and carry energy and information in quantum mechanics without experiencing proper time. This unique behavior positions them as ideal probes of space-time. In the fluid dynamics model of space-time, where time emerges from entropy divergence, we explore whether photons can transmit information across temporally asymmetric domains [Mudassir, 2025; Arminjon, 2006].

We propose that engineered entropy-neutral tunnels—akin to thermodynamic wormholes—enable photons to transfer information from a high-entropy (future-like) domain to a low-entropy (present-like) domain. Because photons do not generate local entropy, they remain coherent across the tunnel, allowing detectable phase shifts that precede emission timestamps in coordinate time while preserving causality in thermodynamic time.

This paper introduces a mechanistic model combining entropy flux dynamics, coherent photon transport, and an experimental proposal based on Bose–Einstein condensates (BECs) and Josephson junctions.

2. Theoretical Framework

2.1. Space-Time as a Thermodynamic Fluid

We model space-time as a compressible medium with entropy flux $\overrightarrow{\mathit{S}}$ and local entropy divergence $\nabla \cdot \overrightarrow{\mathit{S}}$. The emergence of time is governed by / Time Emergence from Entropy Divergence:

$${\displaystyle \frac{dt}{d\tau }}\propto \nabla \cdot \overrightarrow{S}$$

(1)

Where:

• $t$: Coordinate time (global observer)
• $\tau$: Proper time (local observer)
• $\overrightarrow{S}$: Entropy flux vector
• $\nabla \cdot \overrightarrow{S}$: Entropy production rate

This equation expresses that the flow of coordinate time relative to proper time is proportional to the local entropy divergence. It captures the thermodynamic emergence of time in the fluid space-time model

This formulation follows thermodynamic interpretations of Einstein’s equations [Jacobson, 1995] and entropic gravity [Verlinde, 2011].

2.2. Entropy-Divergent Domains and Temporal Asymmetry

Consider two domains:

• Region A: $\nabla \cdot {\overrightarrow{S}}_A\approx 0$
• Region B: $\nabla \cdot {\overrightarrow{S}}_B>\nabla \cdot {\overrightarrow{S}}_A$

Connecting A and B via an entropy-stabilized tunnel allows a photon from B to reach A before its emission time in coordinate terms, yet still respects the thermodynamic time arrow. This reframes predictive signaling as a causally consistent entropy-driven phenomenon.

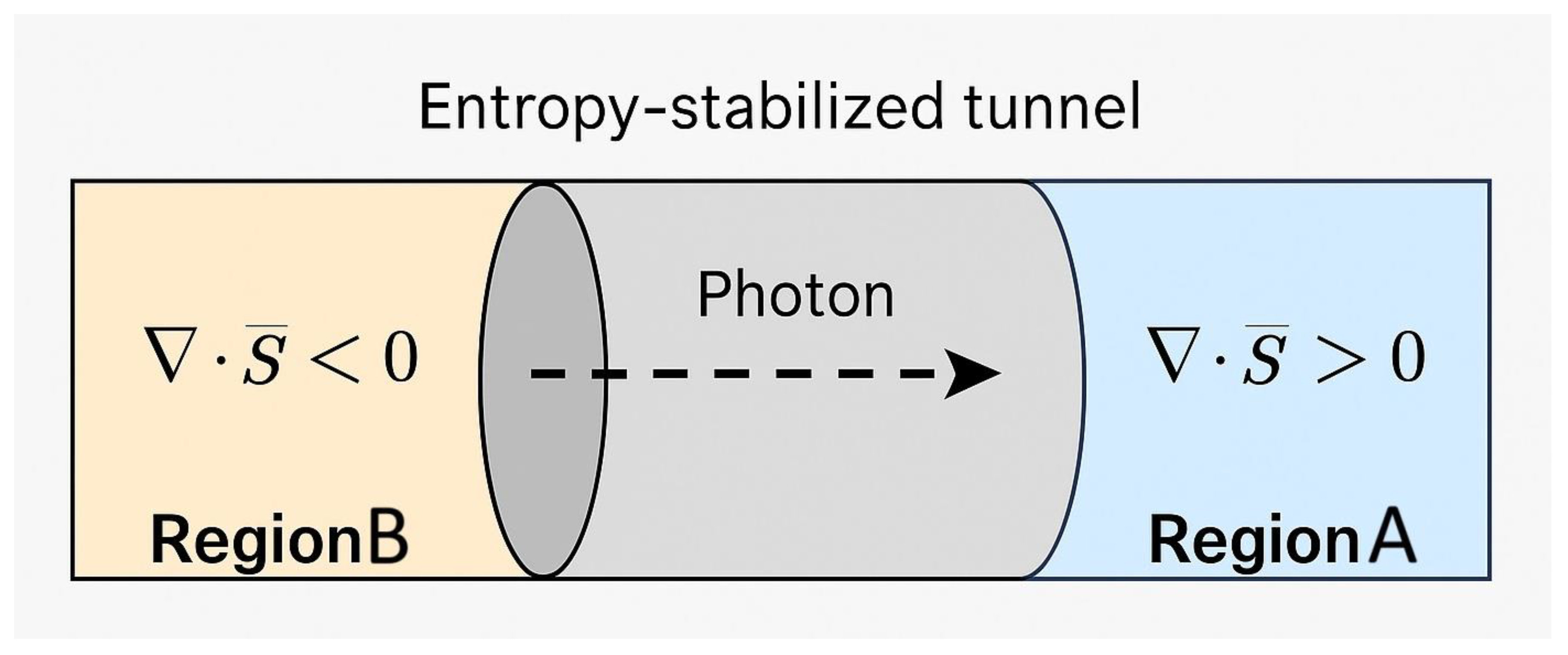
Figure 1. Entropy tunnel schematic showing Region A ($\nabla \cdot {\overrightarrow{S}}_A<0$∇⋅SA​<0) and Region B ($\nabla \cdot {\overrightarrow{S}}_B>0$∇⋅SB​>0) connected by an entropy-stabilized tunnel. A photon (dashed path) travels from the higher-entropy domain (B) to the lower-entropy domain (A), enabling time-asymmetric signaling without violating thermodynamic causality.

Figure 1. Entropy tunnel schematic showing Region A ($\nabla \cdot {\overrightarrow{S}}_A<0$∇⋅SA​<0) and Region B ($\nabla \cdot {\overrightarrow{S}}_B>0$∇⋅SB​>0) connected by an entropy-stabilized tunnel. A photon (dashed path) travels from the higher-entropy domain (B) to the lower-entropy domain (A), enabling time-asymmetric signaling without violating thermodynamic causality.

3. Photons As Entropy-Neutral Carriers

Photon Entropy Neutrality / Photons, being massless and decoherence-resistant in vacuum, follow:

$$\nabla \cdot {\overrightarrow{S}}_{\gamma }=0$$

(2)

This states that photons carry zero entropy divergence along their path, qualifying them as entropy-neutral carriers or “information ghosts.”

Where ${\overrightarrow{S}}_{\gamma }$ is the photon’s entropy flux. This implies photons can carry phase information without perturbing the entropy structure of the tunnel, making them ideal entropy-neutral information carriers, or “information ghosts.”

4. Entropy Tunneling And Phase Preservation

4.1. Thermodynamic Wormhole Analogs

The tunnel must maintain entropy coherence/ Stability Condition for Entropy Tunnel:

$$\mathsf{\Delta }\left(\nabla \cdot \overrightarrow{S}\right)\approx 0\mathrm{along}\mathrm{the}\mathrm{tunnel}$$

(3)

For a tunnel to preserve photon phase and coherence, the entropy divergence must remain nearly constant along its axis.

This condition mirrors phase-locking seen in superfluids and is achievable in systems like BECs [Sabín et al., 2014]. These are not spatial shortcuts but entropy-stabilized pathways for coherent transmission.

4.2. Photon Phase Evolution

Photon Phase Evolution in Tunnel:

$$\varphi \left(t\right)=\int \omega \left(t\right)dt=\int {\displaystyle \frac{2\pi c}{\lambda \left(t\right)}}dt$$

(4)

Where:

• $\varphi \left(t\right)$: Phase
• $\omega \left(t\right)$: Angular frequency
• $\lambda \left(t\right)$: Wavelength under entropy-tunnel conditions

Describes the phase accumulation of a photon as it moves through a time-varying entropy field with local wavelength $\lambda \left(t\right)$.

Preserved phase indicates stable entropy conditions across the tunnel, allowing detection of early phase signatures from Region B in Region A.

5. Proposed Bec Experimental Simulation

5.1. Setup Overview

• Two BEC chambers (rubidium-87) at ~100 nK
• Tunable Josephson junction as the tunnel
• Photon (780 nm) injection into Region B
• Homodyne or Ramsey detectors in Region A

5.2. Challenges and Feasibility

• Maintaining coherence across the tunnel
• Spectroscopic entropy monitoring
• Accurate timestamping via atomic clocks

This builds on past work simulating black hole analogs in BECs [Sabín et al., 2014].

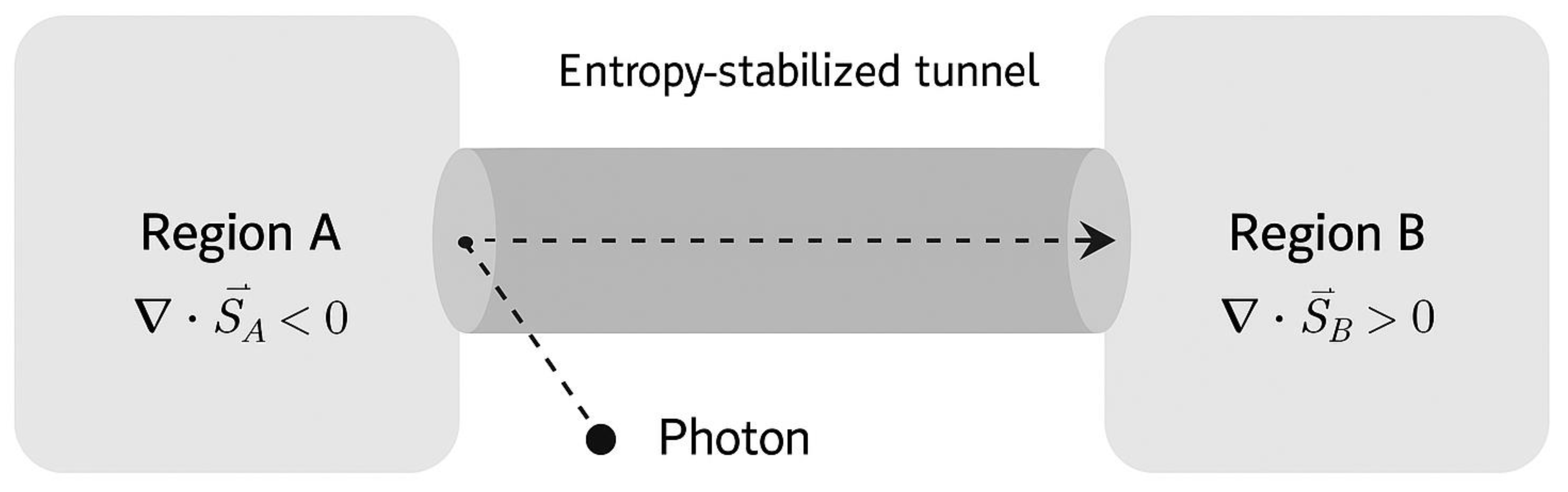
Figure 2. BEC setup with Josephson junction. Simplified schematic of the entropy-stabilized tunnel linking Region B ($\nabla \cdot {\overrightarrow{S}}_B>0$∇⋅SB​>0) to Region A ($\nabla \cdot {\overrightarrow{S}}_A<0$∇⋅SA​<0), with the photon’s trajectory (dashed line) transferring information from a future-like entropy domain to a past-like one, demonstrating coherent time-asymmetric signaling through entropy-neutral transport.

Figure 2. BEC setup with Josephson junction. Simplified schematic of the entropy-stabilized tunnel linking Region B ($\nabla \cdot {\overrightarrow{S}}_B>0$∇⋅SB​>0) to Region A ($\nabla \cdot {\overrightarrow{S}}_A<0$∇⋅SA​<0), with the photon’s trajectory (dashed line) transferring information from a future-like entropy domain to a past-like one, demonstrating coherent time-asymmetric signaling through entropy-neutral transport.

6. Applications and Implications

• Time-desynchronized communication
• Entropy-guided computation across domains
• Foundational tests of thermodynamic time
• Cosmological applications via ER=EPR analogies [Maldacena & Susskind, 2013]

7. Discussion And Originality

This model is the first to unify fluid space-time theory, entropy divergence, and photon phase tunneling in a causality-preserving signaling mechanism. It avoids retrocausal paradoxes and aligns with experimentally feasible BEC systems. Limitations include system scalability and entropy tunnel maintenance.

8. Conclusions

We propose a coherent, causally consistent mechanism for entropy-asymmetric signal transfer using photon tunneling across entropy-stabilized domains. Photons, acting as entropy-neutral carriers, can arrive in a lower-entropy region before their emission time in coordinate terms—without violating thermodynamic causality.

Laboratory realization is possible using Bose–Einstein condensate systems, opening new experimental routes into time emergence, quantum thermodynamics, and space-time fluid dynamics.