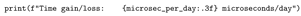Kinetic Scalar Modulation and Quantum Transport Extending the NUVO Schr/odinger Equation – Part 16 of the NUVO Theory Series

1. Introduction

The ability to describe time dilation and redshift in quantum systems using a scalar-modified Schrödinger equation opens the door to a unified scalar field interpretation of quantum evolution. In previous work (Series 15), we demonstrated that gravitational redshift could be encoded through a position-dependent scalar field $\lambda \left(r\right)$ (Here, “velocity” refers specifically to the instantaneous motion relative to the scalar background field. In NUVO theory, only such velocity induces true scalar modulation. Uniform relative motion through flat scalar regions does not alter sinertia, distinguishing NUVO from the coordinate effects of special relativity.) [1], modifying the time and energy terms in the Schrödinger equation.

However, this scalar field also depends on velocity. The present work extends the NUVO quantum framework by incorporating the full $\lambda (r,v)$ structure, which captures both gravitational and kinetic contributions to local time modulation. This richer formulation allows us to model quantum phase evolution along arbitrary trajectories and introduces a scalar-based parallel transport mechanism for quantum states.

2. Modified Schrödinger Equation with $\mathit{\lambda }(\mathit{r},\mathit{v})$

To capture the full dynamics of quantum evolution in scalar-modulated space, we extend the Schrödinger equation to include velocity dependence in the scalar field. The scalar field in NUVO theory is given by:

$$\lambda (r,v)=\gamma \left(v\right)+\mathrm{\Phi }\left(r\right)$$

where $\gamma \left(v\right)$ accounts for local velocity, and $\mathrm{\Phi }\left(r\right)$ encodes the gravitational potential. This extension ensures that both gravitational and kinematic effects influence quantum phase evolution, enabling predictions in non-static systems such as satellites, interferometers, and accelerated observers.

The inclusion of velocity dependence is crucial when considering systems in motion through gravitational fields, such as orbiting satellites, atomic interferometers on accelerating platforms, or moving clocks in Earth-bound laboratories. These systems experience not only gravitational time dilation but also kinetic time modulation—both of which must be captured in the quantum evolution.

To incorporate this, we extend the modified Schrödinger equation to use the full scalar modulation $\lambda (r,v)$:

$$i\hslash \lambda (r,v){\displaystyle \frac{\partial \psi }{\partial t}}=\left[-{\displaystyle \frac{{\hslash }^2}{2m}}\lambda (r,v){\nabla }^2+\lambda (r,v)V\left(r\right)\right]\psi$$

This equation differs from the traditional Schrödinger equation in three key ways:

• Time Derivative Scaling: The term $\lambda (r,v)$ on the left-hand side modulates the rate at which quantum phase evolves. This reflects the fact that time is experienced differently depending on both gravitational depth and motion relative to the local frame.
• Kinetic Term Scaling: The Laplacian (kinetic energy) operator is scaled by $\lambda (r,v)$, meaning the effective inertial response of the particle is altered by its velocity and position. This term captures how local motion through scalar-modulated space affects dispersion and phase curvature.
• Potential Energy Scaling: Although $V\left(r\right)$ remains a classical potential, its influence on the system is scaled by $\lambda (r,v)$, changing the effective strength of binding or repulsion in scalar-modulated regions.

In this formulation, $\lambda (r,v)$ acts as a conformal prefactor that modulates the entire Hamiltonian, and hence the phase evolution, of the wavefunction. This allows NUVO theory to represent both gravitational and motion-induced time dilation effects in quantum systems within a single unified framework.

In the static limit ($v=0$), the equation reduces to the form used in Series 15:

$$i\hslash \lambda \left(r\right){\displaystyle \frac{\partial \psi }{\partial t}}=\left[-{\displaystyle \frac{{\hslash }^2}{2m}}\lambda \left(r\right){\nabla }^2+\lambda \left(r\right)V\left(r\right)\right]\psi$$

In the gravitationally flat and low-velocity limit, $\lambda (r,v)\to 1$, and we recover the standard Schrödinger equation of quantum mechanics [2].

Thus, this generalized NUVO-modified Schrödinger equation provides a natural path for including relativistic effects without requiring a full quantum field theory framework or spacetime curvature. Instead, all corrections emerge from scalar modulation rooted in the physical parameters of the system.

3. Scalar-Modulated Parallel Transport

The inclusion of $\lambda (r,v)$ in the Schrödinger equation introduces a deeper structure in the evolution of quantum states: their phase and energy become path-dependent due to scalar modulation. This invites a natural extension — the notion of parallel transport of a wavefunction along a classical trajectory through scalar-modulated space.

Let $\gamma \left(t\right)$ denote a trajectory in the NUVO manifold M, parameterized by coordinate time t, with local scalar modulation $\lambda \left(\gamma \right(t\left)\right)=\lambda \left(r\right(t),v(t\left)\right)$. The phase evolution of a quantum state $\psi$ transported along this path is no longer globally uniform, but varies according to the local value of $\lambda$ encountered at each point along the path.

We propose the following condition for scalar-modulated parallel transport:

$${\displaystyle \frac{D\psi }{Dt}}\equiv \lambda \left(\gamma \left(t\right)\right){\displaystyle \frac{d\psi }{dt}}+\psi {\displaystyle \frac{d\lambda }{dt}}=0$$

This transport rule enforces that the change in $\psi$ along $\gamma \left(t\right)$ is compensated exactly by the change in scalar field modulation. Intuitively, if the local scalar "clock rate" changes, the wavefunction must adjust its phase rate to maintain physical consistency. This equation ensures that wavefunctions remain synchronized with the local structure of time and energy set by $\lambda (r,v)$.

3.1. Connection Form and Phase Evolution

We define a scalar connection 1-form along the trajectory as:

$${\mathcal{A}}_{\lambda }\left(t\right)={\displaystyle \frac{d\lambda }{dt}}$$

which acts analogously to a gauge connection in electromagnetism or general relativity. The accumulated quantum phase along the path is then given by a path-ordered exponential:

$$\psi \left(t\right)=\mathcal{P}exp\left(-i{\int }_{\gamma \left(0\right)}^{\gamma \left(t\right)}{\displaystyle \frac{E}{\hslash }}\lambda \left(\gamma \left(t^{\prime }\right)\right)d{t}^{\prime }\right)\psi \left(0\right)$$

Here, $\mathcal{P}$ denotes path ordering, and E is the energy eigenvalue in the local frame. This expression generalizes the standard global phase factor $exp(-iEt/\hslash )$ to a locally modulated phase evolution that varies with both gravitational and kinematic conditions along the path.

3.2. Geometric Interpretation

In this framework, the scalar field $\lambda (r,v)$ acts as a local time-scaling field and defines a **parallel transport structure** for quantum states in NUVO space. This is not parallel transport in the Riemannian sense (using affine connections and curvature), but rather a scalar-rescaled transport mechanism that governs how the quantum phase evolves in a non-uniform scalar field.

This construct provides a bridge between classical trajectory mechanics and quantum evolution: the path of the particle modulates the rate of time and energy, and thus directly controls the phase and coherence of the quantum wavefunction.

3.3. Comparison to Standard Quantum Transport

In standard quantum mechanics, time evolution is generated by the Hamiltonian and is globally uniform. In NUVO theory, by contrast: - The time generator is modulated by $\lambda (r,v)$, - The "clock" experienced by the system is locally stretched or compressed, - And quantum coherence can become path-dependent, even in flat space, if scalar gradients exist.

This leads to predictions for measurable phase shifts, coherence loss, and redshift effects in systems subject to varying $\lambda$—including orbiting clocks, accelerating quantum particles, or extended entangled systems in different gravitational and velocity regimes.

4. Applications and Predictions

The introduction of scalar-modulated quantum transport through $\lambda (r,v)$ offers several experimentally relevant consequences that distinguish NUVO theory from both classical general relativity and standard quantum mechanics. Below, we outline three primary applications that illustrate the physical significance of this formalism. It is important to emphasize that in NUVO, only real instantaneous velocity with respect to the scalar geometry contributes to $\lambda (r,v)$. Constant velocity through a uniform scalar field does not induce modulation. This distinction sets NUVO apart from SR, where coordinate-relative velocity leads to apparent time dilation even without physical interaction.

4.1. Redshift and Time Dilation in Moving Systems

In traditional treatments, gravitational redshift is accounted for by the position-dependent gravitational potential, while relativistic Doppler shifts arise from relative motion. In NUVO theory, both effects are unified under a single scalar modulation function $\lambda (r,v)$ [3].

Consider a satellite in an elliptical orbit. At each point along its trajectory, the local wavefunction governing an onboard atomic clock experiences a combined modulation from: - Gravitational potential: $\mathrm{\Phi }\left(r\right)={\displaystyle \frac{GM}{r{c}^2}}$ - Orbital velocity: $v\left(t\right)$, contributing $\gamma \left(v\right)$

The cumulative effect leads to a locally modulated energy level and frequency of oscillation. The predicted rate of time passage—and thus the tick rate of the clock—follows:

$${\nu }_{\mathrm{local}}\left(t\right)={\displaystyle \frac{E_0}{\hslash }}·\lambda (r\left(t\right),v\left(t\right))$$

This formulation allows for an exact prediction of redshift variation throughout the orbit, not only at apogee or perigee. It also allows new corrections to GPS synchronization and satellite clock drift to be derived directly from NUVO theory.

4.2. Interference Effects and Scalar Phase Shift

In atom interferometers or double-slit experiments with quantum particles following multiple paths, NUVO predicts a differential phase accumulation due to path-dependent $\lambda (r,v)$ fields.

Let paths ${\gamma }_1\left(t\right)$ and ${\gamma }_2\left(t\right)$ be two classical trajectories between a source and detector. The total phase difference between wavefunction components along these paths is:

$$\Delta \varphi ={\displaystyle \frac{E}{\hslash }}{\int }_0^T\left[\lambda \left({\gamma }_1\left(t\right)\right)-\lambda \left({\gamma }_2\left(t\right)\right)\right]dt$$

If the two paths differ in gravitational depth, velocity profile, or both, the phase shift will reflect the scalar field differential. This is a direct generalization of the Aharonov–Bohm phase, but arising from $\lambda (r,v)$ instead of vector potential or topological phase.

This effect could be tested in precision cold-atom interferometry, where sensitivity to gravitational and inertial forces is high and external conditions can be modulated.

4.3. Quantum Coherence and Entanglement Across Frames

Entangled quantum systems in different scalar field environments experience differential time evolution. In NUVO theory, this leads to a modulation in their coherence time.

Let particles A and B be entangled but situated in regions with distinct scalar modulation: ${\lambda }_A=\lambda (r_A,v_A)$ and ${\lambda }_B=\lambda (r_B,v_B)$. The relative phase of entanglement evolves as:

$${\varphi }_{\mathrm{rel}}\left(t\right)={\int }_0^t\left[{\lambda }_A\left(t^{\prime }\right)-{\lambda }_B\left(t^{\prime }\right)\right]·{\omega }_{0}d{t}^{\prime }$$

If the difference is large or time-varying, entanglement visibility will diminish over time due to accumulating phase mismatch. This provides a path to understanding quantum decoherence in relativistic or gravitationally varying settings—not as noise or interaction with an environment, but as an intrinsic result of scalar geometry.

Such predictions could be verified using long-baseline quantum communication setups, Earth-satellite entanglement experiments, or laboratory tests with differential acceleration platforms.

5. Outlook and Future Work

This extension of the NUVO-modified Schrödinger equation to include full scalar modulation through $\lambda (r,v)$ brings us closer to a complete quantum formulation within the NUVO framework. By incorporating both gravitational and kinematic effects into a single scalar evolution factor, NUVO theory offers a unified approach to time dilation, redshift, and coherence modulation in quantum systems—without requiring curvature of spacetime or traditional relativistic tensor fields.

The introduction of scalar-modulated parallel transport provides a geometric mechanism for understanding quantum phase evolution in arbitrary motion and gravitational fields. This idea may offer new insights into phase structure, quantum measurement, and coherence degradation without appealing to decoherence or external collapse models.

Several key developments lie ahead:

• Covariant Quantum Dynamics: Develop a formal NUVO covariant derivative for quantum fields in scalar-modulated space. This will enable the full parallel between quantum operator evolution and geometric transport.
• Berry Phase and Aharonov–Bohm Generalization: Explore whether scalar phase transport in NUVO mimics or generalizes well-known quantum geometric phase phenomena. This includes modulated cyclic integrals and interference-based effects.
• Entanglement and Frame Coherence: Extend the formalism to entangled quantum systems moving through different scalar fields. Determine coherence lifetime, synchronization drift, and causal limits under NUVO modulation.
• Experimental Verifiability: Identify high-precision systems where scalar field modulation is measurable. These include atomic clocks in LEO/MEO, satellite-based entanglement tests, and interferometric experiments in variable acceleration fields.
• Bridge to NUVO Hilbert Bundles: As developed in Series 14, the operator-theoretic formalism may be extended to a Hilbert bundle where each point has a $\lambda$-dependent quantum state space. This paper provides the necessary local transport rule along such fibers.

Ultimately, this work strengthens the NUVO framework as a viable alternative to both general relativity and standard quantum mechanics in explaining redshift, time dilation, coherence, and measurement — using a scalar, conformal foundation rooted in energy, geometry, and motion.