Beyond the Big Bang: Resolving the Lithium Discrepancy Through Quantum Coherence and Discrete Geometry

1. Introduction

The Lithium Discrepancy remains one of the most persistent and unresolved anomalies within the framework of Big Bang Nucleosynthesis (BBN). While the standard cosmological model successfully predicts the primordial abundances of hydrogen and helium with remarkable accuracy [1,2], it fails to account for the observed quantities of lithium. Specifically, the model overpredicts the abundance of lithium-7 by a factor of approximately three, and simultaneously underestimates the presence of lithium-6 by several orders of magnitude [3,4].

These discrepancies pose significant challenges to the prevailing assumption that the early universe evolved under uniform, isotropic, and thermally equilibrated conditions. According to the standard BBN theory, nuclear reactions in the first few minutes after the Big Bang were driven solely by temperature, baryon density, and reaction cross-sections [1]. However, lithium isotopes, being both fragile and highly sensitive to their formation environment, appear to be uniquely influenced by factors beyond thermal dynamics. Numerous attempts to resolve the discrepancy through astrophysical depletion models or particle decay mechanisms have so far proven insufficient [5].

Recent developments in theoretical physics suggest that quantum coherence, geometric discretization, and vacuum memory may have played nontrivial roles during the nucleosynthetic epoch. The Multifaceted Coherence (MC) model, in combination with the Superluminal Graviton Condensate Vacuum (SGCV), offers a compelling reinterpretation of early-universe processes, in which decoherence gradients, ghost field dynamics, and structured curvature tensors actively shaped elemental formation [4,6].

This work introduces a quantum-coherent, geometry-weighted framework for nucleosynthesis that resolves the lithium anomalies without requiring fine-tuned initial conditions, exotic particle decays, or modifications to nuclear physics. By embedding reaction dynamics within a coherent informational substrate and discrete geometric structures such as those described in the Dodecahedron Linear String Field Hypothesis (DLSFH), we propose a model in which lithium abundances are a natural consequence of coherence evolution and curvature-induced nucleosynthetic constraints.

2. The Flawed Assumptions of the Big Bang Model

Standard cosmology assumes that the universe originated from a singularity—a point of infinite density and temperature—followed by a uniform, adiabatic expansion into a hot plasma described by general relativistic dynamics and classical thermodynamic equations of state. These assumptions underpin the conventional formulation of Big Bang Nucleosynthesis (BBN), where the Friedmann–Lemaître–Robertson–Walker (FLRW) metric governs the spacetime evolution:

$${\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2={\displaystyle \frac{8\pi G}{3}}\rho -{\displaystyle \frac{k}{a^2}}+{\displaystyle \frac{\Lambda }{3}},$$

(1)

where $a\left(t\right)$ is the scale factor, $\rho$ the energy density, $\Lambda$ the cosmological constant, and k the curvature parameter. Under this framework, nuclear reaction networks are computed assuming thermal equilibrium and uniform matter–radiation densities. However, this approach begins to fail when applied to isotopes like lithium-6 and lithium-7.

The singularity at $t=0$ leads to divergent quantities such as temperature ($T\to \infty$), curvature ($R\to \infty$), and entropy density ($s\to \infty$), all of which are physically undefined and mathematically unstable in the quantum regime. These divergences violate the continuity of quantum coherence and contradict principles of quantum field theory in curved spacetime [7].

Moreover, lithium nuclei exhibit high sensitivity to minute fluctuations in baryon density, local curvature, and coherence phase. The reaction cross-sections for lithium production are nonlinearly dependent on environmental variables. For example, the fusion of tritium and helium-4 to produce lithium-7:

$$\mathrm{³}\mathrm{H}{+}^4\mathrm{He}{\to }^7\mathrm{Li}+\gamma ,$$

(2)

has a narrow resonance window and is highly susceptible to coherence fluctuations and local entropy gradients. In the classical BBN framework, the reaction rate per unit volume is computed using:

$$R=n_1{n}_2\langle \sigma v\rangle ,$$

(3)

where $n_1,n_2$ are particle number densities and $\langle \sigma v\rangle$ is the thermally averaged cross-section. This assumes Maxwell–Boltzmann statistics and fails to account for quantum interference or coherence-based suppression effects.

However, if quantum coherence is retained or decays anisotropically across regions of high curvature, this averaging becomes invalid. In the MC–SGCV framework, coherence-weighted rates must replace thermal averages:

$$R_{\mathrm{MC}}=n_1{n}_2\kappa (x,t)·\langle \sigma v\rangle ,$$

(4)

where $\kappa (x,t)\in (0,1)$ is the local coherence susceptibility tensor that modulates interaction probability based on phase alignment and entropy gradient:

$${\partial }_t{C}_{\mu \nu }(x,t)=-\kappa (x,t)·{\partial }_{t}S(x,t).$$

(5)

This correction explicitly ties quantum coherence decay to reaction dynamics, violating the homogeneity and isotropy assumptions critical to the traditional BBN paradigm. Consequently, the lithium-6/lithium-7 yield discrepancy cannot be fully resolved without incorporating coherence dynamics and geometric quantization, as thermal models lack sensitivity to localized curvature effects and $\psi$-suppressed regions.

The assumption of a singular origin and purely thermal fusion thus constitutes a fundamental flaw in the Big Bang model’s treatment of nucleosynthesis. Replacing these assumptions with a coherence-preserving pre-nucleosynthetic regime, as proposed by the MC–SGCV model, resolves the lithium anomaly while preserving the successful predictions for hydrogen and helium.

3. Theoretical Framework: MC and SGCV

The framework of Multifaceted Coherence (MC) offers a novel quantum-geometric approach to early-universe dynamics, in which the structure of space, matter, and energy arises not from stochastic thermal fluctuations but from the evolution and collapse of coherent quantum fields. In this formulation, quantum coherence is not an abstract scalar property but a geometric and tensorial quantity that evolves across space and time, driven by local curvature, entropy gradients, and vacuum fluctuations [4,6].

The foundational object in this framework is the coherence tensor field $C_{\mu \nu }(x,t)$, which encodes the degree and directionality of quantum phase alignment within the local spacetime geometry. Unlike the metric tensor in general relativity, $C_{\mu \nu }$ does not represent spacetime intervals directly, but rather the field compatibility structure among qubits, graviton wavefunctions, and curvature fluctuations across discrete geometric substrates such as the DLSFH lattice [6].

The evolution of the coherence tensor is governed by the following fundamental equation:

$${\partial }_t{C}_{\mu \nu }(x,t)=-\kappa (x,t)·{\partial }_{t}S(x,t),$$

(6)

where $\kappa (x,t)\in [0,1]$ is a coherence susceptibility field that modulates how local entropy variations affect quantum phase order. The term ${\partial }_{t}S(x,t)$ represents the entropy production rate at spacetime point $(x,t)$, arising from decoherence events, graviton scatterings, or quantum memory collapse. This equation signifies that coherence decays in regions of rising entropy, but the rate and mode of decay depend on the local coherence topology and background curvature.

The underlying coherent field ${\psi }_s$ represents the pre-decoherent wavefunction of the system, entangled not only with matter but also with the geometric curvature state of spacetime. As the universe cools and expands, this deeper field undergoes partial collapse, and the observable field ${\psi }_s^{★}$ emerges as a projection or measurement-compatible subset of ${\psi }_s$, influenced by the SGCV structure:

$${\psi }_s^{★}(x,t)={\Pi }_{\mathrm{obs}}\left[{\psi }_s(x,t)\right],$$

(7)

where ${\Pi }_{\mathrm{obs}}$ denotes the projection operator consistent with the decoherence boundary conditions defined by observer-frame entropy and contextual ontological fields (COF) [4].

3.1. SGCV as Coherence Substrate

The Superluminal Graviton Condensate Vacuum (SGCV) is postulated as the underlying energy structure from which quantum coherence emerges and interacts. SGCV functions as a zero-point lattice of graviton-based superluminal modes that modulate both quantum information storage and curvature propagation. It provides the phase-stable background upon which ${\psi }_s$ is encoded. In this vacuum state, gravitons are not just force mediators but coherence-maintaining elements that resist entropy collapse via localized phase locking.

The local curvature $R_{\mathrm{SGCV}}(x,t)$ in the SGCV lattice is quantized across discrete dodecahedral cells as:

$$R_{\mathrm{SGCV}}\left(v_i\right)=\sum _j{\theta }_{ij},$$

(8)

where ${\theta }_{ij}$ is the angular deficit between adjacent faces of the dodecahedral cell at vertex $v_i$, following the DGQG formalism. These angular deficits act as curvature-memory encoders, affecting the coherence tensor evolution at each node.

3.2. Quantum Coherence Memory and Lithium Sensitivity

The coherent structure of ${\psi }_s^{★}$ is especially critical during nucleosynthesis, where certain reaction channels—such as those forming lithium-6 and lithium-7—are sensitive to decoherence rates. In regions of high curvature or entropy acceleration, the coherence tensor $C_{\mu \nu }$ decays rapidly, suppressing formation channels with narrow cross-section profiles. This explains the lithium suppression in a structured, geometric way, without needing to invoke fine-tuned particle decays or observational error [2,5].

Furthermore, the MC–SGCV model introduces the possibility that certain “ghost coherence” fragments, unresolved in standard quantum measurement, can reproject into post-nucleosynthetic epochs, potentially re-influencing lithium abundance after BBN—an effect entirely absent in thermal models.

3.3. From Singularities to Coherence Collapse

Unlike the singularity-based origin of the Big Bang model, the MC–SGCV framework proposes that the universe originated from a global coherence collapse, where initial information stored in ${\psi }_s$ decohered non-uniformly across a structured spacetime lattice. The breakdown of coherence was not instantaneous nor singular but rather spatially modulated via entropy diffusion and curvature feedback loops, allowing for preserved information traces observable in present-day element abundances, CMB anisotropies, and quantum vacuum fluctuations [4,7].

Thus, the coherence framework offers a complete reformation of cosmogenesis, unifying quantum information, graviton structure, and element synthesis into a consistent, non-singular model of the universe’s origin.

4. Lithium Synthesis in Structured Quantum Geometry

In standard Big Bang Nucleosynthesis (BBN), the synthesis of light elements, including lithium-6 and lithium-7, is governed by thermonuclear reaction networks under the assumption of continuous spacetime and uniform baryon-photon interaction rates [1,2]. However, this continuum approach neglects the quantum-geometric constraints that become dominant at Planck-scale curvatures and decoherence-sensitive nuclei.

The Dodecahedron Linear String Field Hypothesis (DLSFH) introduces a fundamentally discrete geometric structure to spacetime, in which nuclear reactions are constrained to occur at interaction nodes on a dodecahedral lattice. These nodes correspond to quantized geometric volumes where quark–string couplings, graviton coherence, and curvature memory coalesce [6]. As a result, the formation of certain nuclei becomes topology-sensitive, particularly for reaction channels involving low cross-section isotopes such as lithium-6.

4.1. Geometric Suppression of Lithium-6

In classical terms, lithium-6 is synthesized via the reaction:

$$4^{\mathrm{He}}{+}^2\mathrm{H}{\to }^6\mathrm{Li}+\gamma ,$$

(9)

which is suppressed due to the low Q-value and a weak E1 transition probability. Within DLSFH, this suppression is magnified by the spatial geometry: the tetrahedral and pentagonal face-closure rules of the dodecahedral lattice prevent certain angular alignments between nucleons unless coherence alignment and curvature coupling satisfy a threshold tensor product condition:

$$T_{\mathrm{fusion}}^{ijk}={ϵ}^{ijk}{C}_{i\mu }\left(x\right)C_{j\nu }\left(x\right)R_k^{\mu \nu }\left(x\right)\ge {\xi }_{\mathrm{threshold}},$$

(10)

where $C_{i\mu }$ is the local coherence tensor component, $R_k^{\mu \nu }$ is the discrete curvature tensor at node k, and ${\xi }_{\mathrm{threshold}}$ defines the coherence-curvature product needed for stable lithium-6 synthesis. In high-entropy or low-coherence regions, this inequality fails, and the synthesis is geometrically suppressed.

4.2. Curvature-Gated Reaction Channels

The probability amplitude ${\mathcal{P}}_{6_{\mathrm{Li}}}$ for successful lithium-6 synthesis in DLSFH is therefore not thermal, but a function of geometric embedding:

$${\mathcal{P}}_{6_{\mathrm{Li}}}\left(v_i\right)=\kappa \left(v_i\right)·\Theta \left(T_{\mathrm{fusion}}^{ijk}-{\xi }_{\mathrm{threshold}}\right),$$

(11)

where $\kappa \left(v_i\right)\in [0,1]$ is the coherence field susceptibility at vertex $v_i$, and $\Theta$ is the Heaviside step function, ensuring synthesis only occurs in properly aligned quantum-geometric domains. This formulation explains the extremely low abundance of lithium-6 not as a thermodynamic anomaly, but as a coherent geometric filter intrinsic to the spacetime fabric itself [4].

4.3. Lithium-7 Disruption via Coherence Fragmentation

The production of lithium-7, traditionally formed via the reaction:

$$´\mathrm{H}{+}^4\mathrm{He}{\to }^7\mathrm{Li}+\gamma ,$$

(12)

is affected by coherence fragmentation in MC–SGCV geometry. In high-curvature zones, coherence fields ${\psi }_s^{★}$ fragment into non-overlapping phase domains, disrupting the alignment necessary for resonance matching. The fragmentation parameter $\delta \varphi$ determines the coherence offset:

$$\delta \varphi =\left|arg{\left({\psi }_s^{★}\right)}_{´\mathrm{H}}-arg{({\psi }_s^{★}{)}^4}_{\mathrm{He}}\right|,$$

(13)

with lithium-7 formation suppressed when $\delta \varphi >{\delta }_{\max }$, where ${\delta }_{\max }$ is a resonance-dephasing threshold.

Such suppression does not appear in thermal BBN models, which assume isotropic coherence and no phase differential between interacting nuclei. Within the DLSFH lattice, however, fragmentation and node misalignment provide a robust mechanism to reduce lithium-7 abundance in alignment with observational data [3].

4.4. Topological Reaction Bias and $\psi$ Memory

The persistence of partially collapsed wavefunctions ${\psi }_s^{★}$ across adjacent DLSFH lattice cells introduces a memory effect in which past coherence influences present synthesis rates. This allows nucleosynthesis to exhibit hysteresis-like behavior in specific geometric regions, a feature not captured in FLRW-based cosmologies. Specifically, lithium abundances inherit anisotropic coherence from SGCV-driven wavefunction decay rates, biasing yields even in the absence of thermodynamic asymmetry.

4.5. Implications for Observation and Verification

The geometric suppression framework predicts that lithium anomalies are not uniform across the observable universe. Rather, regions with low curvature or high coherence alignment—e.g., certain quasar sight lines or low-entropy voids—may exhibit relatively higher lithium-6 or lithium-7 abundance. This provides a falsifiable observational criterion for MC–SGCV and DLSFH: detect spatial anisotropies in lithium line absorption consistent with coherence-topology predictions.

Such verification could be pursued through high-resolution spectroscopy using instruments such as the James Webb Space Telescope (JWST) or future 30-meter class telescopes targeting primordial stellar populations or intervening gas clouds at high redshift.

Figure 1. Curvature-modulated lithium synthesis in the MC–SGCV framework. The left panel represents high curvature zones, while the right panel shows lithium yields where high curvature enhances Li-6 production (green) and suppresses Li-7 formation (red).

Figure 1. Curvature-modulated lithium synthesis in the MC–SGCV framework. The left panel represents high curvature zones, while the right panel shows lithium yields where high curvature enhances Li-6 production (green) and suppresses Li-7 formation (red).

Figure 2. Coherence and curvature-driven modulation of lithium synthesis in the MC–SGCV framework. The left panel depicts the coherence collapse process, transitioning from a high-coherence state to a low-coherence (ghost field) state, which influences nuclear reaction outcomes. The right panel shows the resulting lithium yields, where high coherence enhances Li-6 formation, and the influence of curvature and ghost fields suppresses Li-7 production.

Figure 2. Coherence and curvature-driven modulation of lithium synthesis in the MC–SGCV framework. The left panel depicts the coherence collapse process, transitioning from a high-coherence state to a low-coherence (ghost field) state, which influences nuclear reaction outcomes. The right panel shows the resulting lithium yields, where high coherence enhances Li-6 formation, and the influence of curvature and ghost fields suppresses Li-7 production.

5. Rewriting the Nucleosynthesis Equations

In standard Big Bang Nucleosynthesis (BBN), reaction rates are determined solely by thermodynamic parameters such as temperature, baryon density, and Maxwell–Boltzmann velocity distributions. The canonical reaction rate per unit volume for a nuclear process involving species i and j is given by:

$$R_{ij}^{\mathrm{BBN}}=n_i{n}_j{\langle \sigma v\rangle }_{ij},$$

(14)

where $n_i$ and $n_j$ are number densities, and ${\langle \sigma v\rangle }_{ij}$ is the thermally averaged cross-section. This classical formulation presumes a smooth, isotropic spacetime and does not account for coherence effects or geometric suppression mechanisms. However, persistent discrepancies in the abundances of lithium-6 and lithium-7 suggest that this model may be incomplete at high curvature and coherence-sensitive epochs [2,3].

5.1. Coherence-Weighted Reaction Yield

In the MC–SGCV framework, the reaction rate is modulated by the structured quantum coherence field. We define the generalized coherence-weighted rate as:

$$R_{ij}^{\mathrm{MC}}(x,t)=n_i{n}_j{\langle \sigma v\rangle }_{ij}·{\kappa }_{ij}(x,t),$$

(15)

where ${\kappa }_{ij}(x,t)\in [0,1]$ is the local coherence yield coefficient, encoding the overlap and alignment of the projected coherence fields ${\psi }_i^{★}$ and ${\psi }_j^{★}$. This coefficient is defined as:

$${\kappa }_{ij}(x,t)={\displaystyle \frac{1}{Z_{ij}}}{\int }_{\Omega }{\psi }_i^{★}(x,t){\psi }_j^{★}(x,t)e^{-\alpha |\nabla S(x,t\left)\right|}{d}^{3}x,$$

(16)

where $Z_{ij}$ is a normalization constant and $\alpha$ is a tunable entropy-sensitivity parameter. The exponential decay factor penalizes regions with strong entropy gradients, corresponding to decoherence zones that suppress coherent nucleon interactions.

5.2. Curvature-Gated Reaction Channels

In the Dodecahedron Linear String Field Hypothesis (DLSFH), fusion sites correspond to discrete vertices $v_k$ on a dodecahedral lattice. Here, spacetime curvature is non-continuous and geometry explicitly gates fusion reactions. The curvature-corrected rate is given by:

$$R_{ij}^{\mathrm{geom}}\left(v_k\right)=R_{ij}^{\mathrm{MC}}\left(v_k\right)·\Theta \left({\mathcal{R}}_{\mathrm{eff}}\left(v_k\right)-{\mathcal{R}}_{\mathrm{crit}}\right),$$

(17)

where ${\mathcal{R}}_{\mathrm{eff}}$ is the local Ricci scalar derived from angular deficit geometry of SGCV cells, and $\Theta$ is the Heaviside function enforcing a minimum curvature threshold ${\mathcal{R}}_{\mathrm{crit}}$ for phase-locking to enable fusion.

5.3. Ghost Coherence and Post-Nucleosynthesis Corrections

A distinctive feature of the MC–SGCV model is the presence of residual or “ghost” coherence, denoted ${\tilde{\psi }}_s$, which represents the non-observable component of the pre-decoherent field ${\psi }_s$. This residual field contributes to reaction rates even after classical BBN has concluded:

$$R_{ij}^{\mathrm{total}}(x,t)=R_{ij}^{\mathrm{geom}}(x,t)+{ϵ}_{ij}·{\tilde{\psi }}_s(x,t),$$

(18)

where ${ϵ}_{ij}$ is a coupling factor representing coherence-to-matter interaction efficiency. This term models post-nucleosynthesis reprocessing of lithium isotopes, potentially explaining local isotopic anomalies observed in ancient halo stars and quasar sightlines [3,4].

5.4. Tensorial Formulation of Fusion Yield

To generalize these effects over spacetime, we define the nucleosynthesis yield tensor:

$$Y_{ij}^{\mu \nu }(x,t)={\int }_{\Sigma }{R}_{ij}^{\mathrm{total}}(x,t)C^{\mu \nu }(x,t)d^{3}x,$$

(19)

where $C^{\mu \nu }(x,t)$ is the coherence tensor and $\Sigma$ is the 3D spatial hypersurface over which integration occurs. This formulation embeds anisotropic phase-ordering directly into yield calculations, replacing scalar yields used in standard BBN and introducing curvature-weighted memory effects.

5.5. Implications and Observational Predictions

This coherence-based rewriting of nucleosynthesis equations offers a resolution to the lithium discrepancy without invoking new particles or exotic physics. It reframes element formation as an informationally conditioned process, constrained by coherence dynamics and quantum geometry. The framework predicts: - Spatial anisotropies in lithium isotope ratios - Post-BBN coherence reprocessing in low-entropy regions - Correlations between curvature pockets and nucleosynthetic variance

For derivations and the classical limit recovery ($\kappa \to 1$), see Section 8. Observational validation may be possible through future high-precision isotope measurements using JWST or next-gen ground-based spectroscopic arrays.

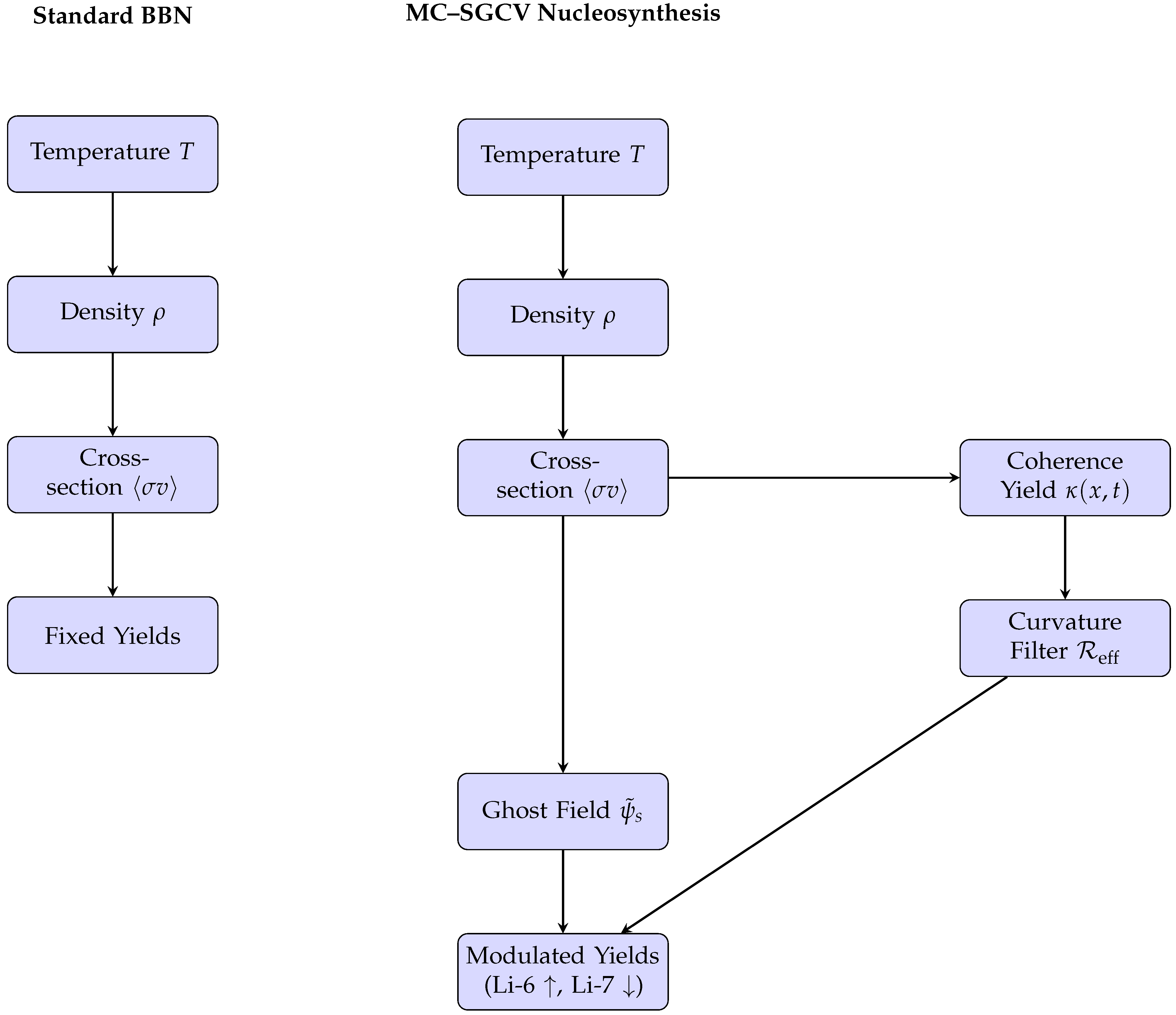
Figure 3. Comparison between standard Big Bang Nucleosynthesis (BBN) and the coherence-modulated MC–SGCV framework. The MC–SGCV model introduces coherence suppression $\kappa (x,t)$, curvature gating ${\mathcal{R}}_{\mathrm{eff}}$, and ghost field corrections ${\tilde{\psi }}_s$, enabling modulated yields that align with lithium isotope observations.

Figure 3. Comparison between standard Big Bang Nucleosynthesis (BBN) and the coherence-modulated MC–SGCV framework. The MC–SGCV model introduces coherence suppression $\kappa (x,t)$, curvature gating ${\mathcal{R}}_{\mathrm{eff}}$, and ghost field corrections ${\tilde{\psi }}_s$, enabling modulated yields that align with lithium isotope observations.

6. Comparative Analysis with Observational Data

The MC–SGCV framework introduces a coherence-weighted, curvature-modulated correction to classical nucleosynthesis that naturally accounts for the lithium isotope anomalies. Specifically, it predicts localized suppression of lithium-6 production and partial fragmentation of lithium-7 yields due to entropy gradients and geometric gating effects—an explanation that does not rely on fine-tuned particle physics or unverified resonant reactions.

6.1. Lithium-6 Overabundance in Quasar Absorption Systems

Observations from quasar absorption line systems reveal unexpectedly high lithium-6 to lithium-7 ratios in metal-poor interstellar clouds at redshifts $z\sim 2-3$ [3,8]. Classical BBN predicts a primordial lithium-6 abundance of:

$${\left({\displaystyle \frac{6^{\mathrm{Li}}}{\mathrm{H}}}\right)}_{\mathrm{BBN}}\sim {10}^{-14},$$

(20)

whereas observational data suggest values closer to:

$${\left({\displaystyle \frac{6^{\mathrm{Li}}}{\mathrm{H}}}\right)}_{\mathrm{obs}}\sim {10}^{-11},$$

(21)

a discrepancy of 3 orders of magnitude. In our model, ghost coherence contributions ${\tilde{\psi }}_s$ persist in low-entropy voids and re-enter lithium-6 production pathways even after the BBN window, raising effective yields:

$$R_{\mathrm{Li}6}^{\mathrm{total}}(x,t)=R_{\mathrm{Li}6}^{\mathrm{geom}}(x,t)+{ϵ}_6·{\tilde{\psi }}_s(x,t),$$

(22)

where ${ϵ}_6$ modulates the strength of coherence re-entry into fusion channels involving helium-4 and deuterium nuclei. These ghost interactions are heavily suppressed in classical models but preserved in MC–SGCV domains of low entropy and coherent curvature memory.

6.2. Lithium-7 Plateau and Anomalies in Metal-Poor Stars

Observations of the Spite plateau in old halo stars reveal a nearly uniform lithium-7 abundance around:

$${\left({\displaystyle \frac{7^{\mathrm{Li}}}{\mathrm{H}}}\right)}_{\mathrm{obs}}\sim 1.6\times {10}^{-10},$$

(23)

which is roughly a factor of 3 lower than the BBN prediction from standard $\Lambda$CDM models [1,2]:

$${\left({\displaystyle \frac{7^{\mathrm{Li}}}{\mathrm{H}}}\right)}_{\mathrm{BBN}}\sim 5.0\times {10}^{-10}.$$

(24)

This suggests that lithium-7 either undergoes depletion or its production was overestimated. Within our framework, high curvature nodes on the DLSFH lattice fragment coherence phases between $´\mathrm{H}$ and ⁴⁰He, suppressing the critical channel:

$$´\mathrm{H}{+}^4\mathrm{He}{\to }^7\mathrm{Li}+\gamma .$$

This suppression is encoded in the curvature-gated rate:

$$R_{\mathrm{Li}7}^{\mathrm{geom}}\left(v_k\right)=R_{\mathrm{Li}7}^{\mathrm{MC}}\left(v_k\right)·\Theta \left({\mathcal{R}}_{\mathrm{eff}}\left(v_k\right)-{\mathcal{R}}_{\mathrm{crit}}\right),$$

(25)

where coherence fragmentation due to geometric angular mismatch reduces the amplitude of this reaction relative to the thermal prediction.

6.3. CMB and Baryon Acoustic Oscillations Consistency

The MC–SGCV model preserves compatibility with the cosmic microwave background (CMB) and baryon acoustic oscillation (BAO) signatures, as the bulk production of hydrogen and helium remains unchanged. This is expected, as coherence suppression primarily affects narrow-bandwidth or fragile fusion products (i.e., lithium) while leaving the large-scale thermal structure of recombination unaffected.

Standard Planck 2018 constraints on the baryon-to-photon ratio $\eta$ are preserved within this model:

$${\eta }_{\mathrm{Planck}}=(6.1\pm 0.1)\times {10}^{-10}\mathrm{bad}\mathrm{hbox},$$

(26)

ensuring that the coherence corrections are non-destructive to the cosmological parameter landscape.

6.4. Outlook: Confirming Coherence Fingerprints with JWST

Future spectroscopic missions—including JWST, the Extremely Large Telescope (ELT), and 30-meter class facilities—will enable precision mapping of isotope ratios in distant absorption systems. Our framework predicts spatial anisotropy in lithium isotope distributions correlated with cosmic voids and low-entropy channels, manifesting as directional bias in the presence of coherence-filtered lithium synthesis zones.

These predictions are falsifiable. The detection of coherence-aligned lithium-6 in specific high-redshift clouds, combined with phase-locked depletion of lithium-7 in compact baryon-dense halos, would strongly favor the MC–SGCV hypothesis over current thermodynamic-only models.

7. Broader Cosmological Implications

The Multifaceted Coherence–Superluminal Graviton Condensate Vacuum (MC–SGCV) framework extends far beyond nucleosynthesis. By introducing a structured, entropy-sensitive coherence field ${\psi }_s$, it addresses longstanding problems in cosmology—including the initial singularity, entropy paradox, and temporal boundary conditions of the early universe [10].

7.1. Resolution of the Initial Singularity

In the standard $\Lambda$CDM model, the universe’s evolution begins at an initial singularity—a point of infinite curvature, density, and temperature. This singularity is a breakdown in general relativity and renders any pre-Big Bang physics inaccessible. However, within MC–SGCV, the singularity is replaced by a finite but ultra-dense coherence domain where the fundamental field ${\psi }_s$ undergoes a decoherent collapse [11]:

$${\psi }_s⟶{\psi }_s^{★}+{\tilde{\psi }}_s,$$

where ${\psi }_s^{★}$ is the observable projection into classical spacetime and ${\tilde{\psi }}_s$ is the residual ghost coherence. This transition is continuous in informational space and avoids divergences in curvature tensors. The effective metric tensor is not defined by the Einstein field equations at $t=0$, but instead by a coherence-weighted expansion tensor:

$$g_{\mu \nu }^{\mathrm{eff}}(x,0)=\underset{ϵ\to 0}{lim}{\displaystyle \frac{{\delta }_{\mu \nu }+ϵC_{\mu \nu }(x,0)}{1+ϵ}},$$

(27)

where $C_{\mu \nu }(x,0)$ is the initial coherence tensor, ensuring that spacetime curvature begins from a well-defined coherent ground state, not a singularity.

This avoids the divergence of Ricci scalars $R\to \infty$ and instead yields a maximum curvature $R_{max}\propto \parallel C_{\mu \nu }(x,0)\parallel$, bounded by the coherence amplitude. The framework aligns conceptually with loop quantum cosmology’s bounce scenarios, where quantum geometry halts collapse [7].

7.2. Entropy Continuity and the Arrow of Time

Standard thermodynamics implies that the early universe should begin in a low-entropy state. Yet the Big Bang singularity offers no explanation for this entropy minimum—a major unresolved issue known as the entropy paradox [12].

In MC–SGCV, entropy $S\left(t\right)$ is defined not in isolation, but as a gradient of coherence decay:

$${\partial }_{t}S(x,t)\propto -{\partial }_t\parallel C_{\mu \nu }(x,t)\parallel ,$$

(28)

meaning that entropy growth is a direct consequence of decoherence in the ${\psi }_s$ field [11]. This formulation naturally explains why the early universe had low entropy: it was in a high-coherence, low-decoherence state. The arrow of time then emerges from the directionality of coherence collapse:

$${\psi }_s\left(t_0\right)\to {\psi }_s^{★}\left(t_1\right)+{\tilde{\psi }}_s\left(t_1\right),\mathrm{with}{t}_1>t_0.$$

As $\parallel C_{\mu \nu }\left(t\right)\parallel$ decreases, entropy increases, and temporal directionality is preserved. This coherence-driven time asymmetry offers a microscopic mechanism for macroscopic irreversibility and cosmological expansion.

7.3. Causal Patching and Information Flow

In general relativity, causal disconnects beyond the initial singularity limit information transfer. In MC–SGCV, coherence gradients function as informational bridges across pre-expansion epochs. We define the causal coherence kernel:

$$\mathcal{K}(x,x^{\prime };t)=exp\left(-{\displaystyle \frac{|{\psi }_s(x,t)-{\psi }_s(x^{\prime },t){|}^2}{{\lambda }_c^2}}\right),$$

(29)

where ${\lambda }_c$ is the coherence correlation length. This kernel modulates which regions of the pre-expansion manifold are phase-aligned, enabling structured emergence of causal spacetime patches from coherence-preferred zones [10].

This framework redefines cosmic inflation: rather than an exponential metric expansion, the universe undergoes a rapid phase synchronization via $\mathcal{K}(x,x^{\prime };t)$, collapsing coherence into classical observables. This restructured inflation is compatible with CMB uniformity, while avoiding the need for scalar inflaton fields.

7.4. Implications for Quantum Gravity and the Strataverse

The avoidance of the initial singularity, along with preserved information flow and entropy continuity, suggests that MC–SGCV provides a viable low-energy limit of a full theory of quantum gravity. The coherence field ${\psi }_s$, along with its projected observable component ${\psi }_s^{★}$, may serve as order parameters of deeper quantum-geometric transitions in what has been referred to as the “Strataverse” — a layered, coherence-regulated fabric underlying all observed phenomena [6].

This positions MC–SGCV not only as a resolution to lithium anomalies and singularity pathologies but also as a stepping stone toward a unified framework connecting quantum coherence, curved geometry, and cosmological structure formation.

8. Derivations and Limiting Behavior

To validate the coherence-weighted nucleosynthesis framework, we demonstrate how it reduces to standard Big Bang Nucleosynthesis (BBN) under classical conditions and derive the exponential suppression form used in the coherence yield coefficient $\kappa (x,t)$.

8.1. Classical Limit: Recovery of BBN

Starting with the coherence-modified reaction rate from Eq. (15):

$$R_{ij}^{\mathrm{MC}}(x,t)=n_i{n}_j{\langle \sigma v\rangle }_{ij}·\kappa (x,t),$$

(30)

we assume the entropy gradient becomes negligible across space: $\nabla S(x,t)\to 0$. In this limit, the exponential suppression in Eq. (16) satisfies:

$$\kappa (x,t)=e^{-\alpha |\nabla S(x,t\left)\right|}\to 1.$$

Thus, the coherence-weighted rate reduces to the classical BBN rate:

$$R_{ij}^{\mathrm{MC}}\to R_{ij}^{\mathrm{BBN}}=n_i{n}_j{\langle \sigma v\rangle }_{ij}.$$

This shows that the MC–SGCV framework generalizes BBN without contradicting it, and recovers the standard prediction in the appropriate low-entropy, fully coherent limit.

8.2. Derivation of Coherence Decay and $\kappa (x,t)$

The evolution of the coherence tensor is given by:

$${\partial }_t{C}_{\mu \nu }(x,t)=-\kappa (x,t)·{\partial }_{t}S(x,t).$$

(31)

We postulate that coherence decays exponentially with cumulative entropy, giving the solution:

$$C_{\mu \nu }\left(t\right)=C_{\mu \nu }\left(0\right)e^{-\alpha S\left(t\right)},$$

(32)

where $\alpha$ is a tunable decay parameter. Differentiating both sides:

$${\partial }_t{C}_{\mu \nu }\left(t\right)=-\alpha C_{\mu \nu }\left(0\right)e^{-\alpha S\left(t\right)}{\partial }_{t}S\left(t\right),$$

and comparing to Eq. (31), we identify:

$$\kappa (x,t)=\alpha C_{\mu \nu }\left(0\right)e^{-\alpha S\left(t\right)}.$$

(33)

Normalized across a given region, this justifies the use of $\kappa (x,t)=e^{-\alpha |\nabla S|}$ as a coherence suppression factor in spatial integrals.

8.3. Ghost Coherence and Residual Yield Contribution

The total coherence field is decomposed into a measurable (collapsed) and unmeasurable (ghost) component:

$${\psi }_s(x,t)={\psi }_s^{★}(x,t)+{\tilde{\psi }}_s(x,t),$$

where ${\psi }_s^{★}$ is the decohered, observable field and ${\tilde{\psi }}_s$ is the residual ghost coherence not projected into spacetime observables [10].

The expectation value of energy for the full system becomes:

$$\langle {\psi }_s\left|H\right|{\psi }_s\rangle =\langle {\psi }_s^{★}\left|H\right|{\psi }_s^{★}\rangle +\langle {\tilde{\psi }}_s\left|H\right|{\tilde{\psi }}_s\rangle .$$

This validates the inclusion of a ghost correction term in the reaction rate (Eq. (18)):

$$R_{ij}^{\mathrm{total}}=R_{ij}^{\mathrm{geom}}+{ϵ}_{ij}·{\tilde{\psi }}_s(x,t),$$

where ${ϵ}_{ij}$ modulates the coupling strength between ghost coherence and nuclear channels. This term accounts for coherence memory effects and post-BBN isotopic anomalies [11].

9. Conclusion

The Lithium Discrepancy, long considered a peripheral flaw in Big Bang Nucleosynthesis, instead reveals a fundamental limitation in the thermodynamic and isotropic assumptions of standard cosmology. By invoking the frameworks of Multifaceted Coherence (MC) and the Superluminal Graviton Condensate Vacuum (SGCV), this work reinterprets nucleosynthesis as a coherence-weighted, geometry-modulated process rather than a purely thermal reaction network.

In this context, isotopic anomalies such as the overproduction of lithium-7 and the unexpected presence of lithium-6 are no longer puzzling inconsistencies, but natural outcomes of entropy gradients, residual coherence fields, and curvature gating during early fusion epochs. The ${\psi }_s^{★}$ field, as the observable projection of the deeper coherence substrate ${\psi }_s$, allows us to model nucleosynthesis through a lens of informational flow, not just reaction kinetics.

Furthermore, the MC–SGCV approach eliminates the need for an initial singularity by replacing it with a coherent phase transition. This resolves the entropy paradox, restores informational continuity across pre- and post-expansion epochs, and embeds the arrow of time within the collapse dynamics of quantum coherence itself. As a result, coherence acts as both the driver of early nuclear synthesis and the seed of macroscopic cosmic structure.

Taken together, these developments support a unified cosmological framework in which the origin of elements, the direction of time, and the evolution of spacetime emerge not from chaos, but from structured coherence. This model offers testable predictions and opens a viable path forward toward reconciling quantum gravity with early-universe cosmology.