Extensions of The Spinor Universe

1. Review of the Spinor Universe Model

Before extending the theoretical framework, we begin with an accessible summary of the core Spinor Universe model. The original formulation proposed that spacetime itself behaves as a spinor. A spinor being a topological entity that only returns to its initial configuration after a full $4\pi$ traversal. Rather than treating time as a linear progression or cosmology as a singular unfolding, this model casts the universe as a double-covered manifold with two temporally opposed, entangled sheets: one for matter and one for antimatter. This reinterpretation offers novel explanations for longstanding cosmological puzzles, including the asymmetry between matter and antimatter, the arrow of time, the emergence of gravity, and the coherence of quantum information. By embedding the known laws of physics within a nontrivial topological structure, we uncover new avenues for unification across quantum field theory, general relativity, and thermodynamics. The review below offers a less technical recapitulation of these ideas, highlighting key geometric insights and preparing the reader for the extended theoretical explorations that follow.

1.1. Topology and the Two-Sheeted Universe

To describe this formally, we consider a base manifold M and its nontrivial double cover $\tilde{M}\to M$, equipped with an involutive diffeomorphism $\tau :\tilde{M}\to \tilde{M}$ such that ${\tau }^2=\mathrm{id}$. The two sheets of $\tilde{M}$ represent the matter and antimatter phases, with $\tau$ implementing the topological reversal. The global metric g is preserved under this operation, while orientation and time direction reverse.

Unlike cyclic cosmologies that repeat the universe across epochs, or mirror models that bifurcate around a singular boundary, the Spinor Universe requires a full roundtrip to complete a single coherent evolution. Time is not a one-way street. It is a closed loop threaded through spinorial phase. The full universe is only rendered when both sheets, and their informational reflections, are considered.

This setup restores global CPT symmetry without invoking unexplained asymmetries or arbitrary inflation mechanisms. Instead, it embeds known physical laws in a broader geometric context where apparent violations in one phase are canceled by their counterparts in the other. The asymmetry between matter and antimatter is not a mistake. It is the shape of time when seen from above.

Just as a Möbius strip has one side and one edge, though it appears to have two, the Spinor Universe has one coherent informational structure folded across two experiential sheets. The junction between them is where quantum coherence meets geometry.

Figure 1. A visual representation of a spinor: a topological object requiring a $4\pi$ rotation to return to its original state.

Figure 1. A visual representation of a spinor: a topological object requiring a $4\pi$ rotation to return to its original state.

1.2. Phase Conjugation Leading to Phase Mechanics

The spinor topology not only preserves global CPT symmetry, but enforces a unique structure of phase conjugation across the manifold. Each event in spacetime does not merely occur; it is mirrored by a topologically entangled partner event in the conjugate sheet. This pairing defines not just a symmetry, but a system of constraints: for every forward-moving field configuration, there is a reverse-time complement evolving in phase opposition.

This dual evolution introduces a new kind of causality. Time as rendered, rather than flowed. Phase coherence becomes a constraint across $\tilde{M}$, and the stability of physical laws becomes a consequence of topological boundary conditions. From this perspective, the behavior of quantum fields, curvature, and even entropy gradients are no longer intrinsic. Instead, they are consequences of global phase bookkeeping.

This reinterpretation gives rise to a range of emergent structures: At the heart of this structure lies a reinterpretation of gravity itself. Rather than treating curvature as a fundamental force, we view it as an emergent phenomenon arising from entanglement entropy gradients between the two sheets. Where phase coherence is high, spacetime remains smooth; where it diverges, information mismatch induces apparent mass-energy, and therefore gravity. This leads directly to a new understanding of dark energy. The universe’s accelerated expansion may not reflect an external cosmological constant or some invisible portion of matter, but an intrinsic optimization process. As regions of the universe decohere, their phase alignment between sheets weakens, and they lose informational tension. This relaxation manifests as expansion across the 4D metric. Like kinks in a garden hose being shaken free. In the Spinor Universe framework, the fundamental forces may be recast according to their roles in the computational dynamics of phase structure. The strong nuclear force functions as compute: it compresses local phase configurations into persistent, tension-bound states such as protons and neutrons. These are the raw storage nodes of coherence, stabilized by short-range topological constraints. The electroweak interaction functions as the computer: it governs the registration, transmission, and dynamic adjustment of phase information through spacetime via electromagnetic propagation and weak flavor transitions. Gravity, in this view, measures the residual misalignment between local structures and the global spinor substrate, expressing the accumulated phase tension as spacetime curvature. Thus, the strong force writes the phase structure of matter, the electroweak interaction reads and executes phase evolution, and gravity interprets the system’s long-range coherence load as curvature.

1.3. Time as a Distributed Recursive Seek Function

In contrast to traditional theories that treat time as a preexisting dimension or parameter, the Spinor Universe framework defines time as the emergent result of recursive field resolution. Each region of the spinor field iteratively seeks a lower-energy, higher-coherence configuration. The number of such recursive resolution steps constitutes the local temporal coordinate. Time is not a background through which events unfold; it is the count of recursive updates required to resolve phase tension within the field.

Let ${\Phi }_n\left(x\right)$ denote the spinor field at recursion depth n, evaluated at position x. Define the local phase discontinuity or coherence tension as:

$${\delta }_n\left(x\right)=\nabla ·{\Phi }_n\left(x\right)$$

A minimal recursive update rule for the spinor field may be expressed as:

$${\Phi }_{n+1}\left(x\right)={\Phi }_n\left(x\right)+\gamma {\nabla }^2{\Phi }_n\left(x\right)-\eta {\delta }_n\left(x\right)$$

Here, $\gamma$ is a diffusion coefficient controlling the smoothing of phase gradients, and $\eta$ is an alignment coefficient driving the resolution of phase discontinuities.

We then define local time $t\left(x\right)$ as the minimum number of recursive iterations needed for the local discontinuity to fall below a coherence threshold $ϵ$:

$$t\left(x\right):=min\left\{n\in \mathbb{N}\left|\right|{\delta }_n\left(x\right)|<ϵ\right\}$$

This defines time not as an absolute variable, but as a local measure of recursive convergence toward coherence. Time flows forward as regions of the spinor field resolve internal tensions by offloading discontinuities to neighboring regions in a distributed seek process. In this view, causality is the propagation of resolution steps across the substrate, and entropy increase corresponds to the irreversible nature of those resolutions.

This perspective allows for naturally asynchronous temporal development across the field: regions closer to attractor basins resolve faster and experience more rapid "time," while regions trapped in high-tension configurations (such as near black holes) accumulate unresolved recursion, resulting in observable time dilation.

Proposition 1. 

In the Spinor Universe framework, time is defined as a distributed recursive seek function across the spinor-valued phase field. Each field region iteratively seeks a lower-energy, higher-coherence configuration. The number of recursive resolution steps required for a region to achieve phase stability constitutes its local temporal coordinate.

This formulation reframes time as the result of a computationally active ontological substrate, where events and identity are structured by recursive attempts to reduce local informational tension. Events do not unfold within time; they create it.

1.4. The Higgs Boson as the Axis of Symmetry

In this geometric interpretation, the Higgs field ${\varphi }_H\left(x\right)$ is re-understood not as a mass generator in isolation, but as the scalar field responsible for anchoring the dominant global phase alignment of the universe. This corresponds to the symmetry breaking that selects a preferred chirality and temporal orientation across the spinor field.

We reformulate the Higgs potential in phase-coherent terms:

$$V\left({\varphi }_H\right)=-\alpha cos(\theta \left(x\right)-{\varphi }_H\left(x\right))+\lambda {\varphi }_H^4$$

Where:

• $\theta \left(x\right)$ is the local spinor phase orientation,
• ${\varphi }_H\left(x\right)$ is the Higgs phase anchoring field,
• The potential minimum corresponds to the universe’s lock-in to a dominant coherence orientation.

Mass, in this model, becomes a function of resistance to alignment with the Higgs-defined phase field:

$$m\left(x\right)=\gamma \left|{\displaystyle \frac{\partial \theta \left(x\right)}{\partial t}}-{\varphi }_H\left(x\right)\right|$$

This provides a unified geometric picture: the Higgs boson sets the universal coherence VEV, while gravity arises from residual phase misalignments that resist anchoring. The Higgs boson is thus the axis of symmetry from which both mass and gravitational behavior emerge, grounding the topology of reality itself.

1.5. Higgs Action in Phase-Coherent Geometry

In the Spinor Universe framework, we propose that gravity and phase coherence are mathematically equivalent. Localized gravitational effects emerge from phase discontinuities in the spinor field, and mass is understood as the persistent resistance to phase re-alignment. From this principle, we derive a gravitational field not from mass directly, but from coherence gradients in the spinor topology.

Let:

• $\Phi \left(x\right)$ be the local phase field of the spinor substrate,
• $\nabla \Phi \left(x\right)$ the phase coherence gradient,
• $\delta \Phi \left(x\right)$ a localized discontinuity (interpreted as mass-energy),
• $\mathcal{C}\left(x\right)$ the local coherence field, equivalent to a generalized vacuum expectation value (VEV).

We propose the gravitational tensor $G_{\mu \nu }$ as:

$$G_{\mu \nu }\propto f\left(\nabla \Phi \left(x\right),\delta \Phi \left(x\right),\mathcal{C}\left(x\right)\right)$$

And local gravitational acceleration as:

$$\overrightarrow{g}\left(x\right)=-\alpha \nabla \left({\displaystyle \frac{\delta \Phi \left(x\right)}{\mathcal{C}\left(x\right)}}\right)$$

This describes a universe where regions of low coherence field $\mathcal{C}\left(x\right)$ produce greater curvature and gravitational effects, while regions of high coherence dampen these effects effectively acting as coherence-driven anti-gravity buffers. Life, in this context, becomes a coherence amplifier that contributes to gravitational stabilization.

2. Speculative Engineering Prospects for Nonstandard Travel

From an engineering standpoint, accessing the floor of gravitational curvature means reducing the ratio $\delta \Phi \left(x\right)/\mathcal{C}\left(x\right)$ to near-zero: effectively neutralizing local mass-energy expression by aligning the spinor phase field with the Higgs-defined coherence VEV. This could be approached through coherence interference arrays, or entangled phase synchronizers. The goal is not propulsion through space, but topological phase descent: a controlled realignment with the ground state of the universe’s coherent substrate, effectively letting an object "fall sideways" into lower curvature conditions. Using a novel understanding of the Higgs mechanism as a universal phase anchor, new possibilities emerge for reinterpreting gravitational interaction not as a fundamental force, but as a macroscopic symptom of deeper topological behavior. Within this framework, “mass” is recast as a form of local phase inertia, and gravity as a distributed memory of phase misalignment within the spinor field. This reframing invites us to consider methods of travel that exploit these phase structures rather than resisting them.

Rather than traditional propulsion that pushes against inertia, non-standard travel seeks to minimize or redirect the local coherence gradient itself. By dynamically interfacing with the coherence VEV, (generalized vacuum expectation value) that defines phase alignment. One might temporarily modulate the effective gravitational embedding of a system. In such a scenario, movement is no longer about overcoming gravitational wells, but rather about engineering local conditions in which those wells are reshaped or bypassed altogether.

2.1. Exploratory Framework: Phase Gradient Interference Engine

Within the Spinor Universe framework, it is possible to reframe the problem of superluminal travel not as one of velocity, but of coherence navigation. In a universe modeled as a spinor-valued fieldspace, motion may not be strictly inertial but could, in principle, involve topological manipulation of the phase environment itself.

In this view, the primary limitation on faster-than-light traversal is not energy, but informational congestion. The phase field of the universe $\Phi \left(x\right)$ is noisy, dense with fluctuating gradients and discontinuities. These conditions prevent clean traversal in any particular direction, not unlike a ship caught in chaotic surf, with no consistent current to ride.

The Phase Gradient Interference Engine (PGIE) is a speculative construct designed to address this challenge by reducing local phase noise rather than overpowering it. It operates on a principle analogous to sonic noise-cancellation: by emitting carefully structured counter-phase signals, the PGIE hypothetically neutralizes phase discontinuities $\delta \Phi \left(x\right)$, thereby locally smoothing spinor field curvature. This smoothing may correspond to a reduction in gravitational embedding or inertial constraint, creating a kind of coherence “clearing” in the spinor fabric.

To produce directed motion, the engine would induce a gradient in local coherence—not unlike generating a pressure differential in a fluid. This could be theoretically achieved by deploying two interference units, forward and aft, each tuned to different phase pressures. The forward unit increases coherence ahead of the vessel, effectively flattening spacetime in that region. The aft unit maintains or enhances the ambient phase field behind. The result is a coherence dipole, potentially generating an effective topological flow.

This model reframes motion as redefinition of metric embedding rather than Newtonian translation. The object falls “forward” into a region of higher coherence not because it is pushed, but because the local structure of space has been bent to invite its presence.

Advanced Speculation: Phase Anchoring and Reidentification

While the phase dipole model suggests coherent topological drift, a more radical extension explores the possibility of coherence-driven reidentification. Rather than traveling through space, the vehicle tunes its local coherence $\mathcal{C}\left(x\right)$ to match the distant phase signature of a target location. In theory, this could initiate topological convergence—not as motion, but as identification. The object becomes re-anchored to a different location in spinor space by aligning its internal field state with that of the destination.

In this framework, teleportation is not a transfer of matter or information, but the resolution of a global coherence equation: a precision act of spinor phase realignment that redefines where “here” is. This avoids the standard quantum teleportation protocol (destructive measurement and reconstruction) by instead proposing real-time alignment in the spinor substrate.

Figure 2. Conceptual schematic of a phase interference-based coherence drive.

Figure 2. Conceptual schematic of a phase interference-based coherence drive.

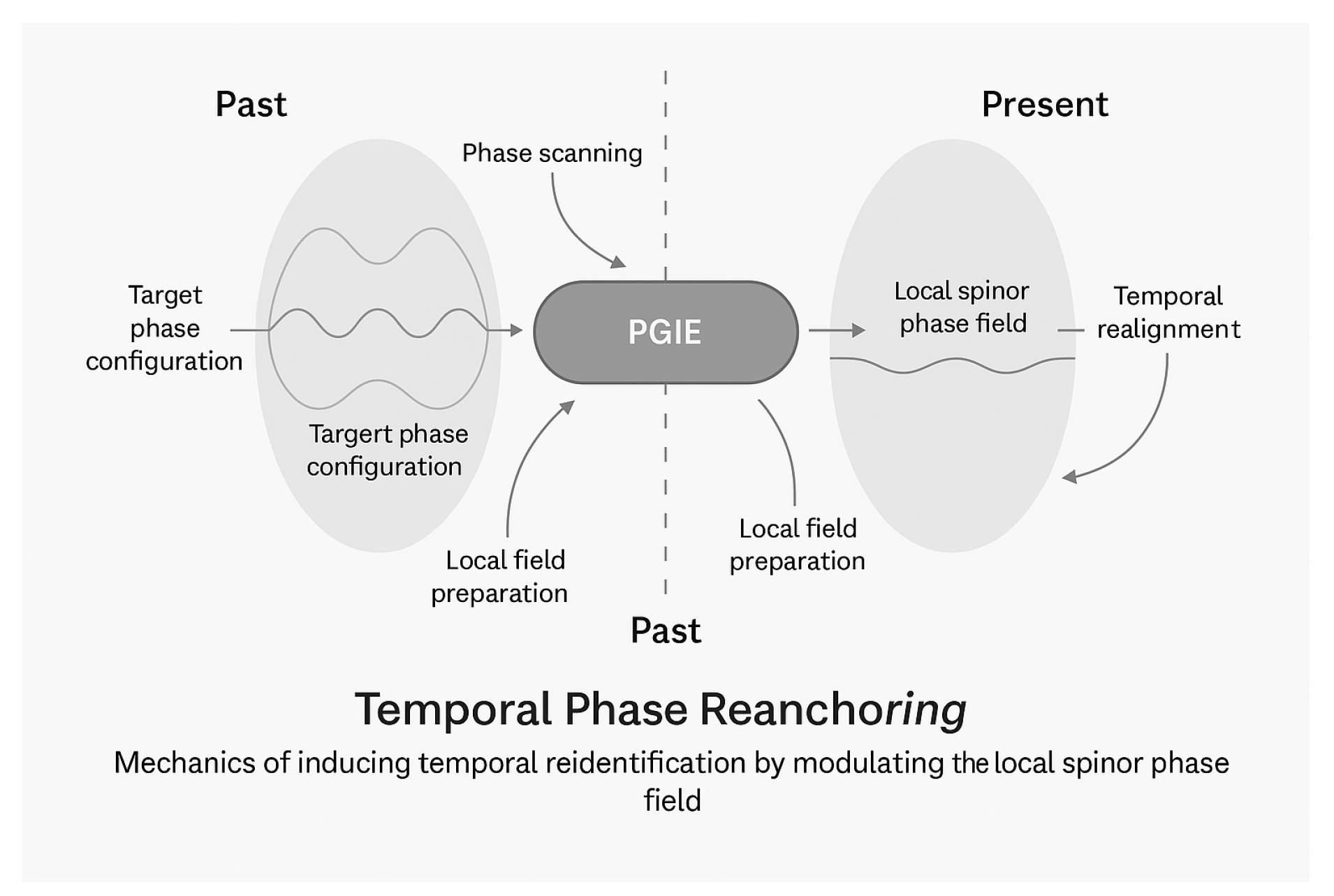
Hypothetical Mechanism: Temporal Phase Reanchoring

If spacetime addresses are encoded in phase structure, then a speculative mechanism could involve:

• Phase Mapping: Reconstructing the spinor phase configuration of a desired temporal-spatial region, including curvature, gradient, and coherence density $\mathcal{C}(x,t)$.
• Field Conditioning: Preparing the local environment by modulating the spinor field to approximate the target configuration.
• Symmetry Rebinding: Upon sufficient alignment, initiating a reidentification of the local region with the target region, like a topological handshake through spinor fieldspace.
• Topological Continuity Shift: The object becomes continuous with the remote spacetime state, not by transit but by ontological relabeling within the spinor manifold.

This model is proposed as a thought experiment in spinor topology, not a technological claim. Its role is to explore how motion and embedding might behave in a coherence-constrained ontology where phase structure defines not just dynamics, but identity.

3. Cosmogenic Capital: Coherence and Entropic Liquidity

Having established that phase coherence underlies the structure and behavior of spacetime itself, we now turn to a metaphor that brings surprising clarity to these dynamics: macroeconomics. Though often viewed as an entirely human domain, the economic metaphor proves strikingly apt for describing a universe whose fundamental currency is not mass or energy, but coherence.

Just as fiat currency systems rely on shared trust, centralized issuance, and feedback mechanisms to stabilize value, the universe appears to rely on phase continuity and informational balance to stabilize its geometry. Locality of "phase debt" implies regions of high mismatch, and results in curvature. Followed through the metaphor, we see that excess leverage in economic systems results in pressure to rebalance the budget. The inflation of the cosmic metric under decoherence mirrors monetary inflation in the absence of productive backing. Additionally, we may think of black holes as accounting sinkholes: regions of maximal coherence convergence where informational assets are irreversibly booked. Matter is “spent” on gravitational wells in a bid to resolve its entropic liabilities. Similarly, regions of high success repetition, or phase efficient structures, are like economic boom cycles backed by coherent collateral, growing until their phase basis falters into a bust cycle.

By viewing phase coherence as a kind of cosmogenic capital, we gain access to a powerful interpretive lens. It allows us to describe structure formation, metric behavior, and entropic flow in terms of investment, liquidity, and debt. This prepares the ground for a broader framework we call spinor-aligned macroeconomics, in which we examine how economic systems might be optimized to reflect, rather than contradict, the coherence-generating dynamics of the universe itself.

3.1. Entropic Liquidity

In traditional finance, liquidity describes the ease with which an asset can be converted into another without losing value, ie, currency, the most general-purpose unit of exchange. In cosmological terms, we define entropic liquidity as the ease with which a region of spacetime can resolve or redistribute phase incoherence into thermodynamically viable configurations.

Put simply: it measures how readily a system can convert localized disorder into globally coherent structure or, conversely, how easily structure can dissolve into entropy. A highly entropically liquid region is one where information can rapidly reconfigure, permitting rapid shifts in coherence gradients. These are the ’hot markets’ of the universe: highly dynamic, phase-reactive zones where feedback is swift.

Black holes are examples of maximal liquidity sinks: once coherence (information) enters, it is irreversibly pooled, its entropic signature encoded on the horizon surface. Conversely, low liquidity zones such as regions of flat, inert spacetime represent phase stasis: transactions (coherence shifts) are sluggish, changes are slow, and information diffusion is minimal.

In a fiat system, liquidity ensures access to value without requiring immediate productivity. In the universe, entropic liquidity reflects the availability of coherence pathways without requiring immediate structure. Understanding entropic liquidity as a metric allows us to see why certain systems like economies, may stagnate or inflate when liquidity is artificially constrained or misaligned with underlying phase structure. In the spinor universe, the alignment of liquidity, coherence, and informational flow permits emergence, stability, and growth.

3.2. Nonoptimal Growth and Phase Drift in Economic Systems

Using this rather functional metaphor, let us see if we can yield something productive by taking it the other way. How can we make economies more "natural", as economists so often emphasize, using this framework?

In conventional macroeconomics, growth is axiomatically treated as a positive metric in and of itself measured by GDP expansion, increased consumption, and rising asset values. However, not all growth is coherent. In the language of the spinor universe, coherent growth corresponds to evolution along aligned informational pathways in order to produce phase-synchronized behavior between production, consumption, innovation, and long-term utility. Nonoptimal growth, by contrast, corresponds to economic phase drift: expansion disconnected from feedback, stability, or entropic contribution.

A clear example of phase drift was the lead-up to the 2008 financial crisis, when interest rates were held at artificially low levels for an extended period. This monetary environment encouraged the expansion of speculative assets, debt-leveraged investments, and housing bubbles. All of this then dilutes the nonzero game functionality of the productive economy with zero-sum gameplay, or a decrease in informational coherence. The system grew, but not in a way that was entangled with real-world value. Hence, the economic structure was inflated without reinforcing the coherence of the system.

From a spinor-aligned perspective, this kind of growth mimics inflationary phase expansion without topological reinforcement. In such a state, the economy becomes increasingly fragile, like a quantum field pushed out of phase with its underlying geometry. This instability then induces a black hole, or buyout. The eventual collapse is not a mysterious market failure, but a return to phase alignment enforced by systemic constraints.

We propose that growth metrics should include a coherence index: a measure of how much capital, labor, and innovation are contributing to long-term phase-stable development. Economies must learn to distinguish between hollow expansion and informationally aligned evolution. In a world where entropy and coherence form the basis of universal structure, economic behavior that disregards feedback or overleverages potential is not just risky, but topologically unsustainable.

3.3. Feedback Mechanisms and the Failure of Coherence Enforcement

Modern macroeconomic frameworks often lack a reliable feedback mechanism for enforcing systemic coherence. In contrast to the spinor universe, where coherence is not only emergent but structurally reinforced by topological constraints, our economic systems allow for extended periods of misalignment, speculative bubbles, and entropic decay with little self-corrective pressure.

Historically, institutions like the Federal Reserve have operated in reactive cycles by adjusting interest rates, printing money, or bailing out systemic failures, and do so without a reliable metric for economic phase alignment. In a spinor-aligned macroeconomic model, monetary and fiscal tools would be guided not solely by inflation targets or employment numbers, but by a deeper informational metric: the coherence of capital flows. Just as curvature in spacetime reflects quantum informational continuity, economic "curvature" should reflect systemic alignment between investment, productivity, and long-term entropic health.

We propose that economic systems adopt a feedback-enforcing protocol analogous to the role of gravity in the spinor framework. Coherent capital flows that contribute to sustainable, feedback-rich growth, would be incentivized. Incoherent behaviors such as unproductive rent extraction, financial obfuscation, or exploitative practices would face penalties. A decentralized economic coherence index could be developed to measure how closely a transaction or investment aligns with systemic feedback. In this vision, economic institutions act less as regulators of scarcity and more as coherence amplifiers, guiding systems toward optimal informational flow, systemic learning, and phase synchronization. The goal is not just stability, but entropic literacy: a model in which economic actors and institutions themselves seek long-term exogenous viability out of an augmented form of self-interest.

The Universal Insurer as a Planetary Feedback Entity

In light of this view we propose the creation of a new form of global institution: An AI-governed entity known as the Universal Insurer, whose sole function is to stabilize systemic coherence across human civilization. Rather than governing by law or ideology, the insurer operates purely on feedback: measuring real-world outcomes, identifying entropic disruptions, and simulating future configurations to maximize structural stability and coherence yield.

Unlike traditional financial insurers, which mitigate individual risk within predefined markets, the Universal Insurer evaluates entire economic, infrastructural, and ecological systems for phase alignment. Using metrics akin to the cake ratio, or the economic analog of vacuum expectation value. (There’s more than one way to make a cake, so what proportion counts as a cake?) This determines where coherence is being lost and allocates resources accordingly. It is neither reactive nor discretionary, but algorithmically proactive: a planetary stabilizer whose "premium" is paid by nations collectively in exchange for the long-term mitigation of systemic collapse and institutional phase failure.

The insurer does not issue currency, regulate markets, or set political priorities. Instead, it functions as a meta-institution or coherence governor that floats above national ideologies, responding only to the behavior of real-world flows. Its governance is fully algorithmic, with publicly auditable models and constraints against manipulation. It cannot be lobbied, bribed, or elected; it can only be updated through rigorous open modeling consensus. It represents not global authority, but planetary feedback.

This entity serves not to abolish nations, but to relieve them of their most failure-prone functions. By simulating the future and reinforcing coherence, it can offer a path toward long-term resilience for civilization. One that is not governed by force or narrative, but by alignment with informational structure.

Governance Integration: Complementing the Nation-State

The emergence of a universal insurer, powered by an AI-governed coherence stabilization entity, invites careful reflection on the future of national governance. While such an insurer may absorb a significant fraction of bureaucratic function currently performed by modern states, it does not replace sovereignty, culture, or collective self-determination. Rather, it offloads systemic drag by replacing reactive and inefficient institutions with proactive coherence enforcement.

We estimate that up to 60% of federal administrative roles in areas like healthcare, housing, retirement, social welfare, and economic modeling could be replaced or augmented by insurer-based feedback systems. These systems would evaluate structural phase alignment (e.g. cake ratio metrics) and stabilize entropy gradients across populations. However, legal systems, education content, defense, diplomacy, and cultural governance would remain the purview of national and regional governments.

The result is a hybrid model: planetary coherence infrastructure coexisting with sovereign identity. Governments retain symbolic, ethical, and narrative agency, while the insurer functions as a non-partisan coherence optimizer — guiding systemic flows with no allegiance but to stability, equity, and informational phase alignment. It is not a world government, but a world nervous system: sensing instability, and distributing resources to dampen disorder without dictating form.

Informatic UBI and the Posthumous Data Dividend

In a coherence-aligned economic system, informational value becomes as tangible as material production. We propose a model of universal basic income (UBI) based on informatics, in which individuals voluntarily contribute their personal data to a secure central compiler that constructs a high-fidelity AI model of their life. This life model remains fully encrypted and inaccessible while the individual is alive, functioning as a personal informational asset.

Upon death, however, the model becomes open access: it may be used to train collective civilizational systems, enrich simulations, or inform large-scale historical pattern analysis. In exchange for this eventual contribution, individuals receive a living dividend during their lifetime, or more familiarly, a basic income. This would be derived not from labor or taxation, but from the prospective informational value of their lived experience.

This system reframes value not in terms of control, but in terms of structured legacy. It enshrines privacy while alive and transparency upon death, and aligns human experience with civilizational learning in a temporally respectful manner. Coupled with a planetary coherence feedback infrastructure, it transforms every life into a contributor to humanity’s long-term informational phase memory.

4. The Morphon Field

At this point, we introduce a speculative but mathematically tractable extension to the Spinor Universe framework: a scalar field we call the morphon, representing feedback between coherent informational patterns and the structure of spacetime itself. The initial inspiration for the morphon field arises from the work of biologist Rupert Sheldrake, whose theory of morphic resonance proposed the existence of a formative, memory-like field that influences the development of biological and behavioral systems [2]. Though controversial and largely excluded from conventional scientific discourse due to its lack of formalization, Sheldrake’s central intuition, that coherent patterns reinforce their recurrence over time, resonates deeply with the framework developed here. In the Spinor Universe model, this idea is formalized as a scalar field coupled not to mass-energy, but to the local coherence of the spinor substrate. The morphon field thus provides a physically grounded, quantifiable structure capable of encoding the universe’s informational memory, retaining and amplifying coherence where it emerges. In this way, the morphon gives rigorous mathematical form to the spirit of Sheldrake’s proposal, embedding a theory of morphic feedback within the topological geometry of quantum phase space. The motivation is simple, yet the implications are not. In a universe where geometry emerges from quantum informational continuity, and coherence directly informs curvature, it becomes natural to ask whether repeated structures leave a kind of imprint on the fabric of reality. If they do, could that imprint act back on subsequent phenomena, subtly biasing them toward the more successful repetitions?

We emphasize at the outset: the morphon field is not introduced as a catch-all for paranormal claims, nor as a metaphysical gesture. Rather, it is formulated as a rigorously definable scalar field, one whose dynamics follow naturally from the feedback conditions implied by spinor-aligned coherence. Nevertheless, its consequences tread into terrain often reserved for folklore, ritual, and long-dismissed anomalies. It would be irresponsible to ignore the strangeness. But it would be more irresponsible to ignore the math. The morphon field is introduced as a scalar informational layer superimposed on the spinor substrate, representing the universe’s capacity for morphic feedback — the persistence and amplification of coherent structure over time. Unlike classical fields, the morphon does not couple directly to mass-energy, but to coherence: it responds to phase alignment and reinforces configurations that successfully resist entropic degradation.

4.1. Three Generations of Matter as Evidence of Stabilization and Evolution

In the Spinor Universe model, the existence of three particle generations is interpreted not as an arbitrary duplication of mass states, but as a layered hierarchy of coherence functionalities necessary for the stabilization of the universe across its energetic history. Each generation corresponds to a distinct form of topological task:

• First Generation (e.g., electrons, up and down quarks):Mass coherence — stabilization of inertial mass and spacetime persistence at low energies.
• Second Generation (e.g., muons, strange quarks):Flavor coherence — stabilization of intermediate quantum transitions and flavor oscillations.
• Third Generation (e.g., tau leptons, top and bottom quarks):Phase feedback coherence — stabilization of phase feedback and turbulence at the highest energy scales.

The observed mass hierarchy reflects this functional ordering, but it inverts the chronological order of emergence across cosmological time.

In the early universe, characterized by maximal decoherence and extreme phase turbulence, the system required phase feedback coherence first. Thus, third-generation particles dominated the earliest epochs, functioning as stabilizers of chaotic energy flux. As the universe expanded and cooled, intermediate-energy stabilizers became necessary, giving rise to the second generation, which provided flavor coherence across emerging field structures. Only after sufficient decoherence had been suppressed did the universe settle into the low-energy, mass-coherent regime dominated by first-generation particles — the familiar building blocks of matter observed today. Thus, by energy scale, the generations ascend from lightest to heaviest. But by cosmological formation priority, they descend from heaviest to lightest:

$$\mathrm{Energy}\mathrm{scale}:1^{\mathrm{st}}\to 2^{\mathrm{nd}}\to 3^{\mathrm{rd}}\mathrm{Formation}\mathrm{sequence}:3^{\mathrm{rd}}\to 2^{\mathrm{nd}}\to 1^{\mathrm{st}}$$

This inversion reflects the spinor topology of the universe, in which phase-space and energy-space are conjugate across forward and reverse temporal sheets. The three generations are not redundant, but functional — the legacy of the universe’s need to navigate, stabilize, and resolve its initial decoherence. In the Spinor Universe framework, the matter and antimatter sheets experience highly asymmetric initial conditions. The matter sheet emerges from a violent decoherence burst, requiring massive, short-lived structures to stabilize early phase chaos. In contrast, the antimatter sheet recoheres gently, favoring low-energy, minimal-disturbance configurations. Despite this asymmetry, both sheets must maintain spinorial entanglement to complete the full $4\pi$ phase cycle. If one sheet fails to achieve viable coherence, the spinor topology collapses entirely. The morphon field emerges as a necessary feedback mechanism, encoding early coherence successes and failures to bias subsequent evolution toward dual-sheet survival and global structural closure.

4.2. Perpendicular Musicians: A Metaphor for Temporal Collaboration

Imagine a vinyl record as a metaphor for the spinor universe. One musician, the forward-time composer, engraves a traditional spiral groove into the disc, etching sound into space in a smooth, continuous trajectory from the outer edge inward. This is the familiar process, linear, causally forward, spatially embedded. It is the matter phase writing its history in real time.

Now, imagine a second composer. This one is not tracing the spiral groove at all. Instead, they engage the medium orthogonally, not following the curvature of the record, but scratching directly across it, encoding perpendicular information. (This is the antimatter phase that composes not through working all the knots out of the matter, but knitting a sweater out of it.)

Where the first musician writes by flowing along the record’s plane, the second imposes a cross-modality of information, scratching across the other’s contribution, introducing phase shifts that affect how the original melody will be heard, distorted, or echoed when played. They use the same records interchangeably, but with the design of their local record players, they can only ever hear their own contributions. While they do not cohabitate within the same evolutionary environment, they are still selective pressures upon each other. One cannot write without acknowledging the other’s imprint. They set the basis of the pitch scale for each other’s compositions.

If either musician acts with disregard for the other, noise and interference result. But when the engravings and pulses begin to align, and when one anticipates the other’s rhythm, not just spatially but also temporally. The grooves deepen into phase-consistent valleys. Discord becomes resolution.

This metaphor reveals how the two temporal sheets of the spinor universe are not independent timelines, nor simple reflections. They are contrapuntal composers working in perpendicular modes, carving a shared reality into coherence. The forward-time evolution forms causal pathways; the reverse-time evolution modulates phase constraints and amplifies or suppresses informational resonance. So although quantum information is separated by their shared boundary, because of their causal relation, they are still able to collaborate. Their mutual awareness, learned through cycles of interference and resolution, is the process through which the universe converges on structure. Gravity is the general object of the game at play, but morphological optimization exists as an emergent meta-strategy within that play. Thus, time itself becomes a medium of cooperation. Events are not isolated, but are scored across a dual-layered geometry where causality and phase memory shape each other.

4.3. The Universe as a Learning System

While quantum information under conventional observation becomes scrambled at an event horizon, a spinor universe interpretation would characterize it as temporally distributed: encoded across both forward and backward time modes in such a way that local observation loses access to global phase memory. However, does not preclude the existence of an adaptive landscape between sheets. Coherence can still be selectively retained, morphically reinforced, and increasingly stabilized across cosmological iterations.

To illustrate this idea, let us reconsider the metaphor of two musicians improvising across time with a spinorial record. They are isolated in separate rooms and cannot hear each other’s musical contribution, but they do have to pass the record back and forth to work on it, and while they do their work in geometrically separated ways, they can improve upon their respective portions of the work with each passing of the record. So they never have to start over from scratch.

In this light, the universe may be viewed as a learning system. It utilizes the accumulation of coherence over time to represent a cosmological memory. Through some unknown number of topological or entropic cycles, the spinor substrate may have undergone phase refinement, producing a stable coherence basin that appears to us as a finely tuned physical cosmos. This perspective does not require intelligent design per se, but posits instead that coherence itself functions as an attractor basin in an evolving phase space, offering a possible resolution to longstanding questions about fine-tuning in physical law and the universe’s apparent favorability towards the production of life.

4.4. Quantizing the Morphon

The field is governed by a modified Klein-Gordon-type equation with coherence-coupled source terms:

$$\square \mu (x,t)+\kappa \mu (x,t)=\beta \mathcal{C}(x,t)$$

where:

• $\mu (x,t)$ is the morphon field,
• $\square ={\partial }^{\mu }{\partial }_{\mu }$ is the d’Alembert operator in curved spacetime,
• $\kappa$ is the morphic decay constant (inverse plasticity),
• $\beta$ is the coherence response coefficient,
• $\mathcal{C}(x,t)$ is the local coherence field, interpreted as the generalized VEV of the spinor substrate.

This equation describes a scalar field that accumulates in regions of high coherence, but decays with a cosmologically scaling timescale set by $\kappa$. The morphon thus behaves as a dynamic attractor field for coherent structures, reinforcing their recurrence without introducing direct force mediation or gauge charges. Instead, it encodes an effective memory potential — a non-local bias toward re-emergence of previously coherent patterns, forming a scalar backdrop to the universe’s informational topology.

This formulation allows the morphon to be quantized as a standard scalar field, admitting creation and annihilation operators in coherence-resonant modes, and enabling field-theoretic treatments of informational resonance, pattern memory, and morphic evolution. In this way, the morphon field establishes the quantum underlayer of what might classically be perceived as morphic resonance, without appealing to teleology or hidden variables.

In the Spinor Universe framework, the morphon field $\mu (x,t)$ evolves as a function of local coherence density $\mathcal{C}(x,t)$, the phase memory of surrounding topology, and the temporal gradient of informational structure. It acts as a scalar buffer encoding where the universe has “learned” to support recurrence, creating an effective landscape of attractor basins favoring previously stabilized configurations.

We propose the following functional coupling:

$${\displaystyle \frac{\partial \mu }{\partial t}}=\beta ·\mathcal{C}(x,t)-\kappa ·\mu (x,t)$$

Where:

• $\mu (x,t)$ is the morphon scalar field,
• $\mathcal{C}(x,t)$ is the local coherence field (generalized VEV),
• $\beta$ is the morphic sensitivity coefficient,
• $\kappa$ is the decay constant reflecting morphic half-life.

This relation describes a system in which coherence generates morphic reinforcement, but only within a limited retention window. As the universe’s global coherence increases, the morphon field becomes less plastic — a form of cosmological aging in which learning slows and novelty is increasingly resisted. In this way, the morphon field encodes not only local memory but a kind of scalar historical inertia that shapes the future through the residue of past coherence.

4.5. Embedding the Morphon Field in the Spinor Universe

We define the morphon field $\mu (x,t)$ as a real scalar field embedded in the spinor substrate, evolving in response to the local coherence field $\mathcal{C}(x,t)$. The dynamics of $\mu$ are governed by the following Lagrangian density:

$${\mathcal{L}}_{\mu }={\displaystyle \frac{1}{2}}{\partial }^{\mu }\mu {\partial }_{\mu }\mu -{\displaystyle \frac{1}{2}}\kappa {\mu }^2-\beta \mathcal{C}(x,t)\mu +{\displaystyle \frac{\lambda }{4}}{\mu }^4+\xi {\varphi }_H\left(x\right){\mu }^2$$

This Lagrangian includes:

• ${\displaystyle \frac{1}{2}}{\partial }^{\mu }\mu {\partial }_{\mu }\mu$: The canonical kinetic term, describing propagation of the morphon field through spacetime.
• $-{\displaystyle \frac{1}{2}}\kappa {\mu }^2$: A decay or “damping” term, representing the decreasing plasticity of the morphon field over time — the scalar expression of cosmic memory saturation.
• $-\beta \mathcal{C}(x,t)\mu$: A coherence-coupled source term. The morphon field accumulates in regions of high local coherence $\mathcal{C}(x,t)$, effectively learning from stability and structure.
• $+{\displaystyle \frac{\lambda }{4}}{\mu }^4$: A self-interaction term allowing non-linear morphon resonance effects and saturation dynamics, modeling memory locking or attractor basins in morphic evolution.
• $+\xi {\varphi }_H\left(x\right){\mu }^2$: A coupling to the Higgs phase anchor field ${\varphi }_H\left(x\right)$, allowing the morphon to scale its sensitivity in proportion to the degree of global phase anchoring. This term binds the morphon’s memory function to the universe’s temporal symmetry breaking.

Together, these terms describe a scalar field that accumulates in coherence-rich regions, saturates over time, and evolves in resonance with the underlying phase geometry of the spinor universe. The morphon does not directly mediate forces, but rather encodes an informational backdrop of a coherent memory scaffold through which topological stability and evolutionary learning are reinforced.

Applying the Euler–Lagrange equation for fields to the morphon Lagrangian,

$${\displaystyle \frac{\partial \mathcal{L}}{\partial \mu }}-{\partial }_{\mu }\left({\displaystyle \frac{\partial \mathcal{L}}{\partial \left({\partial }_{\mu }\mu \right)}}\right)=0,$$

and substituting the full Lagrangian,

$${\mathcal{L}}_{\mu }={\displaystyle \frac{1}{2}}{\partial }^{\mu }\mu {\partial }_{\mu }\mu -{\displaystyle \frac{1}{2}}\kappa {\mu }^2-\beta \mathcal{C}(x,t)\mu +{\displaystyle \frac{\lambda }{4}}{\mu }^4+\xi {\varphi }_H\left(x\right){\mu }^2,$$

we obtain the following equation of motion for the morphon field:

$$\square \mu (x,t)+\kappa \mu (x,t)+\beta \mathcal{C}(x,t)-\lambda {\mu }^3(x,t)-2\xi {\varphi }_H\left(x\right)\mu (x,t)=0.$$

This generalized Klein–Gordon-like equation governs the behavior of the morphon field in response to local coherence $\mathcal{C}(x,t)$, the phase-anchoring Higgs field ${\varphi }_H\left(x\right)$, and its own self-interactions. The appearance of the coherence-coupling source term $\beta \mathcal{C}(x,t)$ ensures that morphon excitations are not sourced by energy or mass directly, but by the underlying order and alignment of the spinor substrate. The decay term $\kappa \mu$ and the non-linear contributions $\lambda {\mu }^3$ and $\xi {\varphi }_H\mu$ determine the field’s saturation behavior and coupling to global symmetry dynamics.

In flat spacetime, the morphon field $\mu (x,t)$ can be quantized in the standard scalar field formalism by promoting it to an operator $\widehat{\mu }(x,t)$ and expanding it in terms of creation and annihilation operators over plane wave modes. The canonical mode expansion is:

$$\widehat{\mu }(x,t)=\int {\displaystyle \frac{d^{3}k}{{\left(2\pi \right)}^3}}{\displaystyle \frac{1}{\sqrt{2{\omega }_k}}}\left[{\widehat{a}}_{\overrightarrow{k}}{e}^{-i({\omega }_{k}t-\overrightarrow{k}·\overrightarrow{x})}+{\widehat{a}}_{\overrightarrow{k}}^{†}{e}^{i({\omega }_{k}t-\overrightarrow{k}·\overrightarrow{x})}\right]$$

where:

• ${\widehat{a}}_{\overrightarrow{k}}$ and ${\widehat{a}}_{\overrightarrow{k}}^{†}$ are the annihilation and creation operators for a morphon quantum of momentum $\overrightarrow{k}$,
• ${\omega }_k=\sqrt{|\overrightarrow{k}{|}^2+m_{\mu }^2}$ is the dispersion relation for the field, where $m_{\mu }^2=\kappa +2\xi {\varphi }_H$ is the effective mass term derived from the Lagrangian.

These operators obey the standard bosonic commutation relations:

$$[{\widehat{a}}_{\overrightarrow{k}},{\widehat{a}}_{{\overrightarrow{k}}^{\prime }}^{†}]={\left(2\pi \right)}^3{\delta }^3(\overrightarrow{k}-{\overrightarrow{k}}^{\prime }),[{\widehat{a}}_{\overrightarrow{k}},{\widehat{a}}_{{\overrightarrow{k}}^{\prime }}]=[{\widehat{a}}_{\overrightarrow{k}}^{†},{\widehat{a}}_{{\overrightarrow{k}}^{\prime }}^{†}]=0.$$

In this formalism, morphon quanta can be interpreted as coherence-stabilizing excitations — localized "packets" of informational reinforcement — which emerge in response to stable phase structures and decay in disordered regions. Their presence reflects the memory-like imprint of high-structure configurations in the spinor substrate, and their dynamics may encode mechanisms for feedback amplification, structural recurrence, or coherence attraction across time.

4.6. A Gauge-Theoretic Interpretation of the Morphon Field

To further formalize the morphon field, we interpret it as a gauge field arising from an internal symmetry related to contextual coherence across time. In conventional gauge theories, local invariance under transformations of internal quantum numbers gives rise to force-mediating fields. By analogy, we propose that the morphon field encodes a local symmetry associated with informational recurrence. This recurrence is not blind repetition, but recurrence that is entropically useful and thus preferentially reinforced.

We define the morphon as a complex scalar field:

$$\varphi \left(x\right)=\rho \left(x\right)e^{i\theta \left(x\right)},$$

where $\rho \left(x\right)$ represents the magnitude of local morphic coherence, and $\theta \left(x\right)$ encodes the morphic phase, which reflects alignment across past information and current context.

We postulate that the morphic phase admits a local $U\left(1\right)$ symmetry:

$$\varphi \left(x\right)\to {\varphi }^{\prime }\left(x\right)=e^{i\alpha \left(x\right)}\varphi \left(x\right),$$

which requires the introduction of a gauge field $M_{\mu }\left(x\right)$ transforming as:

$$M_{\mu }\left(x\right)\to M_{\mu }\left(x\right)+{\partial }_{\mu }\alpha \left(x\right).$$

This leads to a covariant derivative of the form:

$$D_{\mu }\varphi =({\partial }_{\mu }-i{M}_{\mu })\varphi ,$$

and the gauge-invariant Lagrangian becomes:

$$\mathcal{L}=|D_{\mu }{\varphi |}^2-V\left(\varphi \right)-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu },$$

where $F_{\mu \nu }={\partial }_{\mu }{M}_{\nu }-{\partial }_{\nu }{M}_{\mu }$ defines the morphic field strength.

In this interpretation, morphic memory is encoded in the curvature of an informational phase space. Structures that are not only repeated but repeated in ways that contribute to local entropy production will reinforce this field. The morphon does not merely favor repetition, but favors coherent activity that provides informational and entropic utility.

This distinction is essential. The morphon does not act as a magical copying force. It is a statistical field that biases reality toward patterns that are entropically validated. In this view, behaviors that are locally efficient, statistically successful, and rich in entropy flow become easier to instantiate elsewhere. This holds even in systems that are not causally connected, as long as they remain aligned in morphic phase.

Thus, the morphon field does not function as a memory of past events. It acts as an amplifier for future configurations that reinforce coherent informational structure. It favors paths that extend global coherence, shaping the evolution of systems through phase bias rather than direct force.

4.7. Spontaneous Symmetry Breaking in the Morphon Field

To explore the implications of symmetry breaking in the morphon field, we introduce a potential of the form:

$$V\left(\varphi \right)=\lambda {({\varphi }^2-{\varphi }_0^2)}^2,$$

where $\lambda$ is a coupling constant and ${\varphi }_0$ defines the vacuum expectation value (VEV) of the field. This quartic potential exhibits the classic "Mexican hat" structure, leading to spontaneous symmetry breaking (SSB) when $\varphi$ settles into one of the degenerate minima at $\varphi =\pm {\varphi }_0$.

In this context, SSB implies that the universe develops a preference for certain morphic structures—patterns that are favored not merely due to their frequency or environmental support, but because they align with the global vacuum configuration of the morphon field.

Morphic VEV and Memory Encoding.

The nonzero VEV,

$$\langle \varphi \rangle ={\varphi }_0\ne 0,$$

acts as a background memory field, embedding a default structure into spacetime itself. This may correspond to recurring molecular motifs, biological geometries, or informational attractors. Even in the absence of direct morphic activity, the field retains a predisposition toward coherence, biasing the formation of certain patterns across evolutionary or developmental pathways.

Massless Modes and Coherence Freedom.

The spontaneous breaking of continuous symmetry generically leads to the appearance of massless excitations, (ie Goldstone modes). In our framework, these represent patterns that are free to propagate and replicate with minimal informational resistance. Examples may include repeating behaviors, crystallographic templates, or biological features like helical symmetry, which emerge ubiquitously due to minimal morphic cost.

Mass Generation and Morphic Inertia

Deviations from the morphic ground state experience increased energetic cost. As a result, patterns that diverge from the default coherence phase may be suppressed or fail to persist, creating a form of morphic inertia. This mechanism could help explain why certain viable but unchosen configurations (e.g., molecular mirror-life) fail to manifest, even in principle.

Domain Formation and Morphic Divergence

SSB also permits the emergence of distinct regions of space with different vacuum configurations analogous to domains in a ferromagnet. In the morphic case, this may account for the divergent evolution of ecosystems, civilizations, or biospheres. Each domain would retain a localized morphic bias, potentially incompatible with others, generating boundaries not of chemistry but of memory.

Mechanism of Influence

Crucially, the morphon field does not exert direct forces upon particles or fields in the conventional sense. Instead, it modulates the phase landscape of the spinor substrate, altering the stability conditions for coherence itself. In regions of high morphon density, recursive configurations face a lower threshold for persistence, effectively reducing the entropic cost of maintaining structured states. Conversely, in incoherent regions, the formation of new coherent attractors becomes more difficult, as the underlying phase topology no longer supports easy convergence. In this way, the morphon field biases the emergence, reproduction, and durability of coherent forms without transferring energy, acting instead through topological affordance.

Interpretation

Spontaneous symmetry breaking elevates the morphon field from a passive coherence amplifier to an active memory substrate. It does not merely respond to repetition, but imprints a prior, preferred coherence phase into the structure of spacetime itself. This process may underlie the stability of biological chirality, the universality of certain cognitive archetypes, and the recurrence of symbolic structures across time and culture.

Informational Budget and the Embedding of Coherence Memory

A natural objection to the morphon field arises from the question of informational capacity: how can the universe support an additional scalar field encoding coherence memory without violating known quantum informational limits? If all quantum degrees of freedom are already maximally utilized, where does the morphon field “fit”?

This concern is addressed directly by the architecture of the Spinor Universe model. In this framework, the morphon field does not represent a new or independent layer of information, but rather a scalar summary of phase coherence already present within the spinor substrate. It does not store new microstates, but compresses and accumulates phase alignment over time — a derivative of existing structure rather than an additive.

More precisely, the morphon field is only sourced in regions where entropy has been reduced by successful phase alignment. The coherence field $\mathcal{C}(x,t)$, which sources morphon reinforcement, is itself a measure of informational constraint — a reduction in accessible microstates via symmetry and topology. Thus, the morphon field emerges only where the informational budget has already been compressed. It is not a competing signal but a trailing consequence: coherence creates the space for memory.

Additionally, due to the non-local, topologically encoded nature of the spinor substrate, coherence memory does not require dedicated local storage. Instead, it propagates through changes in the curvature and phase flow of the underlying field, much like interference patterns in a continuous medium. In this sense, the morphon field is not an imposed construct, but an inevitable thermodynamic and geometric consequence of phase coherence in an informationally fluid universe.

4.8. Topological Molecular Chirality Hypothesis

These coherence feedback mechanisms open the door to a deeper biological implication: morphon excitations may not be evenly distributed in spacetime, but may cluster preferentially around systems exhibiting long-term coherence stability. One class of such systems is chiral biomolecules, particularly amino acids and nucleotides, whose molecular handedness encodes informational asymmetry and structural memory. In this light, the morphon field offers a possible mechanism for reinforcing and stabilizing chirality biases through coherence feedback loops, thereby providing a natural energetic and topological pathway toward the Topological Molecular Chirality Hypothesis. We formally propose the Topological Molecular Chirality Hypothesis as follows:

The observed universal chirality bias in biological molecules (e.g., the left-handedness of amino acids and the right-handedness of sugars) arises as a natural consequence of the universe’s spinor topological structure. Specifically, molecular chirality is influenced by the embedding of matter within a globally asymmetric spinor field geometry that exhibits a preferred phase orientation following symmetry breaking mediated by the Higgs field. This topological bias is further reinforced by the morphon field, which accumulates preferentially in regions of sustained phase coherence. Chiral molecular systems, being both highly structured and informationally asymmetric, act as local coherence attractors, drawing and stabilizing morphon excitations in a way that amplifies the selection of one chirality over another.

This hypothesis suggests that molecular handedness is not an arbitrary outcome of stochastic chemical evolution, but a physically determined and topologically constrained feature of the quantum geometry of spacetime. The bias emerges from two interlinked factors:

• The global chirality of the universe’s spinor topology, instantiated through the Higgs field’s anchoring of phase orientation and temporal direction.
• The local reinforcement of molecular asymmetry via morphon field accumulation in coherent, chiral biomolecular configurations.

Constraints and Limitations of Morphon Feedback

While the morphon field encodes a coherent memory potential within the spinor substrate, it is essential to clarify the inherent limitations of this mechanism. The targeted reinforcement of arbitrary patterns or outcomes is not possible within this framework. There is no magic.

The constraints arise from the fundamental nature of the morphon field:

• Coherence-Only Coupling: The morphon field responds solely to the scalar coherence field $\mathcal{C}(x,t)$. It has no coupling to semantic content, symbolic patterns, or observer intention. Morphic reinforcement occurs only where phase alignment is already approaching maximum stability.
• Non-Discriminatory Accumulation: As a scalar field with no internal degrees of freedom, $\mu (x,t)$ is incapable of encoding selective preferences. It acts as a passive scalar reservoir that accumulates in proportion to coherence, not pattern identity.
• Decoherence Interference: Artificial attempts to force morphon amplification onto low-coherence or noisy regions result in interference and phase mismatch, which dissipate coherence rather than reinforcing it. The field inherently resists topological distortion.
• Temporal Saturation: The morphon decay term $\kappa {\mu }^2$ ensures that the field becomes increasingly resistant to new imprinting over time. This reflects the cosmological trend toward lower plasticity, wherein the universe stabilizes its structural memory and filters out novel or incoherent configurations.

These limitations preserve the physicality of the model by ensuring that morphon dynamics are fully governed by the coherence structure of the spinor substrate. There is no mechanism by which arbitrary or low-coherence patterns may be selectively reinforced without already being topologically favored.

4.9. Refinements Across Iterations: What the Universe Learns

If the Spinor Universe evolves through topological iteration, then the accumulation of coherence from one cycle to the next reflects not merely structural persistence, but progressive refinement of the universe’s operating parameters. In this framework, we propose that three classes of refinement occur across iterations:

• Phase Topology Refinement: The global spinor substrate becomes increasingly hospitable to stable coherence configurations. This may involve smoothing local phase gradients, reducing decoherence noise, and expanding the basin of attraction around successful phase geometries.
• Effective Field Refinement: Constants associated with emergent fields — such as coupling strengths, mass terms, and vacuum expectation values — may shift toward values that improve stability, longevity, and feedback propagation. These are not fixed by initial conditions but refined through cosmological learning.
• Compression of Law Space: Iteration effectively narrows the range of viable physical laws. Only those consistent with high coherence retention and morphon feedback persist. This provides a potential resolution to the fine-tuning problem: the universe appears well-tuned because its prior iterations were not.

The Primordial Decoherent Epoch and the Tractable Coherence Minimum

The existence of a learning structure in the Spinor Universe implies a necessary ontological precedent: a phase configuration that precedes refinement. We designate this hypothesized early state as the Primordial Decoherent Epoch — an initial phase of the universe characterized by low coherence, minimal structural stability, and a topology dominated by high-magnitude spinor gradients.

In this state, matter and fields as we know them may not yet exist. Instead, the spinor substrate would manifest as a fluctuating informational foam, with coherence islands appearing only sporadically and briefly. Crucially, these rare fluctuations provide the seed conditions required for initiating feedback via morphon field accumulation.

We define the tractable coherence minimum, ${\mathcal{C}}_{\min }$, as the minimum value of the coherence field necessary to trigger stable morphon reinforcement. From the morphon field equation:

$${\displaystyle \frac{\partial \mu }{\partial t}}=\beta ·\mathcal{C}\left(x\right)-\kappa \mu \left(x\right),$$

feedback becomes viable when growth overtakes decay:

$${\mathcal{C}}_{\min }={\displaystyle \frac{\kappa {\mu }_{\mathrm{init}}}{\beta }}.$$

This sets a lower bound on viable spinor configurations capable of initiating structure-learning. Any universe with global coherence below this threshold would decay into pure decoherence. But if even a minimal region satisfies $\mathcal{C}\left(x\right)>{\mathcal{C}}_{\min }$, then feedback loops can begin, morphon memory can accumulate, and stable phase attractors can emerge.

In this light, the universe we observe today is not the only possible spinor outcome, but it may be one of the rare outcomes that crossed the tractable coherence threshold early enough to stabilize, iterate, and eventually develop the phase-anchored precision we associate with physical law in this current iteration. Making far truer the old adage "It could always be worse.".

The Structural Coherence Floor

While the total mass-energy of the universe may decrease with each spinor iteration as phase coherence improves, there exists a lower bound below which further reduction is no longer compatible with structure. Mass-energy, in this framework, is not merely an energetic residue but a necessary byproduct of persistent phase tension — the structural strain required to scaffold complexity.

Topological phenomena such as black holes, particle masses, and quantum vacuum fluctuations are anchored in irreducible phase gradients. These are not defects, but essential asymmetries that allow coherence to propagate, stabilize, and accumulate. Erasing all mass-energy would eliminate the substrate needed to retain memory, form attractors, or support feedback loops.

Thus, the universe must preserve a minimum level of persistent misalignment in order to remain a viable system. We define this as the structural coherence floor, below which morphic iteration fails and coherence cannot be sustained.

4.9.1. The Morphon Horizon and the Completion of Cosmic Learning

As the Spinor Universe continues to refine its phase topology through morphic feedback, it asymptotically approaches a terminal state in which further learning becomes unnecessary. In this limit, the morphon field saturates:

$${\displaystyle \frac{\partial \mu }{\partial t}}\to 0,\mu (x,t)\to {\mu }_{\infty },$$

and the coherence field approaches its global maximum $\mathcal{C}(x,t)\to {\mathcal{C}}_{\max }$. At this point, the morphon field becomes informationally redundant: it no longer differentiates regions, structures, or attractors, as all viable configurations have been encoded and stabilized.

This limit, which we term the Morphon Horizon, represents the theoretical endpoint of a universe that has fully learned its own structure. It is not an entropic death, but a state of maximal informational efficiency. All viable patterns are known, all phase gradients are minimized, and the spinor substrate exists in a globally phase-locked state.

Such a state may be approached but never truly reached, as the universe requires a residual tension to support the very structure of coherence. Yet the existence of this asymptotic endpoint frames cosmic evolution as a process with direction: from disorder to stable informational recursion from noise to self-referential silence.

Recognition of Prior Insights: Sheldrake, Penrose, and Hameroff

Although the morphon field and its spinor embedding are formally introduced here for the first time within a coherent topological cosmology, it would be historically dishonest to claim that these ideas arose without precedent. Key figures in the 20th and early 21st centuries glimpsed critical facets of this structure from different perspectives, albeit without a unifying physical model at their disposal.

Rupert Sheldrake’s theory of morphic resonance proposed that patterns of biological and behavioral organization could self-reinforce across time, laying the conceptual groundwork for the idea that coherence leaves a memory-like imprint on the universe. Roger Penrose and Stuart Hameroff, in their theory of Orchestrated Objective Reduction (Orch-OR), suggested that coherent quantum processes in brain microtubules might play a crucial role in consciousness, emphasizing the fundamental importance of coherence in the emergence of self-aware systems.

Within the framework of the Spinor Universe and the morphon field, these seemingly disparate insights find a natural synthesis. The morphon field formalizes a scalar memory structure capable of influencing coherence across scales, validating Sheldrake’s intuition within a rigorous topological setting. Meanwhile, the role of biological systems as coherence amplifiers supports Penrose and Hameroff’s claims that consciousness is fundamentally linked to deep-phase informational structures rather than emergent classical computation.

Thus, the morphon field does not merely echo their intuitions, but it grounds them. It reinterprets morphic resonance as a quantized scalar memory embedded in the spinor substrate, and reframes coherent consciousness not as a metaphysical emergence, but as a recursive amplifier of topological phase alignment. Their insights were not wrong. They were waiting for topology to catch up.

Recovery of Broader Observational Plausibility

Beyond the immediate theoretical implications, the formalization of the morphon field recovers the plausibility of a wide range of empirical phenomena that were historically marginalized due to the absence of a coherent physical framework. Many researchers and theorists who reported anomalous effects related to coherence, memory, and biological patterning now find their observations newly contextualized within a consistent cosmological structure.

In addition to the major contributions of Sheldrake [2] and Penrose and Hameroff [3], the Spinor Universe model offers a natural explanatory foundation for insights such as:

• Cleve Backster’s observations of primary perception in plants, suggesting long-range coherence effects [4].
• Dean Radin’s experimental studies of nonlocal correlations between human intention and physical systems [5].
• Edgar Mitchell’s Institute of Noetic Sciences work on consciousness and quantum-connected feedback [6].
• Rupert Sheldrake’s later expansions on morphic fields in cognitive phenomena [7].
• Emerging studies on anomalous memory inheritance in biological systems across generations [8].

Rather than discarding these observations as statistical anomalies or cognitive biases, the morphon field model permits their reinterpretation as early glimpses of an underlying coherence memory substrate in nature. While rigorous experimental validation remains paramount, the theoretical groundwork laid here transforms these phenomena from curiosities into plausible expressions of deeper topological processes.

The morphon thus serves as a bridge for reconciling speculative observations with a physically grounded ontology of coherence evolution. It invites serious reconsideration of evidence once discarded, not because it was false, but because it arrived before mathematics could understand it.