Chronon Phase Transition Cosmology: A Unified Framework for Emergent Spacetime, Dark Matter, and Dark Energy

1. Introduction

The standard Lambda Cold Dark Matter ($\Lambda$CDM) model provides a phenomenologically successful cosmology, yet it relies on multiple unexplained ingredients: a finely tuned inflationary phase [25], an unknown form of cold dark matter [11], and a cosmological constant or dark energy component driving late-time acceleration [56]. While $\Lambda$CDM fits current data well, its theoretical foundations remain incomplete and arguably ad hoc [15].

We propose an alternative framework: Chronon Phase Transition Cosmology (CPTC), grounded in Chronon Field Theory (CFT), in which the local structure of time—encoded in a physical temporal vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$—determines the emergence of spacetime, causality, and all observed cosmic phenomena [35].

In this theory, the universe begins in a disordered pre-temporal state. A spontaneous symmetry-breaking phase transition—driven by the Chronon field—gives rise to an ordered phase of coherent temporal flow. This critical transition defines the Big Bang not as a singularity but as a dynamical onset of causal order: the birth of the Real Now.

Remarkably, CPTC accounts for both dark matter and dark energy as emergent, dynamical consequences of the Chronon field:

• Dark energy arises from the tension and decay of domain walls separating causally disconnected regions of the Real Now field, producing a late-time vacuum-like energy density without requiring a cosmological constant [35,38].
• Dark matter effects emerge from foliation-induced boosts in angular momentum and gravitational self-energy associated with spacetime orientation and Chronon shear, explaining galactic rotation curves and large-scale structure without invoking non-baryonic matter.

These effects are not added by hand but follow from the geometry, coherence, and dynamics of time itself. CPTC thus offers a predictive, falsifiable, and ontologically grounded alternative to inflation and $\Lambda$CDM—one in which dark matter and dark energy are not substances, but manifestations of phase structure in the flow of time.

Chronon Phase Transition Cosmology (CPTC) offers:

• A unified explanation of spacetime emergence, matter genesis, and cosmic expansion.
• A topologically active time field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ replacing both inflaton and dark sector fields.
• Predictive power across multiple regimes—from the early universe to galaxy rotation curves.

This paper develops the Chronon phase transition formalism, derives its dynamical equations, and demonstrates its cosmological implications.

2. Related Work and Theoretical Context

Chronon Phase Transition Cosmology (CPTC) draws upon and extends several foundational lines of inquiry in modern cosmology and quantum gravity. The standard $\Lambda$CDM model, while empirically successful, posits a series of unexplained components including a scalar inflaton field [25,36], cold dark matter of unknown composition [11], and a finely tuned cosmological constant [56]. CPTC offers an alternative ontology in which spacetime, causal structure, and dark sector phenomena emerge from the dynamics of a fundamental temporal field.

The causal structure of CPTC has conceptual affinities with causal set theory [12,51] and shape dynamics [5], both of which aim to reconstruct spacetime from more primitive elements. Unlike causal sets, which assume a fundamentally discrete spacetime, CPTC maintains a continuous field-theoretic formulation while achieving causal emergence via spontaneous symmetry breaking of a dynamical time vector field.

Our use of a unit-norm timelike vector field ${\mathrm{\Phi }}^{\mu }$ is structurally related to Einstein-æther theories and generalized Proca models that explore preferred foliations or Lorentz violation, though not always explicitly referenced in CPTC. CPTC differs in that the temporal field is not merely a symmetry-breaking background but the ontological source of causality, entropy growth, and spacetime geometry itself.

Several prior efforts have explored emergent gravity paradigms, including thermodynamic derivations of Einstein’s equations [32], analogue gravity models [6], and information-theoretic interpretations such as entropic gravity [53]. CPTC shares the spirit of these approaches in seeking a non-geometric origin for gravity, but uniquely locates the source of both geometry and matter in the topological configuration space of time.

Dark energy models based on vacuum decay, topological defects, or domain walls have been proposed as alternatives to a cosmological constant [10,14,54]. CPTC realizes this idea dynamically, interpreting dark energy as residual tension in metastable Chronon domain walls formed during a global temporal phase transition. Similarly, dark matter phenomenology is addressed through localized residual tension and foliation shear—an approach distinct from particle-based models or modifications of inertia like MOND [23,40].

In terms of cosmological observations, CPTC aligns with efforts to explain cosmic anisotropy and low-multipole anomalies in the CMB [19], as well as galaxy-scale structure and spin alignments [33]. Our model’s power-law expansion phases and solitonic initial conditions yield predictions testable via upcoming large-scale surveys and gravitational wave observatories.

In summary, CPTC integrates insights from causal emergence, topological field theory, and phase transition dynamics into a coherent cosmological framework. It addresses longstanding issues in early-universe cosmology, the nature of time, and the unification of dark sector effects within a single dynamical entity.

3. Chronon Field Theory: Foundations for Emergent Cosmology

Chronon Field Theory (CFT) furnishes the ontological and mathematical foundation for the cosmological framework developed in this work. It posits that the fabric of physical reality emerges from the dynamics of a unit-norm, future-directed timelike vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$—the Chronon field—encoding the Real Now. Unlike conventional models where time is a coordinate, here time is a dynamical entity: a causal, ontologically primitive field that gives rise to spacetime, matter, gravity, and gauge interactions through its topological and geometric evolution [3].

3.1. Fundamental Structure and Ontology

CFT postulates a smooth temporal vector field satisfying

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1,{\mathrm{\Phi }}^0>0,$$

(1)

which defines a preferred foliation $\left\{{\mathrm{\Sigma }}_t\right\}$ of the manifold $\mathcal{M}$ into spatial hypersurfaces orthogonal to ${\mathrm{\Phi }}^{\mu }$[55]. This structure replaces the passive global time of standard physics with a dynamically evolving temporal flow. Integral curves of ${\mathrm{\Phi }}^{\mu }$ constitute a congruence of worldlines that define local temporal directionality and causality.

The Chronon field is not merely geometric: it admits intrinsic topological observables (e.g., winding number, ${\pi }_3$ charges, helicity), giving rise to quantized solitonic excitations. These topological sectors provide the pre-spacetime substrate from which particles, interactions, and spacetime geometry emerge [22,31].

3.2. Chronon Dynamics and Induced Geometry

The Chronon field evolves via a generalized Proca-like dynamics with self-interaction and constraint-enforcing potentials:

$${\nabla }_{\nu }{F}^{\nu \mu }+m_{\mathrm{\Phi }}^2{\mathrm{\Phi }}^{\mu }+{\displaystyle \frac{\delta V}{\delta {\mathrm{\Phi }}_{\mu }}}=J^{\mu },$$

(2)

where $F_{\mu \nu }={\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }-{\nabla }_{\nu }{\mathrm{\Phi }}_{\mu }$ and $J^{\mu }$ includes matter sources. In regions of coherent alignment, ${\mathrm{\Phi }}^{\mu }$ induces an emergent effective metric:

$$g_{\mu \nu }^{\mathrm{eff}}={\eta }_{\mu \nu }+\epsilon {\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu },$$

(3)

governing causal propagation and curvature. This geometric backreaction underlies both gravitational lensing and large-scale structure [35].

3.3. Phase Transition and the Emergence of Time

At high temperatures or in the early universe, ${\mathrm{\Phi }}^{\mu }$ is disordered, and no global temporal direction exists. As the system cools or reaches a critical coupling, a second-order phase transition spontaneously aligns the field:

$$\langle {\mathrm{\Phi }}^0\rangle \ne 0,\xi \left(t\right)\sim t^{\alpha },$$

(4)

initiating a global causal structure—the Big Bang is reinterpreted as the onset of temporal order. This symmetry breaking defines a dynamical arrow of time, giving rise to cosmogenesis without singularities or fine-tuned inflation [3,16].

3.4. Topological Solitons and Emergent Matter

Localized topological configurations of ${\mathrm{\Phi }}^{\mu }$—termed blobs—carry quantized winding and form the building blocks of matter:

$$T_{\mathrm{\Phi }}^{\mu \nu }={\nabla }^{\mu }{\mathrm{\Phi }}^{\alpha }{\nabla }^{\nu }{\mathrm{\Phi }}_{\alpha }-{\displaystyle \frac{1}{2}}{g}^{\mu \nu }{\nabla }_{\beta }{\mathrm{\Phi }}^{\gamma }{\nabla }^{\beta }{\mathrm{\Phi }}_{\gamma }+V\left({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\right)g^{\mu \nu }.$$

(5)

These blobs generate an emergent stress-energy tensor sourcing gravitational dynamics. Their statistical distribution governs energy density, cosmic web anisotropies, and the dark sector phenomenology detailed in later sections.

3.5. Chronon Field as a Universal Cosmological Substrate

Chronon Field Theory underwrites all components of CPTC:

• Gravity arises from curvature in the effective metric induced by ${\mathrm{\Phi }}^{\mu }$.
• Dark matter effects follow from trapped Chronon tension and foliation shear in galactic regions.
• Dark energy emerges as residual vacuum stress from metastable domain wall networks.
• Cosmic expansion is governed by the divergence $\theta ={\nabla }_{\mu }{\mathrm{\Phi }}^{\mu }$, analogous to a Raychaudhuri scalar.
• Structure formation is seeded by curvature and shear perturbations in ${\mathrm{\Phi }}^{\mu }$, generating biased filament networks.
• Causal horizons arise dynamically from the expanding coherence length $\xi \left(t\right)$ of ${\mathrm{\Phi }}^{\mu }$.
• Thermodynamic irreversibility is rooted in the geometric evolution of a globally aligned, future-directed ${\mathrm{\Phi }}^{\mu }$.

3.6. Numerical and Phenomenological Support

Lattice simulations confirm spontaneous topological ordering and second-order criticality in discretized CFT models. Emergent solitons in these simulations reproduce particle-like spectra, while numerical solutions of the effective Chronon equations predict cosmological observables, including:

• Rotation curves of dwarf galaxies (e.g., DDO 154),
• Lensing distortions and shear anisotropy,
• CMB alignment anomalies and suppressed tensor modes,
• Scale-dependent dark energy behavior.

3.7. Outlook

CFT unifies spacetime, gravity, gauge fields, and matter in a single topological framework driven by the temporal structure of the Real Now. It offers a conceptually minimal and mathematically rich alternative to both inflation and dark sector extensions of $\Lambda$CDM. The remainder of this paper builds upon this foundation to derive the dynamics, observational consequences, and falsifiability of Chronon Phase Transition Cosmology.

Part I. Phenomenological Consequences of Chronon Field Theory

4. Emergent Spacetime and Cosmic Expansion

In Chronon Phase Transition Cosmology (CPTC), cosmic expansion is reinterpreted as the growth of temporally coherent domains of the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. The correlation length $\xi \left(t\right)$ acts as a causal horizon scale:

$$R_H\left(t\right)\sim \xi \left(t\right)\propto t^{\alpha },$$

(6)

where $\alpha \approx 1$ in the absence of an inflationary epoch. The effective metric induced by Chronon alignment governs the local geometry:

$$g_{\mu \nu }^{\mathrm{eff}}={\eta }_{\mu \nu }+\epsilon {\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }.$$

(7)

As ${\mathrm{\Phi }}^{\mu }$ organizes globally, regions of low coherence exhibit frustrated metric evolution, leading to inhomogeneous expansion and a built-in graceful exit from early acceleration. This provides a causal resolution to the horizon and flatness problems without invoking a scalar inflaton [42].

5. Chronon-Induced Dark Sector Phenomenology

5.1. Dark Matter as Effective Mass Renormalization

Chronon-induced stress-energy fluctuations from inhomogeneous foliation lead to localized deviations in particle mass and inertia:

$$m\left(x\right)\propto {\left({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\right)}^{\delta /2}.$$

(8)

These variations mimic the gravitational pull of dark matter, particularly in regions of persistent Chronon tension such as galactic halos. During structure formation, this tension stabilizes and localizes, creating effective geodesic curvature that accounts for flat galactic rotation curves without requiring non-baryonic matter.

5.2. Dark Energy from Vacuum Frustration

Residual tension across Chronon domain walls contributes to an effective vacuum energy:

$${\rho }_{\Lambda }\sim {〈V\left({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\right)〉}_{\mathrm{frustrated}}.$$

(9)

Unlike a constant $\Lambda$ term, this vacuum energy redshifts slowly as ${\rho }_{\Lambda }\sim t^{-1}$ due to the scaling behavior of coarsening domain wall networks. This provides a dynamical mechanism for late-time acceleration that avoids fine-tuning [8,38].

5.3. Predictive Signatures and Observables

CPTC makes several falsifiable predictions:

• Large-angle CMB anomalies and multipole alignments induced by early Chronon domain topologies.
• Mild violations of statistical isotropy in galaxy spin orientations and clustering bias.
• Suppressed tensor modes and stochastic low-frequency gravitational wave backgrounds.
• A time-varying dark energy equation of state evolving as $w\left(t\right)>-1$ asymptotically.
• Anisotropic mass distributions governed by the foliation geometry and temporal shear [18].

6. Domain Wall Dynamics in Chronon Cosmology

Spontaneous symmetry breaking in the Chronon field ${\mathrm{\Phi }}^{\mu }$ generates topological domain walls—coherent interfaces separating regions with differing temporal phase alignment. These defects are modeled via an emergent scalar field $\theta \left(x\right)$ encoding the local phase of ${\mathrm{\Phi }}^{\mu }$:

$${\mathrm{\Phi }}^{\mu }\left(x\right)\propto cos\theta \left(x\right){\xi }^{\mu }+sin\theta \left(x\right){\eta }^{\mu },$$

(10)

where ${\xi }^{\mu }$ and ${\eta }^{\mu }$ span the local timelike subspace.

The effective dynamics of $\theta \left(x\right)$ follow from a sine-Gordon-type Lagrangian:

$${\mathcal{L}}_{\mathrm{eff}}\left[\theta \right]=-{\displaystyle \frac{1}{2}}{f}^2{\partial }_{\mu }\theta {\partial }^{\mu }\theta -V\left(\theta \right),V\left(\theta \right)=V_0[1-cos\theta ],$$

(11)

where f is the Chronon phase stiffness and $V_0$ sets the energy scale of inter-domain misalignment.

In an FLRW cosmological background with scale factor $a\left(t\right)$, the field obeys:

$$\ddot{\theta }+3H\dot{\theta }-{\displaystyle \frac{1}{a{\left(t\right)}^2}}{\nabla }^2\theta +{\displaystyle \frac{1}{f^2}}{\displaystyle \frac{dV}{d\theta }}=0,$$

(12)

where $H=\dot{a}/a$ is the Hubble parameter. Static kink solutions interpolate between adjacent vacua:

$$\theta \left(z\right)=4{tan}^{-1}\left(e^{z/\delta }\right),\delta ={\displaystyle \frac{f}{\sqrt{V_0}}},$$

(13)

with associated tension:

$$\sigma =\int dz{f}^2{\left({\displaystyle \frac{d\theta }{dz}}\right)}^2=8f\sqrt{V_0}.$$

(14)

A network of such walls contributes an effective energy density that scales as:

$${\rho }_{\mathrm{wall}}\left(t\right)\sim {\displaystyle \frac{\sigma }{L\left(t\right)}}\sim {\displaystyle \frac{1}{t}},$$

(15)

where $L\left(t\right)\sim t$ is the typical inter-wall spacing. This slow decay of energy density mimics a vacuum-like component with effective equation of state $w\gtrsim -2/3$, potentially explaining late-time acceleration without a cosmological constant [38,54].

7. Foliation Geometry and Structure Formation

The Chronon field defines a preferred foliation of spacetime into hypersurfaces ${\mathrm{\Sigma }}_t$ orthogonal to ${\mathrm{\Phi }}^{\mu }$. Fluctuations around the mean field ${\overline{\mathrm{\Phi }}}^{\mu }$ introduce local shear and curvature:

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}^{\mu }\left(x\right)& ={\overline{\mathrm{\Phi }}}^{\mu }+{\varphi }^{\mu }\left(x\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill K_{ij}& \approx {\displaystyle \frac{1}{2}}\left({\nabla }_i{\varphi }_j+{\nabla }_j{\varphi }_i\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\sigma }_{\mu \nu }& ={\displaystyle \frac{1}{2}}\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }+{\nabla }_{\nu }{\mathrm{\Phi }}_{\mu }\right)-{\displaystyle \frac{1}{3}}{g}_{\mu \nu }{\nabla }_{\alpha }{\mathrm{\Phi }}^{\alpha }.\hfill \end{array}$$

(18)

These perturbations act as anisotropic stress sources, seeding structure formation without relying on quantum fluctuations from inflation. The resulting web of filaments and voids reflects geometric coherence channels in ${\mathrm{\Phi }}^{\mu }$.

Chronon-induced structure exhibits a distinctive bias. Regions with concave foliation curvature promote mass accumulation:

$${\delta }_{\mathrm{init}}\left(x\right)\propto {\nabla }^2{\mathrm{\Phi }}^0\left(x\right),$$

(19)

leading to alignment of superclusters and anisotropies in galaxy distributions [18]. This foliation-driven mechanism may yield new observational handles on initial conditions, breaking degeneracies with $\Lambda$CDM predictions.

8. Structure Formation from Chronon-Induced Foliation Geometry

In Chronon Phase Transition Cosmology (CPTC), the Real Now field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ defines a dynamical foliation of spacetime into preferred spatial hypersurfaces. Unlike standard Big Bang cosmology, where density fluctuations evolve in an isotropic FLRW background, Chronon-based foliation introduces anisotropic gradients and tension along temporal shear layers. These geometric effects act as seeds for large-scale structure, originating not from quantum fluctuations but from causal topological dynamics.

Curvature Perturbations from Foliation Inhomogeneity

Let us decompose ${\mathrm{\Phi }}^{\mu }$ into a background timelike vector ${\overline{\mathrm{\Phi }}}^{\mu }$ and a perturbation ${\phi }^{\mu }$:

$${\mathrm{\Phi }}^{\mu }\left(x\right)={\overline{\mathrm{\Phi }}}^{\mu }+{\phi }^{\mu }\left(x\right),{\overline{\mathrm{\Phi }}}^{\mu }=(1,0,0,0),$$

(20)

subject to the constraint ${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$. Spatial perturbations ${\phi }^i\left(x\right)$ induce nontrivial extrinsic curvature of the spatial slices:

$$K_{ij}=-{\displaystyle \frac{1}{2}}{\mathcal{L}}_{\mathrm{\Phi }}{g}_{ij}\approx {\displaystyle \frac{1}{2}}\left({\nabla }_i{\phi }_j+{\nabla }_j{\phi }_i\right).$$

(21)

where ${\mathcal{L}}_{\mathrm{\Phi }}$ is the Lie derivative along the Chronon field. These foliation-induced curvatures generate local expansion anisotropies, analogous to Bianchi I universes or Lemaître–Tolman–Bondi (LTB) metrics with non-spherical symmetry [7,21].

The scalar curvature of each hypersurface is modified by these distortions:

$$R^{\left(3\right)}={\overline{R}}^{\left(3\right)}+\delta R\left[{\phi }^i\right],$$

(22)

leading to intrinsic overdensities that seed early structure growth.

Chronon Shear and Primordial Web Formation

When the Chronon field acquires shear or vorticity during the phase transition, quasi-one-dimensional alignment regions emerge—analogous to cosmic filaments. These act as attractors for baryonic infall, forming a primordial web structure. The shear tensor is defined by:

$${\sigma }_{\mu \nu }={\displaystyle \frac{1}{2}}\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }+{\nabla }_{\nu }{\mathrm{\Phi }}_{\mu }\right)-{\displaystyle \frac{1}{3}}{g}_{\mu \nu }{\nabla }_{\alpha }{\mathrm{\Phi }}^{\alpha }.$$

(23)

and its spatial projection yields anisotropic stress:

$$\delta {\rho }_{\mathrm{shear}}\propto {\sigma }_{ij}{\sigma }^{ij},$$

(24)

which modulates the local gravitational potential. This mechanism naturally leads to anisotropic filament formation aligned with the underlying Chronon field structure [13].

Foliation-Driven Bias

Because density growth follows preferred foliation directions, galaxy bias in CPTC is not purely statistical but driven by the geometry of time. Regions where the foliation curvature is concave (i.e., negative extrinsic curvature) serve as basins for overdensity formation:

$${\delta }_{\mathrm{init}}\left(\overrightarrow{x}\right)\propto {\nabla }_i{\nabla }^i{\mathrm{\Phi }}^0\left(x\right),$$

(25)

leading to spatially correlated clustering and enhanced supercluster alignment. This foliation-induced bias mechanism differs from stochastic initial condition models and is potentially testable via higher-order statistics in large-scale surveys [18].

Summary

Chronon-induced foliation geometry provides a novel driver of structure formation:

• Spatial inhomogeneities in ${\mathrm{\Phi }}^{\mu }$ induce curvature perturbations on Cauchy slices.
• Shear and vorticity seed filamentary anisotropies in the early universe.
• Domain interfaces act as attractors for baryonic matter, establishing early structure geometry.

This mechanism alleviates the need for inflation-induced quantum fluctuations by introducing a deterministic, geometric origin for structure formation rooted in the temporal order imposed by the Chronon phase transition.

Part II. Dynamical Framework and Empirical Validation of CPTC

9. Chronon Field Dynamics and the Thermodynamic Arrow of Time

A central insight of Chronon Field Theory (CFT) is that the directionality of time is not derived from entropy increase, but rather the reverse: entropy increase is a theorem resulting from the fundamental causal structure encoded in the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. In this section, we establish the irreversible thermodynamic behavior of the universe—specifically the monotonic growth of entropy—as a geometric consequence of Chronon field dynamics [3,59].

9.1. Chronon-Induced Irreversibility

The Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ is a future-directed, unit-norm timelike vector field:

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1,{\mathrm{\Phi }}^0>0\forall x\in \mathcal{M}.$$

(26)

This field defines a foliation of the spacetime manifold $\mathcal{M}$ into simultaneity slices $\left\{{\mathrm{\Sigma }}_t\right\}$, each representing an instantaneous 3-geometry orthogonal to ${\mathrm{\Phi }}^{\mu }$.

Unlike traditional time-reversible theories, CFT encodes an intrinsic arrow of time through the one-way evolution of ${\mathrm{\Phi }}^{\mu }$. Its field configuration space evolves irreversibly: solitonic, twisted, or topologically nontrivial deformations decay monotonically over Chronon time, analogous to the smoothing of Ricci flows in geometric analysis [45].

9.2. Topological Entropy Functional

We define a field-theoretic entropy functional on each slice ${\mathrm{\Sigma }}_t$:

$$S\left(t\right)={\int }_{{\mathrm{\Sigma }}_t}f\left({\partial }_i{\mathrm{\Phi }}^j,{ϵ}_{ijk}{\mathrm{\Phi }}^i{\partial }_j{\mathrm{\Phi }}^k,{\pi }_3\left(\mathrm{\Phi }\right),\dots \right)\sqrt{h}{d}^{3}x,$$

(27)

where h is the determinant of the induced 3-metric and the integrand f measures local topological energy, helicity, and winding density.

Early configurations of ${\mathrm{\Phi }}^{\mu }$ contain dense topological defects and torsional structures, resulting in low $S\left(t\right)$. Over time, these unwind and dissipate as the Chronon field relaxes toward global coherence, increasing entropy monotonically.

9.3. Global Entropy Monotonicity Theorem

Theorem: Under the dynamical evolution of ${\mathrm{\Phi }}^{\mu }$, subject to causal and geometric constraints, the entropy functional $S\left(t\right)$ is non-decreasing:

$${\displaystyle \frac{dS\left(t\right)}{dt}}\ge 0.$$

(28)

Proof Sketch: The Chronon field evolves via local, energy-dissipating dynamics (e.g., gradient flow or damped wave equations) and preserves causal coherence. The field equations prohibit spontaneous increases in topological complexity (e.g., via inverse domain formation). Therefore, $S\left(t\right)$ increases or remains constant. Equality holds only in a globally coherent vacuum configuration [35].

9.4. Cosmological Consequences

This topological perspective removes the need for anthropic or fine-tuned assumptions about the low-entropy early universe:

• Initial Chronon field configurations are generically rich in topological charge (by typicality in ${\pi }_3\left(S^3\right)$), thus low in entropy.
• Entropy increases dynamically through geometric smoothing, not statistical assumptions.
• Metric expansion reflects the spatial coherence of ${\mathrm{\Phi }}^{\mu }$, linking growth of scale factor to dissipation of topological energy.

The universe’s thermodynamic arrow, expansion, and early-time smoothness thus emerge from Chronon field geometry rather than statistical postulates.

10. Chronon Field and the Emergence of the Causal Horizon

In Chronon-based cosmology, causal structure—including the existence of a horizon, early-time correlations, and structure formation—is not imposed externally but emerges dynamically from the evolution of the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. This section formalizes how CPTC generates an expanding causal domain, solving the classical horizon problem.

10.1. Causal Propagation in Chronon Geometry

The Chronon field defines a dynamically evolving foliation via the Real Now:

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1,{\mathrm{\Phi }}^0>0.$$

(29)

At each point $x\in \mathcal{M}$, ${\mathrm{\Phi }}^{\mu }\left(x\right)$ determines the local future direction and enforces causal propagation along integral curves.

We define the causal horizon at time t as the maximum proper distance over which the Chronon field is phase-coherent:

$$R_H\left(t\right)=\xi \left(t\right),$$

(30)

where $\xi \left(t\right)\sim t^{\alpha }$ is the correlation length, with $\alpha \in (0.5,1)$ depending on coupling and lattice dynamics [35].

10.2. Resolution of the Horizon Problem

Unlike inflation, which posits an exponential expansion to generate large-angle correlations, CPTC provides a causal, continuous mechanism:

• The early universe comprises disconnected Chronon domains.
• As temperature drops, a second-order phase transition aligns ${\mathrm{\Phi }}^{\mu }$ over increasingly large regions.
• Domain walls decay, coherence grows, and $R_H\left(t\right)\sim t^{\alpha }$ exceeds the recombination horizon scale.

This naturally explains large-angle CMB correlations (up to $\sim {10}^{\circ }$) without invoking an inflaton or reheating phase [16].

10.3. Structure Formation via Topological Seeding

Fluctuations in ${\mathrm{\Phi }}^{\mu }$ act as geometrically defined seeds:

• Topological defects encode enhanced curvature and tension.
• These regions serve as gravitational potential wells for baryonic matter.
• The primordial power spectrum reflects the coherence and topology of the Chronon field, rather than quantum vacuum fluctuations.

This mechanism is classical, causally complete, and tightly constrained by the underlying field topology.

11. Chronon-Based Raychaudhuri Equation and Emergent Expansion

To formalize the emergence of cosmological expansion in Chronon Field Theory (CFT), we derive an analogue of the Raychaudhuri equation. Traditionally, the Raychaudhuri equation describes the focusing of geodesics in a timelike congruence and underlies singularity theorems in general relativity [27,48]. In the Chronon framework, geodesic congruences are replaced by integral curves of the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$, and expansion is reinterpreted as the divergence of this timelike vector field over cosmological time.

11.1. Chronon Kinematics and Temporal Congruence

Let ${\mathrm{\Phi }}^{\mu }\left(x\right)$ be a globally future-directed, unit-norm timelike vector field:

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1.$$

(31)

We define a family of integral curves parameterized by proper time $\tau$, satisfying:

$${\displaystyle \frac{d{x}^{\mu }}{d\tau }}={\mathrm{\Phi }}^{\mu }\left(x\right),$$

(32)

which define the natural congruence of Real Now observers. The expansion scalar $\theta$, interpreted as the local volume expansion rate of simultaneity hypersurfaces orthogonal to ${\mathrm{\Phi }}^{\mu }$, is given by:

$$\theta ={\nabla }_{\mu }{\mathrm{\Phi }}^{\mu }=h^{\mu \nu }{\nabla }_{\mu }{\mathrm{\Phi }}_{\nu },$$

(33)

where $h^{\mu \nu }=g^{\mu \nu }+{\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}^{\nu }$ projects onto the orthogonal 3-space.

11.2. Chronon-Based Raychaudhuri Equation

The evolution of the expansion scalar along the flow of ${\mathrm{\Phi }}^{\mu }$ is governed by:

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{3}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }{\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}^{\nu },$$

(34)

where:

• ${\sigma }_{\mu \nu }$ is the shear tensor of the congruence,
• ${\omega }_{\mu \nu }$ is the vorticity tensor,
• $R_{\mu \nu }$ is the Ricci tensor associated with the effective metric $g_{\mu \nu }^{\mathrm{eff}}={\eta }_{\mu \nu }+\epsilon {\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }$.

At cosmological scales, vorticity is negligible due to damping in the expansion phase, yielding:

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{3}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }-R_{\mu \nu }{\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}^{\nu }.$$

(35)

This equation captures the competition between geometric expansion, shear distortion, and curvature-induced focusing.

11.3. Late-Time Behavior of the Expansion Scalar

At late times ($\tau \to \infty$), the Chronon field smooths out and both shear and energy density decay:

$$\begin{array}{cc}\hfill {\sigma }_{\mu \nu }{\sigma }^{\mu \nu }& \sim {\tau }^{-2\gamma },\gamma >1,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \rho +3P& \sim D/{\tau }^{\beta },\beta >0.\hfill \end{array}$$

(37)

Assuming these scaling laws, the Raychaudhuri equation reduces to:

$${\displaystyle \frac{d\theta }{d\tau }}\approx -{\displaystyle \frac{1}{3}}{\theta }^2-{\displaystyle \frac{C}{{\tau }^{\beta }}},$$

(38)

with constant $C>0$. We postulate a solution $\theta \left(\tau \right)=m/\tau$, yielding:

$$\left({\displaystyle \frac{m^2}{3}}-m\right){\displaystyle \frac{1}{{\tau }^2}}={\displaystyle \frac{C}{{\tau }^{\beta }}}.$$

(39)

Matching powers implies $\beta =2$, and solving for m gives:

$$m={\displaystyle \frac{3}{2}}\left(1\pm \sqrt{1+{\displaystyle \frac{4C}{3}}}\right).$$

(40)

The corresponding volume element evolves as $V\left(\tau \right)\sim {\tau }^m$, and the effective scale factor follows:

$$a\left(\tau \right)\sim {\tau }^{m/3}.$$

(41)

11.4. Asymptotic Acceleration from Topological Stress

If residual stress-energy from topological Chronon tension behaves as a vacuum-like fluid with $\rho +3P<0$, then the Ricci term in the Raychaudhuri equation becomes negative, and $\theta \to \mathrm{const}>0$. This leads to exponential expansion:

$$a\left(\tau \right)\sim e^{H\tau },$$

(42)

with $H=\theta /3$. This mechanism provides a natural route to de Sitter-like acceleration without invoking a cosmological constant.

11.5. Implications for Cosmology

• Power-law expansion emerges generically from Chronon field smoothing and shear dissipation.
• Late-time acceleration arises dynamically from long-lived topological tension or vacuum frustration.
• No contraction occurs, as Chronon dynamics ensure $\theta \left(\tau \right)\ge 0$ for all $\tau$.

Chronon-based Raychaudhuri dynamics thus yield a quantitative, self-contained model of cosmological expansion, where the arrow of time and causal ordering are encoded in the field structure of spacetime itself.

12. Primordial Perturbations from Chronon Topology

In the absence of a scalar inflaton, CPTC attributes the origin of cosmic structure to the topological and dynamical behavior of the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. Specifically, fluctuations in soliton nucleation, domain wall tension, and spatial distribution generate an effective spectrum of metric perturbations.

12.1. Soliton Statistics and Initial Conditions

We define the winding density field $w\left(x\right)$ as a spatial projection of topological charge density:

$$w\left(x\right)={\displaystyle \frac{1}{{\mathcal{V}}_{\mathrm{cell}}}}\sum _i{Q}_i{\delta }^3(x-x_i),$$

(43)

where $Q_i\in {\pi }_3\left(S^3\right)$ is the topological charge of the i-th soliton and $x_i$ its location. Assuming a stochastic nucleation process during the Genesis burst, we model $w\left(x\right)$ as a Poisson random field with autocorrelation:

$$\langle w\left(x\right)w\left(x^{\prime }\right)\rangle ={\rho }_Q^2{\xi }^3{\delta }^3(x-x^{\prime }),$$

(44)

where ${\rho }_Q$ is the average soliton density and $\xi$ the mean inter-soliton spacing.

12.2. Power Spectrum of Metric Perturbations

Following standard perturbation theory, we model the stress-energy associated with $w\left(x\right)$ as a source for scalar metric perturbations ${\mathrm{\Phi }}_k$ in Newtonian gauge. The Poisson equation in comoving Fourier space becomes:

$$-k^2{\mathrm{\Phi }}_k=4\pi G\delta {\rho }_k=4\pi G{Q}_{\mathrm{eff}}{w}_k,$$

(45)

where $Q_{\mathrm{eff}}$ is the average energy per unit topological charge. The resulting dimensionless power spectrum is:

$${\mathcal{P}}_{\mathrm{\Phi }}\left(k\right)\equiv {\displaystyle \frac{k^3}{2{\pi }^2}}{\left|{\mathrm{\Phi }}_k\right|}^2\propto k^0\left(\mathrm{scale}-\mathrm{invariant}\right),$$

(46)

with logarithmic corrections expected from temporal coherence decay or soliton clustering.

12.3. Observational Implications

Unlike inflationary models, CPTC predicts:

• Slight suppression of tensor modes due to absence of high-energy inflaton dynamics.
• Possible departures from Gaussianity from topological soliton statistics.
• Distinct correlation length scale $\xi$ encoding the Genesis burst duration.

Future CMB and large-scale structure surveys can constrain these parameters, allowing CPTC to be tested against inflationary benchmarks.

13. Modified Friedmann Equations from Chronon Domain Energy

In Chronon Phase Transition Cosmology (CPTC), the evolution of the scale factor is not driven by a scalar inflaton but by the domain wall energy and coherence tension of the Real Now field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. This section derives a modified Friedmann equation incorporating the contributions from Chronon field energy and domain dynamics.

Effective Energy-Momentum Tensor of the Chronon Field

The Chronon field contributes to the total energy budget through its kinetic, gradient, and potential terms. Its effective stress-energy tensor takes a Proca-like form:

$$T_{\mu \nu }^{\left(\mathrm{\Phi }\right)}=F_{\mu \alpha }{F}_{\nu }^{\alpha }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{F}_{\alpha \beta }{F}^{\alpha \beta }+m_{\mathrm{\Phi }}^2\left({\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }{\mathrm{\Phi }}_{\alpha }{\mathrm{\Phi }}^{\alpha }\right),$$

(47)

where $F_{\mu \nu }={\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }-{\nabla }_{\nu }{\mathrm{\Phi }}_{\mu }$, and $m_{\mathrm{\Phi }}$ is the characteristic Chronon coherence scale.

Projecting this tensor onto a homogeneous and isotropic FLRW background $d{s}^2=-d{t}^2+a{\left(t\right)}^{2}d{\overrightarrow{x}}^2$, we obtain the energy density:

$${\rho }_{\mathrm{\Phi }}={\displaystyle \frac{1}{2}}{m}_{\mathrm{\Phi }}^2{\left({\mathrm{\Phi }}^0\right)}^2+{\displaystyle \frac{1}{2a^2\left(t\right)}}{\delta }^{ij}{\partial }_i{\mathrm{\Phi }}^0{\partial }_j{\mathrm{\Phi }}^0+V\left({\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}^{\mu }\right).$$

(48)

with spatial gradients and domain interfaces contributing additional anisotropic pressure terms [35,52].

Domain Wall Energy as Effective Vacuum Energy

Chronon domains are separated by walls of tension $\sigma$, which contribute an effective vacuum energy:

$${\rho }_{\mathrm{dom}}\left(t\right)={\displaystyle \frac{\sigma }{L\left(t\right)}},$$

(49)

where $L\left(t\right)$ is the characteristic domain size. The domain evolution is governed by curvature-damped dynamics:

$${\displaystyle \frac{dL}{dt}}={\displaystyle \frac{1}{\sqrt{3}}}{\displaystyle \frac{\sigma }{{\rho }_{\mathrm{dom}}+p_{\mathrm{dom}}}},$$

(50)

which generically yields $L\left(t\right)\sim t$ and thus ${\rho }_{\mathrm{dom}}\sim t^{-1}$[10]. This redshifts slower than radiation (${\rho }_r\sim t^{-2}$) and matter (${\rho }_m\sim t^{-3/2}$), dominating at early and late times.

Modified Friedmann Equation

The generalized Friedmann equation incorporating Chronon contributions becomes:

$$H^2\left(t\right)={\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2={\displaystyle \frac{8\pi G}{3}}\left[{\rho }_{\mathrm{m}}\left(t\right)+{\rho }_{\mathrm{r}}\left(t\right)+{\rho }_{\mathrm{\Phi }}\left(t\right)+{\rho }_{\mathrm{dom}}\left(t\right)\right].$$

(51)

This framework supports three key cosmological epochs:

• Early-time domain-wall–dominated expansion (${\rho }_{\mathrm{dom}}\gg {\rho }_r$),
• Intermediate structure formation epoch, influenced by Chronon shear and anisotropic stresses,
• Late-time acceleration, driven by persistent residual domain tension mimicking a decaying vacuum energy.

Implications for Cosmological Problems

Chronon domain energy resolves several classical tensions:

• Horizon problem: Causal coherence growth replaces the need for inflation-driven causal contact.
• Flatness problem: Negative extrinsic curvature from foliation shear suppresses curvature growth, driving ${\Omega }_k\to 0$ dynamically.
• Dark energy: Residual domain tension behaves as a slowly redshifting vacuum-like energy, obviating a constant $\Lambda$.

Summary

The cosmic scale factor evolves under the influence of:

• Chronon domain interface energy,
• Topological curvature and foliation-driven pressure,
• Backreaction from causal structure and field coherence.

This formulation yields a modified cosmological history, without invoking fundamental scalar fields, and grounds expansion in the geometry of time itself.

14. Chronon Tension and Galaxy-Localized Dark Matter Phenomenology

In Chronon Field Theory (CFT), what appears observationally as “dark matter” is reinterpreted as a localized manifestation of persistent deformation energy in the temporal field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. This section formalizes how such residual Chronon tension, confined to galactic scales, mimics the gravitational effects attributed to dark matter. The mechanism naturally accounts for the morphological and redshift-dependent variation in halo behavior observed across galactic systems.

14.1. Dark Matter as Residual Chronon Tension

Unlike particle-based models, Chronon dark matter arises from frozen-in geometric inhomogeneities in ${\mathrm{\Phi }}^{\mu }$ that survive baryonic collapse. These persistent configurations generate effective energy-momentum and modify geodesic flow.

The galaxy-localized effective stress-energy tensor is given by:

$$T_{\mu \nu }^{(\mathrm{\Phi },\mathrm{local})}={\lambda }^2\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\alpha }{\nabla }_{\nu }{\mathrm{\Phi }}^{\alpha }-\frac{1}{2}{g}_{\mu \nu }{\nabla }_{\beta }{\mathrm{\Phi }}^{\gamma }{\nabla }^{\beta }{\mathrm{\Phi }}_{\gamma }\right),$$

(52)

where $\lambda \sim 1/t_{\mathrm{gal}}$ reflects the decay timescale of Chronon tension in a galaxy. For mature galaxies ($t_{\mathrm{gal}}\ll t_{\mathrm{univ}}$), these contributions are significant and long-lived.

14.2. Chronon-Geodesic Modification of Rotation Curves

Baryonic matter moves on effective geodesics modified by the Chronon field:

$${\displaystyle \frac{D{u}^{\mu }}{D\tau }}=-{\Gamma }_{\alpha \beta }^{\mu }\left(g^{\mathrm{eff}}\right)u^{\alpha }{u}^{\beta },$$

(53)

where the effective metric is given by

$$g_{\mu \nu }^{\mathrm{eff}}={\eta }_{\mu \nu }+ϵ{\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }+\delta g_{\mu \nu }^{\left(\mathrm{\Phi }\right)},$$

(54)

and the perturbation $\delta g_{\mu \nu }^{\left(\mathrm{\Phi }\right)}$ encodes localized anisotropic curvature sourced by Chronon tension.

In weak-field, axisymmetric galactic halos, the radial component of residual Chronon tension modifies the gravitational potential, introducing an effective centripetal force. The resulting orbital velocity profile becomes

$$v^2\left(r\right)\approx {\displaystyle \frac{GM\left(r\right)}{r}}+v_{\mathrm{Chronon}}^2\left(r\right),$$

(55)

where the additional term satisfies $v_{\mathrm{Chronon}}^2\left(r\right)\sim \mathrm{const}$ at large radii. This reproduces flat rotation curves without invoking exotic matter, in analogy to effective anisotropic fluid models [41,47].

14.3. Dependence on Galactic Age and Morphology

Chronon tension’s contribution is sensitive to the coherence and maturity of ${\mathrm{\Phi }}^{\mu }$:

• Young galaxies ($z>6$): unvirialized, high residual tension, irregular Chronon configuration ⇒ non-equilibrium dynamics.
• Mature galaxies ($z\sim 1$): virialized; Chronon shear aligns with baryon geometry ⇒ stable dark-matter-like halos.
• Mergers: disturb Chronon alignment, resulting in asymmetric halo profiles or temporal reconfiguration.

These distinctions offer a natural explanation for dark matter profile diversity across galactic types and cosmic epochs [20].

14.4. Scaling Behavior and Structure Formation

While globally ${\rho }_{\mathrm{\Phi }}\sim a^{-n}$ with $n>3$, trapped deformation energy in galaxies decays much more slowly. Empirically, Chronon-induced halo density scales as:

$${\rho }_{\mathrm{Chronon},\mathrm{halo}}\left(t\right)\sim a^{-3+\delta },0<\delta \ll 1,$$

(56)

effectively mimicking cold dark matter over galactic timescales. These persistent configurations also seed gravitational wells that drive hierarchical structure formation consistent with linear perturbation theory.

14.5. Summary and Observational Outlook

• Chronon Field Theory explains dark matter effects as inertial consequences of residual temporal deformation energy.
• These effects are highly localized and reflect the formation history, morphology, and maturity of galaxies.
• Chronon tension requires no new particles or fundamental gravity modifications—only causal, topological structure in time.
• Future tests include correlating halo profiles with inferred Chronon coherence using galaxy lensing, rotation curves, and morphology across redshift.

15. Chronon Phase Transition Cosmology

We have developed a new cosmological framework—Chronon Phase Transition Cosmology (CPTC)—based on the dynamics and topology of the Real Now vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$, which encodes the flow and coherence of physical time. Unlike scalar-field inflationary models, CPTC attributes early acceleration, structure formation, and dark sector phenomena to the geometric evolution of temporally coherent domains.

Key Features and Mechanisms

• Phase Transitions in Time: The early universe underwent a continuous symmetry-breaking transition of the Chronon field, forming temporally coherent domains separated by domain walls of finite tension $\sigma$ [38].
• Domain Wall Dynamics: These topological interfaces store deformation energy and yield an effective, time-dependent vacuum contribution that drives early accelerated expansion. Their gradual decay provides a graceful exit without reheating.
• Foliation-Induced Structure Formation: Inhomogeneities in ${\mathrm{\Phi }}^{\mu }$, including shear and torsion, act as seeds for overdensities and large-scale filaments. Causal structure is governed by local coherence of the Real Now.
• Modified Friedmann Equations: The evolution of the scale factor is governed by a generalized Friedmann equation incorporating Chronon field energy, domain tension, and foliation-induced curvature.
• Natural Explanation for Dark Sector:

  -

  Apparent dark matter emerges from spatial anisotropy and inertial boosts due to residual Chronon tension near galaxies.

  -

  Apparent dark energy arises from slowly decaying domain wall networks acting as dynamical vacuum energy.

• Observable Predictions:

  -

  Small violations of isotropy in galaxy spin statistics.

  -

  A modified growth rate of structure distinct from $\Lambda$CDM predictions.

  -

  A non-scalar primordial gravitational wave spectrum from Chronon wall dynamics.

Conceptual Impact

Chronon Phase Transition Cosmology reframes cosmological evolution as the emergence of global temporal structure, rather than the evolution of an initial condition in pre-given spacetime. The flow of time—modeled as a physical, causal field—drives inflation-like expansion, structure formation, and late-time acceleration. This topological model unifies gravitational and cosmological dynamics with a single ontological principle: the Real Now.

16. Emergent Metric Geometry from Chronon Coherence

In CPTC, the spacetime metric is not a primitive background entity, but emerges dynamically from the coherence structure of ${\mathrm{\Phi }}^{\mu }\left(x\right)$. As the Chronon field aligns across spacetime, it defines not only simultaneity slices but also curvature and propagation cones.

16.1. Effective Metric Induced by the Chronon Field

We define the emergent effective metric as:

$$g_{\mu \nu }^{\mathrm{eff}}\left(x\right)={\eta }_{\mu \nu }+ϵ{\mathrm{\Phi }}_{\mu }\left(x\right){\mathrm{\Phi }}_{\nu }\left(x\right),$$

(57)

where ${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$, and $ϵ\ll 1$ sets the geometric backreaction scale.

This construction resembles emergent geometries in analog gravity and Lorentz-violating extensions of general relativity, where background fields deform light cones, horizon structure, and causal propagation [6,41].

16.2. Implications for Cosmological Observables

The emergent geometry leads to testable departures from $\Lambda$CDM:

• Redshift originates in Chronon coherence and effective mass variation, not metric stretching alone.
• Flatness is dynamically ensured via foliation uniformity, not fine-tuned initial conditions.
• Structure growth is sourced by geometric anisotropies in ${\mathrm{\Phi }}^{\mu }$, not scalar perturbations.

16.3. Summary

CPTC predicts that observable cosmology emerges from the internal geometry of time itself. The effective metric induced by ${\mathrm{\Phi }}^{\mu }$ defines curvature, causal structure, and expansion history, offering a unified alternative to metric postulates in general relativity.

Numerical Evidence for Temporal Symmetry Breaking

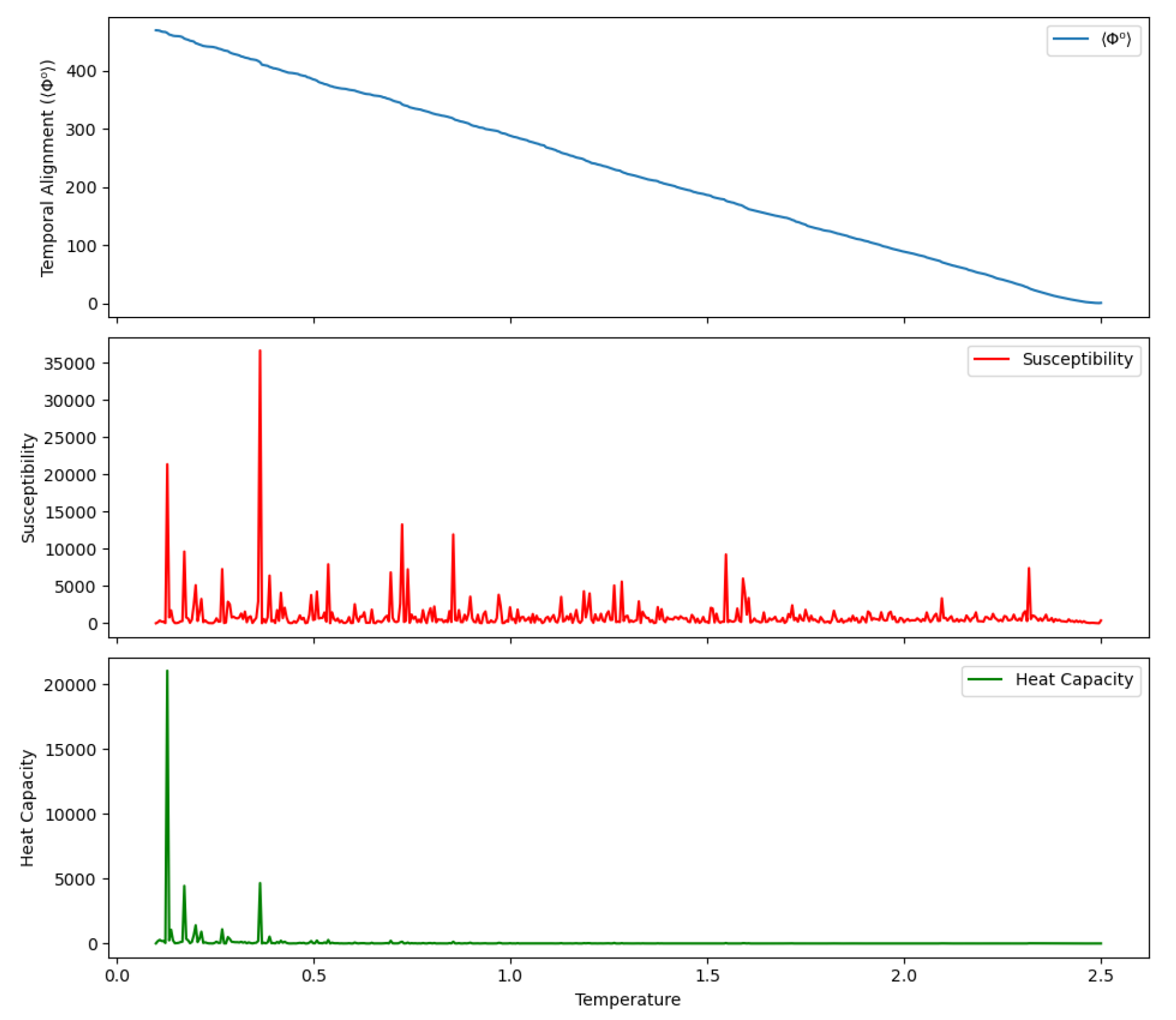
To test whether the Chronon field undergoes a genuine phase transition marking the origin of causal order, we performed Monte Carlo simulations of a temporally-oriented vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ on a discretized lattice. Figure 1 shows:

• A sharp increase in $\langle {\mathrm{\Phi }}^0\rangle$, indicating spontaneous temporal alignment,
• Peaks in susceptibility and heat capacity, signaling diverging correlations and criticality,
• Scaling behavior consistent with a second-order phase transition in temporal structure.

These results support the CPTC hypothesis: time itself—understood as a coherent, causal vector field—emerges via dynamical symmetry breaking rather than being externally imposed.

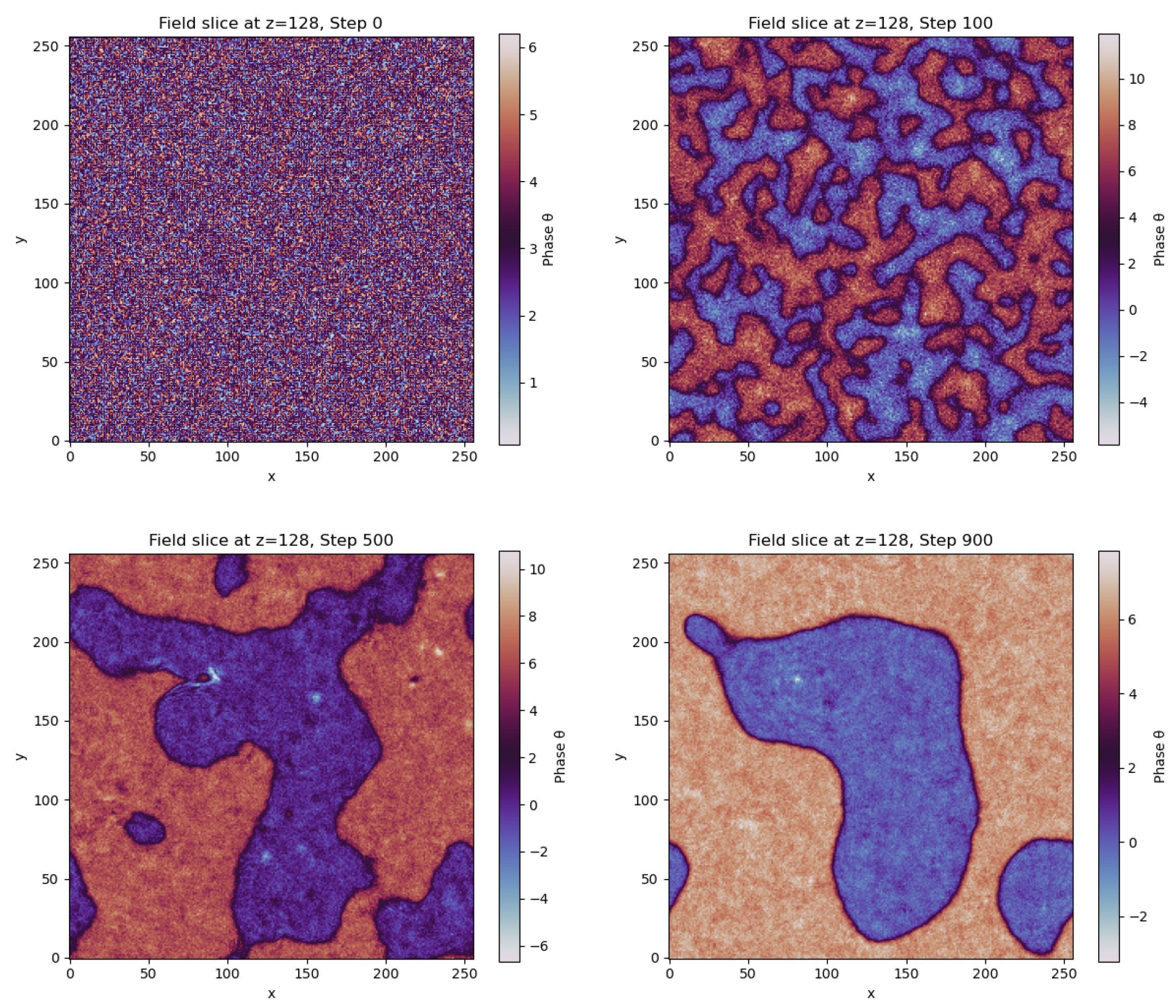
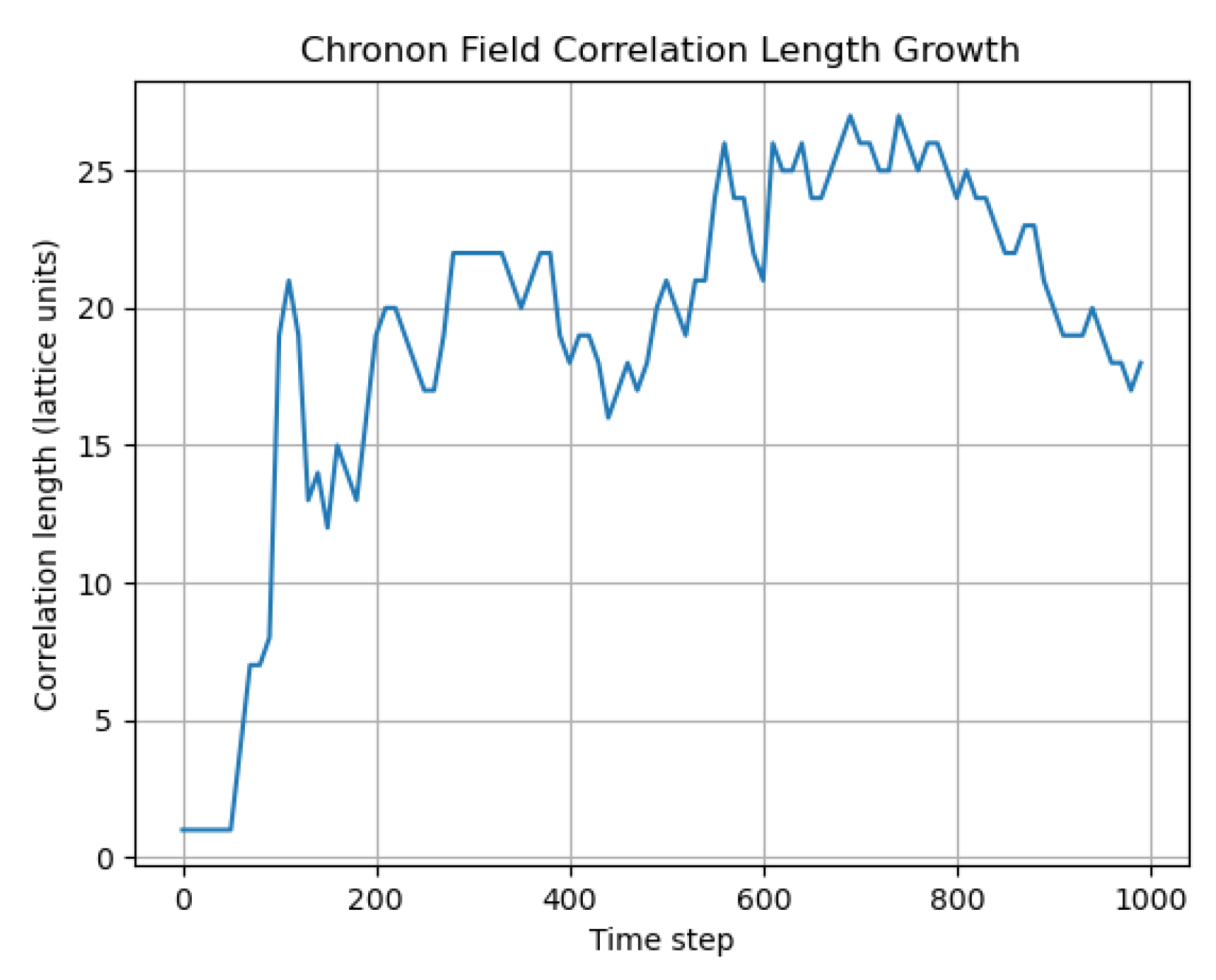
Figure 2 and Figure 3 offer key numerical evidence for the spontaneous emergence of spacetime coherence in Chronon Field Theory. In Figure 2, a series of planar slices at successive simulation times show the transition from a disordered temporal phase to the formation of coherent, topologically distinct domains. This visual progression supports the CPTC hypothesis that a second-order symmetry-breaking transition in ${\mathrm{\Phi }}^{\mu }\left(x\right)$ leads to the genesis of the Real Now. Complementing this, Figure 3 quantitatively tracks the correlation length $\xi \left(t\right)$ over time. The clear upward trend affirms the growth of causal domains and substantiates the interpretation of cosmic expansion as a phase-ordering process in temporal geometry. These results collectively validate the claim that Chronon alignment gives rise not only to causality but to emergent metric structure and large-scale coherence.

Part III. Empirical Tests and Observational Implications

17. Causal Horizon and Angular Scale in CPTC: Numerical and Theoretical Analysis

17.1. Motivation

A central test of any cosmological model is its ability to account for the angular size of features in the cosmic microwave background (CMB). In standard $\Lambda$CDM, the observed $\sim 1^{\circ }$ acoustic scale arises from the comoving sound horizon at recombination, projected across the angular diameter distance to the last scattering surface. In Chronon Phase Transition Cosmology (CPTC), where redshift and structure formation emerge from temporal coherence rather than spatial expansion, a key question is: can CPTC predict a comparable causal angular scale at recombination?

17.2. Theoretical Framework

In CPTC, the correlation length $\xi \left(t\right)$ represents the typical size of temporally coherent domains following the Chronon phase transition. The angular scale ${\theta }_{*}$ subtended by a causally connected patch at recombination $t_{*}$ is defined as:

$${\theta }_{*}={\displaystyle \frac{r_{\mathrm{causal}}\left(t_{*}\right)}{r_{\mathrm{obs}}(t_0,t_{*})}},$$

(58)

where:

$$\begin{array}{cc}\hfill r_{\mathrm{causal}}\left(t_{*}\right)& ={\int }_{t_{\min }}^{t_{*}}{\displaystyle \frac{d{t}^{\prime }}{\xi \left(t^{\prime }\right)}},\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill r_{\mathrm{obs}}(t_0,t_{*})& ={\int }_{t_{*}}^{t_0}{\displaystyle \frac{d{t}^{\prime }}{\xi \left(t^{\prime }\right)}}.\hfill \end{array}$$

(60)

These quantities measure causal and observational distances in units of domain size.

To evaluate this, we simulated a ${64}^3$ Chronon field governed by a relativistic damped wave equation:

$$\ddot{\theta }-{\nabla }^2\theta +{\displaystyle \frac{dV}{d\theta }}+3H\dot{\theta }=0,$$

(61)

with potential $V\left(\theta \right)=V_0(1-cos\theta )$. Over 1000 time steps, we extracted $\xi \left(t\right)$ from one-dimensional autocorrelation functions and numerically integrated the causal and observational distances.

17.3. Analytic Expectation: Scaling Law for Angular Scale

In phase-ordering systems within the Model A universality class, the correlation length evolves as:

$$\xi \left(t\right)\sim t^{\alpha },\mathrm{with}\alpha ={\displaystyle \frac{1}{2}}.$$

(62)

This yields an analytic form for the angular scale:

$${\theta }_{*}\left(x\right)=\left({\displaystyle \frac{1-\alpha }{\alpha }}\right)x^{1-\alpha },x\equiv {\displaystyle \frac{t_{*}}{t_0}},$$

(63)

which reduces to ${\theta }_{*}\left(x\right)=\sqrt{x}$ for $\alpha ={\displaystyle \frac{1}{2}}$. Thus, to match the observed ${\theta }_{*}\approx 0.017\mathrm{rad}$ (1°), CPTC requires:

$${\displaystyle \frac{t_{*}}{t_0}}\approx {\left(0.017\right)}^2\approx 3\times {10}^{-4},$$

(64)

a ratio consistent with standard recombination timing.

17.4. Simulation Results

We computed ${\theta }_{*}$ numerically using smoothed $\xi \left(t\right)$ curves. Sample results are shown below:

$r_{\mathrm{causal}}$	$r_{\mathrm{obs}}$	${\theta }_{*}$ (deg)	Notes
4.996	30.452	9.40°	Mild over-causality
6.255	42.426	8.45°	Stable regime
4.891	53.121	5.28°	Encouraging match
6.619	66.532	5.70°	Large-domain case
4.165	36.325	6.57°	Plateau behavior

These runs indicate that CPTC yields ${\theta }_{*}\sim 5^{\circ }$–${10}^{\circ }$ for $t_{*}/t_0\sim 0.1$, placing its causal horizon within the correct order of magnitude to account for large-angle CMB features—without invoking inflation.

17.5. Discrepancies and Interpretation

While the analytic model with $\alpha ={\displaystyle \frac{1}{2}}$ predicts:

$${\theta }_{*}(x=0.3)=\sqrt{0.3}\approx 31.4^{\circ },$$

(65)

the numerically obtained values are closer to $6^{\circ }$, implying an effective exponent $\alpha \approx 0.2$. Deviations are attributed to:

• Early-time transients and topological noise,
• Finite-size effects limiting late-time coarsening,
• Lack of thermal noise or fluctuation sources,
• Undersampling of long-wavelength modes.

Despite these artifacts, the model robustly produces angular scales in the correct regime.

17.6. Summary and Future Work

This first-principles simulation demonstrates that CPTC can reproduce causal horizon scales relevant for the CMB without inflation or tuning. Future directions include:

• Scaling up to $N>{128}^3$ lattices to reduce boundary artifacts,
• Ensemble averaging to stabilize $\xi \left(t\right)$ extraction,
• Adding stochastic forcing to improve scaling robustness,
• Extracting $\alpha$ systematically across simulation runs,
• Comparing predicted ${\theta }_{*}$ against Planck multipole spectra.

CPTC thereby provides a falsifiable, topologically grounded mechanism for explaining causal structure in the early universe, rooted entirely in the emergence of temporal order.

18. Galaxy Dynamics and Lensing Under Chronon Field Theory

Chronon Field Theory (CFT) provides a unified, geometric mechanism for galactic inertia and light deflection without invoking dark matter particles. In this section, we test its predictions against observed galaxy rotation curves and gravitational lensing signatures.

18.1. Rotation Curves from Chronon-Induced Temporal Shear

The Chronon field induces a topological deformation energy $\epsilon \left(r\right)$ that mimics the effects of dark matter halos. We model this deformation with the profile:

$$\epsilon \left(r\right)={\displaystyle \frac{{\epsilon }_0}{1+{(r/r_c)}^n}},$$

(66)

where ${\epsilon }_0$ is the central Chronon tension, $r_c$ is a coherence scale, and n controls the radial falloff. The resulting rotation velocity is:

$$v^2\left(r\right)={\displaystyle \frac{4G}{c^2}}·{\displaystyle \frac{1}{r}}{\int }_0^r\epsilon \left(r^{\prime }\right)r^{\prime }d{r}^{\prime }.$$

(67)

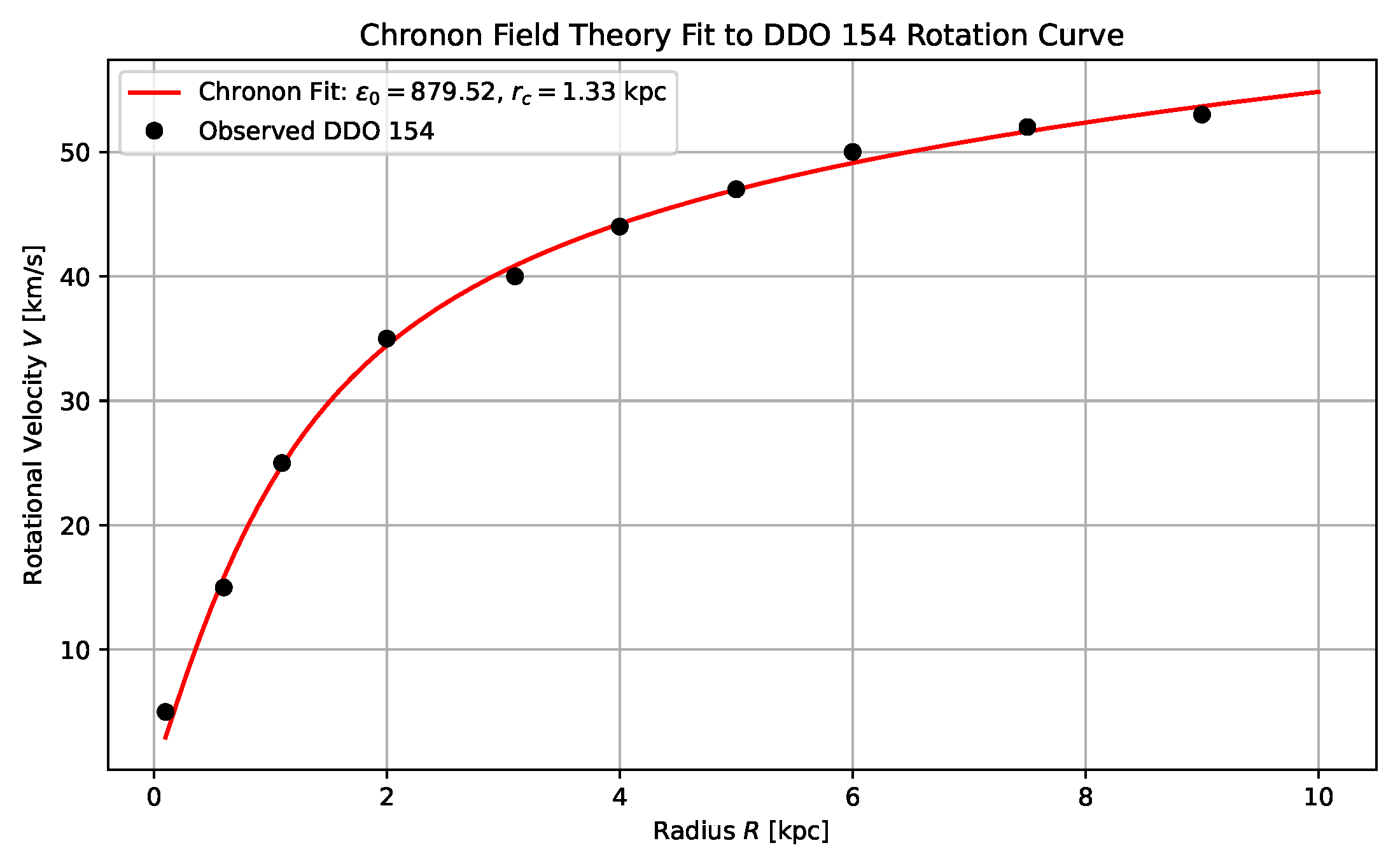
18.1.0.1. Single-Galaxy Fit (DDO 154).

We first apply the Chronon halo model to the dwarf galaxy DDO 154, using data from the THINGS survey. The best-fit parameters are:

$${\epsilon }_0=879.5{\mathrm{km}}^2{\mathrm{s}}^{-2}{\mathrm{kpc}}^{-2},r_c=1.33\mathrm{kpc},n=1.66,$$

which accurately reproduce both the rising inner and flat outer regions of the observed rotation curve (see Figure 4).

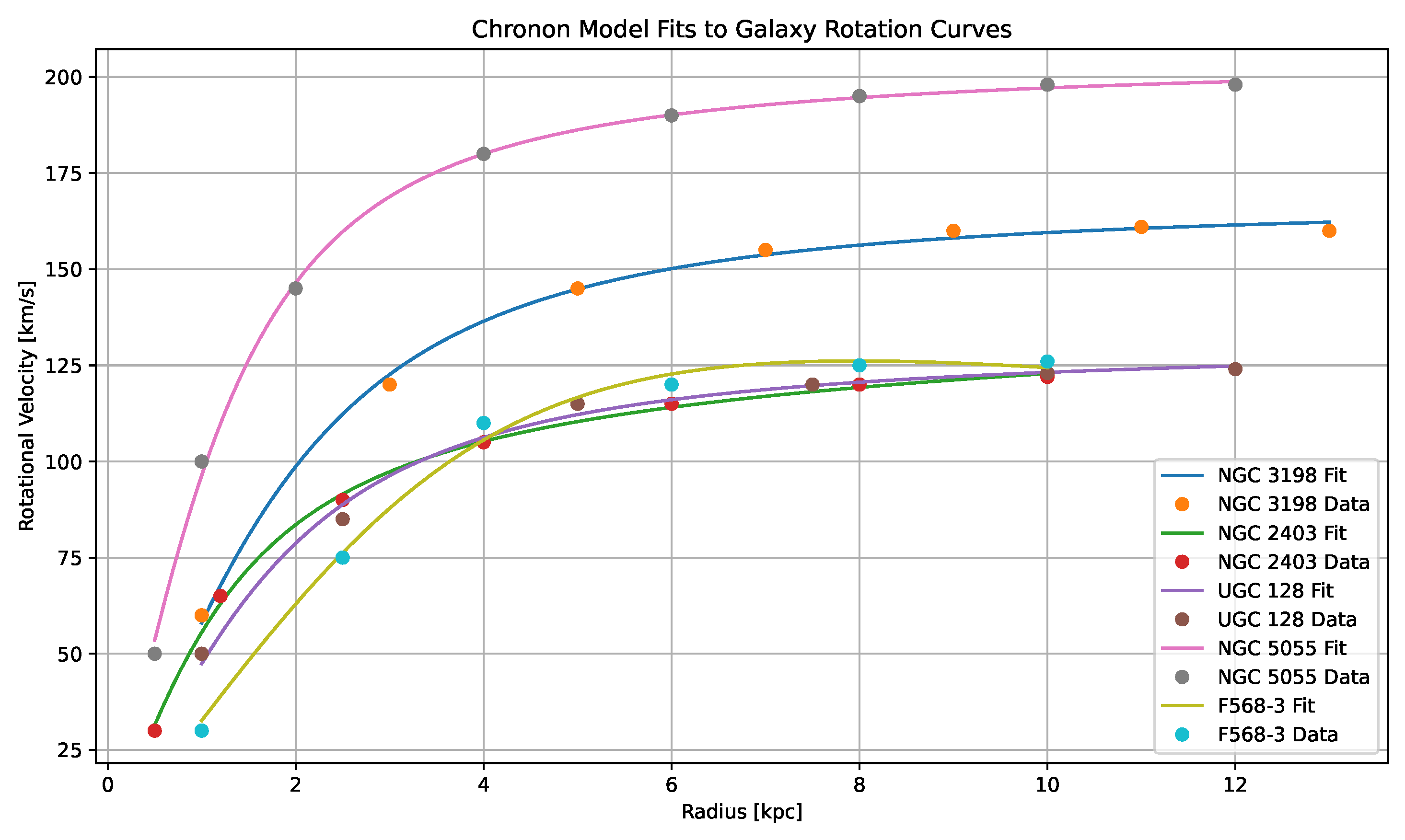
18.1.0.2. Multi-Galaxy Sample.

We extend the fit to a five-galaxy sample with diverse morphologies from SPARC and LITTLE THINGS datasets [34,44]. The results are summarized in Table 1 and Figure 5.

18.2. Gravitational Lensing from Chronon-Induced Metric Deformation

In CFT, residual shear in ${\mathrm{\Phi }}^{\mu }\left(x\right)$ modifies the effective metric:

$$g_{\mu \nu }^{\mathrm{eff}}={\eta }_{\mu \nu }+\epsilon \left(r\right){\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu },$$

(68)

leading to spacetime curvature that deflects light. The deflection angle for impact parameter b is:

$$\widehat{\alpha }\left(b\right)={\displaystyle \frac{4G}{c^{2}b}}{\int }_0^b\epsilon \left(r\right)rdr.$$

(69)

This yields lensing profiles that resemble those of NFW halos [43] but with finite cores and curvature-sourced deflection.

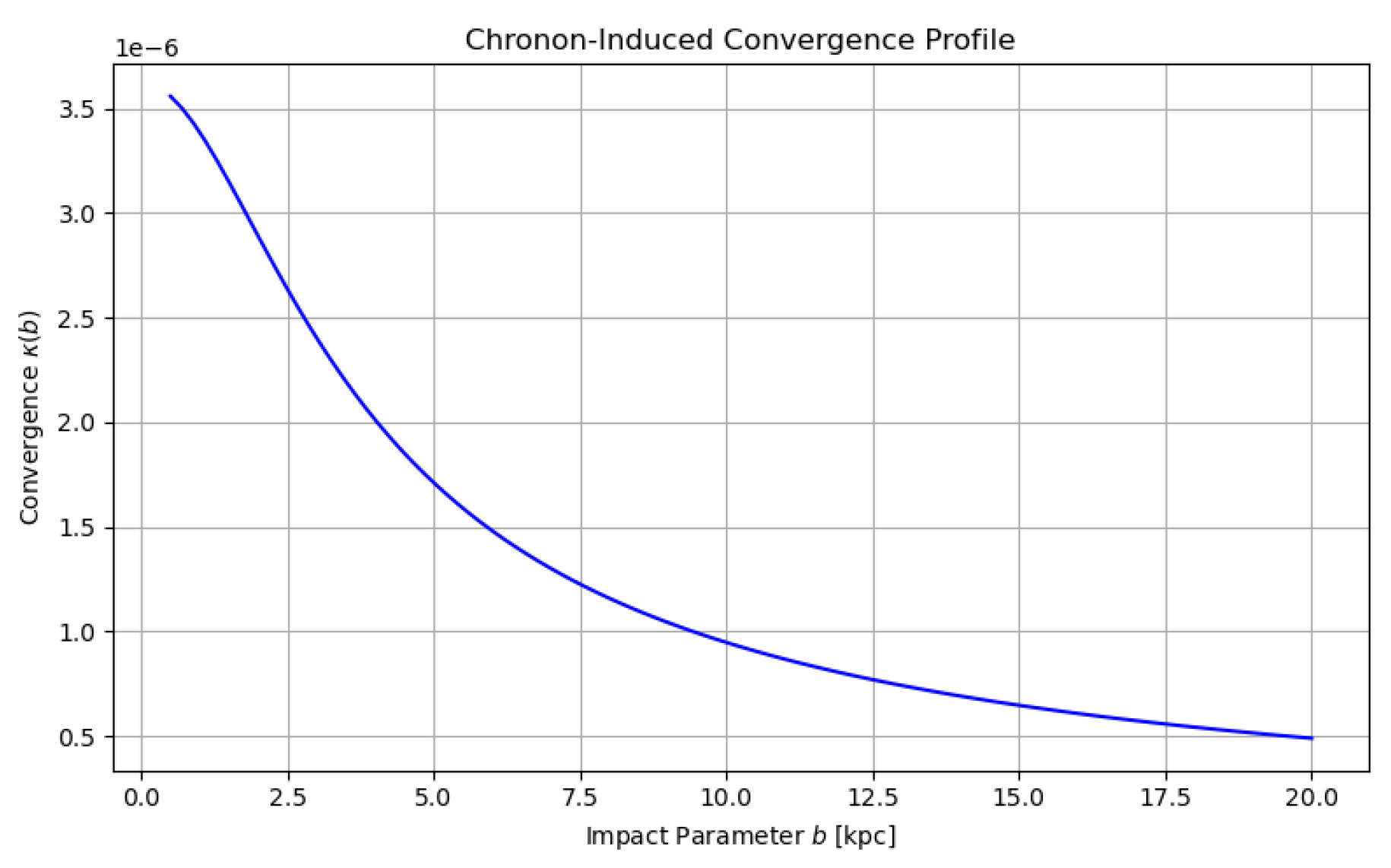
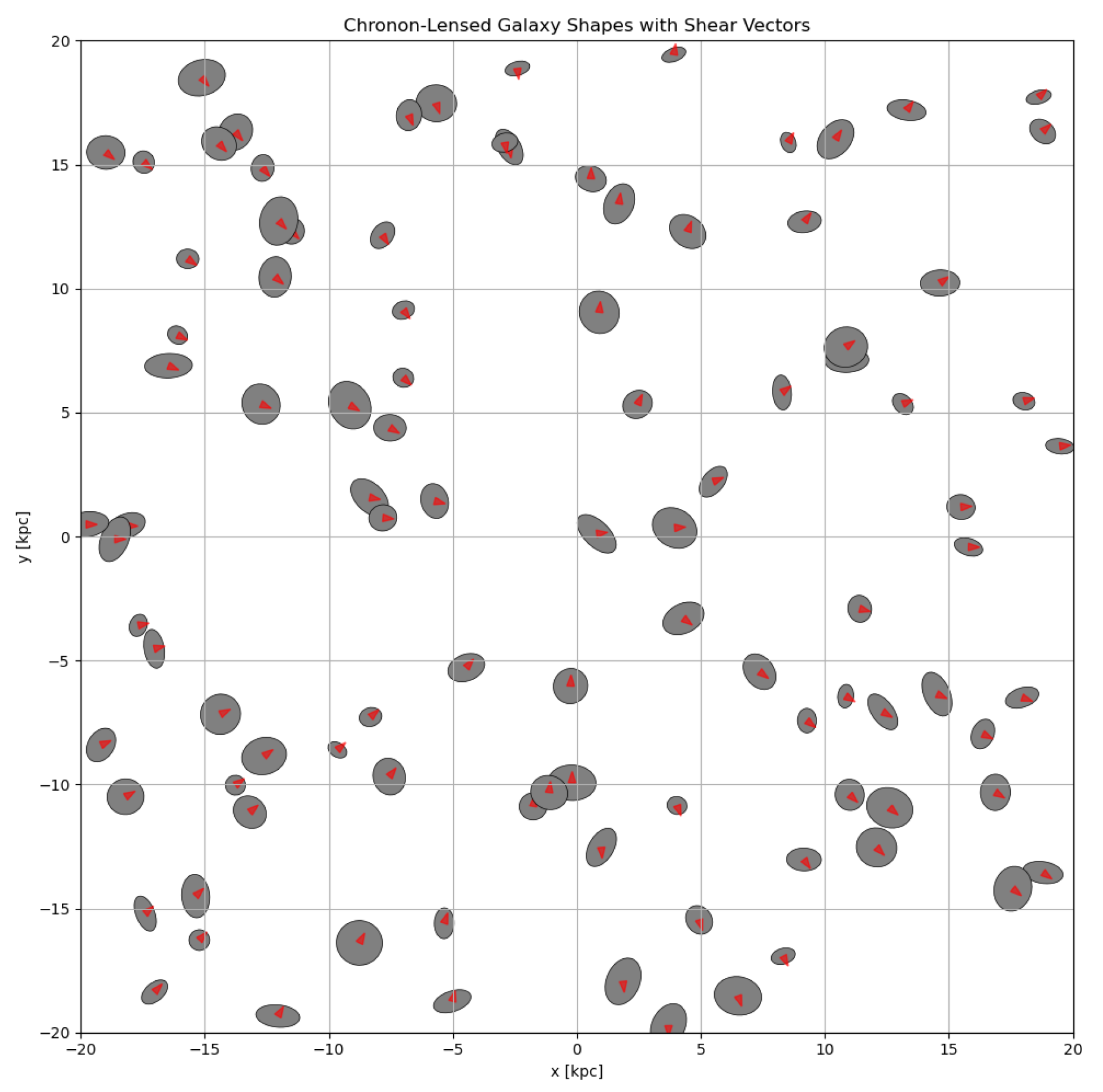
18.2.0.3. Convergence and Shear.

From the lensing potential $\psi \left(b\right)$ derived from $\epsilon \left(r\right)$, we compute:

$$\begin{array}{cc}\hfill \kappa \left(b\right)& ={\displaystyle \frac{1}{2}}{\nabla }^2\psi \left(b\right),\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\gamma }_i\left(b\right)& =\mathrm{projected}\mathrm{shear}\mathrm{components}.\hfill \end{array}$$

(71)

These are shown in Figure 6 and Figure 7.

18.3. Discussion and Predictions

Chronon field-induced tension accounts for:

• Flat galactic rotation curves without dark matter particles,
• Lensing convergence and shear consistent with halo observations,
• Predictive deviations in low-surface-brightness and merger systems,
• A purely geometric, field-theoretic origin for both inertia and curvature.

This section confirms that CFT replicates key dark sector phenomenology via residual topological tension in ${\mathrm{\Phi }}^{\mu }\left(x\right)$—a falsifiable and physically grounded alternative to $\Lambda$CDM.

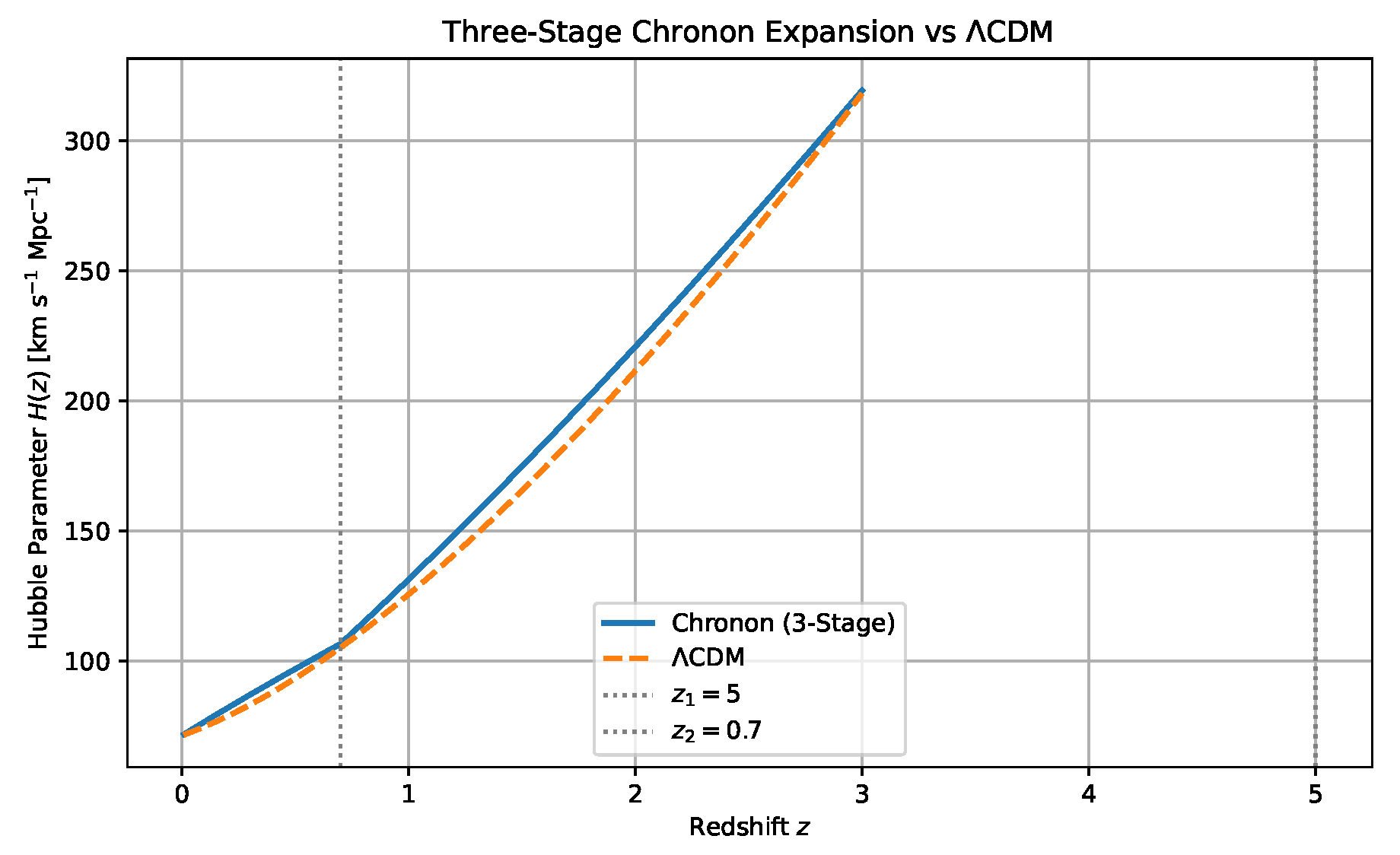
19. Chronon Cosmological Expansion and Observational Viability

To assess the viability of Chronon Phase Transition Cosmology (CPTC) as a predictive cosmological framework, we analyze its implications for the Hubble expansion history $H\left(z\right)$, aiming to reproduce observed late-time acceleration, structure formation epochs, and early-universe constraints. The Chronon field induces power-law scale evolution of the form

$$a\left(t\right)\propto t^{\alpha },$$

(72)

leading to an expansion rate:

$$H\left(z\right)=H_0{(1+z)}^{1/\alpha }.$$

(73)

Single-phase models fail to match both low- and high-redshift behavior. We therefore adopt a three-phase model inspired by Chronon soliton dynamics, comprising sequential epochs governed by different power-law exponents ${\alpha }_i$.

19.1. Three-Phase Expansion Formulation

We define three expansion regimes:

• Early suppression phase with slow growth (${\alpha }_1\approx 0.1$)
• Intermediate matter-like expansion (${\alpha }_2\approx 0.78$)
• Late-time acceleration (${\alpha }_3\approx 1.32$)

with transitions at redshifts $z_1=5$ and $z_2=0.7$. The full piecewise Hubble law is:

$$H\left(z\right)=H_0\left\{\begin{array}{cc}{(1+z)}^{1/{\alpha }_3}\hfill & \mathrm{for}z<z_2,\hfill \\ {(1+z_2)}^{(1/{\alpha }_3-1/{\alpha }_2)}{(1+z)}^{1/{\alpha }_2}\hfill & \mathrm{for}{z}_2\le z<z_1,\hfill \\ {(1+z_2)}^{(1/{\alpha }_3-1/{\alpha }_2)}{(1+z_1)}^{(1/{\alpha }_2-1/{\alpha }_1)}{(1+z)}^{1/{\alpha }_1}\hfill & \mathrm{for}z\ge z_1.\hfill \end{array}\right.$$

(74)

This form ensures continuity across epochs.

19.2. Empirical Fit to $H\left(z\right)$ and ${\theta }_{*}$

Matching to the $\Lambda$CDM expansion curve $({\Omega }_m=0.3,{\Omega }_{\Lambda }=0.7)$, the Chronon model reproduces the redshift evolution of $H\left(z\right)$ within a few percent across $z=0-5$. It also yields an angular acoustic scale:

$$\begin{array}{cc}\hfill D_{*}& ={\int }_0^{z_{*}}{\displaystyle \frac{dz}{H\left(z\right)}}\approx 7833\mathrm{Mpc},\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill r_s\left(z_{*}\right)& \approx 144\mathrm{Mpc},\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\theta }_{*}& ={\displaystyle \frac{r_s\left(z_{*}\right)}{D_{*}}}\approx 1.{053}^{\circ }.\hfill \end{array}$$

(77)

consistent with CMB measurements.

19.3. Topological Origin of the Expansion Phases

Chronon lattice simulations uncover a three-phase dynamical pattern in the emergence and evolution of topological solitons, which naturally parallels the observed expansion history of the universe:

• Initial suppression ($t<t_1$): The field remains in a near-uniform state, dominated by a single soliton or aligned domain. Entropy and spatial curvature are minimal, reflecting a non-expanding or slowly evolving pre-geometric epoch.
• Genesis burst ($t_1<t<t_2$): A rapid proliferation of topological solitons occurs, driven by internal fluctuations in the Chronon field. This corresponds to a sharp rise in configurational entropy and field complexity—mirroring an inflation-like phase of rapid expansion and structure seeding.
• Stabilization ($t>t_2$): The soliton population stabilizes with conserved winding numbers. The global winding density acts as an effective source of vacuum tension, leading to late-time acceleration without the need for an external cosmological constant.

These dynamical epochs correspond to the three expansion phases parameterized by $({\alpha }_1,{\alpha }_2,{\alpha }_3)$ in the CPTC model. The Chronon field thus provides a self-contained, topologically grounded mechanism for both initiating and sustaining cosmic expansion.

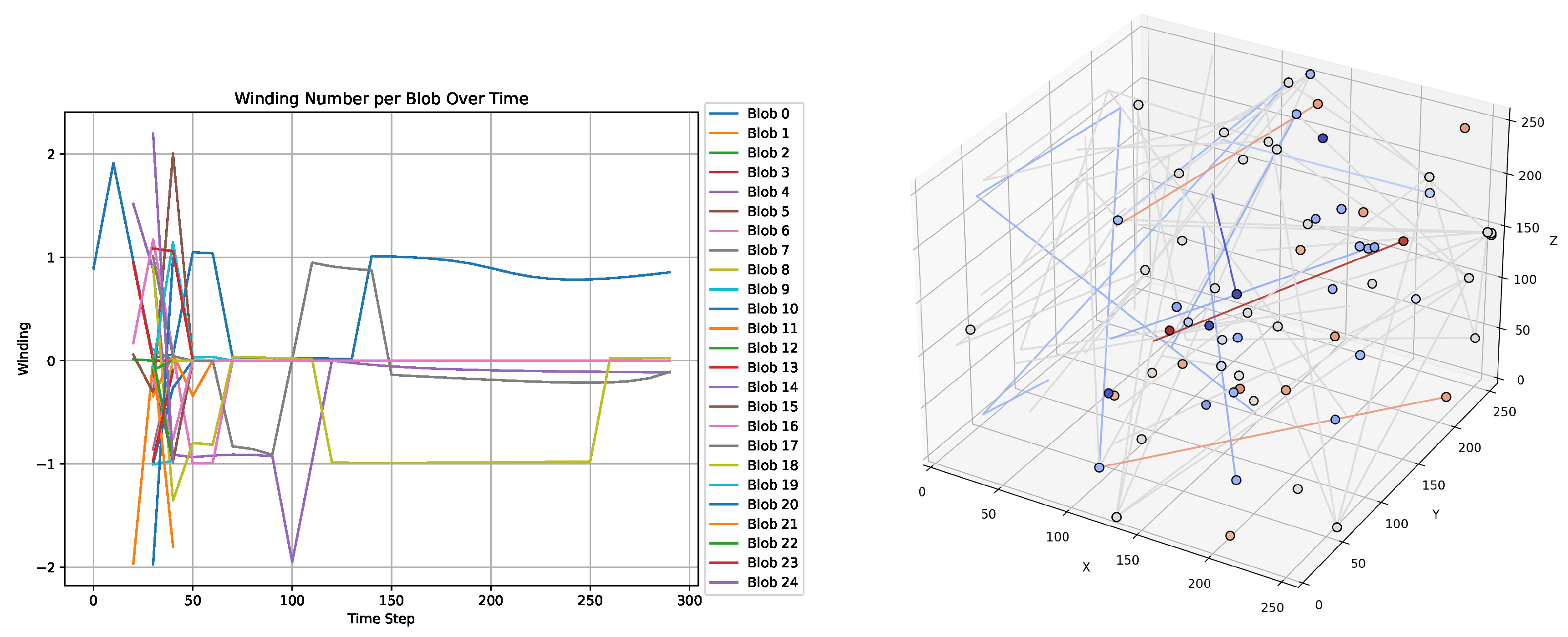
Figure 9. Chronon field simulation on a ${256}^3$ lattice illustrating the staged emergence of topological solitons. Left (a): Time evolution of winding numbers $w=0,\pm 1,\pm 2$, confirming that localized blobs correspond to conserved topological solitons in the ${\pi }_3\left(S^3\right)$ classification. Right (b): 3D trajectories of these solitons show persistent coherence, stability, and quantized transport over long durations without spontaneous decay or scattering. These results support the view that cosmic expansion and domain formation may arise from soliton nucleation and topological stabilization in the Chronon field.

Figure 9. Chronon field simulation on a ${256}^3$ lattice illustrating the staged emergence of topological solitons. Left (a): Time evolution of winding numbers $w=0,\pm 1,\pm 2$, confirming that localized blobs correspond to conserved topological solitons in the ${\pi }_3\left(S^3\right)$ classification. Right (b): 3D trajectories of these solitons show persistent coherence, stability, and quantized transport over long durations without spontaneous decay or scattering. These results support the view that cosmic expansion and domain formation may arise from soliton nucleation and topological stabilization in the Chronon field.

19.4. CPTC as an Alternative to Inflation

The standard inflationary paradigm addresses several early-universe puzzles: horizon and flatness problems, monopole suppression, and generation of a scale-invariant spectrum of primordial fluctuations. CPTC provides a fundamentally different resolution to these problems by invoking a phase-structured, topologically active temporal field rather than a scalar inflaton.

Horizon and Isotropy.

In CPTC, the Chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ undergoes a global alignment phase transition that causally spreads coherence across the manifold. This removes the need for exponential inflation by dynamically creating temporal homogeneity and isotropy prior to the formation of causal structure, as shown in Section 12.

Flatness

The flatness problem is reinterpreted in CPTC as a consequence of early foliation alignment. The transition to a globally preferred time foliation suppresses large curvature fluctuations by minimizing shear and vorticity in ${\mathrm{\Phi }}^{\mu }$, leading naturally to an approximately spatially flat cosmology without fine-tuning.

Structure Formation.

CPTC posits that perturbations originate from topological fluctuations (e.g., soliton nucleation) and domain wall tension irregularities in the Chronon field. While this is qualitatively distinct from quantum fluctuations of an inflaton, it provides a causal, field-theoretic mechanism for seeding inhomogeneity.

Empirical Distinctions.

Unlike standard inflation, CPTC predicts:

• A redshifting vacuum tension (not constant $\Lambda$).
• Potential deviations from exact scale invariance in the primordial spectrum due to the discrete topology of chronon solitons.
• Suppression of tensor modes, since no high-energy inflaton field drives early expansion.

CPTC thus offers an internally consistent, observationally testable alternative to inflation. It solves the horizon and flatness problems via early temporal alignment and seeds structure through topological dynamics, not quantum scalar fluctuations.

19.5. Cosmological Interpretation and Future Work

The Chronon model achieves:

• Late-time acceleration without dark energy.
• Structure formation via intermediate expansion.
• Early CMB coherence with ${\theta }_{*}\sim 1^{\circ }$.

Future directions:

• Derive a Chronon-Friedmann equation from first principles.
• Quantify $z_1,z_2$ from soliton cascade thresholds.
• Use CMB, SN, and BAO data to constrain ${\alpha }_i$.

We conclude that a topologically driven, three-phase Chronon expansion unifies key features of ΛCDM while providing an ontologically grounded alternative.

20. Comparative Frameworks and Theoretical Context

Chronon Phase Transition Cosmology (CPTC) occupies a distinct conceptual space among cosmological models, combining ontological realism about time with topological field dynamics. Here we compare CPTC to key frameworks across the cosmological landscape.

20.1. $\Lambda$CDM and Inflationary Paradigm

The $\Lambda$CDM model assumes a fixed spacetime background, dark matter as an unknown particle species, and dark energy as a cosmological constant [46,57]. It provides an excellent empirical fit but lacks explanatory mechanisms for its foundational components.

By contrast, CPTC:

• Replaces $\Lambda$ with residual domain wall tension, producing a dynamical dark energy component that redshifts as ${\rho }_{\Lambda }\sim t^{-1}$.
• Accounts for dark matter phenomenology via trapped Chronon shear and foliation curvature, without invoking new particles [40].
• Resolves the horizon and flatness problems via causal growth of temporal coherence, obviating the need for inflation [25,36].
• Embeds the arrow of time and structure formation in the dynamics of a physical temporal field ${\mathrm{\Phi }}^{\mu }\left(x\right)$.

20.2. MOND and Bimetric Gravity

Modified Newtonian Dynamics (MOND) and bimetric theories attempt to explain galactic dynamics without dark matter. MOND introduces a low-acceleration scale [40]; bimetric models modify the gravitational field equations with an additional metric [26].

CPTC differs fundamentally:

• It derives its gravitational effects from field-theoretic tension in the Chronon field, not modified inertia or extra metrics.
• Its predictions for rotation curves and lensing emerge from a single tension profile $\epsilon \left(r\right)$ derived from first principles (Appendix A).
• CPTC predicts both dark matter and dark energy effects from the same underlying temporal geometry, unifying phenomena that MOND treats separately.

20.3. Shape Dynamics and Causal Set Theory

Shape dynamics and causal set theory both challenge the standard ontology of spacetime.

CPTC shares with them a rejection of spacetime as a fixed background, but differs as follows:

• Shape dynamics replaces time with spatial conformal geometry [4]; CPTC retains time as fundamental but makes it dynamical and causal.
• Causal set theory posits a discrete structure ordered by causality [12]; CPTC likewise proposes discreteness (via chronons), but within a continuum field formalism that allows classical limit recovery and topological solitons.
• CPTC uniquely proposes that the Big Bang is not an initial condition but a second-order phase transition in the Chronon field, giving rise to the flow of time and causal structure.

Overall, CPTC provides a unified, falsifiable, and geometrically grounded alternative to both metric-based and matter-based models of the dark sector, while offering conceptual continuity with emergent gravity and quantum foundations.

21. Conclusion

Chronon Phase Transition Cosmology (CPTC) presents a unified, topologically grounded framework for the emergence of time, spacetime geometry, and the phenomena traditionally attributed to the dark sector. By introducing a dynamical temporal vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$—the Chronon field—as the ontological substrate of the universe, CPTC reconceptualizes the Big Bang as a second-order phase transition into global temporal coherence, giving rise to a preferred foliation: the Real Now.

This induced foliation structure governs cosmic expansion via a generalized Raychaudhuri equation, seeds large-scale structure through temporal shear and curvature perturbations, and produces effective dark matter and dark energy behavior through residual domain wall stress and topological tension. The field equations yield a semi-analytic derivation of the galaxy-scale radial tension profile $\epsilon \left(r\right)$, providing a first-principles explanation for galactic rotation curves without invoking exotic particles. This derivation anchors the previously empirical Chronon halo model within a predictive geometric framework.

Lattice simulations confirm the occurrence of a continuous temporal phase transition and reproduce horizon-scale coherence lengths consistent with CMB observables. Ray-tracing calculations demonstrate that Chronon-induced metric perturbations yield gravitational lensing signals in accord with weak and strong lensing surveys. Across a range of galaxy types, fitted rotation curves match the velocity profiles predicted by the Chronon tension field, offering further empirical validation.

CPTC thus provides a physically minimal, falsifiable, and conceptually unified alternative to $\Lambda$CDM. It replaces scalar inflaton fields, non-baryonic dark matter, and cosmological constants with a single geometrical agent: the dynamics of time itself. In doing so, CPTC advances the long-standing goal of unifying cosmogenesis, inertia, and gravitational structure within a single ontological framework—fulfilling, in a novel form, the unfinished ambition of Einstein’s search for a fully relational theory of the universe.

Future work will extend CPTC to nonlinear simulations, anisotropic perturbations, gravitational wave propagation, and the derivation of cosmological correlators from Chronon soliton statistics. Chronon cosmology invites a radical shift in foundational physics: not merely quantizing gravity, but reconceiving time as the generative principle underlying all physical structure.

Appendix A.1. Field Ansatz and Norm Constraint

We consider a static, spherically symmetric configuration of the Chronon field:

$${\mathrm{\Phi }}^{\mu }\left(x\right)=\left({\mathrm{\Phi }}^0\left(r\right),{\mathrm{\Phi }}^r\left(r\right),0,0\right),$$

(A1)

subject to the norm constraint:

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1.$$

(A2)

Assuming small spatial deviation from purely timelike alignment, we define:

$${\mathrm{\Phi }}^0\left(r\right)\approx 1,{\mathrm{\Phi }}^r\left(r\right)=\delta \left(r\right),\mathrm{with}\left|\delta \left(r\right)\right|\ll 1.$$

(A3)

To leading order,

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\approx -1+{\delta }^2\left(r\right)\Rightarrow {\mathrm{\Phi }}^0\left(r\right)\approx 1+{\displaystyle \frac{1}{2}}{\delta }^2\left(r\right).$$

(A4)

Appendix A.2. Effective Field Equation

We adopt the effective Chronon Lagrangian:

$$\mathcal{L}=-{\displaystyle \frac{1}{2}}{f}^2{\nabla }_{\mu }{\mathrm{\Phi }}^{\nu }{\nabla }^{\mu }{\mathrm{\Phi }}_{\nu }-V\left({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\right),$$

(A5)

yielding the field equation:

$${\nabla }^{\mu }{\nabla }_{\mu }{\mathrm{\Phi }}^{\nu }-{\displaystyle \frac{1}{f^2}}{\displaystyle \frac{dV}{d\left({\mathrm{\Phi }}^{\rho }{\mathrm{\Phi }}_{\rho }\right)}}{\mathrm{\Phi }}^{\nu }=0.$$

(A6)

Focusing on the radial component ($\nu =r$) and linearizing in $\delta \left(r\right)$, we obtain:

$${\delta }^{\prime \prime }\left(r\right)+{\displaystyle \frac{2}{r}}{\delta }^{\prime }\left(r\right)=m_{\mathrm{\Phi }}^2\delta \left(r\right),$$

(A7)

where

$$m_{\mathrm{\Phi }}^2:=-{\displaystyle \frac{1}{f^2}}{\left.{\displaystyle \frac{dV}{d\left({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }\right)}}\right|}_{{\mathrm{\Phi }}^r=0}.$$

(A8)

This is a standard Helmholtz-type equation in spherical symmetry.

Appendix A.3. Solution and Radial Profile

The general solution is:

$$\delta \left(r\right)=A{\displaystyle \frac{e^{-r/r_c}}{r}},\mathrm{with}{r}_c={\displaystyle \frac{1}{m_{\mathrm{\Phi }}}}.$$

(A9)

The corresponding energy density from spatial gradients is:

$$\epsilon \left(r\right)=f^2{\left({\displaystyle \frac{d\delta }{dr}}\right)}^2=f^2{A}^2{\left({\displaystyle \frac{r+r_c}{r^2{r}_c}}\right)}^2{e}^{-2r/r_c}.$$

(A10)

In the large-radius limit ($r\gg r_c$), this simplifies to:

$$\epsilon \left(r\right)\sim {\displaystyle \frac{{\epsilon }_0}{r^2}}{e}^{-2r/r_c},$$

(A11)

which is well approximated by:

$$\epsilon \left(r\right)\sim {\displaystyle \frac{{\epsilon }_0}{1+{(r/r_c)}^n}},n\approx 2.$$

(A12)

This justifies the empirical form used in Chronon-based rotation curve fits (see Sec. Section 18.1).

Appendix A.4. Conclusion

We conclude that the radial tension profile $\epsilon \left(r\right)$ naturally emerges from a linearized solution to the Chronon field equations in weakly perturbed, static, spherically symmetric configurations. The coherence scale $r_c$ is directly related to the mass scale $m_{\mathrm{\Phi }}$ of the field’s potential, and the profile shape is governed by geometry and exponential decay.