Submitted:
12 May 2025
Posted:
13 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
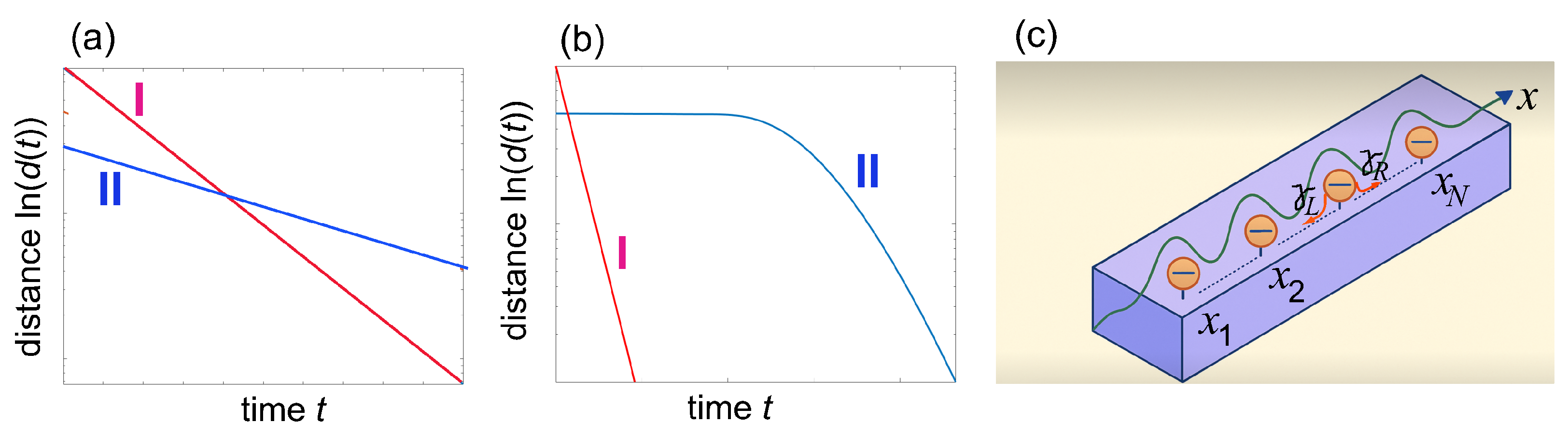
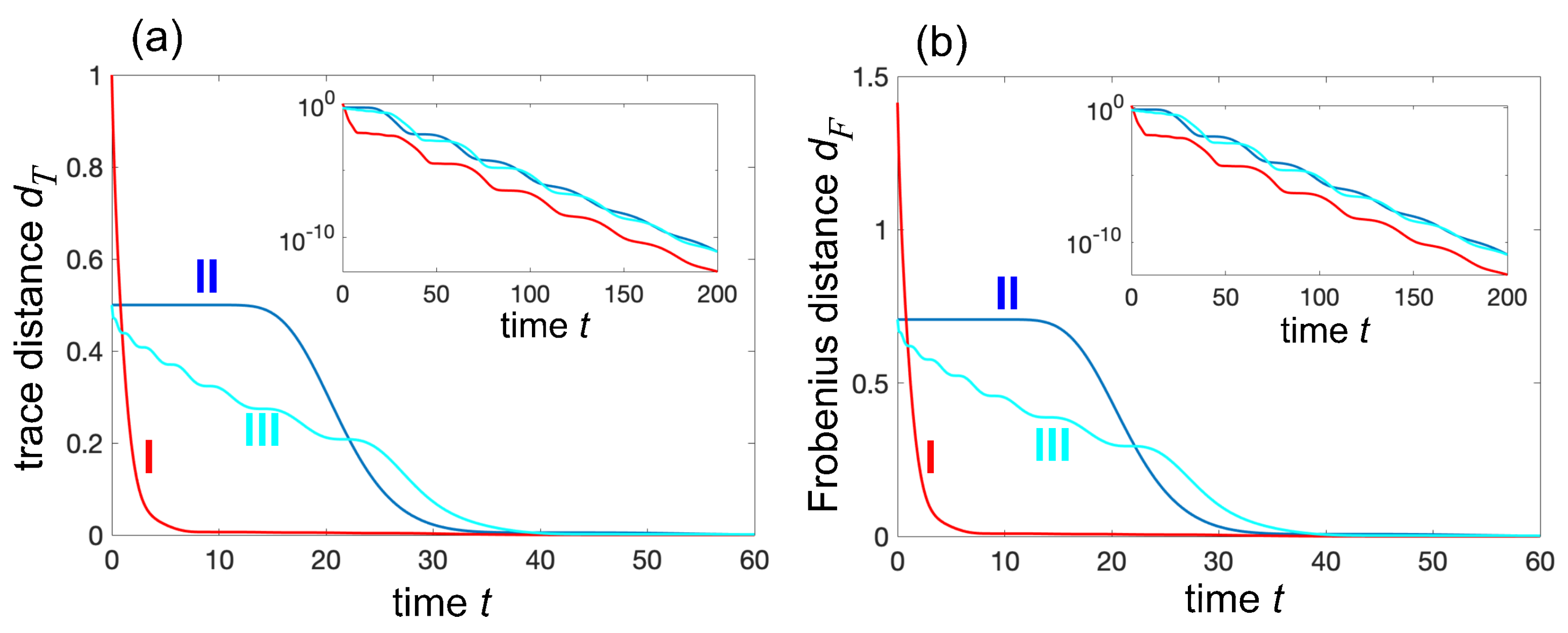
2. Mpemba Effect from Non-Normal Dynamics in Markovian Open Quantum Systems
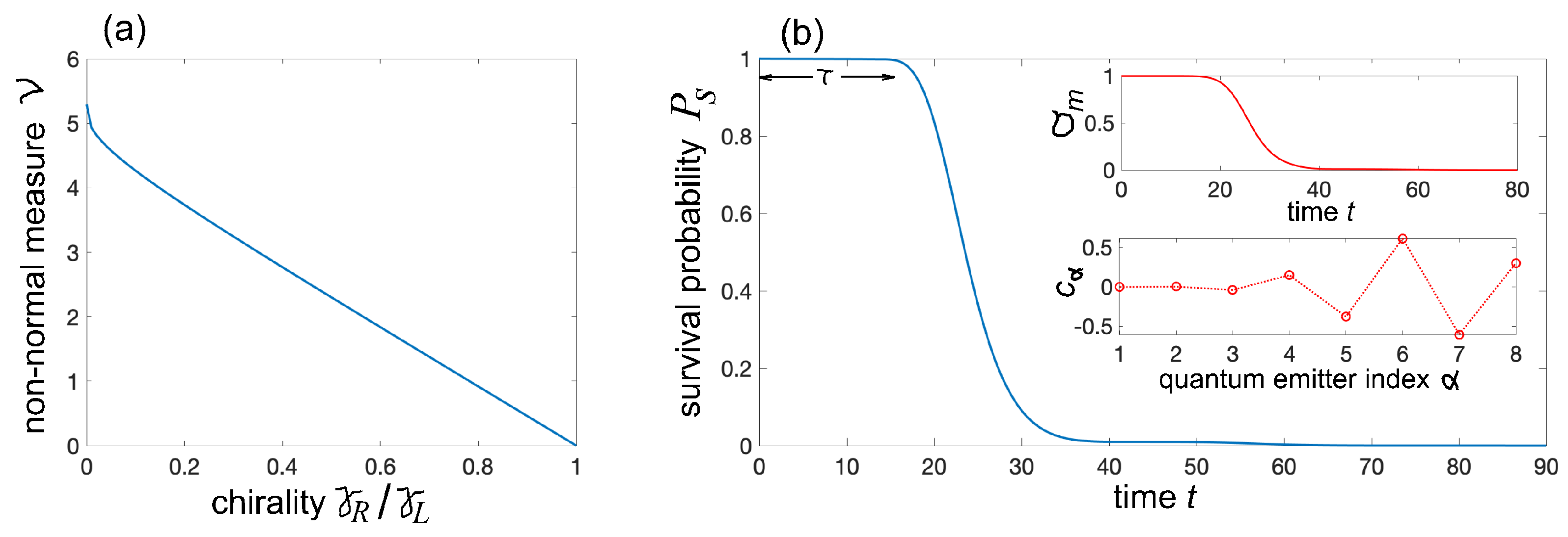
3. Non-Normal Mpemba Effect in Waveguide Quantum Electrodynamics
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Evolution Equations of the Density Matrix Elements
References
- E. B. Mpemba and D. G. Osborne, Cool? Phys. Educ. 1969, 4, 172. [Google Scholar]
- G. S. Kell, The Freezing of Hot and Cold Water. Am. J. Phys. 1969, 37, 564. [Google Scholar] [CrossRef]
- M. Jeng, The Mpemba effect: when can hot water freeze faster than cold? Am. J. Phys. 2006, 74, 514. [Google Scholar] [CrossRef]
- J. Bechhoefer, A. Kumar, and R. Chétrite, A fresh understanding of the Mpemba effect. Nature Rev. Phys. 2021, 3, 534–2021. [Google Scholar] [CrossRef]
- A. Lasanta, F. Vega Reyes, A. Prados, and A. Santos, When the Hotter Cools More Quickly: Mpemba Effect in Granular Fluids. Phys. Rev. Lett. 2017, 119, 148001. [Google Scholar] [CrossRef]
- Z. Lu and O. Raz, Nonequilibrium thermodynamics of the Markovian Mpemba effect and its inverse. Proc. Nat. Acad. Sci. 2017, 114, 5083. [Google Scholar] [CrossRef]
- I. Klich, O. Raz, O. Hirschberg, and M. Vucelja, Mpemba index and anomalous relaxation. Phys. Rev. X 2019, 9, 021060. [Google Scholar]
- A. Kumar and J. Bechhoefer, Exponentially faster cooling in a colloidal system, Nature 2020, 584, 64.
- M. Baity-Jesi, E. Calore, A. Cruz, L. A. Fernandez, J. M. Gil-Narvion, A. Gordillo-Guerrero, D. Iniguez, A. Lasanta, A. Maiorano, E. Marinari, V. Martin-Mayor, J. Moreno-Gordo, A. Munoz-Sudupe, D. Navarro, G. Parisi, S. Perez-Gaviro, F. Ricci-Tersenghi, J. J. Ruiz-Lorenzo, S. F. Schifano, B. Seoane, A. Tarancon, R. Tripiccione, and D. Yllanes, The Mpemba effect in spin glasses is a persistent memory effect. Proc. Nat. Acad. Sci. 2019, 116, 15350. [Google Scholar]
- G. Teza, R. Yaacoby, and O. Raz, Relaxation shortcuts through boundary coupling. Phys. Rev. Lett. 2023, 131, 017101. [Google Scholar] [CrossRef]
- T. V. Vu and H. Hayakawa, Thermomajorization Mpemba Effect, Phys. Rev. Lett. 2025, 134, 107101.
- G. Teza, J. G. Teza, J. Bechhoefer, A. Lasanta, O. Raz, and M. arXiv:2502.01758, M: thermal relaxation; arXiv:2502.01758 2025.
- A. Nava and M. Fabrizio. Lindblad dissipative dynamics in the presence of phase coexistence. Phys. Rev. B 2019, 100, 125102. [Google Scholar] [CrossRef]
- F. Carollo, A. Lasanta, and I. Lesanovsky. Exponentially Accelerated Approach to Stationarity in Markovian Open Quantum Systems through the Mpemba Effect. Phys. Rev. Lett. 2021, 127, 060401. [Google Scholar] [CrossRef]
- S. K. Manikandan, Equidistant quenches in few-level quantum systems. Phys. Rev. Res. 2021, 3, 043108. [Google Scholar] [CrossRef]
- S. Kochsiek, F. Carollo, and I. Lesanovsky. Accelerating the approach of dissipative quantum spin systems towards stationarity through global spin rotations. Phys. Rev. A 2022, 106, 012207. [Google Scholar] [CrossRef]
- F. Ivander, N. Anto-Sztrikacs, and D. Segal, Hyperacceleration of quantum thermalization dynamics by bypassing long-lived coherences: An analytical treatment. Phys. Rev. E 2023, 108, 014130. [Google Scholar] [CrossRef] [PubMed]
- F. Ares, S. Murciano, and P. Calabrese, Entanglement asymmetry as a probe of symmetry breaking. Nature Commun. 2023, 14, 2036. [Google Scholar] [CrossRef]
- Y. -L. Zhou, X.-D. Yu, C.-W. Wu, X.-Q. Li, J. Zhang, W. Li, and P.X. Chen, Accelerating relaxation through Liouvillian exceptional point. Phys. Rev. Research 2023, 5, 043036. [Google Scholar] [CrossRef]
- A. K. Chatterjee, S. Takada and H. Hayakawa, Quantum Mpemba effect in a quantum dot with reservoirs. Phys. Rev. Lett. 2023, 131, 080402. [Google Scholar] [CrossRef]
- M. Moroder, O. Culhane, K. Zawadzki, and J. Goold. Thermodynamics of the quantum Mpemba effect. Phys. Rev. Lett. 2024, 133, 140404. [Google Scholar] [CrossRef]
- A. K. Chatterjee, S. Takada and H. Hayakawa, Multiple quantum Mpemba effect: exceptional points and oscillations. Phys. Rev. A 2024, 110, 022213. [Google Scholar] [CrossRef]
- L. Kh. Joshi, J. Franke, A. Rath, F. Ares, S. Murciano, F. Kranzl, R. Blatt, P. Zoller, B. Vermersch, P. Calabrese, C. F. Roos, and M. K. Joshi, Observing the quantum Mpemba effect in quantum simulations. Phys. Rev. Lett. 2024, 133, 010402. [Google Scholar]
- C. Rylands, K. Klobas, F. Ares, P. Calabrese, S. Murciano, and B. Bertini, Microscopic origin of the quantum Mpemba effect in integrable systems. Phys. Rev. Lett. 2024, 133, 010401. [Google Scholar] [CrossRef]
- S. Murciano, F. S. Murciano, F. Ares, I. Klich, and P. Calabrese, Entanglement asymmetry and quantum Mpemba effect in the XY spin chain, J. Stat. Mech. 2024, 013103.
- K. Chalas, F. K. Chalas, F. Ares, C. Rylands, and P. Calabrese, Multiple crossing during dynamical symmetry restoration and implications for the quantum Mpemba effect. J. Stat. Mech. 0310. [Google Scholar]
- S. Yamashika, F. Ares, and P. Calabrese, Entanglement asymmetry and quantum Mpemba effect in two-dimensional free-fermion systems. Phys. Rev. B 2024, 110, 085126. [Google Scholar] [CrossRef]
- A. Nava and R. Egger, Mpemba effects in open nonequilibrium quantum systems. Phys. Rev. Lett. 2024, 133, 136302. [Google Scholar] [CrossRef]
- S. A. Shapira, Y. Shapira, J. Markov, G. Teza, N. Akerman, O. Raz and R. Ozeri, Inverse Mpemba Effect Demonstrated on a Single Trapped Ion Qubit. Phys. Rev. Lett. 2024, 133, 010403. [Google Scholar] [CrossRef]
- X. Wang and J Wang, Mpemba effects in nonequilibrium open quantum systems. Phys. Rev. Research 2024, 6, 033330. [Google Scholar] [CrossRef]
- D. Liu, J. Yuan, H. Ruan, Y. Xu, S. Luo, J. He, X. He, Y. Ma, and J. Wang, Speeding up quantum heat engines by the Mpemba effect. Phys. Rev. A 2024, 110, 042218. [Google Scholar] [CrossRef]
- F. Caceffo, S. F. Caceffo, S. Murciano, and V. Alba, Entangled multiplets, asymmetry, and quantum Mpemba effect in dissipative systems. J. Stat. Mech. 6310. [Google Scholar]
- S. Liu, H.-K. Zhang, S. Yin, and S.-X. Zhang, Symmetry Restoration and Quantum Mpemba Effect in Symmetric Random Circuits. Phys. Rev. Lett. 2024, 133, 140405. [Google Scholar] [CrossRef]
- S. Longhi, Bosonic Mpemba effect with non-classical states of light. APL Quantum 2024, 1, 046110. [Google Scholar] [CrossRef]
- S. Longhi, Laser Mpemba effect, Opt. Lett. 2025, 50, 2069.
- S. Longhi, Mpemba effect and super-accelerated thermalization in the damped quantum harmonic oscillator, Quantum 2025, 9, 1677.
- J. W. Dong, H. F. Mu, M. Qin, and H. T. Cui, Quantum Mpemba effect of localization in the dissipative mosaic model. Phys. Rev. A 2025, 111, 022215. [Google Scholar] [CrossRef]
- J. Zhang, G. Xia, C.-W. Wu, T. Chen, Q. Zhang, Y. Xie, W.-B. Su, W. Wu, C.-W Qiu, P. Chen, W. Li, H. Jing. Y.-L. Zhou, Observation of quantum strong Mpemba effect. Nature Comms. 2025, 16, 301. [Google Scholar]
- S. Yamashika, P. S. Yamashika, P. Calabrese, and F. Ares, Quenching from superfluid to free bosons in two dimensions: entanglement, symmetries, and quantum Mpemba effect. arXiv:2410.14299, arXiv:2410.14299 2024.
- J. Furtado and A. C. Santos, Strong Quantum Mpemba Effect with Squeezed Thermal Reservoirs. arXiv:2411.04545, arXiv:2411.04545 2024.
- S. Liu, H.-K. S. Liu, H.-K. Zhang, S. Yin, S.-X. Zhang, H. Yao, Quantum Mpemba effects in many-body localization systems. arXiv:2408.07750, arXiv:2408.07750 2024.
- D. Qian, H. D. Qian, H. Wang, and J. Wang, Intrinsic Quantum Mpemba Effect in Markovian Systems and Quantum Circuits. arXiv:2411.18417, arXiv:2411.18417 2024.
- S. Longhi, Quantum Mpemba effect from initial system-reservoir entanglement. arXiv:2504.21758, arXiv:2504.21758 2025 (to appear in APL Quantum).
- M. Boubakour, S. M. Boubakour, S. Endo, T. Fogarty, and T. Busch, Dynamical invariant based shortcut to equilibration in open quantum systems. arXiv:2401.11659, arXiv:2401.11659 2025.
- D. J. Strachan, A. D. J. Strachan, A. Purkayastha, S. R. Clark, Non-Markovian Quantum Mpemba effect. arXiv:2402.05756, arXiv:2402.05756 2024 (to appear in Phys. Rev. Lett.).
- F. Ares, P. F. Ares, P. Calabrese, and S. Murciano, The quantum Mpemba effects. arXiv:2502.08087, arXiv:2502.08087 2025.
- L. Trefethen, A. Trefethen, S. C. Reddy, and T. Driscol, Hydrodynamic stability without eigenvalues. Science 1993, 261, 578. [Google Scholar] [CrossRef]
- B. F. Farrell and P.J. Ioannou, Variance maintained by stochastic forcing of non-normal dynamical systems associated with linearly stable shear flows. Phys. Rev. Lett. 1994, 72, 1188. [Google Scholar] [CrossRef]
- K. G. Makris, L. Ge, and H.E. Türeci, Anomalous Transient Amplification of Waves in Non-normal Photonic Media. Phys. Rev. X 2014, 4, 041044. [Google Scholar]
- M. Asllani, R. Lambiotte, and T. Carletti, Structure and dynamical behavior of non-normal networks. Science Adv. 2018, 4, eaau9403. [Google Scholar] [CrossRef]
- S. Longhi, Anomalous dynamics in multilevel quantum decay. Phys. Rev. A 2018, 98, 022134. [Google Scholar] [CrossRef]
- S. Longhi, Quantum decay in a topological continuum. Phys. Rev. A 2019, 100, 022123. [Google Scholar] [CrossRef]
- T. Mori and T. Shirai, Resolving a Discrepancy between Liouvillian Gap and Relaxation Time in Boundary-Dissipated Quantum Many-Body Systems. Phys. Rev. Lett. 2020, 125, 230604. [Google Scholar] [CrossRef] [PubMed]
- T. Haga, M. Nakagawa, R. Hamazaki, and M. Ueda, Liouvillian Skin Effect: Slowing Down of Relaxation Processes without Gap Closing. Phys. Rev. Lett. 2021, 127, 070402. [Google Scholar] [CrossRef] [PubMed]
- T. Mori and T. Shirai, Symmetrized Liouvillian Gap in Markovian Open Quantum Systems. Phs. Rev. Lett. 2023, 130, 230404. [Google Scholar] [CrossRef]
- G. Lee, A. McDonald, and A. Clerk, Anomalously large relaxation times in dissipative lattice models beyond the non-Hermitian skin effect. Phys. Rev. B 2023, 108, 064311. [Google Scholar] [CrossRef]
- K. Shimomura and M. Sato, General Criterion for Non-Hermitian Skin Effects and Application: Fock Space Skin Effects in Many-Body Systems. Phys. Rev. Lett. 2024, 133, 136502. [Google Scholar] [CrossRef]
- H. Pichler, T. Ramos, A.J. Daley, and P. Zoller, Quantum optics of chiral spin networks. Phys. Rev. A 2015, 91, 042116. [Google Scholar] [CrossRef]
- M. Bello, G. Platero, J.I. Cirac, and A. González-Tudela , Unconventional quantum optics in topological waveguide QED. Science Adv. 2019, 5, eaaw0297. [Google Scholar] [CrossRef]
- A. S. Sheremet, M. I. Petrov, I. V. Iorsh, A. V. Poshakinskiy, and A. N. Poddubny, Waveguide quantum electrodynamics: Collective radiance and photon-photon correlations. Rev. Mod. Phys. 2023, 95, 015002. [Google Scholar] [CrossRef]
- F. Ciccarello, P. Lodahl, and D. Schneble, Waveguide Quantum Electrodynamics. Opt. & Photon. News 2024, 35, 34. [Google Scholar]
- H. P. Breuer and F. Petruccione, The Theory of Open Quantum Systems ( Oxford University Press, USA, 2002).
- S, Kumar, Wishart and random density matrices: Analytical results for the mean-square Hilbert-Schmidt distance, Phys. Rev. A 2020, 102, 012405. [CrossRef]
- P. Solano, P. Barberis-Blostein, F. K. Fatemi, L. A. Orozco, and S. L. Rolston, Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nature Commun. 2017, 8, 1857. [Google Scholar] [CrossRef] [PubMed]
- C. Liedl, F. Tebbenjohanns, C. Bach, S. Pucher, A. Rauschenbeutel, and P. Schneeweiss, Observation of Superradiant Bursts in a Cascaded Quantum System. Phys. Rev. X 2024, 14, 011020. [Google Scholar]
- A. Goban, C.-L. Hung, J. D. Hood, S.-P. Yu, J. A. Muniz, O. Painter, and H. J. Kimble, Superradiance for Atoms Trapped along a Photonic Crystal Waveguide. Phys. Rev. Lett. 2015, 115, 063601. [Google Scholar] [CrossRef]
- P. Lodahl, S. Mahmoodian, and S. Stobbe, Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–2015. [Google Scholar] [CrossRef]
- P. Forn-Diaz, J. J. Garcia-Ripoll, B. Peropadre, J.-L. Orgiazzi, M. A. Yurtalan, R. Belyansky, C. M. Wilson, and A. Lupascu, Ultrastrong coupling of a single artificial atom to an electromagnetic continuum in the nonperturbative regime. Nature Phys. 2017, 13, 39. [Google Scholar] [CrossRef]
- Z. Wang, H. Li, W. Feng, X. Song, C. Song, W. Liu, Q. Guo, X. Zhang, H. Dong, D. Zheng, H. Wang, and D.-W. Wang, Controllable Switching between Superradiant and Subradiant States in a 10-qubit Superconducting Circuit. Phys. Rev. Lett. 2020, 124, 013601. [Google Scholar] [CrossRef] [PubMed]
- M. Zanner, T. Orell, C.M.F. Schneider, R. Albert, S. Oleschko, M.L. Juan, M. Silveri, and G. Kirchmair, Coherent control of a multi-qubit dark state in waveguide quantum electrodynamics, Nature Phys. 2022, 18, 538.
- M. Scigliuzzo, G. Calajò, F. Ciccarello, D. Perez Lozano, A. Bengtsson, P. Scarlino, A. Wallraff, D. Chang, P. Delsing, and S. Gaspariinetti, Controlling Atom-Photon Bound States in an Array of Josephson-Junction Resonators, Phys. Rev. X 2022, 12, 031036.
- P. Henrici, Bounds for Iterates, Inverses, Spectral Variation and Fields of Values of Non-Normal Matrices, Numer. Math. 1962, 4, 24.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).



