Submitted:
27 April 2025
Posted:
28 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Classical and Quantum Response Theory
3. Quantum Dissipation Function for Time Indpendent Perturbations
4. Self Adjoint Quantum Dissipation Operator
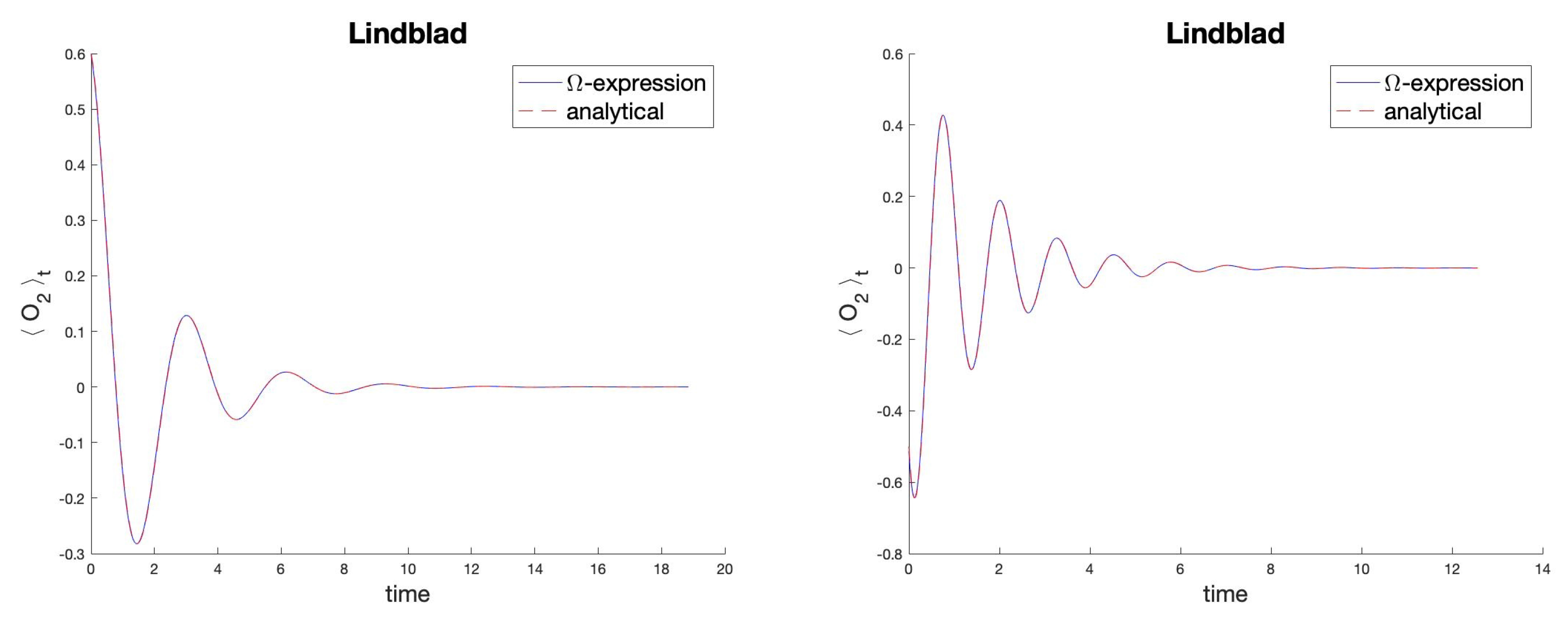
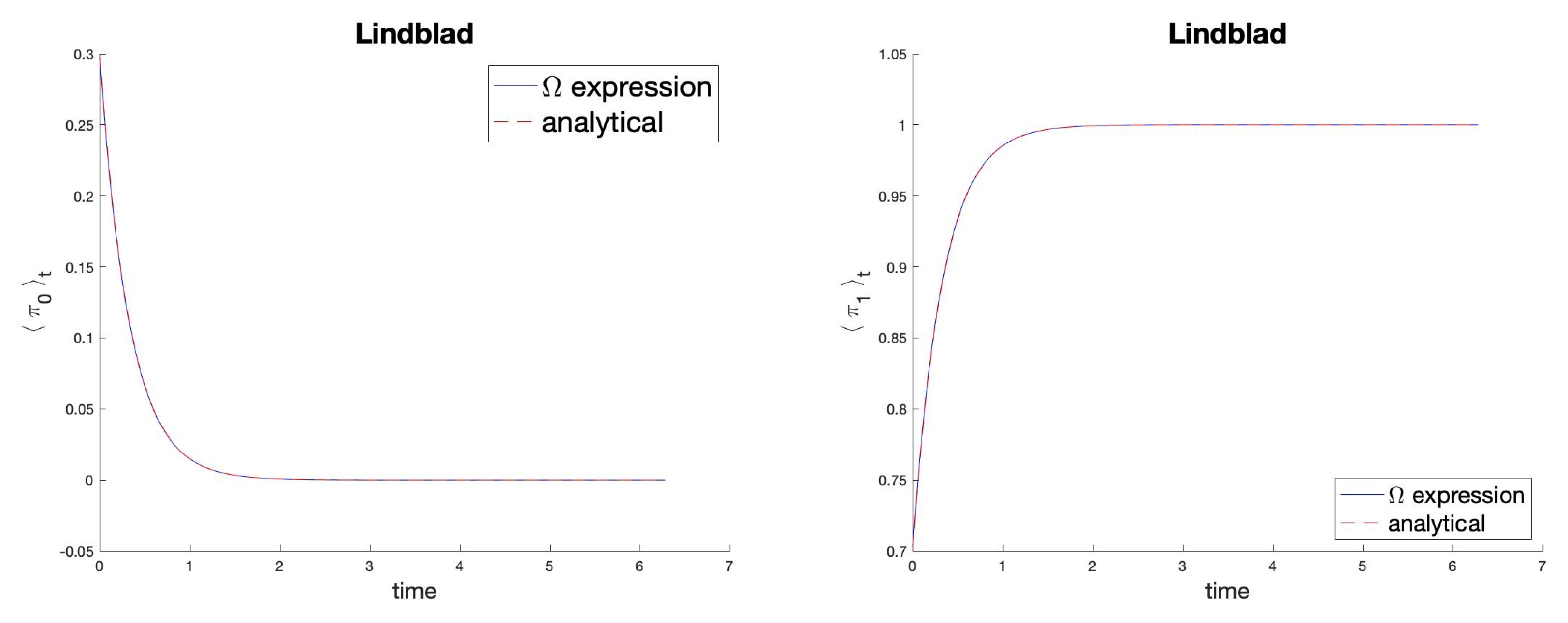
5. Applications to Qubits and Numerical Tests
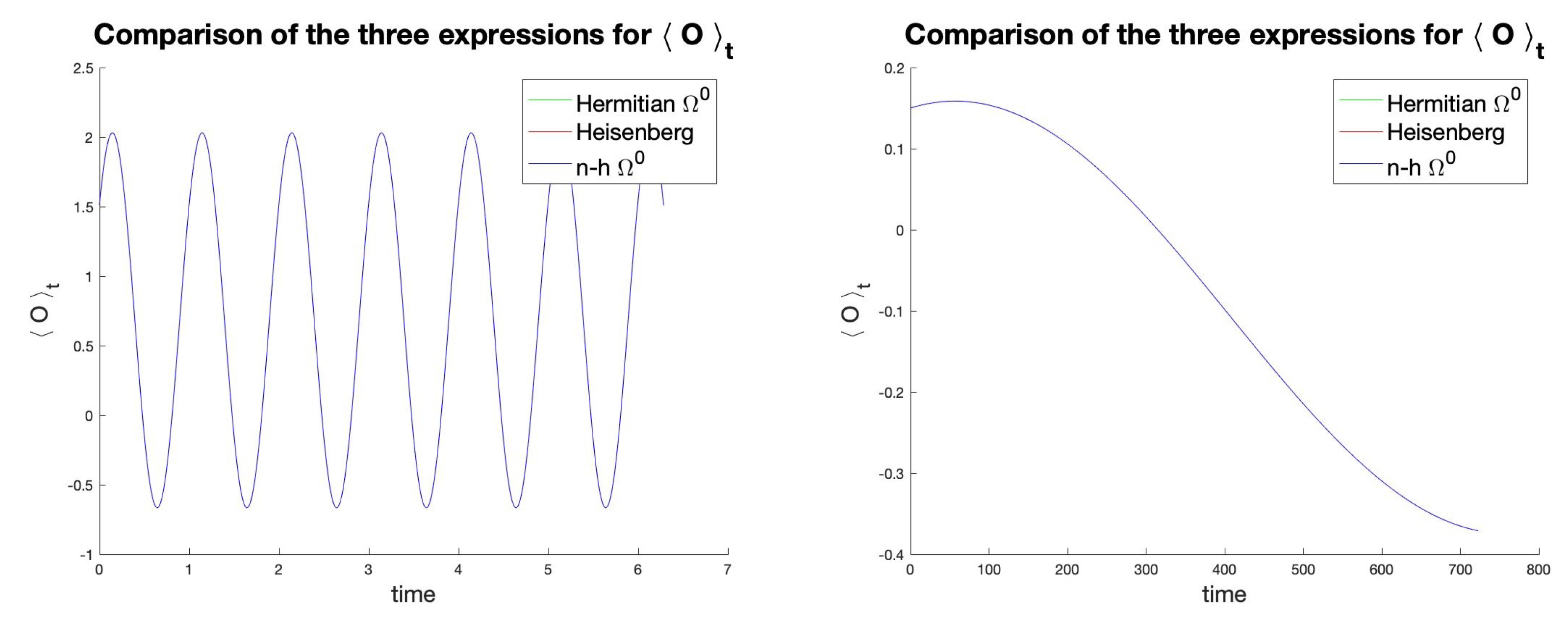
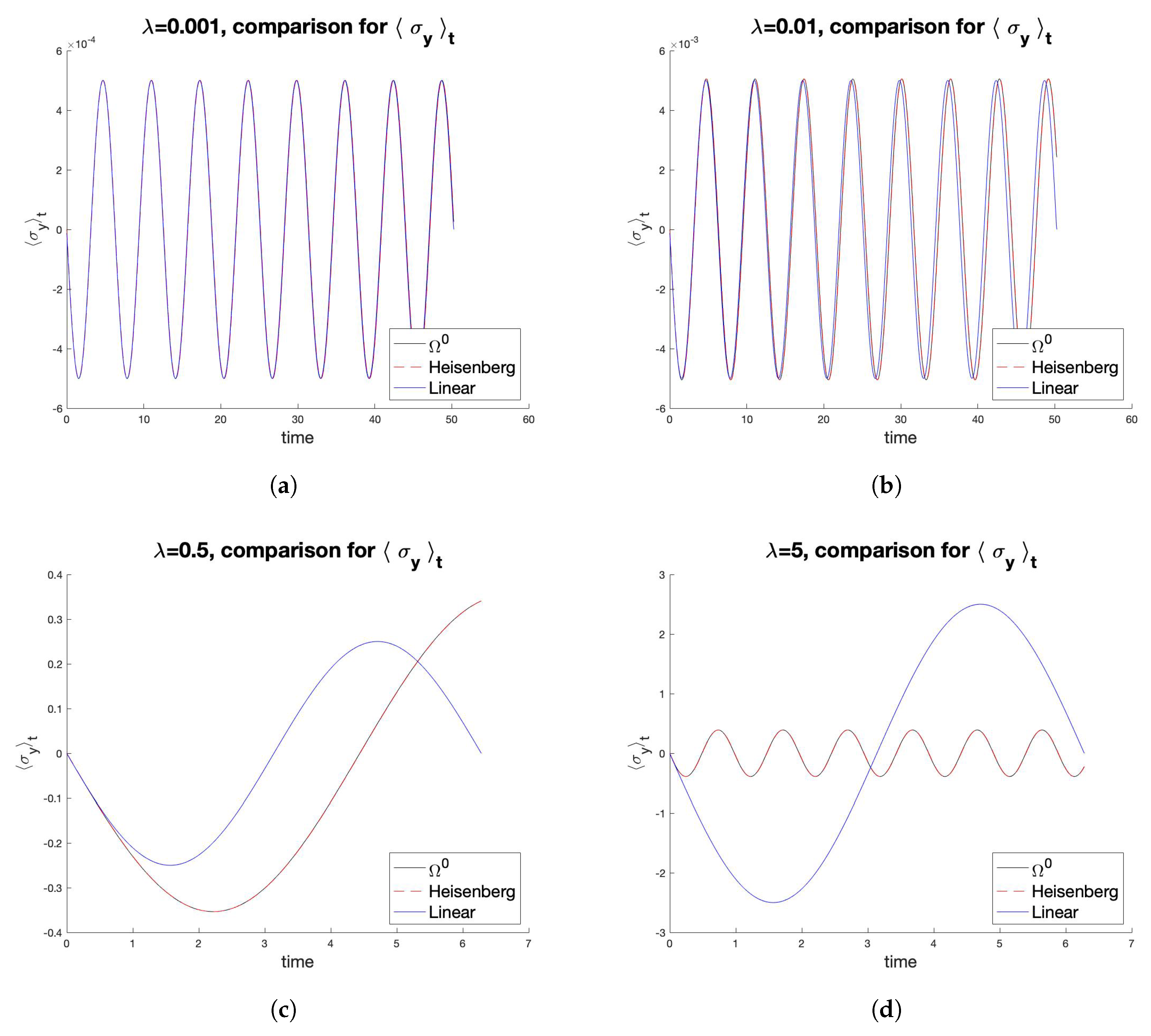
6. Properties of Dissipation and Time Dependent Perturbations
7. The Dissipation Operator for Open Quantum Systems
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Callen, H.B.; Welton, T.A. Irreversibility and generalized noise. Physical Review 1951, 83, 34. [CrossRef]
- Greene, R.F.; Callen, H.B. On the formalism of thermodynamic fluctuation theory. Physical Review 1951, 83, 1231. [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Reports on progress in physics 1966, 29, 255. [CrossRef]
- Green, M.S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. The Journal of chemical physics 1954, 22, 398–413. [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. Journal of the physical society of Japan 1957, 12, 570–586. [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation–dissipation: response theory in statistical physics. Physics reports 2008, 461, 111–195. [CrossRef]
- J Evans, D.; P Morriss, G. Statistical mechanics of nonequilbrium liquids; ANU Press, 2007.
- Feynman, R.P. Simulating physics with computers. In Feynman and computation; cRc Press, 2018; pp. 133–153.
- Schaller, G. Open quantum systems far from equilibrium; Vol. 881, Springer, 2014.
- Breuer, H.P.; Petruccione, F. The theory of open quantum systems; Oxford University Press, USA, 2002.
- Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information; Cambridge university press, 2010.
- Cai, Z.; Babbush, R.; Benjamin, S.C.; Endo, S.; Huggins, W.J.; Li, Y.; McClean, J.R.; O’Brien, T.E. Quantum error mitigation. Reviews of Modern Physics 2023, 95, 045005. [CrossRef]
- Avron, J.E.; Fraas, M.; Graf, G.M.; Kenneth, O. Quantum response of dephasing open systems. New Journal of Physics 2011, 13, 053042. [CrossRef]
- Avron, J.; Fraas, M.; Graf, G. Adiabatic response for Lindblad dynamics. Journal of Statistical Physics 2012, 148, 800–823. [CrossRef]
- Narayan, O. Linear response formula for open systems. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics 2011, 83, 061110. [CrossRef]
- Campos Venuti, L.; Zanardi, P. Dynamical response theory for driven-dissipative quantum systems. Physical Review A 2016, 93, 032101. [CrossRef]
- Shen, H.; Li, D.; Yi, X. Non-Markovian linear response theory for quantum open systems and its applications. Physical Review E 2017, 95, 012156. [CrossRef]
- Konopik, M.; Lutz, E. Quantum response theory for nonequilibrium steady states. Physical Review Research 2019, 1, 033156. [CrossRef]
- Mehboudi, M.; Parrondo, J.M.; Acin, A. Linear response theory for quantum Gaussian processes. New journal of physics 2019, 21, 083036. [CrossRef]
- Levy, A.; Rabani, E.; Limmer, D.T. Response theory for nonequilibrium steady states of open quantum systems. Physical Review Research 2021, 3, 023252. [CrossRef]
- Nakamura, K. Quantum chaos: a new paradigm of nonlinear dynamics; Vol. 3, CUP Archive, 1994.
- Scully, M.O.; Zubairy, M.S. Quantum optics; Cambridge university press, 1997.
- Mukherjee, B.; Sengupta, K.; Majumdar, S.N. Quantum dynamics with stochastic reset. Physical Review B 2018, 98, 104309. [CrossRef]
- Cirillo, E.N.; Colangeli, M.; Rondoni, L. Transport in quantum multi-barrier systems as random walks on a lattice. Journal of Statistical Physics 2019, 176, 692–709. [CrossRef]
- Dubey, V.; Chetrite, R.; Dhar, A. Quantum resetting in continuous measurement induced dynamics of a qubit. Journal of Physics A: Mathematical and Theoretical 2023, 56, 154001. [CrossRef]
- Evans, D.J.; Searles, D.J. Equilibrium microstates which generate second law violating steady states. Physical Review E 1994, 50, 1645. [CrossRef]
- Evans, D.; Cohen, E.; Morriss, G. Probability of second law violations in shearing steady flows, 1993. Phys. Rev. Lett, 70, 2401.
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in stationary states. Journal of Statistical Physics 1995, 80, 931–970. [CrossRef]
- Jarzynski, C.; Wójcik, D.K. Classical and quantum fluctuation theorems for heat exchange. Physical review letters 2004, 92, 230602. [CrossRef]
- Searles, D.J.; Rondoni, L.; Evans, D.J. The steady state fluctuation relation for the dissipation function. Journal of Statistical Physics 2007, 128, 1337–1363. [CrossRef]
- Searles, D.J.; Evans, D.J. Ensemble dependence of the transient fluctuation theorem. The Journal of Chemical Physics 2000, 113, 3503–3509. [CrossRef]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Advances in Physics 2002, 51, 1529–1585. [CrossRef]
- Evans, D.J.; Searles, D.J.; Williams, S.R. On the fluctuation theorem for the dissipation function and its connection with response theory. The Journal of chemical physics 2008, 128. [CrossRef]
- Jepps, O.G.; Rondoni, L. A dynamical-systems interpretation of the dissipation function, T-mixing and their relation to thermodynamic relaxation. Journal of Physics A: Mathematical and Theoretical 2016, 49, 154002. [CrossRef]
- Amadori, D.; Colangeli, M.; Correa, A.; Rondoni, L. Exact response theory and Kuramoto dynamics. Physica D: Nonlinear Phenomena 2022, 429, 133076. [CrossRef]
- Iannella, L.; Rondoni, L. Exact Response Theory for Time-Dependent and Stochastic Perturbations. Entropy 2023, 26, 12. [CrossRef]
- Maffioli, L.; Smith, E.R.; Ewen, J.P.; Daivis, P.J.; Dini, D.; Todd, B. Slip and stress from low shear rate nonequilibrium molecular dynamics: The transient-time correlation function technique. The Journal of Chemical Physics 2022, 156. [CrossRef]
- Bernardi, S.; Searles, D.J. Local response in nanopores. Molecular Simulation 2016, 42, 463–473. [CrossRef]
- Hunter, M.A.; Demir, B.; Petersen, C.F.; Searles, D.J. New framework for computing a general local self-diffusion coefficient using statistical mechanics. Journal of Chemical Theory and Computation 2022, 18, 3357–3363. [CrossRef]
- Searles, D.J.; Sanderson, S. Fluctuation theorems and distribution functions for polar molecules in an electric field. arXiv preprint arXiv:2401.02862 2024.
- Sanderson, S.; Petersen, C.F.; Searles, D.J. Machine learning a time-local fluctuation theorem for nonequilibrium steady states. Progress of Theoretical and Experimental Physics 2023, 2023, 083A01. [CrossRef]
- Andrieux, D.; Gaspard, P. Quantum work relations and response theory. Physical review letters 2008, 100, 230404. [CrossRef]
- Evans, D.J.; Searles, D.J.; Williams, S.R. Fundamentals of classical statistical thermodynamics: dissipation, relaxation, and fluctuation theorems; John Wiley & Sons, 2016.
- Touchette, H.; Harris, R.J. Large deviation approach to nonequilibrium systems. Nonequilibrium statistical physics of small systems: fluctuation relations and beyond 2013, pp. 335–360.
- Schwabl, F. Quantum mechanics; Springer Science & Business Media, 2007.
- Teta, A.; et al. A Mathematical Primer on Quantum Mechanics; Springer, 2018.
- Sinaĭ, A. Introduction to ergodic theory; Vol. 18, Princeton University Press, 1976.
- Jepps, O.G.; Rondoni, L. Deterministic thermostats, theories of nonequilibrium systems and parallels with the ergodic condition. Journal of Physics A: Mathematical and Theoretical 2010, 43, 133001. [CrossRef]
- Pan, L.; Chen, X.; Chen, Y.; Zhai, H. Non-Hermitian linear response theory. Nature Physics 2020, 16, 767–771. [CrossRef]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-hermitian physics. Advances in Physics 2020, 69, 249–435. [CrossRef]
- Caruso, S.; Giberti, C.; Rondoni, L. Dissipation function: Nonequilibrium physics and dynamical systems. Entropy 2020, 22, 835. [CrossRef]
- Rammer, J. Quantum field theory of non-equilibrium states. Quantum Field Theory of Non-equilibrium States 2011.
- Stockburger, J.T.; Motz, T. Thermodynamic deficiencies of some simple Lindblad operators: A diagnosis and a suggestion for a cure. Fortschritte der Physik 2017, 65, 1600067. [CrossRef]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. Europhysics Letters 2014, 107, 20004. [CrossRef]
- De Jong, W.A.; Metcalf, M.; Mulligan, J.; Płoskoń, M.; Ringer, F.; Yao, X. Quantum simulation of open quantum systems in heavy-ion collisions. Physical Review D 2021, 104, L051501. [CrossRef]
- Hu, Z.; Xia, R.; Kais, S. A quantum algorithm for evolving open quantum dynamics on quantum computing devices. Scientific reports 2020, 10, 3301. [CrossRef]
- Santos, J.P.; Céleri, L.C.; Landi, G.T.; Paternostro, M. The role of quantum coherence in non-equilibrium entropy production. npj Quantum Information 2019, 5, 23. [CrossRef]
- Lindblad, G. Expectations and entropy inequalities for finite quantum systems. Communications in Mathematical Physics 1974, 39, 111–119. [CrossRef]
- Sasaki, R.; Tateyama, Y.; Searles, D.J. Constant-Current Nonequilibrium Molecular Dynamics Approach for Accelerated Computation of Ionic Conductivity Including Ion-Ion Correlation. PRX Energy 2025, 4, 013005. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).