Submitted:
06 May 2025
Posted:
06 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Computational Methods, Results and Discussion
2.1. Electronic Structure Calculations: Reference Data on Interaction Energies
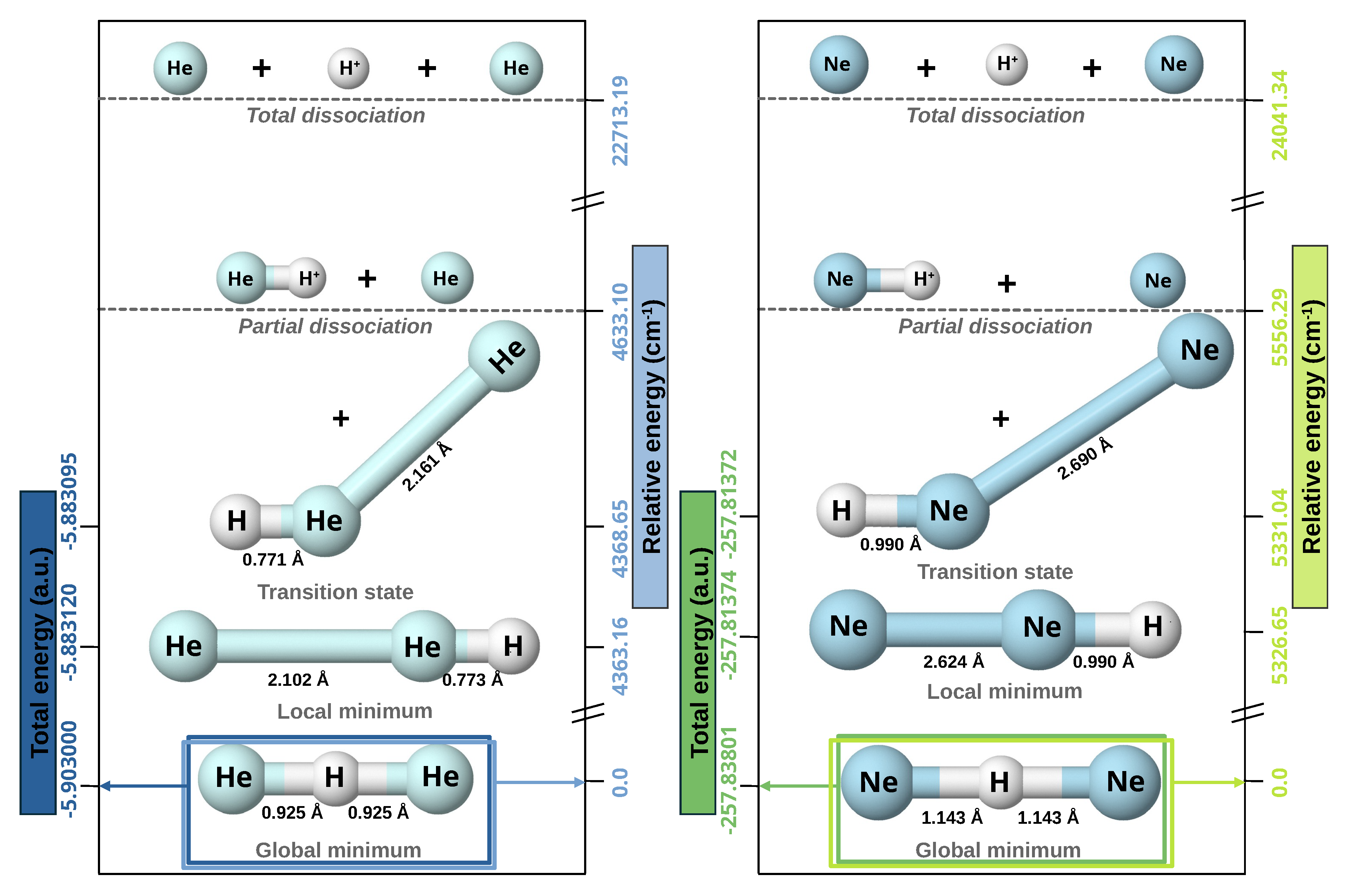
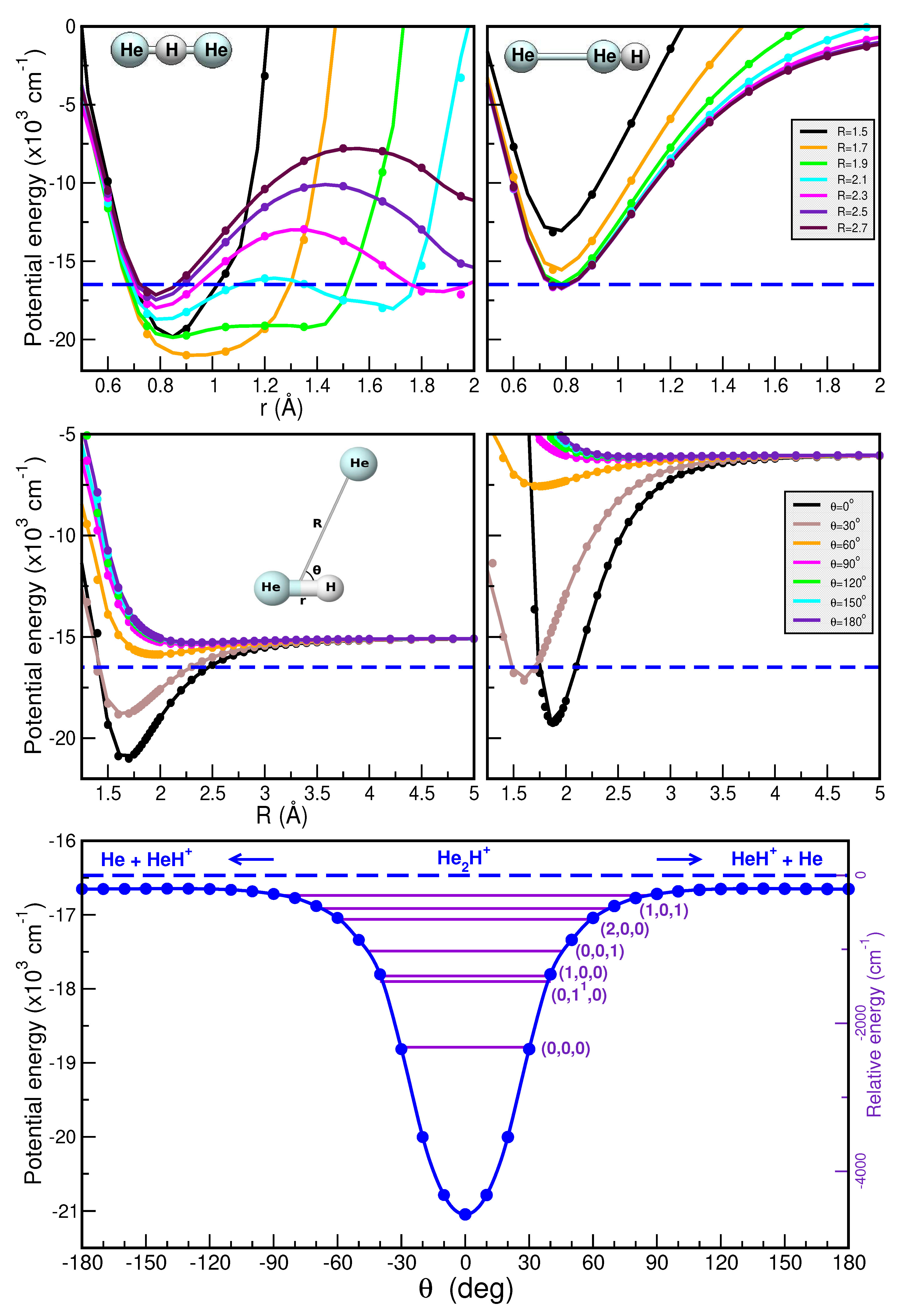
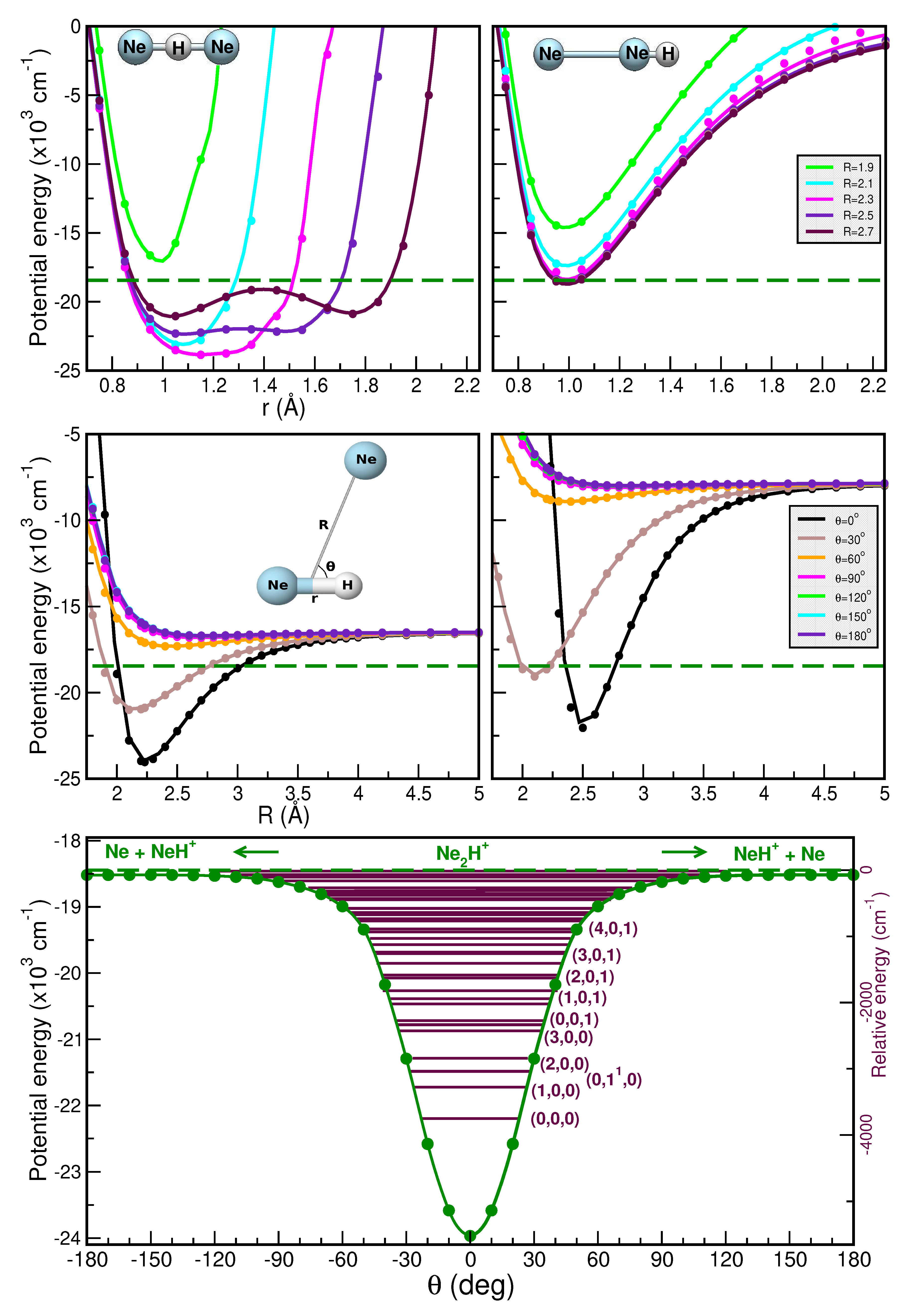
2.1.1. Optimized Structures and Dissociative Energetics
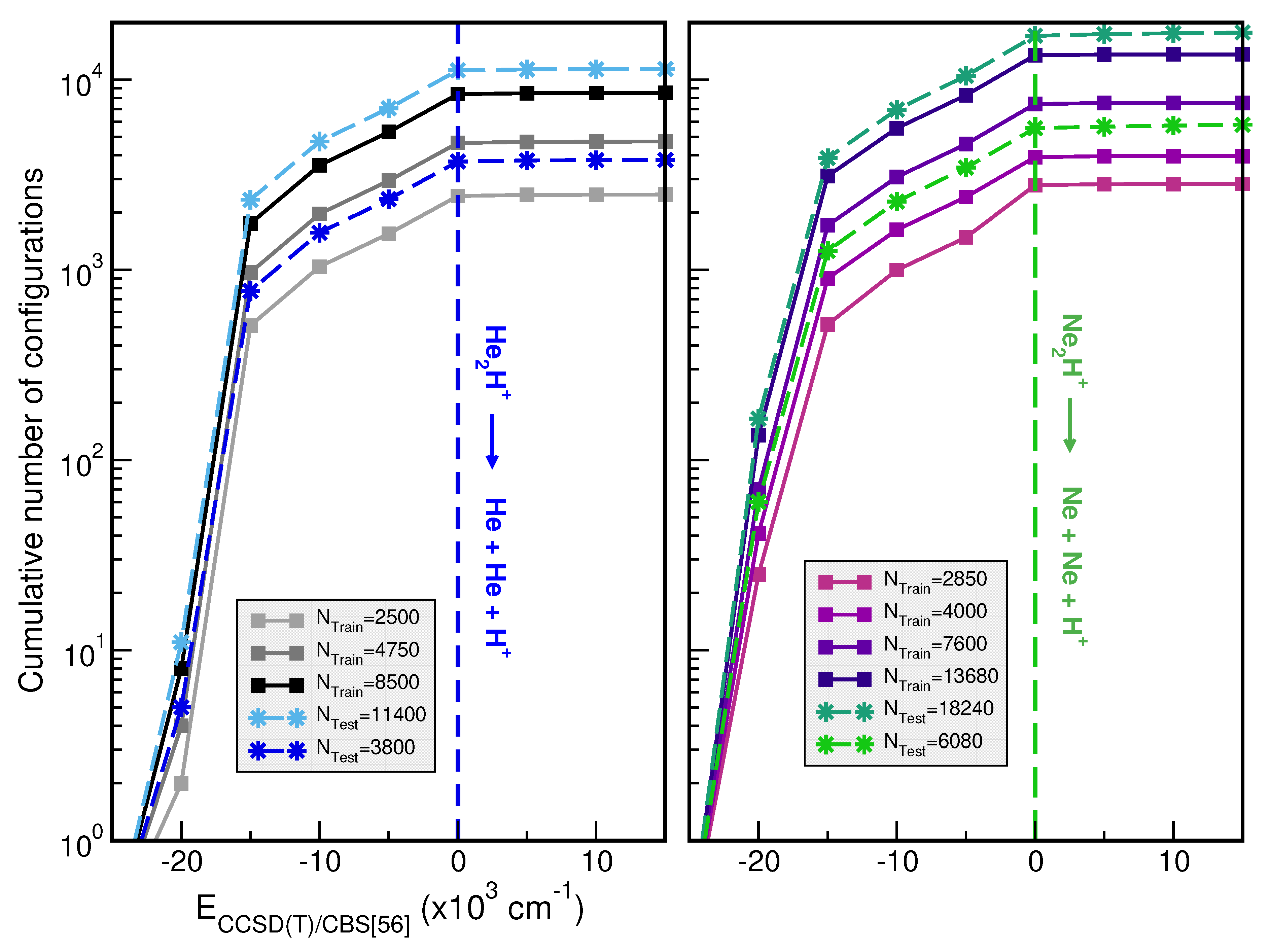
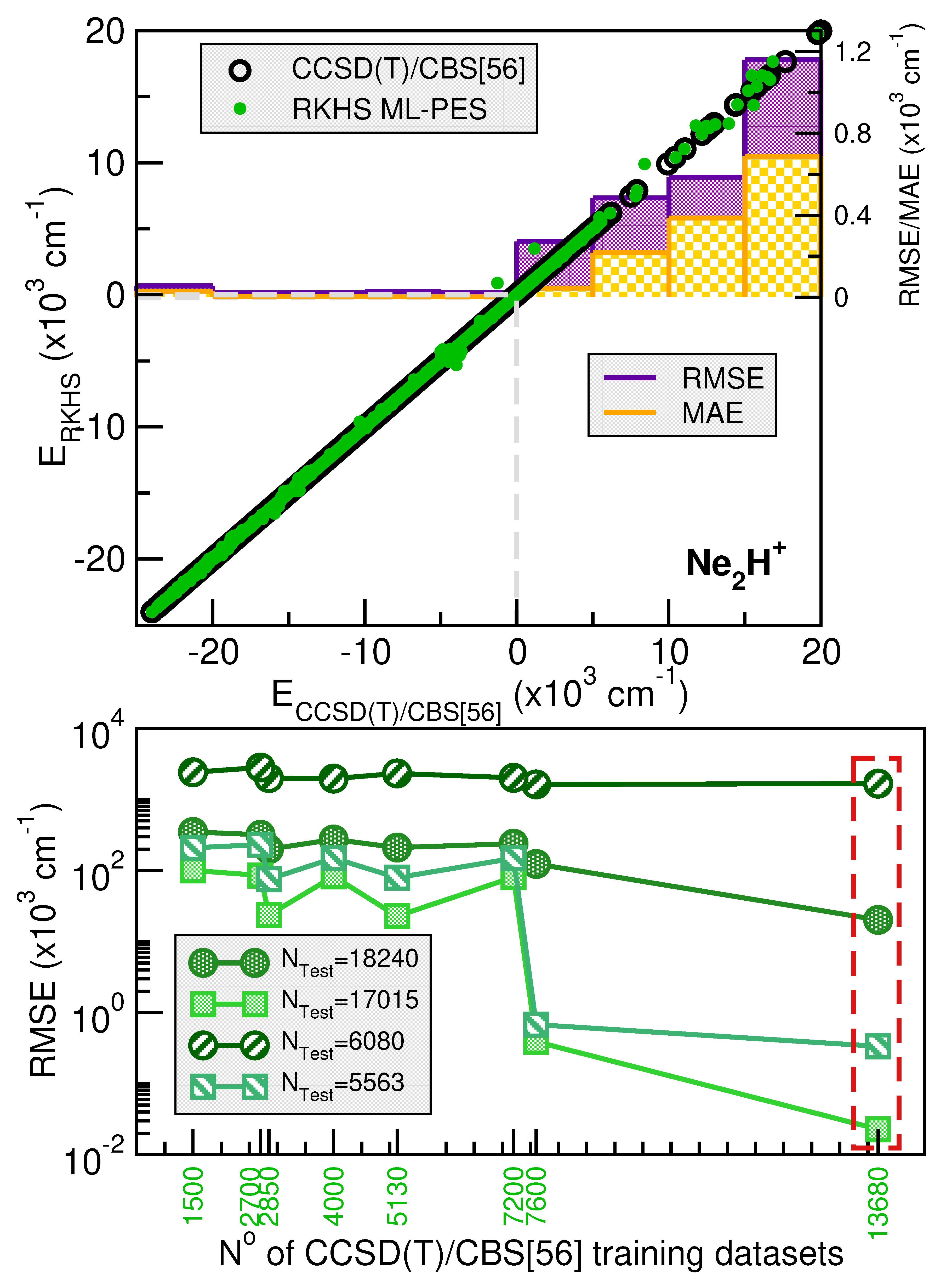
2.1.2. Training and Testing Datasets
2.2. Potential Energy Surface Representations: Topology and Quality
2.2.1. RKHS ML-PESs Methodology
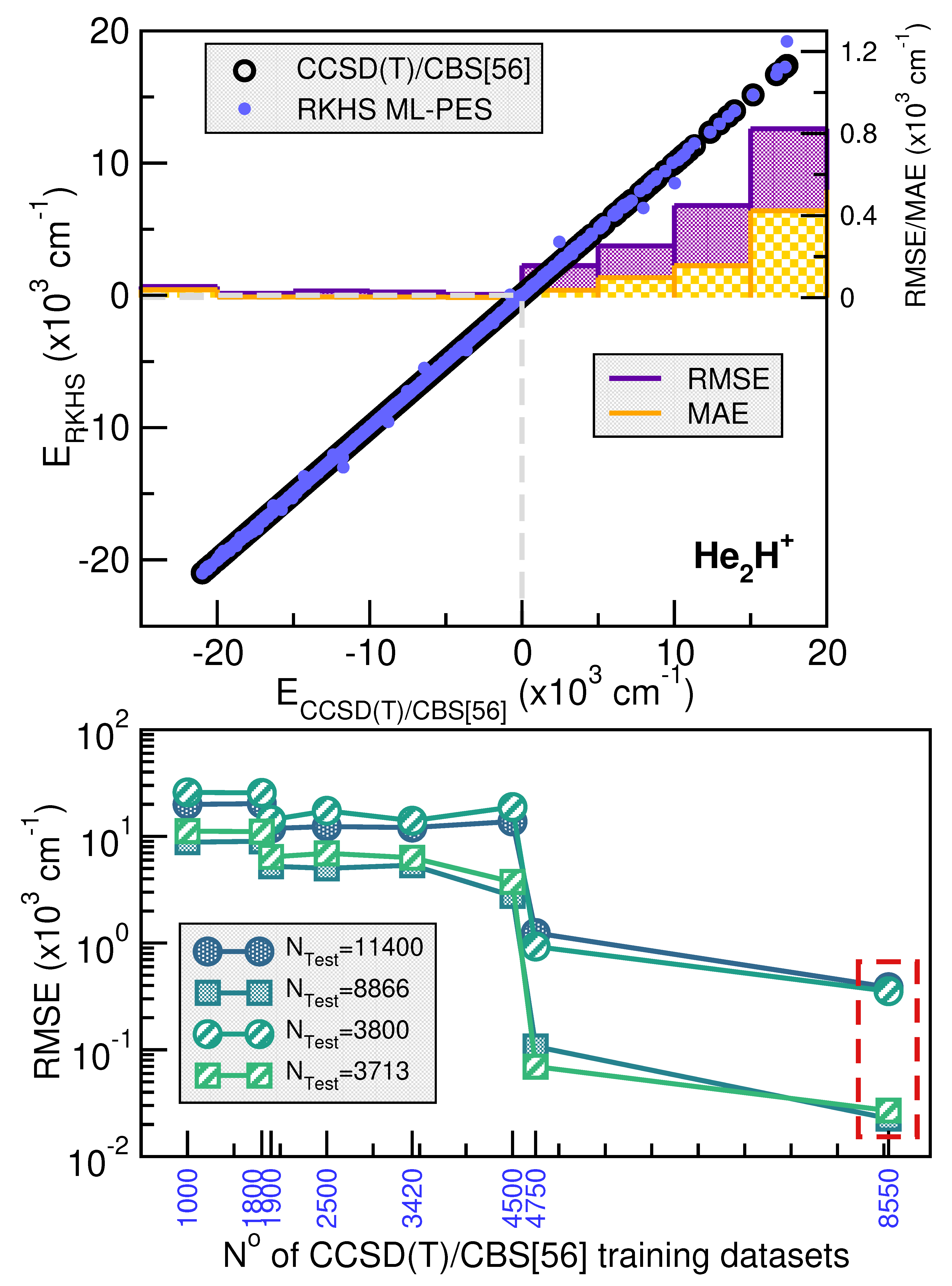
2.2.2. Validation of the RKHS ML-PES Models
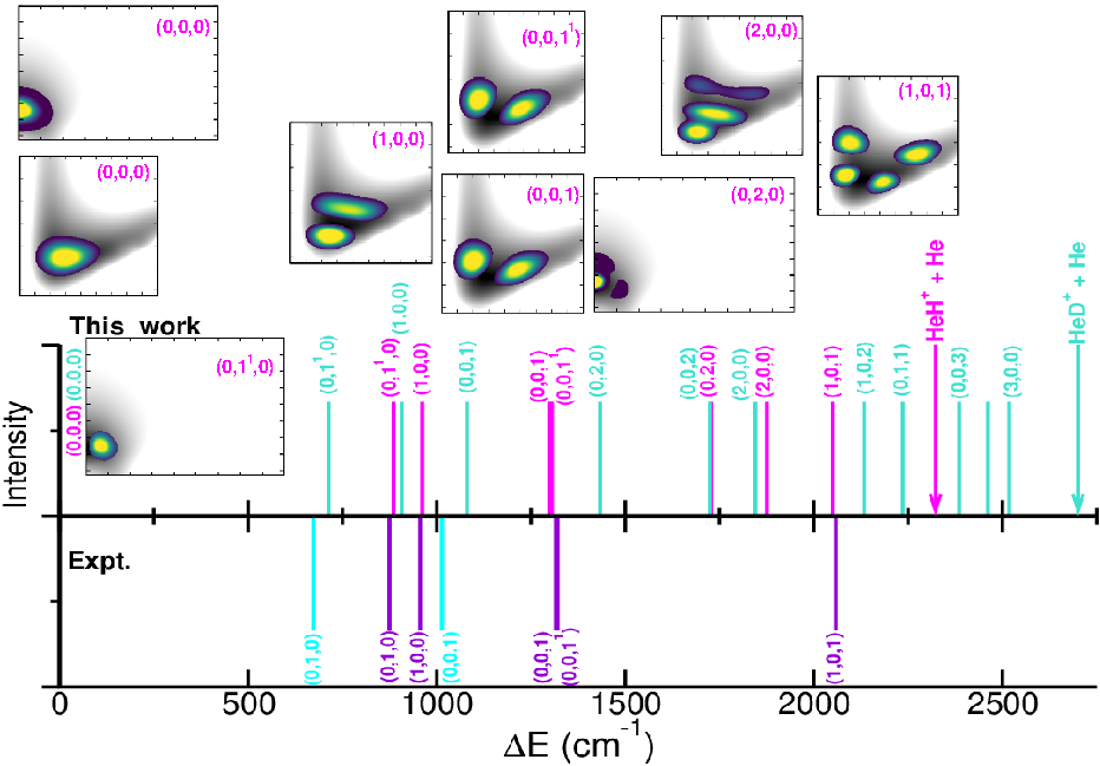
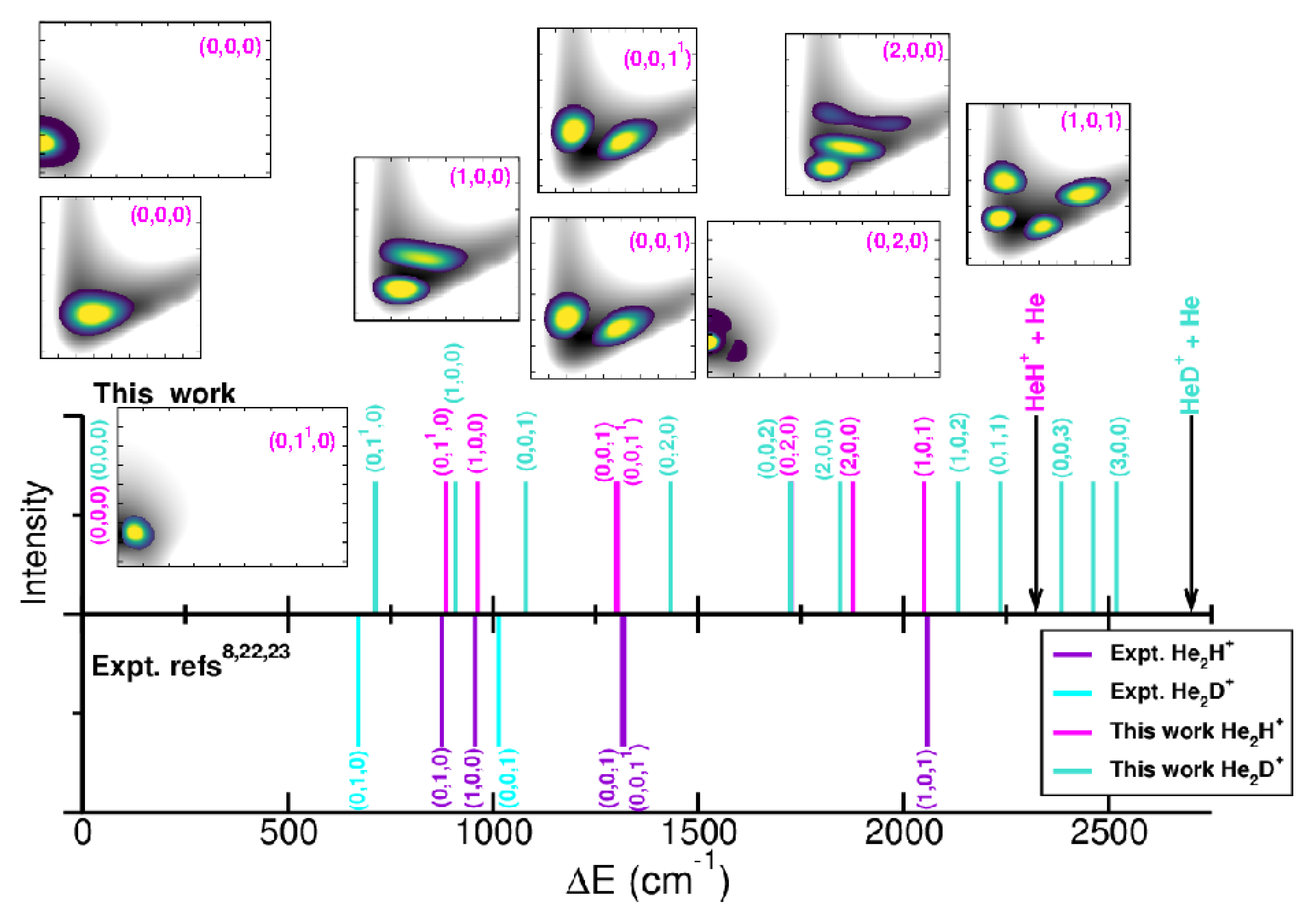
2.3. Bound-State Quantum Calculations: Vibrational Spectral Bands Assignment
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tennyson, J. Accurate variational calculations for line lists to model the vibrational-rotation spectra of hot astrophysical atmospheres. WIREs Comput. Mol. Sci. 2011, 2, 698–715. [Google Scholar] [CrossRef]
- Yu, Q.; Bowman, J.M.; Fortenberry, R.C.; Mancini, J.S.; Lee, T.J.; Crawford, T.D.; Klemperer, W.; Francisco, J.S. Structure, Anharmonic Vibrational Frequencies, and Intensities of NNHNN+. J. Phys. Chem. A 2015, 119, 11623–11631. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.; Carrington, Tucker, J. Computing vibrational spectra using a new collocation method with a pruned basis and more points than basis functions: Avoiding quadrature. J. Chem. Phys. 2023, 158, 144115. [CrossRef]
- Valdés, Á.; Prosmiti, R. First-principles simulations of vibrational states and spectra for and clusters using multiconfiguration time-dependent Hartree approach. Spectrochim. Acta A 2014, 119, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Császár, A.G.; Fábri, C.; Szidarovszky, T.; Mátyus, E.; Furtenbacher, T.; Czakó, G. The fourth age of quantum chemistry: molecules in motion. Phys. Chem. Chem. Phys. 2012, 14, 1085–1106. [Google Scholar] [CrossRef]
- Carrillo-Bohórquez, O.; Valdés, Á.; Prosmiti, R. Computational Energy Spectra of the H2O@C70 Endofullerene. ChemPhysChem 2023, 24, e202300570. [Google Scholar] [CrossRef]
- Valdés, Á.; Cabrera-Ramírez, A.; Prosmiti, R. Confining CO2 inside sI clathrate-hydrates: The impact of the CO2-wate interaction on quantized dynamics. J. Comput. Chem. 2023, 44, 1587–1598. [Google Scholar] [CrossRef]
- Salomon, T.; Baddeliyanage, C.; Schladt, C.; Simkó, I.; Császár, A.G.; Silva, W.G.D.P.; Schlemmer, S.; Asvany, O. High-resolution leak-out spectroscopy of HHe2+. Phys. Chem. Chem. Phys. 2025, 27, 4826–4828. [Google Scholar] [CrossRef]
- Molecules in Space, 2022. Available online: https://cdms.astro.uni-koeln.de/classic/molecules.
- Güsten, R.; Wiesemeyer, H.; Neufeld, D.; Menten, K.; Graf, U.; Jacobs, K.; Klein, B.; Ricken, O.; Risacher, C.; Stutzki, J. Astrophysical detection of the helium hydride ion HeH+. Nature 2019, 568, 357–359. [Google Scholar] [CrossRef]
- Barlow, M.; Swinyard, B.; Owen, P.; Cernicharo, J.; Gomez, H.; Ivison, R.; Krause, O.; Lim, T.; Matsuura, M.; Miller, S.; et al. Detection of a Noble Gas Molecular Ion, 36ArH+, in the Crab Nebula. Science 2013, 342, 1343–1345. [Google Scholar] [CrossRef]
- Müller, H.; Muller, S.; Schilke, P.; Bergin, E.; Black, J.; Gerin, M.; Lis, D.; Neufeld, D.; Suri, S. Detection of extragalactic argonium, ArH+, toward PKS 1830-211. A&A 2015, 582, L4. [Google Scholar]
- NASA’s LADEE Spacecraft Finds Neon in Lunar Atmosphere. https://sservi.nasa.gov/articles/nasas-ladee-spacecraft-finds-neon-in-lunar-atmosphere/, 2015.
- Asvany, O.; Schlemmer, S.; Szidarovszky, T.; Császár, A.G. Infrared Signatures of the and (n = 3–6) Complexes. J. Phys. Chem. Lett. 2019, 10, 5325–5330. [Google Scholar] [CrossRef] [PubMed]
- Kojima, T.M.; Kobayashi, N.; Kaneko, Y. Formation of helium cluster ions HHex+ (x ≤ 14) and H3Hex+ (x ≤ 13) in a very low temperature drift tube. Z Phys D - Atoms, Molecules and Clusters 1992, 23, 181–185. [Google Scholar] [CrossRef]
- Bartl, P.; Leidlmair, C.; Denifl, S.; Scheier, P.; Echt, O. Cationic Complexes of Hydrogen with Helium. Chem. Phys. Chem 2013, 14, 227–232. [Google Scholar] [CrossRef]
- Lundberg, L.; Bartl, P.; Leidlmair, C.; Scheier, P.; Gatchell, M. Protonated and Cationic Helium Clusters. Molecules 2020, 25. [Google Scholar] [CrossRef]
- Apkarian, V.A.; Schwentner, N. Molecular Photodynamics in Rare Gas Solids. Chem. Rev. 1999, 99, 1481–1514. [Google Scholar] [CrossRef] [PubMed]
- Beyer, M.; Lammers, A.; V. Savchenko, E.; Niedner-Schatteburg, G.; E. Bondybey, V. Proton solvated by noble-gas atoms: simplest case of a solvated ion. Phys. Chem. Chem. Phys. 1999, 1, 2213–2221. [CrossRef]
- Fridgen, T.D.; Parnis, J.M. Electron bombardment matrix isolation of Rg/Rg/methanol mixtures (Rg= Ar, Kr, Xe): Fourier-transform infrared characterization of the proton-bound dimers Kr2H+, Xe2H+, (ArHKr)+ and (ArHXe)+ in Ar matrices and (KrHXe)+ and Xe2H+ in Kr matrices. J. Chem. Phys. 1998, 109, 2155–2161. [Google Scholar] [CrossRef]
- Kunttu, H.; Seetula, J.; Räsänen, M.; Apkarian, V.A. Photogeneration of ions via delocalized charge transfer states. I. Xe2H+ and Xe2D+ in solid Xe. J. Chem. Phys. 1992, 96, 5630–5635. [Google Scholar] [CrossRef]
- Tøpfer, M.; Jensen, A.; Nagamori, K.; Kohguchi, H.; Szidarovszky, T.; Császár, A.G.; Schlemmer, S.; Asvany, O. Spectroscopic signatures of and . Phys. Chem. Chem. Phys. 2020. [Google Scholar] [CrossRef]
- Simkó, I.; Schran, C.; Brieuc, F.; Fábri, C.; Asvany, O.; Schlemmer, S.; Marx, D.; Császár, A.G. Quantum Nuclear Delocalization and its Rovibrational Fingerprints. Angew. Chem. Int. Ed. 2023, 62, e202306744. [Google Scholar] [CrossRef] [PubMed]
- Poshusta, R.D.; Haugen, J.A.; Zetik, D.F. Ab Initio Predictions for Very Small Ions. J. Chem. Phys. 1969, 51, 3343–3351. [Google Scholar] [CrossRef]
- Poshusta, R.D.; Siems, W.F. Ab Initio Calculations on He2H+. J. Chem. Phys. 1971, 55, 1995–1996. [Google Scholar] [CrossRef]
- Milleur, M.B.; Matcha, R.L.; Hayes, E.F. Theoretical studies of hydrogen-rare gas complexes: HenH and HenH+ clusters. J. Chem. Phys. 1974, 60, 674–679. [Google Scholar] [CrossRef]
- Dykstra, C.E. The strong hydrogen bond in HeHHe+ and its weak counterpart in He. J. Mol. Struct. THEOCHEM 1983, 103, 131–138. [Google Scholar] [CrossRef]
- Baccarelli, I.; Gianturco, F.A.; Schneider, F. Stability and fragmentation of protonated helium dimers from ab initio calculations of their potential energy surfaces. J. Phys. Chem. A 1997, 101, 6054–6062. [Google Scholar] [CrossRef]
- Kim, S.T.; Lee, J.S. Ab initio study of He2H+ and Ne2H+: accurate structure and energetics. J. Chem. Phys. 1999, 110, 4413–4418. [Google Scholar] [CrossRef]
- Filippone, F.; Gianturco, F.A. Charged chromophoric units in protonated rare-gas clusters: A dynamical simulation. Eur. Phys. Lett. 1998, 44, 585. [Google Scholar] [CrossRef]
- Fortenberry, R.C. Rovibrational Characterization and Interstellar Implications of the Proton-Bound, Noble Gas Complexes: ArHAr+, NeHNe+, and ArHNe+. ACS Earth Space Chem. 2017, 1, 60–69. [Google Scholar] [CrossRef]
- Stephan, C.J.; Fortenberry, R.C. The interstellar formation and spectra of the noble gas, proton-bound HeHHe+, HeHNe+ and HeHAr+ complexes. Mon. Notices Royal Astron. Soc. 2017, 469, 339–346. [Google Scholar] [CrossRef]
- Fortenberry, R.C.; Wiesenfeld, L. A Molecular Candle Where Few Molecules Shine: HeHHe+. Molecules 2020, 25, 2183. [Google Scholar] [CrossRef] [PubMed]
- Panda, A.; Sathyamurthy, N. Bound and Quasibound States of He2H+ and He2D+. J. Phys. Chem. A 2003, 107, 7125–7131. [Google Scholar] [CrossRef]
- Koner, D.; Barrios Herrera, L.; Gonzalez-Lezana, T.; Panda, A. Scattering study of the Ne + NeH+(v0 = 0, j0 = 0) → NeH+ + Ne reaction on an ab initio based analytical potential energy surface. J. Chem. Phys. 2016, 144, 034303. [Google Scholar] [CrossRef] [PubMed]
- Attila, G. Császár, Tamás Szidarovszky, O.A.; Schlemmer, S. Fingerprints of microscopic superfluidity in clusters. Mol. Phys. 2019, 117, 1559–1583. [Google Scholar]
- Lee, J.S.; Secrest, D. A calculation of the rotation–vibration states of He2H+. J. Chem. Phys. 1986, 85, 6565–6575. [Google Scholar] [CrossRef]
- Liang, J.J.; Yang, C.L.; Wang, L.Z.; Zhang, Q.G. A new analytical potential energy surface for the singlet state of He2H+. J. Chem. Phys. 2012, 136, 094307. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Ugalde, J.M.; Andrada, D.M.; Frenking, G. Comparison of Hydrogen and Gold Bonding in [XHX]-, [XAuX]-, and Isoelectronic [NgHNg]+, [NgAuNg]+ (X=Halogen, Ng=Noble Gas). Eur. J. Chem. 2016, 22, 11317–11328. [Google Scholar] [CrossRef]
- Tan, J.A.; Kuo, J.L. A theoretical study on the infrared signatures of proton-bound rare gas dimers (Rg–H+–Rg), Rg=Ne, Ar, Kr, and Xe. J. Chem. Phys. 2019, 150, 124305. [Google Scholar] [CrossRef]
- Murrell, J.N. Molecular potential energy functions; Wiley, 1984.
- Polyansky, O.L.; Prosmiti, R; Klopper, W.; Tennyson, J. An accurate, global, ab initio potential energy surface for the molecule. Mol. Phys. 2000, 98, 261–273.
- Prosmiti, R.; Buchachenko, A.A.; Villarreal, P.; Delgado-Barrio, G. Modeling the potential-energy surface: a first attempt. Theor. Chem. Acc. 2001, 106, 426–433. [Google Scholar] [CrossRef]
- Huang, X.; Braams, B.; Bowman, J.; Kelly, R.; Tennyson, J.; Groenenboom, G.; van der Avoird, A. New ab initio potential energy surface and the vibration-rotation-tunneling levels of (H2O)2 and (D2O)2. J. Chem. Phys. 2008, 128, 034312. [Google Scholar] [CrossRef] [PubMed]
- Braams, B.; Bowman, J. Permutationally invariant potential energy surfaces in high dimensionality. Int. Rev. Phys. Chem. 2009, 28, 577–606. [Google Scholar] [CrossRef]
- Aguado, A.; Barragán, P.; Prosmiti, R.; Villarreal, G.D.B.P.; Roncero, O. A new accurate and full dimensional potential energy surface of based on a triatomics-in-molecules analytic functional form. J. Chem. Phys. 2010, 133, 024306. [Google Scholar] [CrossRef] [PubMed]
- Barragán, P.; Prosmiti, R.; Wang, Y.; Bowman, J. Full-dimensional (15-dimensional) ab initio analytical potential energy surface for the | cluster. J. Chem. Phys. 2012, 136, 224302. [Google Scholar] [CrossRef]
- Arismendi-Arrieta, D.; Riera, M.; Bajaj, P.; Prosmiti, R.; Paesani, F. i-TTM Model for AbInitio-Based Ion-Water Interaction Potentials. 1. Halide-Water Potential Energy Functions. J. Phys. Chem. B 2016, 120, 1822–1832. [Google Scholar] [CrossRef]
- Goncalves, C.; Galvão, B.R.; Mota, V.; Braga, J.; Varandas, A. Accurate Explicit-Correlation-MRCI-Based DMBE Potential-Energy Surface for Ground-State CNO. J. Phys. Chem. A 2018, 122, 4198–4207. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T.J. Neural Network Potential Energy Surfaces for Small Molecules and Reactions. Chem. Rev. 2021, 121, 10187–10217. [Google Scholar] [CrossRef]
- Unke, O.T.; Koner, D.; Patra, S.; Käser, S.; Meuwly, M. High-dimensional potential energy surfaces for molecular simulations: from empiricism to machine learning. Mach. Learn. Sci. Technol. 2020, 1, 013001. [Google Scholar] [CrossRef]
- Noe, F.; Tkatchenko, A.; Muller, K.R.; Clementi, C. Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 2020, 71, 361–390. [Google Scholar] [CrossRef]
- Dral, P. Quantum Chemistry in the Age of Machine Learning. J. Phys. Chem. Lett. 2020, 11, 2336–2347. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Ramezanghorbani, F.; Isayev, O.; Smith, J.; Roitberg, A. TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of the ANI Neural Network Potentials. J. Chem. Inf. Model. 2020, 60, 3408–3415. [Google Scholar] [CrossRef]
- Unke, O.T.; Chmiela, S.; Sauceda, H.E.; Gastegger, M.; Poltavsky, I.; Schütt, K.T.; Tkatchenko, A.; Müller, K.R. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, M.; Ge, F.; Ferré, N.; Dral, P.O.; Barbatti, M. Choosing the right molecular machine learning potential. Chem. Sci. 2021, 12, 14396–14413. [Google Scholar] [CrossRef] [PubMed]
- Montes de Oca-Estévez, M.J.; Prosmiti, R. Quantum computations in heavy noble-gas hydride cations: Reference energies and new spectroscopic data. J. Mol. Graph. Model. 2023, 124, 108562. [Google Scholar] [CrossRef]
- Montes de Oca-Estévez, M.J.; Valdés, Á.; Prosmiti, R. A kernel-based machine learning potential and quantum vibrational state analysis of the cationic Ar hydride (Ar2H+). Phys. Chem. Chem. Phys. 2024, 8, 7060–7071. [Google Scholar] [CrossRef]
- Montes de Oca-Estévez, M.J.; Valdés, Á.; Koner, D.; González-Lezana, T.; Prosmiti, R. Quantum computations on a new neural network potential for the proton-bound noble-gas Ar2H+ complex: Isotopic effects. Chem. Phys. Letts. 2024, 856, 141641. [Google Scholar] [CrossRef]
- Montes de Oca-Estévez, M.J.; Prosmiti, R. Microsolvation of a Proton by Ar Atoms: Structures and Energetics of ArnH+ Clusters. Molecules 2024, 29. [Google Scholar] [CrossRef]
- Dral, P. MLatom: A program package for quantum chemical research assisted by machine learning. J. Comput. Chem. 2019, 40, 2339–2347. [Google Scholar] [CrossRef]
- Abbott, A.; Turney, J.; Zhang, B.; Smith, D.; Altarawy, D.; Schaefer, H. PES-Learn: An Open-Source Software Package for the Automated Generation of Machine Learning Models of Molecular Potential Energy Surfaces. J. Chem. Theory Comput. 2019, 15, 4386–4398. [Google Scholar] [CrossRef] [PubMed]
- Unke, O.; Meuwly, M. PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges. J. Chem. Theory Comput. 2019, 15, 3678–3693. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.; Poltavsky, I.; Müller, K.R.; Tkatchenko, A. sGDML: Constructing accurate and data efficient molecular force fields using machine learning. Comput. Phys. Commun. 2019, 240, 38–45. [Google Scholar] [CrossRef]
- Shao, Y.; Hellström, M.; P.D. Mitev, L.K.; Zhang, C. PiNN: A Python Library for Building Atomic Neural Networks of Molecules and Materials. J. Chem. Inf. Model. 2020, 60, 1184–1193. [CrossRef]
- Ho, T.; Rabitz, H. A general method for constructing multidimensional molecular potential energy surfaces from ab initio calculations. J. Chem. Phys. 1996, 104, 2584–2597. [Google Scholar] [CrossRef]
- T. Hollebeek, T.S.H.; Rabitz, H. A fast algorithm for evaluating multidimensional potential energy surfaces. J. Chem. Phys. 1997, 106, 72223–7227.
- T. Hollebeek, T.S.H.; Rabitz, H. Constructing multidimensional molecular potential energy surfaces from ab initio data. Ann. Rev. Phys. Chem. 1999, 50, 537–570. [CrossRef]
- Ho, T.; Rabitz, H. Proper construction of ab initio global potential surfaces with accurate long-range interactions. J. Chem. Phys. 2000, 113, 3960–3968. [Google Scholar] [CrossRef]
- Ho, T.; Rabitz, H. Reproducing kernel Hilbert space interpolation methods as a paradigm of high dimensional model representations: Application to multidimensional potential energy surface construction. J. Chem. Phys. 2003, 119, 6433–6442. [Google Scholar] [CrossRef]
- Delgado-Tellez, L.; Valdés, A.; Prosmiti, R.; Villarreal, P.; Delgado-Barrio, G. HeI2 interaction potential based on an interpolation scheme. Int. J. Quantum Chem. 2012, 112, 2971–2975. [Google Scholar] [CrossRef]
- Kalemos, A.; Valdés, A.; Prosmiti, R. Theoretical investigation of the HeI2(E3Πg) ion-pair state: Ab initio intermolecular potential and vibrational levels. J. Chem. Phys. 2012, 137, 034303. [Google Scholar] [CrossRef]
- N. Alharzali, H. Berriche, P.V.; Prosmiti, R. Theoretical Study of Cationic Alkali Dimers Interacting with He: L-He and N-He van der Waals Complexes. J. Phys. Chem. A 2019, 123, 7814–7821. [CrossRef]
- N. Alharzali, R.R.S.; Prosmiti, R. Modelling interactions of cationic dimers in He droplets: microsolvation trends in Hen clusters. Phys. Chem. Chem. Phys. 2021, 23, 7849–7859. [CrossRef] [PubMed]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; et al. MOLPRO, version 2012.1, a package of ab initio programs. Available online: http://www.molpro.net.
- DENEB 1.30 beta: The Nanotechnology Software by Atelgraphics. http://www.atelgraphics.com, 2020.
- Montes de Oca-Estévez, M.J.; Prosmiti, R. Computational Characterization of Astrophysical Species: The Case of Noble Gas Hydride Cations. Front. Chem. 2021, 9, 187. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, C. Importance of Angular Correlations between Atomic Electrons. Phys. Rev. 1962, 126, 1015–1019. [Google Scholar] [CrossRef]
- Worth, G.A.; Beck, M.H.; Jäckle, A.; Meyer, H.D. The MCTDH Package, Version 8.2, (2000). H.-D. Meyer, Version 8.3 (2002), Version 8.4 (2007). See http://mctdh.uni-hd.de, 2007.
- Zhang, J.Z.H. Theory and Application of Quantum Molecular Dynamics; World Scientific: Singapore, 1999. [Google Scholar]
- Sukiasyan, S.; Meyer, H.D. On the Effect of Initial Rotation on Reactivity. A Multi-Configuration Time-Dependent Hartree (MCTDH) Wave Packet Propagation Study on the H + D2 and D + H2 Reactive Scattering Systems. J. Phys. Chem. A 2001, 105, 2604–2611. [Google Scholar] [CrossRef]
- Meyer, H.D.; Manthe, U.; Cederbaum, L.S. The Multi-Configurational Time-Dependent Hartree Approach. Chem. Phys. Lett. 1990, 165, 73–78. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The Multiconfiguration Time-Dependent Hartree Method: A Highly Efficient Algorithm for Propagating Wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Meyer, H.D. Studying Molecular Quantum Dynamics with the Multiconfiguration Time-Dependent Hartree Method. WIREs Comput. Mol. Sci. 2012, 2, 351–374. [Google Scholar] [CrossRef]
- Jäckle, A.; Meyer, H.D. Product representation of potential energy surfaces. II. J. Chem. Phys. 1998, 109, 3772–3779. [Google Scholar] [CrossRef]
- Meyer, H.D.; Quéré, F.L.; Léonard, C.; Gatti, F. Calculation and Selective Population of Vibrational Levels with the Multiconfiguration Time-Dependent Hartree (MCTDH) Algorithm. Chem. Phys. 2006, 329, 179–192. [Google Scholar] [CrossRef]
- Doriol, L.J.; Gatti, F.; Iung, C.; Meyer, H.D. Computation of Vibrational Energy Levels and Eigenstates of Fluoroform Using the Multiconfiguration Time-Dependent Hartree Method. J. Chem. Phys. 2008, 129, 224109–1–9. [Google Scholar] [CrossRef] [PubMed]
| [4 | [4 | |||
|---|---|---|---|---|
| This work | From Ref. [37]/Ref. [34] | This work | From Ref. [37]/Ref. [34] | |
| -4633.10 | -4603.92/-4661.88 | – | – | |
| 0 | -2322.6 (0,0,0) | -2321.77 (0,0,0)/-2493.87 | -2700.74 (0,0,0) | -2755.92 (0,0,0)/-2900.37 |
| 1 | -1360.5 (1,0,0) | -1358.16 (1,0,0)/-1539.712 | -1793.2 (1,0,0) | -1775.16 (1,0,0)/-1964.77 |
| 2 | -1022.2 (0,0,1) | -564.18 (2,0,0)/-1133.21 | -1620.4 (0,0,1) | -1384.04 (0,2,0)/-1822.81 |
| 3 | -594.8 (0,2,0) | -462.16 (0,2,0)/-821.88 | -1267.8 (0,2,0) | -916.32 (2,0,0)/-1630.05 |
| 4 | -446.4 (2,0,0) | -422.16 (1,2,0)/-623.47 | -976.8 (0,0,2) | -609.23 (1,2,0)/-1147.73 |
| 5 | -271.8 (1,0,1) | +134.32/-367.79 | -855.9 (2,0,0) | –/-958.19 |
| 6 | +84.6 (2,0,1) | –/-84.69 | -567.5 (1,0,2) | –/-850.11 |
| 7 | +290.2 (1,1,1) | – | -464.8 (0,1,1) | –/-779.13 |
| 8 | +348.3 | – | -315.1 (0,0,3) | –/-537.97 |
| 9 | +426.3 | – | -239.1 | –/-453.28 |
| 10 | – | – | -182.7 (3,0,0) | –/-329.88 |
| 11 | – | – | +45.8 (0,2,1) | –/-278.26 |
| 12 | – | – | +138.0 (1,0,1) | –/-145.99 |
| 13 | – | – | +166.5 | –/-18.55 |
| [20 | [20 | |||
|---|---|---|---|---|
| This work | From Ref. [35 | This work | ||
| -5556.29 | 2D plots | -5807.96 | – | |
| 0 | -3753.3 (0,0,0) | -3971.47 | -4170.5 (0,0,0) | |
| 1 | -3277.8 (1,0,0) | -3514.96 | -3697.2 (1,0,0) | |
| 2 | -2841.8 (2,0,0) | -3068.13 | -3260.8 (2,0,0) | |
| 3 | -2426.7 (3,0,0) | -2634.21 | -3119.9 (0,0,1) | |
| 4 | -2335.0 (0,0,1) | -2535.81 | -3078.9 (0,2,0) | |
| 5 | -2273.6 (0,2,0) | -2444.67 | -2843.1 (3,0,0) | |
| 6 | -2022.5 (4,0,0) | -2213.99 | -2693.1 (1,0,1) | |
| 7 | -1946.0 (1,0,1) | -2152.69 | -2631.3 (1,1,0) | |
| 8 | -1826.9 (1,1,0) | -2005.90 | -2435.6 (4,0,0) | |
| 9 | -1632.0 (5,0,0) | -1809.10 | -2322.8 (2,0,1) | |
| 10 | -1589.5 (2,0,1) | -1784.91 | -2217.0 (2,1,0) | |
| 11 | -1414.3 (2,1,0) | -1585.69/-1586.49 | -2185.5 (0,1,1) | |
| 12 | -1268.0 (3,0,1) | -1434.86/-1435.67 | -2056.3 (5,0,0) | |
| 13 | -1243.4 (6,0,1) | -1420.34/-1422.76 | -1977.9 | |
| 14 | -1143.5 (1,0,1) | -1292.10/-1294.52 | -1966.8 (4,0,1) | |
| 15 | -1039.7 (3,1,0 ) | -1200.96/-1204.19 | -1940.6 (0,3,0) | |
| 16 | -942.5 (4,0,1) | -1096.91/-1104.98 | -1814.2 | |
| 17 | -898.6 | -1051.75/-1063.04 | -1779.4 (1,1,1) | |
| 18 | -819.9 | -993.68/-995.29 | -1701.8 | |
| 19 | -766.6 | -926.73/-933.99 | -1631.0 (4,0,1) | |
| 20 | -734.7 | -903.34/-905.76 | -1584.5 | |
| 21 | -674.5 | -821.07/-831.56 | -1521.1 | |
| 22 | -639.2 | -1449.2 | ||
| ... | ... | |||
| 34 | -16.0 | -897.2 | ||
| ... | ... | |||
| 70 | -7.0 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





