Experimental Evidence of High Renewable Energy Employing a Symmetric Circuit with a Divergent Current Density

1. Introduction

The depletion of fossil fuels such as crude oil and natural gas has created societal energy problems. Moreover, the limited availability of high-cost crude oil has caused economic problems. To mitigate these concerns, countries are attempting to introduce renewable energies [1–6], but such alternatives cannot (in most cases) satisfy 100% of the demand. Moreover, most renewable energies fluctuate with natural climate variations, complicating the system, planning, and control methods [7]. The most promising of the existing renewable energies are solar and wind power [8,9] but they require high costs as will be described. Furthermore, fossil fuel consumption is a cause of rising CO₂ concentration [10,11]. The spread of renewable energy sources must be considered from both economic and technological perspectives. Highly efficient, low-cost energy generation is of major importance [12,13].

To reduce the atmospheric CO₂ concentration, existing renewable energy sources such as solar and wind power must be widely adopted. However, the integration of renewable energy into the existing power systems risks frequency and voltage disruptions. Moreover, effective performance from the existing energy sources requires many expensive storage batteries.

Japan has declared a goal of net-zero carbon by 2050, but simulations [14,15] have shown that meeting this goal might be impossible without breakthrough technologies.

The main problems with the existing renewable energy and nuclear power generation are summarized below.

1)

Renewable energy sources depend on the weather, necessitating large and expensive storage batteries. Moreover, introducing renewable energy sources to the existing energy systems will destabilize the outputs.

2)

Simulations assessing the possibility of achieving net-zero carbon in Japan have included nuclear power generation [16] without considering its dangers. For instance, the Fukushima nuclear accident in Japan in 2011 caused extensive damage.

3)

Although the seriousness of fossil fuel use differs in different countries (e.g., Japan and the United Sates [17]), introducing renewable energy incurs high costs in all countries [16].

To solve the above problems, this paper proposes a new system for stable energy production meeting the demands of Japan, i.e., the required amount of energy in the right place at the right time. Moreover, our system is highly efficient with low costs.

Our previously proposed energy-generating system [18,19] could not generate sufficiently large amounts of energy, although they could provide stable energies. The present paper proposes a new concept for generating a large amount of renewable energy using a highly symmetric circuit with significantly low costs. When certain conditions are satisfied, the circuit provides an apparent divergent current with no Joule heating to both paired light-emitting diodes (LEDs) and paired direct current (DC) motors, boosting the electric power. This power-generation phenomenon is verified in both theory and experiments. We discuss the good agreement between the theory and experiments, and will describe whether the results satisfy the purpose and motivation of this study.

2. Materials and Methods

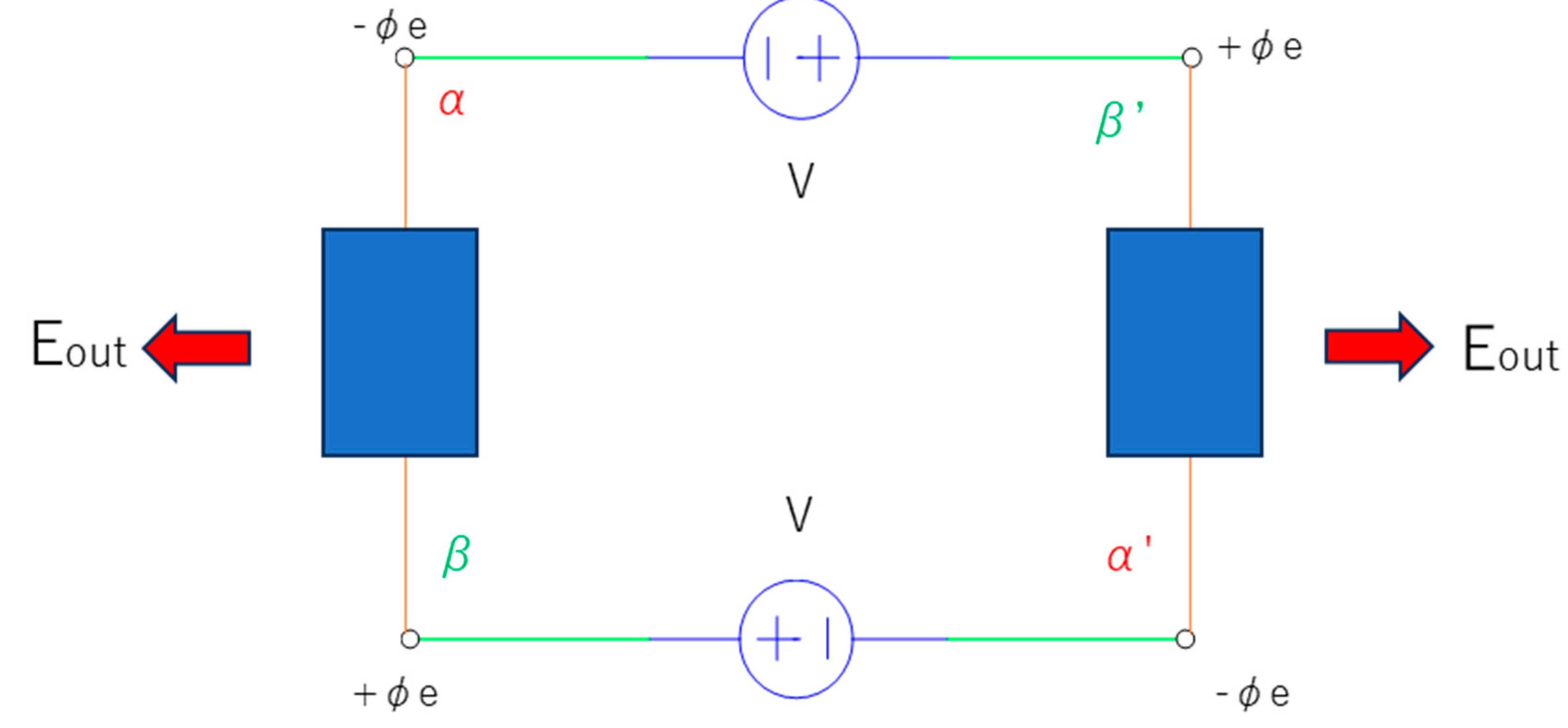
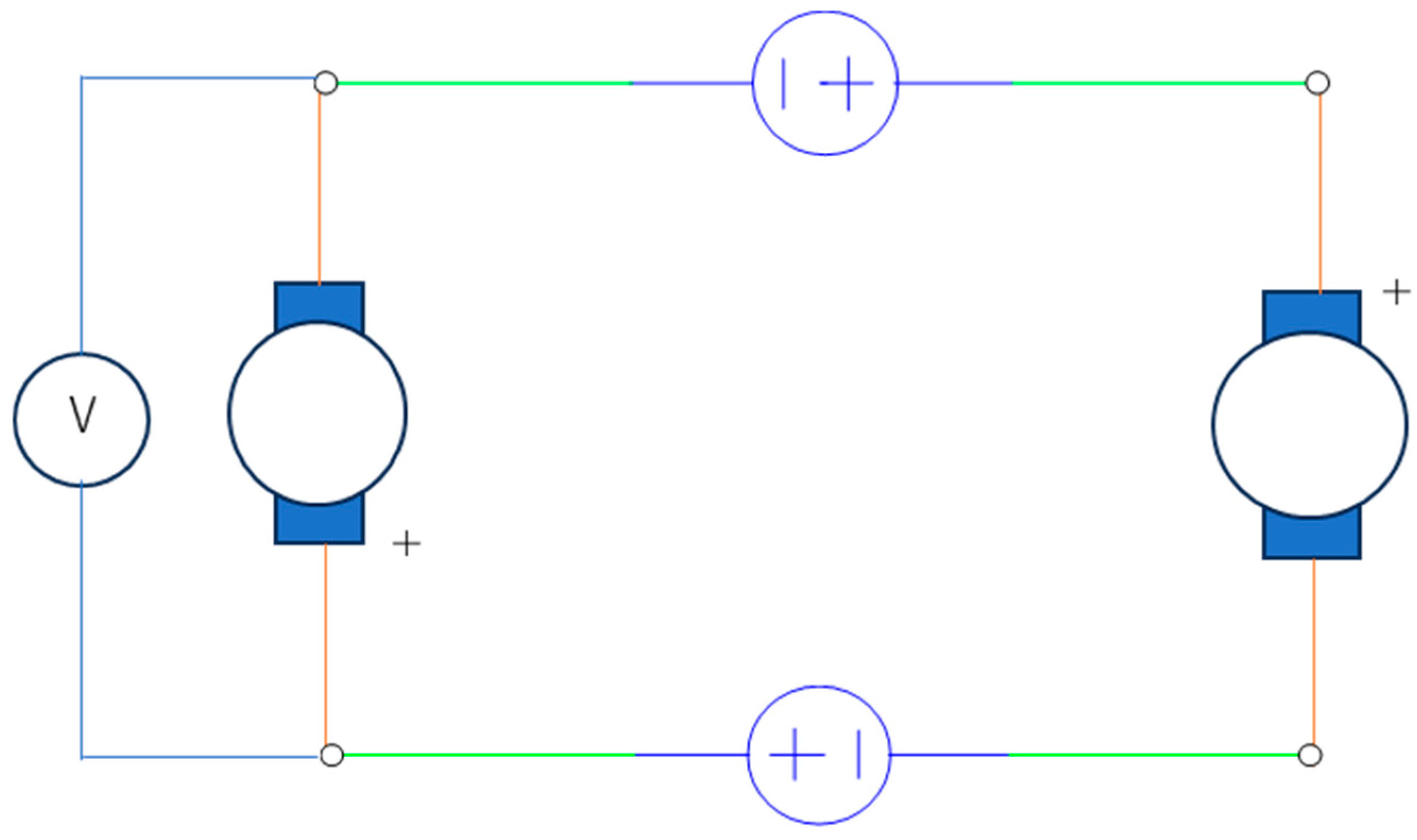
Figure 1 is a schematic of the presented model near its initial state. The circuit employs two same-output voltage sources V and two identical loads which are not pure electrical loads, as they must output an energy of E_out per electron. As shown in the figure, this circuit system is highly symmetric. The voltage (V) is expressed in terms of the electric potential (φ_e) as follows:

$$V\equiv {\phi }_e-\left(-{\phi }_e\right)=2{\phi }_e$$

(1)

Figure 1. Circuit configuration near the initial state, consisting of identical loads (blue blocks) that must output an energy of E_out per electron. Note that φ_e is the electric potential, and then α, β, α^’, and β^’ are taps. Moreover, V is the output of a voltage source.

Figure 1. Circuit configuration near the initial state, consisting of identical loads (blue blocks) that must output an energy of E_out per electron. Note that φ_e is the electric potential, and then α, β, α^’, and β^’ are taps. Moreover, V is the output of a voltage source.

Note that α, β, α^’ and β^’ in Figure 1 are the names of taps.

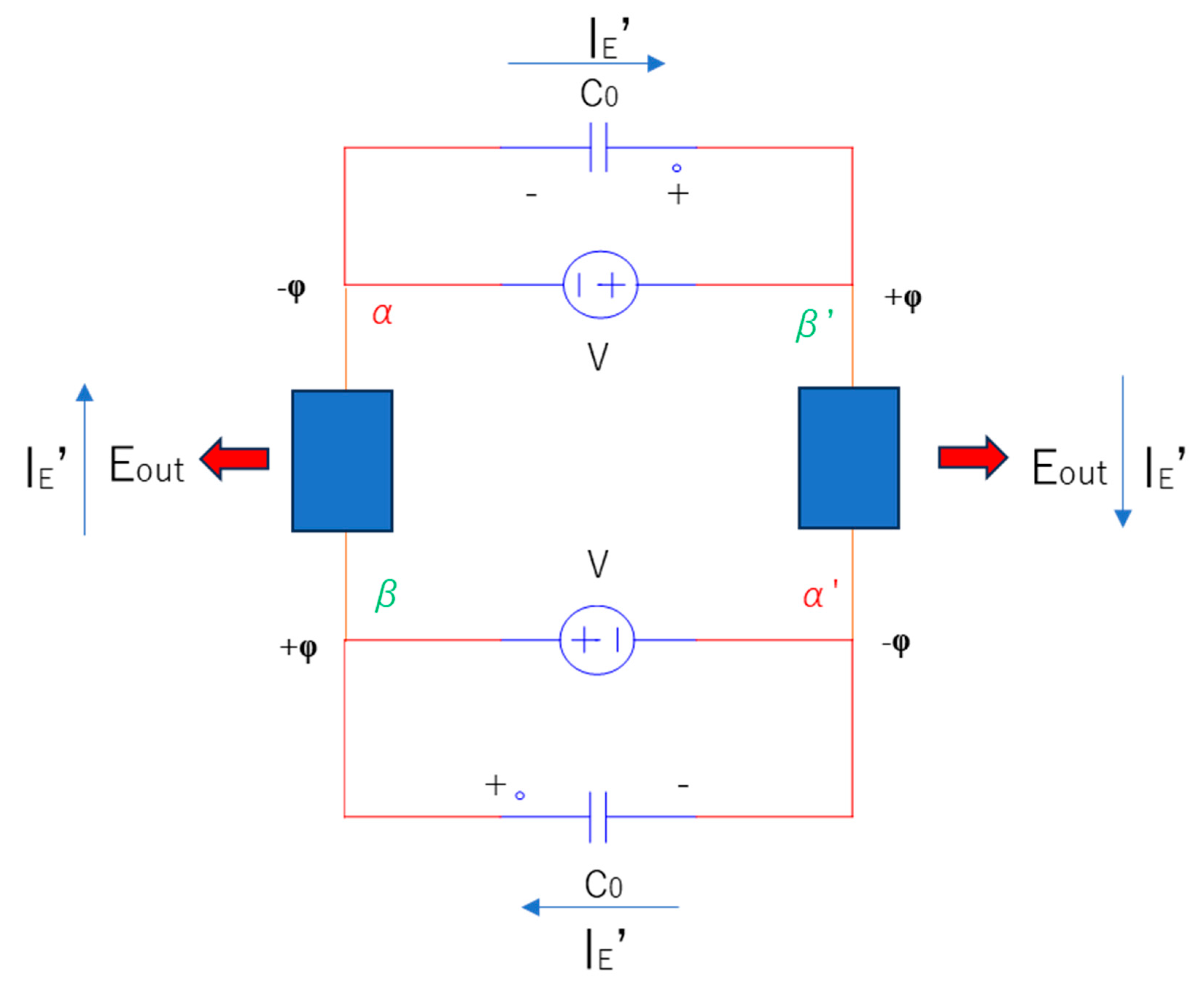
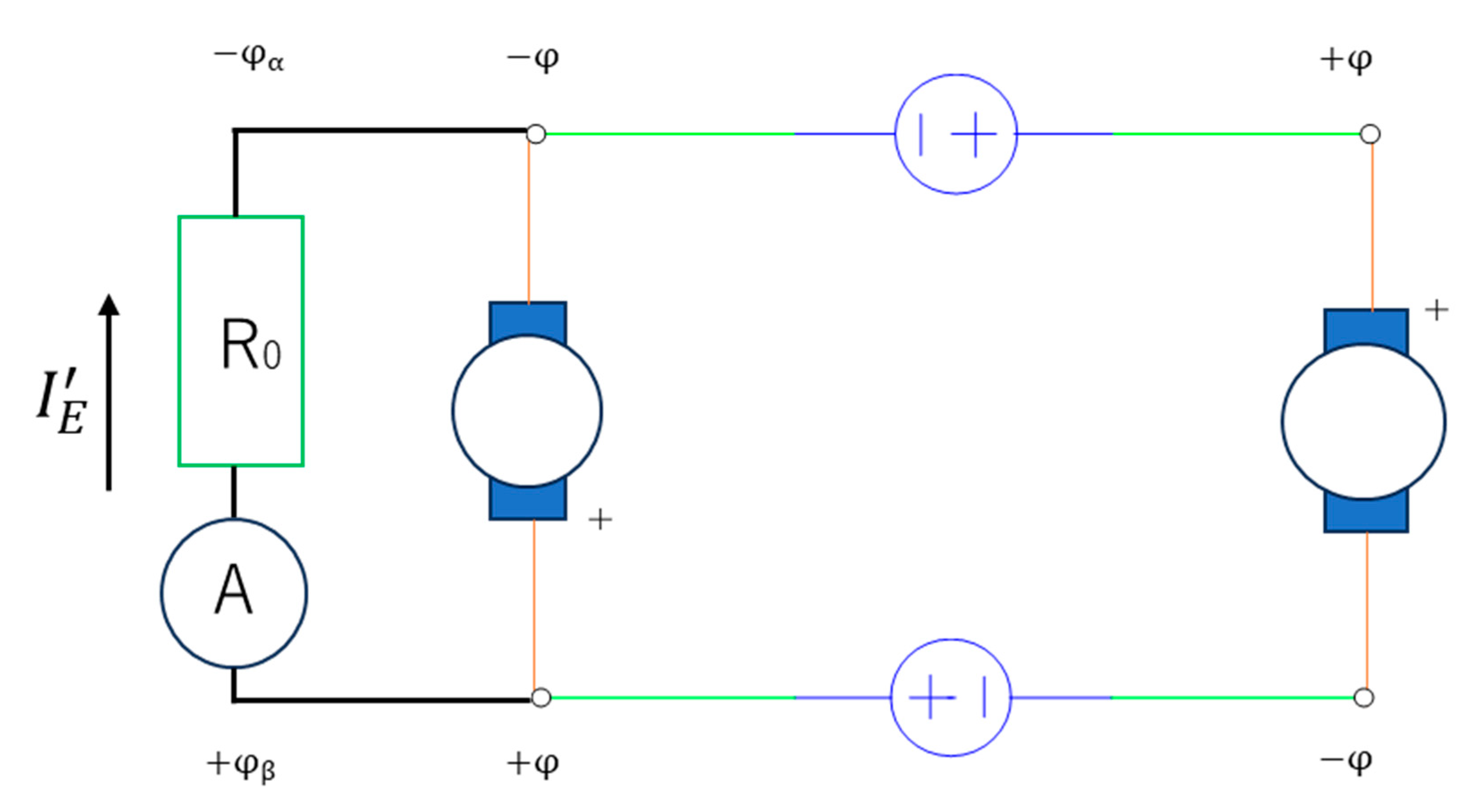
The principle of the model is shown in Figure 2, which (unlike Figure 1) includes a pair of stray capacitors C₀ embedded in a vacuum. At initial time t = 0, the stray condensers C₀ are shorted. (Note that a condenser is generally shorted at the initial state due to its voltage–current characteristic.) Moreover, completely at t=0, the loads do not output the energies due to no current because the stary condenser C₀ are shorted and thus at t=0, all the currents in the system are distributed to the stray condenser C_0. At some transition time t = t_c, which is essentially equal to the time constant (${\tau }_{CR}$) (i.e., the product of the capacitance (C₀) and load resistance (R) of the load), there is a transient current (i) in the loads and an emergent electric potential (φ) defined as follows:

$$E_{out}=2e\phi$$

(2)

where e is the electron charge.

Figure 2. Schematic at the transition time t_c with stray capacitors C₀. The paired condensers repetitively store and discharge energy, generating a constant current $I_E^{\mathrm{\text{'}}}$

Figure 2. Schematic at the transition time t_c with stray capacitors C₀. The paired condensers repetitively store and discharge energy, generating a constant current $I_E^{\mathrm{\text{'}}}$

. The voltage sources V in this state are dead apart from momentary activity near the initial state. Note that α, β, α^’, and β^’ are taps. Moreover, E_out is the output energy per electron from a load.

At time (t_c), considering the above definition of the emergent electric potential (φ), the following condition must be satisfied:

$$2\times {\displaystyle \frac{1}{2}}{C}_0{\left(2\phi \right)}^2>R{i}^2{t}_c$$

(3)

The right-hand side of this inequality indirectly defines the energy of the voltage source V, which essentially equals to the Joule heating. The coefficient “2” in the left-side implies that there are two condensers. Note that, the resistance (R) is the net one including the loads, lead and contact resistances. Thus, for an electron, we can rewrite the condition (3) as:

$$\left|e\phi \right|>{\displaystyle \frac{1}{2}}{k}_{B}T$$

(4)

where k_B and T denote the Boltzmann constant and temperature, respectively. Note that both the sides of inequality (4) imply the avarage energy of an electron.The left-side implies a work which an electron receives from the condenser. In most situations, the temperature is the room temperature (i.e.$,T\approx 300\left[K\right]$) but inequality (4) implies that Joule heating is ineffective.

As discussed later, the term $\left(e\phi \right)$ equals the kinetic energy.

When the above condition is satisfied, the energies stored in the condensers are discharged, because the energy balance between the condenser C₀ and the voltage source V breaks. Under the energy-conservation law, energy interchange between the paired up-condenser and down-condenser in Figure 2 induces a constant current (I_E^’) along the C₀-load-to-C₀-load loop. Because the condensers C₀ are embedded in a vacuum and cannot be touched, a divergent current (I_E^’) is generated. Note that if the inequality is not satisfied, the condensers never discharge their current but if the inequality is satisfied, the voltage sources V momentary operate until the condensers begin discharging at time (t_c) and are dormant thereafter, thereby generating energy.

We now discuss the emergent electric potential (φ)after steady-state, $t\ge t_c$In the vicinity of tap α or β at t = t_c, we have:

$$d{\phi }_e\equiv \overrightarrow{E_e}\times d\overrightarrow{s}$$

(5)

And

$$d{\phi }_{c0}\equiv \overrightarrow{E_{c0}}\times d\overrightarrow{s}$$

(6)

where E_e and E_c0 denote the ohmic and condenser-associated electric fields, respectively.

Note that the vector (ds) aligns along the direction of (I_E^’).

Given that the condenser discharges the current at this time, we have:

$$d{\phi }_{c0}=-E_{c0}ds$$

(7)

Moreover,

$${\phi }_e=E_{e}ds$$

(8)

However, in the vicinity of a tap, because ${\phi }_e={\phi }_{c0}$, we have:

$$d{\phi }_e=d{\phi }_{c0}$$

(9)

giving rise to

$$E_e=E_{c0}=0$$

(10)

This equation implies that the ohmic voltage is ineffective. The volatge of the condenser is updated because of the existence of the left energy of the condition (3). The electric potential is defined as:

$$2e\phi \equiv E_{out}$$

(11)

with

$$\left|\phi \right|>\left|{\phi }_e\right|$$

(12)

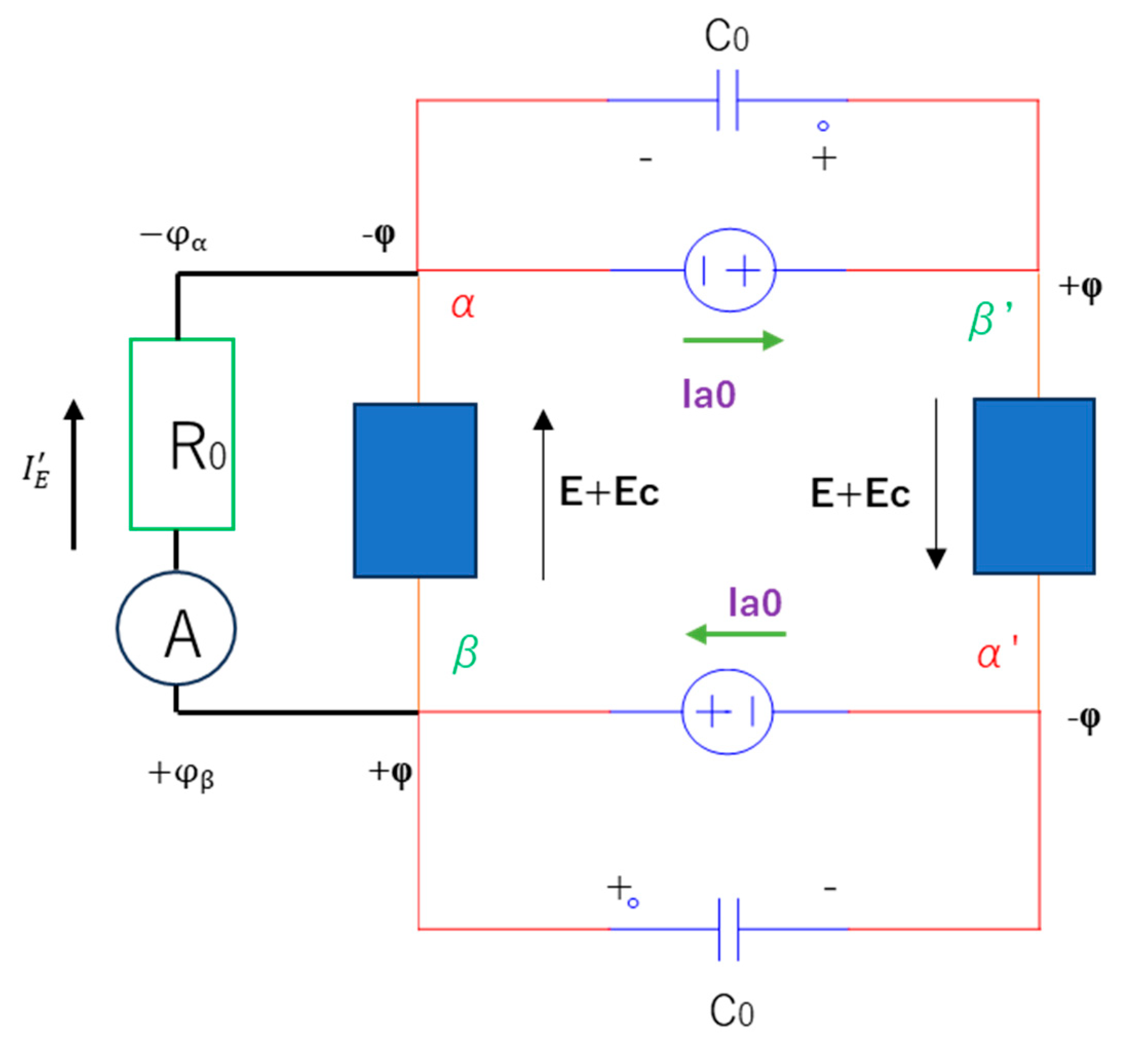
This emergent electric potential (φ) is demonstrated in Figure 3. Note that the electric potential (φ) is not ohmic but a new electric potential of the stray condenser during time $t\ge t_c$Let us introduce wave function contributing to the electron motion.

The general form of the Hamiltonian is:

$$H_{total}\equiv H_G+H_{eff}$$

(13)

where the first and second terms describe the center-of-mass motion and the net electron–electron interaction, respectively. As will be discussed soon, the following assumption holds:

$$H_G\gg H_{eff}$$

(14)

Moerover, as will be described, assuming that the scalar $\left|e\phi \right|$ is distributed along x-axis and provides the center-of- mass motion that is equal to the kinetic energy, this scalar results in a relatively large kinetic energy. Thus, the rest momenta along the other dimentions can be neglected. The reason why $\left|e\phi \right|$ results in the center-of-mass motion is that it is a constant and does not depend on relative ordinates. Therefore, one-dimension motion is allowed. Then, let us consider reason of the formation of the approxiamtion (14). We can assume a uniform electrical potential (φ) at tap α or β, implying that each electron has approximately the same electrical potential (φ) because whether the potential (φ) is macroscopic or microscopic cannot be discerned. This implies that, as (φ) cannot coexist with a Coulomb interaction potential (φ_M), the Hamiltonian (H_eff) is sufficiently small. Note that the satisfaction of the condition (4) implies no Joule heating and thus we do not need to consider many electrons’ interaction. That is, one-particle picutre is allowed. Moreover, the condition (4) also implies that an electron penetrates lattices. Thus, the electron receives no external forces.

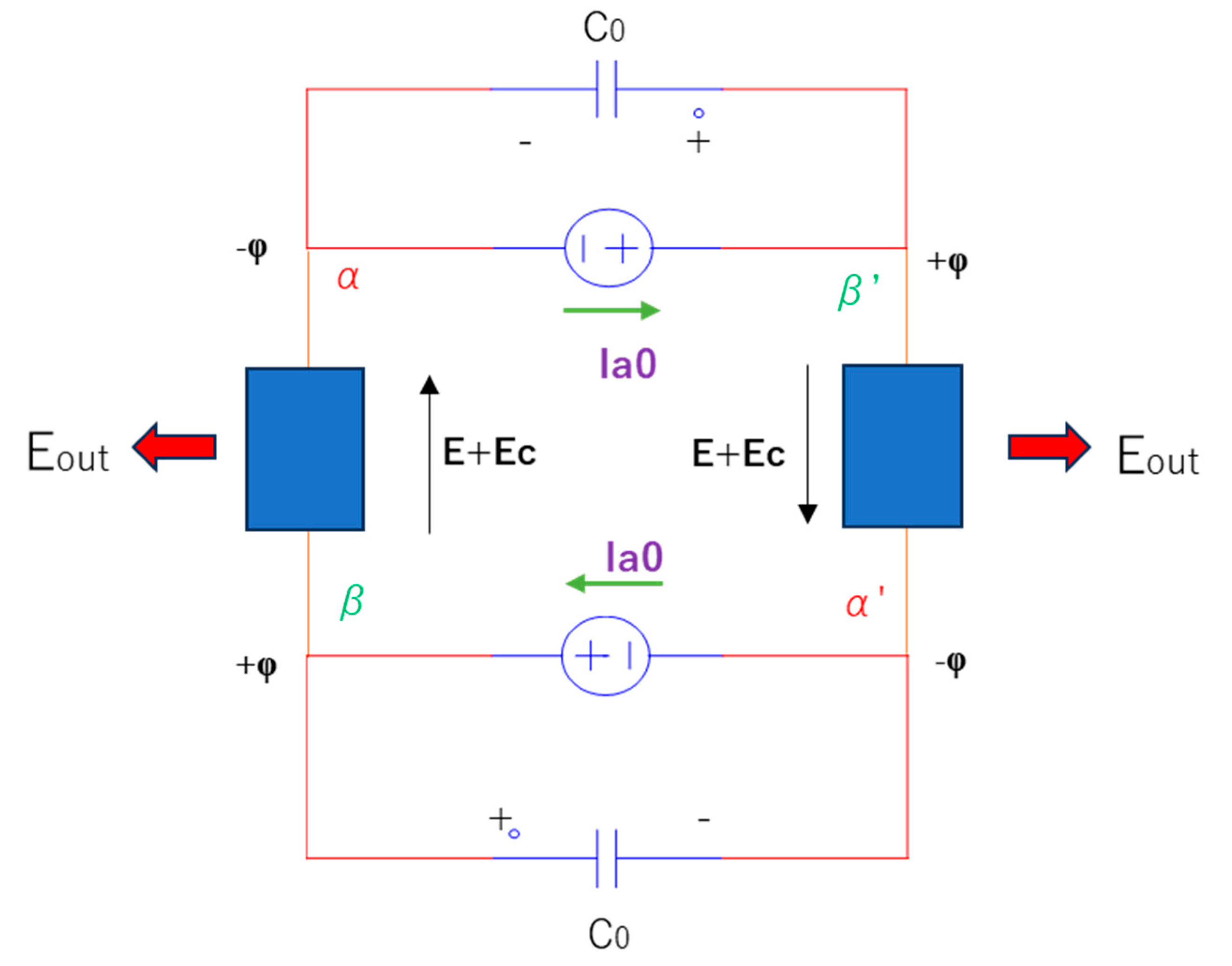
Figure 3. Schematic showing the distribution of the emergent electric potential φ associated with the output energy E_out. The voltage sources $V=2{\phi }_e$ steadily decay.

Figure 3. Schematic showing the distribution of the emergent electric potential φ associated with the output energy E_out. The voltage sources $V=2{\phi }_e$ steadily decay.

The Hamiltonians at tap α are:

$$-{\displaystyle \frac{{ħ}^2}{2m}}{\displaystyle \frac{d^2}{d{x}^2}}+\left(+e\phi \right)\equiv H_{\alpha \uparrow }+H_{\alpha \downarrow }$$

(15)

, 

where m, $H_{\alpha \uparrow }$, and $H_{\alpha \downarrow }$denote the mass of an electron, the Hamiltonian of up-spin electron, and the Hamiltonian of down-spin electron, respectively. Note that, due to the symmetry, the Hamiltonians of tap α^’ are the same forms as those of tap α, Eq. (15). Moreover, as discussed, each Hamiltonian essentially implies one-particle picture.

The exclusion prenciple claims that the energies of up- and down-spin electrons are the same.

Therefore, we consider degeneracies here.

$${\displaystyle \frac{{ħ}^2{k}_{\alpha }^2}{2m}}\equiv \left|+e\phi \right|$$

(16)

where k is the wavenumber.

Thus,

$$k_{\alpha }=\pm {\displaystyle \frac{\sqrt{2me\phi }}{ħ}}$$

(17)

Thus, the wavefunctions with each spin are

$${\psi }_{\alpha \uparrow }=\left|\psi \right|\exp \left(j{\displaystyle \frac{\sqrt{2me\phi }}{ħ}}x\right)\mathrm{and}{\psi }_{\alpha \downarrow }=\delta \left(x\right)$$

(18)

Note that we employed a delta function as the egenfunction of the position.

For the case of tap α^’ we alter the correspondence of the first and second terms of Eq. (15).

$${\psi }_{{\alpha }^{\text{'}}\downarrow }=\left|\psi \right|\exp \left(-j{\displaystyle \frac{\sqrt{2me\phi }}{ħ}}x\right)\mathrm{and}{\psi }_{{\alpha }^{\text{'}}\uparrow }=\delta \left(x\right).$$

(19)

Note that (j) is the imaginary unit. Similarly to tap α, tap β satisfies the following Hamiltonians:

$$-{\displaystyle \frac{{ħ}^2}{2m}}{\displaystyle \frac{d^2}{d{x}^2}}+\left(-e\phi \right)\equiv H_{\beta \downarrow }+H_{\beta \uparrow }$$

(20)

From the exclusion principle,

$${\displaystyle \frac{{ħ}^2{k}_{\beta }^2}{2m}}\equiv \left|-e\phi \right|$$

(21)

Where

$$k_{\beta }=\mp {\displaystyle \frac{\sqrt{2me\phi }}{ħ}}.$$

(22)

The wave functions of β is:

$${\psi }_{\beta \downarrow }=\left|\psi \right|\exp \left(j{\displaystyle \frac{\sqrt{2me\phi }}{ħ}}x\right)\mathrm{and}{\psi }_{\beta \uparrow }=\delta \left(x\right).$$

(23)

For the case of tap β^’, we alter the correspondence of the first and second terms of Eq. (20):

$${\psi }_{{\beta }^{\text{'}}\uparrow }=\left|\psi \right|\exp \left(-j{\displaystyle \frac{\sqrt{2me\phi }}{ħ}}x\right)\mathrm{and}{\psi }_{{\beta }^{\text{'}}\downarrow }=\delta \left(x\right).$$

(24)

The Slater determinant:

$${\psi }_E\equiv {\displaystyle \frac{1}{\sqrt{2}}}\left({\psi }_{\alpha \uparrow }{\psi }_{\beta \downarrow }-{\psi }_{\alpha \downarrow }{\psi }_{\beta \uparrow }\right)+{\displaystyle \frac{1}{\sqrt{2}}}\left({\psi }_{{\alpha }^{\text{'}}\uparrow }{\psi }_{{\beta }^{\text{'}}\downarrow }-{\psi }_{{\alpha }^{\text{'}}\downarrow }{\psi }_{{\beta }^{\text{'}}\uparrow }\right)$$

(25)

In the above equation, the delta functions are substitued.

$${\psi }_E={\displaystyle \frac{1}{\sqrt{2}}}({\psi }_{\alpha \uparrow }{\psi }_{\beta \downarrow }-{\psi }_{{\alpha }^{\text{'}}\downarrow }{\psi }_{{\beta }^{\text{'}}\uparrow })$$

(26)

Thus,

$${\psi }_E={\displaystyle \frac{1}{\sqrt{2}}}{\left|\psi \right|}^2\{\exp \left(j{\displaystyle \frac{2\sqrt{2me\phi }}{ħ}}x\right)-\exp \left(-j{\displaystyle \frac{2\sqrt{2me\phi }}{ħ}}x\right)\}.$$

(27)

The first and second terms of the above equation correspond to the left and right sides of the circuit in Figure 3, respectively. The first and second terms are considered to be related through the Einstein–Podolosky–Rosen correlation [20].

Here, we consider only the first term of Eq. (27).

The uncertainty relation gives

$$∆p∆x\approx {\displaystyle \frac{1}{2}}ħ.$$

Because the momentum (p) is constant as ($ħk)$, the uncertainty $(∆x)$ becomes infinite, defying the classical physical motion of an electron from one tap to the other. The wavefunction of the left part of the circuit is:

$${\psi }_L\equiv \left|{\psi }_L\right|\mathrm{e}\mathrm{x}\mathrm{p}\left[j{\displaystyle \frac{2\sqrt{2me\phi }}{ħ}}x\right].$$

(28)

The probability density (j_E) of the flow:

$$j_E={\displaystyle \frac{ħ}{2mj}}({\psi }_L^{*}{\displaystyle \frac{d{\psi }_L}{dx}}-{\psi }_L{\displaystyle \frac{d{\psi }_L^{*}}{dx}})$$

(29)

is solved as:

$$j_E={\displaystyle \frac{ħ}{2m}}{\displaystyle \frac{4\sqrt{2me\phi }}{ħ}}{\left|{\psi }_L\right|}^2$$

(30)

Herein, we separately consider paired LEDs or paired DC motors as the loads.

DC motor loads

From the normalization condition:

$$\int {\left|{\psi }_L\right|}^{2}dv\equiv 1$$

(31)

we have

$${\left|{\psi }_L\right|}^2{\lambda }^3=1,$$

(32)

where λ is the wavelength of an electron.

The wavenumber (k) is defined as:

$$k\equiv {\displaystyle \frac{1}{\lambda }}$$

(33)

Thus,

$${\left|{\psi }_L\right|}^2\approx k^3$$

(34)

The wavenumber is also derived as:

$$k={\displaystyle \frac{2\sqrt{2me\phi }}{ħ}},$$

(35)

from which the flow probability density (j_E) is obtained as:

$$j_E={\displaystyle \frac{4\sqrt{2me\phi }}{2m}}({{\displaystyle \frac{2\sqrt{2me\phi }}{ħ}})}^3$$

(36)

That is,

$$j_E={\displaystyle \frac{64m^2{e}^2}{m{ħ}^3}}{\phi }^2$$

(37)

To obtain the net current density [A/m²], we multiply Eq. (37) by the electronic charge (e):

$$j_{E=}^{\text{'}}{\displaystyle \frac{64m{e}^3}{{ħ}^3}}{\phi }^2\approx 2\times {10}^{17}{\phi }^2$$

(38)

Here, the area (S_i) is considered as a unit cell; for example,

$$S_i\cong {(1.5\times {10}^{-9})}^2{m}^2$$

(39)

Importantly, the net observed current ${(I}_E^{\text{'}})$ is then derived as:

$$I_E^{\text{'}}\approx 0.45{\phi }^2\left[A\right]$$

(40)

LED loads

Under the normalization condition:

$$\int {\left|{\psi }_L\right|}^{2}dv\equiv 1$$

(41)

we again have:

$${\left|{\psi }_L\right|}^2{\lambda }^3=1$$

(42)

but here we consider the momentum (k_L) of a photon with wavenumber [21]:

$$k_L={\displaystyle \frac{2\pi }{\lambda }}$$

(43)

The photon imparts its momentum to an electron and hole and thus the wave number of a carrier becomes a half of Eq. (43), considering the conservation of the momentum.

$${\left|{\psi }_L\right|}^2={\displaystyle \frac{1}{{\pi }^3}}{k}^3$$

(44)

And

$$j_E={\displaystyle \frac{4\sqrt{2me\phi }}{2m}}({{\displaystyle \frac{2\sqrt{2me\phi }}{ħ}})}^3{\displaystyle \frac{1}{{\pi }^3}}={\displaystyle \frac{64m^2{e}^2}{m{ħ}^3}}{\displaystyle \frac{1}{{\pi }^3}}{\phi }^2$$

(45)

Similarly to the DC motor, the LED loads obtain a net current density of:

$$j_E^{\text{'}}={\displaystyle \frac{64m{e}^3}{{ħ}^3}}{\displaystyle \frac{1}{{\pi }^3}}{\phi }^2\approx 6.4\times {10}^{15}{\phi }^2[A/m^2]$$

(46)

As the net current is contributed by an electron and a hole, we have:

$$j_{E,net}^{\text{'}}\approx 2\times j_E^{\text{'}}=1.3\times {10}^{16}{\phi }^2[A/m^2]$$

(47)

Within the area (S_i) of a unit cell, e.g.,

$$S_i\cong {(1.8\times {10}^{-9})}^2{m}^2$$

(48)

the net current is

$$I_E^{\text{'}}\approx 0.04{\phi }^2\left[A\right]$$

(49)

Next, the DC-motor loads must satisfy two conditions. Let us consider these conditions:

The general motion equation of a motor is [22] as follows:

$$V_a=R_a{I}_a+L{\displaystyle \frac{d{I}_a}{dt}}+E$$

(50)

where R_a [Ω], I_a [A], L [H], and E [V] denote the inner resistance, working current, inductance, and reverse electromotive force, respectively.

Let us first obtain the general solution from Eq. (50). To obtain this solution, setting the nonhomogeneous term ${(V}_a-E)$to zero, the general solution is immediately obtained as:

$$I_a=I_a\left(0\right)\exp (-{\displaystyle \frac{R_a}{L}}t).$$

(51)

At completely t = 0 when all currents flow into the condensers C₀ in our system, the initial current in the motor is zero; that is:

$$I_a\left(0\right)\equiv 0$$

(52)

Moreover, the special solution of Eq. (50) is derived by:

$$I_a\equiv A=const$$

(53)

Thus, by the substitution to Eq. (50),

$$A={\displaystyle \frac{V_a-E}{R_a}}$$

(54)

and thus the net solution, i.e., the sum of the general solution and the special solution, is:

$$I_a=I_a\left(0\right)\exp \left(-{\displaystyle \frac{R_a}{L}}t\right)+{\displaystyle \frac{V_a-E}{R_a}}=0+{\displaystyle \frac{V_a-E}{R_a}}.$$

(55)

The transient equation of the motors in our system is then given by:

$$V_a=R_a{I}_a+E$$

(56)

Where

$$\left|E\right|\equiv k_E{\Omega }_m$$

(57)

In this equation, the proportionality constant (k_E) depends on the magnetic flux, and (Ω_m) is the rotational velocity.

The current (I_a) is considered as the constant current under zero load (I_a0).

Under the working condition:

$$E_{out}>k_{B}T$$

(58)

of our system,

importantly, the motor must satisfy:

$$R_a{I}_{a0}<k_E{\Omega }_{m0}$$

(59)

where Ω_m0 is the speed under zero load.

We now derive the second mandatory condition of the motors. To this end, we discuss the voltages of the motor. At $t=t_c$, because the voltages of the condenser C₀ and voltage source V are canceled, the net input voltage $V_a=2{\phi }_e\equiv 0$ (see Eq. (10)). From Eq. (56), we then have:

$$E\equiv E_c=-R_a{I}_{a0}$$

(60)

meaning that (I_a0) is an induced loop current not induced by the voltage source. That is, this equation garantees that the induced current is (I_a0). As will be mentioned, the above voltage in a motor induces this current to the other motor. This implies that the corresponding energy in Eq. (60) in a motor becomes the input in the other motor.

When the induced current starts to be discharged by the inductor L, as a generator,

$$V_a\equiv V_c=E<0$$

(61)

where V_c is the discharging voltage of the inductor L. Note that, as a generator, (V_a) alternatively becomes the output voltage. As described, unlike Eq. (60), Eq. (61) considers the input. This is related to the existence of the paired motors.

As will be mentioned, the above equation (61) neglects the Joule heating term of Eq. (56). As a result, the motor voltage becomes the superposition of (E_c) and (E), as shown in Figure 4. Thus, the net energy of an electron is (i.e., the updated condenser voltage):

$$E_{eff}\equiv e\left|E+E_c\right|\equiv 2e\phi$$

(62)

To superpose the voltages of Eqs. (60) and (61), the time scale of them must be the same as (t_c),which is not contradictory to the next condition (63).

Let us consider the reason why the Joule heating is neglected. To form the above Eq. (62), i.e., the electric potentials (φ) are emerged, the motors must satisfy:

$$2\times {\displaystyle \frac{1}{2}}L{I}_{a0}^2>R{i}^2{t}_c$$

(63)

where R denotes the net resistance as described in the condition (3). Note that the current (i) of the right-side implies the ohmic current but it will decay when the condition (63) is met. Instead, the current (I_a0) appears, at $t=t_c$. Considering that Eq. (62) contains the voltage (2φ), which implies the voltages for both stray condenser C₀ and the inductor L, the condition (63) must be compatible with condition (3). See Figure 4. That is, the right-sides of both conditions are indirectly equal to that of the voltage source V, and both the energies of the stray condenser and the inductor must dominate over the energy of the voltage source V. Moreover, because the motors are paired in our system, they reciprocally provide and receive energy. Provided that the second condition above is satisfied, the Joule heating term is absent and the motor receives a relatively large input voltage near the initial state, as discussed in the Results section. Moreover, we will show that because the voltage of a motor is:

$$E_{eff}/e\equiv \left|E+E_c\right|\equiv 2\phi >V=2{\phi }_e$$

(64)

implying that the voltage sources V are nonoperational, the loop current (I_a0) is conserved steadily.

The macroscopic current (I_a0) can coexist with the microscopic current ${(I}_E^{\text{'}})$ in the load but the two currents are not superposed, so an additive current does not appear. Thus, if a current meter is connected in series with a motor, it records either the current (I_a0) or the current $\left(I_E^{\text{'}}\right)$ at each moment, presenting widely fluctuating currents to the experimental observer. Accordingly, we set a detour for the current $\left(I_E^{\text{'}}\right)$ in the system with paired DC motors (Figure 5). In the Results section, we will discuss the importance of:

$$I_E^{\text{'}}\gg I_{a0}$$

(65)

Here, let us introduce the output electric power (W_R0). The incremental value in the right-side motor in Figure 5 is

$${dW}^{\text{'}}\equiv I_E^{\text{'}}\left(0\right)\times 2d\phi$$

(66)

Where

$$I_E^{\text{'}}\left(0\right)\equiv 0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2=const.$$

(67)

Considering the symmetry in Figure 5, i.e., because the voltage ($2d\phi$) in the right-side motor is eccentially equal to that of the left-side motor_, Eq. (66) must equal to the incremental electric power (dW) in the left side motor.

Generally, we have, in the resistence and in the left motor of Figure 5,

$$2d{\phi }_{\alpha ,\beta }=R_{0}d{I}_E^{\text{'}}\mathrm{and}d{\phi }_{\alpha ,\beta }\equiv pd\phi$$

(68)

That is,

$$2d\phi ={\displaystyle \frac{R_0}{p}}d{I}_E^{\text{'}}$$

where p is the propotional constant. The reason to introduce this constant will be discussed in the Discussion section. Eqs. (68) and (68-2) imply the current $I_E^{\text{'}}$ is common to the left motor and the resistance. Considering Eq. (66),

$$dW=I_E^{\text{'}}\left(0\right){\displaystyle \frac{R_0}{p}}d{I}_E^{\text{'}}$$

(69)

Given $I_E^{\text{'}}=0.45{\phi }^2$of the left-side motor, we obtain

$$dW=I_E^{\text{'}}\left(0\right){\displaystyle \frac{R_0}{p}}\times d\left(0.45{\phi }^2\right)=0.45I_E^{\text{'}}\left(0\right){\displaystyle \frac{R_0}{p}}\times 2\phi d\phi$$

(70)

Figure 5. Harvesting of the divergent current $I_E^{\mathrm{\text{'}}}$ in the system with DC motor loads. The macroscopic current $I_{a0}$ interferes with the microscopic current $I_E^{\mathrm{\text{'}}}$, necessitating a detour. As described in the main body, it can be interpreted that the current $I_E^{\mathrm{\text{'}}}\left(0\right)$ in the left-side motor alternatively chooses the detour: The emergent electric potential $\left|\phi \right|=\left|{\displaystyle \frac{E+E_c}{2}}\right|=const.$ provides a constant current $I_E^{\mathrm{\text{'}}}=0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2,which$is independent of the resistance $R_0.$ Therefore, a large resistance (for example, 1.0 MΩ) allows the current flow. For the same reason, this equation is not an ohmic equation so Joule heating is absent. Note that $\left|{\phi }_{\alpha ,\beta }\right|$ will be described in the Discussion section.

Figure 5. Harvesting of the divergent current $I_E^{\mathrm{\text{'}}}$ in the system with DC motor loads. The macroscopic current $I_{a0}$ interferes with the microscopic current $I_E^{\mathrm{\text{'}}}$, necessitating a detour. As described in the main body, it can be interpreted that the current $I_E^{\mathrm{\text{'}}}\left(0\right)$ in the left-side motor alternatively chooses the detour: The emergent electric potential $\left|\phi \right|=\left|{\displaystyle \frac{E+E_c}{2}}\right|=const.$ provides a constant current $I_E^{\mathrm{\text{'}}}=0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2,which$is independent of the resistance $R_0.$ Therefore, a large resistance (for example, 1.0 MΩ) allows the current flow. For the same reason, this equation is not an ohmic equation so Joule heating is absent. Note that $\left|{\phi }_{\alpha ,\beta }\right|$ will be described in the Discussion section.

Integrating both sides of Eq. (70) gives

$$W_{R0}=0.45R_0{I}_E^{\text{'}}\left(0\right){\phi }^2\left[W\right]$$

(71)

where W_R0 is the electric power in the resistance (R₀), which was defined by $W_{R0}=pW$.

Provided that the conditions in our system are satisfied, Eq. (71) is not a Joule-heating expression.

The absence of Joule heating can be explained by the dead voltage sources, as frequently described in this paper. The voltage sources are only temporarily active in the vicinity of the initial time.

Note that, although the general current $I_E^{\text{'}}$ was considered and because this current is common to the resistance and the left motor that is, for the symmetry, equal to that of the right-side motor $I_E^{\text{'}}\left(0\right)$, the derivation that results in Eq. (71) makes us interpret that $I_E^{\text{'}}\left(0\right)$ in the left-side motor chooses the the path of the resistance (R₀) instead of the path of the left-side motor. Note that the current $I_E^{\text{'}}$ cannnot coexist simultaneously in both the left motor and the resistance because of the Kirchhoff’s current law.

3. Results

We first present the results of the paired-LED system with:

$$E_{out}\equiv 2e\phi$$

(72)

Or

$$E_{out}\equiv ħ\omega$$

(73)

where ω is the angular frequency. The divergent current is

$$I_E^{\text{'}}=0.04({{\displaystyle \frac{ħ\omega }{2e}})}^2$$

(74)

Given the approximate wavelength (λ) of a blue LED:

$$\lambda =460\left[\mathrm{nm}\right]$$

(75)

the angular frequency is calculated as:

$$\omega ={\displaystyle \frac{2\pi c}{\lambda }}\approx 4.1\times {10}^{15}[\mathrm{rad}/s]$$

(76)

Thus,

$$I_E^{\text{'}}=0.04{\phi }^2=0.04({{\displaystyle \frac{ħ\omega }{2e}})}^2\approx 0.04\times ({1.34)}^2\approx 71\left[\mathrm{mA}\right]$$

(78)

The voltage is

$$2\times 1.34=2.68$$

(79)

The above current and voltage are valid.

The results of the LED system are summarized in the following three figures: a schematic configuration of the circuit, a photograph of the initial experimental setup, and a photograph of the experimental result.

Figure 6. Schematic of divergent current $I_E^{\mathrm{\text{'}}}$ generation in the system with LED loads. As described in the main text, the divergent current $I_E^{\mathrm{\text{'}}}$ drives the LEDs and the voltage sources die at steady-state.

Figure 6. Schematic of divergent current $I_E^{\mathrm{\text{'}}}$ generation in the system with LED loads. As described in the main text, the divergent current $I_E^{\mathrm{\text{'}}}$ drives the LEDs and the voltage sources die at steady-state.

We now present the results of the paired motor system.

Figure 7. Photograph of our tester, included for the reasons given in the Discussion.

Figure 7. Photograph of our tester, included for the reasons given in the Discussion.

Figure 8. Photograph of the paired DC motors (MABUCHI motor RE-280RA), marked with black dots to confirm whether the motors rotate during the experiment.

Figure 8. Photograph of the paired DC motors (MABUCHI motor RE-280RA), marked with black dots to confirm whether the motors rotate during the experiment.

Table 1 lists the specifications of the employed DC motor, and Figure 7 and Figure 8 show a potable tester and the employed paired motors, respectively.

Figure 9 and Figure 10-1 present the three stages of the paired motor experiments: the circuit configurations, the preparations of the experiments, and the experimental results.

Figure 9. Schematic of the circuit for measuring an emergent electric potential. The voltage of the voltage source is compared with that of the DC motor, which implies the emergent electric potential.

Figure 9. Schematic of the circuit for measuring an emergent electric potential. The voltage of the voltage source is compared with that of the DC motor, which implies the emergent electric potential.

Figure 10. Schematic of the experiment for harvesting the current I_E^'. As in Figure 5, a detour avoids interference between the induced macroscopic current I_a0 and the microscopic current I_E^'. As the mathematical form of the current I_E^' (0) is independent of the load R_0 and differs from Ohm’s law, the current flows even when the load R_0 is large. For the same reason, the load resistance R_0 generates no Joule heating. Note that |φ_(α,β) | will be described in the Discussion section.

Figure 10. Schematic of the experiment for harvesting the current I_E^'. As in Figure 5, a detour avoids interference between the induced macroscopic current I_a0 and the microscopic current I_E^'. As the mathematical form of the current I_E^' (0) is independent of the load R_0 and differs from Ohm’s law, the current flows even when the load R_0 is large. For the same reason, the load resistance R_0 generates no Joule heating. Note that |φ_(α,β) | will be described in the Discussion section.

Figure 9-2. Experimental setup for measuring the emergent electric potential. The voltage sources are two stabilized power supplies, one with a red light display; the other with a blue display. The two DC motors are not rotating at this time, as evidenced by the stationary black dots. The emergent electric potential is measured by a voltmeter (foreground).

Table 2 compares the experimentally observed currents $I_E^{\text{'}}\left(0\right)$ with the theoretical currents determined as:

$$I_E^{\text{'}}\left(0\right)\equiv 0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2$$

(80)

where (E + E_c)/2 is the emergent electric potential (φ) with

$$\phi >{\phi }_e=V/2$$

(81)

As the emergent electric potential must not be significantly larger than the input electric potential (φ_e), we approximate

$$\left|{\displaystyle \frac{E+E_c}{2}}\right|\approx 1.2{\phi }_e$$

(82)

as a compromise. As shown, Table 2 confirms sufficient agreements between the experimental and theoretical values.

Table 3 lists the generated electric power (W_R0) for different input voltages (2φ_e)_. Note that, in this table, (φ) in Eq. (71) is again defined by Eq. (82).The values of Table 3 are sufficiently large, which are almost equal to those of nuclear power stations. This implies that the values of Table 3 have provided significant technical merits.

For comfirmation, we validate Eq. (71); that is:

$$W_{R0}=0.45R_0{I}_E^{\text{'}}\left(0\right){\phi }^2$$

(83)

in the paired motor system. The electric power of the LED is obtained simply by replacing coefficient 0.45 [A/V²] with 0.04 [A/V²] as:

$$W_{LED}=0.04R_0{I}_E^{\text{'}}\left(0\right){\phi }^2$$

(84)

Assuming

$$I_E^{\text{'}}\left(0\right)=71\left[\mathrm{mA}\right]$$

(85)

And

$$\phi =1.34$$

(86)

we obtain

$$R_0={\displaystyle \frac{2\times 1.34V}{71mA}}\approx 38[V\Omega$$

(87)

from which $W_{LED}$ is calculated as:

$$W_{LED}\approx 0.193[W\Omega$$

(88)

On the other hand, the direct electric power W’_LED is defined as simply

$$W_{LED}^{\text{'}}\equiv I_E^{\text{'}}\times 2\phi$$

(89)

Then we get:

$$W_{LED}^{\text{'}}\approx 0.190\left[W\right]$$

(90)

Thus

$$W_{LED}\approx W_{LED}^{\text{'}}$$

(91)

validating the expression of W_LED. Considering that Eq. (83) (i.e., Eq. (71)) differs only in the coefficient (i.e., $0.04\to 0.45$), it is allowed to mention that the above result (91) also validates Eq. (71).

based on the previous results.

listed in Table 2.

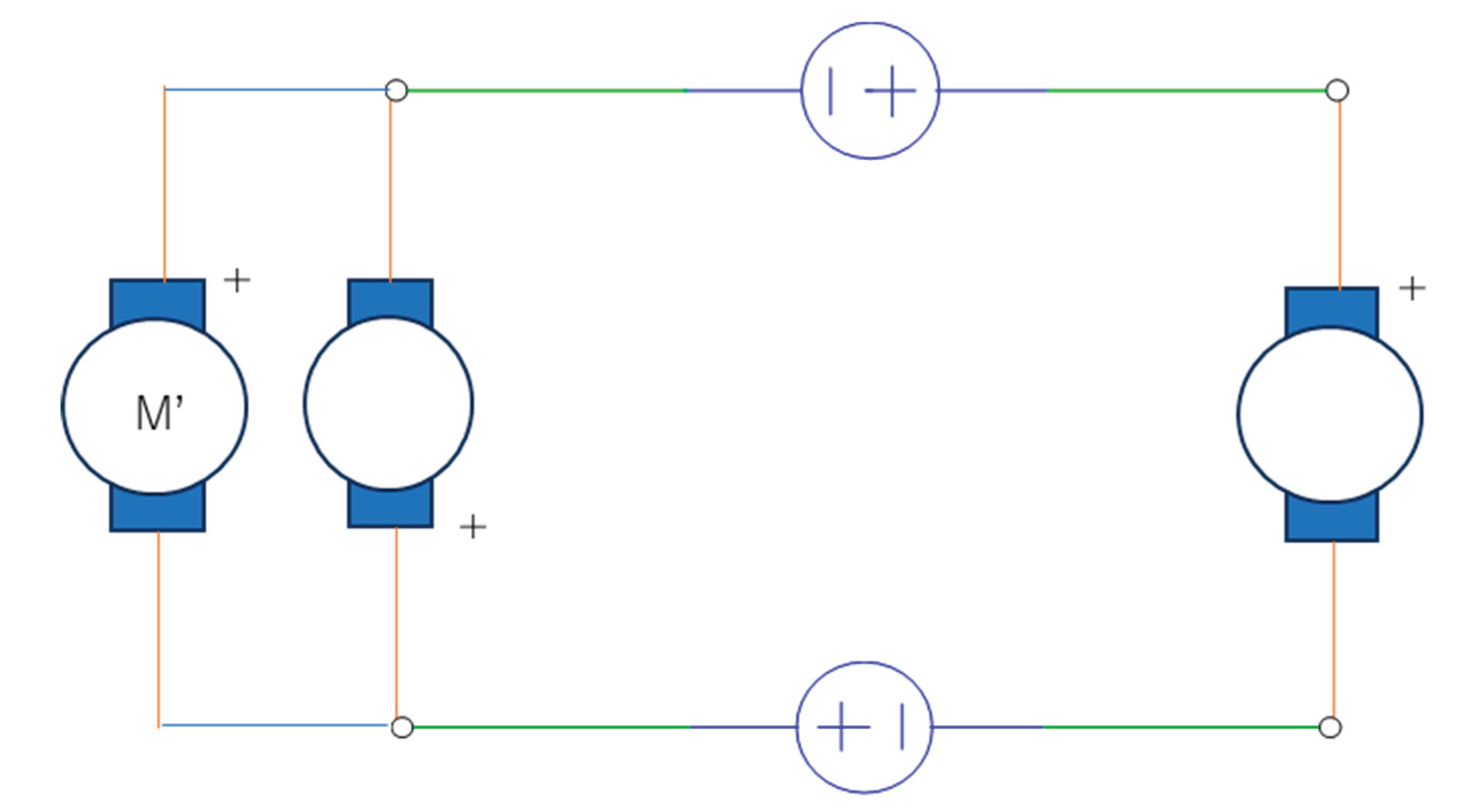
Figure 11 shows the circuit configuration when another motor is employed as the detour. The detour motor operated only when its polarity was reversed from that of the paired motors. In this configuration, the additional motor exchanged energy with the left member of the motor pair. The exchanged energy is:

$$U_M={\displaystyle \frac{1}{2}}L{I}_E^{\text{'}2},$$

(92)

where E [V] are exchanged among $\left(E+E_c\right)$ [V], because the voltage (E_c) indirectly implies the loop current (I_a0) and if the motor M’ included this voltage (E_c), its current would also be the same loop current (I_a0). This case would claim that the current through the left menber of the paired motors becomes zero, considering the Kirchhoff’s current law. However, acutal experiments show that the left motor of the paired motors is still rotating. Accordingly, the voltage that makes the motor M’ work is $E$[V].

4. Discussion

4.1. Why Can a Large Current Flow into the 1.0-MΩ Resistor?

A circuit containing a resistance (R) typically exhibits ohmic characteristics, meaning that its current depends on (R). However, in the present study,

$$I_E^{\text{'}}\left(0\right)\equiv 0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2=const$$

which is independent of the resistance (R), meaning that the current flows through any resistor. The large current flow through the 1.0-MΩ resistor is explained not only by this phenomenon, but also by the absence of Joule heating under the imposed conditional inequalities.

4.2. Condition and Selection of the Paired Motor

To ensure that the paired DC motors satisfy the conditional inequalities (59) and (63), we recommend motors with relatively large inductances. However, inductors with excessive inductance should be avoided because they increase the internal resistance. Therefore, the paired DC motors must be carefully selected. This paper employs the previously discussed MABUCHI motor RE-280RA [23]. A trial experiment using coreless motors as the paired DC motors failed to display the phenomenon described here, possibly because coreless motors with relatively small inductances cannot satisfy the requisite conditions (59) or (63).

4.3. Why Is a Relatively Large Resistance Needed When Harvesting the Current?

To answer this question, we revisit Eq. (80):

$$I_E^{\text{'}}\left(0\right)\equiv 0.45{\left({\displaystyle \frac{E+E_c}{2}}\right)}^2$$

, which implies that the voltage between taps α and β is $(E+E_c)$ [V]. When harvesting the current through a detour, the resistance (R₀) should be sufficiently large to satisfy (see Figure 10-1)

$$\left|{\phi }_{\alpha ,\beta }\right|\ge \left|{\displaystyle \frac{E+E_c}{2}}\right|$$

(93)

where the left-side are electric potentials at tap α or β as a result of the flow of the current $I_E^{\text{'}}\left(0\right)$ to the resistance (R₀). Note that, even when the condition (93) is met, the emergent electric potential $\left|\phi \right|$ at each tap remains as $\left|{\displaystyle \frac{E+E_c}{2}}\right|$, because the current $I_E^{\text{'}}\left(0\right)$ must be constant, not increase. The reason is that, considering that Eq. (57) is formed and that no Joule heating implies the zero load of a motor, the zero-load motor implies that the rotational speed (${\Omega }_m)$ is the maximum ${(\Omega }_{m0})$. Thus, the absolute value of the voltage (E) under zero load is the maximum value.Thus the voltage of a motor $\left|E+E_c\right|$ is conserved. Thus, the electric potentials $\left|{\phi }_{\alpha ,\beta }\right|$ are not superposed at each tap. Assuming another stray condenser C_0R parallel to both the sides of the paired motors, the stray condenser C_0R of the left-side retains the electric potentials $\left|{\phi }_{\alpha ,\beta }\right|$ by charging energy, consuming the time constant: At the transient state, the sum of the current (i_c) in the stray condenser C_0R and the current $\left(I_{E,t}^{\text{'}}\right)$ in the resistance (R₀) is equal to the constant current $I_E^{\text{'}}\left(0\right)$. First, the current $I_E^{\text{'}}\left(0\right)$ flows along the stray condenser C_0R but at the steady state this current flows through the resistance (R₀). Although the resultant $\left|{\phi }_{\alpha ,\beta }\right|$ appear, the electric potentials $\left|\phi \right|$ do not increase as described.

If the condition (93) is satisfied, the current $I_E^{\text{'}}\left(0\right)$ chooses the path along the detour instead of the path of the motor. This can be accepted by the fact that initially the motor inductor L generates magnetic field energy by the current $I_E^{\text{'}}\left(0\right)$ and thus to reduce this energy at most, the current $I_E^{\text{'}}\left(0\right)$ instead chooses the path of the resistance (R₀). To put it precisely, the current $I_E^{\text{'}}\left(0\right)$ chooses the shorted stray condenser C_0R. Note that, if this condition is not satisfied and because a discharged current occurs from the inductor L of the left motor to the resistance (R₀) due to a decrease in the absolute value of the voltgae (E), the current $I_E^{\text{'}}\left(0\right)$ forms a loop current along R₀-L and therefore this current decreases up to almost zero. To meet the condition (93), therefore, it is needed to employ a relatively large resistance as the detour.

When a current meter is placed along the detour, the electric potential at both the taps α and β should also satisfy the above condition. According to Figure 10-1, a relatively large load (R₀) will enlarge the electric potential (φ_α). Moreover, our tester with a relatively large flow divider of a 10-A range is justified for boosting the electric potential (φ_β). Note that, if a current meter that is to detect a small current is employed, the electric potential (φ_β) becomes small.

Moreover, the phenomenon detected in the many experiments of this paper could not be detected by an autorange detector. Such a detector should be employed in a follow-up study, but an internal resistance that varies with the electrical signals might violate the above condition (93). Perhaps, there is a macroscopic current (i_A) in autotange meter and thus this current (i_A) might interefere with the microscopic current ${(I}_E^{\text{'}})$. Therefore, an autorange meter was not employed in our present experiments (Figure 7).

When another motor M’ is employed as a detour, energy exchanges between the inductors give rise to a constant current $\left(I_E^{\text{'}}\right)$. As the additional motor has a very small internal resistance, it demonstrates the potential of supplying the current $\left(I_E^{\text{'}}\right)$ to a small resistance via the observed phenomenon.

4.4. Recap of the Key Concept

This paper describes a novel concept and a highly symmetric circuit for renewable energy generation. A circuit satisfying the requisite conditions generates a divergent current with no Joule heating. The divergent current drives both paired-LED and paired-DC-motor systems, generating large amounts of energy. The phenomenon is demonstrated both theoretically and experimentally, with good agreement between the theoretical and experimental results.

4.4. Significances of This Paper

Many countries are attempting to mitigate the pending energy crisis with solar cells, wind power, and biomass energy sources. However, natural energy produced by renewable energy sources inevitably fluctuate and destabilize the energy system. Stability can be restored only by introducing many storage batteries that increase the costs. More seriously, fossil fuel energies are major CO₂ emitters, whereas nuclear power stations (which release no CO₂) destroy the environment with radioactive materials and their wastes.

Our proposed methodology generates a large amount of energy using a highly symmetric circuit. The main contributions are listed below.

1)

The net generated energy almost equals that of a nuclear power station, implying a sufficiently high energy density.

2)

The system can be introduced at low cost (<10,000 yen).

3)

The system generates no dangerous substances.

4)

This system can provide the required amount of energy at the right time at the right place.

In summary, our simple-to-build system generates comparable energy to a nuclear power station.

5. Conclusion

This study proposes and verifies (theoretically and experimentally) a new circuit-based renewable-energy source. The system outputs a very high electric power and high energy density without natural fluctuations or dangerous substance production. That is, it harvests the required amount of energy at the proper time at the proper place.

Various motor types were experimentally trialed in the paired-motor system, but a more systematic experiment would consolidate the aforementioned conditions. Moreover, the capacitance of the stray capacitor is expected to slightly vary with humidity and atmospheric pressure. This expectation must be clarified in future work. Finally, the inapplicability of the autorange meter must be rationalized.

Additional Information

This study is unrelated to any competing interests such as funding, employment, or personal financial interests. Moreover, this study is unrelated to nonfinancial competing interests. This reasearch did not receive any specific grant from funding agencies in the public, commercial, or not-for- profit sectors.

Moreover, all original contributions and data associated with this study are included in the article. All data (raw) are presented as photographs in the Result section. Further inquiries can be directed to the corresponding author.