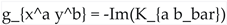On the Dynamical Stability of String Compactifications: Why Chaotic Moduli Evolution is Incompatible with Observed Cosmology

Miltiadis Karazoupis

doi:10.20944/preprints202504.2449.v1

Submitted:

28 April 2025

Posted:

29 April 2025

You are already at the latest version

Abstract

String theory compactifications provide a promising framework for unifying gravity and quantum mechanics, predicting extra spatial dimensions whose geometry and topology determine low-energy physics. The dynamics of the associated moduli fields—scalar fields parameterizing the size and shape of these extra dimensions—are governed by an effective potential derived from supergravity, influenced by background fluxes and non-perturbative effects. This potential landscape is typically high-dimensional and highly nonlinear, possessing features known to permit chaotic behaviour in dynamical systems. This paper examines the mathematical structure of moduli dynamics in Type IIB flux compactifications. We delineate the established properties of the governing equations—nonlinearity, coupling, high dimensionality, and sensitivity to discrete flux choices—which are necessary prerequisites for chaos. We then define dynamical chaos precisely, focusing on Sensitive Dependence on Initial Conditions (SDIC) characterized by positive Lyapunov exponents. By analysing the strict mathematical consequences of SDIC, we demonstrate that chaotic evolution of moduli fields leads to an exponential loss of predictability, can potentially enhance vacuum decay rates, and prevents the reliable stabilization required to match cosmological observations, such as the stability of fundamental constants, the controlled evolution during and after inflation, and the apparent longevity of our universe. We conclude that the observed features of our universe impose a strong phenomenological constraint, requiring that the effective low-energy dynamics originating from string theory must reside within a non-chaotic regime. Viable string vacua capable of describing our universe must therefore correspond to configurations where chaotic dynamics and associated instabilities are either absent or strongly suppressed.

Keywords:

string theory

;

compactification

;

moduli fields

;

moduli stabilization

;

string landscape

;

dynamical systems

;

chaos theory

;

lyapunov exponents

;

cosmology

;

cosmological stability

Subject:

Physical Sciences - Theoretical Physics

Introduction

String theory stands as a leading candidate for a quantum theory of gravity, offering a consistent framework that potentially unifies all fundamental forces and particles (Green, Schwarz and Witten, 1987; Polchinski, 1998). A key prediction of critical superstring theory is the existence of ten spacetime dimensions. To reconcile this with our observed four-dimensional universe (R^(3,1)), the theory posits that the extra six spatial dimensions are compactified on a small internal manifold, typically taken to be a Calabi-Yau (CY) space (X_6) to preserve N=1 supersymmetry in four dimensions (Candelas et al., 1985).

The precise geometry and topology of this internal manifold are not fixed by the theory a priori but are described by a set of continuous parameters known as moduli fields, collectively denoted Preprints 157679 i001

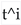. These moduli appear as massless scalar fields in the effective four-dimensional theory and correspond to deformations of the CY manifold's size (Kähler moduli, Preprints 157679 i002

), shape (complex structure moduli, Preprints 157679 i003

), and the value of the string coupling constant (encoded in the axio-dilaton, Preprints 157679 i004

).

Classically, these moduli fields are massless, parameterizing continuous families of degenerate vacuum solutions. The existence of such massless scalars is phenomenologically problematic: they would mediate long-range fifth forces and lead to time-varying fundamental constants (like the fine-structure constant or particle masses), both of which are strongly constrained by observation (Uzan, 2011; Olive and Pospelov, 2008). This constitutes the "moduli problem" of string cosmology.

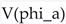Significant progress towards resolving this problem came with the understanding that background fluxes (quantized field strengths threading cycles of the CY manifold) and non-perturbative effects (like Euclidean D-brane instantons or gaugino condensation) can generate a non-trivial scalar potential, denoted Preprints 157679 i005

, for the moduli fields (Giddings, Kachru and Polchinski, 2002; Kachru et al., 2003; Balasubramanian et al., 2005). This potential, derived within the framework of four-dimensional N=1 supergravity, can potentially stabilize all moduli at specific values, giving them masses and fixing the parameters of the effective theory. The seminal work by Gukov, Vafa and Witten (2000) provided the structure of the flux-induced superpotential, W, while frameworks like KKLT (Kachru et al., 2003) and the Large Volume Scenario (LVS) (Balasubramanian et al., 2005; Conlon, Quevedo and Suruliz, 2005) demonstrated explicit (though often fine-tuned) mechanisms for achieving stabilization, typically resulting in metastable de Sitter or stable Minkowski/AdS vacua.

The inclusion of fluxes, which can take numerous discrete values, leads to an exponentially large number of possible potential functions V and corresponding vacuum states, collectively known as the "string landscape" (Susskind, 2003; Douglas, 2003). While finding stable or metastable minima within this landscape is crucial, it is only part of the story. The universe must dynamically evolve into such a vacuum state during its cosmological history. 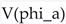This necessitates studying the dynamics of the moduli fields governed by the potential Preprints 157679 i005

, particularly in the early universe.

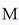The scalar potentials arising in flux compactifications are typically complex functions defined on a high-dimensional moduli space, denoted Preprints 157679 i006

. They exhibit strong nonlinearities and couplings between different moduli fields. Such features are well-known prerequisites for complex dynamical behavior, including chaos, in many areas of physics and mathematics (Strogatz, 2015). The possibility that moduli dynamics could be chaotic raises profound questions about the predictability of string theory, the ability to dynamically reach and persist within stable vacuum configurations, and the likelihood of achieving a cosmological evolution consistent with observations. This paper investigates the implications of chaotic dynamics for the cosmological viability of string compactifications.

Literature Review

The study of moduli dynamics in string compactifications sits at the intersection of string theory, supergravity, cosmology, and dynamical systems theory. The literature relevant to our investigation can be broadly categorized as follows:

Moduli Stabilization Mechanisms

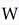The fundamental challenge of massless moduli fields arising from compactification was recognized early on. The development of flux compactifications provided a powerful mechanism to generate potentials for these fields. Giddings, Kachru and Polchinski (2002) demonstrated how turning on background fluxes (F₃, H₃) in Type IIB theory leads to a superpotential Preprints 157679 i007

that depends on the complex structure moduli ( Preprints 157679 i003

) and the axio-dilaton ( Preprints 157679 i004

), potentially stabilizing them. Their work laid the foundation for constructing vacua with broken supersymmetry and stabilized moduli, utilizing the superpotential structure identified by Gukov, Vafa and Witten (2000).

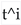However, flux potentials typically do not stabilize the Kähler moduli ( Preprints 157679 i002

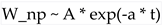). Addressing this required incorporating non-perturbative effects. The KKLT scenario (Kachru et al., 2003) proposed using Euclidean D3-brane instantons or gaugino condensation on D7-branes to generate non-perturbative contributions to the superpotential, Preprints 157679 i008

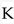. This, combined with the flux potential and an uplifting mechanism (e.g., anti-D3-branes), could stabilize all moduli in a metastable de Sitter vacuum. An alternative approach, the Large Volume Scenario (LVS) (Balasubramanian et al., 2005; Conlon, Quevedo and Suruliz, 2005), utilizes a combination of fluxes, leading-order α' corrections to the Kähler potential Preprints 157679 i009

, and non-perturbative effects to stabilize Kähler moduli at exponentially large volumes, naturally generating a hierarchy between the Planck scale and the supersymmetry breaking scale. These scenarios demonstrated the existence of mechanisms for full moduli stabilization within string theory.

The String Landscape and Statistical Approaches

The realization that fluxes can be chosen in a vast number of ways (~ 10⁵⁰⁰ or more estimated in typical CYs, see Ashok and Douglas, 2004) led to the concept of the string landscape (Susskind, 2003; Douglas, 2003). This landscape consists of a huge ensemble of possible vacuum states with different properties (stabilized moduli values, cosmological constant, particle physics content). Understanding the distribution and properties of these vacua became a central theme (Denef and Douglas, 2004). Statistical methods have been employed to study the prevalence of certain features, like the distribution of the cosmological constant (Bousso and Polchinski, 2000) or the likelihood of achieving specific stabilization schemes (e.g., Martínez-Pedrera, Mehta and Rummel, 2013) or desirable phenomenological properties within ensembles of random supergravity theories (Marsh et al., 2014). 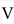While powerful, these statistical studies often focus on the properties of the minima of the potential Preprints 157679 i011

, rather than the dynamics governing how these minima might be reached.

Cosmological Dynamics of Moduli

Stabilizing moduli is necessary but not sufficient; the universe must dynamically evolve to the stabilized minimum. The cosmological dynamics of moduli fields, especially during and after inflation, have been extensively studied (see reviews like Baumann and McAllister, 2015; Cicoli, 2013). Key issues include:

Initial Conditions: Where do moduli fields start in the early universe? Random initial conditions might lead to overshoot problems, where fields roll past desirable minima (Brustein and Steinhardt, 1993). Addressing the initial conditions problem remains a significant challenge.
Inflationary Dynamics: If moduli fields play the role of the inflaton or are coupled to it, their dynamics are crucial for the success of inflation. Multi-field inflation models derived from string theory often exhibit complex trajectory behaviour in field space (e.g., Dias, Frazer and Liddle, 2012; Marsh et al., 2013; Bachlechner et al., 2017), which can affect predictions for cosmological observables.
Post-Inflationary Evolution: After inflation, moduli fields typically oscillate around their potential minima, potentially dominating the energy density and leading to cosmological problems (the "cosmological moduli problem") unless they decay sufficiently early (Banks, Kaplan and Nelson, 1994; de Carlos et al., 1993).

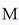These studies highlight that the path taken through the moduli space Preprints 157679 i006

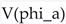is critically important. The complexity of the potential Preprints 157679 i005

suggests that this path could be highly non-trivial.

Chaos in Dynamical Systems

Chaos theory provides the mathematical framework for understanding complex, unpredictable behaviour in deterministic systems (Strogatz, 2015; Ott, 2002). A defining feature is Sensitive Dependence on Initial Conditions (SDIC), quantified by positive Lyapunov exponents ( Preprints 157679 i010

). Chaos arises generically in systems with sufficient nonlinearity, coupling, and dimensionality. Tools like phase space analysis, Poincaré sections, bifurcation diagrams, and Lyapunov exponent calculations are standard methods for detecting and characterizing chaos.

Studies Suggesting Complex Dynamics in String Theory

While rigorous proofs of chaos for generic moduli dynamics are scarce, several studies point towards the possibility of complex behaviour:

Numerical Simulations: Studies of specific inflationary models derived from string theory, particularly multi-field models like N-flation (Dimopoulos et al., 2008) or axion monodromy inflation (Silverstein and Westphal, 2008; McAllister, Silverstein and Westphal, 2010), often reveal complex dynamics and sensitivity to initial conditions, although not always explicitly framed as chaos (e.g., Underwood, 2011; Sumitomo and Tye, 2012).
Random Potentials: Some works model the string landscape using random potentials. Analyses of particle motion in such random potentials often exhibit features associated with chaotic dynamics or diffusion (Aazami and Easther, 2006; Marsh et al., 2013).
Fractal Basin Boundaries: In systems with multiple attractors (minima), the boundaries between their basins of attraction can be fractal, a common indicator of underlying chaotic dynamics (Grebogi, Ott and Yorke, 1983). This possibility has been explored in landscape contexts, where trajectories starting near such boundaries exhibit extreme sensitivity (McDonald and Vilenkin, 2018).
Explicit Calculations in Simplified Models: Investigations of simplified toy models capturing features of string potentials, such as coupled fields with exponential terms (common in supergravity), sometimes demonstrate chaotic regimes for certain parameter ranges (e.g., Copeland, Liddle and Lyth, 1998, although pre-dating modern landscape studies).

Identified Gap

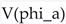The literature firmly establishes the existence of complex, high-dimensional, nonlinear potentials Preprints 157679 i005

in string compactifications and highlights the crucial role of moduli dynamics in cosmology. Studies often reveal complex behavior and sensitivity in specific models or statistical ensembles. However, there is often a gap between observing complexity in simulations and demonstrating chaos according to its mathematical definition (positive Lyapunov exponents, mixing) for realistic potentials derived from supergravity. Furthermore, a systematic analysis connecting the formal definition of chaos directly to the phenomenological requirements of a viable cosmology (stable constants, predictable inflation) is needed. This paper aims to bridge this gap by focusing on the implications of SDIC, arguing that its presence is fundamentally incompatible with observed cosmological stability, irrespective of whether generic string dynamics are proven chaotic in full mathematical detail.

Research Questions

Building upon the established framework of string compactifications, the existence of the string landscape, the cosmological role of moduli fields, and the fundamental principles of dynamical systems theory, this paper seeks to address the following specific questions:

Mathematical Structure: What are the demonstrable mathematical properties (dimensionality, nonlinearity, coupling, parameter dependence) of the dynamical system governing the evolution of moduli fields () derived from Type IIB flux compactifications, as established in the literature, and how do these properties relate to the known prerequisites for chaotic behaviour?
Definition and Implications of Chaos: What is the precise mathematical definition of dynamical chaos relevant to this system, with a specific focus on Sensitive Dependence on Initial Conditions (SDIC) as characterized by positive maximal Lyapunov exponents (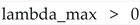)? Crucially, what are the direct and unavoidable mathematical consequences of SDIC regarding the predictability and stability of trajectories within such a system?
Cosmological Viability: How do the mathematical consequences of chaotic moduli dynamics (specifically, the exponential divergence of trajectories implied by SDIC) compare with the observational requirements for a viable cosmological model describing our universe? In particular, how does SDIC conflict with:

◦

The need for reliable stabilization of moduli to ensure time-independent fundamental constants?

◦

The required predictability of cosmological epochs like inflation and reheating?
Constraint on Viable Vacua: Does the potential incompatibility imply that any string vacuum state (defined by a specific choice and corresponding potential ) that aims to describe our observed universe must necessarily exhibit non-chaotic dynamics () in the relevant regions of moduli space and during the relevant cosmological eras?

By addressing these questions, this paper aims to provide a clear argument, grounded in the established mathematical definitions and consequences of chaos, for why chaotic evolution of fundamental scalar fields like moduli is phenomenologically disfavored, thereby imposing a significant dynamical constraint on viable models within the string landscape.

Analysis and Results

This section details the mathematical structure of the dynamical system governing moduli evolution, defines chaos precisely with a focus on its implications, analyzes the consequences of chaotic dynamics—including enhanced vacuum instability—and confronts these consequences with the requirements for cosmological viability, directly addressing the research questions.

The Dynamical System: Moduli Evolution in Supergravity

As established in the literature reviewed and detailed in frameworks like Type IIB flux compactifications (Grana, 2006; Douglas and Kachru, 2007), the evolution of moduli fields phi_a (where a indexes the different complex moduli) is governed by a system of coupled, second-order, nonlinear differential equations derived from N=1 supergravity (Wess and Bagger, 1992). The key ingredients are the Kähler potential K(phi, phi_bar) and the superpotential W(phi) (incorporating flux contributions W_flux and non-perturbative W_np terms). These determine the scalar potential V via the standard formula:

V(phi, phi_bar) = exp(K) * ( K^{a b_bar} * D_a W * D_{b_bar} W_bar - 3 * |W|^2 )

where K^{a b_bar} is the inverse of the Kähler metric K_{a b_bar}, defined as:

K_{a b_bar} = partial_a partial_{b_bar} K

D_a W is the Kähler-covariant derivative:

D_a W = partial_a W + (partial_a K) * W

D_{b_bar} W_bar is its complex conjugate:

D_{b_bar} W_bar = partial_{b_bar} W_bar + (partial_{b_bar} K) * W_bar

and |W|^2 is shorthand for W * W_bar. Note that partial_a denotes partial / partial phi^a and partial_{b_bar} denotes partial / partial phi_bar^b.

The equations of motion for the real scalar components phi^M (where M runs over all real degrees of freedom) in a spatially flat Friedmann-Lemaître-Robertson-Walker (FLRW) cosmological background with scale factor a(t) and Hubble parameter H = dot(a)/a take the form of geodesic motion on the field-space manifold equipped with metric g_{MN} (derived from K_{a b_bar}), subject to potential forces and Hubble friction:

ddot(phi)^M + Gamma^M_{NP} * dot(phi)^N * dot(phi)^P + 3 * H * dot(phi)^M + g^{MN} * partial_N V = 0

Here, ddot(phi)^M denotes the second time derivative, dot(phi)^N the first time derivative, Gamma^M_{NP} are the Christoffel symbols associated with the field-space metric g_{MN}, defined as:

Gamma^M_{NP} = (1/2) * g^{MK} * (partial_N g_{PK} + partial_P g_{NK} - partial_K g_{NP})

and g^{MN} is the inverse metric. partial_N denotes partial / partial phi^N.

This dynamical system possesses several mathematical properties identified as prerequisites for chaotic behaviour (Strogatz, 2015; Ott, 2002):

High Dimensionality: The number of real moduli fields (e.g., 2 * h^(2,1) + 2 * h^(1,1) + 2 for complex structure, Kähler, and axio-dilaton fields in Type IIB) can be large in typical Calabi-Yau compactifications, leading to a high-dimensional phase space (Kreuzer and Skarke, 2000).
Nonlinearity: Strong nonlinearities are inherent in the supergravity structure. They arise from the exponential factor exp(K), terms like |D W|^2 and |W|^2 in V, logarithmic dependencies in K (e.g., K ~ -log(Vol)), transcendental functions in W_flux, non-perturbative exponential terms in W_np (e.g., ~ exp(-a*t^i)), and the velocity-squared kinetic terms involving Christoffel symbols Gamma^M_{NP} which depend on the field positions phi^M.
Coupling: Fields are generically coupled. This occurs through off-diagonal terms in the field-space metric g_{MN} (derived from K_{a b_bar}), through the Christoffel symbols Gamma^M_{NP} in the kinetic terms, and through cross-terms involving different fields within the potential V.
Parameter Dependence: The system depends critically on the discrete choices of background fluxes N_flux. Different flux choices lead to different forms of W and thus different potential landscapes V, creating a vast "landscape" of different dynamical systems (Denef and Douglas, 2004).

These established properties provide the necessary mathematical foundation for the potential emergence of chaotic dynamics in moduli evolution.

Mathematical Definition of Chaos and Sensitive Dependence (SDIC)

While complex behaviour is expected, chaos has a precise mathematical definition. A deterministic dynamical system is typically defined as chaotic if it exhibits the following three properties on some invariant set (often an attractor or a repeller) (Strogatz, 2015; Ott, 2002):

Sensitive Dependence on Initial Conditions (SDIC): Trajectories starting arbitrarily close together diverge exponentially, on average.
Topological Transitivity (or Mixing): The dynamics eventually map any given region of the invariant set to overlap with any other region; trajectories explore the entire set over time.
Density of Periodic Orbits: Unstable periodic orbits are dense within the invariant set.

For the purpose of predictability and cosmological stability, the most crucial property is SDIC. It is formally quantified by the maximal Lyapunov exponent, lambda_max. Consider a trajectory Phi(t) in the phase space (containing positions phi^M and velocities dot(phi)^M) and an infinitesimally close trajectory Phi(t) + delta Phi(t). The separation vector delta Phi(t) evolves according to the linearized equations of motion: d(delta Phi)/dt = J(Phi(t)) * delta Phi, where J is the Jacobian matrix of the flow. The maximal Lyapunov exponent is defined as the maximum average exponential rate of divergence of this separation vector:

lambda_max = lim_{t -> infinity} (1/t) * ln ( ||delta Phi(t)|| / ||delta Phi(0)|| )

where ||...|| denotes a suitable norm in the tangent space, and the limit assumes the initial separation delta Phi(0) is aligned along the direction of maximal expansion (Benettin et al., 1980).

Definition: The dynamics are chaotic if lambda_max > 0. A positive maximal Lyapunov exponent signifies that, on average, the separation between nearby trajectories grows exponentially:

||delta Phi(t)|| ~ ||delta Phi(0)|| * exp(lambda_max * t)

Note: Proving lambda_max > 0 for the full moduli dynamics derived from generic Calabi-Yau compactifications is analytically intractable and computationally challenging due to the high dimensionality and complexity. While numerical studies in simplified or specific string-inspired models sometimes find positive Lyapunov exponents (e.g., early work by Brustein and Steinhardt, 1993; Copeland, Liddle and Lyth, 1998), our analysis focuses not on proving chaos exists generically, but on the unavoidable consequences if lambda_max > 0 holds in cosmologically relevant scenarios.

Consequences of SDIC (lambda_max > 0)

If the dynamical system governing moduli evolution exhibits SDIC (lambda_max > 0) in a relevant region of phase space and during a relevant cosmological epoch, the following consequences are mathematically unavoidable:

Exponential Loss of Predictability: The exponential divergence exp(lambda_max * t) implies that any uncertainty in the initial conditions delta Phi(0) is amplified exponentially over time. To predict the state Phi(t) with a desired accuracy epsilon after time t, the initial state Phi(0) must be known with an accuracy delta Phi(0) ~ epsilon * exp(-lambda_max * t). This required precision shrinks exponentially, rapidly becoming physically impossible to achieve for any significant evolution time t. Long-term prediction becomes impossible in practice.
Extreme Sensitivity to Parameters: Just as the system is sensitive to initial conditions, chaotic systems are often extremely sensitive to small changes in system parameters (Ott, 2002). In our context, this suggests that small variations in the underlying parameters defining the potential V (beyond the discrete flux choice, e.g., parameters in W_np or coefficients of alpha' or loop corrections to K) could lead to vastly different dynamical behaviour, further hindering predictability.
Complex Phase Space Structure: Systems with positive Lyapunov exponents often exhibit complex structures in phase space. For instance, if multiple stable minima (attractors) exist, the boundaries separating their basins of attraction can be fractal (Grebogi, Ott and Yorke, 1983). Trajectories starting near such boundaries exhibit transient chaos and unpredictable final states, making it uncertain which minimum the system will eventually settle into, even if it does settle.
Enhanced Vacuum Instability and Potential for Accelerated Decay: Beyond hindering predictable stabilization, chaotic dynamics can actively compromise the stability of potential minima, particularly metastable ones common in string landscape scenarios (e.g., KKLT de Sitter vacua). Mechanisms include:

◦

Dynamical Exploration and Effective Barrier Reduction: Chaotic trajectories explore a large volume of phase space. This exploration might uncover pathways over or through potential barriers that are not apparent in static analyses. The kinetic energy gained during chaotic oscillations can help overcome barriers classically, or the system might dynamically reach configurations where tunneling barriers are effectively lowered, potentially enhancing decay rates Gamma ~ exp(-S), where S is the bounce action.

◦

Increased Probability of Escape: The erratic nature of chaotic motion means the system doesn't simply oscillate stably within a potential well. It constantly probes the boundaries of its basin of attraction. This increases the likelihood, compared to regular motion, of finding an escape route, especially from shallow or complex minima.

◦

Potential for Resonant Effects: Chaotic systems exhibit a broad spectrum of frequencies. It's conceivable that certain frequencies within the chaotic motion could resonate with quantum tunneling modes or other instability triggers, potentially leading to significantly accelerated decay, although this is likely highly model-dependent.

◦

Implication: Even if a suitable metastable minimum exists, chaotic dynamics during the approach or even transiently within the basin could drastically shorten its lifetime, rendering it cosmologically unviable.

Confrontation with Cosmological Requirements

We now compare these consequences of SDIC — exponential loss of predictability, extreme sensitivity, complex phase structure, and enhanced vacuum instability — with the requirements for a cosmologically viable model capable of describing our observed universe:

Requirement 1: Stable Moduli and Time-Independent Constants: Our universe exhibits stable fundamental constants (electron mass, fine structure constant, etc.) to high precision (Uzan, 2011; Olive and Pospelov, 2008). In string theory, these constants depend on the vacuum expectation values (VEVs) of the moduli fields phi_a. Achieving stable constants requires the moduli to be dynamically stabilized at fixed values phi_a = phi_0, corresponding to a minimum of the potential V.

◦

Conflict with SDIC: If the dynamics near the minimum phi_0 or along the trajectory leading to it were chaotic (lambda_max > 0), reliable stabilization would be compromised. The exponential divergence means that trajectories starting near an intended path to the minimum would rapidly deviate. Even if a minimum exists, reaching it from generic initial conditions becomes highly improbable without extreme fine-tuning. The system might wander indefinitely or be easily perturbed out of shallow minima. Furthermore, chaotic dynamics can actively destabilize minima by enhancing pathways for vacuum decay, potentially destroying the required long-term stability even if a minimum is momentarily reached. The very nature of SDIC resists settling reliably into and remaining within a specific state.
Requirement 2: Predictable Cosmological Evolution (e.g., Inflation): Key cosmological epochs, such as inflation, must proceed predictably to explain observations like the cosmic microwave background (CMB) anisotropies and large-scale structure (Baumann and McAllister, 2015). Successful inflation requires a controlled roll of the inflaton field, a specific number of e-folds, and a predictable end (reheating).

◦

Conflict with SDIC: If the inflaton is a modulus field or is significantly coupled to moduli exhibiting chaotic dynamics, the inflationary trajectory phi_a(t) becomes subject to SDIC. The number of e-folds, the amplitude of generated density perturbations (which depend on the potential and field velocities), and the conditions at the end of inflation would become exponentially sensitive to the pre-inflationary values of phi_a. This would destroy the predictive power of the inflationary scenario, making it impossible to reliably achieve the conditions observed in our universe from generic initial conditions. Any successful prediction would appear as an extreme fine-tuning of initial state parameters, contrary to the motivation for inflation.

Result: Fundamental Conflict

The analysis reveals a fundamental conflict between the mathematical consequences of chaotic dynamics (specifically SDIC, lambda_max > 0, leading to exponential loss of predictability, unreliable stabilization, and potentially enhanced vacuum decay) and the requirements of cosmological stability and predictability derived from observation. Chaotic evolution of the fundamental scalar fields (moduli) determining the properties of our universe leads to outcomes that are incompatible with observation.

Discussion

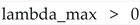The analysis presented establishes a direct conflict between the mathematical definition of chaotic dynamics, specifically Sensitive Dependence on Initial Conditions (SDIC) characterized by Preprints 157679 i012

, and the fundamental requirements for a cosmologically viable effective field theory derived from string theory. Our results demonstrate that if the evolution of moduli fields Preprints 157679 i001

were governed by chaotic dynamics during crucial cosmological periods, the resulting exponential sensitivity and potential for enhanced vacuum instability would render the universe's evolution unpredictably dependent on initial conditions and potentially too short-lived, fundamentally contradicting the observed stability, predictability, and longevity of our cosmos.

Interpreting the Main Result

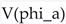It is crucial to emphasize the logic of our argument. We have not proven that moduli dynamics in generic string compactifications are chaotic. Establishing this for the complex, high-dimensional potentials Preprints 157679 i005

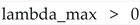derived from supergravity remains a formidable challenge, both analytically and computationally. Instead, our analysis focuses on the implications if chaos, as defined mathematically ( Preprints 157679 i012

), were present. We have shown that the primary characteristic of chaos—SDIC—leads to consequences (exponential loss of predictability, unreliable stabilization, and potential enhancement of vacuum decay rates) that are irreconcilable with observations such as the time-independence of fundamental constants, the requirements for successful inflation and reheating, and the apparent long-term stability of our universe.

Therefore, the observed nature of our universe acts as a powerful phenomenological filter. Regardless of whether chaotic dynamics are common or rare across the vast string landscape, the specific vacuum state and dynamical history corresponding to our universe must belong to a non-chaotic regime. 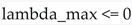The equations of motion governing the evolution towards, and stabilization within, our vacuum must exhibit Preprints 157679 i014

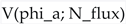in the relevant domain of phase space and during the relevant cosmological eras. Any potential Preprints 157679 i015

arising from a specific flux choice Preprints 157679 i016

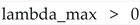that induces chaotic dynamics ( Preprints 157679 i012

) in regions crucial for cosmological evolution or leads to chaos-induced vacuum decay on timescales shorter than observed cannot describe our universe.

Implications for the String Landscape

The concept of the string landscape encompasses a vast number of potential vacuum states defined by different choices of compactification manifolds (X_6) and background fluxes ( Preprints 157679 i016

) (Susskind, 2003; Douglas, 2003). Much research has focused on identifying vacua within this landscape that possess desirable static properties, such as N=1 supersymmetry (possibly broken), the correct gauge group and matter content for the Standard Model, and a small positive cosmological constant (Denef and Douglas, 2004). 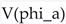Our analysis adds a crucial dynamical constraint: viability requires not only finding a suitable minimum in the potential Preprints 157679 i005

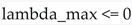but also ensuring that the dynamics governing the evolution towards and stabilization within that minimum are non-chaotic ( Preprints 157679 i014

) and do not trigger premature decay.

This suggests that regions of the landscape corresponding to flux choices Preprints 157679 i016

that induce chaotic potentials (at least in the cosmologically relevant field ranges and epochs) are effectively ruled out as descriptions of our universe. The requirement of non-chaotic, stable dynamics acts as a selection principle, potentially significantly restricting the subset of viable vacua within the landscape beyond static considerations alone. It underscores the importance of studying not just the minima of the landscape potential but also the dynamical trajectories that populate or avoid these minima, and the stability of those minima against dynamical perturbations.

Addressing Potential Subtleties

Several subtleties might arise when considering the role of chaos:

Localized Chaos: Could chaos exist but be confined to regions of moduli space far from the eventual vacuum, or limited to very early cosmological times before observable structures are set? While possible, this does not negate the core issue. If the trajectory towards the final vacuum must pass through a chaotic region, SDIC during that phase could still render the final outcome unpredictable, highly sensitive to unmeasurable initial conditions, or even trigger decay before stabilization. Furthermore, if inflation involves moduli fields, chaotic dynamics (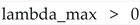) during this critical period would be disastrous for predictability. The requirement seems to be non-chaotic behavior along the entire relevant cosmological trajectory.
Strength of Stabilization: Could stabilization mechanisms create potential wells so deep and steep that they effectively suppress chaos near the minimum? A stable minimum, by definition, corresponds to locally convergent dynamics (negative eigenvalues of the stability matrix, implying local ). However, the basin of attraction leading to that minimum could still be affected by chaos. If the approach involves traversing regions where 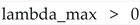, predictability is lost. Furthermore, complex systems can exhibit fractal basin boundaries even when the attractors themselves are simple fixed points (Grebogi, Ott and Yorke, 1983), making the final state exquisitely sensitive to initial conditions near the boundaries. Crucially, even if the minimum is deep, chaotic dynamics within the basin might explore escape routes or trigger instabilities (as discussed in 4.3.4) that would not occur with regular dynamics, potentially leading to decay. The stability of the final point does not guarantee a predictable or safe path to it.
Transient Chaos: Systems can exhibit chaotic behavior for a finite time before settling into a regular state (transient chaos) (Ott, 2002). While potentially less severe than sustained chaos, significant exponential divergence during the transient phase could still amplify initial uncertainties to unacceptable levels, impacting predictability. This is particularly relevant if the transient chaotic phase coincides with critical events like the end of inflation or reheating, where sensitivity can spoil desired outcomes. Moreover, even transient chaos could be sufficient to dynamically probe instability pathways and trigger vacuum decay if the system passes near regions of instability during the chaotic phase.

These considerations suggest that simply finding a stable minimum is insufficient; the dynamics over the relevant cosmological history must avoid the exponential sensitivity and potential destabilization characteristic of chaos.

Predictability in Fundamental Theory

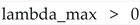The potential for chaotic dynamics touches upon fundamental questions about predictability in physics. While quantum mechanics introduces inherent indeterminacy, classical chaos in deterministic systems represents a different kind of unpredictability arising from nonlinearity and sensitivity. If the fundamental scalar fields governing the universe's properties were subject to chaotic evolution ( Preprints 157679 i012

), it would imply a practical limit to our ability to predict the state of the universe, even with perfect knowledge of the underlying laws, due to the impossibility of specifying initial conditions with infinite precision. Furthermore, if chaos actively promotes vacuum decay, it would challenge the very persistence of any realized state. The apparent regularity, predictability, and longevity of our universe, as evidenced by the success of precision cosmology, strongly suggest that such chaotic dynamics are not dominant in the effective laws governing its large-scale evolution.

Dynamical Selection

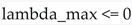In conclusion, the requirement of non-chaotic evolution ( Preprints 157679 i014

) provides a powerful dynamical selection criterion for viable models within the string landscape. It complements static selection criteria (correct particle spectrum, gauge group, etc.) and potentially anthropic arguments. A universe capable of evolving complex structures, including observers, likely requires a degree of stability, predictability, and longevity that is fundamentally incompatible with chaotic dynamics governing its defining parameters. The existence of our stable, predictable universe is therefore evidence that the underlying string theory dynamics, for the specific configuration realized, operate within a non-chaotic and dynamically stable regime.

Conclusion

This paper has investigated the dynamical behaviour of moduli fields arising from string theory compactifications, specifically focusing on the potential for chaotic evolution and its implications for cosmological viability. 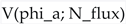We outlined the standard framework of Type IIB flux compactifications, leading to an effective four-dimensional N=1 supergravity theory where the dynamics of Kähler moduli, complex structure moduli, and the axio-dilaton are governed by a scalar potential Preprints 157679 i015

determined by the choice of background fluxes Preprints 157679 i016

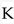, the Kähler potential Preprints 157679 i009

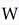, and the superpotential Preprints 157679 i007

.

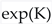Our analysis highlighted the structure of this theory, noting that the resulting dynamical system possesses key mathematical features known to be prerequisites for chaos: high dimensionality, strong nonlinearities stemming from the supergravity structure (e.g., Preprints 157679 i018

,

, non-perturbative terms), coupling between different moduli fields via the Kähler metric and potential terms, and a critical dependence on the discrete choice of fluxes.

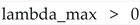We then provided a mathematical definition of dynamical chaos, centering on the concept of Sensitive Dependence on Initial Conditions (SDIC), quantified by a positive maximal Lyapunov exponent ( Preprints 157679 i012

). The core of our analysis focused on the direct and unavoidable mathematical consequences of SDIC: an exponential amplification of initial uncertainties leading to a fundamental loss of long-term predictability, the inherent difficulty in reliably stabilizing moduli at fixed values, and the potential for chaotic dynamics to actively enhance vacuum instability and accelerate decay processes.

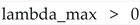By comparing these consequences with the requirements for a successful cosmological model, we identified a stark incompatibility. The observed stability of fundamental constants in our universe necessitates reliable moduli stabilization at fixed values, a process fundamentally undermined by the exponential divergence and potential destabilization inherent in chaotic dynamics ( Preprints 157679 i012

). Similarly, the predictability required for crucial epochs like cosmic inflation, which successfully explains large-scale cosmic properties, is destroyed if the underlying scalar field dynamics exhibit SDIC. Furthermore, the apparent longevity of our universe is inconsistent with dynamics that might trigger rapid, chaos-induced vacuum decay.

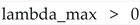Therefore, our central conclusion is that chaotic evolution of moduli fields ( Preprints 157679 i012

) is phenomenologically disallowed in any string vacuum configuration aiming to describe our observed universe. The stability, predictability, and required longevity inherent in cosmological observations act as a powerful dynamical filter on the string landscape. 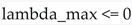While the string landscape potentially contains regions or flux choices leading to chaotic dynamics, the specific configuration corresponding to our universe must reside in a regime where the dynamics are non-chaotic ( Preprints 157679 i014

) during all cosmologically relevant periods and in the relevant regions of moduli space, and where these dynamics do not lead to premature vacuum decay.

This finding imposes a significant constraint on model building within string theory, complementing static requirements (particle content, gauge groups) with a crucial dynamical condition. It underscores the importance of studying not just the minima of the landscape potential but also the dynamical trajectories that lead to them and the stability of those minima against dynamical perturbations. Ultimately, the existence of our stable, predictable, long-lived universe provides compelling evidence that the fundamental dynamics governing its parameters, if described by string theory, must operate in a non-chaotic and dynamically stable manner.

Appendix A

This appendix provides supplementary mathematical details on the N=1 supergravity framework, the derivation of the equations of motion, the field space geometry, the definition of Lyapunov exponents, and examples of nonlinear terms, aiming to make the paper's arguments self-contained.

N=1 Supergravity Framework Details

The low-energy effective action describing the dynamics of moduli fields in Type IIB compactifications is typically given by four-dimensional N=1 supergravity coupled to chiral superfields Preprints 157679 i020

(whose scalar components are the complex moduli Preprints 157679 i021

) (Wess and Bagger, 1992; Freedman and Van Proeyen, 2012). The bosonic part of the Lagrangian relevant for the scalar dynamics in curved spacetime (ignoring fermions and gauge fields for simplicity) is determined by two key functions of the complex scalar fields Preprints 157679 i021

:

Kähler Potential 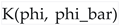: A real function whose second derivatives define the Kähler metric of the scalar field manifold:

where and . This metric determines the scalar kinetic terms. Its inverse is denoted .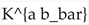
Superpotential : A holomorphic function ().

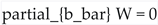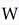From these, we define the Kähler-covariant derivative of Preprints 157679 i007

:

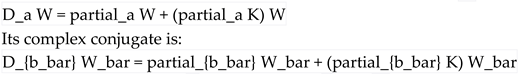
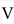The scalar potential Preprints 157679 i011

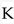is derived from Preprints 157679 i009

and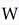

via the standard formula:

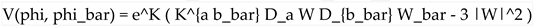where

. This potential governs the interactions and self-interactions of the scalar moduli fields.

The kinetic terms for the complex scalar fields in a general spacetime background with metric Preprints 157679 i032

are given by:

Field Space Metric (Real Fields)

For analyzing the dynamics, it is often convenient to work with real scalar components. We decompose the complex scalars Preprints 157679 i020

into real and imaginary parts. Let the set of all real scalar components be denoted by Preprints 157679 i034

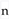. For example, if we have Preprints 157679 i043

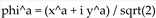complex fields Preprints 157679 i046

, then

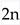represents the Preprints 157679 i035

real fields Preprints 157679 i036

.

The metric Preprints 157679 i037

on the space of real fields Preprints 157679 i034

can be derived from the Kähler metric Preprints 157679 i044

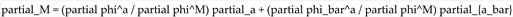. Using the chain rule ( Preprints 157679 i045

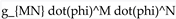), the kinetic term Preprints 157679 i047

(in a flat spacetime for simplicity, Preprints 157679 i038

) must match Preprints 157679 i048

. This yields relations like:

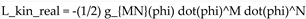The full kinetic Lagrangian in terms of real fields is Preprints 157679 i049

. The factor of 1/2 arises from the standard definition of real scalar kinetic terms.

Equations of Motion (Real Fields)

This is the geodesic equation on the field space manifold with metric Preprints 157679 i037

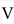, including the force term from the potential Preprints 157679 i011

and the Hubble friction term Preprints 157679 i055

.

Lyapunov Exponents: Conceptual Basis

It is defined formally via the limit:

Calculating Lyapunov exponents typically requires numerically integrating both the original nonlinear equations for Preprints 157679 i060

and the linearized equations for Preprints 157679 i061

over long times. Techniques like Gram-Schmidt orthogonalization are often employed periodically on the set of vectors spanning the tangent space to prevent numerical overflow and to extract the different exponents (Benettin et al., 1980; Ott, 2002).

Examples of Nonlinear Terms in V

Kähler Potential: (Nonlinear logarithms)
Exponential Factor: 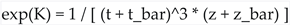(Highly nonlinear in 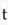and )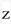
Derivatives of K:

◦

◦
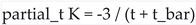
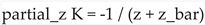
Derivatives of W:

◦

◦
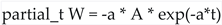
Kähler-Covariant Derivatives:

◦

◦

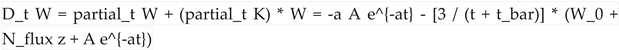
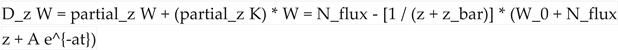
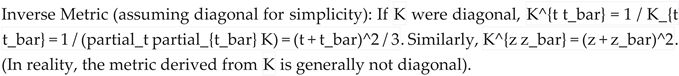
Moduli Space Geometry and Dynamics

This geometric aspect adds another layer of complexity. The kinetic terms themselves are nonlinear (quadratic in velocities Preprints 157679 i074

) and depend on position ( Preprints 157679 i075

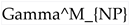) through the metric components in Preprints 157679 i076

. Geodesic motion (motion under no potential, Preprints 157679 i077

) on a curved manifold can itself be chaotic. For instance, geodesic motion on a surface of constant negative curvature is a classic example of chaotic dynamics (Ott, 2002). While the potential Preprints 157679 i011

often dominates the dynamics in string cosmology, the underlying geometry can also play a role, particularly if the potential is relatively flat or if the space has regions of significant negative curvature, which tends to enhance the divergence of nearby trajectories (related to the geodesic deviation equation).

References

Aazami, A.; Easther, R. (2006) Cosmology from random potentials. Journal of Cosmology and Astroparticle Physics 2006(03), 013. [CrossRef]
Ashok, S.K.; Douglas, M.R. (2004) Counting flux vacua. Journal of High Energy Physics 2004(01), 060. [CrossRef]
Bachlechner, T.; Marsh, M.C.D.; McAllister, L.; Wrase, T. (2017) Searching the landscape of random supergravities. Journal of High Energy Physics 2017(1), 123. [CrossRef]
Balasubramanian, V.; Berglund, P.; Conlon, J.P.; Quevedo, F.; Suruliz, K. (2005) Systematics of moduli stabilisation in Calabi-Yau flux compactifications. Journal of High Energy Physics 2005(03), 007. [CrossRef]
Banks, T.; Kaplan, D.B.; Nelson, A.E. (1994) Cosmological implications of dynamical supersymmetry breaking. Physical Review D 49(2), 779–787. [CrossRef]
Baumann, D.; McAllister, L. (2015) Inflation and String Theory; Cambridge University Press. [CrossRef]
Becker, K.; Becker, M.; Haack, M.; Louis, J. (2002) Supersymmetry breaking and alpha-prime corrections to flux induced potentials. Journal of High Energy Physics 2002(06), 060. [CrossRef]
Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.-M. (1980) Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part 1: Theory and Part 2: Numerical application. Meccanica 15(1), 9–30. [CrossRef]
Berg, M.; Haack, M.; Pajer, E. (2006) Constructing string vacua with stabilized moduli. Physical Review D 73(4), 046006. [CrossRef]
Bousso, R.; Polchinski, J. (2000) Quantization of four-form fluxes and dynamical neutralization of the cosmological constant. Journal of High Energy Physics 2000(06), 006. [CrossRef]
Brustein, R.; Steinhardt, P.J. (1993) Challenges for superstring cosmology. Physics Letters B 302(2-3), 196–201. [CrossRef]
Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. (1985) Vacuum configurations for superstrings. Nuclear Physics B 258, 46–74. [CrossRef]
Cicoli, M. (2013) String Loop Effects in Flux Compactifications and Inflation. Classical and Quantum Gravity 30(21), 214002. [CrossRef]
Conlon, J.P.; Quevedo, F.; Suruliz, K. (2005) Large-volume flux compactifications: Moduli spectrum and D3/D7 inflation. Journal of High Energy Physics 2005(08), 007. [CrossRef]
Copeland, E.J.; Liddle, A.R.; Lyth, D.H. (1998) Chaotic hybrid inflation. Physical Review D 58(6), 063508. [CrossRef]
de Carlos, B.; Casas, J.A.; Quevedo, F.; Roulet, E. (1993) Model independent properties and cosmological implications of the dilaton and moduli sectors of 4-d strings. Physics Letters B 318(3), 447–456. [CrossRef]
Denef, F.; Douglas, M.R. (2004) Distributions of flux vacua. Journal of High Energy Physics 2004(05), 072. [CrossRef]
Dias, M.; Frazer, J.; Liddle, A.R. (2012) Multifield consequences for D-brane inflation. Journal of Cosmology and Astroparticle Physics 2012(06), 020. [CrossRef]
Dimopoulos, S.; Kachru, S.; McGreevy, J.; Wacker, J.G. (2008) N-flation. Journal of Cosmology and Astroparticle Physics 2008(08), 003. [CrossRef]
Douglas, M.R. (2003) The statistics of string/M theory vacua. Journal of High Energy Physics 2003(05), 046. [CrossRef]
Douglas, M.R.; Kachru, S. (2007) Flux compactification. Reviews of Modern Physics 79(2), 733–796. [CrossRef]
Freedman, D.Z.; Van Proeyen, A. (2012) Supergravity; Cambridge University Press. [CrossRef]
Giddings, S.B.; Kachru, S.; Polchinski, J. (2002) Hierarchies from fluxes in string compactifications. Physical Review D 66(10), 106006. [CrossRef]
Grana, M. (2006) Flux compactifications in string theory: A comprehensive review. Physics Reports 423(3), 91–158. [CrossRef]
Grebogi, C.; Ott, E.; Yorke, J.A. (1983) Fractal basin boundaries, long-lived chaotic transients, and unstable-unstable pair bifurcation. Physical Review Letters 50(13), 935–938. [CrossRef]
Green, M.B.; Schwarz, J.H.; Witten, E. (1987) Superstring Theory; Cambridge University Press; (2 Volumes); ISBN 978-0521357524, 978-0521357531.
Gukov, S.; Vafa, C.; Witten, E. (2000) CFT's from Calabi-Yau four-folds. Nuclear Physics B 584(1-2), 69–108, Erratum-ibid. B608 (2001) 477-478. [CrossRef]
Kachru, S.; Kallosh, R.; Linde, A.; Trivedi, S.P. (2003) De Sitter vacua in string theory. Physical Review D 68(4), 046005. [CrossRef]
Kreuzer, M.; Skarke, H. (2000) Complete classification of reflexive polyhedra in four dimensions. Advances in Theoretical and Mathematical Physics 4(6), 1209–1230. [CrossRef]
Marsh, D.J.; McAllister, L.; Wrase, T. (2013) Inflation and the Starobinsky Model in Flux Compactifications. Journal of High Energy Physics 2013(12), 078. [CrossRef]
Marsh, M.C.D.; McAllister, L.; Wrase, T. (2014) The wasteland of random supergravities. Journal of High Energy Physics 2014(3), 102. [CrossRef]
Martínez-Pedrera, D.; Mehta, P.; Rummel, M. (2013) Finding the needle in the haystack: the statistics of locating desired vacua in the landscape. Journal of High Energy Physics 2013(6), 110. [CrossRef]
McAllister, L.; Silverstein, E.; Westphal, A. (2010) Gravity waves and linear inflation from axion monodromy. Physical Review D 82(4), 046003. [CrossRef]
McDonald, J.I.; Vilenkin, A. (2018) Fractal boundaries in the string theory landscape. Journal of Cosmology and Astroparticle Physics 2018(03), 006. [CrossRef]
Olive, K.A.; Pospelov, M. (2008) Environmental dependence of masses and coupling constants. Physical Review D 77(4), 043524. [CrossRef]
Ott, E. (2002) Chaos in Dynamical Systems, 2nd ed.; Cambridge University Press. [CrossRef]
Polchinski, J. (1998) String Theory. Cambridge University Press; (2 Volumes); ISBN 978-0521633031, 978-0521633048.
Silverstein, E.; Westphal, A. (2008) Monodromy in the CMB: Gravity waves and string inflation. Physical Review D 78(10), 106003. [CrossRef]
Strogatz, S.H. (2015) Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; Westview Press; ISBN 978-0813349107.
Sumitomo, Y.; Tye, S.H.H. (2012) A Stringy Mechanism for A Small Vacuum Energy - Multi-moduli Cases -. Journal of Cosmology and Astroparticle Physics 2012(11), 006. [CrossRef]
Susskind, L. (2003) The Anthropic Landscape of String Theory. arXiv:preprint hep-th/0302219. [CrossRef]
Underwood, B. (2011) A systematic study of D-brane inflation. Journal of High Energy Physics 2011(11), 097. [CrossRef]
Uzan, J.-P. (2011) Varying Constants, Gravitation and Cosmology. Living Reviews in Relativity 14(1), 2. [CrossRef]
Wess, J.; Bagger, J. (1992) Supersymmetry and Supergravity, 2nd ed.; Princeton University Press; ISBN 978-0691025308.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.